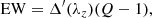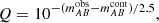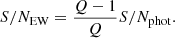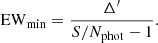| Issue |
A&A
Volume 647, March 2021
|
|
|---|---|---|
| Article Number | A158 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202039146 | |
| Published online | 26 March 2021 | |
J-PAS: Measuring emission lines with artificial neural networks
1
Instituto de Astrofísica de Andalucía (CSIC), PO Box 3004, 18080 Granada, Spain
e-mail: gimarso@iaa.es
2
Departamento de Física, Universidade Federal de Santa Catarina, PO Box 476, 88040-900 Florianópolis, SC, Brazil
3
Centro de Estudios de Física del Cosmos de Aragón (CEFCA), Unidad Asociada al CSIC, Plaza San Juan, 1, 44001 Teruel, Spain
4
Donostia International Physics Center (DIPC), Manuel Lardizabal Ibilbidea, 4, San Sebastián, Spain
5
Ikerbasque, Basque Foundation for Science, 48013 Bilbao, Spain
6
Observatório Nacional, Ministério da Ciencia, Tecnologia, Inovação e Comunicações, Rua General José Cristino, 77, São Cristóvão, 20921-400 Rio de Janeiro, Brazil
7
Instituto de Física, Universidade de São Paulo, Rua do Matão 1371, CEP 05508-090 São Paulo, Brazil
8
Departamento de Física, Universidade Federal do Rio Grande do Norte, 59072-970 Natal, RN, Brazil
9
Núcleo de Astrofísica e Cosmologia (Cosmo-ufes) & Departamento de Física, Universidade Federal do Espírito Santo, 29075-910 Vitória, ES, Brazil
10
Instituto de Física, Universidade Federal da Bahia, 40210-340 Salvador, BA, Brazil
11
Observatório do Valongo, Universidade Federal do Rio de Janeiro, 20080-090 Rio de Janeiro, RJ, Brazil
12
Departamento de Astronomia, Instituto de Astronomia, Geofísica e Ciências Atmosféricas, Universidade de São Paulo, São Paulo, Brazil
13
PPGCosmo & Departamento de Fśica, Universidade Federal do Espírito Santo, 29075-910 Vitória, ES, Brazil
14
Instruments4, 4121 Pembury Place, La Cañada-Flintridge, CA 91011, USA
15
Academia Sinica Institute of Astronomy & Astrophysics (ASIAA), 11F of Astronomy-Mathematics Building, AS/NTU, No. 1, Sect. 4, Roosevelt Road, Taipei 10617, Taiwan
16
Department of Astronomy, University of Michigan, 311West Hall, 1085 South University Ave., Ann Arbor, USA
17
Department of Physics and Astronomy, University of Alabama, Box 870324, Tuscaloosa, AL, USA
18
INAF, Osservatorio Astronomico di Trieste, via Tiepolo 11, 34131 Trieste, Italy
19
IFPU, Institute for Fundamental Physics of the Universe, via Beirut 2, 34151 Trieste, Italy
Received:
10
August
2020
Accepted:
29
December
2020
In the years to come, the Javalambre-Physics of the Accelerated Universe Astrophysical Survey (J-PAS) will observe 8000 deg2 of the northern sky with 56 photometric bands. J-PAS is ideal for the detection of nebular emission objects. This paper presents a new method based on artificial neural networks (ANNs) that is aimed at measuring and detecting emission lines in galaxies up to z = 0.35. These lines are essential diagnostics for understanding the evolution of galaxies through cosmic time. We trained and tested ANNs with synthetic J-PAS photometry from CALIFA, MaNGA, and SDSS spectra. To this aim, we carried out two tasks. First, we clustered galaxies in two groups according to the values of the equivalent width (EW) of Hα, Hβ, [N II], and [O III] lines measured in the spectra. Then we trained an ANN to assign a group to each galaxy. We were able to classify them with the uncertainties typical of the photometric redshift measurable in J-PAS. Second, we utilized another ANN to determine the values of those EWs. Subsequently, we obtained the [N II]/Hα, [O III]/Hβ, and O 3N 2 ratios, recovering the BPT diagram ([O III]/Hβ versus [N II]/Hα). We studied the performance of the ANN in two training samples: one is only composed of synthetic J-PAS photo-spectra (J-spectra) from MaNGA and CALIFA (CALMa set) and the other one is composed of SDSS galaxies. We were able to fully reproduce the main sequence of star-forming galaxies from the determination of the EWs. With the CALMa training set, we reached a precision of 0.092 and 0.078 dex for the [N II]/Hα and [O III]/Hβ ratios in the SDSS testing sample. Nevertheless, we find an underestimation of those ratios at high values in galaxies hosting an active galactic nuclei. We also show the importance of the dataset used for both training and testing the model. Such ANNs are extremely useful for overcoming the limitations previously expected concerning the detection and measurements of the emission lines in such surveys as J-PAS. Furthermore, we show the capability of the method to measure a EW of 10 Å in Hα, Hβ, [N II] and [O III] lines with a signal-to-noise ratio (S/N) of 5, 1.5, 3.5, and 10, respectively, in the photometry. Finally, we compare the properties of emission lines in galaxies observed with miniJPAS and SDSS. Despite the limitation of such a comparison, we find a remarkable correlation in their EWs.
Key words: Galaxy: evolution / surveys / techniques: photometric / methods: data analysis
© ESO 2021
1. Introduction
The study of the formation and evolution of galaxies through cosmic time has been addressed in recent decades through an understanding of how their physical properties leave footprints in the spectral energy distribution (see e.g., Díaz-García et al. 2019, and references therein). Both the analysis of the light coming from stars and the ionized interstellar gas can be converted, via well-known recipes, to physical quantities such as the stellar mass, star formation rate (SFR), dust attenuation, luminosity-age, and gas-phase metallicity. In addition, they may unveil the main ionization mechanism responsible for the optical emission lines that we can observe in the spectrum (for some of the most recent reviews on these topics, see Conroy 2013; Madau & Dickinson 2014; Kewley et al. 2019).
The most massive and youngest stars that lie within galaxies are responsible for the ultraviolet emission in the spectrum, but very often, the presence of dust grains does not allow ultraviolet photons to travel freely through the interstellar medium; consequently, this makes it difficult to constrain the SFR from the blue part of the spectrum alone. However, those stars can actually ionize the surrounding interstellar gas. Very rapidly, hydrogen atoms recombine, leaving tracks the in form of emission lines at a particular wavelength in the spectrum. The Balmer series places Hα at 6562.8 Å, hence, it is less affected by dust extinction and serves as an excellent tracer for measuring SFRs up to z ∼ 0.4 in the optical range (Catalán-Torrecilla et al. 2015).
Other lines, such as the forbidden [O III]λλ4959, 5007 Å and [N II]λλ6548, 6584 Å doublets1, are sensitive to the gas-phase metallicity, which is ideal for investigating the metal enrichment of gas throughout cosmic time (Maiolino & Mannucci 2019). The [N II]/Hα and [O III]/Hβ ratios, among others, were used to construct the so-called BPT diagrams (Baldwin et al. 1981), which distinguish galaxies where the gas has been ionized due to the presence of an active galactic nucleus (AGN) from those where the main ionization mechanism comes from high rates of star formation in the galaxy or shock-ionized gas regions.
Even though spectroscopic surveys have revolutionized astronomy across a number of fields, they provide a limited picture of the universe in many senses. Both multi-object spectroscopy (MOS) and integral field units (IFUs) surveys are partially biased due to the pre-selection of samples, where some properties such as fluxes, redshift, or galaxy-size are limited to a certain range. Some of these issues can partially be solved with narrow band photometric surveys. Although they have been historically limited to few filters, they can act as low-resolution spectrographs and they are able to map the sky quickly and deeply – therefore they offer a more comprehensive snapshot of the universe. Needless to say, some astrophysical analyses will always require the highest possible spectral resolution to fully exploit all the information encoded in the spectrum.
One of the most competitive astrophysical surveys designed to overcome the weaknesses of both photometry and spectrography, functioning halfway between them, could well be the Javalambre-Physics of the Accelerating Universe (J-PAS, Benitez et al. 2014). It will sample the optical spectrum with 56 narrow-band filters for hundreds of millions of galaxies and stars over ∼8000 deg2. This is equivalent to a resolving power of R ∼ 50 (J-spectrum hereafter). Initially thought to explore the origin and nature of the dark energy in the universe, J-PAS is also ideal for galaxy evolution studies and to detect emission line objects (Bonoli et al. 2020). However, the large number of galaxies peaking over a wide range of redshift makes it difficult to employ traditional methods, such as subtracting from the emission line flux the image of the stellar continuum (Vilella-Rojo et al. 2015). Furthermore, line fluxes will contribute to several J-PAS filters, which also vary with the redshift of the object. Consequently, it is necessary for new techniques and algorithms to be developed in order to completely leverage the capability of J-PAS.
Machine learning techniques have effectively become a powerful tool across many fields where large quantities of data are available. The capability of these algorithms to find patterns in the data without making any empirical or theoretical assumptions has turned out to be their main advantage. In recent decades, astrophysical surveys are increasingly releasing vast amounts of data, which brings the opportunity of employing the most sophisticated up-to-date algorithms in order to analyze them faster and more efficiently. The applications range from the estimation of photometric redshifts (Pasquet et al. 2019; Cavuoti et al. 2017) and the identification of stars (Whitten et al. 2019) up through the classification of galaxies (Domínguez Sánchez et al. 2018) and the separation between galaxies and stars (Baqui et al. 2021) up to the determination of the SFR (Delli Veneri et al. 2019; Bonjean et al. 2019) – to cite some of the most recent research. In this work, we developed a new method based on artificial neural networks (ANN) to detect and measure some of the main emission lines in the optical range of the spectrum: Hα, Hβ, [N II], and [O III].
This paper is organized as follows. In Sect. 2, we present the J-PAS data together with data from other surveys that have been used to train and test the ANNs. In Sect. 3, we describe in detail the main characteristics of the ANNs along with a discussion of how they can be trained and tested to deal with the uncertainties associated to the data. In Sect. 4, we show the performance of ANNs in SDSS simulated data sets and discuss its main weaknesses. In Sect. 5, we test our method in galaxies that have been observed both in miniJPAS and SDSS. Finally, we present a summary in Sect. 6 and point out the steps needed to improve and extend the performance of the ANN in detecting and measuring emission lines.
2. J-PAS and spectroscopic data
In this section, we present J-PAS and the spectroscopic data used throughout this paper for training and testing the model.
2.1. J-PAS
J-PAS is an astrophysical survey (Benitez et al. 2014) that is aimed at mapping out close to 8000 deg2 of the northern sky with 56 bands, namely, 54 narrow-band filters in the optical range plus 2 medium-band – one in the near-UV (uJAVA band) and another in the NIR (J1007 band). With a separation of 100 Å, each narrow-band filter has a full width at half maximum (FWHM) of ∼145 Å, whereas the FWHM of the uJAVA band is 495 Å and the J1007 is a high-pass filter. The observations will be carried out with the 2.55 m telescope (T250) at the Observatorio Astrofísico de Javalambre, a facility developed and operated by CEFCA, in Teruel (Spain) using the JPCam, a wide-field 14 CCD-mosaic camera with a pixel scale of 0.2267 arcsec and an effective field of view of ∼4.7 deg2 (see Cenarro et al. 2019; Taylor et al. 2014; Marin-Franch et al. 2015). The survey is expected to detect objects with an apparent magnitude equivalent to iAB < 22.5, up to z ∼ 1 and with a photo-z precision of δz ≤ 0.003(1 + z) for luminous red galaxies.
The J-PAS project started its observations taking data with the Pathfinder camera observing four AEGIS fields with 60 optical bands amounting to 1 deg2. These data allow us to build a complete sample of galaxies up to rSDSS ≤ 22.5 mag (Bonoli et al. 2020). More than 60.000 objects have been detected and can be downloaded from the website of the survey2. We describe the survey, referred as to miniJPAS, in greater detail in Sect. 5.1 One example of how a nearby star-forming galaxy looks at the J-PAS resolution is shown in Fig. 1. The transmission curves of the J-PAS system are also shown in Fig. 1.
 |
Fig. 1. Synthetic photometry (colored dots) of an emission line galaxy model (gray line) at z = 0.044 in the J-PAS photometric system. |
2.2. CALIFA survey
The Calar Alto Legacy Integral Field Area (CALIFA, Sánchez et al. 2012; García-Benito et al. 2015) is an integral field spectroscopy survey which observed 600 spatially resolved galaxies in the local universe (0.005 < z < 0.03). The observations were taken with the 3.5 m telescope at the Calar Alto observatory with the Postdam Multi Aperture Spectrograph (PMAS, Roth et al. 2005) in the PPaK mode (Kelz et al. 2006), which contains 331 fibers of 2.7″ in diameter. With a field of view of 71″×64″ and a spatial sampling of 1 arcsec/spaxel, CALIFA observed each galaxy in the wavelength range of 3700 − 7300 Å with two different overlapping setups. Here, we use the spectra taken in the low-resolution setup (V500) that provides spectra from 3745 to 7500 Å with a spectral resolution of 6 Å to generate J-PAS synthetic photometry.
There are measurements of the emission lines available for a total of 275 787 spectra corresponding to 466 galaxies processed through the reduction pipeline of García-Benito et al. (2015). These spectra include emission patterns of many different zones within the galaxy. Therefore, even though the integrated spectra of CALIFA galaxies might not be heterogeneous enough to build a training set, the individual zones cover plenty of diverse physical states. The properties of the stellar populations and the state of the ionized interstellar gas change from one region to another in each individual galaxy. Hence, with the amount of galaxies observed with CALIFA, we can expect to see a rich representation of the most likely physical scenarios. The emission lines in each zone were measured from the residuals spectra obtained after subtracting the stellar continuum with STARLIGHT (Cid Fernandes et al. 2005).
2.3. MaNGA survey
The Mapping Nearby Galaxies at Apache Point Observatory (MaNGA, Bundy 2015) is an ongoing integral field spectroscopic survey that plans to observe spatially resolved spectra for ten thousand galaxies in the nearby universe (z < 0.15). With a wavelength coverage of 3600 − 10 300 Å at a resolution of R ∼ 2000, MaNGA is equipped with an IFU, in total 19 fibers of 12″ and 127 of 32″. In this work, we use the catalog available in3 and processed by PIPE3D pipeline in MaNGA SDSS-IV datacubes Sánchez et al. (2016a,b). The analysis of the stellar populations and ionized gas provides spatially-resolved information of the strongest emission lines in the optical range for a total of 4 670 507 spaxels from 2755 galaxies.
2.4. SDSS survey
The Sloan Digital Sky Survey (SDSS, York et al. 2000) contains spectroscopic measurements for more than three million astronomical objects and deep images of one third of the sky in five optical bands. The spectra were taken with a fiber of 3″ in diameter and a spectral coverage of 3800 − 9200 Å at a resolution of R ∼ 2000. Here, we use the publicly available MPA-JHU DR8 catalog from the Max Planck Institute for Astrophysics and Johns Hopkins University (Kauffmann et al. 2003b; Brinchmann et al. 2004). All the information regarding the catalog and the fitting procedure of the galaxy physical properties can be consulted online4. The catalog provides a total of 818 333 galaxies with redshift up to z ∼ 0.35. We only consider galaxies with reliable emission line measurements. As described in the data-model of the catalog, we can do that by excluding objects with RELIABLE = 0 and/or ZWARNING > 0 from the sample. We also discard galaxies where J-PAS synthetic magnitudes can not be calculated due to the lack of data in certain wavelength range of SDSS spectra. Finally, we ended up with 701 975 galaxies.
3. Method of analysis
In this section, we describe the architecture of the network in Sect. 3.1 and the strategies used for training and testing the model in Sect. 3.2. We also explain how to deal with photo-redshift uncertainty in Sect. 3.3, how errors can be estimated in Sect. 3.4, and how to treat missing data in Sect. 3.5.
3.1. Architecture of the Network
In this paper we use a class of ANN that is referred to as a fully connected neural network. The implementation was carried out with Tensorflow (Abadi et al. 2015) and Keras libraries (Chollet 2015) in Python. It is composed of a set of layers which have a specific number of neurons. The first layer contains the inputs (features) of the network. In our application, the inputs are the colors of J-PAS measured with respect to the filter corresponding to Hα for each spectrum. For instance, in nearby galaxies (z < 0.015), the Hα emission line will be captured by the J0660 band. Then the color in the filter Ji is defined as the difference respect to the magnitude measured in the J0660 band (Ci = mAB(J0660)−mAB(Ji)). The final layer contains the output of the network, sometimes also named targets in the machine learning argot. Our targets are the equivalent width (EW) of Hα, Hβ, [N II], and [O III]. We built two different ANNs: one performs a regression task and obtains the values of these EWs, this network will be referred to as ANNR. The other, ANNC, carries out a classification between galaxies without emission lines (below a given threshold) and emission line galaxies by imposing cuts in the EWs of the mentioned lines. We could have performed this classification based on the values yielded by the ANNR but an algorithm specifically constructed for a given task will always give better results.
As we mentioned earlier on in this paper, emission line fluxes have contribution to different bands according to the redshift of the source and the width of the emission line. The redshift might be treated as an input in the model but that would imply to train the ANN with a uniform distribution in this parameter, otherwise the ANN would not be able to make predictions equally at all redshifts. Furthermore, this approach would reduce our sample size and limit our range of predictability due to the different redshift coverage of CALIFA, MaNGA, and SDSS. For these reasons, we trained a different ANN for each redshift, going from 0 to 0.35 with a step of 0.001. We shifted all the spectra of the training set in wavelength at the same redshift and we computed the colors within the common wavelength range between J-PAS and the spectroscopic surveys described in Sect 2. This range depends on the redshift and, consequently, the number of inputs vary between 28 and 39 colors.
Between the input and the output layers, the ANN can hold inner layers, commonly called “hidden” layers, with no restrictions as to the number of layers and neurons in it. There is no standard recipe to find the optimal architecture of a network. Theoretically, with one hidden layer, it is possible to model the most complex function with sufficient amount of neurons. However, deep ANN, that is, those with mores hidden layers, have a much higher parameter efficiency and can, hence, model complex functions by using much fewer neurons (Géron 2019). Therefore, a few hidden layers are normally sufficient if the relation between input and output is not very complex. Certainly, this is our case for this study given the emission lines are clearly visible in the J-spectra. In addition, there are other features, such as the color of the spectra, that can also help to estimate the emission line patterns and are linearly connected to the inputs. In other cases where the relation is more complex, for instance, the estimation of the photometric redshift based on the images of a galaxy (Pasquet et al. 2019), an architecture made up of many more hidden layers will converge faster, obtaining an improved level of performance.
The amount of neurons in the hidden layer varies between the size of the input and the size of the output layers. Our ANNs have 2 hidden layers with 20 neurons each, which is in between the number of inputs (34 colors in average) and the number of outputs (four EWs for the ANNR and two classes in the case of the ANNC). A schematic view of the ANNR used in this work can be seen in Fig. 2.
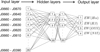 |
Fig. 2. Schematic diagram of the ANNR used for predicting lines emission at rest frame. The J0660 filter is our reference band for colors. |
All the neurons in a given layer are connected to the neurons in the contiguous layer by a matrix of weights, W, and a bias, B:
where Ln refers to layer n. Also, L0 are the inputs of the ANN and g is the activation function of neurons. It worth mentioning the importance of such a function, as it is responsible for the non-linear behavior in the network. Otherwise, the outputs would be simply a linear combination of the inputs, which would not be sufficient to address most of the problems. We use the so-called Rectified Linear Unit (ReLU) activation function (Nair & Hinton 2010), which has become the default activation function in recent years due to its advantages (Glorot et al. 2011).
Typically, ANN are trained using an algorithm commonly referred to as backpropagation. Adjusting the set of weights and bias that minimizes a certain loss-function is the actual process of training. For regression-like problems the most common loss-function is usually a mean square error, while for binomial classification the binary cross entropy is frequently employed. We make use of these functions in our models.
One important aspect to take heed of when when we are training an ANN is to avoid an overfitting. Improving the loss-function indefinitely would lead to the algorithm fitting features of certain data that do not represent the general trend. Consequently, the predictability of the network would be compromised. We can avoid that by imposing a maximum value over the weights that each neuron can carry.
Optimising the architecture of the network is a process that requires tweaking many hyper-parameters. As part of these efforts, we tested different architectures, increasing and decreasing the number of neurons or hidden layers or by using alternative loss functions such as the mean absolute error or the mean relative error for regression. Sometimes even different architectures can obtain very similar results. The model that we describe in this paper is among the ones we tested that better perform.
3.2. Training strategy
We generate synthetic J-PAS data by convolving the spectra presented in Sect. 2 with the J-PAS filter system. Since the wavelength coverage of CALIFA, MaNGA, SSDS, and J-PAS are different, in our model, we only use the common wavelength range of the four instruments at z = 0, which is 3810 − 6850 Å.
The training sample is built differently, depending on whether we are dealing with a classification or a regression task. In a classification problem, an unbalanced number of classes in the training sample might under-predict the minor class (see e.g., Ali et al. 2015, for a review in the topic). Therefore, when is possible, a balance training set is more desirable. In regression-like problems the optimal training set is the one that better covers the parameter space of the target variables. For instance, a training set built for classifying galaxies above and below 3 Å in the EW of Hα will be different from one that aims to compute the same EW in the range between 0 and 20 Å. Simply because we would need many more galaxies in the interval from 3 to 20 Å than would be needed below 3 Å.
Considering the data that we have at hand, there are other aspects that need to be taken into account to build the training sample. First, in order to ensure the algorithm receives the most reliable information, we would wish to select only the spectra where emission lines have been measured with high signal-to-noise ratio (S/N). However, being too strict in the selection criterium induces a bias towards line-emmiting galaxies and reduces significantly the size of the sample. Second, while CALIFA and MaNGA have observed the nearby universe spatially resolving the physical properties of the interstellar medium within galaxies, SDSS can only see the inner parts of nearby galaxies but with the advantage of covering distances further away in the universe. It has been shown how spatial resolution affects the location of points (spaxels) in the BPT, possibly altering AGN classification or simulating it via mixed spectral featured (Gomes et al. 2016). Finally, the emission line catalogs obtained from these surveys have been derived with different fitting tools, which makes it difficult to compare them in equal terms.
In essence, there is not a simple and unique way of putting together all these data and build the training set that better represents the universe as J-PAS will look at it. Instead, we propose to train the ANN with different training sets in order to understand the source of errors and inaccuracies of the model.
3.2.1. Training and testing sets in the ANN for classification
With the aim of identifying galaxies with low and high emission lines, we train a ANN classifier to perform a binary classification based on the EW of Hα, Hβ, [N II] or [O III]. This type of classification might allows us to disentangle the structure of the bimodal distribution found in the EW of Hα in CALIFA and SDSS galaxies (Bamford et al. 2008; Lacerda et al. 2018). In these works the authors found that the mentioned bimodal distribution has its minimum around 3 Å. In the regime of low emission the J-PAS filter system is not sensitive enough to detect emission lines and hence, it is only via machine learning, which can extract features from the J-spectra much more complex, it is possible to address this problem.
Galaxies are considered emitting-line galaxies or Class 1 according to the following criteria:
and Class 2 in the rest of our cases. We trained several classifiers where EWmin takes the following values: 3, 5, 8, 11, and 14 Å. In short, if a galaxy has an EW greater than the EWmin in any of these lines, it will be considered as Class 1. If all the EWs in a galaxy are below the threshold then it will be tagged as Class 2.
In most of the cases, Hα is the most powerful emission line and, consequently, it determines whether galaxies belong to one class or other. There is nothing special in the values chosen for EWmin except that they are in the regime of low emission. With the ANN classifier we prove that this regime can be explored in J-PAS. In addition, any other EWmin around these values could be implemented in the future.
The combination of data from different surveys used in this work does not improve or worsen the performance of the ANN classifier. Consequently, for the sake of simplicity, we train only with CALIFA synthetic J-spectra and we test with SDSS galaxies. We do not impose any cut in the errors of the EWs, but we ensure to have the same amount of J-spectra in both classes in the training set. We end up with 200 000 synthetic J-spectra to perform the training.
3.2.2. Training and testing sets in the ANN for regression
For the purpose of obtaining the values of the EWs of galaxies in J-PAS, we propose two training sets. The first one, which we call the CALMa set, is only composed of CALIFA and MaNGA synthetic J-spectra, while the second one, the SDSS set, includes only SDSS galaxies.
We test the performance of the model by randomly removing 15 000 synthetic J-spectra from the training samples: 5000 from CALIFA, 5000 from MaNGA and 5000 from SDSS. Those synthetic J-spectra are considered as validation or test samples depending on the training sample. For instance, if we train with the CALMa set, we use MaNGA and CALIFA samples to tune the hyper-parameters of the model (validation samples) and SDSS galaxies to actually evaluate the model; and the other way around: if we train with the SDSS sample, SDSS galaxies plays the role of the validation sample and CALIFA and MaNGA synthetic J-spectra are used for testing purpose. In this way, we ensure that the color terms that might appear as a result of fitting tools used to derive the emission lines or the instruments that obtained the spectra are not playing a major role in the prediction made by the ANN. If that were the case, building samples with different surveys in the training and testing sets would allow us to identify any potential bias arising from such circumstances.
We add only those synthetic J-spectra to the training set that have emission lines with an error below a certain threshold. In the case of MaNGA galaxies, spaxels with a S/N below 10 in the flux of Hα, Hβ, [N II] or [O III] were discarded. However, we were more flexible with spaxels in CALIFA and SDSS galaxies, going down to a S/N of 2.5. Such flexibility allows us to increase the amount of low-emitting galaxies in the samples. In addition, when it comes to the CALMa set, we achieved a more equilibrated weight between the prominence of CALIFA and MaNGA in the training sample. We also excluded from the training set those spectra where the EWs are greater than 600 Å (these are very rare cases, 10 in total). Since the loss function is quadratic in the EWs, this type of spectra force the ANNR to fit, at the same time, two antagonistic regimes: low-emitting and extreme emission line galaxies. Consequently, it would worsen the performance of the ANNR in the range of interest. Finally, we ended up with a training set of 134 000 synthetic J-spectra from CALIFA, 280 270 from MaNGA that altogether make up the CALMa set, as well as 135 300 galaxies in the SDSS set.
3.3. Photo-redshift uncertainty
Even though J-PAS will provide redshifts with a high precision (δz ≤ 0.3%5 for luminous red galaxies Benitez et al. 2014), the performance of the ANN could be compromised in certain cases. Let us assume, for example, that we aim to compute the EWs of a galaxy at redshift 0.3 with Δz = 0.003. In the best-case scenario, the galaxy redshift would be between 0.296 and 0.304. According to our redshift bin, we have eight possible ANNs to test with. While in the vicinity of the true redshift the ANN can do a reasonably good job, in the extremes, the EWs would dramatically be underestimated. Since colors are computed with respect to a filter far away from the one corresponding to Hα, the ANN will interpret as an absorption line what indeed is an emission line. Although the probability density functions (PDFs) of the photo-z can help to improve the predictability in assigning weights to each redshift; whenever we found a non-Gaussian PDF with, for instance, an asymmetric distributions with two peaks, it would be difficult for the ANN to make reasonable predictions.
One way to obtain better results in galaxies where the uncertainty in the redshift is high is to consider only the configurations (redshifts) that maximize a certain function. Certainly, for emission line galaxies, the redshift where the sum of all EWs reaches the highest value is close to the true redshift. However, this redshift overestimates the EWs in galaxies with low emission. In order to minimize such an effect, we average over the five configurations (redshifts) that maximize the sum of all EWs within the photo-redshift uncertainty (Δz). The fact that these configurations might be found in non-contiguous redshift bins can help in those cases where there are asymmetric PDF distributions of photo-redshifts.
As we go on to discuss in Sect. 4.4, this method is capable of somehow recomputing the distance of the galaxy, correcting a possible deviation from the spectroscopic redshift in galaxies where ∑EWi > 20 Å. Therefore, the method of the five maximum, hereafter 5max, can certainly help the ANNR to improve its performance but cannot be used with the ANNC. Most probably, it would increase the amount of false positives as the redshift uncertainty increases. In Sect. 4, we quantify how the error in the redshift can impact the predictions of the ANNC and the ANNR. Fortunately, the ANNC is less sensitive to that effect (see Fig. 3 and Table 1).
 |
Fig. 3. ROC curve of the ANNC for EWmin = 3 Å as a function of the redshift uncertainty for 10 000 SDSS galaxies. The legend shows the areas under the ROC curves for each Δz. In Table 1 we show these values for other EWmin settings. Blue dashed line shows the performance of a random classifier. |
Area under the ROC curve as a function of the redshift uncertainty and the EWmin used in the classification.
3.4. Estimation of errors
The uncertainty of the ANN method can be estimated by considering three sources of error: the error of the photometry, the error in the photometric redshift, and the intrinsic error of the ANN training. Before the training actually starts, weights and biases in ANN can be set to a certain value by initialising randomly according to any distribution function. Generally, each initialization state will converge to different local minimum of the loss-function. Even though it is possible to find the state that leads to the best score over the validation sample, it is usually a Monte Carlo approach called the committee (this is, the mean of the individual predictions of a set of ANN) that will be a more robust and accurate estimate of the targets. Thus, the variations of the outputs in each individual member of the committee with respect to the mean provide an estimation of the uncertainty in the predictions intrinsically associated to the training procedure. The paragraphs bellow details the steps to follow in order to account for the contribution of each uncertainty to the errors budget.
Photometric error: we input the ANN with N + 1 different values of the magnitude, where one corresponds to the nominal value and the other N are randomly drawn from a Gaussian distribution centred on the nominal value and with standard deviation equal to the photometric error. The median (M) and the median absolute deviation (MAD) of N + 1 predictions give us the prediction and the weight of one member in one committe:
where i stands for the committe member and zj for the redshift.
ANN intrinsic error: the prediction of the committe in a given redshift can be estimated by computing the average (AVG) of all members in the committe with the weights obtained above. The error of the committe is simply the MAD of m(N + 1) prediction, where m refers to the number of members in the committe. We found that averaging over five members is enough to obtain reliable results:
Photo-redshift uncertainty: we compute the median value of n committes, one for each redshift. In the case of the ANNR we select the five maximum setting (see Sect. 3.3) and for the ANNC, we consider all the redshift within the error range:
Finally, the error is the quadratic sum of the median error of all committees plus the dispersion of these committees respect to the median, which gives us the contribution of the redshifts uncertainty.
If the spectroscopic redshift of the object were known, the expression above would be simply: 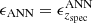 .
.
3.5. Missing data
There are a number of problems, both related to the data reduction or the observation, that could lead to incomplete or missing data. Consequently, a fraction of our sample will lack photometric measurements in some of the filters used by the ANN. Certainly, many such objects would have to be rejected automatically if the photometry is not reliable in the bands capturing the emission lines. However, there will be galaxies where the photometry might be problematic only in the some of the bands dominated by the stellar continuum. For instance, in the miniJPAS area, among the galaxies that are below 0.35 in redshift and 22.7 magnitudes in the rSDSS band (2291), 30% of them have at least one band where the photometry is not reliable. Most of the galaxies in this sample (70%) have a median S/N below 10. Naturally, this fraction will decrease as the median S/N of the sample increases.
One solution to address the problem of missing date requires training several ANN and considering different configurations where part of the data is accessible. Nevertheless, this would imply testing the performance of the ANN in many scenarios and would be computationally very expensive. The other solution is to replace the missing data in the corresponding filter with the fluxes obtained from the spectral fitting of the stellar continuum. Several spectral fitting codes can be used, such as MUFFIT (Díaz-García et al. 2015) or BaySeAGal (Amorim et al., in prep.). This analysis provides reliable photometric predictions for the missing data, as well as information regarding their stellar population properties (e.g., stellar mass, age, and extinction, which is always necessary for a more comprehensive picture). Furthermore, the stellar continuum is needed for obtaining absolute emission line fluxes. We follow this technique to treat the missing data in J-PAS.
4. Validation of the method
In this section we perform several tests to study the predictability and limitations of the model. First, we evaluate the capability of the ANNC in Sect. 4.1. Second, in Sect. 4.2, we compare the predictions of the EWs obtained by the ANNR and trained with the CALMa set with the SDSS testing sample. In Sect. 4.3, we compare the performance of the different training sets proposed in Sect. 3.2.2. In Sect. 4.4, we test the 5max method and we study the impact of the redshift uncertainty on the ANNR predictions as a function of the EW in Sect. 4.5. Finally, in Sect. 4.6 we estimate the minimum EW measurable in function of the S/N of the photometry for each of the emission lines predicted by the ANN.
4.1. Classifying galaxies
The ANNC is trained with the CALIFA training sample. To evaluate its efficiency, we explicitly selected a subset of 10 000 galaxies from the SDSS catalog with the same amount of classes, that is: 5000 galaxies that belong to Class 1 and 5000 to Class 2. (see Sect. 3.2.1). Galaxies in each class are picked at random from the entire catalog. For each galaxy, the ANNC yields a number between 0 and 1 indicating the probability of being one of the two classes. As we discuss in Sect. 4.4, the 5max method (Sect. 3.3) is not suitable for galaxies without emission lines. Most probably, it would increase the amount of false positives as the redshift uncertainty increases. Since we have noticed that the ANNC is less sensitive to redshift and is able to classify galaxies even when its uncertainty is high, we simply compute the average of each one of the predictions within the redshift interval defined by δz.
We show in Fig. 3 the receiver operating characteristic (ROC) curve, which represents the true positive rate (TPR) versus the false positive rate (FPR) for EWmin = 3 Å. We also show how the ROC curve varies as a function of the redshift uncertainty. The ANNC scores very high even when δz = 0.01 and loses efficiency gradually as the uncertainty in the redshift increases. We summarize in Table 1 the area under the ROC curves for others EWmin. The ROC curves do not show remarkable changes in function of the EWmin used in the classification.
4.2. Emission-line galaxies: EWs, line ratios and BPT diagram
In this section, we discuss how the CALMa training set (see Sect. 3.2.2) scores in the SDSS testing sample. We use the spectroscopic redshift provided in the catalog without considering any error so as to separate the uncertainties intrinsically associated to the model from those related to redshift. We do not consider the errors of SDSS spectra; rather, we add Gaussian noise to each magnitude 100 times, assuming an average S/N of 10. This allows us to treat all galaxies in the same manner and assume higher errors.
The testing set from CALIFA, MaNGA, and SDSS are composed of 5000 synthetic J-spectra with S/N in the EWs above 10. This criterion excludes many galaxies with a low-ionization nuclear emission-line region (LINER). We also exclude the spectra where the EWs are greater than 600 Å to test the model in the range of which we trained the ANNR. Hence, even though we are able to identify strong and weak emission lines galaxies, their EWs might not be accurate due to these selection criteria on the training sample.
4.2.1. Equivalent widths
Figure 4 compares the EWs predicted by the ANNR and those in the SDSS testing sample (extracted from the MPA-JHU DR8 catalog). We do not plot the errors yielded by the ANNR for visual reasons. A complete analysis of the errors estimated by the ANNR, as discussed in Sect. 3.4, is performed in Sect. 4.6. The plots on the left are color-coded with the density of points and the ones in the middle with the redshift of the galaxy. The histograms on the right represents the relative difference between the ANNR predictions and the SDSS testing set. We constrain better the EW of Hα followed by Hβ, [O III] and [N II] (see median and median absolute deviation in Fig. 4). The Hα line, which is the most powerful one, presents less dispersion and bias. Hβ and [O III] lines are recovered with similar precision and [N II] line shows more dispersion and bias. We observe that [N II] line saturates at high values, that is to say, the EWs tend to be underestimated as the strength of the line increases. The same effect occurs in the [O III] line in form of a second branch. We analyze this effect in Sect. 4.2.2. We do not observe strong color gradients in the plots color-coded with the redshift, indicating we are not biased with regard to the distance of the objects.
 |
Fig. 4. EWs of Hα, Hβ, [N II] and [O III] predicted by the ANNR compared to SDSS testing sample. The ANNR is trained with the CALMa set. The color-code represents the probability density function defined by a Gaussian kernel (right panel) and the redshift of the objects (left panel). The histograms in are normalized to one and show the relative difference between both values. Black and blue numbers are the median and the median absolute deviation of the difference. Black and grey dashed lines on the left are lines with slope one and the best linear fit respectively. We perform a sigma clipping fit with σ = 3 to exclude outliers. The red dashed line represents the median. |
In summary, the EWs of Hα, Hβ, [N II], and [O III] can be predicted with a relative standard deviation of 8.4%, 13.7%, 14.8%, and 15.7% respectively. Hα, Hβ, [N II], and [O III] lines presents a relative bias of 0.03%, 5.0%, 4.8%, and −6.4% respectively. In a future work, we will study the distribution of all these values using a real and complete sample of galaxies from miniJPAS.
4.2.2. Ratios between emission lines
Based on the EWs, we can easily obtain the ratios of [N II]/Hα and [O III]/Hβ under the approximation that each couple has the same stellar continuum. From that, we also obtain the metallicity indicator O 3N 2 ≡ log{([O III]/Hβ)/([N II]/Hα)} (Pettini & Pagel 2004). Figure 5 shows the comparison between the logarithmic ratios obtained with ANNR and the SDSS testing sample. As in Fig. 4, the plots are color-coded with the density of points (left column) and the redshift of the galaxy (middle panel). The histograms on the right show the logarithmic difference between the ANNR predictions and the SDSS testing set.
 |
Fig. 5. Comparison between [N II]/Hα, [O III]/Hβ and 5O 3N 2 ratios estimated by the ANNR and SDSS testing sample. Same scheme of Fig. 4. The ANNR is trained with the CALMa set. |
The [N II]/Hα ratio is predicted within 0.092 dex and a bias of −0.02 dex. The [O III]/Hβ ratio is slightly better constrained, with no bias and a dispersion of 0.078 dex. Finally, the O 3N 2 is recovered within 0.108 dex and a bias of 0.04 dex. The saturation of the [N II] line at high values is responsible of the same effect observed in the [N II]/Hα ratio. Since MaNGA and CALIFA surveys observed galaxies spatially resolved, the number of star-forming regions is much more numerous in the training sample and consequently the ANNR has few spectra to constrain the ratio of [N II]/Hα in galaxies hosting an AGN. To a lesser extent, that also occurs in the [O III]/Hβ ratio for galaxies with values higher than 3.2 and in the form of a second branch in the [O III] line.
4.2.3. BPT diagram
In Fig. 6, we compare the BPT diagram recovered by the ANNR (left plot) and the one obtained from the SDSS testing sample (right plot). Galaxies are color-coded with the density of points and are grouped into four classes by three dividing lines: star-forming, composite, Seyfert, and LINER. The solid curve is derived empirically using the SDSS galaxies (Kauffmann et al. 2003a, hereafter ka03). The dashed curve is determined by using both stellar population synthesis models and photoionization (Kewley et al. 2001, hereafter Ke01). The dotted line is a empirical division between Seyfert and LINER found by (Schawinski et al. 2007, hereafter S07). The sequence of metal enrichment experienced by star-forming galaxies from high to low values of the [O III]/Hβ ratio is clearly visible and well reproduced in the diagram. We will refer to that as the SF-wing. However, the saturation of the [N II]/Hα and [O III]/Hβ ratios produces the migration of galaxies from right to left and from top to bottom lowering the percentage of Seyferts (from 10.04% to 6.78%), composite (from 15.4% to 10.33%) and LINERS galaxies (from 1.7% to 0.21%) and increasing the percentage of star-forming galaxies (from 74.29% to 83.27%).
 |
Fig. 6. BPT diagram obtained with the ANNR and SDSS testing sample from the MPA-JHU DR8 catalog. The ANNR is trained with the CALMa set. The color-code indicates the density of points. The solid (ka03), dashed (Ke01) and dotted lines (S07) define the regions for the four main ionization mechanism of galaxies. The percentage for each group is shown in black. |
Another way to look at this is offered by Fig. 7. We show the direction towards the location which galaxies should be placed in the BPT according to the SDSS MPA-JHU DR8 catalog. The vectors are color-coded with the distance of each galaxy between the two BPT diagrams and those at a greater distance are plotted last. On average, star-forming galaxies deviate 0.10 dex while Seyfert and composite galaxies do 0.12 dex. In the right panel of Fig. 7, we plot the angular distribution of star-forming, Seyfert, and composite galaxies. The angle is defined as a clockwise rotation towards the x axis. While star-forming galaxies do not show any preferential direction, Seyfert and composite galaxies point with an average angle of 45° in the diagram. The CALMa set is very good at predicting the SF-wing because the main ionization mechanism in most of the regions in CALIFA and MaNGA galaxies is dominated by star-formation process. However, galaxies with a high [N II]/Hα ratio are more difficult to constrain.
 |
Fig. 7. BPT diagram obtained by the ANNR trained with the CALMa set. Arrows point in the direction towards the location where galaxies should be placed according to their position in the SDSS MPA-JHU DR8 catalog. The color represents the distance for each point between the two BPT diagrams. The solid (ka03), dashed (Ke01) and dotted lines (S07) define the regions for the four main ionization mechanisms of galaxies. The percentage for each group is shown in black. The histograms on the rights represent the angular distribution of the arrows for Star forming, Seyfert and composite galaxies. The angle is defined as a clockwise rotation towards the x axis. |
4.3. Comparison between different ANNR training sets
As we pointed out in the Sect. 3.2.2 we trained the ANNR with two different training samples. In Appendix A, we show the results obtained with the SDSS training set in the SDSS testing sample. A quick look at these plots (Appendices A.1–A.3) proves the importance of testing the model on data with a different observational setup and calibration. Considering the fact that the EWs are estimated from a pseudo-spectrum (J-spectrum) with a much lower resolving power, the performance of the SDSS training set in SDSS testing sample is outstanding. Nevertheless, it would not be realistic to deduce from that the actual capability of this method to predict in J-PAS data. Testing the CALMa training set with SDSS galaxies or vice versa gave us a better picture of the weakness and inaccuracies of the model. For instance, the predictions made by ANNR that were trained with SDSS set on the [N II]/Hα and [O III]/Hβ ratios of MaNGA and CALIFA spaxels tend to be overestimated. This is the opposite effect observed when the ANNR is trained with CALMa training set and tested on SDSS galaxies. The performance on the validation samples, that is, the data that belongs to the same survey, is generally better.
For the sake of illustrating the performance of both training sample (SDSS test and CALMa set) in each one of the testing sets (CALIFA, MaNGA and SDSS), we created a comparison table (Table 2). As it can be seen, there will always be a line that is better recovered in one particular simulation, for example, Hα in CALMa versus SDSS, however, the overall performance of the ANNR is generally more accurate using data from the same survey.
Relative difference between the EWs (in percentage) and ratios (in dex) predicted by ANNR and the values provided by the testing samples.
4.4. The 5max method in practice
A simple test to confirm the capability of the 5max method for retrieving the redshift of the object is to verify whether the average redshift over the five configuration is far from the true redshift. Normally, we would compute the EWs only in the redshift within the PDF of photo-zs before applying the 5max, but let us assume we do not have any information regarding the redshift of the object. Then, we have to calculate the EWs in all the redshift from 0 to 0.35 inside the grid and pick only the five redshifts that maximize their sum. Figure 8 shows this scenario where points are color-coded with the spectroscopic redshift. For emission line galaxies (∑EWi > 20 Å), this method is able to obtain the redshift of the object with high precision; what is more, the redshift is not needed as an input. Nevertheless, the 5max is not able to retrieve the redshift of the object when galaxies have low emission. The set of redshifts that maximizes the sum of the EWs is largely uncertain and consequently we do need the PDFs to constrain the redshift value.
 |
Fig. 8. δz obtained from the difference between the spectroscopic redshift and the median redshift in the 5max setting in function of the sum of the EWs provided in the SDSS catalog for a total of 10 000 galaxies. Points are color-coded with the spectroscopic redshift. |
4.5. Dependency on the equivalent width and redshift uncertainty
In order to explore the limitation of the model as a function of the redshift uncertainty and the EW of each one of the emission lines, we assembled galaxies in bins by the EW provided in the SDSS catalog and computed the ratio (R) between the predicted and observed EW. Each bin contains 500 galaxies in the interval 10γ < EWSDSS < 10γ + 0.1 with γ ranging from 0.8 to 2.5 for Hα, from 0.8 to 2.2 for [O III], from 0.8 to 1.8 for Hβ and from 0.8 to 1.8 for [N II]. As we observe in Fig. 9, Hα is clearly more affected by the 5max strategy when EW(Hα) ≤ 101.2 Å. Independently of the redshift uncertainty, the ANNR trained with the CALMa set has more difficulties to constrain the [N II] line underestimating its value as the EW increases. It also presents more dispersion, which is an indication of the different galaxy population found at such EW bins. This is, the percentage of galaxies hosting an AGN is higher. Nonetheless, we are able to constrain the EW of galaxies with a bias less than 10% for most of the lines – even with high uncertainty in the redshift.
 |
Fig. 9. Each point represents the median ratio between the predicted and the observed SDSS EWs and bars indicate the mean absolute deviation. Each bin contains 500 galaxies in the interval 10γ < EWSDSS < 10γ + 0.1 with γ ranging from 0.8 to 2.5 for Hα, from 0.8 to 2.2 for [O III], from 0.8 to 1.8 for Hβ and from 0.8 to 1.8 for [N II]. From left to right and top to bottom we increase the uncertainty in the redshift. Dashed blue lines point to a ratio of 1.15 and 0.85 respectively. Dash black line represent zero bias between the predicted and observed EWs. |
4.6. EW limit
The minimum EW measurable in a photometry system using a traditional method depends only on the S/N of the photometry and the effective width of filters in the system. Let us assume that an emission line falls within one filter (fi) and we know with high precision the redshift of the object. The EW of an emission line can be computed assuming the line is infinitely thin, as:
where Δ′ is the effective width of filter fi and Q is the ratio between the flux with and without emission line see (see Pascual et al. 2007, for details) or simply:
in AB magnitudes. Then, if we are able to estimate the flux of the stellar continuum in the filter tracing the emission line, obtaining the EW is straightforward. The S/N of such line can be expressed in terms of Q and the S/N of the photometry in the filter fi through the following equation:
The minimum EW measurable can be written as:
For S/Nphot = 10 only lines with EW greater that 16.1 Å can be measured in a filter width of 145 Å.
In Fig. 10, we determine the relation between the S/N of each line obtained with the ANN in function of the S/N of the photometry. As before, we assume no errors in the redshift of the objects. We analyze here the same galaxies used in the previous section in order to study the dependence with the EW. Each color represents the average S/N obtained in the line for 500SDSS galaxies with the same EW. The red dashed line follows Eq. (5) for EW = 10 Å, which is the lowest EW bin considered in the simulations. All the lines estimated with the ANN can be measured with a precision higher than a method based on the contrast between the emission line flux and the stellar continuum.
 |
Fig. 10. Predicted S/N of Hα, Hβ, [O III] and [N II] lines in function of the S/N in the photometry. For a given S/N in the photometry, each point represent the mean S/N obtained in the line for 500 SDSS galaxies in the interval (color-coded) γ < logEWSDSS < γ + 0.1 with γ ranging from 0.8 to 2.5 for Hα, from 0.8 to 2.2 for [O III], from 0.8 to 1.8 for Hβ and from 0.8 to 1.8 for [N II]. Errors bars indicate the mean absolute deviation. Dashed red line represents Eq. (5) for EW = 10 Å. |
Hβ is the line that can be obtained with the highest S/N for the same EW, with even better precision than Hα. This is not surprising since the algorithm has learned the implicit relation between Hα and Hβ constrained by the Balmer series and the amount of interstellar dust. Therefore, an EW in Hβ of 10 Å, which corresponds on average to an EW in Hα of about 30 Å, is measured with the same S/N. More complex relations, such as the one between Hα and [N II] has also been learned, but we observe a flattening of the S/N of the [N II] line for the highest EW with an increase in the scatter. This regime is populated with more AGN-like galaxies and consequently it is more difficult to constrain it with the CALMa set. This finding agrees with the behaviour observed in Fig. 9, where higher values of [N II] are systematically underestimated. Finally, the [O III] line is generally more difficult to constrain as we obtain lower S/N. Nevertheless, it can be recovered with better precision than a method based only on the photometry contrast.
To sum up, with an ANN one can measure a EW of 10 Å in Hα, Hβ, [N II], and [O III] lines with a S/N in the photometry of 5, 1.5, 3.5, and, 10 respectively. However, methods based on the photometry contrast need for the same EW a S/N in the photometry of at least 15.5. These facts illustrate once again the capability of machine learning algorithms to go beyond in precision and accuracy respect to traditional methods when large amount of data sets are available.
5. Comparison between miniJPAS and SDSS
In this section, we analyze and compare the data from the SDSS survey that has also been observed with miniJPAS in the AEGIS field. First, we describe the miniJPAS survey in Sect. 5.1. We analyze and compare the properties of galaxies in terms of their emission lines in Sect. 5.2.
5.1. The miniJPAS survey
The miniJPAS survey (Bonoli et al. 2020) is the result of the J-PAS-Pathfinder observation phase carried out with the 2.55 m telescope (T250) at the Observatorio Astrofísico de Javalambre in Teruel (Spain). miniJPAS was observed with the Pathfinder camera, the first instrument installed in the T250 before the arrival of the Javalambre Panoramic Camera (JPCam, Cenarro et al. 2019; Taylor et al. 2014; Marin-Franch et al. 2015). The JPAS-Pathfinder instrument is a single CCD direct imager (9.2k × 9.2k, 10 μm pixel) located at the center of the T250 FoV with a pixel scale of 0.23 arcsec pix−1, that is vignetted on its periphery, providing an effective FoV of 0.27deg2. The miniJPAS data includes four pointings of 1 deg2 in total along the Extended Groth Strip (called the AEGIS field). We use the same photometric system of J-PAS. Thus, AEGIS was observed with 56 narrow band filters covering from ∼3400 to ∼9400 Å. Observations in the four broad bands (uJPAS, and SDSS g, r, and i) were also taken. More than 60 000 objects were detected in the r band, allowing to build a complete sample of extended sources up to r ≤ 22.7 (AB). A detailed description of the survey is in Bonoli et al. (2020). The data is accessible and open to the community through the web page of the survey6.
5.2. The miniJPAS versus SDSS
For this comparison, we selected all galaxies observed with SDSS and miniJPAS with redshift below z ≤ 0.35 and a minimum average S/N of 20 in J-PAS narrow band filters. By a visual inspection we get rid of all QSOs in the sample. We ended up with a total of 89 objects. Whenever photometry measurements are lacking or the S/N in a particular filter is below 2.5, we replace it with the best-fit obtained from the stellar population analysis of the galaxy, as we discuss in Sect. 3.5. For this comparison, we employ BaySeAGal (Amorim, in prep.), a Bayesian parametric approach which assumes a tau-delayed star formation model for the star-formation history.
Generally, galaxy properties vary within the galaxy: the distribution of the gas, its temperature and its density, the distribution of interstellar dust or the stellar populations change as a function of the position in the galaxy (González Delgado et al. 2015). Consequently, if the SFR of a galaxy were higher in the outer parts, the galaxy would look younger in the integrated spectrum than in the central part. Similarly, the AGN of a galaxy would not leave the same imprint in the spectrum if the integrated areas covered regions dominated by other ionization mechanisms. Therefore, ideally, it would be optimal to analyse the same region in both surveys, which implies integrating over the same area. However, the aperture corresponding to the 3 arcsec fiber of SDSS is not sufficiently large to ensure that the point spread function (PSF) of the J-PAS filter system is not affecting the photometry in the filters where the seeing is worse. For this reason, we make use of the MAG_PSFCOR photometry which corrects each magnitude individually by considering the light profile of the galaxy and the PSF for each filter (Molino et al. 2014, 2019). As a consequence, the integrated area varies from galaxy to galaxy, going from 2 to 7 arcsec, and should be taken into account to interpret fairly this comparison. Although the ANNR only use colors as inputs, we scale the SDSS spectrum to match the rSDSS J-PAS magnitude in each galaxy for a visual inspection.
Figure 11 shows the EWs obtained by the ANNR on J-PAS photometric data (Col. 1) and on the synthetic J-PAS magnitudes obtained after convolving SDSS spectra with J-PAS filters (Col. 2) and assuming an average S/N of 20. We compare those values with the EWs derived as a result of fitting a Gaussian function to each one of the emission lines in the spectrum (x-axis). We do not include in this comparison the emission lines where EWs are below 1 Å, which indeed are compatible with zero. The number of galaxies in each row are from top to bottom 57, 37, 64, and 31. We find an excellent agreement when it comes to SDSS synthetic magnitudes, which is in line with the simulations performed with the SDSS dataset. We also find a remarkable correlation in Hα, Hβ and [N II] with J-PAS magnitudes, but we obtain in most of the cases higher values with an increase in the dispersion (see median and MAD in Fig. 11). The agreement is less favourable for the [O III] line. Nevertheless, we should bear in mind the limited number of galaxies used here in order to avoid drawing any conclusion that may not be supported from a statistical point of view. Instead, we consider more appropriate to analyze the origin of these discrepancies by visually examining each object.
 |
Fig. 11. Comparison between the EWs of Hα, [N II], Hβ and [O III] measured in the SDSS spectra and the predictions made by the ANN on miniJPAS data using the MAG PSFCOR (left panel) and synthetic J-PAS magnitudes obtained from the SDSS spectra (right panel). Black and blue numbers are the median and the median absolute deviation of the difference. Dashed black line is line with slope one. |
In Fig. 12, we show several galaxies analyzed in this comparison. We re-scaled the SDSS spectrum to match the rSDSS J-PAS magnitude. We compare the values of the EWs measured in the SDSS spectrum (black) with the values predicted by the ANNR (blue) for each one of these galaxies. On the bottom part, we show in each filter the difference between J-PAS data and SDSS synthetic photometry, which can certainly help to shed light on the origin of the discrepancies.
 |
Fig. 12. Examples of J-PAS galaxies in the AEGIS field with SDSS spectrum. The SDSS spectrum is re-scaled to match the rSDSS J-PAS magnitude. Diamonds correspond to the filters not used by the ANN. Blue and black numbers show, respectively, the predictions made by the ANNR on the EWs and the values measured in the SDSS spectrum. On the top-left part of the plot, we indicate the J-PAS ID of the object, its redshift and the prediction of the ANNC for EWmin = 3 Å. At the bottom, we show the difference in magnitude between the synthetic fluxes obtained from SDSS spectra and J-PAS data. Dashed lines mark from left to right the position of [O II], Hβ, [O III], and Hα emission lines. |
In the first row of Fig. 12, we display three examples of emission line galaxies where the agreement in most of the EWs is remarkable. Although ANNs are often difficult to interpret, it is evident after a visual inspection that the filters capturing the fluxes of the emission lines are the most relevant in determining the values of the EWs. The excess in the flux of Hα in galaxy 2243–8838 explains the increase in its EW respect to what it is obtained from a direct measurement in the spectrum or with the synthetic fluxes by means of the ANNR. In the same vein, the drop in the flux observed in the [O III] line in galaxy 2241–12 850 clarifies the differences found in the EW. Second-order terms include the relation between emission lines (Balmer decrement or recombination lines) and the colors of galaxies. Certainly, the excess in the flux of Hβ in galaxy 2243-9127 does not only increase the value of such line, but it also contributes to the enlargement the EW of Hα.
In the second row of Fig. 12, we show early-type galaxies (ETGs) where the differences between J-PAS data and SDSS synthetic fluxes are negligible. The ANNC estimates very low probability for these galaxies to have any emission line with a EW greater than 3 Å, which is in agreement with the measurements performed in SDSS spectra. As we discussed in Sect. 4.5 the ANNR tends to overestimate the EWs in the regime of low emission and consequently a zero level bias appears in these galaxies. Nonetheless, for many of these lines the values are compatible with the uncertainty and never overcome the 3 Å limit.
Finally, in the third row of Fig. 12 we focus our attention on galaxies where the fluxes seen by J-PAS and SDSS present evident differences in the blue part of the spectrum. The integrated areas in J-PAS are probably capturing regions with greater populations of young stars in 2243–9209 and 2406–4867 galaxies. Such populations raise the number of ionizing photons and this is responsible for the increase in the EWs of emission lines that we observe. The opposite effect occurs in galaxy 2406–5886, the galaxy looks redder with J-PAS data and the flux in Hα is less intense. Therefore, the predictions of the ANNR in the EWs are below the values measured in the SDSS spectrum.
To sum up, despite of the fact that this comparison suffer from several difficulties and it would need many more galaxies to be statistically robust, results are coherent with the simulations presented in Sect. 4 and lay the foundations to better understand and interpret the whole sample of galaxies observed in the AEGIS field, which we will analyze in a future work.
6. Summary and conclusions
We have developed a new method based on ANNs to measure and detect emission lines in J-PAS up to z = 0.35. We can classify galaxies according to the EWs of the emission lines, even with high uncertainty in the redshift. This will allow us to better study the density function of emitting-line galaxies in J-PAS.
Using the synthetic photometry of CALIFA, MaNGA or SDSS spectra, we trained an ANNR to estimate the EWs of Hα, Hβ, [N II], and [O III] lines. We present two training samples to undertake this task.
First, we trained the ANNR with only synthetic J-spectra from MaNGA and CALIFA surveys and we used SDSS to evaluate the performance of the model. The lack of a large enough number of AGN-like synthetic J-spectra leads to a saturation of [N II]/Hα and [O III]/Hβ ratios at high values, which compromises the ability of the model to deal with galaxies where the main ionization mechanism is not dominated by star-formation processes. Nevertheless, we are able to constrain those ratios within 0.078 and 0.092 dex. Furthermore, we are able to reach 0.070 and 0.087 dex, respectively, if one considers only star-forming galaxies. This is a significant improvement in the precision previously. While a method based on the photometry contrast need for an EW of 10 Å a S/N in the photometry of at least 15.5, the ANN can measure the same EW in Hα, Hβ, [N II], and [O III] lines with a S/N in the photometry of 5, 1.5, 3.5, and, 10 respectively.
Second, we trained the ANNR with SDSS galaxies and we revealed the importance of testing the model with data coming from different surveys. Otherwise, the performance of the model may be overestimated. While the SDSS training set scores very high with SDSS testing sample, the performance worsens when we compare it with the MaNGA or CALIFA test sample.
Finally, we estimate the EWs of a set of galaxies observed both in SDSS and miniJPAS. We compare the performance of ANNR in the synthetic SDSS fluxes with the performance in the fluxes measured by J-PAS. Despite the difficulty of comparing data from different surveys in equal terms, we reached an overall agreement. We argue that the origin of the discrepancies might be attributed to differences between the integration areas in miniJPAS and SDSS and/or photometry artefacts that appear as a result of the PSF. Many more data would be needed to be conclusive.
In this work, our model is limited to redshift below z = 0.35 in order to ensure Hα line is measurable with the J-PAS filter system. However, J-PAS will be able to detect galaxies up to z ∼ 1. Other emission lines, such as the [O III]λλ 3726,3729 doublet, are visible in the optical range up to redshift z < 1.6 and have been used as tracer of star formation in many works (Kewley et al. 2004; Sobral et al. 2012). An ultimate version of the model should take into account those facts and build a more sophisticated and complete training sample to be able to overcome the limitations and inaccuracies mentioned so as to fully exploit the potentiality of J-PAS. Our main conclusions are summarized below:
-
The ANNC can classify galaxies according to the EWs of the emission lines beyond the contrast that can directly be measured with sufficient significance in J-PAS (∼16 Å) and in the case of high uncertainty in the redshift as well.
-
The ANNR trained with the CALMa set can estimate the EWs of Hα, Hβ, [N II], and [O III] in SDSS galaxies with a relative standard deviation of 8.4%, 13.7%, 14.8%, and 15.7%, respectively. The Hα, Hβ, [N II], and [O III] lines present a relative bias of 0.03%, 5.0%, 4.8%, and −6.4% respectively. For a S/N of 3, the minimum EW measurable in Hα, Hβ, [O III] and [N II] lines is 18, 6, 40, and, 13 Å, respectively.
-
The [N II]/Hα is constrained within 0.092 dex and a bias of −0.02 dex and the [O III]Hβ ratio with no bias and a dispersion of 0.078 dex in SDSS galaxies. The O 3N 2 is recovered within 0.108 dex and a bias of 0.04 dex.
-
We found an overall correlation between miniJPAS and SDSS galaxies in the EW of Hα, Hβ and, [N II] lines. The correlation in the EW of [O III] is less strong. More data will be needed to unveil the origin of such discrepancy. Certainly, the problems associated with the integrated areas play an important role.
In summary, machine learning methods are essential tools in the era of big data in astronomy. The method we present in this paper will provide a useful tool in the analysis of emission lines in J-PAS and it will allow to go deeper in the understanding of galaxy formation and evolution.
Acknowledgments
G.M.S., R.G.D., R.G.B., E.P., J.R.M., L.A.D.G. and J.M.V. acknowledge support from the State Agency for Research of the Spanish MCIU through the “Center of Excellence Severo Ochoa” award to the Instituto de Astrofísica de Andalucía (SEV-2017-0709) and the projects AYA2016-77846-P and PID2019-109067-GB100. L.A.D.G. acknowledges support from the Ministry of Science and Technology of Taiwan (grant MOST 106-2628-M-001-003-MY3) and from the Academia Sinica (grant AS-IA-107-M01). P.O.B. acknowledge support from the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES) – Finance Code 001. R.A.D. acknowledges support from the CNPq through BP grant 308105/2018-4, and FINEP grants REF. 1217/13 – 01.13.0279.00 and REF 0859/10 – 01.10.0663.00 and also FAPERJ PRONEX grant E-26/110.566/2010 for hardware funding support for the JPAS project through the National Observatory of Brazil and Centro Brasileiro de Pesquisas Físicas. S.C. thanks CNPq, grant No. 307467/2017-1. V.M. thanks CNPq (Brazil) and FAPES (Brazil) for partial financial support. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 888258. LSJ acknowledges support from Brazilian agencies FAPESP (2019/10923-5) and CNPq (304819/201794). A.C. acknowledges support from PNPD/CAPES. J.M.V. acknowledges financial support from research projects AYA2016-79724-C4-4-P, PID2019-107408GB-C44 from the Spanish Ministerio de Ciencia e Innovación. The authors acknowledge the following people for providing valuable comments and suggestions on the first draft of this paper: Stravos Akras, Joel Bregman, Salvador Duarte Puertas, Jorge Iglesias, Yolanda Jimenez Teja, Jose Miguel Rodriguez Espinosa, David Sobral and, Adi Zitrin. This research made use of Python (http://www.python.org), Numpy (Van Der Walt et al. 2011); of Matplotlib (Hunter 2007), a suite of open-source Python modules that provides a framework for creating scientific plots and, Astropy, the community-developed core python package (Astropy Collaboration 2013, 2018). Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the US Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org. This study makes use of the results based on the Calar Alto Legacy Integral Field Area (CALIFA) survey (http://califa.caha.es/). This project made use of the MaNGA-Pipe3D dataproducts. We thank the IA-UNAM MaNGA team for creating this catalogue, and the ConaCyt-180125 project for supporting them. Funding for the J-PAS Project has been provided by the Governments of España and Aragón though the Fondo de Inversión de Teruel, European FEDER funding and the MINECO and by the Brazilian agencies FINEP, FAPESP, FAPERJ and by the National Observatory of Brazil. Based on observations made with the JST/T250 telescope and PathFinder camera for the miniJPAS project at the Observatorio Astrofísico de Javalambre (OAJ), in Teruel, owned, managed, and operated by the Centro de Estudios de Física del Cosmos de Aragón (CEFCA). We acknowledge the OAJ Data Processing and Archiving Unit (UPAD) for reducing and calibrating the OAJ data used in this work. Funding for OAJ, UPAD, and CEFCA has been provided by the Governments of Spain and Aragón through the Fondo de Inversiones de Teruel; the Aragón Government through the Research Groups E96, E103, and E16_17R; the Spanish Ministry of Science, Innovation and Universities (MCIU/AEI/FEDER, UE) with grant PGC2018-097585-B-C21; the Spanish Ministry of Economy and Competitiveness (MINECO/FEDER, UE) under AYA2015-66211-C2-1-P, AYA2015-66211-C2-2, AYA2012-30789, and ICTS-2009-14; and European FEDER funding (FCDD10-4E-867, FCDD13-4E-2685).
References
- Abadi, M., Agarwal, A., Barham, P., et al. 2015, TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, software available from tensorflow.org [Google Scholar]
- Ali, A., Shamsuddin, S. M., & Ralescu, A. 2015, SOCO, 2015 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bamford, S. P., Rojas, A. L., Nichol, R. C., et al. 2008, MNRAS, 391, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Baqui, P. O., Marra, V., Casarini, L., et al. 2021, A&A, 645, A87 [EDP Sciences] [Google Scholar]
- Benitez, N., Dupke, R., Moles, M., et al. 2014, ArXiv e-prints [arXiv:1403.5237] [Google Scholar]
- Bonjean, V., Aghanim, N., Salomé, P., et al. 2019, A&A, 622, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonoli, S., Marín-Franch, A., Varela, J., et al. 2020, ArXiv e-prints [arXiv:2007.01910] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K. 2015, IAU Symp., 311, 100 [Google Scholar]
- Catalán-Torrecilla, C., Gil de Paz, A., Castillo-Morales, A., et al. 2015, A&A, 584, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cavuoti, S., Amaro, V., Brescia, M., et al. 2017, MNRAS, 465, 1959 [NASA ADS] [CrossRef] [Google Scholar]
- Cenarro, A. J., Moles, M., Cristóbal-Hornillos, D., et al. 2019, A&A, 622, A176 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chollet, F., et al. 2015, Keras https://github.com/fchollet/keras [Google Scholar]
- Cid Fernandes, R., Mateus, A., Sodré, L., Stasińska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C. 2013, ARA&A, 51, 393 [Google Scholar]
- Delli Veneri, M., Cavuoti, S., Brescia, M., Longo, G., & Riccio, G. 2019, MNRAS, 486, 1377 [CrossRef] [Google Scholar]
- Díaz-García, L. A., Cenarro, A. J., López-Sanjuan, C., et al. 2015, A&A, 582, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz-García, L. A., Cenarro, A. J., López-Sanjuan, C., et al. 2019, A&A, 631, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domínguez Sánchez, H., Huertas-Company, M., Bernardi, M., Tuccillo, D., & Fischer, J. L. 2018, MNRAS, 476, 3661 [NASA ADS] [CrossRef] [Google Scholar]
- García-Benito, R., Zibetti, S., Sánchez, S. F., et al. 2015, A&A, 576, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Géron, A. 2019, Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems (O’Reilly Media) [Google Scholar]
- Glorot, X., Bordes, A., & Bengio, Y. 2011, Proc. Mach. Learn. Res., 15, 315 [Google Scholar]
- Gomes, J. M., Papaderos, P., Vílchez, J. M., et al. 2016, A&A, 586, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González Delgado, R. M., García-Benito, R., Pérez, E., et al. 2015, A&A, 581, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003a, MNRAS, 341, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003b, MNRAS, 346, 1055 [Google Scholar]
- Kelz, A., Verheijen, M. A. W., Roth, M. M., et al. 2006, PASP, 118, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Geller, M. J., & Jansen, R. A. 2004, AJ, 127, 2002 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Nicholls, D. C., & Sutherland, R. S. 2019, ARA&A, 57, 511 [Google Scholar]
- Lacerda, E. A. D., Cid Fernandes, R., Couto, G. S., et al. 2018, MNRAS, 474, 3727 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., & Mannucci, F. 2019, A&ARv, 27, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Marin-Franch, A., Taylor, K., Cenarro, J., Cristobal-Hornillos, D., & Moles, M. 2015, IAU General Assembly, 29, 2257381 [Google Scholar]
- Molino, A., Benítez, N., Moles, M., et al. 2014, MNRAS, 441, 2891 [NASA ADS] [CrossRef] [Google Scholar]
- Molino, A., Costa-Duarte, M. V., Mendes de Oliveira, C., et al. 2019, A&A, 622, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nair, V., & Hinton, G. E. 2010, Proceedings of the 27th International Conference on International Conference on Machine Learning, ICML’10 (Madison, WI, USA: Omnipress), 807 [Google Scholar]
- Pascual, S., Gallego, J., & Zamorano, J. 2007, PASP, 119, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquet, J., Bertin, E., Treyer, M., Arnouts, S., & Fouchez, D. 2019, A&A, 621, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Roth, M. M., Kelz, A., Fechner, T., et al. 2005, PASP, 117, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Kennicutt, R. C., Gil de Paz, A., et al. 2012, A&A, 538, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez, S. F., Pérez, E., Sánchez-Blázquez, P., et al. 2016a, RM&AC, 52, 171 [Google Scholar]
- Sánchez, S. F., Pérez, E., Sánchez-Blázquez, P., et al. 2016b, RM&AC, 52, 21 [Google Scholar]
- Schawinski, K., Thomas, D., Sarzi, M., et al. 2007, MNRAS, 382, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Best, P. N., Matsuda, Y., et al. 2012, MNRAS, 420, 1926 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, K., Marín-Franch, A., Laporte, R., et al. 2014, J. Astron. Instrum., 3, 1350010 [Google Scholar]
- Van Der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- Vilella-Rojo, G., Viironen, K., López-Sanjuan, C., et al. 2015, A&A, 580, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitten, D. D., Placco, V. M., Beers, T. C., et al. 2019, A&A, 622, A182 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
Appendix A: SDSS training set
In this section, we show how the SDSS training set scores in the SDSS testing sample. This represents the ideal situation where the testing set is included within the parameter space of the training set. In other words, the testing sample is a subset of the training set and consequently the only uncertainties found in the targets variables (EWs) area associated to the capability of the ANNR algorithm to decode the information provided by the inputs (J-spectrum). Nonetheless, we cannot infer from that the actual potential of the ANNR to predict in J-PAS data. As we discussed in the main body of this paper, herein lies the reason why the ANNR must be tested with data with different observational setup and calibrations.
In Fig. A.1, we plot the EWs predicted by the ANNR versus the EWs provided by the SDSS testing sample from the MPA-JHU DR8 catalog. This plot follows the same scheme of Fig. 4. As happened with the CALMa training set, we constrain better the EW of Hα followed by Hβ, [O III] and [N II]. However, the [N II] line is recovered with no bias and it does not saturate at high values.
 |
Fig. A.1. EWs of Hα, Hβ, [N II] and [O III] predicted by the ANNR compared to SDSS testing sample. The ANNR is trained with the SDSS training set. The color-code represents the probability density function defined by a Gaussian kernel (right panel) and the redshift of the objects (left panel). The histograms in grey are normalized to one and show the relative difference between both values. The histograms in blue are the ones in Fig. 4 and are shown for a visual comparison. Black and blue numbers are the median and the median absolute deviation of the difference. Black and grey dashed lines on the left are lines with slope one and the best linear fit respectively. We perform a sigma clipping fit with σ = 3 to exclude outliers. Red dashed line represents the median. |
In Fig. A.2, we show the comparison between the logarithmic ratios of [N II]/Hα, [O III]/Hβ and O 3N 2 in a similar way as we did in Fig. 5. The [N II]/Hα ratio is predicted within 0.089 dex and a bias of 0.019 dex and the [O III]/Hβ ratio within 0.08 dex and a bias of 0.027 dex. As a result, the O 3N 2 is recovered within 0.12 dex and a bias of 0.014.
 |
Fig. A.2. Comparison between [N II]/Hα, [O III]/Hβ and O 3N 2 ratios estimated by the ANNR and SDSS testing sample. The ANNR is trained with the SDSS training set Same scheme of Fig. A.1. |
Finally, we show in Fig. A.3 a comparison of the BPT diagram recovered by the ANNR (left plot) and the one obtained from the SDSS testing sample (right plot) following, once again, the same scheme of Fig. 6. The similarity between those diagrams is remarkable. We are not only able to recover properly the SF-wing but also the AGN branch, obtaining similar percentages of galaxies in all the regions.
 |
Fig. A.3. BPT diagram obtained with the ANNR and SDSS MPA-JHU DR8 catalog where the color-code indicates the density of points. The ANNR is trained with the SDSS training set. The solid (ka03), dashed (Ke01) and dotted lines (S07) define the regions for the four main ionization mechanism of galaxies. The percentage for each group is shown in black. |
All Tables
Area under the ROC curve as a function of the redshift uncertainty and the EWmin used in the classification.
Relative difference between the EWs (in percentage) and ratios (in dex) predicted by ANNR and the values provided by the testing samples.
All Figures
 |
Fig. 1. Synthetic photometry (colored dots) of an emission line galaxy model (gray line) at z = 0.044 in the J-PAS photometric system. |
| In the text | |
 |
Fig. 2. Schematic diagram of the ANNR used for predicting lines emission at rest frame. The J0660 filter is our reference band for colors. |
| In the text | |
 |
Fig. 3. ROC curve of the ANNC for EWmin = 3 Å as a function of the redshift uncertainty for 10 000 SDSS galaxies. The legend shows the areas under the ROC curves for each Δz. In Table 1 we show these values for other EWmin settings. Blue dashed line shows the performance of a random classifier. |
| In the text | |
 |
Fig. 4. EWs of Hα, Hβ, [N II] and [O III] predicted by the ANNR compared to SDSS testing sample. The ANNR is trained with the CALMa set. The color-code represents the probability density function defined by a Gaussian kernel (right panel) and the redshift of the objects (left panel). The histograms in are normalized to one and show the relative difference between both values. Black and blue numbers are the median and the median absolute deviation of the difference. Black and grey dashed lines on the left are lines with slope one and the best linear fit respectively. We perform a sigma clipping fit with σ = 3 to exclude outliers. The red dashed line represents the median. |
| In the text | |
 |
Fig. 5. Comparison between [N II]/Hα, [O III]/Hβ and 5O 3N 2 ratios estimated by the ANNR and SDSS testing sample. Same scheme of Fig. 4. The ANNR is trained with the CALMa set. |
| In the text | |
 |
Fig. 6. BPT diagram obtained with the ANNR and SDSS testing sample from the MPA-JHU DR8 catalog. The ANNR is trained with the CALMa set. The color-code indicates the density of points. The solid (ka03), dashed (Ke01) and dotted lines (S07) define the regions for the four main ionization mechanism of galaxies. The percentage for each group is shown in black. |
| In the text | |
 |
Fig. 7. BPT diagram obtained by the ANNR trained with the CALMa set. Arrows point in the direction towards the location where galaxies should be placed according to their position in the SDSS MPA-JHU DR8 catalog. The color represents the distance for each point between the two BPT diagrams. The solid (ka03), dashed (Ke01) and dotted lines (S07) define the regions for the four main ionization mechanisms of galaxies. The percentage for each group is shown in black. The histograms on the rights represent the angular distribution of the arrows for Star forming, Seyfert and composite galaxies. The angle is defined as a clockwise rotation towards the x axis. |
| In the text | |
 |
Fig. 8. δz obtained from the difference between the spectroscopic redshift and the median redshift in the 5max setting in function of the sum of the EWs provided in the SDSS catalog for a total of 10 000 galaxies. Points are color-coded with the spectroscopic redshift. |
| In the text | |
 |
Fig. 9. Each point represents the median ratio between the predicted and the observed SDSS EWs and bars indicate the mean absolute deviation. Each bin contains 500 galaxies in the interval 10γ < EWSDSS < 10γ + 0.1 with γ ranging from 0.8 to 2.5 for Hα, from 0.8 to 2.2 for [O III], from 0.8 to 1.8 for Hβ and from 0.8 to 1.8 for [N II]. From left to right and top to bottom we increase the uncertainty in the redshift. Dashed blue lines point to a ratio of 1.15 and 0.85 respectively. Dash black line represent zero bias between the predicted and observed EWs. |
| In the text | |
 |
Fig. 10. Predicted S/N of Hα, Hβ, [O III] and [N II] lines in function of the S/N in the photometry. For a given S/N in the photometry, each point represent the mean S/N obtained in the line for 500 SDSS galaxies in the interval (color-coded) γ < logEWSDSS < γ + 0.1 with γ ranging from 0.8 to 2.5 for Hα, from 0.8 to 2.2 for [O III], from 0.8 to 1.8 for Hβ and from 0.8 to 1.8 for [N II]. Errors bars indicate the mean absolute deviation. Dashed red line represents Eq. (5) for EW = 10 Å. |
| In the text | |
 |
Fig. 11. Comparison between the EWs of Hα, [N II], Hβ and [O III] measured in the SDSS spectra and the predictions made by the ANN on miniJPAS data using the MAG PSFCOR (left panel) and synthetic J-PAS magnitudes obtained from the SDSS spectra (right panel). Black and blue numbers are the median and the median absolute deviation of the difference. Dashed black line is line with slope one. |
| In the text | |
 |
Fig. 12. Examples of J-PAS galaxies in the AEGIS field with SDSS spectrum. The SDSS spectrum is re-scaled to match the rSDSS J-PAS magnitude. Diamonds correspond to the filters not used by the ANN. Blue and black numbers show, respectively, the predictions made by the ANNR on the EWs and the values measured in the SDSS spectrum. On the top-left part of the plot, we indicate the J-PAS ID of the object, its redshift and the prediction of the ANNC for EWmin = 3 Å. At the bottom, we show the difference in magnitude between the synthetic fluxes obtained from SDSS spectra and J-PAS data. Dashed lines mark from left to right the position of [O II], Hβ, [O III], and Hα emission lines. |
| In the text | |
 |
Fig. A.1. EWs of Hα, Hβ, [N II] and [O III] predicted by the ANNR compared to SDSS testing sample. The ANNR is trained with the SDSS training set. The color-code represents the probability density function defined by a Gaussian kernel (right panel) and the redshift of the objects (left panel). The histograms in grey are normalized to one and show the relative difference between both values. The histograms in blue are the ones in Fig. 4 and are shown for a visual comparison. Black and blue numbers are the median and the median absolute deviation of the difference. Black and grey dashed lines on the left are lines with slope one and the best linear fit respectively. We perform a sigma clipping fit with σ = 3 to exclude outliers. Red dashed line represents the median. |
| In the text | |
 |
Fig. A.2. Comparison between [N II]/Hα, [O III]/Hβ and O 3N 2 ratios estimated by the ANNR and SDSS testing sample. The ANNR is trained with the SDSS training set Same scheme of Fig. A.1. |
| In the text | |
 |
Fig. A.3. BPT diagram obtained with the ANNR and SDSS MPA-JHU DR8 catalog where the color-code indicates the density of points. The ANNR is trained with the SDSS training set. The solid (ka03), dashed (Ke01) and dotted lines (S07) define the regions for the four main ionization mechanism of galaxies. The percentage for each group is shown in black. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



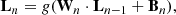
![$$ \begin{aligned}&\mathrm{EW}(\mathrm{H}\alpha ) > \mathrm{EW}_{\min } \parallel \mathrm{EW}(\mathrm{H}\beta ) > \mathrm{EW}_{\min } \parallel \nonumber \\&\mathrm{EW}([\mathrm{O}\,iii ]) > \mathrm{EW}_{\min } \parallel \mathrm{EW}([\mathrm{O}\,iii ])> \mathrm{EW}_{\min }, \end{aligned} $$](/articles/aa/full_html/2021/03/aa39146-20/aa39146-20-eq2.gif)
![$$ \begin{aligned} \begin{aligned}&P_{iz_j} = {M} \left[p^{iz_j}_{0},p^{iz_j}_{1},\ldots ,p^{iz_j}_{N+1}\right], \\&W_{iz_j} = 1/\mathrm{MAD}\left[p^{iz_j}_{0},p^{iz_j}_{1},\ldots ,p^{iz_j}_{N+1}\right], \end{aligned} \end{aligned} $$](/articles/aa/full_html/2021/03/aa39146-20/aa39146-20-eq3.gif)
![$$ \begin{aligned} {\begin{aligned}&P_{z_j} = \mathrm{AVG}\left[P_{0z_j},P_{1z_j},\ldots ,P_{mz_j};W_{0z_j},W_{1z_j},\ldots ,W_{mz_j}\right], \\&\epsilon ^\mathrm{ANN}_{z_j} = \mathrm{MAD} \left[p^{1z_j}_{0},\ldots ,p^{1z_j}_{N+1},p^{2z_j}_{0},\ldots ,p^{2z_j}_{N+1},\ldots ,p^{mz_j}_{0},\ldots ,p^{mz_j}_{N+1}\right]. \\ \end{aligned}} \end{aligned} $$](/articles/aa/full_html/2021/03/aa39146-20/aa39146-20-eq4.gif)
![$$ \begin{aligned} \begin{aligned}&P_{\mathrm{ANN}_R} = { M} \left[P_{z_0}({\max }_0),P_{z_1}({\max }_1),\ldots ,P_{z_4}({\max }_4)\right], \\&P_{\mathrm{ANN}_C} = { M} \left[P_{z_0},P_{z_1},\ldots ,P_{z_n}\right]. \end{aligned} \end{aligned} $$](/articles/aa/full_html/2021/03/aa39146-20/aa39146-20-eq5.gif)
![$$ \begin{aligned} {\begin{aligned}&\epsilon _{\rm ANN} = \sqrt{{M}\left[\epsilon ^\mathrm{ANN}_{z_0},\epsilon ^\mathrm{ANN}_{z_1},\ldots ,\epsilon ^\mathrm{ANN}_{z_n}\right]^2 + \mathrm{MAD}\left[P_{z_0},P_{z_1},\ldots ,P_{z_n}\right]^2}.\\ \end{aligned}} \end{aligned} $$](/articles/aa/full_html/2021/03/aa39146-20/aa39146-20-eq6.gif)