| Issue |
A&A
Volume 646, February 2021
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202038180 | |
| Published online | 03 February 2021 | |
A puzzling non-detection of [O III] and [C II] from a z ≈ 7.7 galaxy observed with ALMA
1
Observational Astrophysics, Department of Physics and Astronomy, Uppsala University, Box 516 751 20 Uppsala, Sweden
e-mail: christian.binggeli@physics.uu.se
2
Department of Physics, School of Advanced Science and Engineering, Waseda University, 3-4-1 Okubo, Shinjuku, Tokyo 169-8555, Japan
3
Waseda Research Institute for Science and Engineering, 3-4-1 Okubo, Shinjuku, Tokyo 169-8555, Japan
4
Department of Environmental Science and Technology, Faculty of Design Technology, Osaka Sangyo University, 3-1-1, Nakagaito, Daito, Osaka 574-8530, Japan
5
Tomonaga Center for the History of the Universe (TCHoU), Faculty of Pure and Applied Sciences, University of Tsukuba, Tsukuba, Ibaraki 305-8571, Japan
6
Department of Space, Earth and Environment, Chalmers University of Technology Onsala Space Observatory, 439 92 Onsala, Sweden
7
Theoretical Astrophysics, Department of Physics and Astronomy, Uppsala University, Box 516, 751 20 Uppsala, Sweden
8
Institute for Cosmic Ray Research, The University of Tokyo, Kashiwa, Chiba 277-8582, Japan
9
Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, UK
10
National Astronomical Observatory of Japan, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
11
Department of Astronomical Science, The Graduate University for Advanced Studies, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
12
Faculty of Science, Hokkaido University, N10 W8, Kitaku, Sapporo, Hokkaido 060-0810, Japan
13
Kyoto University Research Administration Office, Yoshida-Honmachi, Sakyo-ku, Kyoto 606-8501, Japan
14
Shikoku Gakuin University, 3-2-1 Bunkyocho, Zentsuji, Kagawa 765-0013, Japan
15
Division of Particle and Astrophysical Science, Graduate School of Science, Nagoya University, Aichi 464-8602, Japan
16
The Open University of Japan, 2-11 Wakaba, Mihama-ku, Chiba 261-8566, Japan
17
RIKEN Cluster for Pioneering Research, 2-1 Hirosawa, Wako-shi, Saitama 351-0198, Japan
18
Institute of Astronomy, School of Science, The University of Tokyo, 2-21-1 Osawa, Mitaka, Tokyo 181-0015, Japan
Received:
16
April
2020
Accepted:
25
November
2020
Context. Characterizing the galaxy population in the early Universe holds the key to understanding the evolution of these objects and the role they played in cosmic reionization. However, there have been very few observations at the very highest redshifts to date.
Aims. In order to shed light on the properties of galaxies in the high-redshift Universe and their interstellar media, we observe the Lyman-α emitting galaxy z7_GSD_3811 at z = 7.664 with bands 6 and 8 at the Atacama Large Millimeter/submillimeter Array (ALMA).
Methods. We target the far-infrared [O III] 88 μm and [C II] 158 μm emission lines and dust continuum in the star-forming galaxy z7_GSD_3811 with ALMA. We combine these measurements with earlier observations in the rest-frame ultraviolet (UV) in order to characterize the object and compare the results to those of earlier studies that observed [O III] and [C II] emission in high-redshift galaxies.
Results. The [O III] 88 μm and [C II] 158 μm emission lines are undetected at the position of z7_GSD_3811, with 3σ upper limits of 1.6 × 108 L⊙ and 4.0 × 107 L⊙, respectively. We do not detect any dust continuum in band 6 nor band 8. The measured rms in the band 8 and band 6 continua are 26 and 9.9 μJy beam−1, respectively. Similar to several other high-redshift galaxies, z7_GSD_3811 exhibits low [C II] emission for its star formation rate compared to local galaxies. Furthermore, our upper limit on the [O III] line luminosity is lower than the previously observed [O III] lines in high-redshift galaxies with similar UV luminosities. Our ALMA band 6 and 8 dust continuum observations imply that z7_GSD_3811 likely has a low dust content, and our non-detections of the [O III] and [C II] lines could indicate that z7_GSD_3811 has a low metallicity (Z ≲ 0.1 Z⊙).
Key words: galaxies: high-redshift / galaxies: ISM / galaxies: evolution / dark ages, reionization, first stars
© ESO 2021
1. Introduction
In order to provide a complete picture of the cosmic reionization and the evolution of galaxies across cosmic time, we need to understand the nature of the galaxy population present during the first billion years after the Big Bang. The properties of these objects and their interstellar media (ISM) are, however, still poorly understood, and characterizing physical properties of the galaxy population at the very highest redshift remains a challenging task. This is not least due to the lack of observational facilities that can provide us with high-quality spectra in the rest-frame optical and ultraviolet (UV), but it is also due to the limited number of currently observable features that allow for reliable spectroscopic confirmation of possible high-redshift candidates. While the challenge of obtaining high-quality spectra in the rest-frame optical and UV may have to wait until the launch of the James Webb Space Telescope (JWST), the Atacama Large Millimeter/submillimeter Array (ALMA) has provided us with an excellent way to probe these galaxies and their ISM through far-infrared (FIR) emission lines and FIR dust emission since these features fall into ALMA wavelengths at high redshifts.
In recent years, many ALMA studies of high-redshift galaxies have been aimed at observing two such FIR emission lines: the [C II] 158 μm line (see e.g., Carniani et al. 2018; Matthee et al. 2019; Harikane et al. 2020, for a summary of such observations), and the [O III] 88 μm line (Inoue et al. 2016; Laporte et al. 2017; Carniani et al. 2017; Hashimoto et al. 2018, 2019a; Tamura et al. 2019; Harikane et al. 2020). While the [C II] line arises predominantly in photo-dissociation regions (PDRs), where hydrogen is neutral, the [O III] line originates in H II-regions (e.g., Abel et al. 2005). These lines can thus be used to examine a range of properties, such as the ionization state and chemical properties at high redshifts (e.g., Vallini et al. 2015, 2017; Harikane et al. 2018, 2020; Katz et al. 2019). For example, high [O III]-to-[C II] ratios may be an indication of a low neutral hydrogen content, which is associated with high Lyman continuum escape fractions (e.g., Inoue et al. 2016), and thus could help us understand the reionization of the Universe.
A number of studies targeting the [C II] 158 μm line in high-redshift star-forming galaxies have reported surprisingly weak lines compared to local objects with similar star formation rates (SFRs; e.g., Ota et al. 2014; Schaerer et al. 2015; Maiolino et al. 2015). In their analysis of a compilation of galaxies at z ∼ 5−9, Harikane et al. (2020) found that they exhibit a deficit in [C II] with respect to the local [C II]-SFR relation. They also found that this deficit increases with stronger Lyα emission, which is consistent with the results of Carniani et al. (2018) and Harikane et al. (2018). Several mechanisms have been proposed to explain the origin of weak [C II] emission in high-redshift galaxies, such as low metallicity, increased ionization parameters, lower PDR covering fraction, and increased PDR densities in combination with a lower C/O abundance ratio or cosmic microwave background (CMB) effects (e.g., Vallini et al. 2015; Harikane et al. 2018, 2020). It has also been suggested that the possible weakness of [C II] emission in high-redshift galaxies may be a result of a selection bias due to selecting in the UV (Katz et al. 2019). On the other hand, when analyzing a compilation of z ≈ 6−7 galaxies similar to the one used by Harikane et al. (2020), Matthee et al. (2019) do not find that high-redshift galaxies deviate from the local [C II]-SFR relation at SFR ≳ 30 M⊙ yr−1. They do, however, find a possible deviation at lower SFRs. Schaerer et al. (2020) also find good agreement between z ∼ 4−6 star-forming galaxies from the ALPINE-ALMA survey (Le Fèvre et al. 2020; Béthermin et al. 2020; Faisst et al. 2020) and local galaxies. When combined with earlier measurements at z > 6, they find only a slightly steeper [C II]-SFR relation than the local one. Furthermore, in contrast to Harikane et al. (2020), Schaerer et al. (2020) do not find a strong dependence of L[C II]/SFR on the Lyα equivalent width.
The [O III] 88 μm emission line has been observed to be brighter than the [C II] 158 μm line in low-metallicity dwarf galaxies (e.g., Cormier et al. 2015) and is expected to also be so in the high-redshift Universe where metallicities generally should be lower (Inoue et al. 2014a). Indeed, as pointed out by Hashimoto et al. (2019a), the hunt for [O III] 88 μm emission in galaxies z > 6 has thus far been extremely successful, with successful detections all the way up to z ∼ 9 (Hashimoto et al. 2018). Recent results also seem to indicate that [O III] emission in high-redshift galaxies is in better agreement with local galaxies with similar SFRs compared to the [C II] line, suggesting a relatively tight correlation between the SFR and [O III] emission even at z > 6 (Harikane et al. 2020). The number of studies aimed at observing the [O III] line at high redshifts is, however, to date, significantly lower than those targeting the [C II] line.
In this study, we present ALMA observations targeting [C II] 158 μm, [O III] 88 μm, and dust continuum emission in the z = 7.664 Lyα-emitting galaxy z7_GSD_3811 (Song et al. 2016). The paper is organized as follows: in Sect. 2, we briefly describe the target object. In Sect. 3, we describe our ALMA band 6 and band 8 observations of [C II] and [O III] emission, respectively. In Sect. 4, we present our results from ALMA observational constraints from combining these with rest-frame UV data. In Sect. 5, we present results from spectral energy distribution (SED) fitting by combining earlier data with our ALMA data. Finally, in Sect. 6 we discuss and summarize our findings. Throughout the paper, we assume the following cosmological parameters: H0 = 70 km s−1 Mpc−1, Ωm = 0.3, and ΩΛ = 0.7. We use the AB magnitude system (Oke & Gunn 1983). All quoted uncertainties represent 68% confidence intervals.
2. Target
We present ALMA observations of the galaxy z7_GSD_3811 (Finkelstein et al. 2015; Song et al. 2016), a bright (F160W = 25.8 mag) Lyman break galaxy (LBG) in the Great Observatories Origins Deep Survey South (GOODS-S; Giavalisco et al. 2004) field. The object has been observed with the Hubble Space Telescope (HST) and HAWK-I at the Very Large Telescope (VLT) within the Cosmic Assembly Near-infrared Deep Extragalactic Legacy Survey (CANDELS; Grogin et al. 2011; Koekemoer et al. 2011). Spectroscopic follow-up observations using Keck/MOSFIRE have detected a Lyα line at z = 7.6637 ± 0.0011 with a rest-frame equivalent width EW(Lyα)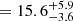 (Song et al. 2016), making it one of the highest-redshift objects to be spectroscopically confirmed. The detected Lyα line places z7_GSD_3811 at a redshift where the [O III] 88 μm and [C II] 158 μm emission lines fall within ALMA band 8 and 6, respectively. Furthermore, there are several earlier studies of high-redshift galaxies with similar UV luminosities (
(Song et al. 2016), making it one of the highest-redshift objects to be spectroscopically confirmed. The detected Lyα line places z7_GSD_3811 at a redshift where the [O III] 88 μm and [C II] 158 μm emission lines fall within ALMA band 8 and 6, respectively. Furthermore, there are several earlier studies of high-redshift galaxies with similar UV luminosities (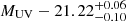 , Song et al. 2016) that have led to detections in [C II] (Pentericci et al. 2016; Carniani et al. 2018) and [O III] (Inoue et al. 2016; Tamura et al. 2019). Thus, z7_GSD_3811 should be a suitable target for expanding the currently limited number of [O III]-detected objects, but also for examining the ISM in the high-redshift Universe through a combination of [O III], [C II] and dust continuum emission.
, Song et al. 2016) that have led to detections in [C II] (Pentericci et al. 2016; Carniani et al. 2018) and [O III] (Inoue et al. 2016; Tamura et al. 2019). Thus, z7_GSD_3811 should be a suitable target for expanding the currently limited number of [O III]-detected objects, but also for examining the ISM in the high-redshift Universe through a combination of [O III], [C II] and dust continuum emission.
3. ALMA observations and imaging
Our ALMA observations of z7_GSD_3811 were performed between April and September 2018 as part of ALMA cycle 5 (Project ID: 2017.1.00190.S, PI: A. Inoue). Observations were performed in ALMA bands 6 and 8 targeting the [C II] 158 μm and [O III] 88 μm emission lines along with dust continuum around 152 μm and 87 μm rest-frame. Four spectral windows (SPWs) centered at approximately 219.4, 221.1, 234.0, and 236.0 GHz, each with a bandwidth of 1875 MHz and a resolution of 3.9 MHz, were used in band 6. For the band 8 observations, four SPWs were placed at approximately 391.6, 393.3, 403.7, and 405.5 GHz, each with a bandwidth of 1875 MHz and a resolution of 7.8 MHz. In band 6, this corresponds to a velocity bandwidth of ∼2400−2600 km s−1 per SPW and a velocity resolution of ∼5 km s−1. In band 8, the velocity bandwidth is ∼1400 km s−1 per SPW, and the velocity resolution is ∼6 km s−1. In both bands, one of the SPWs was centered around the position of the expected emission line of interest ([C II] 158 μm at 219.37 GHz in band 6, and [O III] 88 μm at 391.63 GHz in band 8) given the Lyα redshift, while a spare SPW was placed at higher frequency in case of a large blueshift relative to the Lyα emission line. The two remaining SPWs in each band were used in order to get observations of the dust continuum around 152 μm and 87 μm in bands 6 and 8, respectively. z7_GSD_3811 was observed in band 6 in April and September of 2018, with a median precipitable water vapor (PVW) of 1.3−1.8 mm, and in band 8 in August and September of the same year, with a median PVW of 0.3−0.7 mm. A summary of the observations is presented in Table 1.
Summary of ALMA observations.
For the band 6 observations, the quasar (QSO) J0522-3627 was used for bandpass and flux calibration for the executions performed in April 2018, while the QSO J0423-0120 was used for the execution performed in September 2018. In band 8, J0522-3627 was used for bandpass and flux calibration for all executions. In both bands, the QSO J0348-2749 was used for phase calibration for all the executions. We also used archival band 6 data from cycle 3 (Project ID: 2015.1.00821.S, PI: S. Finkelstein) observed in March and May 2016. The setup of the SPWs in these observations is similar to the setup used in the cycle 5 observations, with a total of four SPWs with bandwidths of 2000 MHz centered at similar frequencies (see Table 1). However, these observations were performed with a lower spectral resolution (15.6 MHz, corresponding to ∼20 km s−1). For the execution performed in March 2016, the QSO J0334-4008 was used both for bandpass and flux calibration. For the execution performed in May, the same flux calibrator was used while J0522-3627 was used for bandpass calibration. For both execution blocks, J0348-2749 was used for phase calibration.
The data have been reduced and calibrated using a standard pipeline running on Common Astronomy Software Application (CASA) version 5.1.1–5 for the band 6 data taken in cycle 5, while a newer version (5.4.0-68) was used for the band 8 data. For the cycle 3 band 6 data, CASA version 4.5.3 was used. Data from different execution blocks and the different cycles was combined before imaging. Imaging was done using the CASA task clean. In the cleaning procedure, we first produced a dirty image from which the rms (root-mean-square) was measured. We verify that the measured rms in these images is consistent with the theoretically expected noise level. For the clean image, we set the cleaning threshold to twice the rms measured in the dirty image.
Our imaging procedure is as follows: we created image cubes and continuum images using a natural weighting. For line images, we made cubes with several different spectral resolutions ranging from the native spectral resolution down to a resolution of ∼200 km s−1 in both bands. Our synthesized beam in the band 6 continuum image is 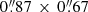 , with a position angle of PA = −81° . The corresponding values for the band 8 continuum image is
, with a position angle of PA = −81° . The corresponding values for the band 8 continuum image is 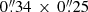 , PA = −88°. The synthesized beams in our [C II] and [O III] images are
, PA = −88°. The synthesized beams in our [C II] and [O III] images are 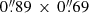 , PA = −84° and
, PA = −84° and 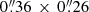 , PA = 89°, respectively. Given the apparent size of the source in the UV images (with an estimated diameter of
, PA = 89°, respectively. Given the apparent size of the source in the UV images (with an estimated diameter of 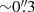 ) and the synthesized beam in band 8, we also created tapered images using several different tapering parameters up to
) and the synthesized beam in band 8, we also created tapered images using several different tapering parameters up to 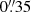 . This results in a beam major axis of
. This results in a beam major axis of 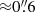 in both line and continuum images, and an increase in the measured rms up to a factor of ∼1.2. We also created [C II] image cubes with a tapering parameter of
in both line and continuum images, and an increase in the measured rms up to a factor of ∼1.2. We also created [C II] image cubes with a tapering parameter of 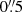 since recent results indicate that the [C II]-emitting region may be two to three times larger than the UV component (Carniani et al. 2018, 2020). This results in a beam major axis of
since recent results indicate that the [C II]-emitting region may be two to three times larger than the UV component (Carniani et al. 2018, 2020). This results in a beam major axis of 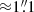 , which should make sure we are covering over three times the UV size. This also leads to an increase in the noise level by a factor of ∼1.1. We inspected the cubes and images taking into account the possible velocity offset between the FIR lines and Lyα, but none of the above strategies lead to significant detections of line nor continuum emission that could be associated with the target. We have assessed the Gaussianity of the pixel noise distribution in all the images used to define upper limits on the non-detections in this paper. We adopted a 3σ threshold as an upper limit for a non-detection in our analysis.
, which should make sure we are covering over three times the UV size. This also leads to an increase in the noise level by a factor of ∼1.1. We inspected the cubes and images taking into account the possible velocity offset between the FIR lines and Lyα, but none of the above strategies lead to significant detections of line nor continuum emission that could be associated with the target. We have assessed the Gaussianity of the pixel noise distribution in all the images used to define upper limits on the non-detections in this paper. We adopted a 3σ threshold as an upper limit for a non-detection in our analysis.
The flux calibration of ALMA data using QSOs (as is our case) relies on the frequent monitoring of a reference sample of QSOs in bands 3 and 7. This strategy provides an estimate of their intrinsic flux and spectral index and allows the extrapolation of their fluxes to the observed dates and frequencies. While the relative uncertainty on the flux calibration reported by the ALMA pipeline is generally below ∼10% for the data used here, the variability of the QSOs may introduce an additional uncertainty1. In order to get a handle on the flux uncertainty due to this variation, we extracted historical measurements of the flux calibrators from the ALMA source catalog and used the maximum and minimum spectral index within a month around each observing date to estimate the uncertainty in the extrapolated flux density for our observing frequencies and dates. Given the monitoring intervals of our calibrators and the different criteria that can be established to estimate the spectral index (e.g., involved bands and contemporaneity of measurements) we consider this to be a conservative and robust estimate. For our band 8 observations, we find that the variability exhibited by J0522-3627 can lead to a difference in the derived flux density on the order of 30%. Using a similar procedure for the band 6 observations, we find that the corresponding value is around 10%.
4. Results
In the following sections, we present upper limits of the [O III] 88 μm and [C II] 158 μm emission lines along with upper limits for the 87 μm and 152 μm dust continuum measurements since no line or continuum emission is detected (see Figs. 1 and 2). We also present results obtained by combining our ALMA upper limits and data in the rest-frame UV of z7_GSD_3811. In the GOODS-S field, a small systematic offset between ALMA and HST images has been observed (see e.g., Dunlop et al. 2017). We have therefore used the coordinates from the Hubble Legacy Fields (HLF) GOODS-S catalog (Whitaker et al. 2019), which have been corrected using the Gaia DR2 catalog (Gaia Collaboration 2016, 2018). We also used images from the HLF GOODS-S data release 2.0 (Illingworth et al., in prep.). We compared the position of a foreground detected object (see Sect. 4.2) and the HST image with the corrected coordinates. We find that that these are consistent within 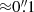 .
.
 |
Fig. 1. ALMA observations drawn at (− 3, −2, −1, 1, 2, 3) × σ overlaid on the HST F160W image of z7_GSD_3811. The positive and negative contours are drawn with solid and dashed lines, respectively. The white hatched ellipse in the bottom of each frame shows the synthesized beam of ALMA. Top left: [O III] line contours for an image collapsed over 400 km s−1 around 391.63 GHz, where σ = 44 mJy km s−1 beam−1. Top right: [C II] line contours for an image collapsed over 400 km s−1 around 219.37 GHz, where σ = 19 mJy km s−1 beam−1. Bottom left: dust continuum contours at 87 μm, where σ = 26 μJy beam−1. Bottom right: dust continuum contours at 152 μm, where σ = 9.9 μJy beam−1. |
4.1. Upper limits for the [O III] and [C II] line fluxes
In order to search for [O III] and [C II] line-emission, we visually inspected the image cubes around the position of z7_GSD_3811 at different velocity slices relative to the expected position of the lines given the source redshift. For the [O III] line, we searched for line emission between ≈ − 2000 to 700 km s−1 relative to the expected position of the line (391.63 GHz at z = 7.6637), while for [C II] the range that we used to search for line emission is ≈ − 2900 to 1300 km s−1 relative to the expected position (219.37 GHz at z = 7.6637). As mentioned in Sect. 3, the SPWs were arranged in this way in order to account for a possible velocity offset between the Lyα redshift and the [O III] and [C II] lines. Since the cycle 3 and cycle 5 band 6 observations cover slightly different frequency ranges and have different spectral resolution, some edge channels were excluded in the imaging step.
Given the lack of a clear detection from visual inspection, we also performed a systematic search for statistically significant features in our ∼50 (40),100 and 200 km s−1 cubes in band 8 (band 6), including tapered versions. Ideally, in order to claim a firm detection, we would want a signal at the 5σ level. Although, we also looked for more marginal features that match the expected properties of the lines. In the search for potential signal, we selected all pixels above three times the image rms (3σ) within 1″ of the target position. We analyzed these further by visually inspecting spectra extracted at the locations and creating moment-0 maps around channels of high intensity. We also looked at groups of pixels that were outside our 1″ area, in cases where these gave rise to any pixels above 3σ inside the area. In this procedure, we did not find any potential line emission signal with a peak signal-to-noise ratio (S/N) larger than 3 at the position of the UV component of z7_GSD_3811 (see also the [C II] and [O III] cube spectra extracted within one beam area at the position of the target in Fig. 2). In the [O III] cube, we are able to find features such that the collapsed moment maps contain some pixels that reach above 4σ within ∼1″ of the position of z7_GSD_3811 (at distances of 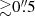 ). In addition to the spatial offset, these features are very narrow compared to earlier [O III] detections, with full width half maxium (FWHM) velocities ≲40 km s−1, and exhibit large velocity offsets relative to Lyα (≳600 km s−1), and thus are unlikely to belong to the [O III] line. Similarly, we find two marginal features at a ∼3.6−3.9σ level around the target position in the [C II] cube that also exhibit significant spatial (
). In addition to the spatial offset, these features are very narrow compared to earlier [O III] detections, with full width half maxium (FWHM) velocities ≲40 km s−1, and exhibit large velocity offsets relative to Lyα (≳600 km s−1), and thus are unlikely to belong to the [O III] line. Similarly, we find two marginal features at a ∼3.6−3.9σ level around the target position in the [C II] cube that also exhibit significant spatial (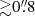 ) and spectral (≳700 km s−1) offsets. In most of our collapsed maps, we are also able to find collections of negative pixels at the same significance as the positive ones when inspecting a larger region of the image, and therefore cannot reliably distinguish these features from noise. We also inspected the pixel noise distributions in the collapsed images to see if there were any clear deviations from Gaussian noise. For the brightest features, we calculateed an integrated S/N by fitting a 2D-Gaussian using the CASA task imfit and separately imaged the data taken at different observation times in order to see if the signal was consistent within these.
) and spectral (≳700 km s−1) offsets. In most of our collapsed maps, we are also able to find collections of negative pixels at the same significance as the positive ones when inspecting a larger region of the image, and therefore cannot reliably distinguish these features from noise. We also inspected the pixel noise distributions in the collapsed images to see if there were any clear deviations from Gaussian noise. For the brightest features, we calculateed an integrated S/N by fitting a 2D-Gaussian using the CASA task imfit and separately imaged the data taken at different observation times in order to see if the signal was consistent within these.
 |
Fig. 2. [C II] (top) and [O III] (bottom) spectrum of z7_GSD_3811 shown at a resolution of ≈21 km s−1 and ≈24 km s−1, respectively. The spectra have been extracted in circular apertures with areas approximately equal to the beam areas. The horizontal axis shows the velocity relative to Lyα and the dashed lines show the 1σ noise level obtained by randomly placing a large number of apertures over the image and adopting the variation in the flux as the noise. |
We find a very narrow FWHM ≈ 30 km s−1, at ≈ − 1250 km s−1 relative to Lyα ) potential signal at 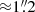 to the southwest of the target in band 8. When imaged with a beam of
to the southwest of the target in band 8. When imaged with a beam of 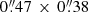 (corresponding to a
(corresponding to a 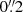 taper), and collapsed over ≈70 km s−1, the peak pixel reaches 5σ. However, the integrated S/N given by imfit is only ≈3.1. Given the large spectral and spatial offset relative to the UV component of z7_GSD_3811 and the narrow line-width, this possible signal is unlikely to belong to our target. We also note that there are some positive channels around −240 km s−1 in the [O III] spectrum shown in Fig. 2. When fitted with a Gaussian, we find a line-width around 100 km s−1. By optimally selecting channels to collapse in order to maximize the S/N, we find that one pixel reaches 3σ at the eastern edge of the UV component, ≈0.1″ from the center. This feature has a line-width and velocity offset that is consistent with expected values for [O III]; however, given its very marginal significance, we were unable to identify this as the line. After all these checks, we were unable to find any potential [C II] and [O III] emission that could be reliably distinguished from noise and which could be associated with our target. We also note that none of the potential emission features found within 1″ exhibit integrated S/Ns > 3. Since we were unable to detect any of the targeted lines, we proceeded to derive upper limits.
taper), and collapsed over ≈70 km s−1, the peak pixel reaches 5σ. However, the integrated S/N given by imfit is only ≈3.1. Given the large spectral and spatial offset relative to the UV component of z7_GSD_3811 and the narrow line-width, this possible signal is unlikely to belong to our target. We also note that there are some positive channels around −240 km s−1 in the [O III] spectrum shown in Fig. 2. When fitted with a Gaussian, we find a line-width around 100 km s−1. By optimally selecting channels to collapse in order to maximize the S/N, we find that one pixel reaches 3σ at the eastern edge of the UV component, ≈0.1″ from the center. This feature has a line-width and velocity offset that is consistent with expected values for [O III]; however, given its very marginal significance, we were unable to identify this as the line. After all these checks, we were unable to find any potential [C II] and [O III] emission that could be reliably distinguished from noise and which could be associated with our target. We also note that none of the potential emission features found within 1″ exhibit integrated S/Ns > 3. Since we were unable to detect any of the targeted lines, we proceeded to derive upper limits.
As mentioned in Sect. 2, z7_GSD_3811 has a detected emission line that is consistent with Lyα at z = 7.6637. There is, however, a possibility that this line belongs to the [O II] λ3727 doublet at z ≈ 1.8. This scenario is discussed by Song et al. (2016), who, while unable to rule out a low-redshift interpretation, argue that the asymmetric line-profile, the photometric redshift determination and non-detection in optical (and stacked optical) bands in combination with their SED fitting suggest that the detected line is Lyα at a redshift of z ≈ 7.7.
In order to make a reasonable assumption on the line-width expected for the [C II] and [O III] lines, we looked at other high-redshift objects. In the case of [C II], there are several successful detections in the high-redshift Universe (see e.g., Matthee et al. 2019; Harikane et al. 2020, for a summary). Looking at objects with similar UV luminosities as z7_GSD_3811, typical line-widths are vFWHM,[C II] ≈ 50−150 km s−1 (Pentericci et al. 2016; Carniani et al. 2018). In the case of [O III]-detected objects with similar UV luminosities, these exhibit line-widths of ![$ {\mathit{v}_{FWHM\mathrm{[{\mathrm{O}\,\textsc{iii}}]}} = 80 {-} 150 \, \mathrm{km \, s^{-1}}} $](/articles/aa/full_html/2021/02/aa38180-20/aa38180-20-eq18.gif) (Inoue et al. 2016; Tamura et al. 2019). Thus, as our fiducial line width for both the [C II] and [O III] line width, we used 100 km s−1. Considering the luminosities that we derive from our upper limits, this [C II] line-width is also in good agreement with values presented in Kohandel et al. (2019) and Schaerer et al. (2020). However, throughout the paper, we also show the results that are obtained if one assumes a four times larger line-width, which is similar to the Lyα line-width (Song et al. 2016). In order to estimate an upper limit to the line fluxes, we thus calculated the integrated rms in a collapse of Δv = 100 and 400 km s−1 around the expected positions of the lines given the source redshift (391.63 and 219.37 GHz for the [O III] and [C II] line, respectively). It is likely that the Lyα line exhibits a velocity offset relative to the actual systemic redshift (see e.g., Hashimoto et al. 2019a). However, with the exception of an atmospheric line around −800 km s−1 in band 8 and an increased rms around −700 km s−1 in band 6 due to some completely flagged channels in the cycle 3 data, our rms is relatively invariant in the observed range. Between v = −500 km s−1 and v = 250 km s−1, the variation in the integrated rms for a 100 km s−1 wide line can be up to approximately ±2% in band 8 and +2%, − 4% in band 6. Thus, different assumptions on the line centers should not alter our results significantly.
(Inoue et al. 2016; Tamura et al. 2019). Thus, as our fiducial line width for both the [C II] and [O III] line width, we used 100 km s−1. Considering the luminosities that we derive from our upper limits, this [C II] line-width is also in good agreement with values presented in Kohandel et al. (2019) and Schaerer et al. (2020). However, throughout the paper, we also show the results that are obtained if one assumes a four times larger line-width, which is similar to the Lyα line-width (Song et al. 2016). In order to estimate an upper limit to the line fluxes, we thus calculated the integrated rms in a collapse of Δv = 100 and 400 km s−1 around the expected positions of the lines given the source redshift (391.63 and 219.37 GHz for the [O III] and [C II] line, respectively). It is likely that the Lyα line exhibits a velocity offset relative to the actual systemic redshift (see e.g., Hashimoto et al. 2019a). However, with the exception of an atmospheric line around −800 km s−1 in band 8 and an increased rms around −700 km s−1 in band 6 due to some completely flagged channels in the cycle 3 data, our rms is relatively invariant in the observed range. Between v = −500 km s−1 and v = 250 km s−1, the variation in the integrated rms for a 100 km s−1 wide line can be up to approximately ±2% in band 8 and +2%, − 4% in band 6. Thus, different assumptions on the line centers should not alter our results significantly.
The measured rms in our collapsed [O III] images is 23 and 44 mJy km s−1 beam−1 for Δv = 100 and 400 km s−1, respectively. For the corresponding [C II] images, we measure an rms of 9.8 and 19 mJy km s−1 beam−1, respectively. Continuum-subtracting the spectrum would lead to an increase in the rms in the channels excluded from the fitting (e.g., Sault 1994), thus depending on the assumed line width. Since our spectrum is compatible with zero, we proceeded without performing continuum subtraction. We show collapsed line images and spectra in Figs. 1 and 2, respectively.
Assuming that the target is unresolved with the native beam sizes, these fluxes correspond to 3σ upper limits on the line luminosities of L[O III] < 1.6 × 108 L⊙, L[O III] < 3.2 × 108 L⊙ for the [O III] line assuming a line-width of Δv = 100 and 400 km s−1, respectively. The corresponding values for [C II] are L[C II] < 4.0 × 107 L⊙ and L[C II] < 7.5 × 107 L⊙. Since the rms scales as the square-root of the line-width, the 3σ upper-limits obtained for 400 km s−1 are comparable to the value one would obtain for a 6σ upper limit assuming a 100 km s−1 line.
4.2. Upper limits for the 87 μm and 152 μm dust continuum
In order to create dust continuum images, we combined all four SPWs in each band and created collapsed images around 87 μm and 152 μm for the band 8 and band 6 data, respectively. Since no significant line emission was detected (see Sect. 4.1), we used the full frequency ranges in each band. While no FIR continuum was detected at the location of z7_GSD_3811, a foreground continuum source was detected in both the band 6 and band 8 dust continuum images2. Before measuring the rms in the continuum images, we masked out the detected foreground object. Our measured rms in the 87 μm image is 26 μJy beam−1. In the 152 μm image, we measure an rms of 9.9 μJy beam−1. The continuum images are shown in Fig. 1. We note that masking out channels corresponding to 400 km s−1 around the expected positions of the line centers from the continuum images leads to an insignificant increase in the measured rms (≤3%).
We estimated the total infrared (IR) dust luminosity (LIR) by integrating a modified black-body (De Breuck et al. 2003) curve over 8–1000 μm while assuming an emissivity index of βd = 1.5 and a dust temperature of Td = 45 K. These values are largely consistent with assumptions made in other studies (e.g., Ouchi et al. 2013; Schaerer et al. 2015; Inoue et al. 2016; Hashimoto et al. 2018; Matthee et al. 2019) and to that observed in Knudsen et al. (2017). Observations of local galaxies suggest that these have slightly lower dust temperatures (≈20−40 K; Rémy-Ruyer et al. 2013). On the other hand, recent studies suggest that the dust temperatures in high-redshift galaxies may be significantly higher (Bakx et al. 2020). In order to get a handle on the variation in LIR for different assumptions regarding the dust temperature we also estimated LIR assuming dust temperatures of 35 and 55 K. In this procedure, we corrected for dust heating and the background effect of the CMB following Ota et al. (2014). We note that the correction factor for CMB effects at 87 μm when assuming Td = 45 K is basically unity, while a value of ≈0.88 is found for the 152 μm dust continuum. The obtained 3σ upper limits to the total IR dust luminosities around 87 μm and 152 μm are LIR, 87 μm, 45 K < 9.3 × 1010 L⊙ and LIR, 152 μm, 45 K < 9.1 × 1010 L⊙, respectively. We will use these values in the forthcoming analysis (see Table 2). For comparison, if we instead assume a dust temperature of 35 K or 55 K, we find: LIR, 87 μm, 35 K < 6.7 × 1010 L⊙, LIR, 152 μm, 35 K < 4.9 × 1010 L⊙, LIR, 87 μm, 55 K < 1.4 × 1011 L⊙, and LIR, 152 μm, 55 K < 1.7 × 1011 L⊙.
Summary of properties of z7_GSD_3811 measured and derived using HST and ground-based imaging, ground-based spectroscopy, and ALMA observations.
4.3. The [C II]-SFR relation
As mentioned in Sect. 1, several studies have found that [C II] emission in high-redshift objects often is weak compared to local galaxies with similar SFRs. Using the UV magnitude and the relationship between UV luminosity and SFR by Kennicutt & Evans (2012), we find a UV SFR for z7_GSD_3811 of 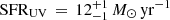 . Here, we used the UV magnitude from Song et al. (2016) presented in Table 2, and assumed that the error bars are symmetric and equal to the larger error presented there. Whereas the UV luminosity gives us an estimate of the non-obscured SFR, the IR luminosity can be converted to an estimate of the dust-obscured star formation. Using the corresponding relationship for the IR luminosity (Kennicutt & Evans 2012) and the upper limit on the total IR luminosity obtained via the band 6 ALMA data, we derived an IR SFR of SFRIR < 4.5 M⊙ yr−1 (1σ) for a dust temperature of 45 K.
. Here, we used the UV magnitude from Song et al. (2016) presented in Table 2, and assumed that the error bars are symmetric and equal to the larger error presented there. Whereas the UV luminosity gives us an estimate of the non-obscured SFR, the IR luminosity can be converted to an estimate of the dust-obscured star formation. Using the corresponding relationship for the IR luminosity (Kennicutt & Evans 2012) and the upper limit on the total IR luminosity obtained via the band 6 ALMA data, we derived an IR SFR of SFRIR < 4.5 M⊙ yr−1 (1σ) for a dust temperature of 45 K.
Following Matthee et al. (2019), we used this 1σ upper-limit to the IR SFR as our upper error bar to the UV+IR SFR (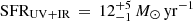 ). In order to see how our values compare to other high-redshift detections, we compare our derived UV+IR SFR and upper limit to the [C II] luminosity to galaxies at z > 6 from the recently published compilation by Matthee et al. (2019). We derived IR and UV SFRs for the galaxies included in the compilation in the same way as for z7_GSD_3811 using the UV magnitudes and IR luminosities presented in Matthee et al. (2019). While this compilation does have a UV magnitude for BDF-3299, we derived a value using the Lyα and intergalactic medium (IGM) -corrected Y band observation and inferred UV-slope from Vanzella et al. (2011). We find MUV ≈ −20.4 for this object, which is 0.5 magnitudes fainter than the original value in the compilation3. In the same way as for z7_GSD_3811, we used upper limits on the IR SFRs as upper limits to the UV+IR SFRs. While we derived UV and IR SFRs for all objects in a consistent manner, we also note that several objects in the compilation have published SFRs from SED fitting. These can in certain cases be significantly larger (or smaller) than the values we obtain using the method described here. For non-detections in [C II], we have gone back to the individual publications and rescaled all the upper limits to the same line-width as z7_GSD_3811 (i.e., 100 km s−1) by assuming that the velocity-integrated rms scales as the square root of the line width. For BDF-3299 and SXDF-NB1006-2, we have used the updated measurements from Carniani et al. (2020). In Fig. 3, we show the position of z7_GSD_3811 and the compilation objects in the [C II]-SFR plot. We also show the local relation for HII/Starburst galaxies and metal-poor dwarf galaxies from De Looze et al. (2014). The shaded region in the figure shows the 1σ dispersion in the relations. We note that the relation for metal-poor dwarf galaxies is extrapolated to higher SFR.
). In order to see how our values compare to other high-redshift detections, we compare our derived UV+IR SFR and upper limit to the [C II] luminosity to galaxies at z > 6 from the recently published compilation by Matthee et al. (2019). We derived IR and UV SFRs for the galaxies included in the compilation in the same way as for z7_GSD_3811 using the UV magnitudes and IR luminosities presented in Matthee et al. (2019). While this compilation does have a UV magnitude for BDF-3299, we derived a value using the Lyα and intergalactic medium (IGM) -corrected Y band observation and inferred UV-slope from Vanzella et al. (2011). We find MUV ≈ −20.4 for this object, which is 0.5 magnitudes fainter than the original value in the compilation3. In the same way as for z7_GSD_3811, we used upper limits on the IR SFRs as upper limits to the UV+IR SFRs. While we derived UV and IR SFRs for all objects in a consistent manner, we also note that several objects in the compilation have published SFRs from SED fitting. These can in certain cases be significantly larger (or smaller) than the values we obtain using the method described here. For non-detections in [C II], we have gone back to the individual publications and rescaled all the upper limits to the same line-width as z7_GSD_3811 (i.e., 100 km s−1) by assuming that the velocity-integrated rms scales as the square root of the line width. For BDF-3299 and SXDF-NB1006-2, we have used the updated measurements from Carniani et al. (2020). In Fig. 3, we show the position of z7_GSD_3811 and the compilation objects in the [C II]-SFR plot. We also show the local relation for HII/Starburst galaxies and metal-poor dwarf galaxies from De Looze et al. (2014). The shaded region in the figure shows the 1σ dispersion in the relations. We note that the relation for metal-poor dwarf galaxies is extrapolated to higher SFR.
 |
Fig. 3. [C II] 158 μm luminosity versus the UV+IR SFR. The yellow star shows the upper limit of z7_GSD_3811 assuming a line-width of 100 km s−1, while the dash and arrow show the upper limit obtained if we assume a line-width of 400 km s−1. The pink line and orange dashed line show the relation for local HII/starburst galaxies and metal-poor dwarf galaxies by De Looze et al. (2014), where the shaded regions correspond to the 1σ dispersion in the relations. The dotted and dash-dotted lines show the relations from the ALPINE-ALMA survey, derived by Schaerer et al. (2020, see text). The dark gray circles show objects from the compilation by Matthee et al. (2019) with z > 6. For BDF-3299 and SXDF-NB1006-2, we show updated [C II] measurement from Carniani et al. (2020). For this sample, we have rescaled the upper limits to line-widths of 100 km s−1. A few galaxies from the compilation that are also detected in [O III] are indicated by their names and a lighter gray color. All upper limits are at the 3σ level. |
Our upper limit on the [C II] line places z7_GSD_3811 below the local relations by De Looze et al. (2014). As can be seen in Fig. 3, several other objects with similar SFR also fall below the local relations. As is the case for z7_GSD_3811, many of these are undetected in [C II]. Even if we assume a [C II] line that is four times wider, our upper limit still places z7_GSD_3811 below the local relations, although with a smaller offset. The dotted line in Fig. 3 shows the relation by Schaerer et al. (2020), where they have used detections and 3σ upper limits from the ALPINE-ALMA survey in combination with earlier z > 6 measurements. Schaerer et al. (2020) correct for hidden star formation for those objects that are undetected in the IR by using the average IRX-β relationship by Fudamoto et al. (2020). Our upper limit on the [C II] luminosity places z7_GSD_3811 at a position that is below this relation in case we assume a 100 km s−1, although, only marginally so when we consider uncertainties related to the fits of Schaerer et al. (2020). For the assumption of a wider line, the upper limit is placed just above the relation. Schaerer et al. (2020) find that using more conservative upper limits (6σ) for the non-detections in their sample still leads to a relation that is somewhat steeper than the local one (the dash-dotted line in Fig 3). Our upper limit on the [C II] luminosity could in principle make z7_GSD_3811 consistent with this relation under the assumption of a 400 km s−1 line-width. This would also be the case if we used a 6σ upper limit for our 100 km s−1 line.
4.4. IRX-β
Dust-correcting rest-frame UV observations of galaxies requires making assumptions regarding the dust attenuation curve, or in other words, how a given amount of dust affects the shape of the spectrum. Since the heated dust emits at IR wavelengths, one way to try to constrain the dust-attenuation curve in galaxies is to look at the relation between the infrared excess (IRX; the IR-to-UV luminosity ratio) and the UV continuum slope (β). While no clear consensus has been reached regarding the dust attenuation curve at higher redshifts, there are studies that seem to favor a steep attenuation law similar to that of the Small Magellanic cloud (SMC) over a flatter Calzetti et al. (2000) law (e.g., Reddy et al. 2006; Capak et al. 2015; Bouwens et al. 2016).
We calculated the position of z7_GSD_3811 in the IRX-β plane and compare it to the positions of other high-redshift objects (z > 6) from the compilation by Matthee et al. (2019) in Fig. 4. Following Ono et al. (2010), we find a UV slope for z7_GSD_3811 using the F125W and F160W fluxes available in the official CANDELS catalog (Guo et al. 2013). We obtain F125W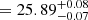 , F160W
, F160W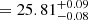 and β ≈ −1.7 ± 0.5. The magnitudes derived from the CANDELS catalog differ slightly from the ones presented in Song et al. (2016). If we would use the values presented there (25.8 and 25.9, for the two filters, respectively) we would obtain a significantly bluer UV slope β ≈ −2.4. Indeed, Song et al. (2016) find that their best fit SED also exhibits a significantly bluer UV slope
and β ≈ −1.7 ± 0.5. The magnitudes derived from the CANDELS catalog differ slightly from the ones presented in Song et al. (2016). If we would use the values presented there (25.8 and 25.9, for the two filters, respectively) we would obtain a significantly bluer UV slope β ≈ −2.4. Indeed, Song et al. (2016) find that their best fit SED also exhibits a significantly bluer UV slope 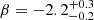 . However, considering the large uncertainties related with these UV slopes, these values are largely consistent with each other. In Fig. 4, we use β ≈ −1.7 ± 0.5. For the calculation of the IRX, we used the 3σ upper limit on the IR dust luminosity from the band 6 observations, a dust temperature of 45 K and a dust emissivity index of βd = 1.5 in order to be consistent with the IR luminosities presented in Matthee et al. (2019). For both the literature sample and z7_GSD_3811, UV luminosities are calculated as LUV = νLν at 1500 Å rest-frame, where Lν is the rest-frame luminosity in units of erg Hz−1 s−1 and ν is the frequency corresponding to 1500 Å. For z7_GSD_3811, we used the UV magnitude from Song et al. (2016) presented in Table 2. We obtain log10(IRX) ≲ 0.11 (see Fig. 4).
. However, considering the large uncertainties related with these UV slopes, these values are largely consistent with each other. In Fig. 4, we use β ≈ −1.7 ± 0.5. For the calculation of the IRX, we used the 3σ upper limit on the IR dust luminosity from the band 6 observations, a dust temperature of 45 K and a dust emissivity index of βd = 1.5 in order to be consistent with the IR luminosities presented in Matthee et al. (2019). For both the literature sample and z7_GSD_3811, UV luminosities are calculated as LUV = νLν at 1500 Å rest-frame, where Lν is the rest-frame luminosity in units of erg Hz−1 s−1 and ν is the frequency corresponding to 1500 Å. For z7_GSD_3811, we used the UV magnitude from Song et al. (2016) presented in Table 2. We obtain log10(IRX) ≲ 0.11 (see Fig. 4).
 |
Fig. 4. Relation between the IR-to-UV luminosity ratio (IRX) and the UV slope β. The yellow star shows the upper limit on the IRX calculated from the band 6 observations z7_GSD_3811. We also show the IRX and UV slopes of galaxies from the compilation of Matthee et al. (2019, dark gray circles). IRX values are calculated under the assumption of a dust temperature of 45 K and a dust emissivity index of βd = 1.5. The solid and dashed line represent the Calzetti and SMC dust laws calculated following Bouwens et al. (2016). The dotted line shows the IRX-β relation from the ALPINE-ALMA survey data, derived by Fudamoto et al. (2020, see text). Galaxies from the Matthee et al. (2019) compilation that are also detected in [O III] are indicated by their names and a lighter gray color. Upper limits on the IRX are at the 3σ level. |
In Fig. 4, we show the IRX-β relations of the Calzetti and SMC dust laws calculated following Bouwens et al. (2016) assuming an intrinsic UV slope β0 = −2.23. We also show the recently derived relation for z ∼ 5.5 galaxies from the ALPINE-ALMA survey (Fudamoto et al. 2020), which is even steeper than the SMC relation. The ALPINE-ALMA relation uses an intrinsic UV slope β0 = −2.62 derived by Reddy et al. (2018) based on the binary population and spectral synthesis models (BPASS; Eldridge & Stanway 2012; Stanway et al. 2016). Our upper limit on the IRX in z7_GSD_3811 is largely consistent with either of the three relations. While the related uncertainties are large, the bluer UV slope obtained by Song et al. (2016) would place z7_GSD_3811 above all three relations. Deeper dust continuum observations and future spectroscopic measurements of the UV slope in z7_GSD_3811 will likely give more insight into which of these relations best describes the object.
4.5. [O III] and UV luminosity
In Fig. 5, we show the ratio between the [O III] and UV luminosities as a function of the UV luminosity for z7_GSD_3811 and a number of high-redshift detections (z ≳ 6; Inoue et al. 2016; Laporte et al. 2017; Carniani et al. 2017; Hashimoto et al. 2018, 2019a; Tamura et al. 2019; Harikane et al. 2020). While there are detections of [O III] emissions from other types of objects, such as QSOs and submillimeter-galaxies (see e.g., Marrone et al. 2018; Walter et al. 2018; Novak et al. 2019; Hashimoto et al. 2019b), we limit this discussion to “normal” star-forming galaxies. In order to calculate the UV luminosities of the objects shown in Fig. 5, we used published values of MUV where these were available and the closest available photometry in the rest of the cases. We then calculated the UV luminosity in the same way as discussed in Sect. 4.4. For B14-65666 (Hashimoto et al. 2019a) and SXDF-NB1006-2 (Inoue et al. 2016), we used the values from the compilation of Matthee et al. (2019). For BDF-3299 (Carniani et al. 2017), we used the magnitude derived in Sect. 4.3. In the case of J1211-0118, J0235-0532, and J0217-0208 we used MUV = −22.8, −22.8, and −23.3 from Harikane et al. (2020), respectively. For MACS1149-JD1 (Hashimoto et al. 2018), MACS0416_Y1 (Tamura et al. 2019), and A2744_YD4 (Laporte et al. 2017), we used the HST F160W magnitude (Zheng et al. 2017), the F140W magnitude (Tamura et al. 2019), and the F140W magnitude from Zheng et al. (2014), respectively. While we consider effects of lensing magnification, the lensing errors are not included. For A2744_YD4, MACS1149-JD1, and MACS0416_Y1, we used lensing magnifications of 1.8 (Laporte et al. 2017), 10 (Hashimoto et al. 2018), and 1.43 (Tamura et al. 2019; Kawamata et al. 2016), respectively.
 |
Fig. 5. [O III] to UV luminosity ratio shown as a function of the UV luminosity. The yellow star shows the upper limit on the [O III] luminosity in z7_GSD_3811 assuming a line-width of 100 km s−1, while the dash and arrow show the corresponding upper limit assuming a line-width of 400 km s−1. The gray circles show [O III]-detected objects at z > 7 (Inoue et al. 2016; Laporte et al. 2017; Carniani et al. 2017; Hashimoto et al. 2018, 2019a; Tamura et al. 2019; Harikane et al. 2020), while squares show the three recent detections by Harikane et al. (2020) at z ∼ 6. The UV luminosity has been calculated with lensing considered, however, the errors in the lensing magnification are not included in this figure. |
Our upper limit places z7_GSD_3811 below the majority of the [O III]-detected objects, and the LO III/LUV ratio from our upper limit is a factor of ∼12 and ∼5 times lower than the ratio observed in MACS0416_Y1 (Tamura et al. 2019) and SXDF-NB1006-2 (Inoue et al. 2016), respectively. Both of which have similar UV luminosities as z7_GSD_3811. The object with the closest LO III/LUV-ratio is A2744-YD4 (Laporte et al. 2017), in which [O III] is detected with a ∼4σ significance. Even if we assume a four times wider line, the upper limit places z7_GSD_3811 below earlier detections of [O III] with similar UV luminosities.
In Fig. 6, we show a comparison between our upper limit on the LO III/LUV and nearby dwarf galaxies originally from Madden et al. (2013), De Looze et al. (2014), and Cormier et al. (2015), compiled by Inoue et al. (2016). In this figure, the horizontal axis shows the oxygen abundance relative to the Sun ([O/H] = log10(nO/nH) − log10(nO/nH)⊙), where we use 12 + log10(nO/nH)⊙ = 8.69 (Asplund et al. 2009). Our 3σ upper limit places z7_GSD_3811 at similar LO III/LUV ratio as nearby dwarf galaxies that have an oxygen abundance of ≈4% to 30% of the solar abundance. The mean oxygen abundance of nearby dwarf galaxies with LO III/LUV lower than z7_GSD_3811 is ≈9% of the solar value. This value does not change significantly in the case that we assume a four times wider line. We note, however, that the set of nearby dwarf galaxies represents a limited sample, and contains few galaxies with high SFR and high oxygen abundance.
 |
Fig. 6. [O III] to UV luminosity ratio (LO III/LUV) plotted against the oxygen abundance relative to the sun ([O/H] = log10(nO/nH)−log10(nO/nH)⊙). The hatched area shows the upper limit on z7_GSD_3811 based on our 3σ upper limit on the [O III] assuming a line-width of 100 km s−1, while the yellow line shows the corresponding value if we assume a four times wider line. The dark gray diamonds show local dwarf galaxies from Madden et al. (2013), De Looze et al. (2014), and Cormier et al. (2015) compiled by Inoue et al. (2016). |
5. SED fitting
In order to get an understanding of the possible stellar populations that may lead to results that are consistent with the HST, VLT and ALMA observations, we performed SED fitting using the PANHIT code (Mawatari et al. 2020). We used measurements from HST (F105W, F125W, F160W) and ground based infrared photometry (VLT/HAWK-I Ks) from the CANDELS catalog (Guo et al. 2013) combined with the ALMA upper limits on the [O III] 88 μm emission (assuming a line-width of 100 km s−1) and dust continuum emission in band 6 and band 8. We did not include the upper limit on the [C II] line due to the difficulty of accurately modeling lines that receive contributions from both H II regions and PDRs (e.g., Abel et al. 2005; Nagao et al. 2011; Inoue et al. 2014a). For the ALMA continuum observations, we created mock-filters with a top-hat shape, with frequency width corresponding to the four SPWs in each band. The central frequency of this filter was set to be the center in the continuum image in each band. We assumed a Chabrier initial mass function (IMF; Chabrier 2003) and a single stellar component. Since z7_GSD_3811 remains undetected in all but four filters, we assumed the simplified case of a constant SFR. The stellar models in PANHIT come from GALAXEV (Bruzual & Charlot 2003), nebular emission (continuum and lines) are from Inoue (2011) and Inoue et al. (2014b) and dust FIR emission is implemented using the empirical templates by Rieke et al. (2009). The nebular emission models from Inoue (2011) and Inoue et al. (2014b) are implemented in PANHIT using a scheme in which different densities are assumed for the regions where the FIR and UV/optical lines are formed. The UV/optical lines are calculated as an average over densities between log10(nH/cm−3) = 0.0−2.0, while the [O III] 88 μm line is calculated using a density of log10(nH/cm−3) = 1.0. The metallicity range used for the fitting was Z = 0.0001 – 0.02, while a Calzetti et al. (2000) attenuation curve with AV = 0−0.5 with steps of AV = 0.05 was used to account for possible dust-reddening and dust emission. In the SED-fitting procedure, we fixed the redshift to z = 7.664 and the escape fraction of ionizing photons to zero. This leaves us with seven observed data-points and four parameters to be fitted, leading to three degrees of freedom. In order to account for IGM attenuation of the model spectra shortward of Lyα, PANHIT uses the model proposed in Inoue et al. (2014b). For a more in-detail description of the PANHIT SED-fitting code, see Mawatari et al. (2020) and the PANHIT webpage4.
Formally, the best-fitting solution (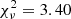 ) obtained from PANHIT gives a high age of 0.57 Gyr and a low metallicity of Z = 0.0004. The SFR of the model is 7.95 M⊙ yr−1, with a stellar mass of M⋆ = 3.05 × 109 M⊙ and a dust-extinction of AV = 0.00 magnitudes. Considering the age of the Universe at z = 7.664 is only ∼0.67 Gyr, this high age can certainly be questioned. In the context of constant SFR models, while cosmic star formation may well start at ∼100 Myr after the Big Bang, we do not expect galaxies to maintain a constant SFR from this time until z ∼ 7.7 since simulations generally suggest increasing SFRs over time. We have also performed tests with exponentially increasing SFRs, which produce fits that are not essentially different than the ones obtained from a constant SFR model. If we restrict the age of our constant SFR models to 300 Myr, as would seem more realistic given star formation histories (SFHs) of simulated galaxies (e.g., the simulations by Shimizu et al. 2016), we end up with three solutions with very similar chi-square but very different properties (see Fig. 7 and Table 3).
) obtained from PANHIT gives a high age of 0.57 Gyr and a low metallicity of Z = 0.0004. The SFR of the model is 7.95 M⊙ yr−1, with a stellar mass of M⋆ = 3.05 × 109 M⊙ and a dust-extinction of AV = 0.00 magnitudes. Considering the age of the Universe at z = 7.664 is only ∼0.67 Gyr, this high age can certainly be questioned. In the context of constant SFR models, while cosmic star formation may well start at ∼100 Myr after the Big Bang, we do not expect galaxies to maintain a constant SFR from this time until z ∼ 7.7 since simulations generally suggest increasing SFRs over time. We have also performed tests with exponentially increasing SFRs, which produce fits that are not essentially different than the ones obtained from a constant SFR model. If we restrict the age of our constant SFR models to 300 Myr, as would seem more realistic given star formation histories (SFHs) of simulated galaxies (e.g., the simulations by Shimizu et al. 2016), we end up with three solutions with very similar chi-square but very different properties (see Fig. 7 and Table 3).
 |
Fig. 7. PANHIT SEDs of three selected models with ages < 0.3 Gyr (see text). The yellow line shows an old (0.29 Gyr), low-metallicity (Z = 0.0004) model (Low Z), the pink line shows a model with the same age but high metallicity (Z = 0.02 ; High Z) and the blue line shows a young, low-metallicity model (Young; Age = 2 Myr, Z = 0.0001). The main panel shows the spectrum in the rest-frame UV and optical, with upper limits and measured photometry from HST and VLT/HAWK-I. The small panels show our ALMA upper limits on the dust continuum (top panel) and the [O III] emission line (bottom panel). Upper limits are at the 3σ level and are indicated with arrows. We note that the dust-continuum fluxes of the three models (crosses) overlap in the top panel. |
Properties of the three selected SED-fitting solutions (see text) and their predicted line luminosities.
These three solutions are statistically indistinguishable, and their relative probabilities are sensitive to percent level variations in our [O III] upper limit. Here we find a Young solution (with an age of 2 Myr) with low metallicity (Z = 0.0001), and two older solutions (with ages of 0.29 Gyr), one with a high metallicity (Z = 0.02) and the other with a low metallicity (Z = 0.0004). Hence, the SED fitting does not uniquely favor a low metallicity solution. It should be noted, however, that while the high metallicity solution has a relatively low chi-square, the [O III] emission of the model is only ∼5% weaker than the observed 3σ upper limit. In the case of the young model, the relatively red UV slope obtained from the CANDELS catalog is reproduced with strong nebular emission, as seen in Fig 7. At such a young age, all of the models with valid fits have metallicities Z ≲ 0.0004. Using an SMC dust extinction law instead of the Calzetti et al. (2000) attenuation law yields no significant difference in the properties of the best-fit models because of the strong pressure toward negligible dust content set by our upper limits on the dust continuum. We also tested our results in a modified version of PANHIT, where the user can specify dust temperature and dust emissivity index. We used the same parameters as in Sect. 4.2 (Td = 45 K, βd = 1.5). While the individual chi-squares of the solutions change, we find that the favored solutions remain largely the same, with slightly higher dust contents (AV = 0.05–0.1). However, if we assume a higher dust temperature (Td = 80 K, as proposed to explain the recent observations of MACS0416_Y1 by Bakx et al. 2020), solutions with higher dust attenuation/thermal reemission (AV = 0.3–0.4) can attain acceptable chi-squares. An effect of this is that PANHIT favors low-metallicity solutions with dust-reddened continua (which, in this case, attain 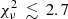 ) over high-metallicty solutions without dust.
) over high-metallicty solutions without dust.
In principle, observations of rest-frame UV/optical emission lines should provide us with a way to disentangle the different solutions suggested by PANHIT. For this purpose, we use PANHIT to estimate line luminosities for selected lines that we should be able to target with the upcoming JWST. Lines such as [O II] λ3727, Hβ, and [O III] λ5007 should fall within the wavelength range of JWST/NIRSpec at the source redshift. Furthermore, Hα should be observable with JWST/MIRI. Using the JWST exposure time calculator5 (Pontoppidan et al. 2016), we can estimate the time required to detect these lines with a given S/N. We set the assumed line-width to be 100 km s−1 and used no continuum and treated the object as a point-source. The line fluxes obtained from PANHIT are shown in Table 3. For all three models, Hβ and [O III] λ5007 are bright enough to be observed with an S/N of ≳5 given an exposure time of approximately one hour with the JWST/NIRSpec multi-object spectrograph using the Prism setting. In the case of [O II] λ3727, we find that we should get an S/N of ∼5 with approximately one hour of exposure for the old high-metallicity solution. For the other two solutions, the line is too weak to be detected with an S/N of ∼5 within a reasonable exposure time. All three models predict Hα strengths that should be detectable with an S/N of ∼5 given an exposure time of approximately six hours using MIRI medium resolution spectroscopy. In addition, He IIλ1640 should fall within the JWST/NIRSpec wavelength range at these redshifts. This line has been suggested as a signature of very metal-poor stellar populations (e.g., Schaerer 2003; Raiter et al. 2010), although recent results highlight that the connection between detections of He II and low metallicity is not entirely clear (e.g., Kehrig et al. 2015, 2018; Senchyna et al. 2017, 2020; Berg et al. 2018; Schaerer et al. 2019). In any case, the He IIλ1640 flux predicted for the models discussed here is not bright enough to be observed with the JWST/NIRSpec within a reasonable exposure time.
6. Discussion and summary
We have presented recent ALMA observations targeting FIR [O III] 88 μm, [C II] 158 μm emission lines and dust continuum in the high-redshift galaxy z7_GSD_3811. The object is not detected in line nor continuum images. We therefore present upper limits of the line and dust continuum emission. In Sect. 4, we show that our UV+IR SFR and 3σ upper limit on the [C II] luminosity would place z7_GSD_3811 below the De Looze et al. (2014) relations for local HII/Starburst galaxies and local low-metallicity dwarfs.
Similar results have been found in a number of studies targeting [C II] in high-redshift galaxies (e.g., Ota et al. 2014; Schaerer et al. 2015; Maiolino et al. 2015; Matthee et al. 2019), and there are several studies discussing the topic and possible explanations (see e.g., Vallini et al. 2015; Carniani et al. 2018; Harikane et al. 2018, 2020). However, as discussed in Sect.1, Schaerer et al. (2020) find better consistency between high-redshift and local objects and derive a [C II]-SFR relation at high redshifts that is only marginally steeper than the local relation for HII/Starburst galaxies. Our upper limit on the [C II] luminosity places z7_GSD_3811 below this relation, although only marginally so when we consider the uncertainties in the fitted relation by Schaerer et al. (2020). As shown in Sect. 4.3 this does also depend on our assumption on the line-width. Formally, our upper limit could be consistent with either of the relations shown in Fig. 3 given a substantial scatter. However, out of these, the slightly steeper relation derived by Schaerer et al. (2020) using measurements and 3σ upper from the ALPINE survey and earlier z > 6 data causes the least tension with our results.
Other studies that have examined the [C II]-SFR relation at high redshifts have found that the [C II]/SFR ratio is anti-correlated with the rest-frame equivalent width of Lyα, albeit with a significant scatter in observed [C II]/SFR versus EW(Lyα) (Carniani et al. 2018; Harikane et al. 2018, 2020). Compared to the relations in Harikane et al. (2018, 2020), our [C II] upper-limit is lower than indicated by the modest Lyα equivalent-width in z7_GSD_3811 (EW(Lyα) ≈ 16 Å; Song et al. 2016). On the other hand, Schaerer et al. (2020) find no such strong anti-correlation, which would seem to be in line with our findings of a modest Lyα equivalent-width combined with weak [C II]. Of course, at these redshifts, absorption of Lyα in the IGM is likely to have a large effect on the observed emission line. Thus, it is possible that the actual equivalent width is significantly larger.
In our search for [O III] emission from high-redshift galaxies, z7_GSD_3811 represents the first non-detection, placing it at an LO III/LUV ratio that is ∼5−12 times lower than those observed in earlier high-redshift detections in galaxies with similar UV luminosities (Inoue et al. 2016; Tamura et al. 2019). One possible explanation for this could be that z7_GSD_3811 contains fewer metals than the other [O III] detected objects. The mean oxygen abundance of local low-metallicity dwarf galaxies that exhibit LO III/LUV lower than our upper limit is ≈10% of the solar value (see Fig. 6). If the results of Steidel et al. (2016), indicating an enhancement of the oxygen abundance at high redshift, extend to z ∼ 7.7, this could, in principle, mean that the metallicity may be even lower. Steidel et al. (2016) argue that such an effect can be explained by a scenario in which the ISM enrichment is dominated by metals produced by core-collapse supernovae. However, due to a lower Lyman continuum emissivity at high metallicities, the relation between [O III] 88 μm and metallicity flattens and may actually turn over around Z ≈ 0.2 Z⊙ (Inoue et al. 2014a). Thus, we emphasize that our upper limit does not exclude the possibility that the object has a higher metallicity as the dwarf galaxy sample shown in Fig. 6 contains few objects at these metallicities. Although, the non-detection of dust emission suggests that a high metallicity is unlikely.
In the case of [C II], we also expect this line to be weaker in low metallicity environments. The relation between weak [C II] versus SFR and metallicity in high-redshift galaxies is, however, still not entirely clear. For example, while Harikane et al. (2020) find a connection between the PDR density and CMB effects on the [C II] luminosity, they do not find a significant effect on the [C II] luminosity as a function of the metallicity in their model. Such an effect is on the other hand seen in the simulations by Vallini et al. (2015), where the authors find that lower gas metallicities could explain the deficit in [C II] versus SFR observed in some high-redshift galaxies. If we compare our upper limit to the [C II] luminosity and our UV SFR to the [C II]-SFR relation by Vallini et al. (2015), we find that the values we obtain are consistent with a metallicity of Z ≲ 0.08 Z⊙ for a line-width of Δv = 100 km s−1. In the case that we assume a four times wider line, this upper limit is relaxed to Z ≲ 0.12 Z⊙. Since the simulations used to calibrate the relationship in Vallini et al. (2015) are using a Salpeter (1955) IMF, we convert our UV SFR to this IMF in order to be consistent.
As shown in Sect. 5, while low metallicity SED-fitting solutions are consistent with our observations, we find that these are not exclusive. Indeed, assuming a “modest” SFR and relatively high age of (0.29 Gyr), solutions with approximately solar metallicity, in the case that the [O III] line luminosity lies just below our ALMA upper limit, are also derived from the SED fitting with similar probabilities. The low LO III/LUV ratio compared to high-redshift objects with similar UV luminosities (SXDF-NB1006-2 and MACS0416_Y1; Inoue et al. 2016; Tamura et al. 2019) could thus also be explained by a difference in the SFHs of these objects.
When we take the SED-fitting results in conjunction with our [C II]-SFR and LO III/LUV compared to observations of local galaxies, this suggests that a likely explanation to the weak [C II], [O III] and dust continuum emission is that z7_GSD_3811 has a low metallicity. In addition, objects with stellar masses around 109 M⊙ and metallicities of 0.5−1 Z⊙ should be rare at these redshifts according to the simulation of Shimizu et al. (2016). As discussed in Sect. 4.4, the CANDELS catalog fluxes indicate a slightly red UV slope. Thus, the non-detection in the dust continuum “forces” PANHIT to increase the age of the object in order to match the UV slope, due to the strong pressure toward negligible dust content set by our upper limits on the dust continuum. With the limited number of observations in the rest-frame optical and UV, it is difficult to accurately constrain the SFH and age (and therefore also the SFR) of the object. A result of this is that we find a solution that exhibits a significantly lower age (2 Myr) that also fits the observations. This solution is similar to the ones suggested for SXDF-NB1006-2 and MACS0416_Y1 (Inoue et al. 2016; Tamura et al. 2019). In this case, the flat/red UV slope is explained by nebular continuum emission. This effect is also expected in the case of very metal-poor starburst galaxies, including the extreme case of a population III -dominated object (Raiter et al. 2010). If the SFR actually is as high as predicted by this solution (SFR = 77 M⊙ yr−1), this could indicate that the object contains very little metals. As we discuss in Sect. 5, JWST will likely be able to detect Hβ and Hα in z7_GSD_3811, which should give us a much better handle on the SFR and possibly also on the metallicity given our ALMA upper limit on the [O III] line.
There are, of course also other mechanisms that could lead to weak [O III] emission, such as high escape fractions of ionizing photons from H II regions. However, with the limited number of observational constraints, it is difficult to meaningfully constrain the escape fraction. Additionally, since the [O III] and [C II] lines are sensitive to the density in the environment where they are formed (e.g., Simpson 1975), increased ISM densities could lead to both weak [O III] and [C II] emission (Harikane et al. 2020). Comparing our [O III] upper limit and UV SFR to the cloudy modeling by Harikane et al. (2020), we find that a low metallicity (Z ≲ 0.2 Z⊙), a high density (log10(nH/cm−3)≳3.0), or a low ionization parameter (log10(Uion)≲ − 3.0) is required to explain the low [O III] luminosity, which is in line with our earlier arguments. If it is the case that the density is high in z7_GSD_3811, a possible way to examine this would be to target the [O III] 52 μm emission line since this line is expected to be stronger than the 88 μm line at high densities (Simpson 1975; Pereira-Santaella et al. 2017). In addition, our FIR dust continuum observations indicate that z7_GSD_3811 likely contains relatively little dust. This is also consistent with the results from our SED fitting, where a majority of the best-fit models contain no dust. These results do, as shown in Sect. 5, of course, depend on the assumed dust temperature at high redshifts. If dust temperatures as high as 80 K (as recently suggested by Bakx et al. 2020) are common at high redshifts, z7_GSD_3811 could actually be subject to higher dust extinction.
As discussed in Sect. 3, we estimate a relative uncertainty on the flux density given the variations in spectral index observed for our flux calibrators. While there is already an uncertainty on the [O III] luminosity coming from our line-width assumption, adding 30% to our 3σ, Δv = 100 km s−1 upper limit would lead to a LO III/LUV ratio of log10(LO III/LUV) ≈ −2.5. This would put our upper limit at a similar LO III/LUV ratio as A2744_YD4, but still significantly lower than that observed in MACS0416_Y1 and SXDF-NB1006-2, which have similar UV luminosities. Similarly, the position of z7_GSD_3811 relative to local dwarf galaxies would not change significantly, and would still be consistent with an oxygen abundance of ≲10% of the solar value. For our band 6 data, the possible additional 10% uncertainty from the flux calibration does not have a significant effect on the results presented here. A strategy currently tested by the ALMA Observatory, where the flux calibration is based on antenna efficiencies has the potential to be more accurate than flux calibration using QSO, especially at higher frequencies, (see the ALMA Technical Handbook6) and thus may help to reduce the contribution of flux uncertainty in future analysis.
In summary, our ALMA results show that z7_GSD_3811 is very weak in [O III], [C II] and FIR dust emission. While the nature of the object remains uncertain, these results may suggest that z7_GSD_3811 has a low metallicity (Z ≲ 0.1 Z⊙) and little dust. This could indicate that the object is in an unevolved phase of chemical evolution and that we are revealing the earliest phase of the galaxy formation process. Furthermore, the lack of a detected [O III] emission line shows that there may be a significantly larger spread in [O III] versus UV luminosity than indicated by earlier observations. If we assume that these objects such as z7_GSD_3811 are more common than currently indicated, we can expect future ALMA studies of [O III] to result in more non-detections. As concerns z7_GSD_3811, future JWST observations should allow us to get a better handle on the current and previous star formation and possibly the metallicity through observations of rest-frame UV/optical continuum and emission lines. This may ultimately clarify the nature of this object and its low [O III] luminosity compared to similar high-redshift objects.
ALMA Technical Handbook; https://almascience.eso.org/documents-and-tools/cycle7/alma-technical-handbook
The position of the foreground object is: RA = 03:32:32.91 Dec = −27:45:41.01 (J2000), outside the zoomed-in images shown in Fig. 1. The position of this source overlaps with an object in the HST F160W image.
MUV ≈ −20.4 leads to a UV SFR that is about a factor of 0.65 lower than what we would obtain using MUV ≈ −20.9 assuming the Kennicutt & Evans (2012) SFR relation. The value we derive is consistent with the UV SFR presented in Maiolino et al. (2015). While there are some spatial offsets between different emission components in BDF-3299, we assume that the UV, [O III] and [C II] emission are associated with the same object.
Panhit webpage, http://www.icrr.u-tokyo.ac.jp/~mawatari/PANHIT/PANHIT.html, maintained by Ken Mawatari.
Acknowledgments
C. Binggeli would like to thank A. Gavel, A. Lavail and M. Sahlén for helpful discussions. M. C. Toribio would like to thank A. M. S. Richards, E. Fomalont and L. T. Maud for useful discussions. A. K. Inoue and K. Mawatari acknowledge the support from the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Numbers 26287034 and 17H01114. A. K. Inoue and T. Hashimoto acknowledge support from the National Astronomical Observatory of Japan (NAOJ) ALMA Grant 2016-01A. T. Okamoto acknowledges the support from JSPS KAKENHI Grant Number 19H01931. Y. Tamura acknowledges support from NAOJ ALMA Scientific Research Grant Number 2018-09B and JSPS KAKENHI Grant Number 17H06130. This publication has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 730562 [RadioNet]. This publication makes use of the following ALMA data: ADS/JAO.ALMA#2017.1.00190.S, ADS/JAO.ALMA#2015.1.00821.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. The authors acknowledges support from the Nordic ALMA Regional Centre (ARC) node based at Onsala Space Observatory. The Nordic ARC node is funded through Swedish Research Council grant No 2017-00648. This research has made use of the VizieR catalog access tool, CDS, Strasbourg, France (DOI: 10.26093/cds/vizier; Ochsenbein et al. 2000), Astropy (http://www.astropy.org), a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018), APLpy, an open-source plotting package for Python (Robitaille & Bressert 2012) and NASA’s Astrophysics Data System (ADS).
References
- Abel, N. P., Ferland, G. J., Shaw, G., & van Hoof, P. A. M. 2005, ApJS, 161, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bakx, T. J. L. C., Tamura, Y., Hashimoto, T., et al. 2020, MNRAS, 493, 4294 [NASA ADS] [CrossRef] [Google Scholar]
- Berg, D. A., Erb, D. K., Auger, M. W., Pettini, M., & Brammer, G. B. 2018, ApJ, 859, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Béthermin, M., Fudamoto, Y., Ginolfi, M., et al. 2020, A&A, 643, A2 [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwens, R. J., Aravena, M., Decarli, R., et al. 2016, ApJ, 833, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P. L., Carilli, C., Jones, G., et al. 2015, Nature, 522, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Carniani, S., Maiolino, R., Pallottini, A., et al. 2017, A&A, 605, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carniani, S., Maiolino, R., Amorin, R., et al. 2018, MNRAS, 478, 1170 [NASA ADS] [CrossRef] [Google Scholar]
- Carniani, S., Ferrara, A., Maiolino, R., et al. 2020, MNRAS, 499, 5136 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Cormier, D., Madden, S. C., Lebouteiller, V., et al. 2015, A&A, 578, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Breuck, C., Neri, R., Morganti, R., et al. 2003, A&A, 401, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Looze, I., Cormier, D., Lebouteiller, V., et al. 2014, A&A, 568, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dunlop, J. S., McLure, R. J., Biggs, A. D., et al. 2017, MNRAS, 466, 861 [Google Scholar]
- Eldridge, J. J., & Stanway, E. R. 2012, MNRAS, 419, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Faisst, A. L., Schaerer, D., Lemaux, B. C., et al. 2020, ApJS, 247, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Finkelstein, S. L., Ryan, R. E., Papovich, C., et al. 2015, ApJ, 810, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Fudamoto, Y., Oesch, P. A., Faisst, A., et al. 2020, A&A, 643, A4 [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giavalisco, M., Ferguson, H. C., Koekemoer, A. M., et al. 2004, ApJ, 600, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Grogin, N. A., Kocevski, D. D., Faber, S. M., et al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y., Ferguson, H. C., Giavalisco, M., et al. 2013, ApJS, 207, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Harikane, Y., Ouchi, M., Shibuya, T., et al. 2018, ApJ, 859, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Harikane, Y., Ouchi, M., Inoue, A. K., et al. 2020, ApJ, 896, 93 [Google Scholar]
- Hashimoto, T., Laporte, N., Mawatari, K., et al. 2018, Nature, 557, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Hashimoto, T., Inoue, A. K., Mawatari, K., et al. 2019a, PASJ, 71, 71 [Google Scholar]
- Hashimoto, T., Inoue, A. K., Tamura, Y., et al. 2019b, PASJ, 71, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A. K. 2011, MNRAS, 415, 2920 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A. K., Shimizu, I., Iwata, I., & Tanaka, M. 2014a, MNRAS, 442, 1805 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A. K., Shimizu, I., Tamura, Y., et al. 2014b, ApJ, 780, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A. K., Tamura, Y., Matsuo, H., et al. 2016, Science, 352, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, H., Galligan, T. P., Kimm, T., et al. 2019, MNRAS, 487, 5902 [NASA ADS] [CrossRef] [Google Scholar]
- Kawamata, R., Oguri, M., Ishigaki, M., Shimasaku, K., & Ouchi, M. 2016, ApJ, 819, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Kehrig, C., Vílchez, J. M., Pérez-Montero, E., et al. 2015, ApJ, 801, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Kehrig, C., Vílchez, J. M., Guerrero, M. A., et al. 2018, MNRAS, 480, 1081 [NASA ADS] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Knudsen, K. K., Watson, D., Frayer, D., et al. 2017, MNRAS, 466, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Kohandel, M., Pallottini, A., Ferrara, A., et al. 2019, MNRAS, 487, 3007 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Laporte, N., Ellis, R. S., Boone, F., et al. 2017, ApJ, 837, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Béthermin, M., Faisst, A., et al. 2020, A&A, 643, A1 [CrossRef] [EDP Sciences] [Google Scholar]
- Madden, S. C., Rémy-Ruyer, A., Galametz, M., et al. 2013, PASP, 125, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Carniani, S., Fontana, A., et al. 2015, MNRAS, 452, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Marrone, D. P., Spilker, J. S., Hayward, C. C., et al. 2018, Nature, 553, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Matthee, J., Sobral, D., Boogaard, L. A., et al. 2019, ApJ, 881, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Mawatari, K., Inoue, A. K., Hashimoto, T., et al. 2020, ApJ, 889, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Nagao, T., Maiolino, R., Marconi, A., & Matsuhara, H. 2011, A&A, 526, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Novak, M., Bañados, E., Decarli, R., et al. 2019, ApJ, 881, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Ochsenbein, F., Bauer, P., & Marcout, J. 2000, A&AS, 143, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Ono, Y., Ouchi, M., Shimasaku, K., et al. 2010, ApJ, 724, 1524 [NASA ADS] [CrossRef] [Google Scholar]
- Ota, K., Walter, F., Ohta, K., et al. 2014, ApJ, 792, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Ellis, R., Ono, Y., et al. 2013, ApJ, 778, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Pentericci, L., Carniani, S., Castellano, M., et al. 2016, ApJ, 829, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira-Santaella, M., Rigopoulou, D., Farrah, D., Lebouteiller, V., & Li, J. 2017, MNRAS, 470, 1218 [NASA ADS] [CrossRef] [Google Scholar]
- Pontoppidan, K. M., Pickering, T. E., Laidler, V. G., et al. 2016, in Observatory Operations: Strategies, Processes, and Systems VI, SPIE Conf. Ser., 9910, 991016 [Google Scholar]
- Raiter, A., Schaerer, D., & Fosbury, R. A. E. 2010, A&A, 523, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reddy, N. A., Steidel, C. C., Fadda, D., et al. 2006, ApJ, 644, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Oesch, P. A., Bouwens, R. J., et al. 2018, ApJ, 853, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2013, A&A, 557, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieke, G. H., Alonso-Herrero, A., Weiner, B. J., et al. 2009, ApJ, 692, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T., & Bressert, E. 2012, APLpy: Astronomical Plotting Library in Python (Astrophysics Source Code Library) [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sault, R. J. 1994, A&AS, 107, 55 [NASA ADS] [Google Scholar]
- Schaerer, D. 2003, A&A, 397, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D., Boone, F., Zamojski, M., et al. 2015, A&A, 574, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D., Fragos, T., & Izotov, Y. I. 2019, A&A, 622, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D., Ginolfi, M., Béthermin, M., et al. 2020, A&A, 643, A3 [CrossRef] [EDP Sciences] [Google Scholar]
- Senchyna, P., Stark, D. P., Vidal-García, A., et al. 2017, MNRAS, 472, 2608 [NASA ADS] [CrossRef] [Google Scholar]
- Senchyna, P., Stark, D. P., Mirocha, J., et al. 2020, MNRAS, 494, 941 [NASA ADS] [CrossRef] [Google Scholar]
- Shimizu, I., Inoue, A. K., Okamoto, T., & Yoshida, N. 2016, MNRAS, 461, 3563 [CrossRef] [Google Scholar]
- Simpson, J. P. 1975, A&A, 39, 43 [NASA ADS] [Google Scholar]
- Song, M., Finkelstein, S. L., Livermore, R. C., et al. 2016, ApJ, 826, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Stanway, E. R., Eldridge, J. J., & Becker, G. D. 2016, MNRAS, 456, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Strom, A. L., Pettini, M., et al. 2016, ApJ, 826, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Tamura, Y., Mawatari, K., Hashimoto, T., et al. 2019, ApJ, 874, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Vallini, L., Gallerani, S., Ferrara, A., Pallottini, A., & Yue, B. 2015, ApJ, 813, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Vallini, L., Ferrara, A., Pallottini, A., & Gallerani, S. 2017, MNRAS, 467, 1300 [NASA ADS] [Google Scholar]
- Vanzella, E., Pentericci, L., Fontana, A., et al. 2011, ApJ, 730, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, F., Riechers, D., Novak, M., et al. 2018, ApJ, 869, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Ashas, M., Illingworth, G., et al. 2019, ApJS, 244, 16 [CrossRef] [Google Scholar]
- Zheng, W., Shu, X., Moustakas, J., et al. 2014, ApJ, 795, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, W., Zitrin, A., Infante, L., et al. 2017, ApJ, 836, 210 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Summary of properties of z7_GSD_3811 measured and derived using HST and ground-based imaging, ground-based spectroscopy, and ALMA observations.
Properties of the three selected SED-fitting solutions (see text) and their predicted line luminosities.
All Figures
 |
Fig. 1. ALMA observations drawn at (− 3, −2, −1, 1, 2, 3) × σ overlaid on the HST F160W image of z7_GSD_3811. The positive and negative contours are drawn with solid and dashed lines, respectively. The white hatched ellipse in the bottom of each frame shows the synthesized beam of ALMA. Top left: [O III] line contours for an image collapsed over 400 km s−1 around 391.63 GHz, where σ = 44 mJy km s−1 beam−1. Top right: [C II] line contours for an image collapsed over 400 km s−1 around 219.37 GHz, where σ = 19 mJy km s−1 beam−1. Bottom left: dust continuum contours at 87 μm, where σ = 26 μJy beam−1. Bottom right: dust continuum contours at 152 μm, where σ = 9.9 μJy beam−1. |
| In the text | |
 |
Fig. 2. [C II] (top) and [O III] (bottom) spectrum of z7_GSD_3811 shown at a resolution of ≈21 km s−1 and ≈24 km s−1, respectively. The spectra have been extracted in circular apertures with areas approximately equal to the beam areas. The horizontal axis shows the velocity relative to Lyα and the dashed lines show the 1σ noise level obtained by randomly placing a large number of apertures over the image and adopting the variation in the flux as the noise. |
| In the text | |
 |
Fig. 3. [C II] 158 μm luminosity versus the UV+IR SFR. The yellow star shows the upper limit of z7_GSD_3811 assuming a line-width of 100 km s−1, while the dash and arrow show the upper limit obtained if we assume a line-width of 400 km s−1. The pink line and orange dashed line show the relation for local HII/starburst galaxies and metal-poor dwarf galaxies by De Looze et al. (2014), where the shaded regions correspond to the 1σ dispersion in the relations. The dotted and dash-dotted lines show the relations from the ALPINE-ALMA survey, derived by Schaerer et al. (2020, see text). The dark gray circles show objects from the compilation by Matthee et al. (2019) with z > 6. For BDF-3299 and SXDF-NB1006-2, we show updated [C II] measurement from Carniani et al. (2020). For this sample, we have rescaled the upper limits to line-widths of 100 km s−1. A few galaxies from the compilation that are also detected in [O III] are indicated by their names and a lighter gray color. All upper limits are at the 3σ level. |
| In the text | |
 |
Fig. 4. Relation between the IR-to-UV luminosity ratio (IRX) and the UV slope β. The yellow star shows the upper limit on the IRX calculated from the band 6 observations z7_GSD_3811. We also show the IRX and UV slopes of galaxies from the compilation of Matthee et al. (2019, dark gray circles). IRX values are calculated under the assumption of a dust temperature of 45 K and a dust emissivity index of βd = 1.5. The solid and dashed line represent the Calzetti and SMC dust laws calculated following Bouwens et al. (2016). The dotted line shows the IRX-β relation from the ALPINE-ALMA survey data, derived by Fudamoto et al. (2020, see text). Galaxies from the Matthee et al. (2019) compilation that are also detected in [O III] are indicated by their names and a lighter gray color. Upper limits on the IRX are at the 3σ level. |
| In the text | |
 |
Fig. 5. [O III] to UV luminosity ratio shown as a function of the UV luminosity. The yellow star shows the upper limit on the [O III] luminosity in z7_GSD_3811 assuming a line-width of 100 km s−1, while the dash and arrow show the corresponding upper limit assuming a line-width of 400 km s−1. The gray circles show [O III]-detected objects at z > 7 (Inoue et al. 2016; Laporte et al. 2017; Carniani et al. 2017; Hashimoto et al. 2018, 2019a; Tamura et al. 2019; Harikane et al. 2020), while squares show the three recent detections by Harikane et al. (2020) at z ∼ 6. The UV luminosity has been calculated with lensing considered, however, the errors in the lensing magnification are not included in this figure. |
| In the text | |
 |
Fig. 6. [O III] to UV luminosity ratio (LO III/LUV) plotted against the oxygen abundance relative to the sun ([O/H] = log10(nO/nH)−log10(nO/nH)⊙). The hatched area shows the upper limit on z7_GSD_3811 based on our 3σ upper limit on the [O III] assuming a line-width of 100 km s−1, while the yellow line shows the corresponding value if we assume a four times wider line. The dark gray diamonds show local dwarf galaxies from Madden et al. (2013), De Looze et al. (2014), and Cormier et al. (2015) compiled by Inoue et al. (2016). |
| In the text | |
 |
Fig. 7. PANHIT SEDs of three selected models with ages < 0.3 Gyr (see text). The yellow line shows an old (0.29 Gyr), low-metallicity (Z = 0.0004) model (Low Z), the pink line shows a model with the same age but high metallicity (Z = 0.02 ; High Z) and the blue line shows a young, low-metallicity model (Young; Age = 2 Myr, Z = 0.0001). The main panel shows the spectrum in the rest-frame UV and optical, with upper limits and measured photometry from HST and VLT/HAWK-I. The small panels show our ALMA upper limits on the dust continuum (top panel) and the [O III] emission line (bottom panel). Upper limits are at the 3σ level and are indicated with arrows. We note that the dust-continuum fluxes of the three models (crosses) overlap in the top panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


