EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 643 (November 2020) A&A, 643 (2020) A52 Full HTML
Free Access
Issue
A&A
Volume 643, November 2020
Article Number A52
Number of page(s) 11
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202037886
Published online 02 November 2020

© ESO 2020

1 Introduction

The supermassive black hole (SMBH) Sgr A* that today lies in the center of our Galaxy, is a low-luminosity, X-ray dim (LX ~ 2 × 1033 erg s−1, Baganoff et al. 2001) galactic nucleus. Nonetheless, some observed phenomena in the Galactic center (GC) region are explained by past more luminous phases of Sgr A* (see Ponti et al. 2013, for a review). For instance, the huge gamma-ray bubble that Fermi-LAT observed 10 kpc above and below the GC may be the remnant of an active phase of Sgr A* a few million years ago (Su et al. 2010; Zubovas et al. 2011). Determining the history of the activity of our Galactic nucleus would allow us to assess the duty cycle of mass accretion of the SMBH (e.g., Park & Ricotti 2012) and thus provide unique insight into the coevolution of the SMBH and galaxies (Di Matteo et al. 2008).

The quest of reconstructing the history of Sgr A* has motivated the interest in characterizing the central molecular zone (CMZ, Morris & Serabyn 1996), the ~100 pc extended region around Sgr A*. The CMZ hosts several molecular cloud complexes (e.g., Sgr A, Sgr B, and Sgr C) that are visible, for instance, in the thermal far-infrared images obtained with the Herschel satellite (Molinari et al. 2011). Interestingly, the physical conditions in the CMZ inferred from infrared observations (i.e., the geometrical size, column density, and gas dynamics) are reminiscent of an AGN torus (Ramos Almeida & Ricci 2017).

The molecular gas in the CMZ is also traced by X-ray reflection spectral features, such as a prominent Fe Kα line and a reflection continuum (Ponti et al. 2013). The lack of X-ray bright sources nearby led Sunyaev et al. (1993) to suggest that the observed emission is the echo of an outburst of Sgr A* that occurred a few hundred years ago and reached a peak luminosity of 1039−40 erg s−1. According to this scenario, the reflected radiation is still visible because of the delay induced by the light travel time between Sgr A* and the clouds in the CMZ.

We sketch two possible scattering geometries of an individual cloud located in front or behind the Sgr A* plane in Fig. 1. Hereafter, we indicate with dproj the distance between the cloud and Sgr A* projected on the plane of the sky, with dlos the line-of-sight displacement of the cloud with respect to the Sgr A* plane, and θ the scattering angle. In addition, c is the speed of light and tlight the light travel time between Sgr A* and the cloud. The two positions depicted in Fig. 1 result in the same effective scattering.

The hypothesis of a previous Sgr A* outburst is appealing because it implies that the X-ray variability of the CMZ is a fossil memory of how our Galactic nucleus acted a few hundred years ago (Muno et al. 2007). Over the years, great effort has been devoted to reconstructing the past light curve of Sgr A* using X-ray spectral, timing, and imaging techniques (Koyama et al. 1996; Murakami et al. 2001). A single-outburst scenario (Ponti et al. 2010), a two-burst scenario (Clavel et al. 2013), and a number of short-lived events (Terrier et al. 2018) have been suggested to explain the data. These flares may be superposed to a long-term high state of Sgr A* (Ryu et al. 2013).

The main source of uncertainty in these studies is that dlos is poorly constrained, which makes it difficult toinfer the time delay tlight and the number of illuminating events. So far, two methods have been used to overcome this problem. Some works searched for correlating variations in multiple regions throughout the CMZ, which provides indications on the number and nature of the illuminatingevents (Clavel et al. 2013; Churazov et al. 2017; Terrier et al. 2018). Conversely, other authors have attempted to derive the line-of-sight positions of individual clumps from a detailed modeling of the iron line and of the reflection continuum (Capelli et al. 2012; Walls et al. 2016; Chuard et al. 2018). These reflection models assume a geometry in which the illuminatingsource is in Sgr A*, which is still debated. Although disfavored as an explanation for the steady part of the emission, alternative sources of illumination, such as cosmic rays from a local source penetrating the clouds (Yusef-Zadeh et al. 2013; Dogiel et al. 2014), are not conclusively ruled out by current data (Mori et al. 2015; Zhang et al. 2015).

An independent way to address these ambiguities is provided by X-ray polarimetry. The reflected emission from a compact illuminating, source is linearly polarized by scattering in the absence of depolarizing agent. The expected polarization angle is normal to the scattering plane and therefore carries clean information of the direction of the illuminating source. The expected polarization degree P depends on the scattering angle θ (McMaster 1961) by 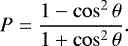(1)

Thus, a measurement of the polarization degree of a molecular cloud allows us to determine dlos because according to the geometry of Fig. 1, 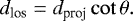(2)

The remaining ambiguity of whether dlos is positive or negative can be broken, for instance, using spectral information (i.e., the dependence of the equivalent width of the iron line on the scattering angle and iron abundances, see Churazov et al. 2017). An X-ray polarization study of the molecular clouds in the GC has the potential of addressing the critical uncertainties that still hamper a full understanding of the origin of the reflection of the nebulae in the GC (Churazov et al. 2002; Marin et al. 2014, 2015; Churazov et al. 2017).

A physical limit of this experiment is the fact that the molecular clouds are embedded in the diffuse unpolarized emission of the GC region (Koyama et al. 1989; Sidoli et al. 1999). In addition to the X-ray reflection from the molecular clouds, the 2–8 keV emission in the GC region comprises the contribution of two diffuse emission components (see Ponti et al. 2013, and references therein) that hereafter we call soft and hard plasma. The soft plasma is traced by the Si XII, Si XIII, S XV, and Ar XVII lines, for example. They are ascribed to a ~1 keV, collisionall-ionized plasma that pervades the GC region and can be sustained by the supernova activity in the region. Conversely, hard plasma is traced by a Fe XXV–Heα line emission at ~6.7 keV that morphologically peaks in the central degree. This component is often modeled as ~6.5 keV thermal plasma. At least a part of it may be ascribed to unresolved point sources such as accreting white dwarf and coronally active stars (Revnivtsev et al. 2007; Yuasa et al. 2012). The remaining emission might be associated with truly diffuse hot gas, possibly originating from supernova remnants.

Because of the complexity of the diffuse emission in the GC region, the synergy between polarimetric and imaging capabilities is a crucial asset for this study because it allows us to resolve the faint molecular clouds from the diffuse emission in the background.The NASA/ASI Imaging X-ray Polarimetry Explorer (IXPE, Weisskopf et al. 2016) that will be launched in 2021 is the first mission that is entirely dedicated to X-ray polarimetry through imaging-capable detectors (i.e., gas pixel detector, GPD, Costa et al. 2001) in the 2–8 keV band, and it will offer the first opportunity to investigate the X-ray polarization of the GC region. The Enhanced X-ray Timing and Polarimetry mission (eXTP, Zhang et al. 2019), which is planned to launch in 2027, will also carry a GPD polarimeter. The effective area of eXTP is expected to be larger by a factor ~4 than that of IXPE, and will therefore allow enlarging the pool of suitable targets.

We evaluate the detectability of the X-ray polarization predicted for the molecular clouds in the GC region by Marin et al. (2015). We simulate IXPE observations of individual candidate targets. With the aid of Chandra maps and spectra, we consider (when possible) the polarization, spectral, and spatial properties of all the emission components (i.e., the cloud, soft plasma, and hard plasma) in each target field. Chandra images are most suitable for this work because the spatial resolution of Chandrais infinite from the IXPE point of view. In addition, we include a realistic model for the instrumental background and for the cosmic X-ray background (CXB). In this way, we are able to quantify how much the polarization degree of the molecular clouds is diluted in the unpolarized environmental radiation. In the ideal case of a detector with an infinite spatial resolution and zero background, the dilution factor is just the ratio between the reflection flux and the total flux (as in, e.g., Marin et al. 2015). In a real observation, the morphological smearing due to a finite point spread function (PSF) and the unpolarized background contribute to increasing the dilution. Our simulation strategy allows us to quantify this additional dilution as well.

Throughout this paper, we quantify the detectability of the polarization by computing the minimum detectable polarization (MDP). The MDP (Weisskopf et al. 2010) is the fundamental quantity for the statistical significance of an X-ray polarization measurement and is defined as 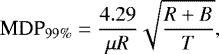(3)

where R is the detected source rate (in counts s−1), B is the background rate, T is the observation time (in seconds), and μ is the adimensional modulation factor of the detector. The MDP99% is not the uncertainty of the polarization measurement, but rather the degree of polarization that can be determined with a 99% probability against the null hypothesis.

The paper is organized as follows. In Sect. 2 we describe the selection and preparation of the Chandra data, and in Sect. 3 we present our simulation procedure. Finally, in Sect. 4 we discuss the results, and in Sect. 5 we summarize our conclusions.

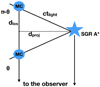thumbnail Fig. 1

Scattering geometry for a molecular cloud located in front or behind the Sgr A* plane. The two positions result in the same effective scattering and polarization degree. In this scheme, dproj is the cloud-Sgr A* distance projected in the plane of the sky, dlos is theline-of-sight displacement of the cloud with respect to the Sgr A* plane, c is the speed of light, tlight is the light travel time between Sgr A* and the cloud, θ and π − θ are the two possible scattering angles.

2 Chandra data preparation

2.1 Chandra data selection

We consider as candidate targets for an X-ray polarimetry observation the molecular clouds for which Marin et al. (2015) computed the polarization properties expected in a theoretical scenario where the source of illumination is a past unpolarized outburst of Sgr A*. The molecular clouds MC1, MC2, Bridge-D, Bridge-E, Bridge-B2 and G0.11-0.11 belong to the Sgr A complex. The Sgr B complex comprises two substructures named Sgr B1 and Sgr B2. Conversely, the clouds Sgr C1, Sgr C2, and Sgr C3 are substructures of the Sgr C complex.

The morphology of the molecular clouds is known from extensive Chandra and XMM-Newton observational campaigns that were carried out in the past 20 yr. The extension of the clouds (see, e.g., Terrier et al. 2018) is typically larger than the nominal PSF of IXPE (which has a radius of ~10″). Furthermore, the diffuse plasma in which the clouds are embedded has an inhomogeneous morphology. In some of the simulations that follow, we therefore use Chandra maps to define the extended spatial morphology of the cloud and the soft and hard plasma component. Moreover, Chandra spectra are used to input the spectral shape of each emission component.

As a first step in the preparation of the IXPE simulations, we retrieved from the public archive the Chandra observations of the Sgr A, Sgr B, and Sgr C complexes. We selected in the archive all the Chandra ACIS-I observations that were taken since 1999 without any gratings in place.

For the Sgr A field, the total Chandra exposure time is ~2.4 Ms. Owing to the superior quality of this dataset, we were able to compute Chandra images of the cloud and the soft and hard plasma in this region (Sect. 2.2). The Chandra field of Sgr B comprises only Sgr B2, and no Chandra observationsinclude Sgr B1, which is therefore excluded from our analysis. The Chandra field of Sgr C comprises Sgr C1 and Sgr C2, and Sgr C3 is included in Chandra Obs-ID 7040. For the Sgr B and Sgr C region the total exposure time of the data available in the Chandra archive is insufficient to produce sensible maps of the emission components separately. For these clouds we therefore use the most recent available Chandra observation for the spectral analysis (Sect. 2.4). We list in Table A.1 all the Chandra observations that we used.

2.2 Chandra maps of the Sgr A field

We processed the Chandra data using the CIAO software (Fruscione et al. 2006), version 4.11, in combination with version 4.8.2 of the Chandra calibration database (CALDB). For each observation, we ran the Chandra_repro routine to create the clean level 2event file. Hence, for the Sgr A region, we created background and continuum-subtracted counts maps of the soft and hard plasma, and the clouds. For all the images, we kept the native ACIS pixel size (i.e., ~0.5″).

We proceeded as follows. For each observation, we created the background event-file using the blank-sky event files that are provided in the Chandra CALDB. For this, we used the blanksky CIAO routine, which customizes a blanksky background file for the input event file, finding the instrument-specific background files in the CALDB and combining and reprojecting them to match the input coordinates.

For each observation we ran the blanksky-image script to create background-subtracted Chandra count maps of each emission component. For the soft plasma, we created a map in the 2.35–3.22 keV energy band, which comprises the S XV and Ar XVII emission lines. For the hard plasma, we created a map centered on the Fe XXV–Heα line (6.62–6.78 keV). The morphology of the molecular gas is given by a Chandra map centered on the Fe–Kα line (6.32–6.48 keV). Finally, for the continuum we used the 4.0–6.32 keV band (e.g., Clavel et al. 2013), which is line free.

For each emission component, we merged as a final step all the images using the CIAO script reproject_image_grid routine, which reprojects all the input images to a common coordinates grid. Using the spectra of the four targets that we selected for the simulations (see the following Sect. 2.3 and Sect. 2.4), we found that a model including an absorbed power law and a 1 keV brehmsstrahlung component adequately interpolate the continuum spectral shape that underlies the S XV, Ar XVII, Fe XXV–Heα, and Fe-Kα line. By averaging the results of this continuum model for the four targets of interest, we derived the scaling factors (0.38, 0.10, and 0.09 for the soft and hard plasma, and the cloud band, respectively) that we used to rescale the continuum images in the band of each emission component. Thus, these scaling factors were optimized for the regions we used the simulations that followed. The final images of each emission component were obtained by subtracting the rescaled continuum count-maps from the signal count maps. We normalized all the maps by dividing by the maximum value. We display the final background- and continuum-subtracted maps of the three emission components in Fig. 2.

2.3 Target identification in the Sgr A field and Chandra maps of individual targets

We searched for the targets analyzed in Marin et al. (2015) in the background- and continuum-subtracted Fe Kα map of the Sgr A field (Fig. 2, first panel). We excluded from our search and thus from the IXPE simulations MC1 and the Bridge D cloud because they are predicted to be basically unpolarized. We identified MC 2, Bridge B2, Bridge E, and G0.11-0.11, which are displayed as circular regions in Fig. 2. In Table 1, we list the central coordinates, the radius, and the projected distance from Sgr A* of each cloud. The cloud sizes are the same of Marin et al. (2015). As a final step in the preparation of the maps for the simulations of the MC2, Bridge B2, Bridge E, and G0.11-0.11 clouds, we created for each emission component smaller Chandra maps cut in the region of interest (i.e., the region listed in Table 1). This is because we simulated IXPE observations of each target individually and on axis. We note, however, that the IXPE field of view is 9′ in radius, and thus a single IXPE pointing of the Sgr A field will catch more than one target. A simulation mapping the entire IXPE field of view will be presented in a future expansion of this work. Here, we simulate each cloud individually, with the aim of collecting useful information in order to decide the best target for a pointing.

We centered each map on the brightest Fe Kα patch. Because the morphology of the clouds varies with time, these coordinates are shifted with respect to those used in Marin et al. (2015). This does not affect the expected polarization degree because it depends mainly on the galactic depth (Eq. (1)). The expected polarization angle may be affected, but changes are expected to be less than one degree (F. Marin, private communication).

In the case of Sgr B1, Sgr C1, Sgr C2, and Sgr C3, we were unable to create the Fe–Kα map to search for the cloud positions. For these clouds we therefore used the same regions as Marin et al. (2015) to extract the spectra from the most recent Chandra observations. The regions used for Sgr B2, Sgr C1, Sgr C2, and Sgr C3 are also listed in Table 1.

Finally, we list in Table 1 all the other cloud data that we input in the IXPE simulations, that is, the polarization degrees and angle resulting from the model of Marin et al. (2015) that were computed assuming a position dlos along the line of sight of the clouds. The assumed distance is the key parameter determining the polarization degree and hence the IXPE detectability. We explore the effect of the assumed distances for our simulations in Sect. 4.

thumbnail Fig. 2

From left to right: background- and continuum-subtracted Chandra maps of the cloud, hard plasma, and soft plasma component in the Sgr A region. Images are smoothed using a 3-pixel Gaussian kernel. The color bar displayed at the bottom has adimensional units because the images are normalized to the maximum value. The regions comprising the targets selected for IXPE simulations (i.e., MC2, Bridge-B2, Bridge-E, and G0.11-0.11) are shown. In the first panel, a circle withthe size of the IXPE PSF is shown for comparison. The direction of Sgr A* is indicated with an arrow.
Table 1

Input data for IXPE simulations of molecular clouds.

2.4 Chandra spectral analysis

The last necessary ingredient for simulating IXPE observations of the selected targets is the spectral shape of each emission component. For all the regions listed in Table 1, we extracted the spectrum from the most recent available Chandra observation. These are highlighted in bold in Table A.1. We confirmed that the extraction regions include no contamination of known bright X-ray sources (listed in, e.g., Terrier et al. 2018).

To extract the spectra, we used the CIAO script specxtract, which creates the source and background spectra and the necessary weighted response matrices. We used the customized blank-sky event file to extract the background spectrum in the same region. We binned the spectra requiring that a minimum of 30 counts is reached in each spectral bin.

We fit all the spectra in the 2.0–8.0 keV band with Xspec version 12.10.1. We used a model including the Galactic absorption, the soft and hard plasma, and the cloud emission. For the Galactic absorption, we used the phabs model, with the hydrogen column density NH as a free parameter. For the plasma components, we used a collisionally ionized plasma model (APEC, Smith et al. 2001)with a temperature set to 1.0 and 6.5 keV for the soft and hard plasma, respectively. We considered solar abundances and set the redshift to zero. For the molecular clouds, we used the neutral reflection PEXMON model (Nandra et al. 2007), where we set (as in, e.g., Ponti et al. 2010) the photon index Γ to 2, the disk inclination to 60°, and the cutoff energy to 150 keV. The free parameters of our fits are therefore the Galactic NH and the normalization of each emission component. We show the spectra of all the clouds in Fig. 3. We list the parameters and errors resulting from our spectral analysis in Table 2. All the spectral fits are statistically acceptable (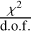 ≤ 1.3).

3 Simulation of IXPE observations

We simulated IXPE observations of the targets listed in Table 1 using the dedicated simulation framework ixpeobssim (Pesce-Rollins et al. 2019). This is a python-based tool that can be fed by an arbitrary source model, including morphological, temporal, spectral, and polarimetric information. Hence, the framework uses the IXPE instrument response functions (i.e., the PSF and the detector effective area) to produce the IXPE-simulated event files. These can be used to create images, spectra, and modulation curves in different bands.

For each target, we performed the simulation in the region listed in Table 1 and centered the field of viewon the coordinates of the target. Within the regions of interest, we simulated all the components that contribute to the diffuse X-ray emission. In addition to the polarized emission of the molecular clouds, we thus included the soft and hard plasma, the cosmic X-ray background, and the instrumental background in our simulations. For each emission component, we input in the simulation the spectrum, the polarization degree, the polarization position angle, and when possible, the spatial morphology. We took the polarization degree and polarization angle of each molecular cloud from the model of Marin et al. (2015), as listed in Table 1. We considered a polarization degree that is constant with energy, but null at the energy of the fluorescence Fe Kα line (6.32–6.48 keV). The fluorescent lines from spherically symmetrical orbitals are unpolarized. Conversely, for the plasma components, we considered a null polarization. In the case of MC2, Bridge-B2, Bridge-E, and G0.11-0.11 we were able to input in the simulator the real morphology of the hard and soft plasma and of the clouds using the Chandra maps described in Sect. 2.3. In the case of the clouds in the Sgr B and Sgr C region, the Chandra data quality did not allow us to compute separate maps of each emission component. We therefore assumed a uniform morphology of all the components in the region of interest for these clouds.

For both the instrumental and the sky background we simulated a null polarization. The internal polarization of the detector is below 1% and thus negligible. For the instrumental background, we took the spectrum from the measurement of the non-X-ray background of the neon-filled detector that flew on board of OSO-8 (Bunner 1978). The gas mixture and absorption coefficient of the OSO-8 detector were similar to the one of the IXPE GPD. For the instrumental background, we simulated a uniform morphology on the detector. In the simulation, the instrumental background is internal to the detector, thus it is not convolved with the instrumental response functions. Finally, for the sky background, we used the parameters of the CXB spectrum of Moretti et al. (2009), and we renormalized it to match the simulated sky area. We simulated it as a sky source with a uniform morphology.

Table 2

Results of the spectral analysis of the molecular clouds described in Sect. 2.4.

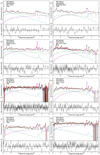thumbnail Fig. 3

From top to bottom: unfolded spectra and residuals to the best-fit model for MC2, Bridge B2, Bridge E, G0.11-0.11, Sgr B2, Sgr C1, Sgr C2, and Sgr C3. The total best-fit model and the reflection component are displayed as a solid line. The spectrum of the hard plasma is displayed as a dashed line. The spectrum of the soft plasma is displayed as a dotted line.
Table 3

Simulations results for the reflection nebulae.

4 Results and discussion

Using the input ingredients described in Sect. 2 and the procedure described in Sect. 3, we simulated IXPE observations of all the targets. We extracted two main quantities from the simulations: the degree to which polarization is diluted by the ambient and background radiation, and which MDP can be reached in a realistic exposure time. These pieces of information serve to evaluate the detectability of the considered targets in an X-ray polarimetric study of the GC.

In order to obtain a sensible measurement of the diluted polarization degree, we proceeded as follows. For all the targets, we ran mock simulations of observations reaching an MDP of at least 1%. Thus, the mock exposure time (i.e., 100 Ms) was chosen to obtain that the absolute error on the polarization degree is 1% or lower. This mimics an ideal case where the statistical uncertainty of the determined polarization degree is negligible. Any observed difference between the determined polarization degree and the theoretical one in these simulations must thus be caused by the mixing between polarized and unpolarized components. We note indeed that in simulations without unpolarized sources in the field of view, the theoretical polarization degree is always recovered within 3% or less when the MDP of the simulation is at least 1%.

In Table 3 we list the diluted polarization degrees resulting from the simulations and compare them with the scaled polarization degrees that result from a simple rescaling using the ratio between the reflection flux and thetotal flux (e.g., Marin et al. 2015). We consider that the scaled polarization degrees are affected by the uncertainty of the spectral decomposition. The ranges given in Table 3 are obtained as P ×(Fcloud ± eFcloud)∕Ftot, where Fcloud and eFcloud are the flux and error, respectively, for the cloudcomponent, Ftot is the total flux and P is the theoretical polarization degree. We observe that the diluted polarization degrees are in some cases lower than the scaled polarization degrees. This additional dilution must be induced by the morphological smearing of the source due to the finite PSF. We illustrate this point in Fig. 4. We ran 100 simulations of G0.11-0.11 for an ideal case of an instrument with infinite spatial resolution and zero background and 100 normal simulations, where the convolution with the instrumental PSF is considered. In this exercise, we considered a mock exposure time of 100 Ms, so that the statistical fluctuations of the simulated polarization degree were within 1%. In Fig. 4, we compare the distribution of the polarization degree obtained in the two cases. We found that an instrument with infinite spatial resolution would observe a polarization degree of ~21%, consistent with what ispredicted by a simple rescaling of the flux. An instrument with the spatial resolution of IXPE would observe an additional dilution of ~5%. This difference is not explained by the statistical fluctuations of the simulation result because that is by design lower than 1% in our simulations. In conclusion, our work shows that the finite spatial resolution of the polarimeter can add a sensible additional dilution depending on the extension and on the morphological details of the source. The quality of the imaging output plays a significant role for an X-ray polarimetric study of the GC region, where the polarized regions have to be resolved out of the surrounding unpolarized emission.

The diluted polarization degrees have to be compared with the MDP that can be achieved in a realistic exposure time. From our IXPE simulations, we computed the MDP in the 2.0–4.0 keV and 4.0–8.0 keV band by running realistic simulations with an exposure time of 2 Ms. We note that polarimetry is a photon- starving science and an exposure time of Megaseconds may be required for faint or lowly polarized sources (e.g., for extragalactic sources such as AGN). Even for bright Galactic sources or extragalactic blazars exposure times of some hundred kiloseconds are typically required.

From the MDP listed in Table 3 we can derive a first indication of the preferable targets for IXPE. We found that the most suitable energy band for searching for polarization signatures is the 4.0–8.0 keV band, where the emission of the molecular clouds dominates the flux output. This exercise indicates that the most promising targets for IXPE observation are G0.11-0.11 and Sgr B2. For these two targets, we found that the diluted polarization degree in the 4.0–8.0 keV band is higher than the MDP that can be reached in a 2 Ms long IXPE observation. Our simulations therefore confirm the preferable targets that were previously suggested by Marin et al. (2015).

However, some caveats must be considered in the planning of an X-ray polarimetric study of the GC. The first issue that we investigated is that the flux of the molecular clouds varies with time. The flux levels we considered are those of 2017 for MC2, Bridge B2, Bridge E, and G0.11-0.11; of 2010 for Sgr B2; of 2014 for Sgr C1 and Sgr C2; and of 2007 for Sgr C3. Our simulations indicate that at these flux levels, an IXPE observation of any of these targets will always be source dominated. For instance, we find that for the faintest target of the pools considered here (i.e., Sgr C3), the instrumental background accounts for 2% of the total counts, while the CXB accounts for 3% of the total counts. Nonetheless, by the time of the IXPE observation, the flux of the molecular clouds may be higher or lower than we considered here. In a recent study of the long-term flux variability of the molecular clouds, Terrier et al. (2018) found that MC2, G0.11-0.11, and Sgr B are fading while the Bridge is brightening up. The trend for Sgr C is more stable, although within a larger uncertainty. It is therefore useful to compute the minimum flux that would be detectable by IXPE in 2 Ms for each target with a signal-to-noise ratio of at least 3. Exploiting our estimates of the background contribution, we determined these flux thresholds and list them in Table 3. We found that the targets in the Sgr A field remain detectable unless the total flux decreases by one (e.g., for MC 2 and Bridge B2) or even two orders of magnitude (e.g., for Bridge E and G0.11-0.11) with respect to the level we considered here. In the case of Sgr B2, the total flux would need to be lower by a factor 3 with respect to the level observed in 2010 (i.e., 1.1 × 10−12 erg s−1 cm−2) to fall below the detection threshold.

In addition to the variability in flux, the molecular clouds in the GC also exhibit variability in morphology. For instance, the brightest centroid in Sgr C2 underwent a displacement of 1.6′ in 12 years (Terrier et al. 2018). We investigated the effect of the morphology for the result of our simulations. At first, we assessed the effect of positioning the simulated IXPE pointing well onto the brightest Fe Kα patch. We tested this issue using the 2 Ms long simulation of the Bridge-B2 cloud, which displays a well-defined bright knot. We find that shifting the IXPE pointing just ~20″ away from the brightest patch causes a loss of ~300 counts and decreases the MDP by 1%. This suggests that it is convenient to center the IXPE pointing on a bright knot in order to maximize the collected counts and thus the chance of detecting a significant polarization.

We therefore evaluated the effect of the morphology on determining the diluted polarization in the region of interest. In Fig. 5, we show as an example the simulated IXPE polarization maps of the two best targets. These were produced from the mock simulations. In these maps, the colored arrows indicate the direction of the polarization angle. In the case of a reflection nebula, this is normal to the projected direction of the illuminatingsource. In the simulated map of Sgr B2, the nebula is uniform in color/polarization degree because it was simulated assuming a uniform morphology for all the components. In the simulated map of G0.11-0.11, that was obtained by starting from the Chandra maps of the different components, and the irregular distribution of color/polarization degree within the nebula reflects the different level of mixing between polarized and unpolarized emission.

Nonetheless, the dilution of the polarization degree averaged over the regions of interest mildly depends on the internal morphology,likely because the substructures are one scale smaller than the IXPE PSF. We verified this point by running simulations of the G0.11-0.11 field assuming a uniform morphology for all the components and a mock exposure time of 100 Ms. The results for the diluted polarization degree are the same within the uncertainty as in the run using the Chandra maps. We are therefore a posteriori confident that our estimates of the polarization dilution in Sgr B2, Sgr C1, Sgr C2, and Sgr C3 are trustworthy.

All in all, we remark that an X-ray observation of the GC would be useful prior the IXPE pointing. With the Spectrum Röntgen Gamma (SRG) on board of eROSITA, for example, it is possible to measure the flux level of the candidate targets. With Chandra or XMM-Newton, it is possible to determine which patches are currently illuminated. This would help in deciding the best pointing.

Finally, in Table 4 we investigate the most critical uncertainty that affects the evaluation of the detectability of the polarization of the molecular cloud. The theoretical polarization degree relies on the poorly constrained line-of-sight distance of the cloud and will be corrected when a more robust determination of dlos is found. We searched in the literature for determinations of the line-of-sight distance of the clouds different from those assumed in Marin et al. (2015) (listed as 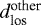in Table 4). These were obtained in works where the scattering angle is derived from modeling of the reflection spectrum (Capelli et al. 2012; Walls et al. 2016; Chuard et al. 2018) and were often loosely constrained. Starting from the range of 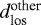, we used Eqs. (1) and (2) to compute the correspondent range of polarization degree (Pother), and we used the dilution factors in the 4.0–8.0 keV band that can be inferred from Table 3 to determine the corresponding range in diluted polarization degree (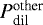). Thus, we were able to verify whether for a different assumption on dlos, the diluted polarization degree of our targets rises or drops below the MDP that can be obtained by IXPE in the 4.0–8.0 keV band in 2 Ms. The values listed in Table 4 confirm the detectability of G011-0.11 and Sgr B2 also for other possible distances reported in the literature. The molecular clouds Bridge B2, Bridge E, and Sgr C1 might be detectable if their real distance along the line of sight lies within the upper bound of the range determined by Capelli et al. (2012) and Chuard et al. (2018).

We also investigated how the enhanced sensitivity of eXTP allows enlarging the pool of suitable targets. The effective area of eXTP will be larger by a factor ~4, which implies (using Eq. (3)) that the MDP for the case of eXTP is lower than those of IXPE by a factor 0.51. When this factor is applied to the MDP values listed in Table 3, this implies that G0.11-0.11, Sgr B2, Sgr C1, Sgr C2, and Sgr C3 are potential targets for eXTP in the 4.0–8.0 keV band. The ranges of diluted polarization degrees obtained in Table 4 by relaxing the constraints on dlos offer a window of eXTP detectability for virtually all the targets. More sensitive telescopes, for instance, the X-ray Polarimetry Probe (XPP, Jahoda et al. 2019) or the New Generation X-ray Polarimeter (NGXRP, Soffitta et al. 2019) mission concept would allow detecting the X-ray polarization of the molecular clouds with shorter exposure times.

In conclusion, an X-ray polarimetric study of the CMZ is a challenging experiment because of the dynamic behavior of the reflection emission and because of the complex gaseous environment in which the nebulae are embedded. In this work, we set up a simulation method that allows realistically assessing how some critical factors (i.e., the variability in flux and morphology of the clouds, and the dilution of the polarization degree in the unpolarized ambient and background radiation) affect the detectability of a reflection nebula observed on axis. Nonetheless, other levels of complexity remain unexplored. In a future expansion of this work, we will produce a simulated IXPE map of the entire Sgr A field of view. This would allow us to investigate, for instance, how the detectability degrades for a nebula off axis and what happens in regions where gas filaments with a different level of polarization are mixed. Because the time required to make a significant measurement of the reflection nebulae in the GC is Megaseconds, the impact on the planning of IXPE observations is significant. Our realistic predictions are therefore important to inform the decision of including these observations in the planning.

thumbnail Fig. 4

Histograms showing the distribution of the polarization degree in the 4.0–8.0 keV band obtained by simulating the cloud G0.11-0.11 for different instrumental resolutions. The orange histogram shows the case with infinite spatial resolution. The blue histogram represents the case with IXPE resolution.
thumbnail Fig. 5

Simulated IXPE polarization maps of G0.11-0.11 (left panel) and Sgr B2 (right panel). The background is color-scaled according to the polarization degree. The colored arrows represent the direction of the polarization angle and are color-scaled accordingly. The color scales for the polarization degree and angle are shown at the right of each figure. The direction of Sgr A* is also indicated for comparison.
Table 4

Polarization obtained for alternative values of dlos reported in the literature.

5 Summary and conclusions

Measuring the X-ray polarization property of a reflection nebula in the GC allows us to confirm (or discard) that they are illuminated by a past outburst of Sgr A* (through the polarization angle) and to determine the position of the nebula along the line of sight (through the polarization degree). These are critical uncertainties that hamper our ability of using the variability of the reflection emission to infer how our Galactic nucleus was behaving a few hundred years ago. Assessing the history of our Galactic nucleus has implications for our understanding of the duty cycle of mass accretion onto SMBH that is believed to drive to the coevolution of SMBH and galaxies.

We have evaluated the feasibility of this experiment with IXPE, which is expected to launch in 2021, and with eXTP, which is scheduled for launch in 2027. We simulated IXPE observations of the molecular clouds MC2, Bridge-B2, Bridge E, G0.11-0.11, Sgr B2, Sgr C1, Sgr C2 and, Sgr C3 considering the polarization properties predicted by the model of Marin et al. (2015). We used the Monte Carlo-based simulation tool ixpeobssim to individually simulate IXPE images of these targets. In our simulations, we considered the spectrum (using Chandra spectra), the polarization properties, and (when possible, using Chandra images) the spatial morphology of the molecular clouds and of the diffuse emission that is comprised in the region of interest. We modeled the diffuse emission of the GC using two thermal plasma components (Tsoft−plasma ~ 1 keV and Thard−plasma ~ 6.5 keV). Finally, we included in our simulations the instrumental background and the cosmic X-ray background. Our strategy is designed to estimate the degree to which the polarization degree of the clouds is diluted by the unpolarized ambient radiation and by the morphological smearing of the sources due to the instrumental PSF.

We determined for each cloud the minimum flux that would be detectable by IXPE in 2 Ms. We find that the molecular clouds considered here become undetectable when the total flux decreases by a factor 3–100 (depending on the cloud) with respect to the level considered here. Moreover, we found that the dilution of the polarization degree ranges between 0.3% and 23% in the 2.0−4.0 keV band and 19% and 55% in the 4.0–8.0 keV band. We note that the morphological smearing of the sources contributes additional dilution, whose value varies from cloud to cloud. The diluted polarization degree does not depend on the internal morphology of the gas in the region of interest.

For the flux levels we considered and the polarization degrees computed by Marin et al. (2015), the most promising targets for IXPE observations are G0.11-0.11 and Sgr B2. For these two cases, we found that the 4.0–8–0 keV polarization, even after being diluted by the surrounding plasma, is detectable by IXPE with a 2 Ms observation. However, the theoretical polarization degree strongly depends on the assumed position of the cloud along the line of sight. If the assumption on the distanceis relaxed within the range reported in the literature, a wider range of possible polarization degrees can be derived. If this is the case, then also Bridge-B2, Bridge-E, and Sgr C1 might be detectable by IXPE in 2 Ms.

Because its effective area is larger by a factor ~4 with the same exposure time, eXTP will be able to detect the 4.0–8.0 keV polarization degree predicted by Marin et al. (2015) of G0.11-0.11, Sgr B2, Sgr C1, Sgr C2, and Sgr C3. When a more relaxed constraint on the distance along the line of sight is considered, then all the targets considered here may be detectable by eXTP.

Acknowledgements

The Italian contribution to the IXPE mission is supported by the Italian Space Agency through agreements ASI-INAF n.2017-12-H.0 and ASI-INFN n.2017.13-H.0. FM acknowledges the support from the Programme National des Hautes Energies of CNRS/INSU with INP and IN2P3, co-funded by CEA and CNES. We thank Gabriele Ponti and Alessandra De Rosa for useful chats about the Chandra data analysis and the eXTP capability. We thank the anonymous referee for the helpful comments that improved this manuscript.

Appendix A Chandra analysis log

Table A.1

Log of the Chandra observations.

References

  1. Baganoff, F. K., Bautz, M. W., Brandt, W. N., et al. 2001, Nature, 413, 45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  2. Bunner, A. N. 1978, ApJ, 220, 261 [NASA ADS] [CrossRef] [Google Scholar]
  3. Capelli, R., Warwick, R. S., Porquet, D., Gillessen, S., & Predehl, P. 2012, A&A, 545, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Chuard, D., Terrier, R., Goldwurm, A., et al. 2018, A&A, 610, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Churazov, E., Sunyaev, R., & Sazonov, S. 2002, MNRAS, 330, 817 [NASA ADS] [CrossRef] [Google Scholar]
  6. Churazov, E., Khabibullin, I., Ponti, G., & Sunyaev, R. 2017, MNRAS, 468, 165 [NASA ADS] [CrossRef] [Google Scholar]
  7. Clavel, M., Terrier, R., Goldwurm, A., et al. 2013, A&A, 558, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Costa, E., Soffitta, P., Bellazzini, R., et al. 2001, Nature, 411, 662 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  9. Di Matteo, T., Colberg, J., Springel, V., Hernquist, L., & Sijacki, D. 2008, ApJ, 676, 33 [NASA ADS] [CrossRef] [Google Scholar]
  10. Dogiel, V. A., Chernyshov, D. O., Kiselev, A. M., & Cheng, K. S. 2014, Astropart. Phys., 54, 33 [CrossRef] [Google Scholar]
  11. Fruscione, A., McDowell, J. C., Allen, G. E., et al. 2006, CIAO: Chandra’s Data Analysis System, SPI Conf. Ser., 6270, 62701V [Google Scholar]
  12. Jahoda, K., Krawczynski, H., Kislat, F., et al. 2019, arXiv e-prints, [arXiv:1907.10190] [Google Scholar]
  13. Koyama, K., Awaki, H., Kunieda, H., Takano, S., & Tawara, Y. 1989, Nature, 339, 603 [NASA ADS] [CrossRef] [Google Scholar]
  14. Koyama, K., Maeda, Y., Sonobe, T., et al. 1996, PASJ, 48, 249 [NASA ADS] [CrossRef] [Google Scholar]
  15. Marin, F., Karas, V., Kunneriath, D., & Muleri, F. 2014, MNRAS, 441, 3170 [NASA ADS] [CrossRef] [Google Scholar]
  16. Marin, F., Muleri, F., Soffitta, P., Karas, V., & Kunneriath, D. 2015, A&A, 576, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. McMaster, W. H. 1961, Rev. Mod. Phys., 33, 8 [NASA ADS] [CrossRef] [Google Scholar]
  18. Molinari, S., Bally, J., Noriega-Crespo, A., et al. 2011, ApJ, 735, L33 [NASA ADS] [CrossRef] [Google Scholar]
  19. Moretti, A., Pagani, C., Cusumano, G., et al. 2009, A&A, 493, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Mori, K., Hailey, C. J., Krivonos, R., et al. 2015, ApJ, 814, 94 [NASA ADS] [CrossRef] [Google Scholar]
  21. Morris, M., & Serabyn, E. 1996, ARA&A, 34, 645 [NASA ADS] [CrossRef] [Google Scholar]
  22. Muno, M. P., Baganoff, F. K., Brandt, W. N., Park, S., & Morris, M. R. 2007, ApJ, 656, L69 [NASA ADS] [CrossRef] [Google Scholar]
  23. Murakami, H., Koyama, K., & Maeda, Y. 2001, ApJ, 558, 687 [NASA ADS] [CrossRef] [Google Scholar]
  24. Nandra, K., O’Neill, P. M., George, I. M., & Reeves, J. N. 2007, MNRAS, 382, 194 [NASA ADS] [CrossRef] [Google Scholar]
  25. Park, K., & Ricotti, M. 2012, ApJ, 747, 9 [CrossRef] [Google Scholar]
  26. Pesce-Rollins, M., Lalla, N. D., Omodei, N., & Baldini, L. 2019, Nucl. Instrum. Meth. Phys. Res. A, 936, 224 [Google Scholar]
  27. Ponti, G., Terrier, R., Goldwurm, A., Belanger, G., & Trap, G. 2010, ApJ, 714, 732 [NASA ADS] [CrossRef] [Google Scholar]
  28. Ponti, G., Morris, M. R., Terrier, R., & Goldwurm, A. 2013, in Cosmic Rays in Star-Forming Environments, eds. D. F. Torres, & O. Reimer, 34, 331 [NASA ADS] [CrossRef] [Google Scholar]
  29. Ramos Almeida, C., & Ricci, C. 2017, Nat. Astron., 1, 679 [Google Scholar]
  30. Revnivtsev, M., Vikhlinin, A., & Sazonov, S. 2007, A&A, 473, 857 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Ryu, S. G., Nobukawa, M., Nakashima, S., et al. 2013, PASJ, 65, 33 [NASA ADS] [CrossRef] [Google Scholar]
  32. Sidoli, L., Mereghetti, S., Israel, G. L., et al. 1999, ApJ, 525, 215 [NASA ADS] [CrossRef] [Google Scholar]
  33. Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [NASA ADS] [CrossRef] [Google Scholar]
  34. Soffitta, P., Bucciantini, N., Churazov, E., et al. 2019, ArXiv e-prints [arXiv:1910.10092] [Google Scholar]
  35. Su, M., Slatyer, T. R., & Finkbeiner, D. P. 2010, ApJ, 724, 1044 [NASA ADS] [CrossRef] [Google Scholar]
  36. Sunyaev, R. A., Markevitch, M., & Pavlinsky, M. 1993, ApJ, 407, 606 [NASA ADS] [CrossRef] [Google Scholar]
  37. Terrier, R., Clavel, M., Soldi, S., et al. 2018, A&A, 612, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Walls, M., Chernyakova, M., Terrier, R., & Goldwurm, A. 2016, MNRAS, 463, 2893 [NASA ADS] [CrossRef] [Google Scholar]
  39. Weisskopf, M. C., Elsner, R. F., & O’Dell, S. L. 2010, On Understanding the Figures of Merit for Detection and Measurement of X-ray Polarization, SPIE Conf. Ser., 7732, 77320E [Google Scholar]
  40. Weisskopf, M. C., Ramsey, B., O’Dell, S., et al. 2016, The Imaging X-ray Polarimetry Explorer (IXPE), SPIE Conf. Ser., 9905, 990517 [Google Scholar]
  41. Yuasa, T., Makishima, K., & Nakazawa, K. 2012, ApJ, 753, 129 [NASA ADS] [CrossRef] [Google Scholar]
  42. Yusef-Zadeh, F., Hewitt, J. W., Wardle, M., et al. 2013, ApJ, 762, 33 [NASA ADS] [CrossRef] [Google Scholar]
  43. Zhang, S., Hailey, C. J., Mori, K., et al. 2015, ApJ, 815, 132 [NASA ADS] [CrossRef] [Google Scholar]
  44. Zhang, S., Santangelo, A., Feroci, M., et al. 2019, Sci. China Phys. Mech. Astron., 62, 29502 [Google Scholar]
  45. Zubovas, K., King, A. R., & Nayakshin, S. 2011, MNRAS, 415, L21 [CrossRef] [Google Scholar]

All Tables

Table 1

Input data for IXPE simulations of molecular clouds.

In the text
Table 2

Results of the spectral analysis of the molecular clouds described in Sect. 2.4.

In the text
Table 3

Simulations results for the reflection nebulae.

In the text
Table 4

Polarization obtained for alternative values of dlos reported in the literature.

In the text
Table A.1

Log of the Chandra observations.

In the text

All Figures

thumbnail Fig. 1

Scattering geometry for a molecular cloud located in front or behind the Sgr A* plane. The two positions result in the same effective scattering and polarization degree. In this scheme, dproj is the cloud-Sgr A* distance projected in the plane of the sky, dlos is theline-of-sight displacement of the cloud with respect to the Sgr A* plane, c is the speed of light, tlight is the light travel time between Sgr A* and the cloud, θ and π − θ are the two possible scattering angles.
In the text
thumbnail Fig. 2

From left to right: background- and continuum-subtracted Chandra maps of the cloud, hard plasma, and soft plasma component in the Sgr A region. Images are smoothed using a 3-pixel Gaussian kernel. The color bar displayed at the bottom has adimensional units because the images are normalized to the maximum value. The regions comprising the targets selected for IXPE simulations (i.e., MC2, Bridge-B2, Bridge-E, and G0.11-0.11) are shown. In the first panel, a circle withthe size of the IXPE PSF is shown for comparison. The direction of Sgr A* is indicated with an arrow.
In the text
thumbnail Fig. 3

From top to bottom: unfolded spectra and residuals to the best-fit model for MC2, Bridge B2, Bridge E, G0.11-0.11, Sgr B2, Sgr C1, Sgr C2, and Sgr C3. The total best-fit model and the reflection component are displayed as a solid line. The spectrum of the hard plasma is displayed as a dashed line. The spectrum of the soft plasma is displayed as a dotted line.
In the text
thumbnail Fig. 4

Histograms showing the distribution of the polarization degree in the 4.0–8.0 keV band obtained by simulating the cloud G0.11-0.11 for different instrumental resolutions. The orange histogram shows the case with infinite spatial resolution. The blue histogram represents the case with IXPE resolution.
In the text
thumbnail Fig. 5

Simulated IXPE polarization maps of G0.11-0.11 (left panel) and Sgr B2 (right panel). The background is color-scaled according to the polarization degree. The colored arrows represent the direction of the polarization angle and are color-scaled accordingly. The color scales for the polarization degree and angle are shown at the right of each figure. The direction of Sgr A* is also indicated for comparison.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.