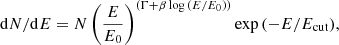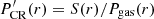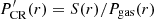| Issue |
A&A
Volume 642, October 2020
|
|
|---|---|---|
| Article Number | A190 | |
| Number of page(s) | 9 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201936896 | |
| Published online | 20 October 2020 | |
MAGIC observations of the diffuse γ-ray emission in the vicinity of the Galactic center⋆
1
Inst. de Astrofísica de Canarias, 38200 La Laguna, Spain
2
Universidad de La Laguna, Dpto. Astrofísica, 38206 La Laguna, Tenerife, Spain
3
Università di Udine and INFN Trieste, 33100 Udine, Italy
4
National Institute for Astrophysics (INAF), 00136 Rome, Italy
5
ETH Zurich, 8093 Zurich, Switzerland
6
Technische Universität Dortmund, 44221 Dortmund, Germany
7
Croatian Consortium: University of Rijeka, Department of Physics, 51000 Rijeka; University of Split – FESB, 21000 Split; University of Zagreb – FER, 10000 Zagreb; University of Osijek, 31000 Osijek; Rudjer Boskovic Institute, 10000 Zagreb, Croatia
8
Saha Institute of Nuclear Physics, HBNI, 1/AF Bidhannagar, Salt Lake, Sector-1, Kolkata 700064, India
9
Centro Brasileiro de Pesquisas Físicas (CBPF), 22290-180 URCA, Rio de Janeiro, RJ, Brasil
10
IPARCOS Institute and EMFTEL Department, Universidad Complutense de Madrid, 28040 Madrid, Spain
11
University of Łódź, Department of Astrophysics, 90236 Łódź, Poland
12
Università di Siena and INFN Pisa, 53100 Siena, Italy
13
Deutsches Elektronen-Synchrotron (DESY), 15738 Zeuthen, Germany
14
Istituto Nazionale Fisica Nucleare (INFN), 00044 Frascati, Roma, Italy
15
Max-Planck-Institut für Physik, 80805 München, Germany
16
Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology (BIST), 08193 Bellaterra, Barcelona, Spain
17
Università di Padova and INFN, 35131 Padova, Italy
18
Università di Pisa and INFN Pisa, 56126 Pisa, Italy
19
ICRANet-Armenia at NAS RA, 0019 Yerevan, Armenia
20
Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas, 28040 Madrid, Spain
21
Universität Würzburg, 97074 Würzburg, Germany
22
Finnish MAGIC Consortium: Finnish Centre of Astronomy with ESO (FINCA), University of Turku, 20014 Turku, Finland; Astronomy Research Unit, University of Oulu, 90014 Oulu, Finland
23
Departament de Física and CERES-IEEC, Universitat Autònoma de Barcelona, 08193 Bellaterra, Spain
24
Japanese MAGIC Consortium: ICRR, The University of Tokyo, 277-8582 Chiba, Japan; Department of Physics, Kyoto University, 606-8502 Kyoto, Japan; Tokai University, 259-1292 Kanagawa, Japan; RIKEN, 351-0198 Saitama, Japan
25
Inst. for Nucl. Research and Nucl. Energy, Bulgarian Academy of Sciences, 1784 Sofia, Bulgaria
26
Universitat de Barcelona, ICCUB, IEEC-UB, 08028 Barcelona, Spain
27
Port d’Informació Científica (PIC), 08193 Bellaterra, Barcelona, Spain
28
Dipartimento di Fisica, Università di Trieste, 34127 Trieste, Italy
29
INAF-Trieste and Dept. of Physics & Astronomy, University of Bologna, Bologna, Italy
Received:
11
October
2019
Accepted:
24
May
2020
Aims. In the presence of a sufficient amount of target material, γ-rays can be used as a tracer in the search for sources of Galactic cosmic rays (CRs). Here we present deep observations of the Galactic center (GC) region with the MAGIC telescopes and use them to infer the underlying CR distribution and to study the alleged PeV proton accelerator at the center of our Galaxy.
Methods. We used data from ≈100 h observations of the GC region conducted with the MAGIC telescopes over five years (from 2012 to 2017). Those were collected at high zenith angles (58−70 deg), leading to a larger energy threshold, but also an increased effective collection area compared to low zenith observations. Using recently developed software tools, we derived the instrument response and background models required for extracting the diffuse emission in the region. We used existing measurements of the gas distribution in the GC region to derive the underlying distribution of CRs. We present a discussion of the associated biases and limitations of such an approach.
Results. We obtain a significant detection for all four model components used to fit our data (Sgr A*, “Arc”, G0.9+0.1, and an extended component for the Galactic Ridge). We observe no significant difference between the γ-ray spectra of the immediate GC surroundings, which we model as a point source (Sgr A*) and the Galactic Ridge. The latter can be described as a power-law with index 2 and an exponential cut-off at around 20 TeV with the significance of the cut-off being only 2σ. The derived cosmic-ray profile hints to a peak at the GC position and with a measured profile index of 1.2 ± 0.3 is consistent with the 1/r radial distance scaling law, which supports the hypothesis of a CR accelerator at the GC. We argue that the measurements of this profile are presently limited by our knowledge of the gas distribution in the GC vicinity.
Key words: gamma rays: general / gamma rays: ISM / Galaxy: center / cosmic rays
Tables and sky maps are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/642/A190
© MAGIC Collaboration 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
The Galactic center (GC) is one of the most extraordinary regions in the very high energy (VHE, > 100 GeV) γ-ray sky, containing a rich variety of sources capable of accelerating charged particles and thereby producing VHE γ-ray emission (van Eldik 2015; Aharonian et al. 2006a; H.E.S.S. Collaboration 2006). If those γ-rays are produced in hadronic interactions, their sources may also contribute to the overall cosmic-ray “sea” filling the region with energized charged particles. This sea of cosmic rays (CRs) is believed to be responsible for the diffuse Galactic plane emission detected by EGRET (Hunter et al. 1997) and later studied by Fermi/LAT (Abdo et al. 2010), as well as the central γ-ray ridge detected with all major Imaging Atmospheric Cherenkov Telescopes (IACTs, H.E.S.S. Collaboration 2006; Archer et al. 2016; Ahnen et al. 2017a). The detected γ-rays originate primarily from deep inelastic nuclear interactions of the high-energetic particles with the surrounding gas, which can also be traced via its emission in the radio band (CS emission, Tsuboi et al. 1999; CO emission, Oka et al. 1998). Thus, deep γ-ray observations in the TeV energy range can be used to infer the underlying CR density, provided that the gas distribution is reliably measured.
This idea has been applied in earlier studies using observations of the central ≈ ± 1° region (in latitude) of the Galaxy (corresponding to ≈300 pc at a distance of 8.5 kpc) with the High Energy Stereoscopic System (H.E.S.S.), suggesting an inhomogeneous distribution of CRs around the GC (Aharonian et al. 2006b; H.E.S.S. Collaboration 2016, 2018). Furthermore, those data indicate that the central super-massive black hole of our Galaxy may itself accelerate particles to PeV (1015 eV) energies.
Observing the GC region with the MAGIC telescopes is only possible at large zenith distances (>58°), implying an increased optical thickness of the atmosphere and larger distance to the shower maximum, which leads to a stronger dilution of the Cherenkov light. On the other hand, for geometric reasons, these data benefit from an increased collection area (≈1 km2, Ahnen et al. 2017a) and, thus, a boost of sensitivity at energies above several TeVs.
Ahnen et al. (2017a) already presented the first part of the MAGIC GC observation campaign in 2012−2015, consisting of ≈70 h of exposure. Apart from the detection of multi-TeV emission from the Galactic plane, those data suggested the presence of a new VHE source close to the so-called radio “Arc” in the GC vicinity, detected also by other telescopes (Archer et al. 2016; H.E.S.S. Collaboration 2018). We continued observing the GC during 2015−2017, adding up to a total exposure time of ≈100 h. In addition, we employ the recently developed 2D likelihood analysis package SkyPrism (Vovk et al. 2018), which provides a more sensitive analysis of extended sources for MAGIC.
This paper is organized as follows. In Sect. 2, we describe the MAGIC observations, the data selection strategy, and the data analysis techniques. In Sect. 3, we provide a detailed description of the various analysis steps and report on their results. In Sect. 4, we estimate the biases, stemming from our background modeling and analysis approach. Finally, Sects. 5 and 6 provide a general discussion and a summary of the obtained results.
2. MAGIC observations of the Galactic center region
The Major Atmospheric Gamma Imaging Cherenkov (MAGIC) telescopes are two 17 m diameter IACTs, located at a distance of 85 m from each other at an altitude of 2200 m a.s.l. at the Roque de los Muchachos Observatory on the Canary Island of La Palma, Spain (28°N, 18°W).
The telescopes record flashes of Cherenkov light produced by extensive air showers (EAS) initiated in the upper atmosphere by γ-ray photons within a field of view of 1.5° (in radius). Both telescopes are operated together in a coincidence trigger stereoscopic mode, in which only events that simultaneously trigger both telescopes are recorded and analyzed (Aleksić et al. 2016). For low-zenith distance observations and for E > 220 GeV, the integral sensitivity of MAGIC is (0.66 ± 0.03)% in units of the Crab Nebula flux (C.U.) for 50 h of observation (Aleksić et al. 2016). At larger zenith angles (above 60°), at which the GC is observable at La Palma, the MAGIC collection area reaches 1 km2 at the energies above 10 TeV (Ahnen et al. 2017a).
MAGIC observations of the GC region which we used for this study were carried out between April 2012 and May 2017 (typically from March to July). The observation time after quality selection cuts is ≈100 h. The data were taken in the so-called “Wobble” mode (Fomin et al. 1994), centered on Sgr A* with a pointing offset of 0.4°.
The acquired data were processed with the standard MAGIC Analysis and Reconstruction Software (MARS, Zanin et al. 2013). The steps involved include the selection of good data quality periods, low-level processing of camera images, calculation of image parameters, and the reconstruction of the energy and incoming direction of the primary γ-rays. The last step is performed using the machine learning technique Random Forests (Albert et al. 2008), where Monte Carlo events and real background data are used for training. This technique is also used for background suppression through event classification.
At the quality selection step, we removed events corresponding to known temporary hardware issues or recorded during bad weather periods. As the full data sample contains some nights with weak moonlight, we also excluded time periods with sky brightness ≳2.5 times the typical dark night sky brightness. Data recorded with higher sky brightness lead to biases when analyzed with the same pipeline that is used for data that has been recorded during dark nights but can, in principle, still be used when accepting a higher energy threshold when applying special analysis settings (see Ahnen et al. 2017b). In order to limit our selection to only good quality data, we applied cuts on several instrument and weather related parameters. These include the mean photomultiplier currents, the event trigger rate, the number of stars detected by the MAGIC star-guider cameras, and the cloud or aerosol induced absorption in the telescope’s field of view. The latter is derived from measurements with an infra-red pyrometer and a LIDAR system (Gaug et al. 2014; Fruck et al. 2014).
3. Data analysis
A high-level analysis of the acquired data was performed with the set of utilities available in the MAGIC SkyPrism package (Vovk et al. 2018). SkyPrism provides a set of routines, aimed at 2D spatial likelihood analysis of MAGIC data, which allows us to self-consistently account for sources of complex morphology within the field of view. Furthermore, it also incorporates algorithms for computing the instrument point spread function, exposure and background maps, which we intensively use throughout the analysis presented here.
3.1. Diffuse background model construction
The wobble observational scheme (Fomin et al. 1994) we used here provides a simultaneous background estimate from comparison of several adjunct (albeit exposed to slightly different sky regions) positions. Still, the applicability of this approach is limited by the distance between the wobble pointings and the target, which in our case is dw = 0.4°. In practice, a source with an extension comparable to or larger than twice the offset distance (0.8°), in the same direction, will still (partially) contribute to the background measured in the same camera region. The diffuse emission of the Galactic plane clearly exceeds this limit, so a special treatment is necessary.
Such contamination of the background map with excess γ-ray signal can be avoided if contributions from locations close to known γ-ray sources are excluded during map construction (Vovk et al. 2018). We thus mask out camera regions that correspond to the Galactic plane and use the rest of the camera (free from known or expected sources) to estimate the corresponding background. This approach, implemented in the SkyPrism package, allows us to significantly reduce the background bias.
Due to the remaining limitations of our background modeling technique and the wobble scheme we used, we cannot completely remove the possible bias in the background estimation from a source as extended as the diffuse Galactic plane emission. Our estimates, described in detail in Sect. 4.1 and illustrated in Fig. 7, demonstrate that in the l = [ − 1.5° ;1.5° ] longitude range along the plane, the remaining bias is within 10−20% of the assumed local source luminosity throughout the Galactic plane and does not exceed 30−50% (equivalent to ≈3% of background) in the outskirts. At the same time, the flux bias is rather constant across the plane and its variations, averaged in the latitude range b = [ − 0.2° ;0.2° ] do not exceed ≈1% of the background, which corresponds to 10−20% of the estimated source flux for a highly extended source.
3.2. MAGIC view of the Galactic center region
The large (>58°) zenith angle GC observations imply an increased energy threshold of ≈1 TeV, although an analysis is also possible at even lower energies given that the studied source is bright enough (Ahnen et al. 2017a). Thus, we performed the spectral analysis in the 400 GeV−50 TeV energy range; the morphology study of the diffuse emission in the GC region was done above γ-ray energies of 1 TeV.
The sky map (above E = 1 TeV) of the GC vicinity, produced with the described diffuse background estimation scheme, is shown in Fig. 1. The Galactic plane is visible over 2° across the image. The significance of this detection, computed using the CS radio emission profile (Tsuboi et al. 1999) as an approximation (see Sects. 3.3 and 3.4 for details of the method), results in a ≈17 standard deviations (σ) incompatibility with the null hypothesis of background and point sources only. Other sources visible in the image are Sgr A*, G0.9+0.1 and the so-called “Arc”, detected with significances of ≈48σ, ≈11σ and ≈6.4σ, respectively, while also propagating uncertainties of the background and exposure model.
 |
Fig. 1. Sky map (excess in units of background) of the GC region in Galactic coordinates at energies above 1 TeV, smeared with a kernel resembling the MAGIC PSF. The pre-trial statistical significance of regions with excess counts is highlighted by green contours at the levels 5σ and 3σ. The (smeared) MAGIC PSF is indicated by 39% and 68% containment contours. The white contours show radio line emission from CS molecules, tracing dense gas (Tsuboi et al. 1999). |
3.3. Galactic plane brightness scan
The CR distribution profile in the GC surroundings should roughly correspond to the brightness distribution of the detected γ-ray emission. Previous measurements have already shown evidence that the ≳100 GeV brightness of the Galactic plane is peaking towards the Sgr A*, indicating a concentration of cosmic-rays (H.E.S.S. Collaboration 2016). The presence of an extended central component, reported by the H.E.S.S. Collaboration (2018), also speaks in favour of this assumption.
The cosmic-ray distribution around the GC can be inferred by solving the integral equation
where S(x, y) is the image plane γ-ray brightness distribution, ρgas and ρCR are the number densities of the gas and CRs, respectively, and A is a factor, which takes into account the proton-proton interaction cross-section, distance to observer, and additional constants. A proper solution of this equation requires knowledge of the full 3D gas density distribution ρgas(x, y, z), which is challenging to obtain. Indeed, while in the image plane (x, y) the resolution of radio surveys reaches ≈0.01° (for instance the CS J = 1−0 emission radio survey of Tsuboi et al. 1999) equivalent to 1−2 pc scale, the line-of-sight distance z can hardly be obtained with an accuracy better than several tens of parsecs. For this reason we solve an approximate expression of Eq. (1):
which splits the problem into the projected gas (directly inferred from the radio data) and cosmic-ray distributions Pgas(x, y) and PCR(x, y) respectively. To avoid degeneracy, we just consider radially symmetric cosmic-ray profiles ρCR ∝ r−α (with r being the distance from the GC) and their projections onto the image plane. These simplifications result in a certain bias of our measurement, which we quantify in Sect. 4.2.
First, we test whether a homogeneous cosmic-ray distribution ρCR = const is consistent with the MAGIC data. For this, we produced an excess event profile of the b = [ − 0.2° ;0.2° ] stripe, centered at the GC position, and the corresponding MAGIC exposure profile using the features of SkyPrism. The resulting, exposure-normalized, Galactic plane profile above 1.2 TeV is shown in Fig. 2. Fitted with a simple model, containing the Sgr A* and G0.9 point sources, the “Arc” source, and the diffuse emission model S(x, y) (computed from the CS emission maps with ρCR = const), it results in χ2/d.o.f. ≈ 69/46 degrees of freedom, equivalent to ≈2.4σ disagreement of the data with the model.
 |
Fig. 2. Top: brightness scan of the b = [ − 0.2° ;0.2° ] stripe of the Galactic plane in the energy range above 1.2 TeV. Blue entries denote the MAGIC measurements, whereas the orange line is the best-fit model to them, composed of the CS profile, Sgr A* point source and the extended “Arc”. Bottom: residuals of the fit in the units of measurement uncertainties. |
In order to investigate if the MAGIC data are in a better agreement with a ρCR ≠ const type cosmic-ray profiles, we used a grid search for the optimal value of α using the profile shown in Fig. 2 and we estimated the cosmic-ray density PCR(d) = S(d)/Pgas(d) as function of the projected off-center distance d using a full maximum likelihood fit of the measured γ-ray brightness around the GC.
The results of the likelihood-profile scan are shown in Fig. 3, where the density ρCR is converted to the cosmic-ray energy density wCR using the same procedure as in H.E.S.S. Collaboration (2016) (formula (2) of the methods section):
 |
Fig. 3. Left: likelihood scan of the cosmic-ray density profile parameter space for ECR ≳ 10 TeV, for a centrally peaked profile of the form ρCR ∝ 1/rα, based on the MAGIC measurements. The scan has been performed for two different model assumptions: (1) only the cosmic-ray population with the power-law distribution exists (solid lines) and (2) the power-law population exist on top of a uniform cosmic-ray density distribution (dashed lines). Magenta crosses mark the best fit values for both assumptions, which nearly exactly overlap for our data. Gray vertical dash-dotted line represents the mean cosmic-ray density from H.E.S.S. Collaboration (2016). The mean cosmic-ray energy density ⟨wCR⟩ estimated here corresponds to the Galactic longitude range [ − 1° ;1° ]. Right: marginalization of the scan over the cosmic-ray profile index only. Green boxes and blue error bars mark the 1 and 2σ confidence ranges correspondingly for assumptions 1 (dark colours) and 2 (light colours). |
where wCR is in eV cm−3, ηN ≈ 1.5 accounts for nuclei heavier than hydrogen, in both CRs and in the target gas. For estimation of the H2 target mass M based on the CS radio maps we used the procedure described by the authors in Sect. 4.2 of Tsuboi et al. (1999):
where the excitation temperature Tex of CS is 30 K, ∫TMB dv is the measured velocity-integrated antenna temperature, A is the area of the GC region, μ(H2) is the mass of the hydrogen molecule and X(CS) = 10−8 is the relative abundance of CS in H2 clouds.
In the scan, we tested two different scenarios where: (1) the ρCR ∝ r−α profile dominates the cosmic-ray density in the region and (2) the peaked cosmic-ray profile is found on top of an underlying homogeneous density, so that ρCR ∝ r−α + const. To account for the background and telescope exposure uncertainties, we have generated 50 random exposure and background maps representing the uncertainty range of our reconstruction method and repeated the scan for each of them. We then averaged the resulting likelihood values in each bin of the scan phase space, which is equivalent to marginalization over these random map representations. The same technique of propagating the uncertainties of the background and exposure models has also been applied throughout the spectral analysis (Sect. 3.4). The resulting averaged values were then used to compute the confidence contours, shown in Fig. 3. In addition to α − wCR combined confidence contours, the right panel of the same figure shows the marginalized uncertainties for the power-law index α for both scenarios (1) and (2), with darker and lighter colours, respectively.
Scenario (1) favours a cosmic-ray density profile with 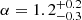 (1σ uncertainty). A similar profile with α = 1.2 ± 0.3 is found for scenario (2), where a homogeneous contribution to the cosmic-ray profile is allowed.
(1σ uncertainty). A similar profile with α = 1.2 ± 0.3 is found for scenario (2), where a homogeneous contribution to the cosmic-ray profile is allowed.
As illustrated in Fig. 4, the full likelihood fit to the obtained sky map is also inconsistent with the ρCR = const assumption. To perform this fit, we first split the CS emission map of Tsuboi et al. (1999; integrated over the radial velocity) into a sequence of concentric rings, with their own normalization factors. Since the CS emission is highly peaked toward the Galactic plane, this is effectively equivalent to a longitudinal split of the Plane inside the b = [ − 0.1° ,0.1° ] stripe. When computing the normalizations of the rings, we’ve also included the Sgr A* point source, as well as G0.9+0.1 and the “Arc” source to the fitted model. The resulting cosmic-ray density profile, shown in Fig. 4 was ultimately fit with the ρCR = const model, yielding χ2 ≈ 22 over 5 degrees of freedom. This corresponds to ≈3.5σ data to model disagreement, indicating a peaked profile.
 |
Fig. 4. Projected cosmic-ray energy density, as obtained from the full likelihood fit to the MAGIC sky map above 1 TeV. The projected distance is counted from the GC position. Measurements of H.E.S.S. Collaboration (2016) are shown in blue for comparison. |
In summary, MAGIC data above 1 TeV indicate a radial cosmic-ray profile with power index α ≈ 0.9−1.4, which is somewhat different to, but still compatible with, earlier findings by H.E.S.S. Collaboration (2016).
3.4. Spectral analysis of the detected sources
To compute the energy spectra of the detected sources in the MAGIC field of view – including the diffuse Galactic plane emission – we used the SkyPrism package. The spatial model used for the fit includes three point sources (Sgr A*, G0.9+0.1 and the Arc source at RA = 17:46:00, Dec = −28:53:00) and the velocity-integrated CS map, re-scaled with the ρCR ∝ r−1.2 best-fit cosmic-ray profile. The fit was performed in the energy range from 400 GeV to 50 TeV with two methods – first, based on energy bins (7 logarithmic energy bins) and second, assuming a certain spectral shape model for each of the sources. In the latter case, we applied a forward folding procedure considering the energy migration matrix during the fit. All spectra were generated from the general form
which can result in a power-law, log-parabola, and power-law with cut-off spectral shape depending on the choice of β and Ecut. The normalization energy for all the sources was set to E0 = 2 TeV, keeping the correlation between the spectral parameters minimal.
To obtain the best fit parameters of the assumed spectral models, we performed a maximal Poissonian likelihood fit to the energy-binned MAGIC sky maps. To ensure a good level of accuracy for the estimated uncertainties, we additionally used the Markov chain Monte Carlo (MCMC) sampler emcee on the parameter space (Foreman-Mackey et al. 2013). The uncertainties of the exposure and background models derived from Monte Carlo simulations and data regions more than 0.3° off the Galactic plane were propagated to the final results by processing 60 random representations through the MCMC sampler and merging the samples. The best-fit values for the detected sources, obtained through this fit, are given in Table 1, along with the corresponding errors and detection significance figures. The obtained spectra (data points and fit results) are shown in Fig. 5. The data points are not the result of spectral unfolding but, rather, spillover corrections based on the energy migration matrix and the fitted spectral shape were applied. The obtained MAGIC spectrum is consistent with the earlier estimate of the Galactic ridge spectral energy density (SED; H.E.S.S. Collaboration 2018), as displayed in Fig. 6. A likelihood ratio test comparing the model for the diffuse component with cut-off to a pure power-law results in the ≈2σ preference for the cut-off for the MAGIC data set.
 |
Fig. 5. MAGIC SEDs of the different components in our model, data points and forward folding fit results (colored bands). For the components corresponding to Sgr A*, the “Arc” and the CR/MC component a power-law shape with exponential cut-off has been used while G0.9+0.1 can be described with a simple power-law. The error bars and bands were computed from the MCMC samples and correspond to 68% confidence range. No spectral unfolding has been applied to the data points, but the effect of spillovers due to energy migration has been corrected for, based on the spectral shapes. Gray arrows indicate the size (length) and direction (orientation) of the SED shifts due to the systematical uncertainties in the analysis (see Sect. 3.4 for details). |
Spectral fit results of the sources, detected in the MAGIC field of view.
The SED shown earlier by H.E.S.S. Collaboration (2016) that led to the speculation about a possible PeV proton accelerator (PeVatron) at the GC, shows a lower average flux and somewhat different spectral shape compared to the other two SEDs in Fig. 6. This difference could be explained by the fact that also the regions in which the fluxes were measured are different. While H.E.S.S. Collaboration (2018) and this work try to include the whole < 1 deg from the GC part of the Galactic ridge, avoiding point sorces, H.E.S.S. Collaboration (2016) used a donut-shaped region for extracting their flux, with a cut-out at the position of the Arc source, and inner and outer radii of 0.15 deg and 0.45 deg, respectively.
 |
Fig. 6. Spectrum of the diffuse Galactic emission, derived from MAGIC data. Dark and light-blue regions mark the 68% and 95% confidence ranges for the assumed power-law with exponential cut-off model. The diffuse spectrum from H.E.S.S. Collaboration (2018), extracted from a similar region, is shown in orange, while the SED obtained from a cut annulus with 0.45 deg outer radius from H.E.S.S. Collaboration (2016) is shown in green. Gray arrows indicate the possible shifts due to the systematical uncertainties in the analysis, similar to Fig. 5. |
We estimate the systematic uncertainties, arising from uncertainties on the energy and flux normalization scales, following the procedure discussed in Ahnen et al. (2017a; based on a detailed study by Aleksić et al. 2016). The resulting estimates are indicated by gray arrows in Figs. 5 and 6, where the vertical arrows indicate the effect of the flux normalization errors at different energies and the horizontal or inclined arrows indicate the effect of the energy scale uncertainty.
4. Estimation of the possible biases in the analysis
4.1. Bias from the background modelling
In order to quantify the bias resulting from the background estimation, we used a simplified simulation of the background map based on the initial assumption on the extension and brightness of the sources in the GC region. In this simulation, we assume that the true signal measured by MAGIC consists of five contributions: extended gas emission (assumed to be traced by the CS map Tsuboi et al. 1999), point-like Sgr A*, the “Arc” source (Archer et al. 2016; Ahnen et al. 2017a; H.E.S.S. Collaboration 2018), point-like G0.9+0.1, and isotropic background. The relative normalizations of these components are taken from the previous analysis of Ahnen et al. (2017a); we used our best fit results for a cross-check. This composite image is then used to sample the photons in the telescope camera coordinates as a function of pointing azimuth and zenith, following the MAGIC pointing during the GC observations. The resulting event list is supplied to the background estimation routine for a comparison of the reconstructed versus the assumed background.
Based on the results, illustrated in Fig. 7, we expect the bias to stay below 2% in units of background flux nearly everywhere in the sky-maps. This translates to a bias of the measured flux of the diffuse emission of more than 40% in some regions along the edges of the Galactic plane, but less than 30% for the brighter regions along the plane and at the center. Still, using the CS map as an approximation for the γ-ray emission, the total bias on the integral flux of the Galactic plane component is estimated to be in the range 7−12%.
 |
Fig. 7. Left: background bias (in units of the true assumed background flux Bkgempty) for the applied background reconstruction technique, estimated with simulations. The map was smeared with the Gaussian kernel with σ = 0.05°; contours indicate ±2% differences with respect to the reference value of 1. Also plotted are the positions of the known γ-ray sources in the Galactic center region as well as the CS emission contours from Tsuboi et al. (1999), corresponding to the integral antenna temperatures of 5, 10 and 15 K, smeared with the same Gaussian kernel. Right: same, but in units of the source flux for the assumed model. Here, only the uncertainties within the region of the used CS gas map are plotted, as the rest of the modelled image contains only background. Such background-only regions are filled with light green. |
4.2. Bias and uncertainty from the assumed gas distribution model
An accurate modeling of the γ-ray emission from GC region requires detailed knowledge of the gas distribution in three dimensions. The angular resolution of MAGIC is better than 0.1°, which translates into ≈15 pc at 8.5 kpc distance from the Earth. As a result, MAGIC can map the profile of γ-ray emission at the projected distances of tens of parsecs from the position of the central supermassive black hole (SMBH); a conversion of this profile to the cosmic-ray density distribution naturally requires, then, that the line-of-sight distances to the gas clouds in the region are known with similar or better accuracy.
This requirement is very difficult to fulfill in practice. At larger distances the locations of the gas clouds are generally inferred from their kinematics, assuming a certain model of gas orbital motion (e.g., Sofue 1995; Nakanishi & Sofue 2003. In the vicinity of the GC, however, this approach can no longer be applied, as the inability to put the source in front or behind the black hole image plane at the scales of tens of parsecs leads to degeneracy in the calculations. The required information – to a certain degree – can be reconstructed using measurements of line-of-sight absorption of the molecular cloud emission, which provides the necessary line-of-sight position estimates (Sawada et al. 2004). Nevertheless, the line-of-sight locations of separate clouds in the GC region can hardly be reconstructed with an accuracy better than ≈50 pc.
In the absence and therefore negligence of the line-of-sight information, Eq. (1) naturally simplifies to Eq. (2), which works only with the projected gas and cosmic-ray densities. Depending on the real distribution ρgas(x, y, z), the transition Eqs. (1) and (2) may bear an oversimplification, resulting in a biased cosmic-ray profile ρCR(r).
We do not attempt to reconstruct a fully realistic structure of the central ≈200 pc of our Galaxy, which would be rather complex (Ferrière et al. 2007). Still, in order to quantify the associated bias in our analysis, we reconstruct the 3D gas distribution in the GC region based on the measurements of Sawada et al. (2004) and Tsuboi et al. (1999). This reconstruction then allows us to compare the profiles obtained accounting for or neglecting the line-of-sight information.
To perform the reconstruction, we used the fact that the 2D CS gas emission images of Tsuboi et al. (1999) are complemented by the radial velocity vrad information, which already provides the line-of-sight information in an indirect way. A mapping of vrad to the missing z coordinate is found in Sawada et al. (2004), where it is given in the (x, z) projection (in our notation). Hence, the measured intensity of the radio emission I(x, y, vrad) can be mapped to a full 3D cube I(x, y, z) through a relation vrad(x, y)↔vrad(x, z). The obtained cube gives an approximate picture of 3D gas distribution in the innermost ≈400 × 400 × 100 pc of the GC region.
Despite the limitations of this approach, based on this 3D cube one can quantify the biases in the calculations from the previous section. In particular, we can check whether the transition Eqs. (1) and (2) still gives a valid estimate for a realistic gas density distribution.
To verify this, we took the example case of a ρCR ∝ r−1 profile and computed the projected cosmic-ray density PCR(r) directly and using the 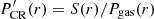 relation. The result of this comparison is shown in Fig. 8, where the exact projected shapes for α = {1, 2} profiles are also given.
relation. The result of this comparison is shown in Fig. 8, where the exact projected shapes for α = {1, 2} profiles are also given.
 |
Fig. 8. Projected cosmic-ray density as a function of the distance from the GC, computed using a 3D reconstruction of the gas distribution in the region. The underlining profile is assumed to have a ρCR ∝ r−1 shape. Blue line shows the true projection, whereas the orange one depicts the |
It is clear from this figure that the inferred profile in the α = 1 case would resemble a steeper one with α′≈1.5. In this way, an α′≈1.0−1.5 measurement, presented in Sect. 3.3, is likely to correspond to the true α ≈ 1 distribution, accounting for this bias. In order to directly check this assumption, we performed a fit of inferred profiles of a form ρCR ∝ r−α + const for α = [0; 2] to the projected cosmic-ray densities, obtained here (Fig. 4) and earlier in H.E.S.S. Collaboration (2016). The results of this test, shown in Fig. 9, indeed suggest that the true, de-projected cosmic-ray profile has a slope of 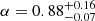 (at 68% confidence level), consistent with the α = 1 assumption.
(at 68% confidence level), consistent with the α = 1 assumption.
 |
Fig. 9. Scan of the cosmic-ray density profile power-law index α with respect to the data in Fig. 4 and earlier measurements from H.E.S.S. Collaboration (2016). The vertical dashed lines mark the derived 1 (blue), 2 (orange) and 3σ (red) confidence intervals. The horizontal dashed line represent the number of degrees of freedom in the fit. The scanned value, α corresponds to the true 3D cosmic-ray distribution and is projected on the plane of the sky using an assumed 3D gas map. See Sect. 4.2 for details. |
In a similar way, we can also estimate the effect of the uncertain line-of-sight measurements on the derived value of α. To reconstruct the effect we randomly shifted the positions of the cube grid cells in the z direction and then regenerated the expected cosmic-ray profiles 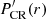 . The random shifts were obtained by adding 10−40 Gaussian-distributed displacements with standard deviations from 50 to 200 pc at random positions within the cube. The amplitude of the Gaussians was fixed to 25 parsec, while their width puts a coherence scale, not allowing the neighbouring bins to have very different shifts. The resulting shifts in the cube do not exceed ≈ ± 50 pc, roughly resembling the corresponding measurement uncertainties.
. The random shifts were obtained by adding 10−40 Gaussian-distributed displacements with standard deviations from 50 to 200 pc at random positions within the cube. The amplitude of the Gaussians was fixed to 25 parsec, while their width puts a coherence scale, not allowing the neighbouring bins to have very different shifts. The resulting shifts in the cube do not exceed ≈ ± 50 pc, roughly resembling the corresponding measurement uncertainties.
The outcome of this calculation is shown in Fig. 10. The comparison with the exact α = {1, 2} profiles projections indicates that the uncertainty in the line-of-sight position measurements can dramatically change the shape of the measured cosmic-ray profile. Within our simulation setup, assuming an α = 1 cosmic-ray profile, we can generally conclude that a measurement of α′≈1.5 is equally likely.
 |
Fig. 10. Projected cosmic-ray density as a function of the distance from the GC, computed using a 3D reconstruction of the gas distribution in the region. The profiles are inferred from the |
It should also be noted that the main evidence for the centrally peaked cosmic-ray profile comes from the measurements in the central ≈30−50 pc, where the uncertainty on the gas content is the highest. Any unaccounted absorption of the molecular radio emission from such dense regions may lead to a general underestimation of the gas content in the direct vicinity of the GC (in addition to the line-of-sight uncertainty) and thereby to a more modest estimate of the cosmic-ray density there.
5. Discussion
Based on deep VHE γ-ray observations using the MAGIC telescopes, we can reconstruct the cosmic-ray distribution profile in the GC region. In this process, we use the simplifications outlined in Sect. 3.3, which result from our partial knowledge of the line-of-sight distribution of the target gas material. This implies that measurements of the cosmic-ray distribution in the GC vicinity can only be improved with more accurate gas observation in other (radio, infra-red, etc.) domains and are not limited by the sensitivity of current γ-ray instruments. Accordingly, even highly sensitive future CTA observations of this region, for an analysis like the one presented here, depend on higher resolution molecular line measurements.
Our estimations, described in Sect. 4.2, indicate that in the absence of such measurements the derived cosmic-ray profile may look sharper than it is in reality. At the same time, the scatter in the profiles, based on the quoted uncertainties in the line-of-sight gas clouds positions, may make any interpretation of the measured shape less reliable. As an example, the α = 1 cosmic-ray profile, simulated in Sect. 4.2, may appear as α between 0.5 and 1.5 depending on the exact locations of the clouds (see Fig. 10).
The existence of a centrally peaked cosmic-ray distribution around GC, revealed by the H.E.S.S. data (H.E.S.S. Collaboration 2016) and confirmed here, however, seems reliable. The MAGIC data suggest an α = 1.2 ± 0.3 profile and therefore do not contradict the α = 1 scenario, in which CRs diffuse outwards from a central source, especially given the considerations outlined above.
This peaked cosmic-ray profile, together with a hard emission spectrum, was interpreted as a signature of PeV cosmic-ray acceleration by SgrA* (H.E.S.S. Collaboration 2016). It should be noted here that alternative explanations for the enhanced density of CRs at GC exist, ranging from millisecond pulsars (Guépin et al. 2018) to dark matter (Lacroix et al. 2016). It has also been shown by Gaggero et al. (2017) that it is possible to consistently model the diffuse γ-ray emission from GC in the Fermi and VHE emission energy range with particles from the Galactic CR sea, nearly without the need of an addition central CR source. The authors also state that in the presence of such a CR sea, the maximum energy of any excess from a central source is even less certain.
MAGIC measurements of the diffuse γ-ray spectrum over a larger region of the central molecular zone, ≈150 pc in width, favor, on a ≈2σ level, a cut-off in the γ-ray spectrum over a pure power law. The 1σ confidence range for the cut-off energy spans from 10 TeV to 80 TeV (see Sect. 3.4). This corresponds to proton energies of ≈0.1−1 PeV, which means that the data are still marginally compatible with the PeVatron scenario.
6. Conclusions
The presence and proximity of a central super-massive black hole make the GC region a unique laboratory for studying comic-ray acceleration near black holes. The above-presented MAGIC observations confirm that the cosmic-ray density profile in the GC vicinity is peaked towards the position of the central SMBH of our Galaxy, similar to what has been pointed out by H.E.S.S. Collaboration (2016). This is consistent with the idea of activity of the latter as a particle accelerator in the recent past or, possibly, even nowadays. The MAGIC data also show that the spectrum of this diffuse γ-ray emission is hard (Γ ≈ 2) and reaches energies of several ten TeV. Our analysis, however, also reveals a hint of the presence of a spectral turnover at around those energies at the 2σ level.
In order to gain further insight to particle acceleration and diffusion in the GC region, including the PeVatron topic, even deeper observations of the GC region by current and next-generation instruments are necessary. The focus should be on energies around and above 10 TeV, where current data sets are still statistics limited. Our study also indicates that such detailed measurements will be very sensitive to the line-of-sight gas distribution assumed and, as such, would require a deeper and higher resolution radio survey of the central 200 pc of our Galaxy.
Acknowledgments
We would like to thank the Instituto de Astrofísica de Canarias for the excellent working conditions at the Observatorio del Roque de los Muchachos in La Palma. We also thank Dario Grasso for the valuable comments. The financial support of the German BMBF and MPG, the Italian INFN and INAF, the Swiss National Fund SNF, the ERDF under the Spanish MINECO (FPA2015-69818-P, FPA2012-36668, FPA2015-68378-P, FPA2015-69210-C6-2-R, FPA2015-69210-C6-4-R, FPA2015-69210-C6-6-R, AYA2015-71042-P, AYA2016-76012-C3-1-P, ESP2015-71662-C2-2-P, FPA2017-90566-REDC), the Indian Department of Atomic Energy, the Japanese JSPS and MEXT, the Bulgarian Ministry of Education and Science, National RI Roadmap Project DO1-153/28.08.2018 and the Academy of Finland grant nr. 320045 is gratefully acknowledged. This work was also supported by the Spanish Centro de Excelencia “Severo Ochoa” SEV-2016-0588 and SEV-2015-0548, and Unidad de Excelencia “María de Maeztu” MDM-2014-0369, by the Croatian Science Foundation (HrZZ) Project IP-2016-06-9782 and the University of Rijeka Project 13.12.1.3.02, by the DFG Collaborative Research Centers SFB823/C4 and SFB876/C3, the Polish National Research Center grant UMO-2016/22/M/ST9/00382 and by the Brazilian MCTIC, CNPq and FAPERJ.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, Phys. Rev. Lett., 104, 101101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006a, ApJ, 636, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006b, Nature, 439, 695 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ahnen, M. L., Ansoldi, S., Antonelli, L. A., et al. 2017a, A&A, 601, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ahnen, M. L., Ansoldi, S., Antonelli, L. A., et al. 2017b, Astropart. Phys., 94, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2008, Nucl. Instrum. Meth. Phys. Res. A, 588, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Ansoldi, S., Antonelli, L. A., et al. 2016, Astropart. Phys., 72, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Archer, A., Benbow, W., Bird, R., et al. 2016, ApJ, 821, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrière, K., Gillard, W., & Jean, P. 2007, A&A, 467, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fomin, V. P., Stepanian, A. A., Lamb, R. C., et al. 1994, Astropart. Phys., 2, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Fruck, C., Gaug, M., Zanin, R., et al. 2014, ArXiv e-prints [arXiv:1403.3591] [Google Scholar]
- Gaggero, D., Grasso, D., Marinelli, A., Taoso, M., & Urbano, A. 2017, Phys. Rev. Lett., 119, 031101 [CrossRef] [PubMed] [Google Scholar]
- Gaug, M., Blanch, O., Dorner, D., et al. 2014, ArXiv e-prints [arXiv:1403.5083] [Google Scholar]
- Guépin, C., Rinchiuso, L., Kotera, K., et al. 2018, JCAP, 2018, 042 [NASA ADS] [CrossRef] [Google Scholar]
- H.E.S.S. Collaboration (Aharonian, F. A.) 2006, Nature, 439, 695 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- H.E.S.S. Collaboration (Abramowski, A., et al.) 2016, Nature, 531, 476 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- H.E.S.S. Collaboration (Abdalla, H., et al.) 2018, A&A, 612, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, S. D., Bertsch, D. L., Catelli, J. R., et al. 1997, ApJ, 481, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Lacroix, T., Silk, J., Moulin, E., & Bœhm, C. 2016, Phys. Rev. D, 94, 123008 [CrossRef] [Google Scholar]
- Nakanishi, H., & Sofue, Y. 2003, PASJ, 55, 191 [Google Scholar]
- Oka, T., Hasegawa, T., Sato, F., Tsuboi, M., & Miyazaki, A. 1998, ApJS, 118, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Sawada, T., Hasegawa, T., Handa, T., & Cohen, R. J. 2004, MNRAS, 349, 1167 [NASA ADS] [CrossRef] [Google Scholar]
- Sofue, Y. 1995, PASJ, 47, 527 [NASA ADS] [Google Scholar]
- Tsuboi, M., Handa, T., & Ukita, N. 1999, ApJS, 120, 1 [NASA ADS] [CrossRef] [Google Scholar]
- van Eldik, C. 2015, Astropart. Phys., 71, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Vovk, I., Strzys, M., & Fruck, C. 2018, A&A, 619, A7 [CrossRef] [EDP Sciences] [Google Scholar]
- Zanin, R., Carmona, E., Sitarek, J., Colin, P., & Frantzen, K. 2013, Proc. of the 33st International Cosmic Ray Conference, Rio de Janeiro, Brasil [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Sky map (excess in units of background) of the GC region in Galactic coordinates at energies above 1 TeV, smeared with a kernel resembling the MAGIC PSF. The pre-trial statistical significance of regions with excess counts is highlighted by green contours at the levels 5σ and 3σ. The (smeared) MAGIC PSF is indicated by 39% and 68% containment contours. The white contours show radio line emission from CS molecules, tracing dense gas (Tsuboi et al. 1999). |
| In the text | |
 |
Fig. 2. Top: brightness scan of the b = [ − 0.2° ;0.2° ] stripe of the Galactic plane in the energy range above 1.2 TeV. Blue entries denote the MAGIC measurements, whereas the orange line is the best-fit model to them, composed of the CS profile, Sgr A* point source and the extended “Arc”. Bottom: residuals of the fit in the units of measurement uncertainties. |
| In the text | |
 |
Fig. 3. Left: likelihood scan of the cosmic-ray density profile parameter space for ECR ≳ 10 TeV, for a centrally peaked profile of the form ρCR ∝ 1/rα, based on the MAGIC measurements. The scan has been performed for two different model assumptions: (1) only the cosmic-ray population with the power-law distribution exists (solid lines) and (2) the power-law population exist on top of a uniform cosmic-ray density distribution (dashed lines). Magenta crosses mark the best fit values for both assumptions, which nearly exactly overlap for our data. Gray vertical dash-dotted line represents the mean cosmic-ray density from H.E.S.S. Collaboration (2016). The mean cosmic-ray energy density ⟨wCR⟩ estimated here corresponds to the Galactic longitude range [ − 1° ;1° ]. Right: marginalization of the scan over the cosmic-ray profile index only. Green boxes and blue error bars mark the 1 and 2σ confidence ranges correspondingly for assumptions 1 (dark colours) and 2 (light colours). |
| In the text | |
 |
Fig. 4. Projected cosmic-ray energy density, as obtained from the full likelihood fit to the MAGIC sky map above 1 TeV. The projected distance is counted from the GC position. Measurements of H.E.S.S. Collaboration (2016) are shown in blue for comparison. |
| In the text | |
 |
Fig. 5. MAGIC SEDs of the different components in our model, data points and forward folding fit results (colored bands). For the components corresponding to Sgr A*, the “Arc” and the CR/MC component a power-law shape with exponential cut-off has been used while G0.9+0.1 can be described with a simple power-law. The error bars and bands were computed from the MCMC samples and correspond to 68% confidence range. No spectral unfolding has been applied to the data points, but the effect of spillovers due to energy migration has been corrected for, based on the spectral shapes. Gray arrows indicate the size (length) and direction (orientation) of the SED shifts due to the systematical uncertainties in the analysis (see Sect. 3.4 for details). |
| In the text | |
 |
Fig. 6. Spectrum of the diffuse Galactic emission, derived from MAGIC data. Dark and light-blue regions mark the 68% and 95% confidence ranges for the assumed power-law with exponential cut-off model. The diffuse spectrum from H.E.S.S. Collaboration (2018), extracted from a similar region, is shown in orange, while the SED obtained from a cut annulus with 0.45 deg outer radius from H.E.S.S. Collaboration (2016) is shown in green. Gray arrows indicate the possible shifts due to the systematical uncertainties in the analysis, similar to Fig. 5. |
| In the text | |
 |
Fig. 7. Left: background bias (in units of the true assumed background flux Bkgempty) for the applied background reconstruction technique, estimated with simulations. The map was smeared with the Gaussian kernel with σ = 0.05°; contours indicate ±2% differences with respect to the reference value of 1. Also plotted are the positions of the known γ-ray sources in the Galactic center region as well as the CS emission contours from Tsuboi et al. (1999), corresponding to the integral antenna temperatures of 5, 10 and 15 K, smeared with the same Gaussian kernel. Right: same, but in units of the source flux for the assumed model. Here, only the uncertainties within the region of the used CS gas map are plotted, as the rest of the modelled image contains only background. Such background-only regions are filled with light green. |
| In the text | |
 |
Fig. 8. Projected cosmic-ray density as a function of the distance from the GC, computed using a 3D reconstruction of the gas distribution in the region. The underlining profile is assumed to have a ρCR ∝ r−1 shape. Blue line shows the true projection, whereas the orange one depicts the |
| In the text | |
 |
Fig. 9. Scan of the cosmic-ray density profile power-law index α with respect to the data in Fig. 4 and earlier measurements from H.E.S.S. Collaboration (2016). The vertical dashed lines mark the derived 1 (blue), 2 (orange) and 3σ (red) confidence intervals. The horizontal dashed line represent the number of degrees of freedom in the fit. The scanned value, α corresponds to the true 3D cosmic-ray distribution and is projected on the plane of the sky using an assumed 3D gas map. See Sect. 4.2 for details. |
| In the text | |
 |
Fig. 10. Projected cosmic-ray density as a function of the distance from the GC, computed using a 3D reconstruction of the gas distribution in the region. The profiles are inferred from the |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



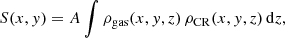
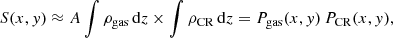
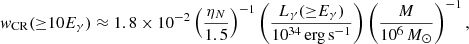
![$$ \begin{aligned} M(\mathrm{H}_2)[M_{\odot }] =&7.5 \times 10^{11} T_{\rm ex}\,[\mathrm{K}]\nonumber \\&\times \frac{\int T_{\rm MB}\,\mathrm{d}{ v} [\mathrm{K\,km\,s^{-1}}] \cdot A[\mathrm{cm}^2] \cdot \mu (\mathrm{H}_2)[M_{\odot }]}{X(\mathrm{CS})}, \end{aligned} $$](/articles/aa/full_html/2020/10/aa36896-19/aa36896-19-eq4.gif)