EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 642 (October 2020) A&A, 642 (2020) A195 Full HTML
Free Access
Issue
A&A
Volume 642, October 2020
Article Number A195
Number of page(s) 11
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/201833947
Published online 20 October 2020

© ESO 2020

1. Introduction

In contrast to standard two-ribbon solar flares (Carmichael 1964; Sturrock 1966; Hirayama 1974; Kopp & Pneuman 1976), circular-ribbon flares are accompanied by brightenings of chromospheric emission in a quasi-circular manner. The simplest model of the magnetic field for these flares (so-called fan-spine configuration) was proposed by Pariat et al. (2009), presenting a structure that consists of a dipolar magnetic field embedded into a dome-structured magnetic field. The principal structural elements are fan lines with an inner and outer spine (see e.g. Fig. 1 in Pariat et al. 2009). The cross-section of the fan lines and the chromosphere plots a quasi-circle. The inner spine draws in the inner ribbon (within the circular ribbon). The outer spine, originating from the domelike structure, can form open magnetic field lines, suggesting the possibility that energetic particles travel outwards from the corona to interplanetary space. Alternately, the outer spine can be anchored at a remote site in the chromosphere (Aulanier et al. 2000; Meshalkina et al. 2009; Kumar et al. 2015). In this case, the outer spine is associated with a loop that is visible in soft X-rays (Fletcher et al. 2001) or in chromospheric line emission (Kumar et al. 2015). The brightening of the circular ribbon is accompanied by the brightening of its remote footpoint (Meshalkina et al. 2009; Kumar et al. 2015; Xu et al. 2017).

The various explanations of the mechanisms of energy release in this type of flare are based on the presence of a quasi-separatrix layer with the magnetic null-point between the fan and dome. In this model of magnetic field configuration, the sheared magnetic field of the sunspots prompts reconnection at the magnetic null-point (Lau & Finn 1990; Aulanier et al. 2000; Su et al. 2009). An observational confirmation of this hypothesis was revealed by Masson et al. (2009). Based on Extreme ultraviolet (EUV) observations, they found an anticlockwise direction for the brightening of the fan magnetic lines. Such brightenings can be explained by slipping or slip-running reconnection. There is evidence by several authors (see, for example, Meshalkina et al. 2009; Reid et al. 2012; Zhang et al. 2015) for detecting the hard X-ray emission with energy above 25 keV in circular-ribbon flares that was interpreted as bremsstrahlung emission by non-thermal electrons.

The processes of particle acceleration and heated plasma motion are usually taking place simultaneously in a solar flare. The structure of the circular ribbon flare defined by the magnetic fan and null point indicates the most probable location for the acceleration and primary energy release. Moreover, in contrast to a two-ribbon flare, the location of this place within the circular-ribbon structure does not move during the flare (Meshalkina et al. 2009; Xu et al. 2017). From this point of view, the circular ribbon flare is a more convenient object for the study of acceleration and energy propagation processes then the classical two-ribbon flare. An analysis of quasi-periodic pulsations (QPPs) in circular ribbon flares can be helpful for diagnostics of wave processes or particle acceleration as pulsation generators. Despite the number of existing studies on circular-ribbon flares, the manifestations of QPPs in this type of flare have rarely been revealed and analysed. In spite of the similar magnetic configurations of circular-ribbon flares where QPPs were observed, the results of these studies indicate various reasons for their onset. Mészárosová et al. (2013) proposed that QPP with periods of 10–83 s observed in radio wavelengths are connected with fast magnetoacoustic waves which propagate along the fan outwards from the magnetic null point. Kumar et al. (2015) found a global standing slow magnetoacoustic wave with a period of 409 s in the hot channels (94 and 131 Å) registered with the Atmospheric Imaging Assembly onboard the Solar Dynamics Observatory (SDO/AIA). The wave was reflected several times between the footpoints of the outer spine. Simultaneously, a period of 202 s was detected in the 6–12 keV X-ray emission in the remote footpoint of outer spine. This periodicity was associated by the authors with possible repetitive reconnection in the fan that caused an acceleration of electrons. The results were obtained in different spectral ranges that correspond to different layers of the solar atmosphere and different mechanisms of emission excitation. We guess that one of the reasons for such heterogeneous results could be that the viewing angle allowed for detecting emission from only one of the structures composing the fan-spine structure of the circular ribbon flare.

To expand on this area of study, we need to find an event such that the angle of view allows us to study each part of the fan-spine structure independently. Moreover, this event should be observed simultaneously at different ranges of the electromagnetic spectrum covering solar atmosphere heights from the chromosphere to the upper layers of the corona. The fan-spine structure located near to the solar disk centre produced a series of consecutive flares suitable for all these criteria on 5 March 2014. We chose for analysis the event presented by Xu et al. (2017). The event consisted of two flares (C2.8 and M1.0 according to the Geostationary Operational Environmental Satellite (GOES) classification) with well-pronounced QPPs seen not only in Hα emission, but in the other wavelengths as well. The purpose of our study is to check if the QPPs observed in the chromospheric Hα emission have the same nature as the QPP in hard X-ray and microwave emissions. We also analyse a connection between the QPP at the fan structure with the QPP at the remote source in order to understand whether they share a common driver for their pulsations.

The paper is organised as follows. The observations are described in Sect. 2. The spatial-temporal features of the flare seen in the multi-wavelength observations are summarised in Sect. 3. The analysis of flare time profiles is carried out in Sect. 4. The detected periodicities are analysed in Sect. 5. The mechanisms are discussed and results are summarised in Sect. 6. Details of the data processing technique are described in Appendix A.

2. Observations

Our analysis is based on observations of the chromospheric emission in Hα line obtained by the New Vacuum Solar Telescope (NVST; Liu et al. 2014). The telescope is equipped with the Lyot filter system with the spectral band-pass in 0.25 Å. The images are obtained with 0.5 arcsec spatial resolution and a 12 s time resolution. We used the data for analysis of the chromospheric response to precipitation of energetic particles and gas-dynamic processes like heating. We take information about the solar flaring plasma behaviour from microwave and X-ray observations.

Microwave flare emission was obtained using data from the Siberian Solar Radio Spectropolarimeter (SSRS), which is the former Badary Broadband Microwave Spectropolarimeter (Zhdanov & Zandanov 2011, 2015). The SSRS observes the solar microwave fluxes at 16 frequencies within the 3.8–8.2 GHz range. The observations are carried out with a cadence of 0.6 s. We found a very faint response in the correlation plots at 17 GHz obtained by the Nobeyama Radioheliograph (Nakajima et al. 1994) but the registered flux is too low to get any valid information about the spatial structure of the microwave source.

We used the data from three different instruments for the analysis of the X-ray emission. The Reuven Ramaty High Energy Solar Spectroscopic Imager (RHESSI; Lin et al. 2002) observed both flares but we cannot use its time profiles for the analysis of QPPs because of several switches between attenuators during the observations. However, the RHESSI data are appropriate for reconstructing the images within the time intervals between the switches. We reconstructed the images at the energies 6–12 keV, 12–25 keV and 25–50 keV. In some time intervals, the numbers of counts were not enough to do correct imaging for all set of energies. We also use the X-ray spectra by RHESSI for estimation of the flare plasma parameters. The Gamma-Ray Burst Monitor (hereinafter, Fermi/GBM) of the Fermi Gamma-ray Space Telescope (Meegan et al. 2009) did not observe the full time interval of interest. The advantage of this instrument is the absence of instrumental artefacts affecting periodicity detection. Thus, we used Fermi/GBM data for proofing solar origin of the signal. The observations both by RHESSI and Fermi/GBM were processed by the standard software (Schwartz et al. 2002). The X-ray time profiles suitable for the periodicity analysis are obtained by Konus, a Gamma-Ray Burst Experiment (Aptekar 1995; Pal’shin et al. 2014) on-board the Wind spacecraft (hereinafter, KW) in the energy band of 20–80 keV. The temporal resolution of these data is 2.944 s. Soft X-ray emission was analysed using GOES within two bands: 1–8 Å and 0.5–4 Å. The time resolution of this data is 2.05 s.

We use the data of SDO to analyse both the line-of-sight magnetograms obtained with the Helioseismic and Magnetic Imager (SDO/HMI; Scherrer et al. 2012) and the images obtained by SDO/AIA (Lemen et al. 2012).

3. Spatial structure and temporal evolution of the flare sources

The circular-ribbon flares occurred in the active region NOAA 11991 close to the solar disk centre (X = 120, Y = −340 arcsec) on 5 March 2014 (Fig. 1). Xu et al. (2017) carried out analysis of the flare topology based on Hα observations and SDO/HMI magnetorgams. They revealed that the principal elements of the fan-spine structure are well mapped in Hα emission (see Fig. 1 in Xu et al. 2017). In Fig. 1, we draw the fan-spine structure over the chromospheric image in the 304 Å SDO/AIA channel which also demonstrates the same form of the flare ribbons as Hα observations. Hereafter, we used the same labels for the flare ribbons (kernels) as Xu et al. (2017). Particularly, the inner ribbon (kernel R1) corresponds to the inner spine. The footpoints of the fan and dome draw the circular ribbon (R2). Note that with time these kernels get strongly entangled so that it becomes impossible to separate their fluxes correctly every time (Xu et al. 2017). Therefore, in this paper, we analyse the whole system R1+R1. The remote footpoint of the outer spine is marked by R3. The authors also detected the ribbon, marked by R4 which appeared later than the other ribbons and after the main phase of the event. The circular ribbon appeared on 4 March 2014 at 08:00 UT and existed till approximately 05:00 UT on 5 March 2014. The comparison of the magnetogram and the location of the chromospheric flare kernels (ribbons R1 + R2) shows that the circular ribbon coincides with the magnetic feature of positive polarity which is surrounded by the features of the negative magnetic polarity (Fig. 2). The remote kernel R3 is connected by the loop to the fan structure R1 and R2. This loop corresponded to the outer spine and is seen in the 171 Å SDO/AIA channel image after the maximum of the second flare (bottom panel of Fig. 2).

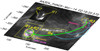thumbnail Fig. 1.

Principal elements of the fan-spine structure involved in the flare SOL2005-05-06 schematically sketched over the SDO/AIA image in the 304 Å band at 02:16:20 UT. The chromospheric kernels are outlined by the yellow ovals: R1+R2 is the circular ribbon structure, where the inner ribbon R1 and the circular ribbon R2 are shown in detail separately at 01:55:49 UT within the dotted rectangle; R3 is the remote ribbon; R4 is the elongated ribbon seen at the decay phase. The fan-spine magnetic structure is drawn in green and magenta: the fan lines (magenta) form the inner spine; the dome lines (green) continue into the outer spine (a long loop anchored at R3 kernel); a quasi-separatrix layer is the surface between magenta and green lines (is not shown here) with the magnetic null-point located between the inner and outer spines (Pariat et al. 2009). Loops in blue connect the sunspot (dark pink) with R3 and R4 kernels.

thumbnail Fig. 2.

SDO/AIA 171 Å maps during the first flare at 01:57:12 UT (top) and during the second flare at 02:07:25 UT (bottom) with the over-plotted contours of hard X-ray emission at 6–12 keV (red), 12–25 keV (light green) and 25–50 keV (white). In the top panel, the X-ray images were reconstructed within 01:55:15–01:55:35 UT (the first peak) by the CLEAN algorithm. The X-ray sources shown by the solid line in the bottom panel were reconstructed within 02:07:00–02:08:40 UT by PIXON algorithm. The contour levels are 50% and 90% of maximum. The X-ray source associated with R4 was obtained by CLEAN algorithm within 02:18:30–02:20:30 UT. The levels are 40%, 60%, and 80% of maximum. The SDO/AIA 304 Å chromosperic kernels are marked by yellow. The magnetic field features of positive and negative polarity are marked by blue and magenta, correspondingly. The absolute value of magnetic feature strength is above 500 G.

The time profile of the Hα emission during interval 01:50–02:40 UT (Xu et al. 2017) could be identified as a set of quasi-periodic pulses. GOES classified them as two events. The first event was a C2.8 GOES class flare with the onset at 01:52 UT and the maximum at 01:58 UT. The second event was an M1.0 GOES class flare with the onset at 02:06 UT and the maximum at 02:10 UT. However, the time profiles in other wavelengths demonstrate a series of peaks between and outside the GOES flares (see Fig. 3) indicating that they are parts of a common process. Therefore, despite the GOES classification, we study these peaks as a single continuous event.

thumbnail Fig. 3.

Normalised time profiles of the flare emission in different spectral ranges. All the time profiles are normalised by their maxima. A colour of each curve within a panel corresponds to the colour of the legend in the panel. Panel a: Hα emission from the sources R1+R2, R1, R3, and R4. Panel b: X-ray flux observed by Fermi/GBM at 25–50 keV and KW at 20–80 keV, and derivative of the GOES flux, at 1–8 Å. Panel c: X-ray fluxes registered by Fermi/GBM 6–12 keV, by GOES at 1–8 Å, and by GOES at 0.5–4 Å. Panel d: microwave fluxes at 8 GHz, 5.7 GHz, and 4 GHz obtained with SSRS. Panel e: X-ray uncorrected fluxes registered by RHESSI at 6–12 keV, 12–25 keV, and 25–50 keV. The RHESSI sources shown in Fig. 2 were reconstructed within time intervals enclosed into pairs of the same-coloured vertical solid lines.

We reconstructed the X-rays images with the CLEAN and PIXON algorithms using the package from Solar Software (Schwartz et al. 2002) based on data of the 4–8 front detectors. The centre of the X-ray sources at 6–12 keV and at 12–25 keV bands coincide with the inner ribbon R1 during the first flare peak (Fig. 2, the top panel). However the 12–25 keV source also covers part of the ribbon R2. In spite of some flux being detected at energies above 25 keV, we could not reconstruct source images for these energies. Later, there are X-ray sources up to 50 keV (Fig. 2, the bottom panel). Compared with its earlier location, the sources moved towards the circular ribbon R2 and localise at one specific part. In spite of the outer-spine loop which connects the fan region (R1 + R2) with the remote source (R3), we did not reveal any X-ray source coinciding with the remote source R3. However, it could be too faint to be distinguished near to the bright source (R1 + R2).

As mentioned above, the Hα emission from the inner ribbon R1 dominates during the impulsive phases of the analysed event (Fig. 3). The exception is the interval between 02:02 UT and 02:07 UT when the maximal emission is produced by the southern chord of circular ribbon R2. The peaks in the time profile of the remote source R3 (red curve) show a delay relative to peaks of the source R1 (blue curve).

The brightening of the elongated ribbon R4 (red curve) occurs at the final phase of the flare activity. However, the variations of the R4 time profile showed a sharp rise of the flux and a complicated structure. One can see in Fig. 2 (bottom panel) that kernel R4 is associated with 6–12 keV X-ray sources. That could be a result of a small flare loop arcade appearance.

4. Analysis of multi-wavelengths spectra and time profiles

The considered events demonstrated a wide range of electromagnetic emission – from optical chromospheric emission to soft and hard X-rays and microwaves. The Hα emission allows us to study relationships between QPPs present in the spatially resolved emission from different flare kernels. However, it is not possible to identify the mechanism responsible for the QPPs using only the Hα data. This emission could be related to both accelerated electrons (non-thermal mechanisms) and heating of the thermal plasma (thermal mechanisms). We need to distinguish the emission mechanisms first using spectral analysis of X-rays and microwave (MW) data. We can use the similarity of the QPPs observed in X-ray and microwave emissions and those in the Hα emission as a marker of the specific mechanism in the kernel. This section is devoted to analysis of spectra of the X-ray and microwave emissions and to analysis of the relationships between time profiles of different emissions.

Figure 4 (left panel) shows the spectra obtained from RHESSI data for the four main peaks marked with dashed vertical lines in Fig. 3. These peaks are clearly seen in X-rays, microwaves, and Hα. We fitted the spectra by two models with albedo correction because of the event location near to the solar disk centre. The first model was simpler and consisted of a thermal bremsstrahlung function and a power-law function (non-thermal emission). Using this model, we got the electron temperature varying from 17 MK to 14 MK during the flares. The second model consisted of multi-thermal bremsstrahlung function where the differential emission measure has a power-law dependence on temperature and thick target bremsstrahlung function. The maximal plasma temperature for this model varied from 23 MK to 14 MK. The estimations of the plasma temperature are similar for both models. The high energy cut-off of the thermal component was not higher than 20 keV during the flares for both models. Thus, we can assume that all X-ray emission above 20 keV is non-thermal, and we can use it as an indicator of electron acceleration processes.

thumbnail Fig. 4.

Left panel: evolution of the X-ray spectra. The observed X-ray spectra (marked by dots) are overplotted by the results of the fitting by a model consisting of an optically thin thermal bremsstrahlung function and power-law function. The average value of the time interval, the observational data, and the results of the fitting are marked by the same colour for each moment in time. Right panel: evolution of the microwave spectra. The observed data (marked by the dots) are over plotted by the result of fitting by the function corresponding to the form of the gyrosynchrotron spectrum. The average value of the time interval, the observational data and the results of the fitting are marked by the same colour for each moment in time. The vertical orange lines mark the 4 GHz and 8 GHz frequencies.

The main peaks in both the microwave and KW hard X-ray emission correlate with the peaks in the time derivatives of the GOES flux manifesting the Neupert effect (Neupert 1968) applicable to the case. The exception was the third X-ray peak at 02:03 UT, approximately, which does not have a strong response in the microwaves. The electron flux is low but still high enough for the generation of gyrosynchrotron emission. We infer that a lack of significant MW emission is the result of a combination of low magnetic field values and the soft, small flux of accelerated electrons. The final answer could be obtained through a modelling of the MW emission, taking into account the peculiarity of the magnetic field topology. However, this is beyond the scope of our current study. All other peaks show peak-to-peak agreement with those peaks seen in the Hα time profiles of the R1+R2 source and R1 source. Hα line centre emission could be both a result of direct ionization of chromospheric plasma by beams of accelerated electrons or plasma heating. The heating could be the result of gas-dynamic expansion following excitation by non-thermal particles or the result of other thermal energy release processes. Thus, the peaks seen in the Hα line profiles could have different origins. In this case, there would be two or more dominating periods in the time profiles of chromosperic emission. Even if we could find a single period accompanied by high-noise background, then we would have several independent models supporting both the thermal and non-thermal nature of the QPPs. That is why we have to use the periodicity obtained from the time profiles of non-thermal X-rays as a marker of the acceleration processes.

Figure 3 (panel c) shows a correlation between the Hα line profiles of the R1+R2 and R1 sources, and thermal X-ray emission. According to the spectral analysis (Fig. 4), the X-ray emission is thermal for energies below about 20 keV. However, observations of Fermi/GBM were stopped at around 02:05 UT, and we have to use X-ray data by GOES for testing the thermal emission of the flares. The GOES band 1–8 Å corresponds to about 1.5–12 keV energy band while emission of the GOES band 0.5–4 Å is equal to 3–25 keV energy band. The 1–8 Å GOES time profile shows a good correlation with the 6–12 keV time profile obtained by Fermi/GBM. All peaks of the GOES time profile correlate with those peak corresponding to Hα kernels. The peaks of the 1–8 Å GOES time profile derivative also demonstrate a good correlation with the non-thermal X-ray emission obtained by Fermi/GBM and KW. Thus, we use both the 1–8 Å band time profile and its derivative as indicators of thermal and non-thermal processes in the event discussed here.

Microwave spectra for the same time periods as the X-ray emission are shown in right panel of Fig. 4. We see that the peak frequency is about 6 GHz and it does not significantly shift towards higher frequencies during the evolution of the analysed event. Thus, the flux at 8 GHz locates optically thin microwave emission and is a direct marker of the emission generated by accelerated electrons. The flux at 4 GHz will be an indicator of the processes generating emission in the optically thick part of the spectrum. Both frequencies are marked by vertical orange lines in the Fig. 4 (right panel).

The peaks seen in the Hα time profiles of the R1+R2 sources together and the R1 source alone (Fig. 3, panel a) appeared at the same time as the main peaks in the hard X-ray (Fig. 3, panel b) and microwave emissions at the selected frequencies (Fig. 3, panel d). The time profiles of microwave fluxes at frequencies above and below the peak frequency show good agreement with each other. We note that time profiles of the microwave fluxes at frequencies above and below the peak frequency show in-phase variations. This fact means that both the optically thin part and optically thick part of the microwave spectrum indicate the same process of electron acceleration without any significant impact of self-absorption by plasma in the flare volume. In other words, both the optically thin and optically thick microwave emission is caused mainly by gyrosynchrotron emission from the same population of accelerated electrons.

Summarising the results presented in the current section, the spectral analysis allowed us to separate emission from thermal and non-thermal generation mechanisms. The similar behaviour of the microwave, non-thermal X-ray, and chromospheric emission gives us evidence that all flux variations have a solar origin and are not artefacts. Thus, these time profiles could be used for periodicity testing and obtaining periodograms for the different Hα sources and different spectral bands. Comparative analyses of periodograms obtained for these emissions and Hα emission will help to reveal which processes dominate in the emission generation of the different flare sources. Moreover, information about periodicity of the different Hα sources will address questions pertaining to the existence of a general process that controls the emission of all flare sources during both events.

5. Periodic properties of the flares

This section includes the results of analysis of QPPs in the multi-wavelength emission of the series of the impulsive energy releases that occurred on 5 March 2014, between 01:50:00 UT and 02:40:00 UT. The details of the technique for the QPP analysis are presented in Appendix A. The results are collected in Figs. 5 and 6; in Table 1 for the impulsive flare phase and in Fig. 7 and Table 2 for the decay phase.

thumbnail Fig. 5.

Results of the wavelet and Fourier analyses of the Hα emission from different flare kernels. The vertical dashed line in panel d indicates the start time of the brightening of the R4 ribbon, 02:13:20 UT.

thumbnail Fig. 6.

Results of the wavelet and Fourier analyses of the microwave and X-ray emission. The vertical dashed line in panel b marks the start time of the brightening of the R4 ribbon. The vertical dashed line in panel e marks the start time of the interval analysed in Fig. 7 (panel a).

thumbnail Fig. 7.

Panels a–c: results of the wavelet and Fourier analyses of the soft X-ray, microwave, and Hα R4 kernel data, during the decay flare phase. Panel d: empirical mode decomposition (EMD) spectrum of the microwave flux at 5.7 GHz. The total energies of the decomposed intrinsic modes are shown by crosses. The blue curve represents the global slope of the spectrum. The 99% confidence intervals are shown by red curves.

Table 1.

Periods (in seconds) with error bars detected during both flares in different emission bands.

The results for each time profile in Figs. 5–7 are split into two sub-panels. The normalised time profile is plotted as a black curve in the left sub-panel. The time profile is normalised over its maximal amplitude, then scaled according to the half maximum of the vertical axis, and, finally, shifted to the top of the panel. The time profile is plotted over the red-colour gradient image which is the wavelet power spectrum. The right sub-panel shows the global wavelet spectrum (black solid curve) with its significance level (dashed curve). A Fourier periodogram normalised over the maximum of the global wavelet spectrum is plotted by the red curve. Both the wavelet Morlet transform and Fourier periodogram were applied to the high-frequency component, which is residual after removing a slowly varying flare trend from the time profile. We obtained the trend via a different method, however, in the figures, we show the results for a Savitzky-Golay polynomial filter having a width of τ = 200 s (see Appendix A for details of the data processing technique). The exceptions are panel c in Fig. 5 and panel d in Fig. 6, where we selected τ = 300 s to allow for longer periods. These τ values are shown in each wavelet spectrum by a horizontal line. It should be noted that smoothing a time profile over a τ value does not mean that the spectral powers in its wavelet of the Fourier spectrum will be zero at the periods P greater than the τ value. Their spectral powers would gradually tend towards zero at longer periods. So, peaks with P >  τ would still be present in the spectrum but their power would be suppressed. Notably, the value of the true periods will not change when changing τ. The right sub-panel collects two curves. The global wavelet spectrum obtained by integration of the wavelet power spectrum over time is shown by the black solid curve.

We checked the significance level for two kinds of noise spectra and found that usage of the white noise leads to most spectral peaks being significant, leading to results that do not provide much information. To the contrary, application of a red noise background spectrum leads to more reasonable constraints on the number of significant components. The 99% significance level according the red noise is plotted as black thin contour over the wavelet spectrum and as the dashed line over the global wavelet spectrum. A Fourier periodogram of the high-frequency signal is plotted by a red curve. The periodogram is normalised over the maximum of the global wavelet power.

The spectral resolution is not the same for longer and shorter periods in the periodogram because its period axis is defined as Pi = 1/fi, where fi is the Fourier frequencies, i = 0…N/2, N is the number of points in the time profile. We need to take into account that the period axis is not regular when estimating the error bars for periods. In the next subsections, we will give the period values in the following format: 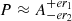P≈ A −e r 2 +e r 1 $ P \approx A^{+er_1}_{-er_2} $ s. Here, A = 1/f is the period (in seconds) corresponding to the Fourier frequency, f, at the peak maximum. The superscript er1 and subscript er2 indicate the differences between A and the two neighbour periods in the period axis. As the period axis is not regular, the values er1 ≠ er2.

5.1. Chromospheric Hα emission

The periodic properties of Hα emission from different sources are collected in Fig. 5. The periodic variations are pronounced in the time profiles associated with both the whole structure R1+R2 and the inner ribbon R1 (the thick black curve in the coloured panels a and b). Wavelet spectra demonstrate well-recognised stripes of a stable period. Wavelet transform detects the period 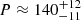P ≈ 140 − 11 + 12 $ P \approx 140^{+12}_{-11} $ s. At the same time, the Fourier periodogram reveals one dominant peak at the period 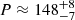P ≈ 148 − 7 + 8 $ P \approx 148^{+8}_{-7} $ s. The peak in global wavelet spectrum (black curve) is wide. Its full width at the half maximum is FWHM ≈ 60 s. The main peak in the periodogram (red curve) is narrower than the corresponding peak in the global wavelet spectrum, FWHM ≈ 10 s. It is obvious from the wavelet spectrum that the periodicity found is associated with the flare activity. No periodicity is evident before the flares nor after the flares. In the wavelet spectrum of the whole circular ribbon structure R1+R2 (Fig. 5, panel a), the periodicity continues for a long time, 1400 s, enveloping nine period cycles in total. The value of the period does not depend on the value of the smoothing interval τ (see Appendix A for details). Therefore, we show the results for τ = 200 s in panels a and b for better visualisation.

The wavelet spectrum of the remote source R3 (Fig. 5, panel c) reveals a number of irregular spots during the flares. The global wavelet spectrum shows a very wide peak with a maximum at P ≈ 152 s with the FWHM ≈ 90 s. A Fourier periodogram demonstrates the set of three peaks with the periods 125 s, 150 s, and 185 s. These peaks have almost equal powers. However, the periods 125 s and 150 s disappear for τ = 300 s, leaving the only significant period 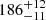186 − 11 + 12 $ 186^{+12}_{-11} $ s. Therefore, we show the results for τ = 300 s.

5.2. Microwave and hard X-ray emissions

In order to study in detail the periodicity found in Hα emission from the circular ribbon structure during two flares, we make a comparative analysis of the periodicities in different wave bands. Multi-periodic behaviour is found both in microwave and hard X-ray emissions (Fig. 6). Each of the wavelet spectra of the microwave emission at 4 GHz, 5.7 GHz, and 8 GHz reveals a period of 157 s that coincide with the flares. Each of the global wavelet spectra shows wide peaks with maxima at the period, 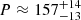P ≈ 157 − 13 + 14 $ P \approx 157 ^{+14}_{-13} $ s.

The Fourier periodograms at these three frequencies show similar, but not identical, compositions of spectral components. The periodogram at 4 GHz shows three peaks with maxima at periods 187 s, 150 s, and 128 s (Fig. 6, panel a). 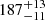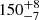However, the periodogram applied to the filtered time series (with the Gaussian-shaped Fourier filter with boundaries 120 s and 200 s enveloping these three spectral peaks) leaves only two significant periods 187 − 11 + 13 $ 187^{+13}_{-11} $ s, 150 − 7 + 8 $ 150^{+8}_{-7} $ s. The global wavelet spectrum does not identify two periods, enveloping them with one broad peak (FWHM ≈ 68 s) with its maximum at P ≈ 172 s. The wavelet transform identifies the period P ≈ 150 s with each flare and the period P ≈ 187 s with the interval between the flares. Also, we note that the period 187 s is comparable with the duration of the flares observed in microwaves. The spectral peak with the period P ≈ 128 s has disappeared from the wavelet spectrum and from the periodogram. This indicates that this peak could be a harmonic of a low-frequency trend (Inglis & Nakariakov 2009).

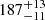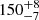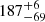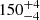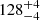In the same way, the periodogram of 5.7 GHz emission contains peaks at periods of 187 − 11 + 13 $ 187^{+13}_{-11} $ s and 150 − 7 + 8 $ 150^{+8}_{-7} $ s (Fig. 6, panel b). Emission at 8 GHz reveals the following set of the periods 187 − 69 + 6 $ 187^{+6}_{-69} $ s, 150 − 4 + 4 $ 150^{+4}_{-4} $ s, and 128 − 4 + 4 $ 128^{+4}_{-4} $ s (Fig. 6, panel c). However, the Fourier filtration method reveals only the first two periods.

The wavelet power spectrum for hard X-ray emission at 20–80 keV demonstrates a complicated period structure from 01:56 UT to 02:15 UT (Fig. 6, panel d). The global wavelet spectrum shows one wide peak with maximum at P ≈ 150 s. The overplotted periodogram shows that the peak consists of one dominant peak 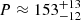P ≈ 153 − 12 + 13 $ P \approx 153^{+13}_{-12} $ s and two secondary, less powerful peaks. 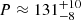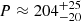The periods of the secondary peaks shown in the figure are P ≈ 131 − 8 + 10 $ P \approx 131^{+10}_{-8} $ s and P ≈ 204 − 20 + 25 $ P \approx 204^{+25}_{-20} $ s. However, the period 204 s is comparable with the duration of the flares themselves, meaning that it is rather a trend than a QPP. The period 131 s is not stable relative to the τ value. Therefore, we do not consider them in the following analysis.

5.3. Soft X-ray emissions

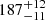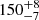The wavelet spectrum of the soft X-ray emission at 1–8 Å and its time derivative are presented in Fig. 6 (panels e and f). Testing by each of the methods mentioned in Appendix A reveals two significant periodic components in the 1–8 Å channel, 187 − 11 + 12 $ 187 ^{+12}_{-11} $ s and 150 − 7 + 8 $ 150^{+8}_{-7} $ s. The time derivative of the flux at 1–8 Å contains the same periods.

5.4. Periods during the flare decay

The brightening of the elongated ribbon R4 started when the emission from the other Hα ribbons and the emission in the other wavelengths reached the decay phase (Fig. 3). In contrast to the microwave emission, the soft X-ray emission still contains strong periodic components connected to the impulsive flare phase. Therefore, in order to avoid the influence of the periodicities related to the flares, we analyse GOES data that started later than Hα and microwave data. Those start times are marked both by dashed vertical line in Figs. 5 and 6 (02:13:20 UT) for the microwave emission and by dotted vertical line in Fig. 6 (02:16:56 UT) — for the soft X-ray emission. The results are shown in Fig. 7 and in Table 2.

Table 2.

Periods (in seconds) with error bars detected during the decay phase in different emission bands.

The global wavelet spectrum of ribbon R4 (Fig. 5 panel d) has a maximum at the period 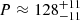P ≈ 128 − 11 + 11 $ P \approx 128^{+11}_{-11} $ s. This period keeps its value and significance for all the considered τ values. There is a secondary peak at 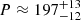P ≈ 197 − 12 + 13 $ P \approx 197^{+13}_{-12} $ s. This period also keeps its value for τ >  200 s. We note that the wavelet spectrum in Fig. 5 (panel d) corresponds to τ = 200 s to emphasise the shorter period, therefore, the 197 s period is not significant there. The longer period is also found in GOES data. Its wavelet spectrum (Fig. 7 panel a) reveals one peak at 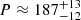P ≈ 187 − 12 + 13 $ P \approx 187^{+13}_{-12} $ s.

The microwave emission at 5.7 GHz contains only a single mode QPPs with 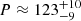P ≈ 123 − 9 + 10 $ P \approx 123^{+10}_{-9} $ s (Fig. 7 panel b). However, when increasing τ up to 300 s, the period of 200 s becomes significant, whereas the 123 s period decreases its power down to below the significance level. In order to perform an independent check of these periods, we applied the method of Empirical Mode Decomposition (EMD). This method decomposes a signal into intrinsic modes which are, in contrast to wavelet and Fourier methods, not restricted a priori to the harmonic functions or their wavelets (see Appendix A for details). The EMD spectrum of the flux at 5.7 GHz is shown in Fig. 7 (panel d). Crosses indicate the total energies for all detected EMD modes. The general slope of the EMD spectrum is plotted by blue curve. For each characteristic time scale (or period), the spectral energy is distributed as a χ2 function with a number of degrees of freedom k >  2, resulting in the existence of two, that is, the upper and lower, confidence intervals (Kolotkov et al. 2016). Thus, the significant EMD modes are those with the total energies outside the area bounded by these intervals. In panel d, the total energy of the 120 s EMD mode is seen to be well above the 99% upper confidence level, coinciding with the 123 s period found in wavelet analysis panel b. The period of 190 s was not detected in the EMD analysis at all. In contrast to the microwave emission at 5.7 GHz, the combination of the mentioned methods did not detect any significant periods at both 4 GHz and 8 GHz.

To summarise, the quasi-periodic variations with a common average period of 150 s are found during the impulsive phase of the flares in the time profiles of Hα emission from the circular ribbon structure, in the microwave emission at 4–8 GHz, in the hard X-ray emission at 20–80 keV, and in soft X-ray emission in 1–8 Å band including its time derivative. The value of the period varies from 148 s to 153 s for different observational bands, but the variations do not exceed the detection errors (see Table 1). We also find a period around 190 s is present in Hα emission from R3 kernel, in microwave emission at 4–8 GHz, and in soft X-ray emission at 1–8 Å. During the decay phase, we also detected the same period around 190 s, within the error bars: the period 187 s in soft X-rays and 197 s in Hα emission from kernel R4. The period with an average value of 125 s is found during the decay flare phase in the emission of the Hα R4 kernel and in the microwave emission at 5.7 GHz.

6. Discussion and conclusions

We chose the circular ribbon flare on 5 March 2014 because of its location near to the disk centre, which allowed us to observe the flare ribbons related to a magnetic fan and the remote flare ribbons with minimal projection effects. Studying this event, we used QPP analysis for understanding relationship between the different flare kernels and processes in the circle ribbon flares. We were interested in revealing the flare kernel (or kernels) that were the source of the observed series of pulses and determining the pulse’s generation mechanism (or mechanisms).

Following the analysis of the time profiles performed in Sect. 4 we found a periodicity (P1) around 150 s in the Hα emission from flare kernels R1, R1+R2, microwave emission and the X-ray emission (panels a–d in Fig. 6). Thus, we can conclude that it is the same periodicity related to R1+R2 kernels and appeared in both X-rays and microwaves. We note that this periodicity is also seen in the GOES time derivative that is used as an indicator of the accelerating processes according to the Neupert effect. The presence of a 150 s periodicity in the hard X-ray emission (20–80 keV), the GOES time derivative, and the 4–8 GHz microwave emission suggests the non-thermal origin of this periodicity. The presence of such a period in soft X-ray flux 1–8 Å indicates that plasma heating were fully caused by the thermalisation of accelerated electrons. Most likely, it is the result of repetitive injections of accelerated electrons. The presence of only this period in the emission from R1+R2 flare kernels implies that the magnetic fan-spine (Fig. 5) is the source of the observed QPPs with a period around 150 s.

The explanation of the 150 s periodicity is likely related to the continuous rotation of the parasitic polarity in the vicinity of the future circular ribbon and apparent motion of the emission source in the circular ribbon R2 reported by Xu et al. (2017). Previous studies (Aulanier et al. 2006; Masson et al. 2009; Reid et al. 2012; Wang & Liu 2012) noted the presence of slipping and slip-running reconnection in the fan-spine and related it to the apparent propagation of the circular ribbon emission. Wang & Liu (2012) found evidence of slipping or slip-running reconnection in their studied events and the emission propagation was in the anticlockwise direction as reported by Xu et al. (2017) for the current event.

We can carry out some estimations based on the assumption that the length of the Hα R2 ribbon during the initial brightening was the result of the primary energy release and precipitation of accelerated electrons. The diameter of the outline of the fan-spine is about 10 arcsec (see Fig. 2), giving the full length of the perimeter to be 23 Mm. As we can see in Fig. 1 in Xu et al. (2017), the initial R2 ribbon length is less than one-quarter of the outline length. Thus, the ribbon length (Lr) is about 6 Mm. We can assume that we observe the direct precipitation of electrons accelerated during the reconnection process within this ribbon length. In this case, the velocity of the process propagation should be up to Lr/P1. So for P1 = 150 s this gives 40 km s−1. Estimations of characteristic slipping reconnection velocities from simulations were around 30 km s−1 (Masson et al. 2009). Observational estimates vary within 20–40 km s−1 (Dudík et al. 2016). This agreement between our estimations and the velocity measurements indicate slipping or slipping running reconnection as the source of quasi-periodicity detected in the R1 and R2 kernels. The other possible drivers of reconnection processes are magnetohydrodynamic (MHD) waves. The sound speed, that is, the characteristic phase speed of the slow magnetoacoustic mode, estimated for the electron temperature 14–17 MK (see Sect. 4) is Cs ≈ 620–680 km s−1. If the reconnection is modulated by the slow MHD wave propagating along an arcade formed by the magnetic fan, the sound speed is an order of magnitude higher than the velocity of process propagation obtained above (about 40 km s−1). The propagation of the fast MHD wave is defined by the phase speed of the fast MHD mode, which is higher than the sound speed. All these estimations of MHD wave characteristics do not support the hypothesis of an MHD wave as the direct reason of the observed 150 s periodicity in the case of wave propagation along the circular arcade. However, we note that in the 3D case, the propagation parameters of MHD waves could change due to various reasons (see Afanasyev & Uralov 2016; Nakariakov & Zimovets 2011), which could potentially explain the observed 150 s periodicity. However, an in-depth analysis required here is beyond of the scope of this study.

According to Fig. 2 (bottom panel) and the 3D magnetic field reconstruction (see Fig. 8 in Xu et al. 2017), the remote flare kernel R3 was connected to the magnetic fan-spine with a loop. So, we could expect that a periodic process in the circular ribbon structure affects the periodic properties of the Hα emission from the R3 kernel, for example, via accelerated electrons passing from the reconnection site to the R3 kernel along the loop. However, we did not detect any period around 150 s in the R3 kernel. The dominant period found in the Hα emission from R3 kernel is 190 s. The 190-s period is absent in the hard X-ray emission that is related to non-thermal electron precipitation only. Moreover, there are obvious differences between the time profiles of the R1, R2, and R3 kernels and the hard X-ray emission. These facts do not support the hypothesis of direct excitation of R3 emission by the same population of accelerated electrons that generated the emission of R1 and R2 kernels.

On the other hand, we found the 190 s period in the microwave and soft X-ray emission. The kernel R3 is the likely source of this period in flare emission as it is located very close to the large sunspot and exhibits the same magnetic polarity as the sunspot. The value of the period is close to the 180 s period oscillation usually observed in sunspots (see e.g. Thomas & Weiss 2008). Thus, oscillations leaking from the sunspot could modulate both the R3 flare Hα emission and the gyrosynchrotron emission of accelerated electrons seen in the microwaves.

Emission of the kernel R4 started during the decay phase of R1, R2, and R3 kernels and there are no hard X-ray emission or response in soft X-ray time derivative. Two periods were detected in kernel R4. The first period, namely, of 190 s, was detected in the soft X-ray emission while the second period, of 125 s, was found in microwave emission. These facts could indicate different origins of detected oscillations.

The similarity of the 190 s QPPs seen both in the Hα emission from kernel R4 and in the soft X-ray emission indicates that a thermal mechanism caused these QPPs. We can attribute the detected 190 s periodicity to the oscillations in the sunspot having characteristic timescales within 2–4 min (see Khomenko & Collados 2015; Sych et al. 2015), or the three-minute sunspot oscillations. However, those oscillations do not have enough energy to generate the flare emission directly. Therefore, the 190 s period could be a result of the modulation of the flare emission from kernel R4 by the three-minute sunspot oscillations.

The second period, of 125 s, found in R4 Hα emission is similar to that found in the microwave emission at 5.7 GHz, indicating a non-thermal mechanism. The fact that this periodicity is detected in only one microwave frequency could result from the low flux densities at other frequencies during the decay phase. We hypothesise that the 125 s period could relate to kink oscillations of the loop connecting the fan (R1+R2) with remote kernel (R3) and seen in EUV emission black (bottom panel in Fig. 2). The loop or outer spine became visible at about 02:00 UT. One can see its transverse oscillations at 171 Å band. The kink oscillations of the loop could cause a null point reconnection (Nakariakov et al. 2006; Reid et al. 2012; Wang & Liu 2012) and generate the accelerated electrons. The kink-oscillations of the loop could result in interaction between the loops relating the kernel R4 with the sunspot. We speculate that part of the electron flux could precipitates and generates the kernel R4 emission. Moreover, the interaction between the loops could be another possible origin of the electron acceleration.

In summary, our conclusion regarding the mechanisms of emission generation based on periodicity properties analysis in the different flare kernels is as follows. We revealed a 150 s periodicity that was simultaneously observed in the spatially resolved Hα flare kernels, soft and hard X-ray emission, and microwave emission. The Hα flare kernels exhibiting this periodicity were related by a magnetic fan-spine structure. The analysis of estimated parameters of the pulses suggests the slipping reconnection mechanism as the origin of these QPPs. We found the 190 s period in both the remote kernel R3 during the impulsive phase and the kernel R4 raised during the decay phase of the event. This periodicity is close to the three-minute oscillations observing in sunspots. However, as the three-minute oscillations typically do not have enough energy to directly generate the flare emission, we suggest that the QPPs of the flare kernels R3 and R4 could be caused by the modulation of their emission by the three-minute wave trains coming from the sunspot. The observational facts indicate a relation between the 125 s period found in the thermal kernel R4 emission and the kink oscillations of the outer spine, which connects the place of the null point reconnection with the remote kernel. This hypothesis, however, requires further study.

Acknowledgments

This research was partly supported by the budgetary funding of Basic Research programs No. II.16 (LKK), No. II.12 (DYK) and No. 0041-2019-0019 (EGK), the grant of the Russian Foundation for Basic Research No. 18-02-00856 (EGK), the grant of the National Natural Science Foundation of China No. 11873091 and Basic Research Program of Yunnan Province No. 2019FA001 (ZX), by the STFC consolidated grant ST/P000533/1 (HASR), and by the STFC consolidated grants ST/P000320/1 and ST/T000252/1 (DYK). Authors thank CSUC “Angara” for SSRS data, teams operating RHESSI, Fermi, SDO, RSTN and GOES for open access to observational data.

References

  1. Afanasyev, A. N., & Uralov, A. M. 2016, Sol. Phys., 291, 3185 [CrossRef] [Google Scholar]
  2. Aptekar, R. L., et al. 1995, Space Sci. Rev., 71, 265 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aulanier, G., DeLuca, E. E., Antiochos, S. K., McMullen, R. A., & Golub, L. 2000, ApJ, 540, 1126 [NASA ADS] [CrossRef] [Google Scholar]
  4. Aulanier, G., Pariat, E., Démoulin, P., & DeVore, C. R. 2006, Sol. Phys., 238, 347 [NASA ADS] [CrossRef] [Google Scholar]
  5. Carmichael, H. 1964, NASA Spec. Publ., 50, 451 [NASA ADS] [Google Scholar]
  6. Dudík, J., Polito, V., Janvier, M., et al. 2016, ApJ, 823, 41 [NASA ADS] [CrossRef] [Google Scholar]
  7. Fletcher, L., Metcalf, T. R., Alexander, D., Brown, D. S., & Ryder, L. A. 2001, ApJ, 554, 451 [NASA ADS] [CrossRef] [Google Scholar]
  8. Gruber, D., Lachowicz, P., Bissaldi, E., et al. 2011, A&A, 533, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Hirayama, T. 1974, Sol. Phys., 34, 323 [NASA ADS] [CrossRef] [Google Scholar]
  10. Huang, N. E., & Wu, Z. 2008, Rev. Geophys., 46, RG2006 [NASA ADS] [CrossRef] [Google Scholar]
  11. Inglis, A. R., & Nakariakov, V. M. 2009, A&A, 493, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Khomenko, E., & Collados, M. 2015, Liv. Rev. Sol. Phys., 12, 6 [CrossRef] [Google Scholar]
  13. Kolotkov, D. Y., Anfinogentov, S. A., & Nakariakov, V. M. 2016, A&A, 592, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Kopp, R. A., & Pneuman, G. W. 1976, Sol. Phys., 50, 85 [NASA ADS] [CrossRef] [Google Scholar]
  15. Kumar, P., Nakariakov, V. M., & Cho, K.-S. 2015, ApJ, 804, 4 [NASA ADS] [CrossRef] [Google Scholar]
  16. Kupriyanova, E. G., Melnikov, V. F., Nakariakov, V. M., & Shibasaki, K. 2010, Sol. Phys., 267, 329 [NASA ADS] [CrossRef] [Google Scholar]
  17. Kupriyanova, E. G., Melnikov, V. F., & Shibasaki, K. 2013, Sol. Phys., 284, 559 [NASA ADS] [CrossRef] [Google Scholar]
  18. Lau, Y.-T., & Finn, J. M. 1990, ApJ, 350, 672 [NASA ADS] [CrossRef] [Google Scholar]
  19. Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
  20. Lin, R. P., Dennis, B. R., Hurford, G. J., et al. 2002, Sol. Phys., 210, 3 [Google Scholar]
  21. Liu, Z., Xu, J., Gu, B.-Z., et al. 2014, Res. Astron. Astrophys., 14, 705 [Google Scholar]
  22. Masson, S., Pariat, E., Aulanier, G., & Schrijver, C. J. 2009, ApJ, 700, 559 [NASA ADS] [CrossRef] [Google Scholar]
  23. Meegan, C., Lichti, G., Bhat, P. N., et al. 2009, ApJ, 702, 791 [NASA ADS] [CrossRef] [Google Scholar]
  24. Meshalkina, N. S., Uralov, A. M., Grechnev, V. V., Altyntsev, A. T., & Kashapova, L. K. 2009, PASJ, 61, 791 [CrossRef] [Google Scholar]
  25. Mészárosová, H., Dudík, J., Karlický, M., Madsen, F. R. H., & Sawant, H. S. 2013, Sol. Phys., 283, 473 [NASA ADS] [CrossRef] [Google Scholar]
  26. Nakajima, H., Nishio, M., Enome, S., et al. 1994, IEEE Proc., 82, 705 [NASA ADS] [CrossRef] [Google Scholar]
  27. Nakariakov, V. M., & Zimovets, I. V. 2011, ApJ, 730, L27 [NASA ADS] [CrossRef] [Google Scholar]
  28. Nakariakov, V. M., Foullon, C., Verwichte, E., & Young, N. P. 2006, A&A, 452, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Nakariakov, V. M., Kolotkov, D. Y., Kupriyanova, E. G., et al. 2019, Plasma Phys. Controlled Fusion, 61, 014024 [NASA ADS] [CrossRef] [Google Scholar]
  30. Neupert, W. M. 1968, ApJ, 153, L59 [NASA ADS] [CrossRef] [Google Scholar]
  31. Pal’shin, V., Charikov, Y., Aptekar, R., et al. 2014, Geomag. Aeron., 54, 943 [CrossRef] [Google Scholar]
  32. Pariat, E., Antiochos, S. K., & DeVore, C. R. 2009, ApJ, 691, 61 [Google Scholar]
  33. Reid, H. A. S., Vilmer, N., Aulanier, G., & Pariat, E. 2012, A&A, 547, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
  35. Scherrer, P. H., Schou, J., Bush, R. I., et al. 2012, Sol. Phys., 275, 207 [Google Scholar]
  36. Schwartz, R. A., Csillaghy, A., Tolbert, A. K., et al. 2002, Sol. Phys., 210, 165 [NASA ADS] [CrossRef] [Google Scholar]
  37. Sturrock, P. A. 1966, Nature, 211, 695 [NASA ADS] [CrossRef] [Google Scholar]
  38. Su, Y., van Ballegooijen, A., Schmieder, B., et al. 2009, ApJ, 704, 341 [NASA ADS] [CrossRef] [Google Scholar]
  39. Sych, R., Karlický, M., Altyntsev, A., Dudík, J., & Kashapova, L. 2015, A&A, 577, A43 [CrossRef] [EDP Sciences] [Google Scholar]
  40. Thomas, J. H., & Weiss, N. O. 2008, Sunspots and Starspots (Cambridge University Press) [CrossRef] [Google Scholar]
  41. Torrence, C., & Compo, G. P. 1998, Bull. Am. Meteorol. Soc., 79, 61 [Google Scholar]
  42. Wang, H., & Liu, C. 2012, ApJ, 760, 101 [Google Scholar]
  43. Xu, Z., Yang, K., Guo, Y., et al. 2017, ApJ, 851, 30 [NASA ADS] [CrossRef] [Google Scholar]
  44. Zhang, Q. M., Ning, Z. J., Guo, Y., et al. 2015, ApJ, 805, 4 [NASA ADS] [CrossRef] [Google Scholar]
  45. Zhdanov, D. A., & Zandanov, V. G. 2011, Cent. Eur. Astrophys. Bull., 35, 223 [Google Scholar]
  46. Zhdanov, D. A., & Zandanov, V. G. 2015, Sol. Phys., 290, 287 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Time series processing method

The procedure described below is applied to each time series under study in a uniform way. The time profiles, first, are interpolated to a regular time axes. We consider different methods of data processing in order to minimise possible effects of the method on the results. We perform the periodic analysis with the de-trended time series, or high-frequency signal, FHF (see Nakariakov et al. 2019). We use a combination of the wavelet (Morlet) technique (Torrence & Compo 1998) and of the Lomb-Scargle periodogram (Scargle 1982) and autocorrelation analysis. The method was tested and described in detail by Kupriyanova et al. (2010). Here we recall its principal steps.

We attract both a smoothing methods and Fourier filtration method to obtain the high-frequency signal. The smoothing method implies, first, calculation of the slowly varying background, or trend, of the original time series. We use both smoothing with the running average (smooth.pro) and a Savitzky-Golay polynomial filter (savgol.pro), both IDL procedures are applied for the same characteristic time window, τ. Then, subtracting the trend from the original time series, we obtain the high-frequency component.

The method of Fourier filtration implies zeroing the spectral power in the Fourier power spectrum of the original time series outside the period band (filter) of interest. The filter boundaries define the lower and higher period values at the half power of the Gaussian bell. So, the periods lower than and higher than the filter are not cut off abruptly but, rather, we smoothly decrease their specral power down to zero. Performing inverse Fourier transform to the filtered spectrum, we obtain the high-frequency component without trend and without high-frequency noise. The de-trended components obtained in these three ways are thus ready for period analysis that follows.

We use a combination of the wavelet technique and of the Lomb-Scargle periodogram to analyse the periods in flare emission. Using both methods, we find the significant spectral peaks. The significance level of a spectral peak is estimated assuming Markov red noise (or Brownian noise; Torrence & Compo 1998). We note that the red noise imposes stronger restrictions for significance of a spectral peak than white noise (Gruber et al. 2011). Those peaks for which spectral power exceed 99% probability level by two methods are believed to be true peaks.

This procedure is repeated for each set of iterations. The reason for the iterations is that the smoothing could lead to an appearance of false peaks in the periodogram and in the wavelet spectrum. In order to avoid these possible artefacts, we obtain the high-frequency component for a set of various τ values in a wide range, from τ = 50 s to τ = 300 s. Changing the τ value affects the statistical significance of the peak in the periodogram. However, it does not change the value of the true period (see e.g. the periodograms in Kupriyanova et al. 2013). Therefore, we believe that the period is true if it satisfies the following conditions: (1) the period value does not depend on the specific τ value; (2) the peak remains significant for different τ values. We do not make checks for longer τ values because in our specific case the characteristic duration of separate flares themselves is, roughly, 300–400 s. The flare repeatability rate is a topic of a separate study, but in this paper we are interested in the fine time structure of the flare emission.

Independently, Gaussian filtration over periods from 120 s to 200 s is applied to verify shorter periods and from 120 s to 300 s to verify longer periods. The visual control of similarity of the high-frequency signals obtained with both smoothing and filtration is performed, and the periods pronounced for all the methods are selected for the following periodic analysis.

Finally, the values of the significant periods obtained with both the wavelet and Fourier methods applied to all the high-frequency signals are compared. Those periods which are similar for all the methods are selected for the diagnostics of processes in the flare volume.

Separately, in order to check the periodic properties of the emissions during the decay phase, we perform the additional analysis using the method of the empirical mode decomposition (EMD). The fundamental difference of this method from the methods based on the Fourier transform described above is that it does not imply a priori any basic functions (Huang & Wu 2008). The method analyses the time scales of the time series itself, collecting the similar time scales into an intrinsic empirical mode. The iteration method distinguishes modes of different time scales, from the low-frequency trend to high-frequency noise. Similarly to the methods based on the Fourier transform, not all intrinsic EMD modes necessarily represent a statistically significant oscillatory process (Kolotkov et al. 2016). Therefore, in this study, we estimate the significance of EMD modes by approximating the shape of the EMD spectrum by a power law function and constructing confidence intervals.

All Tables

Table 1.

Periods (in seconds) with error bars detected during both flares in different emission bands.

In the text
Table 2.

Periods (in seconds) with error bars detected during the decay phase in different emission bands.

In the text

All Figures

thumbnail Fig. 1.

Principal elements of the fan-spine structure involved in the flare SOL2005-05-06 schematically sketched over the SDO/AIA image in the 304 Å band at 02:16:20 UT. The chromospheric kernels are outlined by the yellow ovals: R1+R2 is the circular ribbon structure, where the inner ribbon R1 and the circular ribbon R2 are shown in detail separately at 01:55:49 UT within the dotted rectangle; R3 is the remote ribbon; R4 is the elongated ribbon seen at the decay phase. The fan-spine magnetic structure is drawn in green and magenta: the fan lines (magenta) form the inner spine; the dome lines (green) continue into the outer spine (a long loop anchored at R3 kernel); a quasi-separatrix layer is the surface between magenta and green lines (is not shown here) with the magnetic null-point located between the inner and outer spines (Pariat et al. 2009). Loops in blue connect the sunspot (dark pink) with R3 and R4 kernels.
In the text
thumbnail Fig. 2.

SDO/AIA 171 Å maps during the first flare at 01:57:12 UT (top) and during the second flare at 02:07:25 UT (bottom) with the over-plotted contours of hard X-ray emission at 6–12 keV (red), 12–25 keV (light green) and 25–50 keV (white). In the top panel, the X-ray images were reconstructed within 01:55:15–01:55:35 UT (the first peak) by the CLEAN algorithm. The X-ray sources shown by the solid line in the bottom panel were reconstructed within 02:07:00–02:08:40 UT by PIXON algorithm. The contour levels are 50% and 90% of maximum. The X-ray source associated with R4 was obtained by CLEAN algorithm within 02:18:30–02:20:30 UT. The levels are 40%, 60%, and 80% of maximum. The SDO/AIA 304 Å chromosperic kernels are marked by yellow. The magnetic field features of positive and negative polarity are marked by blue and magenta, correspondingly. The absolute value of magnetic feature strength is above 500 G.
In the text
thumbnail Fig. 3.

Normalised time profiles of the flare emission in different spectral ranges. All the time profiles are normalised by their maxima. A colour of each curve within a panel corresponds to the colour of the legend in the panel. Panel a: Hα emission from the sources R1+R2, R1, R3, and R4. Panel b: X-ray flux observed by Fermi/GBM at 25–50 keV and KW at 20–80 keV, and derivative of the GOES flux, at 1–8 Å. Panel c: X-ray fluxes registered by Fermi/GBM 6–12 keV, by GOES at 1–8 Å, and by GOES at 0.5–4 Å. Panel d: microwave fluxes at 8 GHz, 5.7 GHz, and 4 GHz obtained with SSRS. Panel e: X-ray uncorrected fluxes registered by RHESSI at 6–12 keV, 12–25 keV, and 25–50 keV. The RHESSI sources shown in Fig. 2 were reconstructed within time intervals enclosed into pairs of the same-coloured vertical solid lines.
In the text
thumbnail Fig. 4.

Left panel: evolution of the X-ray spectra. The observed X-ray spectra (marked by dots) are overplotted by the results of the fitting by a model consisting of an optically thin thermal bremsstrahlung function and power-law function. The average value of the time interval, the observational data, and the results of the fitting are marked by the same colour for each moment in time. Right panel: evolution of the microwave spectra. The observed data (marked by the dots) are over plotted by the result of fitting by the function corresponding to the form of the gyrosynchrotron spectrum. The average value of the time interval, the observational data and the results of the fitting are marked by the same colour for each moment in time. The vertical orange lines mark the 4 GHz and 8 GHz frequencies.
In the text
thumbnail Fig. 5.

Results of the wavelet and Fourier analyses of the Hα emission from different flare kernels. The vertical dashed line in panel d indicates the start time of the brightening of the R4 ribbon, 02:13:20 UT.
In the text
thumbnail Fig. 6.

Results of the wavelet and Fourier analyses of the microwave and X-ray emission. The vertical dashed line in panel b marks the start time of the brightening of the R4 ribbon. The vertical dashed line in panel e marks the start time of the interval analysed in Fig. 7 (panel a).
In the text
thumbnail Fig. 7.

Panels a–c: results of the wavelet and Fourier analyses of the soft X-ray, microwave, and Hα R4 kernel data, during the decay flare phase. Panel d: empirical mode decomposition (EMD) spectrum of the microwave flux at 5.7 GHz. The total energies of the decomposed intrinsic modes are shown by crosses. The blue curve represents the global slope of the spectrum. The 99% confidence intervals are shown by red curves.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.