| Issue |
A&A
Volume 641, September 2020
|
|
|---|---|---|
| Article Number | A98 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202038139 | |
| Published online | 16 September 2020 | |
Astrochemical relevance of VUV ionization of large PAH cations★
1
Institut de Recherche en Astrophysique et Planétologie (IRAP), Université de Toulouse (UPS), CNRS, CNES,
9 Avenue du Colonel Roche,
31028
Toulouse, France
e-mail: christine.joblin@irap.omp.eu
2
Synchrotron SOLEIL, L’Orme des Merisiers,
91192
Saint Aubin,
Gif-sur-Yvette,
France
3
INRAE, UAR1008, Transform Department, Rue de la Géraudière,
BP 71627,
44316
Nantes, France
4
Laboratoire de Chimie et Physique Quantiques (LCPQ/IRSAMC), Université de Toulouse (UPS), CNRS,
118 Route de Narbonne,
31062
Toulouse, France
5
Istituto Nazionale di Astrofisica – Osservatorio Astronomico di Cagliari,
Via della Scienza 5,
09047
Selargius (CA), Italy
6
Laboratoire Collisions Agrégats Réactivité (LCAR/IRSAMC), Université de Toulouse (UPS), CNRS,
118 Route de Narbonne,
31062
Toulouse, France
7
Centro de Investigación en Química Biolóxica e Materiais Moleculares (CiQUS) and Departamento de Química Orgánica, Universidade de Santiago de Compostela,
15782
Santiago de Compostela, Spain
Received:
9
April
2020
Accepted:
1
July
2020
Context. As part of interstellar dust, polycyclic aromatic hydrocarbons (PAHs) are processed by an interaction with vacuum ultraviolet (VUV) photons emitted by hot stars. This interaction leads to the emission of not only the well-known aromatic infrared bands, but also electrons, which can significantly contribute to the heating of the interstellar gas.
Aims. Our aim is to investigate the impact of molecular size on the photoionization properties of cationic PAHs.
Methods. Trapped PAH cations of sizes between 30 and 48 carbon atoms were submitted to VUV photons in the range of 9–20 eV from the DESIRS beamline at the synchrotron SOLEIL. All resulting photoproducts including dications and fragment cations were mass-analyzed and recorded as a function of photon energy.
Results. Photoionization is found to be predominant over dissociation at all energies, which differs from the conclusions of an earlier study on smaller PAHs. The photoionization branching ratio reaches 0.98 at 20 eV for the largest studied PAH. The photoionization threshold is observed to be between 9.1 and 10.2 eV, in agreement with the evolution of the ionization potential with size. Ionization cross sections were indirectly obtained and photoionization yields extracted from their ratio with theoretical photoabsorption cross sections, which were calculated using time-dependent density functional theory. An analytical function was derived to calculate this yield for a given molecular size.
Conclusions. Large PAH cations could be efficiently ionized in H I regions and contribute to the heating of the gas by the photoelectric effect. Also, at the border of or in H II regions, PAHs could be exposed to photons of energy higher than 13.6 eV. Our work provides recipes to be used in astronomical models to quantify these points.
Key words: astrochemistry / methods: laboratory: molecular / molecular processes / ISM: molecules / dust, extinction / ultraviolet: ISM
The dataset associated with this work can be found under https://doi.org/10.5281/zenodo.3899775
© G. Wenzel et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Polycyclic aromatic hydrocarbons (PAHs) play a major role in the physics and chemistry of photodissociation regions (PDRs). They strongly absorb the vacuum ultraviolet (VUV) photons emitted by hot stars and relax by emission in the aromatic infrared bands (AIBs). The interaction with VUV photons can lead to other relaxation processes including ionization and dissociation. All these processes together with reactive processes involving in particular electrons and hydrogen (H, H2) govern the evolution of the PAH population in the diffuse interstellar medium (Le Page et al. 2003), in circumstellar disks (Visser et al. 2007), and in reflection nebulae (Montillaud et al. 2013). The results of these chemical models suggest that large PAHs with a typical carbon number, NC, of 50 or more dominate the AIB emission, which led to the grandPAH hypothesis that large and possibly compact PAHs dominate the emission in bright PDRs (Andrews et al. 2015). In some regions associated with these PDRs, large PAHs are expected to be ionized, even reaching the dicationic stage (Tielens 2005; Andrews et al. 2016).
In a previous study we investigated the branching ratio between ionization and fragmentation upon VUV irradiation for medium-sized PAH cations (Zhen et al. 2016) with an NC of between 16 and 24. For all of these cations, fragmentation was observed to be the dominant channel at least up to a photon energy of 13.6 eV which is relevant for H I regions. In the case of larger PAH cations, ionization is expected to be by far the dominant channel as suggested by the study of the hexa-peri-hexabenzocoronene (HBC) cation, C42H , by Zhen et al. (2015). Here, our objective is to quantify the growing importance of ionization as the molecular size increases. Following Zhen et al. (2016), we studied the photoprocessing of PAH cations with an NC between 30 and 48 atoms over the 9.5−20.0 eV VUV range. Photon energies above the Lyman limit are relevant to PAHs observed at the border of ionization fronts in PDRs (Vicente et al. 2013), as well as in H II regions (Compiègne et al. 2007).
, by Zhen et al. (2015). Here, our objective is to quantify the growing importance of ionization as the molecular size increases. Following Zhen et al. (2016), we studied the photoprocessing of PAH cations with an NC between 30 and 48 atoms over the 9.5−20.0 eV VUV range. Photon energies above the Lyman limit are relevant to PAHs observed at the border of ionization fronts in PDRs (Vicente et al. 2013), as well as in H II regions (Compiègne et al. 2007).
Although we also report the branching ratio between ionization and dissociation here, our analysis is focused on ionization. More specifically, we derive the photoionization yield, which is important to model the charge balance of PAHs and its impact on the AIB spectrum (Bakes et al. 2001), but also to evaluate the contribution of these species to the photoelectric heating rate(Bakes & Tielens 1994a; Weingartner & Draine 2001a). The experimental method is described in Sect. 2 and the results are presented in Sect. 3. In Sect. 4, we discuss the astrophysical implications and propose recipes to be used in astrophysical models. We conclude in Sect. 5.
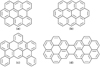 |
Fig. 1 Molecular structures of the studied PAHs, namely (a) benzobisanthene, C30 H |
2 Experimental method and data analysis
We have used the Thermo Scientific™ LTQ XL™ linear ion trap (LTQ ion trap) as described in Milosavljević et al. (2012), which is available at the VUV beamline DESIRS at the synchrotron SOLEIL (Nahon et al. 2012).
The production of PAH cations in the LTQ ion trap was performed using an atmospheric pressure photoionization (APPI) source which required the species of interest to be in solution before their injection with a syringe. This part was a major limitation on the size range of PAHs that we were able to study due to the insolubility of large PAHs. In the present study, we were able to investigate four large PAH cations with NC ranging from 30 to 48, namely (a) benzobisanthene, C30 H , (b) ovalene, C32 H
, (b) ovalene, C32 H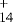 , (c) dibenzophenanthropentaphene (DBPP), C36 H
, (c) dibenzophenanthropentaphene (DBPP), C36 H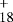 , and (d) dicoronylene, C48 H
, and (d) dicoronylene, C48 H . Sample (b) originated from Janssen Chimica (Belgium), and samples (a) and (c) from the PAH Research Institute in Greifenberg (Dr. Werner Schmidt). The synthesis of compound (d) is briefly reported in Appendix A. The molecular structures of the studied species are depicted in Fig. 1. Emptying the syringe was performed at a constant flow rate for each experiment: 4 μl min−1 for compounds (a) and (b), 6 μl min−1 for compound (c), and 10 μl min−1 for compound (d). The presence of UV irradiation from a Kr discharge lamp ensured a soft creation of PAH cations without fragmentation (Giuliani et al. 2012). The formed cations were then guided through ion optics into the LTQ ion trap in which a constant He pressure of p ≈ 10−3 mbar was held. The ions were cooled by the collisions with He atoms, and the PAH cations of interest, the so-called parent ions, were isolated through specific mass selection and ejection of other species from the ion trap including the 13C isotopomers.
. Sample (b) originated from Janssen Chimica (Belgium), and samples (a) and (c) from the PAH Research Institute in Greifenberg (Dr. Werner Schmidt). The synthesis of compound (d) is briefly reported in Appendix A. The molecular structures of the studied species are depicted in Fig. 1. Emptying the syringe was performed at a constant flow rate for each experiment: 4 μl min−1 for compounds (a) and (b), 6 μl min−1 for compound (c), and 10 μl min−1 for compound (d). The presence of UV irradiation from a Kr discharge lamp ensured a soft creation of PAH cations without fragmentation (Giuliani et al. 2012). The formed cations were then guided through ion optics into the LTQ ion trap in which a constant He pressure of p ≈ 10−3 mbar was held. The ions were cooled by the collisions with He atoms, and the PAH cations of interest, the so-called parent ions, were isolated through specific mass selection and ejection of other species from the ion trap including the 13C isotopomers.
The parent ions were then submitted to the VUV synchrotron radiation which was tuned from 9.5 to 20.0 eV in steps of 0.1, 0.2, 0.3, or 0.5 eV depending on the photon energy range, with the exception of C30 H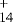 , for which we were able to scan only at low energies up to 15.5 eV. Higher harmonics of the VUV undulator synchrotron radiation with photon energies lower than 16.0 eV were filtered out by a gas filter filled with Ar gas to a pressure of 0.23 mbar. Above 16.0 eV, no such gas filtering is necessary. The photon flux was measured with an IRD AXUV100 calibrated Si photodiode for a monochromator exit slit width of 200 μm and was between 0.8 and 2.8 × 1012 photons s−1 over the studied photon energy range. A typical photon flux can be derived using a previous calibration of the beam size as a function of photon energy (Douix et al. 2017), yielding values of 1.5− 5.2 1014 photons cm−2s−1. In order to limit possible two-photon consecutive absorption processes, we tuned the photon flux by changing (i) the irradiation time from 0.8 to 0.2 s for the lower and higher photon energy ranges, respectively, and (ii) the monochromator exit slit width from 200 μm at low energies to 70 μm at high energies, except for dicoronylene for which values of 400 and 100 μm at low and high energies were used, respectively, to improve the signal-to-noise ratio (S/N). The photon dose was assumed to be linearly proportional to both the irradiation time and the monochromator exit slit width. The probability of two-photon absorption processes could be estimated on the formation of triply charged parent ions, yielding only very small relative intensities below 2% of the total number of photoproducts.
, for which we were able to scan only at low energies up to 15.5 eV. Higher harmonics of the VUV undulator synchrotron radiation with photon energies lower than 16.0 eV were filtered out by a gas filter filled with Ar gas to a pressure of 0.23 mbar. Above 16.0 eV, no such gas filtering is necessary. The photon flux was measured with an IRD AXUV100 calibrated Si photodiode for a monochromator exit slit width of 200 μm and was between 0.8 and 2.8 × 1012 photons s−1 over the studied photon energy range. A typical photon flux can be derived using a previous calibration of the beam size as a function of photon energy (Douix et al. 2017), yielding values of 1.5− 5.2 1014 photons cm−2s−1. In order to limit possible two-photon consecutive absorption processes, we tuned the photon flux by changing (i) the irradiation time from 0.8 to 0.2 s for the lower and higher photon energy ranges, respectively, and (ii) the monochromator exit slit width from 200 μm at low energies to 70 μm at high energies, except for dicoronylene for which values of 400 and 100 μm at low and high energies were used, respectively, to improve the signal-to-noise ratio (S/N). The photon dose was assumed to be linearly proportional to both the irradiation time and the monochromator exit slit width. The probability of two-photon absorption processes could be estimated on the formation of triply charged parent ions, yielding only very small relative intensities below 2% of the total number of photoproducts.
Depending on the acquisition time, a few hundred mass spectra were recorded at each photon energy and averaged to yield one mass spectrum per photon energy step. Following the same procedure, we also recorded blank mass spectra at each photon energy by selecting a mass close to but sufficiently different from each parent ion. This allowed us to perform background subtraction which eliminates contamination peaks from the mass spectra. The averaging procedure provides us with a statistical standard error (see Appendix D). As an example, the background-subtracted mass spectra for ovalene, which has a mass-to-charge ratio of m∕z = 398, are depicted in Fig. 2 at two different photon energies of 9.5 eV and 15.5 eV. The parent ion, C32 H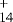 , is well isolated; the 13C isotopic parent ion has a residual contribution of less than 1% remaining in the ion trap. By increasing the photon energy, three different secondary ions can be observed and unambiguously separated, namely the H and 2H/H2 loss, and the main doubly ionized parent ion channels. For the presented example of the ovalene cation, C32 H
, is well isolated; the 13C isotopic parent ion has a residual contribution of less than 1% remaining in the ion trap. By increasing the photon energy, three different secondary ions can be observed and unambiguously separated, namely the H and 2H/H2 loss, and the main doubly ionized parent ion channels. For the presented example of the ovalene cation, C32 H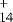 , these species are C32 H
, these species are C32 H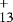 , C32 H
, C32 H , and C32 H
, and C32 H , respectively (see Fig. 2). When extracting the peak intensities as in the following, one has to consider the detector gain efficiency that varies with the charge and the mass of the ions of interest. Recommended scaling factors were therefore applied (see Appendix B).
, respectively (see Fig. 2). When extracting the peak intensities as in the following, one has to consider the detector gain efficiency that varies with the charge and the mass of the ions of interest. Recommended scaling factors were therefore applied (see Appendix B).
3 Results and discussion
3.1 Action spectra and branching ratio
The action spectra are determined following the procedure described in Appendix B yielding relative intensities of the photoproducts as used in a previous study (Zhen et al. 2016). The resulting spectra for the photoionization (dication, denoted I) and photodissociation (fragments, denoted F) channels of the four studied PAH cations are shown in Fig. 3 as a function of the photon energy. The F channel remains small for all investigated PAH cations at all photon energies and is barely notable for the dicoronylene cation in Fig. 3. More specifically, Fig. 4 shows that the branching ratio (BR) for photoionization relative to photodissociation increases significantly with increasing NC with a minimal value of 0.98 in the case of the largest studied cation. This trend of large PAHs differs from what was observed in our earlier study of medium-sized PAH cations for which a larger fraction of fragments was observed (Zhen et al. 2016), but is in line with the ionization BR of about 0.97 at 20 eV derived by Zhen et al. (2015) for the HBC cation, C42 H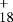 , by operating their home-made ion trap setup at the DESIRS beamline. These latter authors also reported a value of 0.70 ± 0.10 for the ionization BR of the ovalene cation at 20 eV, which can be compared to a value of 0.87 ± 0.02 in our experiment. This difference can be interpreted by the low mass resolution achieved in the former experiments which impacted both the isolation of the 12C parent isotopomer before irradiation and the quantification of the abundance of –H fragments in the photoproducts.
, by operating their home-made ion trap setup at the DESIRS beamline. These latter authors also reported a value of 0.70 ± 0.10 for the ionization BR of the ovalene cation at 20 eV, which can be compared to a value of 0.87 ± 0.02 in our experiment. This difference can be interpreted by the low mass resolution achieved in the former experiments which impacted both the isolation of the 12C parent isotopomer before irradiation and the quantification of the abundance of –H fragments in the photoproducts.
From Fig. 3, we derived appearance energies for the formation of PAH2+ from PAH+, AE2+. The values are listed in Table 1 and compared to the corresponding computed values for the adiabatic ionization potentials, IP2+, which are extracted from the Theoretical Spectral Database of PAHs1 (Malloci et al. 2007a) or calculated at the same level of theory for the missing IP2+ of the DBPP cation according to Malloci et al. (2007b). Experimental and theoretical values are found to be in good agreement considering the accuracy of ~0.3 eV for the calculated values. The trend ofa slow decrease of IP2+ with NC ≳ 30 carbon atoms reported by Malloci et al. (2007b) is confirmed.
 |
Fig. 2 Mass spectra of the ovalene parent cation, C32H |
 |
Fig. 3 Action spectra of the photoproducts, dications (I) and fragments (F), as a function of photon energy for all studied PAH cations, (a) benzobisanthene, (b) ovalene, (c) DBPP, and (d) dicoronylene after absorption of a VUV photon. Relative intensities as explained in Appendix B. |
 |
Fig. 4 Photoionization branching ratio relative to photodissociation as a function of photon energy, for (a) benzobisanthene, C30H |
For doubly ionized PAH cations, 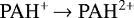 , values of the theoretical adiabatic ionization potentials, IP2+, and measuredappearance energies, AE2+.
, values of the theoretical adiabatic ionization potentials, IP2+, and measuredappearance energies, AE2+.
3.2 Photoionization cross sections
Experimental total action cross sections per carbon atom, 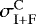 , were obtained following the procedure described in Appendix C. The photoionization cross sections,
, were obtained following the procedure described in Appendix C. The photoionization cross sections, 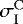 , were then derived using the branching ratio depicted in Fig. 4. The
, were then derived using the branching ratio depicted in Fig. 4. The 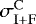 curves are expected to provide a lower value for the absolute photoabsorption cross sections,
curves are expected to provide a lower value for the absolute photoabsorption cross sections, 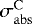 (see Eq. (C.1)). Since
(see Eq. (C.1)). Since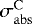 of the studied cations could not be extracted from the performed experiment and have not been reported so far in the literature, we compare these curves with the theoretical photoabsorption cross sections,
of the studied cations could not be extracted from the performed experiment and have not been reported so far in the literature, we compare these curves with the theoretical photoabsorption cross sections, 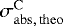 , which were computed using time-dependent density functional theory (TD-DFT) in line with our previous work (Malloci et al. 2004, 2007a) and as described in Appendix E. All obtained cross sections, experimental and theoretical, are displayed in Fig. 5 and compared to each other in the following at high (> 14 eV) and low (<14 eV) energies.
, which were computed using time-dependent density functional theory (TD-DFT) in line with our previous work (Malloci et al. 2004, 2007a) and as described in Appendix E. All obtained cross sections, experimental and theoretical, are displayed in Fig. 5 and compared to each other in the following at high (> 14 eV) and low (<14 eV) energies.
Above 14 eV, the cross sections are globally consistent (see Fig. 5). Still, the values of 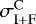 are found to be systematically larger than those of
are found to be systematically larger than those of 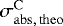 around the peak at 17 eV. In addition, there is a trend of increasing
around the peak at 17 eV. In addition, there is a trend of increasing 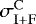 at the peak with molecular size. The case of C48 H
at the peak with molecular size. The case of C48 H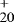 has to be considered with caution though due to a less accurate calibration procedure (see Appendix C). Contrary to the experimental cross sections, the values of
has to be considered with caution though due to a less accurate calibration procedure (see Appendix C). Contrary to the experimental cross sections, the values of 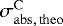 stay close to each other, which is expected from the proportionality of the photoabsorption cross sections with NC. Nevertheless, it is not yet possible to assess the precision of the calculated cross sections. Comparison with an experimental photoabsorption cross section at high energies (up to 30 eV) has so far only been done for neutral anthracene, C14 H10 (Malloci et al. 2004). It is interesting to mention that this comparison reveals overall good agreement between the calculated and measured cross sections but with differences on the band positions and widths (in the theoretical spectra the band width is artificial). Furthermore, around the high-energy peak observed at 18 eV, the discrepancy appears similar to the one illustrated in Fig. 5 in the cases of C32 H
stay close to each other, which is expected from the proportionality of the photoabsorption cross sections with NC. Nevertheless, it is not yet possible to assess the precision of the calculated cross sections. Comparison with an experimental photoabsorption cross section at high energies (up to 30 eV) has so far only been done for neutral anthracene, C14 H10 (Malloci et al. 2004). It is interesting to mention that this comparison reveals overall good agreement between the calculated and measured cross sections but with differences on the band positions and widths (in the theoretical spectra the band width is artificial). Furthermore, around the high-energy peak observed at 18 eV, the discrepancy appears similar to the one illustrated in Fig. 5 in the cases of C32 H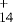 and C36 H
and C36 H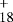 .
.
Below 14 eV, 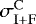 and
and 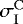 are comparable since the fragmentation is negligible. A plateau is observed from 11.3 to 12.9 eV in these experimental cross sections whereas the theoretical photoabsorption cross section exhibits strong bands (see Figs. 5 and 6). Ionization cross sections in PAHs may also display considerable structure, corresponding both to autoionization resonances and to the opening of channels as energy increases, making additional excited states accessible in the resulting ion with one electron less, i.e., vertical transitions (see e.g., Bréchignac et al. 2014).
are comparable since the fragmentation is negligible. A plateau is observed from 11.3 to 12.9 eV in these experimental cross sections whereas the theoretical photoabsorption cross section exhibits strong bands (see Figs. 5 and 6). Ionization cross sections in PAHs may also display considerable structure, corresponding both to autoionization resonances and to the opening of channels as energy increases, making additional excited states accessible in the resulting ion with one electron less, i.e., vertical transitions (see e.g., Bréchignac et al. 2014).
Theoretical considerations show that the orbital picture of ionization involving valence one-electron bands is severely contaminated by shake-up states, which involve two electrons, one promoted to an excited bound state and the other to the ionization continuum (Deleuze et al. 2001). The authors have shown that in the case of π orbitals, this happens at energies as low as 8 eV for the first ionization (case of neutral PAHs). The density of excited states quickly becomes very large, blending in a quasi-continuum as energy increases (Deleuze et al. 2001). In addition, each electronic excited state may display vibrational structure on top of it, i.e., vibronic states, producing further structure on a smaller scale. Qualitatively, a jump in the ionization cross section is therefore expected when a major channel becomes accessible via a valence one-electron transition, followed by a long plateau-like tail produced by all states coupling to it due to electronic correlation and vibronic coupling. On top of this, there may be electronic transitions to excited states of the parent molecule which have low coupling with the ionization continuum, therefore preferentially relaxing via radiationless transitions to lower electronic states. These do not show in the ionization cross sections. The theoretical method used here to compute the absolute, total cross section does not distinguish among different categories of electronic excitation; they are in principle all included together (except vibronic coupling) and cannot be distinguished in these calculations. More complex techniques involving many-body theory can compute the structure of the ionization cross sections with considerable accuracy (see e.g., Baiardi et al. 2017, for a recent review). However, their computational cost would be extremely high for the species considered here, and they are out of the scope of the present work, in which such detailed structure is not resolved in any case.
Below 14 eV, it is clear that there is a part of the photoabsorption cross section that does not lead to ionization, which we referred to as σ′ in Eq. (C.1). These correspond to excitations which involve fast relaxation via a strong coupling between electronic states and with nuclear states. This leads to vibrational excitation of the parent ion, which is expected to subsequently relax its energy by radiative cooling since no fragmentation is observed. At energies higher than 14 eV, evidence for such transitions, if they exist, is hindered by the precision of our experimental and theoretical data, as discussed above.
4 Astrophysical recipes
4.1 Charge state of astro-PAHs
Several modeling studies on the charge state of astro-PAHs have considered that these species could reach the dication and marginally the trication states (Bakes et al. 2001; Weingartner & Draine 2001a; Andrews et al. 2016). In Fig. 7, we compiled the ionization potentials (IP(Z+1)+) from neutral to cation (Z = 0), cation to dication (Z = 1), and dication to trication (Z = 2), which were obtained from calculations (Malloci et al. 2007b), as well as IPexp and AE(Z+1)+ from experiments (Clar et al. 1981; Hager & Wallace 1988; Zhen et al. 2016, and this work). We compared this data set with two analytical descriptions. Both start from a classical model of the energy it takes to remove one electronic charge from a small, conducting particle. Weingartner & Draine (2001b) considered conducting spheres, and added an empirical correction term to account for both quantum effects and PAH geometry, which is planar and not spherical. This additional term was determined to fit a set of data on first and second ionization potentials of PAHs and led to
![\begin{equation*}\mathrm{IP}^{(Z+1)+}_{\textrm{WD}} \,{=}\, W + \frac{1}{4 \pi \varepsilon_0} \left[ \left( Z+\frac{1}{2} \right) \frac{e^2}{a} + (Z+2) \frac{e^2}{a} \frac{0.03\,\text{nm}}{a} \right] \frac{1\,\mathrm{C}}{e}, \end{equation*}](/articles/aa/full_html/2020/09/aa38139-20/aa38139-20-eq28.png) (1)
(1)
where Z is the ion charge, ε0 is the vacuum permittivity in F ⋅ nm−1, e is the elementary charge in C, W is the work function of bulk graphite, W = 4.4 eV, and a, the effective radius in nm, is proportional to NC via the relation
![\begin{equation*} a \,{=}\, \sqrt[3]{\frac{N_{\mathrm{C}}}{468}}.\end{equation*}](/articles/aa/full_html/2020/09/aa38139-20/aa38139-20-eq29.png) (2)
(2)
In Eq. (1), the first term in square brackets corresponds to the classical conducting sphere model and the second term is the empirical correction. For the data set reported in Fig. 7, we find that, instead of W = 4.4 eV, a value of W = 3.9 eV leads to a better fit (black curves in Fig. 7). A satisfactory model is obtained for all Z values considered (Z = 0, 1, 2). The empirical formula which was adjusted for Z = 0, 1 appears also to be appropriate for Z = 2. The adjustment that we made on the W value corresponds to a vertical shift and somehow depends on the considered data set. For instance, we can see that our reported values for AE(Z+1)+ are systematically slightly above the DFT values (cf. Table 1). Still, our derived value for W appears in line with the values of about 4.0 eV, which were calculated for similar-sized PAHs by Kvashnin et al. (2013).
The second formalism to describe IP(Z+1)+ is given by Bakes & Tielens (1994b) who considered a thin conducting disk instead of a sphere, yielding
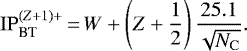 (3)
(3)
The gray curves in Fig. 7 were obtained from Eq. (3) (Bakes & Tielens 1994b) and using W = 3.9 eV, as derived above. The curve provides a very satisfactory description of the data for Z = 0, but tends to increasingly fail for higher Z values. This trend was noticed by Weingartner & Draine (2001b) and we can see that the discrepancy even increases for Z = 2. Tuning the value of W does not change the shape of the curves and this emphasizes the need to include quantum effects in the estimation of IP(Z+1)+.
We can see from Fig. 7 and Eq. (1) that a fraction of the photons absorbed in H I regions can induce ionization ofPAH cations. Taking the absorption and ionization cross sections shown in Fig. 5 and considering the radiation field of the prototypical NGC 7023 NW PDR (Joblin et al. 2018), we can estimate that typically one photon over three absorbed in the [10−13.6] eV range by PAH cations with NC = 30−36 will lead to ionization. The fraction of ionizing events will increase with increasing molecular size as the ionization potential shifts to lower energies. It reaches 0.5 for C48 H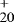 . We also notethat the formation of C
. We also notethat the formation of C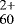 will be more difficult to achieve than that of a PAH2+ of similar size, since the corresponding cations have relatively similar absorption cross sections but the value of AE2+ for C
will be more difficult to achieve than that of a PAH2+ of similar size, since the corresponding cations have relatively similar absorption cross sections but the value of AE2+ for C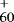 is significantly higher, (10.5 ± 0.1) eV (Douix et al. 2017), compared to8.7 eV for a PAH+ with NC = 60 (see Fig. 7).
is significantly higher, (10.5 ± 0.1) eV (Douix et al. 2017), compared to8.7 eV for a PAH+ with NC = 60 (see Fig. 7).
 |
Fig. 5 Experimentally obtained total action and ionization cross sections per C atom,
|
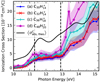 |
Fig. 6 Experimentally obtained photoionization cross sections per C atom, |
 |
Fig. 7 Theoretically calculated ionization potentials, IP(Z+1)+, experimentally obtained IPexp and appearance energies, AE(Z+1)+, as a functionof the number of carbon atoms. For Z = 0, 1, 2, the values refer to the transition |
4.2 Photoionization yield
Photoionization yields of PAH cations were derived for all studied species by dividing the experimental photoionization cross section, 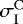 , by the theoretical photoabsorption cross section,
, by the theoretical photoabsorption cross section, 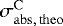 . In Sect. 3.2, we discussed the precision of both the experimental and theoretical cross sections. This can impact the photoionization yields. At energies below 14 eV, the presence of bands in
. In Sect. 3.2, we discussed the precision of both the experimental and theoretical cross sections. This can impact the photoionization yields. At energies below 14 eV, the presence of bands in 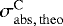 , which are not present in
, which are not present in 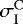 , can induce spectral features in the photoionization yields (e.g., the 12 eV peak obtained for C32 H
, can induce spectral features in the photoionization yields (e.g., the 12 eV peak obtained for C32 H ), which are as precise as the calculated spectrum. Nevertheless, Fig. 8 shows that the photoionization yields display comparable features for the studied molecules, with a rise starting at the ionization thresholds, AE2+, the plateau in the 11.3–12.9 eV range followed by another rise to reach the maximum value. There is some uncertainty on this maximum value because of the unknown contribution from σ′ (cf. Sect. 3.2). In the following, we made the hypothesis that the contribution of σ′ at high energies (20 eV) is minor and that the photoionization yields are limited by the photoionization BR, which never reaches unity as shown in Fig. 4. The mean values at high energies of the photoionization yields were therefore scaled using the ionization BR at 20 eV. The resulting curves are presented in Fig. 8.
), which are as precise as the calculated spectrum. Nevertheless, Fig. 8 shows that the photoionization yields display comparable features for the studied molecules, with a rise starting at the ionization thresholds, AE2+, the plateau in the 11.3–12.9 eV range followed by another rise to reach the maximum value. There is some uncertainty on this maximum value because of the unknown contribution from σ′ (cf. Sect. 3.2). In the following, we made the hypothesis that the contribution of σ′ at high energies (20 eV) is minor and that the photoionization yields are limited by the photoionization BR, which never reaches unity as shown in Fig. 4. The mean values at high energies of the photoionization yields were therefore scaled using the ionization BR at 20 eV. The resulting curves are presented in Fig. 8.
Data on the photoionization yields of neutral PAHs were derived in experimental studies performed by Verstraete et al. (1990) and Jochims et al. (1996). The latter authors proposed a rule of thumb to facilitate the implementation of this yield into models. This consists of a linear function of the photon energy with dependence on the ionization potential. On the basis of our results, we propose the use of a similar approach to describe theevolution of the photoionization yield of PAH cations with molecular size. The resulting function, 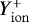 , is based on the above described ionization regimes which occur in different energy ranges (values in eV) as
, is based on the above described ionization regimes which occur in different energy ranges (values in eV) as
\,{=}\, \left\{ \begin{array}{@{}l@{}c@{}l@{}} \begin{array}{@{}l@{}} 0\\ \frac{\alpha}{11.3-\mathrm{IP}^{2+}}(h \nu -\mathrm{IP}^{2+})\\[3pt] \alpha\\[2pt] \frac{\beta(N_{\mathrm{C}})-\alpha}{2.1}\,(h \nu - 12.9) + \alpha\\[3pt] \beta(N_{\mathrm{C}}) \end{array} & \text{for} & \begin{array}{r@{}} h \nu < \mathrm{IP}^{2+}\; \\[3pt] \mathrm{IP}^{2+} \leq h \nu < 11.3\; \\[3pt] 11.3 \leq h \nu < 12.9\; \\[3pt] 12.9 \leq h \nu < 15.0\; \\[3pt] h \nu \geq 15.0, \end{array}\end{array} \right. \end{equation*}](/articles/aa/full_html/2020/09/aa38139-20/aa38139-20-eq40.png) (4)
(4)
where α = 0.3 is the value of the plateau and β depends on NC with
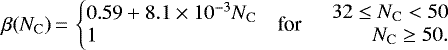 (5)
(5)
The reported β values represent the values at 20 eV of the ionization BR (Fig. 4). These can be considered as maximum values since they neglect a possible contributionof σ′ to the photoabsorption cross section as discussed above. These values were found to increase linearly with size for the studied size range with the dependence given by Eq. (5). Extrapolation to larger sizes leads to a β value of 1 for NC ≥ 50. This trend differs from the case of neutral PAHs for which Jochims et al. (1996) concluded that β = 1 is independentof size, in agreement with previous measurements by Verstraete et al. (1990).
Figure 9 displays examples of $](/articles/aa/full_html/2020/09/aa38139-20/aa38139-20-eq42.png) which were calculated from Eqs. (4) and (5), illustrating the variability of
which were calculated from Eqs. (4) and (5), illustrating the variability of $](/articles/aa/full_html/2020/09/aa38139-20/aa38139-20-eq43.png) with molecular size. No significant variation of this yield is expected for PAH cations with NC ≥ 50. In their PAH evolution model, Andrews et al. (2016) considered the yield of PAH cations based on the recipe given by Jochims et al. (1996) for neutrals but taking into account the appropriate photoionization potential for cations, that is, values of IP2+. To illustratethe impact that this approximation may have on the model results, we report in Fig. 9 these estimated yields and compare them with our recommended yields by integrating from IP2+ to 13.6 eV. We find that for the medium-sized PAHs, as represented by NC = 34, our integrated yield is larger by 19% compared to the previously available one, whereas for large PAHs, as represented by NC = 60, it is smaller by 14%. However, these simple estimates are inconclusive and models have to be run to evaluate the impact on the ionization of the PAH population in specific environments.
with molecular size. No significant variation of this yield is expected for PAH cations with NC ≥ 50. In their PAH evolution model, Andrews et al. (2016) considered the yield of PAH cations based on the recipe given by Jochims et al. (1996) for neutrals but taking into account the appropriate photoionization potential for cations, that is, values of IP2+. To illustratethe impact that this approximation may have on the model results, we report in Fig. 9 these estimated yields and compare them with our recommended yields by integrating from IP2+ to 13.6 eV. We find that for the medium-sized PAHs, as represented by NC = 34, our integrated yield is larger by 19% compared to the previously available one, whereas for large PAHs, as represented by NC = 60, it is smaller by 14%. However, these simple estimates are inconclusive and models have to be run to evaluate the impact on the ionization of the PAH population in specific environments.
 |
Fig. 8 Photoionization yields of the studied cations derived from the ionization and absorption cross sections (see Fig. 5) and scaled as explained in Sect. 4.2. The dashed vertical line marks the 13.6 eV photon energy cut-off for H I regions. |
 |
Fig. 9 Photoionization yields, |
5 Conclusion
We studied the interaction of trapped PAH cations with VUV photons in the range from 9 to 20 eV, also covering photon energies present in HII regions and ionization fronts. Our experimental results provide a wealth of information on both ionization and fragmentation processes. The present article is focused on the detailed analysis of ionization, whereas fragmentation will be the subject of a future, dedicated work. Our initial goal was to explore the properties of large species for NC up to about 80 atoms. However, we were only able to obtain measurements on molecular sizes from 30 to 48 carbon atoms due to the very low solubility of large PAHs. Nevertheless, studies in this range allow us to access the major trends in the ionization properties of PAH cations due to a molecular size increase. Our findings can be summarized as follows.
- (i)
Below 13.6 eV, the formation of a hot ion with subsequent (radiative) cooling is the major relaxation channel, followed by ionization whose yield reaches about 0.5 at 13.6 eV. From a molecular physics point of view, the yield comprises an interesting plateau at a value of 0.3 that extends over the energy range from 11.3 to 12.9 eV. This plateau reveals a spectral range in which there is strong competition between electronic and nuclear states. It would be interesting to investigate the dynamics of the relaxation of excited electronic states in this range using femtosecond (fs) pump-probe experiments (Marciniak et al. 2015).
- (ii)
Contrary to previous studies on neutrals, we were not able to observe that the photoionization yield reaches a value of 1 at high energies. At 20 eV, some dissociation is observed for all studied PAH cations, implying that the maximum of the yield cannot be larger than the branching ratio between ionization and dissociation, which increases with molecular size and reaches 0.98 for the largest studied ion, C48H
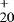 . In addition, we have not included a possible contribution in the photoabsorption events of the formation of a hot ion that would subsequently relax by radiative cooling in isolated conditions. This contribution would further lower the values of the photoionization yield. We have no explanation for the difference observed between neutrals and cations. Whether this is due to a change in their respective properties or the fact that experiments like ours using ion trapping are more sensitive to quantify this effect than experiments carried out on neutrals with different techniques is beyond the scope of this study but would be interesting to investigate.
. In addition, we have not included a possible contribution in the photoabsorption events of the formation of a hot ion that would subsequently relax by radiative cooling in isolated conditions. This contribution would further lower the values of the photoionization yield. We have no explanation for the difference observed between neutrals and cations. Whether this is due to a change in their respective properties or the fact that experiments like ours using ion trapping are more sensitive to quantify this effect than experiments carried out on neutrals with different techniques is beyond the scope of this study but would be interesting to investigate.
Concerning astrophysical applications, we provide recipes to determine both the ionization potential and the photoionization yield of PAH cations as a function of their molecular size, which can be extended to larger sizes (typically NC = 100). This yield can be combined with photoabsorption cross sections that are readily available from calculations using TD-DFT. All this molecular data can be used in models that describe the chemical evolution of PAHs in astrophysical environments. The range of photon energy we studied makes it possible to tackle the evolution of PAHs in extreme astronomical environments such as H II regions and ionization fronts. Observations of PAHs in these environments have so far been scarce due to their technical difficulty, but will become much more accessible thanks to the unique capabilities of the forthcoming James Webb Space Telescope (JWST).
As another example, the cavity around the star in NGC 7023 is expected to be an environment in which large PAH+ and PAH2+ are present (Andrews et al. 2016; Croiset et al. 2016). The presence of dications is expected to impact both the heating of the gas by photoelectric effect and the AIB emission. Some initial IR action spectra of large PAH cations and dications were recorded by Zhen et al. (2017, 2018). These latter authors provide encouraging results suggesting that large ionized PAHs are good candidates for carrying the AIBs. Whether or not the spectral differences between cations and dications will be sufficient to differentiate both charge states in the observations nevertheless remains unclear. Still, we can predict that a detailed modeling approach combined with the wealth of spectral and spatial information, which will be delivered soon by the JWST, will be able to highlight the charge evolution of the PAH population and its impact on the physics and chemistry of PDRs.
Acknowledgements
This paper is dedicated to Sydney Leach, a great scientist who has been a pioneer in laboratory astrophysicsand a major source of inspiration for the whole field. We are grateful to the staff from SOLEIL for the smooth running of the facility. We also wish to acknowledge the insightful comments of the referee on an earlier version of this paper. We acknowledgefunding from the European Research Council under the European Union’s Seventh Framework Programme ERC-2013-SyG, Grant Agreement no. 610256, NANOCOSMOS. This work was also supported by the Agence Nationale de la Recherche (France), under project number ANR-08-BLAN-0065. G. W. thanks the European Union (EU) for support under the Horizon 2020 framework for the Marie Skłodowska-Curie action EUROPAH, Grant Agreement no. 722346. S.Q. and D.P. acknowledgefinancial support from the Spanish Agencia Estatal de Investigación (MAT2016-78293-C6-3-R; AEI/FEDER, UE), Xunta de Galicia (Centro Singular de Investigación de Galicia accreditation 2016–2019, ED431G/09), the European Regional Development Fund-ERDF, and the European FET-OPEN project SPRING, Grant Agreement no. 863098. Finally, this project was granted access to the HPC resources at the CALMIP supercomputing centre under project P20027.
Appendix A Synthesis of dicoronylene, C48H20
Dicoronylene was synthesized following the procedure reported by Cataldo et al. (2011). A mixture of coronene (0.060 g, 0.199 mmol), AlCl3 (4.20 g, 31.2 mmol), NaCl (0.817 g, 14.0 mmol), and CuCl (0.043 g, 0.440 mmol) was stirred at 195 °C for 2 h. Subsequently, an aqueous solution of HCl (10%, 20 ml) was slowly added resulting in the precipitation of a red solid. This solid was filtrated and washed with aqueous solution of HCl (10%, 20 ml), hot water (20 ml) and acetone (3 × 20 ml). The resulting solid was dried to obtain dicoronylene as a red solid (54 mg, 40%).
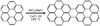 |
Fig. A.1 Schematic of the synthesis of dicoronylene, C48H20, from coronene, C24H12. |
Appendix B Action spectra scaling procedure
From the recorded mass spectra, peak intensities of parent ions and their photoproducts can be deduced. The secondary ions produced upon VUV irradiation consist of the dication with peak intensity SI, and the photofragments with summed peak intensity SF, including the H and 2H/H2 loss channels. Due to detector characteristics, doubly ionized molecules are detected more efficiently than singly ionized molecules. Therefore, the peak intensities derived from the mass spectra have to be scaled by the detector gain efficiency, ε, to retrieve values that scale with abundances. Thermo Scientific™ provides ε+ = 0.29 for parent ions and fragments, ε2+ = 0.42 for dications and a value of 0.54 for trications. There is some gain change with mass but this is a minor correction for the range of studied masses.
The total number of ions in the trap, P0 (in uncalibrated values), can then be calculated with
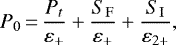 (B.1)
(B.1)
where  is the number of parent ions after irradiation time, t. Building the action spectra requires to derive normalized photoproduct intensities for SI and SF, which can be obtained by first dividing them by P0 and then correcting for the variation of the photon flux, Φ(ν). Indeed the latter evolved in energy due to spectral shape variations. Changes were also made in the irradiation time, t, and monochromator exit slit width, s, so that the total photoproduct intensity remains smaller than ca. 12% of Pt, as seen in the mass spectra. This led to
is the number of parent ions after irradiation time, t. Building the action spectra requires to derive normalized photoproduct intensities for SI and SF, which can be obtained by first dividing them by P0 and then correcting for the variation of the photon flux, Φ(ν). Indeed the latter evolved in energy due to spectral shape variations. Changes were also made in the irradiation time, t, and monochromator exit slit width, s, so that the total photoproduct intensity remains smaller than ca. 12% of Pt, as seen in the mass spectra. This led to
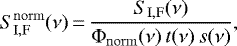 (B.2)
(B.2)
where Φnorm(ν) is normalized to be 1 at its maximum at 9.5 eV. We note that the obtained intensities are in arbitrary units (see Fig. 3) and not in percentage of the total number of ions because of the scaling by the relative photon flux.
Appendix C Photoproduct cross sections scaling procedure
The absorption of a photon by the parent ion leads to different relaxation channels. Considering monochromatic radiation, the photoabsorption cross section, σabs, can therefore be decomposed into the sum of the cross sections for each relaxation channel as
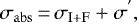 (C.1)
(C.1)
where σI+F is the cross section leading to the production of the secondary products with intensities SI and SF (see Appendix B), and σ′ is the cross section for the creation of a hot ion that will relax its internal energy by radiative cooling and/or collisions with buffer gas (He) in our experiment. These processes cannot be traced in our experiment and only σI+F can be estimated following
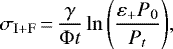 (C.2)
(C.2)
with the photon flux, Φ, in photons cm−2s−1, a form factor, γ, describing the overlap of the photon beam and the ion cloud, the total number of ions, P0, and the number of parent ions, 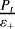 , after irradiation time, t. Plugging P0 from Eq. (B.1) in Eq. (C.2), we get
, after irradiation time, t. Plugging P0 from Eq. (B.1) in Eq. (C.2), we get
 (C.3)
(C.3)
In order to determine cross sections in absolute units, the photon flux, Φ, and the form factor, γ, have to be well known. Douix et al. (2017) managed to record the absolute photoionization cross section, 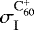 , for the buckminsterfullerene cation, C
, for the buckminsterfullerene cation, C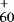 , by carefully measuring these parameters and applying Eq. (C.3), where the term
, by carefully measuring these parameters and applying Eq. (C.3), where the term 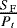 was zero due to the nondissociation of C
was zero due to the nondissociation of C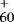 2. In our experiment, we trapped C
2. In our experiment, we trapped C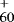 and recorded its dication peak under the same irradiation conditions used for our studied PAHs except dicoronylene as explained below. We were therefore able to derive the value of
and recorded its dication peak under the same irradiation conditions used for our studied PAHs except dicoronylene as explained below. We were therefore able to derive the value of 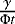 and use this factor to obtain experimental values for σI+F from the photoproduct evolutions of our PAHs according to Eq. (C.3). This scaling procedure yields reasonable cross section values only above the AE2+ of C
and use this factor to obtain experimental values for σI+F from the photoproduct evolutions of our PAHs according to Eq. (C.3). This scaling procedure yields reasonable cross section values only above the AE2+ of C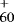 . We bypassed this limitation by scaling the action spectra (see Sect. 3.1 and Appendix B) to the cross sections and replacing the values below the AE2+ of C
. We bypassed this limitation by scaling the action spectra (see Sect. 3.1 and Appendix B) to the cross sections and replacing the values below the AE2+ of C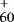 with the values from the scaled action spectra. Finally, to simplify the comparison between species, we divide σI+F of each PAH cation by its respective NC, yielding
with the values from the scaled action spectra. Finally, to simplify the comparison between species, we divide σI+F of each PAH cation by its respective NC, yielding 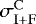 .
.
We note that in this calibration procedure, dicoronylene required a specific treatment. Indeed this ion was studied in different conditions since both the syringe flow rate and the monochromator exit slit width, s, were increased in order to get a sufficient signal. In order to correct at best for these changes, we applied corrections to the 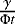 factor in Eq. (C.2) by assuming that not only the photon flux but also the beam overlap with the ion cloud scales linearly with s, the latter is likely disputable but this is the best we could do.
factor in Eq. (C.2) by assuming that not only the photon flux but also the beam overlap with the ion cloud scales linearly with s, the latter is likely disputable but this is the best we could do.
Appendix D Error estimation
Depending on the acquisition time, a few hundred, N, mass spectra, x, are recordedfor each photon energy step. Averaging these mass spectra for each photon energy yields one mean mass spectrum,  , per photon energy with an absolute standard error of
, per photon energy with an absolute standard error of  , where σ is the standard deviation. The error bars, Δf, in Figs. 3 and 4 result from error propagation for a function, f → f(x1, x2,..., xN), according to
, where σ is the standard deviation. The error bars, Δf, in Figs. 3 and 4 result from error propagation for a function, f → f(x1, x2,..., xN), according to
 (D.1)
(D.1)
When determining the cross sections depicted in Fig. 5 following the procedure presented in Appendix Cas well as the obtained photoionization yields shown in Figs. 8 and 9, the error on the cross section of C , which was found to be below 21% by Douix et al. (2017) is used to propagate the errors.
, which was found to be below 21% by Douix et al. (2017) is used to propagate the errors.
Appendix E Theoretical cross section calculations
Theoretical photoabsorption cross sections were obtained using TD-DFT, with the real-time, real-space method of Yabana & Bertsch (1996), as implemented in the OCTOPUS computer code (Tancogne-Dejean et al. 2020). Not all species in this work were considered in our previous work (Malloci et al. 2007a). In addition, since here we need to use theoretical spectra up to relatively high energies (~20 eV), we also took the chance to verify at these energies the convergence of the calculations with respect to the simulation box size and grid spacing, the real-space equivalent of more conventional basis-set convergence for Gaussian-based DFT for example. It is known (Matsuzawa et al. 2001) and mentioned in the OCTOPUS documentation that as a rule of thumb, larger simulation boxes are needed tof obtain converged values for the energies of higher lying electronic excited states, and for the intensities of the transitions involving them. Moreover, when using the real-time, real-space method implemented in OCTOPUS, the photoabsorption spectrum includes both transitions to discrete (bound) electronic states and to the continuum of unbound states. The former tend to converge to well-defined energies in the limit of infinite box size; the latter, instead, are artificially quantized by the boundary conditions of a finite simulation box, whose individual energies keep on changing with changing box size (and shape).
In this context, we started a computational effort to test convergence as a function of box size. This led us to conclude that the spectra in the database of Malloci et al. (2007a) are adequately converged for excitation energies up to ~13 eV, meaning they are suitable for astronomical modeling purposes involving photons up to the Lyman limit. We instead had to consider substantially larger simulation box sizes and denser grid spacing to achieve convergence up to ~20 eV, as required for this work. For our purposes, we found that a “minimal” simulation box can be achieved by considering the union of8 Å radius spheres centered on each atom of the molecule, or by a single larger sphere with an equivalent volume. In addition, a grid spacing of 0.18 Å was needed to achieve convergence. All the calculations were performed on the OLYMPE supercomputer at the mesocentre CALcul en MIdi Pyrénées (CALMIP). We retained from the set of simulations two different converged spectra for each species and averaged them together in order to smooth out the contribution of free electron states and retain discrete ones. Finally, we divided the σabs, theo of each PAH cation by its respective NC, yielding 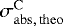 .
.
References
- Andrews, H., Boersma, C., Werner, M. W., et al. 2015, ApJ, 807, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, H., Candian, A., & Tielens, A. G. G. M. 2016, A&A, 595, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baiardi, A., Paoloni, L., Barone, V., Zakrzevski, V. G., & Ortiz, J. V. 2017, J. Chem. Theory Comput., 13, 3120 [CrossRef] [Google Scholar]
- Bakes, E. L. O., & Tielens, A. G. G. M. 1994a, ASPC, 58, 412 [Google Scholar]
- Bakes, E. L. O., & Tielens, A. G. G. M. 1994b, ApJ, 427, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Bakes, E. L. O., Tielens, A. G. G. M., & Charles W. Bauschlicher, J. 2001, ApJ, 556, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Bréchignac, P., Garcia, G. A., Falvo, C., et al. 2014, J. Chem. Phys., 141, 164325 [CrossRef] [Google Scholar]
- Cataldo, F., Ursini, O., Angelini, G., & Iglesias-Groth, S. 2011, Fuller. Nanotub. Car. N., 19, 713 [CrossRef] [Google Scholar]
- Clar, E., Robertson, J. M., Schloegl, R., & Schmidt, W. 1981, J. Am. Chem. Soc., 103, 1320 [CrossRef] [Google Scholar]
- Compiègne, M., Abergel, A., Verstraete, L., et al. 2007, A&A, 471, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Croiset, B. A., Candian, A., Berné, O., & Tielens, A. G. G. M. 2016, A&A, 590, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deleuze, M. S., Trofimov, A. B., & Cederbaum, L. S. 2001, J. Chem. Phys., 115, 5859 [CrossRef] [Google Scholar]
- Douix, S., Duflot, D., Cubaynes, D., Bizau, J.-M., & Giuliani, A. 2017, J. Phys. Chem. Lett., 8, 7 [CrossRef] [Google Scholar]
- Giuliani, A., Giorgetta, J.-L., Ricaud, J.-P., et al. 2012, Nucl. Instrum. Methods Phys. Res. B, 279, 114 [CrossRef] [Google Scholar]
- Hager, J. W., & Wallace, S. C. 1988, Anal. Chem., 60, 5 [CrossRef] [Google Scholar]
- Joblin, C., Bron, E., Pinto, C., et al. 2018, A&A, 615, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jochims, H. W., Baumgaertel, H., & Leach, S. 1996, A&A, 314, 1003 [NASA ADS] [Google Scholar]
- Kvashnin, D. G., Sorokin, P. B., Brüning, J. W., & Chernozatonskii, L. A. 2013, Appl. Phys. Lett., 102, 183112 [CrossRef] [Google Scholar]
- Le Page, V., Snow, T. P., & Bierbaum, V. M. 2003, ApJ, 584, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Malloci, G., Mulas, G., & Joblin, C. 2004, A&A, 426, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malloci, G., Joblin, C., & Mulas, G. 2007a, Chem. Phys., 332, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Malloci, G., Joblin, C., & Mulas, G. 2007b, A&A, 462, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marciniak, A., Despré, V., Barillot, T., et al. 2015, Nat. Commun., 6, 1 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Matsuzawa, N. N., Ishitani, A., Dixon, D. A., & Uda, T. 2001, J. Phys. Chem. A, 105, 4953 [CrossRef] [Google Scholar]
- Milosavljević, A. R., Nicolas, C., Gil, J.-F., et al. 2012, J. Synchrotron Rad., 19, 174 [CrossRef] [PubMed] [Google Scholar]
- Montillaud, J., Joblin, C., & Toublanc, D. 2013, A&A, 552, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nahon, L., de Oliveira, N., Garcia, G. A., et al. 2012, J. Synchrotron Rad., 19, 508 [Google Scholar]
- Tancogne-Dejean, N., Oliveira, M. J. T., Andrade, X., et al. 2020, J. Chem. Phys., 152, 124119 [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2005, The Physics and Chemistry of the Interstellar Medium (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Verstraete, L., Leger, A., D’Hendecourt, L., Defourneau, D., & Dutuit, O. 1990, A&A, 237, 436 [Google Scholar]
- Vicente, S., Berné, O., Tielens, A. G. G. M., et al. 2013, ApJ, 765, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Visser, R., Geers, V. C., Dullemond, C. P., et al. 2007, A&A, 466, 229 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001a, ApJS, 134, 263 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001b, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Yabana, K., & Bertsch, G. F. 1996, Phys. Rev. B, 54, 4484 [CrossRef] [Google Scholar]
- Zhen, J., Castellanos, P., Paardekooper, D. M., et al. 2015, ApJ, 804, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Zhen, J., Rodriguez Castillo, S., Joblin, C., et al. 2016, ApJ, 822, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Zhen, J., Castellanos, P., Bouwman, J., Linnartz, H., & Tielens, A. G. G. M. 2017, ApJ, 836, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Zhen, J., Candian, A., Castellanos, P., et al. 2018, ApJ, 854, 27 [NASA ADS] [CrossRef] [Google Scholar]
The absolute photoionization cross section of C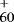 ,
,
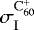 , can be accessed at https://zenodo.org/record/1001072.
, can be accessed at https://zenodo.org/record/1001072.
All Tables
For doubly ionized PAH cations, 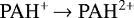 , values of the theoretical adiabatic ionization potentials, IP2+, and measuredappearance energies, AE2+.
, values of the theoretical adiabatic ionization potentials, IP2+, and measuredappearance energies, AE2+.
All Figures
 |
Fig. 1 Molecular structures of the studied PAHs, namely (a) benzobisanthene, C30 H |
| In the text | |
 |
Fig. 2 Mass spectra of the ovalene parent cation, C32H |
| In the text | |
 |
Fig. 3 Action spectra of the photoproducts, dications (I) and fragments (F), as a function of photon energy for all studied PAH cations, (a) benzobisanthene, (b) ovalene, (c) DBPP, and (d) dicoronylene after absorption of a VUV photon. Relative intensities as explained in Appendix B. |
| In the text | |
 |
Fig. 4 Photoionization branching ratio relative to photodissociation as a function of photon energy, for (a) benzobisanthene, C30H |
| In the text | |
 |
Fig. 5 Experimentally obtained total action and ionization cross sections per C atom,
|
| In the text | |
 |
Fig. 6 Experimentally obtained photoionization cross sections per C atom, |
| In the text | |
 |
Fig. 7 Theoretically calculated ionization potentials, IP(Z+1)+, experimentally obtained IPexp and appearance energies, AE(Z+1)+, as a functionof the number of carbon atoms. For Z = 0, 1, 2, the values refer to the transition |
| In the text | |
 |
Fig. 8 Photoionization yields of the studied cations derived from the ionization and absorption cross sections (see Fig. 5) and scaled as explained in Sect. 4.2. The dashed vertical line marks the 13.6 eV photon energy cut-off for H I regions. |
| In the text | |
 |
Fig. 9 Photoionization yields, |
| In the text | |
 |
Fig. A.1 Schematic of the synthesis of dicoronylene, C48H20, from coronene, C24H12. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



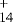
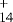
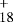
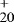
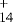
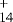
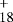
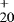
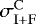
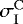
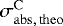
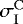
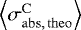
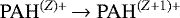
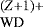
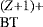
$](/articles/aa/full_html/2020/09/aa38139-20/aa38139-20-eq88.png)