| Issue |
A&A
Volume 670, February 2023
|
|
|---|---|---|
| Article Number | A181 | |
| Number of page(s) | 8 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202245715 | |
| Published online | 27 February 2023 | |
Effect of protonation on the UV/VUV photostability of cyano-substituted anthracene and phenanthrene
1
Université Paris-Saclay, CNRS, Institut des Sciences Moléculaires d’Orsay,
91405
Orsay, France
e-mail: ugo.jacovella@universite-paris-saclay.fr
2
Synchrotron SOLEIL, L’Orme des Merisiers,
91192
Saint-Aubin, Gif-sur-Yvette, France
3
INRAE, UAR1008, Transform Department,
Rue de la Géraudière,
BP 71627,
44316
Nantes, France
4
School of Chemistry, University of New South Wales,
Sydney, NSW
2052, Australia
5
Molecular Horizons and School of Chemistry and Molecular Bioscience, University of Wollongong,
Wollongong, New South Wales
2522, Australia
6
Università di Cagliari, Dipartimento di Fisica,
09042
Monserrato (Cagliari), Italy
7
Istituto Nazionale di Astrofisica – Osservatorio Astronomico di Cagliari,
Via della Scienza 5,
09047
Selargius (CA), Italy
8
Institut de Recherche en Astrophysique et Planétologie (IRAP), CNRS,
9 Avenue du Colonel Roche,
31028
Toulouse, France
Received:
18
December
2022
Accepted:
18
January
2023
Context. The vacuum ultraviolet (VUV) photoprocessing of polycyclic aromatic hydrocarbons (PAHs) has been established as a key piece of the puzzle to understand the life cycle of carbon-based molecules in space. The recent detection of cyano (CN) aromatic species, with unexpectedly high abundance, motivated the current study of investigating their interaction with UV/VUV radiation.
Aims. The aims were to investigate the fate, after VUV photoexcitatation, of medium-size (three rings) CN-PAH radical cations and of their protonated analogs, and thus to assess the effect of protonation on the photostability of the CN-PAHs. Photoproducts (ionic fragments and dications) were mass-analyzed and measured as a function of photon energy. The results were also compared with those for the bare anthracene radical cation to assess the influence of the added CN group.
Methods. The positively charged CN-PAHs were stored in a quadrupole ion trap prior to interrogation by UV/VUV radiation, with photon energies between 4.5 and 13.6 eV, delivered by the DESIRS beamline from the synchrotron SOLEIL.
Results. The HCN/HNC loss channel is present for both radical cations and protonated species, but H2 loss is only apparent for the radical cations. Based on comparison with quantum chemical calculations, radiative and/or collisional processes should be relevant at energies lower than 8 eV, with a stronger propensity for radical cation than protonated CN-PAHs. The cata-condensed 9-CN-anthracene has a nearly two-fold larger photoionization yield at 13.6 eV than peri-condensed 9-CN-phenanthrene.
Conclusions. The photoionization yield of singly and doubly ionized CN-PAHs is greater for radical cations than for protonated analogs. The photoionization yields of CN-PAHs is diminished by protonation and, in the future, similar investigations should target larger protonated CN-PAHs to support a general model for the photo-processing of these relevant molecular systems. Similar processes to those for the bare PAH radical cations may involve the radical cations of CN-PAHs, making their addition important in models that describe the photoelectric heating of interstellar gas.
Key words: ultraviolet: ISM / ISM: molecules / techniques: spectroscopic / molecular processes
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Since 2018, neutral cyano-bearing (CN-bearing) aromatic molecules have been detected in the gas phase within cold objects in our Universe using highly sensitive radio telescopes (McGuire et al. 2018, 2021; McCarthy et al. 2021; Burkhardt et al. 2021; Lee et al. 2021; Cernicharo et al. 2021; Sita et al. 2022). Owing to their large dipole moments, CN-substituted polycyclic aromatic hydrocarbons (PAHs) were thought to be used as proxy molecules to search for apolar PAHs. However, the unexpectedly high-abundance of CN-PAHs then raises questions about the processes leading to their production in interstellar regions. It also highlights the perhaps underestimated importance of CN-substituted molecules to the carbonaceous life cycle in space (McCarthy & McGuire 2021).
It has been evidenced that PAHs should exist under different charge and hydrogenation states and the nature of the PAHs population is mediated by the characteristic of the photon flux (Allain et al. 1996; Le Page et al. 2003; Montillaud et al. 2013). Neutral CN-PAHs can thus serve as precursors of positively charged species such as radical cations and closed-shell protonated cations. Interstellar formation of CN-PAH radical cations can occur via direct photoionization of their neutral counterparts. Although dark parts of molecular clouds are shielded from the ultraviolet (UV) photons from the interstellar radiation field, cloud edges and other photon-dominated regions (PDRs) are exposed to vacuum-ultraviolet (VUV) radiation. PDRs are therefore auspicious environments for direct photoionizion of large neutral species. However, molecules inside dense molecular clouds can still be subjected to VUV radiation (Prasad–Tarafdar Mechanism) generated by the Lyman and Werner bands arising from H2 emission (typically from 6 to 13.6 eV), which results after impact excitation from secondary electrons caused by cosmic rays (Prasad & Tarafdar 1983; Gredel et al. 1989). Protonated CN-PAHs would likely be formed by proton transfer reactions. The standard proton donors in dense molecular clouds are 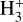 and HCO+ depending on the proton affinity of the molecule to be protonated (Agúndez et al. 2015). Contradictory trends have been found as to the relation between the abundance ratio of a neutral molecule and its protonated analog and the proton affinity of the neutral molecule (Cabezas et al. 2022). The CN-polyynes HC2n+1 N (n = 1–3) have proton affinities ranging from about 750 to 800 kJ mol−1 and observed abundance ratios in TMC-1 ranging from 230 to 380. The calculated proton affinity of CN-naphthalene is of ≈770 kJ mol−1 (Maksić & Eckert-Maksić 1998), similar to the one of HC5N. Using the HC5N/HC5NH+ ratio of 240 and the derived abundance from McGuire et al. (2021) of CN-naphtalene in TMC-1 of ≈7 × 1011 cm−2, we can expect a column density for protonated CN-substituted naphthalene of ≈3 × 109 cm−2.
and HCO+ depending on the proton affinity of the molecule to be protonated (Agúndez et al. 2015). Contradictory trends have been found as to the relation between the abundance ratio of a neutral molecule and its protonated analog and the proton affinity of the neutral molecule (Cabezas et al. 2022). The CN-polyynes HC2n+1 N (n = 1–3) have proton affinities ranging from about 750 to 800 kJ mol−1 and observed abundance ratios in TMC-1 ranging from 230 to 380. The calculated proton affinity of CN-naphthalene is of ≈770 kJ mol−1 (Maksić & Eckert-Maksić 1998), similar to the one of HC5N. Using the HC5N/HC5NH+ ratio of 240 and the derived abundance from McGuire et al. (2021) of CN-naphtalene in TMC-1 of ≈7 × 1011 cm−2, we can expect a column density for protonated CN-substituted naphthalene of ≈3 × 109 cm−2.
Once formed, the positively charged CN-PAHs would further interact with the UV and VUV radiation field present in interstellar and circumstellar media, inducing competing ionization and/or fragmentation mechanisms. The existence of doubly ionized PAHs has been proposed and their possible subsequent role as intermediates in the evolution of the large PAHs has been discussed (Leach 1986; Malloci et al. 2007). This is especially the case since experimental studies have shown that the double ionization mechanism becomes the predominant relaxation path for PAHs with three or more rings, and so even at energies below 13.6 eV (Zhen et al. 2016; Wenzel et al. 2020). PAH dications have even been proposed as carriers of the extended red emission (Witt et al. 2006).
Today 260+ molecules have been identified in interstellar and circumstellar media; among those, roughly 10% are positively charged ones from which approximately 80% are protonated ions1. This observation raises the question of whether the larger number of protonated species compared to regular radical cations reflects a bias in the laboratory astrophysical database or rather arises from intrinsic physical properties such as the photostability under strong UV/VUV radiation. The present study compares the fate of radical cations and protonated tri-cyclic CN-substituted PAHs following UV and VUV photoexcitation.
2 Methods
2.1 Experimental
The influence of protonation on the UV/VUV photostability of CN-PAHs has been studied using action spectroscopy with an LTQ XL™ linear ion trap (Milosavljević et al. 2012) coupled to the DESIRS undulator-based VUV beamline (Nahon et al. 2012) at the SOLEIL synchrotron facility in Saint-Aubin (France). A solution of 10 μM of neutral CN-PAH precursors (9-CN-anthracene and 9-CN-phenanthrene) was prepared in methanol:toluene (50/50) and was introduced into an atmospheric pressure photoionization (APPI) source to generate the protonated species and radical cations from their corresponding neutral counterparts. Under these conditions, toluene was photoionized by the krypton discharge lamp of the ion source and reacted through proton transfer and charge exchange with the CN-anthracene and phenantrene. APPI has been shown to offer some control over the ion produced (Bagag et al. 2007).
The positively charged molecules were guided into the ion trap through a set of ion optics. Helium buffer gas was introduced in the ion trap to reach ≈10−3 mbar and achieve efficient trapping. The ions of interest were protonated species and radical cations of 9-CN-anthracene (9 -CN-AntH+ m/z 204 and 9 -CN-Ant+ m/z 203), and 9-CN-phenanthrene (9 -CN-PheH+ m/z 204 and 9 -CN-Phe+ m/z 203). Monoisotopic ions were selected with a ∆ m/z total width of 1.5 (ie ±0.75). The protonated ions contains a fraction (around 16.7%) of 13C from the radical cations. It appeared that the 13C-containing fragments of the radical cation are not interfering with the fragments produced from the protonated species, with both fragmentation patterns being different. Furthermore, the fragments arising from the 13C-containing precursors are too weak to be measured.
Once selected, the ions were irradiated by the synchrotron radiation in the UV range from 4.5 to 7.5 eV in steps of 0.1 eV, and in the VUV range from 7.0 to 13. eV in steps of 0.2 eV. Higher harmonics of the undulator synchrotron radiation were filtered out by a gas filter filled with Kr gas. An additional Suprasil window was introduced into the synchrotron radiation path when operating in the low-lying energy region (4.5–7.5 eV). The monochromator exit slit width set to 200 m so that the photon flux was of 1012–1013 photons s−1 and the photon resolution was of ≈10 meV at 10 eV. The irradiation time of 1000 ms was set to maintain the photofragmentation yields below 10% to avoid sequential multiphoton absorption processes as can be seen in Fig. 1.
The MassJ package (Giuliani 2021) written in the Julia language (Bezanson et al. 2017) was used to process the data. The shaded zones in Fig. 2 are error bars resulting from the standard statistical error from the averaging process (Giordano 2016) and the error propagation as it was done by Wenzel et al. (2020). The incident photon flux was measured by a calibrated VUV photodiode (IRD AXUV100) to normalize the photodissociation action spectra recorded.
 |
Fig. 1 Top panel (red trace) is a mass spectrum of the protonated 9-CN-anthracene parent ion (C14H9CNH+, m/z = 204) without irradiation. The bottom panel (red trace) is a mass spectrum of the same species irradiated with a photon energy of 5.7 eV, leading to photodissociation. |
 |
Fig. 2 UV/VUV photodissociation spectra of CN-PAH radical cations (left column) and of protonated species (right column). |
2.2 Computational
The structures of the cations have been optimized at the density functional theory (DFT) level using the hybrid exchange-correlation functional B3LYP and the aug-cc-PVDZ basis set to expand molecular orbitals (Lee et al. 1988; Becke 1988; Kendall et al. 1992). The same method was adopted to optimize the corresponding dicationic species to compute adiabatic and vertical second ionization energies. These calculations were performed using the Gaussian 16 software (Frisch et al. 2016). Theoretical photoabsorption cross sections have been calculated by real-time real-space time-dependent density functional theory (TD-DFT), using the method given by Yabana & Bertsch (1996), as implemented in the Octopus software (Tancogne-Dejean et al. 2020), using Trouiller-Martin pseudopotentials (Troullier & Martins 1991) and the local density approximation for the DFT exchange-correlation functional (Dirac 1930; Perdew & Zunger 1981).
Three TD-DFT time evolutions were performed for each molecule, each starting with an initial perturbation along one of the (arbitrary) x, y, and z axes, to recover the full electronic polarisability tensor without assuming any symmetry. Each one was performed in a finite simulation box consisting of the union of a set of spheres, each with a radius of 8 Å, centered around each atom. In this simulation box, all functions were represented in a discrete grid with a spacing of 0.18 Å. This choice of functional, box size, and grid spacing were determined to achieve acceptable accuracy compared to available PAH spectra (Malloci et al. 2007), and to yield good convergence up to ~20 eV (Wenzel et al. 2020). The length of the time integration was 40 h/eV ≃ 165 fs, with 0.002 h/eV ≃ 0.0083 fs time steps, providing good numerical stability of the electronic energy along the numerical time evolution.
The (arbitrary) total length of the time evolution reflects in an (arbitrary) band width in the resulting computed spectrum. We chose a simulation time long enough to ensure that the band width is well below a few tenths of an eV, which is the commonly accepted best accuracy to be expected for this kind of calculation.
The positions of the ions were kept frozen at the optimized geometry all along the time simulation, thereby yielding vertical photoabsorption cross sections, that is not including any rovibronic structure, but just pure electronic transitions. On the other hand, the finiteness of the simulation box gives rise to an artificial quantization of unbound electronic states, causing an oscillatory behavior of the computed cross section at high energies, where it is expected to be smooth. In this case, one should consider the average value across spurious oscillations for comparison with experiment.
3 Results
The VUV action spectra of 9 -CN-Ant+ and 9 -CN-Phe+ over the 4.5–13.6 eV range are presented in the left column of Fig. 2 and the spectra of the corresponding protonated species, that is 9-CN-AntH+ and 9-CN-PheH+, are shown in the right column of Fig. 2. This energy range covers the Lyman-α (10.2 eV) and ends at the ionization energy of atomic hydrogen. The intensities given are relative to the total number of ions (parent plus daughter ions).
The blue curves represent the spectra obtained by monitoring the ion signal of the photofragments corresponding to the loss of HCN and/or HNC (−27 Da). The sequential loss of CN and H is expected to require larger amount of energy than HCN or HNC loss. Furthermore, if sequential loss were a dominant mechanism, as the loss of HCN from the protonated species should lead to a structure similar to that of the loss of CN from the radical cations, we would expect a channel corresponding to the loss of 28 Da (HCN/HNC + H) on the protonated spectra, which is not observed.
The black curves in the spectra of protonated species result from the reaction of background water (+18 Da) with photofragments obtained upon HCN/HNC loss. The appearance energies (AEs) of fragments resulting from HCN and/or HNC loss are ≈5.2 eV for the two protonated species and they are 7.4 and 7.0 eV the 9 -CN-Ant+ and 9-CN-Phen+, respectively. The di-dehydrogenated open-shell ionic photofragments obtained from HCN/HNC loss of the CN-PAH radical cations present no detected reactivity toward residual water in the ion trap; whereas, the mono-dehydrogenated closed-shell ionic photofragments (arylium species) resulting from the HCN/HNC loss of protonated CN-PAHs appear to be very reactive toward water.
The reactivity behavior of C14H9+ formed from 9 -CN-AntH+ and 9 -CN-PhenH+ is different, as can be seen in Fig. 2. In the case of 9 -CN-AntH+, an almost constant fraction of C14H9+ is reacting with water (similar spectra for m/z 177 and 195), whereas the reactivity of C14H9+ from 9 -CN-PhenH+ exhibits a clear photolysis energy dependence. The reactivity of photofragments with water has been previously observed with protonated benzonitrile (Jacovella et al. 2022b) and small protonated N-heterocycles (Hansen et al. 2015; Jacovella et al. 2022a).
Additionally, for the radical cations a dissociative channel corresponding to the loss of an H2 unit (molecular hydrogen at low energies and/or rapid sequential loss of two H atoms at higher energies) has been observed and is shown in yellow (AE of 4.7 and 8.6 eV for 9 -CN-Ant+ and 9 -CN-Phen+, respectively). A striking isomeric effect was thus found for the AE and the intensity of the H2 loss channel. Interestingly, the observed dissociation channels differ from those reported by West et al. (2019) for 9-CN-Ant+ and 9-CN-Phe+ through collision-induced dissociation. In their study, however, they reported an H-loss channel and H2 loss was not observed. We deduce that the available dissociation pathways are different depending on whether thermal heating (collisions) is used on the surface of the electronic ground state or photochemistry (absorption of a photon) where several conical intersections can be explored on the surfaces of excited electronic states. The formation of the dication has been recorded and the corresponding spectra are shown by green curves..
The observed AEs of the dication from the singly cationic species are given in Table 1. These are compared with the theoretical values of the adiabatic and vertical ionization energies (AIEs and VIEs) calculated using DFT (see Methods). For comparison, using the same apparatus Zhen et al. (2016) found an AE of 11.7(1) eV for bare anthracene radical cation, which is 0.5 eV lower in energy than for 9 -CN-Ant+, as is expected from the effective electron-withdrawing effect of the CN group. The calculated ionization energies agree reasonably well for the radical cations with the experimental appearance energies with the trend of AE2+ being slightly larger than AIE2+, as also seen in the work of Wenzel et al. (2020) for bare PAHs. For protonated species, the calculated AIE2+ values are 0.8 and 0.6 eV lower than the AE2+ ones for 9 -CN-AntH+ and 9 -CN-PhenH+, respectively. This appears to be larger than the expected uncertainties and could result from a poor Franck-Condon overlap in the vicinity of the second ionization threshold, as hinted at by the significantly larger values for VIE2+ compared to AIE2+. Another possible explanation could be that the protonated species may include a significant fraction of isomeric structures different from the one we assumed, with slightly higher ionization energies, which would be indistinguishable in this setup.
The black traces in Fig. 3 were obtained by summing the intensity of all photofragments and of the dication. The obtained spectra were compared with the calculated photoabsorption spectra using the aforementioned real time, real space implementation of TD-DFT. Assuming that the relaxation above 10 eV is nearly exclusively governed by fragmentation and ionization processes which are our only observables, the experimental action spectra have been normalized to the theoretical photoabsorption spectra to best reproduce the high-energy region (10 to 13.6 eV). The factors used were 5 × 1016, 1 × 1017, 1 × 1017, and 2 × 1017 for 9 -CN-Ant+, 9 -CN-Phe+, and 9 -CN-AntH+, 9 -CN-PheH+, respectively. The dispersion of these factors, despite the similarity of the average values of the theoretical spectra in the high-energy region, is indicative of the expected uncertainties. Based on these factors and the assumption that no radiative processes take place above 10 eV, we anticipate the errors of our cross section to be on the order of 50%. The theoretical photo-absorption spectra of the protonated species are unable to capture features in the 6–8 eV range that could arise from the presence of other isomers.
The presence of a larger number of structures in the calculated spectra at high energies can partially be attributed to a known artifact. Indeed, the computed wave functions were simulated within a box of finite size, engendering unbound states to be artificially quantized. However, the low-energy (<8 eV) structured bands that are weaker (9 -CN-Ant+) or missing (9 -CN-Phe+) in the experimental photodissociation spectra, compared to the theoretical prediction, may be due to real physical processes. This may indicate that radiative and/or collisional relaxation in the trap with the buffer gas cannot be neglected. This was implicated by Martin et al. (2015) and Zhen et al. (2016) for bare PAH radical cations and further confirmed by Stockett et al. (2022) in the case of 1-CN-naphthalene radical cation (1-CN-Naph+), where efficient recurrent fluorescence (RF) was observed at low internal energies. Based on the He pressure in our ion trap (10−3 mbar), we estimate the collision rate to be 107 s−1. If we assume that about 100 collisions with He are required to de-excite the ions below their dissociation thresholds, we can estimate de-excitation rate through collisions with He of 105 s−1. An estimate of the lower limit of the RF rates has been calculated for the four molecules under investigation using the methodology described in Appendix A. The integrated emission rates through the RF mechanism as a function of excitation energies (R(E)) can be found in Fig. A.3. Table 2 gives the RF rates at two photon energies (4.5 and 8 eV) and the values calculated by Stockett et al. (2022) for 1-CN-Naph+ are also given for comparison. In their study, they show that neglecting the Herzberg-Teller coupling reduced the RF rates by one order of magnitude. In a previous study on anthracene radical cation, Martin et al. (2015) found that their calculated RF rates – obtained with a similar methodology as the one used in our study – were underestimated by at least a factor ~2 to ~3 compared to the experimental results. As a simple test, we also evaluated the influence of the vibrational frequencies in the electronic excited states from which RF arises on computed RF rates (see Fig. A.4). We found that a small variation of 5% alone leads to another increase of one order of magnitude. With all of the aforementioned considerations and the calculated lower limits, it is plausible that recurrent fluorescence can efficiently compete with collisional cooling at excitation energies below 10 eV for small- to medium-sized CN-PAHs.
Experimental appearance energy for the dication from singly charged CN-PAHs (AE2+), as well as their calculated adiabatic ionization energies (AIE2+) and vertical ionization energies (VIE2+).
 |
Fig. 3 Black traces are the intensity of the photo-products (dications + singly ionized photofragments) as a function of VUV photon energy normalized to the photoabsorption cross section in the region [10–13.6 eV]. The red dashed lines are the theoretical photoabsorption spectra. |
Integrated emission rate through recurrent fluorescence at excitation energies of 4.5 and 8 eV.
4 Astrophysical implications and conclusions
Figure 4 displays the intensity ratio of the dication over the sum of all ionic fragments plus dication. When neglecting the radiative and collisional energy loss channels, this ratio may be approximated as a pseudo-photoionization yield. The pseudo-photoionization yields are plotted as a function of photon energy with gold crosses for radical cations and purple circles for protonated species.
The PAH-VUV interaction is a crucial process that partially governs the composition of the PAH population in space and thus the ensuing chemistry. Furthermore, the ionization of PAHs by VUV photons from massive stars is expected to account for a large fraction of the heating of neutral gas in galaxies and thus laboratory data on PAHs and any of their derivatives that are abundant in space are essential to test photoelectric heating models against observational diagnostics (Berné et al. 2022). The substitution of PAHs by a CN functional group does not significantly alter the photoionization yield, considering that for similar and larger sizes, the bare radical cation PAHs presented photoionization yields ranging from 0.2 to 0.5 at 13.6 eV (Zhen et al. 2016). This indicates that the same guiding principles developed by Zhen et al. (2016) and Wenzel et al. (2020) can be applied for radical cations of CN-PAHs.
While Zhen et al. (2016) and Wenzel et al. (2020) have shown that the phototionization yield rapidly becomes the prevalent relaxation route upon VUV excitation as the size of PAHs increases, an important new finding of the present work as seen from Fig. 4 is that protonation can hamper the photoioniza-tion yield. This effect is particularly pronounced in the case of 9 -CN-Ant, where the photoionization yield for 9 -CN-Ant+ reaches ≈0.55 at 13.6 eV, while it is only ≈0.2 at the same photon energy for 9 -CN-AntH+. The photoionization yields are modified by protonation and investigating the protonation effect for other functional groups, they should be targeted for a better understanding of the VUV photoprocessing for the PAH molecular class. Based on the previous work of Stockett et al. (2022) and the comparison between our experimental VUV photodissociation-photoionization spectra and the calculated photoabsorption spectra, we suspect that for CN-PAH species both the radical cations and protonated cases undergo efficient recurrent fluorescence. This relaxation route should be a crucial property for small- to medium-sized species that supports their survival in the harsh conditions of the diffuse interstellar medium (ISM) and thus renders them as potential carriers of the diffuse interstellar bands.
We have presented a first semi-quantitative investigation on the VUV photoprocessing of CN-PAHs in their radical cationic and protonated cation forms. This extends our previous work on protonated benzonitrile (Jacovella et al. 2022b). We hope that this study will instigate quantitative studies on larger CN-PAHs (including protonated species) and possibly further exploration of aspects of radiative cooling such as recurrent fluorescence using electrostatic rings (Stockett et al. 2022). The detection of CN-aromatics in an unexpectedly high abundance and in different types of environments in space definitely establish the importance of their chemistry in space and thus the need for data on these species to be taken into account in astrochemical models.
 |
Fig. 4 Pseudo-photoionization yields as a function of photon energy, for protonated and radical cations 9 -CN-Ant and 9 -CN-Phe. |
Acknowledgements
We are grateful to the staff from SOLEIL for the smooth running of the facility and providing beamtime under project 20191313.
Appendix A Theoretical estimate of recurrent fluorescence
It has long been known that large, isolated molecules may undergo delayed electronic fluorescence, commonly known as “recurrent” or “Poincaré” fluorescence (Leger et al. 1988). This is strictly related to the same process thought to give rise to the observed emission of the aromatic infrared bands by PAHs, under UV irradiation in photodissociation regions (Leger & Puget 1984; Allamandola et al. 1989). A large, isolated molecule, upon absorbing an UV photon, undergoes an electronic transition to an excited electronic state. From there, it very quickly crosses a series of conical transitions all the way down to the ground state, leading to fast conversion of the initial electronic excitation to vibrational excitation. This highly excited molecule, due to vibrational anharmonicity and conical intersections, behaves as a closed, ergodic system, with an equal probability at any given time to be in any state compatible with the conservation of energy and angular momentum. The probability for the molecule to be in a state from which a given transition can occur is given by the ratio between the density of such states and the total density of states. The rate of emission is given by the product of this probability times the Einstein coefficient Av for spontaneous emission, if stimulated emission can be neglected:
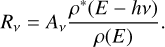 (A.1)
(A.1)
For an electronic transition, ρ* is the density of vibrational states in the electronic excited state from which it arises, whereas ρ is the total density of states, which is dominated by the density of vibrational states in the ground electronic state. Furthermore, Av is related to the absorption-cross section σ (see e. g. Bernath 2020) by the equation
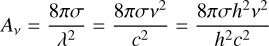 (A.2)
(A.2)
As a first approximation, we can consider only fluorescence transitions from excited electronic states to the ground electronic state, neglecting transitions between two excited states. With this approximation, σ factors are the same photoabsorption cross sections described in Section 2.2, yielding
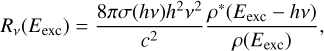 (A.3)
(A.3)
where Rv in this equation is dimensionless. To obtain an actual rate, one has to integrate it over a frequency range, that is
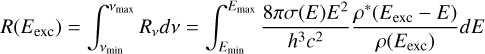 (A.4)
(A.4)
The density of vibrational states in the ground electronic state was obtained in the harmonic approximation using the Beyer-Swinehart direct counting algorithm. For the density of states in the excited electronic state(s), we made the simplifying assumption that for low-lying excited states, vibrational modes and frequencies can be expected to be close to those in the ground electronic state, hence ρ* ≃ ρ.
We note that Rv in Eq. A.3 is proportional to the expected fluorescence spectrum emitted by a sample of molecules excited at energy Eexc. Comparing their spectral distribution for different values of Eexc up to ~14 eV, we find that the predicted emission spectrum is always dominated by the lowest energy permitted transition (Fig. A.1), only in the case of 9-CN-PhenH+ with some contribution from the second lowest one (Fig. A.2). In all cases the emitted photons have energies below ~3 eV. We can then perform, numerically, the integral in Eq. A.4 from Emin = 0 eV to Emax = 5 eV, to obtain an estimate of the total recurrent fluorescence rate as a function of Eexc. The result is shown in Figure A.3.
 |
Fig. A.1 Rv/h for 9-CN-Ant+ at Eexc = 5 eV (top panel) and 12 eV (bottom panel). |
Since all of the approximations involved in this calculation lead to an underestimation, this estimate should be regarded as a lower limit. To get a rough idea of how important this underestimation can be, we repeated the same calculation assuming the minimum of the excited state surface to be very slightly shallower than that of the ground state, resulting in a reduction of vibrational frequencies. Just a mere 5% reduction of the vibrational frequencies in the excited state produces a substantial increase in the ρ* factor, resulting in about an order of magnitude increase of R(Eexc) at Eexc ~ 7 eV. This is shown in Figure A.4. The problem of estimating recurrent fluorescence rates, with a quantitative comparison between theoretical estimates obtained along the lines described above, and experimental data, has been examined in detail for the case of anthracene by Martin et al. (2015). They found that these theoretical predictions underestimate recurrent fluorescence rates by at least a factor ~2-3. More recent data suggest even a somewhat larger underestimation (Joblin 2023; Bernard et al. in prep.).
 |
Fig. A.2 Rv/h for 9-CN-PhenH+ at Eexc = 5 eV (top panel) and 12 eV (bottom panel). |
 |
Fig. A.3 Integrated R(Eexp) as a function of Eexp, assuming – in all cases – the same vibrational frequencies in the ground and excited electronic state involved in the fluorescence. |
 |
Fig. A.4 Integrated R(Eexp) as a function of Eexp for 9CN-anthracene, assuming the vibrational frequencies in excited electronic state(s) involved in the fluorescence to be respectively the same, 98%, and 95% of the vibrational frequencies in the ground electronic state. |
References
- Agúndez, M., Cernicharo, J., de Vicente, P., et al. 2015, A & A, 579, L10 [CrossRef] [EDP Sciences] [Google Scholar]
- Allain, T., Leach, S., & Sedlmayr, E. 1996, A & A, 305, 616 [NASA ADS] [Google Scholar]
- Allamandola, L., Tielens, A., & Barker, J. 1989, ApJS, 71, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Bagag, A., Giuliani, A., & Laprévote, O. 2007, Int. J. Mass Spectrom., 264, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Becke, A. D. 1988, Phys. Rev. A, 38, 3098 [NASA ADS] [CrossRef] [Google Scholar]
- Bernath, P. F. 2020, Spectra of Atoms and Molecules (USA: Oxford University Press) [Google Scholar]
- Berné, O., Foschino, S., Jalabert, F., & Joblin, C. 2022, A & A, 667, A159 [CrossRef] [EDP Sciences] [Google Scholar]
- Bezanson, J., Edelman, A., Karpinski, S., & Shah, V. B. 2017, SIAM Rev., 59, 65 [Google Scholar]
- Burkhardt, A. M., Loomis, R. A., Shingledecker, C. N., et al. 2021, Nat. Astron., 5, 181 [Google Scholar]
- Cabezas, C., Agúndez, M., Marcelino, N., et al. 2022, A & A, 659, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Agúndez, M., Kaiser, R. I., et al. 2021, A & A, 655, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dirac, P. A. M. 1930, Math. Proc. Cambridge Philos. Soc., 26, 376 [CrossRef] [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian~16 Revision C.01 (Wallingford CT: Gaussian Inc.) [Google Scholar]
- Giordano, M. 2016, ArXiv e-prints [arXiv: 1610.08716] [Google Scholar]
- Giuliani, A. 2021, MassJ : Julia package for mass spectrometry data treatment and analysis, Recherche Data Gouv V1, https://doi.org/10.15454/KU1P28 [Google Scholar]
- Gredel, R., Lepp, S., Dalgarno, A., & Herbst, E. 1989, ApJ, 347, 289 [Google Scholar]
- Hansen, C. S., Blanksby, S. J., Chalyavi, N., et al. 2015, J. Chem. Phys., 142, 014301 [NASA ADS] [CrossRef] [Google Scholar]
- Jacovella, U., Hansen, C. S., Giuliani, A., Trevitt, A. J., & Nahon, L. 2022a, MNRAS, 511, 5656 [NASA ADS] [CrossRef] [Google Scholar]
- Jacovella, U., Noble, J. A., Guliani, A., et al. 2022b, A & A, 657, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kendall, R. A., Dunning Jr, T. H., & Harrison, R. J. 1992, J. Chem. Phys., 96, 6796 [NASA ADS] [CrossRef] [Google Scholar]
- Le Page, V., Snow, T. P., & Bierbaum, V. M. 2003, ApJ, 584, 316 [Google Scholar]
- Leach, S. 1986, J. Electron Spectr. Relativ. Phenom., 41, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C., Yang, W., & Parr, R. G. 1988, Phys. Rev. B, 37, 785 [Google Scholar]
- Lee, K. L. K., Changala, P. B., Loomis, R. A., et al. 2021, ApJ, 910, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Leger, A., & Puget, J. 1984, A & A, 137, L5 [NASA ADS] [Google Scholar]
- Leger, A., D'Hendecourt, L., & Boissel, P. 1988, Phys. Rev. Lett., 60, 921 [Google Scholar]
- Maksić, Z. B., & Eckert-Maksić, M. 1998, Theor. Comput. Chem., 5, 203 [CrossRef] [Google Scholar]
- Malloci, G., Joblin, C., & Mulas, G. 2007, Chem. Phys., 332, 353 [Google Scholar]
- Martin, S., Ji, M., Bernard, J., et al. 2015, Phys. Rev. A, 92, 053425 [Google Scholar]
- McCarthy, M. C., & McGuire, B. A. 2021, J. Phys. Chem. A, 125, 3231 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, M. C., Lee, K. L. K., Loomis, R. A., et al. 2021, Nat. Astron., 5, 176 [Google Scholar]
- McGuire, B. A., Burkhardt, A. M., Kalenskii, S., et al. 2018, Science, 359, 202 [Google Scholar]
- McGuire, B. A., Loomis, R. A., Burkhardt, A. M., et al. 2021, Science, 371, 1265 [Google Scholar]
- Milosavljević, A. R., Nicolas, C., Gil, J.-F., et al. 2012, J. Synchrotron Rad., 19, 174 [CrossRef] [Google Scholar]
- Montillaud, J., Joblin, C., & Toublanc, D. 2013, A & A, 552, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nahon, L., de Oliveira, N., Garcia, G. A., et al. 2012, J. Synchrotron Rad., 19, 508 [Google Scholar]
- Perdew, J. P., & Zunger, A. 1981, Phys. Rev. B, 23, 5048 [CrossRef] [Google Scholar]
- Prasad, S. S., & Tarafdar, S. P. 1983, ApJ, 267, 603 [Google Scholar]
- Sita, M. L., Changala, P. B., Xue, C., et al. 2022, ApJ, 938, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Stockett, M. H., Bull, J. N., Cederquist, H., et al. 2022, ArXiv eprint [arXiv:2209.05229] [Google Scholar]
- Tancogne-Dejean, N., Oliveira, M. J. T., Andrade, X., et al. 2020, J. Chem. Phys., 152, 124119 [NASA ADS] [CrossRef] [Google Scholar]
- Troullier, N., & Martins, J. L. 1991, Phys. Rev. B, 43, 1993 [CrossRef] [PubMed] [Google Scholar]
- Wenzel, G., Joblin, C., Giuliani, A., et al. 2020, A & A, 641, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- West, B. J., Lesniak, L., & Mayer, P. M. 2019, J. Phys. Chem. A, 123, 3569 [NASA ADS] [CrossRef] [Google Scholar]
- Witt, A. N., Gordon, K. D., Vijh, U. P., et al. 2006, ApJ, 636, 303 [Google Scholar]
- Yabana, K., & Bertsch, G. F. 1996, Phys. Rev. B, 54, 4484 [CrossRef] [PubMed] [Google Scholar]
- Zhen, J., Castillo, S. R., Joblin, C., et al. 2016, ApJ, 822, 113 [Google Scholar]
Number taken from the www.astrochymist.org website maintained by David E. Woon (U. Illinois, USA).
All Tables
Experimental appearance energy for the dication from singly charged CN-PAHs (AE2+), as well as their calculated adiabatic ionization energies (AIE2+) and vertical ionization energies (VIE2+).
Integrated emission rate through recurrent fluorescence at excitation energies of 4.5 and 8 eV.
All Figures
 |
Fig. 1 Top panel (red trace) is a mass spectrum of the protonated 9-CN-anthracene parent ion (C14H9CNH+, m/z = 204) without irradiation. The bottom panel (red trace) is a mass spectrum of the same species irradiated with a photon energy of 5.7 eV, leading to photodissociation. |
| In the text | |
 |
Fig. 2 UV/VUV photodissociation spectra of CN-PAH radical cations (left column) and of protonated species (right column). |
| In the text | |
 |
Fig. 3 Black traces are the intensity of the photo-products (dications + singly ionized photofragments) as a function of VUV photon energy normalized to the photoabsorption cross section in the region [10–13.6 eV]. The red dashed lines are the theoretical photoabsorption spectra. |
| In the text | |
 |
Fig. 4 Pseudo-photoionization yields as a function of photon energy, for protonated and radical cations 9 -CN-Ant and 9 -CN-Phe. |
| In the text | |
 |
Fig. A.1 Rv/h for 9-CN-Ant+ at Eexc = 5 eV (top panel) and 12 eV (bottom panel). |
| In the text | |
 |
Fig. A.2 Rv/h for 9-CN-PhenH+ at Eexc = 5 eV (top panel) and 12 eV (bottom panel). |
| In the text | |
 |
Fig. A.3 Integrated R(Eexp) as a function of Eexp, assuming – in all cases – the same vibrational frequencies in the ground and excited electronic state involved in the fluorescence. |
| In the text | |
 |
Fig. A.4 Integrated R(Eexp) as a function of Eexp for 9CN-anthracene, assuming the vibrational frequencies in excited electronic state(s) involved in the fluorescence to be respectively the same, 98%, and 95% of the vibrational frequencies in the ground electronic state. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


