EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 640 (August 2020) A&A, 640 (2020) A19 Full HTML
Free Access
Issue
A&A
Volume 640, August 2020
Article Number A19
Number of page(s) 15
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202037851
Published online 03 August 2020

© ESO 2020

1 Introduction

The formation of planets is inherently entangled with the formation and evolution of their natal protoplanetary disks. The physical conditions and chemical composition at the onset of planet formation determine the properties of the resulting planetary systems (e.g., Armitage 2011; Öberg et al. 2011; Morbidelli & Raymond 2016). The key question is therefore the following: At what stage of disk evolution do planets start to form?

The protoplanetary disks around Class II pre-main sequence stars were considered to be the starting point of the planet formation process. However, submillimeter surveys of those disks reveal that the mass reservoir available in Class II disks is much lower than the masses needed to explain the formation of the observed exoplanetary systems (Andrews &Williams 2007a; Greaves & Rice 2010; Williams 2012; Najita & Kenyon 2014; Manara et al. 2018). Structures observed in the disks (e.g., van der Marel et al. 2013; Andrews et al. 2018; Long et al. 2019) are also evidence that planet formation is already underway in the Class II phase. One of the possible solutions to this conundrum is to move the onset of planet formation to the younger disks surrounding Class 0/I protostars (<0.5 Myr; Dunham et al. 2014a), where more material is available (Andrews & Williams 2007b; Greaves & Rice 2011; Ansdell et al. 2017).

There is other evidence for early planet formation. The distribution of different types of meteorites in our Solar System can be explained by the formation of Jupiter’s core in the first million years of the history of the system (Kruijer et al. 2014). There is also evidence for dust growth in the earliest stages of disk formation (e.g., Jørgensen et al. 2007; Kwon et al. 2009; Miotello et al. 2014; Harsono et al. 2018; Hsieh et al. 2019a). Another indication is provided by young sources with structures suggestive of ongoing planet formation (e.g., ALMA Partnership 2015; Sheehan & Eisner 2018). These all suggest that planet formation starts early in disks surrounding much younger Class 0 and Class I protostars rather than in Class II disks.

This begs the following question: What is the amount of material available for planet formation in Class 0/I disks? Greaves & Rice (2011), in a study of a small sample of Class 0 disks known at the time, found that 20–2000 M⊕ of dust mass isavailable in Class 0 disks around low-mass stars. These latter authors concluded that this is sufficient to form the most massive exoplanet systems found to date. An analysis of a sample of Class I disks in Taurus (Andrews et al. 2013) combined with information about the occurrence of exoplanets led Najita & Kenyon (2014) to conclude that Class I disks can explain the population of exoplanetary systems, contrary to Class II disks in the same region. A study of a larger sample of young disks extending to Class 0 protostars is needed to put constraints on planet formation timescales and efficiency.

In the first complete survey of Class 0/I protostars in a single cloud, Perseus, Tychoniec et al. (2018a) used Very Large Array (VLA) 9 mm observations at 75 au resolution to show that there is a declining trend in the dust masses from Class 0 to Class I disks. The median masses for the Class 0 and Class I phase (~250 and ~100 M⊕, respectively) are explained by a significant fraction of the dust being converted into larger bodies already in the Class 0 phase. Moreover, they compared the results for Class 0/I disks in Perseus with Atacama Large Millimeter/submillimeter Array (ALMA) observations of several Class II regions which have mean dust masses in the range 5–15 M⊕ (Ansdell et al. 2017). This suggests that dust masses in the Class 0/I disks are an order of magnitude higher that those for Class II disks. However, we note that the adopted dust mass absorption coefficient (κν - dust opacity) varies in these studies.

ALMA observations by Tobin et al. (2020) in the Orion Molecular Cloud, based on the largest sample of protostars observed in a single region at sub-millimeter wavelengths (379 detections), found much lower mean dust masses for Class 0 and I disks than those in Perseus: 26 and 15 M⊕, respectively. Very low Class I mean dust disk masses (4 M⊕) were also reported in the Ophiuchus star-forming region (Williams et al. 2019). Also in this case, different opacities assumed in those studies could contribute to the difference between the median masses measured.

Comparison of the VLA observations for Perseus with other embedded disk surveys using ALMA is difficult because of the different wavelength range of observations. The VLA observations at 9 mm can have a significant free–free emission contribution, which could result in overestimation of the actual flux coming from the dust (e.g., Choi 2009); although Tychoniec et al. (2018a) applied the correction for a free–free contribution using information from the C-band (4.1 and 6.4 cm) flux densities. On the other hand, the dust emission at those long wavelengths is less likely to be optically thick than that in the ALMA wavelength range (Dunham et al. 2014c). The way forward is to use observations of young disks with VLA and ALMA in the same star-forming region, offering a direct comparison of dust disk masses and a method for determining if the difference in observing wavelengths can be the reason for the described differences. Therefore, in this work we present ALMA observations of protostars in Perseus and compare them with our previous VLA data.

Here, we aim to compare the solid masses of the embedded (Class 0/I) disks with the masses of the exoplanetary systems observed to date to ultimately infer an efficiency of the planet formation. In Sect. 2, we describe the ALMA observations and data analysis. In Sect. 3, the integrated fluxes at 1 and 9 mm are compared; dust masses are then calculated based on those fluxes and are compared with other young and more mature dust disks observed with ALMA. In Sect. 4, we put the inferred masses in the context of known exoplanetary system masses and planet formation models.

2 Observations and analysis

2.1 Observations

In this paper we analyze ALMA Band 6 continuum observations of 44 protostars in the Perseus molecular cloud. The data were obtained in September 2018 with a Cycle 5 program (2017.1.01693.S, PI: T. Hsieh). The absolute flux and bandpass calibrator was J0237+2848, and the phase calibrator was J0336+3218. Continuum images and spectrallines observed in this project are presented in Hsieh et al. (2019b). The continuum bandwidth was ~ 1.85 GHz centered at 267.99 GHz (1.1 mm). The absolute flux calibration uncertainty is on the order of ~30%. The synthesized beam of the continuum observations in natural weighting is 0.′′ 45 × 0.′′ 30. The average spatial resolution of observations(0.′′38) corresponds to 110 au (diameter) at the distance to Perseus (293 ± 22 pc; Ortiz-León et al. 2018). The typical rms value of the continuum images is ~0.1 mJy beam−1.

Additional data on eight disks were obtained in a Cycle 5 program (2017.1.01078.S, PI: D. Segura-Cox). The continuum bandwidth was centered at 233.51 GHz (1.3 mm) with a total bandwidth of 2 GHz. The average synthesized beam of 0.′′ 41 × 0.′′28 provides spatial resolution corresponding to 100 au at the distance of Perseus. The rms value of the images is ~0.05 mJy beam−1. The absolute flux and bandpass calibrator was J0510+1800 and the phase calibrator was J0336+3218. The accuracy of the flux calibration is on the order of ~10%. The measurement sets were self-calibrated and cleaned with the robust parameter 0.5.

We also use the flux densities of 25 disks published in Tobin et al. (2018) which were observed at 1.3 mm with a resolution of 0.′′ 27 × 0.′′16 and sensitivity of 0.14 mJy beam−1. The flux and disk masses in Tobin et al. (2018) are measured using a Gaussian fit in the image domain to the compact component in the system without subtraction of an envelope component. Altogether we compile a sample of 77 Class 0 and Class I disks in Perseus observed with ALMA. In the following, when referring to ALMA data, we refer to “1 mm observations” for brevity, but where the wavelength is used to calculate properties of the source (e.g., disk mass), the exact value of the observed wavelength is used.

The VLA observations come from the VLA Nascent Disks and Multiplicity Survey (VANDAM; Tobin et al. 2015, 2016; Tychoniec et al. 2018b). The sample for the VANDAM survey was prepared based on unbiased infrared and submillimeter surveys of protostars in Perseus (Enoch et al. 2009; Evans et al. 2009; Sadavoy et al. 2014). Fluxes at 9.1 mm (Ka-band), obtained with 0.25′′ resolution from 100 Class 0 and I disks (including upper limits) were reported in Tobin et al. (2016). Tychoniec et al. (2018b) applied a correction for free–free emission based on C-band (4.1 and 6.4 cm) observations. In that work, all sources with a Ka-band spectral index suggestive of emission not coming from dust (α ≪ 2) were marked as upper limits, and we use the same criteria here. We use the 9 mm fluxes corrected for the free–free emission for further analysis.

2.2 Gaussian fitting

Pre-ALMA surveys of embedded sources have found that disk masses are typically only a small fraction of the total envelope mass in the Class 0 phase (1–10%), becoming more prominent as the system evolves in the Class I phase (up to 60%, e.g., Jørgensen et al. 2009). In the much smaller ALMA beam, the envelope contamination is reduced (e.g., Crapsi et al. 2008), but still needs to be corrected for Tobin et al. (2020). Here both components, disk and envelope, are represented by Gaussians.

The CASA (McMullin et al. 2007) v. 5.4.0 imfit task was used to fit Gaussian profiles to the sources. After providing the initial guess, all parameters, namely position, flux, and shape of the Gaussian, were set free during the fit. All sources were inspected by eye to assess the number of necessary Gaussian components. In case of a single source without a noticeable contribution from the envelope, a single compact Gaussian with the size of the synthesized beam was provided as input to the imfit task (Fig. A.1a). In cases where a contribution of the envelope by eye was significant, an additional broad Gaussian with a size of 3′′ was added to the initial guess parameters of the fitting (Fig. A.1b). In two cases (Per-emb-4 and SVS13A2) it was necessary tofix the size of the Gaussian to the synthesized beam size for the fit to converge (Fig. A.1c). Two binary systems with separations below our resolution (Per-emb-2 and Per-emb-5) are treated as single systems with a common disk.

The flux density of the compact Gaussian is assumed to be that of the embedded disk; it is referred to as a “disk” here, even though no evidence for a Keplerian rotation pattern yet exists. We report the measured fluxes of the embedded disks in Table A.1.

The broad component is used only to force the imfit task to not fit extended emission without constraining the compact Gaussian size which would in turn overestimate the flux of the compact emission. It was necessary to add an envelope component to 31 sources out of 51 targets, specifically 20 Class 0 and 11 Class I sources. We assessed the remaining 6 Class 0 sources and 20 Class I sources as not having significant contribution from their envelope.

The envelope flux remaining after subtracting the model of the disk component is measured as the flux in the area of the size of the FWHM of the disk in the residual image. This ratio of the envelope residual flux to the disk flux ranges from less than 1% to usually below 30%. In one case the source is dominated by the envelope emission (Per-emb-51; Fig. A.1d), but after the envelope component subtraction the residual flux is only ~ 6% of that of the disk (Table A.1). The two sources with high values of the ratio, Per-emb-22-B and Per-emb-27B, are heavily affected by the nearby binary component and so the value is not reliable.

We stress that the remaining envelope fraction is not incorporated in the flux density of the disk component, and it is presented toshow that fitting the envelope component is needed to exclude the contamination of the envelope from the disk. Figure A.1 shows that residuals are significantly reduced after removing the envelope contribution, and that without fitting the extended component, some of this emission could contaminate the flux coming from the disk.

thumbnail Fig. 1

ALMA (1.1 and 1.3 mm) integrated fluxes plotted against VLA integrated fluxes at 9.1 mm. A total of 77 sources are plotted but only the 62 sources that are not upper limits are included in fitting the linear function. The best fit to the data is shown with the green line and has a slope of 1.15 ± 0.1. The Class 0 sources are shown in red and Class I sources in blue. Crosses mark sources that are unresolved binaries.

3 Dust disk masses

3.1 Comparison of the integrated fluxes between 1 and 9 mm

Measurements of the continuum emission at different wavelengths allow us to analyze the properties of the emitting material. First, it is important to verify that the fluxes at both 1 mm (ALMA) and 9 mm (VLA) have their origin in the same physical process. This is to confirm that the correction for contamination of the VLA observations by the free–free emission is accurate. In order to do so, we investigate the correlation between the flux densities at both wavelengths and the spectral index of the emission for each source.

The flux densities from the ALMA 1.1–1.3 mm observations are presented in Table A.1. In Fig. 1 we compare the measurements with the VLA 9.1 mm observations (Tobin et al. 2016; Tychoniec et al. 2018a). There is a clear correlation with a close-to-linear slope (1.15 ± 0.10) obtained with the lmfit Python function. The fitting was performed excluding upper limits. The value of the slope indicates that all sources have a similar spectral index between ALMA and VLA wavelengths. Thus, the mechanism responsible for emission at both wavelength ranges is the same. Since it is generally accepted that the ALMA 1 mm emission is dominated by dust thermal emission, we can conclude that this is also the case for the 9 mm VLA observations. The sources with resolved emission at 9 mm can be modelled successfully with the disk (Segura-Cox et al. 2016).

The nature of this emission can also be investigated with the value of the spectral index between the two wavelengths. In the Rayleigh-Jeans approximation, the flux density Fν changes with frequency Fν ~ να, where α is the spectral index. The dust emissivity index β defines the dependence of the dust opacity on the frequency κν ~ νβ. From the observed spectral index, the emissivity index can be derived accordingly: 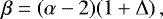β=(α−2)(1+Δ) ,\begin{equation*}\beta = (\alpha - 2)(1&#x002B;\Delta)\, ,\end{equation*}(1)

where Δ is the ratio of optically thick to optically thin emission (Beckwith et al. 1990; Lommen et al. 2007). It is often assumed that emission at millimeter wavelengths is optically thin, in which case Δ = 0 and then β = α − 2.

The spectral index between the ALMA and VLA fluxes is calculated as 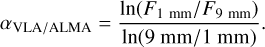αVLA/ALMA=ln(F1 mm/F9 mm)ln(9 mm/1 mm).\begin{equation*}\alpha_{\textrm{VLA/ALMA}}=\frac{\ln (F_{\textrm{1\ mm}}/ F_{\textrm{9\ mm}})}\textrm{ln(9\ mm/1\ mm)}. \end{equation*}(2)

The mean spectral index obtained between ALMA and VLA is α ~ 2.4, with a standard deviation for the sample of 0.5. This indicates that β = 0.4 ± 0.5, which is lower than the typical ISM value, namely ~1.8 for small grains (Draine 2006). The index is also lower than 1, the value typically used for protoplanetary disks, specifically in our previous study of embedded disks in Perseus (Tychoniec et al. 2018a). If emission is optically thin, the low value of β can point to dust growth as is commonly seen in Class II disks (e.g., Natta & Testi 2004; Ricci et al. 2010; Testi et al. 2014). There are other effects that could alter the value of the dust spectral index such as dust porosity (Kataoka et al. 2014), and grain composition (Demyk et al. 2017a,b) but to explain β < 1 some grain growth is required (Ysard et al. 2019).

While the VLA 9 mm flux is unlikely to be optically thick, the ALMA 1 mm emission from young disks can be opaque. Optically thick emission at 1 mm would result in a lower spectral index value. If the indices obtained between 1 and 9 mm αVLA/ALMA are consistent with the Ka-band intraband indices αVLA, it can be assumed that the emission at 1 mm is optically thin so that it is possible to measure the spectral index in a robust way. We calculate the VLA intraband spectral index, which is determined between the two sidebands of the Ka-band observations as follows: 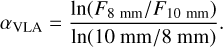αVLA=ln(F8 mm/F10 mm)ln(10 mm/8 mm).\begin{equation*}\alpha_{\textrm{VLA}}=\frac{\ln (F_{\textrm{8\ mm}}/ F_{\textrm{10\ mm}})}\textrm{ln(10\ mm/8\ mm)}. \end{equation*}(3)

Figure A.3 shows the range of the αVLA/ALMA and αVLA values measured. For 23 sources out of 77 we found αVLA/ALMA - αVLA ≤ 0.4, which is in reasonable agreement (see Fig. A.2). For those sources, the emission at both 1 and 9 mm wavelengths is most likely optically thin, and so the spectral index should provide information about the grain size. The mean spectral index of those sources is 2.5, which means that β ~ 0.5. This value confirms that significant dust growth is occurring in the observed disks. The spectral index calculated for the selected optically thin sample (0.5) is similar to that calculated for the full sample (0.4). We therefore proceed in assuming a value of β = 0.5 for the further analysis as an average value, which does not exclude that the 1 mm emission is optically thick. It is also likely that the spectral index varies with the radius of the disk because of optically thick emission close to the protostar and the grain growth further out (Pinilla et al. 2012; van Terwisga et al. 2018), as well as a grain size that depends on radius (Tazzari et al. 2016). Our observed emission is largely unresolved and the measured spectral index is an average of those effects.

The emission at shorter wavelengths is more likely to be optically thick. With at least marginally resolved disks, we can obtain an estimate of the dust optical depth because the extent of the emission allows us to approximate the disk radius. We use the major axis deconvolved from the beam as the diameter of the disk. We then obtain optical depth as τ ~ κνΣ, where κν is dust opacity used to calculate the mass and Σ is averaged surface density. Figure A.4 presents a distribution of calculated optical depths. For all the disks with available major axis value, we get τ < 0.4; and < 0.1 in the vast majority of cases.

Summarizing, we identify dust thermal emission as the dominating physical process responsible for the emission at both 1 mm and 9 mm. What is more, from the sample of sources for which the emission is most likely optically thin, we calculate a spectral index value of 2.5, suggestive of significant grain growth already at these young stages.

3.2 Disk mass measurements

The continuum flux at millimeter wavelengths is commonly used as a proxy of the dust mass of the emitting region. Here we use the collected fluxes for the continuum flux in Perseus with VLA and ALMA to calculate the masses of the embedded disks. The key assumptions used in the calculation, temperature and dust opacity (dust mass absorption coefficient), are discussed. We then proceed to compare the results with other disk surveys both at Class 0/I and at Class II phases.

From the integrated disk fluxes, the dust mass of the disk is calculated following the equation from Hildebrand (1983): 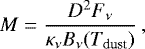M=D2FνκνBν(Tdust) ,\begin{equation*}M=\frac{D^2F_{\nu}}{{\kappa}_{\nu} B_{\nu}(T_{\textrm{dust}})}\, ,\end{equation*}(4)

where D is the distance to the source, Bν is the Planck function for a temperature Tdust, and κν is the dust opacity with the assumption of optically thin emission. The temperature of the dust is set to 30 K, typical for dust in dense protostellar envelopes (Whitney et al. 2003), and disks are assumed to be isothermal. The same temperatureis set for Class 0 and Class I disks. If the decrease of the temperature of dust from Class 0 to Class I is significant, the mass difference diminishes (e.g., Andersen et al. 2019). We consider two cases for the values of κν at 1.3 and 9 mm.

First, because our aim is to compare the results with the Class II disk masses in the literature, most notably the Lupus star-forming region, we use κ1.3 mm = 2.3 cm2 g−1 as used in the determination of masses in Ansdell et al. (2016). Figure 2 (top panel) shows the cumulative distribution function (CDF) for Class II disks in Lupus and Class 0 and I disks in Perseus, all observed with ALMA. The CDF plot is prepared using the survival analysis with the lifelines package for Python (Davidson-Pilon 2017). The CDF plot describes the probability of finding the element of the sample above a certain value. The uncertainty of the cumulative distribution is inversely proportional to the size of the sample and 1σ of the confidence interval is indicated as a vertical spread on the CDF plot. The cumulative distribution function takes into account the upper limits of the measurement, and the median is only reliable if the sample is complete. While the VLA observations sample is complete, the ALMA sample of disks is not, as we assemble ~ 80% of the total sample. Therefore, the VLA median values and distributions are more reliable.

The median dust mass for young disks in Perseus measured with ALMA at 1 mm with the adopted opacity of κ1.3 mm = 2.3 cm2 g−1 is 47 M⊕ and 12 M⊕ for Class 0 and Class I disks, respectively (Fig. 2, top panel). The median is taken from the value corresponding to the 0.5 probability on the CDF plot. The opacity value used here is likely close to the maximum value of the opacity at 1.3 mm (Draine 2006). In an analysis of dust opacity value at 1.3 mm, Panić et al. (2008) find a range between 0.1 and 2 cm2 g−1. Therefore, the dust masses obtained with κ1.3 mm = 2.3 cm2 g−1 from Ansdell et al. (2016) should be considered as a lower limit to the disk masses in Perseus. Only if the grain composition is significantly different from the typical assumption, in particular if dust has a significant fraction of amorphous carbon, will the actual masses of the dust be lower by a factor of a few (Birnstiel et al. 2018), even when compared with the κ1.3 mm = 2.3 cm2 g−1 that we assume to provide a lower limit on the dust disk mass.

Regardless of the uncertainties, there is a clear evolutionary trend from Class 0 to Class II with disk masses decreasing with evolutionary phase. The median dust masses for disks in Perseus measured with ALMA of 47 M⊕ and 12 M⊕ for Class 0 and Class I disks, respectively, are significantly higher than for Class II disks in Lupus which have a median mass of 3 M⊕. We note that this value differs from the 15 M⊕ value reported in Ansdell et al. (2016) because in that work the standard mean is calculated, as opposed to using the median taken from the CDF plot. Also, distances to Lupus disks have been updated with Gaia DR2 distances (Gaia Collaboration 2018). It should be noted that the dust temperature used in Ansdell et al. (2016) was 20 K, while we use 30 K, but the opacity value adopted to calculate the masses is the same. A lower temperature results in an increase of the total mass based on Eq. (4). Therefore, if the temperature were set to 20 K for the Perseus disks, the difference between Class 0/I and Class II disks would be even higher. However, Class 0/I disks are expected to be warmer than Class II disks (Harsono et al. 2015; van’t Hoff et al. 2020).

As an alternative method, considering that ALMA fluxes can be optically thick, we use the VLA flux densities to estimate the disk masses. Here, we adopt κ9 mm = 0.28 cm2 g−1 as provided by dust models of the DIANA project (Woitke et al. 2016) that consider large grains up to 1 cm; we recall that significant grain growth is indicated in our data by the empirically measured value of β =0.5. In Tychoniec et al. (2018a), a value of κ9 mm = 0.13 cm2 g−1 was used, scaled from κ1.3 mm = 0.9 cm2 g−1 of Ossenkopf & Henning (1994) using β = 1. If β = 0.5 is instead used to scalethe opacity κ1.3mm to 9 mm, the value is consistent with that of DIANA.

The median masses measured from the 9 mm observations are 158 M⊕ for Class 0 and 52 M⊕ for Class I (Fig. 2, bottom panel). Those masses are lower than the estimate provided in Tychoniec et al. (2018a) by a factor of two, which stems from the different opacity values used. Additionally, the values quoted in Tychoniec et al. (2018a) are regular medians, taken from the sample of detected disks and the distance to the Perseus star-forming region has been revised from 235 to 293 pc (Ortiz-León et al. 2018) which increases the estimate of the mass.

An important difference between the ALMA and VLA samples is that the VLA sample is complete, as it targeted all known protostars in Perseus (Tobin et al. 2016). Additionally, it is likely that the VLA flux densities are coming from optically thin emission, whereas the ALMA flux densities can become optically thick in the inner regions. We also use a refined model of the dust opacity of the DIANA project (Woitke et al. 2016) including large grains. Therefore, the median masses reported with VLA (158 M⊕ and 52 M⊕ for Class 0 and Class I, respectively) can be considered more robust.

thumbnail Fig. 2

Cumulative distribution plots of the dust disk masses. Top: masses of the Perseus Class 0 and I disks measured with ALMA at 1 mm compared with the Lupus Class II disks measured with ALMA (Ansdell et al. 2016). The opacity value of κ1.3 mm = 2.3  cm2 g−1 is used to calculate the masses. The ALMA sample consist of 77 sources (38 Class 0 and 39 Class I) and the Lupus sample consist of 69 sources. Bottom: masses of the Perseus Class 0 and I disks measured with VLA at 9 mm (red and blue, respectively), compared with the Lupus Class II disks measured with ALMA (Ansdell et al. 2016). The opacity value of κ9 mm =0.28  cm2 g−1 is used to calculate the VLA masses. The VLA sample consist of 100 sources (49 Class 0 and 51 Class I). Medians are indicated in the labels.

3.3 ALMA Class 0/I disk masses for different star-forming regions

Recent ALMA observations of Orion and Ophiuchus reveal masses of embedded Class 0/I dust disks that are somewhat lower than those obtained for Perseus with the VLA (Williams et al. 2019; Tobin et al. 2020). Here, we collect available ALMA observations for Perseus that use the same techniques as other embedded surveys. Such an analysis can reveal the inherent differences between the different protostellar regions.

Figure 3 shows the cumulative distribution of disks observed with ALMA for Orion (Tobin et al. 2020) and for Perseus. The Orion disks were targeted within the VANDAM survey of Orion protostars where 328 protostars were observed with ALMA Band 7 (0.87 mm) at 0.′′1 (40 au) resolution. The sample in Tobin et al. (2020) is divided into Class 0, Class I, and Flat Spectrum sources. We incorporate the Flat Spectrum sources into Class I in the comparison. An opacity value of 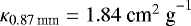κ0.87 mm=1.84 cm2 g−1$\kappa_{0.87\, \textrm{mm}}=1.84\ {\textrm{cm}^{2}\ \textrm{g}}^{-1}$ (Ossenkopf & Henning 1994) has been assumed to calculate the masses in the Orion survey. We use the same reference for opacity at 1.3 mm wavelengths, namely 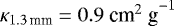κ1.3 mm=0.9 cm2 g−1$\kappa_{1.3\, \textrm{mm}}=0.9\ {\textrm{cm}^{2}\ \textrm{g}}^{-1}$, to calculate the masses from ALMA flux densities in Perseus to compare with the Orion sample. The median for Class 0 dust disk masses is still significantly lower in Orion, 67 M⊕ versus 131 M⊕ in Perseus, but is remarkably similar for Class I: 25 M⊕ versus 33 M⊕. Thus, using ALMA-measured flux densities and the same opacity assumption as Tobin et al. (2020), we find that there are some inherent differences between the population of Class 0 disks in Perseus and Orion. We note that values calculated here are different from those reported in Tobin et al. (2020) because the temperature of the dust was scaled with the luminosity in that work, while we use a constant T = 30 K for a consistent comparison with our sample.

Differences in sound speed or initial core rotation can result in different disk masses (e.g., Terebey et al. 1984; Visser et al. 2009). The initial composition of grains could also affect the dust spectral index. The Orion Molecular Complex seems to show a higher fraction of the amorphous pyroxene than the typical ISM (Poteet 2012). It is likely that such factors are resulting in different observed masses between Orion and Perseus. Tobin et al. (2020) noted that the 9 mm flux density distribution is similar between Perseus and Orion.

The low Class I median masses reported in Ophiuchus (Williams et al. 2019, median mass 3.8 M⊕) are puzzling as they suggest thatthe problem of missing dust mass for planet formation extends from Class II to Class I disks. In our data, the median Class I disk mass median is 11 M⊕ for the sameopacity assumption as in Williams et al. (2019), a factor of three higher. The Ophiuchus sample does not include the entire population of Class I disks in Ophiuchus and may be contaminated with more evolved sources due to the high foreground extinction (van Kempen et al. 2009; McClure et al. 2010). For this reason, we will not include it in the further analysis. Despite those caveats it is possible that the population of young disks in Ophiuchus is less massive than in Perseus and Orion.

thumbnail Fig. 3

Cumulative distribution plots for Perseus disk masses calculated from ALMA flux densities and Orion disk masses from Tobin et al. (2020), both calculated with the same opacity assumptions of κ1.3 mm = 0.9 cm2 g−1. The Perseussample consist of 77 sources (38 Class 0 and 39 Class I), the Orion sample consist of 415 sources (133 Class 0 and 282). Medians are indicated in the labels.

4 Exoplanetary systems and young disks: a comparison of their solid content

Surveys of protoplanetary (Class II) disks around pre-main sequence stars reveal that the dust masses of most disks are not sufficient to explain the inferred solid masses of exoplanetary systems (Williams 2012; Najita & Kenyon 2014; Ansdell et al. 2017; Manara et al. 2018). On the other hand, the results from the younger (Class 0/I) star-forming regions show that the dust reservoir available in younger disks is much higher than in the Class II phase (Tychoniec et al. 2018a; Tobin et al. 2020). Here, we aim to determine whether or not the amount of dust available at the onset of planet formation (Class 0/I disks) agrees with the masses of the exoplanet systems observed for reasonable efficiencies of the planet formation process. Simply, we wish to know whether or not the masses of the embedded disks are high enough to produce the observed population of the most massive exoplanet systems, or whether or not the problem of the missing mass extends even to the youngest disks.

In this analysis we focus on the Perseus sample, the only complete sample that is available for Class 0/I protostars in a low-mass star-forming region; as such, it guarantees that there is no bias towards the more massive disks. However, Perseus may not be a representative star-forming region for the environment of our own Solar System (Adams 2010). Also, because it is difficult to estimate the stellar mass of the Class 0/I sources, making a comparison of planets and disks around similar stellar types is challenging. Therefore, we also include a comparison with the Orion disks. The Orion star-forming region contains more luminous protostars than Perseus; thus it might be more representative of the initial mass function. Another limitation is that we analyze mostly unresolved disks, hence the radial dust distribution in the disk is unknown.

4.1 Exoplanet sample selection

The exoplanet systems masses were obtained from the exoplanet.eu database (Schneider et al. 2011). From the catalog (updated 28.04.2020), we obtained 2074 exoplanets with a provided value for the total mass: either a true mass, or a lower limit to the mass (M × sin (i)). We do not filter for detection method, mass measurement method, or stellar type of the host star. The mass estimation method for the majority of planets with information on a mass detection method provided is a radial velocity method, which introduces a strong bias toward more massive exoplanets. Indeed, 1373 of the exoplanets in our analysis have a total (gas+dust) masses above 0.3 Jupiter masses (MJ). There are 1062 systems with more than one planet where at least one is >0.3 MJ, and 173 systems with a single planet of >0.3 MJ.

Gaseous planets are expected to be less frequent than the rocky low-mass planets (e.g., Mayor et al. 2011). It is estimated that only 17–19% of planetary systems contain a planet more massive than 0.3 MJ within 20 au orbit (Cumming et al. 2008). Therefore, we use only systems containing at least one planet with a total mass of 0.3 MJ and normalize it to 18% of the total population. This is done by setting the 18% value of the CDF plot at the estimated solid fraction of the gaseous planet of 0.3 MJ, which is 27.8 M⊕. We assume that 82% of the systems have masses below that value. By doing so, we focus on the sample of gas giants and their solid material content.

In this work, we focus on a reliably estimated solid mass and its cumulative distribution for the most massive exoplanetary systems. By comparing their CDF to the total dust mass distribution from surveys of young disks, we can answer the pivotal question of whether or not the Class 0/I disks contain enough solids to explain the masses of those systems.

Our study focuses on the dust masses of disks. In order to compare the solid content between the disks and exoplanets, we calculatethe solid content in exoplanets using the formula from Thorngren et al. (2016) for estimating the solid content in gaseous planets. This latter study is based on structural and thermal planetary evolution models relating the metallicity of a gas giant with the total mass of the planet. Importantly, the metals in those gas giants are assumedto be located not only in the core but also in the envelope of a planet. We combined the masses of planets orbiting the same star to retrieve the total dust mass of the system, resulting in 1235 systems in the analysis.

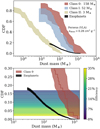thumbnail Fig. 4

Cumulative distribution function of dust disk masses and solid content of exoplanets. Top: cumulative distributionfunction of dust masses for Class 0 (red) and Class I (blue) disks in Perseus and Class II disks (yellow) in Lupus measured with ALMA (Ansdell et al. 2016). In black, the masses of the exoplanet systems are normalized to the fraction of the gaseous planets (Cumming et al. 2008). Perseus disk masses calculated with κ9 mm = 0.28 cm2 g−1 from the VLA fluxes. Medians are indicated in the labels. Bottom: zoom-in to the ranges where exoplanets are present. The color scale shows the efficiency needed for the planet formation for a given bin of the distribution.

4.2 Comparison of young disk dust masses with the solids in exoplanetary systems

In Fig. 4 (top panel) we compare the sample of exoplanetary systems with dust masses of young Class 0 and Class I disks in Perseus with our best estimate of embedded disk dust masses in Perseus, that is, with the complete VLA survey, using the DIANA opacities. Figure 4 (bottom panel) shows efficiency of planet formation for a given bin of the disk and exoplanet distributions. The efficiency is calculated as a ratio of the total mass of the exoplanetary systems at the certain fraction of the cumulative distribution plot divided by the corresponding dust mass of the disk at the same value of the CDF plot. This calculation provides information on how much total dust disk mass will be converted to planets.

In order to reproduce the population of exoplanets with the top 18% most massive disks in Perseus, the efficiency of planet formation would have to be on the order of 15% for Class 0 and 34% for Class I (Fig. 4). The average efficiency is measured by taking the mass at 10% of the cumulative distribution plot (CDF plot is not well sampled for disk masses, and the 10% value is the closest to the mean of the sample with data available). The Class 0/I disk masses in Perseus calculated from the VLA data at 9 mm for the refined value of the dust opacity suggest that on average there is enough mass available at those early phases to form the giant planet systems that we observe.

In Fig. 4 (bottom panel), instead of the average value of the efficiency, we attempt to measure the efficiency per percentage level of the disk masses on the cumulative distribution plot. We note that this analysis has a higher uncertainty than the average value as the distribution of the exoplanets is uncertain. With known masses of a large number of giant planets and expected occurrences of such systems (Cumming et al. 2008) we notice that the most massive exoplanets require efficiencies ~30%, stretching the requirements of some of the planet formation models (see Sect. 4.3). It is also possible that some of the most massive exoplanets or brown dwarfs present in the database do not follow the core accretion formation mechanisms, and excluding them would lower the requirement on efficiency.

If the underlying initial mass function of stars in Perseus is not representative of the stellar initial mass function, it could be that such exosystems were produced from more massive disks than those observed here. Another possibility is that young disks at the Class 0/I phase are still being replenished with material accreting from the envelope (Hsieh et al. 2019b), increasing the amount of effective material available for planet formation. It is also possible that the most massive systems are indeed the most efficient at producing planets.

In Fig. 5 (top panel) the disk masses from the ALMA fluxes in Perseus using the opacity value from Ansdell et al. (2016) are presented. We remind that this is likely the maximum value of the dust opacity at those wavelengths (Panić et al. 2008) and therefore the masses are lower limits. In the bottom panel of Fig. 5, the Orion Class 0/I disk masses measured with ALMA 0.87 mm observations (Tobin et al. 2020) are used.

The comparison of the exoplanet sample with the disk masses for the maximum value of the opacity used with the ALMA data (i.e., lower limit to the disk mass; Fig. 5, top panel) shows that if those opacities were the correct ones, the efficiency of forming planets in the Class 0 phase would be on the order of 33%. The efficiency of the Class I phase would be on the order of 72%. This is in line with our expectations that for our most conservative estimates of disk mass, the efficiencies required for giant planet formation are high, whereas for our best estimate of the dust masses in the young disks, we achieve an average efficiency in agreement with models (see Sect. 4.3). It is also clear that use of dust opacities that result in an order-of-magnitude lower disk masses (Birnstiel et al. 2018) does not provide dust masses that would be compatible with such models. The Orion sample, which contains more luminous protostars and could be more representative of the IMF than Perseus, has comparable disk dust masses in Class I and much lower disk masses in Class 0. The efficiencies required to produce the exoplanet population from the Orion disks dust content, as measured with ALMA, are comparable with those measured for Perseus with VLA observations (Fig. 5 bottom panel): 16 and 45% for Class 0 and Class I, respectively.

Figure 6 presents a different visualization of the distribution of exoplanet systems dust masses compared to the range of disk masses observed in Class 0 and Class I disks in Perseus. The conclusions of our work show that for the complete sample of disks in Perseus and with a large sample of known exoplanets, there is enough solid material in the Class 0 stage to explain the solid content in observed exoplanetary systems. This conclusion is consistent with Najita & Kenyon (2014) and Greaves & Rice (2011) but now with much more robust statistics.

In recent years, several studies, specifically with the use of microlensing observations, have estimated that nearly all stars could host a planet of at least 10 M⊕ (Cassan et al. 2012; Suzuki et al. 2016). Very few cases and irreproducibility of microlensing observations suggest caution should be taken when extrapolating the results to all systems. It should be kept in mind that a large population of wide-orbit planets could pose a challenge to efficiency of planet formation even at the Class 0/I stage (Najita & Kenyon 2014).

Actual timescales for the different phases of low-mass star formation are uncertain. Based on a statistical analysis of a population of protostars, it is estimated that the Class 0 evolutionary phase lasts for ~0.1 Myr after the beginning of the collapse, and the Class I phase ends when the protostar is ~ 0.5 Myr old (Dunham et al. 2014b). More recent estimates of the half-lives of the protostellar phases give Class 0 half-life values of ~0.05 Myr and ~0.08 Myr for Class I (Kristensen & Dunham 2018). Therefore, our results indicate the start of the planet formation begins less than 0.1 Myr after the beginning of the cloud collapse. This is consistent with the ages of the oldest meteorites in our Solar System (Connelly et al. 2012).

thumbnail Fig. 5

Cumulative distribution function of dust masses for Class 0 and Class I disks in Perseus and Orion and Class II disks in Lupus measured with ALMA Top: Perseus disk masses calculated with κ1.3 mm = 2.3 cm2 g−1 from the ALMA fluxes. Bottom: Orion disk masses calculated with the κ0.89 mm = 1.3 cm2 g−1 (Tobin et al. 2020). Medians are indicated in the labels.
thumbnail Fig. 6

Distribution of masses of exoplanetary systems obtained from the exoplanet.eu catalog (Schneider et al. 2011), for the planets around main sequence stars with the measured masses. Shaded areas mark the range of our best estimation of the dust disk masses in Perseus: Class 0 (red) and Class I (blue) calculated from the VLA fluxes with the opacity value of κ9 mm = 0.28 cm2 g−1. Medians of the distributions, 158 and 52 M⊕, for Class 0 and I, respectively, are indicated with the dashed lines. The median mass of the Class II disks in Lupus, 3 M⊕ (Ansdell et al. 2016) is showed in yellow. The masses of the solids in exoplanetary systems are plotted against the stellar mass of the host star. All planets with available information on the mass are included in this plot without introducing the 0.3 MJ threshold.

4.3 The context of planet formation models

It is worthwhile to put our empirical constraints on the solid mass reservoir in the context of planet formation models. Broadly speaking, planets can either form bottom-up through the assembly of smaller building blocks in the so-called core accretion scenario, or top-down in the gravitational instability scenario via direct gravitational collapse of the disk material. In the latter case (see Kratter & Lodato 2016 for a review), planets need not contain rocky cores and we may therefore have overestimated the solid mass locked in planets. In addition, in this view planets form at the very beginning of the disk lifetime when the disk is gravitationally unstable, possibly at even earlier stages than we probe here. If this is the case, our observations do not put constraints on the mass budget required for planet formation since planets would already be formed in the disks we are considering.

Our results are instead relevant for the core accretion scenario. In this case, two large families of models can be defined, differing in the type of building block: planetesimal accretion (e.g., Pollack et al. 1996) and pebble accretion (Ormel & Klahr 2010; Lambrechts & Johansen 2012).

If planets grow by accreting planetesimals, it should be borne in mind that our observations are sensitive only to the dust. Therefore, the efficiency we have defined in this paper should be intended as the product of two efficiencies: the efficiency of converting dust into planetesimals and the efficiency of converting planetesimals into planets. The latter is relatively well constrained from theory and observations. Indeed, the accretion of planetesimals is highly efficient in numerical models (e.g., Alibert et al. 2013) and nearly all planetesimals are accreted into planets over million-year timescales. Observationally, constraints on the mass in planetesimals that are not locked into planets is set by the debris disk population (Sibthorpe et al. 2018). For Sun-like stars, the median planetesimal mass1 is 3 M⊕, which is much smaller than the solid content of giant planets. In this context, the Solar System could be an exception because attempts at explaining its complex history (such as the well-known Nice model, Tsiganis et al. 2005) require instead a much more massive (20–30 M⊕) population of planetesimals past the orbits of Uranus and Neptune that later evolved into the current Kuiper Belt. Even so, this mass is comparable to the mass in the cores of the giant planets, implying an efficiency of planet conversion from planetesimals of ≳ 50%.

Using this value, our observations place empirical constraints on the planetesimal formation efficiency. To satisfy our measurement of a total efficiency of ~ 10%, a planetesimal formation efficiency of ~20% would be needed. There is considerable uncertainty in planetesimal formation models (e.g., Drążkowska & Dullemond 2014, 2018; Lenz et al. 2019), but such an efficiency can in principle be reached by most of the expected conditions in the protoplanetary disks (see Fig. 9 of Lenz et al. 2019 and Table 1 of Drążkowska & Dullemond 2014). Thus, it is possible to explain the observed population of giant planets with the initial dust masses we report in this paper.

If instead planets grow by accreting pebbles, the growth rates can be significantly higher than in planetesimal accretion, but the formation efficiency is lower because most pebbles drift past the forming planets without being accreted (Ormel & Klahr 2010; Ormel 2017). The efficiency of ~ 10% reported here is among the highest that can be reached by pebble accretion (Ormel 2017) and it favours models where the disk is characterized by low turbulence (α < 10−3). Assuming such a value for the turbulence, Bitsch et al. (2019) find that in pebble accretion models that form giant planets, the total planet formation efficiency is 5–15%, which is in line with our findings. This also suggests that, in their models, giant planet formation requires initial dust masses larger than 200−300 M⊕ : we note how this condition is satisfied for ~20% of the Class 0 dust mass distribution. Therefore, the mass constraints derived in this paper from the VLA data are also consistent with pebble accretion, provided that the turbulence in the disk is sufficiently low.

5 Conclusions

This work collects available ALMA and VLA data of a complete sample of Perseus young disks in the Class 0/I phase to provide robust estimates of the disk dust masses at the early phases of star and planet formation. The refined values are used to compare theinferred disk masses with the exoplanetary systems to obtain constraints on when exoplanets start to form.

We find a linear correlation between the fluxes obtained with VLA and ALMA, supporting the fact that thermal dust emission is responsible for the emission at both wavelengths. The value of the dust spectral index measured with ALMA and VLA observations is β =0.5, lower than the commonly used value of β = 1, pointing to significant grain growth occurring already in the Class 0 and I phases. Therefore, compared with our previous study (Tychoniec et al. 2018a) we recalculated the masses with the new dust opacity value from the model that accounts for large grains. The best estimate of the median initial reservoir of dust mass available for planet formation in Perseus is 158 M⊕ and 52 M⊕ for Class 0 and Class I disks, respectively, derived from the VLA data.

Comparison of ALMA observations in Orion and Perseus shows that while disk masses in Class I disks agree well, Class 0 disks are more massive in Perseus than in Orion. This suggests that initial cloud conditions may lead to different masses of disks in the early phases.

We compared dust masses of disks measured with the VLA for Perseus with the observed exoplanet systems. If we assume that planet formation starts with the dust mass reservoir equal to the dust mass of Class I disks in Perseus, an efficiency of ~30% is required to explain the currently observed systems with giant exoplanets. Lower efficiencies of ~15% on average are needed if the Class 0 disks are assumed as the starting point. We find strong evidence that there is enough dust mass in young disks to make planet formation already possible in the first ~0.5 Myr of star formation. Given that low efficiencies are more in line with theoretical core-accretion models, our results are most consistent with significant accumulation of material in larger bodies occurring already at the Class 0 phase.

Acknowledgements

Authors thank the referee for insights that significantly improved the clarity of the paper. Ł.T. and E.v.D. thank Dr. Yao Liu for discussions on dust opacities. ŁT thanks Leon Trapman for discussions that helped in the presentation of results. G.R. acknowledges support from the Netherlands Organisation for Scientific Research (NWO, program number 016.Veni.192.233). J.T. acknowledges support from grant AST-1814762 from the National Science Foundation. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2017.1.01693.S, ADS/JAO.ALMA#2017.1.01078.S, ADS/JAO. ALMA#2015.1.00041.S, and ADS/JAO.ALMA#2013.1.00031.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. Astrochemistry in Leiden is supported by the Netherlands Research School for Astronomy (NOVA). This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 823823 (DUSTBUSTERS). This work was partly supported by the Deutsche Forschungs-Gemeinschaft (DFG, German Research Foundation) – Ref no. FOR 2634/1 TE 1024/1-1. This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2013), http://astropy.org; Matplotlib library (Hunter 2007); NASA’s Astrophysics Data System.

Appendix A Additional figures and tables

thumbnail Fig. A.1

From left to right: observed 1.1 mm ALMA continuum images of the targeted protostars; image of the disk model for the source resulting from the Gaussian fitting (in cases where the envelope component is fitted, only the disk component is shown); residual image after subtracting the disk model from the image; residual image after subtracting both disk and envelope models. From top to bottom: cases that occur in the Gaussian fitting procedure are presented: Per-emb-41, single source, without a noticeable contribution from the envelope; Per-emb-7, contribution of the envelope, as assessed by eye, is significant, an additional broad Gaussian with size of 3′′ was added to the input parameters; Per-emb-54, the central compact component was faint compared to the noise level, it was necessary to fix the size of the Gaussian to the synthesized beam size for the fit to converge. Per-emb-51, the central component has a very small flux compared to the envelope.
thumbnail Fig. A.2

Examples of fitting the spectral index to the fluxes from VLA (8 mm–6.4 cm) and ALMA observations (1 mm). Left: Per-emb-5 has an intra-band Ka-band spectral index in agreement with the spectral index between 1 and 9 mm wavelengths. Center: for Per-emb-19 Ka-band spectral index is too low to be explained only by dust emission, some free–free contamination cannot be excluded. Right: in Per-emb-20, negative spectral index at Ka-band shows that emission is heavily contaminated by other effects, in such cases the Ka-band flux is treated as an upper limit of the dust emission.
thumbnail Fig. A.3

Spectral indices obtained between 1 and 9 mm αVLA/ALMA and Ka-band intraband indices αVLA, only for sources with both values provided. Red points are the sources with consistent spectral indices between VLA/ALMA and VLA Ka-band.
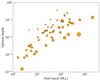thumbnail Fig. A.4

Optical depth as a function of disk dust mass. The size of the circle is proportional to the disk size of the source.
Table A.1

Measured properties of the disks in Perseus molecular cloud.

Table A.2

Masses of the embedded disks in Perseus.

References

  1. Adams, F. C. 2010, ARA&A, 48, 47 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alibert, Y., Carron, F., Fortier, A., et al. 2013, A&A, 558, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. ALMA Partnership, Brogan, C. L., Pérez, L. M., et al. 2015, ApJ, 808, L3 [NASA ADS] [CrossRef] [Google Scholar]
  4. Andersen, B. C., Stephens, I. W., Dunham, M. M., et al. 2019, ApJ, 873, 54 [CrossRef] [Google Scholar]
  5. Andrews, S. M., & Williams, J. P. 2007a, ApJ, 659, 705 [NASA ADS] [CrossRef] [Google Scholar]
  6. Andrews, S. M., & Williams, J. P. 2007b, ApJ, 671, 1800 [CrossRef] [Google Scholar]
  7. Andrews, S. M., Rosenfeld, K. A., Kraus, A. L., & Wilner, D. J. 2013, ApJ, 771, 129 [NASA ADS] [CrossRef] [Google Scholar]
  8. Andrews, S. M., Huang, J., Pérez, L. M., et al. 2018, ApJ, 869, L41 [NASA ADS] [CrossRef] [Google Scholar]
  9. Ansdell, M., Williams, J. P., van der Marel, N., et al. 2016, ApJ, 828, 46 [Google Scholar]
  10. Ansdell, M., Williams, J. P., Manara, C. F., et al. 2017, AJ, 153, 240 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Armitage, P. J. 2011, ARA&A, 49, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Beckwith, S. V. W., Sargent, A. I., Chini, R. S., & Guesten, R. 1990, AJ, 99, 924 [NASA ADS] [CrossRef] [Google Scholar]
  14. Birnstiel, T., Dullemond, C. P., Zhu, Z., et al. 2018, ApJ, 869, L45 [NASA ADS] [CrossRef] [Google Scholar]
  15. Bitsch, B., Izidoro, A., Johansen, A., et al. 2019, A&A, 623, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Cassan, A., Kubas, D., Beaulieu, J. P., et al. 2012, Nature, 481, 167 [NASA ADS] [CrossRef] [Google Scholar]
  17. Choi, M. 2009, ApJ, 705, 1730 [NASA ADS] [CrossRef] [Google Scholar]
  18. Connelly, J. N., Bizzarro, M., Krot, A. N., et al. 2012, Science, 338, 651 [NASA ADS] [CrossRef] [Google Scholar]
  19. Crapsi, A., van Dishoeck, E. F., Hogerheijde, M. R., Pontoppidan, K. M., & Dullemond, C. P. 2008, A&A, 486, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Cumming, A., Butler, R. P., Marcy, G. W., et al. 2008, PASP, 120, 531 [CrossRef] [Google Scholar]
  21. Davidson-Pilon, C. 2017, CamDavidsonPilon/lifelines: 0.11.1 [Google Scholar]
  22. Demyk, K., Meny, C., Leroux, H., et al. 2017a, A&A, 606, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Demyk, K., Meny, C., Lu, X. H., et al. 2017b, A&A, 600, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Draine, B. T. 2006, ApJ, 636, 1114 [Google Scholar]
  25. Drążkowska, J., & Dullemond, C. P. 2014, A&A, 572, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Drążkowska, J., & Dullemond, C. P. 2018, A&A, 614, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Dunham, M. M., Stutz, A. M., Allen, L. E., et al. 2014a, in Protostars and Planets VI (Tucson, AZ: University of Arizona Press), 195 [Google Scholar]
  28. Dunham, M. M., Arce, H. G., Mardones, D., et al. 2014b, ApJ, 783, 29 [NASA ADS] [CrossRef] [Google Scholar]
  29. Dunham, M. M., Vorobyov, E. I., & Arce, H. G. 2014c, MNRAS, 444, 887 [NASA ADS] [CrossRef] [Google Scholar]
  30. Enoch, M. L., Evans, II, N. J., Sargent, A. I., & Glenn, J. 2009, ApJ, 692, 973 [NASA ADS] [CrossRef] [Google Scholar]
  31. Evans, II, N. J., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
  32. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Greaves, J. S., & Rice, W. K. M. 2010, MNRAS, 407, 1981 [NASA ADS] [CrossRef] [Google Scholar]
  34. Greaves, J. S., & Rice, W. K. M. 2011, MNRAS, 412, L88 [NASA ADS] [CrossRef] [Google Scholar]
  35. Harsono, D., Bruderer, S., & van Dishoeck, E. F. 2015, A&A, 582, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Harsono, D., Bjerkeli, P., van der Wiel, M. H. D., et al. 2018, Nat. Astron., 2, 646 [NASA ADS] [CrossRef] [Google Scholar]
  37. Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
  38. Hsieh, T.-H., Hirano, N., Belloche, A., et al. 2019a, ApJ, 871, 100 [NASA ADS] [CrossRef] [Google Scholar]
  39. Hsieh, T.-H., Murillo, N. M., Belloche, A., et al. 2019b, ApJ, 884, 149 [NASA ADS] [CrossRef] [Google Scholar]
  40. Hunter, J. D. 2007, CSE, 9, 90 [Google Scholar]
  41. Jørgensen, J. K., Johnstone, D., Kirk, H., & Myers, P. C. 2007, ApJ, 656, 293 [NASA ADS] [CrossRef] [Google Scholar]
  42. Jørgensen, J. K., van Dishoeck, E. F., Visser, R., et al. 2009, A&A, 507, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Kataoka, A., Okuzumi, S., Tanaka, H., & Nomura, H. 2014, A&A, 568, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Kratter, K., & Lodato, G. 2016, ARA&A, 54, 271 [NASA ADS] [CrossRef] [Google Scholar]
  45. Kristensen, L. E., & Dunham, M. M. 2018, A&A, 618, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Kruijer, T. S., Touboul, M., Fischer-Gödde, M., et al. 2014, Science, 344, 1150 [NASA ADS] [CrossRef] [Google Scholar]
  47. Kwon, W., Looney, L. W., Mundy, L. G., Chiang, H.-F., & Kemball, A. J. 2009, ApJ, 696, 841 [NASA ADS] [CrossRef] [Google Scholar]
  48. Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [Google Scholar]
  49. Lenz, C. T., Klahr, H., & Birnstiel, T. 2019, ApJ, 874, 36 [CrossRef] [Google Scholar]
  50. Lommen, D., Wright, C. M., Maddison, S. T., et al. 2007, A&A, 462, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Long, F., Herczeg, G. J., Harsono, D., et al. 2019, ApJ, 882, 49 [NASA ADS] [CrossRef] [Google Scholar]
  52. Manara, C. F., Morbidelli, A., & Guillot, T. 2018, A&A, 618, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Mayor, M., Marmier, M., Lovis, C., et al. 2011, ArXiv e-prints [arXiv:1109.2497] [Google Scholar]
  54. McClure, M. K., Furlan, E., Manoj, P., et al. 2010, ApJS, 188, 75 [NASA ADS] [CrossRef] [Google Scholar]
  55. McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell (USA: ASP Books), 376, 127 [Google Scholar]
  56. Miotello, A., Testi, L., Lodato, G., et al. 2014, A&A, 567, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Morbidelli, A., & Raymond, S. N. 2016, J. Geophys. Res. Planets, 121, 1962 [NASA ADS] [CrossRef] [Google Scholar]
  58. Najita, J. R., & Kenyon, S. J. 2014, MNRAS, 445, 3315 [NASA ADS] [CrossRef] [Google Scholar]
  59. Natta, A., & Testi, L. 2004, ASP Conf. Ser., 323, 279 [Google Scholar]
  60. Öberg, K. I., Murray-Clay, R., & Bergin, E. A. 2011, ApJ, 743, L16 [NASA ADS] [CrossRef] [Google Scholar]
  61. Ormel, C. W. 2017, Astrophys. Space Sci. Lib., 445, 197 [NASA ADS] [CrossRef] [Google Scholar]
  62. Ormel, C. W., & Klahr, H. H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Ortiz-León, G. N., Loinard, L., Dzib, S. A., et al. 2018, ApJ, 865, 73 [NASA ADS] [CrossRef] [Google Scholar]
  64. Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
  65. Panić, O., Hogerheijde, M. R., Wilner, D., & Qi, C. 2008, A&A, 491, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Pinilla, P., Birnstiel, T., Ricci, L., et al. 2012, A&A, 538, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
  68. Poteet, C. A. 2012, PhD thesis, The University of Toledo, USA [Google Scholar]
  69. Ricci, L., Testi, L., Natta, A., & Brooks, K. J. 2010, A&A, 521, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Sadavoy, S. I., Di Francesco, J., André, P., et al. 2014, ApJ, 787, L18 [NASA ADS] [CrossRef] [Google Scholar]
  71. Schneider, J., Dedieu, C., Le Sidaner, P., Savalle, R., & Zolotukhin, I. 2011, A&A, 532, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Segura-Cox, D. M., Harris, R. J., Tobin, J. J., et al. 2016, ApJ, 817, L14 [NASA ADS] [CrossRef] [Google Scholar]
  73. Sheehan, P. D., & Eisner, J. A. 2018, ApJ, 857, 18 [NASA ADS] [CrossRef] [Google Scholar]
  74. Sibthorpe, B., Kennedy, G. M., Wyatt, M. C., et al. 2018, MNRAS, 475, 3046 [NASA ADS] [CrossRef] [Google Scholar]
  75. Suzuki, D., Bennett, D. P., Sumi, T., et al. 2016, ApJ, 833, 145 [NASA ADS] [CrossRef] [Google Scholar]
  76. Tazzari, M., Testi, L., Ercolano, B., et al. 2016, A&A, 588, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Terebey, S., Shu, F. H., & Cassen, P. 1984, ApJ, 286, 529 [NASA ADS] [CrossRef] [Google Scholar]
  78. Testi, L., Birnstiel, T., Ricci, L., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson, AZ: University of Arizona Press), 339 [Google Scholar]
  79. Thorngren, D. P., Fortney, J. J., Murray-Clay, R. A., & Lopez, E. D. 2016, ApJ, 831, 64 [NASA ADS] [CrossRef] [Google Scholar]
  80. Tobin, J. J., Dunham, M. M., Looney, L. W., et al. 2015, ApJ, 798, 61 [NASA ADS] [CrossRef] [Google Scholar]
  81. Tobin, J. J., Looney, L. W., Li, Z.-Y., et al. 2016, ApJ, 818, 73 [NASA ADS] [CrossRef] [Google Scholar]
  82. Tobin, J. J., Looney, L. W., Li, Z.-Y., et al. 2018, ApJ, 867, 43 [NASA ADS] [CrossRef] [Google Scholar]
  83. Tobin, J. J., Sheehan, P., Megeath, S. T., et al. 2020, ApJ, 890, 130 [CrossRef] [Google Scholar]
  84. Tsiganis, K., Gomes, R., Morbidelli, A., & Levison, H. F. 2005, Nature, 435, 459 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  85. Tychoniec, Ł., Tobin, J. J., Karska, A., et al. 2018a, ApJS, 238, 19 [NASA ADS] [CrossRef] [Google Scholar]
  86. Tychoniec, Ł., Tobin, J. J., Karska, A., et al. 2018b, ApJ, 852, 18 [NASA ADS] [CrossRef] [Google Scholar]
  87. van der Marel,N., van Dishoeck, E. F., Bruderer, S., et al. 2013, Science, 340, 1199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  88. van Kempen, T. A., van Dishoeck, E. F., Salter, D. M., et al. 2009, A&A, 498, 167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. van Terwisga, S. E., van Dishoeck, E. F., Ansdell, M., et al. 2018, A&A, 616, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. van’t Hoff, M. L. R., van Dishoeck, E. F., Jørgensen, J. K., & Calcutt, H. 2020, A&A, 633, A7 [CrossRef] [EDP Sciences] [Google Scholar]
  91. Visser, R., van Dishoeck, E. F., & Black, J. H. 2009, A&A, 503, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Whitney, B. A., Wood, K., Bjorkman, J. E., & Cohen, M. 2003, ApJ, 598, 1079 [NASA ADS] [CrossRef] [Google Scholar]
  93. Williams, J. P. 2012, Meteorit. Planet. Sci., 47, 1915 [NASA ADS] [CrossRef] [Google Scholar]
  94. Williams, J. P., Cieza, L., Hales, A., et al. 2019, ApJ, 875, L9 [Google Scholar]
  95. Woitke, P., Min, M., Pinte, C., et al. 2016, A&A, 586, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Wyatt, M. C., Smith, R., Su, K. Y. L., et al. 2007, ApJ, 663, 365 [NASA ADS] [CrossRef] [Google Scholar]
  97. Ysard, N., Koehler, M., Jimenez-Serra, I., Jones, A. P., & Verstraete, L. 2019, A&A, 631, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
1

As discussed in Wyatt et al. (2007), this value is degenerate with the maximum planetesimal size; here we assume a diameter of 1000 km, and we note that the mass would be even lower if using smaller planetesimals.

All Tables

Table A.1

Measured properties of the disks in Perseus molecular cloud.

In the text
Table A.2

Masses of the embedded disks in Perseus.

In the text

All Figures

thumbnail Fig. 1

ALMA (1.1 and 1.3 mm) integrated fluxes plotted against VLA integrated fluxes at 9.1 mm. A total of 77 sources are plotted but only the 62 sources that are not upper limits are included in fitting the linear function. The best fit to the data is shown with the green line and has a slope of 1.15 ± 0.1. The Class 0 sources are shown in red and Class I sources in blue. Crosses mark sources that are unresolved binaries.
In the text
thumbnail Fig. 2

Cumulative distribution plots of the dust disk masses. Top: masses of the Perseus Class 0 and I disks measured with ALMA at 1 mm compared with the Lupus Class II disks measured with ALMA (Ansdell et al. 2016). The opacity value of κ1.3 mm = 2.3  cm2 g−1 is used to calculate the masses. The ALMA sample consist of 77 sources (38 Class 0 and 39 Class I) and the Lupus sample consist of 69 sources. Bottom: masses of the Perseus Class 0 and I disks measured with VLA at 9 mm (red and blue, respectively), compared with the Lupus Class II disks measured with ALMA (Ansdell et al. 2016). The opacity value of κ9 mm =0.28  cm2 g−1 is used to calculate the VLA masses. The VLA sample consist of 100 sources (49 Class 0 and 51 Class I). Medians are indicated in the labels.
In the text
thumbnail Fig. 3

Cumulative distribution plots for Perseus disk masses calculated from ALMA flux densities and Orion disk masses from Tobin et al. (2020), both calculated with the same opacity assumptions of κ1.3 mm = 0.9 cm2 g−1. The Perseussample consist of 77 sources (38 Class 0 and 39 Class I), the Orion sample consist of 415 sources (133 Class 0 and 282). Medians are indicated in the labels.
In the text
thumbnail Fig. 4

Cumulative distribution function of dust disk masses and solid content of exoplanets. Top: cumulative distributionfunction of dust masses for Class 0 (red) and Class I (blue) disks in Perseus and Class II disks (yellow) in Lupus measured with ALMA (Ansdell et al. 2016). In black, the masses of the exoplanet systems are normalized to the fraction of the gaseous planets (Cumming et al. 2008). Perseus disk masses calculated with κ9 mm = 0.28 cm2 g−1 from the VLA fluxes. Medians are indicated in the labels. Bottom: zoom-in to the ranges where exoplanets are present. The color scale shows the efficiency needed for the planet formation for a given bin of the distribution.
In the text
thumbnail Fig. 5

Cumulative distribution function of dust masses for Class 0 and Class I disks in Perseus and Orion and Class II disks in Lupus measured with ALMA Top: Perseus disk masses calculated with κ1.3 mm = 2.3 cm2 g−1 from the ALMA fluxes. Bottom: Orion disk masses calculated with the κ0.89 mm = 1.3 cm2 g−1 (Tobin et al. 2020). Medians are indicated in the labels.
In the text
thumbnail Fig. 6

Distribution of masses of exoplanetary systems obtained from the exoplanet.eu catalog (Schneider et al. 2011), for the planets around main sequence stars with the measured masses. Shaded areas mark the range of our best estimation of the dust disk masses in Perseus: Class 0 (red) and Class I (blue) calculated from the VLA fluxes with the opacity value of κ9 mm = 0.28 cm2 g−1. Medians of the distributions, 158 and 52 M⊕, for Class 0 and I, respectively, are indicated with the dashed lines. The median mass of the Class II disks in Lupus, 3 M⊕ (Ansdell et al. 2016) is showed in yellow. The masses of the solids in exoplanetary systems are plotted against the stellar mass of the host star. All planets with available information on the mass are included in this plot without introducing the 0.3 MJ threshold.
In the text
thumbnail Fig. A.1

From left to right: observed 1.1 mm ALMA continuum images of the targeted protostars; image of the disk model for the source resulting from the Gaussian fitting (in cases where the envelope component is fitted, only the disk component is shown); residual image after subtracting the disk model from the image; residual image after subtracting both disk and envelope models. From top to bottom: cases that occur in the Gaussian fitting procedure are presented: Per-emb-41, single source, without a noticeable contribution from the envelope; Per-emb-7, contribution of the envelope, as assessed by eye, is significant, an additional broad Gaussian with size of 3′′ was added to the input parameters; Per-emb-54, the central compact component was faint compared to the noise level, it was necessary to fix the size of the Gaussian to the synthesized beam size for the fit to converge. Per-emb-51, the central component has a very small flux compared to the envelope.
In the text
thumbnail Fig. A.2

Examples of fitting the spectral index to the fluxes from VLA (8 mm–6.4 cm) and ALMA observations (1 mm). Left: Per-emb-5 has an intra-band Ka-band spectral index in agreement with the spectral index between 1 and 9 mm wavelengths. Center: for Per-emb-19 Ka-band spectral index is too low to be explained only by dust emission, some free–free contamination cannot be excluded. Right: in Per-emb-20, negative spectral index at Ka-band shows that emission is heavily contaminated by other effects, in such cases the Ka-band flux is treated as an upper limit of the dust emission.
In the text
thumbnail Fig. A.3

Spectral indices obtained between 1 and 9 mm αVLA/ALMA and Ka-band intraband indices αVLA, only for sources with both values provided. Red points are the sources with consistent spectral indices between VLA/ALMA and VLA Ka-band.
In the text
thumbnail Fig. A.4

Optical depth as a function of disk dust mass. The size of the circle is proportional to the disk size of the source.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.