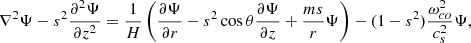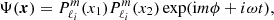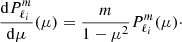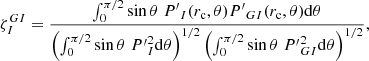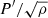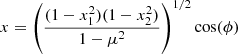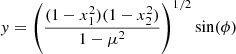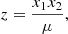| Issue |
A&A
Volume 640, August 2020
|
|
|---|---|---|
| Article Number | A49 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201936653 | |
| Published online | 10 August 2020 | |
First evidence of inertial modes in γ Doradus stars: The core rotation revealed
1
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université de Paris, 5 place Jules Janssen, 92195 Meudon, France
e-mail: Rhita-Maria.Ouazzani@obspm.fr
2
IRAP, Université de Toulouse, CNRS, UPS, CNES, 14 avenue Édouard Belin, 31400 Toulouse, France
3
STAR Institute, Université de Liège, Allée du 6 Août 19, 4000 Liège, Belgium
4
Department of Astronomy, School of Science, The University of Tokyo, 7–3–1 Hongo, Bunkyo-ku, Tokyo 113–0033, Japan
Received:
7
September
2019
Accepted:
8
June
2020
The advent of space photometry with CoRoT and Kepler has allowed for the gathering of exquisite and extensive time series for a wealth of main-sequence stars, including γ Doradus stars, whose detailed seismology was not achievable from the ground. γ Doradus stars present an incredibly rich pulsation spectra, with gravito-inertial modes, in some cases supplemented with δ Scuti-like pressure modes – for the hybrid stars – and, in many cases, with Rossby modes. The present paper aims to show that in addition to these modes which have been established in the radiative envelope, pure inertial modes that are trapped in the convective core can be detected in Kepler observations of γ Doradus stars thanks to their resonance with the gravito-inertial modes. We started by using a simplified model of perturbations in a full sphere of uniform density. Under these conditions, the spectrum of pure inertial modes is known from analytical solutions of the so-called Poincaré equation. We then computed coupling factors, which helped select the pure inertial modes which interact best with the surrounding dipolar gravito-inertial modes. Using complete calculations of gravito-inertial modes in realistic models of γ Doradus stars, we are able to show that the pure inertial and gravito-inertial resonances appear as “dips” in the gravito-inertial mode period spacing series at spin parameters that are close to those predicted by the simple model. We find the first evidence of such dips in the Kepler γ Doradus star KIC 5608334. Finally, using complete calculations in isolated convective cores, we find that the spin parameters of the pure inertial and gravito-inertial resonances are also sensitive to the density stratification of the convective core. In conclusion, we have discovered that certain dips in gravito-inertial mode period spacings that have been observed in some Kepler stars are, in fact, signatures of resonances with pure-inertial modes that are trapped in the convective core. This holds the promise that it would be possible to finally access the central conditions, namely, the rotation and density stratification, of intermediate-mass stars in the main sequence.
Key words: asteroseismology / stars: interiors / stars: rotation / stars: oscillations / convection
© R.-M. Ouazzani et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Angular momentum transport in stellar radiative zones and its evolution over time is a major open issue in stellar physics. Observations of stars in evolved stages that have been provided by the Kepler mission (Beck et al. 2012; Deheuvels et al. 2012; Mosser et al. 2012) have proven that our then-current models of transport were wrong (Eggenberger et al. 2012; Marques et al. 2013). The various attempts to invoke additional mechanisms (Cantiello et al. 2014; Fuller et al. 2014, 2019; Belkacem et al. 2015; Pinçon et al. 2017; Mathis et al. 2018) have not solved this issue or they are still matter of debate.
With the purpose of bringing a main-sequence counterpart to the seismic constraint of rotation in evolved stars, γ Doradus stars g-modes monitored by Kepler have revealed near-core rotation rates in stars which are progenitors of red giants (Van Reeth et al. 2016; Christophe et al. 2018; Li et al. 2019). This has paved the way for the testing of angular momentum transport models against near-core rotation measurements in main-sequence intermediate-mass stars. As a result, Ouazzani et al. (2019) have found that the rotational transport, as formalised by Zahn (1992), does not allow them to reproduce observations of γ Doradus stars. Hence, as for the more evolved stages, another – as yet to be found – mechanism seems to transport angular momentum from the innermost part of the radiative zone outwards. Whether it leads to a rigidification of the rotation profile still remains unproven, but measurements in a handful of stars seem to suggest this is so (Kurtz et al. 2014; Saio et al. 2015; Murphy et al. 2016; Van Reeth et al. 2018; Li et al. 2019).
The constraint of the full internal rotation profile in intermediate-mass stars would be extremely valuable as it would answer the question and allow for further characterisation of the transport mechanism of angular momentum at stake. Once again, γ Doradus stars could help bring on such a constraint. In addition to the g-modes period spacing series, whose interpretation allowed for near-core rotation measurements, these stars harbor pulsations in Rossby modes (Saio et al. 2018; Li et al. 2019) which hopefully bring information on rotational activity in a different cavity than g-modes (Van Reeth et al. 2018, Christophe et al., in prep.). The present paper demonstrates the existence of a signature of pure inertial modes trapped in the convective core within g-modes period spacing series, holding the possibility for a probe of the rotation rate of the convective core.
Inertial waves are caused by the Coriolis acceleration, their frequency in the rotating frame ranging from 0 to 2Ω. They are typically referred to as pure inertial waves when other restoring forces, such as buoyancy or pressure, are absent or negligible. This is relevant for slow motions in stellar convective zones, where turbulent heat transport maintains an isentropic mean stratification or, equivalently, a vanishing Brunt-Väisälä frequency, N. We thus expect convective zones and, in particular, the convective cores of massive and intermediate-mass stars to harbor pure inertial waves. Pure inertial modes in a full sphere have been studied for a fluid of constant density (Bryan 1889; Greenspan 1968; Rieutord 1991) and for isentropic polytropes (Papaloizou & Pringle 1981; Lee et al. 1992; Dintrans & Ouyed 2001; Lockitch & Friedman 1999; Wu 2005). Pure inertial modes trapped in the solar convective zone have been investigated by Guenther & Gilman (1985) and Dziembowski et al. (1987). The coupling of pure inertial modes in stellar convective zones with gravito-inertial modes in adjacent radiative zones has been studied in the case of tidally excited modes in solar-type stars (Ogilvie & Lin 2004) and in massive stars (Papaloizou & Savonije 1997). Lee & Saio (1987) computed oscillatory convective modes present in a rotating convective core with a slightly superadiabatic stratification coupled with gravito-inertial modes or Rossby modes in the radiative enveloppe.
The present article holds the first unambiguous theoretical demonstration of the existence of resonances between gravito-inertial modes in the radiative zone, and pure inertial modes in the convective core in γ Doradus stars. Through a comparison with a γ Doradus star observed by the Kepler mission, we show the first observational signature of pure inertial modes. We start by introducing inertial modes in the case of a sphere of uniform density (Sect. 2.1) and then propose a simple model to describe their coupling with gravito-inertial modes (Sect. 2.2). In Sect. 3, we explore the occurrence of such gravito-inertial – pure inertial resonances in complete calculations. Finally, we investigate the dependency of these resonances on stellar characteristics in Sect. 4 and investigate the diagnosis potential of these resonances with regard to the measurement of rotation in the convective core.
2. Theoretical spectrum of pure inertial modes
While inertial modes in a spherical shell with solid boundaries present complex characteristics, such as singular modes in the inviscid limit (Rieutord & Valdettaro 2018), inertial modes in the full sphere are expected to be smooth and, in the case of a uniform density sphere, they are amenable to analytical solutions (e.g. Greenspan 1968).
Following Wu (2005), it is straightforward to show that, in an isentropic medium (where the Brunt-Vaissala frequency N = 0), small-amplitude adiabatic perturbations show a time and azimuthal (angle ϕ) dependence ∝exp(imϕ + iωt), and are governed by the wave equation :
where s = (2Ω)/ωco is the spin parameter, that is, the ratio of twice the rotation rate Ω (which is taken as uniform here) to the frequency in the co-rotating frame ωco. Ψ is related to the Eulerian pressure perturbation P′ and the equilibrium density ρ0 by 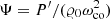 , H = −𝜚0/(d𝜚0/dr) is the density scale height, and
, H = −𝜚0/(d𝜚0/dr) is the density scale height, and 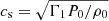 is the sound speed, defined here using the adiabatic exponent Γ1 and the equilibrium pressure P0. Perturbations of the gravitational potential have been neglected through the Cowling approximation. Away from the star surface, and as long as the inertial frequencies are much lower than pressure wave frequencies, the last term can also be neglected. In the next two subsections, we present the properties of inertial modes relevant for our purpose and then construct a simple model for the occurrence of gravito-inertial – inertial mode resonance.
is the sound speed, defined here using the adiabatic exponent Γ1 and the equilibrium pressure P0. Perturbations of the gravitational potential have been neglected through the Cowling approximation. Away from the star surface, and as long as the inertial frequencies are much lower than pressure wave frequencies, the last term can also be neglected. In the next two subsections, we present the properties of inertial modes relevant for our purpose and then construct a simple model for the occurrence of gravito-inertial – inertial mode resonance.
2.1. Inertial modes in a full sphere of uniform density
In the absence of density stratification, H = +∞, the wave equation reduces to the so-called Poincaré equation 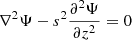 . This equation is separable using the ellipsoidal coordinates (x1, x2, ϕ) defined in Appendix A, and the solution, previously obtained by Bryan (1889), is written as
. This equation is separable using the ellipsoidal coordinates (x1, x2, ϕ) defined in Appendix A, and the solution, previously obtained by Bryan (1889), is written as
where 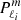 is the associated Legendre polynomial of degree ℓi. For a given pair (ℓi, m), the solution Ψ(x) also holds a frequency dependency through the endpoints of the meridional coordinate intervals, x1 ∈ [μ, 1] and x2 ∈ [ − μ, μ], where μ = ωco/(2Ω) = 1/s. In addition to regularity conditions at the center and along the rotation axis, the boundary condition ξr = 0, applied at the sphere surface, determines the inertial mode frequencies as the non-trivial positive roots of :
is the associated Legendre polynomial of degree ℓi. For a given pair (ℓi, m), the solution Ψ(x) also holds a frequency dependency through the endpoints of the meridional coordinate intervals, x1 ∈ [μ, 1] and x2 ∈ [ − μ, μ], where μ = ωco/(2Ω) = 1/s. In addition to regularity conditions at the center and along the rotation axis, the boundary condition ξr = 0, applied at the sphere surface, determines the inertial mode frequencies as the non-trivial positive roots of :
The detail of the calculations together with a useful discussion on the inertial mode properties can be found in Wu (2005).
Here we focus on the inertial modes which may interact resonantly with dipolar gravito-inertial modes, that is, for symmetry reasons, anti-symmetric zonal (m = 0) modes, symmetric prograde (m = −1) and retrograde (m = 1) modes. For each symmetry class, the set of inertial eigenfrequencies is dense in the [0, 2Ω] interval. However, we shall mostly select low degree ℓi modes. For each pair (ℓi, m), there are [ℓi − |m|−ϵ(ℓi − |m|)]/2 eigenfrequencies, where ϵ(ℓi − |m|) = 0 for even modes and ϵ(ℓi − |m|) = 1 for odd modes. For example, for anti-symmetric zonal (m = 0) modes, one mode is associated with ℓi = 3, two modes with ℓi = 5, three modes with ℓi = 7, and so forth. All modes of a given pair (ℓi, m) have the same number of nodes along a meridian line at the outer sphere, namely ℓi − |m| nodes.
In Table 1, the spin parameters s of the first low ℓi − |m| eigenmodes that can potentially couple with dipolar gravity modes are listed in ascending ℓi − |m|. The spatial distributions of the three (ℓi = 3, 5, 7; m = 0) modes of the first column in the table are displayed on Fig. 1. As we see below, these modes are the most likely to couple with a dipolar zonal mode above the convective core. The remaining three axisymmetric modes of Table 1, one (ℓi = 5; m = 0) mode and two (ℓi = 7; m = 0) modes are shown on Fig. B.1. As apparent from these figures, and as mentioned before, the different modes associated with a pair (ℓi, m) have the same number of nodes along the meridian line at the outer surface but they differ by the number of nodes -on that outer surface meridian line- that are located between the equator and the critical colatitude θc = arccos(μ) = arccos(1/s). For example, the three (ℓi, m) = (7, 0) modes have either no node, one node, or two nodes between the equator and the critical colatitude θc.
 |
Fig. 1. Inertial modes in a uniform density sphere. Each of these modes have a strong spatial matching with the dipolar gravito-inertial mode of the same spin parameter. The dotted line specifies the critical latitude θc = arccos(ω/(2Ω)). |
Inertial-mode spin parameters and coupling coefficients 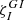 (in parenthesis) with the dipolar Hough function of the same symmetry class and spin parameter.
(in parenthesis) with the dipolar Hough function of the same symmetry class and spin parameter.
2.2. Coupling with gravito-inertial modes
Small-wavelength WKB analysis tells that gravity waves can propagate in regions where ω < N as long as their frequency is sub-inertial, that is, ω < 2Ω (see e.g. Unno et al. 1989). Low-frequency gravity waves can thus propagate from a radiative zone down to a convective core (Dintrans & Rieutord 2000; Prat et al. 2016). If conditions for positive interferences are met, such waves can produce mixed gravito-inertial – pure inertial modes.
Because the spectrum of pure inertial modes is dense in [0, 2Ω], there is always the possibility of a frequency match between a sub-inertial gravity mode in the radiative zone and a pure inertial mode in the core. However, a resonant coupling is expected if there is matching between both their frequencies and their spatial distributions at the convective core boundary. In the well-known case of mixed gravity-pressure modes in slowly rotating evolved stars, the spatial matching is ensured by considering modes with the same spherical harmonic degree. There is no such simplification here as the latitudinal distribution of both pure inertial modes and gravito-inertial modes generally depends on the frequency.
Although a detailed mathematical model of the resonance conditions is beyond the scope of the present paper, we propose here a simplified approach to estimate the occurrences of strong resonant coupling between a pure inertial mode and a gravito-inertial mode, respectively oscillating in the convective core and above it in the radiative zone. We first define a coupling coefficient 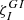 as:
as:
where rc is the radius of the convective core boundary and, 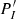 and
and 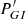 are the latitudinal pressure profile of the inertial and gravito-inertial modes respectively.
are the latitudinal pressure profile of the inertial and gravito-inertial modes respectively.
To compute this coefficient, we begin from the following assumptions: we assume that the latitudinal variations of the gravito-inertial mode is given by the Hough function, that is, the expected form in the framework of the traditional approximation. For the present work, Hough functions are numerically computed by solving Laplace’s tidal equation projected on the basis of spherical harmonics truncated to the degree ℓmax = 500. The linear system to solve is then described in Unno et al. (1989). The latitudinal form of the pure inertial modes results from two assumptions. The first is to neglect the effect of the density stratification. The second is to use the condition ξr = 0 at the convective core radius as a boundary condition to quantise the inertial modes. The inertial modes then take the analytical form given in the previous sub-section. In particular, the pressure perturbation profile at the core radius 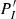 is simply
is simply 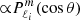 .
.
Using Eq. (4), we compute the coupling coefficients 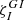 between the uniform-density low-order inertial modes listed in Table 1 and the dipolar Hough functions corresponding to the same spin parameters. We find that the coupling coefficients are either substantial or very small. This property can be readily understood from the geometry of the modes involved. Considering the axisymmetric case, we know that the axisymmetric dipolar Hough functions are single-signed between the equator and the critical colatitude θc corresponding to the spin parameter, and then rapidly go to zero at higher latitudes (Townsend 2003). Thus multiplying them by an inertial mode which also have no node between the equator and θc and integrating over latitude will give a significant normalised coefficient. By contrast, the coupling with inertial modes that have nodes between the equator and θc necessarily will be much smaller. This geometrical interpretation explains why the inertial modes displayed in Fig. 1 have significant values of
between the uniform-density low-order inertial modes listed in Table 1 and the dipolar Hough functions corresponding to the same spin parameters. We find that the coupling coefficients are either substantial or very small. This property can be readily understood from the geometry of the modes involved. Considering the axisymmetric case, we know that the axisymmetric dipolar Hough functions are single-signed between the equator and the critical colatitude θc corresponding to the spin parameter, and then rapidly go to zero at higher latitudes (Townsend 2003). Thus multiplying them by an inertial mode which also have no node between the equator and θc and integrating over latitude will give a significant normalised coefficient. By contrast, the coupling with inertial modes that have nodes between the equator and θc necessarily will be much smaller. This geometrical interpretation explains why the inertial modes displayed in Fig. 1 have significant values of 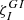 with the axisymmetric dipolar gravito-inertial mode of equivalent spin parameter and why those displayed in Fig. B.1 have very low
with the axisymmetric dipolar gravito-inertial mode of equivalent spin parameter and why those displayed in Fig. B.1 have very low 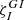 . Similar geometrical interpretations hold for the coupling coefficient of the prograde and retrograde modes.
. Similar geometrical interpretations hold for the coupling coefficient of the prograde and retrograde modes.
Thus, considering dipolar gravito-inertial modes scanning a given frequency range, this simplified model predicts strong coupling with a pure inertial mode at the spin parameters listed in Table 1. The assumptions of the present model are discussed later in this paper.
3. Occurrence of gravito-inertial resonances in complete calculations
In this section, we compute oscillation spectra of realistic models of main-sequence intermediate-mass stars. We wish to further investigate the behaviour of the mixed gravito-inertial – pure inertial modes, while avoiding the assumptions applied in the previous section.
3.1. Stellar and pulsation models
Stellar models were computed with the stellar evolution code CLES (Scuflaire et al. 2008a) for masses between 1.4 and 1.86 M⊙, and with initial helium mass fraction Y = 0.27. We adopted the AGSS09 metal mixture (Asplund et al. 2009) and corresponding opacity tables obtained with OPAL opacities (Iglesias & Rogers 1996), completed at low temperature (log T < 4.1) with Ferguson et al. (2005) opacity tables. We used the OPAL2001 equation of state (Rogers & Nayfonov 2002) and the nuclear reaction rates from the NACRE compilation (Angulo et al. 1999), except for the 14N(p, γ)15O nuclear reaction, for which we adopted the cross-section from Formicola et al. (2004). Surface boundary conditions at T = Teff were provided by ATLAS 9 model atmospheres (Castelli et al. 2003). Convection was treated using the mixing-length theory (MLT) formalism (Böhm-Vitense 1958) with the parameter αMLT = 1.70, close to a solar calibration.
We considered models with turbulent diffusion. Since the CLES code does not include effects of rotation on transport of angular momentum or chemical species, instead we introduced mixing by turbulent diffusion, following the approach of Miglio et al. (2008). This reproduces an effect of rotationally-induced mixing that is quite similar to overshooting, but in addition, it tends to smooth chemical composition gradients inside the star. The coefficient of turbulent diffusion was set to Dt = 700 cm2 s−1 and kept constant to this value during evolution and in every layer of the models. This value was selected from a previous calibration to Geneva models with similar masses (Miglio et al. 2008). The oscillation modes were computed as the adiabatic response of the structure to small perturbations, that is, of the density, pressure, gravitational potential, and velocity field. The ACOR code was developed for this purpose, as presented in Ouazzani et al. (2012, 2015). This oscillation code solves the hydrodynamics equations perturbed by Eulerian fluctuations, performing direct integration of the 2D problem. The numerical method is based on a spectral multi-domain method which expands the angular dependence of eigenfunctions onto spherical harmonics series, and whose radial treatment is particularly well adapted to the behaviour of equilibrium quantities in evolved models (at the interface of convective and radiative regions, and at the stellar surface). The radial differentiation scheme is made by means of a sophisticated finite difference method, which is accurate up to the fifth order in terms of the radial resolution (developed by Scuflaire et al. 2008b, for the LOSC adiabatic code).
According to Ballot et al. (2012) and Ouazzani et al. (2017), the 1D non-perturbative approach, which presents the advantage of requiring less numerical resources, gives satisfactory results compared to the full 2D approach. Throughout this study we therefore work with one-dimensional spherical stellar models. The pulsation modes have been computed using up to 5 spherical harmonics, that is, for a given m, ℓ = 1 to 9 with odd value for dipolar modes. We have made sure, by the mean of convergence tests, that the frequencies do not vary significantly when adding a sixth spherical harmonic in the series. The resulting modes have multiple ℓ characters, they are then assigned an effective angular degree, taking the dominant contribution to the kinetic energy in the series.
3.2. Gravito-inertial resonances in theoretical spectra
Using the set up described in Sect. 3.1, we computed synthetic oscillation spectra for dipolar gravito-inertial modes, assuming a set of uniform rotation values ranging from 7 μHz to 25 μHz. In Fig. 2, we illustrate the period spacing of such synthetic spectra for zonal modes with radial orders ranging from −15 to −49. The pure inertial/gravito-inertial resonances appear clearly in the period spacing series as dips, when a few modes show lower period spacing than their neighbouring modes, for the spectra corresponding to rotation frequencies of 13, 15, 17, 19, 21, and 23 μHz. The vertical lines in Fig. 2 stand at the period of the pure inertial modes computed with the method described in Sect. 2.1. Given the approximations used for their calculations, the agreement with complete calculations is rather striking, all the more so for the lowest rotation rates. The characteristics of the resonances found in the range of excited modes in the complete synthetic spectra of dipolar modes are given in Tables 3–5 for different rotation rates. The interpretation of the discrepancies between the analytical model presented in Sect. 2 and the complete ones is reported to Sect. 4.
 |
Fig. 2. Period spacing as a function of the period for model 1z with different value of the uniform rotation frequency, ranging from 7 μHz to 23 μHz, by increment of 2 μHz, for zonal dipolar modes. Both the period spacings and the periods are shown in the inertial frame of reference. The filled circles are obtained with non-perturbative calculations, while the grey curves are obtained with the traditional approximation of rotation. The vertical lines give the location of the periods of pure inertial modes associated with different rotation rates (only for νrot = 13 to 23 μHz), computed for an incompressible inviscid spherical box as described in Sect. 2.2. |
Concerning prograde modes, which are the ones that are more likely to be observed, the resonances only appear at high rotation rates. For the three models explored in this study, the value of the uniform rotation rate has to be increased up to 25 μHz in order to find a resonance among the modes which are likely to be excited (radial orders around −15 to −60). Special attention should be paid to this case, as the literature has mostly reported observations of prograde modes in γ Doradus and SPB stars. In particular, we believe that the phenomenon of gravito-inertial resonance is responsible for the dips in the period spacing series of dipolar prograde modes in KIC 5608334, reported in Saio et al. (2018). This can be further confirmed by looking at the value of the spin parameter at which this resonance occurs in KIC 5608334: s = 9.01, which is compatible with the values presented in Table 5.
While relaxing the constraint of mode excitation, we look for the next resonances given in Table 3 to confirm that they originate from the coupling with pure inertial modes. We therefore have extended the complete calculations to a broader range of radial orders, from −11 to −191. The spin parameters relative to these eigenvalues are given in Fig. 3. As shown in Fig. 3, three resonances are found and they correspond to the three eigenvalues of the Poincaré problem (indicated in Fig. 3 by the grey vertical lines), for which 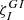 is not negligible (see Table 1). In other words, for each eigenvalue with a coupling coefficient of the order of 0.1 or higher, an associated resonance has been found in the complete calculations. In Fig. 4, we give the 2D maps of the eigenfunctions of the three modes located in the dips of the period spacing series in Fig. 3. These have to be compared to the three panels giving the 2D maps of the pure inertial eigenmodes computed in Sect. 2, which are provided in Fig. 1. From this comparison, we can see clearly that the modes trapped in the convective cores in Fig. 4 closely follow the morphology of the pure inertial modes in a full sphere of uniform density computed in Sect. 2. The mixed morphology of the complete modes clearly confirms their mixed nature: pure inertial in the convective core and gravito-inertial in the surrounding radiative zone.
is not negligible (see Table 1). In other words, for each eigenvalue with a coupling coefficient of the order of 0.1 or higher, an associated resonance has been found in the complete calculations. In Fig. 4, we give the 2D maps of the eigenfunctions of the three modes located in the dips of the period spacing series in Fig. 3. These have to be compared to the three panels giving the 2D maps of the pure inertial eigenmodes computed in Sect. 2, which are provided in Fig. 1. From this comparison, we can see clearly that the modes trapped in the convective cores in Fig. 4 closely follow the morphology of the pure inertial modes in a full sphere of uniform density computed in Sect. 2. The mixed morphology of the complete modes clearly confirms their mixed nature: pure inertial in the convective core and gravito-inertial in the surrounding radiative zone.
 |
Fig. 3. Period spacing as a function of the period for model 1z for a uniform rotation frequency of 21 μHz. Both the period spacings and the periods are shown in the inertial frame of reference. |
 |
Fig. 4. Eigenfunction ( |
3.3. Failure of the traditional approximation to reproduce the resonances
In rotating stars, the equation system for pulsations is not separable in the radial and latitudinal coordinates. The TAR is an approximate treatment that conserves the separability of the system. The first hypothesis is made on the rotation profile by assuming solid-body rotation. The centrifugal distortion is neglected and, hence, spherical symmetry is assumed. Furthermore, considering the properties of low frequency high order g-modes, the TAR neglects the Coriolis force associated with radial motion and radial component of the Coriolis force associated with horizontal motion. Practically, it consists of neglecting the horizontal component of the angular velocity so that Ω = [Ω cos θ,0,0] in the spherical polar coordinates. Finally, we make a Cowling approximation (Cowling 1941), which neglects the perturbation of the gravitational potential. As a result, the motion equation for pulsations can be reduced to an equation for the radial component, which is similar to the one without rotation, and a Laplace tidal equation for the horizontal component, whose eigenfunctions are the Hough functions. For a detailed derivation of these equation, we refer to Unno et al. (1989) Sect. 34.3; or to Lee & Saio (1987).
This approximation has been implemented in the LOSC adiabatic and MAD non-adiabatic oscillation codes, the details of which have been given by Bouabid et al. (2013) and Salmon et al. (2014). We have computed a selection of spectra with this method, for the sake of comparison with the non-perturbative approach, for zonal modes in the model 1z, and for the whole rotation frequency range from 7 to 23 μHz. The results are plotted in Fig. 2, as the grey solid lines. It appears from that figure that the TAR does not model correctly the modes in the neighbourhood of the resonance. While it is in very good agreement far from resonance, it completely misses the change in nature of the mode which endorses a gravito-inertial and pure inertial mixed character.
This result is not surprising since the TAR only applies when Ω ≪ N. Thus, in a convective zone where N = 0, the use of the TAR is not justified. Moreover, they cannot compute pure inertial modes which are not separable in r and θ. Then, as long as the mode is confined in the radiative zone, the TAR reproduces closely enough the complete calculations, but near the resonances when the pure inertial character is significant in the convective core, the TAR fails as expected. Finally, comparing, as in Fig. 2, TAR results with complete calculations can be a way to identify resonances due to pure inertial modes.
4. Impact of the stellar stratification and the rotation rate on the resonances
The density stratification affects inertial waves through the first right hand side term of equation Eq. (1) which is proportional to the inverse of the density scale height and involves first-order derivatives of Ψ. In the short-wavelength limit, second-order derivatives dominate over first-order ones. Moreover, H does not vanish in stellar cores, thus the density stratification term should have a negligible effect in this limit. However, the short-wavelength limit is not expected to be accurate for the low ℓi − |m| modes we are interested in and some effects of the density stratification on the inertial modes are to be expected.
4.1. Location of the resonances for different stellar models
We first investigate this effect by exploring the oscillation spectra of stellar models with various density profiles. We take the three stellar models presented in Table 2. Their stratifications are illustrated through the density profiles plotted in Fig. 5. Indeed the younger the stellar model, the closer to the homogeneous case. In order to find gravito-inertial resonances, we computed synthetic oscillation spectra for dipolar zonal and prograde modes at various uniform rotation rates.
 |
Fig. 5. Density profile, scaled by the central value, for the three stellar models given in Table 2. The dashed line indicates the external boundary of the convective core for each model. |
Parameters of the models explored in detail in this study.
For dipolar zonal modes, as well as dipolar retrograde modes, resonances appear at a relatively slow rotation, as illustrated Fig. 6, and as given in Tables 3 and 4. However, for prograde modes, as mentioned above, it is necessary to push as high as 25 μHz to have the resonance occur in the range of frequency where modes are excited. These values have to be compared to the case of pure inertial mode frequencies computed in a homogeneous sphere given in Table 1: the strongest resonance, in that case, occurs at a spin parameter of s = 1.3246 for the retrograde modes, s = 2.2361 for the zonal modes, and s = 11.3245 for the prograde modes. For the three classes of modes, it appears clearly, as expected, that the resonances are closer to the homogeneous case for the youngest stellar model, than for the second youngest, than for the oldest, ranging from a difference of less than 1% to 3% in the zonal case, 1% to 2% in the retrograde case, and 4% to 24% in the prograde case.
 |
Fig. 6. Period spacings as a function of the period for the three stellar models given in Table 2. Top: for zonal dipolar modes with uniform rotation of 15 μHz. Bottom: for prograde dipolar modes with uniform rotation of 25 μHz. Both the period spacings and the periods are shown in the inertial frame of reference. |
The discrepancy between the homogeneous case and the stellar model case remains relatively small for the retrograde and zonal modes whereas the resonance of the prograde dipolar mode seems to be more sensitive to the density stratification. As mentioned above, pure inertial modes with wavelengths much shorter than the density scaleheight H should not be strongly affected by the density stratification. The wavelengths of the low degree inertial modes considered here are of the order of a fraction of the convective core radius rcc. They are still shorter than the density scale height because rcc ∼ H. This may explain the relatively small effect of the density stratification for retrograde and zonal modes. However, this argument does not hold for prograde inertial modes because their spatial distribution is highly anisotropic with negligible variations in the vertical direction, with such behaviour being related to their high spin parameter. Indeed, estimating the effect of the density stratification by comparing left hand side and right hand terms in Eq. (1), we find that the ratio of the second left hand side term to the second right hand side term is ∼1/(kzH) where kz the vertical component of the wave vector. This ratio and, thus, the effect of the density stratification can not be neglected when kz nearly vanishes, which occurs when the spin parameter is high. In our case, this concerns the three prograde inertial modes with significant coupling listed in Table 1. The behaviour of these inertial-gravito-inertial resonances with rotation is explored in more detail in the next section.
4.2. Pure inertial modes in a sphere with density stratification
Discrepancies between the homogeneous case and the real case can arise either from the difference in stratification, or otherwise from the very crude boundary condition which has been applied at the surface of the sphere in the homogeneous case (Sect. 2). In order to isolate the relevant physical effects, a modified version of the ACOR code has been used, which allows the computation of pure inertial modes in stellar models truncated above the convective cores. The principle here is that the convective core is extracted from a stellar model and the pulsations are then calculated in the complete non-perturbative approach. We imposed a rigid condition at the surface of the convective core which ensures that the radial displacement goes to zero: ξr(r = rcc) = 0. This condition allows the resolution of the core problem without accounting for the radiative envelope.
This modification of the ACOR code allows us to compute pure inertial modes in truncated convective cores taken from the models in Table 2. The results are given in Fig. 7, where the eigenfrequencies computed for the truncated convective cores, which have been converted into spin parameters (in violet), are compared to the values obtained for the resonances in the complete model (in pink), and to the values obtained solving Eq. (1) (also given in Table 1, in grey). The first striking observation, concerning the values of spin parameters obtained in the convective core models, is their constant nature: they do not vary with rotation. We come back to this in the following subsection. Moreover, as expected, the more evolved the model, hence the more stratified, the further away the spin parameters for the truncated core models are from the uniform density case.
 |
Fig. 7. Values of spin parameters as a function of rotation frequency determined through three different methods. In pink are plotted the values computed with ACOR on the stellar model 2 m (see Sect. 3.2), the violet curves correspond to values computed in the truncated convective core of model 2 m (see Sect. 4.2), and the grey constant lines stand for the homogeneous spherical box case (see Sect. 2.1). These are given for dipolar retrograde modes (upper panel), zonal (middle), and prograde ones (lower panel). |
From Fig. 7, it appears clearly that the resonances in the complete models occur systematically much closer to the values corresponding to eigenfrequencies of pure inertial modes determined in the convective core models than in the homogeneous sphere. This does not come as a surprise, but the differences demonstrated here show that the largest discrepancies between the homogeneous case and the complete one come from the hypothesis of homogeneity, rather than from the crude outer boundary condition (ξr = 0 at the surface of the box), which seems to affect the results only marginally.
4.3. Impact of the rotation rate
We have noted in the previous section that the spin parameter at which the resonance between the pure inertial modes and the gravito-inertial modes does not vary with rotation. This is a direct consequence of the fact that in isentropic medium waves are governed by Eq. (1). Indeed, for frequencies much smaller than the acoustic frequencies, the last right hand side term of Eq. (1) is negligible and the wave equation only depends on the spin parameter. Hence, in Table 6 is given one single value of the spin parameter for each models and for each type of modes.
Eigenfrequencies of pure inertial modes in truncated models of convective cores.
This is not exactly the case for the complete models. The correct treatment at a boundary separating two distinct propagation cavities is to ensure the continuity of both pressure and radial displacement. Ogilvie & Lin (2004) discussed this point at a convective/radiative interface. Arguing that in their respective cavities radial displacements of inertial modes are much larger than those of gravito-inertial modes limited by the Brunt-Väisälä frequency, they deduced from the continuity condition that inertial waves see a ξr ≈ 0 condition at the cavity interface. This justification of the boundary condition is only approximate though. In a more accurate model, the conditions at the interface will also depend on the gravito-inertial mode above, which means that the effective boundary condition for the inertial mode and thus its eigenfrequency will depend on parameters such as the Brunt Vaisala frequency. As a result, the resonance will not occur at a fixed spin parameter but will also vary with, for example, the ratio of the rotation rate to the Brunt-Vaisala frequency. In accordance with this understanding, Fig. 7 shows variable spin parameters in full calculations. These variations remain relatively small for the stellar models used in our calculations and in the rotation range considered.
5. Discussion and conclusions
We studied the resonances which can occur between pure inertial modes trapped in convective cores and the gravito-inertial modes in the surrounding radiative envelopes. We show that these resonances leave a clear signature in gravito-inertial modes period spacings which have been found in γ Doradus stars observed during the Kepler nominal mission, including KIC 5608334 (Saio et al. 2018).
We propose a very simple model that provides the spin parameters at which the resonances occur. Comparisons with full calculations show that the model rightly predicts the occurrence of the resonances, while the values of the spin parameters at resonance differ slightly. One of the assumptions of the model, namely the absence of density stratification, was identified as the main source of discrepancy on the resonance spin parameter. As compared to the uniform density model, taking into account density stratification does not change the fact that the resonances occur at fixed spin parameters. The other assumption, namely, vanishing radial displacements at the core radius as a boundary condition for inertial modes, should then account for the remaining deviations with the full calculations.
In this paper, we assume that the convective core is non-magnetic and uniformly rotating. The relevance of such hypotheses might be questioned: indeed, convective cores may be differentially rotating and numerical simulations of A-type star convective cores (see Brun et al. 2005; Augustson et al. 2016, for B stars) show that strong magnetic fields can be generated by a dynamo process. However, in the low Rossby number regime characterising these convective motions, (i) the maxwell stresses are found to largely suppress the differential rotation (no more than a few percents in Brun et al. 2005, based on simulations of a 7-days period rotating star) and (ii) the ratio of the magnetic energy to the kinetic energy of the rotational motions is much smaller than one (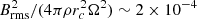 halfway through the convective core for the same simulation). The latter property suggests that the magnetic fields generated in the γ Dor convective cores have either a very small or a negligible effect on the inertial modes. Indeed local and global analysis (e.g. Finlay 2008; Canet et al. 2014) show that the relative deviation of the frequency of an inertial mode provoked by a magnetic field is proportional to this ratio (when this ratio is small). Contrary to magnetic fields, even a small differential rotation would matter, at least for the reason that it will impact the definition of the spin parameter. Baruteau & Rieutord (2013) studied the effect of a differential rotation in the case of an uniform density fluid and showed that it can strongly modify some inertial modes by reducing the volume of their resonant cavity. This effect occurs in specific frequency domains determined by the distribution Ω(r, θ). As an additional effect, the non-axisymmetric inertial modes may be affected by the presence of critical layers when their phase speed equals the azimuthal velocity somewhere in their resonant cavity. Assuming a weak cylindrical differential rotation similar to the one found by Brun et al. (2005) for a seven-day rotating A-star, Ω/Ω0 = 1 + η(r sin θ/R)2 with η = −0.05 and applying the criteria given in Baruteau & Rieutord (2013), we find that the inertial modes producing the dips in the dipolar gravity mode period spacings (see Table 1) are not related to these two strong effects of the differential rotation. In order to further explore the influence of differential rotation on the exact spin parameter of the dips, a dedicated study in a stellar context will be necessary.
halfway through the convective core for the same simulation). The latter property suggests that the magnetic fields generated in the γ Dor convective cores have either a very small or a negligible effect on the inertial modes. Indeed local and global analysis (e.g. Finlay 2008; Canet et al. 2014) show that the relative deviation of the frequency of an inertial mode provoked by a magnetic field is proportional to this ratio (when this ratio is small). Contrary to magnetic fields, even a small differential rotation would matter, at least for the reason that it will impact the definition of the spin parameter. Baruteau & Rieutord (2013) studied the effect of a differential rotation in the case of an uniform density fluid and showed that it can strongly modify some inertial modes by reducing the volume of their resonant cavity. This effect occurs in specific frequency domains determined by the distribution Ω(r, θ). As an additional effect, the non-axisymmetric inertial modes may be affected by the presence of critical layers when their phase speed equals the azimuthal velocity somewhere in their resonant cavity. Assuming a weak cylindrical differential rotation similar to the one found by Brun et al. (2005) for a seven-day rotating A-star, Ω/Ω0 = 1 + η(r sin θ/R)2 with η = −0.05 and applying the criteria given in Baruteau & Rieutord (2013), we find that the inertial modes producing the dips in the dipolar gravity mode period spacings (see Table 1) are not related to these two strong effects of the differential rotation. In order to further explore the influence of differential rotation on the exact spin parameter of the dips, a dedicated study in a stellar context will be necessary.
In future works, it would also be worth investigating whether the dip spin parameters are sensitive to stellar modelling options, especially those that modify the structure near the convective core. Furthermore, beyond the central position of the dip, another interesting development concerns its shape and how that shape is dependent upon the properties of the star. In time, we expect to be able to obtain, given one single series of gravito-inertial modes holding the signature of resonance with a pure inertial mode, the rotation rate both in the convective core and in the surrounding radiative near-core region at once. The diagnostic potential of these resonances hold the promise to eventually probing the central layers of stars on the main sequence.
In this paper, we focus our attention on mixed pure inertial – dipolar gravito-inertial modes because it is mostly dipolar-inertial modes that have been identified so far. However, resonances will also occur with the other gravito-inertial modes. They can be investigated theoretically, as we do in the present work, using the simplified model and the full calculations.
Acknowledgments
This work was supported by the “Programme National de Physique Stellaire” (PNPS) of CNRS/INSU co-funded by CEA and CNES. We thank ISSI “International Space SciencevInstitute”) through the SoFAR “Seismology of Fast Rotating Stars”) program for their support. The authors are very grateful to Hideyuki Saio for his great patience. F.L. and J.B. also would like to thank P.-M. Culpin for his significative contribution at early stages of this work during his Master internship.
References
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Augustson, K. C., Brun, A. S., & Toomre, J. 2016, ApJ, 829, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Ballot, J., Lignières, F., Prat, V., Reese, D. R., & Rieutord, M. 2012, in Progress in Solar/Stellar Physics with Helio- and Asteroseismology, eds. H. Shibahashi, M. Takata, & A. E. Lynas-Gray, ASP Conf. Ser., 462, 389 [NASA ADS] [Google Scholar]
- Baruteau, C., & Rieutord, M. 2013, J. Fluid Mech., 719, 47 [Google Scholar]
- Beck, P. G., Montalban, J., Kallinger, T., et al. 2012, Nature, 481, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Belkacem, K., Marques, J. P., Goupil, M. J., et al. 2015, A&A, 579, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Bouabid, M.-P., Dupret, M.-A., Salmon, S., et al. 2013, MNRAS, 429, 2500 [NASA ADS] [CrossRef] [Google Scholar]
- Brun, A. S., Browning, M. K., & Toomre, J. 2005, ApJ, 629, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Bryan, G. H. 1889, Philos. Trans. R. Soc. London Ser. A, 180, 187 [Google Scholar]
- Canet, E., Finlay, C. C., & Fournier, A. 2014, Phys. Earth Planet. Inter., 229, 1 [Google Scholar]
- Cantiello, M., Mankovich, C., Bildsten, L., Christensen-Dalsgaard, J., & Paxton, B. 2014, ApJ, 788, 93 [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, eds. N. Piskunov, W. W. Weiss, & D. F. Gray, IAU Symp., 210, A20 [Google Scholar]
- Christophe, S., Ballot, J., Ouazzani, R.-M., Antoci, V., & Salmon, S. J. A. J. 2018, A&A, 618, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowling, T. G. 1941, MNRAS, 101, 367 [NASA ADS] [Google Scholar]
- Deheuvels, S., García, R. A., Chaplin, W. J., et al. 2012, ApJ, 756, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Dintrans, B., & Ouyed, R. 2001, A&A, 375, L47 [EDP Sciences] [Google Scholar]
- Dintrans, B., & Rieutord, M. 2000, A&A, 354, 86 [NASA ADS] [Google Scholar]
- Dziembowski, W., Kosovichev, A., & Kozlowski, M. 1987, Acta Astron., 37, 331 [Google Scholar]
- Eggenberger, P., Montalbán, J., & Miglio, A. 2012, A&A, 544, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Finlay, C. C. 2008, Phys. Earth Planet. Interiors, 170, 1 [Google Scholar]
- Formicola, A., Imbriani, G., Costantini, H., et al. 2004, Phys. Lett. B, 591, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Fuller, J., Lecoanet, D., Cantiello, M., & Brown, B. 2014, ApJ, 796, 17 [Google Scholar]
- Fuller, J., Piro, A. L., & Jermyn, A. S. 2019, MNRAS, 485, 3661 [NASA ADS] [Google Scholar]
- Greenspan, H. 1968, The Theory of Rotating Fuilds (Cambridge: Cambridge University Press) [Google Scholar]
- Guenther, D. B., & Gilman, P. A. 1985, ApJ, 295, 195 [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D. W., Saio, H., Takata, M., et al. 2014, MNRAS, 444, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, U., & Saio, H. 1987, MNRAS, 224, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, U., Strohmayer, T. E., & van Horn, H. M. 1992, ApJ, 397, 674 [Google Scholar]
- Li, G., Van Reeth, T., Bedding, T. R., Murphy, S. J., & Antoci, V. 2019, MNRAS, 487, 782 [Google Scholar]
- Lockitch, K. H., & Friedman, J. L. 1999, ApJ, 521, 764 [Google Scholar]
- Marques, J. P., Goupil, M. J., Lebreton, Y., et al. 2013, A&A, 549, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Prat, V., Amard, L., et al. 2018, A&A, 620, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miglio, A., Montalbán, J., Noels, A., & Eggenberger, P. 2008, MNRAS, 386, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 540, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, S. J., Fossati, L., Bedding, T. R., et al. 2016, MNRAS, 459, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I., & Lin, D. N. C. 2004, ApJ, 610, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Ouazzani, R.-M., Dupret, M.-A., & Reese, D. R. 2012, A&A, 547, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ouazzani, R.-M., Roxburgh, I. W., & Dupret, M.-A. 2015, A&A, 579, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ouazzani, R.-M., Salmon, S. J. A. J., Antoci, V., et al. 2017, MNRAS, 465, 2294 [NASA ADS] [CrossRef] [Google Scholar]
- Ouazzani, R. M., Marques, J. P., Goupil, M. J., et al. 2019, A&A, 626, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papaloizou, J., & Pringle, J. E. 1981, MNRAS, 195, 743 [Google Scholar]
- Papaloizou, J. C. B., & Savonije, G. J. 1997, MNRAS, 291, 651 [Google Scholar]
- Pinçon, C., Belkacem, K., Goupil, M. J., & Marques, J. P. 2017, A&A, 605, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prat, V., Lignières, F., & Ballot, J. 2016, A&A, 587, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieutord, M. 1991, Geophys. Astrophys. Fluid Dyn., 59, 185 [Google Scholar]
- Rieutord, M., & Valdettaro, L. 2018, J. Fluid Mech., 844, 597 [Google Scholar]
- Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
- Saio, H., Kurtz, D. W., Takata, M., et al. 2015, MNRAS, 447, 3264 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., Bedding, T. R., Kurtz, D. W., et al. 2018, MNRAS, 477, 2183 [Google Scholar]
- Salmon, S. J. A. J., Montalbán, J., Reese, D. R., Dupret, M.-A., & Eggenberger, P. 2014, A&A, 569, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scuflaire, R., Théado, S., Montalbán, J., et al. 2008a, Ap&SS, 316, 83 [Google Scholar]
- Scuflaire, R., Montalbán, J., Théado, S., et al. 2008b, Ap&SS, 316, 149 [Google Scholar]
- Townsend, R. H. D. 2003, MNRAS, 340, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial oscillations of stars [Google Scholar]
- Van Reeth, T., Tkachenko, A., & Aerts, C. 2016, A&A, 593, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Reeth, T., Mombarg, J. S. G., Mathis, S., et al. 2018, A&A, 618, A24 [NASA ADS] [EDP Sciences] [Google Scholar]
- Wu, Y. 2005, ApJ, 635, 674 [Google Scholar]
- Zahn, J. 1992, A&A, 265, 115 [Google Scholar]
Appendix A: Ellipsoidal coordinates
The Poincaré equation becomes separable using the ellipsoidal coordinates (x1, x2, ϕ) where ϕ is the azimuthal angle of the spherical coordinates and x1 and x2 relations with the cartesian coordinates are written as:
where x1 ∈ [μ, 1] and x2 ∈ [ − μ, μ], and distances have been normalised with the sphere radius. In these coordinates, the surface of the sphere is given by {x1 ∈ [μ, 1],x2 = μ}∪{x1 = μ, x2 ∈ [ − μ, μ]}.
Appendix B: Inertial modes of the full sphere
 |
Fig. B.1. Inertial modes in a uniform density sphere, as computed with the method given in Sect. 2. Each of these modes have a small spatial matching with the dipolar gravito-inertial mode of the same spin parameter. The dotted line specifies the critical latitude θc = arccos(ω/(2Ω)). The top panels show the zonal modes with low coupling coefficients presented in Table 1, whereas the middle and the bottom panels show the tree modes with the highest coupling coefficients for the prograde (m = −1), and the retrograde (m = 1) modes. |
All Tables
Inertial-mode spin parameters and coupling coefficients 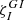 (in parenthesis) with the dipolar Hough function of the same symmetry class and spin parameter.
(in parenthesis) with the dipolar Hough function of the same symmetry class and spin parameter.
Eigenfrequencies of pure inertial modes in truncated models of convective cores.
All Figures
 |
Fig. 1. Inertial modes in a uniform density sphere. Each of these modes have a strong spatial matching with the dipolar gravito-inertial mode of the same spin parameter. The dotted line specifies the critical latitude θc = arccos(ω/(2Ω)). |
| In the text | |
 |
Fig. 2. Period spacing as a function of the period for model 1z with different value of the uniform rotation frequency, ranging from 7 μHz to 23 μHz, by increment of 2 μHz, for zonal dipolar modes. Both the period spacings and the periods are shown in the inertial frame of reference. The filled circles are obtained with non-perturbative calculations, while the grey curves are obtained with the traditional approximation of rotation. The vertical lines give the location of the periods of pure inertial modes associated with different rotation rates (only for νrot = 13 to 23 μHz), computed for an incompressible inviscid spherical box as described in Sect. 2.2. |
| In the text | |
 |
Fig. 3. Period spacing as a function of the period for model 1z for a uniform rotation frequency of 21 μHz. Both the period spacings and the periods are shown in the inertial frame of reference. |
| In the text | |
 |
Fig. 4. Eigenfunction ( |
| In the text | |
 |
Fig. 5. Density profile, scaled by the central value, for the three stellar models given in Table 2. The dashed line indicates the external boundary of the convective core for each model. |
| In the text | |
 |
Fig. 6. Period spacings as a function of the period for the three stellar models given in Table 2. Top: for zonal dipolar modes with uniform rotation of 15 μHz. Bottom: for prograde dipolar modes with uniform rotation of 25 μHz. Both the period spacings and the periods are shown in the inertial frame of reference. |
| In the text | |
 |
Fig. 7. Values of spin parameters as a function of rotation frequency determined through three different methods. In pink are plotted the values computed with ACOR on the stellar model 2 m (see Sect. 3.2), the violet curves correspond to values computed in the truncated convective core of model 2 m (see Sect. 4.2), and the grey constant lines stand for the homogeneous spherical box case (see Sect. 2.1). These are given for dipolar retrograde modes (upper panel), zonal (middle), and prograde ones (lower panel). |
| In the text | |
 |
Fig. B.1. Inertial modes in a uniform density sphere, as computed with the method given in Sect. 2. Each of these modes have a small spatial matching with the dipolar gravito-inertial mode of the same spin parameter. The dotted line specifies the critical latitude θc = arccos(ω/(2Ω)). The top panels show the zonal modes with low coupling coefficients presented in Table 1, whereas the middle and the bottom panels show the tree modes with the highest coupling coefficients for the prograde (m = −1), and the retrograde (m = 1) modes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.