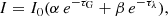| Issue |
A&A
Volume 639, July 2020
|
|
|---|---|---|
| Article Number | L8 | |
| Number of page(s) | 10 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202038157 | |
| Published online | 14 July 2020 | |
Letter to the Editor
ISO-ChaI 52: a weakly accreting young stellar object with a dipper light curve⋆
1
INAF – Osservatorio Astrofisico di Catania, Via S. Sofia 78, 95123 Catania, Italy
e-mail: antonio.frasca@inaf.it
2
European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
3
INAF – Osservatorio Astronomico di Capodimonte, Via Moiariello, 16, 80131 Napoli, Italy
4
INAF – Osservatorio Astronomico di Roma, Via Frascati 33, 00078 Monte Porzio Catone, Italy
5
NASA Ames Research Center, Moffett Blvd, Mountain View, CA 94035, USA
6
INAF – Osservatorio Astronomico di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
7
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
8
Institut für Astronomie und Astrophysik, Eberhard-Karls Universität Tübingen, Sand 1, 72076 Tübingen, Germany
9
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
Received:
13
April
2020
Accepted:
29
June
2020
We report the discovery of periodic dips in the multiband light curve of ISO-ChaI 52, a young stellar object in the Chamaeleon I dark cloud. This is one of the peculiar objects that display very low or negligible accretion in their UV continuum and spectral lines, although they present a remarkable infrared excess emission characteristic of optically thick circumstellar disks. We have analyzed a spectrum obtained at the Very Large Telescope with the X-shooter spectrograph with the tool ROTFIT to determine the stellar parameters. The latter, along with photometry from our campaign with the Rapid Eye Mount telescope and from the literature, have allowed us to model the spectral energy distribution and to estimate the size and temperature of the inner and outer disk. Based on the rotational period of the star-disk system of 3.45 days, we estimate a disk inclination of 36°. The depth of the dips in different bands has been used to gain information about the occulting material. A single extinction law is not able to fit the observed behavior, while a two-component model of a disk warp composed of a dense region with a gray extinction and an upper layer with an extinction as in the interstellar medium provides a better fit to the data.
Key words: stars: pre-main sequence / stars: low-mass / accretion / accretion disks / protoplanetary disks
© ESO 2020
1. Introduction
A key question in the study of planet formation is to explain the evolution of optically thick accretion disks that surround the youngest solar-mass stars and give rise to a remarkable IR excess (class II IR sources) into optically thin debris disks. This evolution includes a phase where only a mild (or no) IR excess is visible (class III sources). Normally, thick disks are observed around classical T Tauri (CTT) stars, which display strong emission lines produced by mass accretion, while the weak-line T Tauri (WTT) stars, with negligible signatures of accretion, are very often detected as class III sources (Hartmann et al. 2005; Lada et al. 2006, and references therein). Generally, these disks persist for a few million years, during which part of the material is accreted onto the star, part is lost through outflows and photoevaporation (e.g., Ercolano & Pascucci 2017; Nisini et al. 2018), and part condenses into centimeter-sized and larger bodies or planetesimals (e.g., Testi et al. 2014). A possible intermediate stage of the T Tauri disk evolution is observationally identified with the so-called transitional disks (TDs), which are characterized by inner holes and gaps in their dust distribution (e.g., Espaillat et al. 2014, and references therein).
A further category of objects has recently emerged with apparently very little or no evidence for accretion in optical (λ > 3400 Å) spectra, but with the near-IR (NIR) emission characteristic of optically thick dust in the inner (few AU) regions of the disk, so that their spectral energy distribution resembles that of class II sources (e.g., Wahhaj et al. 2010; Alcalá et al. 2019; Thanathibodee et al. 2019). The existence of such objects might be explained by slightly different timescales for the decline of disk and accretion processes in young stars (e.g., Fedele et al. 2010). Another possibility is that the accretion is highly variable and mainly occurs during bursts (e.g., Cody et al. 2017). Weak accretion is in general difficult to detect in the region of the Balmer jump. Other diagnostics such as modeling of the Hα line profile (e.g., Espaillat et al. 2008; Thanathibodee et al. 2019) and/or measures of excess emission in near-UV or far-UV spectra (e.g., Alcalá et al. 2019, and references therein) are therefore necessary in these cases of very low accretion rates.
In our X-shooter surveys of the Chamaeleon I (Cha I, Manara et al. 2016, 2017) and Lupus star forming regions (Alcalá et al. 2014, 2017), we have recently detected several such weak accretors. Thereby we have confirmed that some of these disk-bearing objects lack the X-shooter continuum UV excess that is typical of accreting objects. The recent ALMA surveys of Pascucci et al. (2016) in Cha I and of Ansdell et al. (2016a) in Lupus show that the disks around some of these objects are bright in the submillimeter regime and still host a large amount of dust.
Young stellar objects (YSOs) display luminosity variations on different timescales that are due to geometric and intrinsic effects. The variability of nonaccreting objects is mainly related to stellar magnetic activity (cold photospheric spots, flares, etc). For accreting objects, a variety of processes, including hot spots, variable circumstellar extinction, and/or accretion bursts, can cause these variations. A way to efficiently characterize these processes is by photometric multiband imaging techniques. Long-term ground-based observations (e.g., Herbst et al. 2002; Frasca et al. 2009), and more recently, high-precision, high-cadence space photometry (e.g., Venuti et al. 2017; Stauffer et al. 2017), enabled the exploration of different scenarios for the physical process that is involved in the variability of YSOs. An intriguing observed behavior is the recurrent luminosity dips that are likely due to the periodic occultation of the central star by the magnetically warped inner disk edge (e.g., Bouvier et al. 1999, 2003; McGinnis et al. 2015).
In this Letter we report the discovery of quasi-periodic luminosity dips in the weakly accreting object ISO-ChaI 52 (=BYB 18 = 2MASS J11044258−7741571) that were observed simultaneously from the optical to the NIR with the Rapid Eye Mount (REM) telescope at the La Silla observatory. We have also analyzed an intermediate-resolution spectrum of this source (R ≃ 18 000) taken on 18 December 2010 with X-shooter at the ESO Very Large Telescope (VLT; program ID 084.C-1095) with the aim of deriving stellar parameters in support of this study.
2. Observations
The photometric observations were performed with the 60 cm robotic REM telescope located at the ESO-La Silla Observatory (Chile), on 80 nights from 3 April to 1 October 2019. By means of a dichroic, REM simultaneously feeds two cameras at the two Nasmyth focal stations, one for the NIR (REMIR) and one for the optical (ROSS2). The cameras have nearly the same field of view of about 10′×10′ and use wide-band filters (J, H, and K′ for REMIR and Sloan/SDSS g′, r′, i′, and z′ for ROSS2). Due to a technical failure in the REMIR camera, we have NIR data only for the first 20 nights of the campaign. In total, we collected 260, 277, 280, 285, 103, 102, and 108 usable images in g′, r′, i′, z′, J, H, and K′ bands, respectively. Exposure times were 180 s for ROSS2, which simultaneously acquires images in the four Sloan bands, while five ditherings of 7 s each were adopted for each filter of REMIR. Details on the reduction of the photometric data are reported in Appendix A. The reduction of the X-shooter spectrum is performed and described in Manara et al. (2016).
3. Results
3.1. Stellar parameters and accretion diagnostics
We analyzed the X-shooter spectrum with the code ROTFIT (Frasca et al. 2017), which allows us to derive the atmospheric parameters (Teff, log g), the radial velocity (RV), the projected rotational velocity (v sin i), and the veiling (r). Details are given in Appendix B. The results of the ROTFIT analysis are summarized in Table 1. The veiling in the red spectral regions analyzed by us is r < 0.2. Our Teff is fully consistent, within the errors, with the value of 3270 K that was derived by Manara et al. (2016) from the M4 spectral type (SpT) and the SpT–Teff calibration relation of Luhman et al. (2003). Moreover, this spectral type corresponds to Teff = 3200 K and Teff = 3190 K according to the SpT–Teff relations of Pecaut & Mamajek (2013) and Herczeg & Hillenbrand (2014), respectively, which are in perfect agreement with our Teff determination. The Hα line width at 10% of the peak, W10% = 180 ± 18 km s−1, and the Hα flux of 1.2 × 106 erg cm−2 s−1, which we measure on the X-shooter spectrum, both indicate that ISO-ChaI 52 is a nonaccreting object (see, e.g., Fig. 11 in Frasca et al. 2015), as has been noted by Manara et al. (2016, 2017). These authors observed a small excess in the Balmer continuum (see Fig. C.1 in Manara et al. 2016), which translates into an upper limit of −10.34 (rescaled to the Gaia DR2 distance, Manara et al. 2019) for log Ṁacc (M⊙ yr−1), and considered it as a doubtful accretor, at a level compatible with the typical chromospheric emission line activity. We note that the profiles of the Balmer lines and Ca II K line are all rather narrow and symmetric (see Fig. C.1) with no sign of redshifted absorption components or reversals that are frequently observed in the line profiles of accretors (e.g., Thanathibodee et al. 2019; de Albuquerque et al. 2020). The only notable feature is a wing emission, which is stronger on the red side of the Hβ and Hγ profiles and extends up to ≃200 km s−1. This is reminiscent of mass flows or turbulence in the upper atmosphere, which are mostly observed during flare events (see, e.g., Doyle et al. 1988). Moreover, as shown in Fig. C.1, the He I lines λλ5876, 6876 Å are not clearly detected and the Ca II IRT lines display only a filling in of their cores (Fig. C.2) that resembles a purely chromospheric emission. These diagnostics support the scenario that ISO-ChaI 52 is a nonaccreting, or based on the evidence for UV continuum excess derscribed above, a weakly accreting object.
Stellar parameters of ISO-ChaI 52 derived in this work.
3.2. Spectral energy distribution
We used the average values of g′r′i′z′JHK′ magnitudes outside the dips (Fig. 2) to construct the optical/NIR spectral energy distribution (SED). We extended the SED to the blue side and to mid-infrared (MIR) and far-infrared (FIR) wavelengths by adding flux values from the literature. These data are quoted in Table B.1.
We adopted the BT-Settl spectrum (Allard et al. 2012) with Teff = 3200 K, [Fe/H] = 0.0, and log g = 4.0, that is, the spectrum whose parameters are closest to those found with ROTFIT, to fit the optical-NIR portion (from B to J band) of the SED (Fig. 1). Details on the fitting procedure can be found in Appendix B, and some derived parameters are reported in Table 1.
 |
Fig. 1. Spectral energy distribution of ISO-ChaI 52. Mid- and far-infrared fluxes are shown with different symbols, as indicated in the legend. The BT-Settl spectrum (Allard et al. 2012) that provides the best fit to the star photosphere is shown by a gray line. The two black bodies with T = 650 K and T = 100 K that fit the MIR and FIR disk emission are shown by the dotted red and dashed green lines, respectively. The continuous blue line displays the sum of the smoothed photospheric template and the two black bodies. |
The GALEX/NUV flux is clearly in excess with respect to the photosphere. NUV flux excess was observed in older M-type stars and was ascribed to stellar magnetic activity (e.g., Stelzer et al. 2013), but it might be also indicative of mild accretion onto the central star. If this were the case, ISO-ChaI 52 would be somewhat similar to MY Lup, for which accretion is clearly displayed only by UV line and continuum emission revealed by the Hubble Space Telescope (HST; Alcalá et al. 2019).
The SED also displays a significant IR excess at wavelengths longer than about 3 μm that is produced by the circumstellar disk. The IR excess can be fit reasonably well with thermal emission from two sources with two different temperatures. The MIR emission, which is related to the warmer part of the disk, is fit with a blackbody of 650 K with an emitting area 53 times larger than the stellar surface (dotted red line in Fig. 1), while the FIR emission is reproduced by a source with T = 100 K and an area 1.3 × 105 times larger than the stellar surface (dashed green line). The excess IR luminosity estimated as the sum of these two blackbody components is Ldisk ≃ 0.026 L⊙, which is about 22% of the stellar luminosity. This is in close agreement with what has been found for accreting objects in Lupus (Merín et al. 2008) and Cha II (Alcalá et al. 2008), which all display a fractional disk luminosity Ldisk/L* > 8% that is the limit between passive reprocessing disks and accretion disks proposed by Kenyon & Hartmann (1987). The Hertzsprung-Russell (HR) diagram is shown in Fig. B.2 along with the pre-main-sequence evolutionary tracks and isochrones by Baraffe et al. (2015). The position of ISO-ChaI 52 is between the isochrones at 1 and 3 Myr and close to the evolutionary track for a 0.2 M⊙ star.
3.3. REM light curves
ISO-ChaI 52 displays quasi-periodic dimmings throughout the photometric monitoring, which seem to occur about every seven days. The light curves observed in the g′r′i′z′JHK′ bands are highly correlated, and the depth of the dips increases systematically for bluer bands (Fig. 2). These features have been observed in several YSOs from ground- and space-based observations (e.g., McGinnis et al. 2015; Rodriguez et al. 2017; Stauffer et al. 2017, and references therein) and have been ascribed to accretion-driven warps in highly inclined inner disks that may be misaligned with respect to the outer disks (e.g., Bouvier et al. 2003; Ansdell et al. 2016b; Alencar et al. 2018).
 |
Fig. 2. REM multiband optical/NIR light curves of ISO-ChaI 52 for the first 20 days of the campaign. The scales of the vertical axes have been chosen so as to keep the magnitude ranges constant to display the variation amplitudes more clearly. |
We searched for the period of these variations by applying a periodogram analysis (Scargle 1982) to the r′i′z′JH light curves, which are those in which the dips are best observed and where the photometric errors are low enough. To overcome the problem of irregular data sampling, which introduces aliases in the periodogram, we limited the analysis to the first part of the data (50 days for ROSS2 and 20 days for REMIR) and applied the CLEAN iterative deconvolution algorithm (Roberts et al. 1987). We found for all the bands a peak at about 0.29 d−1, corresponding to a period of about 3.45 d, with a false-alarm probability < 0.01, that is, with a confidence level > 99%. The period uncertainty, evaluated following the prescriptions of Horne & Baliunas (1986), is in the range 0.01−0.05 d. A string-length analysis (Dworetsky 1983) produced similar results, with a first deep minimum in string length detected at around 3.5 d, and subsequent minima of similar or shallower depth at multiples of that period value. The peak of the periodogram is broader in the NIR band, as expected from the shorter time baseline of REMIR observations (see Fig. C.3). We cannot exclude that this period is half of the disk rotation period because the main dips are about seven days apart, while smaller dips between them are barely visible. The smaller dips might be produced by another feature on the opposite side of the disk. However, a period of ≃3.5 d would hamper the observation of consecutive dips from Earth because of the day-night cycle. This would explain why the deeper dimmings are seen at about seven days from each other in the first part of the data but are not clearly visible in the second part (August–October 2019, see Fig. A.2). The light curve in the i′ band folded in phase with periods of 3.45 and 6.9 days is shown in Fig. C.4.
4. Discussion and conclusions
Assuming that the occulting material is located near the corotation radius, we can take Prot = 3.45 d as the stellar rotation period and derive the inclination of the rotation axis as 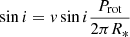 , where we adopted the value of stellar radius given in Table 1, and the more precise value of v sin i = 9.9 ± 0.6 km s−1 reported by Nguyen et al. (2012), which was derived from a high-resolution spectrum. We find sin i = 0.59 ± 0.04 or i = 36° ±4°, in which we have considered the errors on v sin i, R*, and Prot (0.05 d). This value rules out a nearly edge-on inner disk if our best period, and not twice its value (which cannot be excluded, see Sect. 3.3), is the real period. A rotation period of 6.9 d in the above equation would give sin i = 1.18 ± 0.15, which is almost exactly i = 90°. However, an edge-on disk would cause a strong obscuration of the central star, making the object subluminous. This possibility is ruled out because ISO-ChaI 52 is positioned close to the isochrone at 2 Myr in the HR diagram (Fig. B.2). We therefore consider 3.45 d as the more reliable rotation period.
, where we adopted the value of stellar radius given in Table 1, and the more precise value of v sin i = 9.9 ± 0.6 km s−1 reported by Nguyen et al. (2012), which was derived from a high-resolution spectrum. We find sin i = 0.59 ± 0.04 or i = 36° ±4°, in which we have considered the errors on v sin i, R*, and Prot (0.05 d). This value rules out a nearly edge-on inner disk if our best period, and not twice its value (which cannot be excluded, see Sect. 3.3), is the real period. A rotation period of 6.9 d in the above equation would give sin i = 1.18 ± 0.15, which is almost exactly i = 90°. However, an edge-on disk would cause a strong obscuration of the central star, making the object subluminous. This possibility is ruled out because ISO-ChaI 52 is positioned close to the isochrone at 2 Myr in the HR diagram (Fig. B.2). We therefore consider 3.45 d as the more reliable rotation period.
The size of the disk can be estimated on the basis of the IR excess. We described in Sect. 3.2 that the FIR part of the SED can be reproduced by a region that is 1.3 × 105 times larger than the stellar surface and emits as a blackbody with Teff = 100 K. Under this approximation, such an isothermal disk would have a radius of Rdisk ≈ 3 AU, which would correspond to about 15 mas at the distance of ISO-ChaI 52. This is 30 times smaller than the resolution of the ALMA images collected by Pascucci et al. (2016), in which the disk is not resolved (see, e.g., their Figs. 3 and 4).
The depth of the dips in bands of different wavelengths provides useful information on the material occulting the central star. In particular, in the optical bands, the luminosity dimming is largely due to the dust, which differently affects bluer and redder bands, depending on the average size of the grains. We display the extinction Aλ, taken as the depth of the best observed dip (JD = 2458585), as a function of wavelength in Fig. 3. Bearing in mind the radiative transfer equation for a purely absorbing medium, I = I0e−τλ, the extinction Aλ is proportional to the effective optical depth τλ of the layer (Aλ = 1.086 τλ). We have compared the extinction observed during the dip with the extinction law by Cardelli et al. (1989). It is evident from Fig. 3 that the observed extinction is flatter than the typical extinction of the interstellar medium (ISM), which has a total-to-selective extinction ratio RV = AV/E(B − V) = 3.1. It is best reproduced in the g′r′i′z′ bands by a Cardelli law with AV = 0.41 mag and RV = 5.0, which implies an average grain size larger than in the ISM. However, no value of RV is able to reproduce the extinction up to the NIR.
 |
Fig. 3. Extinction taken as the amplitude of the second dip (observed at JD = 2458585) as a function of the filter wavelength (dots). The full lines represent extinction laws at different values of RV = AV/E(B − V) according to Cardelli et al. (1989). The dotted black line is the model by Koutoulaki et al. (2019). The dashed line represents our two-component model (Eq. (1)). All curves are normalized to the observed extinction in the g′ band (λc = 4800 Å). |
A slope in the extinction law flatter than that of the ISM and sometimes a nearly gray extinction have been reported for AA Tau, the prototype of dippers, by Bouvier et al. (1999, 2003) and for the dips of LkCa 15 by Alencar et al. (2018). Koutoulaki et al. (2019) were able to reproduce the extinction curve observed during a dimming event of RW Aur observed with X-shooter, which is much flatter than the ISM, with a power-law distribution of the grain size from a minimum value amin = 0.1 μm to a maximum amax = 150 μm, including the scattering in the effective optical depth. Neglecting the scattering would require even larger grains. An ISM-type extinction (RV = 3.1) would instead be produced by much smaller grains (amax = 0.1 μm). In Fig. 3 we overplot the extinction model by Koutoulaki et al. (2019), scaled to the observed extinction in the g′ band. We note that this curve is flatter than our data, suggesting different conditions for the region that causes the dips in ISO-ChaI 52, as is also expected based on the much deeper dips of RW Aur (2−3 mag in the V band) compared to 0.3 mag dips in r′ for ISO-ChaI 52. Another dipper that displays an extinction effect similar to ISO-ChaI 52 is V354 Mon (Fonseca et al. 2014). Schneider et al. (2018) used X-shooter spectra of this star taken outside and within the dips to derive the properties of the obscuring dust in the disk warp. They showed that it is not possible to reproduce the entire dimmed spectrum by applying a single reddening law to the uneclipsed spectrum. The blue-visible part of the dimmed spectrum could be roughly reproduced by applying a Cardelli law with AV ≃ 1.2 mag and RV = 6.0 to the uneclipsed spectrum, but this left an IR flux excess, similar to what we find for ISO-ChaI 52. A more evolved model, which includes an upper disk layer with an ISM-type extinction and an opaque disk region producing a gray extinction, was able to reproduce their data. We applied a simple two-component model similar to that of Schneider et al. (2018) to our data. In this case, the extinction of the stellar light can be expressed as
where α and β are the fractions of the stellar disk that are occulted by the opaque-gray and thin region of the circumstellar disk, respectively, and τG the optical depth of the gray layer. The best-fitting model (dashed line in Fig. 3) has α = 0.38, β = 0.62, τG = 0.22 (AG ≃ 0.24 mag), and τλ = 5500 ≃ 0.51 (AV = 0.55 mag) with RV = 3.1. Although this is a simple schematic model, it tells us that the feature that occults the central star must contain both small-sized grains (a < 0.5 μm), producing an ISM-type extinction, and larger grains giving rise to a much flatter or gray extinction.
Dips in a weakly accreting object raise the question of what connects the accretion strength and the warp in YSO disks. Stauffer et al. (2015) have analyzed a specific category of dipper stars that share the late SpT and the short-duration (≃1 d) and shallow (0.1−0.4 mag) dips with ISO-ChaI 52. The authors explored alternative scenarios to warped inner disks to explain the origin of the dips, including the occultation of the star by spiral-arm overdensities in the inner disk caused by an embedded planet or by dust entrained into an accretion funnel. The latter model can also explain dips for low-inclination objects. Dippers with nearly face-on outer disks have been found before (e.g., Ansdell et al. 2016b; Scaringi et al. 2016). In particular, Ansdell et al. (2020) found the disk inclination distribution to be consistent with isotropic. The possible explanations they proposed include dust clouds driven by disk winds (which can determine dips in systems with inclinations as low as ∼30°), or misalignments between inner and outer disk (which might be caused by a substellar or planetary companion). Transits of cometary-mass objects have also been proposed for a few nonaccreting dippers (e.g., Scaringi et al. 2016; Ansdell et al. 2019). A dipping behavior may also be observed in objects seen at medium inclinations when the dipole magnetic field of the star exhibits a small tilt angle with respect to its rotation axis, which leads to the formation of accretion streams that extend high above the disk midplane (Bodman et al. 2017). In the following we consider the conditions under which accretion-driven structures, such as disk warps or funnels, might produce dips in ISO-ChaI 52.
Bessolaz et al. (2008) have studied the conditions for a steady accretion flow from a circumstellar disk in the presence of a dipolar stellar magnetic field. There are few measures of photospheric magnetic fields for low-mass (M* ≤ 0.5 M⊙) YSOs with typical values of B* ≈ 1 kG (e.g., Hill et al. 2019; Lavail et al. 2019), but fields of about 100 G and lower have also been observed (e.g., Donati et al. 2010; Morin et al. 2011). Based on Eq. (6) of Bessolaz et al. (2008) and adopting the stellar parameters in Table 1 and the upper limit Ṁacc ≤ 4.6 × 10−11 M⊙ yr−1 (Manara et al. 2019), we derive for ISO-ChaI 52 a disk truncation radius RT ≃ 25 R⊙ for a magnetic field B* = 1 kG. For comparison, the Keplerian corotation radius for Prot = 3.45 d, that is, the period we observe for the dips, is RC ≃ 5.6 R⊙, which would be 8.9 R⊙ when we adopt Prot = 6.9 d. The case of RT > RC corresponds to a propeller regime of star-disk interaction (Ustyugova et al. 2006), where stable funnel-flow accretion is inhibited. To have a steady accretion regime, the photospheric magnetic field should therefore be lower: B* ≤ 70 G for Prot = 3.45 d and B* ≤ 150 G if the period is twice as long. Another possible explanation is that the magnetic field is strong but we underestimate the mass accretion rate. A truncation radius RT ≤ 8.9 R⊙ with a field B* = 1 kG would require a mass accretion rate Ṁacc ≥ 3 × 10−9 M⊙ yr−1, which is about two orders of magnitude higher than the observed upper limit; a higher mass accretion rate is needed for RT ≤ 5.6 R⊙. Examples of YSOs have been reported that have apparently low or no accretion from optical tracers, but significant accretion as drawn from near-UV and far-UV observations (e.g., Alcalá et al. 2019). We note, however, that these objects are hotter than ISO-ChaI 52, which hampers the detection of Balmer continuum excess emission because the contrast with respect to the photospheric emission is low. If Ṁacc in ISO-ChaI 52 were this high, a far stronger UV excess and Balmer continuum than observed would have been detected.
To conclude, a low accretion rate coupled with a relatively weak surface magnetic field can probably give rise to disk warps or accretion structures that are able to produce dips in this low-mass YSO. This work shows that long-term simultaneous multiband photometry ranging from the optical to the NIR domain is effective for studying the circumstellar environment in YSOs.
Acknowledgments
We thank the anonymous referee for her/his useful comments and suggestions. We acknowledge the support from the Italian Ministero dell’Istruzione, Università e Ricerca (MIUR). This work has been partially supported by the project PRIN-INAF-MAIN-STREAM 2017 “Protoplanetary disks seen through the eyes of new-generation instruments”. CFM acknowledges an ESO fellowship. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 823823 (DUSTBUSTERS). This work was partly supported by the Deutsche Forschungs-Gemeinschaft (DFG, German Research Foundation) – Ref no. FOR 2634/1 TE 1024/1-1. LV acknowledges support by an appointment to the NASA Postdoctoral Program at the NASA Ames Research Center, administered by Universities Space Research Association under contract with NASA. GR acknowledges funding from the Dutch Research Council (NWO) with project number 016.Veni.192.233. This research made use of SIMBAD and VIZIER databases, operated at the CDS, Strasbourg, France.
References
- Alcalá, J. M., Spezzi, L., Chapman, N., et al. 2008, ApJ, 676, 427 [Google Scholar]
- Alcalá, J. M., Natta, A., Manara, C. F., et al. 2014, A&A, 561, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alcalá, J. M., Manara, C. F., Natta, A., et al. 2017, A&A, 600, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alcalá, J. M., Manara, C. F., France, K., et al. 2019, A&A, 629, 108 [Google Scholar]
- Alencar, S. H. P., Bouvier, J., Donati, J.-F., et al. 2018, A&A, 620, A195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allard, F., Homeier, D., & Freytag, B. 2012, ASP Conf. Ser., 448, 91 [Google Scholar]
- Ansdell, M., Williams, J. P., van der Marel, N., et al. 2016a, ApJ, 828, 46 [Google Scholar]
- Ansdell, M., Gaidos, E., Williams, J. P., et al. 2016b, MNRAS, 462, L101 [Google Scholar]
- Ansdell, M., Gaidos, E., Jacobs, T. L., et al. 2019, MNRAS, 483, 3579 [Google Scholar]
- Ansdell, M., Gaidos, E., Hedges, C., et al. 2020, MNRAS, 492, 572 [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bessolaz, N., Zanni, C., Ferreira, J., Keppens, R., & Bouvier, J. 2008, A&A, 478, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, L., Herald, J., Efremova, B., et al. 2011, Ap&SS, 335, 161 [Google Scholar]
- Bodman, E. H. L., Quillen, A. C., Ansdell, M., et al. 2017, MNRAS, 470, 202 [Google Scholar]
- Bouvier, J., Chelli, A., Allain, S., et al. 1999, A&A, 349, 619 [NASA ADS] [Google Scholar]
- Bouvier, J., Grankin, K. N., Alencar, S. H. P., et al. 2003, A&A, 409, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Cody, A. M., Hillenbrand, L. A., David, T. J., et al. 2017, ApJ, 836, 41 [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., Van Dyk, S., et al. 2003, 2MASS All-Sky Catalog of Point Sources, University of Massachusetts and Infrared Processing and Analysis Center (IPAC/California Institute of Technology) [Google Scholar]
- de Albuquerque, R. M. G., Gameiro, J. F., Alencar, S. H. P., et al. 2020, A&A, 636, A86 [CrossRef] [EDP Sciences] [Google Scholar]
- Donati, J.-F., Skelly, M. B., Bouvier, J., et al. 2010, MNRAS, 402, 1426 [Google Scholar]
- Doyle, J. G., Butler, C. J., Bryne, P. B., & van den Oord, G. H. J. 1988, A&A, 193, 229 [NASA ADS] [Google Scholar]
- Dunham, M. M., Allen, L. E., Evans, N. J., II, et al. 2015, ApJS, 220, 11 [Google Scholar]
- Dworetsky, M. M. 1983, MNRAS, 203, 917 [NASA ADS] [Google Scholar]
- Ercolano, B., & Pascucci, I. 2017, R. Soc. Open Sci., 4, 170114 [Google Scholar]
- Espaillat, C., Muzerolle, J., Hernández, J., et al. 2008, ApJ, 689, 145 [Google Scholar]
- Espaillat, C., Muzerolle, J., Najita, J., et al. 2014, Protostars and Planets VI (Tucson, AZ: University of Arizona Press), 497 [Google Scholar]
- Fedele, D., van den Ancher, M. E., Henning, Th., et al. 2010, A&A, 510, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fonseca, N. N. J., Alencar, S. H. P., Bouvier, J., Favata, F., & Flaccomio, E. 2014, A&A, 567, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frasca, A., Covino, E., Spezzi, L., et al. 2009, A&A, 508, 1313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frasca, A., Biazzo, K., Lanzafame, A. C., et al. 2015, A&A, 575, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frasca, A., Biazzo, K., Alcalá, J. M., et al. 2017, A&A, 602, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L., Megeath, S. T., Allen, L., et al. 2005, ApJ, 629, 881 [Google Scholar]
- Henden, A. A., Templeton, M., Terrell, D., et al. 2015, APASS: The AAVSO Photometric All-Sky Survey – Data Release 9, AAS Meeting S225, 336.16 [Google Scholar]
- Herbst, W., Bailer-Jones, C. A. L., Mundt, R., Meisenheimer, K., & Wackermann, R. 2002, A&A, 396, 513 [EDP Sciences] [Google Scholar]
- Herczeg, G. J., & Hillenbrand, L. A. 2014, ApJ, 786, 97 [Google Scholar]
- Hill, C. A., Folsom, C. P., Donati, J.-F., et al. 2019, MNRAS, 484, 5810 [Google Scholar]
- Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [Google Scholar]
- Kenyon, S. J., & Hartmann, L. 1987, ApJ, 323, 714 [Google Scholar]
- Koutoulaki, M., Facchini, S., Manara, C. F., et al. 2019, A&A, 625, A29 [EDP Sciences] [Google Scholar]
- Lada, C. J., Muench, A. A., Luhman, K. L., et al. 2006, AJ, 131, 1574 [Google Scholar]
- Lavail, A., Kochukhov, O., & Hussain, G. A. J. 2019, A&A, 630, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luhman, K. L., Stauffer, J. R., Muench, A. A., et al. 2003, ApJ, 593, 1093 [Google Scholar]
- Manara, C. F., Fedele, D., Herczeg, G., & Teixeira, P. 2016, A&A, 585, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manara, C. F., Testi, L., Herczeg, G. J., et al. 2017, A&A, 604, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manara, C. F., Mordasini, C., Testi, L., et al. 2019, A&A, 631, L2 [CrossRef] [EDP Sciences] [Google Scholar]
- McGinnis, P. T., Alencar, S. H. P., Guimarães, M. M., et al. 2015, A&A, 577, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morin, J., Dormy, E., Schrinner, M., & Donati, J.-F. 2011, MNRAS, 418, L133 [CrossRef] [Google Scholar]
- Merín, B., Jørgensen, J., Spezzi, L., et al. 2008, ApJS, 177, 551 [Google Scholar]
- Nguyen, D. C., Brandeker, A., van Kerkwijk, M. H., & Jayawardhana, R. 2012, ApJ, 745, 119 [Google Scholar]
- Nisini, B., Antoniucci, S., Alcalá, J. M., et al. 2018, A&A, 609, A87 [EDP Sciences] [Google Scholar]
- Pascucci, I., Testi, L., Herczeg, G. J., et al. 2016, ApJ, 831, 125 [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [Google Scholar]
- Ribas, A., Espaillat, C. C., Macias, E., et al. 2017, ApJ, 849, 63 [Google Scholar]
- Roberts, D. H., Lehar, J., & Dreher, J. W. 1987, AJ, 93, 968 [Google Scholar]
- Rodriguez, J. E., Ansdell, M., Oelkers, R. J., et al. 2017, ApJ, 848, 97 [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
- Scaringi, S., Manara, C. F., Barenfeld, S. A., et al. 2016, MNRAS, 463, 2265 [Google Scholar]
- Schneider, P. C., Manara, C. F., Facchini, S., et al. 2018, A&A, 614, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Stassun, K. G., Oelkers, R. J., Paegert, M., et al. 2019, AJ, 58, 138 [Google Scholar]
- Stauffer, J., Cody, A. M., McGinnis, P., et al. 2015, AJ, 149, 130 [Google Scholar]
- Stauffer, J., Collier Cameron, A., Jardine, M., et al. 2017, AJ, 153, 152 [Google Scholar]
- Stelzer, B., Marino, A., Micela, G., López-Santiago, J., & Liefke, C. 2013, MNRAS, 431, 2063 [Google Scholar]
- Testa, V., Antonelli, L., Di Paola, A., et al. 2004, SPIE, 5496, 729 [NASA ADS] [Google Scholar]
- Testi, L., Birnstiel, T., Ricci, L., et al. 2014, Protostars and Planets VI (Tucson, AZ: University of Arizona Press), 339 [Google Scholar]
- Thanathibodee, T., Calvet, N., Muzerolle, J., et al. 2019, ApJ, 884, 86 [Google Scholar]
- Ustyugova, G. V., Koldoba, A. V., Romanova, M. M., & Lovelace, R. V. E. 2006, ApJ, 646, 304 [Google Scholar]
- Venuti, L., Bouvier, J., Cody, A. M., et al. 2017, A&A, 599, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wahhaj, Z., Cieza, L., Koerner, D. W., et al. 2010, ApJ, 724, 835 [Google Scholar]
- Wolf, C., Onken, C. A., Luvaul, L. C., et al. 2018, PASA, 35, 10 [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
Appendix A: Photometric data reduction
For the ROSS2 camera, we have generated master flats using the twilight flat-fields taken during the observing run, which are available in the REM archive. The latter were used to correct for pixel-to-pixel sensitivity variations, as well as for the vignetting and illumination of the field of view. After subtraction of the dark-frame, each scientific image was divided by the proper master-flat, depending on the filter. The field of view, as observed in the i′ filter, along with the identification code for our target and the comparison stars reported in Table A.1, is displayed in Fig. A.1.
 |
Fig. A.1. Field of ISO-ChaI 52 as observed by ROSS2 camera with the i′ filter. The identification code (ID in Table A.1) is written next to the stars for which we extracted magnitudes. ID = 1 for ISO-ChaI 52. |
Literature data for some stars in the field of ISO-ChaI 52.
The pre-reduction of the REMIR images is automatically done by the AQuA pipeline (Testa et al. 2004) and the coadded and sky-subtracted frames, resulting from five individual ditherings, are made available to the observer. Aperture photometry for all the stars listed in Table A.1 was performed with DAOPHOT by using the IDL1 routine APER. The photometric errors based on the photon statistics in the NIR bands are typically in the range 0.008−0.018 mag for ISO-ChaI 52 ( ), with average values of 0.013, 0.008, and 0.015 mag in J, H, and K′, respectively. They range instead from 0.003 to 0.006 mag for a brighter star like ISO-ChaI 35 (
), with average values of 0.013, 0.008, and 0.015 mag in J, H, and K′, respectively. They range instead from 0.003 to 0.006 mag for a brighter star like ISO-ChaI 35 (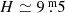 ). In the optical bands, the average photometric errors for ISO-ChaI 52 are 0.013, 0.008, 0.020, and 0.045 mag for z′, i′, r′, and g′, respectively.
). In the optical bands, the average photometric errors for ISO-ChaI 52 are 0.013, 0.008, 0.020, and 0.045 mag for z′, i′, r′, and g′, respectively.
As a result of the field rotation, the center of the field can vary in different pointings of the telescope by as much as a few arcminutes, so that only three stars (stars 1, 2, and 3) are included in all the useful images. We therefore chose star 2 = 2MASS J11042217−7741319, which is the brightest of these three stars and the closest to ISO-ChaI 52, as the comparison object for the purpose of differential photometry. This object is not reported in the literature as a Cha I member although its parallax π = 5.2009 mas is nearly the same as that of ISO-ChaI 52. For each band, we added the magnitude of star 2 listed in Table A.1 to obtain the magnitude of ISO-ChaI 52 and the other stars in the field. The other field stars, even though they have fewer data points, allowed us to verify any possible variability of star 2 and to evaluate the final data uncertainty as the rms of their magnitude differences. To this aim, we calculated the magnitude of star 4 = Glass L adopting star 5 = Glass M as comparison. These two stars are close to each other and are background stars that are unrelated to the Cha I cloud. The rms scatter of the photometry of Glass L throughout the observing season is 0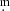 021, 0
021, 0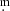 022, 0
022, 0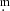 024, and 0
024, and 0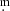 047 for the z′, i′, r′, and g′ band, respectively.
047 for the z′, i′, r′, and g′ band, respectively.
As an example we show in Fig. A.2 the light curves of ISO-ChaI 52, ISO-ChaI 35 (star 3) and Glass L (star 4). The points of ISO-ChaI 35 at JD ≃ 2458583.8, which are about 0.15 mag brighter than those taken 7 h before and 17 h later, are likely taken during a flare because a similar event is also observed in the g′ band as an enhancement of about 0.35 mag, but is not visible in the redder bands. When we consider the magnitude difference between stars 2 and 4, the rms increases slightly to just 0.03 mag and no clear periodicity appears in the data. This confirms that star 2 can be used as a comparison for ISO-ChaI 52.
 |
Fig. A.2. ROSS2 r′ light curve of ISO-ChaI 52 (top panel), ISO-ChaI 35 (middle panel), and Glass L (bottom panel). We have used 2MASS J11042217−7741319 (star 2) for the first two stars and Glass M (star 5) for the latter as comparison stars, adopting the magnitudes listed in Table A.1. The average magnitudes of the last two stars and their rms scatter are provided in the respective panels for the two data segments. |
Appendix B: ROTFIT and SED analysis
The code ROTFIT finds the best photospheric template spectrum (here: BT-Settl, Allard et al. 2012) that reproduces the target spectrum by minimizing the χ2 of the difference between the observed and synthetic spectra in specific spectral segments. The spectral intervals we selected for the analysis with ROTFIT were normalized to the local continuum and contain features that are sensitive to the effective temperature and/or surface gravity, such as the Na I doublet at λ ≈ 819 nm and the K I doublet at λ ≈ 766 − 770 nm (see Fig. B.1).
 |
Fig. B.1. Left panels: continuum-normalized VIS X-shooter spectrum of ISO-ChaI 52 in three regions (full black lines) with the best-fitting synthetic spectrum overplotted (dotted red lines). Right panels: χ2 contour maps in the Teff– log g plane. In each panel, the 1σ confidence level is denoted by the red contour. The best values and error bars on Teff and log g are also indicated. |
 |
Fig. B.2. ISO-ChaI 52 in the HR diagram. See Table 1 for the values of Teff and L* derived with the ROTFIT code. Isochrones and evolutionary tracks by Baraffe et al. (2015) are overplotted as dashed and solid lines; the labels represent their age and mass. |
The SED was built by complementing the g′r′i′z′JHK′ magnitudes observed with REM outside the dips with values from the literature. Notably, we added the Johnson B magnitude reported in the TIC (TESS input catalog, Stassun et al. 2019) and the GALEX-DR5 NUV flux of 4.28 μJy at 2316 Å (Bianchi et al. 2011) at shorter wavelengths. The MIR and FIR fluxes were retrieved from the WISE data release (Wright et al. 2010), from Spitzer IRAC and MIPS data (Dunham et al. 2015), and from Herschel/PACS 100 μm (Ribas et al. 2017). We also included the submillimeter flux at λ = 887 μm, Fν = 4.15 ± 0.16 mJy, reported by Pascucci et al. (2016), which is a disk-integrated value, as the disk is not resolved in the ALMA image (see, e.g., Figs. 3 and 4 in Pascucci et al. 2016). All these values are reported in Table B.1.
Data for the SED of ISO-ChaI 52.
The distance d = 193 ± 3 pc was calculated from the Gaia DR2 parallax of ISO ChaI 52 (π = 5.18 ± 0.07 mas) as d = 1000/π. This high parallax value allows us to neglect small corrections like those proposed by Lindegren et al. (2018) that would decrease the distance by only 1 pc, which is less than the distance error. In the fitting procedure, applied to the fluxes from B to J band, we fixed the distance and the effective temperature and let the stellar radius, R*, and the extinction, AV, vary until a minimum χ2 was reached. The key parameter that affects the results is the effective temperature. We therefore ran the code also with Teff fixed to the extreme values given by the Teff error of 70 K. We found AV = 0.43 ± 0.32 mag, which is lower than the value of 1.2 mag reported by Manara et al. (2016), who analyzed the full calibrated X-shooter spectrum and used real-star spectra of slighlty higher Teff as templates. We note that AV is very sensitive to the intrinsic shape of the flux distribution, that is, to Teff, while the stellar radius, R* = 1.14 ± 0.04 R⊙, is strongly dependent on the distance and on the observed flux near the maximum of the SED, where the extinction plays a minor role.
The stellar luminosity, calculated as 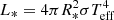 , is L* = 0.123 ± 0.011 L⊙, where the error takes into account the R* and Teff errors and their covariance. This value of L* is higher than the luminosity of 0.09 L⊙ reported by Manara et al. (2016), who adopted a distance d = 160 pc. However, the latter becomes 0.13 L⊙ with the Gaia distance d = 193 pc. This agrees well with our determination.
, is L* = 0.123 ± 0.011 L⊙, where the error takes into account the R* and Teff errors and their covariance. This value of L* is higher than the luminosity of 0.09 L⊙ reported by Manara et al. (2016), who adopted a distance d = 160 pc. However, the latter becomes 0.13 L⊙ with the Gaia distance d = 193 pc. This agrees well with our determination.
Appendix C: Additional plots
 |
Fig. C.1. Profiles of Balmer lines, Ca II K, and He I lines. In each plot, the horizontal dashed green line denotes the continuum level. |
 |
Fig. C.2. X-shooter spectrum of ISO-ChaI 52 in the region of Ca II IRT (solid black line) along with the inactive template (dotted red line). The difference between observed and template spectrum is shown in the bottom of the box, along with the residual emission in the line cores (hatched green areas). |
 |
Fig. C.3. Cleaned periodograms for the photometric data of ISO-ChaI 52 in the HJz′i′r′ bands (from top to bottom). The highest peak in each band corresponds to a period of about 3.45 days. |
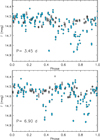 |
Fig. C.4. Light curve in the i′ band folded in phase with the period of 3.45 days (upper panel) and 6.9 days (lower panel). Filled dots refer to the data acquired before the end of May 2019 (JD < 2458630), and open dots are related to the second part of the data (August–October 2019). |
All Tables
All Figures
 |
Fig. 1. Spectral energy distribution of ISO-ChaI 52. Mid- and far-infrared fluxes are shown with different symbols, as indicated in the legend. The BT-Settl spectrum (Allard et al. 2012) that provides the best fit to the star photosphere is shown by a gray line. The two black bodies with T = 650 K and T = 100 K that fit the MIR and FIR disk emission are shown by the dotted red and dashed green lines, respectively. The continuous blue line displays the sum of the smoothed photospheric template and the two black bodies. |
| In the text | |
 |
Fig. 2. REM multiband optical/NIR light curves of ISO-ChaI 52 for the first 20 days of the campaign. The scales of the vertical axes have been chosen so as to keep the magnitude ranges constant to display the variation amplitudes more clearly. |
| In the text | |
 |
Fig. 3. Extinction taken as the amplitude of the second dip (observed at JD = 2458585) as a function of the filter wavelength (dots). The full lines represent extinction laws at different values of RV = AV/E(B − V) according to Cardelli et al. (1989). The dotted black line is the model by Koutoulaki et al. (2019). The dashed line represents our two-component model (Eq. (1)). All curves are normalized to the observed extinction in the g′ band (λc = 4800 Å). |
| In the text | |
 |
Fig. A.1. Field of ISO-ChaI 52 as observed by ROSS2 camera with the i′ filter. The identification code (ID in Table A.1) is written next to the stars for which we extracted magnitudes. ID = 1 for ISO-ChaI 52. |
| In the text | |
 |
Fig. A.2. ROSS2 r′ light curve of ISO-ChaI 52 (top panel), ISO-ChaI 35 (middle panel), and Glass L (bottom panel). We have used 2MASS J11042217−7741319 (star 2) for the first two stars and Glass M (star 5) for the latter as comparison stars, adopting the magnitudes listed in Table A.1. The average magnitudes of the last two stars and their rms scatter are provided in the respective panels for the two data segments. |
| In the text | |
 |
Fig. B.1. Left panels: continuum-normalized VIS X-shooter spectrum of ISO-ChaI 52 in three regions (full black lines) with the best-fitting synthetic spectrum overplotted (dotted red lines). Right panels: χ2 contour maps in the Teff– log g plane. In each panel, the 1σ confidence level is denoted by the red contour. The best values and error bars on Teff and log g are also indicated. |
| In the text | |
 |
Fig. B.2. ISO-ChaI 52 in the HR diagram. See Table 1 for the values of Teff and L* derived with the ROTFIT code. Isochrones and evolutionary tracks by Baraffe et al. (2015) are overplotted as dashed and solid lines; the labels represent their age and mass. |
| In the text | |
 |
Fig. C.1. Profiles of Balmer lines, Ca II K, and He I lines. In each plot, the horizontal dashed green line denotes the continuum level. |
| In the text | |
 |
Fig. C.2. X-shooter spectrum of ISO-ChaI 52 in the region of Ca II IRT (solid black line) along with the inactive template (dotted red line). The difference between observed and template spectrum is shown in the bottom of the box, along with the residual emission in the line cores (hatched green areas). |
| In the text | |
 |
Fig. C.3. Cleaned periodograms for the photometric data of ISO-ChaI 52 in the HJz′i′r′ bands (from top to bottom). The highest peak in each band corresponds to a period of about 3.45 days. |
| In the text | |
 |
Fig. C.4. Light curve in the i′ band folded in phase with the period of 3.45 days (upper panel) and 6.9 days (lower panel). Filled dots refer to the data acquired before the end of May 2019 (JD < 2458630), and open dots are related to the second part of the data (August–October 2019). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.