EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 634 (February 2020) A&A, 634 (2020) A58 Full HTML
Free Access
Issue
A&A
Volume 634, February 2020
Article Number A58
Number of page(s) 10
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201936599
Published online 07 February 2020

© ESO 2020

1. Introduction

Type I X-ray bursts are thermonuclear explosions on the surface layers of weakly magnetized neutron stars (NSs) accreting mass from a low-mass companion (see reviews in Lewin et al. 1993; Strohmayer & Bildsten 2006). The accreted hydrogen and/or helium accumulate steadily on top of the NS surface until they reach ignition temperatures and densities, and a thermonuclear runaway is triggered (e.g. Woosley & Taam 1976; Joss 1978; Wallace & Woosley 1981). The sudden release of nuclear binding energy rapidly heats the NS ocean and atmosphere, and within a few seconds increases the luminosity to its peak value. The burst X-ray spectra are usually fit with a blackbody (kT peaking at 2–3 keV; Swank et al. 1977) that cools down during the burst decay.

Accreting NSs are embedded in the accretion disc, and X-ray bursts are known to influence their surroundings in several ways. In the hot flow paradigm (e.g. Done et al. 2007) the inner accretion disc is believed to puff up in the hard state to a geometrically thick and optically thin hot flow. The hot inner flow Compton up-scatters low-energy photons emitted by the truncated thin disc, the heated NS surface, and possibly the hot flow itself, via synchrotron emission (see e.g. Poutanen & Veledina 2014). The Comptonization produces a power-law-like X-ray spectrum with a high-energy cutoff determined by the hot flow electron temperature. Compared to accreting black holes (BH), the NS surface provides an additional seed photon source for Comptonization. Consequently, as more photons can participate in the up-scattering process, the typical equilibrium electron temperatures of NS systems are much lower than in BH systems (Gilfanov 2010; Done et al. 2007). As the X-ray spectral slope is given by the product of the electron temperature and optical depth, NS systems also have softer X-ray spectra (Burke et al. 2017).

When an X-ray burst occurs in the NS envelope, the number of soft seed photons entering the hot flow increases dramatically. It is therefore expected that successive interactions with these photons will cool the coronal electrons further, resulting in lower electron temperatures and softer Comptonization spectra from the persistent level. The first hints of this effect were seen by the Rossi X-ray Timing Explorer RXTE/HEXTE in the burst light curve of Aql X-1 (Maccarone & Coppi 2003), and subsequently in the RXTE/PCA (Jahoda et al. 1996) light curves of several other bursters: IGR J17473–2721 (Chen et al. 2012), 4U 1636–536 (Ji et al. 2013), GS 1826–24 (Ji et al. 2014a, 2015), and KS 1731–60 and 4U 1705–44 (Ji et al. 2014b). By stacking more than a hundred bursts from the IBIS/ISGRI instrument on board the INTErnational Gamma-Ray Astrophysics Laboratory (INTEGRAL; Winkler et al. 2003), Kajava et al. (2017) detected a clear flux drop above 40 keV in the light curves and spectra of the 4U 1728–34 hard-state bursts. Spectral evidence of X-ray burst-induced coronal cooling was also found in 4U 1636–536 by Chen et al. (2018).

However, a few conflicting cases remain. The flux deficits detected in 4U 1728–34 by Kajava et al. (2017) were not found in the RXTE/PCA light curves by Ji et al. (2014b). Additionally, in ’t Zand et al. (1999) detected an increase of the hard X-ray flux (> 30 keV) in a BeppoSAX burst from GS 1826–24, while Ji et al. (2014a, 2015) detected significant hard X-ray deficits in the RXTE/PCA data of the same source. Degenaar et al. (2016) detected a possible softening of the persistent power-law emission, during a long burst of 4U 1608–52 seen by NuSTAR, but did not find hints of a hard flux decrement. These discrepancies raised the concern that some of the reported flux deficits may be of instrumental origin, such as dead-time effects in the PCA instrument, when the thousands of X-ray burst photons hit the instrument each second, and thus the few high-energy photons above 40 keV may go undetected.

Moreover, significant soft excesses with respect to the hard-state persistent emission were measured in the burst spectra of EXO 0748–676 (Asai & Dotani 2006), SAX J1808.4–3658 (in ’t Zand et al. 2013; Bult et al. 2019), and Aql X-1 (Keek et al. 2018). These excesses suggest a temporary enhancement of the accretion rate induced by the burst, probably via Poynting-Robsertson drag of the accretion flow (Ballantyne & Everett 2005). Enhancements of the persistent emission during X-ray bursts were also inferred by Worpel et al. (2013, 2015) fitting the RXTE/PCA spectra of a large sample of bursters, and by Keek et al. (2014) during a superburst of 4U 1636–536.

GS 1826–24, the “textbook burster” (Bildsten 2000), displays stable bursting behaviour and case 1 mixed H/He bursts (Fujimoto et al. 1981) with quasi-periodic recurrence over long periods of time. This regularity also lead to the nickname “clocked burster” (Ubertini et al. 1999). However, the burst waiting times have actually been observed to vary between roughly 5 and 3 h over the years, in response to variations in the mass accretion rate onto the NS (Cornelisse et al. 2003; Galloway et al. 2004, 2008; Thompson et al. 2008). The accretion rate onto GS 1826–24 is modest, about 13% of the Eddington rate (Chenevez et al. 2016). Thus, it remained in the hard spectral state (or island state; see Hasinger & van der Klis 1989) for years, displaying only brief excursions to a softer X-ray state in 2004 and 2014 during which the accretion rate did not show significant variations (see e.g. Rodi et al. 2016; Chenevez et al. 2016). Its hard-state spectrum can be nicely modelled with a hard (Γ ∼ 1.5) power law with a cutoff at about 50 keV (Cocchi et al. 2010), and a weak high-energy tail that dominates the emission above ∼150 keV (Rodi et al. 2016). In July 2015, GS 1826–24 transitioned to a soft state, where it has remained since then (Strohmayer et al. 2018), except for brief hard-state episodes (Ji et al. 2018). In February 2018, the first superburst from GS 1826–24 was detected by the Gas Slit Camera (GSC, Mihara et al. 2011) on board MAXI (Matsuoka et al. 2009).

As the bursts until 2015 did not reach the Eddington flux (in ’t Zand et al. 1999; Zamfir et al. 2012; Chenevez et al. 2016) the burst temperatures are low enough that their contribution above 30 keV is minimal. Therefore, the IBIS/ISGRI (Ubertini et al. 2003) instrument on board INTEGRAL being sensitive to photons only above ∼17 keV, it does not suffer from the dead-time effects that can severely affect the RXTE/PCA and NuSTAR instruments. In this paper, we present a combined analysis of all INTEGRAL-detected X-ray bursts until 2015, combined with soft-energy data in the same time frame as measured with the RGS on board XMM-Newton (den Herder et al. 2001; de Vries et al. 2014) to study at optimum sensitivity changes in the persistent spectrum during an X-ray burst. The resulting broad-band spectra provide unambiguous evidence of X-ray burst-induced coronal cooling of GS 1826–24. Simultaneously, we find a soft X-ray excess when fitting the burst spectrum using a simple blackbody model.

2. Observations and data reduction

2.1. INTEGRAL

We analysed all the available archival X-ray data of GS 1826–24 since the beginning of the INTEGRAL scientific operations in January 2003 until the spring of 2018, thus covering 15 years of data. We used data from the JEM-X and IBIS/ISGRI instruments. JEM-X, consisting of two identical units X1 and X2, is sensitive in the 3–35 keV range and provides an angular resolution of 3′, while IBIS/ISGRI is sensitive in the 15 keV to 10 MeV range, and provides an angular resolution of 12′. The data were reduced using standard procedures with the INTEGRAL Offline Science Analysis (OSA) provided by the ISDC1. The JEM-X data were analysed using osa v11.0, released in October 2018. The IBIS/ISGRI data were analysed using osa v10.2, released in December 2015. At the time of writing this paper, due to the lack of IBIS/ISGRI calibration files, the validity of OSA11.0 was limited to data later than revolution 1626. Early in the INTEGRAL mission, only one of the two JEM-X units was operated at a time. From revolution 976 onward, JEM-X operated with both units active. Since JEM-X1 was operational almost 14 years out of the 15 we analysed, we based our spectral analysis on the data from JEM-X1 and used JEM-X2 data only to fill the gaps in the long-term light curve, and derive burst recurrence times. The total JEM-X exposure accumulated in GS 1826–24 over this period is 2.17 Ms. However, we limited our spectral analysis to observations where the angular distance between the source location and spacecraft pointing was less than 3.5°, which rendered a total exposure of 954 ks. The selection criteria guaranteed that GS 1826–24 was always within the JEM-X half-response field of view (FOV) and IBIS/ISGRI fully coded FoV (FCFOV), so the measured fluxes and hardness ratios were not affected by flux reconstruction systematic effects towards the edges of the partially coded field of view (PCFOV) that may contaminate the light curves and images. However, to minimize the gaps between successive bursts and improve the calculation of the burst recurrence times, all the available data were used in the burst searching step, as the burst detection times are not sensitive to off-axis effects.

The X-ray bursts were identified on the 2 s binned JEM-X light curves of GS 1826–24 in the 3–25 keV band extracted at the science window level (typical duration from 30 min to 1 h). The burst identification was performed as follows: we computed the mean and standard deviation of the source count rate within each science window, and for each time bin compared the source count rate with these values. When the bin rate exceeded 6σ of the persistent level, we identified the potential onset of an X-ray burst. The peak of the burst and subsequent burst decay were identified in the system light curve to verify that the rise and decay profile were consistent with those of a Type I X-ray burst. The burst detection was further confirmed by extracting the image of the field within a time interval restricted to the burst duration in order to discard contamination to the source light curve by an event originated in another source in the FOV. The burst search resulted in a sample of 148 X-ray bursts2.

Because the hard-state burst peak fluxes and cooling timescales of GS 1826–24 are quite similar over long periods of time (years), we can stack the hard-state bursts together to obtain burst spectra of increased S/N. We identified the periods when GS 1826–24 was in the hard state and from these selected the intervals when GS 1826–24 displayed stable fluxes and bursting properties in order to minimize systematic effects due to poor characterization of the persistent emission or burst spectra. These criteria are fulfilled in the period MJD 52700–54800 (INTEGRAL revolutions 50 to 669). In this period, the IBIS/ISGRI (17–80 keV) flux was in the range 80–130 mCrab and the JEM-X flux (3–25 keV) was 20–60 mCrab. Good time intervals (GTIs) were created to extract and stack five separate spectra along the burst profile, in the intervals 2–12 s, 12–32 s, 32–62 s, 62–112 s, and 112–162 s from the burst onsets.

2.2. XMM-Newton

GS 1826–24 was observed by the Reflection Grating Spectrometer (RGS) on board XMM-Newton in three epochs: 2002, 2003, and 2012. Because the 2002 data set did not overlap with the INTEGRAL observations, we only analysed the 2003 and 2012 data sets. GS 1826–24 was observed during two consecutive revolutions between April 6 and 9, 2003 (revs. 609 and 610; 199 ks total exposure, Kong et al. 2007; in ’t Zand et al. 2013), and in four revolutions between September 12 and 26, 2012 (revs. 2237, 2238, 2243, 2244; 139 ks total exposure). Although quasi-simultaneous with the INTEGRAL data set, the 2012 data were finally dropped from this analysis, as described in Sect. 3.1. We used the XMM-SAS version 17.0.0 to process these data. The data were filtered for high background periods using the SAS task rgsfilter. The spectra and light curves were then generated using the SAS task rgsproc.

Light curves were extracted in the 0.5–2 keV range with a time resolution of 1 s. The burst searching routines described in Sect. 2.1 were also applied to the one-second binned RGS light curve. After filtering for high background, these resulted in the detection of 13 Type I X-ray bursts during the 2003 observations and 8 Type I X-ray bursts during the 2012 observations. The 2003 RGS data set partially overlaps with the INTEGRAL observations. Comparing the two data sets, we identify one X-ray burst detected simultaneously in the barycentric time corrected light curves of RGS (OBS ID 0150390301) and JEM-X (Pointing ID 005900400010.001). This burst was used to calibrate the simultaneity of the JEM-X and RGS burst timescales, and to verify that it was possible to build consistent RGS, JEM-X, and IBIS/ISGRI spectra stacked over the same integration periods along the burst profile (2–12 s, 12–32 s, 32–62 s, 62–112 s, and 112–162 s from the burst onsets).

3. Results

3.1. Persistent emission

The light curves of GS 1826–24 over the 15 years analysed in this work are shown in Fig. 1. We display the IBIS/ISGRI (17–80 keV) and JEM-X (3–25 keV) light curves constructed from the existing INTEGRAL data, complemented with the publicly available daily light curves of MAXI (2–20 keV; Matsuoka et al. 2009) and Swift/BAT (15–50 keV; Krimm et al. 2013). Burst recurrence times derived from this analysis are also shown for reference.

thumbnail Fig. 1.

Light curves of GS 1826–24 during the period analysed in this work. Panel a: Swift/BAT light curve in the 15–50 keV energy range. Panel b: IBIS/ISGRI light curve in the 17–83 keV energy range. Shown in red are the hard-state periods (MJD 52700–54800, MJD 54800–56400), and in light blue and grey, respectively, the dim-hard (MJD 54800–54800) and soft-state periods (MJD 56400 onward). The small vertical lines on top of the light curve indicate the times of detection of Type I X-ray bursts by JEM-X. To build a homogeneous sample, and avoid the systematics effects caused by variations of the persistent emission, burst stacking was performed using the hard-state data from the period MJD 52700–54800. Panel c: JEM-X light curve in the 3–25 keV energy range. Panel d: MAXI light curve in the 2–20 keV energy range. Panel e: recurrence times of the Type I X-ray bursts found in this work. Shown in black are the recurrence times measured directly (see examples in Fig. 2) and in grey the derived recurrence times (as described in the text). The red triangles correspond to the times of detection of the four groups of bursts displayed in Fig. 2.

GS 1826–24 remained persistently in the hard state from its discovery in 1988 until 2015, with bolometric flux in the range 1.8–3.4 × 10−9 erg cm−2 s−1 (Thompson et al. 2008). In 2015 it transited to the soft state, except for brief excursions to the hard state (Ji et al. 2018). Inspecting the IBIS/ISGRI and JEMX light curves, we identify the epochs when GS 1826–24 was detected in the hard state (MJD 52700–57200) and soft state (57200 onward). However, despite the expected stable properties during the hard state, we note a period of reduced (∼80%) X-ray emission in the IBIS/ISGRI and JEM-X light curves (MJD 54800–56400; blue points in Fig. 1b). Because the X-ray fluxes are not as hard in this period compared to the hard state, hereafter we refer to it as the dim hard state.

To prevent variations in the source persistent emission from resulting in systematic effects when stacking the burst spectra, we restricted the analysis of the hard-state burst spectra to the period MJD 52700–54800. Although comparable IBIS/ISGRI fluxes were also measured in the period MJD 56400–57200, the JEM-X flux gradually increased during that epoch (see Fig. 1c), which resulted in artefacts in the derived spectrum. Therefore, these data were not used to build the hard-state spectrum. The hard-state persistent emission spectra were properly fit with a single cutoff power-law model, modified by the interstellar absorption, which uses abundances from Wilms et al. (2000). When fitting the hard-state XMM-Newton/RGS spectrum with high S/N and resolution, the interstellar absorption edges were not clearly described, as detailed in Pinto et al. (2010). Rather than performing a detailed modelling of the absorption by the interstellar medium (ISM), as in Pinto et al. (2010), we instead binned the RGS data by a factor of three and added 3% systematic errors to all the RGS energy bins. Moreover, in the spectral modelling we also added an additional edge near the neon K edge (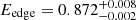 keV, τ = 0.111 ± 0.007), which was needed for a good fit to the data. 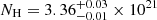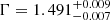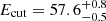The best fitting parameters for the hard-state spectra were cm−2, , keV, 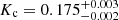(χ2/d.o.f. = 358.8/449), in agreement with Cocchi et al. (2010) and Rodi et al. (2016). Our data do not require an additional Comptonization component, as used by e.g. Rodi et al. (2016), when extending the spectral fits to harder energies (370 keV). We also do not find a significant contribution from the accretion disc in soft X-rays, as claimed by Thompson et al. (2008) and Ono et al. (2016). We also tested the Comptonization models NTHCOMP (Zdziarski et al. 1996; Zycki et al. 1999) and COMPPS (Poutanen & Svensson 1996) available in XSPEC, but these resulted in poorer fits and wavy residuals in the IBIS/ISGRI band and therefore were not considered further.

In the dim hard state the IBIS/ISGRI and JEM-X light curves both showed significant flux variations over time. The combination of these averaged spectra with the September 2012 RGS spectrum results in wavy residuals (unless adding unreasonable model components), likely because at the epoch of the RGS observations the spectra were somewhat harder than the average during 2009–2013 (see Fig. 1). To compare the burst stacked spectra with the persistent emission, we need to average the persistent emission using all the data where we detect bursts. Fitting the average dim-hard-state spectrum, using only the INTEGRAL data we derive the following parameters Γ = 1.67 ± 0.03 and Ecut = 85 ± 6, (χ2/d.o.f. = 29.6/24). The average dim-hard-state burst profiles resemble the hard-state ones (see e.g. the light curve shapes in Fig. 3) and after stacking the dim-hard-state burst spectra, we found qualitatively similar results to those obtained for the hard state (detailed below), but with larger errors, as the stacked dim-hard-state burst spectra are noisier. This is because there are fewer dim-hard-state bursts to stack and the flux is lower than in the hard state. As our main aim is to characterize the burst-induced changes in the Comptonized component, and these are unambiguously determined using the hard-state data set, we concentrate hereafter on the analysis of the influence of the hard-state bursts on the hard-state persistent emission spectra.

3.2. Bursting behaviour

Different bursting properties were observed in the hard, dim hard, and soft states, for which the total number of bursts detected by JEM-X were 90, 49, and 9, respectively. Burst waiting times were computed whenever possible using the JEM-X and RGS data sets. The derived values are displayed in Fig. 1e. In some cases, the source was continuously in the JEM-X FOV for several hours (see Fig. 2), and the burst recurrence times could be directly measured from the data (black points in Fig. 1e). However, gaps are frequent in the JEM-X light curves of GS 1826–24 due to the INTEGRAL dithering strategy and consecutive bursts can be missed (as happens in the two lower panels of Fig. 2). This would result in measured burst recurrence times which are a multiple of the actual values. In such cases we estimated the burst recurrence times by correcting the measured waiting times by the duration of the gaps in the JEM-X light curves (grey points in Fig. 1e).

thumbnail Fig. 2.

Detailed view of four trains of bursts. Top panel: RGS light curve of obs ID 01050390301. The time resolution is 5 s (0.5–2 keV energy range). The other panels provide JEM-X light curves built in the 3–25 keV energy range, with a time resolution of 5 s. For reference, the time of occurrence of these trains of bursts are marked in Fig. 1e. The average recurrence times per panel are (from top to bottom): 3.23 ± 0.05, 3.39 ± 0.05 h, 5.11 ± 0.07 h, and 3.86 ± 0.06 h.

The system consistently displayed quasi-periodic (clocked) burst recurrence times in the hard state (MJD 52700–54800), i.e. over a period of 5 years, when the soft and hard X-ray fluxes displayed roughly constant values. We measure burst waiting times between 3.13 and 3.76 h, consistent with measurements by Galloway et al. (2008) around this period, but significantly shorter than the average burst recurrence time observed between 1996 and 1998 (5.76 h, Ubertini et al. 1999; Galloway et al. 2008), when the system displayed persistent hard-state bolometric fluxes in the range 1.9–2.2 × 10−9 erg cm−2 s−1 (Ubertini et al. 1999; Cocchi et al. 2010), 40–50% lower than the hard-state fluxes we observed (3.8 × 10−9 erg cm−2 s−1).

Contrary to the stable burst waiting times observed during the hard state, the burst recurrence times decreased monotonically from 5.11 to 3.02 h during the dim hard state, while the soft X-ray emission increased (see Fig. 1). Despite the overall decreasing trend, the clocked behaviour still prevailed when looking at the light curves on short timescales (hours; see Fig. 2). The detection of the decreasing burst waiting time happened after a long gap in the JEM-X light curve (between MJD 54300 and 55500), so we could not observe the transition from the quasi-stable bursting regime to the decreasing burst recurrence time regime. The decrease in burst waiting time continued even further during the soft state, when recurrence times of 1.62 h were measured.

We also built the average JEM-X burst profile in the hard, dim hard, and soft states (3–25 keV; see Fig. 3). The burst profiles in the hard and dim hard states were very similar, although with slightly different peak count rates: (130 ± 3 counts s−1 in the hard state and 119 ± 4 count s−1 in the dim hard state)3. Long tails extending up to 100 s after the burst peak were observed in the hard and dim hard average burst profiles. The burst profile changed dramatically in the soft state, when peak count rates of 159 ± 3 counts s−1 were observed, while the burst duration decreased substantially (to ∼15 s). Chenevez et al. (2016) found that most of the soft state bursts of GS 1826–24 reached the Eddington luminosity. If this was also the case for the JEM-X soft state bursts averaged here, we find that the hard and dim hard average bursts would reach peak luminosities of 74% and 81% LEdd, respectively by comparing their average burst peak count rates with soft state average count rate.

thumbnail Fig. 3.

Comparison of the JEM-X (3−25 keV) average burst profiles detected during the three spectral states described in Sect. 3: hard, dim hard, and soft.

We do not observe in our data the long (∼5000 s) X-ray tails detected by in’t Zand et al. (2009) in the GS 1826–24 burst profile light curves, probably due to a poorer JEM-X sensitivity compared to RXTE/PCA. We also note that the typical duration of an INTEGRAL pointing is 1800–3600 s.

3.3. Persistent emission changes during hard-state bursts

We display in Fig. 4 the average burst profiles of GS 1826–24 in the hard state (MJD 52700 to 54800) in four energy bands. The INTEGRAL burst profiles were built averaging the light curves of 48 X-ray bursts, in the JEM-X 3–20 keV energy range (2 s binning) and in the IBIS/ISGRI 18–35 and 35–70 keV energy range (4 s binning). The RGS profile was built averaging the light curves of the 13 bursts detected in the interval MJD 52736–52739.

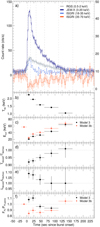thumbnail Fig. 4.

Panel a: average burst profile in four energy bands. The RGS, JEM-X, and IBIS/ISGRI (18–35 keV) light curves refer to the left vertical axis. The IBIS/ISGRI (35–70 keV) light curve refers to the right vertical axes. The profiles were built as described in Sect. 2. The dashed vertical lines indicate the intervals over which the spectra displayed in Fig. 5 were stacked. Panels b and c: evolution of the burst temperature and cutoff energy derived from the fits to the stacked burst spectra, using Model 3 and 3b (free persistent emission parameters). Panels d and e: comparison of the burst temperatures and fluxes derived using the standard fitting procedure (fixed persistent emission parameters: Model 1) with the results derived from Model 3. A dotted line is drawn at the position that equals both values. Panel f: comparison of the power-law flux derived using Models 3 and 3b with the non-bursting persistent emission flux.

The JEM-X 3–20 keV light curve displays the characteristic burst profile of GS 1826–24 in the hard state, with 8 s rise time and a long decay (e-folding decay time was 19.6 s). The burst emission is still detectable in the IBIS/ISGRI light curve in the 18–35 keV range. However, in the 35–70 keV energy range, we observe a clear decrement in the emission of ∼80% with respect to the pre- and post-burst values.

We selected five intervals along the average burst profile (shown in Fig. 4a) and for each hard-state burst we built the corresponding GTI files. The individual burst spectra do not provide the necessary signal-to-noise ratio to perform spectral fits, but when stacking the spectra from the individual bursts we can build spectra that extend up to ∼60 keV. We show in Fig. 5 the persistent spectrum (panel a) and five spectra along the burst profile, spanning times between 2–12 s (panel b), 12–32 s (panel c), 32–62 s (panel d), 62–112 s (panel e), and 112–162 s (panel f) from the burst onsets. During the burst we observe a clear hard X-ray decrement, consistent with the drop observed in the burst average light curves. To account for this, we fitted the stacked burst spectra using five different models. The best fitting parameters are collected in Table 1. Model 1 (where the burst spectrum is fitted with a blackbody model, assuming that the persistent emission spectrum does not change during the burst) corresponds to the standard burst fitting technique (e.g. Kuulkers et al. 2002; Galloway et al. 2008). This model can be rejected with high confidence during the burst peak and decay onset (first two intervals between 2 and 32 s) because it strongly overpredicts the hard X-ray flux and underpredicts the soft X-ray flux, resulting in a soft X-ray excess below ∼2 keV. Model 2 (where we fit the burst spectrum using a blackbody and allow the persistent emission to vary in normalization but not in shape, as in Worpel et al. 2013, 2015) improves the fits significantly, but also can be rejected with high confidence in the 2–32 s intervals because it cannot simultaneously fit the observed hard X-ray deficit and the soft X-ray excess. Using Model 2 we derive an increase in the power-law normalization of about ≈1.3. This corresponds to the fa-parameter in Worpel et al. (2013, 2015). Model 3 (where we fit the burst spectrum using a blackbody component and allow the power-law normalization and cutoff energy to vary) is the best fitting model of the three blackbody cases considered as it allows us to fit simultaneously the observed excess at soft X-rays and the decrement at hard X-rays. For example, during the burst peak (2–12 s interval) we obtain a significant improvement of the fit (Δχ2 = 64.7) for two extra degrees of freedom in the model. We also tried to fit the persistent emission leaving the power-law index as a free parameter, but our fits failed to constrain all the parameters simultaneously.

thumbnail Fig. 5.

Panel a: average hard-state persistent emission spectrum. Shown are the RGS, JEM-X, and ISGRI spectra (in blue, orange, and red, respectively). Panels b–f: average hard-state burst spectra stacked over the five time intervals shown in Fig. 4. The spectral parameters derived from the fits to these spectra are provided in Table 1. The black continuous line shows the resulting spectra (burst+persistent emission) when fitting the data using Model 3, where the CUTOFFPL normalization and cutoff energy during the burst are treated as free parameters (short-dashed line). The dot-dashed line shows the corresponding blackbody component. Highlighted in the data–model panels (in cyan, brown, and pink) are the residuals in the case where the CUTOFFPL component during the burst had been fixed to the best fitting persistent emission (Model 1, long-dashed line). The dotted line shows the corresponding blackbody component.

Table 1.

Best fitting parameters for the burst spectra in the five intervals shown in Fig. 4.

When fitting the burst spectrum with Model 3, we observe an evolution of the cutoff energy during the burst. The cutoff energy drops from the persistent value of 57.6 keV down to 21 keV during the burst peak (2–12 s interval), and then gradually increases to being consistent with the persistent value during the 112–162 s interval (see Table 1, Fig. 4b). Additionally, we observe that the blackbody parameters derived using Model 3 are significantly different from those derived applying the standard burst analysis (Model 1). The blackbody temperatures derived from Model 3 are systematically higher, and at the same time the blackbody luminosity is lower in Model 3 than in Model 1 (see Figs. 4d and e). The standard burst analysis (Model 1) overpredicts the blackbody luminosity in the 2–12 s interval by 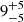%, while in the 32–62 s interval onward, the two methods give similar luminosities (see Fig. 4e).

The Model 3 results suggest that the observed soft X-ray excess could result from the softening of the Comptonized component. However, the soft excess can also be due to inaccurate modelling of the burst spectrum. Theoretical NS atmosphere models show deviations (excesses) of the burst spectra from blackbody shapes, below ∼3 keV (Suleimanov et al. 2011, 2012, 2018). Therefore, we replaced the blackbody component in our Model 1 and Model 3 by the BURSTATMO model, based on the NS atmosphere modelling of Suleimanov et al. (2011, 2012) and fitted again the burst spectra. The BURSTATMO model, available in XSPEC, has five parameters: NS radius (RNS), luminosity expressed as the ratio to the Eddington luminosity (L/LEdd), distance (d), logarithm of gravity (log g), and chemical composition. The BURSTATMO normalization KBURSTATMO is related to the anisotropy of the NS emitting region and other geometrical effects and should be close to unity. We assumed a low metallicity atmosphere (Z = 0.01 × Z⊙), RNS = 10.88 km, log g = 14.3 (which together give a NS mass of MNS = 1.4 M⊙), and d = 5.7 kpc (Chenevez et al. 2016).

The Model 1 fits are improved significantly when we replace the blackbody component with BURSTATMO (Model 1b; see Table 1). In the first three intervals with the highest burst fluxes (2–12, 12–32, and 32–62 s) the BURSTATMO model results in Δχ2 = 65.0, 79.3, 25.5, respectively, for Model 1 for the same number of d.o.f.; however, Model 1b still reproduces the observed hard X-ray flux decrement. The spectral fits are improved further by letting the parameters of the cutoff power-law component vary (Model 3b). When fitting the spectra with Model 3b, the cutoff energy evolves during the burst as observed in Model 3, even though the best fitting values are slightly higher in Model 3b (see Fig. 4c). The BURSTATMO model normalization, KBURSTATMO, is at a constant value for the first 62 s (approximately 0.69 or 0.64 for Model 1b and 3b, respectively), while later on the normalization drops. However, KBURSTATMO depends on the assumed distance, and for d = 7.2 kpc, KBURSTATMO tends to unity.

In Table 1 we also show the cutoff power-law model bolometric fluxes (Fper) during the bursts, computed using the CFLUX model in the 0.01–1000 keV range for Models 3 and 3b (see also Fig. 4e). We note how the cutoff power-law fluxes are practically constant at the same level as outside the bursts, with Fper = (3.80 ± 0.02)×10−9 erg cm−2 s−1 (largest deviations are at the 15% level, with 3σ from the persistent value), even though the best fitting cutoff power-law parameters and in particular the normalization can vary by up to 80%. Excesses of ∼10% in the power-law flux with respect to the flux outside the burst are observed during the burst peak if the burst spectra are measured using a blackbody model, while a flux deficit is observed during the burst peak if we fit the burst spectrum using the BURSTATMO model.

We note that the biggest dissimilarities between BURSTATMO and the standard blackbody model appear at low energies (below ∼2 keV) where the BURSTATMO model predicts an excess emission with respect to the standard blackbody. Modelling our burst spectra with the blackbody model results in a soft excess, which is fitted by an ∼80% increase in the power-law normalization (see Kpl values in Table 1). In contrast, the BURSTATMO model naturally fits the excess, and therefore the power-law component shows a more moderate normalization increase (∼30%). Given that the cutoff energy is very similar in the two models, the hard X-ray photon decrement caused by the decrease in Ecut, together with the different normalization increase in the BURSTATMO and blackbody models, results in the observed differences in the power-law flux.

We also note that the burst luminosity derived with the BURSTATMO model for the 2–12 s interval is 76% of LEdd, very close to the estimate derived from the burst profile comparison in Sect. 3.2, thus supporting the validity of the model.

4. Discussion

The average hard-state burst profiles in four energy bands, selected in the range 0.5–70 keV (see Fig. 4), nicely illustrate the burst-induced coronal cooling effect. While the burst light curves in the 0.5–20 keV energy range (RGS and JEM-X) display the characteristic burst profile (fast rise and exponential decay), and the residual burst emission still contributes to the IBIS/ISGRI 18–35 keV light curve, in the hardest band analysed here (35–70 keV) we observe an abrupt decrement of the hard X-ray emission simultaneous with the burst peak in soft X-rays. The hard X-ray decrement is followed by a gradual rise to pre-burst values simultaneously with the emission decay in the softer bands. The observed depletion of hard X-ray photons is consistent with previous results by Ji et al. (2014a, 2015), who detected significant hard X-ray deficits in the RXTE/PCA light curves of GS 1826–24. Our work thus confirms that the results by these authors are not of instrumental origin in the RXTE/PCA. By stacking the burst spectra along the burst profile we were able to perform time-resolved spectroscopy in the 0.7–60 keV energy range (see Table 1, Fig. 5). The extended energy range, compared to previous works (e.g. Ubertini et al. 1999; Cornelisse et al. 2003; Galloway et al. 2008), allows the simultaneous observation of the burst and persistent emission, and enables the unambiguous characterization of the burst and persistent emission spectral parameters. The resulting spectra confirm the decrement observed in the system 35–70 keV light curve. Simulations of the burst-induced cooling of the corona by Degenaar et al. (2018) based on the EQPAIR model of Coppi (1992) show a gradual electron cooling in response to the burst increasing luminosity, until eventually the hard X-ray emission is suppressed. Our observed decrease in the cutoff energy from about 60 keV down to 21 keV during the burst peak, and the gradual return of the cutoff energy back to its original value in the burst tail resemble the results of these simulations above ∼2 keV (see Fig. 10 in Degenaar et al. 2018). Moreover, we observe that the decrement in hard X-rays is accompanied by a soft X-ray excess (below 2 keV) not directly evident in the burst light curve alone. Enhancements of the persistent emission (below 3 keV) during X-ray bursts were previously observed in EXO 0748–676 (Asai & Dotani 2006), SAX J1808.4–3658 (in ’t Zand et al. 2013) and Aql X-1 (Keek et al. 2018). GS 1826–24 is the first case where both a hard (> 30 keV) flux decrement and an enhancement of the soft X-ray flux are observed simultaneously.

Our spectral analysis does not agree with the traditional assumption that the persistent, Comptonized, emission does not vary during an X-ray burst (van Paradijs & Lewin 1986; Lewin 1993; Kuulkers et al. 2002; Galloway et al. 2008; Model 1 in Table 1). It also shows that the assumption that the spectral shape of the persistent emission is constant during an X-ray burst and only its normalization varies (Worpel et al. 2013, 2015; Model 2 in Table 1) does not provide a proper fit to the data when a broader energy range is used.

The best fits are actually provided by a model where both the persistent emission cutoff energy and normalization are allowed to vary freely (Model 3 and 3b in Table 1). In this case, even if we saw a 30–80% increase of the persistent emission normalization with respect to the pre-burst values (Model 3 and 3b), we actually only find a modest 10% variation of the persistent emission flux, which suggests that in GS 1826–24 the burst does not substantially influence the mass accretion rate. When comparing models 1 to 1b, it is remarkable how much better the NS atmosphere model fits the soft X-ray data compared to the simple blackbody model. This suggests that in GS 1826–24 the soft X-ray excess is not related to the persistent spectrum changes, as in Model 1 the persistent emission is fixed to the pre-burst value. Moreover, when replacing the blackbody component with the atmosphere model, the persistent flux in fact seems to decrease with respect to pre-burst values.

Using NICER observations, with similar soft X-ray coverage, of an Aql X–1 hard-state non-photospheric radius expansion (PRE) burst, Keek et al. (2018) found an enhancement of the persistent emission a factor of 2.5 times the pre-burst values. It is possible that this result is in part due the lack of hard X-ray coverage of this burst, which allowed them to assume that the persistent emission shape did not change during the burst. However, the derived persistent emission enhancement might also be less significant if the burst spectrum was fitted with an atmosphere model instead of a blackbody.

Additionally, our results have important implications due to the textbook reputation of GS 1826–24 (Bildsten 2000). It is the target for making model–theory comparisons, and the inferred variations in the persistent emission during Type I X-ray bursts, previously not accounted for, now suggest that the results of these model comparisons may not be accurate. Our broad-band spectral fits have revealed biases in the determination of the average GS 1826–24 burst spectral parameters (Lbb, Tbb) when the spectra are fitted following the standard fitting approach (Model 1 in Table 1). The bias is more dramatic during the burst peak (Lbb is overestimated by 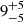% and Tbb is underestimated by 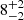%). The discrepancies decrease as the burst decays, being negligible 62 seconds after the burst peak (see Fig. 4). In other words, additionally, the burst-disc-corona interaction generates a much stronger luminosity bias in the peak than in the tail, distorting the burst profile from theoretical expectations.

For example, the burst light curves of GS 1826–24 have been used in the multi-zone KEPLER light curve model (Weaver et al. 1978; Woosley et al. 2004; Heger et al. 2007) to calibrate the dependences between the accretion rate and burst recurrence times, burst energies, and α-values4. The model calibrationstrongly depends on the burst peak luminosities (where we observe larger luminosity biases) as the model parameters are usually selected to bring the observed and predicted peak luminosities into agreement. Actually, large discrepancies are detected between the predicted and observed light curves during the burst rise and tails (> 30 s) when only the peak fluxes are used to normalize the model (Heger et al. 2007; Zamfir et al. 2012), while the discrepancies are smaller if the entire burst light curve is fitted (Zamfir et al. 2012). GS 1826–24 was also used by Cyburt et al. (2016) and Meisel et al. (2019) as a calibration target to study the influence of key nuclear reaction rates on the observed burst profiles derived from the codes KEPLER (Heger et al. 2007) and MESA (Paxton et al. 2011, 2013, 2015, 2018). The burst peak luminosity bias derived in our work is comparable to increasing the key 15O(α, γ)19Ne alpha capture rate (responsible for the rp-process burning breakout from the hot CNO cycle) by a factor of 100 (see Cyburt et al. 2016, their Fig. 6).

The burst peak luminosity bias has additional implications on the NS mass-radius constraints, used in the determination of the equation of state (EOS) of supranuclear matter (Lattimer & Prakash 2007). Neutron star mass and radius are usually constrained from PRE bursts (Lewin et al. 1993). It is assumed that in PRE bursts the luminosity at the touchdown point is equal to the Eddington luminosity. As the normalization of the burst spectrum is related to the emitting area, observations of PRE bursts can be used to put constraints on the NS mass-radius relation. If the flux of the PRE bursts (much brighter than the sub-Eddington GS 1826–24 bursts analysed here) is also overestimated, due to the observed luminosity bias, the NS mass-radius constraints provided by this analysis will be inaccurate.

Alternative NS mass-radius constraints can be derived (for PRE and non-PRE bursts) by comparing the cooling tracks of Type I X-ray bursts with theoretical atmosphere models (Suleimanov & Poutanen 2006; Zamfir et al. 2012; Poutanen et al. 2014; Kajava et al. 2014; Nättilä et al. 2016, 2017). The theoretical atmosphere models in general agree closely with the data, but some residuals are detected in these fits, especially when the flux drops below a certain value (Zamfir et al. 2012; Nättilä et al. 2017; Suleimanov et al. 2017). Although heating of the NS atmosphere by the accreted material could be the reason for these discrepancies (Suleimanov et al. 2018), an additional explanation for these residuals could be the incorrect modelling of the system persistent emission, which is assumed invariant during the burst, and is tied to its pre-burst values. We note that Nättilä et al. (2017) report flux relative errors of 1–5% in the fits to 4U 1702–429 hard-state burst spectra, consistent with the flux biases determined in our work.

On the other hand, the burst-induced persistent emission variation should be proportional to the persistent emission level, which is set by the mass accretion rate. In GS 1826–24 the mass accretion rate (Ṁ ∼ 0.13 ṀEdd) is substantially higher than that of 4U 1702–429 and other atoll sources showing hard-state PRE bursts (Ṁ ∼ 0.01 ṀEdd), and therefore the burst flux bias may not be as significant in these low mass accretion rate sources as it is in GS 1826–24.

5. Summary and conclusions

We have studied the influence of the X-ray burst photons on the hard-state persistent emission of GS 1826–24 using data collected over the period 2003–2008. Time-resolved spectral fits to the burst and persistent emission show an overall change in the persistent emission spectrum during the burst peak, characterized by a simultaneous hard X-ray (> 30 keV) decrement during the burst peak, and an enhancement of the soft X-rays (< 2 keV) with respect to a simple blackbody model. The hard X-ray decrement can be explained by burst-induced cooling of the corona, which does explain the soft X-ray excess. Instead, the soft X-ray excess largely disappears if the burst spectra are fitted with a NS atmosphere model, rather than a pure blackbody. Other mechanisms (such as a temporary enhancement of the mass accretion rate onto the NS due to the partial collapse of the hot flow, or Poynting-Robertson drag of the accretion flow by the burst X-ray photons) are not needed to explain the observed soft X-ray excess as we do not find significant changes in the persistent emission bolometric flux during the bursts.

Our results show that if the burst-induced spectral changes are not taken into account when fitting the burst spectra, the burst luminosity can be overestimated by up to 9% at the peak of the GS 1826–24 bursts, while at around 60 s after the peak the luminosity bias becomes negligible. That means that the interaction between the burst and the accretion flow causes a stronger luminosity bias in the peak than in the tail; therefore, it additionally distorts the burst bolometric light curve, which is used to calibrate theoretical burst models. The accurate determination of the persistent emission for the existing burst data sets is not trivial, as most of them came from instruments operating in a reduced energy range compared to the one used in this work. It is thus not obvious how to correct these bursts for the burst peak luminosity bias found in this work.

1

ISDC Data Centre for Astrophysics, http://www.isdc.unige.ch/

2

Part of this work is also fed into a larger type I X-ray burst database, MINBAR; see http://burst.sci.monash.edu/minbar

3

For reference, 1 Crab = 250 count s−1 in the 3–25 keV energy range.

4

α is defined as the ratio of the time-averaged accretion luminosity to the time-averaged burst luminosity. It can be used to infer the composition of the burning fuel (Bildsten 2000).

Acknowledgments

The authors would like to thank J. J. M. in ’t Zand for useful discussions and valuable comments during the elaboration of this work. We also thank the anonymous referee for the suggestions that helped to improve this manuscript. JJEK acknowledges support from the Academy of Finland grant 295114. JP and VFS were supported by the grant 14.W03.31.0021 of the Ministry of Science and Higher Education of the Russian Federation. The work of V. S. was supported by Deutsche Forschungsgemeinschaft DFG, (grant WE 1312/51-1). Based on observations with INTEGRAL, an ESA project with instruments and science data centre funded by ESA member states (especially the PI countries: Denmark, France, Germany, Italy, Switzerland, Spain) and with the participation of Russia and the USA. Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA. This research has made use of the MAXI data provided by RIKEN, JAXA and the MAXI team.

References

  1. Asai, K., & Dotani, T. 2006, PASJ, 58, 587 [NASA ADS] [Google Scholar]
  2. Ballantyne, D. R., & Everett, J. E. 2005, ApJ, 626, 364 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bildsten, L. 2000, Am. Inst. Phys. Conf. Ser., 522, 359 [NASA ADS] [Google Scholar]
  4. Bult, P., Jaisawal, G. K., Güver, T., et al. 2019, ApJ, 885, L1 [NASA ADS] [CrossRef] [Google Scholar]
  5. Burke, M. J., Gilfanov, M., & Sunyaev, R. 2017, MNRAS, 466, 194 [NASA ADS] [CrossRef] [Google Scholar]
  6. Chen, Y.-P., Zhang, S., Zhang, S.-N., Li, J., & Wang, J.-M. 2012, ApJ, 752, L34 [NASA ADS] [CrossRef] [Google Scholar]
  7. Chen, Y. P., Zhang, S., Qu, J. L., et al. 2018, ApJ, 864, L30 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chenevez, J., Galloway, D. K., in ’t Zand, J. J. M., et al. 2016, ApJ, 818, 135 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cocchi, M., Farinelli, R., Paizis, A., & Titarchuk, L. 2010, A&A, 509, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Coppi, P. S. 1992, MNRAS, 258, 657 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cornelisse, R., in’t Zand, J. J. M., Verbunt, F., et al. 2003, A&A, 405, 1033 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Cyburt, R. H., Amthor, A. M., Heger, A., et al. 2016, ApJ, 830, 55 [NASA ADS] [CrossRef] [Google Scholar]
  13. de Vries, C. P., den Herder, J. W., Gonzalez-Riestra, R., et al. 2014, in Fifteen Years of Experience with the Reflection Grating Spectrometer on XMM-Newton, SPIE Conf. Ser., 9144, 91440R [Google Scholar]
  14. Degenaar, N., Koljonen, K. I. I., Chakrabarty, D., et al. 2016, MNRAS, 456, 4256 [NASA ADS] [CrossRef] [Google Scholar]
  15. Degenaar, N., Ballantyne, D. R., Belloni, T., et al. 2018, Space Sci. Rev., 214, 15 [NASA ADS] [CrossRef] [Google Scholar]
  16. den Herder, J. W., Brinkman, A. C., Kahn, S. M., et al. 2001, A&A, 365, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Done, C., Gierliński, M., & Kubota, A. 2007, A&ARv, 15, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Fujimoto, M. Y., Hanawa, T., & Miyaji, S. 1981, ApJ, 247, 267 [NASA ADS] [CrossRef] [Google Scholar]
  19. Galloway, D. K., Cumming, A., Kuulkers, E., et al. 2004, ApJ, 601, 466 [NASA ADS] [CrossRef] [Google Scholar]
  20. Galloway, D. K., Muno, M. P., Hartman, J. M., Psaltis, D., & Chakrabarty, D. 2008, ApJS, 179, 360 [NASA ADS] [CrossRef] [Google Scholar]
  21. Gilfanov, M. 2010, in X-Ray Emission from Black-Hole Binaries, ed. T. Belloni, 794, 17 [Google Scholar]
  22. Hasinger, G., & van der Klis, M. 1989, A&A, 225, 79 [NASA ADS] [Google Scholar]
  23. Heger, A., Cumming, A., Galloway, D. K., & Woosley, S. E. 2007, ApJ, 671, L141 [NASA ADS] [CrossRef] [Google Scholar]
  24. in ’t Zand, J. J. M., Heise, J., Kuulkers, E., et al. 1999, A&A, 347, 891 [NASA ADS] [Google Scholar]
  25. in’t Zand, J. J. M., Keek, L., Cumming, A., et al. 2009, A&A, 497, 469 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. in ’t Zand, J. J. M., Galloway, D. K., Marshall, H. L., et al. 2013, A&A, 553, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Jahoda, K., Swank, J. H., Giles, A. B., et al. 1996, in EUV, X-Ray, and Gamma-Ray Instrumentation for Astronomy VII, eds. O. H. Siegmund, & M. A. Gummin, Proc. SPIE, 2808, 59 [NASA ADS] [CrossRef] [Google Scholar]
  28. Ji, L., Zhang, S., Chen, Y., et al. 2013, MNRAS, 432, 2773 [NASA ADS] [CrossRef] [Google Scholar]
  29. Ji, L., Zhang, S., Chen, Y., et al. 2014a, ApJ, 782, 40 [NASA ADS] [CrossRef] [Google Scholar]
  30. Ji, L., Zhang, S., Chen, Y.-P., et al. 2014b, A&A, 564, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Ji, L., Zhang, S., Chen, Y., et al. 2015, ApJ, 806, 89 [NASA ADS] [CrossRef] [Google Scholar]
  32. Ji, L., Santangelo, A., Zhang, S., Ducci, L., & Suleimanov, V. 2018, MNRAS, 474, 1583 [NASA ADS] [CrossRef] [Google Scholar]
  33. Joss, P. C. 1978, ApJ, 225, L123 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kajava, J. J. E., Nättilä, J., Latvala, O.-M., et al. 2014, MNRAS, 445, 4218 [NASA ADS] [CrossRef] [Google Scholar]
  35. Kajava, J. J. E., Sánchez-Fernández, C., Kuulkers, E., & Poutanen, J. 2017, A&A, 599, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Keek, L., Ballantyne, D. R., Kuulkers, E., & Strohmayer, T. E. 2014, ApJ, 797, L23 [NASA ADS] [CrossRef] [Google Scholar]
  37. Keek, L., Arzoumanian, Z., Bult, P., et al. 2018, ApJ, 855, L4 [NASA ADS] [CrossRef] [Google Scholar]
  38. Kong, A. K. H., Miller, J. M., Méndez, M., et al. 2007, ApJ, 670, L17 [NASA ADS] [CrossRef] [Google Scholar]
  39. Krimm, H. A., Holland, S. T., Corbet, R. H. D., et al. 2013, ApJS, 209, 14 [NASA ADS] [CrossRef] [Google Scholar]
  40. Kuulkers, E., Homan, J., van der Klis, M., Lewin, W. H. G., & Méndez, M. 2002, A&A, 382, 947 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Lattimer, J. M., & Prakash, M. 2007, Phys. Rep., 442, 109 [NASA ADS] [CrossRef] [Google Scholar]
  42. Lewin, W. H. G. 1993, in Amer. Astron. Soc. Meet. Abstr., BAAS, 25, 1436 [Google Scholar]
  43. Lewin, W. H. G., van Paradijs, J., & Taam, R. E. 1993, Space Sci. Rev., 62, 223 [NASA ADS] [CrossRef] [Google Scholar]
  44. Maccarone, T. J., & Coppi, P. S. 2003, A&A, 399, 1151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Matsuoka, M., Kawasaki, K., Ueno, S., et al. 2009, PASJ, 61, 999 [NASA ADS] [CrossRef] [Google Scholar]
  46. Meisel, Z., Merz, G., & Medvid, S. 2019, ApJ, 872, 84 [NASA ADS] [CrossRef] [Google Scholar]
  47. Mihara, T., Nakajima, M., Sugizaki, M., et al. 2011, PASJ, 63, S623 [Google Scholar]
  48. Nättilä, J., Steiner, A. W., Kajava, J. J. E., Suleimanov, V. F., & Poutanen, J. 2016, A&A, 591, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Nättilä, J., Miller, M. C., Steiner, A. W., et al. 2017, A&A, 608, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Ono, K., Sakurai, S., Zhang, Z., Nakazawa, K., & Makishima, K. 2016, PASJ, 68, S14 [NASA ADS] [CrossRef] [Google Scholar]
  51. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  52. Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
  53. Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
  54. Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Pinto, C., Kaastra, J. S., Costantini, E., & Verbunt, F. 2010, A&A, 521, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Poutanen, J., & Svensson, R. 1996, ApJ, 470, 249 [NASA ADS] [CrossRef] [Google Scholar]
  57. Poutanen, J., & Veledina, A. 2014, Space Sci. Rev., 183, 61 [NASA ADS] [CrossRef] [Google Scholar]
  58. Poutanen, J., Nättilä, J., Kajava, J. J. E., et al. 2014, MNRAS, 442, 3777 [NASA ADS] [CrossRef] [Google Scholar]
  59. Rodi, J., Jourdain, E., & Roques, J. P. 2016, ApJ, 817, 101 [NASA ADS] [CrossRef] [Google Scholar]
  60. Strohmayer, T., & Bildsten, L. 2006, in New Views of Thermonuclear Bursts, eds. W. Lewin, & M. van der Klis (Cambridge: Cambridge University Press), 113 [Google Scholar]
  61. Strohmayer, T. E., Gendreau, K. C., Altamirano, D., et al. 2018, ApJ, 865, 63 [NASA ADS] [CrossRef] [Google Scholar]
  62. Suleimanov, V., & Poutanen, J. 2006, MNRAS, 369, 2036 [NASA ADS] [CrossRef] [Google Scholar]
  63. Suleimanov, V., Poutanen, J., & Werner, K. 2011, A&A, 527, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Suleimanov, V., Poutanen, J., & Werner, K. 2012, A&A, 545, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Suleimanov, V. F., Kajava, J. J. E., Molkov, S. V., et al. 2017, MNRAS, 472, 3905 [NASA ADS] [CrossRef] [Google Scholar]
  66. Suleimanov, V. F., Poutanen, J., & Werner, K. 2018, A&A, 619, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Swank, J. H., Becker, R. H., Boldt, E. A., et al. 1977, ApJ, 212, L73 [NASA ADS] [CrossRef] [Google Scholar]
  68. Thompson, T. W. J., Galloway, D. K., Rothschild, R. E., & Homer, L. 2008, ApJ, 681, 506 [NASA ADS] [CrossRef] [Google Scholar]
  69. Ubertini, P., Bazzano, A., Cocchi, M., et al. 1999, ApJ, 514, L27 [NASA ADS] [CrossRef] [Google Scholar]
  70. Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. van Paradijs, J., & Lewin, W. H. G. 1986, in NATO Advanced Science Institutes (ASI) Series C, eds. J. Truemper, W. H. G. Lewin, & W. Brinkmann, 167, 187 [Google Scholar]
  72. Wallace, R. K., & Woosley, S. E. 1981, ApJS, 45, 389 [NASA ADS] [CrossRef] [Google Scholar]
  73. Weaver, T. A., Zimmerman, G. B., & Woosley, S. E. 1978, ApJ, 225, 1021 [NASA ADS] [CrossRef] [Google Scholar]
  74. Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
  75. Winkler, C., Courvoisier, T. J.-L., Di Cocco, G., et al. 2003, A&A, 411, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Woosley, S. E., & Taam, R. E. 1976, Nature, 263, 101 [NASA ADS] [CrossRef] [Google Scholar]
  77. Woosley, S. E., Heger, A., Cumming, A., et al. 2004, ApJS, 151, 75 [NASA ADS] [CrossRef] [Google Scholar]
  78. Worpel, H., Galloway, D. K., & Price, D. J. 2013, ApJ, 772, 94 [NASA ADS] [CrossRef] [Google Scholar]
  79. Worpel, H., Galloway, D. K., & Price, D. J. 2015, ApJ, 801, 60 [NASA ADS] [CrossRef] [Google Scholar]
  80. Zamfir, M., Cumming, A., & Galloway, D. K. 2012, ApJ, 749, 69 [NASA ADS] [CrossRef] [Google Scholar]
  81. Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
  82. Zycki, P. T., Done, C., & Smith, A. D. 1999, Astrophys. Lett. Commun., 38, 193 [NASA ADS] [Google Scholar]

All Tables

Table 1.

Best fitting parameters for the burst spectra in the five intervals shown in Fig. 4.

In the text

All Figures

thumbnail Fig. 1.

Light curves of GS 1826–24 during the period analysed in this work. Panel a: Swift/BAT light curve in the 15–50 keV energy range. Panel b: IBIS/ISGRI light curve in the 17–83 keV energy range. Shown in red are the hard-state periods (MJD 52700–54800, MJD 54800–56400), and in light blue and grey, respectively, the dim-hard (MJD 54800–54800) and soft-state periods (MJD 56400 onward). The small vertical lines on top of the light curve indicate the times of detection of Type I X-ray bursts by JEM-X. To build a homogeneous sample, and avoid the systematics effects caused by variations of the persistent emission, burst stacking was performed using the hard-state data from the period MJD 52700–54800. Panel c: JEM-X light curve in the 3–25 keV energy range. Panel d: MAXI light curve in the 2–20 keV energy range. Panel e: recurrence times of the Type I X-ray bursts found in this work. Shown in black are the recurrence times measured directly (see examples in Fig. 2) and in grey the derived recurrence times (as described in the text). The red triangles correspond to the times of detection of the four groups of bursts displayed in Fig. 2.
In the text
thumbnail Fig. 2.

Detailed view of four trains of bursts. Top panel: RGS light curve of obs ID 01050390301. The time resolution is 5 s (0.5–2 keV energy range). The other panels provide JEM-X light curves built in the 3–25 keV energy range, with a time resolution of 5 s. For reference, the time of occurrence of these trains of bursts are marked in Fig. 1e. The average recurrence times per panel are (from top to bottom): 3.23 ± 0.05, 3.39 ± 0.05 h, 5.11 ± 0.07 h, and 3.86 ± 0.06 h.
In the text
thumbnail Fig. 3.

Comparison of the JEM-X (3−25 keV) average burst profiles detected during the three spectral states described in Sect. 3: hard, dim hard, and soft.
In the text
thumbnail Fig. 4.

Panel a: average burst profile in four energy bands. The RGS, JEM-X, and IBIS/ISGRI (18–35 keV) light curves refer to the left vertical axis. The IBIS/ISGRI (35–70 keV) light curve refers to the right vertical axes. The profiles were built as described in Sect. 2. The dashed vertical lines indicate the intervals over which the spectra displayed in Fig. 5 were stacked. Panels b and c: evolution of the burst temperature and cutoff energy derived from the fits to the stacked burst spectra, using Model 3 and 3b (free persistent emission parameters). Panels d and e: comparison of the burst temperatures and fluxes derived using the standard fitting procedure (fixed persistent emission parameters: Model 1) with the results derived from Model 3. A dotted line is drawn at the position that equals both values. Panel f: comparison of the power-law flux derived using Models 3 and 3b with the non-bursting persistent emission flux.
In the text
thumbnail Fig. 5.

Panel a: average hard-state persistent emission spectrum. Shown are the RGS, JEM-X, and ISGRI spectra (in blue, orange, and red, respectively). Panels b–f: average hard-state burst spectra stacked over the five time intervals shown in Fig. 4. The spectral parameters derived from the fits to these spectra are provided in Table 1. The black continuous line shows the resulting spectra (burst+persistent emission) when fitting the data using Model 3, where the CUTOFFPL normalization and cutoff energy during the burst are treated as free parameters (short-dashed line). The dot-dashed line shows the corresponding blackbody component. Highlighted in the data–model panels (in cyan, brown, and pink) are the residuals in the case where the CUTOFFPL component during the burst had been fixed to the best fitting persistent emission (Model 1, long-dashed line). The dotted line shows the corresponding blackbody component.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.