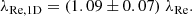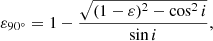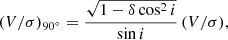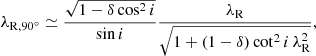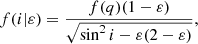| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A59 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201936413 | |
| Published online | 28 November 2019 | |
The CALIFA view on stellar angular momentum across the Hubble sequence
1
Instituto de Astrofísica de Canarias, Vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
e-mail: jfalcon@iac.es
2
Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain
3
Department of Astrophysics, University of Vienna, Türkenschanzstrasse 17, 1180 Vienna, Austria
4
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching b. München, Germany
5
Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
6
Instituto de Astronomía, Universidad Nacional Autónoma de México, Apartado Postal 70-264, México D.F. 04510, Mexico
7
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
8
Instituto de Astrofísica de Andalucía (IAA/CSIC), Glorieta de la Astronomía s/n Aptdo. 3004, 18080 Granada, Spain
9
Observatorio Astronómico, Laprida 854, X5000BGR Córdoba, Argentina
10
Consejo de Investigaciones Científicas y Técnicas de la República Argentina, Avda. Rivadavia 1917, C1033AAJ CABA, Argentina
11
INAF-Osservatorio Astrofisico di Arcetri – Largo Enrico Fermi, 50125 Firenze, Italy
12
Shanghai Astronomical Observatory, Chinese Academy of Sciences, 80 Nandan Road, Shanghai 200030, PR China
13
PITT PACC, Department of Physics and Astronomy, University of Pitts-burgh, Pittsburgh, PA 15260, USA
14
Departamento de Física Teórica, Universidad Autónoma de Madrid, 28049 Madrid, Spain
15
School of Physics and Astronomy, University of St Andrews, North Haugh, St Andrews KY16 9SS, UK
16
Sydney Institute for Astronomy, School of Physics A28, University of Sydney, Sydney, NSW 2006, Australia
17
ARC Centre of Excellence for All-sky Astrophysics in 3D (ASTRO-3D), Australia
18
Departamento de Física, Universidade Federal de Santa Catarina, PO Box 476, 88040-900 Florianópolis, SC, Brazil
19
ETH Zürich, Institute for Astronomy, Wolfgang-Pauli-Str. 27, 8093 Zürich, Switzerland
20
Kapteyn Astronomical Institute, University of Groningen, Postbus 800, 9700 Groningen, The Netherlands
21
Departamento de Física Teórica y del Cosmos, University of Granada, Facultad de Ciencias (Edificio Mecenas), 18071 Granada, Spain
22
Instituto Carlos I de Física Teórica y Computación, Spain
23
Instituto Nacional de Astrofísica, Óptica y Electrónica, Luis E. Erro 1, 72840 Tonantzintla, Puebla, Mexico
Received:
30
July
2019
Accepted:
11
October
2019
We present the apparent stellar angular momentum over the optical extent of 300 galaxies across the Hubble sequence using integral-field spectroscopic (IFS) data from the CALIFA survey. Adopting the same λR parameter previously used to distinguish between slow and fast rotating early-type (elliptical and lenticular) galaxies, we show that spiral galaxies are almost all fast rotators, as expected. Given the extent of our data, we provide relations for λR measured in different apertures (e.g. fractions of the effective radius: 0.5 Re, Re, 2 Re), including conversions to long-slit 1D apertures. Our sample displays a wide range of λRe values, consistent with previous IFS studies. The fastest rotators are dominated by relatively massive and highly star-forming Sb galaxies, which preferentially reside in the main star-forming sequence. These galaxies reach λRe values of ∼0.85, and they are the largest galaxies at a given mass, while also displaying some of the strongest stellar population gradients. Compared to the population of S0 galaxies, our findings suggest that fading may not be the dominant mechanism transforming spirals into lenticulars. Interestingly, we find that λRe decreases for late-type Sc and Sd spiral galaxies, with values that occasionally set them in the slow-rotator regime. While for some of them this can be explained by their irregular morphologies and/or face-on configurations, others are edge-on systems with no signs of significant dust obscuration. The latter are typically at the low-mass end, but this does not explain their location in the classical (V/σ, ε) and (λRe, ε) diagrams. Our initial investigations, based on dynamical models, suggest that these are dynamically hot disks, probably influenced by the observed important fraction of dark matter within Re.
Key words: galaxies: kinematics and dynamics / galaxies: elliptical and lenticular, cD / galaxies: spiral / galaxies: structure / galaxies: evolution / galaxies: formation
© ESO 2018
1. Introduction
After mass, one of the key parameters determining the fate of a galaxy is its angular momentum. A robust result from cosmological simulations is that the angular momentum distribution of dark matter halos is nearly constant with redshift (e.g. Bullock et al. 2001). The amount of angular momentum that is being transferred to the baryons is then believed to set the size of galactic disks (Mo et al. 1998) and to form the basis for the mass-size relation of galaxies (Shen et al. 2003). At the same time, tidal interactions and in particular mergers between galaxies can disturb or even fully destroy the disk so that the memory of the initial angular momentum might well be lost (e.g. Toomre & Toomre 1972).
Galaxy mergers are indeed believed to be an important reason why spheroid-dominated galaxies with surface brightness profiles close to de Vaucouleur (with a Sérsic index n ∼ 4) deviate from the mass-size relation of galaxies with outer surface brightness profiles close to exponential (n ∼ 1). The latter include disk-dominated spiral galaxies, but the relation seems to extend toward lower masses, including dwarf elliptical galaxies (e.g. Kormendy & Bender 2012) and possibly even down to the dwarf spheroidal galaxies (e.g. Brasseur et al. 2011).
Even though stellar rotation is observed in dwarf elliptical galaxies (e.g. Toloba et al. 2011) and possibly even in dwarf spheroidal galaxies (e.g. Battaglia et al. 2008), the motion of their stars remains dominated by dispersion. This implies that the initial angular momentum that set their sizes had been reduced, likely as a result of the mechanisms that are believed to have transformed dwarf disk galaxies into these dwarf spheroid galaxies. Transformation mechanisms which have been proposed, such as tidal interaction and ram pressure stripping, are thought to act stochastically, as reflected in the large diversity in photometric, kinematic and stellar population properties (e.g. Ryś et al. 2013, 2014, 2015), but sudden dramatic changes as a result of, for example, mergers are expected to be rare (Amorisco et al. 2014).
This shows that even if the process of transferring the angular momentum from halo to disk is broadly understood (e.g. Burkert et al. 2016), there still might not be a direct link between the size of the disk of galaxy and its current stellar angular momentum. However, the comparison between current angular momentum and size of galaxies at a given mass provides constraints on the changes in angular momentum and on the mechanisms that caused these changes. The latter mechanisms, in turn, are in all likelihood the same that are responsible for defining the Hubble sequence of galaxies (e.g. Romanowsky & Fall 2012). Clearly, a crucial ingredient in uncovering the evolution of galaxies is a homogeneous and statistically-sound census of the stellar angular momentum in nearby galaxies of all Hubble types.
The SAURON project (de Zeeuw et al. 2002) combines the observed stellar line-of-sight velocity and dispersion fields of 48 early-type galaxies to compute the parameter λRe as a measure of the apparent stellar angular momentum within one effective radius Re (Emsellem et al. 2007). The ATLAS3D survey (Cappellari et al. 2011a) extended this to a volume-limited sample of 260 early-type galaxies out to 42 Mpc to confirm the existence of two families: slow rotators elliptical galaxies with complex stellar velocity fields and fast rotator lenticular as well as elliptical galaxies with regular stellar velocity fields (Krajnović et al. 2011). With the advent of new 2D surveys (e.g. SAMI, Croom et al. 2012; SLUGGS, Arnold et al. 2014; MASSIVE, Ma et al. 2014; MaNGA, Bundy et al. 2015), there has been steady progress in this field over the past decade. While initial samples were still biased towards early-type systems (e.g. Arnold et al. 2014; Fogarty et al. 2014; Veale et al. 2017a), the topic has remained active and has spurred the study of angular momentum in even larger samples of galaxies (including spirals) by the SAMI (Cortese et al. 2016; hereafter C16; van de Sande et al. 2017; hereafter vdS17) and MaNGA (Graham et al. 2018; hereafter G18) survey teams.
The CALIFA survey (Sánchez et al. 2012) of a diameter-selected sample of up to 600 nearby galaxies provides stellar velocity and dispersion fields that not only extend further out in radius, but also cover galaxies of all Hubble types. The goal of this paper is to use the stellar velocity and dispersion maps of 300 observed CALIFA galaxies presented in Falcón-Barroso et al. (2017; hereafter referred to as FLV17), in order to provide a robust census of the apparent stellar angular momentum across the Hubble sequence and investigate the properties of galaxies in some of the most extreme regions of the (λRe, ε) diagram. Part of the results shown here have already been presented in Falcón-Barroso et al. (2015), and have been used in recent literature for comparison with other surveys (e.g. Cappellari 2016; Schulze et al. 2018) or for highlighting the peculiarities of certain types of galaxies (e.g. del Moral-Castro et al. 2019).
The paper is organised as follows. After describing in Sect. 2 the available data for 300 galaxies, we present in Sect. 3 the resulting apparent stellar angular momentum within apertures of different radii and as radial profiles when only long-slit data is available. In Sect. 4, we present the galaxies on the (V/σ, ε) and (λRe, ε) diagrams to investigate the rotational versus pressure support homogeneously among galaxies of all morphologies, showing trends among types and discussing their relation to other global parameters. We conclude our findings in Sect. 5. Appendix A describes the procedures used to deproject our λRe measurements. Table B.1 provides all the quantities used and derived in our study. Throughout we adopt H0 = 70 km s−1 Mpc−1, ΩM = 0.3 and ΩL = 0.7 for respectively the Hubble constant, the matter density and the cosmological constant, although these parameters only have a small effect on the physical scales of the galaxies due to their relative proximity.
2. CALIFA IFU and ancillary data
The Calar Alto Legacy Integral Field Area (CALIFA) survey is the first integral-field spectroscopic (IFS) survey of a diameter selected (45″ < D25 < 80″) sample of up to 600 galaxies in the local universe (0.005 < z < 0.03) of all Hubble types (Sánchez et al. 2012). The so-called CALIFA “mother sample” of 938 galaxies, from which targets are randomly observed based on visibility, is representative in stellar mass over two orders of magnitude 9.4 < log(M⋆/M⊙) < 11.4. This means that after a straightforward volume correction based on D25, the mass (and corresponding luminosity) function over this range is recovered to better than 95% (Walcher et al. 2014). The 65″ × 72″ field-of-view of the employed PMAS/PPAK-IFU (Kelz et al. 2006) covers the full optical extent of the selected galaxies, with a complete filling factor achieved through a three-point dithering scheme, and with a spatial sampling of 1″ that over-samples the spatial resolution by about a factor three (Husemann et al. 2013). The typical Pont-Spread-Function size is FWHM ∼ 2.5″ (Sánchez et al. 2016), that corresponds to an average physical resolution of 0.7 kpc and a range betweeen 0.2 and 1.5 kpc within the considered redshift range.
In this study, we used the high-quality stellar kinematics presented in FLV17 from the V1200 dataset. Briefly, stellar velocity (V) and velocity dispersion (σ) maps were computed using the pPXF code of Cappellari & Emsellem (2004), after the data had been Voronoi binned (Cappellari & Copin 2003) to a signal-to-noise ratio (S/N) of 20 per pixel. We use the Indo-US spectral library (Valdes et al. 2004) as templates over the wavelength range covered by the V1200 grating (i.e. 3750−4550 Å), which includes prominent absorption features such as Ca H+K, Hγ or the Hδ lines. The typical relative uncertainties of our measurements are ∼5% for σ ≥ 150 km s−1. Below that value they increase up to 50% for velocity dispersions as low as 20 km s−1. We refer the reader to FLV17 for more details.
Additional global galaxy properties used here are: (i) distances based on redshift with Hubble flow corrected for Virgo infall (see Walcher et al. 2014); (ii) SDSS redshifts, apparent magnitudes and corresponding colors; (iii) light concentrations based on SDSS r-band 50 and 90 percentile Petrosian radii; (iv) effective radii (Re) estimated using a growth-curve analysis applied to the SDSS images as described in Walcher et al. (2014); (v) stellar masses based on Sunrise spectral energy distribution fits from Walcher et al. (2014); (vi) global star formation rates (SFRs) based on Balmer-decrement corrected Hα fluxes extracted from the CALIFA datacubes (Sánchez et al. 2017); and (vii) stellar population parameters (average ages and age gradients) from García-Benito et al. (2017) using CALIFA data Voronoi binned to reach a target S/N ∼ 20. The resulting spectra of each bin was then processed using PyCASSO (Cid Fernandes et al. 2013; Amorín et al. 2017) using a combination of the GRANADA (González Delgado et al. 2005) and MILES models (Vazdekis et al. 2015) respectively. Reported ages are averages within Re, while radial age gradients are computed performing a robust linear fit over the entire inner Re.
3. Apparent stellar angular momentum
Following Emsellem et al. (2007), we defined the apparent stellar angular momentum as
where Fj, Rj, Vj and σj are the flux, polar radius, velocity, and dispersion per spatial bin j for which the centroid falls within an elliptic aperture with the given semi-major axis R, ellipticity ε, and position angle PA.
We adopted for ε and PA the median values of the outer 10% radial points of, respectively, the ellipticity and position angle profile resulting from an IRAF ellipse model of the SDSS r-band image of each galaxy (Méndez-Abreu et al. 2017). This is in contrast to previous studies (e.g. Emsellem et al. 2007), where the mean ellipticity within Re was used instead (εe). We decided on this option as the effect of non-axisymmetric distortions, which may be caused by, for example, bars, spiral arms, and tidal interactions, are minimized. This is also supported by the close correspondence between the kinematic position angle based on the stellar velocity fields and the latter PA based on the outer radii (see Fig. 2 of Barrera-Ballesteros et al. 2014). We estimated that ellipticities measured within Re are on average 6% smaller than those used here. Nevertheless, we confirmed that there is a good correspondence between the different approaches, aside from extreme cases.
3.1. Global values and aperture transformations
Our dataset allows for the exploration of the specific angular momentum on different aperture sizes. The vast majority of galaxies reach Re (97%), while 61% reach up to 2 Re (see Fig. 4 in FLV17 for details).
Figure 1 shows the normalised observed and deprojected λR distributions measured within 0.5 Re, Re, and 2 Re. For the eight galaxies not reaching one Re with our S/N requirements, we extrapolated their values up to Re based on their integrated profiles, as this extrapolation would be relatively safe (see Fig. 3). We note that we did not attempt to extrapolate values up to 2 Re, as it would be more uncertain. Deprojected λR values were obtained following the prescriptions outlined in Appendix A. In order to provide the most representative distributions for the general population of galaxies, the histograms have been computed by weighting each galaxy contribution by the volume correction factor ( ). The figure shows a mild increase in λR with the aperture size, as expected if the majority of galaxies display clear rotation. While this difference may not be so obvious in the distributions of observed values, it is clearly shown in the deprojected ones, peaking at ∼0.45, ∼0.75, and ∼0.80, respectively, for each aperture.
). The figure shows a mild increase in λR with the aperture size, as expected if the majority of galaxies display clear rotation. While this difference may not be so obvious in the distributions of observed values, it is clearly shown in the deprojected ones, peaking at ∼0.45, ∼0.75, and ∼0.80, respectively, for each aperture.
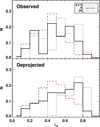 |
Fig. 1. Volume-corrected λR distributions for different aperture sizes (i.e. 0.5 Re, Re, and 2 Re). Top panel: distribution of λR as observed, while bottom panel: distribution of deprojected values (as explained in Appendix A). |
Since data reaching one Re is not always available in other data sets, here we provide transformations between apertures based on our data. This enables us to investigate how well the measured apparent stellar angular momentum at smaller radii can be extrapolated to larger radii. In Fig. 2 we compare λRe with λ0.5 Re and λ2 Re measured within half and twice the half-light radius, respectively, for those galaxies for which the kinematics extends far enough. The dashed curves represent the biweight mean relations:
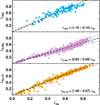 |
Fig. 2. Stellar angular momentum (λR) aperture relations for different aperture sizes. Top and middle panels: relation between λRe with the values of smaller/larger apertures 0.5 Re and 2 Re. Bottom panel: comparison of λRe with that computed with a 1D long-slit along the major axis of the galaxies. The dashed lines indicate the biweight mean values while dotted lines indicate the standard deviation. |
which provide approximate extrapolations for galaxies of all Hubble types. Note that the systematic trend discussed in Fig. 1 is even more evident here. Also, the lack of low λRe and λ2 Re values in the top panel highlights one of the limitations of the CALIFA target selection: large and massive nearby early-type galaxies, which are the main constituents of the slow rotator family (e.g. Emsellem et al. 2011; Veale et al. 2017b) appear in low numbers. Nevertheless, the correlations presented here are in good agreement with those presented in van de Sande et al. (2017) (e.g. λ0.5 Re ≈ 0.79 λRe).
The availability of stellar kinematic maps is rapidly increasing with ongoing and upcoming integral-field spectroscopic instruments and surveys. Even so, much of the stellar kinematic data at higher redshift will remain based on long-slit spectroscopy, which instead provides stellar velocity and dispersion profiles. Assuming the usual major-axis orientation of the long-slit, we use the kinemetry routine (Krajnović et al. 2006) to extract from the stellar kinematic maps of all CALIFA galaxies a major-axis rotation and dispersion profile. In the same way as Eq. (1) for λRe, we then compute λRe, 1D from all radial bins out to the half-light radius Re, resulting in the correlation shown in the bottom panel of Fig. 2. The solid curve represents the biweight mean relation
Our relation differs somewhat from Toloba et al. (2015) (i.e. λRe, 1D ≈ 1.56 λRe), which is likely due to differences in the size and type of galaxy samples used: 300 galaxies of all Hubble types versus 39 dwarf elliptical galaxies in the Virgo cluster. In addition, to aid in the comparison with high redshift measurements, we computed the relation between λRe and (V/σ)Re, 1D. As shown in Eq. (B1) of Emsellem et al. (2011), the relation between λRe and (V/σ) has a quadratic form depending on a single parameter κ. We have fit the relation and obtained a value of κ = 1.1 for all Hubble types, which is the same value derived in the ATLAS3D survey for early-type galaxies.
3.2. Integrated radial profiles
Figure 3 shows the apparent stellar angular momentum λR defined in Eq. (1) as a function of increasing enclosed radius (R) along the major axis, normalized by the effective radius Re of each galaxy. The color represents the Hubble type of the galaxy, from spheroid-dominated ellipticals in red to disk-dominated spirals in blue.
 |
Fig. 3. Integrated λR profiles for our CALIFA sample of 300 galaxies. The profiles are normalized with Re and color-coded by Hubble type (as indicated by the colorbar). |
The elliptical galaxies typically have the lowest λR values at a given (normalized) radius, even though in most cases the angular momentum does gently rise at larger radii. This is in line with the significant net rotation observed from radial velocity measurements of planetary nebulae and globular clusters in the outskirts of elliptical galaxies (e.g. Bellstedt et al. 2017). Moreover, even giant ellipticals like M 87 in the Virgo Cluster that appear round, in deeper images do show in the outskirts significant flattening reflecting at least partial rotational support (e.g. Liu et al. 2005). Additional evidence is found in early-type galaxies with faint spiral-like structures found at large radii (e.g. Gomes et al. 2016). Our findings are consistent with dedicated studies of early-type galaxies reaching up to 5 Re (e.g. Raskutti et al. 2014; Boardman et al. 2017).
Rather unexpected is that the galaxies which have the λR profiles with the largest amplitudes are not the most disk-dominated spiral galaxies. Already in the inner parts, the stars in Sb galaxies have a larger apparent angular momentum than S0 and Sa galaxies, as anticipated from the larger disk-to-total fractions of Sb compared to S0/Sa galaxies. However, the λR values of Sb galaxies are on average also significantly higher than for Sc and Sd galaxies even though the latter are relatively more disk dominated. The most extreme cases in our sample are MCG-02-51-004 (ID: 868), NGC 6301 (ID: 849), and UGC 12518 (ID: 910). See Table B.1 for details.
Since λR, as opposed to V/σ, is normalized in Eq. (1) by the sum of the squares of velocity (V) and dispersion (σ), it not only has a well-defined maximum of unity, but should also be nearly independent of mass – the enclosed total mass is namely proportional to the second velocity moment, which after projection and integration along the line of sight, in turn is proportional to V2 + σ2. Therefore, the difference in λR profiles between galaxies of different morphological type can not merely be the result of a possible difference in mass.
4. Rotation versus pressure support: (V/σ, ε) and (λRe, ε) diagrams
From earlier studies of E/S0 galaxies, in particular from the SAURON project (Emsellem et al. 2007; Cappellari et al. 2007) and ATLAS3D Survey (Emsellem et al. 2011), we know that the slow-rotator and fast-rotator galaxies, apart from their different position in the (λRe, ε)-diagram, do have other distinct properties. Slow rotators often show kpc-scale kinematically distinct cores (KDCs) with similarly-old ages as the rest of the stars in a galaxy that tends to be a quiescent, massive elliptical galaxy with a mildly triaxial intrinsic shape (e.g McDermid et al. 2006). Most elliptical galaxies and nearly all lenticular galaxies are, however, fast rotators having an intrinsic shape, apart from the common presence of bars, that is fully consistent with oblate axisymmetry and spanning a wide range in flattening. They show regular rotation with aligned photometric and kinematic axes even though a KDC is sometimes present, but typically of smaller scale than in slow rotators and containing stars that are on average younger than the main body. A similar picture is revealed by the E (red) and S0 (orange) galaxies from the CALIFA survey.
Figure 4 shows both the more traditional ordered-over-random stellar motion (V/σ)e (left panel) and apparent stellar angular momentum λRe (right panel) as function of the ellipticity ε. The solid curve indicates the demarcation line between slow-rotator and fast-rotator galaxies as inferred from the ATLAS3D survey of elliptical (E) and lenticular (S0) galaxies. The CALIFA survey explores in a homogeneous way galaxies of all Hubble types, as indicated by the color of the symbols. The Sa and Sb galaxies show the expected continuation of fast-rotator E/S0 galaxies: reaching higher values of (V/σ)e and λRe and having on average larger ε, consistent with the increasing dominance of a disk with resulting increase in rotational support and flattening. Interestingly though, the rotational support is decreasing again with Sc and in particular Sd galaxies, some of which reach λRe values close or even below the slow-fast-rotator demarcation line. Still, they remain very different from slow-rotator elliptical galaxies because the spiral galaxies have much larger ε values and hence are intrinsically much flatter. We explore this behavior in more detail in the next section (Sect. 4.1).
 |
Fig. 4. (V/σ, ε)e (left) and (λRe, ε) (right) relations for the CALIFA sample of 300 galaxies. Galaxies are color-coded with Hubble type as indicated by the colorbar. For reference, we plot the ATLAS3D sample with gray crosses. The solid line demarcates the division between Slow and Fast rotators as established by Emsellem et al. (2011). The dashed line in the right panel marks the revised division between Slow and Fast rotators defined by Cappellari (2016). |
We chose to plot in Fig. 4 the ATLAS3D sample for reference, as it provides values for both (V/σ)e and λRe. The comparison of CALIFA with ATLAS3D and other samples in the literature is good overall. While differences in the range of measured ellipticities are small, the biggest discrepancies appear in the range of λRe values. Differences with C16 and vdS17 are mostly on the maximum values of λRe reached. While our largest values are around λRe ∼ 0.85, the SAMI survey galaxies hardly go over 0.8. This is in contrast with the MaNGA sample of G18 that displays λRe values that often reach (and extend past) the theoretical maximum of 1.0. As opposed to G18 galaxies, our sample lacks round, fast rotating galaxies, which may be due to the CALIFA sample selection that precludes the inclusion of large, face-on disks. Interestingly, the range of λRe values of Sánchez et al. (2018) and Fischer et al. (2019), also based on MaNGA data, is consistent with the ones presented here. The sometimes extreme particularities of the beam corrections applied in G18 as opposed to Sánchez et al. (2018) and Fischer et al. (2019) may be at the heart of the large differences between the two studies on the same dataset. The similar effect is also true for when comparing our sample with that of vdS17. In this particular case, differences can be due to the particular definition the SAMI team adopted for Rj in Eq. (1) (e.g. semi-major axis of the ellipse on which spaxel j lies, instead of the circular projected radius to the center). This also results in a lower λRe value as compared to the Polar Rj definition that is adopted here. Regardless of the specific details in the sample selection and peculiarities in the λRe calculation of the three surveys, they are largely complementary.
4.1. Trends with global parameters
To investigate further the properties of galaxies of all morphological types in the (λRe, ε)-diagram, we show in Fig. 5 the relation between λRe and different global parameters, color-coding galaxies according to their Hubble type.
 |
Fig. 5. λRe relations with global parameters for the sample of 300 CALIFA galaxies. Galaxies are color-coded with Hubble type. Top left panel: whisker plot enclosing the interquartile range (IQR), defined at IQR25%–IQR75% for galaxies of each morphological type. The whiskers extend out to the maximum or minimum value of the data, or to 1.5 times IQR25% or IQR75% in case there is data beyond this range. Outliers are identified with small circles. Other panels: relations with r-band absolute magnitude Mr, total stellar mass M⋆, u − r Petrosian color, concentration index R90/R50, and star formation rate SFR. See text for details. |
The top row in Fig. 5 shows the behavior of λRe with Hubble type, r-band absolute magnitude and total stellar mass (from left to right). Not surprisingly the ellipticals display a wide range of λRe values, from the lowest in the sample close to zero to almost 0.6. As originally observed in the SAURON survey, the E family comprises galaxies that includes both slow and fast rotators. The middle and right panels confirm that luminosity and mass are the best predictors for slow rotators, being the dominant population at the high luminosity and mass end. Nevertheless, the increase of λRe with Hubble type would still hold even if slow rotators were not considered. This increasing trend with morphological type was already observed by C16 in the SAMI survey. Interestingly, though, our sample shows a maximum in λRe for the Sb galaxies, with decreasing values for later-types. We have used the much larger MaNGA sample of G18 to check this trend. While there is indeed a turning point at similar stellar masses, this is much milder than observed in our CALIFA sample at low masses. We attribute the difference to the peculiarities of our sample, which is not complete for the low luminosity (and thus mass) end (see FLV17 for more details).
The bottom row shows the relation between λRe with u − r Petrosian color, concentration index (R90/R50, measured as the ratio of 90 and 50 percentile Petrosian radius), and star-formation rates derived from Hα emission line fluxes in Sánchez et al. (2017). Our sample of E/S0/Sa galaxies show a well-defined vertical sequence around the same red color, while later types display bluer colors. The middle panel shows that, slow-rotators aside, the concentration index is clearly related to λRe with larger values reached by the Sb types. This is expected as light concentration is a proxy for the bulge(+bar)-to-total ratio, which in turn is the main driver behind the Hubble morphological classification (e.g. Shimasaku et al. 2001; Strateva et al. 2001). Still, there appears to be some scatter in the relation, consistent with that shown already in C16. The family of Sb galaxies also appear to be the currently higher star-forming systems (right panel). Similarly, going from spiral to elliptical galaxies, the SFR decreases, so it also unsurprising to find the trend of decreasing λR with lower SFR.
The λRe values found for the galaxies in our sample confirm the predominance of Slow rotators in high-mass, high-luminosity systems. We estimate an overall fraction of 28% of Slow rotators with stellar masses above 1011 M⊙, based on the Emsellem et al. 2011 definition. This number sits in the middle of the wide range of predictions provided by the latest surveys (e.g. Emsellem et al. 2011; D’Eugenio et al. 2013; Fogarty et al. 2014; Veale et al. 2017a; van de Sande et al. 2017) which display values between 15% and 80% for masses above 1011 M⊙. Our lower value is likely due to the fact that the CALIFA survey is complete only up to 1011.44 M⊙ (see Walcher et al. 2014, for details).
Despite the limited number of galaxies compared to other surveys, our sample shows two areas with interesting results: (i) the low λRe values for the late-type spirals, and (ii) the particular properties of the fastest rotators.
4.1.1. Low λRe spirals
We have investigated the reasons for the surprisingly low λRe values observed in the latest-type galaxies and found two potential explanations. There is a group of Sc/Sd galaxies with λRe values below 0.35. We have checked and these are both irregular or fairly face-on systems. This naturally explains their unusual location in the (λRe, ε) diagram. The same feature was found by Graham et al. (2018) in their much larger sample of galaxies. The remaining group of Sc/Sd galaxies with λRe values between 0.35 and 0.6 are typically edge-on systems. We have explored whether they present large extinction values, as dust obscuration could prevent the full integration of the stellar kinematics along the line-of-sight and thus led to lower rotation amplitudes. Displaying the bluest colors of the entire sample, this option does not seem to be likely. This is confirmed by the much more detailed study of the extinction in the CALIFA galaxies by González Delgado et al. (2015). We note, however, that simulations suggest that observational estimates could be underestimated for this kind of systems (see Ibarra-Medel et al. 2019, for details). In addition, we have also checked that those galaxies display velocity dispersions well above the point where the limits in the CALIFA spectral resolution are an issue (see Fig. 9 in FLV17).
The large observed ε values for those Sc/Sd galaxies imply that we need a way to keep their dynamically hot stellar disk geometrically thin. We note that they contain small bulges (as observed by their low concentration values), and also are not the highest star-forming galaxies. We postulate that the presence of a relatively large dark matter halo provides an additional vertical force to keep the disk geometrically thin while being dynamically heated. Our initial assessment, based on dynamical models of our sample (Zhu et al. 2018), suggests an enclosed mass that is up to a factor ten larger than the estimated baryonic (stellar plus gas) mass already within the half-light radius. A preliminary confirmation of this was presented in Fig. 3 of Falcón-Barroso et al. (2015). This is in line with previous results in the literature presenting evidence of “thicker” thin disks in late-type spirals (e.g. Yoachim & Dalcanton 2006; Comerón et al. 2011).
4.1.2. Fastest rotators
We have identified a group of 19 galaxies with λRe ≥ 0.82 (i.e. the top 5% of the distribution). They are mostly Sb/Sc galaxies. In Fig. 5 they happen to have intermediate absolute magnitudes, masses, and colors. They are not special in any of those three parameters with respect to other galaxies with lower λRe values. They are peculiar in that they are the highest star-forming galaxies with some of the smallest bulges, as probed by the concentration index1. We have identified at least three other properties that make these galaxies unique. As shown in Fig. 6, they tend to have the largest sizes at a given stellar mass, display some of the strongest average luminosity-weighted inner age gradients measured by García-Benito et al. (2017), and also appear to have rather homogeneous mean stellar population ages within Re of about 1 Gyr (González Delgado et al. 2015). We inspected for any dependence with environment, either local or global, and found no significant trends.
 |
Fig. 6. Top and middle panels: λRe relations with mean age within Re, mean stellar age gradient within Re for our sample of CALIFA galaxies. Bottom panel: stellar mass–size relation. The whisker plot in the middle panel was computed in the same way as in Fig. 5. Galaxies above the 95% percentile of λRe distribution of the sample are marked in blue. The dashed line in the top and middle panels marks that percentile. |
The relative difference between the observed λRe values of this group of galaxies (see top, left panel of Fig. 5) with respect to the S0 population, raises the question whether they could fade into lenticular galaxies. Decades after the discovery of the morphology-density relation (Dressler et al. 1987), the interest in this topic has been revived by the recent results from different groups (e.g. Bedregal et al. 2006; Laurikainen et al. 2010; Kormendy & Bender 2012; Brough et al. 2017; Greene et al. 2017) confirming the initial result, but recasting the observed phenomenon from the Slow/Fast rotator perspective (e.g. Cappellari et al. 2011b). We refer the reader to the extended review on the topic presented in Cappellari (2016). At first sight, based purely on λRe, our results suggest that the transformation between Sa galaxies into S0s is possible. We note, however, that in a fading scenario, both stellar mass and λRe are expected to be conserved. This seems more difficult in the case of Sb and Sc galaxies, for which the difference with respect to the lenticulars in λRe is significant. For Sd galaxies, even though λRe values are consistent with those of lenticulars, their light concentrations are much lower and thus it seems unlikely they will fade into lenticulars with typically much larger bulge-to-disk ratios. Furthermore, the amount of mass in gas for these late-type galaxies can be up to 50% of their baryonic total mass (e.g. Papastergis et al. 2012), making it very difficult to turn all that matter into stars by fading within a Hubble time without substantially increasing the total mass budget of the system. Pre-processing in groups, with tidal interactions and/or major mergers seem to be more likely mechanisms (e.g. Querejeta et al. 2015).
4.2. Trends in the SFR-M⋆ diagram
An interesting way of looking at variations of λRe is through the extensively studied star formation rate–stellar mass relation (e.g. Croton et al. 2006; Cortese et al. 2019), shown in Fig. 7 for our sample. We have divided the diagram in bins of SFR and stellar mass. Each subpanel presents the (λRe, ε) relation for that bin, showing in gray all CALIFA galaxies and highlighting in color those belonging to that bin with their Hubble type. The number on the top-left corner of each inset gives the 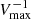 -weighted λRe average for the highlighted galaxies in that bin.
-weighted λRe average for the highlighted galaxies in that bin.
 |
Fig. 7. λRe–ϵ relation as a function of location in the star-formation rate versus total stellar mass (M⋆) relation for the CALIFA galaxies. Each panel shows the complete sample highlighting in color the ones belonging to each specific SFR–M⋆ bin. The number in each subpanel gives the |
The figure shows that the main star-forming sequence is made of galaxies with increasing λRe as both the SFR and stellar mass grow. The high-mass and high star-forming region is populated by Sa/Sb galaxies mostly, whereas the low SFR and stellar mass ends are dominated by later-type galaxies (Sc/Sd). As already highlighted by numerous studies, galaxies departing from the main star-forming sequence are mostly early-type Es and S0s (e.g. Schawinski et al. 2014). It appears that the dynamically coldest disks are found in the most massive and more actively star-forming systems (e.g. Catalán-Torrecilla et al. 2017; Méndez-Abreu et al. 2019). The trends with λRe observed here are supported by a similar analysis with the EAGLE cosmological simulation (Walo-Martín et al., in prep.).
5. Conclusions
This paper presents the CALIFA view on the stellar angular momentum distribution for a sample of 300 galaxies across the Hubble sequence. Our dataset allows us to study the distribution of λR for different apertures (0.5 Re, Re, 2 Re) and provides the relationship between them, including conversions to λR computed with a long-slit along the major axis of the galaxies. Our sample also helps us to investigate the relationship between λR and different global properties of galaxies (e.g. Hubble type, absolute magnitude, u − r color, concentration index, stellar mass, and star formation rate).
In addition, we analyze the distribution of galaxies in the classical (V/σ, ε) and (λRe, ε) diagrams, often used to study the level of rotation over pressure support in galaxies. Our results for early-type (E and S0) galaxies are consistent with previous studies in the literature for the same kind of galaxies. The extension to later-types (Sa to Sd) provided by our sample presents two interesting results. On one side, we find a maximum λRe of around ∼0.85 for large, relatively massive and highly star-forming galaxies (typically Sb systems). On the other hand, rather unexpectedly, we observe relatively low λRe values for low-mass Sc/Sd systems. We will explore these two areas in forthcoming papers for a broader discussion of the nature of S0 galaxies and to investigate the dark matter content of low mass systems.
The results presented here with the CALIFA sample in terms of the stellar angular momentum distribution of galaxies are just the tip of the iceberg of possibilities for extending our understanding of galaxy formation and evolution. Ongoing large surveys have already started to make use of this information in different areas (e.g. vdS17), with a boost in this field coming with the measurement of λRe for thousands of galaxies provided by the MaNGA survey team (e.g. G18). Complementarily, the first studies to relate the radial dependence of λR to the evolution of galaxies are appearing in the literature (e.g. Graham et al. 2017). In the absence of high-quality observations of stellar kinematics for substantial samples of high-redshift galaxies (e.g. z > 1.0), cosmological numerical simulations will allow us to explore the evolution of angular momentum as a function of cosmic time (e.g. Lagos et al. 2018; Schulze et al. 2018; Pillepich et al. 2019; van de Sande et al. 2019).
This is confirmed by the detailed bulge/disk photometric decomposition of Méndez-Abreu et al. (2017) for the limited subset of CALIFA galaxies in common with the sample presented here.
Acknowledgments
We would like to thank the anonymous referee for constructive comments that helped improve some aspects of the original manuscript. This study makes use of the data provided by the Calar Alto Legacy Integral Field Area (CALIFA) survey (http://www.califa.caha.es). Based on observations collected at the Centro Astronòmico Hispano Alemán (CAHA) at Calar Alto, operated jointly by the Max-Planck-Institut für Astronomie and the Instituto de Astrofisica de Andalucia (CSIC). CALIFA is the first legacy survey being performed at Calar Alto. The CALIFA collaboration would like to thank the IAA-CSIC and MPIA-MPG as major partners of the observatory, and CAHA itself, for the unique access to telescope time and support in manpower and infrastructures. The CALIFA collaboration thanks also the CAHA staff for the dedication to this project. Funding and financial support acknowledgements: J. F.-B. from grant AYA2016-77237-C3-1-P from the Spanish Ministry of Economy and Competitiveness (MINECO); GvdV acknowledges funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme undergrant agreement no. 724857 (Consolidator Grant ArcheoDyn). B. G.-L. acknowledge support from the State Research Agency (AEI) of the Spanish Ministry of Science, Innovation and Universities (MCIU) and the European Regional Development Fund (FEDER) under grant with reference AYA2015-68217-P. SFS is grateful for the support of a CONACYT grant CB-285080 and FC-2016-01-1916, and funding from the PAPIIT-DGAPA-IA101217 (UNAM) project. L. Z. acknowledges support from Shanghai Astronomical Observatory, Chinese Academy of Sciences under grant no. Y895201009. L. G. was supported in part by the US National Science Foundation under Grant AST-1311862. RGD from AYA2016-77846-P, AYA2014-57490-P, AYA2010-15081, and Junta de Andalucí a FQ1580. IM from grants AYA2013-42227-P and AYA2016-76682-C3-1-P. RGB, RMGD, IM, and EP acknowledge financial support from the State Agency for Research of the Spanish MCIU through the “Center of Excellence Severo Ochoa” award to the Instituto de Astrofísica de Andalucía (SEV-2017-0709).
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Amorín, R., Fontana, A., Pérez-Montero, E., et al. 2017, Nat. Astron., 1, 0052 [NASA ADS] [CrossRef] [Google Scholar]
- Amorisco, N. C., Evans, N. W., & van de Ven, G. 2014, Nature, 507, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Arnold, J. A., Romanowsky, A. J., Brodie, J. P., et al. 2014, ApJ, 791, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Barrera-Ballesteros, J. K., Falcón-Barroso, J., García-Lorenzo, B., et al. 2014, A&A, 568, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battaglia, G., Helmi, A., Tolstoy, E., et al. 2008, ApJ, 681, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Bedregal, A. G., Aragón-Salamanca, A., & Merrifield, M. R. 2006, MNRAS, 373, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Bellstedt, S., Forbes, D. A., Foster, C., et al. 2017, MNRAS, 467, 4540 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J. 2005, MNRAS, 363, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Boardman, N. F., Weijmans, A.-M., van den Bosch, R., et al. 2017, MNRAS, 471, 4005 [NASA ADS] [CrossRef] [Google Scholar]
- Brasseur, C. M., Martin, N. F., Macciò, A. V., Rix, H.-W., & Kang, X. 2011, ApJ, 743, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Brough, S., van de Sande, J., Owers, M. S., et al. 2017, ApJ, 844, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., Dekel, A., Kolatt, T. S., et al. 2001, ApJ, 555, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Bershady, M. A., Law, D. R., et al. 2015, ApJ, 798, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Burkert, A., Förster Schreiber, N. M., Genzel, R., et al. 2016, ApJ, 826, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2016, ARA&A, 54, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Copin, Y. 2003, MNRAS, 342, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Emsellem, E., Bacon, R., et al. 2007, MNRAS, 379, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Emsellem, E., Krajnović, D., et al. 2011a, MNRAS, 413, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Emsellem, E., Krajnović, D., et al. 2011b, MNRAS, 416, 1680 [NASA ADS] [CrossRef] [Google Scholar]
- Catalán-Torrecilla, C., Gil de Paz, A., Castillo-Morales, A., et al. 2017, ApJ, 848, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Pérez, E., García Benito, R., et al. 2013, A&A, 557, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comerón, S., Elmegreen, B. G., Knapen, J. H., et al. 2011, ApJ, 741, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Cortese, L., Fogarty, L. M. R., Bekki, K., et al. 2016, MNRAS, 463, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Cortese, L., van de Sande, J., Lagos, C. P., et al. 2019, MNRAS, 485, 2656 [NASA ADS] [CrossRef] [Google Scholar]
- Croom, S. M., Lawrence, J. S., Bland-Hawthorn, J., et al. 2012, MNRAS, 421, 872 [NASA ADS] [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- de Zeeuw, P. T., Bureau, M., Emsellem, E., et al. 2002, MNRAS, 329, 513 [NASA ADS] [CrossRef] [Google Scholar]
- del Moral-Castro, I., García-Lorenzo, B., Ramos Almeida, C., et al. 2019, MNRAS, 485, 3794 [NASA ADS] [CrossRef] [Google Scholar]
- D’Eugenio, F., Houghton, R. C. W., Davies, R. L., & Dalla Bontà, E. 2013, MNRAS, 429, 1258 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Lynden-Bell, D., Burstein, D., et al. 1987, ApJ, 313, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Cappellari, M., Krajnović, D., et al. 2007, MNRAS, 379, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Cappellari, M., Krajnović, D., et al. 2011, MNRAS, 414, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Falcón-Barroso, J., Lyubenova, M., & van de Ven, G. 2015, in Galaxy Masses as Constraints of Formation Models, eds. M. Cappellari, & S. Courteau, IAU Symp., 311, 78 [NASA ADS] [Google Scholar]
- Falcón-Barroso, J., Lyubenova, M., van de Ven, G., et al. 2017, A&A, 597, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, J. L., Domínguez Sánchez, H., & Bernardi, M. 2019, MNRAS, 483, 2057 [NASA ADS] [CrossRef] [Google Scholar]
- Fogarty, L. M. R., Scott, N., Owers, M. S., et al. 2014, MNRAS, 443, 485 [NASA ADS] [CrossRef] [Google Scholar]
- García-Benito, R., González Delgado, R. M., Pérez, E., et al. 2017, A&A, 608, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gomes, J. M., Papaderos, P., Vílchez, J. M., et al. 2016, A&A, 585, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González Delgado, R. M., Cerviño, M., Martins, L. P., Leitherer, C., & Hauschildt, P. H. 2005, MNRAS, 357, 945 [NASA ADS] [CrossRef] [Google Scholar]
- González Delgado, R. M., García-Benito, R., Pérez, E., et al. 2015, A&A, 581, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graham, A. W., Janz, J., Penny, S. J., et al. 2017, ApJ, 840, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, M. T., Cappellari, M., Li, H., et al. 2018, MNRAS, 477, 4711 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., Leauthaud, A., Emsellem, E., et al. 2017, ApJ, 851, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Husemann, B., Jahnke, K., Sánchez, S. F., et al. 2013, A&A, 549, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ibarra-Medel, H. J., Avila-Reese, V., Sánchez, S. F., González-Samaniego, A. R., & Rodríguez-Puebla, A. 2019, MNRAS, 483, 4525 [NASA ADS] [CrossRef] [Google Scholar]
- Kelz, A., Verheijen, M. A. W., Roth, M. M., et al. 2006, PASP, 118, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Bender, R. 2012, ApJS, 198, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Krajnović, D., Cappellari, M., de Zeeuw, P. T., & Copin, Y. 2006, MNRAS, 366, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Krajnović, D., Emsellem, E., Cappellari, M., et al. 2011, MNRAS, 414, 2923 [NASA ADS] [CrossRef] [Google Scholar]
- Lagos, C. D. P., Schaye, J., Bahé, Y., et al. 2018, MNRAS, 476, 4327 [NASA ADS] [CrossRef] [Google Scholar]
- Lambas, D. G., Maddox, S. J., & Loveday, J. 1992, MNRAS, 258, 404 [NASA ADS] [Google Scholar]
- Laurikainen, E., Salo, H., Buta, R., Knapen, J. H., & Comerón, S. 2010, MNRAS, 405, 1089 [NASA ADS] [Google Scholar]
- Liu, Y., Zhou, X., Ma, J., et al. 2005, AJ, 129, 2628 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, C.-P., Greene, J. E., McConnell, N., et al. 2014, ApJ, 795, 158 [NASA ADS] [CrossRef] [Google Scholar]
- McDermid, R. M., Emsellem, E., Shapiro, K. L., et al. 2006, MNRAS, 373, 906 [Google Scholar]
- Méndez-Abreu, J., Ruiz-Lara, T., Sánchez-Menguiano, L., et al. 2017, A&A, 598, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Méndez-Abreu, J., Sánchez, S. F., & de Lorenzo-Cáceres, A. 2019, MNRAS, 488, L80 [NASA ADS] [CrossRef] [Google Scholar]
- Mo, H. J., Mao, S., & White, S. D. M. 1998, MNRAS, 295, 319 [Google Scholar]
- Papastergis, E., Cattaneo, A., Huang, S., Giovanelli, R., & Haynes, M. P. 2012, ApJ, 759, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Pillepich, A., Nelson, D., Springel, V., et al. 2019, MNRAS, 490, 3196 [NASA ADS] [CrossRef] [Google Scholar]
- Querejeta, M., Eliche-Moral, M. C., Tapia, T., et al. 2015, A&A, 579, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raskutti, S., Greene, J. E., & Murphy, J. D. 2014, ApJ, 786, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Renzini, A., & Peng, Y.-J. 2015, ApJ, 801, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Romanowsky, A. J., & Fall, S. M. 2012, ApJS, 203, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Ryś, A., Falcón-Barroso, J., & van de Ven, G. 2013, MNRAS, 428, 2980 [NASA ADS] [CrossRef] [Google Scholar]
- Ryś, A., van de Ven, G., & Falcón-Barroso, J. 2014, MNRAS, 439, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Ryś, A., Koleva, M., Falcón-Barroso, J., et al. 2015, MNRAS, 452, 1888 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Avila-Reese, V., Hernandez-Toledo, H., et al. 2018, Rev. Mexicana Astron. Astrofis., 54, 217 [Google Scholar]
- Sánchez, S. F., Kennicutt, R. C., Gil de Paz, A., et al. 2012, A&A, 538, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez, S. F., García-Benito, R., Zibetti, S., et al. 2016, A&A, 594, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez, S. F., Barrera-Ballesteros, J. K., Sánchez-Menguiano, L., et al. 2017, MNRAS, 469, 2121 [NASA ADS] [CrossRef] [Google Scholar]
- Schawinski, K., Urry, C. M., Simmons, B. D., et al. 2014, MNRAS, 440, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Schulze, F., Remus, R.-S., Dolag, K., et al. 2018, MNRAS, 480, 4636 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, S., Mo, H. J., White, S. D. M., et al. 2003, MNRAS, 343, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Shimasaku, K., Fukugita, M., Doi, M., et al. 2001, AJ, 122, 1238 [NASA ADS] [CrossRef] [Google Scholar]
- Strateva, I., Ivezić, Ž., Knapp, G. R., et al. 2001, AJ, 122, 1861 [Google Scholar]
- Toloba, E., Boselli, A., Cenarro, A. J., et al. 2011, A&A, 526, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toloba, E., Guhathakurta, P., Boselli, A., et al. 2015, ApJ, 799, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A., & Toomre, J. 1972, ApJ, 178, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Valdes, F., Gupta, R., Rose, J. A., Singh, H. P., & Bell, D. J. 2004, ApJS, 152, 251 [NASA ADS] [CrossRef] [Google Scholar]
- van de Sande, J., Bland-Hawthorn, J., Brough, S., et al. 2017, MNRAS, 472, 1272 [NASA ADS] [CrossRef] [Google Scholar]
- van de Sande, J., Lagos, C. D. P., Welker, C., et al. 2019, MNRAS, 484, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Coelho, P., Cassisi, S., et al. 2015, MNRAS, 449, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Veale, M., Ma, C.-P., Greene, J. E., et al. 2017a, MNRAS, 471, 1428 [NASA ADS] [CrossRef] [Google Scholar]
- Veale, M., Ma, C.-P., Thomas, J., et al. 2017b, MNRAS, 464, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Walcher, C. J., Wisotzki, L., Bekeraité, S., et al. 2014, A&A, 569, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weijmans, A.-M., de Zeeuw, P. T., Emsellem, E., et al. 2014, MNRAS, 444, 3340 [NASA ADS] [CrossRef] [Google Scholar]
- Yoachim, P., & Dalcanton, J. J. 2006, AJ, 131, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, L., Ven, G. V. D., Bosch, R. V. D., et al. 2018, Nat. Astron., 2, 233 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Deprojection of λRe
For an oblate galaxy, viewed at inclination i, we obtain
as the deprojection of the observed ellipticity ε to the intrinsic ellipticity ε90° when the galaxy would be viewed edge-on (i = 90 ° ). Defining the global anisotropy parameter as 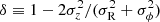 , we infer as shown by Binney (2005)
, we infer as shown by Binney (2005)
for the deprojection of the observed ordered-over-random motion to its edge-on value. Next, inserting this into the approximate relation between λR and V/σ (see Eq. (B1) of Emsellem et al. 2011), we find
as the approximate deprojection of the observed apparent stellar angular momentum λR to its edge-on value λR, 90°.
The inclination of a galaxy can be inferred directly from observations only in special cases, for example when a intrinsically thin and circular disk (in cold gas or corresponding dust) is present, so that its inclination follows directly from the observed ellipticity because 1 − ε = cos i. In general, even if disks are close to axisymmetric, they have a non-negligible intrinsic flattening q which, moreover, will vary from galaxy-to-galaxy.
If we assume that each galaxy is drawn from a group of galaxies with intrinsic shape distribution f(q), the probability of viewing the galaxy at inclination i is given by its observed ellipticity ε as
for 0 ≤ cos i < 1 − ε, and zero otherwise.
We adopt for f(q) a Gaussian distribution with mean and standard deviation (μq, σq), even though it is widely known that this cannot fit the observed ellipticity distribution of a complete (and hence randomly inclined) sample of galaxies. For example, Lambas et al. (1992) introduce even for spiral galaxies an additional Gaussian distribution in the intermediate-to-long axis ratio p with mean around the oblate case of p = 1, but also non-zero dispersion to fit the tail toward rounder galaxies. However, the effect on the inferred (median) inclination is small, even for the mildly triaxial slow-rotator elliptical galaxies, so that we assume an oblate intrinsic shape for all galaxies. Even more so, it turns out that the Gaussian distribution with (μq, σq) = (0.25, 0.12) inferred for 13 482 spirals by Lambas et al. (1992) is nearly identical to the Gaussian distribution with (μq, σq) = (0.25, 0.14) inferred the fast-rotator E/S0 galaxies from the ATLAS3D survey by Weijmans et al. (2014). Henceforth, for all fast-rotator galaxies we adopt the latter Gaussian intrinsic shape distribution, whereas Weijmans et al. (2014) find that the intrinsic shape distribution of the slow-rotator galaxies is well-described by a Gaussian with (μq, σq) = (0.63, 0.09).
Based on axisymmetric dynamical models of 24 E/S0 galaxies, Cappellari et al. (2007) find that their velocity distribution is close to isotropic in the equatorial plane (σR ∼ σϕ) and the remaining anisotropy in the meridional plane (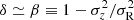 ) is approximately linearly correlated with intrinsic ellipticity ε90°. Based on this correlation, adopting a Gaussian distribution in δ with mean μδ = 0.5 ε90° and standard deviation σδ = 0.1 for 0 ≤ δ ≤ 0.8 ε90° and zero elsewhere, Emsellem et al. (2011) can explain the observed (V/σ, ε)-diagram of the complete sample of ATLAS3D fast-rotator E/S0 galaxies.
) is approximately linearly correlated with intrinsic ellipticity ε90°. Based on this correlation, adopting a Gaussian distribution in δ with mean μδ = 0.5 ε90° and standard deviation σδ = 0.1 for 0 ≤ δ ≤ 0.8 ε90° and zero elsewhere, Emsellem et al. (2011) can explain the observed (V/σ, ε)-diagram of the complete sample of ATLAS3D fast-rotator E/S0 galaxies.
We followed the procedure above for each CALIFA galaxy to approximate the observed λRe values into intrinsic λRe, 90° values at an edge-on view. First by adopting the above fast-rotator or slow-rotator Gaussian intrinsic shape distribution f(q) to obtain the average inclination iav from the median of the corresponding distribution in inclinations given by Eq. (A.4). Second by inserting iav and the observed ellipticity in ε into Eq. (A.1), which provides the approximate intrinsic ellipticity ε90°. Finally, adopting the above Gaussian distribution in the global anisotropy σδ, Eq. (A.3) provides the approximate deprojection to the intrinsic stellar angular momentum λRe, 90° within the effective radius Re.
Appendix B: Table
Stellar angular momentum properties of the CALIFA stellar kinematics sample.
All Tables
All Figures
 |
Fig. 1. Volume-corrected λR distributions for different aperture sizes (i.e. 0.5 Re, Re, and 2 Re). Top panel: distribution of λR as observed, while bottom panel: distribution of deprojected values (as explained in Appendix A). |
| In the text | |
 |
Fig. 2. Stellar angular momentum (λR) aperture relations for different aperture sizes. Top and middle panels: relation between λRe with the values of smaller/larger apertures 0.5 Re and 2 Re. Bottom panel: comparison of λRe with that computed with a 1D long-slit along the major axis of the galaxies. The dashed lines indicate the biweight mean values while dotted lines indicate the standard deviation. |
| In the text | |
 |
Fig. 3. Integrated λR profiles for our CALIFA sample of 300 galaxies. The profiles are normalized with Re and color-coded by Hubble type (as indicated by the colorbar). |
| In the text | |
 |
Fig. 4. (V/σ, ε)e (left) and (λRe, ε) (right) relations for the CALIFA sample of 300 galaxies. Galaxies are color-coded with Hubble type as indicated by the colorbar. For reference, we plot the ATLAS3D sample with gray crosses. The solid line demarcates the division between Slow and Fast rotators as established by Emsellem et al. (2011). The dashed line in the right panel marks the revised division between Slow and Fast rotators defined by Cappellari (2016). |
| In the text | |
 |
Fig. 5. λRe relations with global parameters for the sample of 300 CALIFA galaxies. Galaxies are color-coded with Hubble type. Top left panel: whisker plot enclosing the interquartile range (IQR), defined at IQR25%–IQR75% for galaxies of each morphological type. The whiskers extend out to the maximum or minimum value of the data, or to 1.5 times IQR25% or IQR75% in case there is data beyond this range. Outliers are identified with small circles. Other panels: relations with r-band absolute magnitude Mr, total stellar mass M⋆, u − r Petrosian color, concentration index R90/R50, and star formation rate SFR. See text for details. |
| In the text | |
 |
Fig. 6. Top and middle panels: λRe relations with mean age within Re, mean stellar age gradient within Re for our sample of CALIFA galaxies. Bottom panel: stellar mass–size relation. The whisker plot in the middle panel was computed in the same way as in Fig. 5. Galaxies above the 95% percentile of λRe distribution of the sample are marked in blue. The dashed line in the top and middle panels marks that percentile. |
| In the text | |
 |
Fig. 7. λRe–ϵ relation as a function of location in the star-formation rate versus total stellar mass (M⋆) relation for the CALIFA galaxies. Each panel shows the complete sample highlighting in color the ones belonging to each specific SFR–M⋆ bin. The number in each subpanel gives the |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.