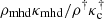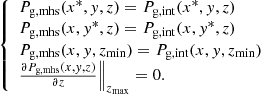| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201936367 | |
| Published online | 11 December 2019 | |
Combining magnetohydrostatic constraints with Stokes profiles inversions
I. Role of boundary conditions
1
Leibniz-Institut für Sonnenphysik, Schöneckstr. 6, 79104 Freiburg, Germany
e-mail: borrero@leibniz-kis.de
2
High Altitude Observatory, NCAR, PO Box 3000, Boulder, CO 80307, USA
3
Instituto de Astrofísica de Canarias, Avd. Vía Láctea s/n, 38205 La Laguna, Spain
4
Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain
Received:
23
July
2019
Accepted:
24
October
2019
Context. Inversion codes for the polarized radiative transfer equation, when applied to spectropolarimetric observations (i.e., Stokes vector) in spectral lines, can be used to infer the temperature T, line-of-sight velocity vlos, and magnetic field B as a function of the continuum optical-depth τc. However, they do not directly provide the gas pressure Pg or density ρ. In order to obtain these latter parameters, inversion codes rely instead on the assumption of hydrostatic equilibrium (HE) in addition to the equation of state (EOS). Unfortunately, the assumption of HE is rather unrealistic across magnetic field lines, causing estimations of Pg and ρ to be unreliable. This is because the role of the Lorentz force, among other factors, is neglected. Unreliable gas pressure and density also translate into an inaccurate conversion from optical depth τc to geometrical height z.
Aims. We aim at improving the determination of the gas pressure and density via the application of magnetohydrostatic (MHS) equilibrium instead of HE.
Methods. We develop a method to solve the momentum equation under MHS equilibrium (i.e., taking the Lorentz force into account) in three dimensions. The method is based on the iterative solution of a Poisson-like equation. Considering the gas pressure Pg and density ρ from three-dimensional magnetohydrodynamic (MHD) simulations of sunspots as a benchmark, we compare the results from the application of HE and MHS equilibrium using boundary conditions with different degrees of realism. Employing boundary conditions that can be applied to actual observations, we find that HE retrieves the gas pressure and density with an error smaller than one order of magnitude (compared to the MHD values) in only about 47% of the grid points in the three-dimensional domain. Moreover, the inferred values are within a factor of two of the MHD values in only about 23% of the domain. This translates into an error of about 160 − 200 km in the determination of the z − τc conversion (i.e., Wilson depression). On the other hand, the application of MHS equilibrium with similar boundary conditions allows determination of Pg and ρ with an error smaller than an order of magnitude in 84% of the domain. The inferred values are within a factor of two in more than 55% of the domain. In this latter case, the z − τc conversion is obtained with an accuracy of 30 − 70 km. Inaccuracies are due in equal part to deviations from MHS equilibrium and to inaccuracies in the boundary conditions.
Results. Compared to HE, our new method, based on MHS equilibrium, significantly improves the reliability in the determination of the density, gas pressure, and conversion between geometrical height z and continuum optical depth τc. This method could be used in conjunction with the inversion of the radiative transfer equation for polarized light in order to determine the thermodynamic, kinematic, and magnetic parameters of the solar atmosphere.
Key words: sunspots / Sun: magnetic fields / Sun: photosphere / magnetohydrodynamics (MHD) / polarization
© ESO 2019
1. Introduction
Inversion codes of the radiative transfer equation applied to spectropolarimetric observations of the solar surface across spectral lines are arguably the most widely used tools to infer the physical parameters of the solar atmosphere (Socas-Navarro et al. 2001; del Toro Iniesta 2003; Bellot Rubio et al. 2006; Ruiz Cobo et al. 2007; del Toro Iniesta & Ruiz Cobo 2016). These observations correspond to the so-called Stokes vector, 𝕀(x, y, λ), where the coordinates (x, y) refer to the solar surface and λ is the wavelength. Applied to this kind of observation, inversion codes provide physical parameters such as the temperature T, three-components of the magnetic field Bx, By, and Bz, and so on, as a function of (x, y, τc), where τc refers to the continuum optical-depth (i.e., far away from any spectral line). This is possible because scanning in wavelength λ is equivalent to sampling layers located at different optical depths in the solar atmosphere. Most if not all current inversion codes for the radiative transfer equation, such as SIR (Ruiz Cobo & del Toro Iniesta 1992), NICOLE (Socas-Navarro et al. 2015), SPINOR (Frutiger et al. 2000; van Noort 2012), and SNAPI (Milić & van Noort 2018), provide the inferred physical parameters as a function of the continuum optical depth τc. This is a consequence of the former being the natural choice to describe the mean-free path of the photons. It is possible to provide the parameters as a function of the coordinate z by applying the following relation between τc and the vertical coordinate z:
where ρ is the density and κc is the continuum opacity. The latter is a nonlinear function of the temperature T and the gas pressure Pg. To evaluate the equation above, T, ρ, and Pg are required. One of these thermodynamic parameters (temperature, gas pressure, or density) can be obtained from the other two by applying a suitable equation of state. There are two main sources of uncertainty when converting from the τc-scale to the z-coordinate or vice versa. The first is the inaccuracy in the top boundary condition for the gas pressure Pg(zmax). This has the effect of shifting the entire z-scale upwards or downwards for each atmospheric column (i.e., at fixed (x, y)). The second source of error is the uncertainty in the determination of T, Pg, and ρ elsewhere outside the upper boundary as a function of z, and has the effect of locally stretching or shrinking the z spacing between discrete τc grid points.
While the T is retrieved by the inversion code itself, ρ and/or Pg must be obtained by other means. This is because these two latter parameters cannot be inferred simultaneously with the temperature (see Pastor-Yabar et al. 2019) unless we provide spectral lines of different ionization stages. Unfortunately, this is not generally the case and therefore density and gas pressure are instead determined through additional constraints, namely the equation of state plus some equilibrium condition. In the case of the aforementioned inversion codes this condition is hydrostatic equilibrium. It is clear however that the assumption of hydrostatic equilibrium is unreliable in many regions of the solar photosphere, making the retrieved gas pressure and density not accurate enough so as to guarantee that the z-scale obtained from Eq. (1) is trustworthy.
Recently, Löptien et al. (2018) made use of the null divergence condition of the magnetic field, ∇ ⋅ B = 0, to obtain a z − τc conversion where the inferred Wilson depression z(τc = 1) is within 100 km of the true Wilson depression. This method however works only for the τc = 1-level and does not attempt to provide realistic values for the density and gas pressure.
Another possibility would be to circumvent Eq. (1) entirely by working directly in the z-scale. To that effect, we recently presented a new inversion code (FIRTEZ; Pastor-Yabar et al. 2019) that solves the forward and inverse equation for polarized radiative transfer directly in the z-scale instead of the τc-scale, thus providing the physical parameters (temperature, magnetic field, etc.) as a function of (x, y, z). Unfortunately FIRTEZ also suffers from similar shortcomings to those of the other inversion codes in that the reliability of the z-scale depends on an accurate determination of the density ρ or gas pressure Pg. We are then left with only one means of improving the accuracy in the inference of ρ and Pg: by dropping the assumption of hydrostatic equilibrium.
Early attempts to determine a more accurate z − τc conversion based on magnetohydrostatic (MHS) instead of hydrostatic equilibrium were by Keller et al. (1990), Solanki et al. (1993), Martinez Pillet & Vazquez (1993), and Mathew et al. (2004). These works considered cylindrical symmetry however. More recently, Puschmann et al. (2010a) developed a new method that does not assume any particular symmetry. Unfortunately, the latter method was not coupled with the inversion code in the sense that the newly retrieved ρ and Pg were not fed back into the inversion algorithm to fit the observed Stokes vector 𝕀(x, y, λ). Puschmann et al. (2010a) noticed for instance that the new gas pressure would appreciably change the continuum in the intensity profiles. Building up from their idea we aim at developing a new method to obtain more realistic densities and gas pressures based also on MHS equilibrium but in such a fashion that the resulting values can be fed back into the inversion code we have developed (FIRTEZ; Pastor-Yabar et al. 2019).
In the present work we assume that the inversion of Stokes profiles provides the temperature T(x, y, z) and magnetic field B(x, y, z) as given by three-dimensional magnetohydrodynamics (MHD) simulations of sunspots (Sect. 2). Furthermore, here we focus only on the effects of the boundary conditions. Errors in the determination of the temperature and magnetic fields via the inversion of Stokes profiles, along with the effects of the limited spatial resolution in the observations, will be addresses in future work. Under this premise, we study the reliability of the inference of the density ρ and gas pressure Pg using hydrostatic equilibrium (Sect. 3) and MHS equilibrium (Sect. 4) and compare our results with the more realistic density and gas pressure from the MHD simulations. The accuracy of the presented methods in the determination of the z − τc conversion (Eq. (1)) is assessed in Sect. 5. The limitations of the method and possible ideas as to how to combine the method presented here with inversion codes for the radiative transfer equation are addressed in Sect. 6. Finally, Sect. 7 summarizes our findings.
2. 3D nongray MHD simulations
Our investigations are based on a nongray three-dimensional MHD simulation of a sunspot following the setup described in Rempel (2012). The resulting sunspot models cover 49.152 × 49.152 × 6.144 Mm3, and were computed using gray radiative transfer and different grid resolutions. To obtain them, we restarted a nongray simulation from the model with 16 × 16 × 12 km3 resolution in Rempel (2012) and evolved it for an additional 15 min with nongray radiative transfer at a higher resolution of 12 × 12 × 8 km. At this resolution the domain has a size of 4096 × 4096 × 768 grid points. Along the third dimension (i.e., direction of gravity) only the upper 192 grid points are needed. These are enough to cover the entire photosphere, which is defined as the region above the τc = 1-level (i.e., continuum optical depth unity level), both in the granulation and umbra, including the Wilson depression. In the granulation surrounding the sunspot the τc = 1-level is located around z ≈ 1000 km. For illustration purposes a map of the magnetic field B at a fixed height of 448 km from the top boundary (i.e., close to τc = 1 in the surrounding granulation) is shown in Fig. 1. The rectangular region limited by the white-dashed lines is the one employed in our study. It encompasses 4096 × 512 × 192 grid points covering 49.152 × 6.144 × 1.536 Mm3. Along the x-axis it runs over the umbra, penumbra, and surrounding granulation. Figure 2 shows z(x, y, τc) for four optical-depth levels (from bottom to top): log τc = [0, −1, −2, −3]. This figure can be viewed as the Wilson depression at different τc-levels. For instance, the z(log τc = 0)-level is located approximately 500−600 km deeper in the umbra (x ≈ 25 Mm) than in the surrounding granulation (x ≈ 0 Mm). These four optical-depth levels have been chosen because they represent what is commonly considered as the photosphere.
 |
Fig. 1. Magnetic field B from the sunspot simulation at a height of 448 km from the upper boundary. The rectangular box in white-dashed lines is the region employed for our study. |
 |
Fig. 2. Geometrical height z for four different optical-depth levels. From bottom to top: log τc = [0, −1, −2, −3]. |
3. Hydrostatic equilibrium
Hydrostatic equilibrium implies that the gas pressure is stratified only due to gravity according to:
where ρ is the density and g = gez is the acceleration due to gravity. On the solar surface g = 2.7414 × 104 cm s−2 (cgs units are employed throughout this paper). The vertical z-component of the equation above translates into
This is a first-order ordinary differential equation that needs only one boundary condition (BC). This BC is typically set at the uppermost boundary zmax, so that Eq. (3) is integrated backwards. Because the gas pressure tends to decay exponentially1 with z, the alternative procedure, that is, setting the BC at zmin and integrating upwards, is usually avoided so as to prevent negative values of Pg, hyd. To study the accuracy to which hydrostatic equilibrium can determine the gas pressure and density we have solved Eq. (3) along the z-direction employing a fourth-order Runge-Kutta method for each grid point (x, y) in the horizontal plane in the three-dimensional domain of the MHD simulation (Sect. 2), and using in each case two different boundary conditions for Pg, hyd(zmax). The first BC takes the gas pressure on the uppermost horizontal plane to be exactly identical to that from the MHD simulations in Sect. 2: Pg, hyd(x, y, zmax) = Pg, mhd(x, y, zmax). The second BC takes the gas pressure on the uppermost horizontal plane to be axisymmetric and equals to:
where ξ = r/Rspot is the normalized radial distance from the center of the Sunspot. To understand where this equation comes from we refer the reader to Sect. 4.2. At this point we simply state that Eq. (4) results in a value for the gas pressure at zmax of about 0.4 and 160 dyn cm−2 in the umbral center (ξ = 0) and surrounding granulation (ξ = 2), respectively. For comparison purposes we note that the three-dimensional MHD simulations yield typical values for the gas pressure at zmax of the order of 102 − 103 dyn cm−2 and 10−1 − 1 dyn cm−2 in the granulation and umbra, respectively.
For the sake of simplicity, results obtained with the aforementioned boundary conditions will be referred to as Phyd, 1 and Pg, hyd, 2, respectively. After obtaining the solution for the hydrostatic gas pressure Pg, hyd, the hydrostatic densities ρhyd, 1 and ρhyd, 2 are obtained by applying the equation of state for ideal gases using the temperature from the MHD simulations:
where Tmhd is the temperature taken from the MHD simulations, u = 1.66053902 × 10−24 g is the atomic mass unit, and k = 1.38064852 × 10−16 erg K−1 is Boltzmann’s constant. The mean molecular weight μ is itself a function of the temperature and is determined solving the Saha and Boltzmann equations (Mihalas 1970, Chap. 3) self-consistently for 92 atomic species. Figure 3 shows the density (top panels) and gas pressure (bottom panels) as a function of the vertical z-axis for three grid points located in the sunspot umbra (right), penumbra (middle), and granulation surrounding the sunspot (left). These grid points are indicated in Fig. 1 as white-filled circles. In solid black we depict the actual values from the MHD simulations (Sect. 2), whereas in solid red and solid blue we show the results after applying hydrostatic equilibrium (Eq. (3)) using the two aforementioned boundary conditions: Pg, hyd(x, y, zmax) = Pg, mhd(x, y, zmax) (Phyd, 1; red), and Phyd, 2(x, y, zmax) given by Eq. (4) (blue; Phyd, 2). By construction, solid black and red curves for the gas pressure (bottom) and density (top) meet at zmax. The vertical dashed lines indicate the location of the z(τc = 1)-level (i.e., Wilson depression).
 |
Fig. 3. Top panels: density as a function of the geometrical height z (i.e., vertical coordinate) for three spatial (x, y) locations corresponding to the sunspot umbra (right), penumbra (middle), and surrounding granulation (left). These locations are indicated by white circles in Fig. 1. Bottom panels: same as top panels but for the gas pressure. Solid black curves correspond to the actual values from the three-dimensional MHD simulation (Sect. 2), whereas colored lines are the hydrostatic results using the two boundary conditions described in the text: Phyd, 1 (red) and Phyd, 2 (blue). The vertical dashed lines indicate the location of the z(τc = 1)-level (i.e., Wilson depression). |
As can be seen, the inferred pressure Pg, hyd and density ρhyd stratification as a function of z, as well as the z(τc = 1)-level, are highly dependent on the upper boundary condition P(zmax). Moreover, the match between the hydrostatic values and the ones from the MHD simulations is in general poor, with discrepancies as large as one order of magnitude in the granulation and penumbra, and up to two orders of magnitude in the umbra (Fig. 3; right panels). Of particular interest is also the fact that, whereas in the MHD simulations (black-solid curves) the gas pressure can increase or decrease with increasing z (bottom-middle panel around z ≈ 1100 km), in the hydrostatic case only ∂Pg, hyd/∂z < 0 is allowed so as to avoid negative densities.
It can be argued that it should be possible to adapt the upper boundary condition (i.e., consider it as a free parameter) so as to improve the match between the hydrostatic solutions (solid red/blue curves) and the MHD (solid black) values. This is equivalent to a change in the integration constant in Eq. (1) mentioned in Sect. 1. While this is certainly a possibility, this idea cannot be applied to real observations because in this case we do not have any information about the real pressure and density, and therefore there is nothing to match Pg, hyd and ρhyd to.
It is important to point out that neither of the two boundary conditions employed above are fully compatible with hydrostatic equilibrium. The reason is that hydrostatic equilibrium is not only represented by the z-derivative of the gas pressure (Eq. (3)), but also by the x and y-derivatives in Eq. (2): ∂Pg, hyd/∂x = ∂Pg, hyd/∂y = 0. This implies that Pg, hyd is constant in planes of fixed z. This condition is not verified by either the solid blue or the red curves in Fig. 3, as at a given z the gas pressure varies horizontally (i.e., it is different in the granulation, penumbra, umbra, etc). Indeed, it is clear that as long as the temperature is also a function of (x, y), hydrostatic equilibrium cannot be maintained in three dimensions. This occurs because if ∂Pg, hyd/∂x = ∂Pg, hyd/∂y = 0 then the same applies (through Eq. (3)) to the density: ∂ρhyd/∂x = ∂ρhyd/∂y = 0. Therefore, the application of the equation of state (Eq. (5)) directly yields: ∂T/∂x = ∂T/∂y = 0.
Thus far, we have demonstrated that the gas pressure and density inferred through hydrostatic equilibrium signficantly differ from the values in the MHD simulations (by as much as two orders of magnitude). The question now is how these inaccuracies translate into z − τc conversion as given by Eq. (1). This is addressed in Fig. 4, where we display z(x, y, τc) at log τc = 0, −1, −2, −3 (from bottom to top). Left and right panels in this figure correspond to the results obtained with the first and second boundary condition, Phyd, 1 and Phyd, 2, respectively. As can be seen by comparison with Fig. 2, the agreement between the hydrostatic solutions and the MHD simulations is rather poor. In particular the Wilson depression between the umbra and surrounding granulation is only about 150 km, whereas in the MHD simulations is closer to 500−600 km. In addition, there is a very strong asymmetry between the penumbra on either side of the umbra, in particular when employing the Phyd, 2 boundary condition given by Eq. (4). While this asymmetry does not appear in the maps of the Wilson depression of the MHD simulations (Fig. 2) it does indeed originate in the simulations, with the left-side penumbra having a stronger magnetic field than the right side due to the presence of a very elongated penumbral filament that protrudes into the umbra in a way that resembles a light bridge. This renders the thermal structure of the left and right sides slightly different. Under hydrostatic equilibrium these different temperatures immediately translate into different pressure and density stratifications with z and thus also a different z − τc conversion.
 |
Fig. 4. Left panels: two dimensional maps of z(x, y, τc) at four different log τc-levels (from bottom to top): 0, −1, −2, −3 using hydrostatic equilibrium and the boundary condition Pg, hyd(x, y, zmax) = Pg, mhd(x, y, zmax). Right panels: same as on the left but using the boundary condition where Pg, hyd(x, y, zmax) is given by Eq. (4). |
4. Magnetohydrostatic equilibrium
Under MHS equilibrium, the momentum equation takes the following form:
which is obtained by adding the Lorentz force term to Eq. (2). This is a system of three first-order partial differential equations. To avoid dealing with such a system of equations we take the divergence of Eq. (6) and transform it into a single second-order partial differential equation:
This equation is now a Poisson-like equation that can be solved provided that the right-hand-side is known. As mentioned in Sect. 1 we are assuming throughout this paper that the inversion of Stokes profiles provides the temperature T and magnetic field, Bx, By, Bz, as a function of (x, y, z). However we are still lacking the knowledge of the density ρmhs(x, y, z), which is in fact one of our unknowns. To circumvent this problem we propose an initial density distribution  , which is then used to determine the right-hand side of Eq. (7). We then solve this equation employing the fishpack2 library (Swarztrauber & Sweet 1975). This yields a gas pressure
, which is then used to determine the right-hand side of Eq. (7). We then solve this equation employing the fishpack2 library (Swarztrauber & Sweet 1975). This yields a gas pressure  which, along with the already known temperature T(x, y, z), is used to obtain a new density
which, along with the already known temperature T(x, y, z), is used to obtain a new density 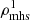 via the equation of state (Eq. (5)). Here,
via the equation of state (Eq. (5)). Here, 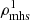 should improve compared to our original estimation
should improve compared to our original estimation 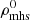 . We then iterate the entire procedure until convergence is achieved, which we define as being the point at which neither the gas pressure nor the density change significantly in several consecutive iterations. In all our tests this occurs within 20−30 iterations.
. We then iterate the entire procedure until convergence is achieved, which we define as being the point at which neither the gas pressure nor the density change significantly in several consecutive iterations. In all our tests this occurs within 20−30 iterations.
Equation (7) is a second-order partial differential equation, thus requiring two boundary conditions per dimension. In our case we employ Dirichlet boundary conditions at all six planes surrounding the domain: Pg, mhs(x*, y, z), Pg,mhs(x,y*,z), Pg, mhs(x, y, z*), where x* refers to both xmin and xmax, and likewise for y* and z*.
4.1. Best-case scenario
We now consider a best-case scenario in which we assume that all values of the gas pressure at the boundaries in the three-dimensional domain indicated by the white box in Fig. 1 are identical to the MHD values:
Further we assume that on the right-hand side of Eq. (7) the density is also given by the values from the MHD simulations. If in the employed simulations (see Sect. 2) the additional terms in the momentum equation that are ignored by the MHS equilibrium, such as the time-derivative of the velocity, and the advection and viscous terms (see Sect. 2.2 Vögler 20033), are negligible, then the gas pressure and density resulting from solving Eq. (7) should be very similar to the values in the MHD simulations. In other words, this test can be considered as a study of how close the MHD simulations are to MHS equilibrium. Gas pressure and density obtained with this test are henceforth referred to as Pmhs, 1 and ρmhs, 1, respectively.
4.2. Practical scenario
We subsequently performed a more practical test, where we do not assume that the upper/lower and side boundary conditions, or the knowledge of the initial density for the iteration of Eq. (7), are given by the MHD simulations (Eq. (8)). Instead we employ empirical boundary conditions that can be applied to actual observations. These boundary conditions result from polynomial approximations interpolated over the angular average of the three-dimensional MHD simulations at different radial distances from the center of the sunspot. To this end we first convert from Cartesian (x, y, z) to cylindrical (ξ, ϕ, z) coordinates in our three-dimensional domain. Here ξ is the normalized radial distance from the center of the sunspot: ξ = r/Rspot. We then perform ϕ-averages (annular) of the logarithm of the gas pressure and density from the MHD simulations for (ξ, z) pairs. Finally, we fit fourth-order polynomials as a function of ξ at each geometrical height zj. Mathematically,
where 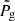 and
and 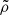 refer to the annular averages. Examples of such polynomial fits are shown in Fig. 5 for four different heights z = 0, 512, 1024, 1528 km. As it can seen, Eq. (4) can be obtained from the equation above by simply taking zj = zmax = 1528 km. These polynomials allow us to recreate the gas pressure and density at any position (r, z) in the three-dimensional domain. Hereafter we refer to these values as interpolated or int for short. We employ these polynomial approximations to build the initial density ρ0 = ρint(r, z) used to iterate the solution of Eq. (7), as well as the gas pressure at the boundaries:
refer to the annular averages. Examples of such polynomial fits are shown in Fig. 5 for four different heights z = 0, 512, 1024, 1528 km. As it can seen, Eq. (4) can be obtained from the equation above by simply taking zj = zmax = 1528 km. These polynomials allow us to recreate the gas pressure and density at any position (r, z) in the three-dimensional domain. Hereafter we refer to these values as interpolated or int for short. We employ these polynomial approximations to build the initial density ρ0 = ρint(r, z) used to iterate the solution of Eq. (7), as well as the gas pressure at the boundaries:
 |
Fig. 5. Logarithm of the density (left) and gas pressure (right) as a function of the normalized radial distance to the center of the sunspot ξ = r/Rspot at four different vertical heights z = 0, 512, 1024, 1528 km. Larger z values correspond to higher atmospheric layers. Black circles correspond to the azimuthal- or ϕ-averages of the MHD simulations (Sect. 2). Red curves are obtained through fourth-order polynomial approximations to the black circles. |
The described procedure implies that the boundary conditions for the gas pressure and initial density are axisymmetric. We emphasize that the interpolated values (solid red lines in Fig. 5) thus obtained are usually within 20% of the mean values (black circles). However, when compared with the actual values from the three-dimensional MHD simulations at individual grid points, differences of an order of magnitude or more are common. It is in this sense that we declare this test to be suitable for real observations since it does not require accurate knowledge of the boundary conditions. We now have all the ingredients needed to solve Eq. (7) iteratively and obtain the gas pressure and density that are consistent with MHS equilibrium and are consistent with the temperatures inferred from the inversion of Stokes profiles: Tinv(x, y, z). Results obtained with these boundary conditions are referred to as Pmhs, 2 and ρmhs, 2.
Examples of the retrieved density and gas pressure in the two scenarios we have just described, for the same three spatial locations as in Fig. 3 (see also white circles in Fig. 1), are displayed in Fig. 6. They are indicated by the dashed red and dashed blue lines for Pmhs, 1 and Pmhs, 2, respectively. It can be readily seen that the agreement between these new results and the ones from the MHD simulations (solid black lines) is not only very good, but is also far better than the hydrostatic case (solid red and solid blue lines in Fig. 3). Of particular interest is the fact that now, the gas pressure Pg, mhs can increase with increasing z without involving negative densities. It is also worth noting that the derived gas pressure and density depend much less on the boundary conditions in the MHS case than in the hydrostatic one. This occurs because in the MHS case the pressure stratification depends strongly on the Lorentz force (second term on the right-hand side of Eq. (7)). Of particular importance are the x and y variations of the magnetic pressure and tension, which couple the results in the horizontal direction, thereby enabling the derived values to quickly forget the boundary condition a few grid points away from the upper boundary in the z-direction.
 |
Fig. 6. Same as Fig. 3 but showing results from MHS equilibrium using different boundary conditions: ideal case scenario (dashed red lines) where boundary conditions are identical to the MHD simulations, and practical scenario (dashed blue lines) where boundary conditions are given by the interpolated model (Eq. (11)). Original values from MHD simulations (Sect. 2) are displayed in solid black lines. |
Using the gas pressure Pg, mhs and density ρmhs from the previous two tests, and assuming that the inversion of Stokes profiles correctly retrieves the temperature from the simulations Tmhd, we now employ Eq. (1) to determine the optical-depth scale τc. Figure 7 shows the geometrical height z for the location of the optical-depth values of log τc = 0, −1, −2, −3 (i.e., Wilson depression at different optical depth levels). Again, results are remarkably good and much better than the hydrostatic case shown in Fig. 4. Of particular interest is the disappearance of the asymmetry between the left and right penumbral sides that was present in the hydrostatic case. Under MHS equilibrium the gas pressure does not depend only on the thermal stratification but also on the Lorentz force. This compensates the different temperatures at either side of the umbra, yielding a Wilson depression in better agreement with the MHD simulations (Fig. 2). It is worth pointing out that z(log τc = −3) with interpolated boundary conditions for the gas pressure (Eq. (11); see uppermost-right panel in Fig. 7) features a very axisymmetric distribution. This occurs because log τc = −3 is close to the upper boundary, and therefore results at this layer can be conditioned by the axisymmetic boundary conditions imposed there.
 |
Fig. 7. Same as Fig. 4 but employing MHS equilibrium and different boundary conditions: ideal case scenario where boundary conditions are identical to the MHD simulations (left panels), and practical scenario where boundary conditions are given by the interpolated model (right panels; Eq. (11)). |
5. Discussion
In the above sections we describe two methods to obtain the gas pressure and density that are consistent with hydrostatic (Sect. 3) and MHS (Sect. 4) equilibrium using different boundary conditions. We have seen that the inferred Pg and ρ are qualitatively much closer to the MHD values in the MHS case than in the hydrostatic one. The same applies to the z − τc conversion. In this section we present a more quantitative study of the reliability in the inference of the gas pressure and density as well as of the reliability in the z − τc conversion.
Figure 8 displays the histograms of the following quantities: log(Pg, mhd/P†) (left-panels) and log(ρmhd/ρ†) (right-panels). Here, P† and ρ† stand for the gas pressure and density obtained in the different tests carried out in this paper: hydrostatic equilibrium using boundary condition Phyd, 1 (solid red line), same but with Phyd, 2 as boundary condition (Eq. (4); solid blue line), MHS equilibrium with Pmhs, 1 boundary conditions (Eq. (8); dashed red line), and MHS equilibrium with Pmhs, 2 boundary conditions (Eq. (11); dashed blue line). To estimate the reliability in the determination of the gas pressure and density we determine, from these histograms, the percentage of points inside the three-dimensional domain where the inferred gas pressure and density are within one order of magnitude from those in the MHD simulations: ∥log(Pg, mhd/P†)∥ ≤ 1 and ∥log(ρmhd/ρ†)∥ ≤ 1. This is equivalent to obtaining the area of each histogram between the abscissa values [ − 1, 1]. Likewise we determine the percentage of points where the inferred gas pressure and density are within a factor of two from those in the MHD simulations: ∥log(Pg, mhd/P†)∥ ≤ 0.3 and ∥log(ρmhd/ρ†)∥ ≤ 0.3. Results for the four tests carried out in this paper are summarized in Table 1. We discuss here only those results where we employed boundary conditions that can be applied to real observations: Phyd, 2 (blue solid-line in Fig. 8) and Pmhs, 2 (blue-dashed line in Fig. 8). Under the assumption of hydrostatic equilibrium the inferred gas pressure and density are within one order of magnitude, and within a factor of two of the correct values, in only about 47 and 23%, respectively, of the grid points in the three-dimensional domain. In the case of MHS equilibrium these numbers increase to about 84 and 55%, respectively. This latter represents a huge improvement over the hydrostatic case and it certainly opens the possibility for inversion codes of the polarized radiative transfer equation to infer for the first time, via MHS constraints, reliable values of the gas pressure and density in the solar atmosphere.
 |
Fig. 8. Histograms of the logarithm of the quotient Pmhd/P† (left) and ρmhd/ρ† (right) in the entire three-dimensional domain, where † indicates the values obtained in the four different tests we have carried out. Solid colored curves represent the inferences in the hydrostatic case (red for boundary condition Phyd, 1; blue for boundary condition Phyd, 2), and dashed coloured curves display the MHS case (red for boundary condition Pmhs, 1; blue for boundary condition Pmhs, 2). See text for details. |
Summary of results in the determination of gas pressure and density.
We now turn our attention to the z − τc conversion. As mentioned in Sect. 1 one of the main sources of uncertainty here is the accuracy in the determination of T, Pg, and ρ elsewhere outside the upper boundary as a function of z, which has the effect of locally stretching or shrinking the z spacing between discrete τc grid points. This effect is determined by the dτc/dz derivative given by Eq. (1). To study it we plot the following ratio in Fig. 9:
 |
Fig. 9. Same as Fig. 8 but for the logarithm of the quotient |
where again the symbol † is used to indicate that the density and continuum opacity, which depend on the temperature and gas pressure, have been obtained using the different approximations and boundary conditions described in Sects. 3 and 4. As this figure shows, the z-spacing between discrete τc points is better retrieved in the MHS case than in the hydrostatic one. We can also see that the differences caused by using different boundary conditions for Pg(zmax) (red vs. blue lines) are small compared to the differences produced by switching from hydrostatic to MHS equilibrium (solid vs. dashed lines).
Once the local stretching or shrinking of the z − τc scale has been studied under different approximations we can address the full z − τc conversion including the effects of the global shift in this scale produced by the choice of boundary conditions. Figure 10 shows histograms of the quantity: z†(log τc)−zmhd(log τc) at four optical-depth values: log τc = [0, −1, −2, −3] (upper-left, upper-right, bottom-left, bottom-right). Here, z†(log τc) represents the z − τc conversion obtained from the same four tests described above. In other words, Fig. 10 displays the histograms of the differences between the maps displayed in Figs. 4 and 7, and the same map from the MHD simulations: Fig. 2. The histograms of z† − zmhd using hydrostatic equilibrium (solid red and solid blue lines) feature a bimodal distribution at all four optical depths studied. The first of the two peaks of the distribution is located at z† − zmhd ≈ 0 to −100 km and is composed by grid points in the granulation that surrounds the sunspot. The second peak is due mostly to grid points in the sunspot umbra as it is located around z† − zmhd ≈ 400 km. The mean of the absolute value of the differences at each optical-depth level, 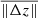 , is in the range 160 − 200 km (see Table 2).
, is in the range 160 − 200 km (see Table 2).
 |
Fig. 10. Histograms of the difference between the inferred height z† and the height in the MHD simulations zmhd for different optical-depth levels: log τc = 0 (upper-left), −1 (upper-right), −2 (bottom-left), and −3 (bottom-right). Solid colored lines represent the inferences in the hydrostatic case (red for boundary condition Phyd, 1; blue for boundary condition Phyd, 2), and dashed colored lines display the MHS case (red for boundary condition Pmhs, 1; blue for boundary condition Pmhs, 2). See text for details. |
Summary of results for the determination of the z − τc conversion.
Histograms of z† − zmhd using MHS equilibrium (color-dashed lines) feature a clear single-peak distribution centered around z† − zmhd ≈ 0 km, and yield a value of 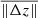 that is a factor three to five better than the hydrostatic case (see Table 2). The mean of the absolute value of the differences,
that is a factor three to five better than the hydrostatic case (see Table 2). The mean of the absolute value of the differences, 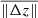 , ranges 10 − 40 km in the best-case scenario, whereas it is about 30 − 70 km in the practical scenario (see Table 2). We reiterate here that the best-case scenario helps us to understand how far or close the MHD simulations are to MHS equilibrium.
, ranges 10 − 40 km in the best-case scenario, whereas it is about 30 − 70 km in the practical scenario (see Table 2). We reiterate here that the best-case scenario helps us to understand how far or close the MHD simulations are to MHS equilibrium.
The width of the histograms around the center value is smaller in the deep photosphere (log τc = 0; upper-left panel in Fig. 10) than in the upper photosphere (log τc = −3; lower-bottom panel in Fig. 10). This is because the approximation of MHS equilibrium starts to break down in the upper photosphere, where the velocity terms that we neglect in Eqs. (6) and (7) (see also description in Sect. 4) begin to play a non-negligible role. Because in this case the histograms feature a single peak that is centered around z† − zmhd ≈ 0 km it is possible to ascribe the width of the histograms to a measure of the standard deviation of the distribution, hence to an error in the determination of z − τc conversion. We refer to this error as σz, τc. Their values are summarized in Table 2 and, as it can be seen, they are comparable to 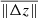 . The numbers presented in Tables 1 and 2 allow us to establish that in the MHS case, the more practical scenario where the boundary conditions are not known but are instead guessed (i.e interpolated), the uncertainty in the determination of the z − τc conversion increases by a factor of two to three with respect to an ideal scenario where the boundary conditions are fully known. However, in the hydrostatic case there is very little difference between both sets of boundary conditions.
. The numbers presented in Tables 1 and 2 allow us to establish that in the MHS case, the more practical scenario where the boundary conditions are not known but are instead guessed (i.e interpolated), the uncertainty in the determination of the z − τc conversion increases by a factor of two to three with respect to an ideal scenario where the boundary conditions are fully known. However, in the hydrostatic case there is very little difference between both sets of boundary conditions.
An additional test that we carried out involves the MHS case (Eq. (7)) with Neumann boundary conditions for the upper-most layer of the three-dimensional domain zmax, while keeping a Dirichlet condition at zmin. In this case, the boundary conditions in Eq. (11) were substituted by:
Results in this case are almost identical to those employing Eq. (11). Density and pressure stratifications become smoother close to zmax compared to those presented as ρmhs, 2 and Pmhs, 2 in Fig. 6 (blue-dashed lines). However, these changes are only minor, and in fact Figs. 7, 8, and 10, as well as Tables 1 and 2 remain almost unchanged.
6. Limitations and implementation in Stokes inversions codes
There are some important limitations in the method we have described to obtain reliable values for the gas pressure, density, and the conversion from z to τc. The first limitation has to do with the knowledge of the Lorentz force term in Eq. (6). We have assumed that this term can be calculated without any issues because the magnetic field B is fully provided by the numerical simulations (Sect. 2). However, whenever B is inferred from the inversion of the Stokes vector we must consider that in fact B is affected by what is referred to as the 180° ambiguity. This ambiguity implies that the inversion cannot distinguish between two possible solutions: B = (Bx, By, Bz) and B† = ( − Bx, −By, Bz), at each (x, y, z) grid point in the observed domain. A number of methods have been developed (Metcalf 1994; Georgoulis 2005; Metcalf et al. 2006) in the past to address this issue. If our method is to be applied to actual inferences of the magnetic field via the inversion of the radiative transfer equation, then we must first solve the 180° ambiguity problem. Failing to do so will certainly return unrealistic values of the electric current, j ∝ ∇ × B, and thus also negatively affect the right-hand side of Eqs. (6) and (7).
The second limitation has to do with the fact that even after correctly solving the 180° ambiguity problem mentioned above, throughout this paper we consider that T(x, y, z) and B(x, y, z) are known, for instance via the application of our recently developed Stokes inversion code in the z-scale (Pastor-Yabar et al. 2019). With this we have shown that it is possible to obtain accurate values for the density ρ(x, y, z) and gas pressure Pg(x, y, z) by applying MHS constraints (Sect. 4). However, one of the main conclusions of Pastor-Yabar et al. (2019) is that T and B can only be properly retrieved by the inversion if Pg (or ρ) is reliably known (see also Sect. 1). This problem can only be solved iteratively, that is, proposing an initial solution for Pg and ρ that is used during the Stokes inversion to obtain T and B. The latter two physical parameters can then be employed to apply the MHS constraints and obtain a better estimation of Pg and ρ that is then sent back into the Stokes inversion. It remains to be proven whether or not this procedure would converge.
An additional limitation that is worth mentioning at this point but is not addressed in this paper concerns the fact that our method works best in the photosphere where the assumption of MHS equilibrium is adequate. Higher up, in particular in the chromosphere, this assumption will surely break down because velocity terms play an important role in the force balance. The main problem here is that Stokes inversion codes use the Doppler effect to retrieve the line-of-sight component of the velocity (vz if at disk center) only and therefore those additional terms cannot be readily evaluated. A possible solution could be to use time-resolved spectropolarimetric observations to infer vx and vy (Welsch et al. 2004; Asensio Ramos et al. 2017).
Another important limitation that needs to be addressed when applying this method to real observations is the fact that, unlike numerical simulations, the inversion of the radiative transfer equation provides the temperature T and magnetic field vector B with different degrees of certainty at each (x, y, z) grid point, in particular along the z-coordinate, with errors increasing quickly below τc = 1 and above τc = 10−4 (actual values will depend on the spectral lines employed in the inversion). How the inaccuracies in the determination of these two physical parameters affect the retrieval of the gas pressure Pg and density ρ remains to be seen. If this effect is too large, extrapolation of the physical quantities or perhaps a switch to hydrostatic equilibrium (i.e., by making the term related to the magnetic field on the right-hand side of Eq. (7) vanish) outside the region where the spectral lines are sensitive might be needed.
7. Conclusions
Here we present a new method to determine the gas pressure and density in the solar atmosphere under the assumption of MHS equilibrium. The method was developed to be used in conjunction with an inversion code for the polarized radiative transfer equation. Therefore, it considers that the temperature T and magnetic field B are known (i.e., given by the inversion) in the three-dimensional domain (x, y, z). The proposed method has been tested with a three-dimensional numerical simulation of a sunspot, and we confirm its potential to retrieve values for the density and gas pressure that are, in more than 80% of the grid points in the domain, within one order of magnitude of the values of the numerical simulation. Moreover, in more than 50% of the domain the retrieval is within a factor of two of the numerical simulation (see Fig. 8 and Table 1). In contrast, we find that the approach based on hydrostatic equilibrium (as extensively used in current inversion codes such as SIR, SPINOR, NICOLE, and SNAPI) determines the correct order of magnitude of these two physical parameters in only about 45% of the domain, whereas a more accurate inference, within a factor of two, occurs only in about 20% of the domain.
Once the pressure and density are known, it is possible to (together with temperatures from the inversion) calculate a z − τc conversion employing Eq. (1). Again we have shown that the application of the MHS solution dramatically improves this conversion compared to the hydrostatic case. Under ideal conditions, when taking as boundary conditions the values of the gas pressure provided by the MHD simulation, our method retrieves the geometrical height z for different τc-levels with an accuracy of some 10 − 40 km. If instead we employ boundary conditions that are more adequate for real applications (i.e., boundary conditions obtained from interpolated models) the error in the determination of the z scale at various τc-levels increases to about 30 − 70 km (see Table 2).
At this juncture it is important to mention that while the method we present here works better with an inversion code for the radiative transfer equation that retrieves the physical parameters in z (Pastor-Yabar et al. 2019), it could also in principle be adapted to inversion codes that retrieve the physical parameters in τc. Therefore, the aforementioned codes that employ hydrostatic equilibrium need not continue to do so.
The most obvious advantage of being able to obtain a reliable z − τc conversion is the ability to determine accurate spatial derivatives of the magnetic field and thus also accurate electric currents (Puschmann et al. 2010b), which are considered as proxies of magnetic reconnection and chromospheric and coronal activity (Priest 1999). In addition, the ability to infer accurate values for the gas pressure and density in the lower solar atmosphere can significantly help to improve methods that extrapolate the magnetic field observed in the photosphere towards the chromosphere and corona (Zhu & Wiegelmann 2018).
The presented method has however a number of limitations such as a limited applicability in the upper solar atmosphere (i.e., chromosphere), where the spatial and temporal derivatives of the velocity play an important role in the momentum equation. It also remains to be seen how this method performs with real observations, where the spatial resolution is much lower than in the numerical simulations, and where the determination of the temperature and magnetic field comes with an attached uncertainty level as a consequence of the application of the inversion process applied to spectropolarimetric observations. We will try to address some of these issues in the future.
Fishpack library can be downloaded here https://www2.cisl.ucar.edu/resources/legacy/fishpack
Acknowledgments
This work was supported by the Deutsche Forschungsgemeinschaft, DFG project number 321818926. JMB acknowledges financial support from the Spanish Ministry of Economy and Competitiveness (MINECO) under the 2015 Severo Ochoa Program MINECO SEV-2015-0548. The authors acknowledge the comments and suggestions for improvement by the referee Dr. Ivan Milić. This material is based upon work supported by the National Center for Atmospheric Research, which is a major facility sponsored by the National Foundation under Cooperative Agreement No. 1852977. This research has made use of NASA’s Astrophysics Data System.
References
- Asensio Ramos, A., Requerey, I. S., & Vitas, N. 2017, A&A, 604, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellot Rubio, L. R. 2006, in Solar Polarization 4, eds. R. Casini, & B. W. Lites, ASP Conf. Ser., 358, 107 [NASA ADS] [Google Scholar]
- del Toro Iniesta, J. C. 2003, Astron. Nachr., 324, 383 [NASA ADS] [CrossRef] [Google Scholar]
- del Toro Iniesta, J. C., & Ruiz Cobo, B. 2016, Liv. Rev. Sol. Phys., 13, 4 [Google Scholar]
- Frutiger, C., Solanki, S. K., Fligge, M., & Bruls, J. H. M. J. 2000, A&A, 358, 1109 [NASA ADS] [Google Scholar]
- Georgoulis, M. K. 2005, ApJ, 629, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, C. U., Steiner, O., Stenflo, J. O., & Solanki, S. K. 1990, A&A, 233, 583 [NASA ADS] [Google Scholar]
- Löptien, B., Lagg, A., van Noort, M., & Solanki, S. K. 2018, A&A, 619, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martinez Pillet, V., & Vazquez, M. 1993, A&A, 270, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Mathew, S. K., Solanki, S. K., Lagg, A., et al. 2004, A&A, 422, 693 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Metcalf, T. R. 1994, Sol. Phys., 155, 235 [Google Scholar]
- Metcalf, T. R., Leka, K. D., Barnes, G., et al. 2006, Sol. Phys., 237, 267 [Google Scholar]
- Mihalas, D. 1970, Stellar Atmospheres (San Francisco: W. H. Freeman & Company) [Google Scholar]
- Milić, I., & van Noort, M. 2018, A&A, 617, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pastor-Yabar, A., Borrero, J., & Ruiz Cobo, B. 2019, A&A, submitted [Google Scholar]
- Priest, E. R. 1999, Ap&SS, 264, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Puschmann, K. G., Ruiz Cobo, B., & Martínez Pillet, V. 2010a, ApJ, 720, 1417 [NASA ADS] [CrossRef] [Google Scholar]
- Puschmann, K. G., Ruiz Cobo, B., & Martínez Pillet, V. 2010b, ApJ, 721, L58 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M. 2012, ApJ, 750, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz Cobo, B. 2007, in Modern Solar Facilities – Advanced Solar Science, eds. F. Kneer, K. G. Puschmann, & A. D. Wittmann, 287 [Google Scholar]
- Ruiz Cobo, B., & del Toro Iniesta, J. C. 1992, ApJ, 398, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Socas-Navarro, H. 2001, in Advanced Solar Polarimetry – Theory, Observation, and Instrumentation, ed. M. Sigwarth, ASP Conf. Ser., 236, 487 [NASA ADS] [Google Scholar]
- Socas-Navarro, H., de la Cruz Rodríguez, J., Asensio Ramos, A., Trujillo Bueno, J., & Ruiz Cobo, B. 2015, A&A, 577, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solanki, S. K., Walther, U., & Livingston, W. 1993, in IAU Colloq. 141: The Magnetic and Velocity Fields of Solar Active Regions, eds. H. Zirin, G. Ai, & H. Wang, ASP Conf. Ser., 46, 48 [NASA ADS] [Google Scholar]
- Swarztrauber, P., & Sweet, R. 1975, Efficient FORTRAN Subprograms for the Solution of Elliptic Partial Differential Equations [Google Scholar]
- van Noort, M. 2012, A&A, 548, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vögler, A. 2003, PhD Thesis, Göttingen University [Google Scholar]
- Welsch, B. T., Fisher, G. H., Abbett, W. P., & Regnier, S. 2004, ApJ, 610, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, X., & Wiegelmann, T. 2018, ApJ, 866, 130 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Magnetic field B from the sunspot simulation at a height of 448 km from the upper boundary. The rectangular box in white-dashed lines is the region employed for our study. |
| In the text | |
 |
Fig. 2. Geometrical height z for four different optical-depth levels. From bottom to top: log τc = [0, −1, −2, −3]. |
| In the text | |
 |
Fig. 3. Top panels: density as a function of the geometrical height z (i.e., vertical coordinate) for three spatial (x, y) locations corresponding to the sunspot umbra (right), penumbra (middle), and surrounding granulation (left). These locations are indicated by white circles in Fig. 1. Bottom panels: same as top panels but for the gas pressure. Solid black curves correspond to the actual values from the three-dimensional MHD simulation (Sect. 2), whereas colored lines are the hydrostatic results using the two boundary conditions described in the text: Phyd, 1 (red) and Phyd, 2 (blue). The vertical dashed lines indicate the location of the z(τc = 1)-level (i.e., Wilson depression). |
| In the text | |
 |
Fig. 4. Left panels: two dimensional maps of z(x, y, τc) at four different log τc-levels (from bottom to top): 0, −1, −2, −3 using hydrostatic equilibrium and the boundary condition Pg, hyd(x, y, zmax) = Pg, mhd(x, y, zmax). Right panels: same as on the left but using the boundary condition where Pg, hyd(x, y, zmax) is given by Eq. (4). |
| In the text | |
 |
Fig. 5. Logarithm of the density (left) and gas pressure (right) as a function of the normalized radial distance to the center of the sunspot ξ = r/Rspot at four different vertical heights z = 0, 512, 1024, 1528 km. Larger z values correspond to higher atmospheric layers. Black circles correspond to the azimuthal- or ϕ-averages of the MHD simulations (Sect. 2). Red curves are obtained through fourth-order polynomial approximations to the black circles. |
| In the text | |
 |
Fig. 6. Same as Fig. 3 but showing results from MHS equilibrium using different boundary conditions: ideal case scenario (dashed red lines) where boundary conditions are identical to the MHD simulations, and practical scenario (dashed blue lines) where boundary conditions are given by the interpolated model (Eq. (11)). Original values from MHD simulations (Sect. 2) are displayed in solid black lines. |
| In the text | |
 |
Fig. 7. Same as Fig. 4 but employing MHS equilibrium and different boundary conditions: ideal case scenario where boundary conditions are identical to the MHD simulations (left panels), and practical scenario where boundary conditions are given by the interpolated model (right panels; Eq. (11)). |
| In the text | |
 |
Fig. 8. Histograms of the logarithm of the quotient Pmhd/P† (left) and ρmhd/ρ† (right) in the entire three-dimensional domain, where † indicates the values obtained in the four different tests we have carried out. Solid colored curves represent the inferences in the hydrostatic case (red for boundary condition Phyd, 1; blue for boundary condition Phyd, 2), and dashed coloured curves display the MHS case (red for boundary condition Pmhs, 1; blue for boundary condition Pmhs, 2). See text for details. |
| In the text | |
 |
Fig. 9. Same as Fig. 8 but for the logarithm of the quotient |
| In the text | |
 |
Fig. 10. Histograms of the difference between the inferred height z† and the height in the MHD simulations zmhd for different optical-depth levels: log τc = 0 (upper-left), −1 (upper-right), −2 (bottom-left), and −3 (bottom-right). Solid colored lines represent the inferences in the hydrostatic case (red for boundary condition Phyd, 1; blue for boundary condition Phyd, 2), and dashed colored lines display the MHS case (red for boundary condition Pmhs, 1; blue for boundary condition Pmhs, 2). See text for details. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



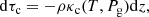
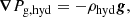
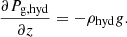
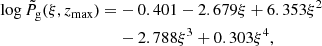
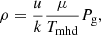
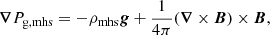
![$$ \begin{aligned} \nabla ^2 P_{\rm g,mhs} = -{ g} \frac{\partial \rho _{\rm mhs}}{\partial z} +\frac{1}{4\pi } {\boldsymbol{\nabla }} \cdot [({\boldsymbol{\nabla }} \times {\boldsymbol{B}}) \times {\boldsymbol{B}}]. \end{aligned} $$](/articles/aa/full_html/2019/12/aa36367-19/aa36367-19-eq7.gif)
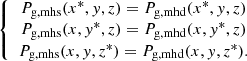
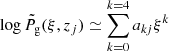
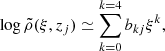
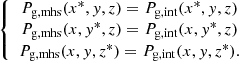
![$$ \begin{aligned} \log \left(\frac{[\mathrm{d}\tau _{\rm c}/\mathrm{d} z]_{\rm mhd}}{[\mathrm{d}\tau _{\rm c}/\mathrm{d} z]^{\dagger }}\right) = \log \left(\frac{\rho _{\rm mhd} \kappa _{\rm c,mhd}}{\rho ^{\dagger } \kappa _{\rm c}^{\dagger }}\right), \end{aligned} $$](/articles/aa/full_html/2019/12/aa36367-19/aa36367-19-eq19.gif)