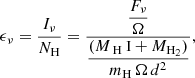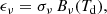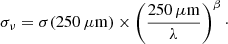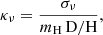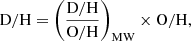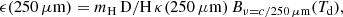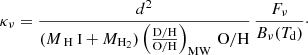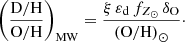| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201936314 | |
| Published online | 31 October 2019 | |
Dust emissivity and absorption cross section in DustPedia late-type galaxies⋆
1
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Florence, Italy
e-mail: sbianchi@arcetri.astro.it
2
INAF – Istituto di Radioastronomia, Via P. Gobetti 101, 40129 Bologna, Italy
3
Sterrenkundig Observatorium, Universiteit Gent, Krijgslaan 281 S9, 9000 Gent, Belgium
4
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, Maryland 21218, USA
5
School of Physics and Astronomy, Cardiff University, The Parade, Cardiff CF24 3AA, UK
6
Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, UK
7
AIM, CEA, CNRS, Université Paris-Saclay, Université Paris Diderot, Sorbonne Paris Cité, 91191 Gif-sur-Yvette, France
8
Institut d’Astrophysique Spatiale, CNRS, Université Paris Sud, Université Paris-Saclay, Bât. 121, 91405 Orsay Cedex, France
9
Central Astronomical Observatory of RAS, Pulkovskoye Chaussee 65/1, 196140 St. Petersburg, Russia
10
St. Petersburg State University, Universitetskij Pr. 28, 198504 St. Petersburg, Stary Peterhof, Russia
11
National Observatory of Athens, Institute for Astronomy, Astrophysics, Space Applications and Remote Sensing, Ioannou Metaxa and Vasileos Pavlou, 15236 Athens, Greece
12
Department of Astrophysics, Astronomy & Mechanics, Faculty of Physics, University of Athens, Panepistimiopolis, 15784 Zografos, Athens, Greece
13
Centre for Astrophysics Research, University of Hertfordshire, College Lane, Hatfield AL10 9AB, UK
Received:
15
July
2019
Accepted:
20
September
2019
Aims. We compare the far-infrared to sub-millimetre dust emission properties measured in high Galactic latitude cirrus with those determined in a sample of 204 late-type DustPedia galaxies. The aim is to verify if it is appropriate to use Milky Way dust properties to derive dust masses in external galaxies.
Methods. We used Herschel observations and atomic and molecular gas masses to estimate ϵ(250 μm), the disc-averaged dust emissivity at 250 μm, and from this, the absorption cross section per H atom σ(250 μm) and per dust mass κ(250 μm). The emissivity ϵ(250 μm) requires one assumption, which is the CO-to-H2 conversion factor, and the dust temperature is additionally required for σ(250 μm); yet another constraint on the dust-to-hydrogen ratio D/H, depending on metallicity, is required for κ(250 μm).
Results. We find ϵ(250 μm) = 0.82 ± 0.07 MJy sr−1 (1020 H cm−2)−1 for galaxies with 4 < F(250 μm)/F(500 μm) < 5. This depends only weakly on the adopted CO-to-H2 conversion factor. The value is almost the same as that for the Milky Way at the same colour ratio. Instead, for F(250 μm)/F(500 μm) > 6, ϵ(250 μm) is lower than predicted by its dependence on the heating conditions. The reduction suggests a variation in dust emission properties for spirals of earlier type, higher metallicity, and with a higher fraction of molecular gas. When the standard emission properties of Galactic cirrus are used for these galaxies, their dust masses might be underestimated by up to a factor of two. Values for σ(250 μm) and κ(250 μm) at the Milky Way metallicity are also close to those of the cirrus. Mild trends of the absorption cross sections with metallicity are found, although the results depend on the assumptions made.
Key words: dust / extinction / infrared: galaxies / galaxies: photometry / galaxies: ISM
DustPedia is a collaborative focused research project supported by the European Union under the Seventh Framework Programme (2007−2013) call (proposal no. 606824, P.I. J. I. Davies, http://www.dustpedia.com). The DustPedia data is publicly available at http://dustpedia.astro.noa.gr
© ESO 2019
1. Introduction
Dust grains of sub-micrometre size constitute a sizeable fraction of all the metals available in the interstellar medium (ISM). Their properties retain the imprint of several processes during the life of a galaxy: grains are formed during star formation (in the atmospheres of giant stars and in the ejecta of supernovae). The grains together with gas are destroyed as they coalesce into protostars. The grains participate in the ISM evolution, when they accrete material from the gas phase or return to it after they are destroyed in supernovae shocks. Knowing their total mass is therefore vital for understanding the chemical evolution of a galaxy (for a recent review, see Galliano et al. 2018).
The dust mass is commonly derived by modelling the spectral energy distribution (SED) in the far-infrared (FIR) and sub-millimetre (submm) wavelength ranges (Hildebrand 1983). The key ingredient in the estimate is knowing the wavelength-dependent FIR absorption (emission) cross section. This is typically derived by modelling the dust properties in the local ISM of the Milky Way (MW). A dust model consists of a mixture of (typically spherical) grains of different sizes and materials. Its composition is constrained by the metal depletion, that is, the difference between the (typically solar) elemental composition and that measured in the ISM gas phase. The missing metals have condensed into dust grains (for a review, see Draine 2003). Models were originally required to reproduce the dependence of extinction on wavelength (the extinction law) in the ultraviolet (UV), optical, and near-infrared (e.g. in the classical work of Mathis et al. 1977; additional constraints on polarisation are needed for models with aspherical grains, see e.g. Siebenmorgen et al. 2014). With the increasing availability of observations at longer wavelengths from balloons and satellites, it has become possible to constrain the models in the FIR to submm. This was done either by comparing the predicted FIR and submm absorption cross section with the cross sections that were estimated under a variety of assumptions in several locations in the Galaxy (Mezger et al. 1982; Draine & Lee 1984) or by simulating the emission due to grains that were exposed to an interstellar radiation field (ISRF) and comparing this emission with the observed emissivity, that is, the surface brightness per column density of hydrogen (Mezger et al. 1982; Désert et al. 1990).
In the past two decades, a common benchmark has been adopted at FIR to submm wavelengths. Dust models are required to reproduce the local MW emissivity, estimated from measurements of the high Galactic latitude cirrus from Far-InfraRed Absolute Spectrophotometer (FIRAS) data (Wright et al. 1991; Reach et al. 1995) or from Diffuse InfraRed Background Experiment (DIRBE) data (Arendt et al. 1998). These two instruments operated on board the Cosmic Background Explorer (COBE; Boggess et al. 1992). The emissivity is predicted for grains that are exposed to the local ISRF (LISRF), estimated by Mathis et al. (1983). Several dust models have been constructed and calibrated using these observational constraints (Dwek et al. 1997; Li & Draine 2001; Draine 2003; Zubko et al. 2004; Compiègne et al. 2011; Jones et al. 2013, 2017; Siebenmorgen et al. 2014). Despite the common starting point, the different choices for the dust materials, size distributions, and other constraints resulted in different absorption cross sections. As a result, dust mass estimates from FIR and submm observations can vary by up to a factor ∼3 from model to model (see e.g. Santini et al. 2014; Casasola et al. 2017; Chastenet et al. 2017; Nersesian et al. 2019; Hunt et al. 2019).
In addition to the uncertainties of evaluating the emission properties of the MW cirrus, variations in dust properties with the environment are also expected because grains can grow by accreting mantles of different compositions or by coagulating in denser media, or because grains are processed in shocked environments (for the former, see Jones et al. 2017; for the latter, Bocchio et al. 2014, and references in the two papers). When the dust mass in external galaxies is estimated using lower resolution observations and global fluxes, there is no guarantee that the properties of the MW cirrus adequately represent the emission from the bulk of the dust. A solution is determining the dust absorption cross section in situ by deriving the dust mass from the mass of metals that is available in the ISM of each galaxy, assuming a universal fraction of metals in dust and simplified dust heating conditions (James et al. 2002). This method requires FIR observations, gas masses, and metallicities and has recently been reassessed by Clark et al. (2016, hereafter C16), who found that the dust absorption cross sections in 22 high-metallicity objects are compatible with previous estimates within a large scatter, and that they did not show large variations from galaxy to galaxy. We here derive the FIR dust emission properties following a similar approach. Based on data from the DustPedia project (Davies et al. 2017), our sample is an order of magnitude larger and spans a wider metallicity range than that of C16. We derive the emissivity, which is least dependent on assumptions and can be used as a benchmark for future dust models. We also derive the absorption cross section after further assumptions on the heating conditions and dust-to-gas ratio.
The paper is organised as follows: in Sects. 2 and 3 we present our sample and method. Section 4 describes MW observations that we used for comparison with our results as well as the dust-to-gas ratio and metallicity estimates that are ingredients of our method. Our results on the dust emissivity are presented and discussed in Sect. 5. The results on the absorption cross section per H atom and per dust mass are reported in Sect. 6. We summarise the work and draw our conclusions in Sect. 7.
2. Sample and dataset
The DustPedia sample (Davies et al. 2017) includes 875 galaxies, almost all the large (D25 > 1′) and nearby (v < 3000 km s−1) objects that have been observed by the Herschel Space Observatory (Pilbratt et al. 2010). For all these galaxies, photometric data are available in up to 34 bands from the UV to the submm (Clark et al. 2018). In the FIR and submm bands, we required that objects have available flux densities at 250 and 500 μm from Herschel’s Spectral and Photometric Imaging Receiver (SPIRE; Griffin et al. 2010). We used fits to the full spectral energy distribution (SED) obtained by Nersesian et al. (2019) using the Code Investigating GALaxy Emission (CIGALE; Boquien et al. 2019) coupled to The Heterogeneous dust Evolution Model for Interstellar Solids (THEMIS; Jones et al. 2017). We also used the procedures of Nersesian et al. (2019) to fit the SED for λ ≥ 100 μm with a single-temperature modified black body (MBB).
The emissivity determination requires knowing the gas column density, therefore we conducted literature searches to collect information on the atomic and molecular gas. H I masses are available for 87% of the DustPedia sample (De Vis et al. 2019; Casasola et al. 2019). We searched for observations of the CO molecule (a tracer for H2) in late-type galaxies (later than Sa, with Hubble stage T ≥ 0.5) that were detected at 250 μm and found them for 255 galaxies (29% of the full DustPedia sample). H2 masses were obtained from the CO observations assuming the CO-to-H2 conversion factor of Amorín et al. (2016), which is dependent on the oxygen abundance as (O/H)−1.5. This is an intermediate choice between using a constant MW-based value (Bolatto et al. 2013) and stronger dependencies on metallicity (Hunt et al. 2015a). Because dust is well detected up to the optical radius R25 = D25/2 (Pohlen et al. 2010; Casasola et al. 2017), we verified that estimates for the gas refer to the same aperture. H I observations are typically taken with beams larger than R25, while most CO observations only cover the central region of a galaxy with a smaller beam. Using averaged radial profiles for each gas component, we implemented aperture corrections to retrieve the mass of atomic and molecular hydrogen within R25 (for a full description, see Casasola et al. 2019).
Global O/H metallicities are available for about 60% of the full DustPedia sample from a literature compilation and archival integral field unit observations (De Vis et al. 2019). Among the various calibrations for the oxygen abundance given by De Vis et al. (2019), we chose the N2 method of Pettini & Pagel (2004), which is compatible with the conversion factor derived by Amorín et al. (2016) and compares well with direct electron-temperature-based determinations at both high and low metallicities (Curti et al. 2017). The N2 metallicities have the advantage that they are available for a larger number of objects, because they require only a limited wavelength coverage of the spectrum.
In summary, we selected all T ≥ 0.5 galaxies that were detected at 250 μm (except for a few objects whose fluxes were flagged because of an insufficient sky coverage), that were detected in atomic gas and in molecular gas, or that were detected in atomic gas with upper limits in molecular gas if the mass of the atomic component was twice higher than the error on the total gas estimate (19% of the final selection; the complementary case of detection in CO with upper limits in H I is not present in our database), for which an N2 metallicity was available, and whose SED coverage was sufficient for an MBB fit. In total, the sample used in this work includes 204 objects.
3. Method
In MW studies, the dust emissivity ϵν is defined as the surface brightness of dust emission Iν per hydrogen column density NH. The normalisation provides information that is independent of the ISM density along the line of sight. For our galaxies, disc-averaged values for Iν and NH can be obtained from the integrated flux density of dust emission Fν and the total hydrogen mass MH = MH I + MH2. The emissivity can then be estimated as
where mH is the mass of the hydrogen atom. The gas masses were derived assuming a galaxy distance d, and the ratio MH/d2 (as well as the emissivity estimate) is thus independent of d. ϵν is also independent of the solid angle Ω because the gas masses and dust flux density refer to the same sky area, that is, the optical disc within R25. Equation (1) should in principle include the contribution of H II to NH. However, this contribution is seldom considered in the MW and difficult to measure in external galaxies. Lacking the data to estimate it, we here neglect H II. We discuss this point further in the next sections.
When all the dust grains in a galaxy are made of the same material, have the same size, and are exposed to the same ISRF, the dust emissivity can be written in the optically thin limit as
where σν is the absorption cross section per hydrogen atom and Bν is the Planck function at the dust temperature Td (we only considered emission at thermal equilibrium because stochastic heating is not dominant for the FIR regime). In the more realistic case of various grain sizes, materials, and heating conditions, σν and Td are different for each grain (Td also depends on the ISRF), and ϵν results from the integral of the second term of Eq. (2) over the dust and ISRF distributions. Nevertheless, the single-temperature simplification is widely used, together with a power-law description of the absorption cross section. At the reference wavelength of 250 μm, it is
Within this MBB approximation, Eq. (2) can be fitted to the observed emissivity SED of Eq. (1) to obtain an SED-averaged representation of σν. We discuss the effect of the single-temperature approximation and of the choice for the power-law index β on the estimate of the absorption cross section later.
The absorption cross section per dust mass is
with D/H the dust-to-hydrogen mass ratio. When the oxygen abundance in the gas (O/H) is a good proxy of the total metal abundance, and when a fixed fraction of metals is locked up in dust grains, D/H should depend linearly on O/H (see, e.g., Draine et al. 2007; Magrini et al. 2011). We used
scaling the ratio on the estimates of D/H and O/H for the MW. Because we used H-normalised quantities, we did not need to consider the contribution of helium (and other metals) to the gas mass. In the Appendix, we show that our approach is analogous to that used by James et al. (2002) and C16 to derive κν.
Using Eqs. (2)–(4), we can write
which clearly shows the expected dependence of the emissivity under the assumptions made here on the dust-to-hydrogen ratio, absorption cross section per dust mass, and dust temperature.
4. MW reference values
We used the MW cirrus emissivity obtained by Bianchi et al. (2017) from Herschel Virgo Cluster Survey data (HeViCS; Davies et al. 2010). The quantity was derived in all SPIRE bands. It can therefore be directly compared with estimates that are available for all the galaxies considered here. The HeViCS emissivity SED, which also uses IRAS and Planck data (Fig. 1, left panel), is in excellent agreement with Planck determinations over much larger sky areas (Planck Collaboration Int. XVII 2014; Planck Collaboration XI 2014). We used ϵ(250 μm) averaged over the whole HeViCS field and the flux (emissivity) ratio F(250 μm)/F(500 μm) to characterise the SED shape. The numerical values of these quantities and of others presented in this section are given in Table 1. Bianchi et al. (2017) furthermore derived σ(250 μm) by fitting the SED with β = 1.6 (Planck Collaboration XI 2014; Fig. 1, right panel).
 |
Fig. 1. Milky Way emissivity ϵν at high Galactic latitude. Left panel: we compare estimates obtained from COBE-DIRBE and Planck data of the south Galactic pole (Planck Collaboration Int. XVII 2014) and from IRAS, Herschel, and Planck data of the HeViCS fields (Bianchi et al. 2017) to those derived from the COBE-FIRAS spectrum. In the right panel, we show MBB fits to the HeViCS data (Bianchi et al. 2017) and to IRAS and Planck data over the whole diffuse high-Galactic latitude cirrus (Planck Collaboration XI 2014), together with the predictions from the THEMIS and Draine et al. (2007) dust models heated by the LISRF. The HeViCS data points are repeated to facilitate comparison. |
Milky Way reference values adopted here (in bold) and other values from the literature.
The HeViCS and Planck Collaboration SEDs agree with FIRAS determinations (Dwek et al. 1997; Draine 2003). A notable exception is the FIRAS spectrum for the high-latitude cirrus in Compiègne et al. (2011; thin purple dot-dashed line in the left panel of Fig. 1). These cirrus estimates only consider the H I contribution to NH and neglect H II (the contribution of high-latitude molecular gas is very low, a few percent at most; Compiègne et al. 2011). Curiously, when Compiègne et al. (2011) included a correction for other contributions to NH (mostly a 20% increase due to H II; see also Draine 2011), their FIRAS emissivity becomes very similar to the other estimates (thick purple dot-dashed line in the left panel of Fig. 1). The discrepancy might be due to different methods, H I observations, and determination of zero-levels in the derivation of the emissivity1.
In Fig. 1 (right panel) we show a few model predictions for dust grains heated by the LISRF2. The THEMIS model (purple dot-dashed line) is able to reproduce the MW SED. Because the model was optimised to reproduce the corrected FIRAS spectrum of Compiègne et al. (2011), it passes through the many other uncorrected estimates we just discussed. Thus, its grain properties have to be considered as scaled on the non-ionised hydrogen alone. The Draine & Li (2007) model (DL07 hereafter; orange dashed line in the figure) was instead originally set to match FIRAS data (see e.g. Li & Draine 2001; Draine 2003), but it has since been rescaled and its predictions at 250 μm are a factor 0.65 lower than observations (see also Bianchi 2013; Planck Collaboration Int. XVII 2014).
To scale Eq. (5), we need estimates of D/H and O/H for the same local medium for which the emissivity is derived. Following Draine et al. (2007), we derived (D/H)MW from the difference between the total metal abundances of the interstellar medium (typically represented by the solar abundances or those of the pre-solar nebula) and the gas-phase abundances measured from absorption line spectra to nearby stars: the missing atoms are depleted into dust. Jenkins (2009) studied the element abundance along several lines of sight in the local Galaxy and parametrised the amount of atoms that are missing from the gas phase with a factor F⋆. We estimated D/H for lines of sight of moderate to high depletion (F⋆ = 0.4 to 1, using Tables 9.5 and 23.1 in Draine 2011). Other values for D/H can be obtained from MW dust grain models. The adopted (D/H)MW and uncertainty encompasses these values. In the same way, we chose (O/H)MW using metallicity measurements from absorption lines of nearby stars and emission lines in local H II regions (see Table 1, which also provides κ(250 μm) obtained from Eq. (4)). With the adopted values, it is ((D/H)/(O/H))MW = 21 ± 6.
5. Emissivity
The emissivities at 250 μm derived for our DustPedia galaxies are shown in Figs. 2–4 as a function of the SPIRE F(250 μm)/F(500 μm) ratio. This FIR colour is available for all galaxies in the sample; it is sensitive to the dust property variation with wavelength (and to a lesser extent to the intensity of the radiation field; Smith et al. 2019). By studying ϵ(250 μm), we wish to provide a reference to benchmark dust models that depends least on assumptions. The estimate of ϵ(250 μm) using Eq. (1) does not require a model for the heating conditions, nor a recipe for the D/H variations across the sample. Still, there is a major uncertainty in ϵ(250 μm): the uncertainty on the CO-to-H2 conversion factor.
 |
Fig. 2. Emissivity ϵ(250 μm) as a function of the F(250 μm)/F(500 μm) ratio. When data on the abscissa (and/or ordinate) are estimated at a level below 2σ, the x (and/or y) error is omitted and an open symbol is used. The red error bar shows the MW estimate from HeVICS. The mean of ϵ(250 μm) and its standard deviation for five bins in F(250 μm)/F(500 μm) is shown by the black error bars (connected by a solid line). The F(250 μm)/F(500 μm) range and the number of galaxies is given for each bin. |
 |
Fig. 3. Emissivity ϵ(250 μm) as a function of F(250 μm)/F(500 μm) for each galaxy (grey datapoints) and for the mean for F(250 μm)/ F(500 μm) bins (same as Fig. 2, but individual error bars are omitted for clarity). Coloured dots in the top panel show the mean and its standard deviation for bins of different morphological types. Red dots in the central panel show the same, but for bins in metallicity (the number of objects for each bin is given in both panels). Bottom panel: the long-dashed line shows the binned mean assuming a constant CO-to-H2 conversion factor, and the short-dashed line shows the mean when the H2 component is neglected. |
 |
Fig. 4. Same as Fig. 2 (individual error bars are omitted for clarity). Left panel: the red line shows the locus of an MBB with β = 1.6 for different temperatures (red dots along the line give the values at Td = 15, 20, 25, 30, 35, and 40 K, from left to right). The purple and orange lines show the loci of dust heated by the LISRF scaled by a factor U for the THEMIS and DL07 grain models, respectively (dots along the lines are for U = 0.1, 0.5, 1, 2, 5, 10, and 20, from left to right). Right panel: the THEMIS dust model (solid purple line) is repeated together with the CMM model from Köhler et al. (2015) for 0.1 < U < 0.5 (dashed purple line). Purple dots are the emissivity values estimated from the CIGALE-THEMIS best-fit SEDs of each galaxy (see text for details). |
5.1. Results
Despite the large scatter of the data points, Fig. 2 shows a mild trend, with a larger ϵ(250 μm) for bluer F(250 μm)/F(500 μm) ratios. The Kendall correlation coefficient is τK = 0.30 (with a negligible probability for the null hypothesis, pK = 0). Although the different properties of dust in various objects might contribute to the scatter, most of it is compatible with the uncertainties in the measurements. In particular, the mean relative error of the emissivity is 28%, dominated by the error on NH (including estimates for the uncertainties in the conversion factor and aperture corrections), while it is 8% for the colour ratio.
The average trend is shown in Fig. 2, where we plot the mean and its standard deviation for five bins in F(250 μm)/F(500 μm) (black error bars and solid line; all means presented in this work are clipped at 4σ to exclude the most extreme outliers, which range from none to four objects at most). The value for the 4 < F(250 μm)/F(500 μm) < 5 bin is entirely consistent with that for the MW cirrus at the same colour ratio (red data point; the numerical value is given in Table 2). For galaxies with higher colour ratios, F(250 μm)/F(500 μm)≳6, an apparent change in the trend is visible.
Emissivity and absorption cross sections for our sample.
Even though our sample is dominated by Sb-Sc galaxies (about half of the objects), a mild dependence of the emissivity on morphology is present. This can be seen in Fig. 3 (top panel), where the mean and its standard deviation are plotted for each of four morphology bins (as defined in Bianchi et al. 2018). The trend is along that with colour ratio, emissivity progressively decreases from Sa-Sab (green) to Scd-Sm (blue). Only the Sm-Ir galaxies (dark blue) do not follow the sequence and fall in between the other types. This behaviour reflects the average FIR colour of each morphology bin: the “peak” temperature of the average SED decreases from Sa-Sab to Scd-Sm, while for Sm-Ir, it is the same as that of Sb-Sc (Bianchi et al. 2018).
The emissivity is also found to mildly correlate with metallicity (τK = 0.31, pK = 0; not shown). In addition to the dependence of the dust properties on elemental abundances, the correlation might again be the reflection of a trend of metallicity with colour ratio (τK = 0.34, pK = 0; not shown), which in turn might come from a concatenation of relations: it is well known that the metallicity correlates with stellar mass (the mass-metallicity relation; Tremonti et al. 2004); in later type spirals of higher stellar mass, a larger radiation fraction is absorbed by dust and is re-emitted in the FIR (Bianchi et al. 2018). The FIR luminosity correlates with the dust temperature, and thus with the colour ratio (Symeonidis et al. 2013; Magnelli et al. 2014). In Fig. 3 (central panel) we show the emissivity versus colour ratio binned according to the metallicity. The metallicity in our sample ranges from 12 + log(O/H) = 7.9 to 9.5. The vast majority of objects has 8.3 ≤ 12 + log(O/H) < 8.9: the three bins in this range align with the emissivity trend with colour ratio (and morphology). The mean for objects in the lowest (and highest) metallicity bin is below (and above) the trend, although the scatter of the objects in these subsample is large (the higher metallicities are also beyond the range of applicability of the N2 calibration; Pettini & Pagel 2004). We also explored the variations of ϵ(250 μm) with other galactic properties derived by Nersesian et al. (2019), such as the bolometric luminosity, the contribution of young and old stars to it, the stellar mass (M⋆), the global and specific star formation rate (sSFR). We found no other correlation stronger than those with colour ratio and metallicity (see below).
Because the metallicities of most of the objects are evenly distributed around the MW value (and close to it), the metallicity-dependent CO-to-H2 conversion factor we adopted does not change greatly throughout our sample. As a result, the emissivities we derived do not depend significantly on the conversion: for a constant Galactic value (e.g. the value recommended by Bolatto et al. 2013), the trend with colour ratio and the absolute value of the emissivity are very similar and virtually indistinguishable within the large uncertainty of the data. This trend is shown by the long-dashed line in Fig. 3 (bottom panel). The short-dashed line in the same figure instead shows the effects of neglecting the molecular gas component in the derivation of ϵ(250 μm) from Eq. (1). The difference with the full derivation (solid line) highlights the galaxies for which H2 is a significant contributor to the gas column density: for the higher colour ratios, F(250 μm)/F(500 μm)≳6, MH2/MH I ≈ 1 to 2. A similar result, with a larger molecular gas fraction for galaxies with a bluer FIR colour, was found by Groves et al. (2015).
Galaxies of type Sb-Sc and those with 8.5 ≤ 12 + log(O/H) < 8.7 have ϵ(250 μm)≈1.2 MJy sr−1 (1020 H cm−2)−1 at F(250 μm)/F(500 μm)≈6 (see top and middle panel in Fig. 3). When the MW is considered as an object of similar morphology (Hodge 1983; van der Kruit 1990) and metallicity, its average ϵ(250 μm) is a factor 1.5 higher than that estimated on the MW cirrus. The difference, however, might be due in part to the warmer dust and in part to a larger contribution of molecular gas in the Galaxy as a whole than in the local high-latitude environment we used as a reference.
5.2. Discussion
In Fig. 4 (left panel) we compare the observed trends with the predictions from the MBB approximation and the THEMIS and DL07 dust grain models. In all cases, the SPIRE fluxes were derived by integrating the SEDs over the instrument filter response functions (The SPIRE Handbook, v. 2.5, 2014). The red line shows the trend of MBB emission with temperature, assuming β = 1.6 (the MW cirrus value). The increase in F(250 μm)/F(500 μm) across most of the range of our sample can be reproduced by dust temperatures raising from Td = 15 K to 40 K (Td ≈ 20 K is the value for the MW cirrus).
The trends for dust models were derived assuming that grains are heated by the LISRF reported by Mathis et al. (1983) scaled by a factor U. The purple and orange lines in Fig. 4 (left panel) show the results for the THEMIS and DL07 models, respectively. When the intensity of the radiation field through U increased (we used values from 0.1 to 20), the model emissivity rises in the same fashion as the MBB does with Td. As expected from Fig. 1 (see also Sect. 4), the THEMIS emissivity for U = 1 passes close to the MW estimate and its trend is very similar to that of the MBB, while the DL07 emissivity is lower and with a higher F(250 μm)/ F(500 μm) ratio (as can be seen by comparing the U = 1 dots in this model and in THEMIS). For F(250 μm)/F(500 μm) ≲ 5.5, the average trend follows the modelled MW-scaled MBB (and THEMIS). For objects with larger F(250 μm)/F(500 μm), the average emissivity is instead a factor ≈0.5 − 0.6 of the MBB predictions (while it is fortuitously matched by DL07). For the bin of the largest F(250 μm)/F(500 μm), the MBB is 9σ away from the sample average.
Apparently, the lower emissivity is found for galaxies with a warmer colour ratio and a larger contribution of molecular hydrogen to NH (Sect. 5.1). This is at odds with theoretical expectations because the grain emissivity should increase in denser environments. For example, Köhler et al. (2015) studied the variations of the THEMIS models in denser media, as the grains accrete layers of aliphatic-rich amorphous carbon, coagulate, and grow ice-mantles. In all these stages the dust emissivity increase for the same U. The changes are expected to occur in regions where UV radiation is strongly attenuated and the ISRF is lower. As a reference, we plot in Fig. 4 (right panel) the emissivity for 0.1 < U < 0.5 from the CMM model of Köhler et al. (2015). In this and other models in that work, the emissivity is higher than the corresponding value from the THEMIS model for diffuse dust.
However, it is not likely that these dense regions contribute significantly to the global FIR emission. In observations at low spatial resolution, the SED could be biased against the emission from cold dust and in favour of grains at hotter temperature (Galliano et al. 2018 call it “a Matriochka effect”; see also Utomo et al. 2019). The emission from regions that contain colder grains, such as those where the emissivity could be enhanced, might contribute little to the global SED, in particular if the filling factor is low. The bias could be even stronger in our work, where we used global fluxes. On the other hand, variation in dust properties is also expected in regions with stronger radiation fields (Jones et al. 2017). It might be wondered whether the dust evolution in this regime might cause the reduced dust emissivity in galaxies with warmer dust. Following Eq. (6) and assuming no variations in the dust temperature and D/H, a smaller ϵ(250 μm) can be obtained by reducing κ(250 μm). Thus, in galaxies with bluer FIR colours with reduced emissivity, the dust masses could be about a factor of two higher than those obtained with the standard properties of the diffuse MW dust. In the companion paper to this work, Casasola et al. (2019) find lower D/H ratios for objects with a larger H2 contribution (that correspond to galaxies that are bluer in the FIR, as shown in Sect. 5.1 and in the bottom panel of Fig. 3). The explanation may be that the dust mass is underestimated when the THEMIS diffuse dust properties are used for these objects. However, in a dust evolutionary scenario the changes in D/H, dust heating, and absorption cross section are probably intertwined. For example, Chastenet et al. (2017) fit the resolved infrared emission in the low-metallicity Large and Small Magellanic Clouds under various assumptions for the dust heating by changing the relative proportion of the material components of THEMIS. The resulting models have higher κ(250 μm) and a lower D/H than the original model. The galaxies with F(250 μm)/F(500 μm)≳6 typically have higher metallicities (Sect. 5.1 and the middle panel of Fig. 3) than the Magellanic Clouds, and thus a reduction in D/H is less likely than a reduction in κ(250 μm). A full dust modelling is needed to conclude, however.
As we discussed in the previous paragraph, the emissivity we derived from the global fluxes might be biased by different heating conditions within each galaxy. In order to estimate the effect of this temperature mixing, we derived mock emissivities from the THEMIS-based CIGALE best-fit SEDs of DustPedia galaxies (Nersesian et al. 2019). The fitting model, following the approach of Draine et al. (2007), assumes that part of the dust is heated by a radiation field characterised by Umin, and another part is heated by a power-law distribution of the heating fields, U−α, with U ≥ Umin and α = 2. Typically, a fit results in most of the dust heated by the Umin component (still including temperature variations depending on the grain size and composition). A small fraction (up to a few percent at most) is instead needed to account for the SED at wavelengths smaller than the thermal peak (see e.g. Draine et al. 2007; Dale et al. 2012; Hunt et al. 2019; Nersesian et al. 2019). Basically, the SED fitting operates by scaling the NH-normalised spectra produced by THEMIS to the true fluxes Fν. The normalisation yields the mass of gas MH that is required for the dust emission, from which the dust mass Md is derived for the (single-value) D/H ratio of the model. By reversing the process, we used the best-fit flux densities and gas masses (from Md) to derive ϵ(250 μm) and F(250 μm)/F(500 μm) for each of the galaxies in our sample, using Eq. (1). The results of the mock derivation of ϵ(250 μm) versus F(250 μm)/F(500 μm) are shown by the purple dots in Fig. 4.
The CIGALE-THEMIS models fit the SED. This means that the mock F(250 μm)/F(500 μm) spans a similar range of values as the observed ones. The mock estimate of ϵ(250 μm) instead relies on the validity of the conversion of the gas mass into a dust mass through the hydrogen-scaled properties of the dust grain model. The mock ϵ(250 μm) is slightly higher than the THEMIS model for the MW (solid purple line) because in the CIGALE fits the fraction of small hydrocarbon solids was allowed to vary with respect to the standard value for diffuse dust. It was found that DustPedia galaxies are typically better fitted by a smaller fraction of hydrogenated carbons than in the MW (for a discussion, see Nersesian et al. 2019). This translates into an increase in FIR emissivity due to the contribution of (larger) carbon grains. The position of the dots for each mock galaxy depends on the fitted value, and in part to a (very small) effect of the temperature mixing. Nevertheless, within the uncertainties of the observations, the mock results still follow those of the THEMIS model. We also tested cases with a larger variation in the heating conditions by removing the Umin component and allowing all the dust to be heated by the U−α distribution (see e.g. Galliano 2018). Allowing α to vary between 1 and 3, we obtained fits to the DustPedia SEDs that are as good as those in Nersesian et al. (2019). Their mock ϵ(250 μm) versus F(250 μm)/F(500 μm) trend (not shown) still follows the trend that was obtained from the original fits. This shows that the mixing of heating conditions (dust temperatures) does not have a significant effect on the emissivity (and on the trend for the galaxies with F(250 μm)/F(500 μm) > 6). Unless the distribution of radiation fields we adopted is too simplistic and unable to describe the full range of heating conditions, the difference between the observed and modelled trends might indicate a difference in the dust grain properties (possibly including a variation in the D/H ratio) for galaxies of bluer FIR colours.
We recall that we did not include the contribution of H II to the gas column density. For the diffuse MW medium, H II is estimated to account for ≈20% of the total hydrogen content (Compiègne et al. 2011; Draine 2011). If this fraction does not change between galaxies, the results presented here are not affected: H II is neglected both in the DustPedia sample and in the MW reference emissivity. Instead, if the fraction of ionised gas increases for galaxies with redder FIR colours, the ϵ(250 μm) trend across the whole F(250 μm)/F(500 μm) range might be reconciled with the modelled trends. Unfortunately, we were unable to find any systematic study on the variation of the fraction of H II in galaxies of different properties. When we use the DL07 model as reference, passing through the average ϵ(250 μm) at higher F(250 μm)/F(500 μm), an increase of ≈40% in NH is needed at F(250 μm)/F(500 μm)≈4.5 for the sample average to fall on the trend (similar results can be found using the other trends in the left panel of Fig. 4, rescaled at higher F(250 μm)/F(500 μm) values). However, this correction would be larger than what is estimated for the MW at the same F(250 μm)/F(500 μm). ϵ(250 μm) is even very weakly anti-correlated with galactic properties from Nersesian et al. (2019) that trace the amount of ionising photons: it is only τK = −0.11 (pK = 3%) for the correlation with the fraction of stellar luminosity coming from young stars (and similar values for the sSFR and the fraction of intrinsic unattenuated photons in the FUV band). It is therefore unlikely that neglicting H II has significantly affected the trend we presented here. The same conclusion might be applied to the contribution of dark (molecular) gas, whose presence might not be revealed because the CO molecule in regions with stronger UV radiation fields is photodissociated (Wolfire et al. 2010). Instead, unaccounted-for H II and dark gas in galaxies at higher F(250 μm)/F(500 μm) would increase the deviation of the ϵ(250 μm) trend from the modelled ones more strongly than what we find here.
6. Absorption cross section
The derivation of the dust absorption cross-section is more uncertain because it requires assumptions on the heating field and on the D/H ratio. We first discuss the absorption cross section per hydrogen atoms, σ(250 μm), where the effects of different dust temperatures are removed. We then consider the absorption cross section per dust mass, κ(250 μm), which further depends on the assumption on the D/H ratio and its variations with metallicity.
6.1. Absorption cross section per hydrogen atom
In Fig. 5 (left panel) we show σ(250 μm) as a function of the global gas metallicity. The dust temperature required to derive σ(250 μm) (Eq. (2)) was obtained by fitting the SED with an MBB of β = 1.6, the same value as derived from fits of the high Galactic latitude cirrus. The black solid line and error bars show the mean (and its standard deviation) for the same bins in metallicity as in Fig. 3. Coloured dots with error bars show the same for the morphology bins. A mild trend of the absorption cross section with metallicity is visible that is compatible with the trend on morphology: objects of later type and lower metallicity have a smaller cross section than earlier type higher metallicity spirals. The scatter is large, however, and the Kendall correlation coefficient is small (τK = 0.21, pK = 0). This faint correlation might be partially due to the small number of data points at low and high metallicity, which have a larger CO-to-H2 correction factor: when it is restricted to the range 8.3 ≤ 12 + log(O/H) < 8.9, τK reduces to 0.1 (pK = 6%). The correlation on this restricted range disappears when a constant MW conversion factor is used (τK = 0.02, pK = 75%).
 |
Fig. 5. Absorption cross section per H atom σ(250 μm) (left panel) and per dust mass κ(250 μm) (right panel) as a function of the metallicity. The two panels show individual measurements as grey dots, with the same convention for open and filled symbols as in Fig. 2. The mean (and its standard deviation) of the quantity of the y-axis for the five metallicity bins defined in Fig. 3 (black error bars connected by a solid line) is shown, and the same, but for the four morphology bins (coloured dots with error bars). We also plot the HeViCS MW estimate of Table 1 (red error bars). Left panel: we also show the mean for each metallicity bin, when the dust temperature is derived with β = 1.8 (dashed line) and 2.0 (dotted line), and the slope for a linear dependence of κ(250 μm) on O/H (green dot-dashed line, arbitrary scale; Eqs. (4) and (5)). Right panel: the black error bar at the left shows the uncertainty in ((D/H)/(O/H))MW. The star indicates the value derived from C16 after rescaling it to the assumptions of this work (see text for details). |
Even when we limit our analysis to the three central bins in metallicity, the average trend appears flatter than (although marginally consistent with) the linear dependence of σ(250 μm) on O/H that is expected from the assumption of a universal dust-to-metal gas fraction (Eqs. (4) and (5); green dot-dashed line in Fig. 5, left panel). However, we note that the trend could have been altered by choosing a single β for the whole sample. Using a larger β would have resulted in lower Td and higher σ(250 μm): for β = 1.8 (close to the value fitted to the THEMIS average cross section; Galliano et al. 2018), the estimate of σ(250 μm) rises by ≈20% (dashed line in Fig. 5, left panel); when β = 2 (as in DL07; Bianchi 2013), it is 55% higher (dotted line). It has been shown that larger apparent β can describe the FIR to submm SED of galaxies with stronger radiation fields better, even without changes in the dust composition (Hunt et al. 2015b). An increase in β for earlier type galaxies with bluer F(250 μm)/F(500 μm) ratios could steepen the average trend of σ(250 μm) vs. O/H and cause it to approach theoretical expectations. The observed trend might also be flatter because of the lower-than-expected ϵ(250 μm) of these galaxies, although the uncertainties associated with the temperature derivation do not make the effect as evident as in the figures of Sect. 5.
The red dot in Fig. 5 (left panel) shows the value derived for the MW cirrus using HeViCS data. For the metallicity bin corresponding to the abundances we adopted for the MW gas (see Sect. 4), the average value of σ(250 μm) of our sample is compatible with the MW estimate, but it is 15% lower. The value becomes fully consistent with that of the MW when the constant conversion factor of Bolatto et al. (2013) is adopted or equivalently, if the Amorín et al. (2016) formula is rescaled to give the exact MW factor at our reference metallicity (see values in Table 2). The value of σ(250 μm) in the cirrus is also close to that of Sb-Sc galaxies (green dot in Fig. 5, left panel), a morphology range that is shared by the Galaxy (see Sect. 5.1). This is also in agreement with the estimates on the Galactic plane by the Planck Collaboration XXI (2011): after deriving the emissivity SED in five Galactocentric rings and fitting them with an MBB, they found that σ(250 μm) at the solar circle is slightly lower than but compatible with the value at high Galactic latitude. Within the uncertainties in the fitting, they also detected no significant variation with Galactocentric radius and within the different ISM components. This confirms that the dust properties in the cirrus are not significantly different from those in the disc.
For different MW regions, an anti-correlation between σ(250 μm) and Td is found. This is generally interpreted as due to local variations in dust composition: for the same emitted power, an increase (decrease) in the absorption cross section results in a decrease (increase) of the temperature (Planck Collaboration XXIV 2011; Martin et al. 2012; Planck Collaboration Int. XVII 2014; Planck Collaboration XI 2014). In optically opaque clouds, the use of a single dust temperature, neglecting the temperature decrease from the outskirts to the core, might contribute to the effect (Ysard et al. 2012). An anti-correlation is also found in our galaxy sample. However, it is weak (τK = −0.17, pK = 0.03%) and largely induced by the uncertainties in Td. Furthermore, in the MW the anti-correlation with Td is also shared by the emissivity (Planck Collaboration Int. XVII 2014), while in our sample the emissivity correlates positively with Td (τK = 0.20, pK = 0).
6.2. Absorption cross section per dust mass
The right panel of Fig. 5 shows κ(250 μm) versus metallicity. The absorption cross section per dust mass was obtained from σ(250 μm) assuming a linear dependence of the D/H ratio on metallicity (Eq. (5)). All errors were propagated to κ(250 μm), except for the uncertainty in the ((D/H)/(O/H))MW normalisation, which applies to all data points (it is shown as the black error bar at the left of Fig. 5, right panel). As for the other panel, we plot the average for metallicity bins, as well as that for bins in morphology (which share the same trend as those in metallicity, as we saw before). Like σ(250 μm), the value of κ(250 μm) for the central bin in metallicity is lower than but consistent with the MW estimate from the HeViCS cirrus (and becomes closer to it for a constant CO-to-H2 conversion factor; see the values in Table 2).
As we discussed above, our method for deriving κ(250 μm) is analogous to that of C16. The main differences are in their choice of reference wavelength (500 μm), CO-to-H2 conversion (from Schruba et al. 2012, with O3N2 metallicity, calibrated as in Pettini & Pagel 2004), dust emission model (two-T MBB with β = 2, although the cold component is dominant), and assumption for the MW value for the (D/H)/(O/H) ratio (see the appendix). When we use the DustPedia dataset (that also includes O3N2 metallicities) and the C16 recipe for the 15 galaxies in common with DustPedia (out of their total sample of 22), we obtain a mean value that agrees with theirs within 10% (although results for individual galaxies differ more because of differences in the data). The galaxies in C16 have metallicities 8.6 < 12 + log10(O/H) < 8.9. Selecting DustPedia objects in the same range, we derived an average correction factor between our values and those obtained assuming the same recipe as C16 (but with a single Td). With this factor, the C16 absorption cross section becomes κ(250 μm) = 2.3 ± 0.1 cm2 g−1 (black star in Fig. 5, right panel). The value is lower than but still marginally consistent with our estimates.
The trend of κ(250 μm) is obviously degenerate with our assumption of a linear dependence of D/H on metallicity: the (marginal) positive correlation of σ(250 μm) with metallicity becomes negative for κ(250 μm), with τH = −0.19 (pK = 0.01%). However, the correlation might be induced by the intrinsic dependence of κ(250 μm) on (the inverse of) O/H and the large uncertainties in metallicity. We verified the trend using proxies of metallicity that were not directly related to the observables we used to derive κ(250 μm): for our sample, M⋆ and 1/sSFR are the quantities that correlate best with metallicity (τK = 0.43 and 0.31, respectively, with pK = 0 in both cases); this is expected because of the mass-metallicity (Tremonti et al. 2004) and fundamental metallicity (Mannucci et al. 2010) relations. For κ(250 μm) vs. M⋆, the strength of the trend is reduced (τK = 0.14, pK = 0.2%), while no significant correlation is found with 1/sSFR (τK = −0.01, with a probability for the null hypothesis pK = 77%). The results are qualitatively similar when we change our reference CO-to-H2 correction factor to a constant one, or when we use a stronger quadratic dependence of the conversion factor on metallicity (such as that derived by Hunt et al. 2015a). The results shown in Fig. 5 (right panel) might thus be consistent with no variation of κ(250 μm) with metallicity, or equivalently, with the assumption that the fraction of metals included in grains is universal.
Instead, theoretical models suggest that the dust-to-metal ratio takes the imprint of the dominant dust-formation mechanism and results in a different dependence of D/H on metallicity (Mattsson & Andersen 2012; Asano et al. 2013). Rémy-Ruyer et al. (2014) found that below a critical metallicity (12 + log(O/H)≲8), the dependence of D/H is steeper than linear. A similar conclusion was drawn by Vílchez et al. (2019), who analysed resolved observations of NGC 628 and M 101. However, these metallicities are absent (or underrepresented for the critical metallicity of 8.4 in Vílchez et al. 2019) from our sample. Nevertheless, the scatter is large and other works have found D/H ∼ (O/H)1.5 − 2 over the full metallicity range in resolved studies (in the MW, Giannetti et al. 2017; and M 101, Chiang et al. 2018) and global studies (De Vis et al. 2019, although at higher metallicity their results are consistent with a constant dust-to-metal ratio). Adopting a steeper dependence of D/H on metallicity would cause κ(250 μm) to be even more negatively correlated with O/H. However, these results depend on various assumptions and ultimately on the use of the same κ(250 μm) for all the objects and environments. Paradoxically, they would require a positive correlation of σ(250 μm) on O/H steeper than what is actually shown in the left panel of Fig. 5.
6.3. Comparison with dust grain models
As a result of the fit to various constraints, dust models are characterised by an effective κν, that is, by the average of the absorption cross section over the grain size distribution and material mix. Typically, the effective κν in the FIR can be described by a power law such as that of Eq. (3) (see Table 1). Moreover, for the chosen grain materials, each model predicts its own D/H ratio, constrained by the observed metal depletions. When we compare our results for κ(250 μm) with those of the models, we need to take into account these differences in β and D/H. We did this in Fig. 6, where we show κ(250 μm) for the MW and for our sample at the MW metallicity, together with the predictions from THEMIS and DL07.
 |
Fig. 6. Absorption cross section per dust mass κ(250 μm) for the MW (red error bar) and for our sample in the MW metallicity bin (black error bar) compared with the values expected from the THEMIS and DL07 grain models (under various assumptions for the D/H ratio and β; see text for details). |
Despite the common value for ϵ(250 μm), the THEMIS model (purple circles in Fig. 6) has a higher effective κ(250 μm) than our measurements. When we scale the model from its original value for D/H to the adopted (D/H)MW (which is equivalent to comparing their respective σ(250 μm)), the difference is smaller. The rescaled THEMIS is still about 2σ away from the MW value. This gap can be further reduced by considering a common β for observations and model. The MW value for κ(250 μm) was derived after fitting the local emissivity SED (Bianchi et al. 2017). For a proper comparison, the emissivity predicted by the model when heated by the LISRF (U = 1) should be fitted accordingly. Using an MBB and allowing the spectral index to vary as well, Köhler et al. (2015) found β ≈ 1.5. The apparent β is smaller than that which describes the effective absorption cross section of the model, β ≈ 1.8. The difference is due to temperature mixing: the SED of the model results from the composition of MBBs at the temperatures attained by grains of different materials and sizes, while the fit considers only one temperature and tries to match the flatter slope by varying both temperature and β. The effect is stronger (and the fitted apparent β smaller than the effective) for radiation fields with a lower intensity (Hunt et al. 2015b). Using β = 1.6, as for the MW and DustPedia estimates, we fitted the U = 1 THEMIS emissivity for 100 < λ/μm < 500 and further reduced the estimate for the model κ(250 μm). When both the O/H and β are matched, the κ(250 μm) fitted to the model is very close to the Galactic value (and to the DustPedia sample average, after the discussion in the previous sections is taken into account). This is expected because the emissivity SED predicted by THEMIS for the MW is not far different from the observed one (Fig. 1).
Nersesian et al. (2019) have shown that the dust masses of DustPedia galaxies can be retrieved equally well (within the observational uncertainties) using the model effective κ(250 μm) coupled with the MBB approximation, or the full model approach accounting for distribution in grain sizes, materials, and ISRF intensities (see also Bianchi 2013). We tested what happens when we use the value of κ(250 μm) obtained from the fit above rescaled to (D/H)MW. In this case the dust masses for DustPedia galaxies are ≈30% higher than when we use the unscaled THEMIS absorption cross section. Half of the relative difference is due to the different choice for D/H and half to the fixed-β MBB approximations. We repeated similar tests for the DL07 model (orange squares in Fig. 6). This time, the adoption of (D/H)MW (lower that the model value) results in a higher κ(250 μm) and dust masses lower by ≈18%. The use of the fixed-β MBB approximation instead leads to dust masses higher by ≈12%: the net effect of both choices is a moderate underestimate of the dust mass by ≈6% with respect to the original DL07 model. The lower predicted emissivity of DL07 (Fig. 1) results in higher dust mass estimates than were obtained with THEMIS. Even when D/H and β are matched, dust masses obtained from the DL07 model would be ≈45% higher than those from THEMIS (because of a correspondingly lower κ(250 μm)). When the original models are used, the DL07-derived masses are about a factor of 3 higher than for THEMIS, as shown by Nersesian et al. (2019) for the DustPedia sample. The low DL07 emissivity is likely the cause of the overestimate of the optical/near-infrared extinction when compared to direct extinction measurements in the MW (Planck Collaboration Int. XVII 2016) and the Andromeda Galaxy (Dalcanton et al. 2015).
The comparison we made with models shows the potential pitfalls of deriving the absorption cross section from FIR observations, which is in particular due to the uncertainties on the D/H ratio and on the MBB approximation. This strengthens our belief that a more reliable characterisation of the dust properties in external galaxies should be made at the ϵ(250 μm) level. This quantity relies on fewer assumptions. This is after all what is commonly done to constrain models for dust in the MW cirrus.
7. Summary and conclusions
We estimated the average dust emissivity ϵ(250 μm) for 204 late-type galaxies belonging to the DustPedia sample (Davies et al. 2017). All our objects have multi-wavelength photometry (Clark et al. 2018), SED-fitted models, and estimates for physical quantities (Nersesian et al. 2019), metallicity (De Vis et al. 2019), and atomic and molecular gas data (De Vis et al. 2019; Casasola et al. 2019). Using the single-T MBB approximation, we derived the absorption cross sections per H-atom σ(250 μm); and per mass κ(250 μm) by adopting a dust-to-hydrogen mass ratio D/H. The results are summarised in Table 2, and the assumptions and MW reference values are listed in Table 1. Our main findings are listed below.
-
In galaxies with global FIR colours similar to that of the Galactic cirrus, ϵ(250 μm) is very close to that measured in the MW and consistent with predictions from the THEMIS model (and from an MBB with β = 1.6). The result is almost independent of the main assumption in the emissivity derivation, that is, the variation of the CO-to-H2 conversion factor with metallicity. This reassures us that MW-based dust models can be used to derive the mass in external galaxies.
-
For galaxies with bluer FIR colours, ϵ(250 μm) is on average smaller than what is implied by its dependence on temperature. These objects are typically of earlier type and higher metallicity, and have an H2 component that contributes significantly if not dominantly to the global gas mass. This might suggest possible variations in dust properties with the environment or the lack (of detection) of dust associated with H2.
-
For objects in the metallicity range of MW gas, the average absorption cross sections, either per H atom, σ(250 μm) or per dust mass, κ(250 μm), are slightly smaller than (by 15%) but compatible with cirrus estimates. The results would become entirely consistent with MW values for a constant CO-to-H2 conversion factor. Mild trends are seen with O/H, although the scatter of the data and the uncertainties in the assumptions prevent a definitive assessment of the variation of the cross sections with metallicity.
One of the main assumptions in this work, as well as in almost all determinations of the dust mass in galaxies, is that the same dust emission properties are valid throughout the whole disc. This appears to be the case for the MW, where σ(250 μm) is found to be the same within each of the gas components on the Galactic plane, and at high latitudes (Planck Collaboration XXI 2011). In this work, we instead found indications that the dust emissivity is reduced for galaxies whose gas mass is dominated by H2. A more definitive assessment of the variation of dust properties with the environment requires resolved observations of dust, gas, and metallicity. In parallel to the current work, a pilot study has been conducted on two DustPedia galaxies, M 74 and M 83: reassuringly, the dust absorption cross section is reduced in these objects in regions of higher gas column density. This qualitatively agrees with our findings (Clark et al. 2019).
Taken at face value, the lower values of ϵ(250 μm) might indicate, without accounting for any D/H variation, that the dust masses for galaxies with bluer FIR colours are underestimated by up to a factor two. While we wait for other observational confirmations of this result, it might be interesting to understand from the theoretical viewpoint whether the exposition of dust grains to strong radiation fields can cause these variations (Jones et al. 2017). Before any other modelling is undertaken, however, we recommend a revision and standardisation of the observational constraints. Comparing the predictions of two commonly used dust grain models, we find discrepancies in the adopted cirrus emissivity, related to both its absolute value and the correction for the H II contribution (accounting for this could reduce ϵ(250 μm) by 20%). Other uncertainties might lie in the definition of the LISFR: Draine (2011) proposed a revisited version of the commonly used spectrum from Mathis et al. (1983), with an energy output increased by about 30% (Bianchi et al. 2017). Finally, a revision is recommended also for the optical extinction per H column density, which is required to scale another main constraint for dust models, the extinction law: the commonly used value (Bohlin et al. 1978) is 40−60% higher than the newer estimates (Liszt 2014; Lenz et al. 2017; Nguyen et al. 2018)
Bianchi et al. (2018) erroneously attributed the discrepancy to a bias in the calibration of FIRAS data, which might only be significant around the 350 μm Planck and Herschel bands (Planck Collaboration VIII 2014), however.
Emission from the THEMIS model has been computed with the DustEM code (Compiègne et al. 2011). The Draine & Li (2007) emission templates are available at https://www.astro.princeton.edu/~draine/
Acknowledgments
We would like to thank the anonymous referee and G. Cresci for useful comments, and L. Verstraete for help with the Compiègne et al. (2011) emissivity. We acknowledge funding from the INAF mainstream 2018 program “Gas-DustPedia: A definitive view of the ISM in the Local Universe, and from the INAF PRIN- SKA 2017 program 1.05.01.88.04”.
References
- Amorín, R., Muñoz-Tuñón, C., Aguerri, J. A. L., & Planesas, P. 2016, A&A, 588, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arendt, R. G., Odegard, N., Weiland, J. L., et al. 1998, ApJ, 508, 74 [Google Scholar]
- Asano, R. S., Takeuchi, T. T., Hirashita, H., & Inoue, A. K. 2013, Earth Planets Space, 65, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S. 2013, A&A, 552, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S., Giovanardi, C., Smith, M. W. L., et al. 2017, A&A, 597, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S., De Vis, P., Viaene, S., et al. 2018, A&A, 620, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bocchio, M., Jones, A. P., & Slavin, J. D. 2014, A&A, 570, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boggess, N. W., Mather, J. C., Weiss, R., et al. 1992, ApJ, 397, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
- Boquien, M., Burgarella, D., Roehlly, Y., et al. 2019, A&A, 622, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casasola, V., Cassarà, L. P., Bianchi, S., et al. 2017, A&A, 605, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casasola, V., Bianchi, S., De Vis, P., et al. 2019, A&A, submitted [Google Scholar]
- Chastenet, J., Bot, C., Gordon, K. D., et al. 2017, A&A, 601, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiang, I.-D., Sandstrom, K. M., Chastenet, J., et al. 2018, ApJ, 865, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, C. J. R., Schofield, S. P., Gomez, H. L., & Davies, J. I. 2016, MNRAS, 459, 1646 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, C. J. R., Verstocken, S., Bianchi, S., et al. 2018, A&A, 609, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clark, C. J. R., De Vis, P., Baes, M., & DustPedia, A. 2019, MNRAS, 489, 5256 [NASA ADS] [CrossRef] [Google Scholar]
- Compiègne, M., Verstraete, L., Jones, A., et al. 2011, A&A, 525, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Curti, M., Cresci, G., Mannucci, F., et al. 2017, MNRAS, 465, 1384 [NASA ADS] [CrossRef] [Google Scholar]
- Dalcanton, J. J., Fouesneau, M., Hogg, D. W., et al. 2015, ApJ, 814, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Aniano, G., Engelbracht, C. W., et al. 2012, ApJ, 745, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, J. I., Baes, M., Bendo, G. J., et al. 2010, A&A, 518, L48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davies, J. I., Baes, M., Bianchi, S., et al. 2017, PASP, 129, 044102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Vis, P., Jones, A., Viaene, S., et al. 2019, A&A, 623, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Désert, F. X., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215 [NASA ADS] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., Dale, D. A., Bendo, G., et al. 2007, ApJ, 663, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., Arendt, R. G., Fixsen, D. J., et al. 1997, ApJ, 475, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Esteban, C., & García-Rojas, J. 2018, MNRAS, 478, 2315 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, F. 2018, MNRAS, 476, 1445 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, F., Galametz, M., & Jones, A. P. 2018, ARA&A, 56, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Giannetti, A., Leurini, S., König, C., et al. 2017, A&A, 606, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Groves, B. A., Schinnerer, E., Leroy, A., et al. 2015, ApJ, 799, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Hodge, P. W. 1983, PASP, 95, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L. K., García-Burillo, S., Casasola, V., et al. 2015a, A&A, 583, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L. K., Draine, B. T., Bianchi, S., et al. 2015b, A&A, 576, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L. K., De Looze, I., Boquien, M., et al. 2019, A&A, 621, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- James, A., Dunne, L., Eales, S., & Edmunds, M. G. 2002, MNRAS, 335, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, A. G., Rachford, B. L., & Snow, T. P. 2005, ApJ, 619, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., Fanciullo, L., Köhler, M., et al. 2013, A&A, 558, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P., Köhler, M., Ysard, N., Bocchio, M., & Verstraete, L. 2017, A&A, 602, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Köhler, M., Ysard, N., & Jones, A. P. 2015, A&A, 579, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lenz, D., Hensley, B. S., & Doré, O. 2017, ApJ, 846, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]
- Liszt, H. 2014, ApJ, 780, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Magnelli, B., Lutz, D., Saintonge, A., et al. 2014, A&A, 561, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magrini, L., Bianchi, S., Corbelli, E., et al. 2011, A&A, 535, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, P. G., Roy, A., Bontemps, S., et al. 2012, ApJ, 751, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsiek, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
- Mattsson, L., & Andersen, A. C. 2012, MNRAS, 423, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, D. M., Jura, M., & Cardelli, J. A. 1998, ApJ, 493, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Mezger, P. G., Mathis, J. S., & Panagia, N. 1982, A&A, 105, 372 [NASA ADS] [Google Scholar]
- Nersesian, A., Xilouris, E. M., Bianchi, S., et al. 2019, A&A, 624, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nguyen, H., Dawson, J. R., Miville-Deschênes, M.-A., et al. 2018, ApJ, 862, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Pilyugin, L. S., Ferrini, F., & Shkvarun, R. V. 2003, A&A, 401, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXI. 2011, A&A, 536, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIV. 2011, A&A, 536, A24 [Google Scholar]
- Planck Collaboration VIII. 2014, A&A, 571, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XVII. 2014, A&A, 566, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XVII. 2016, A&A, 586, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pohlen, M., Cortese, L., Smith, M. W. L., et al. 2010, A&A, 518, L72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Przybilla, N., Nieva, M.-F., & Butler, K. 2008, ApJ, 688, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Reach, W. T., Dwek, E., Fixsen, D. J., et al. 1995, ApJ, 451, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2014, A&A, 563, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ritchey, A. M., Federman, S. R., & Lambert, D. L. 2018, ApJS, 236, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Santini, P., Maiolino, R., Magnelli, B., et al. 2014, A&A, 562, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schruba, A., Leroy, A. K., Walter, F., et al. 2012, AJ, 143, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Siebenmorgen, R., Voshchinnikov, N. V., & Bagnulo, S. 2014, A&A, 561, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, M. W. L., Clark, C. J. R., De Looze, I., et al. 2019, MNRAS, 486, 4166 [NASA ADS] [CrossRef] [Google Scholar]
- Symeonidis, M., Vaccari, M., Berta, S., et al. 2013, MNRAS, 431, 2317 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Utomo, D., Chiang, I. D., Leroy, A. K., Sandstrom, K. M., & Chastenet, J. 2019, ApJ, 874, 141 [NASA ADS] [CrossRef] [Google Scholar]
- van der Kruit, P. C. 1990, in The Milky Way as a Galaxy, eds. I. King, G. Gilmore, & P. C. van der Kruit, 331 [Google Scholar]
- Vílchez, J. M., Relaño, M., Kennicutt, R., et al. 2019, MNRAS, 483, 4968 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., Hollenbach, D., & McKee, C. F. 2010, ApJ, 716, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Mather, J. C., Bennett, C. L., et al. 1991, ApJ, 381, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Ysard, N., Juvela, M., Demyk, K., et al. 2012, A&A, 542, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zubko, V., Dwek, E., & Arendt, R. G. 2004, ApJS, 152, 211 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Analogies with C16
Using Eqs. (1), (2), (4), and (5), we can write
When we neglect the (minor) contribution of an additional component of dust at a warmer temperature, the derivation of κν in C16 (their Eq. (10)) is equivalent to Eq. (A.1), provided that
The parameters in Eq. (A.2) are ξ, a correction to account for the number of elements in the ISM other than H I and H2 (i.e. He – mainly – and metals); εd, a constant dust-to-metal mass fraction; fZ⊙ and (O/H)⊙, the solar metal mass fraction and oxygen abundance, respectively; δO, a correction of the gas oxygen abundance to take the oxygen atoms into account that are depleted into dust (for details, see C16; Clark et al. 2019).
For the values adopted by C16, this is ((D/H)/(O/H))MW = 25 ± 6; for the updated quantities in Clark et al. (2019), this becomes 20 ± 9, which is closer to the value we used here (Sect. 4).
All Tables
Milky Way reference values adopted here (in bold) and other values from the literature.
All Figures
 |
Fig. 1. Milky Way emissivity ϵν at high Galactic latitude. Left panel: we compare estimates obtained from COBE-DIRBE and Planck data of the south Galactic pole (Planck Collaboration Int. XVII 2014) and from IRAS, Herschel, and Planck data of the HeViCS fields (Bianchi et al. 2017) to those derived from the COBE-FIRAS spectrum. In the right panel, we show MBB fits to the HeViCS data (Bianchi et al. 2017) and to IRAS and Planck data over the whole diffuse high-Galactic latitude cirrus (Planck Collaboration XI 2014), together with the predictions from the THEMIS and Draine et al. (2007) dust models heated by the LISRF. The HeViCS data points are repeated to facilitate comparison. |
| In the text | |
 |
Fig. 2. Emissivity ϵ(250 μm) as a function of the F(250 μm)/F(500 μm) ratio. When data on the abscissa (and/or ordinate) are estimated at a level below 2σ, the x (and/or y) error is omitted and an open symbol is used. The red error bar shows the MW estimate from HeVICS. The mean of ϵ(250 μm) and its standard deviation for five bins in F(250 μm)/F(500 μm) is shown by the black error bars (connected by a solid line). The F(250 μm)/F(500 μm) range and the number of galaxies is given for each bin. |
| In the text | |
 |
Fig. 3. Emissivity ϵ(250 μm) as a function of F(250 μm)/F(500 μm) for each galaxy (grey datapoints) and for the mean for F(250 μm)/ F(500 μm) bins (same as Fig. 2, but individual error bars are omitted for clarity). Coloured dots in the top panel show the mean and its standard deviation for bins of different morphological types. Red dots in the central panel show the same, but for bins in metallicity (the number of objects for each bin is given in both panels). Bottom panel: the long-dashed line shows the binned mean assuming a constant CO-to-H2 conversion factor, and the short-dashed line shows the mean when the H2 component is neglected. |
| In the text | |
 |
Fig. 4. Same as Fig. 2 (individual error bars are omitted for clarity). Left panel: the red line shows the locus of an MBB with β = 1.6 for different temperatures (red dots along the line give the values at Td = 15, 20, 25, 30, 35, and 40 K, from left to right). The purple and orange lines show the loci of dust heated by the LISRF scaled by a factor U for the THEMIS and DL07 grain models, respectively (dots along the lines are for U = 0.1, 0.5, 1, 2, 5, 10, and 20, from left to right). Right panel: the THEMIS dust model (solid purple line) is repeated together with the CMM model from Köhler et al. (2015) for 0.1 < U < 0.5 (dashed purple line). Purple dots are the emissivity values estimated from the CIGALE-THEMIS best-fit SEDs of each galaxy (see text for details). |
| In the text | |
 |
Fig. 5. Absorption cross section per H atom σ(250 μm) (left panel) and per dust mass κ(250 μm) (right panel) as a function of the metallicity. The two panels show individual measurements as grey dots, with the same convention for open and filled symbols as in Fig. 2. The mean (and its standard deviation) of the quantity of the y-axis for the five metallicity bins defined in Fig. 3 (black error bars connected by a solid line) is shown, and the same, but for the four morphology bins (coloured dots with error bars). We also plot the HeViCS MW estimate of Table 1 (red error bars). Left panel: we also show the mean for each metallicity bin, when the dust temperature is derived with β = 1.8 (dashed line) and 2.0 (dotted line), and the slope for a linear dependence of κ(250 μm) on O/H (green dot-dashed line, arbitrary scale; Eqs. (4) and (5)). Right panel: the black error bar at the left shows the uncertainty in ((D/H)/(O/H))MW. The star indicates the value derived from C16 after rescaling it to the assumptions of this work (see text for details). |
| In the text | |
 |
Fig. 6. Absorption cross section per dust mass κ(250 μm) for the MW (red error bar) and for our sample in the MW metallicity bin (black error bar) compared with the values expected from the THEMIS and DL07 grain models (under various assumptions for the D/H ratio and β; see text for details). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.