| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A73 | |
| Number of page(s) | 11 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201935828 | |
| Published online | 22 October 2019 | |
Estimating the galaxy two-point correlation function using a split random catalog
1
Department of Physics and Helsinki Institute of Physics, University of Helsinki, Gustaf Hällströmin katu 2, 00014 Helsinki, Finland
e-mail: elina.keihanen@helsinki.fi
2
Scuola Normale Superiore, Piazza dei Cavalieri 7, 56126 Pisa, Italy
3
Department of Mathematics and Physics, Roma Tre University, Via della Vasca Navale 84, 00146 Rome, Italy
4
Dipartimento di Fisica e Astronomia – Alma Mater Studiorum Università di Bologna, Via Piero Gobetti 93/2, 40129 Bologna, Italy
5
INAF – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Piero Gobetti 93/3, 40129 Bologna, Italy
6
INFN – Sezione di Bologna, Viale Berti Pichat 6/2, 40127 Bologna, Italy
7
ICC & CEA, Department of Physics, Durham University, South Road, Durham DH1 3LE, UK
8
INAF, Osservatorio Astronomico di Trieste, Via Tiepolo 11, 34131 Trieste, Italy
9
Aix Marseille Univ., CNRS, CNES, LAM, Marseille, France
10
SISSA, International School for Advanced Studies, Via Bonomea 265, 34136 Trieste, TS, Italy
11
INFN, Sezione di Trieste, Via Valerio 2, 34127 Trieste, TS, Italy
12
Aix Marseille Univ., Université de Toulon, CNRS, CPT, Marseille, France
13
Max-Planck-Institut für Extraterrestrische Physik, Postfach 1312, Giessenbachstr., 85741 Garching, Germany
14
IFPU – Institute for Fundamental Physics of the Universe, Via Beirut 2, 34014 Trieste, Italy
Received:
3
May
2019
Accepted:
24
July
2019
The two-point correlation function of the galaxy distribution is a key cosmological observable that allows us to constrain the dynamical and geometrical state of our Universe. To measure the correlation function we need to know both the galaxy positions and the expected galaxy density field. The expected field is commonly specified using a Monte-Carlo sampling of the volume covered by the survey and, to minimize additional sampling errors, this random catalog has to be much larger than the data catalog. Correlation function estimators compare data–data pair counts to data–random and random–random pair counts, where random–random pairs usually dominate the computational cost. Future redshift surveys will deliver spectroscopic catalogs of tens of millions of galaxies. Given the large number of random objects required to guarantee sub-percent accuracy, it is of paramount importance to improve the efficiency of the algorithm without degrading its precision. We show both analytically and numerically that splitting the random catalog into a number of subcatalogs of the same size as the data catalog when calculating random–random pairs and excluding pairs across different subcatalogs provides the optimal error at fixed computational cost. For a random catalog fifty times larger than the data catalog, this reduces the computation time by a factor of more than ten without affecting estimator variance or bias.
Key words: large-scale structure of Universe / cosmology: observations / methods: statistical / methods: data analysis
© ESO 2019
1. Introduction
The spatial distribution of luminous matter in the Universe is a key diagnostic for studying cosmological models and the physical processes involved in the assembly of structure. In particular, light from galaxies is a robust tracer of the overall matter distribution, whose statistical properties can be predicted by cosmological models. Two-point correlation statistics are very effective tools for compressing the cosmological information encoded in the spatial distribution of the mass in the Universe. In particular, the two-point correlation function in configuration space has emerged as one of the most popular cosmological probes. Its success stems from the presence of characterized features that can be identified, measured, and effectively compared to theoretical models to extract clean cosmological information.
One such feature is baryon acoustic oscillations (BAOs), which imprint a characteristic scale in the two-point correlation function that can be used as a standard ruler. After the first detection in the two-point correlation function of SDSS DR3 and 2dFGRS galaxy catalogs (Eisenstein et al. 2005; Cole et al. 2005), the BAO signal was identified, with different degrees of statistical significance, and has since been used to constrain the expansion history of the Universe in many spectroscopic galaxy samples (see e.g., Percival et al. 2010; Blake et al. 2011; Beutler et al. 2011; Anderson et al. 2012, 2014; Ross et al. 2015, 2017; Alam et al. 2017; Vargas-Magaña et al. 2018; Bautista et al. 2018; Ata et al. 2018). Several of these studies did not focus on the BAO feature only but also analyzed the anisotropies in the two-point correlation function induced by the peculiar velocities (Kaiser 1987), the so-called redshift space distortions (RSD), and by assigning cosmology-dependent distances to the observed redshifts (the Alcock & Paczyński 1979 test). For RSD analyses, see also, for example, Peacock et al. (2001), Guzzo et al. (2008), Beutler et al. (2012), Reid et al. (2012), de la Torre et al. (2017), Pezzotta et al. (2017), Zarrouk et al. (2018), Hou et al. (2018), and Ruggeri et al. (2019).
Methods to estimate the galaxy two-point correlation function (2PCF) ξ(r) from survey data are based on its definition as the excess probability of finding a galaxy pair. One counts from the data (D) catalog the number DD(r) of pairs of galaxies with separation x2 − x1 ∈ r, where r is a bin of separation vectors, and compares it to the number of pairs RR(r) in a corresponding randomly generated (R) catalog and to the number of data-random pairs DR(r). The bin may be a 1D (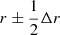 ), 2D, or a 3D bin. In the 1D case, r is the length of the separation vector and Δr is the width of the bin. From here on, “separation r” indicates that the separation falls in this bin.
), 2D, or a 3D bin. In the 1D case, r is the length of the separation vector and Δr is the width of the bin. From here on, “separation r” indicates that the separation falls in this bin.
Several estimators of the 2PCF have been proposed by Hewett (1982), Davis & Peebles (1983), Hamilton (1993), and Landy & Szalay (1993), building on the original Peebles & Hauser (1974) proposal. These correspond to different combinations of the DD, DR, and RR counts to obtain a 2PCF estimate 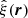 ; see Kerscher (1999) and Kerscher et al. (2000) for more estimators. The Landy–Szalay (Landy & Szalay 1993) estimator
; see Kerscher (1999) and Kerscher et al. (2000) for more estimators. The Landy–Szalay (Landy & Szalay 1993) estimator
(we call this method “standard LS” in the following) is the most commonly used, since it provides the minimum variance when |ξ|≪1 and is unbiased in the limit 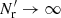 . Here Nd is the size (number of objects) of the data catalog and
. Here Nd is the size (number of objects) of the data catalog and 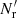 is the size of the random catalog. We define
is the size of the random catalog. We define 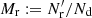 . To minimize random error from the random catalog, Mr ≫ 1 should be used (for a different approach, see Demina et al. 2018).
. To minimize random error from the random catalog, Mr ≫ 1 should be used (for a different approach, see Demina et al. 2018).
One is usually interested in ξ(r) only up to some rmax ≪ Lmax (the maximum separation in the survey), and therefore pairs with larger separations can be skipped. Efficient implementations of the LS estimator involve pre-ordering of the catalogs through kd-tree, chain-mesh, or other algorithms (e.g., Moore et al. 2000; Alonso 2012; Jarvis 2015; Marulli et al. 2016) to facilitate this. The computational cost is then roughly proportional to the actual number of pairs with separation r ≤ rmax.
The correlation function is small for large separations, and in cosmological surveys rmax is large enough so that for most pairs |ξ(r)| ≪ 1. The fraction f of DD pairs with r ≤ rmax is therefore not very different from the fraction of DR or RR pairs with r ≤ rmax. The computational cost is dominated by the part proportional to the total number of pairs needed, 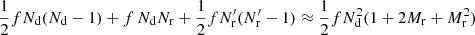 , which in turn is dominated by the RR pairs as Mr ≫ 1. The smaller number of DR pairs contribute much more to the error of the estimate than the large number of RR pairs, whereas the cost is dominated by RR. Thus, a significant saving of computation time with an insignificant loss of accuracy may be achieved by counting only a subset of RR pairs, while still counting the full set (up to rmax) of DR pairs.
, which in turn is dominated by the RR pairs as Mr ≫ 1. The smaller number of DR pairs contribute much more to the error of the estimate than the large number of RR pairs, whereas the cost is dominated by RR. Thus, a significant saving of computation time with an insignificant loss of accuracy may be achieved by counting only a subset of RR pairs, while still counting the full set (up to rmax) of DR pairs.
A good way to achieve this is to use many small (i.e, low-density) R catalogs instead of one large (high-density) catalog (Landy & Szalay 1993; Wall & Jenkins 2012; Slepian & Eisenstein 2015), or, equivalently, to split an already generated large R catalog into Ms small ones for the calculation of RR pairs while using the full R catalog for the DR counts. This method has been used by some practitioners (e.g., Zehavi et al. 20111), but this is usually not documented in the literature. One might also consider obtaining a similar cost saving by diluting (subsampling) the R catalog for RR counts, but, as we show below, this is not a good idea. We refer to these two cost-saving methods as “split” and “dilution”.
In this work we theoretically derive the additional covariance and bias due to the size and treatment of the R catalog; test these predictions numerically with mock catalogs representative of next-generation datasets, such as the spectroscopic galaxy samples that will be obtained by the future Euclid satellite mission (Laureijs et al. 2011); and show that the “split” method, while reducing the computational cost by a large factor, retains the advantages of the LS estimator.
We follow the approach of Landy & Szalay (1993; hereafter, LS93), but generalize it in a number of ways: In particular, since we focus on the effect of the random catalog, we do not work in the limit Mr → ∞. Also, we calculate covariances, not just variances, and make fewer approximations (see Sect. 2.2).
The layout of the paper is as follows. In Sect. 2 we derive theoretical results for bias and covariance. In Sect. 3 we focus on the split LS estimator and its optimization. In Sect. 4 we test the different estimators with mock catalogs. Finally, we discuss the results and present our conclusions in Sect. 5.
2. Theoretical results: bias and covariance
2.1. General derivation
We follow the derivation and notations in LS93 but extend to the case that includes random counts covariance. We consider the survey volume as divided into K microcells (very small subvolumes) and work in the limit K → ∞, which means that no two objects will ever be located within the same microcell.
Here, α, β, and γ represent the relative deviation of the DD(r), DR(r), and RR(r) counts from their expectation values (mean values over an infinite number of independent realizations):
By definition ⟨α⟩ = ⟨β⟩ = ⟨γ⟩ = 0. The factors α, β, and γ represent fluctuations in the pair counts, which arise as a result of a Poisson process. As long as the mean pair counts per bin are large (≫1) the relative fluctuations will be small. We calculate up to second order in α, β, and γ, and ignore the higher-order terms (in the limit Mr → ∞, γ → 0, so LS93 set γ = 0 at this point).
The expectation values for the pair counts are:
where ξ(r) is the correlation function normalized to the actual number density of galaxies in the survey and
is the fraction of microcell pairs with separation r. Here Θij(r): = 1 if xi − xj falls in the r-bin, otherwise it is equal to zero.
The expectation value of the LS estimator (1) is
A finite R catalog thus introduces a (small) bias. (In LS93, γ = 0, so the estimator is unbiased in this limit). This expression is calculated to second order in α, β, and γ (we denote equality to second order by “≂”). Calculation to higher order is beyond the scope of this work. Since data and random catalogs are independent, ⟨αγ⟩ = 0.
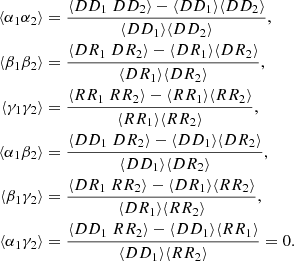
We introduce shorthand notations ⟨α1α2⟩ for ⟨α(r1)α(r2)⟩, ⟨DD1DD2⟩ for ⟨DD(r1)DD(r2)⟩, and similarly for other terms.
For the covariance we get
Terms with γ represent additional variance due to finite 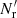 , and are new compared to those of LS93. Also, ⟨β1β2⟩ collects an additional contribution, which we denote by Δ⟨β1β2⟩, from variations in the random field (see Sect. 2.3). The cross terms α1β2 and α2β1, instead depend linearly on the random field, and average to the
, and are new compared to those of LS93. Also, ⟨β1β2⟩ collects an additional contribution, which we denote by Δ⟨β1β2⟩, from variations in the random field (see Sect. 2.3). The cross terms α1β2 and α2β1, instead depend linearly on the random field, and average to the  result. The additional contribution due to finite
result. The additional contribution due to finite 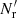 is thus
is thus
From (2),
and so on, so that the covariances of the deviations are obtained from
2.2. Quadruplets, triplets, and approximations
We use
to denote the fraction of ordered microcell triplets, where xi − xk ∈ r1 and xj − xk ∈ r2. The notation ∑* means that only terms where all indices (microcells) are different are included. Here 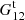 is of the same magnitude as
is of the same magnitude as 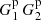 but is larger.
but is larger.
Appendix A gives examples of how the ⟨DD1DD2⟩ and so on in (9) are calculated. These covariances involve expectation values ⟨ninjnlnk⟩, where ni is the number of objects (0 or 1) in microcell i and so on, and only cases where the four microcells are separated pairwise by r1 and r2 are included. If all four microcells i, j, k, and l are different, we call this case a quadruplet; it consists of two pairs with separations r1 and r2. If two of the indices, that is, microcells, are equal, we have a triplet with a center cell (the equal indices) and two end cells separated from the center by r1 and r2.
We make the following three approximations:
-
For microcell quadruplets, the correlations between unconnected cells are approximated by zero on average.
-
Three-point correlations vanish.
-
The part of four-point correlations that does not arise from the two-point correlations vanishes.
With approximations (2) and (3), we have for the expectation value of a galaxy triplet
where ξij := ξ(xj − xi), and for a quadruplet
We use “≃” to denote results based on these three approximations. Approximation (1) is good as long as the survey size is large compared to rmax. It allows us to drop terms other than 1 + ξij + ξkl + ξijξkl in (12). Approximations (2) and (3) hold for Gaussian density fluctuations, but in the realistic cosmological situation they are not good: the presence of the higher-order correlations makes the estimation of the covariance of ξ(r) estimators a difficult problem. However, this difficulty applies only to the contribution of the data to the covariance, that is, to the part that does not depend on the size and treatment of the random catalog. The key point in this work is that while our theoretical result for the total covariance does not hold in a realistic situation (it is an underestimate), our results for the difference in estimator covariance due to different treatments of the random catalog hold well.
In addition to working in the limit 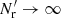 (γ = 0), LS93 considered only 1D bins and the case where r1 = r2 ≡ r (i.e., variances, not covariances) and made also a fourth approximation: for triplets (which in this case have legs of equal length) they approximated the correlation between the end cells (whose separation in this case varies between 0 and 2r) by ξ(r). We use ξ12 to denote the mean value of the correlation between triplet end cells (separated from the triplet center by r1 and r2). (For our plots in Sect. 4 we make a similar approximation of ξ12 as Landy & Szalay 1993, see Sect. 4.2). Also, LS93 only calculated to first order in ξ, whereas we do not make this approximation. Bernstein (1994) also considered covariances, and included the effect of three-point and four-point correlations, but worked in the limit
(γ = 0), LS93 considered only 1D bins and the case where r1 = r2 ≡ r (i.e., variances, not covariances) and made also a fourth approximation: for triplets (which in this case have legs of equal length) they approximated the correlation between the end cells (whose separation in this case varies between 0 and 2r) by ξ(r). We use ξ12 to denote the mean value of the correlation between triplet end cells (separated from the triplet center by r1 and r2). (For our plots in Sect. 4 we make a similar approximation of ξ12 as Landy & Szalay 1993, see Sect. 4.2). Also, LS93 only calculated to first order in ξ, whereas we do not make this approximation. Bernstein (1994) also considered covariances, and included the effect of three-point and four-point correlations, but worked in the limit 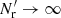 (γ = 0).
(γ = 0).
2.3. Poisson, edge, and q terms
After calculating all the ⟨DD1DD2⟩ and so on (see Appendix A), (9) becomes
for the standard LS estimator.
Following the definition of t and p in LS93, we define
For their diagonals (r1 = r2), we write t, tr, p, pc, pr, q, and qr. Thus, t ≡ t11 ≡ t22, 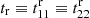 and so on. (We use superscripts for the matrices, e.g., tr(r1, r2), and subscripts for their diagonals, e.g., tr(r)).
and so on. (We use superscripts for the matrices, e.g., tr(r1, r2), and subscripts for their diagonals, e.g., tr(r)).
Using these definitions, (13) becomes
The new part in ⟨β1β2⟩ due to finite size of the random catalog is
Thus only ⟨α1α2⟩ and ⟨β1β2⟩ are affected by ξ(r) (in our approximation its effect cancels in ⟨α1β2⟩). The results for ⟨γ1γ2⟩, ⟨β1γ2⟩, and ⟨α1γ2⟩ are exact. The result for ⟨α1α2⟩ involves all three approximations mentioned above, ⟨α1β2⟩ involves approximations (1) and (2), and ⟨β1β2⟩ involves approximation (1).
We refer to p, pc, and pr as “Poisson” terms and t and tr as “edge” terms (the difference between 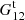 and
and 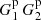 is due to edge effects). While the Poisson terms are strongly diagonal dominated, the edge terms are not. Since
is due to edge effects). While the Poisson terms are strongly diagonal dominated, the edge terms are not. Since 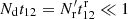 , the q terms are much larger than the edge terms, but they get multiplied by ξ12 − ξ1ξ2 or ξ12. In the limit
, the q terms are much larger than the edge terms, but they get multiplied by ξ12 − ξ1ξ2 or ξ12. In the limit 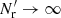 : ⟨β1γ2⟩→0, ⟨γ1γ2⟩→0, ⟨β1β2⟩→t12; ⟨α1α2⟩, and also ⟨α1β2⟩ are unaffected.
: ⟨β1γ2⟩→0, ⟨γ1γ2⟩→0, ⟨β1β2⟩→t12; ⟨α1α2⟩, and also ⟨α1β2⟩ are unaffected.
We see that DD–DR and DR–RR correlations arise from edge effects. If we increase the density of data or random objects, the Poisson terms decrease as N−2 but the edge terms decrease only as N−1 so the edge effects are more important for a higher density of objects.
Doubling the bin size (combining neighboring bins) doubles Gp(r) but makes Gt(r1, r2) four times as large, since triplets where one leg was in one of the original smaller bins and the other leg was in the other bin are now also included. Thus, the ratio 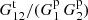 and t are not affected, but the dominant term in p, 1/(1 + ξ)Gp is halved. Edge effects are thus more important for larger bins.
and t are not affected, but the dominant term in p, 1/(1 + ξ)Gp is halved. Edge effects are thus more important for larger bins.
2.4. Results for the standard Landy–Szalay estimator
Inserting the results for ⟨α1α2⟩ and so on into Eqs. (5) and (6), we get that the expectation value of the standard LS estimator (1) is
This holds also for large ξ and in the presence of three-point and four-point correlations. A finite R catalog thus introduces a bias (ξ−1)(4 tr + pr)+4 tr = −pr + (4 tr + pr)ξ; the edge (tr) part of the bias cancels in the ξ → 0 limit.
For the covariance we get
Because of the approximations made, this result for the covariance does not apply to the realistic cosmological case; not even for large separations r, where ξ is small, since large correlations at small r increase the covariance also at large r. However, this concerns only ⟨α1α2⟩ and ⟨α1β2⟩. Our focus here is on the additional covariance due to the size and handling of the random catalog, which for standard LS is
To zeroth order in ξ the covariance is given by the Poisson terms and the edge terms cancel to first order in ξ. This is the property for which the standard LS estimator was designed. To first order in ξ, the q terms contribute. This q contribution involves the triplet correlation ξ12, which, depending on the form of ξ(r), may be larger than ξ1 or ξ2.
If we try to save cost by using a diluted random catalog with 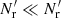 for RR pairs, ⟨γ1γ2⟩ is replaced by
for RR pairs, ⟨γ1γ2⟩ is replaced by 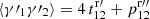 with
with  in place of
in place of  , but
, but 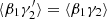 and ⟨β1β2⟩ are unaffected, so that the edge terms involving randoms no longer cancel. In Sect. 4 we see that this is a large effect. Therefore, one should not use dilution.
and ⟨β1β2⟩ are unaffected, so that the edge terms involving randoms no longer cancel. In Sect. 4 we see that this is a large effect. Therefore, one should not use dilution.
3. Split random catalog
3.1. Bias and covariance for the split method
In the split method one has Ms independent smaller Rμ catalogs of size 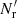 instead of one large random catalog R. Their union, R, has a size of
instead of one large random catalog R. Their union, R, has a size of 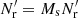 . The pair counts DR(r) and RR′(r) are calculated as
. The pair counts DR(r) and RR′(r) are calculated as
that is, pairs across different Rμ catalogs are not included in RR′. The total number of pairs in RR′ is 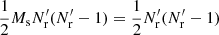 . Here, DR is equal to its value in standard LS.
. Here, DR is equal to its value in standard LS.
The split Landy–Szalay estimator is
Compared to standard LS, ⟨α1α2⟩, ⟨β1β2⟩, and ⟨α1β2⟩ are unaffected. We construct ⟨RR′⟩, ⟨RR′⋅RR′⟩, and ⟨RR′⋅DR⟩ from the standard LS results, bearing in mind that the random catalog is a union of independent catalogs, arriving at
where
The first is the same as in standard LS and dilution, but the second differs both from standard LS and from dilution, since it involves both 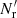 and
and 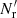 .
.
For the expectation value we get
so that the bias is 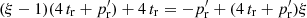 . In the limit ξ → 0 the edge part cancels, leaving only the Poisson term.
. In the limit ξ → 0 the edge part cancels, leaving only the Poisson term.
The covariance is
The change in the covariance compared to the standard LS method is
which again applies in the realistic cosmological situation. Our main result is that in the split method the edge effects cancel and the bias and covariance are the same as for standard LS, except that the Poisson term pr from RR is replaced with the larger pr′.
3.2. Optimizing computational cost and variance of the split method
The bias is small compared to variance in our application (see Fig. 1 for the theoretical result and Fig. 5 for an attempted bias measurement), and therefore we focus on variance as the figure of merit. The computational cost should be roughly proportional to
 |
Fig. 1. Mean ξ(r) estimate and the scatter and theoretical bias of the estimates for different estimators. The dash-dotted line, our theoretical result for the scatter of the LS method, underestimates the scatter, since higher-order correlations in the D catalog are ignored. The dotted line is without the contribution of the q terms, and is dominated by the Poisson (p) terms. The bias is multiplied by 100 so the curves can be displayed in a more compact plot. For the measured mean and scatter, and the theoretical bias we plot standard LS in black, dilution with d = 0.14 in red, and split with Ms = 50 in blue. For the mean and scatter the difference between the methods is not visible in this plot. The differences in the mean estimate are shown in Fig. 5. The differences in scatter (or its square, the variance) are shown in Fig 3. For the theoretical bias the difference between split and dilution is not visible at small r (ξ(r) > 1), where the bias is positive. |
and the additional variance due to finite R catalog in the ξ → 0 limit becomes
Here, Nd and p are fixed by the survey and the requested r binning, but we can vary Mr and Ms in the search for the optimal computational method. In the above we defined the “cost” and “variance” factors c and v.
We may ask two questions:
-
For a fixed level of variance v, which combination of Mr and Ms minimizes computational cost c?
-
For a fixed computational cost c, which combination of Mr and Ms minimizes the variance v?
The answer to both questions is (Slepian & Eisenstein 2015)
Thus, the optimal version of the split method is the natural one where 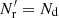 . In this case the additional variance in the ξ → 0 limit becomes
. In this case the additional variance in the ξ → 0 limit becomes
and the computational cost factor 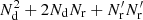 becomes
becomes
meaning that DR pairs contribute twice as much as RR pairs to the variance and also twice as much computational cost is invested in them. The memory requirement for the random catalog is then the same as for the data catalog. The cost saving estimate above is optimistic, since the computation involves some overhead not proportional to the number of pairs.
For small scales, where ξ ≫ 1, the situation is different. The greater density of DD pairs due to the correlation requires a greater density of the R catalog so that the additional variance from it is not greater. From Eq. (19) we see that the balance of the DR and the RR contributions is different for large ξ (the pc term vs. the other terms). We may consider recomputing 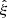 for the small scales using a smaller rmax and a larger R catalog. Considering just the Poisson terms (pc and pr or
for the small scales using a smaller rmax and a larger R catalog. Considering just the Poisson terms (pc and pr or 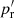 ) with a “representative” ξ value, (27) and (28) become
) with a “representative” ξ value, (27) and (28) become 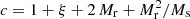 and
and 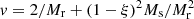 which modifies the above result (Eq. (29)) for the optimal choice of Ms and Mr to
which modifies the above result (Eq. (29)) for the optimal choice of Ms and Mr to
This result is only indicative, since it assumes a constant ξ for r < rmax. In particular, it does not apply for ξ ≈ 1, because then the approximation of ignoring the qr and tr terms in (19) is not good.
4. Tests on mock catalogs
4.1. Minerva simulations and methodology
The Minerva mocks are a set of 300 cosmological mocks produced with N-body simulations (Grieb et al. 2016; Lippich et al. 2019), stored at five output redshifts z ∈ {2.0, 1.0, 0.57, 0.3, 0}. The cosmology is flat ΛCDM with Ωm = 0.285, and we use the z = 1 outputs. The mocks have Nd ≈ 4 × 106 objects (“halos” found by a friends-of-friend algorithm) in a box of 1500 h−1 Mpc cubed.
To model the survey geometry of a redshift bin with Δz ≈ 0.1 at z ∼ 1, we placed the observer at comoving distance 2284.63 h−1 Mpc from the center of the cube and selected from the cube a shell 2201.34–2367.92 h−1 Mpc from the observer. The comoving thickness of the shell is 166.58 h−1 Mpc. The resulting mock sub-catalogs have Nd ≈ 4.5 × 105 and are representative of the galaxy number density of the future Euclid spectroscopic galaxy catalog.
We ignore peculiar velocities, that is, we perform our analysis in real space. Therefore, we consider results for the 1D 2PCF ξ(r). We estimated ξ(r) up to rmax = 200 h−1 Mpc using Δr = 1 h−1 Mpc bins.
We chose standard LS with Mr = 50 as the reference method. In the following, LS without further qualification refers to this. The random catalog was generated separately for each shell mock to measure their contribution to the variance. For one of the random catalogs we calculated also triplets to obtain the edge effect quantity 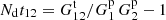 .
.
While dilution can already be discarded on theoretical grounds, we show results obtained using dilution, since these results provide the scale for edge effects demonstrating the importance of eliminating them with a careful choice of method. For the dilution and split methods we also used Mr = 50, and tried out dilution fractions 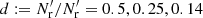 and split factors Ms = 4, 16, 50 (chosen to have similar pairwise computational costs). In addition, we considered standard LS with Mr = 25, which has the same number of RR pairs as d = 0.5 and Ms = 4, but only half the number of DR pairs; and standard LS with Mr = 1 to demonstrate the effect of a small
and split factors Ms = 4, 16, 50 (chosen to have similar pairwise computational costs). In addition, we considered standard LS with Mr = 25, which has the same number of RR pairs as d = 0.5 and Ms = 4, but only half the number of DR pairs; and standard LS with Mr = 1 to demonstrate the effect of a small 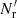 .
.
The code used to estimate the 2PCF implements a highly optimized pair-counting method, specifically designed for the search of object pairs in a given range of separations. In particular, the code provides two alternative counting methods, the chain-mesh and the kd-tree. Both methods measure the exact number of object pairs in separation bins, without any approximation. However, since they implement different algorithms to search for pairs, they perform differently at different scales, both in terms of CPU time and memory usage. Overall, the efficiency of the two methods depends on the ratio between the scale range of the searching region and the maximum separation between the objects in the catalog.
The kd-tree method first constructs a space-partitioning data structure that is filled with catalog objects. The minimum and maximum separations probed by the objects are kept in the data structure and are used to prune object pairs with separations outside the range of interest. The tree pair search is performed through the dual-tree method in which cross-pairs between two dual trees are explored. This is an improvement in terms of exploration time over the single-tree method.
On the other hand, in the chain-mesh method the catalog is divided in cubic cells of equal size, and the indexes of the objects in each cell are stored in vectors. To avoid counting object pairs with separations outside the interest range, the counting is performed only on the cells in a selected range of distances from each object. The chain-mesh algorithm has been imported from the CosmoBolognaLib, a large set of free software C++/python libraries for cosmological calculations (Marulli et al. 2016).
For our test runs we used the chain-mesh method.
4.2. Variance and bias
In Fig. 1 we show the mean (over the 300 mock shells) estimated correlation function and the scatter (square root of the variance) of the estimates using the LS, split, and dilution methods; our theoretical approximate result for the scatter for LS; and our theoretical result for bias for the different methods.
The theoretical result for the scatter is shown with and without the q terms, which include the triplet correlation ξ12, for which we used here the approximation ξ12 ≈ ξ(max(r1, r2)). This behaves as expected, that is, it underestimates the variance, since we neglected the higher-order correlations in the D catalog. Nevertheless, it (see the dash-dotted line in Fig. 1) has similar features to the measured variance (dashed lines).
In Fig. 2 we plot the diagonals of the p, t, and q quantities. This shows how their relative importance changes with separation scale. It also confirms that our initial assumption on small relative fluctuations is valid in this simulation case.
 |
Fig. 2. Quantities p, pc, pr, q, qr, t, and tr for the Minerva shell. The values for the first bin are noisy. The vertical red line marks r = L. |
Consider now the variance differences (from standard LS with Mr = 50), for which our theoretical results should be accurate. Figure 3 compares the measured variance difference to the theoretical result. For the diluted estimators and LS with Mr = 1 the measured result agrees with theory, although clearly the measurement with just 300 mocks is rather noisy. For the split estimators and LS with Mr = 25 the difference is too small to be appreciated with 300 mocks, but at least the measurement does not disagree with the theoretical result.
 |
Fig. 3. Measured difference from LS of the variance of different estimators, multiplied by r2. Dashed lines are our theoretical results. |
In Fig. 4 we show the relative theoretical increase in scatter compared to the best possible case, which is LS in the limit Mr → ∞. Since we do not have a valid theoretical result for the total scatter, we estimate it by subtracting the theoretical difference from LS with Mr = 50 from the measured variance of the latter.
 |
Fig. 4. Theoretical estimate of the scatter of the ξ estimates divided by the scatter in the |
At scales r ≲ 10 h−1 Mpc the theoretical prediction is about the same for dilution and split and neither method looks promising for r ≪ 10 h−1 Mpc where ξ ≫ 1. This suggests that for optimizing cost and accuracy, a different method should be used for smaller scales than that used for large scales. The number of RR pairs with small separations is much less. Therefore, for the small-scale computation there is no need to restrict the computation to a subset of RR pairs, or alternatively, one can afford to increase Mr. For the small scales, we may consider the split method with increased Mr as an alternative to standard LS. We have the same number of pairs to compute as in the reference LS case, if we use Mr = 866 and Ms = 866. We added this case to Fig. 4. It seems to perform better than LS at intermediate scales, but for the smallest scales LS has the smaller variance. This is in line with our conclusion in Sect. 3.2, which is that when ξ ≫ 1, it is not optimal to split the R catalog into small subsets.
We also compared the differences in the mean estimate from the different estimators to our theoretical results on the bias differences (see Fig. 5), but the theoretical bias differences are much smaller than the expected error of the mean from 300 mocks; and we simply confirm that the differences we see are consistent with the error of the mean and thus consistent with the true bias being much smaller. We also performed tests with completely random (ξ = 0) mocks, and with a large number (10 000) of mocks confirmed the theoretical bias result for the different estimators in this case. Since the bias is too small to be interesting we do not report these results in more detail here.
 |
Fig. 5. Differences between the mean ξ(r) estimate and that from the LS, multiplied by r to better display all scales. This measured difference is not the true bias, which is too small to measure with 300 mocks, and is mainly due to random error of the mean. The results for dilution appear to reveal a systematic bias, but this is just due to strong error correlations between nearby bins; for different subsets of the 300 mocks the mean difference is completely different. |
However, we note that for the estimation of the 2D 2PCF and its multipoles, the 2D bins will contain a smaller number of objects than the 1D bins of these test runs and therefore the bias is larger. Using the theoretical results (17) or (24) the bias can be removed afterwards with accuracy depending on how well we know the true ξ.
4.3. Computation time and variance
The test runs were made using a single full 24-core node for each run. Table 1 shows the mean computation time and mean estimator variance for different r ranges for the different cases we tested. Of these r ranges, the r = 80 − 120 h−1 Mpc is perhaps the most interesting, since it contains the important BAO scale. Therefore, we plot the mean variance at this range versus mean computation time in Fig. 6, together with our theoretical predictions. The theoretical estimate for the computation time for other dilution fractions and split factors is
Mean computation time over the 300 runs and the mean variance over four different ranges of r bins (given in units of h−1 Mpc) for each method.
 |
Fig. 6. Measured variance (mean variance over the range r = 80 − 120 h−1 Mpc) vs. computational cost (mean computation time) for the different methods (markers with error bars) and our theoretical prediction (solid lines). The solid lines (blue for the split method, red for dilution, and black for standard LS with Mr ≤ 50) are our theoretical predictions for the increase in variance and computation time ratio when compared to the standard LS, Mr = 50, case, and the dots on the curves correspond to the measured cases (except for LS they are, from right to left, Mr = 25, 12.5, and (50/7); only the first of which was measured). The curve for split ends at Ms = 2500; the optimal case, Ms = Mr, is the circled dot. The error bars for the variance measurement are naive estimates that do not account for error correlations between bins. The theoretical predictions overestimate the cost savings (data points are to the right of the dots on curves; except for the smaller split factors, where the additional speed-up compared to theory is related to some other performance differences between our split and standard LS implementations). This plot would have a different appearance for other r ranges. |
assuming Mr = 50. For standard LS with other random catalog sizes, the computation time estimate is
5. Conclusions
The computational time of the standard Landy–Szalay estimator is dominated by the RR pairs. However, except at small scales where correlations are large, these make a negligible contribution to the expected error compared to the contribution from the DD and DR pairs. Therefore, a substantial saving of computation time with an insignificant loss of accuracy can be achieved by counting a smaller subset of RR pairs.
We considered two ways to reduce the number of RR pairs: dilution and split. In dilution, only a subset of the R catalog is used for RR pairs. In split, the R catalog is split into a number of smaller subcatalogs, and only pairs within each subcatalog are counted. We derived theoretical results for the additional estimator covariance and bias due to the finite size of the random catalog for these different variants of the LS estimator, extending in many ways the original results by Landy & Szalay (1993), who worked in the limit of an infinite random catalog. We tested our results using 300 mock data catalogs, representative of the z = 0.95–1.05 redshift range of the future Euclid survey. The split method maintains the property the Landy–Szalay estimator was designed for, namely cancelation of edge effects in bias and variance (for ξ = 0), whereas dilution loses this cancellation and therefore should not be used.
For small scales, where correlations are large, one should not reduce RR counts as much. The natural dividing line is the scale r where ξ(r) = 1. Interestingly, the difference in bias and covariance between the different estimators (split, dilution, and LS) vanishes when ξ = 1. We recommend the natural version of the split method, Ms = Mr, for large scales where |ξ|< 1. This leads to a saving in computation time by more than a factor of ten (assuming Mr = 50) with a negligible effect on variance and bias. For small scales, where ξ > 1, one should consider using a larger random catalog and one can use either the standard LS method or the split method with a more modest split factor. Because the number of pairs with these small separations is much smaller, the computation time is not a similar issue as for large separations.
The results of our analysis will have an impact also on the computationally more demanding task of covariance matrix estimation. However, since in that case the exact computational cost is determined by the balance of data catalogs and random catalogs, which does not need to be the same as for the individual two-point correlation estimate, we postpone a quantitative analysis to a future, dedicated study. The same kind of methods can be applied to higher-order statistics (three-point and four-point correlation functions) to speed up their estimation (Slepian & Eisenstein 2015).
Acknowledgments
We thank Will Percival and Cristiano Porciani for useful discussions. The 2PCF computations were done at the Euclid Science Data Center Finland (SDC-FI, urn:nbn:fi:research-infras-2016072529), for whose computational resources we thank CSC – IT Center for Science, the Finnish Grid and Cloud Computing Infrastructure (FGCI, urn:nbn:fi:research-infras-2016072533), and the Academy of Finland grant 292882. This work was supported by the Academy of Finland grant 295113. VL was supported by the Jenny and Antti Wihuri Foundation, AV by the Väisälä Foundation, AS by the Magnus Ehrnrooth Foundation, and JV by the Finnish Cultural Foundation. We also acknowledge travel support from the Jenny and Antti Wihuri Foundation. VA acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 749348. FM acknowledges the grants ASI n.I/023/12/0 “Attivit‘a relative alla fase B2/C per la missione Euclid” and PRIN MIUR 2015 “Cosmology and Fundamental Physics: illuminating the Dark Universe with Euclid”.
References
- Alam, S., Ata, M., Bailey, S., et al. 2017, MNRAS, 470, 2617 [NASA ADS] [CrossRef] [Google Scholar]
- Alcock, C., & Paczyński, B. 1979, Nature, 281, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso, D. 2012, ArXiv e-prints [arXiv:1210.1833] [Google Scholar]
- Anderson, L., Aubourg, E., Bailey, S., et al. 2012, MNRAS, 427, 3435 [Google Scholar]
- Anderson, L., Aubourg, E., Bailey, S., et al. 2014, MNRAS, 441, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Ata, M., Baumgarten, F., Bautista, J., et al. 2018, MNRAS, 473, 4773 [NASA ADS] [CrossRef] [Google Scholar]
- Bautista, J. E., Vargas-Magaña, M., Dawson, K. S., et al. 2018, ApJ, 863, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Bernstein, G. M. 1994, ApJ, 424, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Beutler, F., Blake, C., Colless, M., et al. 2011, MNRAS, 416, 3017 [NASA ADS] [CrossRef] [Google Scholar]
- Beutler, F., Blake, C., Colless, M., et al. 2012, MNRAS, 423, 3430 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, C., Kazin, E. A., Beutler, F., et al. 2011, MNRAS, 418, 1707 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Cole, S., Percival, W. J., Peacock, J. A., et al. 2005, MNRAS, 362, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., & Peebles, P. J. E. 1983, ApJ, 267, 465 [NASA ADS] [CrossRef] [Google Scholar]
- de la Torre, S., Jullo, E., Giocoli, C., et al. 2017, A&A, 608, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Demina, R., Cheong, S., BenZvi, S., & Hindrichs, O. 2018, MNRAS, 480, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Grieb, J. N., Sánchez, A. G., Salvador-Albornoz, S., & Dalla Vecchia, C. 2016, MNRAS, 457, 1577 [NASA ADS] [CrossRef] [Google Scholar]
- Guzzo, L., Pierleoni, M., Meneux, B., et al. 2008, Nature, 451, 541 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hamilton, A. J. S. 1993, ApJ, 417, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Hewett, H. C. 1982, MNRAS, 201, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Hou, J., Sánchez, A. G., Scoccimarro, R., et al. 2018, MNRAS, 480, 2521 [Google Scholar]
- Jarvis, M. 2015, Astrophysics Source Code Library [record ascl:1508.007] [Google Scholar]
- Kaiser, N. 1987, MNRAS, 227, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kerscher, M. 1999, A&A, 343, 333 [NASA ADS] [Google Scholar]
- Kerscher, M., Szapudi, I., & Szalay, A. S. 2000, ApJ, 535, L13 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Landy, S. D., & Szalay, A. S. 1993, ApJ, 412, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Lippich, M., Sánchez, A. G., Colavincenzo, M., et al. 2019, MNRAS, 482, 1786 [NASA ADS] [CrossRef] [Google Scholar]
- Marulli, F., Veropalumbo, A., & Moresco, M. 2016, Astron. Comput., 14, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, A., Connolly, A., Genovese, C., et al. 2000, ArXiv e-prints [arXiv:astro-ph/0012333] [Google Scholar]
- Peacock, J. A., Cole, S., Norberg, P., et al. 2001, Nature, 410, 169 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Peebles, P. J. E., & Hauser, M. G. 1974, ApJS, 28, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Percival, W. J., Reid, B. A., Eisenstein, D. J., et al. 2010, MNRAS, 401, 2148 [NASA ADS] [CrossRef] [Google Scholar]
- Pezzotta, A., de la Torre, S., Bel, J., et al. 2017, A&A, 604, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, B. A., Samushia, L., White, M., et al. 2012, MNRAS, 426, 2719 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, A. J., Samushia, L., Howlett, C., et al. 2015, MNRAS, 449, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, A. J., Beutler, F., Chuang, C. H., et al. 2017, MNRAS, 464, 1168 [NASA ADS] [CrossRef] [Google Scholar]
- Ruggeri, R., Percival, W. J., Gil-Marín, H., et al. 2019, MNRAS, 483, 3878 [NASA ADS] [CrossRef] [Google Scholar]
- Slepian, Z., & Eisenstein, D. J. 2015, MNRAS, 454, 4142 [NASA ADS] [CrossRef] [Google Scholar]
- Vargas-Magaña, M., Ho, S., Cuesta, A. J., et al. 2018, MNRAS, 477, 1153 [NASA ADS] [CrossRef] [Google Scholar]
- Wall, J. V., & Jenkins, C. R. 2012, Practical Statistics for Astronomers (Cambridge, UK: Cambridge University Press) [CrossRef] [Google Scholar]
- Zarrouk, P., Burtin, E., Gil-Marín, H., et al. 2018, MNRAS, 477, 1639 [NASA ADS] [CrossRef] [Google Scholar]
- Zehavi, I., Zheng, Z., Weinberg, D. H., et al. 2011, ApJ, 736, 59 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Derivation examples
As examples of how the variances of the different deviations, ⟨αβ⟩ and so on, are derived, following the method presented in LS93, we give three of the cases here: ⟨α1α2⟩ (common for all the variants of LS), and 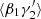 and
and 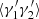 for the split method. The rest are calculated in a similar manner.
for the split method. The rest are calculated in a similar manner.
To derive the ⟨DD1DD2⟩ appearing in the ⟨α1α2⟩ of (15) we start from
where both i, j, and k, l sum over all microcell pairs; ni = 1 or 0 is the number of galaxies in microcell i. There are three different cases for the terms ⟨ninjnknl⟩ depending on how many indices are equal (i ≠ j and k ≠ l for all of them).
The first case (quadruplets, i.e., two pairs of microcells) is when i, j, k, l are all different. We use 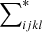 to denote this part of the sum. There are
to denote this part of the sum. There are 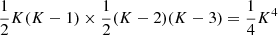 (we work in the limit K → ∞) such terms and they have
(we work in the limit K → ∞) such terms and they have
where δi := δ(xi) is the density perturbation (relative to the actual mean density of galaxies in the survey), ζ is the three-point correlation, and η is the connected (i.e., the part that does not arise from the two-point correlation) four-point correlation. The fraction of microcell quadruplets (pairs of pairs) that satisfy rij ≡ xj − xi ∈ r1 and rkl ∈ r2 is 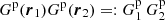 . In the limit of large K the number of other index quadruplets is negligible compared to those where all indices have different values, so we have
. In the limit of large K the number of other index quadruplets is negligible compared to those where all indices have different values, so we have
For the connected pairs (i, j) and (k, l) we have ξ(rij)=ξ(r1)≡ξ1 and ξ(rkl)=ξ(r2)≡ξ2.
The second case (triplets of microcells) is when k or l is equal to i or j. We denote this part of the sum by
It turns out that it goes over all ordered combinations of {i, j, k}, where i, j, k are all different, exactly once, so there are K(K − 1)(K − 2)=K3 such terms (triplets). Here
and
The third case (pairs of microcells) is when i = k and j = l. This part of the sum becomes
where
and
that is, the sum vanishes unless the two bins are the same, r1 = r2.
We now apply the three approximations listed in Sect. 2.2: (1) ξ(rik)=ξ(ril)=ξ(rjk)=ξ(rjl) = 0 in (A.2); (2) ζ = 0 in (A.2) and (A.5); (3) η = 0 in (A.2). We obtain
and using ⟨DD⟩ from (3) we arrive at the ⟨α1α2⟩ result given in Eq. (15).
For the split method, we give the calculation for
below.
First the 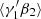 :
:
where
si is the number (0 or 1) of Rμ objects in microcell i, and rl is the number of R objects in microcell l.
There are 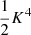 quadruplet terms, for which (see (A.3))
quadruplet terms, for which (see (A.3)) 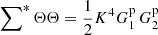 , and
, and
Triplets where i or j is equal to k have ⟨sisknkrl⟩ = 0, since sknk = 0 always (we cannot have two objects, from Rμ and D, in the same cell). There are K3 triplet terms where i or j is equal to l: for them 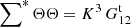 , and
, and
where if sl = 1 then also rl = 1 since Rμ ⊂ R.
Pairs where (i, j)=(k, l) or (i, j)=(l, k) have ⟨skslnkrl⟩ = 0, since again we cannot have two different objects in the same cell. Thus
and we obtain that
which is equal to the ⟨γ1β2⟩ of standard LS.
Then the  :
:
where there are Ms(Ms − 1) terms with μ ≠ ν giving
and Ms terms with μ = ν giving
Adding these up gives
and
This differs both from standard LS and from dilution, since it involves both  and
and  .
.
All Tables
Mean computation time over the 300 runs and the mean variance over four different ranges of r bins (given in units of h−1 Mpc) for each method.
All Figures
 |
Fig. 1. Mean ξ(r) estimate and the scatter and theoretical bias of the estimates for different estimators. The dash-dotted line, our theoretical result for the scatter of the LS method, underestimates the scatter, since higher-order correlations in the D catalog are ignored. The dotted line is without the contribution of the q terms, and is dominated by the Poisson (p) terms. The bias is multiplied by 100 so the curves can be displayed in a more compact plot. For the measured mean and scatter, and the theoretical bias we plot standard LS in black, dilution with d = 0.14 in red, and split with Ms = 50 in blue. For the mean and scatter the difference between the methods is not visible in this plot. The differences in the mean estimate are shown in Fig. 5. The differences in scatter (or its square, the variance) are shown in Fig 3. For the theoretical bias the difference between split and dilution is not visible at small r (ξ(r) > 1), where the bias is positive. |
| In the text | |
 |
Fig. 2. Quantities p, pc, pr, q, qr, t, and tr for the Minerva shell. The values for the first bin are noisy. The vertical red line marks r = L. |
| In the text | |
 |
Fig. 3. Measured difference from LS of the variance of different estimators, multiplied by r2. Dashed lines are our theoretical results. |
| In the text | |
 |
Fig. 4. Theoretical estimate of the scatter of the ξ estimates divided by the scatter in the |
| In the text | |
 |
Fig. 5. Differences between the mean ξ(r) estimate and that from the LS, multiplied by r to better display all scales. This measured difference is not the true bias, which is too small to measure with 300 mocks, and is mainly due to random error of the mean. The results for dilution appear to reveal a systematic bias, but this is just due to strong error correlations between nearby bins; for different subsets of the 300 mocks the mean difference is completely different. |
| In the text | |
 |
Fig. 6. Measured variance (mean variance over the range r = 80 − 120 h−1 Mpc) vs. computational cost (mean computation time) for the different methods (markers with error bars) and our theoretical prediction (solid lines). The solid lines (blue for the split method, red for dilution, and black for standard LS with Mr ≤ 50) are our theoretical predictions for the increase in variance and computation time ratio when compared to the standard LS, Mr = 50, case, and the dots on the curves correspond to the measured cases (except for LS they are, from right to left, Mr = 25, 12.5, and (50/7); only the first of which was measured). The curve for split ends at Ms = 2500; the optimal case, Ms = Mr, is the circled dot. The error bars for the variance measurement are naive estimates that do not account for error correlations between bins. The theoretical predictions overestimate the cost savings (data points are to the right of the dots on curves; except for the smaller split factors, where the additional speed-up compared to theory is related to some other performance differences between our split and standard LS implementations). This plot would have a different appearance for other r ranges. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



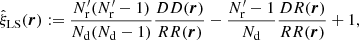
![$$ \begin{aligned}&DD({\boldsymbol{r}}) =: \langle DD({\boldsymbol{r}}) \rangle [1+\alpha ({\boldsymbol{r}})],\nonumber \\&DR({\boldsymbol{r}}) =: \langle DR({\boldsymbol{r}}) \rangle [1+\beta ({\boldsymbol{r}})],\nonumber \\&RR({\boldsymbol{r}}) =: \langle RR({\boldsymbol{r}}) \rangle [1+\gamma ({\boldsymbol{r}})]. \end{aligned} $$](/articles/aa/full_html/2019/11/aa35828-19/aa35828-19-eq8.gif)
![$$ \begin{aligned}&\langle DD({\boldsymbol{r}})\rangle = \frac{1}{2} N_{\rm d}(N_{\rm d}-1)G^\mathrm{p}({\boldsymbol{r}})[1+\xi ({\boldsymbol{r}})],\nonumber \\&\langle DR({\boldsymbol{r}})\rangle = N_{\rm d}N_{\rm r} G^\mathrm{p}({\boldsymbol{r}}),\nonumber \\&\langle RR({\boldsymbol{r}})\rangle = \frac{1}{2} N^{\prime }_{\rm r}(N^{\prime }_{\rm r}-1)G^\mathrm{p}({\boldsymbol{r}}) , \end{aligned} $$](/articles/aa/full_html/2019/11/aa35828-19/aa35828-19-eq9.gif)
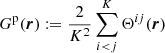
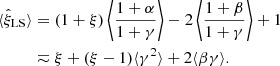
![$$ \begin{aligned} \mathrm{Cov}\left[\hat{\xi }_{\rm LS}({\boldsymbol{r}}_1),\hat{\xi }_{\rm LS}({\boldsymbol{r}}_2)\right]&\equiv \left\langle \hat{\xi }_{\rm LS}({\boldsymbol{r}}_1)\hat{\xi }_{\rm LS}({\boldsymbol{r}}_2)\right\rangle - \left\langle \hat{\xi }_{\rm LS}({\boldsymbol{r}}_1)\right\rangle \left\langle \hat{\xi }_{\rm LS}({\boldsymbol{r}}_2)\right\rangle \nonumber \\&\eqsim (1+\xi _1)(1+\xi _2)\langle \alpha _1\alpha _2\rangle + 4\langle \beta _1\beta _2\rangle \nonumber \\&\quad + (1-\xi _1)(1-\xi _2)\langle \gamma _1\gamma _2\rangle \nonumber \\&\quad - 2(1+\xi _1)\langle \alpha _1\beta _2\rangle - 2(1+\xi _2)\langle \beta _1\alpha _2\rangle \nonumber \\&\quad - 2(1-\xi _1)\langle \gamma _1\beta _2\rangle - 2(1-\xi _2)\langle \beta _1\gamma _2\rangle . \end{aligned} $$](/articles/aa/full_html/2019/11/aa35828-19/aa35828-19-eq12.gif)
![$$ \begin{aligned} \Delta \mathrm{Cov}\left[\hat{\xi }_{\rm LS}({\boldsymbol{r}}_1),\hat{\xi }_{\rm LS}({\boldsymbol{r}}_2)\right] \eqsim &4\Delta \langle \beta _1\beta _2\rangle + (1-\xi _1)(1-\xi _2)\langle \gamma _1\gamma _2\rangle \nonumber \\& - 2(1-\xi _1)\langle \gamma _1\beta _2\rangle - 2(1-\xi _2)\langle \beta _1\gamma _2\rangle . \end{aligned} $$](/articles/aa/full_html/2019/11/aa35828-19/aa35828-19-eq16.gif)
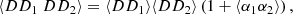
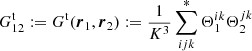
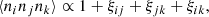
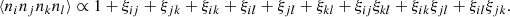
![$$ \begin{aligned}&(1+\xi _1)(1+\xi _2)\langle \alpha _1\alpha _2\rangle \nonumber \\&\qquad \qquad \qquad \simeq \frac{4}{N_{\rm d}} (1+\xi _1)(1+\xi _2)\left[\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2} - 1\right] \nonumber \\&\qquad \qquad \qquad \quad + \frac{2(1+\xi _1)}{N_{\rm d}(N_{\rm d}-1)}\left[ \frac{\delta _{12}}{G^\mathrm{p}_1}- 2(1+\xi _2)\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2} +(1+\xi _2) \right] \nonumber \\&\qquad \qquad \qquad \quad + \frac{4(N_{\rm d}-2)}{N_{\rm d}(N_{\rm d}-1)}(\xi _{12}-\xi _1\xi _2)\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2} ,\nonumber \\&\langle \beta _1\beta _2\rangle \simeq \frac{1}{N_{\rm d}N_{\rm r}}\Biggl \{ N^{\prime }_{\rm r}\left[\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2}-1\right] + N_{\rm d}\left[\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2}-1\right] + 1 \nonumber \\&\qquad \quad \;\; - \frac{2G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2} + \frac{\delta _{12}}{G^\mathrm{p}_1} \Biggr \} + \frac{N_{\rm d}-1}{N_{\rm d}N_{\rm r}}\xi _{12}\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2} ,\nonumber \\&\langle \gamma _1\gamma _2\rangle = \frac{2}{N^{\prime }_{\rm r}(N^{\prime }_{\rm r}-1)}\left\{ 2(N^{\prime }_{\rm r}-2)\left[\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2} - 1\right] + \frac{\delta _{12}}{G^\mathrm{p}_1} - 1\right\} ,\nonumber \\&\langle \alpha _1\beta _2\rangle \simeq \frac{2}{N_{\rm d}}\left[\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2} - 1\right] ,\nonumber \\&\langle \beta _1\gamma _2\rangle = \frac{2}{N^{\prime }_{\rm r}}\left[\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2} - 1\right] ,\nonumber \\&\langle \alpha _1\gamma _2\rangle = 0, \end{aligned} $$](/articles/aa/full_html/2019/11/aa35828-19/aa35828-19-eq26.gif)
![$$ \begin{aligned}&t_{12} := \frac{1}{N_{\rm d}}\left[\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2}-1\right] ,\nonumber \\&t^\mathrm{r}_{12} := \frac{1}{N^{\prime }_{\rm r}}\left[\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2}-1\right] \ = \ \frac{N_{\rm d}}{N^{\prime }_{\rm r}}\,t_{12}, \nonumber \\&p_{12} := \frac{2}{N_{\rm d}(N_{\rm d}-1)}\left[\frac{\delta _{12}}{(1+\xi _1)G^\mathrm{p}_1} - 2\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2} + 1\right] ,\nonumber \\&p^\mathrm{c}_{12} := \frac{1}{N_{\rm d}N_{\rm r}}\left[\frac{\delta _{12}}{G^\mathrm{p}_1} - 2\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2} + 1\right] ,\nonumber \\&p^\mathrm{r}_{12} := \frac{2}{N^{\prime }_{\rm r}(N^{\prime }_{\rm r}-1)}\left[\frac{\delta _{12}}{G^\mathrm{p}_1} - 2\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2} + 1\right],\nonumber \\&q_{12} := \frac{1}{N_{\rm d}}\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2} = t_{12} + \frac{1}{N_{\rm d}} ,\nonumber \\&q^\mathrm{r}_{12} := \frac{1}{N^{\prime }_{\rm r}}\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2} = t^\mathrm{r}_{12} + \frac{1}{N^{\prime }_{\rm r}}\cdot \end{aligned} $$](/articles/aa/full_html/2019/11/aa35828-19/aa35828-19-eq27.gif)
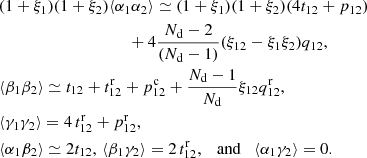
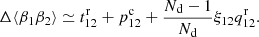
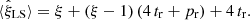
![$$ \begin{aligned} \mathrm{Cov}\left[\hat{\xi }_{\rm LS}({\boldsymbol{r}}_1),\hat{\xi }_{\rm LS}({\boldsymbol{r}}_2)\right]&\equiv \left\langle \hat{\xi }_{\rm LS}({\boldsymbol{r}}_1)\hat{\xi }_{\rm LS}({\boldsymbol{r}}_2)\right\rangle - \left\langle \hat{\xi }_{\rm LS}({\boldsymbol{r}}_1)\right\rangle \left\langle \hat{\xi }_{\rm LS}({\boldsymbol{r}}_2)\right\rangle \nonumber \\&\simeq (1+\xi _1)(1+\xi _2)p_{12} + 4p^\mathrm{c}_{12}\nonumber \\&\quad + (1-\xi _1)(1-\xi _2)\,p^\mathrm{r}_{12} + 4\xi _1\xi _2(t_{12}+t^\mathrm{r}_{12})\nonumber \\&\quad + 4\frac{N_{\rm d}-2}{N_{\rm d}-1}(\xi _{12}-\xi _1\xi _2)q_{12} + 4\frac{N_{\rm d}-1}{N_{\rm d}}\xi _{12}q^\mathrm{r}_{12}. \end{aligned} $$](/articles/aa/full_html/2019/11/aa35828-19/aa35828-19-eq37.gif)
![$$ \begin{aligned} \Delta \mathrm{Cov}\left[\hat{\xi }_{\rm LS}({\boldsymbol{r}}_1),\hat{\xi }_{\rm LS}({\boldsymbol{r}}_2)\right]&\eqsim 4\Delta \langle \beta _1\beta _2\rangle + (1-\xi _1)(1-\xi _2)\langle \gamma _1\gamma _2\rangle \nonumber \\&\quad - 2(1-\xi _1)\langle \gamma _1\beta _2\rangle - 2(1-\xi _2)\langle \beta _1\gamma _2\rangle \nonumber \\&\simeq 4p^\mathrm{c}_{12} + (1-\xi _1)(1-\xi _2)\,p^\mathrm{r}_{12} +4\xi _1\xi _2\,t^\mathrm{r}_{12}\nonumber \\&\quad + 4\frac{N_{\rm d}-1}{N_{\rm d}}\xi _{12}q^\mathrm{r}_{12}. \end{aligned} $$](/articles/aa/full_html/2019/11/aa35828-19/aa35828-19-eq38.gif)
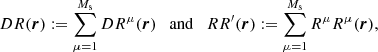
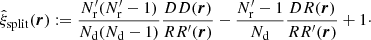
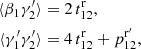
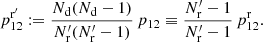
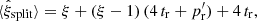
![$$ \begin{aligned} \mathrm{Cov}\left[\hat{\xi }_\mathrm{split} ({\boldsymbol{r}}_1),\hat{\xi }_\mathrm{split} ({\boldsymbol{r}}_2)\right] \simeq &(1+\xi _1)(1+\xi _2)p_{12} + 4\,p^\mathrm{c}_{12} \nonumber \\& + (1-\xi _1)(1-\xi _2)p^{\mathrm{r}^{\prime }}_{12} + 4\xi _1\xi _2(t_{12}+t^\mathrm{r}_{12}) . \end{aligned} $$](/articles/aa/full_html/2019/11/aa35828-19/aa35828-19-eq55.gif)
![$$ \begin{aligned}&\mathrm{Cov}\left[\hat{\xi }^\mathrm{split} _1,\hat{\xi }^\mathrm{split} _2\right] - \mathrm{Cov}\left[\hat{\xi }^\mathrm{LS} _1,\hat{\xi }^\mathrm{LS} _2\right]= (1-\xi _1)(1-\xi _2)(p^{\mathrm{r}^{\prime }}_{12}-p^\mathrm{r}_{12}), \end{aligned} $$](/articles/aa/full_html/2019/11/aa35828-19/aa35828-19-eq56.gif)
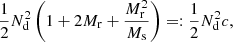
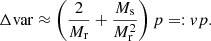
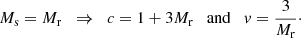
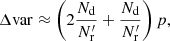
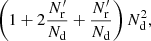
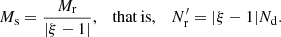
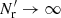
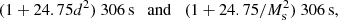
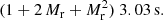
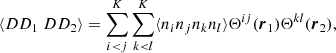
![$$ \begin{aligned}&\langle n_in_jn_kn_l\rangle \nonumber \\&\qquad = \frac{N_{\rm d}}{K}\frac{N_{\rm d} - 1}{K-1}\frac{N_{\rm d}-2}{K-2}\frac{N_{\rm d}-3}{K- 3}\Bigl \langle (1+\delta _i)(1+\delta _j)(1+\delta _k)(1+\delta _l)\Bigr \rangle \nonumber \\&\qquad = \frac{N_{\rm d}(N_{\rm d}-1)(N_{\rm d}-2)(N_{\rm d}-3)}{K^4}\Bigl [1+\langle \delta _i\delta _j\rangle +\langle \delta _k\delta _l\rangle +\langle \delta _i\delta _k\rangle \nonumber \\&\qquad \quad +\langle \delta _i\delta _l\rangle +\langle \delta _j\delta _k\rangle +\langle \delta _j\delta _l\rangle \nonumber \\&\qquad \quad + \langle \delta _i\delta _j\delta _k\rangle +\langle \delta _i\delta _j\delta _l\rangle +\langle \delta _i\delta _k\delta _l\rangle +\langle \delta _j\delta _k\delta _l\rangle +\langle \delta _i\delta _j\delta _k\delta _l\rangle \Bigr ] \nonumber \\&\qquad = \frac{N_{\rm d}(N_{\rm d}-1)(N_{\rm d}-2)(N_{\rm d} -3)}{K^4}\Bigl [1+\xi ({\boldsymbol{r}}_{ij})+\xi ({\boldsymbol{r}}_{kl})+\xi ({\boldsymbol{r}}_{ik})\nonumber \\&\qquad \quad + \xi ({\boldsymbol{r}}_{il})+\xi ({\boldsymbol{r}}_{jk})+\xi ({\boldsymbol{r}}_{jl})\nonumber \\&\qquad \quad + \zeta ({\boldsymbol{x}}_i,{\boldsymbol{x}}_j,{\boldsymbol{x}}_k)+\zeta ({\boldsymbol{x}}_i,{\boldsymbol{x}}_k,{\boldsymbol{x}}_l)+\zeta ({\boldsymbol{x}}_i,{\boldsymbol{x}}_j,{\boldsymbol{x}}_l)+\zeta ({\boldsymbol{x}}_j,{\boldsymbol{x}}_k,{\boldsymbol{x}}_l) \nonumber \\&\qquad \quad + \xi ({\boldsymbol{r}}_{ij})\xi ({\boldsymbol{r}}_{kl})+\xi ({\boldsymbol{r}}_{ik})\xi ({\boldsymbol{r}}_{jl})+\xi ({\boldsymbol{r}}_{il})\xi ({\boldsymbol{r}}_{jk}) \nonumber \\&\qquad \quad +\eta ({\boldsymbol{x}}_i,{\boldsymbol{x}}_j,{\boldsymbol{x}}_k,{\boldsymbol{x}}_l)\Bigr ], \end{aligned} $$](/articles/aa/full_html/2019/11/aa35828-19/aa35828-19-eq80.gif)
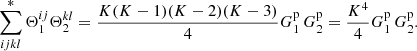
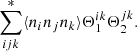
![$$ \begin{aligned} \langle n_in_jn_k\rangle&= \frac{N_{\rm d}}{K}\frac{N_{\rm d}-1}{K-1}\frac{N_{\rm d}-2}{K-2}\Bigl \langle (1+\delta _i)(1+\delta _j)(1+\delta _k)\Bigr \rangle \nonumber \\&= \frac{N_{\rm d}(N_{\rm d}-1)(N_{\rm d}-2)}{K^3}\Bigl [1 +\langle \delta _i\delta _k\rangle +\langle \delta _j\delta _k\rangle +\langle \delta _i\delta _j\rangle + \langle \delta _i\delta _j\delta _k\rangle \Bigr ] \nonumber \\&= \frac{N_{\rm d}(N_{\rm d}-1)(N_{\rm d}-2)}{K^3}\Bigl [1+\xi ({\boldsymbol{r}}_{ik})+\xi ({\boldsymbol{r}}_{jk})+\xi ({\boldsymbol{r}}_{ij})+\zeta ({\boldsymbol{x}}_i,{\boldsymbol{x}}_j,{\boldsymbol{x}}_k)\Bigr ] , \end{aligned} $$](/articles/aa/full_html/2019/11/aa35828-19/aa35828-19-eq84.gif)
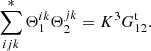
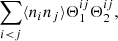
![$$ \begin{aligned} \langle n_in_j\rangle = \frac{N_{\rm d}(N_{\rm d}-1)}{K^2}\left[1+\xi ({\boldsymbol{r}}_{ij})\right] , \end{aligned} $$](/articles/aa/full_html/2019/11/aa35828-19/aa35828-19-eq87.gif)
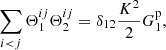
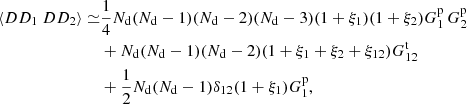
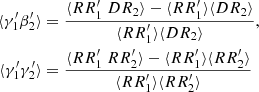
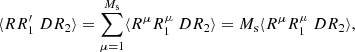
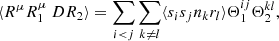
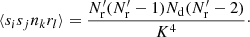
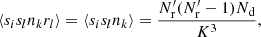
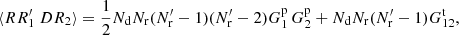
![$$ \begin{aligned} \langle \gamma ^{\prime }_1\beta _2\rangle = \frac{2}{N^{\prime }_{\rm r}}\left[\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2} - 1\right] \ = \ 2\,t^\mathrm{r}_{12} , \end{aligned} $$](/articles/aa/full_html/2019/11/aa35828-19/aa35828-19-eq100.gif)
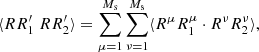
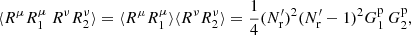
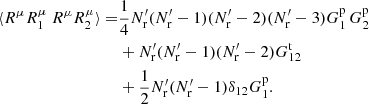
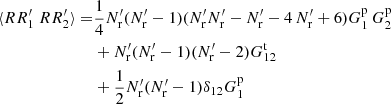
![$$ \begin{aligned} \langle \gamma ^{\prime }_1\gamma ^{\prime }_2\rangle&= \frac{2}{N^{\prime }_{\rm r}(N^{\prime }_{\rm r}-1)}\left\{ 2(N^{\prime }_{\rm r}-2)\left[\frac{G^\mathrm{t}_{12}}{G^\mathrm{p}_1\,G^\mathrm{p}_2} - 1\right] + \frac{\delta _{12}}{G^\mathrm{p}_1} - 1\right\} \nonumber \\&= 4\,t^\mathrm{r}_{12} + p^{\mathrm{r}^{\prime }}_{12} . \end{aligned} $$](/articles/aa/full_html/2019/11/aa35828-19/aa35828-19-eq106.gif)