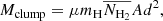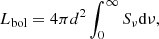| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 49 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201935410 | |
| Published online | 25 October 2019 | |
Fragmentation and filaments at the onset of star and cluster formation
SABOCA 350 μm view of ATLASGAL-selected massive clumps⋆
1
Max-Planck Institute für Radio Astronomy, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: ylin@mpifr-bonn.mpg.de
2
OASU/LAB-UMR5804, CNRS, Université Bordeaux, Allée Geoffroy Saint-Hilaire, 33615 Pessac, France
3
Centre for Astrophysics and Planetary Science, University of Kent, Canterbury CT2 7NH, UK
Received:
6
March
2019
Accepted:
1
September
2019
Context. The structure formation of the dense interstellar material and the fragmentation of clumps into cores is a fundamental step for understanding how stars and stellar clusters form.
Aims. We aim to establish a statistical view of clump fragmentation at subparsec scales based on a large sample of massive clumps selected from the ATLASGAL survey.
Methods. We used the APEX/SABOCA camera at 350 μm to image clumps at a resolution of 8.″5, corresponding to physical scales of < 0.2 pc at a distance < 5 kpc. The majority of the sample consists of massive clumps that are weak or in absorption at 24 μm. We resolved spherical and filamentary structures and identified the population of compact sources. Complemented with archival Herschel data, we derived the physical properties, such as dust temperature, mass, and bolometric luminosity of clumps and cores. We used association with mid-infrared 22−24 μm and 70 μm point sources to determine the star formation activity of the cores. We then statistically assessed their physical properties and the fragmentation characteristics of massive clumps.
Results. We detect emission at 350 μm toward all targets and find that it typically exhibits a filamentary (-like) morphology and hosts a population of compact sources. Using Gaussclumps, we identify 1120 compact sources and derive the physical parameters and star formation activity for 971 of these, 874 of which are associated with 444 clumps. We find a moderate correlation between the clump fragmentation levels with the clump gas density and the predicted number of fragments with a pure Jeans fragmentation scenario. We find a strong correlation between the mass of the most massive fragment and the total clump mass, suggesting that self-gravity may play an important role in the small-scale structure formation of the clumps. Finally, due to the improved angular resolution compared to ATLASGAL, we are able to identify 27 massive quiescent cores with Mcore > 100 M⊙ within 5 kpc; these are massive enough to be self-gravitating, but do not yet show any sign of star formation. This sample therefore comprises promising candidates of massive prestellar cores or deeply embedded high-mass protostars.
Conclusions. The submillimeter observations of the massive clumps that are weak or completely dark at 24 μm reveal rich filamentary structures and an embedded population of compact cores. The maximum core mass is likely determined by the self-gravity of the clump. The rarity of massive prestellar core candidates implies short collapse timescales for dense structures.
Key words: stars: formation / dust / extinction / infrared: ISM
Full Tables 1–3 and a copy of the reduced SABOCA images are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/631/A72
© Y. Lin et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
Despite the significant influence of massive stars on their natal environment and the Galaxy as a whole, their formation process remains poorly constrained. Massive stars (M ≳ 10 M⊙) are considerably rarer than solar-mass stars. They constitute less than ∼10% of the stellar initial mass function (IMF) in mass. The duration of their formation time is short, therefore the deeply embedded early stages are difficult to identify. Adding to the complexity of the high-mass star-forming scenario is that massive stars typically form in clusters (Stahler et al. 2000; Lada & Lada 2003), but the mass assembly and the fragmentation of massive clumps into cores is still not well understood (for recent reviews, see Tan et al. 2014; Motte et al. 2018).
In the past decade, Galactic plane surveys in the far-infrared and submillimeter regime such as the APEX Telescope Large Area Survey of the Galaxy (ATLASGAL, Schuller et al. 2009; Csengeri et al. 2014), the Bolocam Galactic Plane Survey (BGPS, Aguirre et al. 2011), the Herschel infrared Galactic Plane Survey (Hi-Gal, Molinari et al. 2010), and the JCMT Plane Survey (JPS, Moore et al. 2015; Eden et al. 2017) have proven to be excellent finding charts for identifying large samples of massive clumps that exhibit typical physical characteristics of > 103 − 104 M⊙, an extent up to ∼1 pc, and a temperature of ∼20 K, which is typically associated with giant molecular cloud complexes (e.g., Csengeri et al. 2016a; Svoboda et al. 2016; König et al. 2017; Elia et al. 2017; Urquhart et al. 2018). Massive clumps fragment into cores where star formation takes place (Motte et al. 2018). Investigating how the dense gas is structured within massive clumps, and how they fragment and form filaments and cores on a 0.1−0.3 pc scale (e.g., Motte et al. 2007; André et al. 2014) is therefore an important step for understanding the mass assembly process that forms stars and clusters.
Owing to the typically large distance of several kiloparsecs of high-mass star-forming regions, high-angular resolution interferometric studies are required to investigate their structure and fragmentation (e.g., Bontemps et al. 2010; Palau et al. 2013, 2015; Csengeri et al. 2017a; Beuther et al. 2018). It is necessary to reach physical scales of a few thousand to tens of thousand au to resolve the typical Jeans length in these objects, which is 0.1−0.3 pc, assuming a temperature of 20 K and a volume density of 104–105 cm−3, as is characteristic of massive cores or clumps (e.g., Williams et al. 2000; Motte et al. 2007; Wienen et al. 2012; Urquhart et al. 2018). Large areas cannot be mapped with current interferometers in the (sub)millimeter wavelength range. However, ground-based telescopes with sensitive bolometer arrays with large fields of view provide an efficient way to map large regions at a moderate resolution at short wavelengths (350 and 450 μm, i.e., ∼10″, corresponding to a physical scale of 0.1 pc at d∼ 2 kpc). This allows us to conduct a statistical study of fragmentation from clump to core scales (e.g., Motte et al. 2003; Minier et al. 2009; Ragan et al. 2013; Merello et al. 2015; André et al. 2016; Rayner et al. 2017; Heyer et al. 2018). We therefore carried out observations toward more than 200 ATLASGAL-selected sources at 350 μm with the Submillimetre APEX Bolometer array camera (SABOCA, Siringo et al. 2010) at the Atacama Pathfinder Experiment 12 m telescope (APEX, Güsten et al. 2006). These observations achieve an angular resolution of 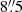 , which is an improvement of a factor of > 2 in terms of angular resolution compared to the ATLASGAL survey. This allows us to identify a population of cores with sizes of 0.1−0.2 pc that are embedded in clumps at distances d ≲ 5 kpc. The angular resolution we achieved corresponds to an intermediate physical scale to separate structures of massive star-forming clumps, which is a missing gap that needs to be closed to link to typical interferometric studies. The sample is twice the size of the sample used by Merello et al. (2015), who targeted a sample of BGPS sources with the SHARC-II camera on the Caltech Submillimeter Observatory (CSO). Combining our results with ancillary submillimeter and infrared data, we estimate the physical parameters of the cores and compare them with the properties of clumps in order to constrain their fragmentation and structure formation. The higher angular resolution compared to ATLASGAL allows us to distinguish between quiescent and star-forming cores and deliver a sample of starless or prestellar massive cores.
, which is an improvement of a factor of > 2 in terms of angular resolution compared to the ATLASGAL survey. This allows us to identify a population of cores with sizes of 0.1−0.2 pc that are embedded in clumps at distances d ≲ 5 kpc. The angular resolution we achieved corresponds to an intermediate physical scale to separate structures of massive star-forming clumps, which is a missing gap that needs to be closed to link to typical interferometric studies. The sample is twice the size of the sample used by Merello et al. (2015), who targeted a sample of BGPS sources with the SHARC-II camera on the Caltech Submillimeter Observatory (CSO). Combining our results with ancillary submillimeter and infrared data, we estimate the physical parameters of the cores and compare them with the properties of clumps in order to constrain their fragmentation and structure formation. The higher angular resolution compared to ATLASGAL allows us to distinguish between quiescent and star-forming cores and deliver a sample of starless or prestellar massive cores.
This paper is organized as follows: in Sect. 2 we present the observations, data reduction, and the complementary data. In Sect. 3 we present our results and the data analysis, including source extraction and determination of physical properties of clumps and SABOCA compact sources. In Sect. 4 we discuss the statistics of the sample in terms of the fragmentation properties and the relation between clump and core properties. Our main results and conclusions are summarized in Sect. 5.
2. Observations and data reduction
2.1. Source selection
Over 10 000 compact sources have been identified in the ATLASGAL survey (Csengeri et al. 2014; Urquhart et al. 2014), and the distance estimates of the majority of them (8007) allow determining their physical parameters (Urquhart et al. 2018). In this study, we used 350 μm SABOCA observations to investigate the small-scale structure of the clumps. Different from the extensive follow-up observations of the brightest submillimeter clumps selected from the ATLASGAL survey using both single-dish (Giannetti et al. 2014, 2017; Csengeri et al. 2016a; Kim et al. 2017, 2018) and interferometric observations (Csengeri et al. 2017a, 2018), this study focuses more on a population of massive clumps with a lower surface density (with typically a lower submillimeter flux density). Our targets were selected to be weak or in absorption at 24 μm based on the Spitzer MIPS GALactic plane survey (MIPSGAL; Carey et al. 2009). This initial sample of 95 clumps was complemented with sources at different evolutionary stages based on their mid-infrared color selection at 24 and 70 μm, mostly having a bolometric luminosity-to-mass ratio (Lbol/M) lower than 10. In addition, we included the data for the brightest 25 sources from the ATLASGAL survey.
Altogether, we targeted 204 ATLASGAL clumps, which is the largest number of clumps targeted with SABOCA. Since we obtained target maps, 371 other ATLASGAL sources have been covered in the fields. On average, we have 2−3 ATLASGAL clumps per field. The total number of observed clumps from the GaussClump compact source catalog of Csengeri et al. (2014) is therefore 575. In Fig. 1 we compare the integrated flux density and Lbol/M of our sample with the same quantities of the whole ATLASGAL sample where available (Urquhart et al. 2018). This shows that our sample is representative of the entire population of submillimeter sources, with a Lbol/M range of 0.1−100 L⊙/M⊙. Many of these sources are good candidates for hosting objects in early stages of high-mass star and cluster formation (see, e.g., Csengeri et al. 2017a). The sample also comprises massive clumps in more advanced stages of high-mass star formation, however, that are associated with bright mid-infrared sources and ultra-compact H II regions exhibiting L/M > 100 L⊙/M⊙. We performed the whole analysis on the entire sample homogeneously, and we clarify in the discussion when we focused on the mid-infrared dark sources.
 |
Fig. 1. Distribution of the integrated flux density and bolometric L/M of all ATLASGAL sources (in blue filled contours, the darker region corresponds to higher density) (Urquhart et al. 2018) and the target sources observed with SABOCA (gray pluses and dots) at different distance ranges. The histograms on the right side and in the top panel show the 1D distributions of integrated flux density and L/M of all ATLASGAL sources (blue) and all target sources (gray), respectively. |
We show the distance distribution of all sources in Fig. 2 for which a distance has been determined by Urquhart et al. (2018); these are primarily kinematic distances. Altogether, this provides us with a distance to 507 clumps, which corresponds to 88% of our sample.
 |
Fig. 2. Distance distribution of the observed ATLASGAL clumps. The vertical dashed line indicates the 5 kpc distance. The filled green region indicates the 2−4 kpc range. |
The entire sample covers a distance range from 1 to 14.5 kpc (Fig. 2), corresponding to a physical resolution between 0.04 and 0.6 pc. The wide range of linear scales (∼10) affects the observed morphologies and derived physical properties. To mitigate any possible observational biases, we restricted our statistical analysis to a distance-limited sample (d ≲ 2 − 4 kpc); this corresponds to physical sizes of 0.07 and 0.15 pc, and thus reduces the range of linear scales to a factor of 2. The majority of the clumps are located within 5 kpc (314 out of the 507 clumps, corresponding to 62% of the sample), 205 of which are located within 2−4 kpc. The more distant sources are mostly luminous OB clusters that tend to be associated with very active star-forming regions, which belong to the 25 strongest submillimeter sources within the ATLASGAL survey, such as the W51 and W43 complexes (e.g., Ginsburg et al. 2015; Motte et al. 2014).
2.2. SABOCA observations and data reduction
We targeted the selected ATLASGAL sources using the SABOCA instrument that is installed at the APEX telescope, which offers ∼8″ angular resolution at 350 μm. We used a raster spiral mapping strategy for each source that mapped a 4′ region centered on the source position. The observations were conducted in 2010 and 2012 with a median precipitable water vapor (PWV) of 0.3 mm and are all less than 0.5 mm. The typical on-source integration time was ∼5 min, which gives a better than ∼160 mJy beam−1 noise level for most of the sources (Fig. 3). This corresponds to a mass sensitivity of 1.84 M⊙ at 3 kpc, assuming a dust temperature of 20 K, κ350 μm = 0.076 cm2 g−1, and a gas-to-dust ratio of 100 (Eqs. (1) and (2)).
 |
Fig. 3. 350 μm peak flux density vs. the 1σ rms noise level observed with SABOCA toward all fields. The histogram on the right side and in the top panel shows the distribution of peak flux densities and the noise levels. |
We used the BoA software (Schuller 2012) with standard procedures and iterative masking for the data reduction. The atmospheric zenith opacity determined from the radiometer in each science scan was used to correct for atmospheric opacity. These values were compared to the results of the skydip measurement and found to be consistent. Mars and standard calibrators, such as IRAS 13134−6264, were regularly observed and used as primary flux calibrators. Typical calibration uncertainties are within 20%. Pointing and focus were updated every 1−2 h. The telescope pointing accuracy is within 2−3″.
We used the standard iterative source-masking reduction procedures optimized for the faint and the bright sources. In the first step of the iterative processing, an initial map is obtained after opacity correction, and then the correlated noise and bad channels are removed. The resulting map is then smoothed by two-thirds of the beam size (yielding a resolution of 9.5″) to achieve a better signal-to-noise ratio. This is then used as an input model for the following iterations to represent the real source structure. The residual flux is modeled by subtracting the model image from the initial map, with a cutoff level at a signal-to-noise ratio of 3. After adding the model back to the image, the process is repeated until the peak flux level remains unchanged. For the final maps, we applied 3″ smoothing, which gives a resolution of 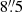 (original beam size ∼8″). We checked the convergence of the data reduction process by examining the relative change of the peak and integrated flux density around the brightest pixels during the iterative process. The pixel size is
(original beam size ∼8″). We checked the convergence of the data reduction process by examining the relative change of the peak and integrated flux density around the brightest pixels during the iterative process. The pixel size is 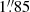 in the final map.
in the final map.
In order to have a uniform and consistent noise level estimation for all fields, we used a wavelet-based estimator implemented in the skimage python package; this assumes a Gaussian noise distribution and calculates the standard deviation in each map (Donoho & Johnstone 1994). Before this estimation, we trimmed the edge of the maps because of the increased noise level due to the non-uniform sampling at the map edges caused by the scanning strategy. We selected several sources to check the derived values and found them to be consistent with measurements made of an emission-free region of the map. The achieved rms noise distribution of all the sources is shown in Fig. 3. The mean noise level for the relatively weak sources (from projects M-0085.F-0046-2010 and M-0090.F-0026-2012) is 0.12 Jy beam−1 with a standard deviation of 0.07 Jy beam−1, and for the brightest sources (M-0085.F-0055-2010), it is 0.21 Jy beam−1 with a standard deviation of 0.10 Jy beam−1.
We find that the rms noise of the brightest sources with a peak flux density of 100 Jy beam−1 is higher by up to a factor of 5 than that of the weaker sources (Fig. 3). Altogether, the sources exhibit a wide range of peak flux density from as low as 1.25 Jy beam−1 up to 600.4 Jy beam−1, with an average of 52.0 Jy beam−1 and a median of 9.0 Jy beam−1 at 350 μm. In agreement with our initial selection from ATLASGAL, this shows that we have very many relatively faint and a few extremely bright clumps.
2.3. Ancillary data
To be able to determine the physical properties of the clumps, we relied on the far-infrared emission of the dust. For this, we used level 2.5/3 archival data from Herschel PACS and SPIRE at 70/160 μm, 250/350 μm, respectively, from the Hi-Gal survey (Molinari et al. 2010, 2016). The zero-point offsets of the SPIRE data were corrected by Planck-HFI data via cross-calibration1; this accounts for the thermal background produced by the instrument itself. Six fields are not covered in Hi-Gal or lie at the edges of the maps. These were excluded from the following analysis.
We complemented the HiGAL data with the combined ATLASGAL and Planck-HFI 870 μm data (Csengeri et al. 2016b). This data product has a considerably wider spatial dynamic range than the ATLASGAL data alone, allowing the recovery of large-scale structures, which can be directly compared with the emission probed by Herschel. To associate the submillimeter emission with mid-infrared sources, we also made use of the MIPSGAL survey and its point source catalog (Gutermuth & Heyer 2015).
3. Results
3.1. SABOCA 350 μm view of ATLAGSAL clumps: filaments and cores
We show examples of massive clumps at 350 μm observed by APEX/SABOCA in Fig. 4, where we also directly compare them with the 24 μm emission from the Spitzer/MIPSGAL survey that probes their star formation activity at a comparable angular resolution of 6″. We detect emission at 350 μm toward all fields, typically tracing emission from the ambient cloud material as well as from compact sources. The images for all the targeted sources are shown in Appendix A.
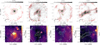 |
Fig. 4. Top panels: examples of 350 μm emission toward ATLASGAL-selected massive clumps obtained with APEX/SABOCA. Contour levels start at 5σ and show five uniformly spaced intervals on a logarithmic scale up to the peak flux density in each field. The green crosses show the position of ATLASGAL sources. Bottom panels: colored images show the 24 μm emission from MIPSGAL on a logarithmic scale, contours are the same as in the top panel of the 350 μm emission. Red crosses mark the positions of the compact sources identified in the SABOCA maps. The target name from the ATLASGAL Gaussclumps catalog is given in each plot. |
The range of peak flux densities of the observed fields spans two orders of magnitude at 350 μm with a typical dynamic range of ∼100, but this is noticeably lower for fields containing brighter sources. The high dynamic range and improved resolution allowed us to conduct a detailed analysis of the overall morphology of the sample in a homogeneous way for the majority of the sources; this is particularly true for the mid-infrared weak sources because of the better sensitivity and dynamic range.
As revealed in Fig. 4, the morphology of the 350 μm emission exhibits a great variety, including isolated compact spherical structures (Fig. 4a) and prominent elongated structures, which are often referred to as filaments (Figs. 4b–d). The structure of the source presented in Fig. 4d reveals a relatively straight filamentary morphology, but we also find a network of connecting filament-like structures and branches, which are illustrated in Figs. 4b and c, for example. These structures are reminiscent of the large-scale filamentary structure of the ISM (e.g., Li et al. 2016). Visual inspection of all the maps in Appendix A indicates that most of the fields exhibit elongated, filament-like emission (67%). This either corresponds to low-intensity uniformly distributed material or consists of brighter emission to which several compact sources are associated. These sources are marked in Table 1 together with the properties of the identified substructures (see more detail in Sect. 4.3). In general, fields dominated by a single bright source at 350 μm represent only a minor fraction of the sample.
Properties of SABOCA sources from Gaussclumps source extraction.
3.2. Extraction of compact sources
We used the Gaussian decomposition algorithm Gaussclumps to identify compact structures embedded within the ATLASGAL clumps2. Originally developed for identifying structures in 3D position-position-velocity data cubes, Gaussclumps assumes that the resolved structures are Gaussian-shaped and iteratively subtracts the fitted structures from the map (Stutzki & Guesten 1990). Gaussclumps is the same tool used to extract the compact sources from the ATLAGSAL survey (Csengeri et al. 2014).
We set the initial guesses of aperture cutoff and aperture FWHM to 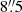 and 1.1 times the angular resolution, respectively. The initial guess for the source FWHM was also set to 1.1 times the angular resolution, and we required the identified substructure by Gaussclumps to have a peak flux higher than three times the rms. There are several other control parameters in the least-squares fitting algorithm. The stiffness parameters s0, sc, and sa adjust the tolerance between the observed intensity, maximum intensity, and its position, respectively, with the corresponding fitted parameters. We performed a series of tests to evaluate how the choices for the stiffness parameters affect the identified sources. We found that using 1, 1, and 10 for s0, sc, and sa results in a more stringent constraint on the fitted peak flux position, and seems to more robustly recover the prominent structures while avoiding the detection of spurious sources at relatively low signal-to-noise levels.
and 1.1 times the angular resolution, respectively. The initial guess for the source FWHM was also set to 1.1 times the angular resolution, and we required the identified substructure by Gaussclumps to have a peak flux higher than three times the rms. There are several other control parameters in the least-squares fitting algorithm. The stiffness parameters s0, sc, and sa adjust the tolerance between the observed intensity, maximum intensity, and its position, respectively, with the corresponding fitted parameters. We performed a series of tests to evaluate how the choices for the stiffness parameters affect the identified sources. We found that using 1, 1, and 10 for s0, sc, and sa results in a more stringent constraint on the fitted peak flux position, and seems to more robustly recover the prominent structures while avoiding the detection of spurious sources at relatively low signal-to-noise levels.
In total, we identified 1120 structures with Gaussclumps within our SABOCA maps, yielding on average 4−5 compact sources within the 4′ maps. We list the parameters of the extracted compact sources in Table 1. In the following, we use the nomenclature commonly adopted in the literature (e.g., Williams et al. 2000; Motte et al. 2007; Zhang et al. 2009; Liu et al. 2012a,b), where clumps means structures with sizes of ∼0.5−1 pc, and cores are structures of ∼0.1 pc that are embedded within a clump. Because most of our analysis and discussions is based on the distance-limited sample, in the following we use the term cores to refer to the compact sources extracted from the SABOCA 350 μm observations because most of them have an FWHM size ≲0.2 pc. When we discuss the properties of SABOCA 350 μm compact sources together with clumps, we use the term fragments instead to indicate their relation.
4. Physical properties of clumps and cores
4.1. Dust temperature and H2 column density maps on the clump scale
We performed a pixel-by-pixel fitting of the far-infrared spectral energy distribution (SED) to compute maps of the dust temperature, Td, and the H2 column density, N(H2). For this, we used PACS 160 μm, SPIRE 250 μm, and 350 μm maps and the combined APEX/LABOCA-Planck-HFI 870 μm data. We first convolved the maps to a common resolution of ∼25″ and then gridded the data onto the same pixel grid. We performed an SED fit of each pixel using a modified-blackbody model:
where in τν = μmHN(H2)κν, mH is the mean molecular weight, and we adopted a value of 2.8, and N(H2) is the gas column density. We adopted a dust opacity law of 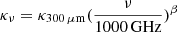 , where κ300 μm = 0.1 cm2 g−1 is the dust opacity per unit mass (gas and dust) at a reference wavelength 300 μm and β is fixed to 1.8, which is the average value found toward the Galactic plane (Planck Collaboration XXV 2011). These parameters have been used for the Herschel Gould Belt Survey (André et al. 2010), the HOBYS (Motte et al. 2010), and the Hi-Gal (e.g., Elia et al. 2017) key programs. This dust emissivity relation yields κ870 μm = 0.0147 cm2 g−1, while the previous ATLASGAL studies, for instance, Csengeri et al. (2014) and König et al. (2017), used a κ870 μm of 0.0185 cm2 g−1, which corresponds to a difference of a factor of 1.25 in the mass estimates. In addition, for the clumps whose fitted temperature was higher than 45 K, we additionally included the PACS 70 μm measurements in the final fits because in this temperature regime the inclusion of the shorter wavelength constrains the fit better. We note that there is emerging evidence that β and Td are anticorrelated (e.g., Juvela et al. 2013), which means that fixing β to a certain value will cause an uncertainty on Td that propagates into the mass estimate. More sophisticated modeling methods are required to accurately recover this anticorrelation (Juvela et al. 2013; Galliano 2018) by properly taking into account observational uncertainties, line-of-sight mixing of different components, etc. In addition, the dust opacity can also increase in a dense and cold cloud as a result of grain growth (dust coagulation, e.g., Ossenkopf & Henning 1994; Planck Collaboration XXV 2011; Ysard et al. 2013). In general, the mass estimates may have an uncertainty of up to a factor of 2−3 as a result of possible variations in dust opacity and emissivity index β.
, where κ300 μm = 0.1 cm2 g−1 is the dust opacity per unit mass (gas and dust) at a reference wavelength 300 μm and β is fixed to 1.8, which is the average value found toward the Galactic plane (Planck Collaboration XXV 2011). These parameters have been used for the Herschel Gould Belt Survey (André et al. 2010), the HOBYS (Motte et al. 2010), and the Hi-Gal (e.g., Elia et al. 2017) key programs. This dust emissivity relation yields κ870 μm = 0.0147 cm2 g−1, while the previous ATLASGAL studies, for instance, Csengeri et al. (2014) and König et al. (2017), used a κ870 μm of 0.0185 cm2 g−1, which corresponds to a difference of a factor of 1.25 in the mass estimates. In addition, for the clumps whose fitted temperature was higher than 45 K, we additionally included the PACS 70 μm measurements in the final fits because in this temperature regime the inclusion of the shorter wavelength constrains the fit better. We note that there is emerging evidence that β and Td are anticorrelated (e.g., Juvela et al. 2013), which means that fixing β to a certain value will cause an uncertainty on Td that propagates into the mass estimate. More sophisticated modeling methods are required to accurately recover this anticorrelation (Juvela et al. 2013; Galliano 2018) by properly taking into account observational uncertainties, line-of-sight mixing of different components, etc. In addition, the dust opacity can also increase in a dense and cold cloud as a result of grain growth (dust coagulation, e.g., Ossenkopf & Henning 1994; Planck Collaboration XXV 2011; Ysard et al. 2013). In general, the mass estimates may have an uncertainty of up to a factor of 2−3 as a result of possible variations in dust opacity and emissivity index β.
Using ATLASGAL and Herschel data, König et al. (2017) determined the properties of 109 ATLASGAL-selected massive clumps from SEDs of mid- to far-infrared data. That study was based on the clump-averaged integrated properties, while here we map the spatial distribution of the physical properties (e.g., dust temperature and gas column density). Examples of the resulting dust temperature and column density maps on the 25″ grid are shown in the top panels of Fig. 5.
 |
Fig. 5. Top panels: dust temperature (Td) and H2 column density (NH2) maps obtained with a pixel-by-pixel SED fitting of PACS 160 μm, SPIRE 250, 350 μm, and combined LABOCA and Planck 870 μm data at 25″ resolution. Bottom panels: same as the top panels, but using the PACS 70 μm and the SABOCA and SPIRE 350 μm combined maps at 10″ resolution. The top and bottom panels are in same color scale for dust temperature and column density maps, respectively. The circles in the top panel indicate the region mapped by SABOCA. |
4.2. Dust temperature and H2 column density maps on the core scale
To obtain the same parameters at the scale of cores, we made use of the high-resolution SABOCA observations for the SED fitting. Because ground-based submillimeter observations are not sensitive to extended emission due to sky noise subtraction, the SABOCA maps do not recover emission from scales larger than ∼0.9−1.0′ (∼60−70% of the instrument field of view of SABOCA) (Siringo et al. 2009). Because the Herschel SPIRE 350 μm covers a similar frequency range (Fig. 6), we can use these data to recover the extended emission. The sampled angular scales of the two data sets overlap between the ∼25″ resolution Herschel 350 μm and the largest angular scales recovered by SABOCA.
 |
Fig. 6. Top panel: transmission of the Herschel/SPIRE and the APEX/SABOCA instruments. Bottom panel: color-correction factors for SABOCA (dashed line) and SPIRE (solid line) as a function of the spectral index of the source. The dash-dotted line shows the conversion factor to scale the SPIRE intensities to the nominal center wavelength of SABOCA. |
To combine the SABOCA and SPIRE 350 μm data, we first calculated the color corrections due to the different shape of the transmission curves and nominal frequencies of the SABOCA and SPIRE instruments. Following a procedure similar to that described in Csengeri et al. (2016a), we determined the central wavelength correction factor from SPIRE to SABOCA (F = 0.97) and color-correction factors for both instruments (CSPIRE = 0.93, CSABOCA = 0.86). These factors were applied to maps made with each instrument before the combination procedure. The transmission curves and the relation between the assumed spectral index and the correction factors are shown in Fig. 6.
An additional complication is that ten of the brightest sources are saturated in the SPIRE 350 μm images. We corrected for this by interpolating between the saturated pixels assuming a 2D Gaussian flux distribution around the center. We find that the interpolated images are in general consistent with the SABOCA images after they are smoothed to the SPIRE 350 μm resolution of 25″. Finally, for all sources, we linearly combined the SABOCA and SPIRE 350 μm images in the Fourier domain using the immerge task of the Miriad software package (Sault et al. 1995). Before the combination, we calculated a weighting factor from the overlapping spatial scales between the two datasets that was then applied to scale the SABOCA flux to match that of the SPIRE 350 μm measurements. For more details on the procedure of the combination, we refer to Lin et al. (2016).
We used these combined maps together with the PACS 70 μm band at a similarly high resolution of ∼10″ after smoothing to estimate the physical properties of the SABOCA sources, such as H2 column density NH2, mass, and average dust temperatures Td. We did this by fitting SEDs to each pixel in the maps to trace the local heating sources and estimate the core-scale temperature and column density. The formulations are the same as when we fit the four bands at a coarser resolution (Sect. 4.1). Assuming that the four-band SED fits in general describe the bulk of the cold component in the coarser resolution maps, we scaled the 70 μm flux densities in order to remove the contribution of a second hotter gas component that is often seen toward deeply embedded protostars and massive young stellar objects (MYSO). The scaling factor is defined as the flux ratio of the observed 70 μm emission map and the extrapolated 70 μm flux based on the SED fit with the four bands. This step is necessary because most of our sources are mid-infrared weak, thus dominated by cold dust that mainly emits at wavelengths longer than ∼100 μm. Hence our method of using only the 70 μm and the 350 μm data would lead to an underestimate of the core masses, with flux at 70 μm predominantly originating from the deeply embedded heating sources.
We find that the scaling factors are generally less than 1.0 for most of our mid-infrared dark and relatively bright evolved sources. However, for the extremely bright OB cluster-forming regions such as G10.6−0.4 and G12.8−0.2 (ATLASGAL names: G010.6237−0.3833 and G012.7914−0.1958), we find a ratio higher than one for the predicted 70 μm flux compared to the observed flux density. These sources are at the edge of prominent compact 70 μm emission features, and because of their more evolved nature, including the 70 μm flux in the SED fits without any scaling provides a better constraint on their temperature fit (e.g., Lin et al. 2016). When the scaling factor exceeded one, we therefore used the original 70 μm fluxes. In Appendix B we present two examples that include one of these extremely bright OB clusters and the statistics of the scaling factors with the derived properties. The difference between the derived values using the original and scaled 70 μm flux density in the SED fits are generally within 20% for the temperature and 50% for the column density depending on the flux-scaling factor, which is discussed in detail in Appendix B. The uncertainties of the fitted column density and dust temperature are within 20%. Examples of the 10″ temperature and column density maps are shown in the bottom panels of Fig. 5. Altogether, we were able to perform a pixel-by-pixel SED fit for 198 of our maps, which includes 971 cores that are identified in the SABOCA maps.
4.3. Statistics of the physical properties of ATLASGAL clumps and SABOCA cores
We derived the physical properties, such as average dust temperature, mass, bolometric luminosity of the identified SABOCA compact sources, and their ATLAGSAL host clumps, from the pixel-by-pixel SED fitting described in Sect. 4.2.
The average dust temperature was calculated from the mean pixel values within the identified Gaussian structures based on the FWHMs reported in Csengeri et al. (2014). Similarly, we calculated the clump masses by summing the column densities (NH2) of each pixel over the source area at distance, d (see Sect. 2.1),
where A stands for the clump area defined by πR2. The radius is defined as R = σ, where 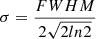 . We estimated the total bolometric luminosity by integrating the fitted SEDs,
. We estimated the total bolometric luminosity by integrating the fitted SEDs,
where Sν is derived by the fitted SED curve described in Sect. 4.1, and is summed within R = σ, as well.
To estimate the physical properties of the 350 μm SABOCA compact sources, we followed the same procedure as described above using the corresponding parameters fit by Gaussclumps and using the high-resolution column density and dust temperature maps (10″). The physical parameters of the individual ATLASGAL clumps and the SABOCA sources are listed in Tables 2 and 3, respectively. We list the general statistics of the clump and core properties in Table 4 for all the sources and the distance limited sample.
ATLASGAL clump properties.
Properties of SABOCA sources, their 24 μm and 70 μm associations, and parental clumps.
Physical properties of ATLASGAL clumps and SABOCA compact sources.
The distribution of the physical properties of the clumps is shown in Fig. 7. The average mass of all of the clumps is 600 M⊙. In total, 65% of the sources have > 100 M⊙, and the most massive clump has a mass of 1 × 104 M⊙; this is one of the more distant sources in our sample. In addition, there are 130 clumps above 650 M⊙, which is the mass limit used by Csengeri et al. (2014) as a threshold for a massive clump to potentially form high-mass stars. The average mass of all the SABOCA sources is 198 M⊙, and for the distance limited sample it is 50 M⊙, which is about three times lower than the values of the clumps (Table 2).
 |
Fig. 7. Distribution of the physical properties of all the observed ATLASGAL clumps and compact sources identified at 350 μm with SABOCA. Top left: mass distribution of clumps and SABOCA compact sources. The vertical lines show mass limits of 40 M⊙ and 650 M⊙. Top right: distribution of sizes that are the measured FWHM size from the Gaussclumps source extraction. Vertical lines show the 0.1 and 0.5 pc range for the definition of cores and clumps. Bottom left: luminosity-to-mass ratio distribution of the clumps and SABOCA compact sources. The vertical dotted lines indicate luminosity-to-mass ratios of 1 and 10, which are taken as empirical evolutionary boundaries in Molinari et al. (2016) for massive clumps. Bottom right: temperature distribution with a vertical line showing 18 K, which is the average temperature for galactic background. |
The mean clump FWHM size of all the clumps and those at 2−4 kpc is 0.68 ± 0.45 pc and 0.42 ± 0.11 pc, corresponding to the typically observed scales for Galactic clumps. The mean FWHM size is 0.31 ± 0.21 pc for all the SABOCA sources, and for the sources in 2−4 kpc, the value is 0.19 ± 0.05 pc, corresponding to a typical core scale.
We also calculated the surface density based on the average column density derived from SED fits, where Σ = μmHN(H2) (g cm−2). Table 4 shows that SABOCA sources typically have higher surface densities on average than the clumps, indicating a concentration of dense gas at smaller scales. The mass surface density of most of the clumps (65%) and cores (78%) is higher than 0.2 g cm−2, which was used to identify promising massive star progenitors by Butler & Tan (2012).
We find dust temperatures between ∼14 K and ∼50 K for the clumps, and on average, we find similar values for clumps and cores. This is expected from our SED fitting method, which is mainly sensitive to the cold component. The most active star-forming clumps have an average dust temperature of > 40 K and correspond to the most massive OB cluster-forming regions in the Galaxy.
Owing to our source selection strategy, we have a large fraction of clumps with low bolometric luminosity and a luminosity-to-mass ratio lower than 10 (74%). A low bolometric luminosity together with a high mass is indicative of an early evolutionary stage (e.g., Motte et al. 2007; Molinari et al. 2016), therefore very many of our targeted clumps are likely to be at early evolutionary stages. We indicate the Lbol/M = 1 and Lbol/M = 10 vertical lines in the luminosity-to-mass ratio distribution plot (Fig. 7). The lines show empirical limits from Molinari et al. (2016) for massive clumps in a starless or prestellar stage, and clumps hosting high-mass ZAMS stars, respectively. The Lbol/M > 10 ratio can also correspond to a qualitatively different heating source, reflecting the presence of deeply embedded UC-H II regions (see Sect. 4.4; see also Kim et al. 2018). The most evolved clumps, with luminosity-to-mass ratios above 100, such as G34.3+0.2, G10.6−0.4, and G333.6+0.2 (Campbell et al. 2004; Liu et al. 2010; Lo et al. 2015, respectively), are clumps residing in well-known extreme Galactic massive star-forming regions.
4.4. Signposts of star-forming activity of the 350 μm SABOCA sources
We used the MIPSGAL point source catalog at 24 μm (∼6″; Gutermuth & Heyer 2015) and the Herschel/Hi-Gal point source catalog at 70 μm (∼8 4; Molinari et al. 2016) to assess the star formation activity of the SABOCA 350 μm compact sources. The angular resolution of these catalogs is similar to that of the SABOCA observations. We also made use of the WISE point source catalog (11″ at 22 μm; Cutri et al. 2012) to complement the mid-infrared surveys because MIPSGAL is saturated at > 2 Jy, while the WISE point source photometry is reliable to ∼330.0 Jy flux density at 22 μm. We also used the existing RMS (Lumsden et al. 2013; Urquhart et al. 2013) and the CORNISH (UC-)H II region catalogs (Kalcheva et al. 2018) to identify the sources associated with H II regions that are likely to be saturated in mid-infrared images. These catalogs have a coordinate range that covers in total ∼30% of our SABOCA (295 out of 971) cores. The higher angular resolution of the SABOCA data allows a better matching with these higher angular resolution ancillary catalogs than ATLASGAL, which is necessary to assess the star-forming activities in the cores.
4; Molinari et al. 2016) to assess the star formation activity of the SABOCA 350 μm compact sources. The angular resolution of these catalogs is similar to that of the SABOCA observations. We also made use of the WISE point source catalog (11″ at 22 μm; Cutri et al. 2012) to complement the mid-infrared surveys because MIPSGAL is saturated at > 2 Jy, while the WISE point source photometry is reliable to ∼330.0 Jy flux density at 22 μm. We also used the existing RMS (Lumsden et al. 2013; Urquhart et al. 2013) and the CORNISH (UC-)H II region catalogs (Kalcheva et al. 2018) to identify the sources associated with H II regions that are likely to be saturated in mid-infrared images. These catalogs have a coordinate range that covers in total ∼30% of our SABOCA (295 out of 971) cores. The higher angular resolution of the SABOCA data allows a better matching with these higher angular resolution ancillary catalogs than ATLASGAL, which is necessary to assess the star-forming activities in the cores.
We cross-matched the position of the SABOCA sources and these catalogs with an angular separation limit of  , corresponding to the angular resolution of SABOCA maps. The distribution of the angular offsets between the SABOCA compact sources and their mid-infrared emission (Fig. 8, left panel) suggests a good positional correlation between the mid-infrared sources and the 350 μm SABOCA peak positions. The dispersion of offsets is in the range of 2−4″, which is consistent with the pointing accuracy of the telescope.
, corresponding to the angular resolution of SABOCA maps. The distribution of the angular offsets between the SABOCA compact sources and their mid-infrared emission (Fig. 8, left panel) suggests a good positional correlation between the mid-infrared sources and the 350 μm SABOCA peak positions. The dispersion of offsets is in the range of 2−4″, which is consistent with the pointing accuracy of the telescope.
 |
Fig. 8. Left: distribution of angular distances between SABOCA sources and their MIR compact source or/and H II region associations. In each bin, the probability of dN/N is normalized by the annular area defined by adjacent angular bins as dN/(N × Area). Right: distribution of distances of star-forming and quiescent SABOCA compact sources. |
We used the association with UC-H II regions, 24/22 μm or 70 μm point sources to distinguish between star-forming and quiescent cores and to assess the statistics of their physical properties. Because the diffuse mid-infrared background emission varies, the completeness of these catalogs is inhomogeneous, however. The sensitivity limit of the MIPSGAL 24 μm survey (5σ, ∼10 mJy) can probe down to 18 L⊙ protostars within 15 kpc following the calculation of Motte et al. (2007) based on IRAS colors from Wood & Churchwell (1989). This suggests that even intermediate-mass protostars could be revealed in our sample. However, as discussed in Gutermuth & Heyer (2015), the MIPSGAL catalog completeness is strongly dependent on the spatial variation of the local emission, therefore the sensitivity limit does not reflect the level of the completeness toward all sources. The sensitivity limit of the PACS 70 μm band of 0.2 Jy (Molinari et al. 2016) corresponds to a luminosity of ∼25 L⊙ at 5 kpc (Dunham et al. 2008). This similarly suggests that at least intermediate-mass protostars should be detected at 70 μm when the spatial variation of the completeness level and source confusion are neglected.
In all the 1120 compact sources identified from the SABOCA maps, of which 971 have physical parameters based on their SED fitting, 13 (1.3%) have UCH II region counterparts. In the remaining sources, 184 (19.0%) are directly associated with 24/22 μm compact sources. In addition, we also have 87 (8.9%) sources that spatially coincide with regions of saturated 24 μm emission, but without 22 μm or 70 μm counterparts. These are ignored in the following analysis. Of the 184 sources that have 24/22 μm compact sources, 18 do not have a 70 μm compact source counterpart. Visual inspection of these 18 sources shows that they are all associated with faint or extended 70 μm emission, and hence they are likely to be below the completeness limit of the PACS 70 μm catalog. Of the remaining sources, 142 (14.6%) have a compact source counterpart only at 70 μm. The remaining 545 (56.1%) sources are either dark at 24/22 μm or are associated with extended or diffuse 70 μm emission, which is not included in the compact source catalog. To summarize, we used the various surveys described above to classify 884 cores, of which 545 cores are found to be quiescent (64%) and 339 cores are forming stars (36%).
Dust extinction may prohibit detection of deeply embedded 24/70 μm compact sources. We calculated the dust opacities at 70 μm based on the derived column densities for quiescent cores with our assumed opacity law (see Sect. 4.1). We find that 90% of the calculated opacities are lower than 1 with a 95% quartile level of opacity ∼2.4, indicating that dust extinction does not significantly affect our classification. However, the effect of source geometry and the uncertainty of dust emissivity may also influence the actual extinction.
To determine whether the nonuniform distances of our sources affect the classification, we show the distance distribution of the star-forming and quiescent cores in Fig. 8 (right panel). The two distributions are similar, with a KS-test yielding p-value = 0.31 and D = 0.08 (p-value > 0.05 and D < Dα at a significance level of α = 0.05), which means that fewer quiescent cores appear at closer distances than star-forming cores, suggesting that the different distances do not bias our classification. However, we caution that these similarities in the distributions might arise because the two opposite biases cancel each other out: at larger distances, the objects tend to be more massive and hence more likely to be already forming stars. This effect counteracts the decreasing likelihood of detecting mid-infrared compact sources. In the following, we restrict our analysis to the distance-limited sample, or to samples in certain distance bins, so that the results are less affected by the classification bias that is due to the varying distance.
5. Discussion
In this section we compare the physical properties of the star-forming and quiescent SABOCA cores (Sect. 5.1), and investigate their capability of forming high-mass stars (Sect. 5.2). We study the fragmentation properties and the clump structure in Sect. 5.3 based on a distance-limited sample of 2−4 kpc. In Sect. 5.4 we identify a sample of massive quiescent SABOCA cores at < 5 kpc that are high-mass prestellar core candidates.
5.1. Physical properties of star-forming and quiescent cores
In Sect. 4.4 we classified the SABOCA cores into two categories according to their radio, mid-, and far-infrared compact source associations: star-forming and quiescent. As discussed in the following paragraphs, our approach is more sensitive to the deeply embedded low- to intermediate-mass protostars than using a single wavelength.
A 24 μm point source associated with a compact 350 μm source suggests the presence of a local heating source that corresponds to one or more protostars. However, the absence of a 24 μm point source does not necessarily mean that there is no star-forming activity. A high optical depth or mid-infrared confusion may inhibit the detection of compact 24 μm sources. In this case, being more sensitive to the outer regions of internally heated cores, the PACS 70 μm compact source association (e.g., Dunham et al. 2008; Ragan et al. 2013) is used to further determine the star-formation activity. While it is clear that the absence of a 24−70 μm point source appears to exclude the presence of a massive YSO, early stage (even up to high-mass) protostars have been detected toward infrared-quiet massive clumps (Bontemps et al. 2010; Feng et al. 2016; Csengeri et al. 2018) and dense cores with luminosities as low as 400 L⊙ (Duarte-Cabral et al. 2013).
In Fig. 9 we show the distribution of the physical parameters of cores located at a distance of 2−4 kpc. This sample consists of 233 quiescent and 129 star-forming cores. We find that the star-forming cores in general have a modestly higher temperature (24.0 K ± 0.75 K) than the quiescent cores (18.9 K ± 0.19 K). We obtain a p-value < 0.001 for a KS-test confirming that the temperatures of the two populations are statistically different. However, we also note that many (43%) star-forming cores have a relatively low dust temperature (< 20 K). Some quiescent cores have temperatures higher than 25 K (5%). Visual inspection of these cores reveals that they are located close to extended nebulosities at 70 μm; these cores may therefore be star-forming cores that remain undetected because of confusion from the nearby bright source or are genuinely quiescent cores whose warmer temperature is caused by external heating.
 |
Fig. 9. Distribution of the physical properties of star-forming and quiescent SABOCA compact sources in the 2−4 kpc distance bin, in red and blue, respectively. Top left: temperature distribution of two categories. Top right: mass distribution. Bottom left: luminosity distribution. Bottom right: surface density distribution. In each plot, the cumulative probability distribution is drawn with respective colors according to the right y-axis. |
The luminosity distribution of the SABOCA cores is presented in the bottom left panel of Fig. 9. This plot shows a similar picture as the dust temperature, with the star-forming cores having higher luminosities. The KS-test results in p-value < 0.001, again indicating a distinct distribution. However, we find many quiescent sources with high luminosities of > 103 L⊙. The number of quiescent sources decreases to zero above Lbol ∼ 103.5 L⊙, which is equivalent to the zero-age main-sequence (ZAMS) luminosity of a B2–B4 star. As discussed in the previous paragraph, these high values of the bolometric luminosities toward quiescent cores are either due to external heating or to a higher level of confusion and blending with nearby sources. It is therefore possible that some of the quiescent cores might be protostellar, but the lack of a corresponding bright 24 μm source suggests that the star formation is still at a very early stage.
The mass distribution of the quiescent and star-forming sources is remarkably similar. Together with their difference in bolometric luminosities, this may suggest that the cores classified as quiescent are in an earlier stage of star formation, and would follow the same evolutionary path as the star-forming cores (Csengeri et al. 2017b, see also discussion in Sect. 5.2). The range of typical core masses is between 10 and 320 M⊙, with an average mass of star-forming and quiescent cores of 53.1 ± 4.2 M⊙ and 45.5 ± 3.1 M⊙, respectively. The KS test yields p-value = 0.26, indicating a similar mass distribution. The typical core masses for star-forming and quiescent cores are not significantly different. The star-forming cores have on average smaller sizes (0.15 ± 0.002 pc in FWHM) than quiescent cores (0.16 ± 0.003 pc in FWHM). The mean mass surface density of star-forming cores (0.50 ± 0.03 g cm−2) is higher than that of the quiescent cores (0.40 ± 0.02 g cm−2). The KS-test yields a p-value ∼ 0.012 (∼1%), indicating that the two distributions are different; star-forming cores have a higher surface density.
The similar mass distribution and relatively different surface density distribution of quiescent and star-forming cores indicate that at the typical scale of ∼0.2 pc, the quiescent cores have assembled enough mass to evolve into protostellar cores when they contract. Cores can contract gravitationally from the moment they first appear because their background is unstable (Naranjo-Romero et al. 2015). In the framework of dynamical evolution cores are clump fed (see also Wang et al. 2010), which is supported by growing observational evidence for gas replenishment beyond the core scale (e.g., Galván-Madrid et al. 2009; Csengeri et al. 2011; Peretto et al. 2013; Liu et al. 2015; Chen et al. 2019). In this case, cores prior to star formation may be expected to have a lower mass than star-forming cores, but because quiescent cores are relatively more extended and their aspect ratio (from Gaussclump) shows them to be less roundish than star-forming cores, the similar mass distributions may not contradict this dynamical evolution scenario. In addition, some of the star-forming cores may be in a state of gas dispersal (Fig. 11). The most luminous of the quiescent cores (L > 102.5 L⊙) have higher surface densities of 0.69 ± 0.13 g cm−2 than their less luminous counterparts with 0.33 ± 0.01 g cm−2. The number of quiescent cores decreases significantly above ∼0.5 g cm2. This may suggest that when a higher mass surface density regime is reached, the cores necessarily form high-mass stars, for which the formation timescales are shorter than for low- and intermediate-mass star formation (Csengeri et al. 2014; Urquhart et al. 2018).
5.2. Fraction of massive star-forming cores
To estimate the fraction of the SABOCA cores that are potential precursors or in the early stage of forming massive stars, we show the mass-radius plot and mass-luminosity diagram of all the samples in Figs. 10 and 11. For this analysis we only used sources located at 1−2 kpc and 2−4 kpc distance ranges, which allows us to compare sources with similar size-scales. We briefly discuss more distant sources for comparison purposes.
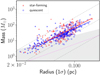 |
Fig. 10. Mass-radius diagram of SABOCA compact sources. The quiescent cores and star-forming cores are indicated with blue and red in 2−4 kpc (hollow markers) and 1−2 kpc (filled markers) distance bins. The dashed lines show the constant volume density of 104, 105, and 106 cm−3. The magenta dotted line indicates Larson’s third relation of approximately 1021 cm−2 column density. The gray filled region is below the empirical threshold of massive star formation from Kauffmann & Pillai (2010), which is scaled to match the dust opacity values we used in this work. Red and blue lines indicate the fitted linear regression for the quiescent and star-forming cores at 2−4 kpc. |
 |
Fig. 11. Luminosity-mass diagram of SABOCA compact sources. The quiescent and star-forming cores are indicated with blue and red in 2−4 kpc (hollow markers) and 1−2 kpc (filled markers) distance bins. The empirical evolutionary tracks for massive clumps with envelope masses of 80, 140, 350, 700, and 2000 M⊙ in Molinari et al. (2008) are shown with gray dots. André et al. (2008) tracks for final stellar masses of 1, 3, 8, 15, and 50 M⊙ are shown as magenta dashed lines. Red and blue lines indicate the fitted linear regression for the quiescent and star-forming cores at 2−4 kpc. |
The mass-radius plot (Fig. 10) shows no clear difference between the star-forming and quiescent cores in mass scale. A substantial number of the cores are found above the empirical threshold for massive star formation introduced by Kauffmann & Pillai (2010), suggesting that very many of them are capable of or are already in the process of forming high-mass stars. In particular, we cover many quiescent cores with a radius of ∼0.2 pc and masses of ∼100 M⊙, corresponding to a mass surface density of ∼0.2 g cm−2, thus representing potentially young regions where massive star formation could occur (e.g., Butler & Tan 2012).
The derived power-law relation of M ∝ rα gives α = 2.67± 0.25 and α = 2.60 ± 0.16 for star-forming and quiescent cores at a distance range of 2−4 kpc, respectively. For sources at 1−2 kpc, the indices are somewhat higher, with α = 3.00 ± 0.62 and α = 3.07 ± 0.32 for the star-forming and quiescent sample, respectively. For sources at 4−8 and 8−12 kpc, more shallower slopes of ∼2.0 are found. These slopes are generally steeper than observed on the even larger clump-scale, where a relation of M ∝ R1.4 − 1.7 is derived (e.g., Urquhart et al. 2018). The trend of a steepening mass-radius relation at a small scale (or smaller distance range) is also seen in Ragan et al. (2013), for example, toward cores in infrared dark clouds, and in Beuther et al. (2018) toward young massive star-forming regions at thousands of au (as reflected in their Fig. 11).
Observationally, the Larson density-size relation (M ∝ R2) could be due to a selection effect of a certain column density threshold, as frequently pointed out in previous works (e.g., Larson 1981; Ballesteros-Paredes & Mac Low 2002; Camacho et al. 2016). In our case, the more distant objects with smaller slopes of the power-law dependence on radius might arise because they correspond to larger physical sizes, and thus receive a larger contribution from their more diffuse envelope. The steepening of the mass-radius relation from a slope of ∼2 to ∼3 corresponds to a change from a constant column density to a constant volume density. Considering that cores are usually embedded in a gaseous environment, the slopes of α = 3, 2, 1 can result from different environments such as a (spherically) uniform medium, a 2D layer, or a centrally concentrated filament, respectively (Myers 2009). This again indicates that at larger distances the amount of envelope gas might affect the slope, that is, cores appear more “concentrated” when a diffuse layer is involved. On the other hand, the different power-law forms of M ∝ R2 or M ∝ R3 might indicate different modes of accretion (Hennebelle 2012), either dominated by turbulence from larger scales or the protocluster self-gravity. Hence the steepening of the mass-radius relation may reflect the successively prevailing role of self-gravity at smaller scales (see also Camacho et al. 2016).
The luminosity and mass distribution for the star-forming versus quiescent cores is shown in Fig. 11. The evolutionary tracks for different final stellar masses and initial envelope masses (André et al. 2008; Molinari et al. 2008) are also included in this plot. These tracks have two main components, a vertical track that represents the main accretion phase, and a horizontal track that indicates the clump gas dispersal phase. Where these lines join, they form an apex that effectively defines the start of the stellar ZAMS lifetime. Most of the quiescent cores are below this apex and are therefore in the early stage of their evolution. Some of the star-forming cores, on the other hand, may be in a phase of gas dispersal. The brightest star-forming cores are clusters around or above the apex, indicating that many have reached the ZAMS stage and the envelope clean-up phase has probably begun (Molinari et al. 2008). Although scattered, the two distributions for quiescent and star-forming cores are clearly distinct for core masses higher than a few tens of M⊙, with star-forming cores having higher luminosities. A linear regression fit between the log-log mass and luminosity gives L ∝ M0.97 ± 0.06 and L ∝ M1.58 ± 0.16 for quiescent and star-forming cores at 2−4 kpc, respectively. Similarly drastic differences in power-law slopes for the sources at 1−2 kpc distance are found, with L ∝ M0.76 ± 0.16 and L ∝ M1.37 ± 0.23 for quiescent and star-forming cores. For sources at 4−8 kpc, the difference in slopes decreases, with quiescent cores having L ∝ M1.20 ± 0.08 and star-forming cores L ∝ M1.40 ± 0.13. Within the uncertainties, for clumps a consistent relationship is found between luminosity and mass with L ∝ M1.3 (e.g., Molinari et al. 2008; Urquhart et al. 2018). The less pronounced difference in the mass-luminosity scaling relation of these two populations with larger distances can be explained if the mid-infrared source association with the submillimeter compact source becomes less robust with increasing distance to distinguish genuine quiescent cores, but also because more distant sources have more ambient gas, as mentioned before, which contributes to the mass but not much to the luminosity. The latter case is consistent with the fact that for sources more distant than 8 kpc, shallower slopes are found for quiescent and star-forming cores as L ∝ M0.81 ± 0.13 and L ∝ M0.91 ± 0.20. In line with our previous results, that is, the mass distribution and the mass-radius relation of the quiescent cores and star-forming cores, the luminosity and mass diagram with evolutionary tracks also suggests that a significant fraction of these cores can form a high-mass star, should they eventually collapse to become a single object.
In Fig. 12 we show the mass distribution of the cores (ΔN/Δlog(M), André et al. 2014), of the SABOCA cores at < 5 kpc. The completeness level of our sample is not straightforward to assess because the sensitivity varies and the dust temperatures are different in each field. We estimated the mass completeness using the highest noise level (0.18 Jy beam−1) for sources at d < 5 kpc, and assumed a dust temperature of 15 K, which is the lowest value we have for the core population. This allowed us to obtain a conservative estimate of the mass completeness limit of cores in the sample. With a flux density of 3σ and a source size close to the beam size, the mass completeness limit is approximately 41.4 M⊙. We fit a power law to the cores at d < 5 kpc above 41.4 M⊙, and find a power-law index of −1.89 ± 0.39. Although the fit has a large uncertainty, the slope is larger than the Salpeter IMF (−1.35) and is also steeper than recent findings of mass distribution of cores in higher angular-resolution studies of the early stages of high-mass protoclusters (e.g., Csengeri et al. 2017a; Motte et al. 2018). This could be explained by the fact that our study is more limited by confusion due to the poorer angular resolution; the slope is fit in a higher mass range than these works, suggesting that there might be intrinsically less massive cores at this larger scale (0.1−0.2 pc). On the other hand, the derived core mass distribution may be described better by a log-normal than a power-law distribution, as shown by previous studies (e.g. Peretto & Fuller 2010). We also find that moving the cutoff mass to a higher value would result in a steeper fitted slope. We also note that different source extraction methods may result in different core mass distributions (e.g., Cheng et al. 2018) and such results should be interpreted with caution.
 |
Fig. 12. Fragment mass distribution of all SABOCA sources. The fitted power-law index of the all the sources at < 5 kpc above our mass completeness (> 41.4 M⊙) is indicated by the green vertical line. |
5.3. Clump structure and fragmentation: Association of cores to clumps
Here we investigate the hierarchical structure of the clumps by assigning the SABOCA cores (child fragments) to their parent clumps in which they are embedded. We focus on the 971 SABOCA sources whose physical properties we derived in the analysis here. Because the Jeans length is typically resolved up to 4 kpc, we again consider a sample in the 2−4 kpc distance range, while the sample located at 1−2 kpc is added in some plots for comparison purpose.
For each parent and child structure, we generated a mask based on their FWHM size from Gaussclumps and assigned the child fragments to their parental clumps based on their overlapping area, as illustrated in Fig. 13. Clumps located at the edge of the SABOCA maps were omitted from this analysis because we may not cover the full extent of the clump. We calculated the fragmentation level in two ways: exactNmm corresponds to the exact sum of the probability of overlapping areas of child fragments within the extent of the parent clump; the other is roundingNmm, which assigns each fragment to the clump with which it has the largest overlapping area. In short, the exactNmm considers fragments that overlap multiple clumps. For example, fragment 3 in Fig. 13, overlaps two clumps, giving 0.20 and 0.33 to the two clumps’ exactNmm, while it is counted to the central clump as 1 in roundingNmm. In this approach, the sum of exactNmm equals that of roundingNmm, while for some clumps, roundingNmm may be zero when a fragment that overlaps it has a larger proportional area inside another clump.
 |
Fig. 13. Example of the fragment allocation criterion toward an example SABOCA mapping field. Left panel: 870 μm LABOCA emission in gray scale, overlaid with ATLASGAL clumps as green dashed ellipses. Middle panel: 350 μm SABOCA emission in gray scale with contour levels from 3σ to the peak flux with 5 linear logarithmic spacing. Each SABOCA core is labeled with a number and is refered to as number x. Green dashed ellipses mark the ATLASGAL clumps as identified in Csengeri et al. (2014). Blue, magenta, and cyan ellipses mark the position of three sets of fragments belonging to several ATLASGAL clumps. Right panel: (slightly zoomed in compared to the middle panel), the overlapping possibilities of each fragment with the ATLASGAL clumps are indicated with arrows. |
We allocated 874 fragments to 444 clumps for the whole sample; the remaining ∼100 SABOCA sources lack a parental clump structure, and 353 fragments to 161 clumps in the 2−4 kpc distance bin, 77 fragments to 37 clumps in the 1−2 kpc distance bin; consequently, each clump averages ∼2 fragments. This is similar to what Merello et al. (2015) find when they extended from a resolution of 33″ to 8.5″. The thermal Jeans mass and Jeans length for a clump with a temperature of 20 K and a volume density of 104–105 cm−3 is 2−6 M⊙ and 0.1−0.3 pc (Bontemps et al. 2010; Palau et al. 2015). Even at a later stage with a typical temperature of 30 K, the Jeans mass is only a factor of two higher, and the Jeans length is only 20% larger. Therefore we resolved the hierarchical fragmentation of clumps to cores on scales of 0.1−1.0 pc. Considering the typical clump properties of our sample, our results suggest that the number of fragments is broadly consistent with the Jeans length that we resolve here: the number of fragments is consistent with the number of predicted Jeans lengths within the clump size. The SABOCA cores have considerably higher masses than that of the thermal Jeans mass by a factor of 10−100, however. This has been found in similar studies of ≲0.1 pc cores or condensations (e.g., Motte et al. 2007; Wang et al. 2011; Csengeri et al. 2017a; Lu et al. 2018).
In Fig. 14 we investigate in detail the fragmentation level of the clumps as a function of their physical properties for sources at a distance of 2−4 kpc. For the analysis, we only considered parental clumps for which at least one fragment lay entirely within the clump. The colored points mark the fragment numbers according to the roundingNmm criterion, and gray points show the exactNmm with each pair linked with dotted lines. Although the different fragment allocation methods may result in quantitatively different fragmentation levels, we find that the general trend of fragmentation is similar. Therefore, both methods give a qualitatively similar picture.
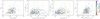 |
Fig. 14. Fragmentation level as a function of clump properties of sources located at a distance at 2−4 kpc. In each plot, data points are color-coded according to the clump size. Gray triangles show the exact fragment number exactNmm; colored dots show the rounding fragment number roundingNmm (see definitions in Sect. 5.3). Dashed contours show the distribution of exactNmm from a Gaussian kernel density estimation. Left: number of fragments as a function of clump mass. Middle left: specific fragment level (Nmm normalized by clump radius) as a function of the clump luminosity-to-mass ratio. Middle right: specific fragment level as a function of the clump density. Right: number of fragments as a function of predicted number of fragments based on a Jeans fragmentation scenario. Gray dashed lines mark the lines of Nmm = 0.15/0.05/0.01 × Mclump/MJeans, clumpTd. |
Comparing the level of fragmentation, that is, the number of fragments with clump mass, L/M and the predicted number of fragments with Jeans scenario, we find a generally significant scatter in the fragmentation levels, while the left panel of Fig. 14 suggests that the number of fragments increases slightly with clump mass. The Spearman correlation coefficient is 0.39 (exactNmm vs. Mclump, 0.38 of roundingNmm vs. Mclump, p-value < 0.001), indicating a moderate correlation. We hereby define the specific fragmentation level as the number of fragments per unit clump size, as Nmm/Rclump. The normalization by clump size is necessary given our limited angular resolution improvement in identifying fragments, such that we tend to pick up more fragments when the clump size is larger. The middle panel shows the specific fragmentation level as a function of the clump luminosity-to-mass ratio, a proxy of the evolutionary stage (e.g., Molinari et al. 2008; Csengeri et al. 2016a; Urquhart et al. 2018). There is a trend of subtle increase in the specific fragmentation as a function of L/M, with a Spearman correlation coefficient of 0.24 (exactNmm/Rclump vs. Lclump, 0.29 of roundingNmm/Rclump vs. Lclump, p-value ∼ 0.015). We caution that a higher Lbol/M ratio could also arise because the most massive (proto)stars are forming within the clump (Ma et al. 2013) rather than an evolved stage characterized by gas dispersal. Finally, comparing the number of fragments with the thermal Jeans fragmentation prediction, we examine the correlation between specific fragment level with clump gas density (middle right panel of Fig. 14), and find a Spearman correlation coefficient of 0.41 (exactNmm/Rclump vs. ρclump, 0.45 of roundingNmm/Rclump vs. ρclump, p-value < 0.001). Based on the clump temperature and gas density, we also find a moderate correlation between the fragment level with the predicted Jeans number (NJeans = Mclump/MJeans), with a Spearman correlation coefficient of 0.31 (exactNmm vs. NJeans, 0.32 of roundingNmm vs. NJeans, p-value ∼ 0.001). We also note that the clumps considered here have a positive correlation of their gas volume density and temperature (T ∝ ρ0.22), corresponding to the gas equation of state (EOS) having a polytropic exponent of γ ∼ 1.22, which is close to the upper limit that is relevant for Galactic molecular clouds (Spaans & Silk 2000). The increase in temperature with density means that the Jeans mass decreases more slowly with density than isothermal gas, favoring less fragmentation. When compared with an assumed initial temperature of 20 K, that is, the clump temperature when fragmentation occurred (e.g., Palau et al. 2015), a stronger correlation between the observed fragmentation level with the predicted Jeans number is found, with a Spearman correlation coefficient of 0.40 (exactNmm vs. NJeans, 0.42 of roundingNmm vs. NJeans, p-value < 0.001). On smaller scales toward more evolved massive clumps, it seems that Jeans fragmentation is at work (e.g., Palau et al. 2015; Beuther et al. 2018; Liu et al. 2018). It is possible that turbulence dominates the fragmentation process at larger scale (e.g., Zhang et al. 2009; Wang et al. 2014) to induce a higher critical mass. We note that there is also evidence that the combined thermal and turbulent pressure is still not sufficient to stabilise the fragments in filamentary clouds (e.g. Lu et al. 2018). The time delay of fragments with a Jeans mass may be explained within the global hierarchical collapse scenario (Vázquez-Semadeni et al. 2019) because the density of the fragments must grow to sufficiently high contrast, and while this happens, the Jeans mass in the contracting clump will have decreased. This implies that the fragment masses, especially in early stage clumps, will in general be higher than the average Jeans mass measured for the clump.
Because Gaussclump is a non-hierarchical source extraction method, the association of child structures to parental structures is ambiguous, which introduces a source of uncertainty in the fragmentation level and the correlations with properties of the parental clumps. Here we provide two sets of fragmentation levels as a first attempt to deal with the association uncertainties. As a further benchmark, we adopt a completely independent method of source extraction (dendrogram, Rosolowsky et al. 2008) which is not hampered by the association issue, and present the same correlations between fragmentation level with clump properties in Appendix C. We find that the moderate correlations we derive here are also present in the dendrogram analysis; some of them show slightly tighter correlations, that is, Nmm vs. Mclump (Spearman correlation coefficient of 0.42), Nmm versus NJeans (Spearman correlation coefficient of 0.48). These results help to solidify the analysis in this section.
Studies of smaller but more homogeneous samples of massive cores and high-mass protostars based on higher angular resolution observations, for instance, thousands of au, did not find a clear correlation between the core properties and fragmentation level, except that a higher central volume density, a higher clump mass may lead to more fragments (Palau et al. 2015). Although we discuss here the core scale and a considerably larger sample, we can only conclude that there is moderate indication of Jeans fragmentation at work, and there is no trend of fragmentation level with clump evolution. It is possible, however, that the overall sample covers a too wide range of Galactic clumps to reveal which clump properties might affect the fragmentation level. In addition, our source selection may not be homogeneous for massive clumps with a luminosity-to-mass ratio range larger than 10 L⊙/M⊙.
In Fig. 15 we illustrate the relationship between the most massive fragment and clump properties for sources in the 1−2 kpc (triangles) and 2−4 kpc (circles) distance bins. For these plots, we again only include cases in which the parental clump has at least one fragment that lies entirely within the clump. When we compare the mass of the most massive fragment with the clump Lbol/M ratio, it seems that more evolved clumps with a higher Lbol/M ratio (Fig. 15, left panel) only host core masses above ∼20 M⊙. We here derive the correlations and regressions only for sources in the 2−4 kpc distance range, and sources in 1−2 kpc distance range are shown in the figure for comparison purpose. We find a strong correlation between the clump mass and the mass of the most massive core. This correlation is statistically significant and has a Spearman coefficient of 0.92 and p-value lower than 0.001. This clearly indicates that more massive cores tend to form in more massive clumps. A linear fit in the logarithmic scale yields a relation of log Mmmf = 0.96log Mclump − 1.18, which corresponds to Mmmf = 0.31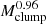 . This relation is close to a fraction of 30% of the clump mass that is assembled in the most massive fragment. In Appendix C we demonstrate that this strong correlation is present when the dendrogram source extraction method is applied, regardless of the distinct concepts behind these algorithms in recognising cloud structures. As a comparison, Merello et al. (2015) found that 19% of the clump mass resides within the total dense substructures seen at 350 μm when they considered the change from 30″ to 8
. This relation is close to a fraction of 30% of the clump mass that is assembled in the most massive fragment. In Appendix C we demonstrate that this strong correlation is present when the dendrogram source extraction method is applied, regardless of the distinct concepts behind these algorithms in recognising cloud structures. As a comparison, Merello et al. (2015) found that 19% of the clump mass resides within the total dense substructures seen at 350 μm when they considered the change from 30″ to 8 5 resolution maps. We note that the exact values of this fraction depend primarily on the relative resolution differences in defining the parental structure and substructures. We also find that the surface density of the most massive fragment correlates well with the clump surface density and has a fitted relation of log Σmmf = 1.02log Σclump + 0.42, close to Σmmf ∼ 1.5Σclump. This indicates that the gas in the cores is denser than that in their parental clumps.
5 resolution maps. We note that the exact values of this fraction depend primarily on the relative resolution differences in defining the parental structure and substructures. We also find that the surface density of the most massive fragment correlates well with the clump surface density and has a fitted relation of log Σmmf = 1.02log Σclump + 0.42, close to Σmmf ∼ 1.5Σclump. This indicates that the gas in the cores is denser than that in their parental clumps.
 |
Fig. 15. Most massive fragment mass as a function of clump properties for sources at a distance of 2−4 kpc (dots) and 1−2 kpc (triangles). Left: mass of the most massive fragment as a function of clump luminosity-to-mass ratio. Vertical lines mark the luminosity-to-mass ratio of 1 and 10. Middle: mass of the most massive fragment mass as a function of clump mass. Gray lines show the 30% and 100% proportion of clump mass; the blue dashed line shows the result of a linear fit on logarithmic scale to sources in the 2−4 kpc distance range of Mfragments = 0.96log Mclumps − 1.18. The relation between cluster mass and maximum stellar mass is indicated by the red dash-dotted line, which is an analytical relation from Weidner et al. (2013), and is scaled up by 3.3 assuming a 30% star-formation efficiency. The eft and middle plots share the same color bar. The clumps are color-coded according to their sizes. Right: surface density of the most massive fragment as a function of clump surface density. Vertical line marks the 0.2 g cm−2 empirical limit from Butler & Tan (2012). The blue dashed line shows the result of a linear fit to sources in the 2−4 kpc distance range of log Σfragments = 1.03log Σclumps + 0.43. |
With the approximate relations between clump and its most massive fragment Σmmf ∼ 1.5Σclump and Mmmf ∼ 0.31Mclump, and when we assume that the clump density profile follows a power-law form as a function of radius n(r)∝r−kρ, a density structure of n(r)∝r−1.5 is obtained, which is equivalent to a mass profile of M(r)∝r1.5 for the enclosed clump. The self-similar density profile of n(r)∝r−kρ with kρ in range of 1.6−1.9 is obtained in gas spheres of high density from simulations of self-gravitating supersonic turbulence (Collins et al. 2012; Murray & Chang 2015). In particular, Murray & Chang (2015) suggested that the n(r)∝r−1.5 is an attractor solution at clump inner radii that is reached over the self-similar gravitational collapse of the clumps, when the density is then independent of time, that is, n(r, t)→n(r). Furthermore, the clump density power-law forms can be directly linked to the power-law tails seen in molecular cloud column density probability distribution functions (N-PDF), ln N ∼ N−s, with s = 2/(kρ − 1) (Federrath & Klessen 2013). kρ ∼ 1.5 thus corresponds to an N-PDF slope of −4. Lin et al. (2017) proposed a tentative critical value of the N-PDF power-law slope of −4 to separate massive star-forming cloud intermediate evolutionary stages, which have a shallower slope, with early or late stages, through an analysis of ten massive star-forming clouds from the infrared dark stage to an evolved stage with embedded luminous OB clusters. Because most of the clumps we considered here have an L/M < 10, which means that they are in a relatively early evolutionary stage (Molinari et al. 2008), this small-scale clump density distribution agrees with the evolution trend of the cloud N-PDF, which is compatible indirect observational evidence of a multi-scale cloud collapse, as in the global hierarchical collapse scenario (Vázquez-Semadeni et al. 2019).
In middle panel of Fig. 15 we also plot the mass of the most massive star in a cluster (Mmax) as a function of the cluster mass (Mecl) (Weidner et al. 2013) scaled up by 3.3 times, together with the relation of masses between the most massive fragments and parental clumps. Here we make the simple assumption that the mass of most massive stellar member that formed in the most massive fragment is proportional to the fragment mass with a constant star formation efficiency (SFE) of 30% regardless of the mass scale. The relation between mmax and Mecl indicates that the mass of the most massive star systematically changes with the cluster mass in stars and is incompatible with a scale-free IMF (Weidner et al. 2013). The sampling procedure that introduces this relation also suggests that star formation is highly regulated, with low-mass stars forming until feedback from the massive stars is able to prevail over the gravity-dominated formation process (Weidner & Kroupa 2006). The fact that the formation of low-mass stars starts early and continues until massive stars are formed is seen in the numerical simulations of cloud formation and collapse by converging flows over a time span of a few megayears (Vázquez-Semadeni et al. 2017). The relation of the most massive fragment and clump mass is compatible with the mmax − Mecl relation, with the most massive core likely to be the progenitor of the most massive stellar member and perhaps fragmenting into somewhat less massive cores, which may also remain unresolved at present, indicating that the reservoir clump mass is essential in regulating the mass distribution at smaller scales. The larger deviation of our observed most massive core-clump mass relation to mmax − Mecl in a wider mass range is understandable because we find that more massive objects tend to have more fragments, as discussed before. With higher angular resolution observations we might resolve the bending of the most massive core-clump mass relation. Numerical simulations of rotating massive cloud cores with radiative feedback have indicated that fragmentation-induced starvation could be a possible scenario that sets the limit of the mass of the most massive stars (Peters et al. 2010).
5.4. Massive quiescent cores: candidate high-mass prestellar cores?
The higher resolution of the 350 μm observations with SABOCA compared to the 870 μm LABOCA maps of ATLASGAL offers the possibility to better distinguish between star-forming and quiescent cores. We take this opportunity to investigate the brightest SABOCA sources in more detail that are quiescent and lack embedded compact sources at 24 and 70 μm. To select the most massive cores, we used our mass estimates measured in a radius of 1σ, corresponding typically to a mass measurement within an FWHM diameter of 0.17 pc for a 0.2 pc core. We selected cores that are located at d < 5 kpc and have M1σ > 100 M⊙, assuming that they are capable of forming at least one early-B or O-type star. Among all SABOCA cores, we find 87 sources that fulfill this distance and mass criteria, of which 34 (37%) are not associated with any embedded compact sources at 24 and 70 μm. The fraction of star-forming versus quiescent cores is higher in this high-mass regime than toward all sources within 5 kpc, where 58% are found to be quiescent. When we consider only the most massive cores, the relative fraction of star-forming versus quiescent cores is significantly higher, which is consistent with other studies (e.g., Csengeri et al. 2014; Urquhart et al. 2018) that have suggested shorter formation timescales for the most massive clumps.
A quiescent massive core with > 100 M⊙ within a typical radius of 0.085 pc has a volume density > 7.5 × 105 cm−3 and a mass surface density of 0.92 g cm−2 assuming a uniform density distribution. However, most of these sources typically have non-flat flux distributions, suggesting a steeper density profile, as is the case for their embedding clump. The bulk of the gas is cold, with dust temperatures between 14 and 25 K, and on average of 18 K. Like the overall population of quiescent cores, the massive quiescent cores also exhibit lower bolometric luminosities between 60 and 2300 L⊙.
To investigate whether these massive quiescent cores could qualify as candidates for extremely elusive and rare high-mass prestellar cores (Csengeri et al. 2017b; Motte et al. 2018; Lu et al. 2018), we visually inspected these candidates, and removed 7 cores from the final list that are too close to and blended with a bright source at 24 μm. This left us with a final list of 27 sources (Table 5). Being embedded in a larger-scale clump, these sources are typically surrounded by other cores, some of which are lower mass and/or star-forming. We do not find any isolated or single candidate high-mass pre-stellar core above the > 100 M⊙ mass limit. An example of the massive quiescent core embedded in clump structure with lower-mass counterparts is shown in Fig. 16
Candidate massive prestellar cores with > 100 M⊙ at < 5 kpc.
 |
Fig. 16. Example of a clump hosting massive quiescent cores. White crosses mark the > 100 M⊙ quiescent cores and the blue cross marks the star-forming cores. The masses for quiescent cores are indicated in the figure. Contour levels are from 7σ to the peak flux with six logarithmic linear levels in between. |
We searched for available ancillary higher angular resolution archival data that would help us to investigate the nature of these cores further, and found that G333.1298−0.5602 and G333.4659−0.1641 have been observed at high angular resolution as part of the SPARKS project using ALMA (Csengeri et al. 2017a, 2018). These studies suggest, however, that the brightest fragments on a 2000 au scale in these sources are high-mass protostellar objects rather than prestellar cores.
To further probe the star formation activity of these cores we examined ancillary data on molecular tracers obtained with the IRAM 30 m telescope described in Csengeri et al. (2016a), and the MALT90 survey observed with the MOPRA telescope (Foster et al. 2013) which are available for all but one of the sources. These observations, however, have a coarser angular resolution than the SABOCA maps are, therefore, only indicative as an independent probe of their star formation activity.
Similarly to Motte et al. (2007), we first investigate here the velocity profiles of the SiO (2–1) line. SiO is a widely used tracer for shocks. It becomes in particular abundant in fast shocks associated with jet activity (e.g., Schilke et al. 1997; Codella et al. 1999). Therefore, high-velocity line wings could be indicative of the presence of jets and outflow activity related to embedded protostars, but it might also originate from a nearby more evolved core if the resolution is lower than our SABOCA maps. We used here the pointed observations of Csengeri et al. (2016a) and the MALT90 maps (Foster et al. 2013), where we extracted and averaged the spectra toward the core position within the MOPRA beam (∼38″). For the MOPRA data, these figures are shown in Appendix D, Fig. D.1. Except for the cores GS351.4379+0.6537 and G351.4416+0.6534, we find no clear evidence of a broad velocity component in this line toward our candidate high-mass prestellar cores, but the lack of SiO line wings could also be due to sensitivity limitations. Where available (6 sources), we checked the IRAM 30 m observations for the CO (1–0) line that is covered by our spectral survey described in Csengeri et al. (2016a) that could be a more sensitive probe for high-velocity outflowing gas. Although the line shape is strongly affected by absorption from the reference position, there is no clear evidence for high-velocity emission that could be related to outflowing gas in this tracer either. The observed line wings of the SiO (2–1) transitions toward GS351.4379+0.6537 and G351.4416+0.6534 are likely due to blending with a star-forming core within the beam of the MOPRA observations. Of the remaining 24 sources, 13 (54%) have detections in the SiO (2–1) line showing a narrow SiO component, and 11 sources show no detection in the SiO (2–1) line at all. To conclude, the SiO (2–1) line does not provide an indication for deeply embedded ongoing star formation activity.
To make use of the available spectroscopic data, we also investigated whether infall signatures on the clump scale could be revealed toward our sample. While Csengeri et al. (2016b) suggested that most of the massive clumps are gravitationally unstable, spectroscopic signatures of infall (e.g., Myers et al. 1996; Mardones et al. 1997; Wu & Evans 2003) could provide an indication that the clump itself is collapsing (however, see Smith et al. 2013). To search for an infall signature, that is, redshifted self-absorption of optically thick lines, we used the HCO+ and H13CO+ (J = 1–0) lines, and where detected, we used a single-Gaussian fit to the H13CO+ line to extract the vlsr of the clump. Although a proper interpretation of these line profiles would require dedicated modeling, visual inspection of the spectra suggests possible infall motions toward 16 sources (60%). The information obtained from molecular line data is listed in Table 5.
Considering a typical star formation efficiency of 20−40% (Tanaka et al. 2017), the SABOCA cores with > 100 M⊙ are good candidates to form at least one massive star. The absence of 24−70 μm emission, together with the indications from SiO/HCO+/H13CO+ tracers, suggests that except for two cores, there is no further indication for star formation activity related to jets and outflows in the sample based on the SiO (2–1) line, while more than half of the clumps hosting half of the cores shows indications of the presence of global infall motions. We identify seven sources where the SiO (2–1) line is not detected and there is no indication for infall. On the clump scale, these sources could be considered as starless massive sources. However, we cannot exclude ongoing low-mass star formation when the core would fragment and form only a low-mass cluster. The physical processes that determine the possibility for a massive core to form high-mass stars are not yet clear.
We conclude that considering all of the available low angular-resolution data, our sample of candidate high-mass prestellar cores is robust, although deeply embedded high-mass protostars have been detected toward mid-infrared quiet massive cores and clumps (Bontemps et al. 2010; Wang et al. 2011; Ohashi et al. 2016; Csengeri et al. 2017a). High angular resolution observations are needed to confirm their nature.
6. Conclusions
We presented the largest sample of Galactic clumps studied at a moderate resolution of 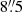 at 350 μm observed with APEX/SABOCA. By combining with available Herschel and LABOCA observations from ATLASGAL, we analyzed the core properties derived from SED fits and investigated the fragmentation as a function of the physical properties of clumps. Our major findings are listed below.
at 350 μm observed with APEX/SABOCA. By combining with available Herschel and LABOCA observations from ATLASGAL, we analyzed the core properties derived from SED fits and investigated the fragmentation as a function of the physical properties of clumps. Our major findings are listed below.
-
Our SABOCA observations detect the 350 μm emission toward all targeted ATLASGAL clumps and reveal a variety of morphology from compact, relatively isolated sources to complex filamentary structures with branches. We find that the majority of the targeted sources exhibit a filamentary structure emission. Fields dominated by a single bright source at 350 μm represent only a minor fraction of the sample.
-
We identified 1120 compact sources at 350 μm using Gaussclumps. We estimated the physical properties toward 971 SABOCA sources from SED fits. The average FWHM size is 0.32 pc, the dust temperature is 21.6 K, the average mass is 198 M⊙, and the average surface density is 0.40 g cm−2. Four hundred and five cores are located at a distance of 2−4 kpc; they have an average FWHM size of 0.19 pc, an average dust temperature of 21.8 K, an average mass of 52 M⊙, and an average surface density of 0.40 g cm−2. We find a systematic shallowing of slopes of the core mass-radius relation as a function of distance, from ∼3 to ∼2.
-
Using the presence of 22−24 μm and 70 μm point sources, we distinguished between star-forming and quiescent SABOCA sources. Most of the sources lack mid- and far-infrared counterparts (56.1%) and are classified as quiescent cores. For the distance-limited sample (2−4 kpc), we find that the quiescent cores have a similar mass range as the star-forming cores but are somewhat more extended and hence less dense and of lower dust temperature (0.16 pc, 0.40 g cm−2, 18.9 K) than the star-forming cores (0.15 pc, 0.50 g cm−2, 24.0 K).
-
We find that on average, each clump hosts two cores, which is broadly consistent with the length scale of thermal Jeans fragmentation. The core masses are, however, a factor of 10−100 times higher than predicted by thermal fragmentation. The observed number of fragments is moderately correlated with the clump density and the number of fragments predicted by pure thermal Jeans fragmentation inferred from the clump properties (correlation coefficient of ≳0.4, p-value ∼ 0.001). We do not find a strong indication that more cores would form as the clumps evolve as traced by their increasing Lbol/M ratio.
-
We find a strong correlation between the clump mass and the mass of the most massive core, close to ∼30% of the clump mass is assembled in the most massive core. The surface density of the most massive fragment is increased compared to the parental clumps.
-
We identified 27 massive (> 100 M⊙) quiescent cores at d < 5 kpc that are promising candidates of massive star-forming progenitors in their earliest stages. Further high-resolution observations are necessary to confirm the nature of these cores and determine whether they might host genuine high-mass prestellar cores.
The procedure is described in http://herschel.esac.esa.int/Docs/SPIRE/spire_handbook.pdf
This is implemented in the GILDAS software package that can be found at http://www.iram.fr/IRAMFR/GILDAS
Acknowledgments
We thank the anonymous referee, whose comments and suggestions helped us to significantly increase the clarity of the paper. Y. Lin thanks Pavel Kroupa for helpful discussions, and Dario Colombo for his suggestions on the Dendrogram analysis. T.Cs. acknowledges support from the Deutsche Forschungsgemeinschaft, DFG, via the SPP (priority programme) 1573 “Physics of the ISM”. The following Herschel data (obsID) was used in this work: 1342183068, 1342183069, 1342184484, 1342184485, 1342186275, 1342186276, 1342189081, 1342189082, 1342189083, 1342189084, 1342189109, 1342189110, 1342189878, 1342189879, 1342203083, 1342203084, 1342203085, 1342203086, 1342203278, 1342203279, 1342203282, 1342203283, 1342203287, 1342203288, 1342203289, 1342203290, 1342203291, 1342203292, 1342203293, 1342203294, 1342204042, 1342204043, 1342204044, 1342204045, 1342204046, 1342204047, 1342204054, 1342204055, 1342204056, 1342204057, 1342204058, 1342204059, 1342204090, 1342204091, 1342204092, 1342204093, 1342204094, 1342204095, 1342204100, 1342204101, 1342204104, 1342204105, 1342204366, 1342204367, 1342204368, 1342204369, 1342204421, 1342204422, 1342204845, 1342204846, 1342207026, 1342207027, 1342207028, 1342207029, 1342207052, 1342207053, 1342207054, 1342207055, 1342214510, 1342214511, 1342214575, 1342214576, 1342214713, 1342214714, 1342214763, 1342214764, 1342218642, 1342218643, 1342218644, 1342218645, 1342218646, 1342218647, 1342218692, 1342218693, 1342218694, 1342218695, 1342218963, 1342218964, 1342218965, 1342218966, 1342218995, 1342218996, 1342218997, 1342218998, 1342218999, 1342219000, 1342219630, 1342219631, 1342231361, 1342231362, 1342231851, 1342231852, 1342231858, 1342231859. This work has made use of the following Python libraries/packages: Astropy (Astropy Collaboration 2018), Matplotlib (Hunter 2007), Numpy (Oliphant 2006), Scipy (Jones et al. 2001), Scikit-image (van der Walt et al. 2014), Pandas (McKinney 2010), PySpecKit (Ginsburg & Mirocha 2011), and APLpy (Robitaille 2019).
References
- Aguirre, J. E., Ginsburg, A. G., Dunham, M. K., et al. 2011, ApJS, 192, 4 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- André, P., Minier, V., Gallais, P., et al. 2008, A&A, 490, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, Protostars and Planets VI (Tucson: University of Arizona Press), 27 [Google Scholar]
- André, P., Revéret, V., Könyves, V., et al. 2016, A&A, 592, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Ballesteros-Paredes, J., & Mac Low, M.-M. 2002, ApJ, 570, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Mottram, J. C., Ahmadi, A., et al. 2018, A&A, 617, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bontemps, S., Motte, F., Csengeri, T., & Schneider, N. 2010, A&A, 524, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butler, M. J., & Tan, J. C. 2012, ApJ, 754, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Camacho, V., Vázquez-Semadeni, E., Ballesteros-Paredes, J., et al. 2016, ApJ, 833, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, M. F., Harvey, P. M., Lester, D. F., & Clark, D. M. 2004, ApJ, 600, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Noriega-Crespo, A., Mizuno, D. R., et al. 2009, PASP, 121, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H.-R. V., Zhang, Q., Wright, M. C. H., et al. 2019, ApJ, 875, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, Y., Tan, J. C., Liu, M., et al. 2018, ApJ, 853, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Codella, C., Bachiller, R., & Reipurth, B. 1999, A&A, 343, 585 [NASA ADS] [Google Scholar]
- Collins, D. C., Kritsuk, A. G., Padoan, P., et al. 2012, ApJ, 750, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Csengeri, T., Bontemps, S., Schneider, N., et al. 2011, ApJ, 740, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Csengeri, T., Urquhart, J. S., Schuller, F., et al. 2014, A&A, 565, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csengeri, T., Leurini, S., Wyrowski, F., et al. 2016a, A&A, 586, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csengeri, T., Weiss, A., Wyrowski, F., et al. 2016b, A&A, 585, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csengeri, T., Bontemps, S., Wyrowski, F., et al. 2017a, A&A, 600, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csengeri, T., Bontemps, S., Wyrowski, F., et al. 2017b, A&A, 601, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csengeri, T., Bontemps, S., Wyrowski, F., et al. 2018, A&A, 617, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cutri, R. M., Wright, E. L., Conrow, T., et al. 2012, Explanatory Supplement to the WISE All-Sky Data Release Products, Tech. rep. [Google Scholar]
- Donoho, D. L., & Johnstone, I. M. 1994, Biometrika, 81, 425 [CrossRef] [MathSciNet] [Google Scholar]
- Duarte-Cabral, A., Bontemps, S., Motte, F., et al. 2013, A&A, 558, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dunham, M. M., Crapsi, A., Evans, II, N. J., et al. 2008, ApJS, 179, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Eden, D. J., Moore, T. J. T., Plume, R., et al. 2017, MNRAS, 469, 2163 [NASA ADS] [CrossRef] [Google Scholar]
- Elia, D., Molinari, S., Schisano, E., et al. 2017, MNRAS, 471, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., & Klessen, R. S. 2013, ApJ, 763, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, S., Beuther, H., Zhang, Q., et al. 2016, ApJ, 828, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, J. B., Rathborne, J. M., Sanhueza, P., et al. 2013, PASA, 30, e038 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, F. 2018, MNRAS, 476, 1445 [NASA ADS] [CrossRef] [Google Scholar]
- Galván-Madrid, R., Keto, E., Zhang, Q., et al. 2009, ApJ, 706, 1036 [NASA ADS] [CrossRef] [Google Scholar]
- Giannetti, A., Wyrowski, F., Brand, J., et al. 2014, A&A, 570, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giannetti, A., Leurini, S., Wyrowski, F., et al. 2017, A&A, 603, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginsburg, A., & Mirocha, J. 2011, Astrophysics Source Code Library [record ascl:1109.001] [Google Scholar]
- Ginsburg, A., Bally, J., Battersby, C., et al. 2015, A&A, 573, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gutermuth, R. A., & Heyer, M. 2015, AJ, 149, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P. 2012, A&A, 545, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heyer, M., Wilson, G. W., Gutermuth, R., et al. 2018, MNRAS, 473, 2222 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open Source Scientific Tools for Python [Google Scholar]
- Juvela, M., Montillaud, J., Ysard, N., & Lunttila, T. 2013, A&A, 556, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalcheva, I. E., Hoare, M. G., Urquhart, J. S., et al. 2018, A&A, 615, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kauffmann, J., & Pillai, T. 2010, ApJ, 723, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, W.-J., Wyrowski, F., Urquhart, J. S., Menten, K. M., & Csengeri, T. 2017, A&A, 602, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, W.-J., Urquhart, J. S., Wyrowski, F., Menten, K. M., & Csengeri, T. 2018, A&A, 616, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- König, C., Urquhart, J. S., Csengeri, T., et al. 2017, A&A, 599, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, Annu. Rev. Astron. Astrophys., 41, 57 [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Li, G.-X., Urquhart, J. S., Leurini, S., et al. 2016, A&A, 591, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, Y., Liu, H. B., Li, D., et al. 2016, ApJ, 828, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., Liu, H. B., Dale, J. E., et al. 2017, ApJ, 840, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H. B., Ho, P. T. P., & Zhang, Q. 2010, ApJ, 725, 2190 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H. B., Jiménez-Serra, I., Ho, P. T. P., et al. 2012a, ApJ, 756, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H. B., Quintana-Lacaci, G., Wang, K., et al. 2012b, ApJ, 745, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H. B., Galván-Madrid, R., Jiménez-Serra, I., et al. 2015, ApJ, 804, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H. B., Chen, H. R. V., Román-Zúñiga, C. G., et al. 2018, ArXiv e-prints [arXiv:1808.07702] [Google Scholar]
- Lo, N., Wiles, B., Redman, M. P., et al. 2015, MNRAS, 453, 3245 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, X., Zhang, Q., Liu, H. B., et al. 2018, ApJ, 855, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Lumsden, S. L., Hoare, M. G., Urquhart, J. S., et al. 2013, ApJS, 208, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, B., Tan, J. C., & Barnes, P. J. 2013, ApJ, 779, 79 [Google Scholar]
- Mardones, D., Myers, P. C., Tafalla, M., et al. 1997, ApJ, 489, 719 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, W. 2010, in Proceedings of the 9th Python in Science Conference, eds. S. van der Walt, & J. Millman, 51 [Google Scholar]
- Merello, M., Evans, II, N. J., Shirley, Y. L., et al. 2015, ApJS, 218, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Minier, V., André, P., Bergman, P., et al. 2009, A&A, 501, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Pezzuto, S., Cesaroni, R., et al. 2008, A&A, 481, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Schisano, E., Elia, D., et al. 2016, A&A, 591, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moore, T. J. T., Plume, R., Thompson, M. A., et al. 2015, MNRAS, 453, 4264 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Schilke, P., & Lis, D. C. 2003, ApJ, 582, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Bontemps, S., Schilke, P., et al. 2007, A&A, 476, 1243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., Zavagno, A., Bontemps, S., et al. 2010, A&A, 518, L77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., Nguyên Luong, Q., Schneider, N., et al. 2014, A&A, 571, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., Bontemps, S., & Louvet, F. 2018, ARA&A, 56, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, N., & Chang, P. 2015, ApJ, 804, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C. 2009, ApJ, 706, 1341 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C., Mardones, D., Tafalla, M., Williams, J. P., & Wilner, D. J. 1996, ApJ, 465, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Naranjo-Romero, R., Vázquez-Semadeni, E., & Loughnane, R. M. 2015, ApJ, 814, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Ohashi, S., Sanhueza, P., Chen, H.-R. V., et al. 2016, ApJ, 833, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Oliphant, T. E. 2006, A Guide to NumPy (USA: Trelgol Publishing), 1 [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Palau, A., Fuente, A., Girart, J. M., et al. 2013, ApJ, 762, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Palau, A., Ballesteros-Paredes, J., Vázquez-Semadeni, E., et al. 2015, MNRAS, 453, 3785 [NASA ADS] [CrossRef] [Google Scholar]
- Peretto, N., & Fuller, G. A. 2010, ApJ, 723, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Peretto, N., Fuller, G. A., Duarte-Cabral, A., et al. 2013, A&A, 555, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peters, T., Klessen, R. S., Mac Low, M.-M., & Banerjee, R. 2010, ApJ, 725, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XXV. 2011, A&A, 536, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ragan, S. E., Henning, T., & Beuther, H. 2013, A&A, 559, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rayner, T. S. M., Griffin, M. J., Schneider, N., et al. 2017, A&A, 607, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robitaille, T. 2019, https://doi.org/10.5281/zenodo.2567476 [Google Scholar]
- Rosolowsky, E. W., Pineda, J. E., Kauffmann, J., & Goodman, A. A. 2008, ApJ, 679, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, in Astronomical Data Analysis Software and Systems IV, eds. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, ASP Conf. Ser., 77, 433 [NASA ADS] [Google Scholar]
- Schilke, P., Walmsley, C. M., Pineau des Forets, G., & Flower, D. R. 1997, A&A, 321, 293 [NASA ADS] [Google Scholar]
- Schuller, F. 2012, in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VI, Proc. SPIE, 8452, 84521T [NASA ADS] [CrossRef] [Google Scholar]
- Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siringo, G., Kreysa, E., Kovács, A., et al. 2009, A&A, 497, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siringo, G., Kreysa, E., De Breuck, C., et al. 2010, The Messenger, 139, 20 [NASA ADS] [Google Scholar]
- Smith, R. J., Shetty, R., Beuther, H., Klessen, R. S., & Bonnell, I. A. 2013, ApJ, 771, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Spaans, M., & Silk, J. 2000, ApJ, 538, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Stahler, S. W., Palla, F., & Ho, P. T. P. 2000, Protostars and Planets IV (Tucson: University of Arizona Press), 327 [Google Scholar]
- Stutzki, J., & Guesten, R. 1990, ApJ, 356, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Svoboda, B. E., Shirley, Y. L., Battersby, C., et al. 2016, ApJ, 822, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, J. C., Beltrán, M. T., Caselli, P., et al. 2014, Protostars and Planets VI (Tucson: University of Arizona Press), 149 [Google Scholar]
- Tanaka, K. E. I., Tan, J. C., & Zhang, Y. 2017, ApJ, 835, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Urquhart, J. S., Thompson, M. A., Moore, T. J. T., et al. 2013, MNRAS, 435, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Urquhart, J. S., Moore, T. J. T., Csengeri, T., et al. 2014, MNRAS, 443, 1555 [NASA ADS] [CrossRef] [Google Scholar]
- Urquhart, J. S., König, C., Giannetti, A., et al. 2018, MNRAS, 473, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- van der Walt, S., Schönberger, J. L., Nunez-Iglesias, J., et al. 2014, PeerJ, 2, e453 [Google Scholar]
- Vázquez-Semadeni, E., González-Samaniego, A., & Colín, P. 2017, MNRAS, 467, 1313 [NASA ADS] [Google Scholar]
- Vázquez-Semadeni, E., Palau, A., Ballesteros-Paredes, J., Gómez, G. C., & Zamora-Avilés, M. 2019, MNRAS, submitted [arXiv:1903.11247] [Google Scholar]
- Wang, P., Li, Z.-Y., Abel, T., & Nakamura, F. 2010, ApJ, 709, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, K., Zhang, Q., Wu, Y., & Zhang, H. 2011, ApJ, 735, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, K., Zhang, Q., Testi, L., et al. 2014, MNRAS, 439, 3275 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., & Kroupa, P. 2006, MNRAS, 365, 1333 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., Kroupa, P., & Pflamm-Altenburg, J. 2013, MNRAS, 434, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Wienen, M., Wyrowski, F., Schuller, F., et al. 2012, A&A, 544, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, J. P., Blitz, L., & McKee, C. F. 2000, Protostars and Planets IV (Tucson: University of Arizona Press), 97 [Google Scholar]
- Wood, D. O. S., & Churchwell, E. 1989, ApJ, 340, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, J., & Evans, II, N. J. 2003, ApJ, 592, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Ysard, N., Abergel, A., Ristorcelli, I., et al. 2013, A&A, 559, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Q., Wang, Y., Pillai, T., & Rathborne, J. 2009, ApJ, 696, 268 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: SABOCA maps
 |
Fig. A.1. SABOCA 350 μm and 24 μm emission from Spitzer/MIPS emission maps of target sources. Contour levels start at 5 × σ and show 5 uniformly spaced intervals on a logarithmic scale up to peak flux density of each field of 350 μm flux. The green crosses show the position of ATLASGAL sources. Coloured images show the 24 μm emission from Spitzer/MIPS on a logarithmic scale, contours are the same as in the top panel of the 350 μm emission red crosses mark the positions of the compact sources identified in the SABOCA maps. The target name from the ATLASGAL Gaussclumps catalog is given in each plot. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
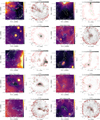 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
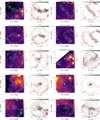 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
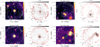 |
Fig. A.1. continued. |
Appendix B: 70 μm scaling factor and comparison between the 25″ and 10″ N(H2) and Td maps
The method we adopted for the 10″ resolution SED fit is based on the assumption that the SED at longer wavelengths of 160, 250, 350 and 870 μm fluxes represent the cold component of gas which dominate the bulk of mass (envelope of cores) at the scale we are probing. Thus the predicted 70 μm fluxes from this SED compared to the observed fluxes provide a correction factor to account for the hot gas component, which otherwise would bias the derived Td to a higher value and hence underestimate the gas column density.
In Fig. B.1 we present 25″ and 10″ resolution column density and dust temperature maps for two fields for sources G10.8278−0.0184 (left panel) and G12.7914−0.1958 (right panel). In the column density and dust temperature maps, the identified SABOCA cores are marked and labeled with a number. The corresponding SED curves for the pixels of these core positions are shown in Fig. B.2. We denote the difference between the derived column density and temperature, N(H2) and Td from the unscaled 70 μm flux and that from the scaled 70 μm as ΔN(H2) and ΔTd. In Fig. B.3 we present the 2D histogram of the pixels in the 10″ derived maps of G10.8278−0.0184, in terms of their 70 μm scaling factor, f with ΔN(H2)/N(H2) and ΔTd/Td, with the color scale indicating the pixel fractions. The anticorrelation between the scaling factor and ΔTd/Td reflects the increase in the dust temperature of these relatively cold sources (< 20 K), that is, core 2 in source G10.8278−0.0184 (left panel of Fig. B.1) is correlated with the increase of the 70 μm flux fraction from the bulk gas component, representing a gradual warm-up process of the envelope. The values of ΔTd/Td are within 30%, depending on the absolute value of the rescaling factor f. ΔN(H2)/N(H2) has a tighter relation to the rescaling factor f; it is almost a linear relation of ΔN(H2)/N(H2) = 0.5f − 0.45.
 |
Fig. B.1. 25″ and 10″ column density and dust temperature maps for source G10.8278−0.0184 and G12.7914−0.1958. The corresponding SED curves for the positions marked by red crosses with number labels are given in the subplots of Fig. B.2 with the same number labels in red. |
 |
Fig. B.2. Example SED curves for pixels in Fig. B.1. The gray dashed line represents the four-band fitted SED curve for the 25″ resolution maps and the black dashed line represents the two-band fitted SED curve for the 10″ resolution maps after rescaling the 70 μm fluxes. Red and magenta crosses mark the fluxes from smoothed 10″ and 25″ PACS 70 μm maps, respectively. Red circles represent the 25″ fluxes for the four-band fits, and black circles show the extrapolated 25″ 70 μm flux from the four-band fits. Right panel: the additional red dashed line in each subplot represents the two-band fitted SED curve for the 10″ resolution maps from unscaled 70 μm fluxes. |
 |
Fig. B.3. Two-dimensional distribution of the 70 μm flux scaling factors with derived Td, N(H2) and ΔN(H2)/N(H2), ΔTd/Td for pixels in 10″ derived maps of source G10.8278−0.0184. |
Scaling down the 70 μm flux according to the extrapolated 70 μm flux of the cold component is not equivalent to fixing the temperature to the coarser resolution temperature map. The left panel of Fig. B.1 shows that the enhanced temperatures of higher than ∼25 K, that is, for cores 1 and 3, and their adjacent region, are better resolved in the 10″ temperature map. In addition, we can now compare the derived fragment mass to the clump mass on a common basis to avoid an overestimate of the temperature due to the inclusion of 70 μm map in the higher resolution fits.
We also show cases in which the scaling factors are larger than 1, that is, cores 2, 7, and 9 in source G12.7914−0.1958 (right panel of Fig. B.1). This is due to external heating by the nearby mid-infrared bright object, therefore there is a mixture of hot and cold dust with the hot component along the line of sight that is not well shielded because the density of its cold component is relatively low. In this case, the four-band fits probe a temperature close to the hot dust and a column density close to the cold component, thus giving a predicted 70 μm flux higher than the observations. These sources should be intrinsically hotter, for which the inclusion of 70 μm flux into the SED would better constrain the Td and N(H2). For these sources, we therefore directly used the unscaled PACS 70 μm fluxes in the high-resolution fit.
Appendix C: Fragmentation analysis: a comparison with dendrogram results
We used Gaussclumps to identify the compact sources in the SABOCA emission maps. Gaussclumps is a non-hierarchical source extraction method, which assumes that cloud structures are composed of multiple Gaussian sources that can overlap. In contrast, another widely used source extraction method, dendrogram, is a hierarchical source identification method, which is discreet in the sense that a given emission area (or pixel) can only belong to a single structure, no overlap is allowed among the structures (of the same level). We explore here the dendrogram representation of the cloud structure seen in the SABOCA maps, and compare these results with Gaussclumps.
There are several parameters to control the dendrogram source extraction, min_value, min_delta, and min_npix, representing the minimum threshold, the minimum significance of a structure compared to its merging level, and the minimum size of a structure. Similarly as we did with Gaussclump, we set the min_value to three times the rms of the SABOCA map, and min_npix as the number of pixels corresponding to the beam size. For min_delta, we set this to zero, as an attempt to pick up the maximum number of sources as well as to be consistent with Gaussclump, which does not have a similar control parameter.
We ran dendrogram on the SABOCA emission maps and applied the extracted structures to the 10″ column density maps in order to derive the physical properties of these structures. We defined the size scale of the structures extracted by dendrogram as the geometrical mean of the area. We similarly assumed that this size scale is representative for the scale of the line-of-sight dimension, and estimated the average gas density (ρclump). For the analysis, we only included structures that have closed contours within the map. We find that the relatively small field of view of the SABOCA maps provides an incomplete view of the structures at the lowest contours, especially for those showing a filamentary structure. A closed contour for the first structure therefore is a condition that strongly limits our statistics.
With dendrogram, we defined the fragmentation level as the number of leaves residing within the lowest parental structure (branch or trunk) in the map. Isolated leaves without any parental structures were omitted. For example, in Fig. C.1, source G19.8835−0.5363 appears to be an isolated structure, while source G334.2000−0.2000 has three leaves (one blue leaf and two red leaves) residing in the lowest branch (outer green contour), which gives one statistic. In general, compared to Gaussclump, dendrogram picks up in addition numerous structures with irregular morphology, that is, the magenta leaves at the edge of G333.7700−0.2500; there are fewer leaves than compact sources identified by Gaussclump, and the average size appears larger. The differences are intrinsically linked with their different ways of defining structures. Although a systematic comparison between these two methods is beyond the scope of this paper, here we benchmark the analysis in Sect. 5.3 to determine whether the choice of source extraction method causes systematic differences in the results.
 |
Fig. C.1. Dendrogram source extraction results of four sources. Left: dendrogram identified multi-level structures overlaid on the SABOCA emission map. Leaves originating from the same top branch structures are marked with the same color (in red, blue, cyan, or magenta) as contour lines. Leaves with brown color are isolated leaf structures, i.e., with no parental structure in the emission map. Orange ellipses are the corresponding schematic ellipse calculated based on the intensity weight. Branches that do not intersect with the map edge, i.e., with closed contours as defined in the text, are marked with lime contour lines. Right: dendrogram tree plot representation of the left panel. Similarly, leaves from same top branch are marked with same color as in the left panel. The horizontal dotted line indicates the 3σ threshold we used for the minimum level as input parameter of the dendrogram identification. |
In Fig. C.2 the fragmentation level is compared with the clump properties, similarly as in Fig. 14. We again find a correlation between the fragmentation level with the parental clump mass, with a Spearman correlation coefficient of 0.42 (p-value < 0.001), although we have smaller statistics here. We again define the specific fragmentation level as the number of fragments normalized by clump size, as Nmm/Rclump. There is no correlation between a specific fragmentation level with clump L/M ratio, with a Spearman correlation coefficient of 0.018. Finally, comparing the fragmentation level with the Jeans fragmentation prediction, we find a Spearman correlation coefficient of 0.30 of a specific fragmentation level with clump gas density (p-value ∼ 0.05). For the comparison of the fragmentation level with the number of Jeans mass predicted by clump dust temperature and gas density, a Spearman correlation coefficient of 0.48 is found (p-value ∼ 0.003). When we assume a fragmentation temperature of 20 K, the Spearman correlation coefficient is 0.44 (p-value < 0.001). These results are broadly consistent with Fig. 14 in Sect. 5.3. The relations of the mass of the most massive fragment with clump L/M and clump mass are also compatible with Fig. 15, despite the drastic difference in the contrast of surface densities between the most massive fragments and their parental clump, as shown in the right panels of Figs. 15 and C.3. We coded the data points in the right panel of Fig. C.3 according to the size difference between the most massive fragment and its parental clump. It is obvious that the large scatter of the two surface density values is related to the relative size difference that defines the parent and child structures, which together again lead to the tight correlation between the mass of the most massive fragment and the parental clump mass. We therefore conclude that the source extraction method and the way we define the fragmentation level by allocating sources in a non-hierarchical way do not affect the analysis results within the scope of this work.
 |
Fig. C.2. Fragmentation level as a function of clump properties of sources located at a distance of 2−4 kpc (dots) and 1−2 kpc (triangles). In each plot, data points are color-coded according to the clump size. Dashed contours show the distribution of sources at 2−4 kpc from a Gaussian kernel density estimation. Left: number of fragments as a function of clump mass. Middle left: specific fragmentation level (normalized by the size of the parent structure) as a function of the luminosity-to-mass ratio of the clump. Middle right: specific fragmentation level as a function of the clump density. Right: number of fragments as a function of the predicted number of fragments based on a Jeans fragmentation scenario. Gray dashed lines mark the lines of Nmm = 0.15/0.05/0.01 × Mclump/MJeans, clumpTd. |
 |
Fig. C.3. Left: mass of the most massive fragment as a function of clump properties for sources at a distance 2−4 kpc (dots) and 1−2 kpc (triangles). Left: mass of the most massive fragment as a function of the luminosity-to-mass ratio of the clump. Vertical lines mark the luminosity-to-mass ratios of 1 and 10. Middle: mass of the most massive fragment as a function of clump mass. Gray lines show the 30% and 100% proportion of the clump mass, and the blue line shows the result of a linear fit on a logarithmic scale to sources in a 2−4 kpc distance range of Mfragments = 0.87log Mclumps − 0.21. The left and middle plots share the same color bar. The clumps are color-coded according to their sizes. Right: surface density of the most massive fragment as a function of clump surface density. The gray line marks the line of equality, and the blue line shows the result of a linear fit to sources in a 2−4 kpc distance range of log Σfragments = 1.51log Σclumps + 1.13. The different sizes of the markers correspond to the size ratios between the size of the parental clump and the size of the most massive fragment, as indicated in the legend, that is, the smaller the size of a marker, the larger size difference between a fragment and its parental clump, up to a factor of 5. |
Appendix D: MALT90 spectrum toward the massive prestellar cores
 |
Fig. D.1. MALT90 spectra toward the > 100 M⊙ quiescent cores at < 5 kpc. The source names are shown in the title. HCO+/H13CO+ and SiO lines are plotted in the top and bottom panels, respectively. The VLSR is indicated with a vertical line in the HCO+/H13CO+ plot. The residual of the H13CO+ fit is shown in green, offset by −0.4 K. |
 |
Fig. D.1. continued. |
 |
Fig. D.1. continued. |
 |
Fig. D.1. continued. |
All Tables
Properties of SABOCA sources, their 24 μm and 70 μm associations, and parental clumps.
All Figures
 |
Fig. 1. Distribution of the integrated flux density and bolometric L/M of all ATLASGAL sources (in blue filled contours, the darker region corresponds to higher density) (Urquhart et al. 2018) and the target sources observed with SABOCA (gray pluses and dots) at different distance ranges. The histograms on the right side and in the top panel show the 1D distributions of integrated flux density and L/M of all ATLASGAL sources (blue) and all target sources (gray), respectively. |
| In the text | |
 |
Fig. 2. Distance distribution of the observed ATLASGAL clumps. The vertical dashed line indicates the 5 kpc distance. The filled green region indicates the 2−4 kpc range. |
| In the text | |
 |
Fig. 3. 350 μm peak flux density vs. the 1σ rms noise level observed with SABOCA toward all fields. The histogram on the right side and in the top panel shows the distribution of peak flux densities and the noise levels. |
| In the text | |
 |
Fig. 4. Top panels: examples of 350 μm emission toward ATLASGAL-selected massive clumps obtained with APEX/SABOCA. Contour levels start at 5σ and show five uniformly spaced intervals on a logarithmic scale up to the peak flux density in each field. The green crosses show the position of ATLASGAL sources. Bottom panels: colored images show the 24 μm emission from MIPSGAL on a logarithmic scale, contours are the same as in the top panel of the 350 μm emission. Red crosses mark the positions of the compact sources identified in the SABOCA maps. The target name from the ATLASGAL Gaussclumps catalog is given in each plot. |
| In the text | |
 |
Fig. 5. Top panels: dust temperature (Td) and H2 column density (NH2) maps obtained with a pixel-by-pixel SED fitting of PACS 160 μm, SPIRE 250, 350 μm, and combined LABOCA and Planck 870 μm data at 25″ resolution. Bottom panels: same as the top panels, but using the PACS 70 μm and the SABOCA and SPIRE 350 μm combined maps at 10″ resolution. The top and bottom panels are in same color scale for dust temperature and column density maps, respectively. The circles in the top panel indicate the region mapped by SABOCA. |
| In the text | |
 |
Fig. 6. Top panel: transmission of the Herschel/SPIRE and the APEX/SABOCA instruments. Bottom panel: color-correction factors for SABOCA (dashed line) and SPIRE (solid line) as a function of the spectral index of the source. The dash-dotted line shows the conversion factor to scale the SPIRE intensities to the nominal center wavelength of SABOCA. |
| In the text | |
 |
Fig. 7. Distribution of the physical properties of all the observed ATLASGAL clumps and compact sources identified at 350 μm with SABOCA. Top left: mass distribution of clumps and SABOCA compact sources. The vertical lines show mass limits of 40 M⊙ and 650 M⊙. Top right: distribution of sizes that are the measured FWHM size from the Gaussclumps source extraction. Vertical lines show the 0.1 and 0.5 pc range for the definition of cores and clumps. Bottom left: luminosity-to-mass ratio distribution of the clumps and SABOCA compact sources. The vertical dotted lines indicate luminosity-to-mass ratios of 1 and 10, which are taken as empirical evolutionary boundaries in Molinari et al. (2016) for massive clumps. Bottom right: temperature distribution with a vertical line showing 18 K, which is the average temperature for galactic background. |
| In the text | |
 |
Fig. 8. Left: distribution of angular distances between SABOCA sources and their MIR compact source or/and H II region associations. In each bin, the probability of dN/N is normalized by the annular area defined by adjacent angular bins as dN/(N × Area). Right: distribution of distances of star-forming and quiescent SABOCA compact sources. |
| In the text | |
 |
Fig. 9. Distribution of the physical properties of star-forming and quiescent SABOCA compact sources in the 2−4 kpc distance bin, in red and blue, respectively. Top left: temperature distribution of two categories. Top right: mass distribution. Bottom left: luminosity distribution. Bottom right: surface density distribution. In each plot, the cumulative probability distribution is drawn with respective colors according to the right y-axis. |
| In the text | |
 |
Fig. 10. Mass-radius diagram of SABOCA compact sources. The quiescent cores and star-forming cores are indicated with blue and red in 2−4 kpc (hollow markers) and 1−2 kpc (filled markers) distance bins. The dashed lines show the constant volume density of 104, 105, and 106 cm−3. The magenta dotted line indicates Larson’s third relation of approximately 1021 cm−2 column density. The gray filled region is below the empirical threshold of massive star formation from Kauffmann & Pillai (2010), which is scaled to match the dust opacity values we used in this work. Red and blue lines indicate the fitted linear regression for the quiescent and star-forming cores at 2−4 kpc. |
| In the text | |
 |
Fig. 11. Luminosity-mass diagram of SABOCA compact sources. The quiescent and star-forming cores are indicated with blue and red in 2−4 kpc (hollow markers) and 1−2 kpc (filled markers) distance bins. The empirical evolutionary tracks for massive clumps with envelope masses of 80, 140, 350, 700, and 2000 M⊙ in Molinari et al. (2008) are shown with gray dots. André et al. (2008) tracks for final stellar masses of 1, 3, 8, 15, and 50 M⊙ are shown as magenta dashed lines. Red and blue lines indicate the fitted linear regression for the quiescent and star-forming cores at 2−4 kpc. |
| In the text | |
 |
Fig. 12. Fragment mass distribution of all SABOCA sources. The fitted power-law index of the all the sources at < 5 kpc above our mass completeness (> 41.4 M⊙) is indicated by the green vertical line. |
| In the text | |
 |
Fig. 13. Example of the fragment allocation criterion toward an example SABOCA mapping field. Left panel: 870 μm LABOCA emission in gray scale, overlaid with ATLASGAL clumps as green dashed ellipses. Middle panel: 350 μm SABOCA emission in gray scale with contour levels from 3σ to the peak flux with 5 linear logarithmic spacing. Each SABOCA core is labeled with a number and is refered to as number x. Green dashed ellipses mark the ATLASGAL clumps as identified in Csengeri et al. (2014). Blue, magenta, and cyan ellipses mark the position of three sets of fragments belonging to several ATLASGAL clumps. Right panel: (slightly zoomed in compared to the middle panel), the overlapping possibilities of each fragment with the ATLASGAL clumps are indicated with arrows. |
| In the text | |
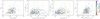 |
Fig. 14. Fragmentation level as a function of clump properties of sources located at a distance at 2−4 kpc. In each plot, data points are color-coded according to the clump size. Gray triangles show the exact fragment number exactNmm; colored dots show the rounding fragment number roundingNmm (see definitions in Sect. 5.3). Dashed contours show the distribution of exactNmm from a Gaussian kernel density estimation. Left: number of fragments as a function of clump mass. Middle left: specific fragment level (Nmm normalized by clump radius) as a function of the clump luminosity-to-mass ratio. Middle right: specific fragment level as a function of the clump density. Right: number of fragments as a function of predicted number of fragments based on a Jeans fragmentation scenario. Gray dashed lines mark the lines of Nmm = 0.15/0.05/0.01 × Mclump/MJeans, clumpTd. |
| In the text | |
 |
Fig. 15. Most massive fragment mass as a function of clump properties for sources at a distance of 2−4 kpc (dots) and 1−2 kpc (triangles). Left: mass of the most massive fragment as a function of clump luminosity-to-mass ratio. Vertical lines mark the luminosity-to-mass ratio of 1 and 10. Middle: mass of the most massive fragment mass as a function of clump mass. Gray lines show the 30% and 100% proportion of clump mass; the blue dashed line shows the result of a linear fit on logarithmic scale to sources in the 2−4 kpc distance range of Mfragments = 0.96log Mclumps − 1.18. The relation between cluster mass and maximum stellar mass is indicated by the red dash-dotted line, which is an analytical relation from Weidner et al. (2013), and is scaled up by 3.3 assuming a 30% star-formation efficiency. The eft and middle plots share the same color bar. The clumps are color-coded according to their sizes. Right: surface density of the most massive fragment as a function of clump surface density. Vertical line marks the 0.2 g cm−2 empirical limit from Butler & Tan (2012). The blue dashed line shows the result of a linear fit to sources in the 2−4 kpc distance range of log Σfragments = 1.03log Σclumps + 0.43. |
| In the text | |
 |
Fig. 16. Example of a clump hosting massive quiescent cores. White crosses mark the > 100 M⊙ quiescent cores and the blue cross marks the star-forming cores. The masses for quiescent cores are indicated in the figure. Contour levels are from 7σ to the peak flux with six logarithmic linear levels in between. |
| In the text | |
 |
Fig. A.1. SABOCA 350 μm and 24 μm emission from Spitzer/MIPS emission maps of target sources. Contour levels start at 5 × σ and show 5 uniformly spaced intervals on a logarithmic scale up to peak flux density of each field of 350 μm flux. The green crosses show the position of ATLASGAL sources. Coloured images show the 24 μm emission from Spitzer/MIPS on a logarithmic scale, contours are the same as in the top panel of the 350 μm emission red crosses mark the positions of the compact sources identified in the SABOCA maps. The target name from the ATLASGAL Gaussclumps catalog is given in each plot. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. B.1. 25″ and 10″ column density and dust temperature maps for source G10.8278−0.0184 and G12.7914−0.1958. The corresponding SED curves for the positions marked by red crosses with number labels are given in the subplots of Fig. B.2 with the same number labels in red. |
| In the text | |
 |
Fig. B.2. Example SED curves for pixels in Fig. B.1. The gray dashed line represents the four-band fitted SED curve for the 25″ resolution maps and the black dashed line represents the two-band fitted SED curve for the 10″ resolution maps after rescaling the 70 μm fluxes. Red and magenta crosses mark the fluxes from smoothed 10″ and 25″ PACS 70 μm maps, respectively. Red circles represent the 25″ fluxes for the four-band fits, and black circles show the extrapolated 25″ 70 μm flux from the four-band fits. Right panel: the additional red dashed line in each subplot represents the two-band fitted SED curve for the 10″ resolution maps from unscaled 70 μm fluxes. |
| In the text | |
 |
Fig. B.3. Two-dimensional distribution of the 70 μm flux scaling factors with derived Td, N(H2) and ΔN(H2)/N(H2), ΔTd/Td for pixels in 10″ derived maps of source G10.8278−0.0184. |
| In the text | |
 |
Fig. C.1. Dendrogram source extraction results of four sources. Left: dendrogram identified multi-level structures overlaid on the SABOCA emission map. Leaves originating from the same top branch structures are marked with the same color (in red, blue, cyan, or magenta) as contour lines. Leaves with brown color are isolated leaf structures, i.e., with no parental structure in the emission map. Orange ellipses are the corresponding schematic ellipse calculated based on the intensity weight. Branches that do not intersect with the map edge, i.e., with closed contours as defined in the text, are marked with lime contour lines. Right: dendrogram tree plot representation of the left panel. Similarly, leaves from same top branch are marked with same color as in the left panel. The horizontal dotted line indicates the 3σ threshold we used for the minimum level as input parameter of the dendrogram identification. |
| In the text | |
 |
Fig. C.2. Fragmentation level as a function of clump properties of sources located at a distance of 2−4 kpc (dots) and 1−2 kpc (triangles). In each plot, data points are color-coded according to the clump size. Dashed contours show the distribution of sources at 2−4 kpc from a Gaussian kernel density estimation. Left: number of fragments as a function of clump mass. Middle left: specific fragmentation level (normalized by the size of the parent structure) as a function of the luminosity-to-mass ratio of the clump. Middle right: specific fragmentation level as a function of the clump density. Right: number of fragments as a function of the predicted number of fragments based on a Jeans fragmentation scenario. Gray dashed lines mark the lines of Nmm = 0.15/0.05/0.01 × Mclump/MJeans, clumpTd. |
| In the text | |
 |
Fig. C.3. Left: mass of the most massive fragment as a function of clump properties for sources at a distance 2−4 kpc (dots) and 1−2 kpc (triangles). Left: mass of the most massive fragment as a function of the luminosity-to-mass ratio of the clump. Vertical lines mark the luminosity-to-mass ratios of 1 and 10. Middle: mass of the most massive fragment as a function of clump mass. Gray lines show the 30% and 100% proportion of the clump mass, and the blue line shows the result of a linear fit on a logarithmic scale to sources in a 2−4 kpc distance range of Mfragments = 0.87log Mclumps − 0.21. The left and middle plots share the same color bar. The clumps are color-coded according to their sizes. Right: surface density of the most massive fragment as a function of clump surface density. The gray line marks the line of equality, and the blue line shows the result of a linear fit to sources in a 2−4 kpc distance range of log Σfragments = 1.51log Σclumps + 1.13. The different sizes of the markers correspond to the size ratios between the size of the parental clump and the size of the most massive fragment, as indicated in the legend, that is, the smaller the size of a marker, the larger size difference between a fragment and its parental clump, up to a factor of 5. |
| In the text | |
 |
Fig. D.1. MALT90 spectra toward the > 100 M⊙ quiescent cores at < 5 kpc. The source names are shown in the title. HCO+/H13CO+ and SiO lines are plotted in the top and bottom panels, respectively. The VLSR is indicated with a vertical line in the HCO+/H13CO+ plot. The residual of the H13CO+ fit is shown in green, offset by −0.4 K. |
| In the text | |
 |
Fig. D.1. continued. |
| In the text | |
 |
Fig. D.1. continued. |
| In the text | |
 |
Fig. D.1. continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.