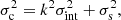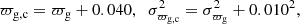| Issue |
A&A
Volume 630, October 2019
|
|
|---|---|---|
| Article Number | A119 | |
| Number of page(s) | 18 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201935885 | |
| Published online | 02 October 2019 | |
Gaia DR2 distances to Collinder 419 and NGC 2264 and new astrometric orbits for HD 193 322 Aa,Ab and 15 Mon Aa,Ab⋆
Centro de Astrobiología, CSIC-INTA, Campus ESAC. C. Bajo del Castillo s/n, 28 692 Villanueva de la Cañada, Madrid, Spain
e-mail: jmaiz@cab.inta-csic.es
Received:
14
May
2019
Accepted:
8
August
2019
Context. On the one hand, the second data release of the Gaia mission (Gaia DR2) has opened a trove of astrometric and photometric data for Galactic clusters within a few kiloparsecs of the Sun. On the other hand, lucky imaging has been an operational technique to measure the relative positions of visual binary systems for a decade and a half. This time is sufficient to apply the results of the technique to the calculation of orbits of some massive multiple systems within ∼1 kpc of the Sun.
Aims. As part of an ambitious research program to measure distances to Galactic stellar groups (including clusters) containing O stars, I start with two of the nearest examples: Collinder 419 in Cygnus and NGC 2264 in Monoceros. The main ionizing source for each cluster is a multiple system with an O-type primary: HD 193 322 and 15 Mon, respectively. For each of the two multiple systems, I aim to derive new astrometric orbits for the Aa,Ab components.
Methods. First, I present a method that uses Gaia DR2 G + GBP + GRP photometry, positions, proper motions, and parallaxes to obtain the membership and distance of a stellar group and applied these values to Collinder 419 and NGC 2264. Second, I present a new code that calculates astrometric orbits by searching the whole seven-parameter orbit space and apply it to HD 193 322 Aa,Ab and 15 Mon Aa,Ab using, as input, literature data from the Washington Double Star Catalog and the AstraLux measurements recently presented by our group in another paper published this year.
Results. I obtain Gaia DR2 distances of 1006+37−34 pc for Collinder 419 and 719 ± 16 pc for NGC 2264; the main contribution to the uncertainties comes from the spatial covariance of the parallaxes. The two NGC 2264 subclusters are at the same distance (within the uncertainties) and show a significant relative proper motion. The distances are shown to be robust. HD 193 322 Aa,Ab follows an eccentric (e = 0.58+0.03−0.04) orbit with a period of 44 ± 1 a and the three stars it contains have a total mass of 76.1+9.9−7.4M⊙. The orbit of 15 Mon Aa,Ab is even more eccentric (e = 0.770+0.023−0.030); it has a period of 108 ± 12 a and a total mass of 45.1+3.6−3.3M⊙ for its two stars.
Key words: astrometry / binaries: visual / methods: data analysis / open clusters: individual: Collinder 419 / open clusters and associations: individual: NGC 2264 / stars: kinematics and dynamics
Full Tables A.1 and A.2 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/630/A119
© ESO 2019
1. Introduction
The second data release (DR2) of the Gaia mission (Prusti et al. 2016) took place in April 2018 (Brown et al. 2018). Gaia DR2 includes optical photometry for over 1.3 × 109 sources in the three bands G, GBP, and GRP and five-parameter astrometry (positions, parallaxes, and proper motions) for a similar number of sources. Gaia DR2 constitutes the largest ever collection of such precise photometry and astrometry. The data are not only precise but also accurate, as several studies have confirmed with respect to the astrometry and photometry (e.g., Arenou et al. 2018; Evans et al. 2018; Lindegren et al. 2018a; Luri et al. 2018; Maíz Apellániz & Weiler 2018; note that this list is incomplete as Gaia DR2 calibration is an ongoing effort). Nevertheless, to achieve the highest accuracy it is important to read the “fine print” of the papers above because there are biases and quality issues lurking in the data. The Gaia team maintains a “known issues” web page1 that should be consulted before using the data (details are given in the next section).
Gaia represents a giant leap for astrometry but, of course, it has limitations. One such limitation is its inability to separate close binaries because few pairs with separations of ∼1″ are listed in DR2, and that is one way in which complementary ground-based observations can fill the information gaps. One technique that can accurately measure the relative positions of visual pairs from ∼50 mas to a few arcseconds is lucky imaging and an instrument that uses that technique is AstraLux at the 2.2 m Calar Alto telescope (Hormuth et al. 2008). I have been using AstraLux for over a decade (Maíz Apellániz 2010) and we have recently presented new results for a number of massive-star pairs (Maíz Apellániz et al. 2019), which are used in this work to derive the relative orbit of two visual binaries.
Collinder 419 is a relatively poorly studied, nearby (for a cluster containing at least one O star) open cluster in Cygnus whose most complete study was performed by Roberts et al. (2010). These authors derived a distance of 741 ± 36 pc based on a color-magnitude diagram (CMD) analysis that is compatible with the HIPPARCOS distance of 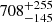 pc for HD 193 322 Aa,Ab (Maíz Apellániz et al. 2008; Sota et al. 2011), which is the brightest object at the cluster core2. Collinder 419 is dominated by HD 193 322; the composition of this complex hierarchical system has recently been reviewed in detail by Maíz Apellániz et al. (2019). In the current work, I only mention that it has an inner binary Ab1,Ab2 with a 312.4 d period (McKibben et al. 1998; ten Brummelaar et al. 2011) that orbits around a third object, Aa, which is the brightest component of the system (Table 1). At a much larger separation (
pc for HD 193 322 Aa,Ab (Maíz Apellániz et al. 2008; Sota et al. 2011), which is the brightest object at the cluster core2. Collinder 419 is dominated by HD 193 322; the composition of this complex hierarchical system has recently been reviewed in detail by Maíz Apellániz et al. (2019). In the current work, I only mention that it has an inner binary Ab1,Ab2 with a 312.4 d period (McKibben et al. 1998; ten Brummelaar et al. 2011) that orbits around a third object, Aa, which is the brightest component of the system (Table 1). At a much larger separation (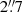 ) I find a fourth component, B. ten Brummelaar et al. (2011) used long-baseline interferometry to derive an eccentric visual orbit for HD 193 322 Aa,Ab (Table 1). HD 193 322 Aa,Ab includes at least two O stars, its integrated spectral type is O9 IV(n), and it clearly dominates the ionizing flux of Collinder 419, as the only other early B-type star in the cluster is HD 193 322 B, which is a B1.5 V(n)p (Sota et al. 2011; ten Brummelaar et al. 2011; Maíz Apellániz et al. 2019).
) I find a fourth component, B. ten Brummelaar et al. (2011) used long-baseline interferometry to derive an eccentric visual orbit for HD 193 322 Aa,Ab (Table 1). HD 193 322 Aa,Ab includes at least two O stars, its integrated spectral type is O9 IV(n), and it clearly dominates the ionizing flux of Collinder 419, as the only other early B-type star in the cluster is HD 193 322 B, which is a B1.5 V(n)p (Sota et al. 2011; ten Brummelaar et al. 2011; Maíz Apellániz et al. 2019).
Literature visual orbits for HD 193 322 Aa,Ab and 15 Mon Aa,Ab.
In contrast, NGC 2264 is a well-studied nearby open cluster in Monoceros that is a frequent target for amateur astronomers, as it is a bright H II region that contains the Cone Nebula, a well-known pillar, and a reflection nebula. Dahm (2008) provided an excellent summary of the literature on the cluster and gave a preferred (short) distance of ∼760 pc, which is consistent with the value later derived using two water masers of 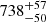 pc (Kamezaki et al. 2014). Other authors, however, have derived longer distances: 950 ± 75 pc (Pérez et al. 1987), 910 ± 50 pc (Neri et al. 1993), and 913 ± 40 pc (Baxter et al. 2009). The HIPPARCOS distance to 15 Mon Aa,Ab, the brightest object in the cluster, is
pc (Kamezaki et al. 2014). Other authors, however, have derived longer distances: 950 ± 75 pc (Pérez et al. 1987), 910 ± 50 pc (Neri et al. 1993), and 913 ± 40 pc (Baxter et al. 2009). The HIPPARCOS distance to 15 Mon Aa,Ab, the brightest object in the cluster, is 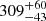 pc (Maíz Apellániz et al. 2008), which is highly discrepant with the other distance measurements; but it should be noted that van Leeuwen (2007) assigned a poor goodness-of-fit value to the HIPPARCOS measurement. Several authors (Caballero & Dinis 2008; Turner 2012; Tobin et al. 2015; González & Alfaro 2017; Venuti et al. 2018) have studied the spatial and dynamical structure of NGC 2264 and determined it is very complex and organized as a double cluster, with the northern, older half centered on 15 Mon and the southern younger half centered on the Cone Nebula. Similar to HD 193 322 and Collinder 419, 15 Mon dominates the ionizing radiation output of NGC 2264 because it contains the only O star(s) in the cluster. 15 Mon Aa,Ab is a close visual binary with an integrated spectral type of O7 V(f)z var and 15 Mon B is a B2: Vn located 3″ away (Maíz Apellániz et al. 2018, 2019). The magnitude difference between Aa and Ab is 1.6 mag, which indicates that Ab is likely to be a late-O or early-B star, but there is no spatially separated spectroscopy to confirm that. Several authors (Gies et al. 1993, 1997; Cvetković et al. 2009, 2010; Tokovinin 2018) have calculated visual orbits that agree on a high eccentricity (0.67 to 0.85) and a periastron passage close to 1996 but wildly disagree on the period, whose values range from 23.6 a to 190.5 a, and other parameters (Table 1).
pc (Maíz Apellániz et al. 2008), which is highly discrepant with the other distance measurements; but it should be noted that van Leeuwen (2007) assigned a poor goodness-of-fit value to the HIPPARCOS measurement. Several authors (Caballero & Dinis 2008; Turner 2012; Tobin et al. 2015; González & Alfaro 2017; Venuti et al. 2018) have studied the spatial and dynamical structure of NGC 2264 and determined it is very complex and organized as a double cluster, with the northern, older half centered on 15 Mon and the southern younger half centered on the Cone Nebula. Similar to HD 193 322 and Collinder 419, 15 Mon dominates the ionizing radiation output of NGC 2264 because it contains the only O star(s) in the cluster. 15 Mon Aa,Ab is a close visual binary with an integrated spectral type of O7 V(f)z var and 15 Mon B is a B2: Vn located 3″ away (Maíz Apellániz et al. 2018, 2019). The magnitude difference between Aa and Ab is 1.6 mag, which indicates that Ab is likely to be a late-O or early-B star, but there is no spatially separated spectroscopy to confirm that. Several authors (Gies et al. 1993, 1997; Cvetković et al. 2009, 2010; Tokovinin 2018) have calculated visual orbits that agree on a high eccentricity (0.67 to 0.85) and a periastron passage close to 1996 but wildly disagree on the period, whose values range from 23.6 a to 190.5 a, and other parameters (Table 1).
In this paper I present new Gaia DR2 distances to Collinder 419 and NGC 2264 and new literature+AstraLux-based visual orbits for HD 193 322 Aa,Ab and 15 Mon Aa,Ab. I pay special attention to the methods used for the calculation of cluster distances and visual orbits, as they will be used in future papers for other targets.
2. Methods and data
2.1. Distances to and membership of stellar groups
There are different properties that can be used to determine the membership and distance of a stellar group (cluster, association, or part thereof): positions, CMDs, trigonometric parallaxes, proper motions, and spectroscopy of individual sources are the most commonly used. In many cases, two or three of these properties are combined. The specific technique chosen depends primarily on the data quality and uniformity, sample completeness, and whether our main interest is determining the initial mass function, structural properties (radius, velocity dispersion), or distance. In a more indirect way, the choice of technique also depends on the number of groups we want to study: for just one group or a few it is possible to do a “manual” (or supervised) in-depth analysis of each star, but if our sample consists of hundreds of objects we will likely attempt a more “automatic” (or unsupervised) technique that does not require such an attention to detail.
A combination of characteristics makes Gaia DR2 an excellent source of information for the task at hand (Brown et al. 2018): (i) It provides a large sample of high-quality, uniform (a) positions, (b) parallaxes, (c) proper motions, and (d) three-band optical photometry in a single catalog derived from a single mission. Future data releases will also provide spectroscopy, spectrophotometry, and information on variability (which exists in DR2 for a limited sample) for a significant fraction of the sample. This minimizes problems derived from catalog cross-matching. (ii) The sky coverage is complete and very uniform. (iii) The magnitude completeness is very good down to G = 20 and there are few stars missing owing to saturation. (iv) The data are well calibrated and different quality indicators are provided.
Nevertheless, this might be more complicated than it appears (the devil is in the details) and it is important to understand the calibration process and corrections needed if biases are to be avoided. In particular: (i) There is a zero point in the parallax3 that several authors have measured to be in the approximate range 30−50 μas. The value is dependent (to different degrees) on magnitude, color, and position, and the zero point for fainter objects is generally lower (Lindegren et al. 2018a give 29 μas for quasars) than for brighter objects, for which it is around 50 μas (Khan et al. 2019 and references therein). (ii) Parallaxes and proper motions are spatially correlated (Lindegren et al. 2018a) so to combine the values from different objects in a stellar group the covariance has to be taken into account. (iii) Some sources have a poor astrometric solution, requiring them to be eliminated (or at least down weighted) from the list used to determine the stellar group properties. The Gaia team recommends the use of the renormalized unit weight error (RUWE) to evaluate the astrometric quality of the Gaia DR2 sources (Lindegren et al. 2018b; Lindegren 2018). (iv) The astrometric uncertainties listed in Gaia DR2 are the internal uncertainties (σint). Before using these uncertainties they have to be converted into external or corrected uncertainties (σc) using the Lindegren et al. (2018b) recipe
where k = 1.08 in all cases and σs is 0.021 mas for G < 13 and 0.043 mas for G ≥ 13 in the case of parallaxes and 0.032 mas a−1 for G < 13 and 0.066 mas a−1 for G ≥ 13 in the case of proper motions. (v) To properly compare the observed magnitudes and colors the updated sensitivity curves of Maíz Apellániz & Weiler (2018) must be used; I note that GBP has different sensitivities for G (as obtained from the Gaia archive) larger or smaller than 10.87 mag. (vi) The G magnitudes obtained from the archive require a correction and the resulting G′ should be used. The Gaia team recommends using the correction from Evans et al. (2018) for stars with G ≤ 6 and that from Maíz Apellániz & Weiler (2018) for fainter stars. (vii) While the G magnitudes are calculated by point spread function (PSF) fitting in an imaging detector configuration, the GBP and GRP magnitudes are calculated by aperture photometry in a slitless-spectroscopy configuration; as previously mentioned, future Gaia data releases will provide spectrophotometry instead of photometry in those bands. Therefore, the GBP and GRP magnitudes can be more easily affected by contamination from nearby sources in crowded regions and by emission lines in nebular regions (Fig. 17 in Evans et al. 2018). In order to flag sources with suspect photometry we define the distance (in magnitudes) in the GBP − G′ versus G′−GRP color plane, dCC, with respect to the stellar locus in Fig. 10 of Maíz Apellániz & Weiler (2018). Objects with large values of dCC (above and to the left in that figure) are likely contaminated. We note that this restriction is nearly equivalent to Eq. (1) of Evans et al. (2018).
The most extensive study of the open cluster population in the Milky Way with Gaia DR2 data to date is that of Cantat-Gaudin et al. (2018). Those authors used a version of the unsupervised UPMASK code (Krone-Martins & Moitinho 2014), which selects groups of stars in the three-dimensional astrometric space of parallaxes and proper motions through k-means clustering to study 1229 clusters. Their list included both Collinder 419 and NGC 2264. Some of the properties, such as central right ascension and declination α + δ, radius that contains 50% of the members r50, probable number of stars N*, central proper motions μα* + μδ, and parallax ϖ, they measured for these two clusters are listed in Table 2, as we use these properties as a reference. The uncertainties listed are the standard deviations of the mean and do not include the effect of covariance.
Properties of Collinder 419 and NGC 2264 from Cantat-Gaudin et al. (2018).
In this section I describe a supervised method to derive distances and membership to stellar groups using Gaia DR2 data. The idea for the method originated during the calculation of the distance to M8 for Campillay et al. (2019). The main differences between the method described in this work and the Cantat-Gaudin et al. (2018) method are that the supervised method: (a) allows the user to fine-tune the membership selection parameters; (b) combines astrometric, photometric, and data quality information (as opposed to astrometric information alone); and (c) is designed to derive distances, which leads to using parallaxes only as a secondary selection parameter in the last step (to minimize biases in the distance measurement). In forthcoming sections I apply the method to calculate the distances to Collinder 419 and NGC 2264 and in future papers this method will be used for other stellar groups with massive stars. The method follows these steps:
– I spectroscopically select one or several stars that are the most massive and luminous in the stellar group. Those are typically O stars with spectral types from the Galactic O-Star Spectroscopic Survey (GOSSS; Maíz Apellániz et al. 2011), but they can also be B stars or late supergiants. Those objects are considered to be as representative of the group in terms of coordinates, proper motions, parallaxes, and extinction and are used as initial guesses for the filters described below.
– I calculate an extinguished isochrone for a GBP − GRP vs. G′ CMD, using the family of extinction laws of Maíz Apellániz et al. (2014), based on the GOSSS spectral type for a reference O star in the group, its extinction parameters from Maíz Apellániz & Barbá (2018), and an isochrone of the appropriate age (1 Ma or 3.2 Ma are the usual choices for a group with O stars). The extinction parameters are used to force the isochrone to go through the observed position of the reference star in the CMD by a vertical displacement.
– I download the Gaia DR2 data for a square (in α + δ) field with a number of objects Nf. I do an initial filtering using three quality indicators: RUWE, dCC, and σϖc. The upper limits on RUWE and dCC (see definitions above) are used to eliminate stars with bad astrometry and contaminated photometry, respectively, and are set by default at 1.4 and 0.2 mag, respectively. The upper limit on σϖc is only used for some groups to filter out background dim objects, which tend to have large parallax uncertainties.
– I define a group center both in coordinates (α + δ) and in proper motion (μα* + μδ) and their respective radii (r and rμ) and filter out the objects outside the circles in coordinates and proper motion. This filtering is similar to that applied by other algorithms such as that used by Cantat-Gaudin et al. (2018).
– I carry out the next filtering based on the positions in the GBP − GRP versus G′ CMD using the extinguished isochrone previously described. As extinction can change significantly across the face of a stellar group (Maíz Apellániz & Barbá 2018), the isochrone is moved diagonally (from top left to bottom right) in the direction defined by the extinction vector4 to define a band of possible extinctions. Objects outside that band are rejected. This filtering is useful to eliminate foreground or background populations with extinctions different than those of the stellar group.
– I should already have, at this point, a relatively clean but still preliminary sample with N*, 0 objects with some possible outliers in parallax. To get rid of those, I compute a preliminary group average parallax, ϖg, 0, as the weighted mean of the parallaxes in the sample (Eqs. (3) and (4) in Campillay et al. 2019); I filter out the objects whose parallaxes ϖ are more than 3σϖc away from ϖg, 0 (normalized parallax criterion), where we are using the external parallax uncertainties defined above. The value of 3σϖc was chosen from the typical sample size of ∼100 cluster members to minimize the sum of false negatives and false positives, but the final result is not very sensitive to change, for instance, in the range 2.5σϖc–3.5σϖc. With that final filtering I compute the weighted mean again to arrive to the group average parallax, ϖg, using N* objects. With the same sample I obtain the group average proper motions μα * ,g and μδ, g. In all three cases the covariance term is required to properly estimate the uncertainties.
– I examine the results using several plots combining coordinates, proper motions, colors, magnitudes, and parallaxes and the process is iterated until a final result is achieved. To minimize subjectivity in the final result (something inherent to a degree in a supervised algorithm), small variations are introduced in the restrictions to ensure that the value of ϖg is robust (i.e., that the resulting changes are smaller than one sigma).
Once I have the final sample and its ϖg, I calculate σϖg using Eq. (5) in Campillay et al. (2019). In most cases, the second (covariance) term dominates the error budget so it is important not to omit it. The next step is to correct the group average parallax for the parallax zero point. Given that it is not constant (see above), I use an average value of 40 μas and also add 10 μas to the uncertainty budget as follows:
where the values above are given in milliarcseconds. The final step is to calculate a distance and an uncertainty to the stellar group using a Bayesian prior. As the object of study are young stellar groups, their spatial distribution is different from that of the general Gaia disk population at ∼1 kpc distances and beyond, which is dominated by much older red giants. Therefore, I use the prior described by Maíz Apellániz (2001, 2005) with the updated Galactic (young) disk parameters from Maíz Apellániz et al. (2008).
2.2. Visual orbits calculation
As mentioned in the introduction, the ionizing flux in Collinder 419 and NGC 2264 is dominated in each case by an O-type visual multiple system, HD 193 322 Aa,Ab and 15 Mon Aa,Ab, respectively, with orbital periods periods measured in decades. In this paper I calculate new orbits for HD 193 322 Aa,Ab and 15 Mon Aa,Ab and in this section I first describe the data and then the method used to calculate the orbits.
2.2.1. Data
The first group of data is from the Washington Double Star Catalog (WDS; Mason et al. 2001), a compilation of separations, position angles, and magnitude differences from literature (including historical) sources and the own authors data. The second group of data is from our own AstraLux observations of HD 193 322 and 15 Mon obtained with the 2.2 m telescope at Calar Alto presented in Maíz Apellániz et al. (2019). The AstraLux data are part of a long running program to observe massive visual binaries (Maíz Apellániz 2010; Maíz Apellániz et al. 2015; Simón-Díaz et al. 2015) and are used in this paper for the calculation of visual orbits. As the pipeline for the processing of AstraLux data has changed significantly since it was described in Maíz Apellániz (2010), I provide an update in this section.
The first change in the pipeline was in the calculation of the geometric distortion. Originally, it was based on observations of the Trapezium stars compared with positions obtained from a WFPC2/HST image. In the new version, I used three different calibration fields: the Trapezium, Cyg OB2−22, and a region in the globular cluster M13. These calibration fields were compared using observations during the same night and subsequent nights; as long as the instrument is not perturbed, the geometric distortion remains stable in consecutive nights. Also, I switched to Gaia DR2 reference coordinates, which include proper motions and can be adapted to the different observation epochs. With the new version I was able to detect and correct systematic effects at the 0.1° level in the orientation for the previous calibration. The detector was aligned with a direction close to the north for each run. Our calibration-field measurements (taken every night) indicated that a typical deviation from true north is ∼1° (which is corrected by the pipeline) and, as mentioned above, the value remains stable during a given campaign. The geometric distortion correction applied was a four-parameter linear transformation (x + y plate scales, rotation, and shear), as the absolute positioning was carried out based on a reference star, with the plate scales and shear changing little between campaigns. I saw no signs of a quadratic component, as expected from the small field of view. Possible pixel-to-pixel effects were not considered because the final products are the result of the combination of 100−1000 recentered exposures and any such effects would be averaged out.
The second change, already partially used by Simón-Díaz et al. (2015), was the implementation of a more realistic model for the PSF. The new PSF model has two position (x and y core coordinates), one flux, and ten shape parameters. The core of the PSF is an obstructed Airy pattern with the parameters of the Calar Alto 2.2 m telescope convolved with a two-dimensional Gaussian (three shape parameters). The PSF also has a Moffat-profile halo (four shape parameters) with a flux fraction and position displacement (three shape parameters) with respect to the core. The implementation of the new PSF model significantly reduced the residuals and allowed for a minimization of the systematic effects (which are included in the uncertainties given in Maíz Apellániz et al. 2019).
The third change in the pipeline was the use of both the 1% and 10% AstraLux products, where the percentage refers to the fraction of (best) lucky images selected. In Maíz Apellániz (2010) only the 1% images were used. The change allowed for a better inclusion of possible PSF systematic effects. The situation in this case is different from the PSF fitting of either Hubble Space Telescope (HST) or standard ground-based imaging. In the first case there are 25−100 mas pixels and in the second case they are an order of magnitude larger, but in both situations PSF boxes of ∼10 × 10 pixels are fitted, as that is the size required to enclose most of the flux without adding much of the background region. With AstraLux we have HST-like core- and pixel-sizes with ground-based-like wing sizes. This forced us to use much larger (in pixels) PSF boxes, containing thousands of pixels as opposed to ∼100. The comparison between the 1% and 10% products analyzes different weights given to the core and wings in such process and, in that way, estimates the systematic effects added by a non-perfect fit to data by a model.
2.2.2. Method
Fitting a visual orbit requires finding seven parameters (e.g., Meeus 1998):
-
P: orbital period
-
T0: epoch of periastron passage
-
e: (true) eccentricity
-
a: semi-major axis
-
i: inclination with respect to the plane of the sky
-
Ω: position angle of the ascending node
-
ω: longitude of the periastron in the direction of motion.
Traditionally (e.g., Tokovinin 1992, software available at http://www.ctio.noao.edu/ atokovin/orbit/), algorithms start with an initial guess and use a χ2 minimization method to find the best solution (or mode in likelihood terms) in the seven-parameter space. The associated uncertainties are calculated from the derivatives at the location of the best solution. This method is relatively fast (solutions are typically reached in seconds) but it has three potential issues, all related to the high dimensionality of the problem. First, the shape of the likelihood is unlikely to be well described by a seven-dimensional ellipsoid, as the problem is highly non-linear, unless the orbit is well characterized and all the epochs have appropriate weights. Therefore, the values of the real uncertainties are likely to be underestimated by the local behavior of the derivatives around the best solution. Second, a complex likelihood can have multiple solutions and different initial guesses can lead to different final solutions. Third, the problems above are aggravated by the presence of epochs with incorrect measurements, which have to be eliminated or at least down weighted.
An alternative, which I used in this work, is to measure the likelihood ℒ = exp(−χ2/2) in a large number of points in the possible parameter space to measure its global properties around the best solution rather than its local properties. This is the technique I use with my software CHORIZOS (Maíz Apellániz 2004) for a very different problem, i.e., the fitting of spectral energy distributions to (spectro-)photometric data. CHORIZOS attacks the problem by first evaluating ℒ in a coarse grid that covers the whole n-dimensional space, where n ranges between 2 and 5. After finding the solutions where ℒ is above a given threshold it creates a fine grid to better characterize the high-likelihood regions (a process that may be repeated with an ultra-fine grid). This strategy works well for most problems for n = 2 or n = 3 but becomes computationally expensive for n = 4 and prohibitive for n = 5. Therefore, it cannot be used for the calculation of visual orbits, where n = 7.
I used a different strategy in this work; this approach allows the algorithm to sweep through the high-likelihood region of the seven-dimensional space in minutes to hours. We first applied it for HD 93 129 Aa,Ab in Maíz Apellániz et al. (2017) and I generalized it for any visual binary.
– I start by selecting a range of possible values for each of the seven parameters. This initial selection may be (and usually is) modified in subsequent iterations so can be started with a very broad range. For the data points that have no measured uncertainties I also select initial values for their uncertainties (or weights).
– I then apply a traditional χ2 minimization method using as guesses 128 different values spread over the parameter space. The purpose of this step is to find different possible minima. The solutions that are found above a selected ℒ threshold are kept as seeds for the next steps.
– I create a grid of possible solutions with 255 uniformly spaced points in each dimension5 and round up the seeds from the previous step to those values.
– I search the adjacent points of the grid (i.e., those whose seven indices are one or zero units away) for those cases that are above the selected ℒ threshold.
– I iterate the previous step until no more points are found. The process leads to an amoeba-like shape that expands through the seven-dimensional space.
– I examine the solution using a two-dimensional parameter and orbit plots (see examples in Sect. 4) to check for two aspects. First, I check whether the selected parameter range is appropriate: Does the likelihood become small at the edges? Is the grid fine enough? Second, I check whether the uncertainties are appropriate: Is the reduced χ2 close to one? Is it true by groups of data from the same source? Are there any clear outliers? The parameter ranges and uncertainties are revised accordingly and the whole procedure is iterated.
As this algorithm searches a large volume in the seven-dimensional space, not only can it evaluate uncertainties (including the correlation matrix) in a more realistic way but it can also reveal the complex shape of the likelihood and new solutions not found using a traditional algorithm. It is not ideal, however, as it is possible to have solutions “escape” through the holes in the grid. This is possible, especially when two parameters are highly correlated, in which case the shape of the likelihood may look more like a snake than an amoeba and slither through the seven-dimensional space avoiding the grid points. To avoid such a problem, which is easily seen in the two-dimensional plots, the algorithm allows for two possible parameter substitutions during the search:
– Periastron distance d ≡ a sin i instead of a. This is useful for highly elliptical incomplete orbits in which the former is much better defined than the latter; P and a are highly correlated but P and d are much less so. We used this substitution in Maíz Apellániz et al. (2017).
– ϖ ≡ ω + Ω, we note that ϖ is an angle, not the parallax. This is useful in some situations in which ω and Ω are anti-correlated (as is the case for the two systems studied in this paper). This substitution was also used in Maíz Apellániz et al. (2017) but with a different sign convention.
3. Distances to and membership of Collinder 419 and NGC 2264
In this section I present the results of the supervised method described above as applied to the Gaia DR2 data for Collinder 419 and NGC 2264. Table 3 lists the filters applied to the data (reference star; RUWE, dCC, and σϖ ranges; central coordinates α + δ and radius r; central proper motion motions μα* + μδ and radius rμ; and color range with respect to the reference star Δ(GBP − GRP)) and the results obtained are summarized. The values tϖ, tμα*, and tμδ are normalized χ2-like tests for the parallax and proper motions: they should be ∼1 if the differences between the individual values and their weighted mean normalized by the uncertainties follow a standard normal distribution and larger if there is an additional source of scatter (distance spread for the parallaxes, internal motion for the proper motions). In Figs. A.1 and A.2 the graphical results of the method are shown. Finally, in Tables A.1 and A.2 the final membership of each cluster is listed. Collinder 419 has an isochrone with an age of 3.2 Ma while that of NGC 2264 has an age of 1 Ma.
Filters applied and results obtained for the distances to and membership of Collinder 419 and NGC 2264.
3.1. Collinder 419
Collinder 419 appears in the top panels of Fig. A.1 as a loosely defined cluster centered around HD 193 322, which is the brightest object on the field. The cluster core has a radius of ∼2′ but r is significantly bigger, as the cluster has a larger halo that extends mostly toward the NE. With the possible exception of the immediate vicinity of HD 193 322, Collinder 419 does not show as an overdensity in the Gaia source density diagram. The vast majority of the sources belong to a Galactic background population at a distance of 2−5 kpc and they show a gradient increasing from NE to SW. That direction is nearly parallel to the Galactic plane, so the effect is likely caused by differential extinction beyond the distance of Collinder 419 and not by a real Galactic disk density gradient.
As Collinder 419 is not well defined by position in the sky, we must turn to the next panel in Fig. A.1 to see its most defining characteristic, i.e., proper motion. The cluster is clearly separated from the field population by ∼2 mas a−1. The next three panels show how the cluster also differs in G′ and GBP − GRP. The CMD indicates that Collinder 419 has a relatively low extinction: Maíz Apellániz & Barbá (2018) give E(4405 − 5495) = 0.381 ± 0.006 and R5495 = 2.972 ± 0.079 for HD 193 322 Aa,Ab, which translates into a E(GBP − GRP)≈0.65. As I am selecting cluster objects with Δ(GBP − GRP) > − 0.30, which corresponds to E(GBP − GRP) > 0.35, this means that there is just a small extinction restriction for a young cluster at the distance of HD 193 322 Aa,Ab. The location of some cluster members toward the left and right of the upper part of the reference extinguished isochrone indicates that there is a differential extinction effect of a few tens in E(4405 − 5495) for the Collinder 419 cluster members. Progressing down the CMD, the cluster members end up preferentially to the right of the reference extinguished isochrone; this is an indication that those lower mass stars have not reached the main sequence yet.
Most of the field population is located at larger distances and consists of two subpopulations. The largest comprises faint stars in the bottom left quadrant of the CMD, which also form the two main density peaks in the color-parallax and magnitude-parallax diagrams. The second population is likely red giant stars, which make up most of the stars to the right of the cluster sequence in the CMD. Such red giant stars are likely the main source for the 18 contaminants rejected by the normalized parallax criterion.
The distance I obtain for Collinder 419 is 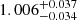 kpc, an uncertainty of 3−4%. We note that most of the uncertainty arises from the spatial covariance term: if it were not included σϖg would be 6 μas instead of 34 μas; the spatial covariance is also the dominant source for the proper motion uncertainties. My value for ϖg is very similar to that derived by Cantat-Gaudin et al. (2018) but the uncertainties are very different because of that. The two values for the distance are very similar, nonetheless (their mode is 1019.2 pc, within one sigma of the value here) but I find significantly more cluster members. With respect to the literature values, the HIPPARCOS distance for HD 193 322 Aa,Ab of Maíz Apellániz et al. (2008) is just over one sigma away (but with a large uncertainty), while the much lower distance of Roberts et al. (2010) derived from a pure CMD analysis is clearly incompatible with the Gaia parallaxes. Collinder 419 is not a rich cluster and, hence, is not able to make a dent in the total Gaia parallax histogram of Fig. A.1. Indeed, only 0.4% of the Gaia stars in the field end up being selected by the algorithm. The value tϖ is very close to one, indicating that the algorithm is identifying a group of stars with differences in distance much smaller than the individual parallax uncertainties. On the other hand, tμα* and tμδ are significantly larger than one, indicating that Gaia is sensitive to the internal cluster motions.
kpc, an uncertainty of 3−4%. We note that most of the uncertainty arises from the spatial covariance term: if it were not included σϖg would be 6 μas instead of 34 μas; the spatial covariance is also the dominant source for the proper motion uncertainties. My value for ϖg is very similar to that derived by Cantat-Gaudin et al. (2018) but the uncertainties are very different because of that. The two values for the distance are very similar, nonetheless (their mode is 1019.2 pc, within one sigma of the value here) but I find significantly more cluster members. With respect to the literature values, the HIPPARCOS distance for HD 193 322 Aa,Ab of Maíz Apellániz et al. (2008) is just over one sigma away (but with a large uncertainty), while the much lower distance of Roberts et al. (2010) derived from a pure CMD analysis is clearly incompatible with the Gaia parallaxes. Collinder 419 is not a rich cluster and, hence, is not able to make a dent in the total Gaia parallax histogram of Fig. A.1. Indeed, only 0.4% of the Gaia stars in the field end up being selected by the algorithm. The value tϖ is very close to one, indicating that the algorithm is identifying a group of stars with differences in distance much smaller than the individual parallax uncertainties. On the other hand, tμα* and tμδ are significantly larger than one, indicating that Gaia is sensitive to the internal cluster motions.
HD 193 322 Aa,Ab itself is not included in the final membership list as it was excluded due to its high RUWE; this is likely an effect of its multiplicity, which is unresolved by Gaia but should manifest in large astrometric residuals6. This is not a problem because the method employed in this work emphasizes a low number of false positives at the price of increasing the number of false negatives. The second brightest (in G′) object in the field, HD 193 159, is a foreground B star located at approximately half the distance to Collinder 419 and with very little extinction. The third brightest object in the field is the first cluster member in the list, i.e., HD 193 322 B, the visual companion to HD 193 322 Aa,Ab. The next object in the membership list is HDE 228 911, a previously known spectroscopic binary. As part of the GOSSS collaboration, we obtained a GOSSS spectrum with the Albireo spectrograph at the Observatorio de Sierra Nevada (OSN) and caught the system in a SB2 state, allowing me to determine that it is made out of a couple of near identical B1.5 V stars (Fig. A.3). The observation was obtained at HJD 2 455 850.283 and the velocity difference between the two components was 325 ± 10 km s−1. Another bright object in the field is HDE 228 882 but its Gaia DR2 parallax puts it beyond Collinder 419 and its GBP − GRP color indicates it experiences a significantly larger extinction. We also obtained a GOSSS spectrum from OSN for HDE 228 882 and derived a spectral type of B0.5 Iab(n) (Fig. A.3). Comparing the two spectra in that figure shows that the second has stronger diffuse interstellar bands (DIBs), as expected from the larger extinction. Roberts et al. (2010) suggested that 2MASS J20175763+4044373 (= IRAS 20161+4035) is also a cluster member and derived a spectral type of M3 III for that star, which appears in principle incompatible with the Collinder 419 isochrone. The Gaia DR2 data hold a surprise for the object: its individual parallax is consistent with being at the same distance as the cluster but its proper motion is highly discrepant with either Collinder 419 or the field population and instead suggests a relative velocity in the plane of the sky close to 50 km s−1. This raises the possibility that 2MASS J20175763+4044373 is a recent runaway from Collinder 419. However, its motion does not trace back to HD 193 322 but to a region of high extinction toward the NE that appears to be associated with the WISE H II region G078.378+02.785. Therefore, another possibility is that G078.378+02.785 is a younger star-forming region at the same distance (a second generation of stars likely triggered by Collinder 419) and that 2MASS J20175763+4044373 is a massive very young PMS object ejected from there ∼105 a ago (as estimated from the flying time). The young age would be consistent with the strong Li I absorption in the spectrum of 2MASS J20175763+4044373 measured by Roberts et al. (2010).
3.2. NGC 2264
The appearance of NGC 2264 in the top panels of Fig. A.2 is different from that of Collinder 419 for four reasons: Aldoretta et al. (2015) there are significantly more cluster members, Arenou et al. (2018) NGC 2264 shows a clear double structure concentrated around two points, Baxter et al. (2009) the position of the cluster is well correlated with nebular emission, and [4] anti-correlated with the overall source density. The last point seems counterintuitive but it can be explained in the context of the third. Young clusters containing O stars still associated with their natal clouds ionize their surfaces creating H II regions but take their time to devour their molecular clouds, generating different extinction-related effects and structures depending on the direction from where we observe them (Walborn et al. 2002; Maíz Apellániz et al. 2004, 2015; Maíz Apellániz & Barbá 2018). The case of NGC 2264 is similar to that of the Orion Nebula: they are nearby, well-resolved H II regions where the main ionizing star (15 Mon for NGC 2264, θ1 Ori C for the Orion Nebula) is located on the near side of the natal cloud. Therefore, we see the H II face on with the ionizing star(s) in the foreground. The H II region has the overall shape of a concave hole in the molecular cloud, which results in a bright region surrounded by a dark region; possible pillars are created by photoevaporation at the edge. In the case of NGC 2264 the Cone Nebula (seen toward the bottom of the DSS2 images in Fig. A.2) is the most prominent example. As the molecular cloud blocks most of the light behind the cluster, the field population (located mostly in the background at distances of 2−5 kpc) is much better seen at the right and left edges of the field shown in Fig. A.2: hence, the anti-correlation between cluster members and overall source density.
As already mentioned, the double cluster structure of NGC 2264 in the optical was previously known, and two additional stellar concentrations were visible in the NIR, indicating that there are additional hidden subclusters (Caballero & Dinis 2008). To study the possible differences between the two subclusters (NGC 2264 N and NGC 2264 S), I repeated the analysis of the whole region for the two subregions in Table 3 and plotted them in the top panels of Fig. A.2. NGC 2264 N is approximately centered on 15 Mon and NGC 2264 S is closer to the Cone Nebula.
As occurred with Collinder 419, NGC 2264 is best differentiated from the field population in the proper-motion diagram, with a separation of ∼3 mas a−1 in Fig. A.2. The CMD indicates that Collinder 419 has a very low extinction: Maíz Apellániz & Barbá (2018) give E(4405 − 5495) = 0.054 ± 0.006 and R5495 = 4.431 ± 0.752 for 15 Mon Aa,Ab,B, which translates into a E(GBP − GRP)≈0.11. I am selecting cluster objects with Δ(GBP − GRP) > − 0.20, which corresponds to E(GBP − GRP) > − 0.09; a negative value is used to include the effect of photometric uncertainties for objects with extinction close to zero. This means that there is no extinction restriction for a young cluster at the distance of 15 Mon Aa,Ab,B, but the isochrone filter is still useful to discard background objects. Going down the isochrone in the CMD we first encounter stars that have already reached the main sequence and then a pre-main sequence (PMS) region that is richer and more separated from the isochrone than in the Collinder 419 case, indicating a younger age and likely a higher cluster mass. I note that the PMS seems to stop around G′ = 18. This is likely an effect of the dCC filter: dim stars immersed in nebulosity such as those in NGC 2264 have contaminated GBP and GRP photometry.
The field population is located mostly beyond NGC 2264. It is similar to that of Collinder 419 but with fewer stars at extreme red colors; this is an an effect of the lower extinction in this direction of the Galaxy, much closer to the anticenter. Most of the 66 contaminants rejected by the normalized parallax criterion are farther than NGC 2264 but a minority (eight) are closer.
The distance we obtain for NGC 2264 is 719 ± 16 pc (an uncertainty of just 2%). As with Collinder 419, most of the uncertainty arises from the spatial covariance term: if it were not included σϖg would be 3 μas instead of 29 μas. Indeed, my value for ϖg is the same as that derived by Cantat-Gaudin et al. (2018) but the uncertainties are very different because of that. I also found significantly more cluster members. With respect to the literature values, the maser distance of Kamezaki et al. (2014) is that closer to the Gaia value because it is less than one sigma away. NGC 2264 is a richer cluster and, hence, its presence is detected in the total Gaia parallax histogram of Fig. A.2: 1.1% of the Gaia stars in the field end up being selected by the algorithm. Similar to Collinder 419, tϖ is close to one, but tμα* and tμδ are even larger, which is a sign that the internal motions are stronger in NGC 2264 (see below).
Comparing the two subclusters, their distances are very similar and from the Gaia DR2 point of view they could be at the same distance from the Sun. We note that their distance in the plane of the sky corresponds to 4.5 pc, which is much smaller than either of the individual distance uncertainties. There is a significant difference in the proper motions, where the two subclusters move in a counterclockwise motion with respect to each other. This relative motion should in principle contribute to the increased values of tμα* and tμδ but it cannot be the main source, as both NGC 2264 N and NGC 2264 S (especially the latter) have high values of those quantities when analyzed separately. Therefore, we must conclude that the internal motions within each subcluster dominate the velocity dispersion.
Neither 15 Mon AaAb nor 15 Mon B are included in the final membership list owing to their high RUWE but, as I already mentioned in the case of Collinder 419, that is not a problem. The second and third objects in the membership list (sorted by G) are HD 47 887 and HD 47 961, which are both B stars. Table A.2 includes many more stars with spectral types than Table A.1; this is a reflection of the different levels of richness and number of previous studies between the two clusters. Progressing down the list the spectral types progressively switch from B to A and then to later types, as expected. Nevertheless, it should be noted that the Simbad spectral types cannot be completely trusted, given the number of errors it contains (see Maíz Apellániz et al. 2016 for some examples).
3.3. Testing the robustness of the distance determinations
A critique of supervised methods is that the user may not select the appropriate parameters and bias the results. To check that the values for ϖg derived in this work are unbiased, I did Monte Carlo simulations for the clusters varying the values of α, δ, r, μα*, μδ, rμ, and Δ(GBP − GRP) within reasonable limits. For Collinder 419 the Monte Carlo simulations yield N* = 64 ± 16 and ϖg = 0.956 ± 0.004 mas and for NGC 2264 they yield N* = 253 ± 39 and ϖg = 1.354 ± 0.002 mas. Those results lead to two conclusions. First, the number of Gaia-detected cluster members is within one sigma of our selected value but in both cases the average is on the low side. This makes sense because supervision is introduced, among other things, to maximize the number of bona fide members so removing the supervision decreases that number on average. Second, and most important, the group parallax is robust. The difference is 1 μas for Collinder 419 and even less than that for NGC 2264. Considering that the main source of error is due to the spatial covariance (more than one order of magnitude larger), I can conclude that supervision (if done properly) does not bias the derived group parallax.
4. Visual orbits of HD 193 322 Aa,Ab and 15 Mon Aa,Ab
In this section I present the results for the relative visual orbits for HD 193 322 Aa,Ab and 15 Mon Aa,Ab. The data used for the calculation of the orbits (including the uncertainties derived from the method itself) are given in Tables 4 and 5. I used the option of fitting ϖ ≡ ω + Ω instead of ω. The seven fitted parameters, d, ω, and total masses MAa, Ab are given in Table 6. In each case a median and percentile-based uncertainties (derived from all calculated orbits) are first given, followed by the result for the mode orbit. For the masses I assume the distances to Collinder 419 and NGC 2264 derived in the previous section and do not include the uncertainties associated with distance. Figure A.4 shows the fitted orbits, Figs. A.5 and A.6 the derived likelihood projected into the planes of each pair of fitted parameters, and Fig. A.7 the normalized fitting residues. Table 7 gives the calculated ephemerides (and their uncertainties) for both systems in the period 1980−2030.
Astrometry used for the calculation of the visual orbit of HD 193 322 Aa,Ab.
Astrometry used for the calculation of the visual orbit of 15 Mon Aa,Ab.
4.1. HD 193 322 Aa,Ab
The orbital solution I obtain for HD 193 322 Aa,Ab is relatively similar to the one derived by ten Brummelaar et al. (2011) but with some significant differences. On the one hand, the values of T0 and a are within one sigma of each other, with improved uncertainties in the new solution. On the other hand, the period is now longer and the orbit is more eccentric, which is a consequence of the better position angle coverage available now. Another significant difference is that I find a larger uncertainty for the inclination. An explanation to that is found in Fig. A.5. Most plots are relatively well approximated by ellipsoids but those involving i have more complex shapes, including a low-probability tail that extends to low values. Such shapes cannot only be described by the derivatives at the location of the mode and correctly characterizing these shapes requires a method that searches the seven-parameter space such as that used in this work. Most parameters have low correlation coefficients but there are some exceptions, most notably a and i, which are positively correlated. There is clearly room for improvement in the orbit, especially as one revolution has not been completed since the first observations (that event would take place by the end of the decade of the 2020s, Table 7) and since there were no observations in the 1990s, when the periastron took place. The next periastron will take place in about 20 years from now.
Applying a distance of 1006 pc to the ten Brummelaar et al. (2011) results, a total mass of 133 ± 29 M⊙ is obtained, which is almost twice of what I obtain in this work. The new value is more realistic, as it requires dividing 76.1 M⊙ among three non-supergiant late-O/early-B stars. The total mass was not such a big problem for ten Brummelaar et al. (2011) because they estimated Collinder 419 to be closer to us and that reduces MAa, Ab, which is proportional to the distance cubed. Indeed, they were aware of this possibility as they mentioned the need for further epochs to resolve the “lingering problems” they had encountered with their mass calculations. Since my value for the distance to Collinder 419 has an uncertainty of 3−4%, the uncertainty for MAa, Ab has an additional (systematic) uncertainty of ∼10%, i.e., comparable to the random uncertainty. Once Gaia DR3 becomes available, it is likely that systematic uncertainty will be reduced.
The ephemerides in Table 7 were calculated using the 1000 most likely orbits plotted in Fig. A.4. The uncertainties in ρ and θ show two minima: one in the second half of the 1980s and another around 2010. Those are the two times when observations were obtained. In between, there is a large increase in uncertainties around the time of the periastron, as the system was moving at maximum speed at the time and no observations are available. Hence, there is a large uncertainty as to where the system was at a particular time even if the periastron is well constrained within ∼1 year. Further into the future uncertainties start growing again as the trajectory is an extrapolation from the latest data. Even though it is not shown, uncertainties continue growing until the next periastron passage around 2040 for the same reasons stated for the previous passage.
Finally, I considered the possibility that the observations taken in the 1980s suffered from the 180° phase error in position angle that sometimes affects speckle interferometry. I was able to calculate a reasonable orbit combining those modified data with the data from 2005 onward but the resulting MAa, Ab was almost one-third lower than the value in Table 6. That is an unphysical result, as it is inconsistent with the existence of three massive stars that include at least two O stars. Therefore, I conclude that the 1980s observations have no phase error.
Fitted orbital parameters, d, ω, and MAa, Ab for HD 193 322 Aa,Ab and 15 Mon Aa,Ab.
4.2. 15 Mon Aa,Ab
As mentioned in the introduction, for 15 Mon Aa,Ab there are five published orbital solutions instead of just one. Looking at these solutions, there is a clear trend of increasing periods from those published in the 1990s to the most recent of Tokovinin (2018) by more than a factor of five between the extremes. That effect is a cautionary tale on the dangers of calculating visual orbits from very incomplete arcs, especially if a thorough search of the parameter space is not performed or bad data points are not eliminated or at least down weighted. The orbital period I find follows the trend of increasing periods of Gies et al. (1993, 1997) and Cvetković et al. (2009, 2010) but stops at a value that is just over half of the Tokovinin (2018) value (which is published without uncertainties). The uncertainty in the period is relatively large (∼10%) and there is indeed a tail that extends to higher values but the likelihood around 190 is very low (Fig. A.6). The new periastron epoch and eccentricity are similar to those of the previous three orbits but with reduced uncertainties. The values for a and i follow the same pattern as the period, with values intermediate between those of Cvetković et al. (2009, 2010) and Tokovinin (2018).
The mass derived for 15 Mon Aa,Ab has a relative uncertainty of less than 10%, which looks surprising given the uncertainties for P and a, the two quantities used to derive it. The explanation is that P and a have a strong positive correlation, as seen in Fig. A.6. The uncertainty on the distance to NGC 2264 is lower than for Collinder 419, leading to an additional systematic uncertainty of ∼7%. Nevertheless, the uncertainty for MAa, Ab is one of the lowest known for an O-type binary, especially considering that most measured systems to date are spectroscopic binaries with poorly constrained inclinations. The total mass we obtain (at a distance of 719 pc) is higher than that derived by Gies et al. (1997) and lower than that derived by Cvetković et al. (2010). It is relatively similar to the value derived from the Tokovinin (2018) orbit but that author does not calculate it explicitly.
The uncertainties for the 15 Mon Aa,Ab ephemerides in Table 7 follow a pattern similar to the HD 193 322 Aa,Ab, with two minima around 1990 and 2012. The maximum in between is not as prominent, however, as in this case the system was observed near periastron. As deduced from Fig. A.4, the uncertainties are expected to grow significantly after 2040, as that part of the orbit near apastron has never been observed. On the other hand, observations in the next decade should constrain the orbital parameters significantly, even though the system will not return to its first observed epoch until around the turn of the century.
Calculated ephemerides and their uncertainties for HD 193 322 Aa,Ab and 15 Mon Aa,Ab in the 1980−2030 period.
5. Future work
My short-term goal is to apply the supervised Gaia method to a number of young clusters containing O stars to derive reliable Gaia DR2 distances. The clusters will be selected using GOSSS data and Maíz Apellániz & Barbá (2018) will be used for the extinction parameters. In the medium term, Gaia DR3 is expected to reduce the systematic effects in the parallaxes and proper motions, especially the zero point offset and the spatial covariance effects. Those reductions should lead to significantly better distances to stellar clusters. In the long term, the final Gaia data release may yield parallaxes good enough to measure distance differences within associations or cluster halos at ∼1 kpc.
Regarding astrometric orbits, I plan to use the existing data to analyze several more systems. I will also continue obtaining new AstraLux epochs to further constrain the HD 193 322 Aa,Ab and 15 Mon Aa,Ab orbits.
There is also room for improvement in our knowledge of HD 193 322 Aa,Ab and 15 Mon Aa,Ab elsewhere. We are monitoring both systems using high-resolution spectroscopy to improve their spectroscopic orbits as part of MONOS (Maíz Apellániz et al. 2019). However, there is a limit to what we can do with spatially unresolved spectroscopy, especially when one of the systems is a fast rotator or the Δm between components is large. One solution would be lucky spectroscopy (Maíz Apellániz et al. 2018) but, unfortunately, the separation is too small. We recently attempted resolving 15 Mon Aa,Ab using that technique but we were only partially successful. It was possible to separate Ab from Aa but the resulting spectrum is too noisy and I can only say that this object is consistent with being a late-O or early-B star. An alternative would be using STIS at HST; my collaborators and I successfully used this technique to separate HD 93 129 Aa,Ab at a point where the separation was even smaller than for the two systems in this paper (Maíz Apellániz et al. 2017). In that way, it would be possible to obtain individual spectra for HD 193 322 Aa, 15 Mon Aa, and 15 Mon Ab, and a combined spectrum for HD 193 322 Ab1,Ab2 that could be separated in velocity. In combination with the results in this paper, reliable spectral types and masses could be derived for all components. As this paper was being refereed my collaborators and I received notice that the HST program we had submitted to do precisely that had been accepted. Barring unexpected events, we expect to have new results on these two systems soon.
We note that Roberts et al. (2010) gave a HIPPARCOS distance of 600 pc but that is just the inverse of the observed parallax from van Leeuwen (2007), which is a biased estimator of the distance when the parallax uncertainty is large. The HIPPARCOS distance given by Sota et al. (2011) uses a distance prior for OB stars (Maíz Apellániz 2001, 2005).
Acknowledgments
I thank an anonymous referee for comments that helped improve the paper, Rodolfo X. Barbá for useful discussions regarding this work, Pablo Crespo Bellido for his help with the testing of the method to measure distances to stellar groups, Alfredo Sota for the processing of the GOSSS spectra of HDE 228 911 and HDE 228 882, Brian Mason for providing me with the WDS detailed data and for his efforts maintaining the catalog, and the Calar Alto staff for their help with the AstraLux campaigns. I acknowledge support from the Spanish Government Ministerio de Ciencia, Innovación y Universidades through grants AYA2016-75 931-C2-2-P and PGC2018-095 049-B-C22. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research has made extensive use of the SIMBAD database, operated at CDS, Strasbourg, France.
References
- Aldoretta, E. J., Caballero-Nieves, S. M., Gies, D. R., et al. 2015, AJ, 149, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Arenou, F., Luri, X., Babusiaux, C., et al. 2018, A&A, 616, A17 [Google Scholar]
- Baxter, E. J., Covey, K. R., Muench, A. A., et al. 2009, AJ, 138, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, A. G. A., Vallenari, A., Prusti, T., et al. 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caballero, J. A., & Dinis, L. 2008, Astron. Nachr., 329, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Campillay, A. R., Arias, J. I., Barbá, R. H., et al. 2019, MNRAS, 484, 2137 [NASA ADS] [CrossRef] [Google Scholar]
- Cantat-Gaudin, T., Jordi, C., Vallenari, A., et al. 2018, A&A, 618, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cvetković, Z., Vince, I., & Ninković, S. 2009, Publ. Astron. Obs. Belgrade, 86, 331 [NASA ADS] [Google Scholar]
- Cvetković, Z., Vince, I., & Ninković, S. 2010, New Astron., 15, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Dahm, S. E. 2008, Handbook of Star Forming Regions, Volume I (ASP), 966 [Google Scholar]
- Evans, D. W., Riello, M., De Angeli, F., et al. 2018, A&A, 616, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gies, D. R., Mason, B. D., Hartkopf, W. I., et al. 1993, AJ, 106, 2072 [NASA ADS] [CrossRef] [Google Scholar]
- Gies, D. R., Mason, B. D., Bagnuolo, Jr., W. G., et al. 1997, ApJ, 475, L49 [NASA ADS] [CrossRef] [Google Scholar]
- González, M., & Alfaro, E. J. 2017, MNRAS, 465, 1889 [NASA ADS] [CrossRef] [Google Scholar]
- Hartkopf, W. I., Tokovinin, A., & Mason, B. D. 2012, AJ, 143, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Horch, E. P., van Altena, W. F., Cyr, Jr., W. M., et al. 2008, AJ, 136, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Horch, E. P., Falta, D., Anderson, L. M., et al. 2010, AJ, 139, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Horch, E. P., Casetti-Dinescu, D. I., Camarata, M. A., et al. 2017, AJ, 153, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Hormuth, F., Brandner, W., Hippler, S., & Henning, T. 2008, J. Phys. Conf. Ser., 131, 012051 [Google Scholar]
- Kamezaki, T., Imura, K., Omodaka, T., et al. 2014, ApJS, 211, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Khan, S., Miglio, A., Mosser, B., et al. 2019, A&A, 628, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krone-Martins, A., & Moitinho, A. 2014, A&A, 561, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L. 2018, GAIA-C3-TN-LU-LL-124-01 [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018a, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018b, https://www.cosmos.esa.int/documents/29201/1770596/Lindegren_GaiaDR2_Astrometry_extended.pdf [Google Scholar]
- Luri, X., Brown, A. G. A., Sarro, L. M., et al. 2018, A&A, 616, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz Apellániz, J. 2001, AJ, 121, 2737 [Google Scholar]
- Maíz Apellániz, J. 2004, PASP, 116, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J. 2005, in The Three-dimensional Universe with Gaia, eds. C. Turon, K. S. O’Flaherty, & M. A. C. Perryman, ESA SP, 576, 179 [Google Scholar]
- Maíz Apellániz, J. 2010, A&A, 518, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz Apellániz, J., & Barbá, R. H. 2018, A&A, 613, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz Apellániz, J., & Weiler, M. 2018, A&A, 619, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz Apellániz, J., Pérez, E., & Mas-Hesse, J. M. 2004, AJ, 128, 1196 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J., Alfaro, E. J., & Sota, A. 2008, ArXiv e-prints [arXiv:0804.2553] [Google Scholar]
- Maíz Apellániz, J., Sota, A., Walborn, N. R., et al. 2011, HSA6, 467 [Google Scholar]
- Maíz Apellániz, J., Evans, C. J., Barbá, R. H., et al. 2014, A&A, 564, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz Apellániz, J., Barbá, R. H., Sota, A., & Simón-Díaz, S. 2015, A&A, 583, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz Apellániz, J., Sota, A., Arias, J. I., et al. 2016, ApJS, 224, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J., Sana, H., Barbá, R. H., Le Bouquin, J.-B., & Gamen, R. C. 2017, MNRAS, 464, 3561 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J., Barbá, R. H., Simón-Díaz, S., et al. 2018, A&A, 615, A161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz Apellániz, J., Trigueros Páez, E., Negueruela, I., et al. 2019, A&A, 626, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, B. D., Wycoff, G. L., Hartkopf, W. I., Douglass, G. G., & Worley, C. E. 2001, AJ, 122, 3466 [Google Scholar]
- Mason, B. D., Hartkopf, W. I., Gies, D. R., Henry, T. J., & Helsel, J. W. 2009, AJ, 137, 3358 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, B. D., Hartkopf, W. I., Raghavan, D., et al. 2011, AJ, 142, 176 [NASA ADS] [CrossRef] [Google Scholar]
- McAlister, H. A., Hartkopf, W. I., Hutter, D. J., Shara, M. M., & Franz, O. G. 1987, AJ, 93, 183 [NASA ADS] [CrossRef] [Google Scholar]
- McAlister, H. A., Hartkopf, W. I., Sowell, J. R., Dombrowski, E. G., & Franz, O. G. 1989, AJ, 97, 510 [NASA ADS] [CrossRef] [Google Scholar]
- McAlister, H. A., Mason, B. D., Hartkopf, W. I., & Shara, M. M. 1993, AJ, 106, 1639 [NASA ADS] [CrossRef] [Google Scholar]
- McKibben, W. P., Bagnuolo, Jr., W. G., Gies, D. R., et al. 1998, PASP, 110, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Meeus, J. 1998, Astronomical Algorithms, 2nd ed. (Richmond: Willmann-Bell) [Google Scholar]
- Neri, L. J., Chavarria, C.-K., & de Lara, E. 1993, A&AS, 102, 201 [NASA ADS] [Google Scholar]
- Pérez, M. R., The, P. S., & Westerlund, B. E. 1987, PASP, 99, 1050 [NASA ADS] [CrossRef] [Google Scholar]
- Prusti, T., de Bruijne, J. H. J., Brown, A. G. A., et al. 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roberts, L. C., Gies, D. R., Parks, J. R., et al. 2010, AJ, 140, 744 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., Le Bouquin, J.-B., Lacour, S., et al. 2014, ApJS, 215, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Simón-Díaz, S., Caballero, J. A., Lorenzo, J., et al. 2015, ApJ, 799, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Sota, A., Maíz Apellániz, J., Walborn, N. R., et al. 2011, ApJS, 193, 24 [NASA ADS] [CrossRef] [Google Scholar]
- ten Brummelaar, T. A., O’Brien, D. P., Mason, B. D., et al. 2011, AJ, 142, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Tobin, J. J., Hartmann, L., Fűrész, G., Hsu, W.-H., & Mateo, M. 2015, AJ, 149, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A. 1992, in IAU Colloq. 135: Complementary Approaches to Double and Multiple Star Research, eds. H. A. McAlister, & W. I. Hartkopf, ASP Conf. Ser., 32, 573 [NASA ADS] [Google Scholar]
- Tokovinin, A. 2018, IAU Commission G1 Circular, 195, 2 [Google Scholar]
- Tokovinin, A., Mason, B. D., & Hartkopf, W. I. 2014, AJ, 147, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A., Mason, B. D., Hartkopf, W. I., Méndez, R. A., & Horch, E. P. 2015, AJ, 150, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A., Mason, B. D., Hartkopf, W. I., Méndez, R. A., & Horch, E. P. 2016, AJ, 151, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, D. G. 2012, Astron. Nachr., 333, 174 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, in Hipparcos, the New Reduction of the Raw Data, (Dordrecht: Springer), Astrophys. Space Sci. Lib., 350 [Google Scholar]
- Venuti, L., Prisinzano, L., Sacco, G. G., et al. 2018, A&A, 609, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walborn, N. R., Maíz Apellániz, J., & Barbá, R. H. 2002, AJ, 124, 1601 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional figures and tables
 |
Fig. A.1. Collinder 419 Gaia DR2 distances and membership results. Top row (left to right): source density diagram, DSS2 blue image, and 2MASS J image. Middle row (left to right): proper motions, color-parallax, and magnitude-parallax diagrams. Bottom row (left to right): color-magnitude diagram, parallax histogram, and normalized-parallax histogram. In all diagrams a heat-type scale (increasing as white-yellow-orange-red-black) is used to indicate the total Gaia DR2 density in a linear scale (except in the CMD, where a log scale is used). In the first four panels the green circle indicates the coordinates or proper motion constraints. In the CMD the green lines show the reference extinguished isochrone (right) and the displaced isochrone used as constraint (left), joined at the top by the extinction trajectory. In all diagrams the blue symbols indicate the objects used in the final sample and the gray symbols those rejected by the normalized parallax criterion. The plotted parallax uncertainties are the external ones. In the parallax histogram black indicate the total Gaia DR2 density, red the sample prior to the application of the normalized parallax criterion, and blue the final sample, while the two green vertical lines delineate the weighted-mean parallax: dotted for ϖg, 0 and solid for ϖg. Black and blue have the same meaning in the normalized parallax histogram, where the green line shows the expected normal distribution. |
 |
Fig. A.2. Same as Fig. A.1 for NGC 2264 with two changes: the top right panel shows a DSS2 red image and two additional circles are used to indicate the subgroups NGC 2264 N and NGC 2264 S in the top three panels. |
 |
Fig. A.3. GOSSS spectrograms of HDE 228 911 and HDE 228 882. |
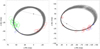 |
Fig. A.4. Plane-of-the-sky orbit plots for HD 193 322 Aa,Ab (left) and 15 Mon Aa,Ab (right). The mode (highest likelihood) orbit is shown as a thick black line; a star marks the orbital center, a dashed line the line of nodes, and a cross the periastron. In both cases the motion is counterclockwise and less than a full revolution has been completed since the first data were obtained. In addition to the mode orbit, the top 1000 orbits by likelihood found by the algorithm are plotted using gray thin lines. Ellipses show the measured data points joined by short lines to the predicted position in the mode orbit. A color code is used to indicate the data source. For HD 193 322 Aa,Ab (Table 4), red is used for McAlister et al. (1989), green for ten Brummelaar et al. (2011), magenta for Aldoretta et al. (2015), and blue for Maíz Apellániz et al. (2019). For 15 Mon Aa,Ab (Table 5), blue is used for Maíz Apellániz et al. (2019) and red for the rest of the sources. North is up and east is left. Using the distances derived in this paper, the plotted regions are 126 AU × 126 AU for HD 193 322 Aa,Ab and 158 AU × 158 AU for 15 Mon Aa,Ab. |
 |
Fig. A.5. Likelihood plots of every parameter pair for the orbital fitting of HD 193 322 Aa,Ab. The levels plotted range between 0.1% and 100% of the maximum collapsed (from the other five parameters) likelihood in each case using a linear scale. The cross denotes the projection of the seven-parameter mode into that plane, which does not necessary correspond to the maximum of the collapsed likelihood. |
 |
Fig. A.7. Normalized separation (top) and position angle (bottom) residue plots for HD 193 322 Aa,Ab (left) and 15 Mon Aa,Ab (right). The vertical position shows the residue position in the normalized O–C sense (data-fit divided by the individual observed uncertainties) and the vertical error bar shows the one-sigma range allowed by the fit. The color code is the same as in Fig. A.4. |
Collinder 419 Gaia DR2 selected sample sorted by G.
NGC 2264 Gaia DR2 selected sample sorted by G.
All Tables
Filters applied and results obtained for the distances to and membership of Collinder 419 and NGC 2264.
Fitted orbital parameters, d, ω, and MAa, Ab for HD 193 322 Aa,Ab and 15 Mon Aa,Ab.
Calculated ephemerides and their uncertainties for HD 193 322 Aa,Ab and 15 Mon Aa,Ab in the 1980−2030 period.
All Figures
 |
Fig. A.1. Collinder 419 Gaia DR2 distances and membership results. Top row (left to right): source density diagram, DSS2 blue image, and 2MASS J image. Middle row (left to right): proper motions, color-parallax, and magnitude-parallax diagrams. Bottom row (left to right): color-magnitude diagram, parallax histogram, and normalized-parallax histogram. In all diagrams a heat-type scale (increasing as white-yellow-orange-red-black) is used to indicate the total Gaia DR2 density in a linear scale (except in the CMD, where a log scale is used). In the first four panels the green circle indicates the coordinates or proper motion constraints. In the CMD the green lines show the reference extinguished isochrone (right) and the displaced isochrone used as constraint (left), joined at the top by the extinction trajectory. In all diagrams the blue symbols indicate the objects used in the final sample and the gray symbols those rejected by the normalized parallax criterion. The plotted parallax uncertainties are the external ones. In the parallax histogram black indicate the total Gaia DR2 density, red the sample prior to the application of the normalized parallax criterion, and blue the final sample, while the two green vertical lines delineate the weighted-mean parallax: dotted for ϖg, 0 and solid for ϖg. Black and blue have the same meaning in the normalized parallax histogram, where the green line shows the expected normal distribution. |
| In the text | |
 |
Fig. A.2. Same as Fig. A.1 for NGC 2264 with two changes: the top right panel shows a DSS2 red image and two additional circles are used to indicate the subgroups NGC 2264 N and NGC 2264 S in the top three panels. |
| In the text | |
 |
Fig. A.3. GOSSS spectrograms of HDE 228 911 and HDE 228 882. |
| In the text | |
 |
Fig. A.4. Plane-of-the-sky orbit plots for HD 193 322 Aa,Ab (left) and 15 Mon Aa,Ab (right). The mode (highest likelihood) orbit is shown as a thick black line; a star marks the orbital center, a dashed line the line of nodes, and a cross the periastron. In both cases the motion is counterclockwise and less than a full revolution has been completed since the first data were obtained. In addition to the mode orbit, the top 1000 orbits by likelihood found by the algorithm are plotted using gray thin lines. Ellipses show the measured data points joined by short lines to the predicted position in the mode orbit. A color code is used to indicate the data source. For HD 193 322 Aa,Ab (Table 4), red is used for McAlister et al. (1989), green for ten Brummelaar et al. (2011), magenta for Aldoretta et al. (2015), and blue for Maíz Apellániz et al. (2019). For 15 Mon Aa,Ab (Table 5), blue is used for Maíz Apellániz et al. (2019) and red for the rest of the sources. North is up and east is left. Using the distances derived in this paper, the plotted regions are 126 AU × 126 AU for HD 193 322 Aa,Ab and 158 AU × 158 AU for 15 Mon Aa,Ab. |
| In the text | |
 |
Fig. A.5. Likelihood plots of every parameter pair for the orbital fitting of HD 193 322 Aa,Ab. The levels plotted range between 0.1% and 100% of the maximum collapsed (from the other five parameters) likelihood in each case using a linear scale. The cross denotes the projection of the seven-parameter mode into that plane, which does not necessary correspond to the maximum of the collapsed likelihood. |
| In the text | |
 |
Fig. A.6. Same as Fig. A.5 for 15 Mon Aa,Ab. |
| In the text | |
 |
Fig. A.7. Normalized separation (top) and position angle (bottom) residue plots for HD 193 322 Aa,Ab (left) and 15 Mon Aa,Ab (right). The vertical position shows the residue position in the normalized O–C sense (data-fit divided by the individual observed uncertainties) and the vertical error bar shows the one-sigma range allowed by the fit. The color code is the same as in Fig. A.4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.