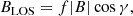| Issue |
A&A
Volume 630, October 2019
|
|
|---|---|---|
| Article Number | A139 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201935856 | |
| Published online | 08 October 2019 | |
Height variation of magnetic field and plasma flows in isolated bright points
Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
e-mail: ckuckein@aip.de
Received:
9
May
2019
Accepted:
26
August
2019
Aims. The expansion with height of the solar photospheric magnetic field and the plasma flows is investigated for three isolated bright points (BPs).
Methods. The BPs were observed simultaneously with three different instruments attached to the 1.5 m GREGOR telescope: (1) filtergrams of Ca II H and blue continuum (4505 Å) with the HiFI, (2) imaging spectroscopy of the Na I D2 line at 5890 Å with the GFPI, and (3) slit spectropolarimetry in the 1 μm spectral range with the GRIS. Spectral-line inversions were carried out for the Si I 10827 Å Stokes profiles.
Results. Bright points are identified in the Ca II H and blue continuum filtergrams. Moreover, they are also detected in the blue wing of the Na I D2 and Si I 10827 Å lines, as well as in the Ca I 10839 Å line-core images. We carried out two studies to validate the expansion of the magnetic field with height. On the one hand, we compare the photospheric Stokes V signals of two different spectral lines that are sensitive to different optical depths (Ca I vs. Si I). The area at which the Stokes V signal is significantly large is almost three times larger for the Si I line – sensitive to higher layers – than for the Ca I one. On the other hand, the inferred line-of-sight (LOS) magnetic fields at two optical depths (log τ = −1.0 vs. −2.5) from the Si I line reveal spatially broader fields in the higher layer, up to 51% more extensive in one of the BPs. The dynamics of BPs are tracked along the Na I D2 and Si I lines. The inferred flows from Na I D2 Doppler shifts are rather slow in BPs (≲1 km s−1). However, the Si I line shows intriguing Stokes profiles with important asymmetries. The analysis of these profiles unveils the presence of two components, a fast and a slow one, within the same resolution element. The faster one, with a smaller filling factor of ∼0.3, exhibits LOS velocities of about 6 km s−1. The slower component is slightly blueshifted.
Conclusions. The present work provides observational evidence for the expansion of the magnetic field with height. Moreover, fast flows are likely present in BPs but are sometimes hidden because of observational limitations.
Key words: Sun: photosphere / Sun: chromosphere / Sun: magnetic fields / methods: data analysis / techniques: polarimetric / techniques: high angular resolution
© ESO 2019
1. Introduction
The immediate atmospheric layer below the solar surface is unstable and dominated by convective motions. These instabilities are observed as a granular pattern which consists, on its smallest scales, of convective cells – granules – and between these cells of dark intergranular lanes. Oftentimes, these relatively dark lanes show small-scale brightenings in various wavelengths such as the molecular bandhead of CH (G-band) (Steiner et al. 2001) or wideband Ca II H and K lines. These very small features are called bright points (BPs) and their average size is on the order of 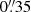 (e.g., Berger et al. 1995; Bovelet & Wiehr 2003). The existence of BPs has been known for many decades (e.g., Mehltretter 1974), although often under different terms. For instance, Muller (1983) called them facular points with a mean lifetime of 18 min. Recently, Liu et al. (2018) investigated the lifetimes of about 1300 isolated BPs of which 10% had lifetimes longer than 7 min while the others had shorter lifetimes.
(e.g., Berger et al. 1995; Bovelet & Wiehr 2003). The existence of BPs has been known for many decades (e.g., Mehltretter 1974), although often under different terms. For instance, Muller (1983) called them facular points with a mean lifetime of 18 min. Recently, Liu et al. (2018) investigated the lifetimes of about 1300 isolated BPs of which 10% had lifetimes longer than 7 min while the others had shorter lifetimes.
Observations indicate a strong correlation between BPs and magnetic flux concentrations (e.g., Viticchié et al. 2010; Yang et al. 2016). However, some studies report that not all BPs present polarization signals. In a statistical study, Beck et al. (2007) find that 94% percent of 447 identified BPs were co-spatial with polarization signals above the noise level. In another work, Berger & Title (2001) analyzed 720 G-band BPs and find that all were of magnetic nature. Realistic 3D radiative magnetohydrodynamic (MHD) simulations support this correlation (e.g., Shelyag et al. 2004). Yet, caution has to be taken since not all small magnetic elements necessarily coincide with G-band or Ca II H brightenings (de Wijn et al. 2009).
Many studies over the past decades were devoted to the inference of the magnetic field strength in BPs. From multi-line inversions, Beck et al. (2007) infer a magnetic field strength in the range of 500–1400 G. The authors treated the filling factor f as a free parameter, meaning that the area occupied by the magnetic component inside of each pixel can vary. This is an important aspect, as BPs are very small features, which are often not fully resolved by current telescopes because of insufficient angular resolution. Therefore, if a unit filling factor is assumed, the inferred magnetic field strength may change (Criscuoli & Uitenbroek 2014). Utz et al. (2013), assuming f = 1, report on field strengths of BPs which formed a two-component distribution with a clear peak in the kilogauss regime around 1300 G to 1500 G and a second tail distribution peaking around a few hundred Gauss. The latter might be due to measurement difficulties, such as capturing the BP before or after the convective collapse. Fields on the order of kilogauss were also found in 3D MHD simulations (Riethmüller et al. 2014), regardless of their presence inside or outside of active regions (Criscuoli & Uitenbroek 2014). Even strong longitudinal magnetic fields can be inferred during the formation process of BPs, reaching up to ∼2000 G (Nagata et al. 2008).
Bright points were observed with very high spatial resolution (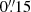 –
–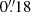 ) using the SUNRISE balloon-borne solar observatory (Solanki et al. 2010). It was found that, when BPs merge, an enhancement of the BP brightness is related to an increase of the magnetic field strength (Requerey et al. 2015). The opposite occurs when BPs fragment. The continuous merging and fragmenting of BPs is likely triggered by the evolution of granules, which constantly compress and stretch the field lines (Martínez González et al. 2011). Kilogauss fields are then related to compressed magnetic structures and lower fields to fragmented BPs. This explains why a two-component magnetic field distribution appears in larger statistical studies. Moreover, SUNRISE data illustrated large asymmetries of the Stokes V profiles in individual network patches (Martínez González et al. 2012). These asymmetries varied across the patch, showing that the internal structure of the magnetic patch was at least partially resolved. The results of the spectral-line inversions and the Stokes V asymmetries suggested a geometry with magnetic field lines that expand with height. Such a geometry matches with classical models (e.g., Spruit 1976; Solanki 1993).
) using the SUNRISE balloon-borne solar observatory (Solanki et al. 2010). It was found that, when BPs merge, an enhancement of the BP brightness is related to an increase of the magnetic field strength (Requerey et al. 2015). The opposite occurs when BPs fragment. The continuous merging and fragmenting of BPs is likely triggered by the evolution of granules, which constantly compress and stretch the field lines (Martínez González et al. 2011). Kilogauss fields are then related to compressed magnetic structures and lower fields to fragmented BPs. This explains why a two-component magnetic field distribution appears in larger statistical studies. Moreover, SUNRISE data illustrated large asymmetries of the Stokes V profiles in individual network patches (Martínez González et al. 2012). These asymmetries varied across the patch, showing that the internal structure of the magnetic patch was at least partially resolved. The results of the spectral-line inversions and the Stokes V asymmetries suggested a geometry with magnetic field lines that expand with height. Such a geometry matches with classical models (e.g., Spruit 1976; Solanki 1993).
Plasma flows related to BPs are found to be directed downward. In the photosphere, using separate observations for the Fe I 5250.5 Å and Fe I 6302 Å lines, the Doppler shifts reach up to 6 km s−1 (Utz et al. 2014; Nagata et al. 2008). Yet, the average values are around 2.4 km s−1. Further up in the atmosphere, in the upper photosphere or lower chromosphere, the line-of-sight (LOS) velocities associated to spectral shifts of the Na I D1 line can yield 7 km s−1 (Jess et al. 2010). Hence, a continuous downflow across several layers of the solar atmosphere seems to take place at BPs. Evidence in this regard was provided by Fischer et al. (2009) who found co-temporal large downflows in BPs encoded in two photospheric spectral lines, one in the deep photosphere (Fe I 6302 Å) and another one in the upper photosphere (Mg I b2).
This work is based on multi-wavelength observations of BPs acquired with the 1.5 m GREGOR solar telescope (Schmidt et al. 2012). Thus, we can investigate some BP parameters with height. Such studies are needed for the modeling of BPs (see, e.g., Gent et al. 2013). Only by multi-wavelength measurements in various heights of the solar atmosphere we will be able to constrain BP models, which are needed for MHD wave propagation and lead to lifelike results (e.g., Fedun et al. 2011). In this study, three carefully selected isolated BPs are analyzed in depth. The spatial resolution is highest in the blue part of the visible spectrum, which facilitates studying the small-scale structure of BPs, whereas the near-infrared spectral range at 1 μm offers a spectropolarimetric diagnostic window, including photospheric and chromospheric lines, to determine the magnetic structure and LOS velocities. Sections 2 and 3 describe the observations, instrumental setup, and data analysis. Section 4 covers the results. The results are discussed in Sect. 5 and the main findings are summarized in the Conclusions (Sect. 6).
2. Observations and data reduction
The target of the observations was a decaying pore, prominently surrounded by a network of BPs and tiny pores, which belonged to active region NOAA 12708. The active region rotated onto the solar disk on 2018 May 04. The observations took place a few days later on 2018 May 09. The location of the pore was close to disk center, at coordinates (x, y)=(62″, −120″), where the cosine of the heliocentric angle is μ = 0.99. The three analyzed BPs are highlighted with a red circle in Fig. 1. They were chosen because they were isolated, that is, far away from the central pore and outside of the densely-packed network of BPs. Furthermore, all three BPs were inside of the FOV of all instruments. The negative polarity of the magnetic field covered almost the entire FOV except for BP (a), which belonged to a small area of positive polarity.
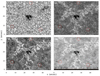 |
Fig. 1. Overview of small AR NOAA 12708. Starting in the upper left panel and moving clockwise: Speckle-restored blue continuum (4505 Å) and Ca II H (3968 Å) images from HiFI, Si I 10827 Å slit-reconstructed blue wing (λ0 − 0.35 Å) from GRIS, and MOMFBD-restored blue-line wing (λ0 − 0.22 Å) image from GFPI of the Na I D2 5890 Å line. We note that the image scales from all instruments are different. The black stripe in the lower part of the Si I λ0 − 0.35 Å image indicates that there are no data available. Red circles identified by letters (a)–(c) indicate the isolated BPs under study. It is interesting to note that the BPs in the Si I λ0 − 0.35 Å panel do not always match the other instruments because it is a slit-reconstructed image in the range of 08:38–09:07 UT. |
The instrumental setup at the 1.5 m GREGOR telescope consisted of three different instruments, which were recording data simultaneously. The analyzed time range spans between 08:38–09:07 UT, roughly 30 min. A detailed description of the used instrumentation follows below.
2.1. Spectropolarimetric rasters scans in the near infrared
The GREGOR Infrared Spectrograph (GRIS, Collados et al. 2012) acquired full-Stokes spectra in the Si I 10827 Å spectral range. The number of accumulations per step were ten, with an exposure time of 100 ms each. The whole map encompassed 300 steps (roughly 30 min), with a step size and pixel size along the slit of 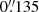 , yielding a field of view (FOV) of 60″ × 40″. The data was dark and flat-field corrected, as well as polarimetrically calibrated using the GREGOR polarimetric unit (Hofmann et al. 2012) and the standard procedures (Collados 1999, 2003). The Stokes profiles were normalized to the average continuum, which was determined from different areas across the FOV excluding regions with significant polarization signals.
, yielding a field of view (FOV) of 60″ × 40″. The data was dark and flat-field corrected, as well as polarimetrically calibrated using the GREGOR polarimetric unit (Hofmann et al. 2012) and the standard procedures (Collados 1999, 2003). The Stokes profiles were normalized to the average continuum, which was determined from different areas across the FOV excluding regions with significant polarization signals.
The spectral range comprised the photospheric Ca I 10838.97 Å and Si I 10827.09 Å lines. Both lines are Zeeman triplets with an effective Landé factor of geff = 1.5 (Balthasar et al. 2016). Moreover, the spectral range included the chromospheric He I 10830 Å triplet. The spectral sampling was 18.04 mÅ pixel−1. The wavelength was calibrated on an absolute scale using the two telluric lines next to the He I 10830 Å triplet and taking into account orbital motions, solar rotation, and gravitational redshift. A detailed description of the wavelength calibration is given in the appendices of Martinez Pillet et al. (1997) and Kuckein et al. (2012a). All reference wavelengths throughout the manuscript were taken from the National Institute of Standards and Technology (NIST, Kramida et al. 2018). Bright points in the near-infrared, within the FOV of GRIS, are well identified in the core of the Ca I line and in the blue wing of the Si I line at λ0 − 0.35 Å (lower right panel of Fig. 1).
2.2. Imaging spectroscopy in the visible
Imaging spectroscopy along the Na I D2 5889.95 Å line (see Table 1) was carried out with the GREGOR Fabry-Pérot Interferometer (GFPI, Puschmann et al. 2012, and references therein). The Na I D2 line maps the upper photosphere to lower chromosphere in the solar atmosphere. The scan along the spectral line comprised 16 wavelength positions on an equidistant grid with a spectral sampling of 56.5 mÅ. The number of images per wavelength position was eight and the exposure time was 40 ms. Between 08:38–09:07 UT 52 scans, with a cadence of 31.6 s, were acquired. The GFPI setup included two synchronized CCD cameras, which were located in the narrow- and broad-band channels of the GFPI. This configuration allowed for image restoration using multi-object multi-frame blind deconvolution (MOMFBD, Löfdahl et al. 2002; van Noort et al. 2005). Before restoration, all images were corrected by the average dark image and divided by the flat field. The FOV after image restoration was 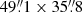 , with a spatial sampling of 0.04″ pixel−1 and no binning. The MOMFBD-restored narrow-band images were finally corrected for the prefilter transmission curve and the blueshift across the FOV. The data reduction and image restoration procedures are part of AIP’s software package sTools1 (Kuckein et al. 2017). The blue wing of the Na I D2 line at λ0 − 0.22 Å reflects well the location of the BPs (lower left panel of Fig. 1).
, with a spatial sampling of 0.04″ pixel−1 and no binning. The MOMFBD-restored narrow-band images were finally corrected for the prefilter transmission curve and the blueshift across the FOV. The data reduction and image restoration procedures are part of AIP’s software package sTools1 (Kuckein et al. 2017). The blue wing of the Na I D2 line at λ0 − 0.22 Å reflects well the location of the BPs (lower left panel of Fig. 1).
Interference filters for HiFI and GFPI.
2.3. Very fast imaging in the violet and blue
The highest spatial resolution was achieved in the violet and blue spectral range using the two synchronized sCMOS cameras of the High-resolution Fast Imager (HiFI, Kuckein et al. 2017; Denker et al. 2018a). Table 1 describes the properties of the two interference filters. The spatial sampling was 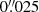 pixel−1. Nevertheless, the angular resolution R of the telescope, following equation R = λ/D (where λ is the wavelength and D is the effective diameter of the primary mirror), yields
pixel−1. Nevertheless, the angular resolution R of the telescope, following equation R = λ/D (where λ is the wavelength and D is the effective diameter of the primary mirror), yields 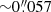 and
and 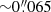 , for Ca II H and blue continuum, respectively. Hence, we oversampled by a factor of about 1.14 and 1.30, respectively.
, for Ca II H and blue continuum, respectively. Hence, we oversampled by a factor of about 1.14 and 1.30, respectively.
The observing strategy with HiFI consisted in repeated bursts of 500 images with a frame rate of 47 Hz and an exposure time of 7 ms (between 08:38 and 09:00 UT) and 6 ms (between 09:00 and 09:07 UT), to adjust for intensity changes because of the rising Sun. A series of 500 images was acquired within 23 s. Dark and flat-field corrections were carried out as part of the data reduction pipeline sTools. Afterward, the 100 best images of each series were identified using the Median Filter-Gradient Similarity (MFGS) algorithm (Deng et al. 2015; Denker et al. 2018b). The selected images were then restored using the speckle-interferometry code KISIP (Wöger & von der Lühe 2008).
The upper panels of Fig. 1 exhibit speckle-restored HiFI images. Bright points are straightforwardly identified in the Ca II H filtergram, whereas the blue continuum image shows less contrast between the BP and its surroundings. The regions of interest and a comparison between the isolated BPs under study in both filters is depicted in Fig. 2.
 |
Fig. 2. Region-of-interest including the three isolated BPs (a)–(c) from Fig. 1. Left column: blue-continuum images; right column: corresponding Ca II H image. The white box shows the size of the FOV of the inversions shown in Fig. 4. |
3. Data analysis
3.1. Alignment
The spatial resolution and FOV of the three instruments is different. In addition, difficulties arise when matching slit-reconstructed images, like the ones acquired with GRIS, to imaging instruments such as GFPI and HiFI. The spatial sampling of GRIS is about 5.4 times larger than the one of HiFI. To accomplish this task, calibration images of the United States Air Force (USAF) resolution target inserted at GREGOR’s focus F3 were used. The standard rotation and correlation procedures from the Interactive Data Language (IDL), as well as the alignment routine for proper motion measurements from Molowny-Horas (1994) and Yi & Molowny-Horas (1995), which belongs to the oslolib, were used to successfully match the images from different instruments. Furthermore, a visual inspection was carried out to verify their coincidence, since all analyzed BPs appear as enhancements of the intensity for all wavelengths.
3.2. Inversions
The Si I 10827 Å line was inverted using the Stokes Inversions based on Response functions (SIR; Ruiz Cobo & del Toro Iniesta 1992) code. The abundance was taken from Grevesse (1984) (7.50 for Si) and the logarithm of the oscillator strength times the multiplicity of the lower level, log gf = 0.363, from Borrero et al. (2003). The used collisional broadening parameters α and σ, which result from the quantum mechanical theory of Anstee, Barklem, and O’Mara, were 0.231 and 2.0412 × 10−14, respectively. The SIR code assumes local thermodynamical equilibrium (LTE) and hydrostatic equilibrium to iteratively solve the radiative transfer equation. The code provides height-dependent physical parameters. The height stratification is expressed in logarithmic units of the optical depth (log τ) at 5000 Å. Up to four nodes across the atmospheric height were used. The microturbulence was kept constant with height. A single magnetic component was used together with a non-magnetic component (only intensity). The latter serves in the inversions to infer the filling factor f. The filling factor accounts for the fraction of magnetic component within the resolution element of the observations and is used to determine the magnetic field strength. The use of a filling factor is necessary for the Si I data, as we are not fully resolving the BPs. This can be clearly seen by comparing the high-resolution Ca II H and blue-continuum filtergrams to the slit-reconstructed Si I map. The non-magnetic component was computed by averaging the Stokes I profiles of a quiet-Sun area within the FOV. Two magnetic components were used for a few pixels to disentangle the atmosphere that produced some specific asymmetries in the Stokes V profiles near BPs (see Sect. 4.4).
The inversions were initialized with three different model atmospheres: the FAL-C and FAL-F models (Fontenla et al. 2006) and the Harvard-Smithsonian reference atmosphere model (HSRA; Gingerich et al. 1971). The FAL-C and HSRA models represent quiet regions of the Sun, whereas FAL-F simulates an active network. The models cover an optical depth range at 5000 Å between 1.4 ≥ log τ ≥ −4.0. The resulting atmospheres, which best fit the observed Stokes profiles were stored. The evaluation of the fits was performed by using a χ2-test, which computes the sum of the squared differences between the observed and synthesized Stokes profiles.
Particular attention needs to be drawn to the line core of the Si I line, since it is formed under non-LTE (NLTE) conditions. The main NLTE effect is that the line core is deeper than under LTE conditions (Bard & Carlsson 2008). Response functions to a given quantity – magnetic field and LOS velocity – allow to determine at which optical depths range the spectral line is sensitive to perturbations on such quantity. The response functions were calculated using one atmospheric model obtained from the inversions of each bright point (a–c). It is found that the Si I line is sensitive to changes in the atmosphere below log τ ≲ −1.0 until almost log τ ∼ −4.0. Shchukina et al. (2017) found NLTE effects also in Stokes Q, U, and V in the inner wings of the Si I line, around Δλ = 0.1 Å. A comparative study inverting the Si I line with and without departure coefficients from LTE with SIR demonstrated that rms variations of the field strength (up to 150 G) and the LOS velocity (up to 0.2 km s−1) exist at log τ = −0.2 (Kuckein et al. 2012b). We consider these variations rather low and will constrain our analysis between −1.0 ≥ log τ ≥ −2.5, hence avoiding smaller optical depths.
4. Results
4.1. Bright point fine structure
The blue continuum at 4505 Å and Ca II H images from HiFI reveal small-scale details in and around the BPs. Rather than point-like features, the observed BPs resemble chains of BPs which appear as elongated tube-like structures (Fig. 2). The length of individual BPs lies in the subarcsecond range, whereas chains of BPs extend a few seconds of arc. Moreover, the thickness of isolated BPs, as shown in Figs. 2a and c, corresponds to 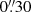 –
–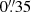 (217–253 km). They lie along intergranular lanes and are very dynamic. Time-evolution movies (not shown) exhibit that their shape is molded by the expansion and displacement of the adjacent granules, which are much larger than the BPs themselves. A detailed analysis of the filtergram time evolution is beyond the scope of this work and is postponed to a future paper.
(217–253 km). They lie along intergranular lanes and are very dynamic. Time-evolution movies (not shown) exhibit that their shape is molded by the expansion and displacement of the adjacent granules, which are much larger than the BPs themselves. A detailed analysis of the filtergram time evolution is beyond the scope of this work and is postponed to a future paper.
4.2. Bright point infrared Stokes profiles
Bright points were easiest identified in the high-spatial resolution HiFI broad-band blue-continuum and Ca II H images. Afterward, the corresponding area was scrutinized in the near-infrared data. Interestingly, BPs are also well distinguished when selecting the blue wing of the Si I line in a slit-reconstructed image, at about λ0 − 0.35 Å away from the line core. The fact that BPs appear bright in the wing of the Si I line, and not in the line core, indicates that the perturbation is located in deep layers of the photosphere, because the Si I line core is formed in the upper photosphere. The same applies to the Na I D2 line, where BPs are best detected in filtergrams of the blue wing, at about λ0 − 0.22 Å away from the line core.
In the three isolated BPs, the Stokes V profiles with the largest amplitude match the brightest intensity in Si I λ0 − 0.35 Å (e.g., Fig. 5). An example showing the four Stokes profiles with highest signal (up to V/Ic ∼ 0.07) in BP (b) is presented in Fig. 3. In this figure, the spectral profiles were slightly smoothed by convolving them with a normalized Gaussian with a FWHM of ∼36 mÅ, which roughly corresponds to the spectral resolution. The red line shows the best fit from the SIR inversions. The dashed vertical line in the lower panel marks the spectral position of Si I λ0 − 0.35 Å, where BPs are most easily identified. The dotted vertical lines mark the wavelengths at rest of Si I 10827 Å and the blue (He I b) and blended red (He I r) components of the He I 10830 Å triplet.
 |
Fig. 3. Four Stokes V/Ic profiles with the largest amplitude belonging to BP (b), and their corresponding Stokes I/Ic profiles. The various Stokes I (V) profiles are shifted by +0.20 (+0.05) along the y-axis or ordinate. The wavelength axis is centered at the Si I line at rest. The red line shows the best fit obtained from the SIR inversion. The dotted vertical lines show the positions at rest of Si I and of the blue (He I b) and red (He I r) components of He I. The dashed vertical line indicates Si I λ0 − 0.35 Å, which corresponds to the image shown in the lower right corner of Fig. 1. |
Upon closer inspection, the Si I profiles of BP (b) shown in Fig. 3 exhibit asymmetries. The Stokes I/Ic red wing appears more tilted compared to the blue wing and Stokes V/Ic shows a much broader and extended red lobe compared to the blue one. A likely explanation for this is the existence of gradients in the physical parameters along the LOS, that is, the quantities vary across different optical depths of the solar atmosphere. Stokes Q and U were not taken into account, as their profiles were at the noise level and therefore not discernible. The standard deviation of the Stokes V/Ic, Q/Ic, and U/Ic profiles computed in the continuum was around 10−3, which is of the same order of magnitude as the standard deviation of the Stokes Q/Ic and U/Ic profiles in the spectral line itself.
No polarization signatures were detected in the He I profiles of the selected BPs (Fig. 3). Stokes V/Ic appears completely flat and the red component of Stokes I/Ic shows some, but very low, absorption. Hence, if polarization signals were present, they were very weak, below the noise level of our data.
4.3. Magnetic field structure and Doppler velocities
Spectral line inversions of the Si I Stokes profiles were carried out for the three selected isolated BPs. We concentrated on a zoom of the region-of-interest in GRIS of about 3″ × 3″, which generously covered the small BPs (white box in Fig. 2). Solely Stokes I and V were taken into account, as the Stokes signals of Q and U were at the noise level. Furthermore, the observed FOV was close to disk center, which assures that the differences between the LOS magnetic field and the vertical magnetic field in the solar reference frame (BLOS ≈ Bvertical) are small. Vertical magnetic fields refer to radially oriented fields.
The longitudinal magnetic field in each pixel was computed using the equation
taken from Landi Degl’Innocenti et al. (1992), where |B| is the magnetic field strength, f the filling factor, and γ the LOS inclination of the magnetic field. All three parameters were inferred during the SIR inversions. The inferred filling factor in the area of the BPs was, on average, in the range of 0.3–0.5.
The longitudinal magnetic field at two different optical depths inferred from the Si I line is shown in Fig. 4. From left to right, the isolated BPs (a)–(c) are depicted. The lower row corresponds to a larger optical depth in the solar atmosphere (log τ = −1.0), whereas the top row corresponds to log τ = −2.5. The first column shows BP (a), which has an inverted color table with respect to BPs (b)–(c), because of the positive polarity. A visual inspection comparing BLOS between the two optical depths reveals that the field covers a larger fraction of the FOV at log τ = −2.5. On the contrary, at log τ = −1.0, the field is more concentrated. Let us further quantify this expansion. Therefore, we identified pixels within the FOV of Fig. 4 close to the BPs, which had BLOS > 100 G or BLOS < −100 G, depending on the polarity of the BP. This value is a good threshold to encompass the LOS magnetic field for all BPs. We found an expansion of the magnetic field with height in all three BPs. In particular, the smallest extension was found for BP (a), with an increment of about 7% of the pixels fulfilling |BLOS|> 100 G. We note that BP (a) has also the smallest size of all the studied BPs (Fig. 2). The largest increment of the area of the magnetic field by 51% was seen in BP (b), followed by 19% for BP (c).
 |
Fig. 4. Longitudinal magnetic field and velocity maps inferred from the Si I 10827 Å inversions of the three isolated BPs at two different optical depths, log τ = −1.0 (bottom) and −2.5 (top). Bright points (a)–(c) are shown from left to right. We note that BP (a) has opposite polarity as compared to BPs (b) and (c). Magnetic fields are clipped between −200 G and +600 G for BP (a), and between −600 G and +200 G for BPs (b–c). LOS velocities are clipped between ±4 km s−1. Negative velocities represent flows along the LOS toward the observer, that is, upflows because of the proximity to disk center. The FOV corresponds to a zoom of the region-of-interest (white box in Fig. 2). |
We repeated a similar experiment comparing the circular polarization signal of the photospheric Ca I 10839 Å line to the Si I line. The former is formed in a rather thin layer corresponding to the deep photosphere (e.g., Felipe et al. 2016), while the latter in the upper photosphere. The middle panels of Fig. 5 compare the absolute maximum amplitude of Stokes Vmax/Ic among both lines. The amplitude of the circular polarization arising from the Ca I line is much smaller than the Si I one. However, this is mainly due to the fact that the spectral line is much shallower than the deep Si I line. What is more important is the spatial extension of the Stokes Vmax/Ic signals in both lines. The Ca I Stokes Vmax/Ic signals appear compact around the BP, whereas the Si I counterpart shows a widespread area centered at the BP. This wider area of the Si I signal provides further evidence of the expansion of the magnetic field lines with height at the isolated BP.
 |
Fig. 5. Zoom of the region-of-interest of 3″ × 3″ belonging to BP (b) from Fig. 2. Lower two panels: intensity of the Si I line in the core (left) and averaged blue wing at around λ0 − 0.35 Å (right), where BPs are well detected. Middle left (right) panel: unsigned maximum signal in Stokes Vmax/Ic from the Si I 10827 Å (Ca I 10839 Å) line. Upper left panel: longitudinal magnetic field at log τ = −1 inferred from the Si I inversions. A zoom of the HiFI blue-continuum image showing the fine structure is exhibited in the upper right panel. Pixels enclosed inside the white contours show atypical Si I Stokes V profiles, with two discernible red lobes like the example shown in Fig. 6. |
The order of magnitude of the longitudinal magnetic fields inferred from the Si I inversions (BLOS) is computed for the three isolated BPs. For this purpose, an average of 5 × 5 pixels (about 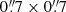 ) centered at the BPs is calculated and then averaged over both heights (log τ = −1.0 and −2.5). The mean LOS magnetic field is in the range of 220–340 G. Individual pixels, with magnetic fields along the LOS of up to 620 G, were found in BP (b).
) centered at the BPs is calculated and then averaged over both heights (log τ = −1.0 and −2.5). The mean LOS magnetic field is in the range of 220–340 G. Individual pixels, with magnetic fields along the LOS of up to 620 G, were found in BP (b).
The Si I inferred LOS velocity maps reveal that the studied isolated BPs are associated with downflows (redshifts). This is not surprising as BPs are located in intergranular lanes, between granules which have rising plasma in their center. The average LOS velocities centered in the same abovementioned box of 5 × 5 pixels for the three BPs is in the range of 0.6–3.1 km s−1 for log τ = −1.0. Moreover, for log τ = −2.5 we find average LOS velocities between 0.0 and 1.8 km s−1. In BPs (b) and (c), the mean velocities clearly decrease with height, whereas BP (a) shows no variation with height, also not in its standard deviation within the 5 × 5 pixels box. Nevertheless, these results have to be interpreted with caution as the Stokes profiles in the BPs show asymmetries which are likely produced by different flows along the LOS (Fig. 3). We will investigate this in the next section.
4.4. Highly redshifted Stokes V lobes
All three isolated BPs reveal signs of asymmetric Stokes V profiles. This becomes evident not only when inspecting the profiles in the center of the BP (Fig. 3), but also even clearer a few pixels away from the center (Fig. 5). For example, for BP (b), two distinguishable red lobes in the Stokes V profile are found within the white contour in Fig. 5. An example of the shape is depicted in Fig. 6. The observed intensity profile in the lower left panel is not symmetric, having a red wing which is wider than the blue wing. Inspecting the Stokes V profile reveals that another magnetized component is inside the resolution element. In order to disentangle the two signals for these pixels, we carried out inversions with two magnetized components and one non-magnetic component, to deduce the velocity of the highly shifted component. The inversions were initialized with a slightly different setup as the regular single magnetic component inversions. More weight was given to Stokes V to assure a good fit to the second magnetic component. To decrease the number of free parameters and focus on the Doppler shift of the second component, the macroturbulence was fixed in both model atmospheres to the theoretical value of the spectral resolution of the data (∼1 km s−1), and only two nodes were used for magnetic field strength, LOS velocity, and inclination of the field. The filling factor was left as a free parameter and served as a parameter to weight the importance of each magnetized atmosphere inside of the pixel. The outcome of the inversion is presented in Fig. 6 as a red solid line in the lower two panels. The Stokes I/Ic and V/Ic profiles which arise from each individual atmosphere, weighted by their corresponding filling factor in the case of Stokes V/Ic, are displayed in the upper panels. The coexistence of two magnetic components is clearly evident within the same resolution element. Both components share similar magnetic field and inclination values, but significantly differ in their Doppler shifts. When averaging the LOS velocities across −1.0 ≥ log τ ≥ −2.5 (16 layers in optical depth), a blue shifted component with a LOS velocity of vLOS, 1 ≈ −1 km s−1 and a standard deviation (across the 16 layers of optical depth) of σ1 = 0.16 km s−1 is found. Conversely, a strongly redshifted component with a LOS velocity of vLOS, 2 ≈ 6 km s−1 and σ2 = 0.08 km s−1 is retrieved (red solid line in the upper panels of Fig. 6). The blueshifted magnetic component has a larger filling factor (f1 ≈ 0.7) compared to the highly redshifted one (f2 ≈ 0.3). Hence, the later contributes less to the observed Stokes profiles.
 |
Fig. 6. Representative example of Stokes I/Ic and V/Ic profiles of a highly redshifted pixel close to the center of BP (b). The profiles are taken from inside of the white contour of Fig. 5. Lower two panels: observations (black dots) and best fit (solid red line) from a two-component SIR inversion. Upper two panels: synthesized profiles arising from the two atmospheric models obtained with SIR which coexist within the same resolution element. Atmosphere 1 (blue solid line) and 2 (red solid line) have a filling factor of about 0.7 and 0.3, respectively. The inferred average LOS velocity and inclination between −1.0 ≥ log τ ≥ −2.5 from this particular fit is vLOS, 1 ∼ −1 km s−1 and γ1 ∼ 172° and vLOS, 2 ∼ 6 km s−1 and γ2 ∼ 169°, for atmospheres 1 and 2, respectively. |
4.5. Na I Doppler shifts
Simultaneous spectral information of the Na I D2 line in the abovementioned BPs is provided by the GFPI. The closest scan in time for each BP was used to compute the Doppler shifts at a line depth which corresponds to λ0 ± 0.22 Å. The reason for choosing this particular filtergram is because BPs show their highest contrast at λ0 − 0.22 Å when scanning with the GFPI along the Na I D2 line. The bisector method was used to infer the shift of the inner wings of the line with respect to the quiet-Sun reference profile, which in turn was determined by averaging areas within the whole FOV, which were absent of dark and bright structures. Line-core fits or fits of the whole spectral line with a Gaussian will yield different velocities. The former will map higher layers in the atmosphere, while the latter will provide an average shift of the whole spectral line.
The upper panels of Fig. 7 illustrate the LOS velocities in a small FOV of about 3″ × 3″ centered at each BP. The depth of the line at which the bisectors were computed is marked with a black arrow in the lower left panel. It corresponds to the fifth wavelength position when scanning along the line (roughly at λ0 − 0.22 Å of the Na I D2 line). The black contours mark intensity enhancements associated with the BPs. The three isolated BPs show a common velocity pattern, which is dominated by moderate-to-low downflows. BPs (a) and (b) exhibit the largest velocities, sporadically reaching up to 1 km s−1.
 |
Fig. 7. Upper row: Doppler shifts for BPs (a)–(c) inside the zoomed region-of-interest, using the bisector method at a line depth, which corresponds to about Na I D2λ0 − 0.22 Å. The arrow in the lower left panel illustrates the depth at which the bisector was computed. Black contours mark the area of the BP. Lower panels: average quiet-Sun profile (dotted line) within the whole FOV (Fig. 1). The large dots correspond to the acquired filtergrams along the Na I D2 line with GFPI. The green solid lines exhibit the brightest 25 profiles belonging to the green box in the upper panels. The dashed vertical line marks the wavelength at rest. |
A closer view of the spectral profiles at the BPs is provided in the lower three panels of Fig. 7. The dotted curve represents the quiet-Sun profile. The Na I D2 intensity profiles belonging to the green box in the upper LOS velocity maps are shown in solid green. The green box, centered at the highest intensity of the BP, comprises 25 pixels. The highest intensity refers to the highest value at the wavelength position corresponding to the black arrow in Fig. 7. One interesting observational feature is the enhancement of the inner blue wing. This naturally explains why BPs are best seen in filtergrams corresponding to λ0 − 0.22 Å. The enhancement in the blue inner wing appears in all three isolated BPs. Conversely, the line core intensity remains close to the one of the quiet-Sun reference profile.
The temporal evolution of the average spectral profile within the green box in Fig. 7 is depicted for each BP in the lower panels of Fig. 8. The color table maps the different times from the beginning of the observations (violet) toward the end of the time series (red). As a comparison, the quiet-Sun profile is represented with a dotted line. In addition, the dashed profile matches in time with the Si I observations. The line core does not show significant changes in intensity during the whole times series. Conversely, the wings of the line appear vertically shifted in intensity, especially in the blue wing. This is the reason why it was used as an indicator for BPs. Overall the profiles do not manifest large Doppler shifts.
 |
Fig. 8. Upper row: time evolution of the average LOS velocities computed within the 5 × 5 px2 green box shown in Fig. 7. The vertical bars indicate ± the standard deviation of the velocities within the same box. The overplotted red dashed line shows the average intensity in the blue wing of Na I D2 inside of the same green box. The arrow marks the time of simultaneous GRIS data. Lower row: average intensity profile generated within the same green box. The color code indicates the time of each profile. The dashed vertical line marks the wavelength at rest. The dotted profile represents the quiet-Sun profile whereas the dashed one corresponds in time to the average profile marked with the arrows in the above panels. |
The upper panels of Fig. 8 track the average LOS velocity (black line) and intensity (red dashed line) of the BPs within the same green box marked in Fig. 7. While the solid line depicts the average velocity, the bars indicate one σ (standard deviation within the same box) up and down. This information reveals how much the velocities fluctuate in the BP. Bright point (a) shows the best correlation between the LOS velocity and the intensity. Both follow a similar decreasing trend. The velocities are larger when the BP is prominently seen (higher intensity). The intensity and LOS velocity in BP (b) oscillates, but is overall persistent. As opposed to BP (a), BP (c) seems to be slowly brightening up, as indicated by the positive trend of the intensity. Often, but not always, peaks in intensity are correlated with peaks in velocity. For instance, the intensity peak at around 11 and 21 min has a redshift of about 0.7 km s−1 and 0.6 km s−1 on average, respectively. The standard deviation of the LOS velocities inside the region of interest is generally small. It only oscillates between 0.01 and 0.16 km s−1 during the almost 30 min of observations.
5. Discussion
5.1. Identification of bright points
The current multi-wavelength study shows that BPs are identified in a variety of wavelengths. From our simultaneous observations, BPs are best recognized in the broad-band (FWHM = 11 Å) Ca II H filtergrams, which is the highest angular-resolution data set of the present work. In addition, their fine structure appears in the blue continuum filtergrams, though with less contrast. Caution has to be taken, since small elongated structures, similar to BPs, also appear in blue continuum images but with neither a Ca II H counterpart nor polarization signals in the near-infrared lines. A good example is seen in Fig. 2, at the middle panel at coordinates (x, y) = (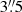 ,
, 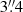 ). This pseudo-BP is almost touching the BP in the blue-continuum filtergram, whereas it is not detectable in the Ca II H filtergram. The question remains if these pseudo-BPs will appear bright in G-band filtergrams, which are typically used to pinpoint BPs.
). This pseudo-BP is almost touching the BP in the blue-continuum filtergram, whereas it is not detectable in the Ca II H filtergram. The question remains if these pseudo-BPs will appear bright in G-band filtergrams, which are typically used to pinpoint BPs.
Furthermore, BPs are well identified in the blue wings of Si I at λ0 − 0.35 Å and Na I D2 at λ0 − 0.22 Å (Fig. 1). This seems to be a common property of other photospheric lines such as the Fe I 5250.5 Å line (Utz et al. 2014). Yet, deeply formed lines such as the Ca I 10839 Å line, also trace BPs in line-core images. On the contrary, higher up in the atmosphere, the chromospheric He I 10830 Å triplet remains unaffected, at least in our studied isolated BPs. In summary, the present data provide evidence of the low-atmospheric nature of BPs. Although BPs were identified in the line core of Na I D1 (which has a similar behavior to the Na I D2 line analyzed in this work), the core rather samples magnetic concentrations in the photosphere, not in the chromosphere (Leenaarts et al. 2010). Jess et al. (2010) reported on BPs in the line core of Na I D1. Their spectral range was just half of the range observed in the present Na I D2 line, and the deduced Doppler shifts reached up to 7 km s−1. We conjecture that their intensity enhancements were mainly related to the strong redshifts of the whole Na I D1 line profile, which then showed the inner blue wing. A LOS velocity of 7 km s−1 corresponds to a Doppler shift of about 0.14 Å for this line.
5.2. Doppler velocities in the bright points
Height-dependent inversions of the Si I 10827 Å line revealed downflows at the three isolated BPs. The LOS velocities were smaller at lower optical depths of the atmosphere, at log τ = −2.5, in two BPs, whereas the other BP remained constant with height. However, when scrutinizing the individual Stokes profiles, we noticed asymmetries in Stokes I and V. Such asymmetries are not uncommon in BPs (e.g., Riethmüller et al. 2014; Martínez González et al. 2012). In our case, in some of the Stokes V profiles, two components became clearly discernible (Fig. 6). The location of these profiles is only a fraction of a second of arc (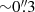 ) away from the center of the BP (within the white contours in Fig. 5), at the border of the BP (see lower right panel in Fig. 5). It is worth to mention that having a spatial variation of the Stokes V asymmetries within the magnetic concentration indicates that the internal structure of the BP is at least partially resolved. However, we do not find single-lobed Stokes V profiles as shown in the SUNRISE high-resolution observations of an individual network patch (Martínez González et al. 2012). An increment of the asymmetries in area and amplitude of Stokes V, away from the core of the BP, was interpreted by Riethmüller et al. (2014) as an indication of a flux-tube canopy. Interestingly, the clearly-discernible two-component Stokes V profiles are not found at the center of the BP. A plausible explanation is that at the center of the BP, the slower component is much stronger than the redshifted one. Hence, it dominates over the weaker component, which still leaves an imprint on the profiles (Fig. 3). The inferred filling factor from the dual magnetic-component inversions further supports this hypothesis. The slower (and stronger) component had a filling factor of 0.7, whereas the weaker component had only 0.3. This unbalance is likely to be even stronger at the center of the BP. Therefore, we assume that two components are present in and around BPs. Both components are possibly coexisting within the same resolution element at different atmospheric optical depths. As a consequence, strong downflows appear in a region of about 1″ × 1″ centered at the BP. The strong LOS velocities reach up to 6 km s−1, which is consistent with downflows inferred from other photospheric lines in BPs, such as the Fe I 6302 Å and 5250 Å lines (Utz et al. 2014; Nagata et al. 2008).
) away from the center of the BP (within the white contours in Fig. 5), at the border of the BP (see lower right panel in Fig. 5). It is worth to mention that having a spatial variation of the Stokes V asymmetries within the magnetic concentration indicates that the internal structure of the BP is at least partially resolved. However, we do not find single-lobed Stokes V profiles as shown in the SUNRISE high-resolution observations of an individual network patch (Martínez González et al. 2012). An increment of the asymmetries in area and amplitude of Stokes V, away from the core of the BP, was interpreted by Riethmüller et al. (2014) as an indication of a flux-tube canopy. Interestingly, the clearly-discernible two-component Stokes V profiles are not found at the center of the BP. A plausible explanation is that at the center of the BP, the slower component is much stronger than the redshifted one. Hence, it dominates over the weaker component, which still leaves an imprint on the profiles (Fig. 3). The inferred filling factor from the dual magnetic-component inversions further supports this hypothesis. The slower (and stronger) component had a filling factor of 0.7, whereas the weaker component had only 0.3. This unbalance is likely to be even stronger at the center of the BP. Therefore, we assume that two components are present in and around BPs. Both components are possibly coexisting within the same resolution element at different atmospheric optical depths. As a consequence, strong downflows appear in a region of about 1″ × 1″ centered at the BP. The strong LOS velocities reach up to 6 km s−1, which is consistent with downflows inferred from other photospheric lines in BPs, such as the Fe I 6302 Å and 5250 Å lines (Utz et al. 2014; Nagata et al. 2008).
This study has been unable to find large Doppler shifts of the Na I D2 line in the three isolated BPs, contrary to the Doppler shifts of up to 7 km s−1 found by Jess et al. (2010) in their data using the Na I D1 line. Nevertheless, these high velocities were not found in all BPs of their observations. In the present data, the Si I Stokes V profiles indicate large flows. Figure 8 illustrates in time the average Na I D2 intensity profiles at the three BPs. There is no indication at any time of large Doppler shifts. Several reasons can be ascribed for the non detection of fast flows in this line. First, the large flows are best seen in the Si I Stokes V profiles and are only faintly intuited in the red wing of Si I Stokes I. Hence, its origin is linked to magnetic structures. Unfortunately, no Stokes V data from Na I D2 was recorded. Therefore, we cannot confirm weather these flows would have left an imprint in the Na I D2 polarimetric signals. Moreover, the low filling factor inferred from the SIR inversions of the fast component (only 0.3), already indicates that this component contributes less than the slower component. Second, the Na I D2 line is a broader line and a second, weaker component would unlikely contribute significantly to the intensity profile. It should be also mentioned that, in general, observations are affected by stray light, which is also the case for GREGOR (e.g., Borrero et al. 2016; Felipe et al. 2016; Denker et al. 2018b). This can affect the apparent size of the BP by mainly smearing effects. Still, it seems that stray-light contamination does not modify the shape of the Stokes profiles, although it can weaken the polarization signals (Quintero Noda et al. 2015). Thus, it is not expected that the present inferred Doppler shifts are significantly influenced by the presence of stray light.
Of particular interest is the case of a forming BP described by Nagata et al. (2008) who deduced a sudden increment of the LOS velocity of ∼6 km s−1 (downward), co-temporal with a significant increment of the longitudinal magnetic field. However, the shape of the Fe I 6302 Å Stokes I profiles from their Fig. 2, closely resembles the intensity profiles shown in our Fig. 3. Likewise, the profiles show asymmetries that are mainly reflected in the red wing, which appears inclined toward the red. This signature is seen before, during, and after the sudden rise of the longitudinal magnetic field. Therefore, this indicates that more than one unresolved component was present in their data all the time within the same resolution element. Thus, the velocities may have been underestimated before and after the sudden increase of the magnetic field.
In the present study, we lack temporal coverage of the near-infrared Stokes profiles. However, we find that all three analyzed BPs, independently of the stage of their life, showed asymmetries in the red wing. This suggests that this phenomenon is rather common, and likely persistent, during the lifetime of BPs. However, more cases of isolated BPs need to be studied. Broader red wings in Stokes V were attributed to downward accelerated and magnetized plasma (Steiner et al. 1998). Such downflows also match with the scenario of convective collapse (Parker 1978) and were already detected in BPs in the upper photosphere using Mg I b2 dopplergrams (Fischer et al. 2009). Higher spatial- and spectral-resolution observations will potentially show more cases of strong downflows associated with BPs.
5.3. Magnetic field expansion with height
It is known that the photospheric magnetic field of small- and large-scale structures expands with height (e.g., Spruit 1976; Solanki 1993; Solanki et al. 1999; Buehler et al. 2015). Such an expansion happens because gas pressure decreases with height and magnetic flux needs to be conserved. For instance, comparing the sizes of BPs by using filtergrams of two photospheric lines, which are sensitive to different optical depths, Rimmele (2004) deduced that the magnetic flux concentration expands with height. Martínez González et al. (2012) studied the asymmetries of Stokes V profiles in a resolved magnetic patch observed with the balloon-borne observatory SUNRISE and suggested a geometry compatible with magnetic features that expand with height. Moreover, simulations showed this expansion by illustrating individual field lines arising from flux sheets in intergranular lanes (Steiner et al. 1998). Here, we search for evidence of such an expansion in observational data of BPs by analyzing different spectral lines and carrying out height-dependent inversions.
First, the circular polarization signals were compared between the Ca I 10839 Å and Si I 10827 Å lines. The former is sensitive to a thin layer in the deep photosphere, while the latter is formed in the upper photosphere. Felipe et al. (2018) estimated a difference of about 300 km in geometrical height between these two lines in the umbra of a sunspot. Likewise, we assume this as an acceptable approximation of the height difference for BPs, which are located deeper along dark intergranular lanes. The spatial extension across the FOV of the Stokes V signals was about a factor of three larger for the Si I line compared to the Ca I line (middle panels of Fig. 5). This difference indicates that the field necessarily spatially expands with height, which is expected because of the decrease of gas pressure.
Secondly, we scrutinized the Si I line itself, which covers several optical depths in the solar atmosphere. To that end, the extension of the inferred longitudinal magnetic field was compared at two optical depths, log τ = −1 and −2.5. All analyzed BPs showed a spatial increment of BLOS of at least 7%. A huge rise in extension of about 51% was deduced for BP (b). This disparity in the percentages is owing to the size of the BPs. Figure 2 shows that all analyzed BPs have a different shape and proportion. Smaller or individual BPs expand less with height. Therefore, it is not surprising that the expansion percentages are different for each BP.
We found rather low values for the longitudinal magnetic fields in BPs, on average 220–340 G. For individual pixels a field strength of up to 620 G was inferred. We note that these values were computed using a filling factor that was determined during the inversions (Eq. (1)). The average filling factor in BPs 1–3 was in the range of 0.30 and 0.50. Compared to lower resolution observations, for instance at the VTT, Beck et al. (2007) inferred values of < 0.15. This is consistent, since higher spatial resolution observations bring along larger filling factors. Furthermore, no linear polarization information was used because the Stokes Q and U signals were at the noise level. We speculate that the transverse magnetic fields might be very small and do not contribute significantly to the magnetic field strength. From simulations, BPs harbor kilogauss magnetic fields (Criscuoli & Uitenbroek 2014). The Si I line is more sensitive to higher layers of the photosphere. The expansion of the magnetic fields with height necessarily implies a decrease of the field strength. We conjecture that this could be the reason for the lower inferred fields. We note also that stray light can weaken the polarization signals (Quintero Noda et al. 2015), thus reducing the inferred field strength.
6. Summary and conclusions
The present work aimed at analyzing the magnetic field expansion with height and the dynamics of three isolated bright points using high-resolution filtergrams and spectropolarimetric data in various spectral lines observed with the 1.5 m GREGOR solar telescope. To the best of our knowledge, the near-infrared spectral range around the Si I 10827 Å line has not yet been explored in relation to BPs. High-resolution filtergrams acquired with the HiFI instrument in broad-band Ca II H and blue continuum (4505 Å) were used to easily identify the BPs. Then, spectroscopic images along the Na I D2 line and one large spectropolarimetric raster scan in the Si I 10827 Å spectral range were used to infer Doppler velocities and LOS magnetic fields. The observations were taken close to disk center. Therefore, we do not expect significant changes between the LOS and local solar reference frames.
The high spatial-resolution filtergrams in the blue-continuum and in the Ca II H line uncover BPs as thin (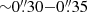 ) features which appear in groups or chains and therefore resemble elongated (few seconds of arc), rather than roundish, structures. The analyzed isolated BPs were visible during the 30 min observations.
) features which appear in groups or chains and therefore resemble elongated (few seconds of arc), rather than roundish, structures. The analyzed isolated BPs were visible during the 30 min observations.
We summarize the most important findings below:
-
The three analyzed isolated BPs were identified simultaneously in Ca II H (3968 Å) and blue continuum (4505 Å) filtergrams. Furthermore, they were best detected in filtergrams in the blue wing of the Na I D2 line (at λ0 − 0.22 Å) and slit-reconstructed images of the Si I 10827 Å line (at λ0 − 0.35 Å), as well as in the line core of the Ca I 10839 Å line.
-
The studied BPs were of magnetic nature, as depicted in Fig. 4. The longitudinal magnetic fields are on average in the range of 220–340 G, with individual pixels of up to 620 G. The fields might be slightly underestimated due to the presence of stray light in the observations.
-
By analyzing the spatial extension of Stokes V signals between the Ca I and the Si I lines (∼300 km height difference), we provided evidence for the expansion of the magnetic field with height in BPs (Fig. 5). The Stokes V signals of Si I occupied about three times the area of the Ca I counterpart. More evidence was provided by comparing the spatial extension of the longitudinal magnetic field inferred from the Si I line at two different optical depths (log τ = −1.0 and −2.5). The field expands between 7% and 51% with height, depending on the size of the BPs (Fig. 4).
-
The LOS velocities deduced from Na I D2 at λ0 − 0.22 Å were moderate to low (≲1 km s−1). Conversely, the Si I Stokes I and V profiles showed asymmetries which were ascribed to gradients along the LOS (Fig. 3). Some of the Stokes V profiles, about
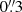 away from the center of the BP, revealed two discernible components. Two-component inversions unveiled downflows of up to 6 km s−1 in one component, while the slower one was slightly blueshifted but had a much larger filling factor (Fig. 6). We speculate that both components are also present at the center of the BP but are masked by the stronger (and slower) component. Asymmetries in the red wing of the Stokes profiles support this argument (Fig. 3). We suggest that more than one component within the resolution element may be common in BPs.
away from the center of the BP, revealed two discernible components. Two-component inversions unveiled downflows of up to 6 km s−1 in one component, while the slower one was slightly blueshifted but had a much larger filling factor (Fig. 6). We speculate that both components are also present at the center of the BP but are masked by the stronger (and slower) component. Asymmetries in the red wing of the Stokes profiles support this argument (Fig. 3). We suggest that more than one component within the resolution element may be common in BPs. -
The He I 10830 Å triplet was not sensitive to the studied isolated BPs. However, we cannot rule out weak polarization signals which may become visible when using larger exposure times.
Our findings shed new light on the dynamics and the magnetic field expansion present in BPs. Further work needs to be carried out to follow the time evolution of Stokes profiles in BPs with high temporal, spatial, and spectral resolution. An important role will play the multi-wavelength capabilities of the next generation of large-aperture telescopes. Such multi-line observations are crucial to better follow the magnetic field lines and flows across the solar atmosphere. We expect further advances with the advent of the 4 m Daniel K. Inouye Solar Telescope (DKIST, Tritschler et al. 2015) and European Solar Telescope (EST, Jurčák et al. 2019).
http://gregor.aip.de/ (requires free registration).
Acknowledgments
The 1.5 m GREGOR solar telescope was built by a German consortium under the leadership of the Leibniz-Institut für Sonnenphysik in Freiburg (KIS) with the Leibniz-Institut für Astrophysik Potsdam (AIP), the Institut für Astrophysik Göttingen (IAG), the Max-Planck-Institut für Sonnensystemforschung in Göttingen (MPS), and the Instituto de Astrofísica de Canarias (IAC), and with contributions by the Astronomical Institute of the Academy of Sciences of the Czech Republic (ASCR). The author thanks Drs. H. Balthasar and S. J. González Manrique for their help during the observations. Drs. H. Balthasar, S. J. González Manrique, I. Kontogiannis, and D. Utz, are greatly acknowledged for helpful discussions and for providing very valuable input on the manuscript. In addition, the author thanks Dr. C. Denker for carefully reading the manuscript and providing suggestions, as well as the anonymous referees for their criticism which led to an improved version of the manuscript. This research has made use of NASA’s Astrophysics Data System. Funding from the Horizon 2020 projects PRE-EST (grant agreement No 739500) and SOLARNET (No 824135) is greatly acknowledged.
References
- Balthasar, H., Gömöry, P., González Manrique, S. J., et al. 2016, Astron. Nachr., 337, 1050 [NASA ADS] [CrossRef] [Google Scholar]
- Bard, S., & Carlsson, M. 2008, ApJ, 682, 1376 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, C., Bellot Rubio, L. R., Schlichenmaier, R., & Sütterlin, P. 2007, A&A, 472, 607 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berger, T. E., & Title, A. M. 2001, ApJ, 553, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, T. E., Schrijver, C. J., Shine, R. A., et al. 1995, ApJ, 454, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Borrero, J. M., Bellot Rubio, L. R., Barklem, P. S., & del Toro Iniesta, J. C. 2003, A&A, 404, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borrero, J. M., Asensio Ramos, A., Collados, M., et al. 2016, A&A, 596, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bovelet, B., & Wiehr, E. 2003, A&A, 412, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buehler, D., Lagg, A., Solanki, S. K., & van Noort, M. 2015, A&A, 576, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collados, M. 1999, in Third Advances in Solar Physics Euroconference: Magnetic Fields and Oscillations, eds. B. Schmieder, A. Hofmann, & J. Staude, ASP Conf. Ser., 184, 3 [NASA ADS] [Google Scholar]
- Collados, M. V. 2003, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, eds. S. Fineschi, 4843, 55 [Google Scholar]
- Collados, M., López, R., Páez, E., et al. 2012, Astron. Nachr., 333, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Criscuoli, S., & Uitenbroek, H. 2014, A&A, 562, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deng, H., Zhang, D., Wang, T., et al. 2015, Sol. Phys., 290, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Denker, C., Kuckein, C., Verma, M., et al. 2018a, ApJS, 236, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Denker, C., Dineva, E., Balthasar, H., et al. 2018b, Sol. Phys., 293, 44 [NASA ADS] [CrossRef] [Google Scholar]
- de Wijn, A. G., Stenflo, J. O., Solanki, S. K., & Tsuneta, S. 2009, Space Sci. Rev., 144, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Fedun, V., Shelyag, S., & Erdélyi, R. 2011, ApJ, 727, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Felipe, T., Collados, M., Khomenko, E., et al. 2016, A&A, 596, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Felipe, T., Kuckein, C., & Thaler, I. 2018, A&A, 617, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, C. E., de Wijn, A. G., Centeno, R., Lites, B. W., & Keller, C. U. 2009, A&A, 504, 583 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontenla, J. M., Avrett, E., Thuillier, G., & Harder, J. 2006, ApJ, 639, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Gent, F. A., Fedun, V., Mumford, S. J., & Erdélyi, R. 2013, MNRAS, 435, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Gingerich, O., Noyes, R. W., Kalkofen, W., & Cuny, Y. 1971, Sol. Phys., 18, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N. 1984, Phys. Scrip. Vol. T, 8, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Hofmann, A., Arlt, K., Balthasar, H., et al. 2012, Astron. Nachr., 333, 854 [NASA ADS] [CrossRef] [Google Scholar]
- Jess, D. B., Mathioudakis, M., Christian, D. J., Crockett, P. J., & Keenan, F. P. 2010, ApJ, 719, L134 [NASA ADS] [CrossRef] [Google Scholar]
- Jurčák, J., Collados, M., Leenaarts, J., van Noort, M., & Schlichenmaier, R. 2019, Adv. Space Res., 63, 1389 [Google Scholar]
- Kramida, A., Ralchenko, Yu., Reader, J., & NIST ASD Team 2018, NIST Atomic Spectra Database (ver. 5.6.1), [Online] (Gaithersburg, MD: National Institute of Standards and Technology), [2018, November 30], https://physics.nist.gov/asd [Google Scholar]
- Kuckein, C., Martínez Pillet, V., & Centeno, R. 2012a, A&A, 542, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuckein, C., Martínez Pillet, V., & Centeno, R. 2012b, A&A, 539, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuckein, C., Denker, C., Verma, M., et al. 2017, in Fine Structure and Dynamics of the Solar Atmosphere, eds. S. Vargas Domínguez, A. G. Kosovichev, P. Antolin, & L. Harra, IAU Symp., 327, 20 [NASA ADS] [Google Scholar]
- Landi Degl’Innocenti, E. 1992, in Magnetic Field Measurements, eds. F. Sanchez, M. Collados, & M. Vazquez, 73 [Google Scholar]
- Leenaarts, J., Rutten, R. J., Reardon, K., Carlsson, M., & Hansteen, V. 2010, ApJ, 709, 1362 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., Xiang, Y., Erdélyi, R., et al. 2018, ApJ, 856, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Löfdahl, M. G. 2002, in Image Reconstruction from Incomplete Data, eds. P. J. Bones, M. A. Fiddy, & R. P. Millane, Proc. SPIE, 4792, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez González, M. J., Asensio Ramos, A., Manso Sainz, R., et al. 2011, ApJ, 730, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez González, M. J., Bellot Rubio, L. R., Solanki, S. K., et al. 2012, ApJ, 758, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez Pillet, V., Lites, B. W., & Skumanich, A. 1997, ApJ, 474, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Mehltretter, J. P. 1974, Sol. Phys., 38, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Molowny-Horas, R. 1994, Sol. Phys., 154, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Muller, R. 1983, Sol. Phys., 85, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Nagata, S., Tsuneta, S., Suematsu, Y., et al. 2008, ApJ, 677, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1978, ApJ, 221, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Puschmann, K. G., Denker, C., Kneer, F., et al. 2012, Astron. Nachr., 333, 880 [NASA ADS] [Google Scholar]
- Quintero Noda, C., Asensio Ramos, A., Orozco Suárez, D., & Ruiz Cobo, B. 2015, A&A, 579, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Requerey, I. S., Del Toro Iniesta, J. C., Bellot Rubio, L. R., et al. 2015, ApJ, 810, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Riethmüller, T. L., Solanki, S. K., Berdyugina, S. V., et al. 2014, A&A, 568, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rimmele, T. R. 2004, ApJ, 604, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz Cobo, B., & del Toro Iniesta, J. C. 1992, ApJ, 398, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, W., von der Lühe, O., Volkmer, R., et al. 2012, Astron. Nachr., 333, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Shchukina, N. G., Sukhorukov, A. V., & Trujillo Bueno, J. 2017, A&A, 603, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shelyag, S., Schüssler, M., Solanki, S. K., Berdyugina, S. V., & Vögler, A. 2004, A&A, 427, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solanki, S. K. 1993, Space Sci. Rev., 63, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., Finsterle, W., Rüedi, I., & Livingston, W. 1999, A&A, 347, L27 [NASA ADS] [Google Scholar]
- Solanki, S. K., Barthol, P., Danilovic, S., et al. 2010, ApJ, 723, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 1976, Sol. Phys., 50, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, O., Grossmann-Doerth, U., Knölker, M., & Schüssler, M. 1998, ApJ, 495, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, O., Hauschildt, P. H., & Bruls, J. 2001, A&A, 372, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tritschler, A., Rimmele, T. R., Berukoff, S., et al. 2015, in 18th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. G. T. van Belle, & H. C. Harris, 18, 933 [NASA ADS] [Google Scholar]
- Utz, D., Jurčák, J., Hanslmeier, A., et al. 2013, A&A, 554, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Utz, D., del Toro Iniesta, J. C., Bellot Rubio, L. R., et al. 2014, ApJ, 796, 79 [NASA ADS] [CrossRef] [Google Scholar]
- van Noort, M., Rouppe van der Voort, L., & Löfdahl, M. G. 2005, Sol. Phys., 228, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Viticchié, B., Del Moro, D., Criscuoli, S., & Berrilli, F. 2010, ApJ, 723, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Wöger, F., & von der Lühe, II, O. 2008, in Advanced Software and Control for Astronomy II, Proc. SPIE, 7019, 70191E [CrossRef] [Google Scholar]
- Yang, Y., Li, Q., Ji, K., et al. 2016, Sol. Phys., 291, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Yi, Z., & Molowny-Horas, R. 1995, A&A, 295, 199 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Overview of small AR NOAA 12708. Starting in the upper left panel and moving clockwise: Speckle-restored blue continuum (4505 Å) and Ca II H (3968 Å) images from HiFI, Si I 10827 Å slit-reconstructed blue wing (λ0 − 0.35 Å) from GRIS, and MOMFBD-restored blue-line wing (λ0 − 0.22 Å) image from GFPI of the Na I D2 5890 Å line. We note that the image scales from all instruments are different. The black stripe in the lower part of the Si I λ0 − 0.35 Å image indicates that there are no data available. Red circles identified by letters (a)–(c) indicate the isolated BPs under study. It is interesting to note that the BPs in the Si I λ0 − 0.35 Å panel do not always match the other instruments because it is a slit-reconstructed image in the range of 08:38–09:07 UT. |
| In the text | |
 |
Fig. 2. Region-of-interest including the three isolated BPs (a)–(c) from Fig. 1. Left column: blue-continuum images; right column: corresponding Ca II H image. The white box shows the size of the FOV of the inversions shown in Fig. 4. |
| In the text | |
 |
Fig. 3. Four Stokes V/Ic profiles with the largest amplitude belonging to BP (b), and their corresponding Stokes I/Ic profiles. The various Stokes I (V) profiles are shifted by +0.20 (+0.05) along the y-axis or ordinate. The wavelength axis is centered at the Si I line at rest. The red line shows the best fit obtained from the SIR inversion. The dotted vertical lines show the positions at rest of Si I and of the blue (He I b) and red (He I r) components of He I. The dashed vertical line indicates Si I λ0 − 0.35 Å, which corresponds to the image shown in the lower right corner of Fig. 1. |
| In the text | |
 |
Fig. 4. Longitudinal magnetic field and velocity maps inferred from the Si I 10827 Å inversions of the three isolated BPs at two different optical depths, log τ = −1.0 (bottom) and −2.5 (top). Bright points (a)–(c) are shown from left to right. We note that BP (a) has opposite polarity as compared to BPs (b) and (c). Magnetic fields are clipped between −200 G and +600 G for BP (a), and between −600 G and +200 G for BPs (b–c). LOS velocities are clipped between ±4 km s−1. Negative velocities represent flows along the LOS toward the observer, that is, upflows because of the proximity to disk center. The FOV corresponds to a zoom of the region-of-interest (white box in Fig. 2). |
| In the text | |
 |
Fig. 5. Zoom of the region-of-interest of 3″ × 3″ belonging to BP (b) from Fig. 2. Lower two panels: intensity of the Si I line in the core (left) and averaged blue wing at around λ0 − 0.35 Å (right), where BPs are well detected. Middle left (right) panel: unsigned maximum signal in Stokes Vmax/Ic from the Si I 10827 Å (Ca I 10839 Å) line. Upper left panel: longitudinal magnetic field at log τ = −1 inferred from the Si I inversions. A zoom of the HiFI blue-continuum image showing the fine structure is exhibited in the upper right panel. Pixels enclosed inside the white contours show atypical Si I Stokes V profiles, with two discernible red lobes like the example shown in Fig. 6. |
| In the text | |
 |
Fig. 6. Representative example of Stokes I/Ic and V/Ic profiles of a highly redshifted pixel close to the center of BP (b). The profiles are taken from inside of the white contour of Fig. 5. Lower two panels: observations (black dots) and best fit (solid red line) from a two-component SIR inversion. Upper two panels: synthesized profiles arising from the two atmospheric models obtained with SIR which coexist within the same resolution element. Atmosphere 1 (blue solid line) and 2 (red solid line) have a filling factor of about 0.7 and 0.3, respectively. The inferred average LOS velocity and inclination between −1.0 ≥ log τ ≥ −2.5 from this particular fit is vLOS, 1 ∼ −1 km s−1 and γ1 ∼ 172° and vLOS, 2 ∼ 6 km s−1 and γ2 ∼ 169°, for atmospheres 1 and 2, respectively. |
| In the text | |
 |
Fig. 7. Upper row: Doppler shifts for BPs (a)–(c) inside the zoomed region-of-interest, using the bisector method at a line depth, which corresponds to about Na I D2λ0 − 0.22 Å. The arrow in the lower left panel illustrates the depth at which the bisector was computed. Black contours mark the area of the BP. Lower panels: average quiet-Sun profile (dotted line) within the whole FOV (Fig. 1). The large dots correspond to the acquired filtergrams along the Na I D2 line with GFPI. The green solid lines exhibit the brightest 25 profiles belonging to the green box in the upper panels. The dashed vertical line marks the wavelength at rest. |
| In the text | |
 |
Fig. 8. Upper row: time evolution of the average LOS velocities computed within the 5 × 5 px2 green box shown in Fig. 7. The vertical bars indicate ± the standard deviation of the velocities within the same box. The overplotted red dashed line shows the average intensity in the blue wing of Na I D2 inside of the same green box. The arrow marks the time of simultaneous GRIS data. Lower row: average intensity profile generated within the same green box. The color code indicates the time of each profile. The dashed vertical line marks the wavelength at rest. The dotted profile represents the quiet-Sun profile whereas the dashed one corresponds in time to the average profile marked with the arrows in the above panels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.