| Issue |
A&A
Volume 630, October 2019
Rosetta mission full comet phase results
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201834851 | |
| Published online | 20 September 2019 | |
Dust of comet 67P/Churyumov-Gerasimenko collected by Rosetta/MIDAS: classification and extension to the nanometer scale
1
Space Research Institute of the Austrian Academy of Sciences,
Schmiedlstrasse 6,
8042 Graz, Austria
e-mail: thurid.mannel@oeaw.ac.at
2
University of Graz,
Universitätsplatz 3,
8010 Graz, Austria
3
European Space Astronomy Centre, Camino Bajo del Castillo, s/n., Urb. Villafranca del Castillo,
28692 Villanueva de la Cañada,
Madrid, Spain
4
Leiden Observatory,
Postbus 9513,
2300 RA Leiden, The Netherlands
5
Space Policy Institute, George Washington University,
20052 Washington DC,
USA
6
Centre de Sciences Nucléaires et de Sciences de la Matière (CSNSM) CNRS-IN2P3/Université Paris Sud, Université Paris-Saclay,
Bât. 104,
91405 Orsay Campus, France
7
Department of Lithospheric Research, University of Vienna,
Althanstrasse 14,
1090 Vienna, Austria
8
Natural History Museum,
Burgring 7,
1010 Vienna, Austria
9
UPMC (Sorbonne Université), CNRS/INSU, LATMOS-IPSL,
Paris, France
10
European Space Research and Technology Centre, Future Missions Office (SREF),
Noordwijk, The Netherlands
11
Institut für Planetologie, Universität Münster,
Wilhelm-Klemm-Strasse 10,
48149 Münster, Germany
Received:
13
December
2018
Accepted:
3
May
2019
Context. The properties of the smallest subunits of cometary dust contain information on their origin and clues to the formation of planetesimals and planets. Compared to interplanetary dust particles or particles collected during the Stardust mission, dust collected in the coma of comet 67P/Churyumov-Gerasimenko (67P) during the Rosetta mission provides a resource of minimally altered material with known origin whose structural properties can be used to further the investigation of the early solar system.
Aims. The cometary dust particle morphologies found at comet 67P on the micrometer scale are classified, and their structural analysis is extended to the nanometer scale.
Methods. We present a novel method for achieving the highest spatial resolution of imaging obtained with the MIDAS Atomic Force Microscope on board Rosetta. 3D topographic images with resolutions down to 8 nm were analyzed to determine the subunit sizes of particles on the nanometer scale.
Results. Three morphological classes can be determined: (i) fragile agglomerate particles of sizes larger than about 10 μm comprised of micrometer-sized subunits that may themselves be aggregates and show a moderate packing density on the surface of the particles. (ii) A fragile agglomerate with a size of about a few tens of micrometers comprised of micrometer-sized subunits that are suggested to be aggregates themselves and are arranged in a structure with a fractal dimension lower than two. (iii) Small micrometer-sized particles comprised of subunits in the size range of hundreds of nanometers that show surface features that are again suggested to represent subunits. Their differential size distributions follow a log-normal distribution with means of about 100 nm and standard deviations between 20 and 35 nm.
Conclusions. The properties of the dust particles found by MIDAS represent an extension of the dust results of Rosetta to the micro- and nanometer scale. All micrometer-sized particles are hierarchical dust agglomerates of smaller subunits. The arrangement, appearance, and size distribution of the smallest determined surface features are reminiscent of those found in chondritic porous interplanetary dust particles. They represent the smallest directly detected subunits of comet 67P.
Key words: comets: individual: 67P/Churyumov-Gerasimenko / space vehicles / space vehicles: instruments / planets and satellites: formation / techniques: miscellaneous / protoplanetary disks
© ESO 2019
1 Introduction
The process that forms planets, asteroids, and comets is usually estimated to have started with collisional aggregation of the smallest dust particles, themselves products of earlier stellar evolution or condensation processes in our early solar system (Tielens et al. 2005; Li & Greenberg 2003; Weidenschilling & Cuzzi 1993). Because they are important in the agglomeration process, these particles have been the focus of many observational and laboratory studies (Blum & Wurm 2008). However, it was not previously possible to investigate the microscopic properties of nearly unaltered individual particles with a known provenance. Former investigations were based on (1) remote observations (Levasseur-Regourd et al. 2008; Hayward et al. 2000), (2) laboratory measurement of returned cometary material (Brownlee et al. 2006; Zolensky et al. 2006), and (3) linking interplanetary dust particles (IDPs) that were collected in the Earth’s stratosphere (Wozniakiewicz et al. 2013; Zolensky et al. 2008; Bradley 2007) and ultracarbonaceous antarctic micrometeorites (UCAMMs; Yabuta et al. 2017; Dartois et al. 2013; Duprat et al. 2010) to cometary material.
The Rosetta mission to comet 67P/Churyumov-Gerasimenko (hereafter 67P) provided the first opportunity of sampling the dust and gas environment of the inner coma of a comet during a two-year period around its perihelion passage in August 2015. The low relative spacecraft-nucleus speeds enabled collection of dust particles by various instruments with only small degrees of alteration. One of the instruments on board Rosetta, the Micro-Imaging Dust Analysis System (MIDAS; Bentley et al. 2016a; Riedler et al. 2007), carried the first Atomic Force Microscope (AFM) that was launched into space, and was specifically designed to probe the properties of the smallest dust particles at the micro- to nanometer scale.
Investigations of the dust particles collected by MIDAS are reported in Bentley et al. (2016b) and Mannel et al. (2016). The most important conclusion of these papers is the structural description of nearly unaltered cometary dust particles in the micrometer-size range: all detected dust particles show a hierarchical agglomerate character. Here we introduce a classification into three groups of the particles that were analyzed by MIDAS: (i) about 10 μ m large particles with subunits that are packed in a moderately dense fashion; these make up the majority of the MIDAS collection. (ii) One large but extremely porous particle. (iii) Small particles a few micrometer in size. Groups (i) and (ii) have been analyzed by Bentley et al. (2016b) and Mannel et al. (2016), and a characterization of the small particles is presented here. In particular, we show that the small particles are not only comprised of some hundred nanometer-sized subunits, as introduced in Bentley et al. (2016b), they also show surface features following a log-normal differential size distribution with means measuring about 100 nm and standard deviations of between 20 and 35 nm. To obtain this resolution, a novel imaging technique was developed that is described in Sect. 2. High-resolution images of a well-preserved dust particle are shown in Sect. 4.1, and the size distributions of the subunits and the smallest identifiable surface features are presented. In Sect. 5.1 they are discussed and compared to the results of IDP and UCAMM analyses, findings of the Stardust mission, and to other Rosetta results. The classification of MIDAS results is shown in Sect. 4.2 and set into the frame of the results obtained about dust during the Rosetta mission in Sect. 5.2. Section 6 gives a brief summary of the main findings.
2 Methods
The MIDASinstrument on board the Rosetta comet orbiter collected dust particles and imaged them with an AFM. A description of the instrument is presented by Riedler et al. (2007), and an overview of its operation and imaging modes is given in Bentley et al. (2016a). Like every AFM, MIDAS used sharp tips to raster the dust surface in order to obtain high-resolution 3D images of nearly unaltered cometary dust. The finite width of the tips became a limiting factor when it was tried to access the smallest features of the dust particles (Bentley et al. 2016a). Therefore a “reverse-imaging mode” was developed, in which an onboard tip calibration sample with sharp spikes was used to probe cometary dust particles that had accumulated on the AFM tips during previous scans. This tip calibration sample was used primarily to image the apex of the tip to determine its shape. It consisted of an array of spikes sharper than the tips with a half-opening angle of 25° ± 5°, 700 nm height, a distance between neighboring spikes of 2.12 μm, and of 3 μm in the diagonal direction (NT-MDT 2018).
As an AFM image is a convolution of the real structure and the tip shape, the tip width and shape can dominate the real resolution in certain situations, in particular, if a steep feature smaller than the tip apex is imaged. Because the calibration spikes are sharper than the MIDAS tips and many thousands of them are available on the tip calibration target in case one becomes blunt or contaminated, the ultimate resolution that was attainable with MIDAS is greatly improved by this reverse-imaging mode.
During MIDAS normal imaging mode (a dynamic intermittent contact mode; Bentley et al. 2016a), only low forces should be applied to the sample. Nevertheless, many of the cometary dust particles that were imaged fragmented, probably because they were highly fragile, and dust was removed from the target or (partially) stuck to the tip. This pick-up of dust could either occur for whole particles at once or through subsequent pick-up of smaller fragments. The adhering dust to the tip was observed by the regular tip images that were acquired using the tip calibration sample. Thus, the particles seen in the tip images have potentially undergone several modifications: on impact with the target, on pick-up by the tip, and in any subsequent scans with this tip. A history of tip usage during and after pick-up is thus given in Appendix A. In general, the overall particle surface structure might be altered and thus is not investigated in greater detail. It is instead assumed that the particles we studied are aggregates of subunits that have a higher internal strength than the parent particle, and thus their sizes and shapes might be still pristine (Hornung et al. 2016; Skorov & Blum 2012).
After successful image acquisition in the reverse-imaging mode, a 3D image of the picked-up particle surface with resolutions of typically 15 or 8 nm is available. Following the methods used previously in Mannel et al. (2016) and Bentley et al. (2016b), the visible surface features of the particles were then identified by visual inspection of the topographic images and their 3D representation. Even the sharper tip calibration spikes cannot penetrate deeply between the individual features, and material that apparently lays between the features was neglected as it cannot be fully imaged. These areas could either be further features hidden by an upper layer, an undefined matrix material, or features with a much smaller radius, which cannot be resolved because of the resolution limit. To prevent incorrect identification of subunits close to the resolution limit, no features with fewer than 9 pixel were marked.
3 Definition of language
The structural description of cometary dust is complex and benefits from a clearly defined vocabulary. A unified dust classification scheme of the Rosetta dust results with a well-defined vocabulary is presented in Güttler et al. (2019). Here we use corresponding terminology, in particular:
a particle is a subordinate term that can be applied to any form of dust agglomerate, fragment, subunit, etc.;
a grain is the smallest building block of the dust, also referred to as fundamental building block. It is identified, for example, based on its mineralogy or high material strength;
an agglomerate consists of structurally distinct smaller parts that can but do not have to be different in properties. These smaller parts are called subunits. Each subunit can again be an agglomerate, but it can also be a grain. In the literature, the word aggregate is often used synonymously to agglomerate, although there is a tendency to use agglomerate for loosely packed material and aggregate for more consolidated stronger material (e.g., Nichols et al. 2002);
a fractal particle is a hierarchical agglomerate whose subunits are arranged following a statistical order that can be described by a fractal dimension (Mannel et al. 2016; Meakin 1991). Although it is conceivable that cometary particles can have fractal dimensions Df > 2, to date, only dust particles with fractal structures of Df < 2 have been detected with certainty (Fulle et al. 2017; Mannel et al. 2016);
in the particular case of MIDAS, a solid particle is defined as a particle that does not show fragmentation or major surface features such as deep trenches between bulbous units if scanned with sufficient resolution.
Furthermore, the sizes of particles and subunits are given as their equivalent diameters, that is, the diameter of a disk with the same area as measured for the feature projected onto the x–y plane.
4 Results
4.1 Dust features on the nanometer scale
One particle, called particle G, was collected during perihelion and was later picked up by a tip (for a more precise description of its collection time and scan history, see Appendix A). It is expected to be rather unaltered because its structure is unchanged in repeated scans (e.g., the images shown in Figs. 1 and 2). It was scanned seven times with resolutions of 15 and 8 nm between its first detection on 12 November 2015 and its last scan on 25 May 2016. The scan that allows the best identification of the particle structure was taken on 8 December 2015. It has a resolution of 15 nm, and a crop of the interesting region is shown in Fig. 1. The highest resolution scan with the least artifacts had a resolution of 8 nm, was taken on 11 May 2016, and a crop of the particle is shown in Fig. 2. The full scans together with key metadata can be found in Appendix D.
Figure 1a shows the 15 nm scan taken on 8 December 2015. The particle is the open, flocculent structure in the center and measures about 1 μm in diameter. It is adhering to the tip that is visible in the bottom right part of the image. The smooth, round shape is the tip apex, the straight line that diminishes in height to the bottom right corner is a structure that supports the tip. It is directly visible that particle G is an agglomerate of several large features that again show distinct surface features. The larger features are clearly separated and are thus treated as subunits comprising the particle. Whether their smaller surface features are also related to subunits is hard to decide based on MIDAS topographic data alone and is discussed in Sect. 5.1.
Figure 1b shows the same image as Fig. 1a, but the subunits are outlined in cyan. As described in Appendix B, the outer rim of the particle may show artificial broadening due to tip-sample convolution depending on the steepness of the particle. The large subunit on the left shows the most severe case: it is elongated to the bottom side due to this tip-sample convolution.
Figure 1c shows the same image as the previous panels, but the surface features are marked in cyan. The subunits marked in Fig. 1b seem to be covered by the surface features, or if the surface features are subunits, the larger units may be completely built of them. However, it is not possible to mark all these surface features, for example, because the discriminatory power related to the resolution is limited, because they apparently cover each other, or because they lie too close to the border. Thus, the marked features in Fig. 1c, as well as those marked in Fig. 2b, are just aselection of the best-visible features. Their spatial density and arrangement cannot be completely mapped.
Figure 2a again shows particle G, the same particle as presented in Fig. 1, but this time, it is scanned with 8 nm resolution and five months later, on 11 May 2016. The structure of particle G remained unchanged, meaning that there was no substantial alteration during the scans such as compression, fragmentation, or displacements of subunits. Additionally, the particle shows no change despite the five-month-long storage in the instrument at a temperature well above 20 °C, possibly up to 35 °C1. This suggests that the particle did not contain volatile materials when it was detected by MIDAS for the first time. It is possible, however, that the particle contained volatile materials that evaporated upon ejection from the nucleus, the travel through the coma, or in the three-month period between the collection and the detection by MIDAS.
The preservation of the structure indicates that particle G remained relatively unaltered at least after pick-up by the tip. When we compare Figs. 1 and 2, the particle in Fig. 2 is slightly stretched horizontally and compressed vertically relative to the particle in Fig. 1. The effect on the measured size of the particle is negligible as the measured equivalent diameter of particle G is 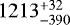 and
and 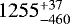 nm in the 15 and 8 nm resolution scans, respectively, and is thus similar in the range of its uncertainties. The effect on the sizes of the smaller subunits is even smaller, thus the inaccuracy due to stretch or compression can be neglected. The slight change in shape of the particle in the different scans is an effect that is due to the longer scanning time of the more highly resolved scan (7 h vs. 22 h), making it more prone to piezo drift as a result of temperature changes. This is especially strong in the slower scanning direction (the horizontal direction in Figs. 1 and 2). More details about this artifact are given in Appendix D.
nm in the 15 and 8 nm resolution scans, respectively, and is thus similar in the range of its uncertainties. The effect on the sizes of the smaller subunits is even smaller, thus the inaccuracy due to stretch or compression can be neglected. The slight change in shape of the particle in the different scans is an effect that is due to the longer scanning time of the more highly resolved scan (7 h vs. 22 h), making it more prone to piezo drift as a result of temperature changes. This is especially strong in the slower scanning direction (the horizontal direction in Figs. 1 and 2). More details about this artifact are given in Appendix D.
The scan shown in Fig. 2b reveals additional deeper-lying features at the rim of the particle that are indicated by white arrows. The color scale needed to be stretched, and especially more shallow features can therefore not be easily recognized in the printed figure. Moreover, the rims of the particle in Fig. 2 show a stronger broadening, which might be an effect caused by the use of different spikes on the calibration target that might have had distinct shapes and aspect ratios.
Figure 2b presents the same image as Fig. 2a, but this time, the surface features are marked in cyan. In comparison to the features outlined in Fig. 1c, most features were found in both scans. However, some features were only found in the 15 nm resolution scan because the particle rims are slightly less broadened, and some features were only found in the 8 nm scan because its resolution is better.
The cumulative size distributions of all marked subunits and features are given in Figs. 3–5. All sizes are listed in Table D.2, and their uncertainties were determined as described in Appendix B. The related differential size distributions can be expected to follow a log-normal function (Wozniakiewicz et al. 2013; Rietmeijer 1993). The trend of the size distribution is easier to determine in the cumulative representation for the given measurement data because the related uncertainties can be handled in a more convenient way (see Appendix B). The cumulative subunit sizes were therefore fit with the integrand ofa log-normal distribution, and the related mean values and standard deviations were denoted as as μlog and σlog. All performed fits passed a Kolmogorov-Smirnov test (KS test). For details about the fitting routine and the KS test, see Appendix C.
Figure 3 shows the sizes of the small surface features on particle G, scanned with 15 nm resolution (see Fig. 1c) fit by the integrand of a log-normal distribution. The arithmetic mean value of the data measures 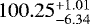 nm, in good agreement with the fitted mean value of μlog = 101.80 ± 0.50 nm. The geometric mean value is slightly lower, with
nm, in good agreement with the fitted mean value of μlog = 101.80 ± 0.50 nm. The geometric mean value is slightly lower, with 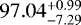 nm, which is an expected behavior as this metric places less weight on the larger sizes. This can be favorable if it is expected that the large subunit sizes lie on the trailing end of a log-normal distribution and should be weighted less strongly. The standard deviation is found to be σlog = 23.97 ± 0.64 nm, and the minimum and maximum subunit sizes are
nm, which is an expected behavior as this metric places less weight on the larger sizes. This can be favorable if it is expected that the large subunit sizes lie on the trailing end of a log-normal distribution and should be weighted less strongly. The standard deviation is found to be σlog = 23.97 ± 0.64 nm, and the minimum and maximum subunit sizes are 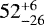 and
and 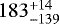 nm.
nm.
Figure 4 shows the small feature sizes on particle G, scanned with 8 nm resolution (see Fig. 2b) together with their fit. The arithmetic mean value of 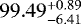 nm is in agreement with the fitted mean value of μlog = 100.12 ± 0.57 nm. The geometric mean value measures
nm is in agreement with the fitted mean value of μlog = 100.12 ± 0.57 nm. The geometric mean value measures 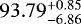 nm. The influence of the two largest subunit sizes on the mean values is clearly reflected in the geometric mean being much smaller than the arithmetic mean. When we compare the mean values determined for the 15 and 8 nm scans, the arithmetic mean values are in agreement, and the fitted mean values are similar. The standard deviation of the 8 nm scan with σlog = 34.51 ± 0.76 nm is slightly broader than the standard deviation found for the 15 nm resolution scan. This indicates a broader distribution, probably caused by the larger size interval of the measured subunit sizes of between
nm. The influence of the two largest subunit sizes on the mean values is clearly reflected in the geometric mean being much smaller than the arithmetic mean. When we compare the mean values determined for the 15 and 8 nm scans, the arithmetic mean values are in agreement, and the fitted mean values are similar. The standard deviation of the 8 nm scan with σlog = 34.51 ± 0.76 nm is slightly broader than the standard deviation found for the 15 nm resolution scan. This indicates a broader distribution, probably caused by the larger size interval of the measured subunit sizes of between 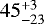 and
and 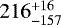 nm.
nm.
The distribution of the larger subunits of particle G as marked in Fig. 1b is shown in black in Fig. 5. The sizes lie between 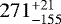 and
and 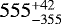 nm, have an arithmetic mean value of
nm, have an arithmetic mean value of 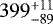 nm, and a geometric mean value of
nm, and a geometric mean value of 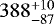 nm. Because of the low statistics, a distinction between a log-normal distribution or a simple line is not possible. The KS test was passed best by the fit of a line with a slope of (3.5 ± 0.3) × 10−3 nm−1.
nm. Because of the low statistics, a distinction between a log-normal distribution or a simple line is not possible. The KS test was passed best by the fit of a line with a slope of (3.5 ± 0.3) × 10−3 nm−1.
The sizes are in very good agreement with the sizes found for the subunits of particle D, an about 1 μ m particle collected pre-perihelion (Bentley et al. 2016b). They are shown in blue in Fig. 5, lie between 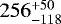 and
and 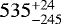 nm, show an arithmetic mean value of
nm, show an arithmetic mean value of 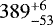 nm, and a geometric mean value of
nm, and a geometric mean value of 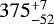 nm. The fitted line has a slope of (3.2 ± 0.3) × 10−3. In contrast to particle G, particle D was only imaged with a resolution of 80 nm and thus no surface features on these subunits were visible. The detection of similarly sized subunits at different resolutions indicates that the determined subunit size is independent of the image resolution. Finding subunits of similar sizes in distinct particles also underlines the suggested hierarchical dust structure with characteristic subunit size regimes (Levasseur-Regourd et al. 2018; Bentley et al. 2016b). As all high-resolution scans of MIDAS show the same kind of surface features as particle G, and because the subunit sizes of particle D and particle G match very well, it is possible that particle D, as well as all subunits of the larger particles E and F visible in Fig. 6, also has surface features in the size range of some hundred nanometers. It can be hypothesized that many of the micrometer-sized particles of comet 67P have the approximately 100 nm surface features visible on particle G.
nm. The fitted line has a slope of (3.2 ± 0.3) × 10−3. In contrast to particle G, particle D was only imaged with a resolution of 80 nm and thus no surface features on these subunits were visible. The detection of similarly sized subunits at different resolutions indicates that the determined subunit size is independent of the image resolution. Finding subunits of similar sizes in distinct particles also underlines the suggested hierarchical dust structure with characteristic subunit size regimes (Levasseur-Regourd et al. 2018; Bentley et al. 2016b). As all high-resolution scans of MIDAS show the same kind of surface features as particle G, and because the subunit sizes of particle D and particle G match very well, it is possible that particle D, as well as all subunits of the larger particles E and F visible in Fig. 6, also has surface features in the size range of some hundred nanometers. It can be hypothesized that many of the micrometer-sized particles of comet 67P have the approximately 100 nm surface features visible on particle G.
In summary, the differential distributions of the small features of particle G follow a log-normal distribution with a mean size about 100 nm and a standard deviation between 20 and 35 nm, where the detected subunits span a total size range between about 50 to 250 nm. The lower limit of feature sizes determined in particle G seems not to be resolution limited because the smallest feature size and mean values remain similar in differently resolved scans. The upper size limit is given by the transition to larger features (marked in Fig 1b). Deep trenches separate the larger features such that they are clearly distinct and are suggested to be subunits. They exhibit the smaller features on their surfaces (marked in Fig. 1c), which indicates that the larger subunits may be comprised by smaller ones.
 |
Fig. 1 Particle G, a 1 μm particle scanned with the MIDAS reverse-imaging mode on 8 December 2015 with a resolution of 15 nm per pixel. The smooth, round shape at the bottom with a fading line to the bottom right corner is the tip with which the particle was picked up, above sits the particle with well-visible substructures. Panel a: particle itself. Panel b: larger subunits. Panel c: smallest identifiable features. |
 |
Fig. 2 Same 1 μm particle G as shown in Fig. 1, but this time scanned with a resolution of 8 nm on 11 May 2016. Panel a: particle itself. Panel b: smallest identifiable features. Compared to Fig. 1, the color scale has to be fully exploited as some lower-lying subunits were imaged (indicated by the white arrows). |
 |
Fig. 3 Cumulative size distribution of the subunits of particle G identified in the 15 nm resolution scan (Fig. 1c). On the left we show the probability that a subunit is smaller than the indicated value, and on the right we show the number of detected subunits. The log-normal fit is shown in blue together with its uncertainty interval in light blue. The verticallines denote the arithmetic (black) and fitted (blue) mean values with shaded uncertainty intervals. |
 |
Fig. 4 Cumulative size distribution of the subunits of particle G identified in the 8 nm resolution scan (Fig. 2b). On the left we show the probability that a subunit is smaller than the indicated value, and on the right we show the number of detected subunits. The log-normal fit is shown in blue together with its uncertainty interval in light blue. The verticallines denote the arithmetic (black) and fitted (blue) mean values with shaded uncertainty intervals. |
 |
Fig. 5 Cumulative size distribution of the larger subunits of particle G (Fig. 1b, black dots) and D (Bentley et al. 2016b, blue triangles). The line fits of the data are shown for particle G in black and particle D in blue, and the arithmetic means of the measured sizes are given as vertical lines with shaded uncertainty intervals. |
 |
Fig. 6 3D rendered images of MIDAS dust particles. Panel a: particle F as example for a large agglomerate particle whose subunits arepacked in a moderately dense fashion on the surface (Mannel et al. 2016). The source scan was taken on 14 October 2015 at 08:08:23 UTC with a resolution of 192 nm. Panel b: large porous agglomerate particle E. The data are taken from a scan on 18 January 2015 at 20:59:28 UTC with a resolution of 210 nm. Panel c: particle G, which is representative for the small particle class. The source scan was taken on 11 May 2016 at 12:08:03 UTC with a resolution of 8 nm and is shown in Figs. 2 and in Appendix D.2. |
4.2 Dust classification
In an attempt to classify the MIDAS dust collection, three distinct particle classes can be identified. We list them briefly below.
(i) Large particles with moderate packing of subunits at the surface
The large (>10 μm) particles are agglomerates with subunit sizes around 1.5 μm (Mannel et al. 2016) that might again consist of smaller subunits that were not visible due to the resolution limit in these scans. The subunits that are visible on the surface are neither packed in the densest possible fashion nor extremely loose; trenches are visible that clearly separate the subunits, but they are generally smaller than the typical size of the subunits, in particular compared to the large porous particles through which the target surface is visible. In contrast to smaller particles detected with MIDAS, the large particles with moderate packing fragment easily into their micrometer-sized subunits. This is interpreted as an indication that the strength that keeps the subunits of the large particles together is weaker than the strength that binds the subunits of the small particles because it is expected that the effective tensile strength increases for smaller aggregates (Hornung et al. 2016; Skorov & Blum 2012). In no case did a disintegrated particle show fragments that differed from those that were observed on the surface of the particle, and thus it is suggested that all large agglomerates internally consist of the same typical subunits as are visible at the surface. No observations indicated that the large particles might have a solid core that is just coated with the observed subunits, or that there are euhedral crystalline parts, meaning crystalline material with clear-cut recognizable crystal faces. The majority of MIDAS detections are large compact agglomerates. An example is particle F, analyzed in Mannel et al. (2016), which is shown as rendered 3D image in Fig. 6a.
(ii) The large porous particle
The large (>10 μm in size) porous particle, called particle E, consists of subunits with similar sizesand shapes as are visible on the surface of the large particles with moderate packing (Mannel et al. 2016). However, as is visible in the rendered 3D image of the particle presented in Fig. 6b, they are extremely loosely assembled. As derived in Mannel et al. (2016), the structure shows a degree of ordering that can be described with a fractal dimension less than two. It is assumed that this structure is characteristic for dust particles built in a cluster–cluster-agglomeration growth process in the solar nebula (Blum & Wurm 2008; Dominik et al. 2007). As shown in Fulle & Blum (2017) and Mannel et al. (2016), the porous large particle might have been preserved since the early solar system, which would make it the structurally most pristine dust particle ever imaged. It is suggested that all dust particles found in comets started with this fractal structure, but the majority was subsequently densified and is now forming the group of particles with a moderate packing of subunits (Blum et al. 2017; Fulle & Blum 2017). MIDAS detected one large porous particle, particle E, but the Grain Impact Analyser and Dust Accumulator (GIADA; Colangeli et al. 2007) demonstrated that there is a whole population of these particles (Fulle et al. 2015, 2017).
(iii) Small particles
The small (about one to a few micrometers) particles show bulb-shaped subunits with a surface packing density that is suggested to be comparable to that of the large particles with moderate packing fashion of the subunits. The 1 μm particles typically consist of subunits with sizes of several hundreds of nanometers. As the individual small particles are similar in size and shape to the fragments of the large particles, it is suggested that they might belong to the same population. One possibility could be that the individually collected small particles are in fact fragments from larger particles that separated before collection, for instance, during ejection from the nucleus or their travel through the cometary coma. Another option could be that they were not integrated into the larger particles during formation in the early solar system, but nevertheless were incorporated into the material of the cometary nucleus. In contrast to the large particles with moderate packing of subunits at the surface, no small particle showed fragmentation or strong alteration during scanning. This indicates that a higher internal strength keeps the smaller particles together. In general, individual small particles are scarce in MIDAS detections, and no individual particle smaller than 1 μ m was detected. Possible reasons are discussed in Sect. 5.2.2.
Particle G shown as rendered 3D version in Fig. 6c, as well as particle D presented in Bentley et al. (2016b), are exemplary particles for the small particle class. All small particles and fragments of larger particles that were scanned with a sufficiently high resolution show subunits with sizes smaller than one hundred nanometers. Thus, it is suggested that the 100 nm surface features are common to all cometary dust of comet 67P, that is to say, the subunits of particle E in Fig. 6b or particle F in Fig. 6a might well show these features if they were scanned with a higher resolution. The same is suggested for the small particle D presented in Bentley et al. (2016b).
5 Discussion
5.1 Comparison of the smallest subunit sizes found in comet 67P and other samples
The investigation of the dust of comet 67P in the reverse-imaging mode of MIDAS was very successful. It was possible to determine the surface structure of the smallest individually collected particles down to a scale smaller than 100 nm. The approximately 1 μm particles show clearly separated features that are interpreted as subunits with mean sizes close to 400 nm. Most interestingly, these subunits again show features with sizes following a log-normal distribution with a mean of about 100 nm. With the purely topographic information provided by MIDAS, it cannot be conclusively decided whether these smallest features are subunits or just surface features. For such a determination, topographical scans with a higher resolution, as well as information on the material properties such as compositional heterogeneity, are required. However, a suggestion can be made based on a comparison to other Rosetta measurements and to typical sizes found for subunits that have been identified in other cometary material.
The best sources for subunit sizes of cometary dust are the returned Stardust samples (Brownlee et al. 2006) from comet 81P/Wild 2, investigations of chondritic porous IDPs (CP IDPs) collected in the stratosphere (Flynn et al. 2013) and Antarctica (Noguchi et al. 2015), as well as UCAMMs (Duprat et al. 2010) gathered on the Antarctic continent. All these materials are susceptible to alteration between the time that they were released from the comet and the investigation in the laboratory. Stardust samples had to survive a high-velocity capture, IDPs and UCAMMs had a long solar system sojourn and might have been altered during their passage of Earth’s atmosphere. Even when we keep these shortcomings in mind, these particles nevertheless represent a great resource to study the properties of their parent bodies such as the sizes of their subunits.
CP IDPs and UCAMMs
Both materials consist of subunits smaller than micrometers that consist of anhydrous materials, mainly olivine, pyroxene, a substance described as glass with embedded metal and sulphides (hereafter GEMS), and iron sulphide (Flynn et al. 2013; Dobrică et al. 2012). A study by Wozniakiewicz et al. (2013) investigated the size distribution of the subunits of CP IDPs. The dust agglomerates were disaggregated and the sizes of the resulting fragments were measured. Thus, the sizes do not primarily refer to compositionally distinct regions (which cannot be determined by MIDAS either), but to the sizes of the consolidated subunits (a quantity that is accessible to MIDAS). Over 5600 subunits of four CP IDPs were analyzed, and their size distributions were found to follow log-normal distributions (Wozniakiewicz et al. 2013). The mean and standard deviation values of the fitted distributions were not determined, but the cumulative size distributions were investigated by a graphical procedure that determined that the geometric means range between 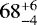 and
and 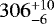 nm and the standard deviations range between about 40 and 200 nm (Wozniakiewicz et al. 2013). The geometric mean value of the small features of particle G agree, although on the smaller side, with the geometric mean valuesfound for the CP IDPs. The distribution of the small features is narrower than that of the CP IDPs, which might be caused by the larger size range that is covered by the subunit sizes of the CP IDPs (from about tens of nanometers up to 1 μm). The narrow nature of the subunit size distribution in dust of comet 67P has been described in earlier studies at larger size scales: on the one hand, for the subunits of a few micrometers comprising the 10 μm particles as detected by MIDAS (Mannel et al. 2016); on the other hand, for the tens of micrometer-sized subunits comprising the 100 μm clusters detected in optical microscope images with a pixel resolution of 14 μm obtained with the Cometary Secondary Ion Mass Analyser (COSIMA; Kissel et al. 2007) (Hornung et al. 2016). The repeated detection of rather distinct subunit sizes supports the image that cometary dust has a hierarchical structure (see also Sect. 5.2.3).
nm and the standard deviations range between about 40 and 200 nm (Wozniakiewicz et al. 2013). The geometric mean value of the small features of particle G agree, although on the smaller side, with the geometric mean valuesfound for the CP IDPs. The distribution of the small features is narrower than that of the CP IDPs, which might be caused by the larger size range that is covered by the subunit sizes of the CP IDPs (from about tens of nanometers up to 1 μm). The narrow nature of the subunit size distribution in dust of comet 67P has been described in earlier studies at larger size scales: on the one hand, for the subunits of a few micrometers comprising the 10 μm particles as detected by MIDAS (Mannel et al. 2016); on the other hand, for the tens of micrometer-sized subunits comprising the 100 μm clusters detected in optical microscope images with a pixel resolution of 14 μm obtained with the Cometary Secondary Ion Mass Analyser (COSIMA; Kissel et al. 2007) (Hornung et al. 2016). The repeated detection of rather distinct subunit sizes supports the image that cometary dust has a hierarchical structure (see also Sect. 5.2.3).
Rietmeijer (1993) derived the subunit size distribution for one CP IDP. The particle was imaged with transmission and scanning electron microscopy, and its subunits were identified by eye. The particle showed about 100 granular units, subunits of carbon-rich chondritic to carbonaceous composition, and polyphase units, most frequently of about 100 nm (Rietmeijer 1993). Their diameters range from 64 to 7580 nm with a mean of 585 nm; all sizes are given with a relative uncertainty of 10 percent. Their size distribution follows a log-normal distribution that is typical for a size-sorting process (Rietmeijer 1993). It is polymodal with overlapping normal distributions described by means between 128 and 3360 nm. The size range covered by the subunits of the investigated CP IDP is much larger than found in particle G, in particular because it trails to much larger sizes. Only the normal distribution with the smallest mean of 128 nm comes close to the observed mean value about 100 nm of the smallest features of particle G, but because no standard deviation for this distribution is given, it is uncertain how well the size distribution of particle G and the investigated CP IDP would match.
Additionally, Rietmeijer (1993) detected about 400 nanocrystals among the constituents of the granular units of two CP IDPs. They had sizes between 1.4 and 636 nm that followed log-normal and log–log-normal distributions with means between 3.1 and 49.6 nm and standard deviations between 0.5 and 7.2 nm. It is conceivable that the subunits of particle G we investigated here also contain similar nanocrystals or particles as small as some nanometers that were not resolved in the 8 nm resolution scans of MIDAS. Whether such nanocrystals should be treated as smallest subunits or if they are constituents that are fused together to form the smallest subunits requires a separate discussion if they do exist.
Dobrică et al. (2012) analyzed three UCAMMs and investigated the apparent sizes of grains that were visible in 80 nm thin sections. They measured 550 mineral subunits (olivines, pyroxenes, and sulfides) and found sizes ranging from 15 nm to 1.1 μm with a geometric mean of about 138 nm and an uncertainty of the size measurements of 5%. Because no fits are available to date, it is not possible to determine how well the size distributions would fit in the range measured by MIDAS. However, as the size range encloses that of the features found in MIDAS particles, the possibility that the size distributions are in agreement is given and could be tested in future projects.
In summary, judging by the size of the detected features in CP IDPs, the smallest subunits found in MIDAS dust particles could correspond to the smallest subunit sizes derived for CP IDPs. However, the size distributions we determined here are narrower, inparticular, they trail less to higher values. This could be an effect of low statistics or a true difference between the samples.
Stardust measurements
The majority of the particles collected by Stardust are olivine and pyroxene silicates with solar isotopic compositions, which suggests an origin in our solar system rather than an interstellar provenance. These polymineralic particles dominate those made of a single mineral even down to sizes smaller than 100 nm, indicating that the dust composition is surprisingly consistent at different scales and that the smallest subunits of the dust may be as small as tens of nanometers (Hörz et al. 2006; Zolensky et al. 2006). The sizes of these smallest single mineral impactors are similar to those of the nanocrystals determined by Rietmeijer (1993). As discussed above, they might also be existing in MIDAS dust particles and might be fused into the 100 nm features. Price et al. (2010) and Wozniakiewicz et al. (2012) investigated the sizes of particles smaller than 10 μm that impacted the aluminum foils of the Stardust probe. The distribution peaks at about 175 nm, but if we assume that the particles areagglomerates of smaller subunits, as indicated by their common polymineralic nature, then the subunit size distribution would peak at sizes below 100 nm (Price et al. 2010). A study of over 450 particles that do not seem to be agglomerates, that is, those that show single mineral impactors of silicate or sulfide, found geometric mean sizes of 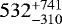 nm for the silicate particles and
nm for the silicate particles and 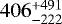 nm for the sulfides (Wozniakiewicz et al. 2013). These sizes are notably larger than the 175 nm (or less) found for the whole dataset. This large spread of subunit sizes could indicate a size distribution with a large width. No fits of these sizedistributions are available, but the figures in Wozniakiewicz et al. (2012) and Price et al. (2010) indicate that the differential sizes may follow a log-normal distribution. When we assume that the smallest subunit sizes are possibly between tens and hundreds of nanometers, the subunit size range found for MIDAS smallest features would be encompassed. The determination of the size distributions for the small Stardust particles and a detailed comparison to the distributions obtained for comet 67P could be the work of an interesting future project.
nm for the sulfides (Wozniakiewicz et al. 2013). These sizes are notably larger than the 175 nm (or less) found for the whole dataset. This large spread of subunit sizes could indicate a size distribution with a large width. No fits of these sizedistributions are available, but the figures in Wozniakiewicz et al. (2012) and Price et al. (2010) indicate that the differential sizes may follow a log-normal distribution. When we assume that the smallest subunit sizes are possibly between tens and hundreds of nanometers, the subunit size range found for MIDAS smallest features would be encompassed. The determination of the size distributions for the small Stardust particles and a detailed comparison to the distributions obtained for comet 67P could be the work of an interesting future project.
Other Rosetta measurements
Although there was no instrument other than MIDAS on board Rosetta that directly measured (sub-)micrometer dust particles, several instruments indirectly detected the presence of smallest dust. The remote-sensing instruments Alice (an ultraviolet imaging spectrometer; Stern et al. 2007) and the Visible and InfraRed Thermal Imaging Spectrometer (VIRTIS; Coradini et al. 2007) suggest that the dust properties change during some dusty outbursts. Bockelée-Morvan et al. (2017a,b) found evidence that during outbursts small (about 100 nm) particles either bound in fractal agglomerates or as individual particles can be ejected. Alice detected higher dust densities (Steffl et al. 2015), and a so-called anomalous feature that was suggested to stem from dust particles that are disrupted to fragments in the nanometer size range when they enter the instrument (Noonan et al. 2016a,b). Additionally, the Langmuir probe of the RPC instrument (Rosetta Plasma Consortium; Carr et al. 2007) detected a lack of photoelectrons from the sunward direction over perihelion. One interpretation is the existence of nanometer-sized dust particles between the comet and the Sun (Johansson et al. 2017).
The indirect detections of dust particles of about 100 nanometer or smaller discussed above suggests that the 100 nm features detected by MIDAS may indeed represent subunits. It might also be hypothesized that the larger dust particles of tens to thousands of micrometers can release their subunits in the nanometer size range under special conditions, for example, during an outburst, close to strong electric fields, or after a longer journey through the solar system.
In conclusion, the sizes of the smallest features detected by MIDAS of about 100 nm are in good agreement with indirect detections of smallest dust particles by other Rosetta instruments. Thus, these smallest features of MIDAS dust particles might not only be surface related, but may represent subunits.
Interstellar dust grains
It is an open question to what extent dust particles that were inherited pristinely from the interstellar medium were available as fundamental building blocks in our early solar system. Based on remote observations, it is expected that interstellar dust consists of silicates and carbon with sizes of mostly about a few hundred nanometers, in a distribution that reaches a few nanometers and up to some micrometers (Li & Greenberg 2003).
The cometary material available for investigation typically shows a very small fraction of identifiable interstellar particles. The Stardust collection held a few candidates for interstellar dust (Westphal et al. 2014; Brownlee et al. 2006), which were mostly complex aggregates with sizes between some micrometers (for those collected in the aerogel) and a few hundred nanometers (for those captured in the aluminum foils). CP IDPs show compositions in agreement with a solar system provenance (Flynn et al. 2016), but a minority, as small as a few parts per million, of micrometer-sized particles shows isotopic ratios that suggest an interstellar origin (Messenger 2000). When we compare this with these low abundances of interstellar particles in cometary dust, it is unlikely that MIDAS particles contain a substantial fraction of interstellar grains. Although the feature sizes identified for particle G would match the expected size range of interstellar particles, we cannot conclude to which extent MIDAS particles contain interstellar dust because we lack compositional data.
5.2 MIDAS dust classification
The classification presented in this paper is meant to give a coarse overview of MIDAS results and an easy approach for comparisonsto studies about cometary dust and of other Rosetta (dust analysis) instruments (Levasseur-Regourd et al. 2018). It is also in agreement with the synthesis of our knowledge about cometary dust, which can be found in Güttler et al. (2019).
5.2.1 Comparison to Rosetta dust results
In a tentative combination of different results of the dust-analyzing instruments on board Rosetta, namely COSIMA, GIADA, and MIDAS, the majority of the dust of comet 67P in the micro- to millimeter range might be (hierarchical) agglomerates with intermediate porosities of about 60–90% and related densities of about 800 kg m-3 (Fulle et al. 2017; Langevin et al. 2017). The large compact agglomerates with moderate packing of the subunits at the surface that are mainly detected by MIDAS might be representatives of this group of cometary dust particles detected by COSIMA and GIADA, but it should be noted that MIDAS large agglomerates are about 10 μm, which is one order of magnitude smaller than the particles that were typically investigated by COSIMA and GIADA. In addition to a majority of compact agglomerates with moderate packing, COSIMA and GIADA found a large dispersion of density values for dust particles of comet 67P: on the one hand, the fluffy fractal particles detected by GIADA and MIDAS show lowest density values that are lower than 1 kg m-3 (Fulle et al. 2017). On the other hand, rather high densities are reached for consolidated, possibly solid particles with densities over 4000 kg m-3 detected by GIADA (Fulle et al. 2017), and by solid and crystalline material detected by COSIMA through their measurement of calcium-aluminum-rich inclusions (Paquette et al. 2016) and due to their detection of crystalline material through specular reflections (Langevin et al. 2017). However, no solid particles have been detected by MIDAS, and the reasons are discussed in the following section.
5.2.2 Lack of solid particles
As an AFM, MIDAS cannot probe the interior of the dust, thus a “solid” particle for MIDAS is defined as one that does not fragment and that does not show a surface with major features such as deep trenches between bulbous units if scanned with sufficient resolution. Typically, large particles show fragmentation and small particles show distinct surface structures. It cannot be excluded that MIDAS scanned particles that had a solid core with a distinct surface layer of bulbous subunits, but there were no indications for this case.
A special subgroup of solid particles is represented by euhedral crystalline material. Despite the suggestion based on COSIMA data of a common admixture of 5 to 15 μm euhedral crystals in their about 100 μm agglomerates (Langevin et al. 2017), MIDAS did not identify any clear-cut crystal shapes. Although a disguise by a surface layer would be conceivable, such a layer would have to be brought in agreement with the detection by COSIMA through specular reflections; one possibility might be a surface layer with pores that are large enough to allow reflection but small enough to hinder the access with the tips of MIDAS. The same obstacles apply to the detection of euhedral crystals in the smallest subunits that were found by MIDAS. Although there is no indication for crystalline material at the smallest scale, a clear decision concerning the amorphous or crystalline nature of the subunits cannot be made with the data that are currently available.
In addition to the difficulties in identifying solid particles, their lack in the MIDAS collection could be caused by a lower capture efficiency: solid particles are expected to have a higher probability than agglomerate particles to bounce back rather than stick on the collection target. Because the same effect applies to COSIMA collections, the detection of solid particles might be best possible with GIADA. However, GIADA can only detect the density of particles with estimated sizes of about 60–150 μm (depending on particle albedo and density, Della Corte et al. 2015); these sizes are slightly above the detection capabilities of MIDAS. When we assume that solid particles are particles with small cross sections and high densities (over 4000 kg m-3), GIADA found a subset of solid particles that might have no clear counterpart in the particle collections of MIDAS and possibly not in that of COSIMA either (Hilchenbach et al. 2017). It is unknown how many solid particles should be expected at the size scale of MIDAS. In conclusion, MIDAS data do not show evidence for solid particles, but this could be caused by an instrumental bias such as collection efficiencies or difficulties with proper identification.
5.2.3 Fragmentation and hierarchy
Fragmentation is observed for large (larger than about 10 μm) particles, but not for small (smaller than about 5 μm) particles. It is assumed that the force that holds the grains in the subunits together is stronger than the force that holds the subunits of the particle together (Hornung et al. 2016; Skorov & Blum 2012). Consequently, fragmentation of the particle in subunits is easier than fragmentation of the subunits in grains. This behavior is in good agreement with the determined hierarchical agglomerate structure. It is unknown how many levels the hierarchy of cometary dust spans, but MIDAS detected smallest features of about 100 nm on subunits with sizes of a few hundred nanometers that comprise particles of about a few micrometers that build agglomerates of about tens of micrometers. Additionally, COSIMA inferred the existence of particles up to the millimeter scale (Levasseur-Regourd et al. 2018; Langevin et al. 2016). When these results are combined, the dust particles at comet 67P show distinct features at scales between 100 and 1 mm.
5.3 Dust of comet 67P: similarities and differences to CP IDPs
Although the origin of CP IDPs remains unknown, they have been strongly suggested to stem from comets based on targeted collections during meteor showers linked to comets (Taylor et al. 2016), modeling of particle trajectories (Poppe 2016; Nesvorný et al. 2010), and compositional, optical, and structural analysis (Flynn et al. 2016; Rietmeijer 1998). Jupiter-family comets were also found to be the main sources of dust particles in Earth’s orbit (Levasseur-Regourd et al. 2019).
Results of the Rosetta mission can be used to further strengthen this link. The COSIMA instrument provided compositional and optical analysis of their tens to hundreds of micrometer-sized cometary dust particles. The composition at the 40 μm scale is a mixture of carbonaceous material and minerals, in agreement with CP IDPs and UCAMMs (Bardyn et al. 2017). The appearance of the dust particles collected by MIDAS and COSIMA at comet 67P is also highly reminiscent of CP IDPs (Levasseur-Regourd et al. 2018; Bentley et al. 2016b; Langevin et al. 2016). Figure 7 illustrates these similarities. Panels a and c show scanning electron microscope images of 8 and 11 μm CP IDPs. Their surfaces are dominated by bulbous (sub-)micrometer-sized subunits (Brownlee 2016; Noguchi et al. 2015; Flynn et al. 2013). Their surfaces are reminiscent of those of the particles detected by MIDAS, for example, that of particle G shown in a MIDAS AFM image in panel b. However, it should be noted that particle G measures only 1 μm, a fraction of the size of typical CP IDPs. Panels d and e in Fig. 7 show transmission electron microscopy images of the subunitsin CP IDPs that are reminiscent of those imaged by MIDAS. Panel d presents a mix of silicate features consisting of tiny platy subunits (black arrows) and larger grains (black areas) in a matrix of volatile carbonaceous material (open arrows) (Rietmeijer & Nuth 2004). Panel e shows polycrystalline silicate grains in a CP IDP with sizes of about 100 nm (Wozniakiewicz et al. 2012). In a visual comparison, their shapes and assembly are similar to those found in particle G. It should be noted, however, that no unambiguous comparison can be drawn as no compositional data are available for MIDAS particles.
In summary, dust of comet 67P and CP IDPs show a similar appearance, and their smallest subunits are similar in size and arrangement. A promising future project may be a quantitative comparison of the optical images of CP IDPs and cometary dust particles to further strengthen the suggested link between cometary dust and CP IDPs.
 |
Fig. 7 Comparison of the MIDAS particle G in panel b with CP IDPs in panels a and c, and with high-resolution images of their constituent subunits in panels d and e. Panel a is taken from Brownlee (2016), panel c from Flynn et al. (2013), panel d from Rietmeijer & Nuth (2004), and panel e from Wozniakiewicz et al. (2012). |
6 Conclusions
The MIDAS atomic force microscope allowed a morphological classification of nearly pristine cometary dust at the micro- and nanometer scale. Three classes were introduced:
- (i)
the large agglomerates of about 10 μm that consist of micrometer-sized subunits in a fragile arrangement with moderate packing density of the subunits at the surface;
- (ii)
the large porous agglomerate of about 10 μm comprised of micrometer-sized subunits in a structure with a fractal dimension less than two;
- (iii)
the small particles of about 1 μm that show subunits that measure several hundred nanometers and have surface features with a mean size of about 100 nm.
The MIDAS dust categories are in good agreement with the results found by other dust-detecting instruments on board Rosetta. In particular, the submicrometer results allow a good extension of the knowledge of cometary dust to the nanometer scale.
The nature of the 100 nm surface features of the small particles cannot be conclusively determined by MIDAS data alone, such that the possibility remains that the next larger subunits of some hundred nanometers are the fundamental building blocks, or conversely, that the fundamental building blocks have not yet been detected as they might be even smaller than the smallest features, that is, smaller than about 50 nm.
The size distributions of the smallest detected surface features were determined, where the differential size distribution was found to follow a log-normal distribution with a mean of about 100 nm and a standard deviation between 20 and 35 nm. The subunit sizes are in agreement with indirect measurements of other Rosetta instruments. It may be that the subunits found in Stardust material or UCAMMs follow similar size distributions, and this should be investigated in future projects. CP IDPs show a subunit arrangement, shape, and size distribution that is similar to the dust of comet 67P, which further strengthens the link between comets and CP IDPs. It also indicates that the smallest 100 nm features detected by MIDAS might indeed be subunits, but it remains uncertain whether they represent the fundamental building blocks of comet 67P.
Acknowledgements
Rosetta is an ESA mission with contributions from its member states and NASA. We also thank the Rosetta Science Ground Segment and Mission Operations Centre for their support in acquiring the presented data. MIDAS became possible through support from funding agencies including the European Space Agency’s PRODEX programme, the Austrian Space Agency, the Austrian Academy of Sciences and the German funding agency DARA (later DLR). T.M. acknowledges funding by the Austrian Science Fund FWF P 28100-N36 and A.C.L.-R. acknowledges support from Centre National d’Études Spatiales in the scientific analysis of the Rosetta mission.
Appendix A Dust collection time, exposure geometry, and scan history related to particle G
Unlike regular MIDAS scans, where a clear strategy of scan, expose, and re-scan was usually employed, the determination of when a tip picked up dust, from which target it originated, and when this dust was first collected requires a careful analysis. Calibration images of the tip in use were commanded periodically (typically once every few weeks) to monitor the tip health, and toward the end of the mission, specifically for the purpose of high-resolution reverse imaging, as described in this paper. After a dust particle that stuck to a tip was identified, all exposures and operations in between had to be examined to determine the likely period of dust collection and the pick-up time.
The tip shown in Figs. 1 and 2 was only used for scans on a target that was exposed during perihelion. The exact exposure geometry is shown in Fig. A.1. The spacecraft had a distance to the comet of between 300and 450 km while the comet was at its closest position to the Sun at about 1.2 au. Following the orientation of the Rosetta probe, MIDAS funnel was pointing at various possible locations around the whole comet with latitudes between +40 and −60 degrees and longitudes between ±50 degrees.
 |
Fig. A.1 Collection geometry for particle G (see Figs. 1 and 2). Green shaded regions show the periods when particles could be collected. Upper panel: comet-spacecraft distance and off-nadir pointing, middle panel: latitude and longitude, and bottom panel: comet-Sun distance. |
The successful images taken with the tip in the normal imaging mode have resolutions of up to 625 nm and do not show obvious dust particles. However, it is still possible that small dust particles that were not visible in these coarse resolution scans existed and were (partly) picked up. The tip image was taken after only four scans of this target and shows a large dust particle attached to the tip. Unfortunately, no previous tip image is available for this tip, and thus the cometary origin of the contaminant must be concluded based on the morphological similarities to other dust particles that adhered to tips and were detected on the targets.
Appendix B Discussion of uncertainties
Although it is tempting to interpret AFM images as one would their optical counterparts, care must be taken as every AFM image is a convolution of the tip and sample shapes. Because the tip convolution is strongly dependent on the tip opening angle, the artifactsare reduced by using the reverse-imaging technique with the calibration standard spikes. In addition, different areas on the calibration sample (with different spikes) were used, and the tip was typically imaged by more than one spike within a given scan. This gave confidence that the features seen in these images were not the result of contamination on the tip calibration sample.
To calculate uncertainties for the feature sizes, two sources of inaccuracies were taken into account. First, the tip-sample convolution leads to a systematic broadening of the measured size. Second, the marking precision of the features introduces a statistical deviation of the size. Systematical and statistical errors are added linearly to arrive at the total uncertainty. As the tip convolution can only broaden the size of positive features but uncertainties in the marking of the subunits can either enlarge or shrink the sizes, the resulting error bars are asymmetric.
The degree of tip convolution depends on the curvature radius of the calibration spike, its opening angle, and the shape of the feature to be imaged. The increase in the diameter Δd is approximated as 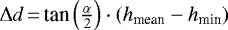 , where
, where 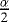 is the half-opening angle of the tip of 25° ± 5°, and the mean and minimum height measured under the marked area are hmean and hmin. A small height difference hmean − hmin leads to a small tip convolution, where the minimum reachable value is given by the apex diameter of the spikes on the calibration target of 20 nm (NT-MDT 2018). The presented calculation is precise for spherical features and will result in an overestimation for more pointed or flatter objects. It thus gives an upper limit of the uncertainty. The calculated uncertainty lies between 14 and 234%, where the lowest values originate from the most flat subunits. Their flanks are shallower than the tip half-opening angle, and thus the broadening is limited to the size of the tip apex (for a 100 nm subunit, this would be a 20% uncertainty due to tip convolution).
is the half-opening angle of the tip of 25° ± 5°, and the mean and minimum height measured under the marked area are hmean and hmin. A small height difference hmean − hmin leads to a small tip convolution, where the minimum reachable value is given by the apex diameter of the spikes on the calibration target of 20 nm (NT-MDT 2018). The presented calculation is precise for spherical features and will result in an overestimation for more pointed or flatter objects. It thus gives an upper limit of the uncertainty. The calculated uncertainty lies between 14 and 234%, where the lowest values originate from the most flat subunits. Their flanks are shallower than the tip half-opening angle, and thus the broadening is limited to the size of the tip apex (for a 100 nm subunit, this would be a 20% uncertainty due to tip convolution).
The extreme values (over about 80%) occur for features that are located at the particle rims. As the sides of the dust that sticks to a tip are not in contact with a target surface but instead adhere to the wall of the tip, the spike on the calibration target can approach from the side and thus create the impression of an arbitrarily lengthened feature. The resulting large height differences lead to correspondingly large tip convolution uncertainties. These cases are clearly identifiable in the cumulative size distributions because of their large uncertainty bars; the error bars that would otherwise have extended, non-physically, below zero diameter have been truncated at zero.
The marking precision of features in the scans depends on the resolution of the scan and the accuracy of the recognition whether a pixel belongs to a feature (i.e., a human factor). To estimate the latter uncertainty, the features were repeatedly marked and the results compared. This led to an assumption of a deviation of 15% in the number of marked pixels. Calculating the deviation of the measured diameter on this basis leads to uncertainties between 7 and 9%. Again, especially the features close to a rim producethe higher error rates. However, as evenly distributed erroneously marked pixels do not have a strong influence on the calculated feature size, the uncertainty due to the marking is in the range of the image resolution or smaller.
Some relatively large uncertainties for the subunit sizes present a challenge when the differential size distribution is determined because the binning cannot be chosen smaller than the maximum uncertainty found for one of the data points. For the presented cases the differential size distribution would only contain two bins, which renders the determination of a distribution function impossible. However, the cumulative size distribution does not face these problems because here no binning is necessary. Thus, this paper investigated the shape of the cumulative size distribution and inferred the properties of the differential size distribution.
Appendix C Fit of the size distributions
The cumulative size distribution of the subunits is expected to follow the integrand of the log-normal distribution,
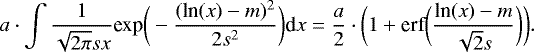 (C.1)
(C.1)
The related mean value μlog and standard deviation σlog for the log-normal distribution are calculated as
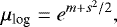 (C.2)
(C.2)
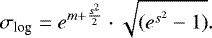 (C.3)
(C.3)
All fits were carried out by the orthogonal distance regression routine of python (scipy.odr)2. The fits take into account the uncertainties of the data and return fit values together with uncertainties. Uncertainties of derived quantities (the mean and standard deviation of the log-normal distribution, see Eqs. (C.2) and (C.3)) are propagated, where their contributions are added quadratically.
The fits were tested by a KS test, where the distance in y-direction between thecumulative size distributions and their empirical distribution functions were calculated. In all cases the determined distances were well below the maximum allowed distance to pass the test (for the 15 nm log-normal fit d15 nm = 0.057 < dmax_15 nm = 0.116, for the 8 nm log-normal fit d8 nm = 0.045 < dmax_8 nm = 0.117, for the line fit of particle G dG = 0.1 < dmax_G = 0.3, and for particle D dD = 0.1 < dmax_D = 0.4).
Appendix D Open access of MIDAS data, raw images, and image processing
The data used in this paper are available in the ESA Planetary Science Archive3 with the product identifiers as given in Tables D.1 and D.2. The tables also contain the key metadata of the scans.
Figures 1 and 2 only contain a crop of the data, thus the full scans are shown in Figs. D.1 and D.2. It is obvious that the images show a slight wavelike bending in x-direction, which is due to thermal drift of the piezo motor (see, e.g., Eaton & West 2010). MIDAS was originally foreseen to operate in a closed-loop design to remove artifacts due to the behavior of the piezo motors, including the thermal drift described above, but this function was lost during launch for the x-direction (Bentley et al. 2016a). The scans presented in this paper are taken with y as fast scanning-direction (from top to bottom) in a closed loop to allow correction for piezo creep, and x as slow scanning-direction (from left to right) in an open loop. Thus, the temperature drift is especially strong in x direction and for longer scanning durations.
 |
Fig. D.1 Full image of the scan taken on 8 December 2015 shown in Fig. 1. The key metadata are given in Table D.1. |
In principle, it is possible to remove the wavelike bending by a polynomial background subtraction. This procedure adjusts the height of the data, but not the step size in the x- and y-directions. This paper analyzed the sizes of the particle and its subunits projected on the x–y plane and did not use the height information other than for feature identification. Because every processing step alters the data and can introduce a bias, it was decided to apply no such processing. To correct deviations of the step size in the x- and y-directions, a dedicated calibration scan would have been necessary, but because of the complex planning pattern of MIDAS (Bentley et al. 2016a), this was not feasible for the scans we presented here. The equivalent diameters of particle G in the analyzed scans are with 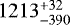 and
and 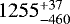 nm for the 15 and 8 nm scan, respectively, similar in the range of uncertainties despite the slight bending. As the error introduced by the thermal drift is even smaller for the smaller subunits, it is assumed that the unprocessed data are still a valid basis for the data analysis we presented.
nm for the 15 and 8 nm scan, respectively, similar in the range of uncertainties despite the slight bending. As the error introduced by the thermal drift is even smaller for the smaller subunits, it is assumed that the unprocessed data are still a valid basis for the data analysis we presented.
 |
Fig. D.2 Full image of the scan taken on 11 May 2016 shown in Fig. 2. The key metadata are given in Table D.2. |
Appendix E Tabulated subunit sizes
The sizes of the subunits and features identified in Figs. 1b and c and in Fig. 2b are given with their uncertainties in Tables E.1–E.2.
References
- Bardyn, A., Baklouti, D., Cottin, H., et al. 2017, MNRAS, 469, S712 [CrossRef] [Google Scholar]
- Bentley, M. S., Arends, H., Butler, B., et al. 2016a, Acta Astronaut., 125, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Bentley, M. S., Schmied, R., Mannel, T., et al. 2016b, Nature, 537, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, J., & Wurm, G. 2008, ARA&A, 46, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blum, J., Gundlach, B., Krause, M., et al. 2017, MNRAS, 469, S755 [CrossRef] [Google Scholar]
- Bockelée-Morvan, D., Rinaldi, G., Erard, S., et al. 2017a, MNRAS, 469, S443 [CrossRef] [Google Scholar]
- Bockelée-Morvan, D., Rinaldi, G., Erard, S., et al. 2017b, MNRAS, 469, S842 [CrossRef] [Google Scholar]
- Bradley, J. P. 2007, in Treatise on Geochemistry, eds. H. D. Holland & K. K. Turekian (Oxford: Pergamon), 1 [Google Scholar]
- Brownlee, D. E. 2016, Elements, 12, 165 [CrossRef] [Google Scholar]
- Brownlee, D., Tsou, P., Aléon, J., et al. 2006, Science, 314, 1711 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Carr, C., Cupido, E., Lee, C. G. Y., et al. 2007, Space Sci. Rev., 128, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Colangeli, L., Lopez-Moreno, J. J., Palumbo, P., et al. 2007, Space Sci. Rev., 128, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Coradini, A., Capaccioni, F., Drossart, P., et al. 2007, Space Sci. Rev., 128, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Dartois, E., Engrand, C., Brunetto, R., et al. 2013, Icarus, 224, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Della Corte, V., Rotundi, A., Fulle, M., et al. 2015, A&A, 583, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobrică, E., Engrand, C., Leroux, H., Rouzaud, J.-N., & Duprat, J. 2012, Geochim. Cosmochim. Acta, 76, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Dominik, C., Blum, J., Cuzzi, J. N., & Wurm, G. 2007, Protostars and Planets V (Tucson, AZ: University of Arizona Press), 783 [Google Scholar]
- Duprat, J., Dobrică, E., Engrand, C., et al. 2010, Science, 328, 742 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Eaton, P., & West, P. 2010, Atomic Force Microscopy (Oxford: Oxford University Press) [CrossRef] [Google Scholar]
- Flynn, G. J., Wirick, S., & Keller, L. P. 2013, Earth Planets Space, 65, 1159 [NASA ADS] [CrossRef] [Google Scholar]
- Flynn, G., Nittler, L., & Engrand, C. 2016, Elements, 12, 177 [CrossRef] [Google Scholar]
- Fulle, M., & Blum, J. 2017, MNRAS, 469, S39 [CrossRef] [Google Scholar]
- Fulle, M., Della Corte, V., Rotundi, A., et al. 2015, ApJ, 802, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Fulle, M., Della Corte, V., Rotundi, A., et al. 2017, MNRAS, 469, S45 [Google Scholar]
- Güttler, C., Mannel, T., Rotundi, A., et al. 2019, A&A, 630, A24 (Rosetta 2 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayward, T. L., Hanner, M. S., & Sekanina, Z. 2000, ApJ, 538, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Hilchenbach, M., Fischer, H., Langevin, Y., et al. 2017, Phil. Trans. R. Soc. London, Ser. A, 375, 20160255 [NASA ADS] [CrossRef] [Google Scholar]
- Hornung, K., Merouane, S., Hilchenbach, M., et al. 2016, Planet. Space Sci., 133, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Hörz, F., Bastien, R., Borg, J., et al. 2006, Science, 314, 1716 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Johansson, F. L., Odelstad, E., Paulsson, J. J. P., et al. 2017, MNRAS, 469, S626 [NASA ADS] [CrossRef] [Google Scholar]
- Kissel, J., Altwegg, K., Clark, B. C., et al. 2007, Space Sci. Rev., 128, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Langevin, Y., Hilchenbach, M., Ligier, N., et al. 2016, Icarus, 271, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Langevin, Y., Hilchenbach, M., Vincendon, M., et al. 2017, MNRAS, 469, S535 [CrossRef] [Google Scholar]
- Levasseur-Regourd, A. C., Zolensky, M., & Lasue, J. 2008, Planet. Space Sci., 56, 1719 [NASA ADS] [CrossRef] [Google Scholar]
- Levasseur-Regourd, A., Agarwal, J., Cottin, H., et al. 2018, Space Sci. Rev., 214, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Levasseur-Regourd, A., Renard, J.-B., Hadamcik, E., et al. 2019, A&A, 630, A20 (Rosetta 2 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, A., & Greenberg, J. M. 2003, in Solid State Astrochemistry, eds. V. Pirronello, J. Krelowski, & G. Manicò (Dordrecht: Springer Science+ Business Media), 120, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Mannel, T., Bentley, M. S., Schmied, R., et al. 2016, MNRAS, 462, S304 [NASA ADS] [CrossRef] [Google Scholar]
- Meakin, P. 1991, Rev. Geophys., 29, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Messenger, S. 2000, Nature, 404, 968 [CrossRef] [PubMed] [Google Scholar]
- Nesvorný, D., Jenniskens, P., Levison, H. F., et al. 2010, ApJ, 713, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Nichols, G., Byard, S., Bloxham, M. J., et al. 2002, J. Pharm. Sci., 91, 2103 [CrossRef] [Google Scholar]
- Noguchi, T., Ohashi, N., Tsujimoto, S., et al. 2015, Earth Planet. Sci. Lett., 410, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Noonan, J., Schindhelm, E., Parker, J. W., et al. 2016a, Acta Astronaut., 125, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Noonan, J., Schindhelm, E., Parker, J. W., et al. 2016b, Proc. SPIE, 9905, 99053J [CrossRef] [Google Scholar]
- NT-MDT. 2018, Spectrum Instruments, Test Grating TGT1, available at http://www.ntmdt-tips.com/products/view/tgt1 (accessed 12 December 2018) [Google Scholar]
- Paquette, J. A., Engrand, C., Stenzel, O., Hilchenbach, M., & Kissel, J. 2016, Meteorit. Planet. Sci., 51, 1340 [NASA ADS] [CrossRef] [Google Scholar]
- Poppe, A. R. 2016, Icarus, 264, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Price, M. C., Kearsley, A. T., Burchell, M. J., et al. 2010, Meteorit. Planet. Sci., 45, 1409 [Google Scholar]
- Riedler, W., Torkar, K., Jeszenszky, H., et al. 2007, Space Sci. Rev., 128, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Rietmeijer, F. J. M. 1993, Earth Planet. Sci. Lett., 117, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Rietmeijer, F. 1998, Rev. Mineral., 36, XIII [Google Scholar]
- Rietmeijer, F. J. M., & Nuth, III, J. A., 2004, in The New Rosetta Targets. Observations, Simulations and Instrument Performances, Astrophys. Space Sci. Lib., eds. L. Colangeli, E. Mazzotta Epifani, & P. Palumbo (Dordrecht: Springer Science+Business Media), 311, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Skorov, Y., & Blum, J. 2012, Icarus, 221, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Steffl, A. J., Feldman, P. D., A’Hearn, M. F., et al. 2015, AAS/Division for Planetary Sciences Meeting Abstracts, 47, 413.08 [NASA ADS] [Google Scholar]
- Stern, S. A., Slater, D. C., Scherrer, J., et al. 2007, Space Sci. Rev., 128, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, S., Messenger, S., & Folco, L. 2016, Elements, 12, 171 [CrossRef] [Google Scholar]
- Tielens, A. G. G. M., Waters, L. B. F. M., & Bernatowicz, T. J. 2005, in Chondrites and the Protoplanetary Disk, eds. A. N. Krot, E. R. D. Scott, & B. Reipurth, ASP Conf. Ser., 341, 605 [NASA ADS] [Google Scholar]
- Weidenschilling, S. J., & Cuzzi, J. N. 1993, in Protostars and Planets III, eds. E. H. Levy & J. I. Lunine (Tucson, AZ: University of Arizona Press), 1031 [Google Scholar]
- Westphal, A. J., Stroud, R. M., Bechtel, H. A., et al. 2014, Science, 345, 786 [NASA ADS] [CrossRef] [Google Scholar]
- Wozniakiewicz, P. J., Bradley, J. P., Ishii, H. A., et al. 2012, ApJ, 760, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Wozniakiewicz, P. J., Bradley, J. P., Ishii, H. A., Price, M. C., & Brownlee, D. E. 2013, ApJ, 779, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Yabuta, H., Noguchi, T., Itoh, S., et al. 2017, Geochim. Cosmochim. Acta, 214, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Zolensky, M. E., Zega, T. J., Yano, H., et al. 2006, Science, 314, 1735 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zolensky, M. E., Nakamura-Messenger, K., Rietmeijer, F., et al. 2008, Meteorit. Planet. Sci., 43, 261 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Particle G, a 1 μm particle scanned with the MIDAS reverse-imaging mode on 8 December 2015 with a resolution of 15 nm per pixel. The smooth, round shape at the bottom with a fading line to the bottom right corner is the tip with which the particle was picked up, above sits the particle with well-visible substructures. Panel a: particle itself. Panel b: larger subunits. Panel c: smallest identifiable features. |
| In the text | |
 |
Fig. 2 Same 1 μm particle G as shown in Fig. 1, but this time scanned with a resolution of 8 nm on 11 May 2016. Panel a: particle itself. Panel b: smallest identifiable features. Compared to Fig. 1, the color scale has to be fully exploited as some lower-lying subunits were imaged (indicated by the white arrows). |
| In the text | |
 |
Fig. 3 Cumulative size distribution of the subunits of particle G identified in the 15 nm resolution scan (Fig. 1c). On the left we show the probability that a subunit is smaller than the indicated value, and on the right we show the number of detected subunits. The log-normal fit is shown in blue together with its uncertainty interval in light blue. The verticallines denote the arithmetic (black) and fitted (blue) mean values with shaded uncertainty intervals. |
| In the text | |
 |
Fig. 4 Cumulative size distribution of the subunits of particle G identified in the 8 nm resolution scan (Fig. 2b). On the left we show the probability that a subunit is smaller than the indicated value, and on the right we show the number of detected subunits. The log-normal fit is shown in blue together with its uncertainty interval in light blue. The verticallines denote the arithmetic (black) and fitted (blue) mean values with shaded uncertainty intervals. |
| In the text | |
 |
Fig. 5 Cumulative size distribution of the larger subunits of particle G (Fig. 1b, black dots) and D (Bentley et al. 2016b, blue triangles). The line fits of the data are shown for particle G in black and particle D in blue, and the arithmetic means of the measured sizes are given as vertical lines with shaded uncertainty intervals. |
| In the text | |
 |
Fig. 6 3D rendered images of MIDAS dust particles. Panel a: particle F as example for a large agglomerate particle whose subunits arepacked in a moderately dense fashion on the surface (Mannel et al. 2016). The source scan was taken on 14 October 2015 at 08:08:23 UTC with a resolution of 192 nm. Panel b: large porous agglomerate particle E. The data are taken from a scan on 18 January 2015 at 20:59:28 UTC with a resolution of 210 nm. Panel c: particle G, which is representative for the small particle class. The source scan was taken on 11 May 2016 at 12:08:03 UTC with a resolution of 8 nm and is shown in Figs. 2 and in Appendix D.2. |
| In the text | |
 |
Fig. 7 Comparison of the MIDAS particle G in panel b with CP IDPs in panels a and c, and with high-resolution images of their constituent subunits in panels d and e. Panel a is taken from Brownlee (2016), panel c from Flynn et al. (2013), panel d from Rietmeijer & Nuth (2004), and panel e from Wozniakiewicz et al. (2012). |
| In the text | |
 |
Fig. A.1 Collection geometry for particle G (see Figs. 1 and 2). Green shaded regions show the periods when particles could be collected. Upper panel: comet-spacecraft distance and off-nadir pointing, middle panel: latitude and longitude, and bottom panel: comet-Sun distance. |
| In the text | |
 |
Fig. D.1 Full image of the scan taken on 8 December 2015 shown in Fig. 1. The key metadata are given in Table D.1. |
| In the text | |
 |
Fig. D.2 Full image of the scan taken on 11 May 2016 shown in Fig. 2. The key metadata are given in Table D.2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


