| Issue |
A&A
Volume 630, October 2019
Rosetta mission full comet phase results
|
|
|---|---|---|
| Article Number | A24 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201834751 | |
| Published online | 20 September 2019 | |
Synthesis of the morphological description of cometary dust at comet 67P/Churyumov-Gerasimenko
1
Max Planck Institute for Solar System Research,
Justus-von-Liebig-Weg 3,
37077 Göttingen,
Germany
e-mail: c.guettler@tu-bs.de
2
Space Research Institute, Austrian Academy of Sciences,
Schmiedlstrasse 6,
8042 Graz, Austria
3
Physics Institute, University of Graz,
Universitätsplatz 5,
8010 Graz, Austria
4
INAF – Istituto di Astrofisica e Planetologia Spaziali,
Via Fosso del Cavaliere 100,
00133 Rome, Italy
5
Dipartimento di Scienze e Tecnologie, Universitá degli Studi di Napoli Parthenope, CDN IC4,
80143 Naples, Italy
6
INAF – Osservatorio Astronomico,
Via Tiepolo 11,
34143 Trieste, Italy
7
LESIA,
Observatoire de Paris, Université PSL, CNRS, Université Paris Diderot, Sorbonne Paris Cité, Sorbonne Université,
5 place J. Janssen,
92195
Meudon Principal Cedex, France
8
IRAP, Université de Toulouse, CNRS, UPS, CNES,
Toulouse, France
9
LATMOS, Sorbonne Université, CNRS, UVSQ, Campus Pierre et Marie Curie,
BC 102, 4 place Jussieu,
75005 Paris, France
10
Institut für Geophysik und extraterrestrische Physik, Technische Universität Braunschweig,
Mendelssohnstr. 3,
38106 Braunschweig, Germany
11
Department of Physics and Astronomy “Galileo Galilei”, University of Padova,
Via Marzolo 8,
35131 Padova, Italy
12
Center of Studies and Activities for Space (CISAS) “G. Colombo”, University of Padova,
Via Venezia 15,
35131 Padova, Italy
13
CNR-IFN UOS Padova LUXOR,
Via Trasea 7,
35131 Padova, Italy
14
Ciencias Espaciales, Instituto de Geofísica, Universidad Nacional Autónoma de México, Coyoacán,
Mexico City 04510, Mexico
15
Instituto de Astrofísica de Andalucía (CSIC),
c/ Glorieta de la Astronomia s/n,
18008 Granada, Spain
16
Department of Physics and Astronomy “Galileo Galilei”, University of Padova,
Vicolo dell’Osservatorio 3,
35122 Padova, Italy
17
Osservatorio Astrofisico di Arcetri, INAF,
Firenze, Italy
18
Universität der Bundeswehr München, LRT-7,
85577
Neubiberg, Germany
19
Institut d’Astrophysique Spatiale, CNRS/Université Paris-Sud,
91405 Orsay, France
20
Physics Department, 206 Allison Laboratory, Auburn University,
Auburn,
AL 36849, USA
21
Konkoly Observatory,
PO Box 67,
1525 Budapest, Hungary
22
Deutsches Zentrum für Luft- und Raumfahrt (DLR), Institut für Planetenforschung,
Rutherfordstraße 2,
12489
Berlin, Germany
Received:
30
November
2018
Accepted:
26
February
2019
Before Rosetta, the space missions Giotto and Stardust shaped our view on cometary dust, supported by plentiful data from Earth based observations and interplanetary dust particles collected in the Earth’s atmosphere. The Rosetta mission at comet 67P/Churyumov-Gerasimenko was equipped with a multitude of instruments designed to study cometary dust. While an abundant amount of data was presented in several individual papers, many focused on a dedicated measurement or topic. Different instruments, methods, and data sources provide different measurement parameters and potentially introduce different biases. This can be an advantage if the complementary aspect of such a complex data set can be exploited. However, it also poses a challenge in the comparison of results in the first place. The aim of this work therefore is to summarize dust results from Rosetta and before. We establish a simple classification as a common framework for intercomparison. This classification is based on the dust particle structure, porosity, and strength and also on its size. Depending on the instrumentation, these are not direct measurement parameters, but we chose them because they were the most reliable for deriving our model. The proposed classification has proved helpful in the Rosetta dust community, and we offer it here also for a broader context. In this manner, we hope to better identify synergies between different instruments and methods in the future.
Key words: comets: general / comets: individual: 67P/Churyumov-Gerasimenko / space vehicles: instruments
© C. Güttler et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1 Introduction
When comets become active, they release gas and dust, of which latter is then carried away by the gas to form the cometary coma. The detailed physical processes of the dust release from the surface are not well known. However, because cometary material is known to exhibit a very low strength (Attree et al. 2018; Groussin et al. 2015) and processes take place under the extremely low cometary gravity (Sierks et al. 2015), the forces required to lift off the dust are likely gentle. This is the mechanism by which a comet, formed 4.57 billion years ago, slowly decomposes back into its building blocks. The level of the primitiveness of these dust particles with respect to their formation time can be debated, but it is clear that they still carry clues to the early formation of comets and our solar system. It must be the ultimate goal of cometary dust studies, whether from Earth or by spacemissions, to interpret results from this point of view and aim to decipher these clues.
It was the purpose of Rosetta, ESA’s Mission to the Origin of the Solar System (Schulz et al. 2009), to provide the data in support of this goal. Three instruments on Rosetta were exclusively dedicated to the study of dust in the coma of comet 67P/Churyumov-Gerasimenko (67P). Several other instruments from the suite of 11 instruments on board Rosetta and 10 instruments on the lander Philae were equally suited and successful in the study of cometary dust. Results of these dust studies are presented in Sects. 3.1–3.6.
Rosetta-era studies of cometary dust are standing on the shoulders of space missions such as Giotto and Vega at 1P/Halley and Stardust at 81P/Wild 2. Giotto was equipped with two dedicated dust instruments, the Dust Impact Detector System (DID), and the Particle Impact Analyzer (PIA), which provided the first in situ data of cometary dust shortly after its release from a comet. Additionally, the Optical Probe Experiment (OPE) retrieved local dust brightness and polarization. The Vega spacecraft were equipped with the dust mass spectrometer PUMA (on Vega 1; Kissel & Krueger 1987; Krueger et al. 1991) and the dust particle detectors SP-1 and SP-2 (on Vega 1 and 2, respectively; Reinhard & Battrick 1986), which all were in situ dust instruments. During its flyby at comet Wild 2, the Stardust spacecraft collected dust particles to bring them to Earth for detailed analyses (Stardust results are described further in Sect. 3.7). Additional in situ information was provided by the Stardust Dust Flux Monitor Instrument (DFMI; Tuzzolino et al. 2004) and Cometary and Interstellar Dust Analyzer (CIDA; Kissel et al. 2004).
Aspects of cometary dust can also be studied from Earth: telescope observations can, for instance, determine levels of activity and the morphology of the large-scale dust tails and trails, thus dynamics of dust particles; photopolarimetric studies allow the interpretation of the dust particle structures. When cometary dust particles are lifted off a comet, they can travel through the solar systemand eventually cross the Earth orbit. They are collected in the Earth stratosphere as interplanetary dust particles (IDPs) or on the Earth surface as micrometeorites (MMs). These aspects are all summarized and discussed in Sects. 3.8 and 3.9.
The main goal of this work is to summarize Rosetta results on cometary dust and make them comparable among themselves, but also with studies that are not based on Rosetta. Here we focus on the morphology and structure of cometary dust particles; for the composition and mineralogy, we refer to Engrand et al. (2016, Rosetta), Zolensky et al. (2006, Stardust) and others. Many results were published by the different Rosetta instrument teams, and because of the nature of the complementary instruments, measurement parameters are different and not directly comparable. We establish in Sect. 2 a clear language and classification for dust particles of different morphologies. This is not a new definition, but we try to summarize the consensus of the community and then rigorously stick to it. Based on this, we summarize in Sect. 3 results from Rosetta, Stardust, and Earth-based observations. As a key result, they are summarized in Table 1 and Fig. 12. They are compared and discussed in Sect. 4, and a short conclusion is presented in Sect. 5.
This work is the result of a series of workshops and discussions, involving the largest part of the Rosetta dust community. It is clear that because such a great wealth of data is still being interpreted, this can only be a first step in a concerted understanding of Rosetta data in particular and cometary dust in general. However, the work is ongoing, and we aim to continue combining our results in the spirit of this paper.
2 Classification
2.1 General nomenclature
Different communities or even different scientists tend to use slightly different nomenclatures. This work is a large collaborative effort, and the aim is to form a broad agreement (or at least identify disagreements). It is therefore critical to be as explicit and precise as possible, which is why we provide the used and agreed nomenclature here. We intend to keep consistence with the nomenclature used in the Stardust (e.g., Brownlee et al. 2006) and planetesimal formation (e.g., Dominik et al. 2007) communities.
A grain is the smallest component we consider in this study. It is a solid particle with a tensile strength (typically >MPa) that exceeds the forces acting in its environment. A grain is likely irregular in shape but homogeneous in composition. It is the constituent that forms the aggregates and agglomerates defined below. Grains were created by condensation, either in the solar system’s protoplanetary disk or earlier in the interstellar medium or AGB-star outflows (e.g., Alexander et al. 2007). We do not specify the grain material in this definition.
The term monomer is often used in this context and must not be confused with the definition of a monomer molecule. In the dust community, monomer is used synonymously with grain, often in theoretical works. We thus propose to keep this term, but restrain its use to spherical or elliptical grains or their mathematical description.
We use the term (dense) aggregate for an intimate assemblage of grains that are rigidly joined together and cannot be readily dispersed. Such dense aggregates might look like grains from the outside, but in fact contain different mineralogical components (grains) in the inside. The smallest components observed in the Stardust sample were these aggregates (Brownlee et al. 2006).
A (porous) agglomerate is constituted of grains or dense aggregates. The binding forces are much smaller than the inner binding forces of grains or aggregates, such that agglomerates are easily dispersed. Agglomerates are the particles that are expected to form through dust agglomeration in the early protoplanetary disk (Dominik et al. 2007).
The terms aggregate and agglomerate are often used synonymously to describe what we define here as agglomerate. However, we see the need to formal distinction between these two. The precise distinction is not always consistent in the literature (e.g., Nichols et al. 2002; Walter 2013), and we choose the definition that is prevalently used in the community when the two are distinguished at all. We propose to address them as dense aggregates and porous agglomerates when the precise wording is important (as dense we consider porosities < 10%, see below).
Furthermore, we distinguish the case of a fractal agglomerate, which is showing a fractal and dendritic nature, implying a very high porosity of typically >99%. For these, the fractal dimension Df defines the relation between mass m and size r as m ∝ rDf (e.g., review by Blum 2006). In our case, the relevant fractal agglomerates have Df < 3 and are typically in the range 1.5–2.5. This is consistent with particles formed by cluster–cluster agglomeration (Blum 2006).
Finally, we use the term particle as a generic term for any unspecified dust particle. This can be anything from a monomer to an agglomerate and implies that the nature of a particle is not further known or considered.
Summary of Rosetta and Stardust classification.
2.2 Structure and porosity classification
Based on the general nomenclature above, we further refine the description of the structures and porosities of dust particles. In addition to the size of a particle, the porosity and structure are parameters that are to some degree accessible for Rosetta’s dust instruments and are a focus of this work. We introduce three groups that prove to be useful in terms of categorizing the Rosetta dust observations summarized below. Each group comprises physical properties and a structure that can explain these properties. Specifically, the three discriminating properties chosen here are (a) porosity, (b) structure, and (c) strength. Various structures are possible within these groups, which are illustrated in Fig. 1 and are separately explained below. Each of these structures isalso compared to examples in nature, laboratory, or theory in Figs. 2–6.
The group solid describes particles with (a) a porosity <10% that are (b) consolidated and (c) exhibit a high strength similar to rock. Particles that fall into this group are the grains and dense aggregates described in Sect. 2.1, and also chondrules or calcium-aluminum-rich inclusions (CAIs). The tensile strength should be in the MPa range and higher, which is only the case for solid particles of low porosity. The latter is chosen to be <10%, to be much smaller than the random close packing of a granular medium (~ 40%, Onoda & Liniger 1990), which enables clearly distinguishing between compressed agglomerates. The most reasonable mechanism that can create these low porosities for cometary particles is thermal processing, that is, compaction through (partial) melting or vapor transport.
We identify two structures that fall into this group. Irregular grains and spherical monomers (SOLID_1 in Fig. 1) are the smallest. Examples of irregular grains used in laboratory analog experiments are shown in Fig. 2 (left). Many different materials have been used in laboratory experiments, while the examples here are from diamond (top left, Poppe et al. 2000) and Forsterite (bottom left, Tamanai et al. 2006). Spherical monomers can easily be formed in the laboratory from supersaturated gas or liquid phases and are also used for analog experiments in astrophysics. All three examples in Fig. 2 (right) are from SiO2, but with different size distributions (top to bottom: Poppe et al. 2000; Colangeli et al. 2003; Brisset et al. 2017). Monomers in nature are not perfectly spherical and have rough surfaces.
When grains form a dense aggregate, we expect a morphology like SOLID_2, which is an idealized (simplified) Stardust particle. Figure 3 shows three thin sections of solid aggregates from Stardust (top: Brownlee 2014; bottom left: Brownlee et al. 2006). Some interplanetary dust particles (IDPs) collected in the Earth’s stratosphere in the NASA Cosmic Dust Catalog1 also resemble this morphology; an example is presented in Fig. 3 (L2021B6, bottom right).
The structures described below are based on agglomerated particles from the solid group. SOLID_1 s are drawn in gray (e.g., silicates) or blue (e.g., ices) to indicate that the composition can vary. However, we wish to leave the shape and composition of the constituent grains open on that scale and therefore assume that the agglomerates below can form out of any of these grains in any mixed state.The composition of many agglomerates in Stardust and Rosetta is known, but this is beyond the scope of this paper.
The second class, group fluffy, describes agglomerates that (a) have a very high porosity (>95%). These (b) are likely fractal and dendritic agglomerates, the only reasonable explanation for extreme porosities, and (c) show a very low strength (Pa range). A visualized example is FLUFFY_1 in Fig. 1. Fractal agglomerates are very well known from the literature, in particular in the context of early planet formation (Blum 2006). The examples in Fig. 4 (left) show fractal agglomerates from SiO2, grown under laboratory conditions. The top example is a small agglomerate of 1.9 μm monomers from Heim et al. (1999), while the lower example is significantly larger and has a fractal dimension of Df ≈1.8 (not measured for this specific agglomerate, but for similar ones that formed under the same condition, Blum 2004). The example on the top right is a fractal agglomerate formed in a computer simulation by ballistic cluster–cluster agglomeration, consists of 8192 monomers, and exhibits a fractal dimension of 1.99 (Wada et al. 2008). The bottom right example is from the Rosetta/MIDAS experiment and is discussed in detail in Sect. 3.1.
Finally, the group porous collects the remaining parameter range with particles of (a) porosities between 10 and 95%. These are (b) considered to be loosely bound agglomerates with (c) an intermediate but rather low strength, typically in the order of 1 Pa to 100 kPa. Laboratory analog experiments demonstrated that in the case of silicates, this depends only mildly on composition (Blum et al. 2006). Because of their higher stickiness in collisions (Gundlach & Blum 2015), ice agglomerates may form easier in the solar nebula. However, their intrinsic cohesion (tensile strength) is very similar to that of silicates (Gundlach et al. 2018b) as long as the temperatures are low. For temperatures above ~ 140 K, micrometer-sized ice particles start to sinter on timescales shorter than ~105 s so that forcometary nuclei close to the ice-evaporation front, the mechanical strength might be increased (Gundlach et al. 2018a). Sintering can also occur for silicates (Poppe 2003) and organics (Kouchi et al. 2002).
Figure 1 provides two examples for this group: POROUS_1 is a van-der-Waals agglomerate with a rather homogeneous structure, bound by surface forces. Similar agglomerates are studied in laboratories and computer simulations. In Fig. 5 we present an SEM image of a loose agglomerate consisting of 0.5 μm solid zirconium silicate particle (top left, Blum & Münch 1993), an IDP from the NASA Cosmic Dust Catalog (L2021A1, bottom left), an x-ray tomography reconstructed cut though an agglomerate from SiO2 monomers (top right, Kothe et al. 2013), and an agglomerate used for numeric simulations (bottom right, Wada et al. 2011).
The substructure might not be as homogeneous, and the second example for the porous group in Fig. 1 (POROUS_2) represents a cluster consisting of smaller agglomerates with voids in between. These hierarchic agglomerates were produced in laboratory experiments, as shown in Fig. 6 (top left). This is a back-light illuminated agglomerate, grown from smaller (100 μm) agglomerates under microgravity conditions (Brisset et al. 2016). The other examples are from Rosetta/COSIMA (top right) and Rosetta/MIDAS (bottom) and are explained in detail in Sects. 3.1 and 3.2. A hierarchic agglomeratestructure can formally be described as being fractal if the agglomerate consists of hierarchically structured (self-similar) sub-agglomerates. In the case of POROUS_2, we assume either one single sub-agglomerate size or a few cascades of substructures, such that all requirements for the porous group are still fulfilled. The strength of these clusters is significantly smaller than POROUS_1 structures if the number of contacts is small at substructure boundaries.
A classification into these three groups is not always unambiguous. The correlation of structure, porosity, and strength is likely but not necessary. It can therefore be possible that a studied particle shares properties of more than one group, such that a classification is not easily possible. This is in particular the case when the structure also shows properties of different groups, as in the mixed cases in Fig. 7.
POROUS_SOLID_1 is a particle from the solid group, sheathed with an agglomerate layer. An example for such an agglomerateis the common picture of a mantled chondrule. A polished cross-section of a rimmed chondrule by Metzler et al. (1992) is shown on the top left of Fig. 8, and an isolated chondrule analog by Beitz et al. (2012) is shown in the top right (inset with different coating technique). Based on a density measurement, this particle would be a member of the solid group, while the outer appearance (e.g., light scattering) would cloak it as a member of the porous group. The Stardust particle T57 Febo (Brownlee et al. 2006, also Fig. 8 bottom left) is another mixed case POROUS_SOLID_2. Depending on the ratio between solid and mixed component, the group would be ambiguous. Finally, a solid particle with an attached fractal structure as depicted in FLUFFY_SOLID_1 was observed in IDPs (NASA Cosmic Dust Catalog, L2021A7, Fig. 8 bottom right), and shares reflection and density properties from the solid and fluffy group. More ambiguities are further discussed in Sect. 3 when they occur.
 |
Fig. 1 Possible dust-particle structures, defined by applying the three main groups defined in Sect. 2.2. The units of larger structures are drawn from circles for illustrative purposes only. In reality, these can be any of the solid group, where colors (gray and blue) also indicate that compositions can vary (e.g., ices). |
 |
Fig. 4 Fractal particles from laboratory experiments (left), computer simulation (top right), and Rosetta/MIDAS (bottom right, left and right of the scale bar; references in the text). The color code and scale bar for the bottom right image denotes height. |
 |
Fig. 5 Agglomerates from the POROUS_1 type in Fig. 1. SEM image of a laboratory analog agglomerate (top left), an IDP (bottom left), a tomographic cross section (top right), and a computer model (bottom right; references in the text). |
 |
Fig. 6 Clusters of agglomerates from the POROUS_2 type in Fig. 1. Sample grown under microgravity (top left), Rosetta/ COSIMA (top right), and Rosetta/MIDAS samples (bottom; references in the text). |
 |
Fig. 7 Classification from Sect. 2.2 and Fig. 1 is not always unambiguous. These examples of mixed cases show aggregate structures that would be classified one way or another, depending on the method applied (e.g., surface microscopy, mass determination, or light scattering). |
3 State of knowledge
In this section we summarize the knowledge on cometary dust with a focus on Rosetta. Sections 3.1–3.6 focus on Rosetta dust instruments. These are all different and thus complementary in nature: the Micro-Imaging Dust Analysis System (MIDAS; see Riedler et al. 2007) collected dust particles and determined their shape and structure with an atomic force microscope. It was thus an in situ instrument with an imaging method. The same is the case for the Cometary Secondary Ion Mass Analyser (COSIMA; see Kissel et al. 2007), where collected particles were studied with a microscope and with a secondary ion mass spectrometer. The Grain Impact Analyser and Dust Accumulator (GIADA; see Colangeli et al. 2007) was another in situ instrument, but without an imaging method. Particles instead crossed a laser curtain, and their size and speed was determined from the signal of scattered light (Grain Detection System; GDS). The particles then collided on the Impact Sensor (IS), where their momentum (thus mass if velocity is known) could be measured if they carried enough momentum. The Optical, Spectroscopic, and Infrared Remote Imaging System (OSIRIS; see Keller et al. 2007), consisting of a narrow- and a wide-angle camera, could observe within the inner coma individual (but still unresolved) dust particles as well as a diffuse signal from a large ensemble of indistinguishable particles. In either case, the interpretation requires an assumption of the light-scattering properties. The Visible and Infrared Thermal Imaging Spectrometer (VIRTIS; see Coradini et al. 2007) could spectrally resolve the diffuse coma to infer color and temperature of the unresolved dust. As OSIRIS and GIADA above, VIRTIS also relied on the scattered light and model assumptions on scattering properties. On the surface of comet 67P, the lander Philae also studied the dust, and we place the focus here on the dust monitor DIM as part of Philae/SESAME (Seidensticker et al. 2007) as well as on the down-looking camera Philae/ROLIS (Mottola et al. 2007) and the cameras for panoramic imaging, Philae/CIVA (Bibring et al. 2007).
Sections 3.7–3.9 extend the picture beyond recent Rosetta findings. We consider constraints from the large body of Earth-based observation as well as studies of cometary dust in laboratories, in particular the samples brought back to Earth by Stardust.
The intention of this section is to summarize the individual results and compile them into a comparative table (Table 1). While the summaries are descriptive and comprehensive, the resulting table is a simplification, which is intended as a framework and an aid to memory for cross-comparison. While individual instrument groups have so far interpreted specific instrument results, we here aim with all Rosetta instrument teams involved to homogenize our understanding and nomenclatures. For a more general and complementary review of cometary dust with a focus on Rosetta, we also refer to the article by Levasseur-Regourd et al. (2018).
3.1 Rosetta/MIDAS
The MIDAS atomic force microscope revealed the surface structure of particles with nanometer resolution for 1–50 μm sized particles. All studied particles show surfaces with textures that can be interpreted as that of an agglomerate consisting of smaller subunits, which could again be of agglomerate structure (Bentley et al. 2016).
One particle was pointed out to exhibit an extraordinarily loose packing of subunits, and a sophisticated structural analysis was conducted (Fig. 4, bottom right; Bentley et al. 2016; Mannel et al. 2016). Subunits range from 0.58 to 2.57 μm with an average of 1.48 μm (Bentley et al. 2016), while it cannot be excluded that these subunits are again agglomerates with subunit sizes smaller than about 500 nm. The particle is expected to have compacted during collection so that its image can be interpreted as a projection of the original structure onto the target plane (Fig. 4, bottom right), which was determined to be fractal with a fractal dimension Df = 1.7 ± 0.1 (as used in Table 1; Mannel et al. 2016). Only a 37 × 20 μm2 area of the particle was scanned, and an attempt to scan the particle with adapted parameters showed that fragmentation destroyed the probably very fragile particle. The representative size (disk of same area) of this particle is about 15 μm diameter, while it might be argued that the lateral extension is no larger than 80 μm, which results in a representative size of 30 μm diameter. We therefore consider a range of 15–30 μm (as used in Table 1) for the MIDAS fluffy group. It should be noted that because this was the only fractal collected by MIDAS and because the overall number of collected particles is unknown but assumed to be low, it is not feasible to determine a ratio of fractal versus non-fractal particles.
All remaining particles with sizes about 10–50 μm show surface features in the order of 1 μm, which we interpret to mean that these are loosely bound subunits (group porous in Sect. 2.2). As an example, Fig. 6 (bottom) shows two of these agglomerates in different sizes: the left particle of ~ 20 μm diameter shows several substructures, of which the structure at the bottom right (≲10 μm) is the most prominent. The particle in the bottom right of Fig. 6, in the size of the previous subunit and measured with higher resolution, again features about four subunits. On the next smaller scale, Fig. 9 shows a 1 μm particle that consists of a few hundred nanometer-sized subunits that again exhibit surface features that might indicate that they are again agglomerates (Mannel et al. 2019). Overall, this indicates that the 10–50 μm sized particles might have a hierarchical structure of agglomerates of agglomerates, resembling the example POROUS_2.
The sizes of cavities compared to the subunits suggests a packing below maximum density, while on the other hand, the density is certainly higher than that of the fractal particle described above. Most of the 10–50 μm sized particles decomposed into many smaller fragments during scanning, which are of similar size as features observed on their surface. This suggests that they at least to a large extent consist of subunits similar to those shaping their surface and are not mistaken as particles resembling the examples POROUS_SOLID_1 or SOLID_2. The sizes of subunits are moreover similar to those of the fractal particle described by Mannel et al. (2016). This could be a sign that the fractal and denser particles have formed out of subunits from a similar reservoir and are at least to a large extent agglomerates.
The smallest individual particles detected are between 1 and 10 μm (Bentley et al. 2016, and Fig. 6 bottom right). They are less numerous than larger particles and did not fragment during scanning, pointing towards a higher strength. Their surfaces are similar to those of the 10–50 μm particles, but in a size range of the large particle subunits. Because the 1–10 μm particles were scanned with higher resolutions, it is possible to resolve features of sizes down to about 500 nm on their surfaces (see Fig. 9, discussed below), and highest resolution scans (8 and 15 nm pixel−1) even resolve features with sizes of about 100 nm. The deep trenches observed between the few hundred nanometer features indicate that the 1–10 μm particles might be agglomerates rather than members of the SOLID_2 class. However, it should be mentioned that they were never seen to disintegrate, and thus they could also have a solid core covered with subunits like POROUS_SOLID_1. Relying on the deep trenching, we suggest to classify 1–10 μm particles as agglomerates with a non-negligible porosity, which overall places MIDAS dust particles of 1–50 μm size into the porous group.
Particles matching the solid group were not strictly observed by MIDAS. Neither porosity nor the inner structure of the dust can be determined with the current data. The size of the smallest refractory subunits cannot be determined either because of the resolution limit of MIDAS and the ambiguity between surface features that is created by roughness or subunits. The smallest identified features have sizes between 50–200 nm (Fig. 9 and Mannel et al. 2019). They were detected in a special imaging mode where the instrument picked up particles or particle fragments that could have alteredthe particles or fragments. It is expected that particle alteration first alters the arrangement of the subunits, and a higher stress is required to change subunit properties. As the subunit size distributions of rather porous looking picked-up particles and more compressed looking particles are similar, we expect that no major alteration ofsubunit sizes occurred. However, if these smallest 50–200 nm sized features are only surface features of consolidatedlarger units, then the next larger units with sizes smaller than about 500 nm would be the candidates for the smallestsolid unit detected by MIDAS. To conclude, with a significant uncertainty, we consider particles of 50–500 nm (as used in Table 1) as the smallest particles, possibly classified into our solid group.
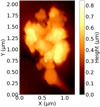 |
Fig. 9 MIDAS image of an agglomerate particle sticking to the side of a tip that was acquired using a calibration target with sharp spikes (Mannel et al. 2019). The smooth round feature at the bottom is the tip apex, and the straight line to the bottom right corner is a structure supporting the tip. The image has a pixel resolution of about 15 nm and was acquired on 8 December 2015. |
3.2 Rosetta/COSIMA
The COSIMA instrument collected dust particles to image them with an optical microscope (COSISCOPE) and then perform secondary ion mass spectroscopy (SIMS). Observed dust particles range from the COSISCOPE resolution limit of 14 μm to around one millimeter (as used in Table 1). During collection, the particles collided with the targets with a varying relative velocity of about a few m s−1 with respect to the Rosetta spacecraft (Rotundi et al. 2015). Upon impact, they therefore fragmented, and the adhering fragments show a power-law size distribution with a differential power-law exponent of − 3.1 on average (Hilchenbach et al. 2016; Merouane et al. 2016).
The fragments were initially classified as compact particles, rubber piles, shattered clusters, and glued clusters (Langevin et al. 2016; Merouane et al. 2016). It was later shown that compact particles are also fragile enough to be broken by mechanical pressure as well as by charge-up in the SIMS ion beam (Hilchenbach et al. 2017). Ellerbroek et al. (2017) furthermore showed in laboratory analog experiments that the four morphological groups defined by Langevin et al. (2016) can be explained through a variation in collection velocity. Based on this and the evidence that all particles can be further broken, we consider all as agglomerates according to the classification in Sect. 2.2. Many particles show substructures, even down to the resolution limit of 14 μm pixel−1, which indicates that they are clusters consisting of smaller components, possibly again agglomerates (similar to POROUS_2 in Fig. 1).
In an attempt to infer mechanical properties from the impact fragmentation, Hornung et al. (2016) used this picture for the impacting agglomerates and inferred a strength (they did intentionally not distinguish between tensile and shear strength) for the initially non-fragmented agglomerate. In their model, the strength is determined by the binding force between sub-agglomerate structures and therefore depends on their sizes, and they obtained around 1000 Pa (as used in Table 1) when subunits of 10–40 μm were assumed, that is, a size of about the COSISCOPE resolution limit.
Observations of substructures of non-fragmented agglomerates were interpreted by Hornung et al. (2016) as macroscopic filling factors2 (on a 60–300 μm scale) in the range of 0.4–0.6. These substructures were in turn assumed to be porous, with the smallest solid unit of ~ 0.2 μm diameter. This is formally described by their size-dependent filling factor ϕ ∝ r−0.4, which implies a hierarchical cascade of substructures and porosities on all scales down to the solid grain. Because the fragmentation model constrains strength boundaries rather than void spaces, the porosity of above 90% quoted by Hornung et al. (2016) is likely not a strong restriction. Based on a hierarchical porosity model for the dust agglomerates, the bulk of the dust particle porosity budget would reside in the size range below 14 μm. The exact values rest on the known and adopted model parameters.
The agglomerates collected by COSIMA were mostly ice-free as the instrument was kept warm inside and particles were studied days to weeks after collection. However, they show a surprisingly high reflectance factor in the 3–22% range (Langevin et al. 2016, 2017). Agglomerates were illuminated with a red LED (640 nm) at phase angles between 72 and 84 deg from two directions (roughly opposite, left and right in the image plane, cf. Langevin et al. 2017, Fig. 1), one after another. The measured reflectance, in particular, the comparison between left and right illumination, was explained with scattering centers inside the agglomerate volume and an optical mean-free path in the 20–25 μm range. The required porosity depends on the size of the scattering centers and is estimated to be in the 50–90% range (Langevin et al. 2017).
The COSIMA results can also provide a clue about the solid group: Paquette et al. (2016) have found compositions that are consistent with CAI material. These were discovered on separated spots in a 30 μm rastered line scan of particle David Toisvesi.2. A possible interpretation would be two or more solid CAI particles (thus SOLID_1) of <30 μm, embedded in an agglomerate of porous nature. Another hint for solid components is provided by specular reflections. Langevin et al. (2017) interpreted these as being produced by 5–15 μm crystalline facets. This would be a grain of type SOLID_1. The size estimate is derived from a comparison to reference olivine particles, which were dispersed on one of the flight targets before launch (Langevin et al. 2017). Because the size constraint from the CAI candidate above is weaker, we consider COSIMA solid particles (SOLID_1 or SOLID_2) in the 5–15 μm range (as used in Table 1).
3.3 Rosetta/GIADA
GIADA measured the scattered light, speed, and momentum of dust particles (Della Corte et al. 2015). On the basis of these data, it is possible to infer the density of a dust particle as it depends on its true shape, composition, and microporosity (Fulle et al. 2016b).
The measurement range of GIADA fell between 0.3 and 100 m s−1 in speed (higher velocities up to 300 m s−1 are less reliable) and 10−10−4 × 10−4 kg m s-1 in momentum, which results in masses between 1.0 × 10−12 and 1.3 × 10−3 kg. The particle equivalent diameters fall between 60 and 200 μm for high-albedo material (kaolinite) and 150 and 800 μm for low-albedo material (amorphous carbon; Della Corte et al. 2016).
All particles measured with GIADA GDS and IS show densities enveloped by dust bulk densities of Fe-sulphides (4600 kg m−3) and hydrocarbons (1200 kg m−3), where either an oblate or prolate ellipsoidal shape with aspect ratios up to 10 was assumed (Fulle et al. 2017). The mean dust bulk density results in 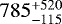 kg m−3, where the large uncertainty arises from the unknown shape. However, an average spherical shape is in good agreement with the prolate and oblate ellipsoids framing the whole data set (except for a few outliers). Fulle et al. (2017) inferred the dust volume filling factor to be 0.59 ± 0.08. With this, the majority of the dust detected by GIADA is described to be porous agglomerates (group porous). Their sizes span the whole detection range of GIADA from roughly 0.15 to 0.8 mm (as used in Table 1).
kg m−3, where the large uncertainty arises from the unknown shape. However, an average spherical shape is in good agreement with the prolate and oblate ellipsoids framing the whole data set (except for a few outliers). Fulle et al. (2017) inferred the dust volume filling factor to be 0.59 ± 0.08. With this, the majority of the dust detected by GIADA is described to be porous agglomerates (group porous). Their sizes span the whole detection range of GIADA from roughly 0.15 to 0.8 mm (as used in Table 1).
Two dust populations drop out of this characterization: first, Fulle et al. (2017) presented particles with a density of around or above 4000 kg m−3 (cluster with small cross-sections in their Fig. 1; for these, the assumed albedo was that of carbon, otherwise the density would be even higher). These densities can only be explained by a compaction mechanism, which has to affect their strengths, making a loose agglomerate structure unlikely. Their sizes are typically <0.5 mm (as used in Table 1) and, according to the classification in Sect. 2.2, they fall into the solid group. It cannot be excluded that the structure resembles POROUS_SOLID_1 in Fig. 7, for instance, if the solid core is large enough. In any case, the measurements demand the existence of macroscopic particles from the solid group.
The other extreme are dust particles that are inferred to be very low density, fluffy agglomerates (Della Corte et al. 2015). In particular, their densities and speeds were so low that these particles had insufficient momentum to produce a signal at the impact sensor. They were only detected by the optical detection measurement subsystem (GDS) as showers of many small dust particles caused by large, low-density parent agglomerates fragmenting directly in front of the instrument (Fulle et al. 2015), where the confinement of the shower restricted the fragmentation to occur in close proximity. The low speed and the fragmentation in front of the spacecraft were explained by Fulle et al. (2015) with electrostatic forces: the fluffy agglomerates were charged in the coma, which led to their disruption if the strength of the electrostatic field exceeded the strength that held the agglomerate together. Fulle et al. (2015) estimated charge, mass, and cross section of the parent agglomerates and derived an upper limit for the equivalent bulk density of lower than 1 kg m−3. Moreover, the velocity of these fluffy agglomerates was lower than the escape velocity from the comet. Assuming that this velocity difference was caused by electrostatic deceleration of the particles at the spacecraft, Fulle & Blum (2017) determined the size of the fluffy agglomerates before breakup to be in the millimeter range. Because the only plausible way to grow such a large and porous particle is fractal growth, Fulle et al. (2016a) calculated a fractal dimension of Df ≈1.87 (as used in Table 1) for the fluffy agglomerates. The GDS showers, that is, the fluffy particles, were often accompanied by the signal of a compact particle at the IS (GDS+IS detection), which is interpreted as the fluffy particles being attached to a compact particle until disruption shortly before detection. It is not known if all fluffy particles were attached to a compact particle as the cross sections of the GDS showers were larger than GIADA’s entrance area, which means that the compact particle did maybe not enter the instrument and escaped detection. Furthermore, GDS detections of single particles with low speeds and not enough momentum to create an IS signal could also have been caused by fluffy particles, although a determination of density, and thus clear assignment to the group fluffy or group porous, is not possible.
The probability of a particle being a fluffy agglomerate is about 23% (as used in Table 1; Fulle & Blum 2017)if all GDS single detections are counted as group porous, or 58% if the latter are counted as group fluffy.
3.4 Rosetta/OSIRIS
With the Rosetta/OSIRIS camera system, dust in the coma of 67P could be studied remotely, thus non-invasively, through observationsin different color filters of the solar light they scatter. We have to distinguish between individual particles, which in most cases were unresolved (smaller than one pixel), and a diffuse signal from a large ensemble of indistinguishable particles.
Individual particles were first described by Rotundi et al. (2015), who determined a dust-particle size distribution, later analyzed in its time evolution by Fulle et al. (2016c) and Ott et al. (2017). Detectable sizes by this method are typically in the range of centimeters and decimeters. Agarwal et al. (2016) studied the larger end of particles observed with OSIRIS, which were close to the comet and far from the spacecraft, with the largest about 80 cm diameter3 (as used in Table 1). Only one particle was detected that was resolved by the cameras (i.e., larger than 1 pixel, Fig. 7 in Fulle et al. 2016c), where the size is largely uncertain but likely larger than a meter. Frattin et al. (2017) studied individual particles in different OSIRIS color filters to assess their composition, and depending on their spectral slope, associated
different particles with organics, silicates, or water ice. All of these particles are expected to fall into the porous group as defined in Sect. 2.2. They are too large to be fractals or grains, and it is unlikely that they are solid.
The smallest individual particles in OSIRIS were observed by Güttler et al. (2017). These were close to the spacecraft (1–100 m), and the smallest measured 0.3 mm in diameter (as used in Table 1). The sizes could have been smaller, depending on the scattering properties of the particles (see discussion in Güttler et al. 2017 and Fulle et al. 2018). Density assumptions in the 100–1000 kg m−3 range can explain the observed acceleration of the particles, either through a rocket force (Güttler et al. 2017) or by pure solar radiation pressure (Fulle et al. 2018). Based on this density, the agglomerates fall into the porous group (as used in Table 1).
The diffuse coma observed under different phase angle conditions was studied by Bertini et al. (2017, 2019). With the comet outside the OSIRIS field of view (FoV; preferably by 90°), the Rosetta spacecraft was rotated around a vector perpendicular to the Sun direction and inside the comet-spacecraft-Sun plane to take images of the coma at a wide range of phase angles. From the overall flux in the images (after filtering cosmics and individual dust particles), they computed a phase curve, which interestingly shows a concave “smile shape”, featuring an absolute minimum at around 90° phase angle (see their Figs. 2–4).
Moreno et al. (2018) succeeded in modeling the full phase function using elongated particles of diameter ≳20 μm, which need to be aligned along the solar radiation direction. In a complementary modeling attempt, Markkanen et al. (2018) could reproduce the OSIRIS phase function at different times using aggregates in the 5–100 μm size range, consisting of sub-micrometer-sized organic grains and micrometer-sized silicate grains. Indication for macroscopic particles (in contrast to dispersed sub-micrometer monomers) is also provided from analogous laboratory experiments by Muñoz et al. (2017). Overall, there are indications for particles smaller than the best OSIRIS resolution in OSIRIS data, but interpretation and detailed studies are still ongoing.
3.5 Rosetta/VIRTIS
The Rosetta/VIRTIS dual-channel spectrometer (Coradini et al. 2007) consisted of two instruments: the point spectrometer VIRTIS-H (operating in the 2–5 μm spectral range with an FoV of 0.033° × 0.10°) and the line-scanning imaging spectrometer VIRTIS-M (operating in the 0.25–5 μm spectral range with an FoV of 3.6° × 3.6°). Because of its low spatial resolution and relatively long integration times (compared to Rosetta/OSIRIS), it could not study individual dust particles. The strength of VIRTIS was the high spectral resolution and the extended wavelength range that covered thermal radiation in the 3–5 μm spectral range. Spectra of the diffuse coma can be modeled to provide remote-sensing information, complementary to other Rosetta instruments.
A comprehensive study of the diffuse coma and outbursts observed with the VIRTIS-H channel on 13 and 14 September 2015 was presented by Bockelée-Morvanet al. (2017a,b) and Rinaldi et al. (2018). The two key results that we pick up here are the particle size distribution in the quiescent coma and the detection of high-temperature grains (see below) during outburst.
Bockelée-Morvanet al. (2017a) modeled the 2–5 μm infrared emission of a collection of porous and fractal particles with Mie and Rayleigh-Gan-Debye theories (see Bockelée-Morvanet al. 2017a for details), in order to explain the 2 μm color, color temperature, and bolometric albedo measured on the spectra. The best fit for the quiescent coma was achieved with a differential power index β of the n(a) ∝ a−β size distribution in the range 2.5–3 (as used in Table 1), consistent with the power index determined by other instruments (Rotundi et al. 2015; Fulle et al. 2016c). The observed 20% excess in color temperature with respect to the equilibrium temperature can be attributed either to the presence of sub-micrometer particles made of absorbing material or, alternatively, to fractal agglomerates with sub-micrometer units. The ratio of fractal versus porous agglomerates influences the minimum size of the particles in the size distribution fitting the measurements. For a relative number of fractal agglomerates of 25% (Fulle & Blum 2017), particles at sizes below ~ 20–30 μm should be underabundant (Bockelée-Morvanet al. 2017b). The scattering and thermal properties of the diffuse coma of 67P are in line with the mean of values measured for moderately active comets, showing that 67P is not atypical in its dust properties (Bockelée-Morvanet al. 2017a).
The material detected shortly after outburst onset showed blue colors and color temperatures as high as 550 and 650 K (Figs. 4 and 5 in Bockelée-Morvanet al. 2017a, and Rinaldi et al. 2018). This was attributed to superheating of very small particles, which were warmed by solar irradiation but could not sufficiently cool through infrared emission. The required particle size to explain the two properties is ~0.1 μm, and particles are believed to be individual, that is, not bound in larger aggregates (see discussion in Bockelée-Morvanet al. 2017a and Rinaldi et al. 2018). Because nanometer-sized particles may not be present in the general background coma, Bockelée-Morvanet al. (2017a) suggested that the outburst was disintegrating loosely bound agglomerates, which were otherwise bound by strong cohesion. These smallest particles could fall into our solid group, although their strength and porosity is not constrained by VIRTIS.
3.6 Rosetta/Philae
3.6.1 DIM
The Dust Impact Monitor (DIM) on board Philae was a cube with 7 cm to a side, designed to detect sub-millimeter- and millimeter-sized dust particles emitted from the nucleus of the comet employing piezoelectric detectors. The cube had three active sensor sides, and each side had a total sensitive area of 24 cm2 (Seidensticker et al. 2007). During the descent of Philae to the surface of 67P, DIM recorded an impact of a cometary dust particle (among many other impact signals identified as false impacts) at 2.4 km from the comet surface (Hirn et al. 2016; Krüger et al. 2015; Flandes et al. 2018). Experiments support the identification of this particle (aerogel was used as a comet analog material to characterize the properties of this particle). They are consistent with a particle radius of 0.9 mm, density of 250 kg m−3, and porosity close to 90%. Data and estimations also indicate that the particle likely moved at near 4 m s−1 with respect to the comet (Podolak et al. 2016; Flandes et al. 2018).
3.6.2 ROLIS
The Rosetta Lander Imaging System (ROLIS) observed the original Philae landing site Agilkia during descent and later Philae’s final rest location Abydos. In the Agilkia region, surface regolith was observed with a best resolution of 0.95 cm pixel−1 (Mottola et al. 2015). In addition to the power-law size distribution of particles, the images reveal that small, decimeter-sized boulders show surface textures down to the resolution limit. At the Abydos site, the material is more lumpy, and no individual particles or pores can be distinguished at the resolution limit of 0.8 cm pixel−1 (Schröder et al. 2017). Dust particles crossing the camera field of view were observed few centimeters as well as several meters from the camera (Figs. 3 and 7, respectively, in Schröder et al. 2017). No size or morphological information can be determined, however.
3.6.3 CIVA
The Comet Infrared and Visible Analyser (CIVA) performed successful observations at the Abydos final landing site. With a best resolution of 0.6 mm pixel−1, the observed surface is in parts interpreted as pebbles with a dominating size of 5–12 mm (Poulet et al. 2016). It should be noted that these are not clearly detached from the surface, which means that the observations are consistent with ROLIS and the interpretation is different. CIVA has observed one isolated signal in the coma, which was interpreted as a detached particle by Bibring et al. (2015, supplement Fig. S5), consistent with ROLIS observations. No further properties of this particle candidate can be determined in this case either.
3.7 Stardust sample collection
The Stardust mission collected and returned cometary dust samples, which are the only cometary samples of known origin available on Earth (Brownlee et al. 2006). The spacecraft made a flyby at the Jupiter-family comet 81P/Wild 2 in January 2004 at 234 km closest distance and 6.1 km s−1 relative velocity. It captured more than 10,000 dust particles between 1 and 100 μm in collectors of 3 cm thick silica aerogel tiles. In addition, the aluminum frame around the aerogel tiles shows impact craters with residues of the particles.
All particles were altered by the capture, dominantly through heating to temperatures above the melting point of silica. Particles larger than a micrometer are often reasonably well preserved due to their higher thermal inertia, while sub-micrometer dust was only able to survive when shielded by a larger particle (Brownlee et al. 2006; Rietmeijer 2016).
3.7.1 Aerogel tracks
Impacts into aerogel are divided into three main classes (Hörz et al. 2006): type A tracks are slender, flute- or carrot-shaped tapering tracks with either a single or multiple styli and/or spikes (cf. Fig. 10a), where a stylus is defined as that part of the particle track that runs about straight, looking like a narrowing tube or a root. The shortest type A tracks of less than 100 μm were initially all classified as type A, although it was then already noted that their morphology of a squat turnip is slightly different (Hörz et al. 2006). Subsequent laboratory work with analog material showed that their impactors are substantially different from the longer type A tracks, thus Kearsley et al. (2012) suggested to reclassify these tracks as type A* (cf. Fig. 10e). Type B tracks show broader, bulbous cavities with one or several styli (cf. Fig. 10b and c),and type C tracks are broad, stubby cavities with no or very little styli (cf. Fig. 10d).
To determine impactor properties from track properties, many efforts of laboratory calibration were carried out, for example, by Kearsley et al. (2012). Impactors that are suggested to match particles of the solid group in our classification are single crystals or glassy grains of sizes between 1 and 10 μm (note that impactor particle diameters smaller than 1 μm are all correlated to type A* tracks; Burchell et al. 2008). These materials are not expected to fragment upon high-velocity capture and indeed are found to produce type A tracks with one stylus (Kearsley et al. 2012). However, type A tracks with one stylus can also be caused by agglomerates of up to 100 μm with coarse subunits larger than about 10 μm. In our classification, this agglomerate would fall in the porous group.
The porous group is suggested to be populated by all agglomerate impactors used in the experimental calibrations,except for the most fragile ones (Kearsley et al. 2012). These impactors of sizes between 1 and 100 μm (Burchell et al. 2008)were found to create type A tracks with single or multiple styli as well as type B tracks. This ambiguity is in good agreement with the continuity between the track shapes of type A and B (Kearsley et al. 2012) and possibly an effect of different aggregate strength depending on the degree of subunit fineness and organic content.
Extremely weak material with highest porosities as suggested in the fluffy group was not used for laboratory calibrations, and a comparison to the impacts created is therefore difficult. The best matches among the used calibration material is expected to be the agglomerates of fine subunits with organic material, or pure organic material. Small impactors of a few 100 nm probably created type A* tracks, and impactors of 10 μm (Burchell et al. 2008) created type C tracks.
In comparison to the Rosetta/GIADA data, these impactors could well be the same materials as the particles creating fluffy detections without a sign of a compact particle in the GIADA instrument. On the other hand, fluffy particles associated with the detection of a compact particle in GIADA (explained by FLUFFY_SOLID_1 in Fig. 7) are suggested to have caused Stardust type B tracks, where the fluffy part would create the bulbous morphology and the compact particle creates the stylus.
 |
Fig. 10 Track morphology terminology for Stardust tracks, derived from Kearsley et al. (2012, Figs. 1 and 12). (a)–(d) from aerogeltracks in Stardust collection. (e) from analog experiment by Kearsley et al. (2012). |
3.7.2 Aluminum foils
Cometary dust particles that collided with the aluminum frame holding the aerogel collector produced hyper-velocity craters and left molten residues inside (Hörz et al. 2006). It was found in laboratory experiments that it is possible to deduce impactor properties such as size, mass, density, and internal structure from crater morphology.
If the morphology of the craters is smoothly bowl-shaped, their suggested impactors are dense and 10–60 μm long, thus could resemble the particles causing type A tracks in aerogel. The residuals in the craters indicate that these particles must not be homogeneous in composition, but can also have consisted of a compact silicate particle of about 3000 kg m−3 accompanied by a fine-grained material mix (Kearsley et al. 2008). This would mean that impactors creating bowl-shaped craters would fall into our solid group or porous group, or a mix of the two (e.g., POROUS_SOLID_1 or POROUS_SOLID_2).
For craters with high and uneven relief, Kearsley et al. (2008) suggest that they are caused by porous agglomerates with low densities, complex shape, and diverse composition. Their model calculations reveal porosities around 75% and densities lower than 1000 kg m−3, which classifies them as members of our porous group. Agglomerate sizes can be up to 100 μm, but their constituents are in the micrometer scale and seem to consist of again smaller particles in the tens of nanometer size range (Kearsley et al. 2008). These smallest grains of tens of nanometers fall into our solid group.
As there are no experimental data on extremely low-density and high-porosity material shot on aluminum foils (Kearsley et al. 2008), there is no counterpart for the fluffy group in these laboratory studies. Interestingly, the distribution of aerogel tracks and aluminum foil craters are only slightly consistent with random impacts and can be interpreted as clustering. It was suggested that particles fragment in the coma, leading to so-called bursts and swarms in dust flux measurements (Tuzzolino et al. 2004; Economou et al. 2012). Clustering of impact features, be it aerogel tracks or aluminum foil impacts, could be the result of particle fragmentation, but the reason for breakup is unknown (Hörz et al. 2006). If millimeter-sized fluffy particles like those detected by Rosetta/GIADA (Sect. 3.3) were present at comet Wild 2, the aluminum foil clusters could even be explained without particle fragmentation, just by direct impact of fluffy particles, or, if breakup is desired, the fragmentation of fluffy particles can be explained by electrostatic charging.
3.8 Interplanetary dust particles and micrometeorites
The largest sample of cometary material on Earth is believed to be in interplanetary dust particles (IDPs) and micrometeorites (MMs). While IDPs are particles collected in the Earth stratosphere, MMs are collected on the ground (e.g., Antarctica and sediments). The association with cometary material is not unambiguous, but several arguments support it on a statistical level.
The zodiacal cloud model of Nesvorný et al. (2010) suggests from a dynamical perspective that 85% of the total mass influx at Earth originates from Jupiter-family comets. Particles smaller than ~ 300 μm should moreover survive frictional heating to arrive in the Earth stratosphere (as IDPs) and even on the surface (as MMs). Interpretations of zodiacal light observations in the visible and infrared domains (Lasue et al. 2009; Rowan-Robinson & May 2013) also indicate that most of the interplanetary dust particles reaching Earth’s vicinity are of cometary origin.
Busemann et al. (2009) connected IDPs collected in April 2003 with comet 26P/Grigg-Skjellerup, which was expected to show an enhanced flux in this time period. From a compositional standpoint, this sample shows very primitive properties: an unusually high abundance of pre-solar grains, organic matter, and fine-grained carbonates. As a classification, Bradley (2003) and Rietmeijer (2002) distinguished IDPs between chondritic and non-chondritic material. Bradley (2003) further sorted the morphological appearance into chondritic porous (CP) and chondritic smooth (CS). The chondritic porous particles are considered the most primitive IDPs, being composed of unhydrated phases and not showing products of aqueous alteration. The IDPs described by Busemann et al. (2009) fall into this chondritic porous group.
The measurement of physical properties (we are particularly interested in porosity and strength) are difficult on this scale. To our knowledge, nothing is published on the strength, but there were some attempts to measure porosities (also see the summary in Rietmeijer 1998). One possibility of IDP porosity measurement is described by Love et al. (1994): the volume was determined with a combination of transmission and scanning electron microscopy (TEM and SEM). For the mass determination, they measured the Fe count rate of IDPs from x-ray fluorescence (see also Flynn & Sutton 1991) and enhanced this mass with the assumption of a chondritic composition. They confirmed with calibration measurements that in their measurement range of 5– 15 μm, the entire volume was excited. The determined density distribution was corrected for a size bias in fall speed (coupling times). The corrected numbers show a large portion of particles with densities near and below 2000 kg m−3 (40% porosity), but higher densities (up to 6000 kg m−3) were also observed.
For larger samples of chondritic IDPs in the 10–100 μm range, Corrigan et al. (1997) produced thin sections and measured direct porosity from SEM images. Their results peak around 4%, and the tail of the distribution (although small numbers) ranges to 53% porosity.
It seems as if our solid and porous group from Sect. 2.2 are represented in the IDP collections. Moreover, there are indications for higher porosities (Rietmeijer 1993), indicating members of the fluffy group.
To further link these studies to our morphologic classification, we studied the classification of MMs. Their link to cometary material is weaker than that of the IDPs, but much material exists, and a classification was presented by Genge et al. (2008). In their Table 1, they defined three groups from the MMs melting state, where we are mostly interested in their unmelted MMs. Furthermore, they defined the subclasses fine grained, coarse grained, refractory and ultracarbonaceous. The fine-grained MMs can be reasonably porous (C3 in their nomenclature, example in Fig. 11, left), falling into our porous group. Their coarse-grained MMs would fall into our solid group, but because of possible alteration of the MMs, we should be careful in connecting these with cometary dust. Genge et al. (2008) also found that particles might not fall into a unique class, as their example from Fig. 11 (right) shows. This mix of coarse- and fine-grained material resembles our examples of mixed cases in Fig. 7, in particular, POROUS_SOLID_2. The refractory and ultracarbonaceous MMs classified by Genge et al. (2008) are likely associated with cometary dust, but are classified by compositional arguments. We therefore do not draw a comparison here.
 |
Fig. 11 SEMimage of micrometeorites (MMs) by Genge et al. (2008). Left: their fine-grained C3 type, associated with our porous group. Right: particle consisting of coarse-grained (top left) and fine-grained (bottom right) components, similar to mixes we have exemplified in Fig. 7, in particular, POROUS_SOLID_2. |
3.9 Earth-based observations of 67P and other comets
3.9.1 Dust tail and trail
Observation and modeling of the dust tail and trail can provide independent clues on particle sizes present in the coma. The shape of the tail and trail from Earth-based observations is mostly determined by (a) the size- and time-dependent dust production rate and velocity, and (b) forces acting on these dust particles (for a review on this topic, see Agarwal et al. 2007). The first is a free parameter constrained by Rosetta, and for the latter, the decisive quantity is the ratio of solar radiation pressure and gravity, which depends on the size, optical properties, and bulk density of a particle (Burns et al. 1979). Tail models are more sensitive to small particle sizes, while the trail is dominated by large particles (≳ 100 μm). Moreno et al. (2017) used 116 tail observations from various telescopes plus trail observations from the last and previous apparitions of comet 67P. With a Monte Carlo model, they propagated the trajectories of dust particles and compared synthetic images generated in this way to the available observations. Motivated by the small amount of (sub-)micrometer particles detected by MIDAS, they used 20 μm as a minimum particle diameter. They let the maximum particle diameter vary from 2 to 80 cm as a function of heliocentric distance (largest size around perihelion). The slope for particles with <2 mm diameter also varies with heliocentric distance. No further evolution of particle sizes in the coma such as fragmentation or sublimation was applied or required. Overall, they reached a good fit to the telescope imaging data, and the dust production rate, an outcome of the model, also shows a reasonable correlation, if not complete, with gas production rates (Hansen et al. 2016).
The size input parameters, albedo, and bulk density were chosen to be consistent with Rosetta. However, the fit to the telescope data confirms their applicability also on the large scale. In particular, the minimum required particle size of 20 μm is interesting. Smaller particles do exist, that is, they can be dispersed and were observed (Bockelée-Morvanet al. 2017a,b, and others), but there are too few of them to manifest themselves in the scattered light of telescope observations. In particular, the steep size distribution adopted for small particles near perihelion (differential size distribution exponent ≤ −3.5) implies that the scattering cross-section is concentrated in the smallest particles near the minimum adopted size. This implies that the cross section of particles <20 μm must be small (i.e., a sharp cutoff in the size distribution around this size) because otherwise either the model coma would become much brighter than the observed coma or the model dust production rate of larger particles would have to be decreased to become inconsistent with Rosetta observations and the surface brightness of the trail. This lack of <20 μm diameter particles is in line with earlier findings at 67P (Agarwal et al. 2010; Fulle et al. 2010) and with Spitzer observations of a larger sample of Jupiter-family comets (Reach et al. 2007). An assessment of the minimum required and maximum allowed population for these sizes would be interesting but is currently not available.
3.9.2 Polarimetry
Remote observations of solar light scattered by dust in cometary comae and tails have been used for more than one hundred years to study its partial linear polarization, as first done on comet Tralles in 1819 (Arago 1858). The linear polarization is connected to chemical composition and physical properties of the dust. During the return of 1P/Halley in 1985–1986, the evolution of the polarization pointed toward significant changes in dust properties during outbursts (Earth-based; Dollfus et al. 1988) and also variations related to jet structures (when Giotto crossed them; Levasseur-Regourd et al. 1999; Fulle et al. 2000). Polarimetric remote observations of comet 67P have been performed during its 2008–2009 and 2013–2016 returns in preparation and support of the Rosetta mission (Hadamcik et al. 2010, 2016; Rosenbush et al. 2017). The interpretation of these data sets requires experimental and numerical simulations to infer information on chemical composition and physical properties of the dust observed in cometary comae (e.g., Levasseur-Regourd et al. 2007). Experimental simulations on numerous samples are obtained with gonio-polarimeters, operating in the laboratory and/or under microgravity conditions (Muñoz & Hovenier 2011, 2015; Levasseur-Regourd et al. 2015).
Agglomerates of sub-micrometer-sized grains best fit the higher polarization observed in cometary jets and after fragmentation or disruption events, while a mixture of porous agglomerates and compact particles are needed to fit whole comae observations (Hadamcik et al. 2006). The polarimetric phase curves of cometary analogs made of porous agglomerates of sub-micrometer-sized Mg-silicates, Fe-silicates, and carbon black grains mixed with compact Mg-silicates grains are comparable to those observed in comae of comets (Hadamcik et al. 2007). Numerical simulations complement the experimental work to infer further dust properties: It has been established that spheres or spheroids, in fact, any solid particles, cannot (even with various size distributions and compositions) reproduce the observational data (Kolokolova et al. 2004) and that models with agglomerates of sub-micrometer-sized particles provide satisfactory results (Kiselev et al. 2015). Simulations indeed strongly suggest that cometary dust is a mixture of (possibly fractal) agglomerates and of compact particles of both non-absorbing silicate-type materials and more absorbing organic-type materials (Levasseur-Regourd et al. 2008; Lasue et al. 2009). The variety of agglomerate and grain structures is thus consistent with the scheme developed in Sect. 2.2, with an emphasis on the porous group.
4 Discussion and interpretation
Using the morphologically motivated classification scheme from Sect. 2.2, we have in Sect. 3 summarized recent results on cometary dust, which culminated in Table 1. We now wish to change the point of view, discuss the results in a comparative manner, and exploit the potential from the complementary design of the individual instruments.
The imaging capabilities of MIDAS and COSIMA provide similar insights on a different but overlapping size scale. Both show the surface, and at some level, the interior, structure of porous dust agglomerates (porous group in Fig. 1), possibly with substructure as in POROUS_2. The MIDAS capability of strength measurement is not yet fully exploited, but from COSIMA we learned that all agglomerates break when the SIMS ion beam is applied. In contrast to this, the measurement parameters of GIADA are size (relying on a light scattering model) and mass, from which we can derive densities and porosities. Sizes are also determined by OSIRIS and VIRTIS: while OSIRIS provided insight on large dust particles up to a meter (again, using a light scattering model), VIRTIS provided constraints on the power-law size distribution and smallest unit size from modeling.
In Fig. 12 we provide a visual representation to allow for a more quantitative comparison of the observed size ranges. Every color represents an instrument (as in Table 1, we include Stardust in the comparison) and the results are grouped by the three groups defined in Sect. 2.2. Much overlap is seen for porous agglomerates in the COSIMA size range (14–300 μm, black dashed box at the top), which overlaps with MIDAS, GIADA, OSIRIS, and Stardust. The overlap confirms that we have the best complementary knowledge for aggregates in this size range. However, it has to be noted that measurements and interpretations (e.g., porosities) are not overall consistent even though they fall into the same group. Instruments and interpretations can have biases, therefore this overlap has the potential to further understand and correct for these.
In the same box (group porous), no agglomerates are smaller than 1 μm. This is a choice we made in Sect. 3.1, where we interpreted sub-micrometer structures scanned by MIDAS as solid components, which is possible but ambiguous. The size of the smallest solid component is an interesting topic with important implications for solar system formation. One particularly noteworthy contribution here is the detection of 100 nm sized particles that are needed to explain the observation of superheating in VIRTIS spectra (Sect. 3.5). We do have imagery evidence of structures on this size scale from MIDAS (Fig. 9): the cauliflower structure in Fig. 9 is interpreted as a porous agglomerate (~ 1 μm) of highly irregular but solid aggregates (100 nm size range). It becomes evident that we lack data on the ≲ 1 μm size range, and we are left with indirect evidence, which should be the focus of upcoming research.
Large particles from the solid group were described by Stardust (aerogel and aluminum foil; 1–100 μm), COSIMA (CAI candidate and specularreflection; 5–15 μm) and GIADA(measurements of high densities; 0.15–0.5 mm). There is no strong evidence for solid particles larger than 1 mm, but neither is there a robust method to distinguish between porous agglomerates and solid particles in the OSIRIS size range. Our choice of group is supported by indirect density measurements on the (sub-)millimeter scale (Güttler et al. 2017; Fulle et al. 2018), but a small fraction of solids could have been unrecognized.
Agglomerates from the fluffy group smaller than 1 cm are found by MIDAS and GIADA, confirming Stardust findings. Their existence as a small fraction of the full dust population is plausible within the context of planetesimal formation (Fulle & Blum 2017). The complete picture as presented in Fig. 12 can be consistent with primordial dust agglomeration: In the comet-forming region, we would expect small solid particles, either falling in from the interstellar cloud or transported out from the inner solar system. These coagulate into fractal agglomerates if allowed by the dynamic environment. Larger agglomerates would restructure in collisions while they grow, such that we expect everything above a threshold size (e.g., millimeter size range, depending on model) to fall into the porous group.
Anotheraspect linked to the primordial growth of these agglomerates is their structure and porosity. Not only does the structure observed by MIDAS and COSIMA show similarities in the build-up from smaller substructures, the same applies in principle to surface boulders observed by OSIRIS and ROLIS. Figure 13 shows the comparison of MIDAS and COSIMA agglomerates (top) and ROLIS and OSIRIS boulders (bottom). It is interesting that morphologies on these different size scales, from sub-micrometer to tens of meters, that is, over seven orders of magnitude, appear similar. At least the organization into substructures is evident on all scales. It is tempting to apply the concept of POROUS_2 in Fig. 1 and extend this to form clusters out of clusters and so forth in a hierarchic structure. The problem with this is that one would expect to add porosity at every step of assembly: if the initial agglomerates (POROUS_1) have a filling factor (1 – porosity) of 0.5, the first cluster of agglomerates (POROUS_2) has a filling factor of 0.52, a cluster of these has a filling factor of 0.53, and so forth. Assuming a size ratio of 10 between cluster sizes and their next smaller component, the filling factor of a 10 m boulder would be 0.57 = 0.008 (99.2% porosity). This is of course absurd and widely inconsistent with the bulk porosity of the comet (Sierks et al. 2015). This exemplifies that structure and porosity have to be treated as individual parameters. It is possible that the structure is the result of an agglomeration process that also involved compaction. In this case, the porosity would be found on the smallest and strongest scales. Porosity as a function of size would thus increase for small sizes until it remains constant at a threshold size, which is expected to be close to the bulk porosity of the comet.
 |
Fig. 12 Visual representation of Table 1 to show where different instruments overlap in their sensitivity range. Openboxes denote unknown size limits, i.e., smaller equal or larger equal than the plotted size. |
 |
Fig. 13 Agglomerates and boulders of comet 67P at different scales from MIDAS (top left, Bentley et al. 2016), COSIMA (top right, Langevin et al. 2016), ROLIS (bottom left, Mottola et al. 2015), and OSIRIS (bottom right, NAC image at 2015-02-14T15:31:05). |
5 Conclusions
This article presented the first summary and intercomparison of results from all Rosetta dust instruments. We established a classification scheme (Sect. 2.2) based on structure, porosity, and strength of fluffy and porous dust agglomerates, compact aggregates, and grains. This classification was compared to results of Stardust and Earth-based observations of probable cometary dust. These include tail and trail observations as well as polarimetric studies. We also reviewed the information of IDPs and MMs from the standpoint of our classification.
Different instruments and methods have different measurement parameters that result in different descriptions of their results. It is therefore a success to be able to describe this amount of data, all within the same framework of our classification. The choice to constrain our classification to morphology, porosity, and strength is a large restriction and can only be a first step in a complementary study of cometary dust after Rosetta. The work needs to be continued and extended, and we hope that the classification we presented will help.
Acknowledgment
We thank all Rosetta instrument teams, the Rosetta Science Ground Segment at ESAC, the Rosetta Mission Operations Centre at ESOC, and the Rosetta Project at ESTEC for their outstanding work, enabling the science return of the Rosetta Mission.
References
- Agarwal, J., Müller, M., & Grün, E. 2007, Space Sci. Rev., 128, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Agarwal, J., Müller, M., Reach, W. T., et al. 2010, Icarus, 207, 992 [NASA ADS] [CrossRef] [Google Scholar]
- Agarwal, J., A’Hearn, M. F., Vincent, J.-B., et al. 2016, MNRAS, 462, S78 [CrossRef] [Google Scholar]
- Alexander, C. M. O., Boss, A. P., Keller, L. P., Nuth, J. A., & Weinberger, A. 2007, Protostars and Planets V (Tucson, AZ: University of Arizona Press), 801 [Google Scholar]
- Arago, F. 1858, Astronomie Populaire, Vol. l. XVIII, t. III., ed. Gide (Flammarion: Paris) [Google Scholar]
- Attree, N., Groussin, O., Jorda, L., et al. 2018, A&A, 611, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beitz, E., Güttler, C., Weidling, R., & Blum, J. 2012, Icarus, 218, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Bentley, M. S., Arends, H., Butler, B., et al. 2016, Acta Astron., 125, 11 [Google Scholar]
- Bertini, I., La Forgia, F., Tubiana, C., et al. 2017, MNRAS, 469, S404 [CrossRef] [Google Scholar]
- Bertini, I., La Forgia, F., Fulle, M., et al. 2019, MNRAS, 482, 2924 [Google Scholar]
- Bibring, J.-P., Lamy, P., Langevin, Y., et al. 2007, Space Sci. Rev., 128, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Bibring, J.-P., Langevin, Y., Carter, J., et al. 2015, Science, 349, aab0671 [CrossRef] [Google Scholar]
- Blum, J. 2004, in Astrophysics of Dust, eds. A. N. Witt, G. C. Clayton, & B. T. Draine, ASP Conf. Ser., 309, 369 [NASA ADS] [Google Scholar]
- Blum, J. 2006, Adv. Phys., 55, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, J., & Münch, M. 1993, Icarus, 106, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, J., Schräpler, R., Davidsson, B. J. R., & Trigo-Rodríguez, J. M. 2006, ApJ, 652, 1768 [NASA ADS] [CrossRef] [Google Scholar]
- Bockelée-Morvan, D., Rinaldi, G., Erard, S., et al. 2017a, MNRAS, 469, S443 [CrossRef] [Google Scholar]
- Bockelée-Morvan, D., Rinaldi, G., Erard, S., et al. 2017b, MNRAS, 469, S842 [CrossRef] [Google Scholar]
- Bradley, J. P. 2003, Treatise on Geochemistry (Amsterdam: Elsevier) 1, 711 [Google Scholar]
- Brisset, J., Heißelmann, D., Kothe, S., Weidling, R., & Blum, J. 2016, A&A, 593, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brisset, J., Heißelmann, D., Kothe, S., Weidling, R., & Blum, J. 2017, A&A, 603, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brownlee, D. E. 1985, Ann. Rev. Earth Planet. Sci., 13, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Brownlee, D. 2014, Ann. Rev. Earth Planet. Sci., 42, 179 [Google Scholar]
- Brownlee, D. E. 2016, Elements, 12, 165 [CrossRef] [Google Scholar]
- Brownlee, D., Tsou, P., Aléon, J., et al. 2006, Science, 314, 1711 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Burchell, M. J., Fairey, S. A. J., Wozniakiewicz, P., et al. 2008, Meteor. Planet. Sci., 43, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, J. A., Lamy, P. L., & Soter, S. 1979, Icarus, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Busemann, H., Nguyen, A. N., Cody, G. D., et al. 2009, Earth Planet. Sci. Lett., 288, 44 [Google Scholar]
- Colangeli, L., Henning, T., Brucato, J. R., et al. 2003, A&ARv, 11, 97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colangeli, L., Lopez-Moreno, J. J., Palumbo, P., et al. 2007, Space Sci. Rev., 128, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Coradini, A., Capaccioni, F., Drossart, P., et al. 2007, Space Sci. Rev., 128, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Corrigan, C. M., Zolensky, M. E., Dahl, J., et al. 1997, Meteorit. Planet. Sci., 32 [Google Scholar]
- Della Corte, V., Rotundi, A., Fulle, M., et al. 2015, A&A, 583, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Della Corte, V., Sordini, R., Accolla, M., et al. 2016, Acta Astron., 126, 205 [CrossRef] [Google Scholar]
- Dollfus, A., Bastien, P., Le Borgne, J.-F., Levasseur-Regourd, A. C., & Mukai, T. 1988, A&A, 206, 348 [NASA ADS] [Google Scholar]
- Dominik, C., Blum, J., Cuzzi, J. N., & Wurm, G. 2007, Protostars and Planets V (Tucson, AZ: University of Arizona Press), 783 [Google Scholar]
- Economou, T. E., Green, S. F., Brownlee, D. E., & Clark, B. C. 2012, Icarus, 222, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Ellerbroek, L. E., Gundlach, B., Landeck, A., et al. 2017, MNRAS, 469, S204 [CrossRef] [Google Scholar]
- Engrand, C., Duprat, J., Dartois, E., et al. 2016, MNRAS, 462, S323 [CrossRef] [Google Scholar]
- Flandes, A., Albin, T., Arnold, W., et al. 2018, Icarus, 302, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Flynn, G. J., & Sutton, S. R. 1991, Lunar Planet. Sci. Conf. Proc., 21, 541 [NASA ADS] [Google Scholar]
- Frattin, E., Cremonese, G., Simioni, E., et al. 2017, MNRAS, 469, S195 [CrossRef] [Google Scholar]
- Fulle, M., & Blum, J. 2017, MNRAS, 469, S39 [CrossRef] [Google Scholar]
- Fulle, M., Levasseur-Regourd, A. C., McBride, N., & Hadamcik, E. 2000, AJ, 119, 1968 [Google Scholar]
- Fulle, M., Colangeli, L., Agarwal, J., et al. 2010, A&A, 522, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fulle, M., Corte, V. D., Rotundi, A., et al. 2015, ApJ, 802, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Fulle, M., Altobelli, N., Buratti, B., et al. 2016a, MNRAS, 462, S2 [CrossRef] [Google Scholar]
- Fulle, M., Della Corte, V., Rotundi, A., et al. 2016b, MNRAS, 462, S132 [CrossRef] [Google Scholar]
- Fulle, M., Marzari, F., Della Corte, V., et al. 2016c, ApJ, 821, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Fulle, M., Della Corte, V., Rotundi, A., et al. 2017, MNRAS, 469, S45 [Google Scholar]
- Fulle, M., Bertini, I., Della Corte, V., et al. 2018, MNRAS, 476, 2835 [NASA ADS] [CrossRef] [Google Scholar]
- Genge, M. J., Engrand, C., Gounelle, M., & Taylor, S. 2008, Meteorit. Planet. Sci., 43, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Groussin, O., Jorda, L., Auger, A.-T., et al. 2015, A&A, 583, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gundlach, B., & Blum, J. 2015, ApJ, 798, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Gundlach, B., Ratte, J., Blum, J., Oesert, J., & Gorb, S. N. 2018a, MNRAS, 479, 5272 [NASA ADS] [CrossRef] [Google Scholar]
- Gundlach, B., Schmidt, K. P., Kreuzig, C., et al. 2018b, MNRAS, 479, 1273 [NASA ADS] [CrossRef] [Google Scholar]
- Güttler, C., Hasselmann, P. H., Li, Y., et al. 2017, MNRAS, 469, S312 [CrossRef] [Google Scholar]
- Hadamcik, E., Renard, J. B., Levasseur-Regourd, A. C., & Lasue, J. 2006, J. Quant. Spectr. Rad. Transf., 100, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Hadamcik, E., Renard, J.-B., Rietmeijer, F. J. M., et al. 2007, Icarus, 190, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Hadamcik, E., Sen, A. K., Levasseur-Regourd, A. C., Gupta, R., & Lasue, J. 2010, A&A, 517, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hadamcik, E., Levasseur-Regourd, A. C., Hines, D. C., et al. 2016, MNRAS, 462, S507 [CrossRef] [Google Scholar]
- Hansen, K. C., Altwegg, K., Berthelier, J.-J., et al. 2016, MNRAS, 462, S491 [Google Scholar]
- Heim, L.-O., Blum, J., Preuss, M., & Butt, H.-J. 1999, Phys. Rev. Lett., 83, 3328 [NASA ADS] [CrossRef] [Google Scholar]
- Hilchenbach, M., Kissel, J., Langevin, Y., et al. 2016, ApJ, 816, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Hilchenbach, M., Fischer, H., Langevin, Y., et al. 2017, Phil. Trans. R. Soc. London, Ser. A, 375, 20160255 [NASA ADS] [CrossRef] [Google Scholar]
- Hirn, A., Albin, T., Apáthy, I., et al. 2016, A&A, 591, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hornung, K., Merouane, S., Hilchenbach, M., et al. 2016, Planet. Space Sci., 133, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Hörz, F., Bastien, R., Borg, J., et al. 2006, Science, 314, 1716 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kearsley, A. T., Borg, J., Graham, G. A., et al. 2008, Meteor. Planet. Sci., 43, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Kearsley, A. T., Burchell, M. J., Price, M. C., et al. 2012, Meteor. Planet. Sci., 47, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, H. U., Barbieri, C., Lamy, P., et al. 2007, Space Sci. Rev., 128, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Kiselev, N., Rosenbush, V., Levasseur-Regourd, A.-C., & Kolokolova, L. 2015, Comets (Cambridge: Cambridge University Press), 379 [Google Scholar]
- Kissel, J., & Krueger, F. R. 1987, Nature, 326, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Kissel, J., Krueger, F. R., Silén, J., & Clark, B. C. 2004, Science, 304, 1774 [NASA ADS] [CrossRef] [Google Scholar]
- Kissel, J., Altwegg, K., Clark, B. C., et al. 2007, Space Sci. Rev., 128, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Kolokolova, L., Hanner, M. S., Levasseur-Regourd, A.-C., & Gustafson, B. Å. S. 2004, in Comets II, eds. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson, AZ: University of Arizona Press), 577 [Google Scholar]
- Kothe, S., Blum, J., Weidling, R., & Güttler, C. 2013, Icarus, 225, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Kouchi, A., Kudo, T., Nakano, H., et al. 2002, ApJ, 566, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Krueger, F. R., Korth, A., & Kissel, J. 1991, Space Sci. Rev., 56, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Krüger, H., Seidensticker, K. J., Fischer, H.-H., et al. 2015, A&A, 583, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Langevin, Y., Hilchenbach, M., Ligier, N., et al. 2016, Icarus, 271, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Langevin, Y., Hilchenbach, M., Vincendon, M., et al. 2017, MNRAS, 469, S535 [CrossRef] [Google Scholar]
- Lasue, J., Levasseur-Regourd, A. C., Hadamcik, E., & Alcouffe, G. 2009, Icarus, 199, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Levasseur-Regourd, A. C., McBride, N., Hadamcik, E., & Fulle, M. 1999, A&A, 348, 636 [NASA ADS] [Google Scholar]
- Levasseur-Regourd, A. C., Mukai, T., Lasue, J., & Okada, Y. 2007, Planet. Space Sci., 55, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Levasseur-Regourd, A. C., Zolensky, M., & Lasue, J. 2008, Planet. Space Sci., 56, 1719 [NASA ADS] [CrossRef] [Google Scholar]
- Levasseur-Regourd, A.-C., Renard, J.-B., Shkuratov, Y., & Hadamcik, E. 2015, Laboratory studies (Cambridge: Cambridge University Press), 35 [Google Scholar]
- Levasseur-Regourd, A.-C., Agarwal, J., Cottin, H., et al. 2018, Space Sci. Rev., 214, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Love, S. G., Joswiak, D. J., & Brownlee, D. E. 1994, Icarus, 111, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Mannel, T., Bentley, M., Schmied, R., et al. 2016, MNRAS, 462, S304 [NASA ADS] [CrossRef] [Google Scholar]
- Mannel, T., Bentley, M. S., Boakes, P. D., et al. 2019, A&A, 630, A26 (Rosetta 2 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markkanen, J., Agarwal, J., Väisänen, T., Penttilä, A., & Muinonen, K. 2018, ApJ, 868, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Merouane, S., Zaprudin, B., Stenzel, O., et al. 2016, A&A, 596, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Metzler, K., Bischoff, A., & Stoeffler, D. 1992, Geochim. Cosmochim. Acta, 56, 2873 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno, F., Muñoz, O., Gutiérrez, P. J., et al. 2017, MNRAS, 469, S186 [CrossRef] [Google Scholar]
- Moreno, F., Guirado, D., Muñoz, O., et al. 2018, AJ, 156, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Mottola, S., Arnold, G., Grothues, H.-G., et al. 2007, Space Sci. Rev., 128, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Mottola, S., Arnold, G., Grothues, H.-G., et al. 2015, Science, 349, aab0232 [CrossRef] [Google Scholar]
- Muñoz, O., & Hovenier, J. W. 2011, J. Quant. Spectr. Rad. Trans., 112, 1646 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz, O., & Hovenier, J. W. 2015, Experimental Scattering Matrices of Clouds of Randomly Oriented Particles (Cambridge: Cambridge University Press), 130 [Google Scholar]
- Muñoz, O., Moreno, F., Vargas-Martín, F., et al. 2017, ApJ, 846, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Jenniskens, P., Levison, H. F., et al. 2010, ApJ, 713, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Nichols, G., Byard, S., Bloxham, M. J., et al. 2002, J. Pharma. Sci., 91, 2103 [Google Scholar]
- Onoda, G. Y., & Liniger, E. G. 1990, Phys. Rev. Lett., 64, 2727 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ott, T., Drolshagen, E., Koschny, D., et al. 2017, MNRAS, 469, S276 [CrossRef] [Google Scholar]
- Paquette, J. A., Engrand, C., Stenzel, O., Hilchenbach, M., & Kissel, J. 2016, Meteor. Planet. Sci., 51, 1340 [Google Scholar]
- Podolak, M., Flandes, A., Della Corte, V., & Krüger, H. 2016, Planet. Space Sci., 133, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Poppe, T. 2003, Icarus, 164, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Poppe, T., Blum, J., & Henning, T. 2000, ApJ, 533, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Poulet, F., Lucchetti, A., Bibring, J.-P., et al. 2016, MNRAS, 462, S23 [CrossRef] [Google Scholar]
- Reach, W. T., Kelley, M. S., & Sykes, M. V. 2007, Icarus, 191, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Reinhard, R., & Battrick, B. 1986, Space Missions to Halley’s Comet (Paris: ESA SP) [Google Scholar]
- Riedler, W., Torkar, K., Jeszenszky, H., et al. 2007, Space Sci. Rev., 128, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Rietmeijer, F. J. M. 1993, Earth Planet. Sci. Lett., 117, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Rietmeijer, F. J. M. 1998, in Planetary Materials, Reviews in Mineralogy, ed. J. J. Papike (Chantilly: Mineralogical Society of America), 36, 2–1 [Google Scholar]
- Rietmeijer, F. 2002, Chemie der Erde / Geochemistry, 62, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Rietmeijer, F. J. M. 2016, Meteor. Planet. Sci., 51, 1871 [NASA ADS] [CrossRef] [Google Scholar]
- Rinaldi, G., Bockelée-Morvan, D., Ciarniello, M., et al. 2018, MNRAS, 481, 1235 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenbush, V. K., Ivanova, O. V., Kiselev, N. N., Kolokolova, L. O., & Afanasiev, V. L. 2017, MNRAS, 469, S475 [CrossRef] [Google Scholar]
- Rotundi, A., Sierks, H., Della Corte, V., et al. 2015, Science, 347, aaa3905 [NASA ADS] [CrossRef] [Google Scholar]
- Rowan-Robinson, M., & May, B. 2013, MNRAS, 429, 2894 [NASA ADS] [CrossRef] [Google Scholar]
- Schröder, S. E., Mottola, S., Arnold, G., et al. 2017, Icarus, 285, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Schulz, R., Alexander, C., Boehnhardt, H., & Glassmeier, K.-H. 2009, Rosetta: ESA’s Mission to the Origin of the Solar System (New YorK: Springer) [Google Scholar]
- Seidensticker, K. J., Möhlmann, D., Apathy, I., et al. 2007, Space Sci. Rev., 128, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Sierks, H., Barbieri, C., Lamy, P. L., et al. 2015, Science, 347, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Tamanai, A., Mutschke, H., Blum, J., & Meeus, G. 2006, ApJ, 648, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Tuzzolino, A. J., Economou, T. E., Clark, B. C., et al. 2004, Science, 304, 1776 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2008, ApJ, 677, 1296 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2011, ApJ, 737, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, D. 2013, Nanomaterials (Hoboken: Wiley-Blackwell), 9 [CrossRef] [Google Scholar]
- Zolensky, M. E., Zega, T. J., Yano, H., et al. 2006, Science, 314, 1735 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Example images of interplanetary dust particles in this work are from the NASA Cosmic Dust Catalog Volume 15 from 1997 (see, e.g., Brownlee 1985, 2016).
The sizes shown in the paper are valid for particles that have a phase function and albedo as described by Kolokolova et al. (2004), in contrast to what is stated in the paper. If they show reflection properties like the nucleus (Güttler et al. 2017), the sizes should be corrected up (increased) by a factor 4.4 (Agarwal, priv. comm.).
All Tables
All Figures
 |
Fig. 1 Possible dust-particle structures, defined by applying the three main groups defined in Sect. 2.2. The units of larger structures are drawn from circles for illustrative purposes only. In reality, these can be any of the solid group, where colors (gray and blue) also indicate that compositions can vary (e.g., ices). |
| In the text | |
 |
Fig. 2 Examples of laboratory analogs for the SOLID_1 types in Fig. 1 (references in the text). |
| In the text | |
 |
Fig. 3 Samples of the SOLID_2 types in Fig. 1 (references in the text). |
| In the text | |
 |
Fig. 4 Fractal particles from laboratory experiments (left), computer simulation (top right), and Rosetta/MIDAS (bottom right, left and right of the scale bar; references in the text). The color code and scale bar for the bottom right image denotes height. |
| In the text | |
 |
Fig. 5 Agglomerates from the POROUS_1 type in Fig. 1. SEM image of a laboratory analog agglomerate (top left), an IDP (bottom left), a tomographic cross section (top right), and a computer model (bottom right; references in the text). |
| In the text | |
 |
Fig. 6 Clusters of agglomerates from the POROUS_2 type in Fig. 1. Sample grown under microgravity (top left), Rosetta/ COSIMA (top right), and Rosetta/MIDAS samples (bottom; references in the text). |
| In the text | |
 |
Fig. 7 Classification from Sect. 2.2 and Fig. 1 is not always unambiguous. These examples of mixed cases show aggregate structures that would be classified one way or another, depending on the method applied (e.g., surface microscopy, mass determination, or light scattering). |
| In the text | |
 |
Fig. 8 Examples for mixed cases in Fig. 7 (references in the text). |
| In the text | |
 |
Fig. 9 MIDAS image of an agglomerate particle sticking to the side of a tip that was acquired using a calibration target with sharp spikes (Mannel et al. 2019). The smooth round feature at the bottom is the tip apex, and the straight line to the bottom right corner is a structure supporting the tip. The image has a pixel resolution of about 15 nm and was acquired on 8 December 2015. |
| In the text | |
 |
Fig. 10 Track morphology terminology for Stardust tracks, derived from Kearsley et al. (2012, Figs. 1 and 12). (a)–(d) from aerogeltracks in Stardust collection. (e) from analog experiment by Kearsley et al. (2012). |
| In the text | |
 |
Fig. 11 SEMimage of micrometeorites (MMs) by Genge et al. (2008). Left: their fine-grained C3 type, associated with our porous group. Right: particle consisting of coarse-grained (top left) and fine-grained (bottom right) components, similar to mixes we have exemplified in Fig. 7, in particular, POROUS_SOLID_2. |
| In the text | |
 |
Fig. 12 Visual representation of Table 1 to show where different instruments overlap in their sensitivity range. Openboxes denote unknown size limits, i.e., smaller equal or larger equal than the plotted size. |
| In the text | |
 |
Fig. 13 Agglomerates and boulders of comet 67P at different scales from MIDAS (top left, Bentley et al. 2016), COSIMA (top right, Langevin et al. 2016), ROLIS (bottom left, Mottola et al. 2015), and OSIRIS (bottom right, NAC image at 2015-02-14T15:31:05). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


