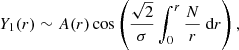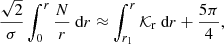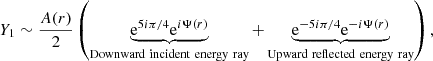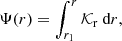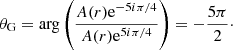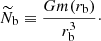| Issue |
A&A
Volume 626, June 2019
|
|
|---|---|---|
| Article Number | A125 | |
| Number of page(s) | 17 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201935327 | |
| Published online | 24 June 2019 | |
Evolution of the gravity offset of mixed modes in RGB stars
1
Institut d’Astrophysique Spatiale, Univ. Paris-Sud, CNRS, Université Paris-Saclay, Bâtiment 121, 91405 Orsay Cedex, France
2
STAR Institute, Université de Liège, 19C Allée du 6 Août, 4000 Liège, Belgium
e-mail: charly.pincon@uliege.be
3
LESIA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, Univ. Paris Diderot, 5 place Jules Janssen, 92195 Meudon, France
4
Department of Astronomy, School of Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku 113-0033 Tokyo, Japan
Received:
21
February
2019
Accepted:
2
May
2019
Context. Observations of mixed modes in evolved low-mass stars enable us to probe the properties of not only the outer envelope of these stars, but also their deep layers. Among the seismic parameters associated with mixed modes, the gravity offset, denoted with εg, is expected to reveal information on the boundaries of the inner buoyancy resonant cavity. This parameter was recently measured for hundreds of stars observed by the Kepler satellite and its value was shown to change during evolution.
Aims. In this article, we theoretically investigate the reasons for such a variation in terms of structure properties, focusing only on the red giant branch.
Methods. Using available asymptotic analyses and a simple model of the Brunt–Väisälä and Lamb frequencies in the upper part of the radiative zone, we derived an analytical expression of εg for dipolar modes and compared its predictions to observations.
Results. First, we show that the asymptotic value of εg well agrees with the mean value observed at the beginning of the ascent of the red giant branch, which results from the high density contrast between the helium core and the base of the convective envelope. Second, we demonstrate that the predicted value also explains the sharp decrease in εg observed for the more luminous red giant stars of the sample. This rapid drop turns out to occur just before the luminosity bump and results from the kink of the Brunt–Väisälä frequency near the upper turning point associated with the buoyancy cavity as stars evolve and this latter nears the base of the convective envelope. The potential of εg to probe the value and slope of the Brunt–Väisälä frequency below the base of the convective region is clearly highlighted.
Conclusions. The observed variation in εg and its link with the internal properties on the red giant branch are now globally understood. This work motivates further analyses of the potential of this parameter as a seismic diagnosis of the region located between the hydrogen-burning shell and the base of the convective envelope, and of the local dynamical processes associated for instance with core contraction, the migration of the convective boundary, or overshooting.
Key words: asteroseismology / stars: oscillations / stars: interiors / stars: evolution
© ESO 2019
1. Introduction
The space-borne missions CoRoT (e.g., Baglin et al. 2006a,b) and Kepler (e.g., Borucki et al. 2010) now allow access to seismic data for thousands of stars, from the main sequence to the core helium burning stages, and even to white dwarfs. These additional constraints have led to a revolution in stellar physics and continue to reveal the dynamics at work in the inner layers of these stars (e.g., Chaplin & Miglio 2013; Di Mauro 2016).
One of the important advances in the field brought by these data results from the detection and study of mixed modes in evolved stars (e.g., Mosser et al. 2016; Hekker & Christensen-Dalsgaard 2017). Mixed modes constitute a peculiar type of eigenmodes that oscillate in a central cavity, or buoyancy cavity, where they behave as gravity modes, and an external cavity, or acoustic cavity, where they behave as pressure modes; both of these cavities are coupled by an evanescent region located between the profiles of the Brunt–Väisälä and Lamb frequencies (see Fig. 1). Assuming that the short-wavelength WKB approximation is met in each cavity (i.e., in the asymptotic limit), their oscillation frequencies satisfy the general quantization relation (Shibahashi 1979; Tassoul 1980; Takata 2016a,b)
 |
Fig. 1. Profile of the modified Brunt–Väisälä and ℓ = 1 Lamb frequencies (thick solid and dashed lines, respectively) for two 1.2 M⊙ red giant models with νmax ≈ 200 μHz (blue) and νmax ≈ 60 μHz (red). These both models correspond to stars at the beginning of the ascent of the RGB and at a point just before the luminosity bump, respectively. The usual Brunt–Väisälä and ℓ = 1 Lamb frequencies, N and S1, are represented by the light thin solid and dashed lines, respectively. The vertical dash-dotted lines indicate the hydrogen-burning shell and the horizontal strip symbolizes a typical 6Δν-wide observed frequency range around νmax, for each model with the corresponding color. The buoyancy and acoustic cavities for a mode of frequency ν are located where 2πν ≤ (𝒩 and 𝒮1) and 2πν ≥ (𝒩 and 𝒮1), respectively. |
where Θg and Θp are frequency dependent phase terms associated with the propagation of waves in the buoyancy and the acoustic cavities, respectively, and q is the coupling factor that quantifies the level of interaction between both cavities through the intermediate evanescent region.
As shown by Eq. (1), the mixed mode frequency pattern contains information on various regions of evolved stars and in particular on their deepest layers. First, observations of mixed modes have led to the measurement, for thousands of stars, of the dipolar period spacing (e.g., Bedding et al. 2011; Mosser et al. 2012a; Vrard et al. 2016), the value of which is sensitive to both the properties of the helium core and the evolutionary stage (e.g., Montalbán et al. 2013; Mosser et al. 2014; Lagarde et al. 2016). The coupling factor of dipolar modes has also been measured for such a large sample of stars and has been shown to vary during evolution because of the structural changes of the region located between the hydrogen-burning shell and the base of the convective envelope (e.g., Mosser et al. 2017; Hekker et al. 2018). Additionally, the rotational splittings of mixed modes have provided important constraints on the redistribution of internal angular momentum during the post-main sequence stage (e.g., Deheuvels et al. 2014; Gehan et al. 2018).
More recently, several works have focused on a new seismic parameter associated with mixed modes, i.e., the gravity offset denoted with εg (e.g., Buysschaert et al. 2016; Hekker et al. 2018; Mosser et al. 2018). This parameter on the order of unity, which appears inside Θg in Eq. (1), mainly depends on the properties of the regions close to boundaries of the buoyancy cavity. Mosser et al. (2018) were able to measure the gravity offset with precision for hundreds of stars on the red giant branch (hereafter, RGB) and on the red clump. The authors showed that the observed value remains about constant at the beginning of the RGB and then rapidly drops before the stars reach the luminosity bump. For more evolved red clump stars, the spread in the measurements turns out to be much larger than for RGB stars.
In this work, we aim at interpreting the evolution of the gravity offset on the RGB from a theoretical point of view in terms of internal structure. For this purpose, the available asymptotic analyses of dipolar mixed modes are considered. The subsequent statements thus assume that the oscillation wavelength is much smaller than the structure scale height in both resonant cavities (i.e., in the WKB approximation). The paper is organized as follows. In Sect. 2, we properly introduce the notion of gravity offset and clearly pave the way for the present investigation. A general physical interpretation of this parameter within the framework of the asymptotic limit is then given in Sect. 3. Using this theoretical background and simple models of the Brunt–Väisälä and Lamb frequencies, we derive in Sect. 4 an analytical expression for εg that explicitly accounts for the structural changes occurring during evolution. This model is subsequently used to explain and interpret the observations by Mosser et al. (2018). We discuss the results in Sects. 5 and 6 is devoted to conclusions.
2. Setting the stage
In this introductory section, we expose the problem and clarify the underlying goals of the present investigation. In all the following, we implicitly focus on dipolar mixed modes. Indeed, among mixed modes that penetrate into the stellar core, only dipolar modes can currently bring us information on the innermost properties of evolved stars since they have the highest amplitude at the surface (e.g., Dupret et al. 2009; Grosjean et al. 2014).
2.1. Empirical introduction of the gravity offset
Before any theoretical study on the subject, the notion of gravity offset was first introduced in an observational context by Mosser et al. (2012b). To fit the asymptotic expression of mixed modes in Eq. (1) to real frequency spectra, Mosser et al. (2012b) parametrized the phase Θg associated with the buoyancy cavity as
where ν is the oscillation cyclic frequency (with σ = 2πν the angular frequency), 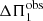 is the observed dipolar period spacing, and
is the observed dipolar period spacing, and 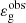 is the so-called observed gravity offset. Within the framework of the fitting procedure,
is the so-called observed gravity offset. Within the framework of the fitting procedure, 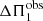 and
and 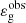 were supposed to be frequency independent in the observed narrow frequency range around νmax, representing the frequency at maximum oscillation power (see Eq. (21) for an expression).
were supposed to be frequency independent in the observed narrow frequency range around νmax, representing the frequency at maximum oscillation power (see Eq. (21) for an expression).
The presence of the dominant first term in the brackets of the right-hand side of Eq. (2) as well as its frequency dependence on 1/ν were motivated by the results of the asymptotic analyses of mixed modes by Shibahashi (1979) and Tassoul (1980). This term is close to the number of radial nodes of a mixed mode in the buoyancy cavity, denoted with ng, which is very large in the asymptotic limit. In contrast, the small term on the order of unity, 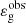 , was introduced for empirical reasons. Indeed, Mosser et al. (2012b) found that the fits of the asymptotic relation to real data were better with non-null values of
, was introduced for empirical reasons. Indeed, Mosser et al. (2012b) found that the fits of the asymptotic relation to real data were better with non-null values of 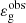 , in particular in subgiant and young red giant stars. Given its role in the asymptotic relation and the π-periodic behavior of the cotangent function in Eq. (1), the value of
, in particular in subgiant and young red giant stars. Given its role in the asymptotic relation and the π-periodic behavior of the cotangent function in Eq. (1), the value of 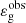 can be measured only modulo unity. A theoretical justification of the empirical expression of Θg in Eq. (2) is therefore needed to give a clear physical meaning to the observed values of the gravity offset.
can be measured only modulo unity. A theoretical justification of the empirical expression of Θg in Eq. (2) is therefore needed to give a clear physical meaning to the observed values of the gravity offset.
2.2. Unclear previous interpretations
The gravity offset of mixed modes has been interpreted through an analogy with the asymptotic analyses of pure gravity modes provided by Provost & Berthomieu (1986) in the case of the Sun, or by Brassard et al. (1992) in the case of ZZ Ceti stars. Nevertheless, the link between the results of these works and the case of mixed modes in evolved stars deserves to be clarified because of different evolutionary stages and structural properties as well as types of oscillation modes.
Actually, the ambiguity also extends to the physical interpretation of the observed values of the period spacing, as already discussed in Takata (2016a, cf. Sect. 4.4 of this paper). Indeed, previous works often considered 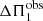 as equal to the asymptotic quantity
as equal to the asymptotic quantity 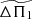 , which appears in the expression of Θg derived by Shibahashi (1979) and Tassoul (1980), and is defined as
, which appears in the expression of Θg derived by Shibahashi (1979) and Tassoul (1980), and is defined as
where r is the radius in the star and N is the usual Brunt–Väisälä frequency (e.g., Unno et al. 1989, for a definition). The bounds of the integral, r1 and r2, correspond to the inner and the upper turning points associated with the buoyancy cavity. In the formulations of Shibahashi (1979) and Tassoul (1980), both represent the physical boundaries of the cavity and are equal to the radii at which σ = N(r). As an illustration, the radial profile of N is shown in Fig. 1 for two 1.2 M⊙ red giant models computed with the stellar evolution code CESTAM (Marques et al. 2013). As input physics, the chemical composition corresponds to a solar mixture, as provided by Asplund et al. (2009), which has solar-calibrated initial helium and metal abundances Y0 = 0.25 and Z0 = 0.013. The OPAL 2005 equation of state and the NACRE nuclear reaction rates were considered. Microscopic diffusion, overshooting, and rotation were neglected and the stellar atmosphere was constructed following the Eddington gray approximation. The mixing-length theory of convection was used with a solar-calibrated parameter αMLT = 1.65. Both models chosen as examples correspond to stars at the beginning of the ascent of the RGB with νmax ≈ 200 μHz and just before the luminosity bump with νmax ≈ 60 μHz, respectively. We note that the radial profiles of the critical frequencies as well as their evolution with time in stars with masses between 1 M⊙ and 2 M⊙ follow the same trend between the beginning of the RGB and the luminosity bump as that depicted in Fig. 1. Indeed, whatever their mass in this range, red giant stars evolve along the Hayashi line in the Herztsprung–Russell diagram and thus share similar properties (e.g., Kippenhahn et al. 2012). In Fig. 1, a typical 6Δν-wide observed frequency range around νmax, as expected from theoretical estimates and observations in RGB stars (e.g., Grosjean et al. 2014; Mosser et al. 2018), is indicated for each model, where Δν is the large frequency separation between two consecutive acoustic radial modes. Since both turning points in the buoyancy cavity are located where σ = N in the asymptotic formulation of Shibahashi (1979) and Tassoul (1980), the variation of a given turning point ri with the oscillation frequency is measured by
As (dlnN/dlnr) is finite in the central regions of each model considered in Fig. 1, the inner turning point r1 depends on σ according to Eq. (4). Similarly, the outer turning point r2 is also frequency dependent for the young red giant model with νmax ≈ 200 μHz. As a consequence, 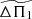 in Eq. (3) is frequency dependent as well. It is therefore clear that this quantity is not representative of the observed period-spacing
in Eq. (3) is frequency dependent as well. It is therefore clear that this quantity is not representative of the observed period-spacing 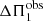 as this latter is supposed to be frequency independent. We also anticipate that the outer turning point r2 is, in contrast, independent of frequency in the more evolved model with νmax ≈ 60 μHz considered in Fig. 1.
as this latter is supposed to be frequency independent. We also anticipate that the outer turning point r2 is, in contrast, independent of frequency in the more evolved model with νmax ≈ 60 μHz considered in Fig. 1.
Since the observed gravity offset and observed period spacing of mixed modes are related to each other by Eq. (2), we need to understand simultaneously the link of both observed parameters with the asymptotic expressions to achieve our purpose. To do so, we have to consider a more detailed examination of the available asymptotic analyses of mixed modes. A similar study was performed by Mosser et al. (2013) in the case of the radial acoustic modes observed in red giant stars. Indeed, for these modes, the authors showed that the observed value of the frequency large separation and the asymptotic value are not equivalent. They then demonstrated the need to consider a second-order expansion around νmax of the asymptotic expression of radial modes derived by Tassoul (1980) to make the link between both and theoretically interpret the observed values. A similar approach is used in this work in the case of mixed modes, as presented in the next section.
2.3. Local asymptotic definitions around νmax
The comparison of any asymptotic expressions of the gravity offset and of the period spacing with the observed values are only relevant if they have equivalent definitions. This can be met if the analytical expression of Θg is proved to have a similar form to Eq. (2) in terms of frequency dependence over the observed frequency range, at least with a level of error lower than the uncertainties on the measurements of the gravity offset denoted with σε. Nevertheless, such an identification is not straightforward since we have seen that Θg can depend on the frequency in a more complicated way than Eq. (2); see the frequency dependence of the bounds of the integral in Eq. (3) for instance.
Actually, whatever the expression of Θg, a theoretical justification for the form given in Eq. (2) can be obtained through a local analysis over a narrow frequency range around νmax, in an analogous way to the case of the radial acoustic modes in red giant stars (Mosser et al. 2013). Indeed, to demonstrate this, we formally rewrite Θg as
where F is a differentiable function of frequency. Using a first-order Taylor expansion of F around ν = νmax, we obtain
where (′) denotes the derivative with respect to frequency. In the last equation, G(ν) is a real function (not necessarily differentiable) such as G(ν)→0 as ν → νmax and that encapsulates all the higher order terms. In a small enough frequency range around νmax, it is always possible to assume that the last term in the right-hand side of Eq. (6) is negligible compared to the preceding ones. Substituting the truncated first-order expansion of Eq. (6) into Eq. (5), Θg is thus about equal around νmax to
which has the same form as Eq. (2) with respect to the frequency dependence. According to Eq. (7), the local asymptotic dipolar period spacing and gravity offset around νmax, denoted with ΔΠ1 and εg in the following, can be identified, respectively, as
and
so that Θg can now be approximated around νmax as
as proposed before through empirical considerations. We see a posteriori that a first-order Taylor expansion of the F function is sufficient in Eq. (6) to reproduce the empirical form in Eq. (2). Nevertheless, we emphasize that the identification in Eqs. (8) and (9) remains accurate if and only if the considered frequency range around νmax is small enough for the higher order terms in Eq. (6) to be negligible. Otherwise, the asymptotic gravity offset would be frequency dependent and could not be representative of the fitted values in the considered frequency range.
The question that naturally follows in practice is thus to know whether this relation is valid over all the observed frequency range around νmax or not with a level of error lower than σε. According to Eqs. (5) and (6), this is met if the remainder around νmax,
is much smaller than σε over the observed frequency range. Therefore, the comparison between the local asymptotic values and the observed values of both parameters are relevant if this latter condition is satisfied. Otherwise, we must conclude that the physical modeling and hypotheses on which the proposed asymptotic expression of Θg is based are insufficient to interpret the observations. This condition is checked before any comparison in the following (see Sects. 4.2 and 5.1).
3. Asymptotic interpretation of the gravity offset
After having set the general context and goals of the present study, we now discuss in more detail the physical meaning of the gravity offset within the framework of the asymptotic limit. All the theoretical background useful for the present investigation is introduced in this section.
3.1. General physical origin
In a first step, it is instructive to discuss the physical origin of the gravity offset from a general point of view using simple considerations. To do so, considering the formulation of mixed modes proposed by Takata (2016b) appears judicious. Using a progressive-wave picture of the oscillations in both cavities and basic wave principles, Takata (2016b) retrieved the asymptotic quantization condition in Eq. (1) and expressed Θg in the very general form1
where 𝒦r is the radial wavenumber, which takes a null value at r1 an r2, and where θG and δ are the phase lags2 introduced after the reflection of an incident wave propagating in the buoyancy cavity toward r1 and r2, respectively, with values in [0, 2π].
On the one hand, the comparison between Eqs. (10) and (12) shows that a first contribution to the gravity offset may result from θG and δ, the phase lags introduced at the reflection near the center and the intermediate evanescent region, respectively. These terms, on the order of unity, seem missing at first sight in the asympotic expression of mixed modes derived by Shibahashi (1979) under the Cowling approximation (e.g., Cowling 1941). Actually, this results from the fact that δ + θG ≈ π in this formulation. Indeed, Shibahashi (1979) first demonstrated that the wave function (i.e., the dependent variable v of his paper) near the innermost (single) turning point r1 takes the form of an Airy function of the first kind, so that the phase lag introduced at the reflection in r1 is equal to θG = +π/2 (e.g., see also Brekhovskikh 1980)3. Secondly, the analysis of Shibahashi (1979) assumed a very thick evanescent region, and therefore the same wave function also takes the form of an Airy function of the first kind close to the outer turning point r2 and δ ≈ +π/2 for the same reasons as mentioned above. As a result, the sum of both phase lags is equal to π in the hypothesis of a thick evanescent region and the last three terms in Eq. (12) cancel out. Takata (2016a) showed later that this does not hold true when the evanescent region is very thin in red giant stars or when the influence of the perturbation of the gravitional potential is taken into account (i.e., in the non-Cowling approximation), as we see in the subsequent sections.
On the other hand, Eq. (12) also shows that another contribution to εg may come from the wavenumber integral, and in particular, from the integral over the region in the vicinity of the turning points. Indeed, far enough away from the turning points, that is in the middle part of the buoyancy cavity, 𝒦r is provided in a good approximation by (e.g., Unno et al. 1989)
This approximation is in fact valid when 2πν ≪ N, which is met in the middle of the buoyancy cavity for the frequency range observed in typical red giant stars (e.g., see Fig. 1). Consequently, the wavenumber integral over the middle part of the buoyancy cavity mostly contributes to the leading-order term in Θg that is proportional to 1/ν. In contrast, near the turning points, the approximation in Eq. (13) is not valid since 𝒦r tends to zero. There, say close to a turning point ri, it is preferable to assume that 𝒦r approximately takes the simple form
where K(ri), α(ri) and Δr(ri) are positive real quantities depending on the properties of the medium near ri, with Δr(ri) chosen such as 𝒦r(r)Δr(ri)≲1 in the considered region. In these considerations, the wavenumber integral over the region where |r − ri|≲Δr(ri) is thus provided in a first approximation by
This simple estimate demonstrates, first, that the contribution of the wavenumber integral in the vicinity of the turning points to the total integral depends on the properties of the region close to ri. Second, this estimate also shows that it is on the order of unity at most since in general α(ri)≳1 and 𝒦r(ri ± Δr)Δr(ri)≲1 by definition.
The value of the gravity offset is therefore related to the properties of the boundaries of the buoyancy cavity (i.e., close to r1 and r2), through the contributions of the phase lags introduced at reflection and of the wavenumber integral in the vicinity of the turning points. As expected from the observational definition, both contributions are on the order of unity at most. In contrast, they turn out to depend on the oscillation frequency since the turning point is in general frequency dependent. This emphasizes the need for a local asymptotic analysis around νmax, that is such as proposed in Sect. 2.3, to disentangle the contributions to each term in the first-order expansion of Θg as a function of frequency that is given in Eq. (7), and thus interpret the observed values. At this stage, the computation of ΔΠ1 and εg still needs the knowledge of the expression of Θg in Eq. (12) for typical red giant stars.
3.2. Link with the structure properties in red giant stars
All the physical information in Eq. (12) is encapsulated in the quantities θG, δ, and 𝒦r. To go further, the link between these quantities and the internal properties is commonly made through more detailed analyses of the stellar oscillation equations considering realistic stellar structure. We discuss and quantify these terms in the light of the asymptotic analysis by Takata (2016a; hereafter T16) for dipolar mixed modes in red giant stars. Regarding εg, this latter work brought two main important theoretical improvements compared to the analyses of Shibahashi (1979) and Tassoul (1980). First, it fully accounts for the effect of the perturbation of the gravitational potential on oscillations (Takata 2006). Second, it considers the limiting case of a very thin evanescent zone. Nevertheless, the hypothesis of a very thick evanescent zone, as usually assumed by previous works (Shibahashi 1979; Tassoul 1980), can be easily retrieved from the result of T16, and thus using this formulation enables us to discuss both cases in a convenient way. In the subsequent paragraphs, we note the main results of T16 concerning the gravity offset but present these in a different way to explicitly make the link with θG, δ, and 𝒦r.
Near the center of the star, the analysis is made very general because of the well-known behaviors of the internal structure and wave-displacement vector that are imposed by the central boundary conditions. First, the treatment of T16 in this region (cf. Sect. 3.3 of T16) is similar to that of Shibahashi (1979) except for an essential difference. Indeed, owing to the influence of the perturbation of the gravitional potential, the behavior of the dependent variable Y1 in T16, which is equivalent to the dependent variable v of Shibahashi (1979) in the limit of the Cowling approximation, differs from an Airy function of the first kind near the innermost turning point r1 (see Sect. 3.1). As a consequence, the phase lag introduced at the reflection in r1 for the variable Y1 turns out to be decreased by π compared to its value in the Cowling approximation; thus it is equal in this case to (modulo 2π)
For sake of simplicity, the basic derivation of θG is detailed in A. Second, the analysis of T16 (cf. Sect. 3.3 and 4 of T16) also accounted for the singularity at the center, which can impact both the location of the innermost turning point r1 and the wavenumber integral over this region and therefore the value of εg. The T16 author finally found
where N is the usual Brunt–Väisälä frequency and the big O Bachmann–Landau notation is used. In Eq. (17), 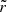 is an arbitrary radius inside the buoyancy cavity that is far enough away from the turning points for the asymptotic limit to be valid and the residual to be negligible (i.e.,
is an arbitrary radius inside the buoyancy cavity that is far enough away from the turning points for the asymptotic limit to be valid and the residual to be negligible (i.e., 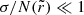 ).
).
In the upper part of the buoyancy cavity (i.e., for 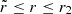 ), T16 (cf. Sect. 3.2 of T16) simultaneously treated both closely-related turning points associated with the evanescent region. As a result, the same wave function (i.e., Y1) takes this time the form of a linear combination of the Weber functions and the phase lag introduced at r2 is given from the argument of Eq. (99) of T164, that is equal to
), T16 (cf. Sect. 3.2 of T16) simultaneously treated both closely-related turning points associated with the evanescent region. As a result, the same wave function (i.e., Y1) takes this time the form of a linear combination of the Weber functions and the phase lag introduced at r2 is given from the argument of Eq. (99) of T164, that is equal to
where the function Ψ is given in Eqs. (85)-(86) of T16 and depends on the properties of the evanescent region. In the case of a very thick evanescent region, we have Ψ → −π/4, which implies δ → +π/2, in agreement with the discussion in Sect. 3.1.
Finally, to compute the expression of Θg, we also have to provide the expression of the radial wavenumber in the upper part of the buoyancy cavity. In the WKB approximation, it is equal to (T16)
where 𝒩 and 𝒮1 are the modified Brunt–Väisälä and ℓ = 1 Lamb frequencies, respectively, which account for the perturbation of the gravitational potential. Both are related to the usual Brunt–Väisälä and Lamb frequencies, N and S1 (see, e.g., Unno et al. 1989, for definitions), through the equalities 𝒩 = N/J and 𝒮1 = S1J, where J = 1 − ρ(r)/ρav(r), and ρ is the local density and ρav is the mean density in the sphere of radius r. As an illustration, their profiles are shown in Fig. 1. This figure shows that the difference between the modified and usual critical frequencies is large only below the hydrogen-burning shell and is negligible in the outer layers. Moreover, we can see that the turning points associated with the buoyancy cavity turn out to satisfy σ = 𝒮1(r1) and σ = 𝒩(r2) in the non-Cowling case. The frequency dependence of the turning points in this case is thus also measured by Eq. (4), but by replacing N in this latter equation with 𝒮1 and with 𝒩 for r1 and r2, respectively. Nevertheless, given the similar behaviors of N and 𝒮1 close to r1 and of N and 𝒩 close to r2, the same conclusions as in the Cowling approximation hold valid about the frequency dependence of r1 and r2. The ambiguity on the physical interpretation of the period spacing and of the gravity offset that was highlighted in Sect. 2.2 therefore persists in the non-Cowling case (Takata 2016a).
3.3. Basic asymptotic expression of Θg in RGB stars
By injecting Eqs. (16)–(18) in Eq. (12), the asymptotic expression of Θg in RGB stars can be rewritten (modulo π)
We retrieve Eq. (136) of T16 who obtained this in a different way, that is through matching the wave functions coming from the different regions (i.e., from the center, evanescent region, and surface). It is also worth mentioning that, under the Cowling approximation, a term with a value of π/2 needs to be added to Eq. (20) owing to the different behavior of the wave function near r1 in the Cowling hypothesis and in the non-Cowling case (see the second paragraph of Sect. 3.2). As seen in Fig. 1 and Eq. (19), this is actually related to the change in nature of the innermost turning point r1, which is located where σ = 𝒮1(r1) in the non-Cowling case instead of σ = N(r1) in the Cowling approximation. This modification leads to a shift of half the radial wavelength in the wave function, whence an additional phase of π/2 in Θg. This point emphasizes the importance of going beyond the Cowling approximation when studying the gravity offset.
According to Eq. (20), identifying the first term in the right-hand side as the main contribution to the leading order term of Θg, we see that the variation in εg on the RGB certainly results from structural changes in the upper part of the radiative zone and the surrounding evanescent region (i.e., between about 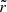 and r2) via both the wavenumber integral and the Ψ function. To relate the value of εg to the internal properties, we thus need to model this region.
and r2) via both the wavenumber integral and the Ψ function. To relate the value of εg to the internal properties, we thus need to model this region.
4. Evolution of εg on the red giant branch
In this section, we investigate the evolution of εg on the RGB. By modeling in a simple way the Brunt–Väisälä and Lamb frequencies between the hydrogen-burning shell and the base of the convective zone, we first obtain an analytical expression for εg, which is subsequently used to interpet the observed variations in  during evolution.
during evolution.
4.1. Simplified modeling of the upper radiative layers
As shown by the propagation diagrams in Fig. 1, the Brunt–Väisälä frequency varies at first approximation as a power law of radius between the hydrogen-burning shell and the base of the convective zone. This behavior is mainly due to the high density contrast existing between the helium core and the convective envelope on the RGB. For young red giant stars (e.g., model with νmax ≈ 200 μHz in Fig. 1), the turning point r2, where 𝒩(r2)=2πν ∼ 2πνmax, is located in the radiative region and depends on the mode frequency since Eq. (4) is non-null here. When stars evolve on the RGB, νmax decreases because of the envelope expansion. Indeed, νmax is about proportional to the acoustic cut-off frequency at the surface and its value is ruled by the scaling law (e.g., Kjeldsen & Bedding 1995; Belkacem et al. 2013)
where M is the stellar mass, R is the stellar radius, and νmax, ⊙ = 3104 μHz is the solar reference value as prescribed by Mosser et al. (2013). Hence, since the increase in R is predominant on the RGB, νmax decreases during evolution. In contrast, the (usual and modified) Brunt–Väisälä frequency increases owing to the core contraction. As a result, the value of νmax becomes low enough at one point on the RGB for r2 to be about equal to the radius of the base of the convective zone, which is denoted with rb. Since r2 ≈ rb and (dln𝒩/dlnr) tends to minus infinity close to rb, Eq. (4) shows that the turning point r2 then becomes frequency independent around νmax for the rest of the evolution on the RGB (e.g., model with νmax ≈ 60 μHz in Fig. 1). Given that εg is sensitive to the properties of the region in the vicinity of the turning points (see Sect. 3), its computation must account for this change of configuration. In the following, we denote the value of the modified Brunt–Väisälä frequency just below the base of the convective region with 𝒩b. We therefore distinguish two cases. First, case a: young stars on the beginning of the ascent of the RGB for which r2 < rb and 2πνmax > 𝒩b; and second, case b: more evolved stars with r2 ≈ rb and 2πνmax ≲ 𝒩b.
Moreover, to express εg, we use several simplifying assumptions. First, the (modified) Brunt–Väisälä frequency is modeled as a decreasing power law of radius with an index β for  , that is,
, that is,
At the base of the convective zone, 𝒩 varies so sharply close to rb that it is assumed to discontinuously change from 𝒩b to about zero. A schematic view of this simplified configuration is shown in Fig. 2. In case a only, we note that
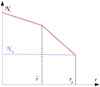 |
Fig. 2. Schematic view of the modified Brunt–Väisälä frequency as a function of radius on a logarithmic scale, as assumed by the simple model presented in Sect. 4.1. The horizontal dashed line indicates the value 𝒩b just below the base of the convective zone at radius rb. The radius |
since 𝒩(r2)=σ at the turning point. Second, for sake of simplicity, we also focus on the case of a thick evanescent region, so that σ ≪ 𝒮1 everywhere in the buoyancy cavity and Ψ ≈ −1/4. Third and lastly, the relation J ≈ const. ≈ 2β/3, which results from the high density contrast between the core and the envelope, is supposed to be met in a good approximation between the hydrogen-burning shell and the base of the convective zone (e.g., see Sect. A.3.1 of T16). All these hypotheses are checked a posteriori in Sect. 5.2 not to modify the final conclusions.
4.2. Asymptotic expressions of ΔΠ1 and εg
Under the previous assumptions, we have to compute the integrals between 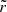 and r2 in Eq. (20) to completely express Θg and then identify εg and ΔΠ1 based on Eqs. (5)–(9).
and r2 in Eq. (20) to completely express Θg and then identify εg and ΔΠ1 based on Eqs. (5)–(9).
4.2.1. Computations in case a (r2 < rb, σ > 𝒩b)
The case a has already been considered by Takata (2016a). Nevertheless, most of the analytical developments in this case are useful to treat case b. For sake of clarity and convenience, we thus propose in the following to detail the computation, considering the hypothesis of a thick evanescent region only.
The first step consists in expressing the frequency dependence of r2 in the upper bound of the first integral that appears in the right-hand side of Eq. (20), denoted with ℐ1 in the following. This latter can be rewritten as
In case a, it results to
where the second integral in Eq. (24) is computed using the change of variable y = 𝒩 with y(r2)=σ and y(rb)=𝒩b.
The second step is to consider the second integral in the right-hand side of Eq. (20), denoted with ℐ2 in the following. Assuming σ ≪ 𝒮1 in Eq. (19), this integral can be rewritten
Then, using the change of variable x = σ/𝒩 and the fact that x(r2)=1, we obtain in case a (e.g., Abramowitz & Stegun 1972)
where 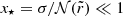 in the asymptotic limit and is neglected in the following.
in the asymptotic limit and is neglected in the following.
The final step consists in injecting Eqs. (25) and (28) in Eq. (20), so that the asymptotic expression of Θg finally reads in case a
where Nb = J𝒩b is the value of the usual Brunt–Väisälä frequency just below rb. According to Eq. (5), the F function is equal in case a to
In the hypothesis of a thick evanescent region, Ψ is about constant and close to −π/4 (see Sect. 3.2). The determination of the local asymptotic period spacing and gravity offset around νmax is thus obtained from Eqs. (8) and (9), that is,
and
where we used the relation β ≈ 3J/2 and Nb ≈ (2β/3)𝒩b. We retrieve the result found by T16 in the hypothesis of a thick evanescent region. We note that the terms in brackets in the right-hand side of Eq. (31) would be equal to the integral between 0 and +∞ of the Brunt–Väisälä frequency if this latter hypothetically varied following Eq. (22) from 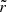 to +∞.
to +∞.
Therefore, the model predicts that 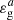 is independent of νmax so that the gravity offset remains constant during evolution for the young red giant stars in case a. Actually, according to Eq. (30), the local first-order analysis around νmax appears to be a very good approximation in case a since the remainder in Eq. (11) originates only from the residual in Eq. (28) that is on the order of x⋆. Indeed, we can check that x⋆ ∼ 0.01 in typical red giant stars so that the remainder is clearly negligible (e.g., see Fig. 1). This result validates the assumptions made in the measurement of
is independent of νmax so that the gravity offset remains constant during evolution for the young red giant stars in case a. Actually, according to Eq. (30), the local first-order analysis around νmax appears to be a very good approximation in case a since the remainder in Eq. (11) originates only from the residual in Eq. (28) that is on the order of x⋆. Indeed, we can check that x⋆ ∼ 0.01 in typical red giant stars so that the remainder is clearly negligible (e.g., see Fig. 1). This result validates the assumptions made in the measurement of 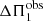 and
and 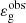 for stars in case a (see Sect. 2.1). We conclude that the local asymptotic values of ΔΠ1 and εg are representative of both observed quantities, respectively; thus their comparison is relevant. Actually, the same conclusions can be reached in the hypothesis of a very thin evanescent region, as discussed in Sect. 5.2.
for stars in case a (see Sect. 2.1). We conclude that the local asymptotic values of ΔΠ1 and εg are representative of both observed quantities, respectively; thus their comparison is relevant. Actually, the same conclusions can be reached in the hypothesis of a very thin evanescent region, as discussed in Sect. 5.2.
4.2.2. Computations in case b (r2 ≈ rb, σ < 𝒩b)
For stars in case b, the upper bound of the first integral in Eq. (20) is frequency independent since r2 must be replaced by rb, so that this integral is merely equal in case b to
To go further, the computation of the second integral in Eq. (20) is similar to Eqs. (26)–(28) in case a, except that the upper bound of the integral is now frequency dependent and equal to xb = 2πν/𝒩b. As a result, we obtain in case b (e.g., Abramowitz & Stegun 1972)
where we again used the relation β ≈ 3J/2 and the fact that x⋆ ≪ 1. Injecting Eqs. (33) and (34) in Eq. (20), we get
Proceeding in a similar way as in Sect. 4.2.1, the F function now reads in case b, according to Eq. (5),
In the hypothesis of a thick evanescent region, Ψ is a constant close to −π/4 and the derivative of F with respect to frequency is thus equal to
As a final step, the local asymptotic period pacing and gravity offset can be computed using Eqs. (8), (9), (36) and (37), that is,
and
Unlike in case a, the local asymptotic gravity offset depends on νmax in case b and therefore must vary during evolution. In this case, the remainder around νmax defined in Eq. (11) is non-null and is equal using Eqs. (5), (6), (11), (36) and (37) to
where xb, max = 2πνmax/𝒩b. We show in Sect. 5.1 that the remainder is not higher than about σε over the observed frequency range of typical red giant stars in case b and thus can be neglected. As a consequence, the definitions of the local asymptotic period spacing and gravity offset given in Eqs. (8) and (9) are representative of the observed values and the comparison between both remains relevant in case b.
4.3. Variation of εg with evolution
4.3.1. Asymptotic predictions of the model
The variation of the gravity offset during the evolution on the RGB can now be discussed in the framework of the model developed in the previous sections. From Eqs. (32) and (39), it is possible to compute εg as a function of the parameter 2πνmax/𝒩b. This ratio monotically decreases with time and thus represents a proxy of the evolutionary stage on the RGB (see B). As expected from stellar models of typical observed RGB stars, the value of this parameter is considered between 0.01 and 100. The result is shown in Fig. 3.
 |
Fig. 3. Local asymptotic value of the gravity offset according to the model considered in Sect. 4.1. It was computed via Eq. (32) in case a (blue) and Eq. (39) in case b (red). The cases a and b are defined in Sect. 4.1. It is shown as a function of the ratio 2πνmax/𝒩b, where 𝒩b is the value of the (modified) Brunt–Väisälä frequency just below the base of the convective zone. Stellar evolution goes from the right to the left. |
For red giant stars such as 2πνmax ≥ 𝒩b (case a), the model predicts that the value of εg remains constant and about equal to 0.22. According to Eq. (32), this peculiar value results from the power-law behavior of the Brunt–Väisälä frequency and from the relation between J and β, which are a direct consequence of the high contrast of density between the helium core and the base of the convective envelope in these stars. Once 2πνmax/𝒩b = 1, the value of εg rapidly drops to reach negative values. This sharp decrease is the consequence of the kink of the Brunt–Väisälä frequency profile near the base of the convective zone. Indeed, while the turning point r2 depends on the oscillation frequency when 2πνmax > 𝒩b, the change in the behavior of 𝒩 near r2 in evolved red giant stars such as 2πνmax < 𝒩b makes r2 frequency independent. As a consequence, the term 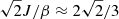 in Eq. (25), which contributes to the value of εg in case a, disappears in Eq. (33). In parallel, 𝒦r becomes discontinuous at r2 in case b and thus does not tend to zero as r tends to r2. The frequency independent integral in Eq. (28) for the case a is thus replaced by the frequency dependent integral in Eq. (34) for the case b. As a result, εg in case b depends on νmax. Moreover, its derivative with respect to νmax turns out to be discontinuous, going from 0 to +∞ at the transition between both cases (in the sense of the evolution), as seen in Fig. 3. Using standard stellar models of 1, 1.2, 1.4, 1.6, 1.8, and 2 M⊙ computed by means of the sellar evolution code CESTAM, the input physics of which is detailed in Sect. 2.2, we estimated based on the scaling relation in Eq. (21) that this transition must happen for values of νmax, t ≈ 110, 95, 80, 70, 60, and 50 μHz, respectively, that is, just before the luminosity bump (e.g, Christensen-Dalsgaard 2015). We note that the higher the mass, the lower the value of νmax, t. Interestingly, Khan et al. (2018) found a similar trend in the observed value of νmax at the luminosity bump.
in Eq. (25), which contributes to the value of εg in case a, disappears in Eq. (33). In parallel, 𝒦r becomes discontinuous at r2 in case b and thus does not tend to zero as r tends to r2. The frequency independent integral in Eq. (28) for the case a is thus replaced by the frequency dependent integral in Eq. (34) for the case b. As a result, εg in case b depends on νmax. Moreover, its derivative with respect to νmax turns out to be discontinuous, going from 0 to +∞ at the transition between both cases (in the sense of the evolution), as seen in Fig. 3. Using standard stellar models of 1, 1.2, 1.4, 1.6, 1.8, and 2 M⊙ computed by means of the sellar evolution code CESTAM, the input physics of which is detailed in Sect. 2.2, we estimated based on the scaling relation in Eq. (21) that this transition must happen for values of νmax, t ≈ 110, 95, 80, 70, 60, and 50 μHz, respectively, that is, just before the luminosity bump (e.g, Christensen-Dalsgaard 2015). We note that the higher the mass, the lower the value of νmax, t. Interestingly, Khan et al. (2018) found a similar trend in the observed value of νmax at the luminosity bump.
As 2πνmax/𝒩b keeps decreasing with evolution after the transition, the model predicts that εg smoothly decreases. Indeed, the integral in Eq. (34), which actually represents the error made by computing the wavenumber integral in the upper part of the buoyancy cavity using the approximate expression for the radial wavenumber given in Eq. (13), tends to zero as the oscillation frequency decreases. In the case of very evolved stars for which 2πνmax ≪ 𝒩b, the value of the gravity offset is then expected to approach −0.25, that is, the limit value of the phase Ψ as the evanescent region becomes very thick.
4.3.2. Observed values
Mosser et al. (2018) measured the value of the gravity offset in 196 RGB stars observed by the Kepler satellite, that is, with values of the period spacing lower than 150 s and in a mass range between about 1 M⊙ and 2 M⊙ (e.g., Mosser et al. 2014). The median uncertainty on 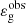 for this sample of stars is about σε ∼ 0.08, which turns out to be large for a parameter smaller than unity. Given the intrinsic difficulty of measuring this parameter, we thus consider only the stars with error bars on
for this sample of stars is about σε ∼ 0.08, which turns out to be large for a parameter smaller than unity. Given the intrinsic difficulty of measuring this parameter, we thus consider only the stars with error bars on 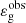 below 2σε ∼ 0.16. The resulting selected sample consists in 187 red giant stars. We checked that the rejected stars do not belong to a peculiar subset regarding the mass and evolutionary state and that the observed values of the coupling factor, period spacing, and large separation in these stars follow the same trend as the whole sample. Further analyses of the power spectra of the rejected stars are nevertheless needed to fully confirm that such large uncertainties originate from errors in the fits rather than structural peculiarities, which is out of scope of this paper.
below 2σε ∼ 0.16. The resulting selected sample consists in 187 red giant stars. We checked that the rejected stars do not belong to a peculiar subset regarding the mass and evolutionary state and that the observed values of the coupling factor, period spacing, and large separation in these stars follow the same trend as the whole sample. Further analyses of the power spectra of the rejected stars are nevertheless needed to fully confirm that such large uncertainties originate from errors in the fits rather than structural peculiarities, which is out of scope of this paper.
4.3.3. Comparison: Model versus observations
The values of the gravity offset in the 187 selected RGB stars are reported in Fig. 4 as a function of νmax. As shown in Fig. 4, the authors noticed an accumulation of values in the range [0.2, 0.35] for νmax ≳ 110 μHz. In contrast, for νmax ≲ 110 μHz, Fig. 4 shows that 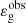 rapidly decreases in average by an amount of about 0.2 and that its value can even becomes negative for several stars.
rapidly decreases in average by an amount of about 0.2 and that its value can even becomes negative for several stars.
 |
Fig. 4. Observed values of the gravity offset adapted from Mosser et al. (2018) as a function of νmax in RGB stars (+ symbols). The color code indicates the seismic mass computed following Mosser et al. (2013). The error bars are also represented for each data point. The horizontal magenta dashed line corresponds to the asymptotic value expected from Eq. (32) for RGB stars in case a and in the low coupling hypothesis (see Sect. 4.1 for the definition of the cases a and b). This value is included in the dark gray rectangle that corresponds to the values predicted by Takata (2016a), considering typical structures of stars in the early RGB phase (see Sect. 5.2). The clear gray domain represents the asymptotic prediction that is expected from Eq. (39) for RGB stars in case b. Guided by stellar models, the transition is assumed to occur between νmax ≈ 50 μHz (red solid line) and νmax ≈ 110 μHz (blue solid line), depending on stellar mass (see main text). The prediction of the analytical model is plotted as a function of νmax by assuming that the parameter 𝒩b in Eq. (39) is constant. The black solid line shows the prediction for a transition at νmax = 130 μHz. In contrast, the clear blue domain corresponds the prediction for a value at the transition of νmax, t = 110 μHz, assuming that |
To compare the observations with the theoretical predictions of the analytical model, we need to make assumptions on the value of νmax at the transition between cases a and b, denoted with νmax, t (i.e., for which 2πνmax = 𝒩b), and on the evolution of the ratio 2πνmax/𝒩b for stars in case b. First, we assume that νmax, t takes values between 50 μHz and 110 μHz in the considered mass range, as estimated through standard stellar models of typical red giant stars (see Sect. 2.2 for details on the input physics). Second, as suggested by the 1.2 M⊙ stellar models in Fig. 1, 𝒩b generally increases between the beginning of the RGB and the luminosity bump while νmax decreases. Indeed, a rough estimate of 𝒩b just below the base of the convective zone is provided according to the definition of 𝒩 with J(rb)∼1 by
where G is the gravitational constant and m(r) represents the mass inside the shell of radius r. Using stellar models in the considered mass range, we checked that Eq. (41) is a good proxy of the actual value of the Brunt–Väisälä frequency just below the base of the convective envelope since it follows the same trend during evolution. At the beginning of the ascent of the RGB, the inner convective boundary deepens inside the star until a point just before the luminosity bump where it starts receding. This leads to the well-known first convective dredge-up of the chemical elements. In the first part of the RGB, 𝒩b increases because of the predominant effect of the decrease in rb. In the subsequent short recession phase after the convective boundary has attained its minimum and before the luminosity bump, 𝒩b can be regarded as about constant. In parallel, the expansion of the envelope is so rapid at this evolutionary state that νmax decreases more rapidly than 𝒩b increases. This trend is observed in all the considered mass range (see Appendix B for more details). In order to model this in a simple way, we assume in the following that 𝒩b decreases as 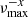 with x a real between zero and unity. Under this hypothesis, we have
with x a real between zero and unity. Under this hypothesis, we have
As a first step, the decrease in the ratio can be supposed to be mainly due to the decrease in νmax, and therefore 𝒩b can be considered as a constant (i.e., x = 0). The resulting predicted value of εg in case b, for νmax, t = 50 − 110 μHz, are represented by the light gray domain in Fig. 4. As a test, the corresponding prediction of the model for a slightly higher value of νmax, t at 130 μHz, which corresponds to a transition occurring at an earlier evolutionary state in the considered mass range, is represented by the black solid line. In the opposite limiting case, 𝒩b can be supposed to increase as rapidly as νmax decreases (i.e., x = 1). The result is indicated in the same figure by the blue dashed line for νmax, t = 110 μHz. The clear blue domain represents the analytical predictions for x between zero and unity at νmax, t = 110 μHz. We see that the higher the value of x, the sharper the decrease in εg as νmax decreases.
Figure 4 shows that observations and theory are in a noteworthy agreement. On the one hand, the observed values in stars with νmax ≳ 110 μHz and their error bars are compatible with the constant asympotic value of 0.22 predicted by the analytical model. On the other hand, the global drop in 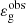 for νmax ≲ 110 μHz is also well reproduced by the theoretical expectations. Indeed, the rapid decrease in
for νmax ≲ 110 μHz is also well reproduced by the theoretical expectations. Indeed, the rapid decrease in 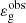 occurs about at the same evolutionary stage as predicted through stellar models, that is, for νmax ∼ 50 − 110 μHz in the considered mass range. Moreover, the mean amplitude of the drop in
occurs about at the same evolutionary stage as predicted through stellar models, that is, for νmax ∼ 50 − 110 μHz in the considered mass range. Moreover, the mean amplitude of the drop in 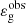 reasonably agrees with the predictions of the analytical model. In the framework of this model, we thus conclude that the stars for which the value of
reasonably agrees with the predictions of the analytical model. In the framework of this model, we thus conclude that the stars for which the value of 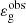 is slightly lower than about 0.22 correspond to stars that have just spent the transition between cases a and b (i.e., such as 2πνmax/𝒩b ∼ 1) and for which the gravity offset starts rapidly decreasing. Furthermore, it is also worth mentioning that less massive stars visually seem to undergo the transition and take negative values before the more massive stars, as predicted through stellar models (see Sect. 4.3.1 and B). However, given the small amount of data for the less and the more massive stars of the sample at the transition compared to other observed stars, a statistical test of this trend currently appears to be difficult. In later stages, for νmax ≲ 50 μHz, we expect to observe values between about −0.1 and −0.25. Again, because of the difficulty to observe gravity-dominated mixed modes in these stars (e.g., Grosjean et al. 2014), there are few data available to statistically test this prediction.
is slightly lower than about 0.22 correspond to stars that have just spent the transition between cases a and b (i.e., such as 2πνmax/𝒩b ∼ 1) and for which the gravity offset starts rapidly decreasing. Furthermore, it is also worth mentioning that less massive stars visually seem to undergo the transition and take negative values before the more massive stars, as predicted through stellar models (see Sect. 4.3.1 and B). However, given the small amount of data for the less and the more massive stars of the sample at the transition compared to other observed stars, a statistical test of this trend currently appears to be difficult. In later stages, for νmax ≲ 50 μHz, we expect to observe values between about −0.1 and −0.25. Again, because of the difficulty to observe gravity-dominated mixed modes in these stars (e.g., Grosjean et al. 2014), there are few data available to statistically test this prediction.
For the frequency range νmax, t = 50 − 110 μHz, Fig. 4 shows that accounting for the increase in 𝒩b along with evolution after the transition extends the predicted domain toward lower values of εg (i.e., see the clear blue domain in Fig. 4). As an illustration, we can consider the case of the 1.2 M⊙ red giant model with νmax ≈ 60 μHz in Fig. 1. For this stellar model, we estimated 2πνmax/𝒩b ≈ 0.5 so that the value of εg predicted by Eq. (39) is close to −0.1, as reported in Fig. 4. As said in Sect. 4.3.1, we also estimated from its evolutionary sequence that νmax, t ≈ 95 μHz at the transition. If 𝒩b was constant, we would have, in contrast, 2πνmax/𝒩b = νmax/νmax, t ≈ 0.63 from Eq. (42) and εg ≈ −0.04 according to Eq. (39). Therefore, accounting for the increase in 𝒩b is necessary for a value of εg = −0.1 to be compatible with the value of νmax, t ≈ 95 μHz at the transition in this standard stellar model. Nevertheless, Fig. 4 shows that slightly higher values of νmax, t can also lead on their own to lower values of εg at a given value of νmax in case b (i.e., see the black solid line in Fig. 4). Therefore, a value of εg = −0.1 at νmax ≈ 60 μHz can be explained not only by an increase in 𝒩b during evolution for νmax, t ≈ 95 μHz, as in the 1.2 M⊙ red giant model considered in Fig. 1, but also by a slightly higher value of νmax, t between 95 μHz and 130 μHz at a constant value of 𝒩b, or by the simultaneous effect of both. While the progressive increase in 𝒩b during evolution results from the inward migration of the base of the convective zone at this evolutionary stage, the increase in the value of νmax, t can physically result from the presence of overshooting at the inner convective boundary. This point is discussed in more detail in Sect. 5.5. We emphasize that both effects tend to improve the agreement with observations in case b, compared to the predictions obtained with the range of values for νmax, t that are estimated through standard stellar models without overshooting and considering 𝒩b as a constant during evolution.
Nevertheless, we notice four stars that exhibit discrepancies compared to the observed general trend and theoretical predictions. First, for νmax ∼ 70 μHz, the stars KIC 3749487 and KIC 10387370 have 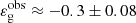 and
and 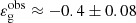 , respectively. These observations turn out to be well lower than the predicted range of values. Actually, the error bars in KIC 3749487 are compatible with the lower limit of −0.25 expected from the model. In this star, the abnormal value of εg could therefore be explained within the framework of the model by a much more rapid increase in 𝒩b with evolution and/or a higher value of νmax, t at the transition. In contrast, the value measured in KIC 10387370 is too low compared to the predicted lower limit and thus is incompatible with the model. Second, for 150 μHz ≲ νmax ≲ 200 μHz, the stars KIC 2584478 and KIC 12008916 exhibit values of
, respectively. These observations turn out to be well lower than the predicted range of values. Actually, the error bars in KIC 3749487 are compatible with the lower limit of −0.25 expected from the model. In this star, the abnormal value of εg could therefore be explained within the framework of the model by a much more rapid increase in 𝒩b with evolution and/or a higher value of νmax, t at the transition. In contrast, the value measured in KIC 10387370 is too low compared to the predicted lower limit and thus is incompatible with the model. Second, for 150 μHz ≲ νmax ≲ 200 μHz, the stars KIC 2584478 and KIC 12008916 exhibit values of 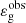 that are well below the values measured in dozens of other stars at the same evolutionary stage with similar masses but in agreement with the predictions of the model. We checked that the seismic properties of these four stars (e.g., period spacing, coupling factor, core rotation rate; see Table C.1) follow the mean trend of the whole considered RGB sample, except the gravity offset. Rather than different structures, errors in the observed fits or underestimated uncertainties are thus certainly the most plausible explanation for these outliers. The four outliers therefore do not statistically hinder the global agreement between observations and theory. More detailed analyses of these four stars are nonetheless needed to attest the reasons for their deviations from the global trend, which is beyond the scope of this work.
that are well below the values measured in dozens of other stars at the same evolutionary stage with similar masses but in agreement with the predictions of the model. We checked that the seismic properties of these four stars (e.g., period spacing, coupling factor, core rotation rate; see Table C.1) follow the mean trend of the whole considered RGB sample, except the gravity offset. Rather than different structures, errors in the observed fits or underestimated uncertainties are thus certainly the most plausible explanation for these outliers. The four outliers therefore do not statistically hinder the global agreement between observations and theory. More detailed analyses of these four stars are nonetheless needed to attest the reasons for their deviations from the global trend, which is beyond the scope of this work.
In conclusion, the general trend observed in the variation of 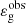 with evolution can be globally explained through the asymptotic expressions and the model that we developed. Red giant stars with νmax ≳ 110 μHz exhibit values of the gravity offset about constant and close to 0.22. This mean value is the consequence of the high contrast of density between the core and the envelope. For red giant stars with νmax ∼ 50 − 110 μHz, the rapid decrease observed in the gravity offset by a mean value of about 0.2 occurs when νmax becomes so low that the outermost turning point r2 associated with the buoyancy cavity becomes and remains about equal to the radius of the base of the convective zone, rb, during the subsequent evolution on the RGB. This is the consequence of the kink in the Brunt–Väisälä frequency profile at the interface between the radiative and convective regions. This clear signature in
with evolution can be globally explained through the asymptotic expressions and the model that we developed. Red giant stars with νmax ≳ 110 μHz exhibit values of the gravity offset about constant and close to 0.22. This mean value is the consequence of the high contrast of density between the core and the envelope. For red giant stars with νmax ∼ 50 − 110 μHz, the rapid decrease observed in the gravity offset by a mean value of about 0.2 occurs when νmax becomes so low that the outermost turning point r2 associated with the buoyancy cavity becomes and remains about equal to the radius of the base of the convective zone, rb, during the subsequent evolution on the RGB. This is the consequence of the kink in the Brunt–Väisälä frequency profile at the interface between the radiative and convective regions. This clear signature in 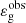 happens just before the luminosity bump. Furthermore, accounting for the effects of the inward migration of the base of the convective or of overshooting in this region tends to improve the agreement between the model and observations in the more evolved red giant stars with νmax ≲ 110 μHz.
happens just before the luminosity bump. Furthermore, accounting for the effects of the inward migration of the base of the convective or of overshooting in this region tends to improve the agreement between the model and observations in the more evolved red giant stars with νmax ≲ 110 μHz.
To finish, we emphasize that the agreement between observations and theory is remarkable given the difficulty to measure 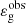 . Indeed, since the number of radial nodes in the buoyancy cavity is very large and typically close to ng ∼ 100 in red giant stars, a difference as small as 0.5% between
. Indeed, since the number of radial nodes in the buoyancy cavity is very large and typically close to ng ∼ 100 in red giant stars, a difference as small as 0.5% between 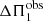 and ΔΠ1 leads to a difference of values of 0.5 between
and ΔΠ1 leads to a difference of values of 0.5 between 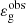 and εg. The present result therefore confirms the robustness of both the measurement method and the validity of the asymptotic analyses in red giant stars.
and εg. The present result therefore confirms the robustness of both the measurement method and the validity of the asymptotic analyses in red giant stars.
5. Discussion
In this last section, we discuss the results and main assumptions used in this work.
5.1. Validity of the local asymptotic definitions in RGB stars
In this work, we considered local definitions around νmax for εg and ΔΠ1 (see Sect. 2.3). The comparison between the local asymptotic expressions and observed values is relevant if both quantities are equivalent over all the observed frequency range around νmax, which can be checked a posteriori.
For stars in case a, we showed in Sect. 4.2.1 that the local asymptotic expressions are representative of the observed values. In the framework of the considered model, the equivalence between both actually turned out to be easy to confirm. For stars in case b, the answer to this question is less straightforward. In order to check the validity of comparing local asymptotic expressions to observations in case b, we can proceed as follows. We still assume in a good approximation that the observed frequencies belong to a 6Δν-wide frequency range centered around νmax as expected from theoretical estimates and observations in typical RGB stars (e.g., Grosjean et al. 2014; Mosser et al. 2018). Using the Δν − νmax scaling law for RGB stars, that is (e.g., de Assis Peralta et al. 2018),
where νmax and Δν are expressed in μHz, the typical width of the observed frequency range, δν, on both sides of νmax is equal to
For typical observed red giant stars in case b, we have 50 μHz ≲ νmax ≲ 110 μHz (e.g., see Fig. 4), so that we obtain
Using Eq. (40), it is possible to check for the considered range of νmax that the remainder over the observed frequency range νmax ± δν satisfies the inequality
As a result, the remainder is smaller than or comparable to the typical uncertainties on the observed values of the gravity offset.
Therefore, given the current precision on the measurement of these parameters, we conclude that the local asymptotic expressions of εg and ΔΠ1 defined in Sect. 2.3 are both sufficient and representative of the observed values. The impact of the remainder on the comparison with the observed values performed in Sect. 4 is thus negligible and does not modify the main conclusions, as mentioned before.
5.2. Sensitivity of the results on the assumptions
The theoretical expression of εg relies on several simplifying hypotheses regarding the structure of the region between the hydrogen-burning shell and the base of the convective zone. Here, we propose to discuss the sensitivity of the result on these assumptions.
On the one hand, we assume that the evanescent region is thick. While this is met at first approximation for evolved red giant stars in case b, it is questionable for younger stars in case a as shown by the observations of Mosser et al. (2017). Takata (2016a) analytically treated the other limiting case of a very thin evanescent zone by assuming that 𝒮1 varies as a similar power law of radius to 𝒩. In this hypothesis, the value of εg is expected to remain between 0.2 and 0.35 despite a large set of typical configurations considered for the evanescent region. This is in agreement with the observations (e.g., see gray rectangle in Fig. 4), as already mentioned by Mosser et al. (2018). Moreover, given the small sensitivity of εg to the properties of the evanescent region (see Fig. 4 of T16), we expect that its variation over the observed frequency range to be much smaller than σε ∼ 0.08. As a conclusion, the local asymptotic definitions of the period spacing and gravity offset remain representative of the observed values in the case of a thin evanescent region, and thus their comparison is also relevant.
On the other hand, it is obvious that the transition between cases a and b is more progressive than assumed in the model presented in Sect. 4.1 (e.g., compare Figs. 1 and 2). In this region, it seems more reasonable to assume that the logarithmic derivative of 𝒩, denoted with β⋆, can vary with radius, that is,
The exponent β⋆ is supposed to be much higher than unity and to tend rapidly to infinity near rb. In this intermediate case, the estimate of the integrals in Eqs. (24) and (26) can be obtained using two main assumptions. First, we can assume that the frequency dependent quantities β⋆(r2) and J(r2) do not vary too much over the observed frequency range around νmax. As a result, the integral ℐ1 in Eq. (24) can be computed around νmax by replacing rb with r2(νmax), such that the result is similar to Eq. (25) by replacing 𝒩b with 2πνmax, that is,
where r2, max = r2(νmax). Second, as νmax decreases and r2 tends to rb, the main contribution to the integrals in Eq. (26) comes from the region near r2 since 𝒩 in the integrands sharply decrases with lnr at the base of the convective zone. As a result, Eq. (26) can be crudely estimated in a similar way to Eq. (28) by assuming that J and β⋆ are constant and equal to their values at r2(ν), that is,
where the first assumptions J ≈ J(r2, max) and β⋆ ≈ β⋆(r2, max) over the observed frequency range were used. Following the same reasoning as in Sect. 4.2.1, the local asymptotic expression of the gravity offset is thus similar to Eq. (32), that is,
except that the relation β = 3J/2 in the previous picture does not hold true in this case between β⋆ and J. Nevertheless, J(r2, max)∼1 in evolved red giant stars close to the transition, so that the evolution of εg depends only on the evolution of β⋆(r2, max). This latter parameter is equivalent to the frequency dependent arcsine function in Eq. (39). Because of the sharp kink of the Brunt–Väisälä frequency, the increase in β⋆(r2, max) due to the decrease in νmax can be assumed to be so rapid close to the transition that it can mimic the sharp decrease in the value of εg that was predicted by the model developed in Sect. 4. Using Eq. (50), the rapid decrease in εg resulting from the change in β⋆ from 3/2 to infinity is equal to 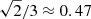 , which reasonably agrees with the observations in Fig. 4 given the crude assumptions used to derive Eq. (50). In these considerations, the same conclusions are therefore reached, the drop in the value of εg results from the kink in the Brunt–Väisälä frequency near the turning point r2 at the transition.
, which reasonably agrees with the observations in Fig. 4 given the crude assumptions used to derive Eq. (50). In these considerations, the same conclusions are therefore reached, the drop in the value of εg results from the kink in the Brunt–Väisälä frequency near the turning point r2 at the transition.
In summary, despite the simple modeling we used, it appears to be sufficient for our purpose and does not impact our interpretation of the observed global variations in εg in terms of internal structure.
5.3. Simultaneous variations in ΔΠ1 and q
While εg exhibits a rapid characteristic decrease for stars at the transition between cases a and b, we can wonder whether simultaneous rapid variations in the period-spacing ΔΠ1 and in the coupling factor q of mixed modes are observable or not.
Regarding ΔΠ1, Eqs. (31) and (38) also predict a sharp increase at the transition between cases a and b. Indeed, ΔΠ1 is expected to decrease smoothly for stars in case a owing to the increase both in the integral of the Brunt–Väisälä frequency between 0 and rb and in the parameter 𝒩b during evolution. After the transition, an extra term appears in Eq. (38) depending on νmax. As a result, the derivative of the period spacing with respect to νmax is discontinuous and tends to infinity at the transition, whence an expected sharp increase during the evolution. The maximum relative amplitude of the jump in ΔΠ1 predicted by the model can be estimated considering that the ratio 2πνmax/𝒩b varies quasi-instantaneously from unity to zero at the transition while N and 𝒩b remain about unmodified. According to Eqs. (31) and (38), and the fact that 𝒩b ∼ 2πνmax at the transition, the relative rapid variation in the period spacing at the transition is thus expected to be lower than
This transition occurs for stars around νmax ≈ 80 μHz, which corresponds to ΔΠ1 ≈ 75 s (e.g., Vrard et al. 2016). Following Eq. (51), this is equivalent to a rapid relative increase smaller than 0.15% in ΔΠ1. This variation is too low to be clearly detected since it is on the order of the relative precision on the period spacing for these stars (Mosser et al. 2018). This implies that εg is more sensitive than ΔΠ1 to the transition, which is reasonable since εg corresponds to the (small) higher order term in the phase term Θg while ΔΠ1 represents the leading-order term that is mainly sensitive to the properties of the region in the middle of the buoyancy cavity.
Besides, the coupling factor depends on the wave transmission factor through the evanescent region and thus on the properties of this region (e.g., Takata 2016b). The evanescent region is located between the profiles of 𝒩 and 𝒮1, that is, between turning points r2 and r3 for which σ = 𝒩(r2) and σ = 𝒮1(r3). Without going into the details, we thus understand that the coupling factor is also likely to be sensitive to the kink in the Brunt–Väisälä frequency at the transition between cases a and b since it significantly modifies the structure of the evanescent region (e.g., see Fig. 1). The factor q could therefore potentially present a noticeable change of trend during evolution that would be associated with this transition. For the considered stars, that is, for 50 μHz ≲ νmax ≲ 110 μHz, we did not perceive any obvious change of behavior as a function of νmax in the observed values of q obtained by Mosser et al. (2017). The lack of data for νmax ≲ 80 μHz and the current uncertainties on the measurements partly make the search for such a feature difficult. Analytical studies of the coupling factor around the transition will be useful to guide future observational investigations but need for further theoretical efforts. Indeed, in addition to consider the effect of the kink in the Brunt–Väisälä frequency on the variation of q with evolution, the analysis will also have to deal with the influence of the spike in the Brunt–Väisälä frequency and of the discontinuity in the Lamb frequency at the base of the convective region resulting from the presence of a sharp molecular weight gradient (see Sect. 5.4). This will demand going beyond the picture given by the current asymptotic analyses of mixed modes provided by Shibahashi (1979) and Takata (2016a).
Therefore, we conclude that neither ΔΠ1 nor q can currently bring us a signature on the transition between cases a and b as clear as that observed in εg. More detailed analyses should be performed in the future to find evidence of a given signature associated with the transition in these parameters.
5.4. Possible effect of the μ-gradient at the base of the convective zone
Figure 1 shows that a spike in the (modified) Brunt–Väisälä frequency exists at the base of the convective zone for evolved red giant stars in case b. This is the consequence of a strong molecular weight gradient (or μ-gradient). This μ-gradient causes the luminosity bump in the later stage when the hydrogen-burning shell reaches the associated zone. Since the luminosity bump is observationally detected (e.g., Khan et al. 2018), there is no doubt on the existence of this μ-gradient in real stars.
Such a sharp variation can slightly perturb the oscillation period and create a so-called buoyancy glitch (e.g., Brassard et al. 1992; Miglio et al. 2008; Cunha et al. 2015). Indeed, as shown by Cunha et al. (2015), the presence of a sharp μ-gradient inside the buoyancy cavity locally results in a discontinuity in the wave function derivative with respect to radius, leading to an additional phase term in the expression of Θg in Eq. (20). It is thus obvious that this feature can modify the physical interpretation of the observed values of the gravity offset in case b if its contribution to Θg is of the same order as the asymptotic predictions obtained without considering the glitch. We propose to discuss its impact in a simple way focusing on stars that have just spent the transition, that is, for which 2πνmax ∼ 𝒩b. Indeed, most of the observed values of the gravity offset in case b were obtained for 50 μHz ≲νmax ≲ 110 μHz (e.g., see Fig. 4), which corresponds to the νmax frequency range of the stars just after the transition that is expected from stellar models (e.g., see Fig. 1). To go further, we adapt the formulation of buoyancy glitches given by Cunha et al. (2015; hereafter C15). In other words, we assume that the spike in N2 can be modeled by a Dirac δ function located at r⋆ and with an amplitude A⋆. However, in contrast to C15, we do not assume that this sharp feature is located far away from the turning point r2. Instead, we assume that r⋆ is very close to r2, where the radial wavenumber vanishes. Under these considerations, the discontinuity in the wave function derivative with respect to radius at r⋆ that is provided by Eq. (11) of C15 becomes
where Φin(r) and Φout(r) are the wave functions below and above r⋆, respectively. Equation (52) shows that the derivative of the wave function remains continuous at first approximation near r⋆. This holds true whatever the amplitude of the μ-gradient since kr(r⋆)≈kr(r2)≡0 in the considered hypothesis. As a result, the contribution of the additional phase term associated with the glitch to Θg must be of higher order than εg.
In conclusion, we find that the impact of the spike in the Brunt–Väisälä frequency at the base of the convective zone is small at first approximation and does not modify the interpretation of the global observed variations of the gravity offset in evolved red giant stars. This result will have to be confirmed by more detailed analyses based either on theoretical developments or stellar models, accounting both for a more realistic shape of the spike in N and for slightly different values between r⋆ and r2, as observed in Fig. 1. This must be subject to future works, which are beyond the scope of this paper.
5.5. Overshooting below the convective region
To match the observed location of the luminosity bump in low-mass stars with stellar models, Khan et al. (2018) included overshooting below the convective envelope. They demonstrated that an adiabatic extent of the convective zone of about 0.3H on average over the mass and metallicity ranges of their sample, where H is the pressure scale height, is sufficient to fit the observations. This work gives a clear evidence that overshooting at the base of the convective region must be taken into account in red giant stars and thus has the potential to modify the value of the gravity offset.
However, while overshooting decreases the radius of the base of the convective region rb, it does not change the formal profile of the (modified) Brunt–Väisälä frequency just below rb. Indeed, it is possible to check in typical red giant models including overshooting that 𝒩 still varies at first approximation as a power law of radius between the hydrogen-burning shell and the convective envelope before sharply vanishing close to rb. Therefore, the assumptions used in Sect. 4.1 remain valid and the analytical expressions of the gravity offset provided in Eqs. (32) and (39) are not modified in the presence of overshooting.
For young red giant stars in case a, the expression of εg in Eq. (32) is independent of the internal structure, so that overshooting has no effect on the value of the gravity offset predicted by the model. For more evolved stars in case b, the expression of εg in Eq. (32) depends on the internal structure only through the ratio 2πνmax/𝒩b. Therefore, the effect of overshooting on εg at a given value of νmax can only result from its impact on 𝒩b. Since the base of the convective region is deeper with overshooting, the value of 𝒩b is higher according to Eq. (41). As shown in B, this trend is well reproduced in stellar models. Moreover, it turns out that the variation rate of 𝒩b as a function of νmax before the luminosity bump is comparable with or without overshooting. As a result, at a given value of νmax, overshooting leads only to higher νmax, t at the transition between cases a and b (i.e., for which 2πνmax, t ≈ 𝒩b). For instance, we found that the inclusion of an adiabatic overshoot region of about 0.3H in a 1.2 M⊙ evolutionary sequence with the same input physics as described in Sect. 2.2 leads to an increase in νmax, t from about 95 μHz to about 115 μHz.
As a conclusion, the effect of overshooting is already included in the analytical model through the parameter νmax, t. Indeed, as shown by simple considerations and stellar models, the thicker the overshooting region, the higher the value of νmax, t since the lower the value of rb (see B). Moreover, for reasonable values of the overshoot thickness based on the study of the luminosity bump (Khan et al. 2018), it appears that its effect tends to reinforce the agreement between the model and observations, as mentioned in Sect. 4.
5.6. Seismic diagnoses with εg
In Sect. 4, we demonstrated that the global variation in the gravity offset during the evolution exhibits a clear signature on the RGB that is related to the kink in the Brunt–Väisälä frequency at the interface between the radiative and convective zones. Moreover, our analytical model also provides a first insight into the potential of the gravity offset of mixed modes to probe this region in more detail.
Indeed, on the one hand, for young red giant stars in case a, the model predicts a constant value of 0.22 for εg in the weak coupling limit. Nevertheless, in the strong coupling limit, Takata (2016a) showed that the value of εg depends both on the slope of 𝒩 in this region and on the thickness of the evanescent region. The structure of this region is ruled by the high density contrast between the core and envelope, which depends on the core contraction. The gravity offset in case a has therefore the potential to inform us of the contraction rate of the helium core. On the other hand, for more evolved red giant stars in case b, the model predicts that the value of εg depends only on 𝒩b at a given value of νmax. As discussed in Sect. 4.3.3 and in B, the value of 𝒩b mainly depends on the location of the base of the convective region. Therefore, its value may inform us of the migration of the convective boundary with time, and in particular around the convective first dredge-up, and on overshooting in this region.
In practice, despite the good precision on the measurement of the gravity offset, which results from a precision on the measurement of ΔΠ1 better than 0.5%, the uncertainties on its value can appear at first sight to be too large to provide us with detailed constraints on the region close to r2 for a given star in case a. Indeed, as mentioned in Sect. 4.1, the sensitivity of εg to the structural properties is on the order of the error bars for stars in case a according to the analytical result of Takata (2016a) (e.g., see the dark gray rectangle in Fig. 4). In contrast, for more evolved stars after the transition, the observed variations in  can certainly give us more detailed insights into the internal properties. To illustrate this point, we can consider for instance a 1.2 M⊙ star with νmax ≈ 60 μHz and εg = −0.1. To explain this value, Eq. (39) requires 2πνmax/𝒩b ≈ 0.5. As previously discussed in Sect. 4.3.3 and Sect. 5.5, such a value of 𝒩b at νmax ≈ 60 μHz can result either from the progressive increase of 𝒩b owing to the inward migration of the convective boundary or from a slightly higher value of νmax, t caused, for instance, by overshooting. Indeed, without overshooting, we estimated through stellar models that νmax, t ≈ 95 μHz for a stellar mass of 1.2 M⊙. In order to fit the observed value at νmax = 60 μHz with the analytical expression in Eq. (39), given the assumption that
can certainly give us more detailed insights into the internal properties. To illustrate this point, we can consider for instance a 1.2 M⊙ star with νmax ≈ 60 μHz and εg = −0.1. To explain this value, Eq. (39) requires 2πνmax/𝒩b ≈ 0.5. As previously discussed in Sect. 4.3.3 and Sect. 5.5, such a value of 𝒩b at νmax ≈ 60 μHz can result either from the progressive increase of 𝒩b owing to the inward migration of the convective boundary or from a slightly higher value of νmax, t caused, for instance, by overshooting. Indeed, without overshooting, we estimated through stellar models that νmax, t ≈ 95 μHz for a stellar mass of 1.2 M⊙. In order to fit the observed value at νmax = 60 μHz with the analytical expression in Eq. (39), given the assumption that 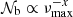 , we find that a value of x ≈ −0.5 is needed. In contrast, if 𝒩b is considered as a constant, we find that an increase in the value of νmax, t to about 120 μHz is needed for the prediction of the analytical model to match the given value of εg at νmax = 60 μHz. Stellar models show that this can be achieved with an adiabatic extent of the convective region of about 0.3H. In reality, such a value of εg at νmax = 60 μHz may result from both effects. Equivalently, we note that the different picture considered for stars close to the transition in Sect. 4.1 requires β⋆(r2, max)∼5 in Eq. (50) (with J(r2, max)≈1) to explain εg = −0.1. In this view, the slope of the Brunt–Väisälä at r2, max plays the same role as the ratio 2πνmax/𝒩b in Eq. (39) and thus may be sensitive at a given value of νmax to overshooting and the migration speed of the base of the convective zone.
, we find that a value of x ≈ −0.5 is needed. In contrast, if 𝒩b is considered as a constant, we find that an increase in the value of νmax, t to about 120 μHz is needed for the prediction of the analytical model to match the given value of εg at νmax = 60 μHz. Stellar models show that this can be achieved with an adiabatic extent of the convective region of about 0.3H. In reality, such a value of εg at νmax = 60 μHz may result from both effects. Equivalently, we note that the different picture considered for stars close to the transition in Sect. 4.1 requires β⋆(r2, max)∼5 in Eq. (50) (with J(r2, max)≈1) to explain εg = −0.1. In this view, the slope of the Brunt–Väisälä at r2, max plays the same role as the ratio 2πνmax/𝒩b in Eq. (39) and thus may be sensitive at a given value of νmax to overshooting and the migration speed of the base of the convective zone.
The analytical model that was developed therefore supports the gravity offset as a promising source of information on the base of the convective region. Further studies will have to be performed to assess the ability of this parameter to constrain stellar models. Refinement in the analytical model that was developed in this work, fully accounting for instance for a realistic shape of the Brunt–Väisälä frequency, the sharp μ-gradient at the base of the convective region, or a better representation of the evolution of 𝒩b as a function of νmax, will help guide such investigations.
6. Conclusions
In this paper, we addressed from a theoretical point of view the variations in the gravity offset of mixed modes that were observed on the RGB by Mosser et al. (2018). After having properly introduced the notion of gravity offset, we considered the asymptotic analyses of mixed modes by Shibahashi (1979) and Takata (2016a,b) to make the link between the internal properties of stars and the observed values. First, we clearly showed in general terms that this parameter is related to the properties of the boundaries of the buoyancy cavity through the contributions of the phase lags introduced at reflection and of the wavenumber integral in the vicinity of the turning points (i.e., close to r1 and r2). We also demonstrated that its value must remain on the order of unity. Then, by modeling at first approximation the Brunt–Väisälä frequency as a power law of radius between the hydrogen-burning shell and the base of the convective zone, we obtained simplified local asymptotic expressions for the period spacing and gravity offset, denoted with ΔΠ1 and εg, respectively, over a narrow frequency range around νmax. These local asymptotic values were shown to be representative of the observed values. As a result, the observed quantities could be analyzed within the asymptotic framework.
The considered model predicts a constant value for εg close to 0.22 in the first part of the ascent of the RGB. This peculiar value is the result of the power-law behavior of the Brunt-Väisälë frequency between the hydrogen-burning shell and the base of the convective zone, which is a direct consequence of the high density contrast compared to the helium core. At a peculiar instant just before the luminosity bump, it is expected to drop rapidly by a mean value of about 0.2 in the directly following stages. This fall in the value of the gravity offset is a consequence of the kink of the Brunt–Väisälä frequency near the base of the convective region when the outer turning point associated with the buoyancy cavity becomes and remains very close to this latter region during the subsequent evolution on the RGB evolution. Using stellar models, we estimated that this transition must occur around 50 μHz ≲ νmax ≲ 110 μHz for a typical mass range of the observed red giant stars. These predictions are in global agreement with the observed variations. As a result, we conclude that the drop observed in the value of the gravity offset in red giant stars is the signature of the kink of the Brunt–Väisälä frequency at the transition between the radiative and convective regions. The simplified assumptions on the structure of the upper layers of the radiative zone that were considered in the model were checked a posteriori not to modify the conclusions. For more evolved stars, for which the visibility of gravity-dominated mixed modes is too low to be observed, the model predicts a lower limit of −0.25.
The agreement between theoretical predictions and global trend in the observations of the gravity offset validates both the use of the asymptotic expressions to interpret the data and the relevancy of the measurements. We demonstrated that no clear signature of the transition such as that observed in εg is currently expected to be detected in the period spacing and the coupling factor of mixed modes. However, both seismic parameters certainly remains sensitive to this transition. More thorough analyses of the data guided by new theoretical developments will be needed in the future to detect a signature associated with the transition in these parameters. This will provide additional support for the relevancy of the present conclusions regarding εg.
To conclude, this work represents a first step toward a methodic exploitation of the gravity offset for the characterization of red giant stars, and in particular for the study of the region located between the helium core and the base of the convective envelope. The ability of this parameter to probe the profile of the Brunt–Väisälä frequency in this region allows us to constrain the contraction rate of the helium core, the migration of the base of the convective zone, and the efficiency and the extent of the convective boundary mixing in this region. In this work, we showed in particular that accounting for these ingredients tends to improve the agreement between the predictions of the analytical model and the observations. This promising potential calls for further investigations. The next step will directly consist in extending this study to red clump stars. The analysis will have to carefully take into account the presence of a convective core in these central helium-burning stars, which will be subject of a future work.
The quantization condition of mixed modes is provided by Eqs. (15)–(19) of Takata (2016a), where the variable XG is equal to the wavenumber integral over the buoyancy cavity.
The phase lags are defined as the argument of the amplitude ratio of the reflected plane wave to the incident plane wave, which are associated with one given wave dependent variable. In this formulation, the direction of the propagation is determined by that of the propagation of the wave energy, that is of the group velocity.
Unlike a phase loss of −π/2 found by Brekhovskikh (1980), we obtain a phase gain of +π/2 since, in the case of gravity waves, the direction of the propagation of the wave energy is in the opposite direction of the phase velocity (e.g., Unno et al. 1989).
Acknowledgments
C. P. especially thank M.-J. Goupil and K. Belkacem for their fruitful comments on the paper and their unwavering support. The authors also thank the entire Kepler team, whose efforts made these results possible, as well as the anonymous referee whose comments greatly helped improve the final version of the paper. M. T. is grateful to Paris Observatory for the support of his stay at the observatory. During this work, C. P. was partially funded by a postdoctoral research grants from CNRS (France) and from F.R.S.-FNRS (Belgium). M. T. is partially supported by JSPS KAKENHI Grant Number 18K03695. We appreciate the financial support from the Programme National de Physique Stellaire (CNRS/INSU). B. M. acknowledges the support of the International Space Institute (ISSI) for the program AsteroSTEP (Asteroseismology of STEllar Populations).
References
- Abramowitz, M., & Stegun, I. A. 1972, Handbook of Mathematical Functions (New York: Dover) [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baglin, A., Auvergne, M., Barge, P., et al. 2006a, in ESA Special Publication, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, 1306, 33 [Google Scholar]
- Baglin, A., Auvergne, M., Boisnard, L., et al. 2006b, in 36th COSPAR Scientific Assembly, COSPAR Meeting, 36, 3749 [Google Scholar]
- Bedding, T. R., Mosser, B., Huber, D., et al. 2011, Nature, 471, 608 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Belkacem, K., Samadi, R., Mosser, B., Goupil, M. J., & Ludwig, H. G. 2013, in Progress in Physics of the Sun and Stars: A New Era in Helio- and Asteroseismology, eds. H. Shibahashi, & A. E. Lynas-Gray, ASP Conf. Ser., 479, 61 [NASA ADS] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brassard, P., Fontaine, G., Wesemael, F., & Hansen, C. J. 1992, ApJS, 80, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Brekhovskikh, L. M. 1980, Appl. Math. Mech., 16, 161 [CrossRef] [Google Scholar]
- Buysschaert, B., Beck, P. G., Corsaro, E., et al. 2016, A&A, 588, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaplin, W. J., & Miglio, A. 2013, ARA&A, 51, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J. 2015, MNRAS, 453, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Cowling, T. G. 1941, MNRAS, 101, 367 [NASA ADS] [Google Scholar]
- Cunha, M. S., Stello, D., Avelino, P. P., Christensen-Dalsgaard, J., & Townsend, R. H. D. 2015, ApJ, 805, 127 [Google Scholar]
- de Assis Peralta, R., Samadi, R., & Michel, E. 2018, Astron. Nachr., 339, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Deheuvels, S., Doğan, G., Goupil, M. J., et al. 2014, A&A, 564, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Mauro, M. P. 2016, Frontier Research in Astrophysics II, held 23–28 May, 2016 in Mondello (Palermo), Italy (FRAPWS2016), Online at https://pos.sissa.it/cgi-bin/reader/conf.cgi?confid=269, 29 [Google Scholar]
- Dupret, M.-A., Belkacem, K., Samadi, R., et al. 2009, A&A, 506, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehan, C., Mosser, B., Michel, E., Samadi, R., & Kallinger, T. 2018, A&A, 616, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grosjean, M., Dupret, M.-A., Belkacem, K., et al. 2014, A&A, 572, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., & Christensen-Dalsgaard, J. 2017, A&ARv, 25, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., Elsworth, Y., & Angelou, G. C. 2018, A&A, 610, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khan, S., Hall, O. J., Miglio, A., et al. 2018, ApJ, 859, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., Weigert, A., & Weiss, A. 2012, Stellar Structure and Evolution (Berlin, Heidelberg: Springer-Verlag) [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Lagarde, N., Bossini, D., Miglio, A., Vrard, M., & Mosser, B. 2016, MNRAS, 457, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Marques, J. P., Goupil, M. J., Lebreton, Y., et al. 2013, A&A, 549, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miglio, A., Montalbán, J., Noels, A., & Eggenberger, P. 2008, MNRAS, 386, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Montalbán, J., Miglio, A., Noels, A., et al. 2013, ApJ, 766, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Mosser, B., & Miglio, A. 2016, The CoRoT Legacy Book: The Adventure of the Ultra High Precision Photometry from Space, ed. CoRot Team, 197 [Google Scholar]
- Mosser, B., Elsworth, Y., Hekker, S., et al. 2012a, A&A, 537, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012b, A&A, 540, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Michel, E., Belkacem, K., et al. 2013, A&A, 550, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Benomar, O., Belkacem, K., et al. 2014, A&A, 572, L5 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Mosser, B., Pinçon, C., Belkacem, K., Takata, M., & Vrard, M. 2017, A&A, 600, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Gehan, C., Belkacem, K., et al. 2018, A&A, 618, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinçon, C., Belkacem, K., Goupil, M. J., & Marques, J. P. 2017, A&A, 605, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Provost, J., & Berthomieu, G. 1986, A&A, 165, 218 [NASA ADS] [Google Scholar]
- Shibahashi, H. 1979, PASJ, 31, 87 [NASA ADS] [Google Scholar]
- Takata, M. 2006, PASJ, 58, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Takata, M. 2016a, PASJ, 68, 109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takata, M. 2016b, PASJ, 68, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Tassoul, M. 1980, ApJ, 43, 469 [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial Oscillations of Stars (Tokyo: University of Tokyo Press) [Google Scholar]
- Vrard, M., Mosser, B., & Samadi, R. 2016, A&A, 588, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Value of θG in the non-Cowling case
Following Takata (2016a; hereafter T16), the dependent variable Y1 inside the buoyancy cavity is provided by Eqs. (16), (114), and (116) of his paper. The dependent variable Y1 reads in the asymptotic limit
where A(r) is a real slowly varying amplitude. According to Eq. (112) of T16, we can rewrite the phase in the cosine function of Eq. (A.1) such as
where r1 is the innermost turning point. Injecting Eq. (A.2) into Eq. (A.1), we obtain
where the quantity
represents the rapidly varying wave phase that increases with respect to radius. A time dependence of e−iσt is assumed for the oscillation variables in T16 and in this study. Therefore, the first (second) term inside the brackets of Eq. (A.3) corresponds to the progressive (regressive) component. Since the group velocity is in the opposite direction of the phase velocity in the buoyancy cavity, it is related to a downward incident (upward reflected) energy ray. Within the framework of the formulation of mixed modes by Takata (2016b), the phase lag θG at the reflection in r1 for the variable Y1 is thus given by the argument of the ratio of the reflected to the incident wave amplitude in the sense of the group velocity, that is,
In the Cowling approximation, the variable Y1, which is equivalent to the variable v in Shibahashi (1979), takes in contrast the form of an Airy function of the first kind near r1. Following the same reasoning as in the previous paragraphs, we can show that θG = +π/2 in this case (e.g., see discussion in Sect. 3.1).
Appendix B: Evolution of 𝒩b with νmax before the luminosity bump
The parameter 𝒩b represents the value of the modified Brunt–Väisälä frequency just below the base of the convective zone. Its value is well defined only in the ideal case where 𝒩 varies as a power law in the radiative zone and discontinuously drops to about zero at the base of the convective zone, as schematically represented in Fig. 2. However, as mentioned in Sect. 5.2, stellar models suggest that 𝒩 vanishes more progressively at the base of the convective zone so that a clear definition of this parameter can be subject to discussions (e.g., see an attempt of definition in Pinçon et al. 2017). Moreover, the transition from an adiabatic to a radiative temperature gradient at the base of the convective zone, which is related to the profile of 𝒩 in this region, is still subject to uncertainties in stellar modeling. For these reasons, we choose to discuss the variation of this parameter during evolution using orders of magnitude through the proxy 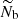 , defined by
, defined by
The evolution of 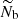 as a function of νmax is plotted in Fig. B.1 for several evolutionary sequences of models with masses between 1 M⊙ and 2 M⊙. Most of these evolutionary sequences were built using the same standard input physics as used to build the 1.2 M⊙ models considered as illustration in Sect. 2.2. Only one of these models, which has a mass of 1.2 M⊙, includes adiabatic overshooting below the convective zone. The thickness of the overshooting region was assumed to be equal to about 0.3H, with H the pressure scale height at the base of the convective zone, which is close to the mean value derived by Khan et al. (2018) to match the observed location of the luminosity bump in low-mass stars. The considered frequency range for νmax correspond to stars between the beginning of the RGB and the luminosity bump. In Fig. B.1, we see that
as a function of νmax is plotted in Fig. B.1 for several evolutionary sequences of models with masses between 1 M⊙ and 2 M⊙. Most of these evolutionary sequences were built using the same standard input physics as used to build the 1.2 M⊙ models considered as illustration in Sect. 2.2. Only one of these models, which has a mass of 1.2 M⊙, includes adiabatic overshooting below the convective zone. The thickness of the overshooting region was assumed to be equal to about 0.3H, with H the pressure scale height at the base of the convective zone, which is close to the mean value derived by Khan et al. (2018) to match the observed location of the luminosity bump in low-mass stars. The considered frequency range for νmax correspond to stars between the beginning of the RGB and the luminosity bump. In Fig. B.1, we see that 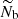 generally increases as νmax decreases at this evolutionary stage, except for a short phase before the luminosity bump (corresponding to the rapid variation visible at low values of νmax in Fig. B.1). Indeed, on the first part of the RGB, the base of the convective zone progressively deepens into the interior of the stars with respect to both the mass and radius coordinates. At a certain stage just before the luminosity bump, it attains a minimum and starts slightly receding. This results in the first dredge-up of the chemical elements (e.g., Kippenhahn et al. 2012). Since
generally increases as νmax decreases at this evolutionary stage, except for a short phase before the luminosity bump (corresponding to the rapid variation visible at low values of νmax in Fig. B.1). Indeed, on the first part of the RGB, the base of the convective zone progressively deepens into the interior of the stars with respect to both the mass and radius coordinates. At a certain stage just before the luminosity bump, it attains a minimum and starts slightly receding. This results in the first dredge-up of the chemical elements (e.g., Kippenhahn et al. 2012). Since 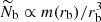 , this parameter is more sensitive to the decrease in rb than in m(rb) and thus increases in the first part of the RGB, as depicted in Fig. B.1. In the short phase just after the convective boundary has attained its minimum and before the luminosity bump,
, this parameter is more sensitive to the decrease in rb than in m(rb) and thus increases in the first part of the RGB, as depicted in Fig. B.1. In the short phase just after the convective boundary has attained its minimum and before the luminosity bump,  decreases so slowly that it can be regarded as constant at first approximation. We also see that the inclusion of an adiabatic overshooting region at the base of the convective region significantly modifies the value of
decreases so slowly that it can be regarded as constant at first approximation. We also see that the inclusion of an adiabatic overshooting region at the base of the convective region significantly modifies the value of  . Indeed, in this case, the radius of the base of the convective region is smaller than without overshooting while its mass coordinate remains about constant, so that
. Indeed, in this case, the radius of the base of the convective region is smaller than without overshooting while its mass coordinate remains about constant, so that  must be higher for the same reasons as before. Nevertheless, we see in Fig. B.1 that the variation rate of
must be higher for the same reasons as before. Nevertheless, we see in Fig. B.1 that the variation rate of  as a function of νmax remains comparable during evolution with or without overshooting. Moreover, we checked by varying the overshooting length that the thicker the overshooting region, the higher
as a function of νmax remains comparable during evolution with or without overshooting. Moreover, we checked by varying the overshooting length that the thicker the overshooting region, the higher 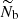 , as expected from the previous arguments.
, as expected from the previous arguments.
 |
Fig. B.1. Evolution of |
In Fig. B.2, we see that 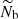 increases more slowly than νmax decreases during evolution. This is because the stellar radius increases more rapidly than rb decreases at these stages. As a result, it is obvious that the ratio
increases more slowly than νmax decreases during evolution. This is because the stellar radius increases more rapidly than rb decreases at these stages. As a result, it is obvious that the ratio 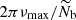 decreases during evolution more slowly than
decreases during evolution more slowly than 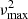 , as assumed in Sect. 4.3.3. Figure B.2 also shows that at a given value of νmax, the higher the mass, the higher this ratio. This confirms the fact the higher the mass, the lower the value of νmax, t at the transition between cases a and b (i.e., when
, as assumed in Sect. 4.3.3. Figure B.2 also shows that at a given value of νmax, the higher the mass, the higher this ratio. This confirms the fact the higher the mass, the lower the value of νmax, t at the transition between cases a and b (i.e., when 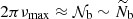 ). Moreover, since the thicker the overshooting region, the higher
). Moreover, since the thicker the overshooting region, the higher 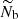 at a given value of νmax, we deduce that the lower the ratio
at a given value of νmax, we deduce that the lower the ratio 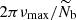 so that the higher the value of νmax, t at the transition, as shown in Fig. B.2.
so that the higher the value of νmax, t at the transition, as shown in Fig. B.2.
 |
Fig. B.2. Same caption as in Fig. B.1 but for the ratio |
In summary, considering that 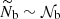 , we conclude the following for stellar masses between 1 M⊙ and 2 M⊙:
, we conclude the following for stellar masses between 1 M⊙ and 2 M⊙:
-
The value of 𝒩b increases at the beginning of the ascent of the RGB until a short phase just before the luminosity bump where it remains about constant.
-
The ratio 2πνmax/𝒩b decreases more slowly than
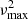 during evolution since the envelope expansion is faster than the migration of the convective boundary toward the center.
during evolution since the envelope expansion is faster than the migration of the convective boundary toward the center. -
The thicker the overshooting region below the convective region or the lower the stellar mass, the higher the values of 𝒩b and of νmax, t.
Appendix C: Seismic properties of the four outliers
The seismic properties of the four outliers depicted in Fig. 4 are summarized in C.1 following the data provided by Mosser et al. (2018).
Seismic properties of the four outliers discussed in Sect. 4.3.3.
All Tables
All Figures
 |
Fig. 1. Profile of the modified Brunt–Väisälä and ℓ = 1 Lamb frequencies (thick solid and dashed lines, respectively) for two 1.2 M⊙ red giant models with νmax ≈ 200 μHz (blue) and νmax ≈ 60 μHz (red). These both models correspond to stars at the beginning of the ascent of the RGB and at a point just before the luminosity bump, respectively. The usual Brunt–Väisälä and ℓ = 1 Lamb frequencies, N and S1, are represented by the light thin solid and dashed lines, respectively. The vertical dash-dotted lines indicate the hydrogen-burning shell and the horizontal strip symbolizes a typical 6Δν-wide observed frequency range around νmax, for each model with the corresponding color. The buoyancy and acoustic cavities for a mode of frequency ν are located where 2πν ≤ (𝒩 and 𝒮1) and 2πν ≥ (𝒩 and 𝒮1), respectively. |
| In the text | |
 |
Fig. 2. Schematic view of the modified Brunt–Väisälä frequency as a function of radius on a logarithmic scale, as assumed by the simple model presented in Sect. 4.1. The horizontal dashed line indicates the value 𝒩b just below the base of the convective zone at radius rb. The radius |
| In the text | |
 |
Fig. 3. Local asymptotic value of the gravity offset according to the model considered in Sect. 4.1. It was computed via Eq. (32) in case a (blue) and Eq. (39) in case b (red). The cases a and b are defined in Sect. 4.1. It is shown as a function of the ratio 2πνmax/𝒩b, where 𝒩b is the value of the (modified) Brunt–Väisälä frequency just below the base of the convective zone. Stellar evolution goes from the right to the left. |
| In the text | |
 |
Fig. 4. Observed values of the gravity offset adapted from Mosser et al. (2018) as a function of νmax in RGB stars (+ symbols). The color code indicates the seismic mass computed following Mosser et al. (2013). The error bars are also represented for each data point. The horizontal magenta dashed line corresponds to the asymptotic value expected from Eq. (32) for RGB stars in case a and in the low coupling hypothesis (see Sect. 4.1 for the definition of the cases a and b). This value is included in the dark gray rectangle that corresponds to the values predicted by Takata (2016a), considering typical structures of stars in the early RGB phase (see Sect. 5.2). The clear gray domain represents the asymptotic prediction that is expected from Eq. (39) for RGB stars in case b. Guided by stellar models, the transition is assumed to occur between νmax ≈ 50 μHz (red solid line) and νmax ≈ 110 μHz (blue solid line), depending on stellar mass (see main text). The prediction of the analytical model is plotted as a function of νmax by assuming that the parameter 𝒩b in Eq. (39) is constant. The black solid line shows the prediction for a transition at νmax = 130 μHz. In contrast, the clear blue domain corresponds the prediction for a value at the transition of νmax, t = 110 μHz, assuming that |
| In the text | |
 |
Fig. B.1. Evolution of |
| In the text | |
 |
Fig. B.2. Same caption as in Fig. B.1 but for the ratio |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



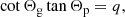
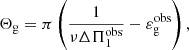
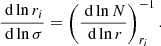
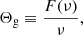
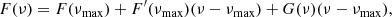
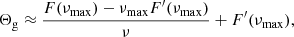
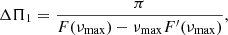
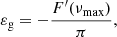
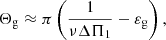
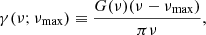
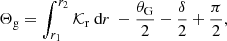
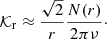
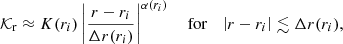
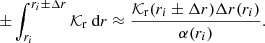
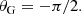
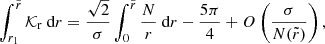
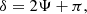
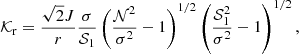
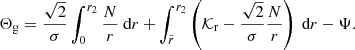
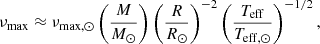
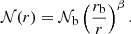
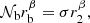
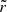
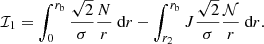
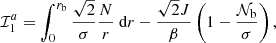
![$$ \begin{aligned} \mathcal{I} _2\approx \int _{\tilde{r}}^{r_2} \sqrt{2} J \left[ \left(\frac{\mathcal{N} ^2}{\sigma ^2}-1 \right)^{1/2}-\frac{\mathcal{N} }{\sigma }\right] \frac{\text{ d}r}{r} \cdot \end{aligned} $$](/articles/aa/full_html/2019/06/aa35327-19/aa35327-19-eq45.gif)
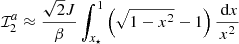
![$$ \begin{aligned}&= \frac{\sqrt{2} J}{\beta } \left[ 1-\frac{\pi }{2}+O\left(x_\star \right)\right] , \end{aligned} $$](/articles/aa/full_html/2019/06/aa35327-19/aa35327-19-eq47.gif)
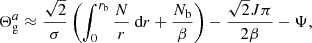
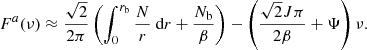
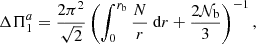
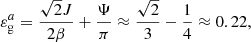
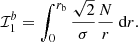
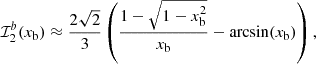
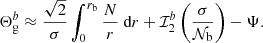
![$$ \begin{aligned} F^b(\nu ) \approx \frac{\sqrt{2}}{ 2\pi } \left(\int _{0}^{r_{\rm b}} \frac{N}{r} \text{ d}r \right) + \frac{\mathcal{N} _{\rm b}}{2\pi } \left[ \mathcal{I} _2^b(x_{\rm b})- \Psi \right] x_{\rm b} . \end{aligned} $$](/articles/aa/full_html/2019/06/aa35327-19/aa35327-19-eq60.gif)
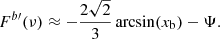
![$$ \begin{aligned} \Delta \Pi _1^b = \frac{2 \pi ^2}{ \sqrt{2}}\left[\int _{0}^{r_{\rm b}} \frac{N}{r} \text{ d}r + \frac{2 \mathcal{N} _{\rm b}}{3} \left(1-\sqrt{1-\left(\frac{2\pi \nu _{\rm max}}{\mathcal{N} _{\rm b}}\right)^2}~\right)\right]^{-1} , \end{aligned} $$](/articles/aa/full_html/2019/06/aa35327-19/aa35327-19-eq62.gif)
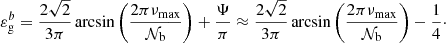
![$$ \begin{aligned} \gamma (\nu ;\nu _{\rm max})&\approx \frac{1}{\pi } \left[\mathcal{I} _2^b\left(x_{\rm b}\right)-\mathcal{I} _2^b\left(x_{\mathrm{b,max}}\right) \right]\nonumber \\&\quad +\frac{2 \sqrt{2} }{3 \pi }\left(\sqrt{1-x_{\mathrm{b,max}}^2}~-1\right)\left(\frac{1}{x_{\rm b}}-\frac{1}{x_{\mathrm{b,max}}}\right) , \end{aligned} $$](/articles/aa/full_html/2019/06/aa35327-19/aa35327-19-eq64.gif)
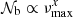
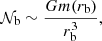
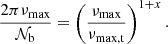
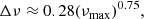
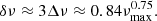
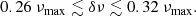
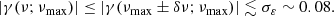
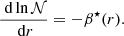
![$$ \begin{aligned} \mathcal{I} _1 \approx \frac{\sqrt{2}}{\sigma }\left[\int _{0}^{r_{2,\mathrm{max}}} \frac{N}{r} \text{ d}r + \frac{2\pi \nu _{\rm max}J(r_{2,\mathrm{max}})}{\beta ^\star (r_{2,\mathrm{max}})}\right] - \frac{\sqrt{2}J(r_{2,\mathrm{max}})}{\beta ^\star (r_{2,\mathrm{max}})} , \end{aligned} $$](/articles/aa/full_html/2019/06/aa35327-19/aa35327-19-eq90.gif)
![$$ \begin{aligned} \mathcal{I} _2 \approx \frac{\sqrt{2} J(r_{2,\mathrm{max}})}{\beta ^\star (r_{2,\mathrm{max}})} \left[ 1-\frac{\pi }{2}\right] , \end{aligned} $$](/articles/aa/full_html/2019/06/aa35327-19/aa35327-19-eq91.gif)
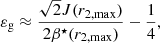
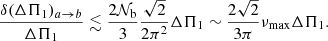
![$$ \begin{aligned} \left[\frac{\text{ d} \Phi _{\rm in}}{\text{ d} r}-\frac{\text{ d} \Phi _{\rm out}}{\text{ d} r} \right]_{r_\star } = A_\star k_{\rm r}^2(r_\star ) \Phi _{\rm in}(r_\star ) \approx 0 , \end{aligned} $$](/articles/aa/full_html/2019/06/aa35327-19/aa35327-19-eq95.gif)