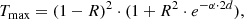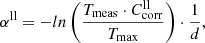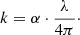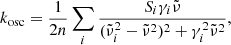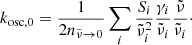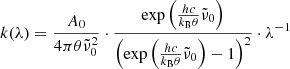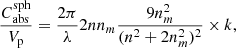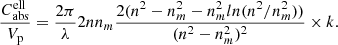| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 13 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201834805 | |
| Published online | 13 May 2019 | |
Far-infrared continuum absorption of forsterite and enstatite at low temperatures
Friedrich-Schiller-University Jena, Astrophysical Institute and University Observatory, Schillergaesschen 2-3, 07745 Jena, Germany
e-mail: harald.mutschke@uni-jena.de
Received:
10
December
2018
Accepted:
19
March
2019
Context. The far-infrared continuum opacity of cold dust is an important quantity for the study of debris disks in planetary systems and of protoplanetary disks. Forsterite and enstatite are considered to be the most abundant crystalline dust species in such environments.
Aims. The optical constants of these minerals at wavelengths above 80 μm, which govern the opacity, and their temperature dependence are poorly known. Our aim is to fill in this lack of information with new laboratory data.
Methods. We present spectroscopic transmission measurements on forsterite and enstatite single crystals of up to 10 mm thickness at wavelengths between 45 and 500 μm and for temperatures down to 10 K. We compare our results to literature data originating from powder transmission and from reflection spectroscopy.
Results. The imaginary parts of the refractive indices calculated from the measurements show very strong temperature dependences, which to that extent are not seen in reflection-based data or in powder measurement data. The temperature dependences can be described by a simple theoretical model taking the contributions of single-phonon absorption and phonon difference processes into account. We also observe, for the first time, enstatite absorption bands at 87.5 μm and 116.6 μm wavelengths.
Conclusions. The single-crystal optical constants of forsterite and enstatite predict an extremely small submillimeter opacity of crystalline silicate dust at low temperatures, which would make these particles almost invisible in the thermal radiation of cold dust. Thus, it is important to understand why absorption measurements with mineral powders resulted in much higher opacity values.
Key words: methods: laboratory: solid state / techniques: spectroscopic / opacity / solid state: refractory / circumstellar matter / dust, extinction
© ESO 2019
1. Introduction
Observations at far-infrared and submillimeter wavelengths are an important tool for the study of cold dusty astronomical objects such as interstellar clouds, protoplanetary disks, and debris disks in planetary systems. The observed wavelength-dependent flux can be converted into dust masses, temperatures, and spatial distributions if the dust opacity is known in the wavelength ranges of the absorbed stellar radiation and of the thermal dust emission (e.g., Krivov et al. 2008). In both these spectral regions, the visible/near-infrared and the far-infrared/submillimeter, the opacity is often determined by relatively weak continuum absorption since the frequencies are outside of the ranges of strong spectral resonances (UV, mid-infrared), at least for insulating solids.
In most astrophysical objects, the bulk of the dust consists of silicate particles. While these silicates are mostly non-crystalline (amorphous) in interstellar space, crystalline silicates play an important role in stellar environments. Among these minerals, the Mg-rich olivine and orthopyroxene minerals forsterite (Mg2SiO4) and enstatite (MgSiO3) are thought to be the most abundant. Because of their high thermal stability, forsterite and enstatite are predicted to be the first silicates that condense from a cooling gas of solar composition (Gail et al. 2003). Thus, it is not surprising that their spectral signatures were found to dominate the infrared spectra of stellar outflows (in addition to amorphous silicates, e.g., Molster et al. 2002) and protoplanetary disks (Juhász et al. 2010). Forsterite and enstatite are also abundant in primitive solar system materials, such as cometary dust (Bradley et al. 2003) and chondrules in meteorites. Thus, they can also be expected to occur in debris disks of extrasolar planetary systems, although olivines with a higher iron content have been shown to occur in transient dust in several of these systems (Olofsson et al. 2012).
In the wavelength range around 70 μm, both forsterite and enstatite have lattice vibration bands, which were expected to show up in the emission spectra of cold dust, for example in protoplanetary disks. The search for them with the Herschel space telescope has led to a number of detections of the 69 μm forsterite vibration band (e.g., Sturm et al. 2010; de Vries et al. 2012). These detections proved the Mg-richness of at least a significant fraction of the olivine minerals in the respective objects since the wavelength position of this band is strongly composition sensitive (Sturm et al. 2013). Enstatite bands have unfortunately not been detected in Herschel spectra. The interpretation of all these observations was supported by dedicated laboratory work where the dependence of infrared band positions, widths, and strengths on composition, grain size, grain shape, temperature, and structural perfectness has been investigated (e.g., Koike et al. 2006, and references therein). Laboratory results on the forsterite 49 μm and 69 μm bands, for instance, made their widths and positions usable as a dust thermometer (Chihara et al. 2001; Bowey et al. 2002; Suto et al. 2006). Most of these laboratory measurements have been performed on powdered minerals. In a few cases, the complex refractive index at low temperatures was also determined by reflection measurements on polished crystals (Suto et al. 2006; Demichelis et al. 2012; Zeidler et al. 2015).
Similarly, a number of laboratory studies have been undertaken to determine the continuum absorption coefficient of amorphous and crystalline silicates in the visible (e.g., Zeidler et al. 2011; Pitman et al. 2013) and in the far-infrared/submillimeter spectral ranges (Mennella et al. 1998; Chihara et al. 2001; Boudet et al. 2005; Coupeaud et al. 2011; Mutschke et al. 2013; Demyk et al. 2017a,b). Studying the latter is especially demanding, since most of the physical absorption mechanisms relevant at these low photon energies show a strong temperature dependence. Amorphous silicates have been quite comprehensively studied in this respect. The relatively large differences found between the absorptivities of different amorphous samples can probably be understood as a consequence of the variability of stoichiometries and disorder (e.g., Demyk et al. 2017a). For olivine and pyroxene minerals the situation is different since the crystal structures are well defined. The far-infrared continuum absorption of crystals should be determined by contributions from single phonons, i.e., the long-wavelength wings of the infrared bands, and from phonon difference processes, i.e., the excitation of a higher energy lattice vibration at the cost of the photon energy plus de-excitation of a lower energy vibration (Hadni et al. 1970; Mishima et al. 1983; Henning & Mutschke 1997). Both absorption processes are expected to be strongly temperature dependent, the former because of narrowing of the bands towards low temperature, the latter due to the gradual disappearance of the required low-energy lattice vibrations.
Temperature-dependent data for olivine powders embedded in polyethylene pellets were measured by Mennella et al. (1998, for iron-poor olivine, Mg1.8Fe0.2SiO4, and for fayalite, Mg0.12Fe1.88SiO4) and by Chihara et al. (2001, for forsterite, Mg2SiO4). While Chihara et al. (2001) covered the wavelength range up to 100 μm (∼70 μm at temperature θ = 4.2 K), the measurements by Mennella et al. (1998) extend to 2 mm in wavelength (down to θ = 24 K). Both of these works find a steepening of the wavelength-dependent absorption decay at low temperatures. The absolute values of the mass absorption coefficient at low temperature, however, differ significantly, i.e., they are higher by more than one order of magnitude (at λ = 100 μm) in the Mennella et al. results. On the other hand, Mutschke et al. (2013) measured an olivine powder (Mg1.84Fe0.16SiO4, sample originally prepared by Imai et al. 2009) similar to that measured by Mennella et al. (1998) at θ = 10 K and found values closer to those measured by Chihara et al. (2001). Furthermore, Coupeaud et al. (2011) measured samples of originally amorphous silicates, which have been crystallized at high temperature. In contrast to the results of the other authors, they do not find any temperature dependence of the mass absorption coefficient. Their absorption values are comparable to those by Mennella et al. (1998); however, their materials contain a large portion of other crystallization products such as periclase (MgO).
Mutschke et al. (2013) presented the first low-temperature transmission measurements on an olivine single crystal (Mg1.78Fe0.22SiO4) in the 100 μm wavelength range and found a continuum absorption, which was again an order of magnitude lower (at θ = 10 K) than the lowest values measured on powders. The difference between the room temperature and the 10 K absorption amounted to more than one order of magnitude, but also at room temperature the values were a factor of 3.7 lower than those measured with the olivine powder. It was found that the 10 K values coincided roughly with the predictions from optical constants measured by reflection spectroscopy of forsterite (Suto et al. 2006), i.e., to continuum absorption values which derive from the wings of the Lorentzian band profiles. The large difference between far-IR absorption coefficients measured on powders and those calculated from such optical constants had been noted previously by Fabian et al. (2001) and Sogawa et al. (2006).
For pyroxene minerals, there is less information about their low-temperature absorption coefficient at far-infrared wavelengths. Chihara et al. (2001) measured far-infrared spectra at room-temperature and at liquid helium temperature of synthetic ortho- and clinoenstatite (MgSiO3), and of diopside (CaMgSi2O6) powders up to a wavelength of 100 μm. For orthoenstatite, the behavior of the continuum absorption with temperature and the absorption values are comparable to those of their forsterite; for the other two materials it could be similar, as far as the continuum is recognizable beneath the phonon bands in the 60–75 μm wavelength region. A detailed analysis of these phonon bands for orthoenstatite was carried out by Demichelis et al. (2012). While their reflection spectra, measured at θ = 60 K with a synthetic crystal, extend to about 100 μm in wavelength, they also present positions and oscillator strengths derived by ab initio calculations, which cover some additional bands at long wavelengths (up to 115 μm) that were not detected in the measurements. Unfortunately, they do not present the full set of oscillator parameters. However, for bands up to the 50 μm wavelength range, these values are available from the measurements by Zeidler et al. (2015) on a natural enstatite crystal, e.g., at temperatures of 10 K and 100 K. Thus, an estimate of the continuum absorption produced by the band wings can be calculated from a combination of these data, but it is currently unknown how this corresponds to the powder data.
Some important questions arise from the situation discussed above:
1. Up to what wavelengths and temperatures do the long-wavelength wings of single-phonon infrared bands determine the continuum absorption coefficient of crystalline silicates? How strong are the contributions from phonon difference processes at relevant temperatures?
2. Are mass absorption coefficients that are measured on single crystals systematically lower than those measured on powders? Is the higher absorption of powder samples a result of grain morphology and lattice distortion (see Imai et al. 2009) or of scattering losses (Fabian et al. 2001)?
Finding answers for these questions will be important for clarifying the contribution of crystalline silicates to the thermal emission of cold dust, in particular in (proto-)planetary systems.
In order to strengthen the experimental basis for the case of single crystals, we present in this paper laboratory measurements of the absorption coefficient of single-crystal forsterite and orthopyroxene at temperatures down to 10 K. The goal of these measurements is to provide data for individual crystal axes, and for a synthetic sample (forsterite) that can be compared to the previously measured natural olivine. The far-infrared absorption of natural orthoenstatite is measured for the first time in single-crystal form. The above questions are extensively discussed by comparing our results to both powder absorption data and reflection-based data and to a simple model of the two physical absorption components.
2. Experiment
2.1. Samples
We used a synthetic forsterite single crystal of cubic shape with 10 mm long edges, manufactured by Oxide Corporation, which was kindly provided by Prof. Dr. H. Zacharias, Institute of Physics, University of Münster. The crystal was clear without color, but with a considerable number of small internal bubbles. The crystal surfaces were cut perpendicular to the main crystallographic directions, i.e., [100], [010], and [001]. The orientation of the crystal surfaces was checked by infrared reflection spectroscopy with polarized radiation. The infrared spectra showed good agreement with previous measurements (Sogawa et al. 2006; Suto et al. 2006) and there was no indication of surface misorientation. X-ray photoelectron spectra showed no features attributable to Fe (Suhasaria et al. 2015).
For the measurements on enstatite, we used plates of different thicknesses from two natural single crystals. One of them, originating from Burma, had already been used by Zeidler et al. (2015) for reflection spectroscopy and, as described there, a smaller piece with approximate dimensions 10 × 5 × 5 mm had been cut from the crystal. While the crystallographic c-axis is parallel to one of the larger surfaces of this piece, the orientations of the other axes are undefined for this surface. Therefore, we named this sample E(nstatite)B(urma)[xx0], according to the only partly known direction of the surface normal. As was done in Zeidler et al. (2015), we used this sample for measurements with polarization parallel to the c-axis (hereafter c-polarization). The thickness of this piece, after polishing the rear side, was within (4.01 ± 0.03 mm) over the entire plate. From the bigger piece described by Zeidler et al. (2015), which had a polished surface in the a,b-plane (dimensions 10 × 5 mm), we cut a 5 mm thick plate parallel to this surface. After polishing the rear side, it had a thickness of (5.02 ± 0.04 mm). This sample is denoted EB[001] and was used for measurements in a- and b-polarization. This crystal has the stoichiometry Mg0.92Fe0.09SiO3, as found by energy-dispersive X-ray analysis (Zeidler et al. 2015).
In addition, thinner plates of a different enstatite crystal originating from Kilosa District, Morogoro Region, Tanzania, have been prepared at the Institute of Mineralogy, University of Jena. The stoichiometry of this enstatite is MgFe0.1SiO2.9. The two plates, which had been used for the transmission spectroscopy, were cut perpendicular to the a and b crystallographic axes, respectively, and polished to a thickness of 0.6 mm, at lateral dimensions of approximately 10 × 8 mm. These samples are denoted E(nstatite)K(ilosa)[100] and EK[010], respectively.
2.2. Transmission spectroscopy
We used a Bruker 113v Fourier transform infrared (FTIR) spectrometer with Mylar beam splitters, a mercury discharge lamp as the light source, and a deuterated tri-glycine sulfate (DTGS) detector for the measurements. The samples were mounted inside a double-walled liquid helium cooled cryostat (CryoVac Konti Spectro B) with polyethylene windows, which was placed in the spectrometer’s sample chamber. The sample mount allows the user to switch between the sample and an empty reference channel. Both channels were equipped with diaphragms of identical aperture (5 mm). The samples were cooled by helium contact gas transferring heat to the cold sample chamber walls, which ensures uniform cooling of the sample from all sides.
Polarized radiation was produced by a wire-grid polarizer (carrier material polyethylene, degree of polarization >98%) placed in front of the cryostat entrance window. The orientation of the polarizer with respect to the crystallographic axes of the sample was controlled by observing infrared reflection spectra of the mounted samples and minimizing the bands designating unwanted crystal-axis contributions. Using this method, the polarizer is aligned to the desired crystal axis with a precision of about ±3 degrees.
Transmission measurements were typically started at a sample temperature of 300 ± 2 K; additional measurements were taken at 200 K, 150 K, 100 K, 75 K, 50 K, and 10 K during cooling-down of the sample. For each measurement, the sample temperature was stabilized to about ±1 K accuracy, before reference and sample spectra were taken with 64 scans of the FTIR spectrometer each. Depending on the transparency of the samples, which varied strongly with the temperature, measurements in up to three spectral ranges of the FTIR instrument (defined by the use of different beam splitters) were performed during a single temperature step, i.e., 650–150 cm−1, 220–50 cm−1, and 120–20 cm−1. These spectra generally showed a good overlap (better than 1% of the transmission) and were merged to obtain spectra covering the full spectral range of interest.
3. Results
3.1. Forsterite transmission spectra
The transmission of the forsterite crystal was measured with the beam direction parallel to each of the three crystallographic axes. In two of the three orientations (beam along the [010] and [001]-axes) the measurements were performed with both of the possible polarization directions (measurements denoted F[010]a for a-polarization, F[010]c for c-polarization, and so forth); in the third orientation, only one polarization direction was measured (F[100]c). For some of the polarization directions, spectra were recorded only for selected temperatures, i.e., series F[010]c consists only of spectra for 10 K, 50 K, and 300 K, while series F[001]a lacks a 10 K spectrum.
Figure 1 shows the measured transmission spectra (Tmeas, solid and dashed lines) plotted over the wavenumber (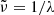 in cm−1); the corresponding wavelengths (30 μm–500 μm) can be inferred from the upper axes. Spectra for a-polarization are given in panel (a), b-polarization in (b), c-polarization in (c). The two incomplete series F[001]a and F[010]c are plotted as dashed lines. The former has been scaled by a factor of 1.8 in order to demonstrate the good agreement to series F[010]a after multiplicative scaling (see Sect. 3.2).
in cm−1); the corresponding wavelengths (30 μm–500 μm) can be inferred from the upper axes. Spectra for a-polarization are given in panel (a), b-polarization in (b), c-polarization in (c). The two incomplete series F[001]a and F[010]c are plotted as dashed lines. The former has been scaled by a factor of 1.8 in order to demonstrate the good agreement to series F[010]a after multiplicative scaling (see Sect. 3.2).
The strong temperature dependence of the transmission of the forsterite crystal is easily recognizable in all three polarization directions. While measurable transmission is detected only below 50 cm−1 at room temperature, the crystal becomes transparent already below 250 cm−1 at 10 K. For each temperature, the transmission increases towards smaller wavenumbers, apart from absorption bands positioned at 202 cm−1 (particularly strong in a-polarization, but weaker also in c-polarization) and 145 cm−1 (in b-polarization, very weak in a- and c-polarization). These bands are the already mentioned 49 μm and 69 μm single-phonon bands of forsterite, respectively. They are excited exclusively by a- and b-polarized radiation, respectively, the weaker appearances in other polarization directions are due to the small error of the polarizer alignment and to the beam divergence of the FTIR spectrometer (±7.5 deg).
Apart from these bands, a relatively weak minimum at ∼90 cm−1 also appears in several of the spectra for a-polarization. As there is no such long-wavelength infrared band predicted by theory (Iishi 1978) and the band is not present at 10 K, we think that it is an artifact of the measurement setup. We note that the position of the band is one of the intensity minima created by multiple reflection in the inner cryostat windows. These minima occurring with a period of 18 cm−1 are sometimes not well compensated by the reference measurements and lead either to periodic structures in the spectrum (e.g., in the 10 K and 50 K spectra in Fig. 1b), or coincide for unknown reasons with erratic peaks (mainly maxima) in the enstatite spectra (see Sect. 3.3).
 |
Fig. 1. Temperature-dependent transmission spectra of the forsterite crystal for orientation of the electric field parallel to the a-axis (panel a), b-axis (panel b), and c-axis (panel c). Complete temperature series (F[010]a, F[001]b, F[100]c) are plotted as solid lines, the two incomplete series as dashed lines. The F[001]a curves have been scaled by a factor of 1.8; they approximately match the F[010]a curves for the same temperatures. Dotted lines: calculated maximum transmission curves taking into account the intensity reflected by the crystal surfaces. |
3.2. Maximum transmission curves and measurement errors
The dotted lines in Fig. 1 indicate the theoretical maximum transmission curves 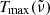 for each measurement, which are defined by the loss of intensity due to reflection at the crystal surfaces. These curves have been calculated from the optical constants by Suto et al. (2006) as
for each measurement, which are defined by the loss of intensity due to reflection at the crystal surfaces. These curves have been calculated from the optical constants by Suto et al. (2006) as
where R is the reflectivity (normal incidence) at a crystal surface calculated from the optical constants, d the sample thickness, and α the linear absorption coefficient. For θ = 10 K, the 50 K data by Suto et al. (2006) have been used, for θ = 75 K the 100 K data. The expression R2 ⋅ exp(−α ⋅ 2d) takes a first-order contribution from internally reflected radiation into account, which becomes significant at reasonable transparency of the crystal. For this calculation, the term exp(−α ⋅ 2d) can be approximated with sufficient accuracy by (Tmeas/(1 − R)2)2.
It is evident, that the measured transmission spectra reach maximum values, which are partly higher than the calculated limit (by about 20%) and partly considerably lower (by up to 33%). The former case happened exclusively at measurements with the beam in [010] direction (Figs. 1a,c), while the latter is mainly associated with the [001] direction (Figs. 1a,b; we note that without scaling series F[001]a would have maximum values 33% below the theoretical curves). The disagreement among the spectra measured with the same polarization direction and the excess over the theoretical limit both indicate strong errors in the measured absolute transmission values. Similar errors were already noted by Mutschke et al. (2013) and were mainly assigned to the displacement of the beam by refraction at the sample surfaces. For the very thick samples used here, and the complicated optical path with four partly bent cryostat windows, such beam displacements can influence the detected signal significantly. Transmission values apparently above the physical limits could be due to a beam misalignment in the reference measurements, caused by the windows. Beam refraction by the sample can then increase the intensity at the detector above the reference level. In the measurements with the 5 mm thick enstatite sample (see next section), we find this effect again and with a similar magnitude. We checked that room temperature spectra measured without cryostat are consistent with this view, i.e., showed lower transmission values that were in agreement with the physical limits. Unfortunately, the room temperature data are not suitable for a precise correction of these errors because of the narrow transparency range and the strong noise in the corresponding spectral region.
For the data showing a strongly reduced transmission, it is conceivable that the transmission through the crystal was influenced by scattering losses caused by the internal bubbles. As these were not homogeneously distributed within the crystal, they affected the measurements mainly in the [001] orientation. For both of these error sources, scattering losses and refraction losses, it can be expected that they cause spectrally flat errors, i.e., loss of a fixed percentage of the beam intensity. The spectra measured with the same polarization and at the same temperature, but with different beam direction, can indeed be transferred into each other by applying the same constant factor for all temperatures, as is demonstrated in Fig. 1a. Unfortunately, it cannot be decided from our data by what factor the errors would be eliminated because the absorption in the sample cannot be easily distinguished from the errors.
The flattening of the low-temperature spectra (especially the 10 K spectra) at small wavenumbers towards a slope close to that of the theoretical curves might indicate, however, that the correct transmission curves are approaching these limits, in which case the absorption by the sample would be very low. We take this assumption for producing lower limit absorption spectra; i.e., we multiply each temperature series (see Sect. 3.4) with a correction factor 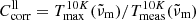 , where the transmission values taken at the wavenumber
, where the transmission values taken at the wavenumber 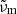 with the highest Tmeas value in the spectrum measured at θ = 10 K. These correction factors are the same for the measurements with the same sample orientation and range between 0.83 and 1.50 (see Table 1). To estimate the upper limits of absorption we take for the moment
with the highest Tmeas value in the spectrum measured at θ = 10 K. These correction factors are the same for the measurements with the same sample orientation and range between 0.83 and 1.50 (see Table 1). To estimate the upper limits of absorption we take for the moment 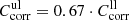 , assuming that the absorption of the forsterite would be at most as high as the losses measured with the F[001] spectra, which reach only 67% of the theoretical maximum transmission. We show in Sect. 3.4 that this error range can be reduced by physical arguments. Moreover, because of these and other errors, e.g., noise and fringes, we take transmission values of 5% below the maximum transmission and 2% above zero as the limits of detectable absorption for all our measurements.
, assuming that the absorption of the forsterite would be at most as high as the losses measured with the F[001] spectra, which reach only 67% of the theoretical maximum transmission. We show in Sect. 3.4 that this error range can be reduced by physical arguments. Moreover, because of these and other errors, e.g., noise and fringes, we take transmission values of 5% below the maximum transmission and 2% above zero as the limits of detectable absorption for all our measurements.
Correction factors for lower and upper limit absorption 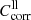 and
and 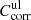 applied to the transmission spectra (Eq. (2)), maximum error values Δα, and usable range of the linear absorption coefficient α for the individual measurements of forsterite (F[100], F[010], F[001]) and enstatite (EB[xx0], EB[001], EK[100], EK[010]).
applied to the transmission spectra (Eq. (2)), maximum error values Δα, and usable range of the linear absorption coefficient α for the individual measurements of forsterite (F[100], F[010], F[001]) and enstatite (EB[xx0], EB[001], EK[100], EK[010]).
3.3. Enstatite transmission spectra
The transmission of the thick enstatite samples (enstatite Burma) was measured for a- and b-polarization with the 5 mm thick sample (EB[001]a, and b) and for c-polarization with the 4 mm thick sample (EB[xx0]c). A coarser grid of sample temperatures (300 K, 200 K, 100 K, and 10 K) than for forsterite was chosen for the enstatite measurements because the major changes in the spectra already occurred above 100 K. The transmission spectra are shown in Figs. 2a–c as the dashed lines. The onset of transparency shifts with these samples from 50–90 cm−1 at θ = 300 K to 100–120 cm−1 for θ = 10 K, the higher values occurring with the 4 mm thick sample. Generally, the transparency range at low temperatures does not extend to wavenumbers as high as for the forsterite (we note the different wavenumber scales in Fig. 1 and Fig. 2) despite the smaller sample thickness. The spectra of the 5 mm thick EB[001] sample in a- and b-polarization, measured at low temperatures, exceed the theoretical maximum transmission limits by up to 20%. Here, the considerations about errors by beam displacement presented in Sect. 3.2. apply again. Thus, similar to the forsterite case, we correct the EB[001]a,b spectra by multiplying with a constant factor 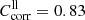 in order to calculate lower limit absorption spectra (see Sect. 3.4). For EB[xx0]c, the original spectra can be used to calculate the lower limit absorption (
in order to calculate lower limit absorption spectra (see Sect. 3.4). For EB[xx0]c, the original spectra can be used to calculate the lower limit absorption (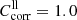 ). For the upper limits, we estimate for both cases
). For the upper limits, we estimate for both cases 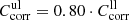 , i.e., slightly higher absorption than the detected loss in any measured low-temperature spectrum at low wavenumber.
, i.e., slightly higher absorption than the detected loss in any measured low-temperature spectrum at low wavenumber.
 |
Fig. 2. Same as Fig. 1, but for enstatite (temperatures only 300 K, 200 K, 100 K, 10 K). The solid and the dash-dotted lines (the latter only in panel c) are the transmission spectra of the 0.6 mm thick enstatite slabs, while the dashed lines are the transmission spectra measured on the 5 mm and 4 mm samples (the latter for the c-polarization). Dotted lines: calculated maximum transmission curves taking the reflection at the crystal surfaces into account. |
For the thin enstatite samples (enstatite Kilosa), the transmission in a- and c-polarization was measured with the sample cut perpendicular to the [010] axis (EK[010]a,c) and the transmission in b- and c-polarization with the sample cut perpendicular to the a-axis (EK[100]b,c). Series EK[100]c contains only spectra for 300 K and 200 K, which are plotted as dash-dotted lines in Fig. 2c, while all other spectra of the thinner samples are plotted as solid lines. With these spectra, the wavenumber range with non-zero transmission is extended to 130–150 cm−1. At small wavenumbers, the transmission spectra of the thin plates approach the curves of the calculated theoretical limits (dotted lines; see previous section for the formula and Sect. 4.2 for the optical constants used). However, for the EK[100] data the approach is not as close as for the EK[010] data, as clearly indicated by the direct comparison in Fig. 2c. The discrepancy between the two spectra amounts to roughly 10% in transmission. Thus, we estimate 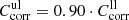 with
with 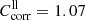 for EK[100] and
for EK[100] and 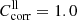 for EK[010].
for EK[010].
The spectra also show absorption bands at about 86 cm−1 in a-polarization (also seen for the thicker samples) and at about 114 cm−1 in b-polarization. These two bands had been predicted by the ab initio calculations by Demichelis et al. (2012), but to our knowledge here they are being experimentally confirmed for the first time. Other structures appearing in the spectra are, on the one hand, narrow fringes (period ∼3.0 cm−1) originating from multiple reflection in the thin samples and, on the other hand, a number of strong peaks (maxima at ∼72 cm−1 and ∼56 cm−1) in a few of the spectra, which are clearly artifacts. As already noted (Sect. 3.1), they appear at wavenumbers, where multiple reflection in the cryostat windows causes weak beam intensity and must be due to strong noise or incomplete compensation of these spectral features of the setup. We exclude the corresponding narrow spectral ranges from further data evaluation.
3.4. Absorption coefficient spectra
Spectra of the linear absorption coefficient of our forsterite and enstatite samples at different temperatures are calculated from the measured sample transmission Tmeas(λ) after multiplication with the lower and upper limit correction factors 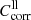 and
and 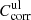 discussed in Sects. 3.2 and 3.3 and summarized in Table 1. For the spectral variable, we switch from
discussed in Sects. 3.2 and 3.3 and summarized in Table 1. For the spectral variable, we switch from 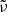 to
to 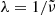 . According to the Lambert-Beer law, the lower limit absorption coefficient, e.g., is calculated as
. According to the Lambert-Beer law, the lower limit absorption coefficient, e.g., is calculated as
while for the upper limit 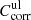 has to be used. The wavelength- and temperature-independent difference
has to be used. The wavelength- and temperature-independent difference 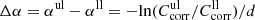 is the uncertainty of the absorption coefficient resulting from possible beam displacement and scattering in the measurement and is also given in Table 1. For most samples with the exception of the thin enstatite slabs, it is of the order of 0.5 cm−1. In addition, Table 1 lists the maximum range of linear absorption coefficients that we consider detectable by the respective measurements due to noise and fringes, i.e., corresponding to a sample transmission between 2% and 95% of Tmax (Sect. 3.2). All absorption spectra are (approximately) restricted to these ranges in the following, unless they are even further limited by the exclusion of noted artifacts.
is the uncertainty of the absorption coefficient resulting from possible beam displacement and scattering in the measurement and is also given in Table 1. For most samples with the exception of the thin enstatite slabs, it is of the order of 0.5 cm−1. In addition, Table 1 lists the maximum range of linear absorption coefficients that we consider detectable by the respective measurements due to noise and fringes, i.e., corresponding to a sample transmission between 2% and 95% of Tmax (Sect. 3.2). All absorption spectra are (approximately) restricted to these ranges in the following, unless they are even further limited by the exclusion of noted artifacts.
Figure 3 shows in color the resulting lower limit absorption coefficient spectra for selected temperatures. We note the following:
 |
Fig. 3. Lower and upper limits (αll and αul = αll + Δα) of the linear absorption coefficient for forsterite (upper panels) and enstatite (lower panels) in the three polarization directions: a-polarization (left), b-polarization (middle), and c-polarization (right). The data resulting from sample F[100] and EB[xx0] are plotted as squares, F[010] and EK[010] as solid lines, F[001] and EB[001] as circles, EK[100] as plus symbols. Lower limits are plotted in color, upper limits with Δα according to Table 1 are plotted in gray. Spectra calculated for 100 K forsterite with reduced Δα = 0.1, 0.2, and 0.3 cm−1 are shown as thin black lines, labeled with the Δα values. For clarity, the spectra are only shown for selected temperatures, as indicated in the legends. The dashed and dotted straight lines indicate power laws proportional to 1/λ and 1/λ2, respectively. The wavelength scales in the upper and lower panels are not the same. |
– the forsterite spectra measured with different sample orientation (circles and solid lines) coincide well with each other over the whole wavelength range (panels a and c); the same is true for the spectra of the two thin enstatite samples (plus symbols and solid lines) in c-polarization (panel f, only the 300 K measurements are shown);
– the lower limit spectra of the thin and thick enstatite samples overlap and continue to shorter/longer wavelengths with a similar slope;
– the slope of all lower limit spectra away from the bands, i.e., at long wavelengths, is similar and close to an inverse quadratic dependence on wavelength.
The first point confirms that a multiplicative correction is applicable, i.e., it leads to consistent results from different measurements in the same polarization. The second point could indicate that the lower limit enstatite spectra are more correct than the upper limit spectra, for which the absorption coefficients measured on thick and thin samples do not agree. However, this is not entirely conclusive because the thin and the thick enstatite samples were not made from the same crystal, although the chemical composition of the two crystals is very similar.
However, the third point may provide a physical argument to restrict the error range. The upper limits for the absorption coefficient spectra corresponding to the error values listed in Table 1 are shown in Fig. 3 as gray lines and symbols. These spectra show a shallower decrease with wavelength, in particular at low temperatures. For enstatite, the slope at the longest wavelengths of the upper limit spectra is approximately proportional to the inverse wavelength, which is represented by the dashed lines in Fig. 3, while for the forsterite it is even flatter than that. For the imaginary part of the refractive index (k, see next section), this would mean that it would be constant in the former case and even increasing with wavelength in the latter. This behavior of k would require electromagnetic transitions with a probability that increases towards lower frequencies, which is not likely to occur in dielectric crystals according to our knowledge. In fact, the single-phonon transitions (IR bands) located at shorter wavelengths are supposed to cause a decrease in the absorption coefficient proportional to λ−2, and the phonon difference processes, which are expected to dominate the absorption spectrum at higher temperatures, should also produce a λ−2 spectral decrease (e.g., Mishima et al. 1983). Moreover, the spectral slope found with the absorption coefficients of forsterite and enstatite powders (Mennella et al. 1998; Chihara et al. 2001; Imai et al. 2009; Mutschke et al. 2013) is typically an inverse quadratic dependence on wavelength or steeper.
Thus, a slope of the absorption coefficient that is shallower than 1/λ will be considered unlikely in the following. This means for the forsterite spectra, that we narrow the error range to Δα = 0.1 cm−1, which corresponds (at 100 K) to the lowest of the thin black lines plotted in Fig. 3. Additionally, where possible we now select the measurements that are less affected by fringe structures for further data evaluation. For forsterite in a- and c-polarization, we use the F[010] measurements; where data are lacking in these series the spectra of the other series will be used. For enstatite in c-polarization, we choose the complete series EK[010].
Figure 4 presents the resulting lower and upper limit absorption coefficient spectra at 10 K, which were not shown in Fig. 3. It demonstrates that, independent of the polarization direction, the absorption level beneath the visible bands is considerably higher for our enstatite than for the forsterite. More clearly than in the 100 K spectra (Fig. 3), it decreases with a very steep slope (power-law exponent β = 5 or steeper) up to a wavelength of at least 150 μm. Similar slopes have been reported for the olivine crystal by Mutschke et al. (2013) up to about 100 μm, and for the forsterite powder by Chihara et al. (2001) up to about 80 μm. In our opinion, these steep slopes indicate that the absorption coefficients have not yet reached a real continuum behavior; i.e., they are still governed by the shoulders of the infrared bands. This would mean that the differences in the absorption coefficients between these crystals (see also Sect. 4.1) would arise from different widths and positions of the single-phonon bands located at shorter wavelengths. With increasing temperature (Fig. 3), the slope of the enstatite spectra becomes flatter in this wavelength range (λ < 150 μm), which is likely a consequence of broadening of the IR bands (mainly seen in the 100 K spectra) and of the increasing phonon difference-process absorption, which adds a contribution with a pure β = 2 slope (see Sect. 4.4) to the absorption spectra. This contribution should be dominant in the 300 K spectra. At wavelengths longer than 150 μm, the continuum absorption ( β ≤ 2 depending on the correction factor) is clearly reached at temperatures of 100 K and higher.
 |
Fig. 4. Lower and upper limit absorption coefficient spectra at a temperature of 10 K in the three polarization directions. The dashed lines correspond to the spectra of the thick enstatite samples (enstatite Burma). For clarity, the upper limit spectra for the thin enstatite samples are not shown. The lower and upper black dotted lines indicate λ−2 and λ−5 spectral slopes, respectively. |
For the forsterite, already at 10 K we seem to observe a flattening of the spectral slope at wavelengths above 70 μm. Unfortunately, due to the errors in our measurements, this remains uncertain because we cannot guarantee that the lower limit spectra are indeed the spectra with the lowest possible values. Thus, we still have no safe information as to what values the absorption coefficient at 100 μm and beyond decreases at a temperature of 10 K.
4. Discussion
4.1. Comparison to mass absorption coefficients from transmission spectroscopy
Before calculating the imaginary part of the refractive index, we compare the absorption coefficients to literature data that have been derived from transmission spectroscopy of powders and crystal plates. For the former, we choose the results by Chihara et al. (2001) because their work contains spectra of both forsterite and enstatite. A more complete collection of powder absorption coefficients was presented by Mutschke et al. (2013), who also measured absorption coefficients for an olivine powder with 8% iron (original hand-milled sample by Imai et al. 2009), which we include in the comparison. As was done in that paper, we transform the linear mass absorption coefficient of the single crystals (this work and the olivine plate from Mutschke et al. 2013) into the mass-normalized absorption coefficient 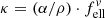 ( ρ = 3.3 g cm−3), taking a conversion factor
( ρ = 3.3 g cm−3), taking a conversion factor 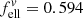 for the absorption of ellipsoidal particles versus compact material into account (see Appendix A). The embedding of the powders into a polyethylene (PE) matrix is corrected by a factor
for the absorption of ellipsoidal particles versus compact material into account (see Appendix A). The embedding of the powders into a polyethylene (PE) matrix is corrected by a factor 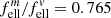 . The conversion factors are identical for both minerals as the far-infrared refractive indices are very similar. The approximate κ values at 100 μm wavelength and 300 K and 10 K temperature are compared in Table 2. For the forsterite data by Chihara et al. (2001), we have recalculated the extrapolation from 80 μm to 100 μm because the estimates by Mutschke et al. (2013) were very rough.
. The conversion factors are identical for both minerals as the far-infrared refractive indices are very similar. The approximate κ values at 100 μm wavelength and 300 K and 10 K temperature are compared in Table 2. For the forsterite data by Chihara et al. (2001), we have recalculated the extrapolation from 80 μm to 100 μm because the estimates by Mutschke et al. (2013) were very rough.
Comparison of the mass-normalized absorption coefficient κ for ellipsoidal particles in a vacuum at λ = 100 μm.
From the comparison in Table 2 we find that the absorption coefficients measured with powders are a factor of 4–10 larger than those measured with single crystals already at room temperature. At low temperature the single-crystal absorption can be up to two orders of magnitude smaller than that measured with powders (for the synthetic forsterite); for the natural crystals it is a factor of 4 (enstatite, upper limit) to 67 (olivine, lower limit) smaller. Thus, our new results confirm, in particular for synthetic forsterite, that there is an extreme difference between the absorption behavior of a single crystal and a powder (Mutschke et al. 2013).
It is interesting that the natural olivine crystal absorbs about one order of magnitude stronger at 10 K than the synthetic forsterite. For powder spectra, the difference is still a factor of 3. If, for the olivine, the absorption coefficient at λ = 100 μm is still governed by the infrared bands (as for enstatite; see previous section), this could simply reflect the well-known band shift and broadening due to the iron content of the olivine (e.g., Fabian et al. 2001). In addition, it is not excluded that a higher defect density in the natural crystal may lead to an enhanced continuum absorption (Imai et al. 2009), for example by the activation of acoustic vibration modes. Measurements at longer wavelengths could help to clarify this issue.
4.2. Comparison to optical constants from reflection measurements
The imaginary part of the refractive index, k, was calculated from the linear absorption coefficient spectra by applying
from the Lambert-Beer law. The spectra for forsterite (upper panel) and enstatite (lower panel) are displayed in Fig. 5. For multiple data at the same temperature and polarization we omitted the noisier values, as already mentioned.
 |
Fig. 5. Imaginary part of the refractive index for forsterite (upper panels) and enstatite (lower panels) in the three polarization directions: a-polarization (left), b-polarization (middle), c-polarization (right). Lower limit spectra are plotted as symbols and solid lines in colors and upper limit spectra in gray (for selected temperatures). The measured data are compared with literature data derived from reflection spectroscopy by Suto et al. (2006) for forsterite (dashed lines, 50 K and 300 K) and Zeidler et al. (2015) for enstatite (10 K and 300 K, with an extension using data from Demichelis et al. 2012, as described in the text). |
In addition, we show literature data of k. These were taken from Suto et al. (2006) in the case of the forsterite, i.e., calculated from the Lorentzian oscillator parameters given by these authors as
where 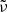 in our notation is identical to ω in theirs;
in our notation is identical to ω in theirs; 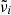 are the oscillator resonance frequencies; γi the damping parameters;
are the oscillator resonance frequencies; γi the damping parameters; 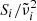 the oscillator strengths, which are equivalent to fi in the notation of Demichelis et al. (2012) and Δεi in Zeidler et al. (2015); and n is the real part of the refractive index, which is also calculated from the Lorentzian oscillator model. In the case of enstatite, we took the oscillator data by Zeidler et al. (2015), but modified them for wavelengths above about 50 μm using the data from Demichelis et al. (2012). In particular, we replaced the lowest frequency oscillators in the Zeidler et al. (2015) data for a- and c-polarization (∼176 cm−1 and ∼141 cm−1, respectively), which were marginally detected or even possibly misdetected by the predicted modes at 87.4 cm−1 and 144.8 cm−1 for a-polarization and the measured double-peak at 137.1 cm−1 and 147.1 cm−1 for c-polarization. For b-polarization, we added the predicted modes at 114.6 cm−1 and 200.6 cm−1 to the Zeidler et al. (2015) data. For the damping parameters in the Lorentzian oscillator description of these modes, which was not specified by Demichelis et al. (2012), we chose uniformly 1 cm−1.
the oscillator strengths, which are equivalent to fi in the notation of Demichelis et al. (2012) and Δεi in Zeidler et al. (2015); and n is the real part of the refractive index, which is also calculated from the Lorentzian oscillator model. In the case of enstatite, we took the oscillator data by Zeidler et al. (2015), but modified them for wavelengths above about 50 μm using the data from Demichelis et al. (2012). In particular, we replaced the lowest frequency oscillators in the Zeidler et al. (2015) data for a- and c-polarization (∼176 cm−1 and ∼141 cm−1, respectively), which were marginally detected or even possibly misdetected by the predicted modes at 87.4 cm−1 and 144.8 cm−1 for a-polarization and the measured double-peak at 137.1 cm−1 and 147.1 cm−1 for c-polarization. For b-polarization, we added the predicted modes at 114.6 cm−1 and 200.6 cm−1 to the Zeidler et al. (2015) data. For the damping parameters in the Lorentzian oscillator description of these modes, which was not specified by Demichelis et al. (2012), we chose uniformly 1 cm−1.
The two most striking results from the comparison in Fig. 5 are first, that the k values derived from our transmission measurements show a much stronger temperature dependence than those calculated from the oscillator model and second, that the k values measured at very low temperature are much lower than those predicted by this model. The first result was expected because the reflection-spectroscopy data on which the model is based do not contain information about excitations other than the single-phonon infrared bands. The strong temperature dependence could thus originate from the expected additional contribution of phonon difference processes, which are only detected in the transmission measurements. The second point was surprising because the absorption coefficient should not fall below the value of the single-phonon contribution at any temperature. Consequently, if the measured values are correct, the oscillator model predicts k values for the long-wavelength wings of the single-phonon bands that are much too high.
In the long-wavelength (low-frequency) limit and for 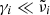 , which is valid for forsterite and enstatite (see, e.g., Suto et al. 2006), Eq. (4) reduces to
, which is valid for forsterite and enstatite (see, e.g., Suto et al. 2006), Eq. (4) reduces to
Since the parameters 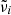 and
and 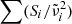 are tightly constrained by the measured band positions and by the low-frequency refractive index
are tightly constrained by the measured band positions and by the low-frequency refractive index 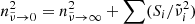 , which can be determined from the reflectivity at long wavelengths, we conclude that the damping parameters γi resulting from the analysis of the reflection spectra at low temperatures are apparently much too high to correctly describe the long-wavelength absorption spectrum beyond the bands. Damping parameters of single-phonon bands typically decrease with decreasing temperature due to the reduction of phonon interaction (e.g., Zeidler et al. 2013, and references therein). For forsterite, this leads to the clear decrease in the continuum absorption in the oscillator-model spectra by a factor of about 3 from θ = 300 K to θ = 50 K, which is roughly consistent with the change in damping parameters for many oscillators of forsterite reported by Suto et al. (2006). This refers mainly to modes in the 15–40 μm wavelength region, which cause the largest contributions to Eq. (5). In the case of the oscillator-based enstatite data, the effect is unfortunately not seen; the temperature dependence of the calculated continuum absorption is sometimes even inverse to the expected. In our opinion, this is due to the uncertainty of the oscillator parameters especially for weak bands in the Zeidler et al. (2015) data; for most of the strong bands, the damping coefficients show the expected decrease with falling temperature (Zeidler et al. 2015).
, which can be determined from the reflectivity at long wavelengths, we conclude that the damping parameters γi resulting from the analysis of the reflection spectra at low temperatures are apparently much too high to correctly describe the long-wavelength absorption spectrum beyond the bands. Damping parameters of single-phonon bands typically decrease with decreasing temperature due to the reduction of phonon interaction (e.g., Zeidler et al. 2013, and references therein). For forsterite, this leads to the clear decrease in the continuum absorption in the oscillator-model spectra by a factor of about 3 from θ = 300 K to θ = 50 K, which is roughly consistent with the change in damping parameters for many oscillators of forsterite reported by Suto et al. (2006). This refers mainly to modes in the 15–40 μm wavelength region, which cause the largest contributions to Eq. (5). In the case of the oscillator-based enstatite data, the effect is unfortunately not seen; the temperature dependence of the calculated continuum absorption is sometimes even inverse to the expected. In our opinion, this is due to the uncertainty of the oscillator parameters especially for weak bands in the Zeidler et al. (2015) data; for most of the strong bands, the damping coefficients show the expected decrease with falling temperature (Zeidler et al. 2015).
A possible reason why the low-temperature damping parameters determined from reflection spectroscopy are too high to accurately describe the long-wavelength absorption could be the spectral vicinity of a multitude of bands in the 15–40 μm wavelength region. The coupling between these bands may lead to difficulties with the simple Lorentzian oscillator model, for instance in the sense that the damping for a certain mode should not be taken as a frequency-independent parameter, but instead as a function of the distance to adjacent phonon resonances. Energetically more isolated vibration modes such as the forsterite 49 μm and 69 μm bands show a much larger decrease in the damping constant at low temperatures, for example a factor of 10 decrease for the former and 16 for the latter (θ = 300 → 50 K; Suto et al. 2006). However, this may also be a consequence of the lower mode energy, so that the above explanation remains a speculation.
4.3. Single-phonon bands of enstatite at λ > 60 μm
We noted already in Sect. 3.3 that the two bands seen in our spectra at 86 cm−1 (116 μm) in a-polarization and at 114 cm−1 (88 μm) in b-polarization have to our knowledge been detected for the first time in a measurement; they had previously been predicted by Demichelis et al. (2012) via ab initio calculations. Another predicted and so far undetected mode at 144.8 cm−1 (a-polarization, 69.1 μm) is, unfortunately, outside of our measurement range, meaning that the thin enstatite sample was opaque at this wavelength (Fig. 2a). According to the predictions by the Lorentzian oscillator model displayed in Fig. 5d, this is surprising and indicates that either this band is much stronger and broader than assumed, causing the strong absorption increase towards 80 μm wavelength, or that there is another strong band not correctly parameterized in the oscillator data. Measurements with a strongly reduced sample thickness would thus be required to detect this band.
The two detected bands appear almost at the predicted positions, namely at 116.6 μm (114.4 predicted) and 87.5 μm (87.3 predicted). Both band positions shift by about 1 μm upon warming to 300 K. The damping parameter of 1 cm−1 chosen for both of them in our Lorentzian oscillator model is too small by a factor of 2–3 in both cases according to the measurements. The oscillator strength predicted by Demichelis et al. (2012) seems to be approximately correct. A precise analysis of oscillator parameters from our spectra is difficult because it requires a correct oscillator model at shorter wavelengths, which is currently beyond our scope. We note that the mentioned bands are probably too weak (an order of magnitude weaker than the ∼70 μm double band in c-polarization) to play any role in dust observations.
4.4. Temperature dependence of the continuum absorption
Finally, we wanted to evaluate whether the measured continuum k values at all temperatures can be fitted by a simple model that takes the temperature-dependent absorption by single phonons and by phonon difference processes into account. Both contributions are assumed to vary proportionally to the inverse wavelength according to Eq. (5) for the single-phonon contribution and to Eq. (6) for the phonon difference-process absorption, which corresponds to the slope of the measured lower limit spectra at long wavelengths. The magnitude of the single-phonon absorption, given by the sum over all 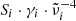 in Eq. (5) will be simply adjusted to the literature oscillator data at θ = 300 K. For lower temperatures, we chose that all γi follow the same (adjustable) second-order polynomial in θ because several authors have pointed out a quadratic dependence of oscillator damping parameters on temperature (Ipatova et al. 1967; Gervais & Piriou 1974). Following Zeidler et al. (2013), the constant term of the polynomial is omitted.
in Eq. (5) will be simply adjusted to the literature oscillator data at θ = 300 K. For lower temperatures, we chose that all γi follow the same (adjustable) second-order polynomial in θ because several authors have pointed out a quadratic dependence of oscillator damping parameters on temperature (Ipatova et al. 1967; Gervais & Piriou 1974). Following Zeidler et al. (2013), the constant term of the polynomial is omitted.
For the phonon difference-process absorption, we apply the model by Mishima et al. (1983):
Here, h is Planck’s constant, c the vacuum speed of light, and kB the Boltzmann constant. For the scaling constant A0, we use the value 1.188 × 105 cm−1 K determined by Mishima et al. (1983). The parameter 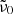 , which when multiplied by c represents the unknown average frequency of the participating phonons, is adjusted to fit the measured data. For the model to be valid, the wavelengths where it is applied should be sufficiently smaller than 1/
, which when multiplied by c represents the unknown average frequency of the participating phonons, is adjusted to fit the measured data. For the model to be valid, the wavelengths where it is applied should be sufficiently smaller than 1/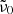 . The temperature dependence of k is mainly governed by the factor
. The temperature dependence of k is mainly governed by the factor 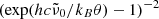 , which arises from the occupation numbers of the participating phonon states and vanishes at low θ.
, which arises from the occupation numbers of the participating phonon states and vanishes at low θ.
Figure 6 shows the temperature dependence of the measured k values (lower limit values; red dots) with error bars, for a wavelength of 200 μm, which is sufficiently far away from the single-phonon resonances and is covered by most spectra. Only for θ = 10 K are the values estimates obtained by extrapolating the spectra by eye. We selected arbitrarily the a-polarization data for forsterite and the c-polarization data for enstatite. Also shown are the values calculated from the Lorentzian oscillator model (green squares); we used the θ = 300 K data point to estimate the single-phonon contribution (green solid line) by fitting the polynomial to this value. The oscillator-model data at lower temperature are only shown for completeness; our model does not follow these data for the reasons discussed in Sect. 4.2. Instead, we adjusted the linear and quadratic contributions in a way that the curve matches the lower limit k values at 10 K and 50 K/100 K for forsterite/enstatite as closely as possible, or stays at least below these values.
 |
Fig. 6. Temperature dependence of the imaginary part of the refractive index for forsterite in a-polarization (upper panel) and enstatite in c-polarization (lower panel) at λ = 200 μm (lower limit values; red dots with error bars). The oscillator-model data are represented by the green filled squares. The red solid lines represent model curves built from the contributions of phonon difference processes (Mishima model) plus the contributions of single-phonon absorption; the green solid line is the single-phonon contribution alone. Also shown are simple linear, quadratic, and mixed linear/quadratic curves (black dotted, dashed, and dash-dotted lines) in order to check their compatibility with the measured data (see text). |
An important question is whether single-phonon absorption following such a temperature dependence could explain the complete data including those at higher temperatures. Thus, we also display in Fig. 6 polynomials (linear, quadratic, and mixed) that would match the measured k at θ = 300 K. For forsterite, it is evident that the polynomial curves cannot fit all the measured temperature-dependent data since their behavior is too flat at high temperatures and too steep at intermediate temperatures. For enstatite, the measured data are consistent with a quadratic behavior, which supports the relatively strong single-phonon contribution in our model, compared to forsterite.
A much better fit to the measured k values is obtained when the single-phonon absorption and the Mishima et al. (1983) model (Eq. (6)) are added. Only a single parameter (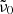 ) was adjusted to fit the measured k values at temperatures above 100 K. The complete models for forsterite and enstatite are represented by the red solid lines in Fig. 6. For low temperatures, the difference-process contribution becomes negligible, i.e., the red and green curves are identical; for the higher temperatures, the model matches almost perfectly the measured data. This is also seen in Fig. 7 where we compare the wavelength-dependent model to the measured lower limit spectra in the same two polarization directions. For temperatures of 75 K and higher, the model matches the k spectra in the continuum (i.e., above λ = 70 μm for forsterite, λ = 150 μm for enstatite) very well. At lower temperatures, the model proposes a lower absorption level compared to the measured data; however, the uncertainty of the data and the fact that the 10 K enstatite spectrum has probably not yet reached the continuum level at the measured wavelengths, have to be considered here.
) was adjusted to fit the measured k values at temperatures above 100 K. The complete models for forsterite and enstatite are represented by the red solid lines in Fig. 6. For low temperatures, the difference-process contribution becomes negligible, i.e., the red and green curves are identical; for the higher temperatures, the model matches almost perfectly the measured data. This is also seen in Fig. 7 where we compare the wavelength-dependent model to the measured lower limit spectra in the same two polarization directions. For temperatures of 75 K and higher, the model matches the k spectra in the continuum (i.e., above λ = 70 μm for forsterite, λ = 150 μm for enstatite) very well. At lower temperatures, the model proposes a lower absorption level compared to the measured data; however, the uncertainty of the data and the fact that the 10 K enstatite spectrum has probably not yet reached the continuum level at the measured wavelengths, have to be considered here.
 |
Fig. 7. Spectra of the imaginary part of the refractive index (lower limit values) for forsterite in a-polarization (solid lines, upper panel) and enstatite in c-polarization (circles and solid lines, lower panel) compared to the best-fit continuum absorption model (see also Fig. 6). The dashed lines represent the full model (single-phonon plus phonon difference-process contributions); the dash-dotted lines are the single-phonon components alone for θ = 300 K. |
The model is very limited as well. First, the single-phonon contribution is very uncertain since it is unknown whether it is correctly represented by the literature oscillator data at 300 K. Larger contributions by the single-phonon absorption seem unlikely and provide a poor match, at least in case of the forsterite. Smaller contributions have been tested, and we found that the Mishima et al. (1983) model would still be able to fit the measured data very well. For this, just a smaller representative phonon frequency 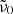 would be required. Using only one such frequency in the model is another strong simplification, since many phonons contribute to the difference-process absorption. The numbers determined in our fit correspond approximately to phonons of the strong 33 μm band complex, which is the strong band with the lowest resonance frequency in all polarization directions for this material. Similarly, for enstatite in c-polarization there is a very strong band at 414 cm−1 (Demichelis et al. 2012). However, for the other polarization directions we would obtain similar
would be required. Using only one such frequency in the model is another strong simplification, since many phonons contribute to the difference-process absorption. The numbers determined in our fit correspond approximately to phonons of the strong 33 μm band complex, which is the strong band with the lowest resonance frequency in all polarization directions for this material. Similarly, for enstatite in c-polarization there is a very strong band at 414 cm−1 (Demichelis et al. 2012). However, for the other polarization directions we would obtain similar 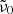 values, although for these crystal axes there are strong phonon bands at much lower frequencies. So, the interpretation of this value and the whole model should be taken with caution.
values, although for these crystal axes there are strong phonon bands at much lower frequencies. So, the interpretation of this value and the whole model should be taken with caution.
5. Conclusions
Even within the uncertainties of our data, we can conclude from our results and the discussion above that forsterite and enstatite single crystals have very low absorption coefficients, and thus emissivities at the temperatures typical for dust in protoplanetary disks, debris disks, and the interstellar medium. The optical constants extrapolated from the oscillator fits to reflection spectra may provide a roughly correct estimate only at temperatures around 100 K (forsterite) or 200 K (enstatite); they fail to reproduce the 10 K absorption level, likely because of the limitations of the simple Lorentzian oscillator description. They also do not reproduce the absorption at higher temperatures because phonon difference processes dominate the absorption in that case.
Both the literature oscillator data and our single-crystal absorption coefficients predict that the opacity of forsterite and enstatite dust is much lower than that of amorphous silicate dust. This is demonstrated in Fig. 8. If mixtures of amorphous and crystalline dust are considered, then the total opacity decreases almost linearly with the crystallinity of the dust (upper panel). Only if the fraction of amorphous silicate falls below 5% does the crystalline dust become visible. The numbers in Fig. 8 are calculated for spherical grains in order to make them comparable to typical astronomical simulations and compatible to the values given for amorphous silicates by Boudet et al. (2005). For ellipsoidal grains, see the conversion factors in Appendix A. In the lower panel of Fig. 8, the same data is depicted in a different way. Crystalline dust can be added to any simulation of thermal dust emission at θ = 100 K using amorphous silicate, without becoming visible up to approximately 20 times the volume of the amorphous dust.
 |
Fig. 8. Opacity values for three selected wavelengths for mixtures of crystalline and amorphous silicate dust at θ = 100 K. Solid lines are for our forsterite, dashed lines for enstatite. Upper panel: the total mass-normalized cross section is plotted over the fraction of MgSiO3 glass (Boudet et al. 2005) in composite particles with crystalline grains. Lower panel: we plot the dependence on the admixture of crystalline dust, given in multiples of the amount of glassy material. |
These values would have to be changed considerably if powder transmission data were used. So far, it is completely unclear why such measurements on crystalline silicate powders embedded in polyethylene pellets find mass absorption coefficients that are up to two orders of magnitude higher at low temperature. A possibility could be the presence of structural defects in the silicate grains in the powders (Imai et al. 2009), which could, for example, lead to an activation of acoustic vibration modes that do not absorb IR radiation in perfect crystals. However, experimental problems such as scattering losses caused by inhomogeneities in the density distribution of the sample (Häßner et al. 2018) may also play a role. A clarification of this issue would be very important for modeling and interpretation of the submillimeter emission from cold dust.
Acknowledgments
We are grateful to Prof. H. Zacharias, Physikalisches Institut, WWU Münster, Germany, for providing the forsterite crystal, and to M. Lippold, D. Schmidt, and Prof. F. Langenhorst, Institut für Geowissenschaften, FSU Jena, for providing the thin enstatite samples. This work has been supported by the Deutsche Forschungsgemeinschaft (DFG) through grant MU 1164/9-1 within the Research Unit FOR2285 “Debris disks in Planetary Systems”.
References
- Bohren, C. F., & Huffman, D. R. 1983, Absorption and Scattering of Light by Small Particles (New York: Wiley) [Google Scholar]
- Boudet, N., Mutschke, H., Nayral, C., et al. 2005, AJ, 633, 272 [Google Scholar]
- Bowey, J. E., Barlow, M. J., Molster, F. J., et al. 2002, MNRAS, 331, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Bradley, J. 2003, in Lecture Notes in Physics, ed. T. K. Henning (Berlin: Springer Verlag), Astromineralogy, 609, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Chihara, H., Koike, C., & Tsuchiyama, A. 2001, Publ. Astron. Soc. Japan, 53, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Coupeaud, A., Demyk, K., Meny, C., et al. 2011, A&A, 535, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Demichelis, R., Suto, H., Noël, Y., et al. 2012, MNRAS, 420, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Demyk, K., Meny, C., Lu, X.-H., et al. 2017a, A&A, 600, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Demyk, K., Meny, C., Leroux, H., et al. 2017b, A&A, 606, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Vries, B. L., Acke, B., Blommaert, J. A. D. L., et al. 2012, Nature, 490, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, D., Henning, T., Jäger, C., et al. 2001, A&A, 378, 228 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Gail, H. P. 2003, in Lecture Notes in Physics, ed. T. K. Henning (Berlin: Springer Verlag), Astromineralogy, 609, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Gervais, F., & Piriou, B. 1974, Phys. Rev. B, 10, 1642 [NASA ADS] [CrossRef] [Google Scholar]
- Hadni, A. 1970, in Far-Infrared Properties of Solids, eds. S. S. Mitra, & S. Nudelman (New York: Plenum Press), 561 [CrossRef] [Google Scholar]
- Häßner, D., Mutschke, H., Blum, J., Zeller, T., & Gundlach, B. 2018, MNRAS, 481, 5022 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, T., & Mutschke, H. 1997, A&A, 327, 743 [NASA ADS] [Google Scholar]
- Iishi, K. 1978, Am. Mineral., 63, 1198 [Google Scholar]
- Imai, Y., Koike, C., Chihara, H., et al. 2009, A&A, 507, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ipatova, I. P., Maradudin, A. A., & Wallis, R. F. 1967, Phys. Rev., 155, 882 [NASA ADS] [CrossRef] [Google Scholar]
- Juhász, A., Bouwman, J., Henning, T., et al. 2010, ApJ, 721, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Koike, C., Mutschke, H., Suto, H., et al. 2006, A&A, 449, 583 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivov, A. V., Müller, S., Löhne, T., & Mutschke, H. 2008, ApJ, 687, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Mennella, V., Brucato, J. R., Colangeli, L., et al. 1998, ApJ, 496, 1058 [NASA ADS] [CrossRef] [Google Scholar]
- Mishima, O., Klug, D. D., & Whalley, E. 1983, J. Chem. Phys., 78, 6399 [NASA ADS] [CrossRef] [Google Scholar]
- Molster, F. J., Waters, L. B. F. M., Tielens, A. G. G. M., Koike, C., & Chihara, H. 2002, A&A, 382, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mutschke, H., Zeidler, S., & Chihara, H. 2013, Earth Planets Space, 65, 1139 [NASA ADS] [CrossRef] [Google Scholar]
- Olofsson, J., Juhász, A., Henning, T., et al. 2012, A&A, 542, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pitman, K. M., Hofmeister, A. M., & Speck, A. K. 2013, Earth Planets Space, 65, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Sogawa, H., Koike, C., Chihara, H., et al. 2006, A&A, 451, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sturm, B., Bouwman, J., Henning, T., et al. 2010, A&A, 518, L129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sturm, B., Bouwman, J., Henning, T., et al. 2013, A&A, 553, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suhasaria, T., Thrower, J. D., & Zacharias, H. 2015, MNRAS, 454, 3317 [NASA ADS] [CrossRef] [Google Scholar]
- Suto, H., Sogawa, H., Tachibana, S., et al. 2006, MNRAS, 370, 1599 [NASA ADS] [CrossRef] [Google Scholar]
- Zeidler, S., Posch, T., Mutschke, H., Richter, H., & Wehrhan, O. 2011, A&A, 526, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zeidler, S., Posch, T., & Mutschke, H. 2013, A&A, 553, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zeidler, S., Mutschke, H., & Posch, T. 2015, ApJ, 798, 125 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Conversion factors for absorption coefficients in the limits of small particles and small absorption
The formulae for absorption cross sections Cabs of particles in the Rayleigh limit (Bohren & Huffman 1983) for radiation with vacuum wavelength λ can be simplified if the imaginary part of the refractive index of the particle material k is much smaller than the real part n. For spherical particles the volume-normalized absorption cross section (particle volume Vp) is then
where nm is the refractive index of the (non-absorbing) embedding medium. For ellipsoidal particles with a continuous distribution of form factors (CDE model, Bohren & Huffman 1983), the simplified formula is given by
The volume-normalized cross sections can be directly compared to the linear absorption coefficient αbulk = 2π/λ ⋅ k of a bulk material since the optical depth through an ensemble of N particles (filling factor F = NVp/V) within the beam with cross section A is
with (F d) the projected sample thickness, while αbulk = τ/d. Similarly, the mass absorption coefficient κ = αpart/ρ (with the mass density ρ) can be compared to αbulk/ρ. We denote the ratios αpart/αbulk ≡ κρ/αbulk as the conversion factors 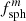 and
and 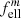 for embedded spherical and ellipsoidal particles, respectively. The symbols
for embedded spherical and ellipsoidal particles, respectively. The symbols 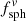 and
and 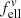 are used for non-embedded (nm = 1) particles. The conversion factors depending on the material refractive index are plotted in Fig. A.1. Values used in this paper can be found at the intersections with the vertical dotted line.
are used for non-embedded (nm = 1) particles. The conversion factors depending on the material refractive index are plotted in Fig. A.1. Values used in this paper can be found at the intersections with the vertical dotted line.
 |
Fig. A.1. Conversion factors for mass- or volume-normalized absorption coefficients of particles relative to bulk material in the small-absorption limit (k ≪ n). Curves for variable material refractive index are given for the cases of small PE-embedded (refractive index nm = 1.52) and non-embedded (matrix vacuum) spherical and ellipsoidal (CDE model, Bohren & Huffman 1983) particles. The curves are labeled with the symbols used in the text. The vertical dotted line indicates an average value of the refractive index for forsterite and enstatite in the submillimeter spectral range (n = 2.66). |
All Tables
Correction factors for lower and upper limit absorption 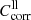 and
and 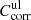 applied to the transmission spectra (Eq. (2)), maximum error values Δα, and usable range of the linear absorption coefficient α for the individual measurements of forsterite (F[100], F[010], F[001]) and enstatite (EB[xx0], EB[001], EK[100], EK[010]).
applied to the transmission spectra (Eq. (2)), maximum error values Δα, and usable range of the linear absorption coefficient α for the individual measurements of forsterite (F[100], F[010], F[001]) and enstatite (EB[xx0], EB[001], EK[100], EK[010]).
Comparison of the mass-normalized absorption coefficient κ for ellipsoidal particles in a vacuum at λ = 100 μm.
All Figures
 |
Fig. 1. Temperature-dependent transmission spectra of the forsterite crystal for orientation of the electric field parallel to the a-axis (panel a), b-axis (panel b), and c-axis (panel c). Complete temperature series (F[010]a, F[001]b, F[100]c) are plotted as solid lines, the two incomplete series as dashed lines. The F[001]a curves have been scaled by a factor of 1.8; they approximately match the F[010]a curves for the same temperatures. Dotted lines: calculated maximum transmission curves taking into account the intensity reflected by the crystal surfaces. |
| In the text | |
 |
Fig. 2. Same as Fig. 1, but for enstatite (temperatures only 300 K, 200 K, 100 K, 10 K). The solid and the dash-dotted lines (the latter only in panel c) are the transmission spectra of the 0.6 mm thick enstatite slabs, while the dashed lines are the transmission spectra measured on the 5 mm and 4 mm samples (the latter for the c-polarization). Dotted lines: calculated maximum transmission curves taking the reflection at the crystal surfaces into account. |
| In the text | |
 |
Fig. 3. Lower and upper limits (αll and αul = αll + Δα) of the linear absorption coefficient for forsterite (upper panels) and enstatite (lower panels) in the three polarization directions: a-polarization (left), b-polarization (middle), and c-polarization (right). The data resulting from sample F[100] and EB[xx0] are plotted as squares, F[010] and EK[010] as solid lines, F[001] and EB[001] as circles, EK[100] as plus symbols. Lower limits are plotted in color, upper limits with Δα according to Table 1 are plotted in gray. Spectra calculated for 100 K forsterite with reduced Δα = 0.1, 0.2, and 0.3 cm−1 are shown as thin black lines, labeled with the Δα values. For clarity, the spectra are only shown for selected temperatures, as indicated in the legends. The dashed and dotted straight lines indicate power laws proportional to 1/λ and 1/λ2, respectively. The wavelength scales in the upper and lower panels are not the same. |
| In the text | |
 |
Fig. 4. Lower and upper limit absorption coefficient spectra at a temperature of 10 K in the three polarization directions. The dashed lines correspond to the spectra of the thick enstatite samples (enstatite Burma). For clarity, the upper limit spectra for the thin enstatite samples are not shown. The lower and upper black dotted lines indicate λ−2 and λ−5 spectral slopes, respectively. |
| In the text | |
 |
Fig. 5. Imaginary part of the refractive index for forsterite (upper panels) and enstatite (lower panels) in the three polarization directions: a-polarization (left), b-polarization (middle), c-polarization (right). Lower limit spectra are plotted as symbols and solid lines in colors and upper limit spectra in gray (for selected temperatures). The measured data are compared with literature data derived from reflection spectroscopy by Suto et al. (2006) for forsterite (dashed lines, 50 K and 300 K) and Zeidler et al. (2015) for enstatite (10 K and 300 K, with an extension using data from Demichelis et al. 2012, as described in the text). |
| In the text | |
 |
Fig. 6. Temperature dependence of the imaginary part of the refractive index for forsterite in a-polarization (upper panel) and enstatite in c-polarization (lower panel) at λ = 200 μm (lower limit values; red dots with error bars). The oscillator-model data are represented by the green filled squares. The red solid lines represent model curves built from the contributions of phonon difference processes (Mishima model) plus the contributions of single-phonon absorption; the green solid line is the single-phonon contribution alone. Also shown are simple linear, quadratic, and mixed linear/quadratic curves (black dotted, dashed, and dash-dotted lines) in order to check their compatibility with the measured data (see text). |
| In the text | |
 |
Fig. 7. Spectra of the imaginary part of the refractive index (lower limit values) for forsterite in a-polarization (solid lines, upper panel) and enstatite in c-polarization (circles and solid lines, lower panel) compared to the best-fit continuum absorption model (see also Fig. 6). The dashed lines represent the full model (single-phonon plus phonon difference-process contributions); the dash-dotted lines are the single-phonon components alone for θ = 300 K. |
| In the text | |
 |
Fig. 8. Opacity values for three selected wavelengths for mixtures of crystalline and amorphous silicate dust at θ = 100 K. Solid lines are for our forsterite, dashed lines for enstatite. Upper panel: the total mass-normalized cross section is plotted over the fraction of MgSiO3 glass (Boudet et al. 2005) in composite particles with crystalline grains. Lower panel: we plot the dependence on the admixture of crystalline dust, given in multiples of the amount of glassy material. |
| In the text | |
 |
Fig. A.1. Conversion factors for mass- or volume-normalized absorption coefficients of particles relative to bulk material in the small-absorption limit (k ≪ n). Curves for variable material refractive index are given for the cases of small PE-embedded (refractive index nm = 1.52) and non-embedded (matrix vacuum) spherical and ellipsoidal (CDE model, Bohren & Huffman 1983) particles. The curves are labeled with the symbols used in the text. The vertical dotted line indicates an average value of the refractive index for forsterite and enstatite in the submillimeter spectral range (n = 2.66). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.