| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201834325 | |
| Published online | 16 May 2019 | |
Secondary eclipse of the hot Jupiter WASP-121b at 2 μm★
1
Konkoly Observatory of the Hungarian Academy of Sciences,
Budapest,
1121
Konkoly Thege ut. 15-17,
Hungary
e-mail: kovacs@konkoly.hu
2
Institute of Theoretical Physics, Eötvös University,
Budapest,
1117
Pázmány Péter sétány 1A,
Hungary
Received:
26
September
2018
Accepted:
3
April
2019
Ground-based observations of the secondary eclipse in the 2MASS K band are presented for the hot Jupiter WASP-121b. These are the first occultation observations of an extrasolar planet that were carried out with an instrument attached to a 1 m class telescope (the SMARTS 1.3 m). We find a highly significant eclipse depth of (0.228 ± 0.023)%. Together with other planet atmosphere measurements, including the Hubble Space Telescope near-infrared emission spectrum, current data support more involved atmosphere models with species producing emission and absorption features, rather than simple smooth blackbody emission. Analysis of the time difference between the primary and secondary eclipses and the durations of these events yields an eccentricity of e = 0.0207 ± 0.0153, which is consistent with the earlier estimates of low or zero eccentricity, but with a smaller error. Comparing the observed occultation depth in the K band with the one derived under the assumption of zero Bond albedo and full heat redistribution, we find that WASP-121b has a deeper observed occultation depth than predicted. Together with the sample of 31 systems with K-band occultation data, this observation lends further support to the idea of inefficient heat transport between the day and night sides for most of the hot Jupiters.
Key words: planets and satellites: atmospheres / methods: data analysis
Photometric time series are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/625/A80
© ESO 2019
1 Introduction
When it is combined with other pieces of information (such as planet mass), the low thermal radiation of extrasolar planets is direct evidence of their substellar nature. In addition to this independent verification, measuring the radiation spectrum yields a wealth of information on atmospheric structure and basic orbital parameters. Because of their low temperatures (relative to the temperatures of their host stars), the best chance of detection clearly lies in the infrared. From the first detection, employing the mid-infrared instrument of the Spitzer Space Telescope by Deming et al. (2005), many systems have been observed not only by space-based, but also by ground-based instruments attached to 4-m class telescopes. Here we report the multiple detection of the secondary eclipse1 of the hot Jupiter (HJ) WASP-121b in the 2MASS K band by A Novel Dual Imaging CAMera (ANDICAM) attached to the 1.3 m telescope of the SMARTS Consortium2.
The transiting extrasolar planetary system WASP-121 was discovered by Delrez et al. (2016) using the wide-field telescopes of the SuperWASP project (Pollacco et al. 2006, see also Anderson et al. 2018 for the latest update). The analysis of these and the subsequent spectroscopic followup observations revealed that WASP-121b is a very hot Jupiter, with a maximum photospheric temperature above 3000 K. This is expected because the planet very closely orbits an F star (Porb = 1.27 days). The close orbit and the extended planet radius3 of Rp = 1.87 RJ with a standard mass of Mp = 1.18 MJ imply rather strong tidal dissipation, leading to Roche-lobe filling and then to a speedy disruption within some hundred million years, assuming a stellar tidal dissipation factor Qstar < 108 (see Delrez et al. 2016; and for the signature of a strongly evaporating atmosphere, the near-UV observations of Salz et al. 2019). In addition, the planet has probably experienced a strong dynamical interaction with some nearby third body, as can be inferred from the large projected spin-orbit angle of 258° ± 5° (see Delrez et al. 2016). Interestingly, secondary eclipses were observed multiple times by the same authors in the Sloan-z′ band by the 60 cm TRAPPIST telescope; to our knowledge, this is the first occultation detection from the ground by a telescope of this size. The significant detection of the occultation depth of a mere (0.060 ± 0.013)% resulted in the first direct estimation of the planet temperature. Important followup observations (both during the primary and secondary eclipses) have been made by Evans et al. (2016, 2017, 2018) using the Hubble Space Telescope’s (HST) Wide Field Camera 3 in the near-infrared, the Spitzer/IRAC detector at 3.6 μm, and HST/STIS in the UV. These data indicate a weak H2O emission during occultation and absorption during transit, implying temperature inversion due to some high-altitude absorber. In spite of the successful fit of the HST emission spectrum, and quite currently the transmission spectrum observed by the same instrument, the authors caution that the solution is not unique (e.g., type of absorber and precision of the fit at different wavelengths). These issuesare not unique to WASP-121b, they are also present in other very hot Jupiters (e.g., WASP-33b, Kepler-13Ab; see Parmentier et al. 2018). In spite of the considerable progress made in the past ten years, there is a substantial lack of understanding the relations between the physical parameters of the systems and the thermal properties of their planets (see the uniform analysis by Adams & Laughlin 2018 of ten systems with full infrared phase curves).
The purpose of this work is to add a flux value to the emission spectrum of WASP-121b at a single waveband and thereby increase the number of constraints on future atmosphere modeling of the planet. Furthermore, timing estimates are presented to give more stringent limits on the orbital eccentricity, which is a valuable parameter for analyzing the dynamical history of the system.
Secondary eclipse observations of WASP-121b in the near-infrared.
2 Observations and analysis method
Photometricobservations in the 2MASS K and Cousins I bands (effective wavelengths of 2.2 and 0.8 μm, respectively) have been made by using the ANDICAM instrument in a beam-splitting mode, allowing simultaneous data acquisition in the two bands4. On each night, the target was monitored continuously, by allowing ample amount of pre- and after-event time (permitted by the actual sky position) to reliably fix the out-of-eclipse (OOE) baseline for the event, which lasted for almost 3 h. An exposure time of 15–20 s was used, resulting in an overall cadence of 70–500 s because of the overheads, related to read-outs, varying movements due to dithering, and other data acquisition steps. The observing log with some associated parameters is given in Table 1.
For the K-band observations, dithering was used to decrease the higher sensitivity against detector non-uniformity in the near-infrared. We found this method useful because we did not have a priori information on pixel sensitivity. This method also includes some risk, however, because by testing different parts of the CCD, we may bump into bad positions, leading to light curves of larger scatter that is associated with the particular dither position. Our strategy has proven to be useful in general and led to a higher quality result in theend.
By stacking several images, we show the dither pattern in Fig. 1 for one of the nights. The number of dither positions changed from night to night, and their durations varied. The image (already corrected for flat field) spectacularly exhibits sequences of rings, which are reminiscent of the trace of earlier dewdrops. In spite of their high visibility, their effect has been proven to be less damaging for the data quality than the varying pixel sensitivity (which is considerably more difficult to spot because the pixels lack the type of spatial correlation that the rings have).
To produce the photometric time series that was to be used to derive the basic occultation parameters, we proceeded as follows. First we computed simple relative fluxes at various but fixed circular apertures from 10 to 20 pixel radii with an increment of2 pixels. After much experimenting and inspecting the final product of the full detrending procedure to be described below, we find that an aperture with a pixel radius of 16 yields the light curve with the smallest scatter. All results presented in this paper refer to this aperture size.
By using the relative fluxes (target over comparison star flux, hereafter raw flux) and folding the data with the orbital period, we can determine whether we can see some sign of an occultation event. The result is shown in Fig. 2. The pale dots show that the raw fluxes are very noisy, and the event with the expected depth of 0.1–0.2% is hopelessly buried in the noise. We can determine the reason of this somewhat unexpected high level of noise by examining the individual light curves associated with the various dither positions5. The highlighted light curves show a strong dependence on the dither position, leading to both zero-point shifts and nightly trends. Therefore (not entirely unexpectedly), we must employ some detrending method that is likely the cause of the trends and zero-point shifts. The detrending step is vital and therefore quite common in the extraction of planetary signals in general, and in particular, in deriving wavelength-dependent transit depths for the exquisite accuracy needed to estimate emission or transmission spectra (e.g., Stevenson et al. 2012; Kreidberg et al. 2015).
It is well known that ground-based instruments detect stellar light deformed by the multiplicative noise and systematics originating from the Earth’s atmosphere and from the environment or instrument. In addition, we also have an additive noise source from the sky background,
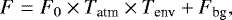 (1)
(1)
where F is the detected and F0 is the true stellar flux. The transmission functions of the Earth’s atmosphere and the instrument are denoted by Tatm and Tenv, respectively, and the background flux is given by Fbg. In traditional photometric reductions the atmospheric and instrumental effects are filtered out with the aid of comparison stars near the target, using the assumption of the close similarity in the transmission functions for the target and its neighboring companions. However, when higher accuracy is required, this method usually fails because of the lack of complete equivalence between the transmission functions of the target and the comparison stars (for faint targets, the additive background noise is an additional problem).
Because we lack an obvious exact solution of the problem (similarly to the method followed in other studies, e.g., Bakos et al. 2010; Delrez et al. 2016), we opted for an approximate solution. Here we took the logarithm of the target to comparison star flux ratios F∕Fc, and fit the data with the linear combination of the presumed signal and certain external photometric parameters (e.g., position, and width of the point spread function, PSF). In addition, we treated each light curve of the different dither positions individually, with particular zero-points and trends (but with the same underlying signal). That is, we used a least-squares minimization for the following expression:
![\begin{eqnarray*}\hspace*{-6pt}& & \mathcal D = \sum_{j=1}^M \sum_{i=1}^{N_{\textit{j}}} w_{\textit{j}}\bigg[\log\Bigg({F_{\textit{j}}(i) \over F_{\textit{j}}^{\textrm{c}}(i)}\Bigg) - E_{\textit{j}}(i)\bigg]^2,\\[3pt] \hspace*{-6pt}& & E_{\textit{j}}(i) = a_{0,\it j} + a_{x,\it j}X_{\textit{j}}(i) + a_{y,\it j}Y_{\textit{j}}(i) + A \log(F_{\textrm{trap}}(i)). \end{eqnarray*}](/articles/aa/full_html/2019/05/aa34325-18/aa34325-18-eq2.png)
Here all data were sorted by the orbital phase. We assumed that there are M dither positions altogether with Nj data points at the jth dither. Because our extensive tests showed that neither arbitrary polynomial nor additional external parameters are needed to reach a detection with a high signal-to-noise ratio (S/N), we only used the pixel position components (X, Y) of the target to correct for instrumental effects. The stellar flux during the occultation was approximated by a trapezoidal function Ftrap with fixed ingress and egress time, duration, and eclipse center of 0.015, 0.120 and 2457764.65485 days, respectively, corresponding to those given by Delrez et al. (2016). The weights {w} were constant for the same dither index and proportional to the reciprocal of the variance of the residuals around the best-fitting trapezoidal. Because the solution was not known, the weights were iterated during the process of solution. Finally, the data were converted back into relative intensities, with an OOE normalization of 1.0 for the fitted trapezoidal. The error of the occultation depth was computed as
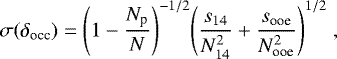 (4)
(4)
where s14 and sooe are sums of the squared residuals in the in-the-eclipse and OOE phases, respectively, with associated number of data points N14 and Nooe. The factor in front (with Np parameters fitted to N data points)represents the debiasing of the error due to the decrease of the degrees of freedom, because of parameter fitting. The S/N of the detection is the ratio of the average eclipse depth to this error,
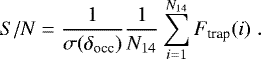 (5)
(5)
 |
Fig. 1 Dithering pattern used during the near-infrared observations. The image shows the 2.4′ × 2.4′ FOV of the ANDICAM near-infrared camera, attached to the 1.3 m telescope of the SMARTS Consortium. The target (WASP-121=2MASS 07102406-3905506) is in the middle, the comparison star 2MASS 07102364-3905561 is in the lower left corner. North is up and west is to the left. Circles around the target and the comparison star show the aperture sizes used to estimate the stellar and background fluxes. |
 |
Fig. 2 Simple photometric flux ratios ordered by the orbital period (pale dots). Some dithers are annotated to show the nightly trends (or the lack of them, i.e., number 9). Dither 6 (gray dots) is plotted also after employing zero-point shift and detrending by the position vector (black dots, see Sect. 2 for details). |
Occultation depths for WASP-121 in the 2MASS K band.
3 Occultation parameters
First we fixed all secondary eclipse parameters (except for the occultation depth) by assuming a circular orbit and the validity of the parameters derived for the transit by Delrez et al. (2016). Following the procedure described in Sect. 2, we computed the best-fitting occultation depth under various conditions, concerning the number of clipped points and the omitted dither light curves. The result is shown in Table 2. Except perhaps for the extreme choices of data trimming parameters (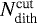 and
and 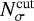 ), the occultation depth is relatively stable. To avoid too sparsely populated dither light curves and to avoid overtrimming the data, we opted for the case of
), the occultation depth is relatively stable. To avoid too sparsely populated dither light curves and to avoid overtrimming the data, we opted for the case of 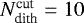 and
and 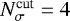 . The folded light curve obtained in this way is shown in Fig. 3. The resulting secondary eclipse depth is 0.00228 ± 0.00023.
. The folded light curve obtained in this way is shown in Fig. 3. The resulting secondary eclipse depth is 0.00228 ± 0.00023.
To determine the level of the systematics filtering, we computed the autocorrelation function (ACF) of the residuals after subtracting the best-fitting trapezoidal as shown in Fig. 3. In units of the orbital period, the ACF was computed with steps of 0.00123 up to 0.115, that is, close to the length of the full eclipse event. As a sanity check, we also computed the ACF for many Gaussian white-noise realizations. The result is shown in Fig. 4. The residuals are almost uncorrelated. The basic correlation length is smaller than ~0.005 in units of the orbital period. This value is lower than one-half of the ingress duration. It seems that the decorrelation method we applied yields nearly white-noise residuals, which supports the validity of the pure statistical error estimation given by Eq. (4). We also note that similar short-timescale correlations are observable in other studies that investigated systematics, in particular, in the analysis of the HST data by Evans et al. (2017).
Although the noise is rather high, the relatively large number of data points led to a detection with high S/N. Therefore, it is tempting to examine whether our assumption on the applicability of the transit parameters holds, and if there is a way to further constrain the eccentricity by the best-fitting occultation center and event duration. To this aim, we mapped the quality of the fit as a function of ΔTc (tested occultation center time minus the one calculated from the transit with the assumption of circular orbit) and t14 (occultation duration).
To further examine the issue of eccentricity, the secondary eclipse data of Delrez et al. (2016) were investigated in addition to our data. Because the observations were made in the Sloan z′ band, the signal is considerably shallower than in the 2MASS K (Ks) band. Nevertheless, the number of data points (6260 flux measurements on seven nights) compensates for this, and yields a confident detection of S∕N = 7.5, with δocc = 0.000697 ± 0.000081 and a residual standard deviation of 0.003190. This depth is larger by 0.000096 than the one derived by Delrez et al. (2016), but the difference is within 1σ, and could be accounted for by the lower number of detrending parameters used in our code. We found it satisfactory to use only the pixel coordinates, and avoid correcting with a polynomial and other parameters because these do not yield an appreciable improvement in the quality of the fit and may in addition lead to a depression of the occultation depth.
The (ΔTc, t14) maps are shown in Figs. 5 and 6 for the Ks and Sloan z′ data, respectively. As expected, the topology of both maps confirms the rather small (if any) deviations from the parameters predicted by the transit with the assumption of circular orbit. Furthermore, the Sloan z′ data are more restrictive than the Ks data, even though the S/N value is higher for the latter. This is because the parameter maps also yield information on the sensitivity of the solution on the neighboring parameter values and not only on a specific combination of the parameters, which might be better or worse, depending on the functional form of the variance on these parameters and noise level. The better quality of the Sloan z′ data is also visible in the nearly three times smaller error of the derived occultation depth.
The currently available secondary eclipse parameters are summarized in Table 3. The errors of the items associated with this paper have been computed in the following way. After the best-fitting trapezoidal was found, we added Gaussian white noise with the observed standard deviations of the residuals corresponding to this solution, and then the best-fitting trapezoidal to these simulated data was searched for. By repeating the process 500 times, we computed statistically stable estimates of the formal errors. The ingress and egress time was always fixed to the observed values given by thetransit data of Delrez et al. (2016), and we repeated this with the remaining parameters, depending on which parameter was tested for errors (e.g., in the case of the occultation center, we fixed the duration and the ingress and egress times). Although this approach is primarily dictated by keeping the execution time within a reasonable limit, our error estimates for the moment of the occultation time is in perfect agreement with the one predicted by the analytic formula of Deeg & Tingley (2017). The errors of O–C were taken equal to those of Tocc because the errors of the computed occultation times (C) have been proven to be negligible.
The available observations suggest a small (or zero) eccentricity. Because the more precise estimation also requires knowledge of the eclipse duration, the lack of this parameter for the most accurate HST and Spitzer observations prevents us from including these data in the analysis. Therefore we used only the occultation parameters derived from the SMARTS and TRAPPIST observations.
Following Winn (2010), by omitting the negligible inclination effect, we use the following formula to estimate the eccentricity:
![\begin{eqnarray*}e = \Bigg[\Bigg({\pi \over 2}{\Delta T_{\textrm{c}} \over P}\Bigg)^2 + {\Bigg({{r14-1} \over {r14+1}}\Bigg)^2}\Bigg]^{1 \over 2} \hskip 1mm ,\end{eqnarray*}](/articles/aa/full_html/2019/05/aa34325-18/aa34325-18-eq9.png) (6)
(6)
where P is the orbital period, ΔTc is the observed time of the occultation center minus the predicted time from the transit, assuming zero eccentricity; r14 = t14(occ)∕t14(tra), which is the ratio of the secondary and primary eclipse durations.
Assuming that the errors are independent of the eclipse times and durations both for the primary and the secondary eclipses and that these errors are also uncorrelated with the error of the period, we can use this equation to estimate the eccentricity and its pure statistical error.
For the transit and for the period, we took the values given in Table 4 of Delrez et al. (2016). For the secondary eclipse, we used the values shown in Table 3 of this paper. Errors were assumed to be Gaussian. Then, Eq. (6) yields e = 0.0207 ± 0.0153 when we use the SMARTS and e = 0.0314 ± 0.0222 when we use the TRAPPIST data. These eccentricity values were also tested using the transit center values of Evans et al. (2018) for the HST/STIS G430Lv2 band (we obtained very similar results for the other bands as well). We note that this test is not entirely consistent because we used the transit duration value of Delrez et al. (2016): Evans et al. (2018) did not give this parameter for their data. We obtain for the SMARTS and TRAPPIST data e = 0.0198 ± 0.0157 and e = 0.0312 ± 0.0224, respectively, that is, very close to the values estimated on the basis of the transits of Delrez et al. (2016).
Concluding, we note that Delrez et al. (2016) quoted a 3σ upper limit of e = 0.07 from the global analysis of the photometric and radial velocity data. Our independent analysis agrees quite well with theirs.
 |
Fig. 3 Systematics-filtered folded flux ratios normalized to 1.0 in the OOE part. Average fluxes (in 30 phase bins) are shown by blue dashes, and the best-fitting trapezoidal secondary eclipse approximation is plotted as the yellow continuous line. |
 |
Fig. 4 Blue dots: autocorrelation function (ACF) of the residuals of the trapezoidal fit to the final dataset shown in Fig. 3. Red dots: ACF of generated uncorrelated noise. Error bars are for the standard deviations of the ACF values of the random datasets. The time lag is given in units of the orbital period. The inset shows the immediate neighborhood of ACF at zero time-shift. |
 |
Fig. 5 Intensity plot for the unbiased estimate of the variance of the residuals between the data and the occultation model scanned in the parameter space of the displacement of the occultation center ΔTc and the duration of the event t14. We employ iterative 4σ clipping to find the best solution for each parameter combination. |
 |
Fig. 6 Same as in Fig. 5, but for the TRAPPIST data. The better contrast of the best solution is attributed to the significantly larger number of data points for the TRAPPIST data. |
Observed secondary eclipse times for WASP-121b.
4 Comparison with planet atmosphere models
At the time of writing, the following secondary eclipse observations are available for WASP-121b: the Sloan z′ data at 0.9 μm by Delrez et al. (2016), and the HST data in 1.1–1.6 μm and the Spitzer data at 3.6 μm, both by Evans et al. (2017). The main panel in Fig. 7 shows these two single-band data points, the band-averaged value of the HST spectral data, and our occultation depth in the K band at 2.2 μm (see also Table 4 for the actual numerical values we used). The data are overplotted on the recent planetary atmosphere models of Evans et al. (2017) and Parmentier et al. (2018). We note that although the “No dissociation” model very clearly shows that element dissociation needs to be considered in modeling HJ atmospheres, it is unphysical, and it is included merely to show the extreme case of neglecting this important physical process. This model was constructed using chemical equilibrium chemistry in the atmospheric structure module of the global circulation model, but the H2O abundance was considered fixed in computing the spectrum. However, the model labeled “Solar composition” is consistent in this respect and shows that the currently available data overall agree with it6, without any special assumption or adjustment. Unfortunately, the situation is somewhat more involved because several other possibilities yield spectra that are rather similar to that of the “Solar composition” model. For example, the heavy metal content of the “Solarcomposition” model might be increased by a factor of three, without any essential effect on the emission spectrum; see Parmentier et al. (2018) for further details.
The blackbody lines (gray and black) in Fig. 7 show the effect of heat transport from the day to the night side. When we assume zero Bond albedo in both cases, the black line displays the case of heat transport with maximum efficiency (AB = 0, ε = 1.0; see Cowan & Agol 2011; Lopez-Morales & Seager 2007). It is clear that all available data exclude this possibility and support circulation models that are rather inefficient, resulting in a higher day-side temperature. For WASP-121b, this temperature seems to be close to 2700 K, corresponding to ε= 0.57, assuming AB = 0. In a comparison with the models of Evans et al. (2017), who also used this planet temperature, we find that their “retrieved” model slightly underestimates our occultation depth by 1.7σ, but the mismatch for the blackbody line of 2700 K is only 0.4σ.
By scanning the planet temperature, we find that the best-fitting blackbody model to the four single-band data points (weighted equally, and also using the broadband value at 1.4 μm derived from the HST/WFC3 spectrum by Evans et al. 2017) is reached when Tp = 2652 K. The RMS and the χ2 value of the residuals is 0.170 ppt and 17.6, respectively. All points are within or close to 1σ, except for the point at 0.9 μm, which deviates by 3.8σ. For the solar composition model of Parmentier et al. (2018), we obtain 0.234 ppt and 41.2 for the RMS and χ2, respectively.These high values result from the Spitzer and HST/WFC3 data, with deviations of 3.2σ and 5.6σ, respectively (the other two points deviate by less than 0.5σ). Repeating the same comparison for the retrieved model of Evans et al. (2017), we obtain 0.222 ppt and 26.4 for the RMS and χ2. Now all points deviate near 1σ (the 2.2 μm point by 1.7σ), except for the HST/WFC3 point, which deviates by 4.7σ. From these tests it seems that there is no strongly preferred model by the single-band data. The preferred status of the blackbody model is due to the adjusted planet temperature, which turned out to be lower by 50 K than the one used by the detailed atmospheric models. The nearly common outlier status of the HST/WFC3 band-averaged point7 indicates both the value of precise observational data in selecting the best-fitting atmosphere model and the caution we must take using broadband data because at higher wavelength resolution, the data fit the retrieval model of Evans et al. (2017) quite well.
It is important to note that the status of the outliers might change with a different way of handling systematics. As mentioned, overcorrecting the systematics may lead to a lower occultation depth (e.g., we obtained a greater depth from the 0.9 μm data by ~0.1 ppt than the depth derived by Delrez et al. 2016, quite likely because our derivation lacked polynomial correction).
Concerning the slightly preferred retrieval model of Evans et al. (2017), the fact that our measurement deviates by 1.7σ from their model spectrum indicates that although additional fine-tuning is needed, the basic characteristics of the observations are matched well. On the other hand, the required VO abundance is some thousand times the solar value, which warrants some caution (see Evans et al. 2017 and Parmentier et al. 2018 for further discussion of this issue with the emission spectrum).
Additional complications come from the more extensive data that are available from HST and ground-based transmission spectrum measurements. The recent analysis of these data by Evans et al. (2018) lends further support to a high (10–30-times solar) VO abundance and lack of TiO. Furthermore, these data also pose some challenges in explaining the steep rise of the absorption in the near-ultraviolet regime. (Which trend if further amplified by the recent near-ultraviolet data by the Swift satellite; see Salz et al. 2019.) Evans et al. (2018) invoked sulfanyl (SH) as a possible absorber because the standard explanation by Rayleigh scattering fails in the case of WASP-121b, due to the high atmospheric temperature that is implied by Rayleigh scattering only.
Unfortunately, the currently available data on WASP-121b populate the more easily measurable part of the emission spectrum still too sparsely. In the waveband between 2 and 4 μm (where the CO and H2O emissions are the most pronounced) additional data would be of great help. High S/N measurements carried out by instruments such as CRIRES at the Very Large Telescope (VLT) would be clearly capable to map this crucial region. In addition to determining the abundances of the molecules above, this might also constrain the abundances derived from the shorter wavelength part of the spectrum, where gathering data with high S/N is more difficult.
 |
Fig. 7 Comparison of the single-band secondary eclipse depths (including the band-averaged HST/WFC3 data, turquoise dot) with the planetary atmosphere models of Parmentier et al. (2018) [Par18] and Evans et al. (2017) [Eva17]. Vertical error bars show 3σ statistical uncertainties, and horizontal bars indicate the widths of the individual wavebands. We caution that the “No dissociation” model is unphysical, and is shown merely to highlight the effect of omitting dissociation in computing the spectrum (see text for further details). The blackbody lines correspond to different efficiency of the day and night heat transport (black: fully efficient; gray: no heat transport). For completeness, the inset shows the HST observations of Evans et al. (2017) with their spectrum retrieval model and the solar composition model of [Par18]. For better visibility, we use 1σ error bars here. |
Secondary eclipse depths of WASP-121b.
5 Inefficiency of the day- to night-side heat transport
In agreement with other studies (e.g., Adams & Laughlin 2018, and references therein), our data support the lack of efficient day- to night-side heat transport (see Fig. 7). This conclusion is further strengthened when we compare the predicted and observed occultation depths using all currently available data. Based on the list of Alonso (2018), we collected the secondary eclipse depths measured in the 2MASS K band for 32 hot Jupiters (see Croll et al. 2015; Cruz et al. 2015; Zhou et al. 2015, Martioli et al. 2018; and this paper). The observed depths as a function of the expected value (assuming zero Bond albedo and fully efficient heat transport) are shown in Fig. 8. The figure clearly shows a nearly uniform offset, with no apparent dependence on the expected depth. The effect is exacerbated if we consider more realistic albedos, as suggested by recent analyses of full-orbit phase curves; see Adams & Laughlin (2018).
We arrive at a similar conclusion when we examine the difference between the observed and calculated occultation depths as a function of the temperature at the substellar point, for instance. Although we admit that a more complete characterization of the heat distribution by directly measuring the night- and day-side fluxes is required (i.e., Komacek & Showman 2016), no correlation seems to exist between the heat redistribution efficiency and planet temperature based on the 2.2 μm measurements alone (see Cowan & Agol 2011; Komacek & Showman 2016 advocating the existence of such a correlation). In support of our result, it is interesting to note that a similar study by Baskin et al. (2013), based on Spitzer 3.6 and 4.5 μm data, has led to the same conclusion.
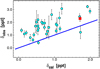 |
Fig. 8 Observed vs. calculated secondary eclipse depths for the 32 extrasolar planets known today with emission measurements at ~2.2 μm. Nearly all observations lie above the equality line, corresponding to the calculated and expected blackbody value, assuming effective heat transport from the day to the night side. WASP-121b is shown as a red square. Error bars show 1σ statistical errors. |
6 Conclusions
We presented the first secondary eclipse measurements of an extrasolar planet in the near-infrared using a 1 m class telescope. With the ANDICAM imager attached to the 1.3 m telescope of the SMARTS Consortium, we detected an occultation depth of (0.228 ± 0.023)% in the 2MASS K band from observations made in three nights of the very hot Jupiter WASP-121b. We compared this value with theoretical planetary spectra of Parmentier et al. (2018) and Evans et al. (2017) and found that it perfectly fits the former model, using solar composition, atmospheric circulation, and molecular dissociation. However, when all available secondary eclipse data are considered (Sloan z′, HST and Spitzer data; see Delrez et al. 2016 and Evans et al. 2017), it seems that the VO-enhanced model of Evans et al. (2017) is preferred over the solar composition model, but with a less favorable match to our data. Although the 2700 K blackbody line also yields an acceptable overall fit to the available data, the more detailed HST spectrum is not reproduced well. Additional data in the (2–4)μm regime would be very useful to verify model predictions on CO and H2 O emissions and build a more coherent planet atmosphere model.
Although our observations were made in a single waveband, they yield a reasonably solid piece of information on both the orbital and atmospheric characterization of the WASP-121 system. Together with future emission data in the (2– 4) μm band, they will allow us to prove or refute the existence of the CO, H2O emission feature on the day side that is predicted by the models in this waveband.
Acknowledgements
We thank Laetitia Delrez for sending us the secondary eclipse observations presented in the discovery paper on WASP-121. We are grateful to Vivien Parmentier for making the relevant planet atmosphere models accessible to us and helping in comprehending the models. The professional help given by the SMARTS staff at the Yale University during the data acquisition period is much appreciated. We also thank the referee for the critical notes on our early interpretation of the planet atmosphere models. The observations have been supported by the Hungarian Scientific Research Fund (OTKA, grant K-81373). T.K. acknowledges the support of Bolyai Research Fellowship. Additional grants (PD 121223and K 129249) from the National Research, Development and Innovation Office are also acknowledged.
Appendix A Night-by-night occultation depths
We briefly examine the night-by-night stability of the occultation signal presented in this paper from the merged data for the three observation nights (see Sect. 3). The nightly data are treated in the same way as the merged data. The derived occultation depths with their statistical errors and some additional parameters are given in Table A.1. We note that the errors shown are unbiased because we considered the number of fitted parameters (Np) and the number of clipped data points (Nclip). All nightly occultation values are within the 1σ error ranges, scattered around the merged value. Figures A.1–A.3 show the nightly data and the corresponding fits.
Night-by-night occultation depths of WASP-121 in the 2MASS K band.
 |
Fig. A.1 Separate trapezoidal eclipse fit to the systematics-filtered secondary eclipse light curve observed on 2016 February 26. The flux ratio is normalized to 1.0 in the OOE part of the light curve. The best-fitting trapezoidal is shown by the yellow line (with a black silhouette for better visibility). The 30-bin averages of the light-curve points are shown by the blue dashes. |
References
- Adams, A. D., & Laughlin, G. 2018, AJ, 156, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso, R. 2018, Handbook of Exoplanets (London: Springer) [Google Scholar]
- Anderson, D. R., Temple, L. Y., Nielsen, L. D., et al. 2018, MNRAS, submitted, [arXiv:1809.04897] [Google Scholar]
- Bakos, G. Á., Torres, G., Pál, A., et al. 2010, ApJ, 710, 1724 [NASA ADS] [CrossRef] [Google Scholar]
- Baskin, N. J., Knutson, H. A., Burrows, A., et al. 2013, ApJ, 773, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, N. B., & Agol, E. 2011, ApJ, 729, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Croll, B., Albert, L., Jayawardhana, R., et al. 2015, ApJ, 802, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Cruz, P., Barrado, D., Lillo-Box, J., et al. 2015, A&A, 574, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deeg, H. J., & Tingley, B. 2017, A&A, 599, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delrez, L., Santerne, A., Almenara, J.-M., et al. 2016, MNRAS, 458, 4025 [NASA ADS] [CrossRef] [Google Scholar]
- Deming, D., Seager, S., Richardson, L. J., & Harrington, J. 2005, Nature, 434, 740 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Evans, T. M., Sing, D. K., Wakeford, H. R., et al. 2016, ApJ, 822, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, T. M., Sing, D. K., Kataria, T., et al. 2017, Nature, 548, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, T. M., Sing, D. K., Goyal, J. M., et al. 2018, AJ, 156, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Kreidberg, L., Line, M. R., Bean, J. L., et al. 2015, ApJ, 814, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Komacek, T. D., & Showman, A. P. 2016, ApJ, 821, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez-Morales, M., & Seager, S. 2007, ApJ, 667, L191 [NASA ADS] [CrossRef] [Google Scholar]
- Martioli, E., Colón, K. D., & Angerhausen, D. 2018, MNRAS, 474, 4264 [NASA ADS] [CrossRef] [Google Scholar]
- Parmentier, V., Line, M. R., Bean, J. L., et al. 2018, A&A, 617, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Salz, M., Schneider, P. C., Fossati, L., et al. 2019, A&A, 623, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stevenson, K. B., Harrington, J., Fortney, J. J., et al. 2012, ApJ, 754, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N. 2010, ArXiv e-prints [arXiv:1001.2010v5] [Google Scholar]
- Zhou, G., Bayliss, D. D. R., Kedziora-Chudczer, L., et al. 2015, MNRAS, 454, 3002 [NASA ADS] [CrossRef] [Google Scholar]
For additional details on the instrument, access images, see http:// www.astro.yale.edu/smarts/1.3m.html; http://archive.noao.edu/search/query/
The radius quoted here is the one that appears in the abstract of the discovery paper. We use the radius based on the HST measurements of Evans et al. (2017); see Sect. 4.
Unfortunately, the signal, hampered by weather and instrumental limitations, in the Cousins I band was too weak to yield any useful planetary atmospheric constraint, so we decided to discard it. The expected occultation depth in this band is ~0.5 ppt, yielding a less than 3σ detection with the data at hand.
By admitting the existence of systematic differences for the HST near-infrared measurements of Evans et al. (2017); see inset of Fig. 7.
It is important to note that we used the errors given by Evans et al. (2017) estimated by considering only the statistical errors. However, the true range of the fluxes is nearly twenty times larger, implying the inadequacy of the statistical errors in this case.
All Tables
All Figures
 |
Fig. 1 Dithering pattern used during the near-infrared observations. The image shows the 2.4′ × 2.4′ FOV of the ANDICAM near-infrared camera, attached to the 1.3 m telescope of the SMARTS Consortium. The target (WASP-121=2MASS 07102406-3905506) is in the middle, the comparison star 2MASS 07102364-3905561 is in the lower left corner. North is up and west is to the left. Circles around the target and the comparison star show the aperture sizes used to estimate the stellar and background fluxes. |
| In the text | |
 |
Fig. 2 Simple photometric flux ratios ordered by the orbital period (pale dots). Some dithers are annotated to show the nightly trends (or the lack of them, i.e., number 9). Dither 6 (gray dots) is plotted also after employing zero-point shift and detrending by the position vector (black dots, see Sect. 2 for details). |
| In the text | |
 |
Fig. 3 Systematics-filtered folded flux ratios normalized to 1.0 in the OOE part. Average fluxes (in 30 phase bins) are shown by blue dashes, and the best-fitting trapezoidal secondary eclipse approximation is plotted as the yellow continuous line. |
| In the text | |
 |
Fig. 4 Blue dots: autocorrelation function (ACF) of the residuals of the trapezoidal fit to the final dataset shown in Fig. 3. Red dots: ACF of generated uncorrelated noise. Error bars are for the standard deviations of the ACF values of the random datasets. The time lag is given in units of the orbital period. The inset shows the immediate neighborhood of ACF at zero time-shift. |
| In the text | |
 |
Fig. 5 Intensity plot for the unbiased estimate of the variance of the residuals between the data and the occultation model scanned in the parameter space of the displacement of the occultation center ΔTc and the duration of the event t14. We employ iterative 4σ clipping to find the best solution for each parameter combination. |
| In the text | |
 |
Fig. 6 Same as in Fig. 5, but for the TRAPPIST data. The better contrast of the best solution is attributed to the significantly larger number of data points for the TRAPPIST data. |
| In the text | |
 |
Fig. 7 Comparison of the single-band secondary eclipse depths (including the band-averaged HST/WFC3 data, turquoise dot) with the planetary atmosphere models of Parmentier et al. (2018) [Par18] and Evans et al. (2017) [Eva17]. Vertical error bars show 3σ statistical uncertainties, and horizontal bars indicate the widths of the individual wavebands. We caution that the “No dissociation” model is unphysical, and is shown merely to highlight the effect of omitting dissociation in computing the spectrum (see text for further details). The blackbody lines correspond to different efficiency of the day and night heat transport (black: fully efficient; gray: no heat transport). For completeness, the inset shows the HST observations of Evans et al. (2017) with their spectrum retrieval model and the solar composition model of [Par18]. For better visibility, we use 1σ error bars here. |
| In the text | |
 |
Fig. 8 Observed vs. calculated secondary eclipse depths for the 32 extrasolar planets known today with emission measurements at ~2.2 μm. Nearly all observations lie above the equality line, corresponding to the calculated and expected blackbody value, assuming effective heat transport from the day to the night side. WASP-121b is shown as a red square. Error bars show 1σ statistical errors. |
| In the text | |
 |
Fig. A.1 Separate trapezoidal eclipse fit to the systematics-filtered secondary eclipse light curve observed on 2016 February 26. The flux ratio is normalized to 1.0 in the OOE part of the light curve. The best-fitting trapezoidal is shown by the yellow line (with a black silhouette for better visibility). The 30-bin averages of the light-curve points are shown by the blue dashes. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1, but for the night shown in the upper right corner. |
| In the text | |
 |
Fig. A.3 Same as Fig. A.1, but for the night shown in the upper right corner. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


