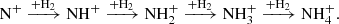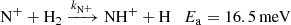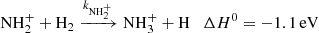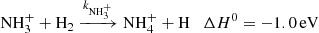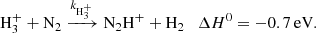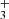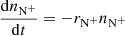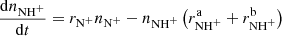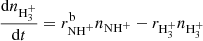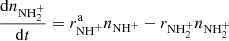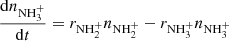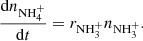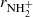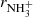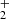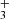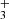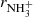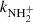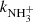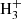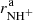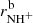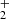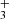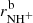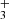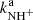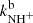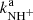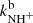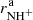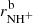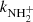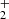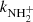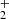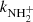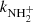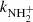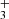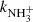© ESO 2019

1. Introduction

Nitrogen is among the six most abundant elements in the Universe. Owing to the dominance of hydrogen in the Universe, it is not surprising that nitrogen hydrides are present in the interstellar medium (ISM). Ammonia was the first polyatomic molecule discovered in interstellar space (Cheung et al. 1968). Later, other nitrogen hydrides were detected: NH by Meyer & Roth (1991), NH₂ by van Dishoeck et al. (1993), and NH₃D⁺ by Cernicharo et al. (2013). Atomic and molecular nitrogen were also observed in the ISM (Nieva & Przybilla 2012; Knauth et al. 2004). For information on recent observations of nitrogen hydrides, see the results from the Herschel/HIFI instrument (Persson et al. 2010, 2012; Caselli et al. 2017), and from the SOFIA instrument (Wyrowski et al. 2016). For a detailed description of interstellar chemistry of nitrogen hydrides, see for example Rist et al. (2013) and Harju et al. (2017) and the reviews by Le Gal et al. (2014), Gerin et al. (2016), and Acharyya & Herbst (2015). Despite some differences between observed values and the modelled predictions of populations of nitrogen hydrides (see e.g. Le Gal et al. 2014; Persson et al. 2012; Novotný et al. 2014 and references therein), it is generally accepted that the main pathway to gas-phase formation of ammonia in the ISM is a chain of hydrogen abstraction reactions followed by the dissociative recombination of NH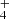 (Herbst & Klemperer 1973; Le Gal et al. 2014; Gerin et al. 2016). The suggested pathway of the gas-phase formation of the NH 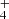in the ISM starting from N⁺ is (Le Gal et al. 2014)

(1)

In current understanding of nitrogen chemistry, the production of N⁺ in the low-temperature (10 K) dark clouds results from dissociative ionization of N₂ in reaction with He⁺ (Hily-Blant et al. 2013; Le Gal et al. 2014). Alternatively, the chain may also be initiated by 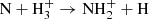, although this reaction has a high activation energy (Herbst et al. 1987; Scott et al. 1997; Le Gal et al. 2014). It is expected that neutral NH₃ molecules are consequently formed in the dissociative recombination of 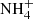ions with electrons. Other hydrides can also be formed by the recombination of ions from this sequence with electrons (Florescu-Mitchell & Mitchell 2006). To model the production of ammonia in the ISM it is important to know the rate coefficients of all the reactions in the chain (1) for temperatures down to 10 K.

The first binary ion-molecule reaction of the chain is

(2)

with a corresponding reaction rate coefficient denoted as k_N⁺. Since the enthalpy of this reaction is not yet known with sufficient precision, we provide the activation energy E_a obtained by Zymak et al. (2013). The enthalpies of the other hydrogen abstraction reactions were taken from Rist et al. (2013). This endothermic reaction of the N⁺ ion with molecular hydrogen has been studied using several well-established experimental techniques (e.g. Adams & Smith 1985; SIFDT, Marquette et al. 1988; CRESU, and Gerlich 1993; 22-pole ion trap). It has also been studied in our laboratory using the 22-pole ion trap instrument with consideration of para- and ortho-spin configurations of the reacting hydrogen molecule (Zymak et al. 2013; Plašil et al. 2014).

The next reaction of the chain (1) is

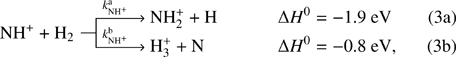
where 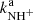and 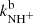are reaction rate coefficients of channels with production of 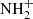and H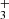, respectively. We also define the overall rate coefficient of the reaction of NH⁺ ion with H₂ as 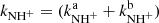. The enthalpy of the proton transfer channel (3b) was calculated from the corresponding proton affinities (Hunter & Lias 1998). Reaction (3) was studied at 300 K by Fehsenfeld et al. (1967; FA), Kim et al. (1975; ICR), and Adams et al. (1980; SIFT). At 15 K, it was studied by Gerlich (1993; ion trap). The production of H 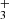ion (reaction (3b)) was only reported by Adams et al. (1980).

The produced 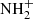ion further reacts with H₂ in reaction

(4)

with a reaction rate coefficient 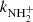. This reaction was studied by Fehsenfeld et al. (1967; FA), Kim et al. (1975; ICR), and Adams et al. (1980; SIFT) at 300 K. Using an ion trap instrument, the rate coefficient of the reaction (4) was measured at 15 K by Gerlich (1993).

The final reaction of chain (1) is

(5)

with a rate coefficient 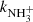. This reaction was studied experimentally over broad range of temperatures by Fehsenfeld et al. (1975), Kim et al. (1975), Smith & Adams (1981), Luine & Dunn (1985), Böhringer (1985), Barlow & Dunn (1987), Adams & Smith (1984), and Gerlich (1993). It was also studied theoretically by Herbst et al. (1991) and recently by Álvarez-Barcia et al. (2016). At temperatures above 300 K, the measured temperature dependence of the rate coefficient of the exothermic reaction (5) exhibits dependence typical for endoergic reactions. If the temperature dependence of 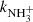measured at temperatures above 300 K is extrapolated towards lower temperatures relevant for interstellar clouds using Arrhenius dependence (Fehsenfeld et al. 1975), then the values will be far too low to explain the observed NH₃ abundances. This problem was solved when measurements at temperatures below 100 K indicated that the temperature dependence of the reaction rate coefficient has a local minimum, and then slowly increases with temperature decreasing below 50 K. These temperature dependences of rate coefficients of ion-molecule reactions with minimum have been observed several times (e.g. Smith & Adams 1981) and they are typical of exothermic reactions proceeding by tunnelling through a potential barrier (Ng et al. 1994). The observed increase in the reaction rate coefficient 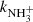at low temperatures due to the tunnelling is sufficient for reaction (5) to play an important role in interstellar chemistry.

The recent observations of nitrogen hydrides in many areas of the ISM have led to the modelling of their production and destruction in the corresponding environments. This requires the knowledge of the rate coefficients of reactions playing a role in the production and destruction of nitrogen hydrides at temperatures down to 10 K. The present contribution reports the results of the studies of the reactions of ions NH⁺, NH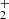, and NH 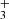with H₂ at temperatures from 15 to 300 K using a 22-pole radio frequency (RF) ion trap. After a brief description of the instrument and typical measuring procedures, new data including measured temperature dependences of the reaction rate coefficients (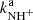, , 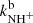, 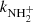and 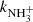) are presented. The new results are compared with values from previous experiments and with available theoretical predictions.

2. Experiment and data analysis

The experiments were carried out by means of a linear RF 22-pole ion trap instrument operating at temperatures (T_22PT) from 10 to 300 K. The basics of storing ions in RF fields have been described thoroughly by Gerlich (1992, 1995). Only a very short description of the apparatus and its operation are given here (for details, see e.g. Gerlich 1992; Gerlich et al. 2011; Plašil et al. 2011; Zymak et al. 2013). The ion trap is surrounded by a copper box, which is mounted onto a cold head of a closed-cycle helium refrigerator. Helium and hydrogen are introduced into the trap via leak valves and optionally in short pulses (∼10 ms) via a piezo valve (Gerlich 2008).

The primary reactant ions are produced by electron bombardment of the precursor gas in a storage ion source (SIS). In the present experiments, a mixture of N₂ and H₂ was used as a source gas. The produced ions were periodically extracted from the ion source and mass selected with a quadrupole mass filter. The mass-selected (primary) ions were transferred into the 22-pole ion trap, filled with a mixture of He buffer gas and H₂ reactant gas. The helium number density used in the experiments was in the range of 10¹³ − 10¹⁴ cm⁻³ during the measurements and it was temporarily increased to 10¹⁵ cm⁻³ during the injection of ions into the trap by adding He via the piezo valve. In the present experiments, normal hydrogen was used as a reactant gas with number densities in the trap varying from 10¹⁰ up to 10¹² cm⁻³. In normal H₂, the para/ortho ratio is 1/3, corresponding to the thermal equilibrium at 300 K (for discussion, see Zymak et al. 2013; Hejduk et al. 2012). As the rotational excitation in hydrogen gas is thermalized only within para and ortho manifolds, H₂ gas flowing through the gas inlet system into the trap volume is not thermalized at trap temperatures below 200 K (Zymak et al. 2013; Hejduk et al. 2015). The gas number density inside the ion trap is determined using a spinning rotor gauge and a calibrated ionization gauge with estimated uncertainty of 20%. This constant systematic uncertainty is not included in the error bars of our figures, which indicate the relative uncertainties.

At the number densities of He buffer gas and H₂ reactant gas in the present experiment, the kinetic energy of the injected ion was cooled by hundreds of collisions with He atoms prior to colliding with H₂. After various trapping times, the ions were extracted from the trap and after passing through a second quadrupole mass filter, they were detected with an MCP detector. The standard measuring procedure is based on filling the ion trap at a fixed frequency with a well-defined number of primary ions and by analysing the content of the ions in the ion trap after different trapping (reaction) times. The data are analysed under the assumption that the numbers of detected ions are proportional to the numbers of ions in the ion trap. In the following text these relative numbers of different ions of particular mass detected (counted) after trapping time t are denoted n_x(t), where the index x refers to the various ions in the ion trap. For easier comparison of the experimental results, the data plotted in the figures were normalized by dividing by the total number of detected ions n_Σ0 = ∑n_x(t₀), where t₀ is the shortest trapping time. The symbol Σ(t) in the figures indicates the normalized total number of ions in the trap, Σ(t) = ∑n_x(t)/n_Σ0. The mass discrimination of the detection system is considered in the data analysis (see e.g. Kovalenko et al. 2018, for details) and for some ions (H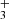 in comparison with NH⁺), it was calibrated using a suitable chemical reaction (see Sect. 3.1).

In recent experiments with our apparatus (Zymak et al. 2013; Plašil et al. 2012; Roučka et al. 2018) and in other 22-pole ion trap experiments (Hauser et al. 2015; Endres et al. 2017) it has been confirmed that the collisional temperature (here denoted simply T) is slightly higher than the temperature of the copper box surrounding the ion trap (nominal ion trap temperature, T_22PT). At the present experimental conditions, we can safely assume that the collisional temperature in the interaction of ions with H₂ does not exceed the ion trap temperature by more than 10 K. For simplicity of presentation, we define the collisional temperature as T = T_22PT + 5 K with an uncertainty of ±5 K.

To illustrate the character of the results from the ion trap experiment, the typical data measured in an experiment with injection of N⁺ ions into the ion trap filled with He buffer gas and H₂ reactant gas are shown in Fig. 1. Plotted are the time evolutions of normalized numbers (n_x(t)/n_Σ0) of N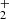⁺, NH⁺, NH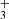, NH, NH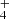, and H 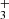ions in the ion trap. The mass discriminations for particular ions are considered in the evaluation of the measured data. Owing to the large differences between the values of the rate coefficients of the reactions in chain (1), the data were collected in small time steps over a broad time interval. The dominant process after the injection of N⁺ ions is their reaction with H₂ in which the NH⁺ ions are formed. The NH⁺ ions further react with H₂, producing N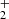H and H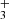. The NH 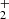ions consequently react with H₂ to produce NH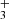. Finally, the NH 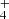ions are produced in slow reactions of NH 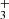with H₂. From the time evolution of the normalized number of H 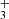ions it can be seen that at very long trapping times H 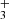ions are slowly removed by reactions with N₂ (see e.g. Marquette et al. 1989) that penetrates into the trap volume from the ion source:

(6)

Fig. 1. Measured time evolutions of normalized numbers (nx(t)/nΣ0) of N+, NH+, NH, NH, NH, and H ions in the trap filed with He/H2 gas mixture after the injection of N+ ions from the SIS. The collisional temperature is T = 16 K, hydrogen number density is [H2]=5.7 × 1010 cm−3 and helium number density is [He]=5.6 × 1013 cm−3. The fitted solution of the corresponding system of rate equations is indicated with the solid lines. The crosses (x) indicate the sum of the normalized numbers (Σ(t)) of all ions in the ion trap.

Open with DEXTER

At low temperatures (⪅40 K), this process becomes negligible because the number density of N₂ in the trap is reduced by condensation on the walls of the trap.

The time evolution of the numbers of ions in the ion trap after injection of N⁺ ions can be described by the following set of differential balance equations, which can be derived from the chemical Eqs. (2)–(6):

(7)

(8)

(9)

(10)

(11)

(12)

The reactions are parametrized by the reaction rates r_x, which are proportional to the reaction rate coefficients and the number densities of the neutral reactants, i.e. r_x = k_x[H₂] in the case of reactions with H₂ and in Eq. (9). The rate coefficients of the reactions (2)–(6) can therefore be determined by fitting the solution of the corresponding set of differential rate equations to the experimental data with the reaction rates and initial numbers of ions as free parameters. From the fitted rates r_x at given hydrogen density [H₂], we calculate the corresponding reaction rate coefficients as k_x = r_x/[H₂]. An example of a fitted solution is also shown in Fig. 1.

In measurements with NH⁺ and NH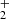 primary ions, the system can be simplified by setting n_N⁺ and (n_N⁺, n_NH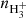⁺, ) to zero, respectively. Special attention should be paid to the possible excitation of the intermediate ions produced in the sequence of reactions in trap. Details concerning the studies of specific reactions are discussed in Sect. 3.

To confirm that the observed reaction rates are indeed caused by binary reactions with H₂ and to evaluate the possible loss of ions due to other (background) processes, we measured the time evolutions of the relative numbers of the ions at several number densities of hydrogen in the ion trap. In these particular experiments, N⁺ ions were injected into the ion trap (see example in Fig. 1). The examples of the dependences of the reaction loss rates (r_x) on [H₂] for the reactions (2)–(5) measured at T = 18 K are shown in Fig. 2. The values of 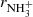were obtained from the fits of the measured time evolutions of relative number of ions at long trapping times, i.e. from evolutions of 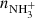and 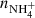(not shown in Fig. 1; see Fig. 9 below). The linearity of the dependences plotted in Fig. 2 confirms that the time evolutions of the relative numbers of particular ions in the ion trap are controlled by binary ion-molecule reactions with H₂. The measured loss rates can be expressed by the formula, r_x = k_x[H₂]+r_xbg, where r_xbg is the background loss rate for particular ions. The corresponding binary reaction rate coefficients k_N⁺, k_NH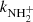⁺, , and 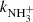are given by the slope of the plotted dependences. The value of k_N⁺(18 K) = (1.0 ± 0.4)×10⁻¹⁰ cm³ s⁻¹ obtained from the data plotted in Fig. 2 is in very good agreement with the values obtained in previous studies (Zymak et al. 2013). The values of the other reaction rate coefficients obtained from the data in Fig. 2 are discussed below.

Fig. 2. Measured reaction loss rates rN+, rNH+, , and of N+, NH+, NH, and NH ions, respectively, as a function of H2 number density. The primary N+ ions are injected into the ion trap from the SIS. The collisional temperature is T = 18 K and helium number density is [He]=8 × 1013 cm−3. For the relatively slow reaction of NH ions, the plotted values of are multiplied by a factor of 2000. The corresponding binary reaction rate coefficients kN+, kNH+, , and given by the slope of the plotted dependences are indicated in the legend.

Open with DEXTER

In order to increase the accuracy of the measured reaction rate coefficients for reactions of particular ions, these ions are produced in the SIS and injected into the ion trap. The corresponding reaction rate coefficient can then be calculated from the decay (time evolution) of the relative number of this particular ion. The obvious advantage of the determination of the rate coefficient from the decrease in the relative number of the studied ion is that the decrease in the relative number of the injected ions is influenced only by the reaction of particular ions with the reactant gas.

3. Results and discussion

3.1. Reaction NH⁺ + H₂

We measured the rate coefficients for the atom abstraction reaction (3a) and for the proton transfer reaction (3b) at the ion trap temperatures from 10 up to 130 K. In these experiments, NH⁺ ions were produced by electron bombardment of the mixture of H₂ and N₂ gases in the SIS and injected into the trap. The typical time evolutions of the normalized numbers of primary and product ions are shown in Fig. 3.

Fig. 3. Measured time evolutions of the normalized numbers (nx(t)/nΣ0) of indicated ions in the trap. A+(15 Da) indicates a normalized number of ions with mass 15 Da (mixture of 14NH+ and 15N+ ions). The measurements were performed at T = 34 K, [H2]=6.2 × 1010 cm−3, and [He]≈1014 cm−3. The solid lines are least-squares fits, which were used to determine the reaction rate coefficients. The dash-dotted straight line indicates the decrease in the normalized numbers of 14NH+ ions and the dotted line indicates the normalized numbers of 15N+ ions. The crosses (×) indicate the sum of the normalized numbers of all ions in the ion trap, Σ(t). The normalized numbers of ions are increased by a factor of 2.

Open with DEXTER

Since the mass filters in our instrument cannot resolve between ¹⁴NH⁺ and the ¹⁵N⁺ isotope, we also injected a small fraction of ¹⁵N⁺. This mixture of ¹⁴NH⁺ and ¹⁵N⁺ ions (mass 15 Da) is denoted A⁺(15 Da). The relative populations of ¹⁴NH⁺ and ¹⁵N⁺ ions injected to the ion trap are influenced by the natural abundance of ¹⁵N in N₂ and by kinetics in the ion source at particular conditions (partial pressures of gases, electron energy, and storage time in the SIS). The decrease in the normalized number of A⁺(15 Da) is exponential (dash-dotted straight line in semi-log plot) with a leveling at ∼0.025 (dotted line indicated as ¹⁵N⁺). This leveling of the A⁺(15 Da) numbers was not observed when ¹⁴NH⁺ ions were produced directly in the trap in the reaction of H₂ with ¹⁴N⁺ ions (with well-known isotopic composition; see the example in Fig. 1). This confirms that the slowly reacting ions are ¹⁵N⁺ ions. The presence of ¹⁵N⁺ is considered in the data analysis. Owing to its small rate coefficient, the reaction of ¹⁵N⁺ with H₂ does not influence the evaluation of the rate coefficient k_NH⁺. Nevertheless, we take it into account, assuming that it has the same rate coefficient as the ¹⁴N⁺ + H₂ reaction (Zymak et al. 2013).

From the data plotted in Fig. 3, we can see the decrease in the relative number of NH⁺ ions and the production of N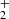H and H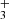 ions. To obtain the branching ratio for the reactions (3a) and (3b), the ion detection system had to be calibrated. We obtained the discrimination of the detection system between ions of mass 3 Da and 16 Da by measuring the discrimination between mass 3 Da and 17 Da using a calibration reaction of 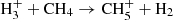(Bohme et al. 1980) and by taking into account the discrimination between mass 16 Da and 17 Da known from the present experiment with reaction .

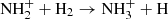We verified the binary character of the reactions (3a) and (3b) at the present experimental conditions by measuring the dependences of the reaction rates 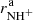and 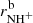on hydrogen number density. The examples of the dependences measured at temperature T = 20 K are shown in Fig. 4. The number density of H₂ leaking from the ion source has also been measured and is accounted for in our figures.

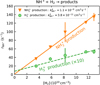Fig. 4. Measured dependences of the reaction rates and , corresponding to the production of NH and H ions, on H2 number density. The plotted values of (corresponding to H production) are increased by a factor of 10. The mean helium number density was of the order of 1014 cm−3. The collisional temperature is T = 20 K. In these experiments, the primary NH+ ions were produced in the SIS and injected into the ion trap. The values of the binary reaction rate coefficients and obtained from the slopes of the corresponding dependences are shown in the legend.

Open with DEXTER

By fitting the measured time evolutions of the relative numbers of ions in the ion trap, the reaction rate coefficients 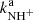and 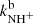for the reaction channel (3a) and (3b) were obtained. The temperature dependences of the reaction rate coefficients 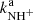and 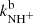are shown in Fig. 5. Also plotted is the value of k_NH⁺ measured at 300 K by Kim et al. (1975). There is just one value of the reaction rate coefficient k_NH⁺ measured in the ion trap experiment at 15 K by Gerlich (1993). In the ion trap experiment, Gerlich measured the overall reaction rate coefficient k_NH⁺ (see Fig. 5). Production of H 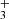ions was observed only in the selected ion flow tube (SIFT) studies of Adams et al. (1980). At 300 K, they observed 85% of NH 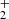and 15% of H 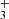products. The corresponding values of 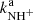and 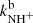are plotted in Fig. 5. If we extrapolate our data from 130 K towards 300 K as a constant, then there is good agreement with the previously obtained values of k_NH⁺ by Kim et al. (1975) and 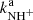by Adams et al. (1980). However, the value of 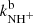for the production of H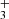, measured by Adams et al. (1980) is almost a factor of 4 higher than the present value at 130 K. Values recommended by the Kinetic Database for Astrochemistry (KIDA, Wakelam et al. 2012) and by the University of Manchester Institute of Science and Technology (UMIST) Database for Astrochemistry (McElroy et al. 2013) are also included in Fig. 5.

Fig. 5. Measured temperature dependences of the reaction rate coefficients and of the reactions (3a) and (3b), respectively. The data were binned and averaged for presentation. The raw data without binning are indicated with the smaller points. The stars (at 20 K) indicate the reaction rate coefficients obtained from the dependences of and on [H2] (Fig. 4). The horizontal solid line (kL) indicates the value of the Langevin collisional rate coefficient. Results of Kim et al. (1975), Adams et al. (1980), and Gerlich (1993) are indicated with the open symbols. The values taken from the KIDA (Wakelam et al. 2012) and UMIST (McElroy et al. 2013) databases are also plotted.

Open with DEXTER

There have been several previous studies of reaction of NH⁺ with H₂; however, this is the first study giving the temperature dependences of the reaction rate coefficients 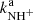and 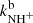from 15 up to 130 K, i.e. for astrophysically relevant temperatures.

3.2. Reaction NH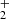 + H₂

As mentioned above, in the experiments where N⁺ ions were injected into the ion trap and NH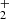 ions were produced in the chain of reactions with H₂, we observed the dependence of the measured reaction rate coefficient 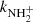on partial pressures of gases in the ion trap and on the trapping time. This is presumably connected with internal excitation of NH 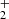ions formed in exothermic reactions, which did not encounter enough collisions with He and H₂ for collisional de-excitation prior to the hydrogen abstraction reaction. To avoid uncertainties, the NH 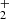ions were produced in the SIS and injected into the ion trap. The primary NH 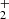ions were produced by electron bombardment of the mixture of N₂ and H₂ with number density ratio [N₂]:[H₂]≈10 : 3. In these experiments, the temperature of the ion trap was varied from 10 K to 300 K. An example of measured time evolutions of the normalized numbers of primary NH 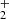and produced NH 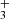ions is shown in Fig. 6. The exponential decrease in the normalized numbers of NH 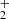ions over two orders of magnitude indicates a reaction with a constant reaction rate coefficient.

Fig. 6. Measured time evolutions of the normalized numbers (nx(t)/nΣ0) of the primary NH ions and of the produced NH ions. The measurements were performed at the collisional temperature T = 39 K, hydrogen number density [H2]=6.2 × 1010 cm−3, and helium number density [He]∼1014 cm−3. The solid lines are fits of the measured data. The crosses (x) indicate the sum of the normalized numbers of all ions in the ion trap, Σ(t).

Open with DEXTER

Two examples of dependences of the reaction rates 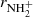on [H₂] for reaction (4) measured at T = 18 K and T = 24 K are shown in Fig. 7. The linearity of the obtained dependences confirms that the time evolution of the relative numbers of NH 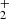ions in the ion trap is controlled by a binary reaction with H₂. The slope of the obtained linear dependence is given by the rate coefficient 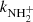for the corresponding binary reaction.

	Fig. 7. Measured dependence of the reaction rate rNH2f of NH ions on H2 number density. The helium number density is [He]∼1.1 × 1014 cm−3. The collisional temperatures are T = 18 K and 24 K. The corresponding values of the binary reaction rate coefficient are given by the slope of the plotted dependences. The primary NH ions were produced in the SIS and injected into the ion trap.
Open with DEXTER

The measured temperature dependence of the rate coefficient 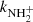between 15 and 300 K is shown in Fig. 8. Also plotted are the results of previous studies at 300 K (Kim et al. 1975; Adams et al. 1980), which are in agreement (within experimental accuracy) with the present value of 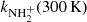. Gerlich (1993) measured the rate coefficient 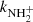of reaction (4) at 15 K using a 22-pole ion trap with injection of N⁺ ions. From time evolutions of the number of ions in the trap filled with mixture of He and H₂, he obtained the reaction rate coefficient 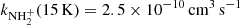(point G in Fig. 8). At similar conditions in present experiments using the injection of N⁺ ions into the ion trap, we obtained 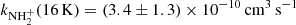(point A, the value obtained from the data shown in Fig. 1) and 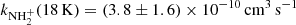(point B, the value obtained from the data shown in Fig. 2). The present results (point A and B) and the value from Gerlich (1993) (point G) are in rather good agreement, but we note again, that they were measured with short relaxation time, i.e. at conditions without sufficient relaxation of reacting ions (see also discussion in Gerlich 1993). The values of 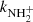recommended by KIDA (Wakelam et al. 2012) and UMIST (McElroy et al. 2013) are also indicated in Fig. 8. KIDA and UMIST only use values measured at 300 K, and the differences in the measured temperature dependences are obvious.

Fig. 8. Temperature dependence of the rate coefficient of the reaction (4). The upward pointing triangles indicate the binned values measured in the present experiments with the injection of NH ions into the ion trap. The raw data without binning are indicated with the smaller points. The stars indicate the reaction rate coefficients obtained from the [H2] dependences (see Fig. 7). The horizontal straight line (kL) indicates the value of the Langevin collisional rate coefficient. The values of measured in previous experiments at 300 K by Kim et al. (1975; ICR) and by Adams et al. (1980; SIFT) are indicated with the open triangles. The labels A and B indicate values of obtained in the present experiments with the injection of N+ ions into the trap at 16 and 18 K, respectively. The label G indicates the value of measured in similar conditions in ion trap at 15 K by Gerlich (1993).

Open with DEXTER

In the experiments with injection of N⁺ or NH⁺ ions, we observed that at temperatures below ∼100 K the measured values of 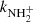are dependent on processes of formation of NH 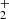ions. The detailed investigation of this phenomenon, including dependence on para/ortho population of H₂, will be a subject of further studies in our laboratory and are not discussed here.

3.3. Reaction NH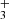 + H₂

The exothermic reaction (5) of NH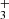 ion with H₂ has been studied many times owing to fundamental interest and to its predicted role in the formation of NH₃ in interstellar clouds (Herbst & Klemperer 1973; Le Gal et al. 2014; Gerin et al. 2016). Recent theoretical calculations of the temperature dependence of the reaction rate coefficient 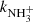for temperatures down to 20 K (Álvarez-Barcia et al. 2016) are in qualitative agreement with the experiments; nevertheless, at temperatures between 30 and 100 K the calculated reaction rate coefficient is smaller than the available experimental values. To provide further experimental evidence, we measured the reaction rate coefficients at temperatures ranging from 15 to 100 K. In these experiments, N⁺ ions were injected into the ion trap and in a sequence of hydrogen abstraction reactions, NH 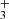ions were formed there (see example in Fig. 1). Since reaction (5) is slow in the temperature range covered, the NH 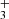ions formed in the ion trap have thousands of collisions with He and H₂ prior to the reaction. We can expect that in these collisions NH 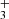ions are thermalized. To see the eventual influence of excitation/de-excitation of NH 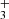ions in collisions with H₂ the data were collected using a broad range of hydrogen densities (see the example of the data plotted in Fig. 2). The example of the measured time evolutions of the normalized numbers (n_x(t)/n_Σ0) of the primary NH 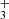ions and of the produced NH 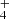ions measured at long storage time is shown in Fig. 9. The data plotted in Fig. 9 were measured at identical experimental conditions as data plotted in Fig. 1, the only difference is in the time scale. We also monitored the time evolution of the normalized numbers of H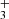, N⁺, NH⁺, and NH 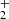ions in the trap (see the example plotted in Fig. 1), but in Fig. 9 these data are not included. As we can see from the data plotted in Fig. 1, the ions N⁺, NH⁺, and NH 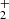are within 0.2 s removed from the trap in the sequence of fast reactions with H₂.

Fig. 9. Measured time evolutions of normalized numbers (nx(t)/nΣ0) of NH and NH ions in the trap filed with He/H2 gas mixture after the injection of N+ ions from the SIS and fast formation of NH ions. The collisional temperature is T = 16 K, hydrogen number density is [H2]=5.7 × 1010 cm3 s−1 and helium number density is [He]=5.6 × 1013 cm3 s−1. The fitted solution of the corresponding system of rate equations is indicated with the solid lines. The crosses (×) indicate the sum of the normalized numbers of all ions in the ion trap (Σ(t)).

Open with DEXTER

The values of 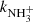obtained from the fits of measured time evolutions of n_x(t) at long trapping times (i.e. with long relaxation times) at temperatures from 15 up to 100 K are plotted in Fig. 10. We can see the agreement of the present results with the previous experimental results over the covered range of temperatures; in other words, our experiment confirms that the recently calculated reaction rate coefficient by Álvarez-Barcia et al. (2016) is systematically lower than the experimental data at low temperatures.

Fig. 10. The temperature dependence of the reaction rate coefficient . The binned present data measured with long trapping times are indicated with the full diamonds. The raw data without binning are indicated with the smaller points. Present data measured with short trapping time are indicated with a red star (label A). The points labelled as G1 and G2 are the values measured by Gerlich (1993) using short and long trapping time, respectively. Previous experimentally determined binary rate coefficient are taken from Fehsenfeld et al. (1975), Kim et al. (1975), Smith & Adams (1981), Adams & Smith (1984), Luine & Dunn (1985), Böhringer & Arnold (1985), Böhringer (1985), Barlow & Dunn (1987). The plotted theoretical temperature dependences were calculated by Herbst et al. (1991) (dashed line) and by Álvarez-Barcia et al. (2016) (solid line). The dash dotted line indicates the Arrhenius dependence obtained by the fit of the data measured at temperatures above 300 K (Fehsenfeld et al. 1975). Included are also the temperature dependences recommended by KIDA (Wakelam et al. 2012) and by UMIST (McElroy et al. 2013).

Open with DEXTER

When the trapping time was short (⪅100 ms) and the time for the relaxation of produced NH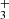 ions was not long enough, we observed a substantial increase in the reaction rate coefficient 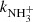in comparison with values obtained in experiments using long trapping time. An example of a value of 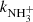obtained from the fit of time evolutions of n_x(t) at a short trapping time (i.e. with a short relaxation time) is plotted in Fig. 10, labelled A (non-thermalized 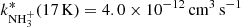). A similar increase in the reaction rate coefficient at short trapping time was observed by Gerlich with his ion trap experiment at 15 K (Gerlich 1993). His results obtained at short and long trapping times are labelled G1 and G2 in Fig. 10. At He pressures used in the ion trap in the present experiments (with NH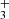) we did not observe any effect of a ternary reaction. The temperature dependences of 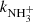recommended by KIDA (Wakelam et al. 2012) and by UMIST (McElroy et al. 2013) are also plotted in Fig. 10.

4. Summary

Following our previous studies of the reaction of N⁺ ions with molecular hydrogen, we studied the chain of hydrogen abstraction reactions of NH⁺, NH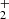, and NH 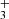ions with molecular hydrogen leading to the formation of NH ions at temperatures relevant for interstellar clouds. Using the 22-pole ion trap apparatus, we measured the temperature dependences of the rate coefficients of the reactions of NH⁺, NH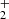, and NH 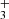ions with H₂ at temperatures down to 15 K.

In the reactions of NH⁺ ions, we observed two products: NH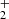 (∼97%) and H 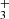(∼3%) (see Figs. 3–5). There have been several previous studies of the reaction of NH⁺ with H₂, but this is the first study giving the temperature dependences of the reaction rate coefficients 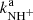and 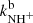at astrophysically relevant temperatures. In the covered temperature range, from 15 to 130 K, both reaction rate coefficients are approximately constant (see Fig. 5). The value of 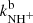obtained in our experiment at 130 K, 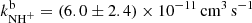is approximately 4 times lower than the only previously available value, which was obtained at 300 K (Adams et al. 1980, 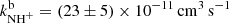). Although these values are not directly comparable due to the difference in temperatures, it is unlikely that the reaction rate coefficient, which is constant below 130 K, would change by a factor of 4 between 130 K and 300 K. There are several systematic effects that can specifically affect the measurement of such a minor reaction channel. We are not able to discuss the possible sources of error in the experiment of Adams et al. (1980), such as different detection efficiencies and diffusion rates for H 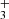and NH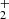. In our study, the detection efficiency was calibrated in experiments with H 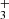and CH₄ (see Sect. 3.1) at otherwise identical conditions to the NH⁺ experiments. The standard deviation of the detection efficiency was smaller than 10% at given experimental conditions, although it can vary by tens of percentage points with change of potentials in the extraction and detection system. The other systematic effect is related to the kinetic energy release of the reaction. Although we do not know what fraction of the 0.8 eV reaction exothermicity is converted to kinetic energy of the products, it is possible that the H 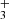ion gains sufficient energy to escape from the trap. However, we did not observe any variation in the branching ratio with trap RF amplitude or He pressure, which would indicate this effect.

The temperature dependence of the rate coefficient of the reaction of NH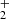 ion with H₂ was measured for temperatures from 15 to 300 K (see Fig. 8). The only observed product of the reaction was the 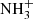ion. The rate coefficient of this reaction drops monotonically from 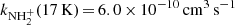to 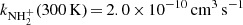. At 300 K, our value of 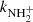is in agreement with the results of both previous studies (Kim et al. 1975; Adams et al. 1980). At 15 K, our value is significantly higher than that of Gerlich (1993). Our tests indicate that this might be due to insufficient relaxation of the NH 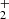ions in the experimental procedure of Gerlich (1993). Our experiments were carried out with an injection of NH 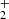ions from the SIS to the ion trap, and the decay of the number of primary ions was observed over long trapping times to exclude the influence of the process of formation and relaxation of NH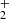. The time dependence of the NH 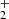ion formation process and its relaxation in He or H₂ collisions is discussed. The detailed investigation of this phenomenon, including dependence on para/ortho population of H₂, will be a subject of further studies in our laboratory and is not discussed here. This is the first study giving the temperature dependence of the reaction rate coefficient 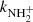from 15 K to 300 K.

Due to the astrophysical significance, the temperature dependence of the rate coefficient of the reaction of NH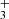 with H₂, producing NH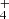, was also studied. The measured temperature dependence of the reaction rate coefficient has a minimum at temperatures around 70 K (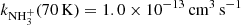). At lower temperatures the value of 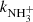slowly increases with decreasing temperature. The presented data for the reaction of NH 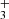ions with H₂ are in agreement with previous experimental values. The recently calculated reaction rate coefficient of Álvarez-Barcia et al. (2016) is systematically lower than all the experimental data at temperatures below 150 K, although the discrepancy is close to the experimental error.

Studies of the reactions of NH⁺, NH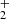, and NH 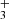ions with D₂, HD, and para-H₂ are in preparation.

Acknowledgments

We thank the Technische Universität Chemnitz and the Deutsche Forschungsgemeinschaft for lending the 22-pole trap instrument to the Charles University team. We thank Prof. Dieter Gerlich for the discussion and helpful suggestions. This work was partly supported by the Czech Science Foundation (GACR 17-19459S, GACR 17-18067S), and by Charles University (project Nr. GAUK 1584217, 1144616, 1168216).

References

All Figures

	Fig. 1. Measured time evolutions of normalized numbers (nx(t)/nΣ0) of N+, NH+, NH, NH, NH, and H ions in the trap filed with He/H2 gas mixture after the injection of N+ ions from the SIS. The collisional temperature is T = 16 K, hydrogen number density is [H2]=5.7 × 1010 cm−3 and helium number density is [He]=5.6 × 1013 cm−3. The fitted solution of the corresponding system of rate equations is indicated with the solid lines. The crosses (x) indicate the sum of the normalized numbers (Σ(t)) of all ions in the ion trap.
Open with DEXTER
In the text

	Fig. 2. Measured reaction loss rates rN+, rNH+, , and of N+, NH+, NH, and NH ions, respectively, as a function of H2 number density. The primary N+ ions are injected into the ion trap from the SIS. The collisional temperature is T = 18 K and helium number density is [He]=8 × 1013 cm−3. For the relatively slow reaction of NH ions, the plotted values of are multiplied by a factor of 2000. The corresponding binary reaction rate coefficients kN+, kNH+, , and given by the slope of the plotted dependences are indicated in the legend.
Open with DEXTER
In the text

	Fig. 3. Measured time evolutions of the normalized numbers (nx(t)/nΣ0) of indicated ions in the trap. A+(15 Da) indicates a normalized number of ions with mass 15 Da (mixture of 14NH+ and 15N+ ions). The measurements were performed at T = 34 K, [H2]=6.2 × 1010 cm−3, and [He]≈1014 cm−3. The solid lines are least-squares fits, which were used to determine the reaction rate coefficients. The dash-dotted straight line indicates the decrease in the normalized numbers of 14NH+ ions and the dotted line indicates the normalized numbers of 15N+ ions. The crosses (×) indicate the sum of the normalized numbers of all ions in the ion trap, Σ(t). The normalized numbers of ions are increased by a factor of 2.
Open with DEXTER
In the text

	Fig. 4. Measured dependences of the reaction rates and , corresponding to the production of NH and H ions, on H2 number density. The plotted values of (corresponding to H production) are increased by a factor of 10. The mean helium number density was of the order of 1014 cm−3. The collisional temperature is T = 20 K. In these experiments, the primary NH+ ions were produced in the SIS and injected into the ion trap. The values of the binary reaction rate coefficients and obtained from the slopes of the corresponding dependences are shown in the legend.
Open with DEXTER
In the text

	Fig. 5. Measured temperature dependences of the reaction rate coefficients and of the reactions (3a) and (3b), respectively. The data were binned and averaged for presentation. The raw data without binning are indicated with the smaller points. The stars (at 20 K) indicate the reaction rate coefficients obtained from the dependences of and on [H2] (Fig. 4). The horizontal solid line (kL) indicates the value of the Langevin collisional rate coefficient. Results of Kim et al. (1975), Adams et al. (1980), and Gerlich (1993) are indicated with the open symbols. The values taken from the KIDA (Wakelam et al. 2012) and UMIST (McElroy et al. 2013) databases are also plotted.
Open with DEXTER
In the text

	Fig. 6. Measured time evolutions of the normalized numbers (nx(t)/nΣ0) of the primary NH ions and of the produced NH ions. The measurements were performed at the collisional temperature T = 39 K, hydrogen number density [H2]=6.2 × 1010 cm−3, and helium number density [He]∼1014 cm−3. The solid lines are fits of the measured data. The crosses (x) indicate the sum of the normalized numbers of all ions in the ion trap, Σ(t).
Open with DEXTER
In the text

	Fig. 7. Measured dependence of the reaction rate rNH2f of NH ions on H2 number density. The helium number density is [He]∼1.1 × 1014 cm−3. The collisional temperatures are T = 18 K and 24 K. The corresponding values of the binary reaction rate coefficient are given by the slope of the plotted dependences. The primary NH ions were produced in the SIS and injected into the ion trap.
Open with DEXTER
In the text

	Fig. 8. Temperature dependence of the rate coefficient of the reaction (4). The upward pointing triangles indicate the binned values measured in the present experiments with the injection of NH ions into the ion trap. The raw data without binning are indicated with the smaller points. The stars indicate the reaction rate coefficients obtained from the [H2] dependences (see Fig. 7). The horizontal straight line (kL) indicates the value of the Langevin collisional rate coefficient. The values of measured in previous experiments at 300 K by Kim et al. (1975; ICR) and by Adams et al. (1980; SIFT) are indicated with the open triangles. The labels A and B indicate values of obtained in the present experiments with the injection of N+ ions into the trap at 16 and 18 K, respectively. The label G indicates the value of measured in similar conditions in ion trap at 15 K by Gerlich (1993).
Open with DEXTER
In the text

	Fig. 9. Measured time evolutions of normalized numbers (nx(t)/nΣ0) of NH and NH ions in the trap filed with He/H2 gas mixture after the injection of N+ ions from the SIS and fast formation of NH ions. The collisional temperature is T = 16 K, hydrogen number density is [H2]=5.7 × 1010 cm3 s−1 and helium number density is [He]=5.6 × 1013 cm3 s−1. The fitted solution of the corresponding system of rate equations is indicated with the solid lines. The crosses (×) indicate the sum of the normalized numbers of all ions in the ion trap (Σ(t)).
Open with DEXTER
In the text

	Fig. 10. The temperature dependence of the reaction rate coefficient . The binned present data measured with long trapping times are indicated with the full diamonds. The raw data without binning are indicated with the smaller points. Present data measured with short trapping time are indicated with a red star (label A). The points labelled as G1 and G2 are the values measured by Gerlich (1993) using short and long trapping time, respectively. Previous experimentally determined binary rate coefficient are taken from Fehsenfeld et al. (1975), Kim et al. (1975), Smith & Adams (1981), Adams & Smith (1984), Luine & Dunn (1985), Böhringer & Arnold (1985), Böhringer (1985), Barlow & Dunn (1987). The plotted theoretical temperature dependences were calculated by Herbst et al. (1991) (dashed line) and by Álvarez-Barcia et al. (2016) (solid line). The dash dotted line indicates the Arrhenius dependence obtained by the fit of the data measured at temperatures above 300 K (Fehsenfeld et al. 1975). Included are also the temperature dependences recommended by KIDA (Wakelam et al. 2012) and by UMIST (McElroy et al. 2013).
Open with DEXTER
In the text