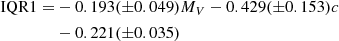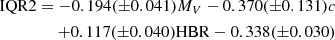| Issue |
A&A
Volume 624, April 2019
|
|
|---|---|---|
| Article Number | A24 | |
| Number of page(s) | 15 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201935110 | |
| Published online | 02 April 2019 | |
Empirical estimates of the Na–O anti-correlation in 95 Galactic globular clusters
INAF-OAS Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Gobetti 93/3, 40129 Bologna, Italy
e-mail: eugenio.carretta@inaf.it
Received:
23
January
2019
Accepted:
11
February
2019
Large star-to-star abundance variations are direct evidence of multiple stellar populations in Galactic globular clusters (GCs). The main and most widespread chemical signature is the anti-correlation of the stellar Na and O abundances. The interquartile range (IQR) of the [O/Na] ratio is well suited to quantifying the extent of the anti-correlation and to probe its links to global cluster parameters. However, since it is quite time consuming to obtain precise abundances from spectroscopy for large samples of stars in GCs, here we show empirical calibrations of IQR[O/Na] based on the O, Na abundances homogeneously derived from more than 2000 red giants in 22 GCs in our FLAMES survey. We find a statistically robust bivariate correlation of IQR as a function of the total luminosity (a proxy for mass) and cluster concentration c. Calibrated and observed values lie along the identity line when a term accounting for the horizontal branch (HB) morphology is added to the calibration, from which we obtained empirical values for 95 GCs. Spreads in proton-capture elements O and Na are found for all GCs in the luminosity range from MV = −3.76 to MV = −9.98. This calibration reproduces in a self-consistent picture the link of abundance variations in light elements with the He enhancements and its effect on the stellar distribution on the HB. We show that the spreads in light elements seem already to be dependent on the initial GC masses. The dependence of IQR on structural parameters stems from the well known correlation between c and MV, which is likely to be of primordial origin. Empirical estimates can be used to extend our investigation of multiple stellar populations to GCs in external galaxies, up to M 31, where even integrated light spectroscopy may currently provide only a hint of such a phenomenon.
Key words: stars: abundances / stars: atmospheres / stars: Population II / globular clusters: general
© ESO 2019
1. Introduction
The dawn of observations of multiple stellar populations in Galactic globular clusters (GCs) dates back to more than 30 years ago. Since then, a major effort has been devoted to quantifying the amount of the stellar component whose composition deviates from the typical pollution given by core-collapse supernovae (SNe) in a metal-poor environment.
The first attempts concerned the dichotomy of CN and CH bandstrengths observed in GC stars (primarily giants, see the focus review by Smith 1987). The ratios of CN-weak to CN-strong stars were used as fingerprints of the star to star abundance variations in GCs and to investigate possible links to global cluster parameters (see e.g. Norris 1987, and, more recently Kayser et al. 2008; Pancino et al. 2010). This approach essentially discriminates two main components: first generation (FG) stars, with the typical chemical pattern of metal-poor halo stars, and second generation (SG) stars, whose composition was very likely altered by the nuclearly processed matter ejected from massive stars of the first component. This, in short, is the classical scenario summarized, together with its history, drawbacks and open issues, in a number of reviews with all the necessary references (Kraft 1994; Gratton et al. 2004, 2012; Bastian & Lardo 2018).
An obvious advantage of CH/CN-based indicators is that the method can be easily extended to large samples by using suitable photometric bandpasses sensitive to C and N absorption features (see e.g. Briley 1997; Briley et al. 2001; Milone et al. 2012a; Monelli et al. 2013). Among the cons, we mention the warning put forward by G.H. Smith and collaborators (see Smith et al. 2013; Smith 2015), that probably photometry and spectroscopy may not see exactly the same things, most photometric indexes being “blind” to the alterations in the abundances of heavier elements. As a consequence, it is more difficult to quantify the contributions when higher ranges of temperatures are involved in the proton-capture reactions of the complete CNO cycle (Denisenkov & Denisenkova 1989; Langer et al. 1993) responsible for alterations in species such as O and Na, not to mention Mg and Al.
A typical example is provided by the anti-correlation of Na with O abundances in GC stars discovered by the Lick-Texas group about 30 years ago (see Kraft 1994; Gratton et al. 2004 for references). As large samples of stars in several GCs became routinely available thanks to efficient, high multiplex spectrographs, Carretta (2006) proposed to use the interquartile range IQR of the [O/Na] distribution to quantify the extent of this main chemical signature of multiple populations in GCs. Being defined as the middle 50% of a data sample, the IQR is a robust indicator, insensitive to outliers, not very sensitive to small number statistics and upper limits. The IQR is driven by the fraction of stars where the changes in composition are more evident (Carretta et al. 2010a). The IQR[O/Na] seems to be a good tool to probe the interplay between the internally processed matter and the leftover pristine gas resulting in the formation of SG stars.
However, despite the modern instrumentation, this approach may be time consuming, if very fertile. During our FLAMES survey devoted to the link between the Na–O anti-correlation and horizontal branch (HB) morphology (Carretta et al. 2006) we invested about 12 years to collect homogeneous abundances for more than 2500 red giant branch (RGB) stars in 25 GCs. From this unprecedented database, we found that IQR[O/Na] is well correlated with the present-day total cluster mass, as expressed for example, by the proxy of total absolute magnitude MV. Moreover, the larger the extent of the anti-correlation, the higher the maximum temperature reached by stars populating the HB in the GCs (Carretta et al. 2007a). The IQR[O/Na]–MV correlation, although very significant, shows some scatter, and in Carretta et al. 2014a) we uncovered that the residuals around this relation are not randomly distributed, but they are correlated very well with the cluster concentration parameter c, once the core-collapse GCs are excluded (see Fig. 1).
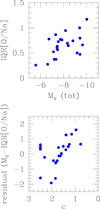 |
Fig. 1. IQR[O/Na] for Galactic GCs as a function of the total absolute magnitude MV (upper panel), and residual around this relation as a function of the cluster concentration c (lower panel). Both panels are reproduced from Carretta et al. (2014a). |
These relations are so statistically robust that we can use almost all the GCs in our FLAMES survey as calibrators and provide a multivariate relation to empirically estimate the extent of the Na–O anti-correlation in many more objects, even without spectroscopic observations of individual stars. These empirical estimates are then possible even for small or distant GCs, poorly studied not only with high-resolution spectroscopy, but also neglected by most photometric surveys.
Moreover, beside their use as probes of multiple populations in never-before-explored GCs, the derived relations may hide in plain sight deeper physical meanings. The present-day total mass of a GC is nothing but a reflection of its initial mass, as combined with internal dynamical processes and external dynamical evolution due to interactions with the host Galaxy in almost a Hubble time. In a sense, these processes can be summarized in the parameter c (e.g. Murray & Lin 1992; Djorgovski 1991). The elusive cluster-to-cluster spreads in He are accounted for by a parameter describing the HB morphology. These are the ingredients of the new calibration proposed in the present work.
This new tool can be applied to a large number of GCs belonging to the different Galactic sub-populations, providing empirical estimates of the Na–O anti-correlation for about 80% of the whole GC system of the Milky Way. Moreover, the range of application extends at least up to galactic systems where HB stars can be currently resolved in GCs, such as the M 31 galaxy. A better and statistically robust understanding of the links between the global cluster properties and the multiple population phanomenon is then possible.
The paper is organized as follows: we describe in Sect. 2 how our empirical calibration is derived and how it can be improved. Sanity checks, the application to the Galactic GCs, and the link with the properties of different globular cluster sub-populations are illustrated in Sect. 3. These results are discussed in Sect. 4, with emphasis on the link between initial and present-day GC masses. A summary is given in Sect. 5.
2. Calibration of the Na–O extension in GCs
The main outcome of our FLAMES survey is represented by homogeneous Fe abundances for more than 2500 RGB stars and Na, O abundances for most of them, allowing us to derive the observed values of IQR[O/Na]. The most updated versions of the IQR[O/Na]–MV correlation and the one of its residual as a function of concentration c is given in Bragaglia et al. (2017, their Fig. 5).
2.1. First calibration
The first calibration we may think of is then simply an update of the bivariate analysis shown in Carretta et al. (2014a), where the derived IQR can be calibrated as a combination of the cluster total absolute magnitude MV and concentration c. The updated sample simply consists in adding the value for NGC 6139 (Bragaglia et al. 2015) and the recent reanalysis of NGC 6388 with a larger sample of stars (Carretta & Bragaglia 2018).
Among the calibrators, three core-collapse GCs present in our FLAMES survey (NGC 6752, NGC 6397, and NGC 7099) as well as NGC 6535 (Bragaglia et al. 2017) are not considered. The last one is not listed as core-collapse in the Harris (1996) and 2010 on-line edition; hereinafter H10 catalogue. However, its position in the residual-c plane appears to be clearly discrepant with respect to the other GCs, indicating some peculiarity for this cluster, as discussed in Bragaglia et al. (2017). NGC 6535 is a GC with an inverted mass function (Halford & Zaritsky 2015), with a current MV = −4.75 (H10) and a large IQR[O/Na]. This GC was severely depleted of its low mass stars by interaction with the Galaxy. For NGC 6535 to lie on the relation defined by the other GCs we would need to assume a luminosity at least 2 mag brighter than the current one. This uncertainty makes this object not well suited as a good calibrator.
The relevant data for the remaining 22 GCs used as calibrators are listed in Table 1. The values for MV, c, and total metallicity [Fe/H] are from H10, the HB index or ratio, HBR (Zinn 1986; Lee 1989, 1990), is from Mackey & van den Bergh (2005), and the observed IQR[O/Na] values are from the studies whose references are given in the last column. For the clusters NGC 1851 (M 54), showing a small (noticeable) iron spread and the Na–O anti-correlation in each metallicity component, we adopted the total values as in Fig. 1. For the classification of GCs in Galactic populations (halo, bulge, disc) we followed Carretta et al. (2010a).
Relevant parameters for calibrating GCs from our FLAMES survey.
Our first calibration is then:
with rms = 0.166 and a Pearson regression coefficient rP = 0.67 (22 GCs). The two-tail probability to be a random result is p = 6.5 × 10−4.
2.2. A missing ingredient
In Fig. 2 the calibrated IQR1 is plotted as a function of the actually observed values of IQR[O/Na] for our 22 calibrating GCs. Different symbols, used throughout this paper, individuate GCs of the bulge and/or disc (hereafter bulge/disk; filled squares), inner halo (triangles), and outer halo (circles) components, as well as those associated to the dwarf spheroidal galaxy Sagittarius, currently disrupting in our Galaxy (pentagons).
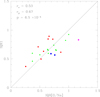 |
Fig. 2. Comparison of the IQR1 values from the first calibration (Eq. (1)) with the observed values IQR[O/Na] for 22 calibrating GCs. The Spearman rank correlation (rS) coefficient, the Pearson linear correlation (rP) coefficients and its p-value are listed in the panel. Different symbols individuate different Galactic populations (see text). |
As shown by the Spearman rank correlation coefficient rS and the Pearson linear correlation coefficient rp, the relation between IQR1 and IQR[O/Na] is good, statistically significant at more than 99.9% level of confidence. However, the calibrated values deviate from the equality line: something is still missing.
By looking at the residuals IQR1–IQR[O/Na] it is easy to understand what this factor may be. Positive residuals are found for GCs mostly with a red HB morphology (e.g. 47 Tuc, NGC 362, M 71), whereas negative residuals are more common for GCs with a bluer HB (e.g. NGC 288, M 79, NGC 4833, M 80, M 12 etc.). This fact gives us a hint to improve the calibration: the missing factor must be related to the distribution of stars along the HB.
This conclusion is further strengthened by Fig. 3 where the residuals of the calibrated values IQR1 with respect to the observed IQR[O/Na] are plotted as a function of various recent and older parameters describing the HB morphology. The widely used HBR index measures the mean location in colour of the bulk of HB population through the ratio (B − R)/(B + V + R) where B, V, and R are the numbers of blue, variable, and red HB stars. Recio-Blanco et al. (2006) used the maximum temperature reached by stars on the bluest part of the HB, 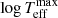 , estimated with the zero-age HB models by Cassisi et al. (1999). Dotter et al. (2010) computed the Δ(V − I) parameter as the median colour difference between HB and RGB at the level of the HB in the GCs of the ACS survey (Sarajedini et al. 2007). Finally, in the rightmost panel, the residuals are plotted as a function of the integrated, reddening corrected, UV colours from the FUV e NUV bands observed with Galex (Dalessandro et al. 2012).
, estimated with the zero-age HB models by Cassisi et al. (1999). Dotter et al. (2010) computed the Δ(V − I) parameter as the median colour difference between HB and RGB at the level of the HB in the GCs of the ACS survey (Sarajedini et al. 2007). Finally, in the rightmost panel, the residuals are plotted as a function of the integrated, reddening corrected, UV colours from the FUV e NUV bands observed with Galex (Dalessandro et al. 2012).
 |
Fig. 3. Residuals from the calibration of Eq. (1) as a function of various parameters for the HB morphology. Above each panel the Spearman and Pearson correlation coefficients are listed, as well as the p-values and the number of calibrating GCs used in the respective relations. |
All the shown relations are statistically significant, some at a confidence level exceeding 99.9%, even when the parameters are available for a limited number of calibrating GCs. It is clear that, beside structural parameters such as MV and c, the morphology of the HB is a parameter that must be included in a calibration that aims to correctly reproduce the observed extension of the Na–O anti-correlation.
2.3. Final calibration
There has been ample discussion on the best parameter for describing the distribution of GC stars on the HB, from the classical comparison of old and new parameters by Fusi Pecci (1993) to more recent works introducing variations or new parameters (Dotter et al. 2010; Dalessandro et al. 2012; Milone et al. 2014).
Each operative definition comes with its pros and cons. Indexes tailored to better represent the coolest part of the HB are affected by uncertainties concerning the reddening estimates, blurring of AGB and RGB stars, possible difficulties to individuate the terminal points of the red HB (see in particular the discussion in Fusi Pecci 1993, their Sect. 3.3). On the other hand, other parameters are somewhat blind to the red extremes, being purposedly defined to handle the hotter regions of the HB distribution. Among the drawbacks, uncertainties in the end point of long blue tails, also related to possible contamination by field stars. Parameters such as Ltail (Fusi Pecci 1993), 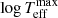 (Recio-Blanco et al. 2006), and L2 (Milone et al. 2014) allow a finer HB-type resolution among GCs with long blue tails on the HB. A common shortcoming is however that in most analyses they are measured on optical (and sometimes old and shallow) CMDs, where the completeness of faint extreme blue tail stars may become a relevant issue, as discussed by Dalessandro et al. (2012).
(Recio-Blanco et al. 2006), and L2 (Milone et al. 2014) allow a finer HB-type resolution among GCs with long blue tails on the HB. A common shortcoming is however that in most analyses they are measured on optical (and sometimes old and shallow) CMDs, where the completeness of faint extreme blue tail stars may become a relevant issue, as discussed by Dalessandro et al. (2012).
After scrutinizing various options, we adopted the classical HBR index for several reasons. This parameter may not be ideally suited for all HB types, but is straightforward to compute, it is available for the vast majority of Galactic GCs, and it is model independent. HBR values are also given for very small GCs, usually neglected in most photometric surveys, allowing us to apply the calibration down to the very low mass regime. The index, or some close variants, can be computed from deep HST CMDs of clusters even in the M 31 galaxy (see e.g. Perina et al. 2012), as well as in closer external galaxies such as the Magellanic Clouds and the Fornax dSph (e.g. Mackey & Gilmore 2004). Finally, the entry for HBR is also available for M 54, the second most massive GC in the Milky Way, while no data are found for this cluster concerning other parameters (except for L2, Milone et al. 2014). As well as sampling the high mass end of the GCs mass function, this provides the side benefit of including in the calibrating dataset a cluster of extra-Galactic origin, M 54 being a confirmed member of Sgr (Bellazzini et al. 2008). We may use this occurrence as a test for the applicability of the results to other GC systems. Adopting this HB index we “lose” NGC 5139 (ω Cen) for which HBR is not given, but this is a cluster with many peculiarities, besides hosting multiple populations (see e.g. the review by Gratton et al. 2004).
By adding the term in HBR, our finally adopted calibration is:
with rms = 0.141 and rp = 0.79 (22 GCs). The improvement in this calibration with respect to IQR1 (Eq. (1)) is immediately evident: the two-tail probability to be a random result is now down to p = 1.2 × 10−5, the scatter is decreased, and the calibrated IQR2 explains ∼18% more of the variability in the response (i.e. the extent of the Na–O anti-correlation) due to adding the HB morphology description to the predictors.
In Fig. 4 we compare the new calibrated values IQR2 to the observed ones IQR[O/Na] for our 22 GCs. Now all the values satisfactorily lie around the identity line: no statistically significant correlation of the residuals IQR2–IQR[O/Na] as a function of global parameters is found.
 |
Fig. 4. Comparison of the IQR2 values from our final calibration (Eq. (2)) with the observed values IQR[O/Na] for 22 calibrationg GCs. Symbols and labels are as in Fig. 2. |
At first glance comparing Figs. 2 and 4, we see that to correctly reproduce the one-to-one correspondence with the observed spreads of Na and O abundances it is necessary to introduce a correcting factor describing the distribution of HB stars in GCs.
On a second level, the goodness of this calibration bears a deeper physical meaning. All the observed IQR[O/Na] values are computed in our calibrating clusters from samples of red giants. The link between the chemical abundances of light elements in RGB stars and the distribution in colour of stars in the next evolutionary phase on the HB once again points towards the well known connection existing between the multiple population phenomenon and the HB in GCs. Besides the structural parameters of a GCs there should be another ingredient that is able to explain the coupling of different observations in two distinct evolutionary phases, likely related to how multiple stellar populations formed and evolved in the clusters.
This ingredient was predicted theoretically some time ago (D’Antona et al. 2002) and is already well known from monovariate relations. Carretta et al. (2007a) find a very strong correlation between chemical variations in proton-capture elements and the highest temperature reached on the ZAHB by GC stars. Ever since, this relation holds for any new GC studied to date (see e.g. Carretta & Bragaglia 2018). Enhanced He abundance was individuated as the culprit: associated to stars with highly depleted O and enhanced Na abundances, it results in decreased envelope masses, forcing the stars to spend the following HB phase segregated at very high temperature regimes. If the alterations in O and Na are due to proton-capture reactions in H burning at high temperature, whose main outcome is of course He, then this is essentially the relation connecting the variegated HB morphology and the multiple population phenomenon in GCs.
3. Application to galactic GCs
The calibration for IQR2 can be then applied to all Galactic GCs for which the parameters MV, c, and HBR are known. We considered the GCs listed in the H10 catalogue with parameter c < 2.5. The HBR values were taken from Mackey & van den Bergh (2005), except for Terzan 8, whose HBR is from Carretta et al. (2010a). For the division of GCs into different Galactic sub-populations we followed the classification scheme described in the Appendix A of Carretta et al. (2010a).
Excluding GCs without an HBR value, like NGC 5139 (ω Cen), and AM-1, a poorly studied cluster whose IQR2 turned out to be slightly negative (probably due to some problems in the parameters), we could apply Eq. (2) and provide new empirical predictions for the extent of the Na–O anti-correlation for 95 GCs. We also add the 22 GCs used as calibrators. Three more GCs in our FLAMES survey (NGC 6397, NGC 6752, and NGC 7099 = M 30) are classified core-collapse; while they were not used as calibrators, they have observed IQR[O/Na] values directly derived by our group (Carretta et al. 2007c, 2009a,b) and we included them in the sample. A grandtotal of 120 galactic GCs (∼80% of all classical GCs in the Milky Way) with extension of the Na–O anti-correlation on the scale defined by our very homogeneous survey is then available. IQR2 values for individual GCs are listed in the Appendix, Table A.1.
3.1. Sanity checks: Multiple populations, He, and HB
This large dataset enables us to perform statistically robust tests to verify how reliable the final calibration is. First, we compare in Fig. 5 the run of IQR1 (left panel) and IQR2 (right panel) as a function of the cluster metallicity [Fe/H]. As is evident in the left panel, IQR1 does not show any correlation with metallicity. The Student’s t-test returns a two-tail probability of p = 0.23. On the other hand, IQR2 is found correlated with [Fe/H] and the relation is statistically very robust (p = 6.7 × 10−5).
 |
Fig. 5. Extensions of the Na–O anti-correlation IQR1 (left panel) and IQR2 (right panel) from the calibrations Eqs. (1) and (2), respectively. Symbols are as in Fig. 2. Black points indicate the calibrating GCs from our FLAMES survey, and their shape indicate the Galactic sub-population. Symbols and label are as in Fig. 4. |
All the main classes of polluters proposed to explain the spread of Na, O (and other light elements) observed in GCs do not alter the cluster initial metallicity (see Gratton et al. 2012; Bastian & Lardo 2018). Remarkably, even in the so-called iron complex GCs, where intrinsic dispersions in [Fe/H] are measured, a Na–O anti-correlation is detected in each individual metallicity component (e.g. NGC 1851, Carretta et al. 2011; M 22, Marino et al. 2011; NGC 6273, Johnson et al. 2015). When the term for the HB enters in the calibration for IQR2, so does implicitly also the dependence on metallicity, which is the first parameter driving the HB morphology. This self-consistently explains the correlation (or the lack thereof) observed in Fig. 5.
A second consistency check for our calibrations is based on the He variations expected in multiple stellar populations. Stellar models He-enhanced reach the H-exhaustion point earlier than their counterparts with lower He. For a mixture of stellar populations differing in their He content we must then expect a spread in colour on the main sequence (MS), or even split sequences in the most extreme cases (e.g. Milone et al. 2012a,b). Thus, if our calibrated extents of the Na–O anti-correlation correctly account for concomitant enhancement of He after the nuclear processing producing Na-enhanced, O-depleted matter, a correlation with the colour spreads along the MS should be seen.
For 56 GCs in our dataset Gratton et al. (2010) estimated the colour spreads δ(B − V) and δ(V − I) expected along the MS from the computed He spreads corresponding to the mass dispersion along the HB. These two parameters, derived independently, are found to be strongly correlated with our empirical estimates of the Na–O anti-correlation extent in Fig. 6. Again, different approaches (spectroscopic and photometric) at two different evolutionary phases (RGB and MS) concur to the same general, consistent picture.
 |
Fig. 6. Calibrated extent of the Na–O anti-correlation IQR2 as a function of the colour spreads in B − V and V − I along the MS from Gratton et al. (2010). Symbols and labels are as in the previous figures. |
As a third consistency check, we can test whether a correlation is found with more direct estimates of He abundances. However, the limitations for a spectroscopic derivation of the He content in GC stars are even more severe than those concerning O and Na, both among HB and RGB stars (see discussions in Gratton et al. 2010; Dupree et al. 2011; Pasquini et al. 2011; Milone et al. 2018) so that it is still necessary to resort to vicarious measurements. Recently, Milone et al. (2018) have produced estimates of the maximum He variation in 57 GCs by comparing multi wavelength HST photometry to synthetic spectra computed with abundances appropriate for FG and SG stars.
In Fig. 7 our calibrated values IQR2 are plotted against their δYmax estimates for 53 GCs in common. There is a strong correlation, significant at a level of confidence exceeding 99.9%. There is also a noticeable scatter, and for this we offer two explanations. First, as already discussed in Fusi Pecci (1993), the effects of a secondary parameter may result in correlations that appear to be less clean than those generated by primary parameters. The dependence of IQR2 on He is mediated by the HB morphology, because the ZAHB evolution of He enhanced stars is preferentially spent at bluer locations. However, the He content was tagged only as a third parameter for the HB by Gratton et al. (2010).
 |
Fig. 7. Calibrated IQR2 values for the extension of the Na–O anti-correlation as a function of the maximum variations in He derived from photometry (Milone et al. 2018). GCs defined as type-II are encircled, and the position of NGC 6388 is labelled (see text). |
Second, beside the statistical impact, there could be a more physical meaning, because of the different dependence on stellar mass for the alterations and following release of He, O, and Na in the polluting matter (see e.g. Gratton et al. 2010, 2012). Let us consider the two most favourite candidate polluters, intermediate-mass AGB stars (Ventura et al. 2001) and fast rotating massive stars (FRMS; Decressin et al. 2007). For both candidates the phase at which He is produced is the same: the main sequence. However, the production and release of He is accompanied by O-depletion and Na-enhancement at the same evolutionary phase in FSRM, while it is delayed until the hot-bottom burning in the AGB phase in the AGB scenario, where the production of He is somewhat decoupled from that of O and Na. Thus, the trend and scatter in Fig. 7 could perhaps be seen as the action of AGB polluters or possibly even of a mixture of polluters, with FRMS working at the very early phases and the contribution from AGB stars entering at the appropriate (longer) timescale. We note that the estimates δYmax from Milone et al. 2019 show significant correlations with the colour spreads δ(B − V) and δ(V − I) from Gratton et al. (2010: two-tail p = 0.0022 and 0.0010, respectively), although with some scatter.
Finally, we note that the GCs in Fig. 7 seem to approximatively follow two different branches, and eight out of nine type-II GCs (as defined in Milone et al. 2017, and marked with open circles in our figure) lie on the upper branch. These are the GCs usually called iron-complex or anomalous from their intrinsic dispersion in Fe, as well as heavier elements like those from s-process. Photometrically, almost all type-II GCs show split sub-giant branches (SGBs), with the faint SGB continuing up to a red RGB. As mentioned above, in these GCs the multiple population phenomenon appears in each metallicity component (e.g. Carretta et al. 2011, 2010b,c; Marino et al. 2015; Johnson et al. 2015 for NGC 1815, M 54, NGC 5286, and NGC 6273, respectively). The only exception in Fig. 7 is NGC 6388, clearly located on the lower “branch”. However, from high resolution spectroscopy there is no sign of an intrinsic dispersion in [Fe/H] in this massive GC (σ[Fe/H] = 0.041 dex from the direct analysis of 24 RGB stars in Carretta & Bragaglia 2018 and σ[Fe/H] = 0.051 from 151 giants in Carretta & Bragaglia, in prep.; both values are fully compatible with observational errors only). In passing we also note that NGC 6388 is the only GC defined as type-II for which Milone et al. (2017) could not clearly establish the connection faint SGB-RGB.
Hence, it seems that all genuine iron complex (or type-II) GCs are segregated on the (tentative) upper branch in Fig. 7. Taken at face value, this observation indicates that these GCs have much-too-high IQR values if compared to their estimated maximum variation in He. While a deeper study of the full links between spectroscopic and photometric properties of GCs is desirable, it is beyond the immediate purposes of the present work. We limit the extent of our study here, and summarize the results of this section below.
The extension of the Na–O anti-correlation can be calibrated as a function of structural parameters of the GCs. The observed values of spreads in O and Na are best reproduced when the HB morphology is accounted for in the empiric calibration. Its reliability is corroborated because the calibration correctly returns a dependence on metallicity, the first parameter governing the HB morphology. Moreover, the He enhancement predicted to go along with the alterations in O and Na is well incorporated by the calibration, as shown by the correlation of IQR2 with the colour spreads on the MS phase and with estimates of He variations deduced from UV photometry.
We suggest that the spread observed in the relation between the extent of the Na–O anti-correlation and the He spread in GCs may be ascribed either to the decoupling in AGB stars between the peaks of He and O, Na changes in the polluting matter or to the presence of different classes of polluters acting at different times. The last hypothesis is endorsed by several existing cases of discrete groups observed along the anti-correlations of proton-capture elements, where the stellar components with extreme and intermediate composition cannot be reproduced using only one class of massive polluters (NGC 6752: Carretta et al. 2012; NGC 2808: Carretta et al. 2018; NGC 6388: Carretta & Bragaglia 2018).
All these tests confirm the coherent picture of multiple stellar populations in GCs, where O-depleted and Na, He-enhanced stars help to simultaneously explain the observed extent of the Na–O anti-correlation, the distribution of stars in HB and the spreads in colour along the MS. We can thus be confident that the adopted empirical calibration returns a reliable, quantitative estimate of the nuclear processing and chemical modifications occurred at early times in GCs.
3.2. Na–O anti-correlation across GCs in the Milky Way
With the above calibration, empirical estimates for the Na–O anti-correlation can be derived for 120 Galactic GCs, including the most distant or smallest ones, that up to now were not investigated for multiple stellar populations neither with spectroscopic nor photometric means.
In Fig. 8 we plot the calibrated IQR2 values as a function of the total absolute magnitude MV from H10. For 25 GCs analysed in our FLAMES survey in this figure we use the observed IQR[O/Na] values (black symbols).
 |
Fig. 8. Calibrated IQR2 values from Eq. (2) as a function of the total absolute magnitude from H10. Observed IQR[O/Na] values are used for 25 GCs from our FLAMES survey (black symbols). |
The high-luminosity end of our relation is secured by the presence of the massive GC M 54 in the calibrating sample. Formally, our empirical calibration (Eq. (2)) should be valid only down to the faintest MV magnitude in our calibrating sample, corresponding to NGC 6838 = M 71 (black square at MV = −5.61). Hence, for about a dozen GCs we are formally in an extrapolation regime. We note, however, that no indication of departures from linearity is evident from both Fig. 4 and Fig. 8. The increased scatter in the latter may be well ascribed to increasing uncertainties in the literature estimates of parameters. Supporting evidence is given by two GCs below the above threshold, Pal 5 and Terzan 8 (MV = −5.17 and −5.07, respectively). In both these small clusters SG stars are directly found using high resolution spectroscopy (Smith et al. 2002; Carretta et al. 2014b, respectively), providing an unambigous chemical tagging, although for very few stars.
With these caveats in mind, we can provide estimates of IQR2 for GCs as faint as Pal 13 (MV = −3.76). Formally, for any spatially resolved GC whose structure can be reasonably approximated by King (1966) models it is possible to derive a value for the extension of the putative Na–O anti-correlation due to hosted multiple populations. Due to the dependence on different parameters in Eq. (2), however, the smallest extent we estimate does not correspond to Pal 13. The record holder seems to be the GC 1636-283, also known as ESO452-SC11, with IQR2 = 0.025. This tiny bulge GC (estimated mass of only a few thousand solar masses, Simpson et al. 2017) lies at the mass border between globular and open clusters, so the small derived value for IQR2 could simply be an artefact of the calibration, mistaken for a real value. Fortunately, the recent spectroscopic analysis by Simpson et al. (2017) shows star-to-star abundance variations in this GC, not only from CN absorption features, but also from direct measurements of Na abundances. Incidentally, this example well points out the strength of our calibration: Simpson et al. complain that it is highly unlikely that many other member stars in this GC can be reached for abundance analysis, whereas an estimate of inhomogeneities is easily obtained from our approach.
Among the GCs in Fig. 8 with the smallest IQR2 values, another noteworthy cluster is Liller 1. With MV = −7.32 and IQR2=0.114 this object is located a little way off the main locus defined by the other GCs. However, a relevant revision of its structural parameters has been proposed by Saracino et al. (2015), who found Liller 1 to be less concentrated than previously estimated (c = 1.74 ± 0.15 instead of 2.3). From Eq. (2) this update would change the value of IQR2 from 0.114 to 0.321, more in agreement with the moderately high mass estimated for this GC.
To compare the derived extension of Na–O anti-correlation in GCs of different Galactic sub-populations in Fig. 9 (left panel) we plotted IQR2 as a function of the the distance in kpc from the Galactic plane. We also show the average values for the individual populations of bulge/disc, inner, and outer halo GCs (BD, IH, and OH): 0.503 (rms = 0.240, 58 GCs), 0.678 (rms = 0.209, 32 GCs), and 0.562 (rms = 0.227, 24 GCs), respectively. A Student’s t-test shows that the only statistically significant difference is between the mean values for BD and IH GCs (t = 3.60, 88 degrees of freedom, two-tailed probability P < 0.001), as also confirmed by a Kolmogorov–Smirnov test on the cumulative distributions of IQR2 (Fig. 9, right panel).
 |
Fig. 9. Left panel: calibrated IQR2 values as a function of the distance in kpc from the Galactic plane (H10). Horizontal lines are traced at the average values of the corresponding galactic populations (same colour coding). Right panel: cumulative distribution of IQR2 for GCs of different sub-populations. The P values from two-sample Kolmogorov–Smirnov (K–S) tests are indicated. |
However, before concluding that (inner) halo GCs did experience, on average, a greater degree of processing than bulge/disc GCs, as would seem judging from the extent of the Na–O anti-correlation, we caution that it is necessary to look at the intrinsic properties of the parent cluster sub-populations.
This is done in Fig. 10, where the cumulative distributions of the parameters entering in the calibrating Eq. (2) are shown. From the luminosity functions in the left panel, the inner halo hosts more luminous (i.e. massive) GCs than both outer halo and disc. Many small GCs are found in the disc, contrary to the common sense of expecting small GCs more efficiently destroyed in the more crowded and denser central galactic regions. As discussed in, for example, Carretta et al. (2010a), this evidence suggests that differences in LFs might be more related to the formation mechanisms than to destruction processes, although this may even not be the whole story. From the middle panel of Fig. 10 we also may appreciate that GCs in the disc are more compact than those of both inner halo and outer halo, and are better suited to resist to disruption in the ensuing evolution. Finally, disc GCs have basically redder HB morphologies than outer halo GCs, whereas in turn IH GCs have bluer HBs. These properties of IH GCs, in particular the coupling between high GC mass and blue HB morphology, have been known for more than ten years (Recio-Blanco et al. 2006; Lee et al. 2007).
 |
Fig. 10. Left, middle, and right panels: cumulative distributions of total absolute magnitude MV, concentration c, and HBR index for GCs of different Galactic sub-populations. Probabilities from K–S tests are indicated in each panel. |
We conclude that the larger IQR2 values found for IH GCs are fully consistent with the distribution of parameters appropriate for this particular Galactic sub-population. In Carretta et al. (2010a) from a limited sample of 19 GCs we concluded that mass and metallicity are among the main parameters driving the chemical signatures of multiple populations, with an additional contribution given by the location in the Galaxy. The proposed empirical calibration and the discussion above allow a better understanding of why this occurs: the extent of the chemical processing between different stellar generations is modulated by the distribution of structural parameters and HB morphology (whose first parameter is indeed the metallicity).
The same line of reasoning does apply to the difference in the estimates of the Na–O anti-correlation in GCs with a different origin. In Fig. 11 left panel) we reproduced the age–metallicity relations obtained by Leaman et al. (2013) for GCs formed in situ in the Galactic disc and those likely originated in smaller systems, later accreted and disrupted in the Milky Way. The size of the symbols in this figure are proportional to the IQR2 values, and clearly indicate that the extension of the Na–O anti-correlation is larger in the accreted component, as is confirmed statistically by the K–S test on the cumulative distributions plotted in Fig. 11 (right panel). It is easy to verify, using the classification provided by Leaman et al., that the accreted GCs are more massive and have bluer HBs than the GCs formed in situ. Again, the differences in the extent of the multiple population phenomenon are driven and explained by the mean properties of the parent cluster populations, even concerning the environment where they originally formed, as in this example.
 |
Fig. 11. Left panel: age–metallicity relation from Leaman et al. (2013) for GCs formed in situ in the MW disc (blue points) and GCs likely formed in smaller stellar systems and later accreted in the MW (red points). The size of the symbols are proportional to the IQR2 values. Right panel: cumulative distributions of GCs with different origin. The P value from two-sample K–S tests is indicated. |
4. Discussion
The case of the globular cluster Pal 5 is emblematic to better understand the dependence of IQR2 from structural cluster parameters. The extended tidal tails associated to Pal 5 (e.g. Odenkirchen et al. 2001, 2003) are a direct evidence of a large mass loss due to severe tidal disruption in the potential well of our Galaxy. Clearly the present-day total mass of GCs (as portrayed by the total luminosity) is only a lower limit of the initial GC mass. Yet, not only direct proofs of SG composition do exist for Pal 5, but also our calibration for IQR2 provides a value for the extension of the Na–O anti-correlation (IQR2 = 0.426) which locate this GC right in the middle of the relation defined by all GCs. We argue that our calibration represents a good empirical way to approach the initial conditions of GCs, where the dependence on the (unknown) initial mass is included in the present day mass and all the Gyr-long history of dynamical evolution due to internal and external dynamical processes is modelled by the concentration parameter.
4.1. The new calibration in context
In Fig. 12 we summarize the ingredients of our calibration by using the correlation between concentration c and luminosity; well known for some time (see e.g. Djorgovski & Meylan 1994; hereinafter DM94). In this figure, the shape of the symbols represent the different Galactic sub-populations, while the colours code the different HB morphologies. Symbol size is proportional to the IQR2 values.
 |
Fig. 12. Left panel: correlation between concentration c and total absolute magnitude MV for MW GCs. The size of symbols is proportional to the IQR2 value, their shape indicates the Galactic population, and the colours refer to the HB morphology, as detailed by the legend in the right panel. |
The largest impact is due to the total cluster mass. At any given value of concentration there is a clear gradient, the larger is the mass the more extended is the Na–O anti-correlation, regardless if GCs belong to the bulge/disc or halo population. Again, this strongly corroborates the idea that mass is the main driving parameter. The second parameter is the concentration: at any fixed MV the IQR decreases as c increases. These trends explain the observed relations in Fig. 1 and the dependence on structural parameters of our resulting empirical calibration. This adds the “axis” represented by the chemistry of multiple stellar populations to this plot.
Photometry may also lend supporting evidence, when the parameters c and MV are simultaneously considered, as shown in Fig. 13. Here we plot again the c − MV correlation but this time the symbol sizes are proportional to the fraction of FG stars N1/Ntot estimated from HST photometry by Milone et al. (2017). Although the sample is now more limited (about the half of the sample used in the present work) this figure is clearly specular to Fig. 12. GCs with larger fractions of FG stars (small fractions of SG stars) are confined at smaller luminosities (masses) at any given concentration.
 |
Fig. 13. Correlation between concentration and luminosity for Galactic GCs, where are only plotted GCs with fraction of FG stars estimated in Milone et al. (2017) from HST photometry. Symbol sizes are proportional to the fractions, in steps of 10% from about 10 to about 70%. |
The existence of more extended Na–O anti-correlations in more loose GCs seem to conflict with the idea that SG stars usually form more centrally concentrated (but see Gratton et al. 2012 and Bastian & Lardo 2018 for exceptions). Carretta et al. (2014a) put forward the possibility that low concentration GCs were originally more massive than present day, but lost more mass, since at fixed mass the impact of tidal shocks is inversely proportional to the density of a cluster (Spitzer 1958). This hypothesis is addressed in Sect. 4.2 below.
Finally, Fig. 12 is more than a compact summary of our empirical calibration. As discussed in the pioneering studies by Djorgovski (1991) and DM94 the correlation between luminosity and concentration also represents a summary of the initial conditions and the following dynamical evolution of the GC system. The concentration parameter can be assumed as a measure of the dynamical evolutionary stage of clusters since most of these systems are lead toward higher and higher concentration by the combined impact of internal evolution and environment-induced effects. Two-body relaxation pushes stars on the high velocity tail of the Maxwellian velocity distribution, where they can be more efficiently affected by the Galactic tidal field and escape the cluster, whose concentration increases (e.g. Murray & Lin 1992; DM94). Since at any given MV concentration and central relaxation time trc are anti-correlated, the zone of avoidance at low luminosities and high c reflects the results of dynamical evolution, which drives low mass clusters with short trc toward tidal disruption or core-collapse (DM94). On the other hand, the absence of luminous GCs of low concentration is simply explained as a fossil record of the initial conditions, as no mechanism is able to explain this second empty region (e.g. Djorgovski 1991).
Bellazzini et al. (1996; B96) attempted to disentangle the relative weight of evolutionary vs primordial mechanisms in GCs of different galactic sub-populations by simulating a series of King models in the assumptions that c and MV were either correlated or uncorrelated. Although their definition of inner and outer GC populations is different from the one adopted in the present work, by comparing the output of their simulations with the distribution of real Galactic GCs of various sub-populations they concluded that the correlation between concentration and luminosity must be of primordial origin, being strong for the outer halo GCs, populating regions where the tidal field is weak, and less clear or absent for inner halo GCs, where it may have been somewhat mitigated by the effects of dynamical evolution. More massive GCs are thus born with higher central concentration.
However, we must not forget that while current masses may be estimated from total luminosities or kinematics, the original masses of GCs are usually only educated guesses, even if the two quantities must be obviously correlated (see e.g. Kruijssen 2015; Balbinot & Gieles 2018). The greatest unknown is represented by the dynamical evolution processes required to map the initial masses in what is currently observed in GCs of the different Galactic sub-populations.
4.2. Present and initial masses, and dynamical mass loss
The IQR2 values show a good correlation with a combination of present-day structural parameter MV and c and B96 also found the relation between cluster absolute magnitude and concentration be mostly primordial in origin. Since MV is not supposed to change very much during the lifetime of a cluster (Murray & Lin 1992), all together these observations may point out that the impact of the cluster dynamical evolution is minimal; just the minimum required to empty the region at high c, faint MV.
This occurrence would seem to be in agreement with the theoretical work by Reina-Campos et al. (2018) who addressed the impact of cluster disruption on multiple populations by deriving statistical estimates of the initial-to-present mass ratios from E-MOSAICS cosmological simulations. By using the sample of GCs with fractions of enriched SG stars Fenrich derived from photometry (Milone et al. 2017), they concluded that dynamical evolution (tidal shocks and/or evaporation) cannot explain the rise of this fraction as the cluster mass increases. Similar arguments are used by Kruijssen (2015) in his two-phase model, in particular for metal-poor GCs. Reina-Campos et al. (2018) conclude that dynamical mass loss could not have a large effect on the present day masses of GCs and the detected fractions as well as the ratios FG/SG must probably reflect initial values. Were this the case, a big problem would arise for the mass-budget limited models, because one of the strongholds more frequently used to alleviate the so called mass-budget problem is the preferential loss of FG stars up to 90% of the cluster mass to simultaneously account for the scarce yields of nuclearly polluted matter and the large observed fraction of SG stars in GCs (see Gratton et al. 2012; Bastian & Lardo 2018 for extensive discussion of this issue). Usually, in this approach primordial proto-GCs are assumed to have been much more massive than today, factors from 10 to 100 are required to eliminate the mass-budget problem, in stern contrast with the estimates of the initial masses given above.
The main role is supposed to be played by the fast mass loss from stellar evolution: gas expulsion and ejecta from FG Supernovae cause the cluster to expand, and stars to escape, reducing the original mass by half in the first Gyr (Vesperini et al. 2010; Khalaj & Baumgardt 2015; Baumgardt et al. 2019). According to most scenarios for multiple populations, at this epoch the Na–O anti-correlation must be completely developed and SG stars more centrally concentrated. As a consequence, the preferential mass loss of FG stars results into a dramatic increase of the SG fraction in GCs at early times of their lifetime. In the next phase, two-body relaxation realizes spatial mixing of the different population, so that the ensuing dynamical evolution acts more or less in the same way on different components and the ratio SG/FG stabilizes (e.g. Vesperini et al. 2010).
We may tackle this issue since our calibration of IQR2 provides sufficiently large statistics to have a better insight. When observed, best currently available proper motions of real Galactic GCs from Gaia DR2 (Gaia Collaboration 2018) are used to compute realistic orbits for the GCs we may see how the resulting changes in masses compare with the Na–O anti-correlation.
Baumgardt et al. (2019; BHSB) and Balbinot & Gieles (2018) derived the ratio between the current masses and the inizial masses of Galactic GCs essentially by assuming a mass loss law and playing backward the orbital motions of GCs until their primordial masses correctly reproduce the observed present day values. While we used the study of Baumgardt et al. (2019) we note that the correlation between their estimates and those by Balbinot & Gieles (2018) is significant, at better than 99.9%.
The derived initial values are on average ∼15 times the present values (see Fig. 14), with a clear trend proceding toward the outskirts of the Galaxy. Bulge/disc GCs were originally 23.1 (σ = 80.7, 76 objects) times more massive, on average, while this number decreases to 6.4 times (σ = 10.4, 34 GCs) for inner halo GCs. Outer halo GCs and those associated to Sgr were found on average only 4.5 (σ = 2.5, 27 objects) and 4.3 (σ = 3.3, seven objects) times more massive than the current values, respectively. No cluster is located rightward the line traced at Mini = 2 Mnow, that simply models a 50% mass loss from stellar evolution.
 |
Fig. 14. Comparison of present and initial GC masses from Baumgardt et al. (2019). Filled symbols are as in Fig. 2, whereas empty symbols indicate core-collapse GCs. The line is traced at Mini = 2 Mnow. |
In Fig. 15 the correlation c − MV is again represented by dividing the GCs in various Galactic sub-populations. However, this time the size of symbols reflects the initial masses as estimated in Baumgardt et al. (2019), not the present day masses. Not all the current faint clusters were originally born with small masses. Classic example are the bulge/disc GCs 1636-283 (ESO452-SC11) and Terzan 4, present day absolute magnitudes < − 4.5 and c ∼ 1. According to Baumgardt et al. they were born with initial masses comparable to those of M 15 or 47 Tuc (with MV > −9.0). Their orbital parameters show that these GCs spent almost an Hubble time near the central regions of the Galaxy, likely affected by (even severe) tidal shocks. During their lifetimes the dynamical evolution reduced their masses to a few per cent of the original ones.
 |
Fig. 15. Correlation between concentration and luminosity for Galactic GCs. Different colour and shapes represent the various Galactic populations as in Fig. 12. Symbol sizes are proportional to the initial masses estimated by Baumgardt et al. (2019). In unit of 105 M⊙ the adopted ranges for the scaling of sizes are 0–1, 1–10, 10–20, and > 20. |
Apart from these and other few cases, masses are rather smoothly translated into the present day absolute magnitudes (masses), with a simple scaling. Thus, the comparison of Fig. 15 with Fig. 12 easily allows to see that the extent of the Na–O anti-correlation is apparently already dictated by the original mass of clusters. Baumgardt et al. (2019) also found for the least dynamically evolved GCs a slope of the mass function about 1 dex higher than a Kroupa mass function in the range 0.2–0.8 M⊙. The authors considered this result as an evidence that GC started with a bottom light mass function. In this case, due to the fewer low-mass stars present, a larger fraction of stars may be polluted, partly alleviating the tension between the expected and observed SG fractions.
Finally, in Fig. 16 we plot the difference between initial and present day masses (Baumgardt et al. 2019, and priv. comm.) as a function of the tidal radius in pc from the fit of N-body models1. No evidence of extended GCs losing more mass than the compact clusters is found, as advanced instead in Carretta et al. (2014a) to explain more extended anti-correlations in more loose GCs.
 |
Fig. 16. Mass loss from Baumgardt et al. (2019), in unit of 105 M⊙, as a function of the tidal radius for Galactic GCs. Symbols are as Fig. 14. |
Remarkably, the conclusion from this section is that the present-day masses of GCs seem to preserve essentially the ranking provided by the initial masses, apart from a few exception. When the observed IQR[O/Na] values for our 22 calibrators are correlated either to MV or log Mini we derive the same value of the Pearson correlation coefficient (rP = −0.48 and rP = 0.48 respectively). The bottom line is that both correlations are equally significant, at a confidence level greater than 99.9%.
However, taking into account the number of assumptions still entering the computation of the initial GC masses (and we cannot know their original concentration), we stand for a calibration including the present day masses, as expressed by the proxy of total luminosities, a rather simple quantity to be measured. In addition, our empirical calibration offers a precious tool with which to examine globular clusters in nearby galaxies putting them on the same scale and allowing a meaningful comparison with GCs of the Galactic system. This will be the subject of a forthcoming paper.
5. Summary and future work
The extent of the Na–O anti-correlation observed in GCs is an useful quantitative measure of the impact of multiple population phenomenon in a globular cluster. Obtaining this measure requires a large investment of observing time even with high multiplex spectrographs at 8–10 m class telescopes.
We the used 22 GCs from our unprecedented homogeneous FLAMES survey to calibrate observed IQR[O/Na] values in term of structural parameters and HB morphology. We find that the combination of total absolute cluster magnitude (a proxy for the cluster present-day mass) and concentration is very well correlated to the extent of the Na–O anti-correlation in GCs. When a term describing the HB morphology is added, our empirical calibration returns values on the identity line with respect to the observed values on our system, based on more than 2000 red giant in 22 GCs.
We were able to provide empirical estimates of the Na–O anti-correlation in 95 Galactic GCs. When added to the 25 GCs observed in our FLAMES survey, we can homogeneously provide quantitative estimates of the multiple population phenomenon in a large sample of 120 GCs (80% of all GCs in the Milky Way). The calibration cannot be applied to core-collapse GCs, but direct observation of Na–O abundances in at least three GCs show that the anti-correlation is preserved even after the core-collapse.
The large number of data points allow us to uncover that the main differences in the extent of the multiple population phenomenon are a direct reflection of the mean properties of the parent cluster sub-population (outer and inner halo, disc) in the Galaxy (luminosity function, distribution of sizes and concentration). This accounts for the findings by Carretta et al. (2010a) that the chemical signatures of multiple populations included a contribution due to the location in the Galaxy.
Galactic clusters that feature a large Na–O anti-correlation are segregated along the correlation between c and MV, at high luminosities (mass) values at each given concentration. This well known correlation explains the dependence of our calibrated IQR2 on structural parameters. A comparison with recent estimates of initial masses suggests that the extension of Na–O anti-correlation is already dependent on the original GC masses. The following dynamical evolution seems essentially to preserve this dependence through a scaling of the masses to the present-day values, apart a few exceptions (mostly GCs spending most of their lifetimes in the central regions of the Galaxy, where the effects of tidal interaction are strong). We thus recommend to adopt the present calibration using the observed total absolute magnitudes MV that are easily obtained from the observations and are not affected by assumptions regarding the estimates of initial GC masses.
Moreover, this calibration can be easily applied to GC systems in nearby external galaxies: a forthcoming paper will be devoted to this. A first check is already provided by GCs in our Galaxy that are associated to the closest external galaxy, the dwarf spheroidal Sgr (Ibata et al. 1994). The disruption of this dSph released in the Milky Way a number of GCs, all listed in the Harris (1996) catalogue, and in Table A.1. According to our calibration the properties of these migrant GCs cannot be distinguished from autochthonous Milky Way GCs in this context. We conclude that our empirical calibration is a useful compact way to represent and quantify the properties of multiple populations in GCs.
Acknowledgments
I would like to thank the referee for a constructive review. I wish to thank Angela Bragaglia for valuable help and suggestions, Emanuele Dalessandro for useful discussions, Antonio Sollima and Holger Baumgardt for providing their estimates of initial GC masses, and Raffaele Gratton who first pointed out the role of the concentration. This research has made use of the SIMBAD database (in particular Vizier), operated at CDS, Strasbourg, France, and of the NASA’s Astrophysical Data System.
References
- Balbinot, E., & Gieles, M. 2018, MNRAS, 484, 2479 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., & Lardo, C. 2018, ARA&A, 56, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., Hilker, M., Sollima, A., & Bellini, A. 2019, MNRAS, 482, 5138 [Google Scholar]
- Bellazzini, M., Vesperini, E., Ferraro, F. R., & Fusi Pecci, F. 1996, MNRAS, 279, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Bellazzini, M., Ibata, R. A., Chapman, S. C., et al. 2008, AJ, 136, 1147 [NASA ADS] [CrossRef] [Google Scholar]
- Bragaglia, A., Carretta, E., Sollima, A., et al. 2015, A&A, 583, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bragaglia, A., Carretta, E., D’Orazi, V., et al. 2017, A&A, 607, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Briley, M. M. 1997, AJ, 114, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Briley, M. M., Smith, G. H., & Claver, C. F. 2001, AJ, 122, 2561 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E. 2006, AJ, 131, 1766 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E. 2015, ApJ, 810, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E. 2016, ArXiv e-prints [arXiv:1611.04728] [Google Scholar]
- Carretta, E., & Bragaglia, A. 2018, A&A, 614, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2006, A&A, 450, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Recio-Blanco, A., Gratton, R. G., Piotto, G., & Bragaglia, A. 2007a, ApJ, 671, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2007b, A&A, 464, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., Lucatello, S., & Momany, Y. 2007c, A&A, 464, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009a, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., & Lucatello, S. 2009b, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010a, A&A, 516, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010b, A&A, 520, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010c, ApJ, 714, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Lucatello, S., Gratton, R. G., Bragaglia, A., & D’Orazi, V. 2011, A&A, 533, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., Lucatello, S., & D’Orazi, V. 2012, ApJ, 750, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2013, A&A, 557, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2014a, A&A, 564, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2014b, A&A, 561, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2015, A&A, 578, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Lucatello, S., et al. 2018, A&A, 615, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassisi, S., Castellani, V., degl’Innocenti, S., Salaris, M., & Weiss, A. 1999, A&AS, 134, 103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalessandro, E., Schiavon, R. P., Rood, R. T., et al. 2012, AJ, 144, 126 [NASA ADS] [CrossRef] [Google Scholar]
- D’Antona, F., Caloi, V., Montalbán, J., Ventura, P., & Gratton, R. 2002, A&A, 395, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Antona, F., Vesperini, E., D’Ercole, A., et al. 2016, MNRAS, 458, 2122 [NASA ADS] [CrossRef] [Google Scholar]
- Decressin, T., Meynet, G., Prantzos, N., Charbonnel, C., & Ekstrom, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Denisenkov, P. A., & Denisenkova, S. N. 1989, A. Tsir., 1538, 11 [NASA ADS] [Google Scholar]
- D’Ercole, A., Vesperini, E., D’Antona, F., McMillan, S. L. W., & Recchi, S. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Djorgovski, S. 1991, ASPC, 13, 112 [NASA ADS] [Google Scholar]
- Djorgovski, S., & Meylan, G. 1994, AJ, 108, 1292 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Sarajedini, A., Anderson, J., et al. 2010, ApJ, 708, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Dupree, A. K., Strader, J., & Smith, G. H. 2011, ApJ, 728, 155 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Fusi Pecci, F., Ferraro, F. R., Bellazzini, M., et al. 1993, AJ, 105, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Helmi, A., et al.) 2018, A&A, 616, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Carretta, E., & Bragaglia, A. 2012, A&ARv, 20, 50 [CrossRef] [Google Scholar]
- Gratton, R. G., Lucatello, S., Bragaglia, A., et al. 2006, A&A, 455, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Lucatello, S., Bragaglia, A., et al. 2007, A&A, 464, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Carretta, E., Bragaglia, A., Lucatello, S., & D’Orazi, V. 2010, A&A, 517, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Halford, M., & Zaritsky, D. 2015, ApJ, 815, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Irwin, M. J., & Gilmore, G. 1994, Nature, 370, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, C. I., Rich, M. R., Pilachowski, C. A., et al. 2015, AJ, 150, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Kayser, A., Hilker, M., Grebel, E. K., & Willemsen, P. G. 2008, A&A, 486, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khalaj, P., & Baumgardt, H. 2015, MNRAS, 452, 924 [NASA ADS] [CrossRef] [Google Scholar]
- King, I. R. 1966, AJ, 71, 64 [Google Scholar]
- Kraft, R. P. 1994, PASP, 106, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D. 2015, MNRAS, 454, 1658 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, G. E., Hoffman, R., & Sneden, C. 1993, PASP, 105, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Leaman, R., VandenBerg, D. A., & Mendel, J. T. 2013, MNRAS, 436, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y. W. 1989, PhD Thesis, Yale University [Google Scholar]
- Lee, Y. W. 1990, ApJ, 363, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y.-W., Gim, H. B., & Casetti-Dinescu, D. I. 2007, ApJ, 661, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Mackey, A. D., & Gilmore, G. F. 2004, MNRAS, 355, 504 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mackey, A. D., & van den Bergh, S. 2005, MNRAS, 360, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Marino, A. F., Sneden, C., Kraft, R. P., et al. 2011, A&A, 532, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marino, A. F., Milone, A. P., Karakas, A. I., et al. 2015, MNRAS, 450, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A., Piotto, G., Bedin, L., et al. 2012a, ApJ, 744, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Piotto, G., Bedin, L., et al. 2012b, A&A, 537, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milone, A. P., Marino, A. F., & Dotter, A. 2014, ApJ, 785, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Piotto, G., Renzini, A., et al. 2017, MNRAS, 464, 3636 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Marino, A. F., Renzini, A., et al. 2018, MNRAS, 481, 5098 [NASA ADS] [CrossRef] [Google Scholar]
- Monelli, M., Milone, A. P., Stetson, P. B., et al. 2013, MNRAS, 431, 2126 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, S. D., & Lin, D. N. C. 1992, ApJ, 400, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. 1987, ApJ, 313, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Odenkirchen, M., Grebel, E. K., Rockosi, C. M., et al. 2001, ApJ, 548, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Odenkirchen, M., Grebel, E. K., Dehnen, W., et al. 2003, AJ, 126, 2385 [NASA ADS] [CrossRef] [Google Scholar]
- Pancino, E., Rejkuba, M., Zoccali, M., & Carrera, R. 2010, A&A, 524, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasquini, L., Mauas, P., Káufl, H. U., & Cacciari, C. 2011, A&A, 531, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perina, S., Bellazzini, M., Buzzoni, A., et al. 2012, A&A, 546, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Recio-Blanco, A., Aparicio, A., Piotto, G., De Angeli, F., & Djorgovski, S. G. 2006, A&A, 452, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reina-Campos, M., Kruijssen, J. M. D., Pfeffer, J., Bastian, N., & Crain, R. A. 2018, MNRAS, 481, 2851 [NASA ADS] [CrossRef] [Google Scholar]
- Saracino, S., Dalessandro, E., Ferraro, F. R., et al. 2015, ApJ, 806, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Sarajedini, A., Bedin, L. R., Chaboyer, B., et al. 2007, AJ, 133, 1658 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, J. D., De Silva, G., Martell, S. L., Navin, C. A., & Zucker, D. B. 2017, MNRAS, 472, 2856 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. H. 1987, PASP, 99, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. H. 2015, PASP, 127, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. H., Sneden, C., & Kraft, R. P. 2002, AJ, 123, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. H., Modi, P. N., & Hamren, K. 2013, PASP, 125, 1287 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, Jr., L. 1958, ApJ, 127, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., D’Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Vesperini, E., McMillan, S. L. W., D’Antona, F., & D’Ercole, A. 2010, ApJ, 718, L112 [NASA ADS] [CrossRef] [Google Scholar]
- Zinn, R. J. 1986, in Stellar Populations, eds. C. A. Norman, A. Renzini, & M. Tosi (Cambridge: Cambridge Uiversity Press), 73 [Google Scholar]
Appendix A: Derived values for IQR2
In the following table we list the relevant parameters and the results from the calibration of IQR2 (Eq. (2)). The values for total absolute magnitude MV, concentration c, metallicity [Fe/H] are from Harris (1996, 2010 on-line edition). The Galactic population is the same as in Table 1 and is adopted from Carretta et al. (2010a), whereas the HBR values are from Mackey & van den Bergh (2005) except for Terzan 8, whose HB index is taken from Carretta et al. (2010a).
Note that the values of IQR2 are actually the observed IQR[O/Na] values for the 22 calibrating GCs in Table 1, as well as for the three core-collapse GCs NGC 6397, NGC 6752, and NGC 7099 (M 30). These three GCs are studied in our FLAMES survey, but not used to derive the calibration for IQR2.
Relevant parameters and calibrated IQR2 values for Galactic GCs.
All Tables
All Figures
 |
Fig. 1. IQR[O/Na] for Galactic GCs as a function of the total absolute magnitude MV (upper panel), and residual around this relation as a function of the cluster concentration c (lower panel). Both panels are reproduced from Carretta et al. (2014a). |
| In the text | |
 |
Fig. 2. Comparison of the IQR1 values from the first calibration (Eq. (1)) with the observed values IQR[O/Na] for 22 calibrating GCs. The Spearman rank correlation (rS) coefficient, the Pearson linear correlation (rP) coefficients and its p-value are listed in the panel. Different symbols individuate different Galactic populations (see text). |
| In the text | |
 |
Fig. 3. Residuals from the calibration of Eq. (1) as a function of various parameters for the HB morphology. Above each panel the Spearman and Pearson correlation coefficients are listed, as well as the p-values and the number of calibrating GCs used in the respective relations. |
| In the text | |
 |
Fig. 4. Comparison of the IQR2 values from our final calibration (Eq. (2)) with the observed values IQR[O/Na] for 22 calibrationg GCs. Symbols and labels are as in Fig. 2. |
| In the text | |
 |
Fig. 5. Extensions of the Na–O anti-correlation IQR1 (left panel) and IQR2 (right panel) from the calibrations Eqs. (1) and (2), respectively. Symbols are as in Fig. 2. Black points indicate the calibrating GCs from our FLAMES survey, and their shape indicate the Galactic sub-population. Symbols and label are as in Fig. 4. |
| In the text | |
 |
Fig. 6. Calibrated extent of the Na–O anti-correlation IQR2 as a function of the colour spreads in B − V and V − I along the MS from Gratton et al. (2010). Symbols and labels are as in the previous figures. |
| In the text | |
 |
Fig. 7. Calibrated IQR2 values for the extension of the Na–O anti-correlation as a function of the maximum variations in He derived from photometry (Milone et al. 2018). GCs defined as type-II are encircled, and the position of NGC 6388 is labelled (see text). |
| In the text | |
 |
Fig. 8. Calibrated IQR2 values from Eq. (2) as a function of the total absolute magnitude from H10. Observed IQR[O/Na] values are used for 25 GCs from our FLAMES survey (black symbols). |
| In the text | |
 |
Fig. 9. Left panel: calibrated IQR2 values as a function of the distance in kpc from the Galactic plane (H10). Horizontal lines are traced at the average values of the corresponding galactic populations (same colour coding). Right panel: cumulative distribution of IQR2 for GCs of different sub-populations. The P values from two-sample Kolmogorov–Smirnov (K–S) tests are indicated. |
| In the text | |
 |
Fig. 10. Left, middle, and right panels: cumulative distributions of total absolute magnitude MV, concentration c, and HBR index for GCs of different Galactic sub-populations. Probabilities from K–S tests are indicated in each panel. |
| In the text | |
 |
Fig. 11. Left panel: age–metallicity relation from Leaman et al. (2013) for GCs formed in situ in the MW disc (blue points) and GCs likely formed in smaller stellar systems and later accreted in the MW (red points). The size of the symbols are proportional to the IQR2 values. Right panel: cumulative distributions of GCs with different origin. The P value from two-sample K–S tests is indicated. |
| In the text | |
 |
Fig. 12. Left panel: correlation between concentration c and total absolute magnitude MV for MW GCs. The size of symbols is proportional to the IQR2 value, their shape indicates the Galactic population, and the colours refer to the HB morphology, as detailed by the legend in the right panel. |
| In the text | |
 |
Fig. 13. Correlation between concentration and luminosity for Galactic GCs, where are only plotted GCs with fraction of FG stars estimated in Milone et al. (2017) from HST photometry. Symbol sizes are proportional to the fractions, in steps of 10% from about 10 to about 70%. |
| In the text | |
 |
Fig. 14. Comparison of present and initial GC masses from Baumgardt et al. (2019). Filled symbols are as in Fig. 2, whereas empty symbols indicate core-collapse GCs. The line is traced at Mini = 2 Mnow. |
| In the text | |
 |
Fig. 15. Correlation between concentration and luminosity for Galactic GCs. Different colour and shapes represent the various Galactic populations as in Fig. 12. Symbol sizes are proportional to the initial masses estimated by Baumgardt et al. (2019). In unit of 105 M⊙ the adopted ranges for the scaling of sizes are 0–1, 1–10, 10–20, and > 20. |
| In the text | |
 |
Fig. 16. Mass loss from Baumgardt et al. (2019), in unit of 105 M⊙, as a function of the tidal radius for Galactic GCs. Symbols are as Fig. 14. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.