| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A165 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201834853 | |
| Published online | 28 March 2019 | |
HD 219666 b: a hot-Neptune from TESS Sector 1★
1
Thüringer Landessternwarte Tautenburg,
Sternwarte 5,
07778 Tautenburg,
Germany
e-mail: mesposito@tls-tautenburg.de
2
Department of Physics, University of Warwick,
Gibbet Hill Road,
Coventry,
CV4 7AL, UK
3
Centre for Exoplanets and Habitability, University of Warwick,
Gibbet Hill Road,
Coventry,
CV4 7AL, UK
4
Dipartimento di Fisica, Università degli Studi di Torino,
via Pietro Giuria 1,
10125
Torino, Italy
5
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas,
4150-762 Porto, Portugal
6
Department of Space, Earth and Environment, Chalmers University of Technology, Onsala Space Observatory,
439 92 Onsala, Sweden
7
Leiden Observatory, University of Leiden,
PO Box 9513,
2300 RA Leiden, The Netherlands
8
Departamento de Física e Astronomia, Faculdade de Ciencias, Universidade do Porto, Rua Campo Alegre,
4169-007 Porto, Portugal
9
Department of Astronomy, Graduate School of Science, The University of Tokyo,
Hongo 7-3-1, Bunkyo-ku,
Tokyo
113-0033, Japan
10
Space Research Institute, Austrian Academy of Sciences,
Schmiedlstrasse 6,
8041 Graz, Austria
11
European Southern Observatory,
Alonso de Cordova 3107,
Vitacura, Santiago, Chile
12
Departamento de Astrofísica, Centro de Astrobiología (INTA-CSIC), Campus ESAC (ESA)Camino Bajo del Castillo s/n 28692 Villanueva de la Cañada, Spain
13
Universidad de Buenos Aires, Facultad de Ciencias Exactas y Naturales, Buenos Aires, Argentina
14
CONICET – Universidad de Buenos Aires, Instituto de Astronomía y Física del Espacio (IAFE), Buenos Aires, Argentina
15
Department of Astrophysical Sciences, Princeton University,
4 Ivy Lane,
Princeton,
NJ
08544, USA
16
Geneva Observatory, University of Geneva,
Chemin des Mailettes 51,
1290 Versoix, Switzerland
17
Stellar Astrophysics Centre, Deparment of Physics and Astronomy, Aarhus University,
Ny Munkegrade 120, 8000 Aarhus C, Denmark
18
Instituto de Astrofísica de Canarias,
C/ Vía Láctea s/n,
38205 La Laguna,
Tenerife, Spain
19
Departamento de Astrofísica, Universidad de La Laguna,
38206
Tenerife, Spain
20
Institute of Planetary Research, German Aerospace Center,
Rutherfordstrasse 2,
12489 Berlin, Germany
21
Department of Astronomy and McDonald Observatory, University of Texas at Austin,
2515 Speedway,
Stop C1400, Austin,
TX 78712, USA
22
Department of Physics and Kavli Institute for Astrophysics and Space Research, MIT,
Cambridge, MA 02139, USA
23
Aix-Marseille Université, CNRS, CNES, LAM, Marseille, France
24
National Astronomical Observatory of Japan, NINS,
2-21-1 Osawa, Mitaka,
Tokyo 181-8588, Japan
25
Rheinisches Institut für Umweltforschung an der Universität zu Köln,
Aachener Strasse 209,
50931 Köln, Germany
26
Department of Earth and Planetary Sciences, Tokyo Institute of Technology,
Meguro-ku, Tokyo, Japan
27
Department of Earth, Atmospheric and Planetary Sciences, MIT,
77 Massachusetts Avenue,
Cambridge,
MA 02139, USA
28
Zentrum für Astronomie und Astrophysik, Technische Universität Berlin,
Hardenbergstr. 36 10623 Berlin, Germany
29
Astrobiology Center, NINS,
2-21-1 Osawa, Mitaka,
Tokyo
181-8588, Japan
30
Astronomy Department and Van Vleck Observatory, Wesleyan University,
Middletown,
CT 06459, USA
31
Institut für Geologische Wissenschaften, Freie Universität Berlin,
Malteserstr. 74–100 12249 Berlin, Germany
32
Institut de Ciències de l’Espai (ICE, CSIC), Campus UAB, Bellaterra, Spain
33
Institut d’Estudis Espacials de Catalunya (IEEC),
Barcelona, Spain
34
Landessternwarte Königstuhl, Zentrum für Astronomie der Universität Heidelberg,
Königstuhl 12,
69117 Heidelberg, Germany
35
INAF – Osservatorio Astrofisico di Torino,
Via Osservatorio 20,
10025 Pino Torinese, Italy
36
JST, PRESTO,
7-3-1 Hongo, Bunkyo-ku,
Tokyo
113-0033, Japan
Received:
13
December
2018
Accepted:
4
February
2019
We report on the confirmation and mass determination of a transiting planet orbiting the old and inactive G7 dwarf star HD 219666 (M⋆ = 0.92 ± 0.03 M⊙, R⋆ = 1.03 ± 0.03 R⊙, τ⋆ = 10 ± 2 Gyr). With a mass of Mb = 16.6 ± 1.3 M⊕, a radius of Rb = 4.71 ± 0.17 R⊕, and an orbital period of Porb ≃ 6 days, HD 219666 b is a new member of a rare class of exoplanets: the hot-Neptunes. The Transiting Exoplanet Survey Satellite (TESS) observed HD 219666 (also known as TOI-118) in its Sector 1 and the light curve shows four transit-like events, equally spaced in time. We confirmed the planetary nature of the candidate by gathering precise radial-velocity measurements with the High Accuracy Radial velocity Planet Searcher (HARPS) at ESO 3.6 m. We used the co-added HARPS spectrum to derive the host star fundamental parameters (Teff = 5527 ± 65 K, log g⋆ = 4.40 ± 0.11 (cgs), [Fe/H]= 0.04 ± 0.04 dex, log R′HK = −5.07 ± 0.03), as well as the abundances of many volatile and refractory elements. The host star brightness (V = 9.9) makes it suitable for further characterisation by means of in-transit spectroscopy. The determination of the planet orbital obliquity, along with the atmosphericmetal-to-hydrogen content and thermal structure could provide us with important clues on the formation mechanisms of this class of objects.
Key words: planets and satellites: detection / planets and satellites: fundamental parameters / techniques: radial velocities / stars: fundamental parameters / techniques: photometric / planets and satellites: individual: HD 219666 b
© ESO 2019
1 Introduction
Following the success of the Kepler space mission (Borucki 2016), in April 2018 NASA launched a new satellite, the Transiting Exoplanet Survey Satellite (TESS, Ricker et al. 2015). By performing a full-sky survey, TESS is expected to detect approximately 10 000 transiting exoplanets (TEPs; Barclay et al. 2018; Huang et al. 2018a). Most interestingly, nearly 1000 of them will orbit host stars with magnitudes V ≲ 10 (as of November 2018 there are 56 known TEPs around stars with V < 10, only 13 of which have masses <20 M⊕, according to the NASA exoplanet archive1). Bright host stars are suitable for precise radial-velocity (RV) measurements that can lead to planet mass determinations down to a few Earth masses, and to estimates of the planet bulk density for TEPs. In-transit precise RVs also allow us to measure the planet orbital obliquity through the observation of the Rossiter-McLaughlin effect (see, e.g. Triaud 2017). High-signal-to-noise ratio (S/N) number spectra are very much needed for transmission spectroscopy studies aimed at the detectionof atomic and molecular species, and the characterisation of the thermal structure of planet atmospheres (Snellen et al. 2010; Bean et al. 2013).
TESS has a field of view of 24° × 96°, and will cover almost the full sky in 26 Sectors, each monitored for about 27 days. Full frame images (FFIs) are registered every 30 min, while for a selected sample of bright targets (~16 000 per Sector) pixel sub-arrays are saved with a two-minute cadence. The first TESS data set of FFIs from Sectors 1 and 2 was released on December 6, 2018, and the TESS Science Office, supported by the Payload Operations Centre at MIT, had already issued TESS data alerts for a number of transiting planet-host star candidates, the so-called TESS objects of interest (TOIs). Preliminary two-minute cadence light curves and target pixel files (Twicken et al. 2018) are made publicly available for download at the MAST web site2.
Several TESS confirmed planets have already been announced: π Mensae c (TOI-144), a super-Earth orbiting a V = 5.65 mag G0 V star (Huang et al. 2018b; Gandolfi et al. 2018); HD 1397 b (TOI-120), a warm giant planet around a V = 7.8 mag sub-giant star (Brahm et al. 2018; Nielsen et al. 2019); HD 2685 b (TOI-135), a hot-Jupiter hosted by an early F-type star (Jones et al. 2019); and an ultra-short-period Earth-like planet around the M-dwarf star LHS 3844 (TOI-136; Vanderspek et al. 2019). Here we report on the detection and mass determination of a Neptune-like planet (Mb ≃ 16.6 M⊕, Rb ≃ 4.7 R⊕) on a Porb ≃ 6 day orbit around the bright (V = 9.9) G7 V star HD 219666 (TOI-118; Tables 1 and 2).
The work presented here is part of the ongoing RV follow-up effort carried out by two teams, namely the KESPRINT consortium (see, e.g. Johnson et al. 2016; Van Eylen et al. 2016; Dai et al. 2017; Gandolfi et al. 2017; Barragán et al. 2018; Prieto-Arranz et al. 2018) and the NCORES consortium (see, e.g. Armstrong et al. 2015; Lillo-Box et al. 2016; Barros et al. 2017; Lam et al. 2018; Santerne et al. 2018). Both teams were recently awarded two large programs with the High Accuracy Radial velocity Planet Searcher (HARPS) spectrograph at the ESO-3.6 m telescope to follow up TESS transiting planet candidates. The two consortia have joined forces to make better use of the instrument, optimise the scientific return of the available observing time, and tackle more ambitious planet detections and characterisations.
This paper is organised as follows. Section 2 describes the TESS photometric data, our custom light-curve extraction and assessment of the light contamination factor. Section 3 reports on our spectroscopic follow-up observations, which were used to confirm the planetary nature of the transiting companion, and to derive the fundamental parameters and metal abundances of the host star (Sect. 4). The joint analysis of transit light curves and RV data is described in Sect. 5. Finally we discuss our results in Sect. 6.
Main identifiers, coordinates, parallax, and optical and infrared magnitudes of HD 219666.
2 TESS photometry
HD 219666 was observed by TESS in Sector 1 (CCD #2 of Camera #2) and falls in a region of the sky that will not be further visited by TESS. Sector 1 was monitored continuously for ~27.9 days, from 2018-07-25 (BJDTDB = 2458325.29953) to 2018-08-22 (BJDTDB = 2458353.17886), with only a 1.14 day gap (from BJDTDB = 2458338.52472 to BJDTDB = 2458339.66500) when the satellite was repointed for data downlink. In addition, between BJDTDB = 2458347 and BJDTDB = 2458350, the TESS light curve shows a higher noise level caused by the spacecraft pointing instabilities. The corresponding data-points were masked out and not included in the analysis presented in this paper.
Fundamental parameters and elemental abundances of HD 219666.
2.1 Custom light-curve preparation
To check that the SPOC aperture is indeed an optimal choice, we extracted a series of light curves from the pixel data using contiguous sets of pixels centred on HD 219666. We first computed the 50th–95th percentiles (in 1% steps) of the median image, and then selected pixels with median counts above each percentile value to form each aperture. We then computed the 6.5 h combined differential photometric precision (CDPP; Christiansen et al. 2012) of the light curve resulting from each of these apertures, and we found that the aperture that minimised the CDPP was slightly larger than the SPOC aperture shown in Fig. 1. However, we opted to use the PDCSAP light curve produced from the SPOC aperture, which has lower levels of systematic noise as a result of the processing performed by the SPOC pipeline (Ricker & Vanderspek 2018).
The median-normalised light curve that we used in our analysis is shown in Fig. 2.
 |
Fig. 1 5′ × 5′ archival image taken in 1980 from the SERCJ survey, with the SPOC photometric aperture overplotted in blue (TESS pixel size is 21′′), and the positions of Gaia DR2 sources (J2015.5) within 2′ of HD 219666 indicated by circles. HD 219666 is in red, nearby sources contributing more than 1% of their flux to the aperture arein orange (see Sect. 2.2), and other sources are in green. |
2.2 Limits on photometric contamination
To investigate the possibility of contaminating flux from nearby stars within the SPOC photometric aperture, we compared the Gaia DR2 (Gaia Collaborations 2018) sources with the aperture and an archival image of HD 219666 from the SERC-J survey3. To do so, we executed a query centred on the coordinates of HD 219666 from the TESS Input Catalog4 (TIC; Stassun et al. 2018) using a search radius of 3′. The archival image, taken in 1980, shows HD 219666 to be offset from its current position by ~4.8′′. The proper motion is not sufficient to completely rule out chance alignment with a background source, but such an alignment with a bright source is qualitatively unlikely. We also note the non-detection by Gaia of any other sources within ~30′′ of HD 219666. Figure 1 shows Gaia DR2 source positions overplotted on the archival image, along with the SPOC photometric aperture. Using a 2D Gaussian profile with a FWHM of ~25′′ to approximate the TESS point spread function (PSF), and a negligible difference between the GRP and T bandpasses, we found that the transit depth of HD 219666 should be diluted by no more than 0.1%, even considering partial flux contributions from nearby stars outside the aperture. Furthermore, we found that HD 219666 is the only star in or near the aperture that is bright enough to be the source of the transit signal, given the observed depth and assuming a maximum eclipse depth of 100%.
3 HARPS observations
We acquired 21 high-resolution (R ≈115 000) spectra of HD 219666 with the HARPS spectrograph (Mayor et al. 2003) mounted at the ESO-3.6 m telescope of La Silla observatory (Chile). The observations were performed between 02 October and 05 November 2018 UTC, as part of the large observing programmes 1102.C-0923 (PI: Gandolfi) and 1102.C-0249 (PI: Armstrong). We reduced the data using the dedicated HARPS Data Reduction Software (DRS) and extracted the RVs by cross-correlating the echelle spectra with a G2 numerical mask (Baranne et al. 1996; Pepe et al. 2002; Lovis & Pepe 2007). Table 3 lists the HARPS RVs and their uncertainties, along with the BIS and FWHM of the cross-correlation function (CCF), the Ca II H and K Mount-Wilson S-index, and S/N per pixel at 5500 Å.
The generalised Lomb-Scargle (GLS; Zechmeister & Kürster 2009) periodogram of the HARPS RV measurements (Fig. 3, first panel) shows a significant peak at the frequency of the transit signal (f1 = 0.166 d−1; vertical dashed red line), with a false alarm probability5 (FAP) lowerthan 0.1 % (horizontal dashed blue line). The peak has no counterpart in the periodograms of the activity indicators, as shown in the second, third, and fourth panels of Fig. 3. This provides strong evidence that the signal detected in our Doppler data is induced by an orbiting companion and confirms the presence of the transiting planet with a period of about 6 days. The periodogram of the RV measurements shows additional peaks symmetrically distributed to the left and right of the dominant frequency. We interpreted these peaks as aliases of the orbital frequency, as shown bythe position of the peaks in the periodogram of the window function (Fig. 3, fifth panel).
4 Stellar fundamental parameters
The determination of the stellar parameters from the spectrum of the host star is crucial in order to derive the planetary parameters from transit and RV data. The three most important planetary parameters are the mass, Mb, the radius Rb, and the age τb, all of them only derivable with knowledge of the same parameters for the host star, M⋆, R⋆, and τ⋆. Therefore, we have used two independent methods in order to determine the stellar parameters with the highest degree of confidence available today. To this aim, we used the co-added HARPS spectrum, which has a S/N per pixel of ~300 at 5500 Å.
In one of the methods, we used version 5.22 of the Spectroscopy made easy (SME) code (Valenti & Piskunov 1996; Valenti & Fischer 2005; Piskunov & Valenti 2017). The SME code calculates synthetic spectra, using a grid of stellar models and a set of initial (assumed) fundamental stellar parameters and fits the result to the observed high-resolution spectrum with a chi-square minimisation procedure. The code contains a large library of different 1D and 3D model grids. In our analysis of the co-added HD 219666 HARPS spectrum, we used the ATLAS12 model atmosphere grid (Kurucz 2013). This is a set of 1D models applicable to solar-like stars. The observed spectral features that we fit are sensitive to the different photospheric parameters, including the effective temperature Teff, metallicity [M/H], surface gravity log g⋆, micro- and macro-turbulent velocities vmic and vmac, and the projected rotational velocity v sin i⋆. In order to minimise the number of free parameters we adopted the calibration equation of Bruntt et al. (2010) to estimate vmic and we fitted many isolated and unblended metal lines to determine v sin i⋆.
We used several different observed spectral features as indicators of each fundamental stellar parameter. The Teff was primarily determined by fitting the wings of Balmer lines, which for solar-type stars are almost totally dependent on the temperature and weakly dependent on gravity and metallicity (Fuhrmann et al. 1993). The surface gravity log g⋆ was determined by fitting the line profiles of the Ca I lines at 6102, 6122, 6162, and 6439 Å, and the profiles of the Mg I triplet at 5160–5185 Å. Results were then checked by fitting also the line wings of the sodium doublet at 5896 and 5890 Å using a sodium abundance determined from a number of fainter lines. In this case all three ions provided the same value for log g⋆. Using this method we derived an effective temperature Teff = 5450 ± 70 K, surface gravity log g⋆ = 4.35 ± 0.06 (cgs), iron content of [Fe/H] = +0.06 ± 0.03 dex, calciumcontent of [Ca/H] = 0.12 ± 0.05 dex, magnesium [Mg/H] = 0.18 ± 0.10 dex, and sodium [Na/H] = 0.15 ± 0.01 dex. The vmic used was 0.9 ± 0.1 km s−1, and we found v sin i⋆ = 2.2 ± 0.8 km s−1 and vmac = 2.8 ± 0.9 km s−1.
In an independent analysis, stellar atmospheric parameters (Teff, log g⋆, vm ic, and [Fe/H]) and respective error bars were derived using the methodology described in Sousa (2014) and Santos et al. (2013). Briefly, we made use of the equivalent widths (EWs) of 224 Fe I and 35 Fe II lines, as measured in the combined HARPS spectrum of HD 219666 using the ARES v2 code6 (Sousa et al. 2015), and we assumed ionisation and excitation equilibrium. The process makes use of a grid of ATLAS model atmospheres (Kurucz 1993) and the radiative-transfer code MOOG (Sneden 1973). This method provides effective temperatures in excellent agreement with values derived using the infrared flux method that are independent of the derived surface gravity. The resulting values are Teff = 5527 ± 25 K, log g⋆ = 4.34 ± 0.04 (cgs), vmic = 0.90 ± 0.04 km s−1, and [Fe/H] = 0.04 ± 0.02 dex. The surface gravity corrected for the systematic effects discussed in Mortier et al. (2013) has a value of log g⋆ = 4.40 ± 0.04 (cgs).
The two sets of spectroscopic parameters obtained using the two independent methods described above are in good agreement. While we have no reason to prefer one method over the other, in the following analyses we adopted the values derived using the EW method. We stress that the quoted uncertainties are internal error bars that do not account for the choice of spectral lines and/or atmospheric models. Following Sousa et al. (2011), we accounted for systematic effects by quadratically adding 60 K, 0.1 (cgs), and 0.04 dex to the nominal uncertainty of the effective temperature, surface gravity, and iron content, respectively. The adopted values of Teff = 5527 ± 65 K, log g⋆ = 4.40 ± 0.11 (cgs), and [Fe/H] = 0.04 ± 0.04 dex are listed in Table 2.
Stellar abundances of the elements were also derived using the same tools and models as for stellar parameter determination, as well as using the classical curve-of-growth analysis method, assuming local thermodynamic equilibrium (LTE). Although the EWs of the spectral lines were automatically measured with ARES, for the elements with only two or three lines available we performed careful visual inspection of the EWs. For the derivation of chemical abundances of refractory elements we closely followed the methods described in Adibekyan et al. (2012, 2015) and Delgado Mena et al. (2017). Abundances of the volatile elements O and C were derived following the method of Delgado Mena et al. (2010) and Bertran de Lis et al. (2015). Since the two spectral lines of oxygen are usually weak and the 6300.3 Å line is blended with Ni and CN lines, the EWs of these lines were manually measured with the task splot in IRAF. We noticed that for several individual spectra of the star, the 6300 Å region was contaminated by the telluric [OI] emission line. We excluded these contaminated spectra when measuring the EW of the stellar oxygen line at 6300.3 Å. Lithium and sulfur abundances were derived by performing spectral synthesis with MOOG (Delgado Mena et al. 2014). The final abundances of the elements are presented in Table 2. It is worth noting that the abundances of Na, Mg, and Ca derived with this EW method are in agreement with the abundances obtained with the spectral fitting method. Perhaps it is also interesting to note that the star seems to be enhanced in several α elements (Mg, Si, Ti) and show under-abundance of some heavy elements (e.g. Ba and Y). Such a chemical composition is typical for the so-called high-α metal-rich stars first discovered by Adibekyan et al. (2011, 2013). The origin of this population is not yet fully clear, but most probably these stars are migrators from the inner Galaxy (Adibekyan et al. 2011; Anders et al. 2018).
We derived the stellar radius (R⋆) combining the Tycho BT, VT magnitudes, the Gaia G, GBP, GRP photometry, and 2MASS J, H, Ks magnitudes (see Table 1) with our spectroscopic parameters (Teff, log g⋆, [Fe/H]; see Table 2) and the Gaia’ parallax (10.590 ± 0.028 mas, Gaia Collaborations 2018, see Table 2). We corrected the Gaia G photometry for the magnitude dependent offset using Eq. (3) from Casagrande & VandenBerg (2018), and adopted a minimum uncertainty of 0.01 mag for the Gaia magnitudes to account for additional systematic uncertainties in the Gaia photometry. We added 0.06 mas to the nominal Gaia’s parallax to account for the systematic offset found by Stassun & Torres (2018), Riess et al. (2018), and Zinn et al. (2018). Followingthe method described in Gandolfi et al. (2008), we found that the reddening along the line of sight to the star is consistent with zero and did not correct the apparent magnitudes. The bolometric correction for each band-pass was computed using the routine from Casagrande & VandenBerg (2018). We determined a stellar radius of R⋆ = 1.03 ± 0.03 R⊙.
We used the BAyesian STellar Algorithm (BASTA, Silva Aguirre et al. 2015) to determine a stellar mass of M* = 0.92 ± 0.03 M⊙ and an age of τ⋆ = 10 ± 2 Gyr by fitting the stellar radius R*, effective temperature Teff and iron abundance [Fe/H] to a large, finely-sampled grid of GARSTEC stellar models (Weiss & Schlattl 2008).
From the Ca II H and K S-index values provided by the HARPS DRS, we calculated 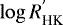 = −5.07 ± 0.03 (Lovis et al. 2011). Using the activity-rotation empirical relationships reported in Noyes et al. (1984) and Mamajek & Hillenbrand (2008), we derived a stellar rotation period of Prot = 34 ± 6 and 37 ± 4 days respectively, which are in good mutual agreement. An upper limit to Prot of 22
= −5.07 ± 0.03 (Lovis et al. 2011). Using the activity-rotation empirical relationships reported in Noyes et al. (1984) and Mamajek & Hillenbrand (2008), we derived a stellar rotation period of Prot = 34 ± 6 and 37 ± 4 days respectively, which are in good mutual agreement. An upper limit to Prot of 22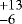 days can be inferred from the stellar radius and v sin i⋆, which is compatible with good alignment between the stellar rotation axis and the planetary orbital axis. We note that the 27.9 day duration of the TESS observations is not long enough to attempt a reliable estimation of the photometric stellar rotational period.
days can be inferred from the stellar radius and v sin i⋆, which is compatible with good alignment between the stellar rotation axis and the planetary orbital axis. We note that the 27.9 day duration of the TESS observations is not long enough to attempt a reliable estimation of the photometric stellar rotational period.
 |
Fig. 2 TESS light curve of HD 219666. The red arrows point to the four planet-transit occurrences. |
HARPS RV measurements of HD 219666.
 |
Fig. 3 Generalised Lomb-Scargle periodogram of the HARPS RVs (first panel), the CCF BIS and FWHM (second and third panels, respectively), the Ca II H and K S-index (fourth panel), and of the window function (fifth panel). The vertical dashed red line marks the frequency of the transit signal. The horizontal dashed blue line marks the FAP = 0.1% level. |
HD 219666 system parameters.
5 Joint analysis of the transit and Doppler data
We performed a joint fit to the TESS light curve (Sect. 2) and the 21 HARPS measurements (Sect. 3) using the code pyaneti (Barragán et al. 2019). The code uses a Bayesian approach for the model parameter estimations, and samplesthe posteriors via Markov chain Monte Carlo (MCMC) methods.
We selected 10 h of photometric data-points centred around each of the four transits observed byTESS and flattened the four segments using a second-order polynomial fitted to the out-of-transit data. We fitted the transit light curves using the limb-darkened quadratic model of Mandel & Agol (2002). We set Gaussian priors on the limb-darkening coefficients adopting the theoretical values predicted by Claret (2017) along with a conservative error bar of 0.1 for both the linear and the quadratic limb-darkening term. The transit light curve poorly constrains the scaled semi-major axis (a∕R⋆). We therefore set a Gaussian prior on a∕R⋆ using the orbital period and the derived stellar parameters (Sect. 4) via Kepler’s third law.
The RV model consists of a Keplerian equation. Following Anderson et al. (2011), we fitted for 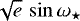 and
and 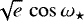 , where e is the eccentricity and ω⋆ is the argument of periastron. We also fitted for an RV jitter term to account for instrumental noise not included in the nominal uncertainties, and/or for RV variations induced by stellar activity. We imposed uniform priors for the remaining fitted parameters. Details of the fitted parameters and prior ranges are given in Table 4.
, where e is the eccentricity and ω⋆ is the argument of periastron. We also fitted for an RV jitter term to account for instrumental noise not included in the nominal uncertainties, and/or for RV variations induced by stellar activity. We imposed uniform priors for the remaining fitted parameters. Details of the fitted parameters and prior ranges are given in Table 4.
We used 500 independent Markov chains initialized randomly inside the prior ranges. Once all chains converged, we used the last 5000 iterations and saved the chain states every ten iterations. This approach generates a posterior distribution of 250 000 points for each fitted parameter. Table 4 lists the inferred planetary parameters. They are defined as the median and 68% region of the credible interval of the posterior distributions for each fitted parameter. The transit and RV curves are shown in Figs. 4 and 5, respectively.
An initial fit for an eccentric orbit yielded e = 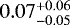 , which is consistent with zero within less than 2σ. We determined the probability that the best-fitting eccentric solution could have arisen by chance if the orbit were actually circular using Monte Carlo simulations. Briefly, we created 105 sets of synthetic RVs that sample the best-fitting circular solution at the epochs of our observations. We added Gaussian noise at the level of our measurements and fitted the simulated data allowing for an eccentric solution. We found that, given our measurements, there is a 35% probability that an eccentric solution with e ≥ 0.07 could have arisen by chance if the orbit were actually circular. As this is above the 5% significance level suggested by Lucy & Sweeney (1971), we decided to conservatively assume a circular model. We note that the eccentric solution provides a planetary mass that is consistent within less than 1-σ of the result from the circular model.
, which is consistent with zero within less than 2σ. We determined the probability that the best-fitting eccentric solution could have arisen by chance if the orbit were actually circular using Monte Carlo simulations. Briefly, we created 105 sets of synthetic RVs that sample the best-fitting circular solution at the epochs of our observations. We added Gaussian noise at the level of our measurements and fitted the simulated data allowing for an eccentric solution. We found that, given our measurements, there is a 35% probability that an eccentric solution with e ≥ 0.07 could have arisen by chance if the orbit were actually circular. As this is above the 5% significance level suggested by Lucy & Sweeney (1971), we decided to conservatively assume a circular model. We note that the eccentric solution provides a planetary mass that is consistent within less than 1-σ of the result from the circular model.
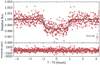 |
Fig. 4 Phase-folded and normalized TESS photometric data with our best fitting transit light curve. |
 |
Fig. 5 Phase-folded HARPS RV data points with our best fitting circular RV curve. The blue error bars correspond to the nominal RV uncertainties calculated by the HARPS DRS while the grey ones account for the RV jitter term. The bottom panel shows the RV residuals that have a rms of 1.7 m s −1. |
6 Discussion and conclusion
HD 219666 b has almost the same mass as Neptune (Mb = 16.6 ± 1.3 M⊕) but a larger radius (Rb = 4.71 ± 0.17 R⊕). With an orbital period of Porb ≃ 6 days and an equilibrium temperature of Teq ≃ 1073 K, it is a new member of a relatively rare class of exoplanets: the hot-Neptunes. Figure 6 shows that HD 219666 b lies in a region of the mass−radius diagram that is scarcely populated. The comparison with rocky planets composition models (Zeng et al. 2016) suggests that HD 219666 bholds a conspicuous gas envelope.
The existence of a hot-Neptunes “desert” has already been pointed out (see, e.g. Szabó & Kiss 2011; Mazeh et al. 2016; Owen & Lai 2018), and HD 219666 b falls close to the lower edge of the desert in the mass−period diagram (see Fig. 1 in Mazeh et al. 2016), and well inside the desert in the radius−period diagram (see Fig. 7). The relative paucity of hot-Neptunes (as compared to hot super-Earths and hot-Jupiters) could be interpreted as a consequence of two different formation mechanisms for short-period planets: in situ formation for terrestrial planets (Ogihara et al. 2018; Matsumoto & Kokubo 2017), and formation at larger separations followed by inward migration for giant planets (Nelson et al. 2017). Intermediate-mass planets like HD 219666 b would then be either the upper tail of terrestrial planets or the lower tail of giant-planet distributions. Alternatively, giant and small close-in planets could have a common origin but a dramatically different atmospheric escape history (Lundkvist et al. 2016; Ionov et al. 2018; Owen & Lai 2018). Other mechanisms have been proposed to explain the observed hot-Neptune desert. Matsakos & Königl (2016) advanced an explanation based on high-eccentricity migration followed by tidal circularization. They interpreted the two distinct segments of the desert boundary as a consequence of the different slopes of the empirical mass-radius relation for small and large planets. Batygin et al. (2016) advocated the in situ formation of close-in super-Earths and hot-Jupiters alike. In the rare cases when a core mass of Mcore ≳ 15M⊕ was reached, rapid gas accretion would lead to the formation of a gaseous giant planet. In this way the relative occurrence of Earth-, Neptune- and Jupiter-like close-in planets can be explained.
To determine whether or not in-situ formation of a planet so close to its star is even possible, wecalculate the isolation mass of a planet orbiting with a period of 6 days around a 0.9 M⊙ star. This is the mass of the planet that can form assuming that it grows by consuming all the planetesimals that are within its gravitational influence. Assuming a typical T Tauri disc with a mass of 0.01M⊙ within 100 AU, a gas-to-dust ratio of 100 and a surface mass density profile of Σ ∝R−3∕2 (a steep profile enables as much material as possible to be made available in the inner disc for planet formation), the available rocky material is ≈ 5 × 10−3 M⊕. Even if the gas-to-dust ratio was a factor of ten lower (Ansdell et al. 2016) the resulting mass is still nowhere near the mass of the planet reported in this study. We point out that this calculation assumes no accretion through the disc when in reality rocky material could drift inwards and build up the core. From the perspective of pebble accretion, Lambrechts et al. (2014) showed that the pebble isolation mass – the core mass at which the drift of pebbles ceases, stopping the accretion of rocky material onto the core – at the radial location of the reported planet is approximately 1 M⊕, and simulations of planet growth by pebble accretion in evolving discs also show that a high mass of rocky material cannot be produced in the inner discs (Bitsch et al. 2015). The ~1 M⊕ upper limit to the rocky material that could have been accreted in situ must be compared with an estimate of the Mcore of HD 219666 b. According to Lopez & Fortney (2014), HD 219666 b, given its mass and radius, should have a H/He envelope which contributes 10–20% of its total mass, that is the 80 to 90% of the mass (13–15 M⊕) belongs to the rocky core. Therefore, we conclude that it is more likely that HD 219666 b formed further out and migrated inwards.
We derived the atmospheric mass-loss rate of HD 219666 b using the interpolation routine presented by Kubyshkina et al. (2018), which is based on a large grid of hydrodynamic upper atmosphere models. The main assumption is that the planet hosts a hydrogen-dominated atmosphere, which, given the measured bulk density, appears to be valid. For the computation, we employed the system parameters listed in Table 2 and a high-energy stellar flux (hereafter referred to as XUV flux) at the planetary distance to the star of 573.8 erg cm−2 s−1, obtained by scaling the solar XUV flux, derived from integrating the solar irradiance reference spectrum (Woods et al. 2009) below 912 Å, to the distance of the planet and the radius of the host star. This is a good assumption because the host star has a mass close to solar and appears to be rather inactive and old. We obtained a hydrogen mass-loss rate of about 1.2 × 1010 g s−1, which is comparable to what is obtained employing the energy-limited formula (5.2 × 109 g s−1; Erkaev et al. 2007). This indicates that, for this planet, atmospheric expansion and mass loss are driven mostly by atmospheric heating due to absorption of the stellar XUV flux, with an additional component due to the intrinsic thermal energy of the atmosphere and low planetary gravity (Fossati et al. 2017). The obtained mass-loss rate corresponds to 0.06 M⊕ Gyr−1, suggesting that mass loss does not play a major role in the current evolution of the planetary atmosphere. However, this does not account for the fact that the star was probably more active in the past, particularly during the first few hundred million years, up to about 1 Gyr (Jackson et al. 2012; Tu et al. 2015), when the XUV fluxes could have been up to about 500 times larger than the current estimate. This would lead to mass-loss rates about 500 times higher. It is therefore likely that atmospheric escape played a significant role in shaping the early planetary atmospheric evolution.
HD 219666 b is an interesting target for further atmospheric characterisation, given its equilibrium temperature of ~1070 K, since the range of expected temperatures at the terminator (depending on the planet’s albedo and energy transport) straddles widely different atmospheric chemical compositions under thermochemical equilibrium. Using the properties of the system, we modelled the transmission spectrum of the planet using the Python Radiative Transfer in a Bayesian framework7 (Cubillos et al., in prep.), which is based on the Bayesian Atmospheric Radiative Transfer package (Blecic 2016; Cubillos 2016), and simulated James Webb Space Telescope (JWST) observations with Pandexo (Batalha et al. 2017). These models consider opacities from the main spectroscopically active species expected for exoplanets at these wavelengths: H2 O and CO2 from Rothman et al. (2010); CH4, NH3, and HCN from Yurchenko & Tennyson (2014); CO from Li et al. (2015); Na and K from Burrows et al. (2000); Rayleigh opacities from H, He, and H2 (Kurucz 1970; Lecavelier Des Etangs et al. 2008); and collision-induced absorption from H2 –H2 (Borysow et al. 2001; Borysow 2002) and H2–He (Borysow et al. 1988, 1989; Borysow & Frommhold 1989). We compressed the HITEMP and ExoMol databases with the open-source repack package (Cubillos 2017) to extract only the strong, dominating line transitions.
Figure 8 shows estimated transmission spectra of HD 219666 b assuming a cloud-free atmosphere, in thermochemical equilibrium (Blecic et al. 2016) for solar elemental composition, at two illustrative atmospheric temperatures that lead to different transmission spectra. By combining NIRISS SOSS and NIRSpec G395H observations, one could potentially constrain the atmospheric chemistry and temperatureof the planet with a single-transit observation with each instrument. The transmission spectrum at wavelengths shorter than 2 μm constrain the H2O abundance for both models, setting the baseline to constrain the abundances of other species. At longer wavelengths, either CH4 (T = 600 K model) or CO/CO2 (T = 1000 K model) dominate the carbon chemistry at the probed altitudes (Fig. 8, bottom panels), producing widely different features in the transmission spectrum (Fig. 8, top panel).
An important clue to the formation mechanism of HD 219666 b could come from the knowledge of its orbital obliquity with respect to the stellar equatorial plane, which can be estimated through the observation of the Rossiter–McLaughlin (RM) effect. We calculated that the RV amplitude of the RM effect is of ~3 m s−1, meaning that it would probably be detectable with HARPS, and certainly with ESPRESSO (Pepe et al. 2010). Remarkably, there are only two hot-Neptunes with a reported measure of the orbital obliquity, GJ 436 b (Bourrier et al. 2018) and HAT-P-11 b (Winn et al. 2010), and both have a misaligned orbit.
Given the precise RV measurements from HARPS and the mid-transit time from the TESS mission, we can also constrain the presence of co-orbital planets (or trojans) to HD 219666 b, by putting upper limits to their mass Mt (assuming there are no other planets in the system or they are far enough to not perturb the RVs in the time span of our observations). We followed the technique described in Leleu et al. (2017), and subsequently applied in Lillo-Box et al. (2018a,b), to model the RV data by including the so-calledα parameter, which accounts for the possible mass imbalance between the L4 and L5 regions in the co-orbital region of the planet. The parameter α is defined as 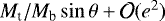 , where θ is the resonant angle representing the difference between the mean longitudes of the trojan and the planet. We set Gaussian priors on the time of transit and period of the planet, and left the rest of the parameters (i.e. e cosω, e sin ω, α, γ, and Kb) with uniform broad priors. We also included a slope term and a jitter term to account for white noise. The result of this analysis provides parameters compatible with the prior joint analysis and allows us to set constraints on co-orbital planets in the system. In particular, we find α = − 0.14 ± 0.22, which assuming the estimated planet mass provides an upper limit (95% confidence level) of Mt = 4.6 M⊕ at L5 and no constraint (i.e. up to the mass of the planet) at L4.
, where θ is the resonant angle representing the difference between the mean longitudes of the trojan and the planet. We set Gaussian priors on the time of transit and period of the planet, and left the rest of the parameters (i.e. e cosω, e sin ω, α, γ, and Kb) with uniform broad priors. We also included a slope term and a jitter term to account for white noise. The result of this analysis provides parameters compatible with the prior joint analysis and allows us to set constraints on co-orbital planets in the system. In particular, we find α = − 0.14 ± 0.22, which assuming the estimated planet mass provides an upper limit (95% confidence level) of Mt = 4.6 M⊕ at L5 and no constraint (i.e. up to the mass of the planet) at L4.
In conclusion, we report the discovery of a hot-Neptune transiting the bright (V = 9.9) G7 V star HD 219666. The collaboration between the KESPRINT and NCORES consortia has made possible a rapid spectroscopic follow-up with HARPS, leading to the confirmation and characterisation of the planet candidate detected by TESS. HD 219666 b adds to a list of only five Neptune-like planets (0.5 < Mp < 2 MNep with 1 MNep = 17.2 M⊕) transiting a V < 10 star. We carried out detailed analyses to derive the fundamental parameters and the elemental abundances of the host star. We discuss the possibility of further characterisation of the planet, in particular by examining the potential of JWST in-transit observations to detect the presence of molecular features in transmission spectra.
 |
Fig. 6 Mass−radius diagram for planets with masses Mp < 25 M⊕ and radii Rp < 6 R⊕, as retrieved from the catalogue for transiting planets TEPCat (available at http://www.astro.keele.ac.uk/jkt/tepcat/; Southworth 2011). Planets whose masses and radii are known with a precision better than 25% are plotted with grey circles. Composition models from Zeng et al. (2016) are displayed with different lines and colours. The red circle marks the position of HD 219666 b. Planets closer in mass to HD 219666 b are labelled. |
 |
Fig. 7 Planet radius as a function of the orbital period. As for Fig. 6, data are retrieved from TEPCat. The position of HD 219666 b is shown by a red circle. The black dashed lines delimit the hot-Neptunes desert as derived in Mazeh et al. (2016). |
 |
Fig. 8 Model transmission spectra of HD 219666 b (top panel). The dots and error bars denote simulated single-transit JWST transmission observations with NIRISS SOSS and NIRSpec G395H (wavelength coverage at bottom) for two underlying models (solid curves) at temperatures of 600 and 1000 K (see legend). CH4 shows strongabsorption bands at 1.7, 2.3, and 3.3 μm in the 600 Kmodel; whereas CO and CO2 show their strongest absorption features at wavelengths beyond 4 μm in the 1000 K model. Bottom panels: composition of the main species that shape the transmission spectrum. Depending on the atmospheric temperature, carbon favours either higher CH4 (temperatures lower than ~900 K) or CO/CO2 abundances (otherwise). |
Acknowledgements
We thank the anonymous referee for her/his useful comments. This paper includes data collected by the TESS mission, which are publicly available from the Mikulski Archive for Space Telescopes (MAST). Funding for the TESS mission is provided by NASA’s Science Mission directorate. M.E. acknowledges the support of the DFG priority program SPP 1992 “Exploring the Diversity of Extrasolar Planets” (HA 3279/12-1). D.B. acknowledges support by the Spanish State Research Agency (AEI) Project No. ESP2017-87676-C5-1-R and No. MDM-2017-0737 Unidad de Excelencia “María de Maeztu” – Centro de Astrobiología (INTA-CSIC). D.J.A. gratefully acknowledges support from the STFC via an Ernest Rutherford Fellowship (ST/R00384X/1). This work was supported by FCT – Fundação para a Ciência e a Tecnologia through national funds and by FEDER through COMPETE2020 – Programa Operacional Competitividade e Internacionalização by these grants: UID/FIS/04434/2013 & POCI-01-0145-FEDER-007672; PTDC/FIS-AST/28953/2017 & POCI-01-0145-FEDER-028953 and PTDC/FIS-AST/32113/2017 & POCI-01-0145-FEDER-032113. X.D. is grateful to the Branco-Weiss fellowship − Society in Science for its financial support. P.J.W. is supported by the STFC Consolidated Grant ST/P000495/1. S.H. acknowledges support by the fellowships PD/BD/128119/2016 funded by FCT (Portugal). This work has made use of the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna. This publication makes use of The Data & Analysis Center for Exoplanets (DACE), which is a facility based at the University of Geneva (CH) dedicated to extrasolar planets data visualisation, exchange and analysis. DACE is a platform of the Swiss National Centre of Competence in Research (NCCR) PlanetS, federating the Swiss expertise in Exoplanet research. The DACE platform is available at https://dace.unige.ch. We thank the Swiss National Science Foundation (SNSF) and the Geneva University for their continuous support to our planet search programs. This work has been in particular carried out in the frame of the National Centre for Competence in Research “PlanetS” supported by the Swiss National Science Foundation (SNSF). S.C.C.B., N.C.S., S.G.S, V.A. and E.D.M. acknowledge support from FCT through Investigador FCT contracts nr. IF/01312/2014/CP1215/CT0004, IF/00169/2012/CP0150/CT0002, IF/00028/2014/CP1215/CT0002, IF/00650/2015/CP1273/CT0001, and IF/00849/2015/CP1273/CT0003. This work is partly supported by JSPS KAKENHI Grant Numbers JP18H01265 and 18H05439, and JST PRESTO Grant Number JPMJPR1775. P.G.B. acknowledges the support of the MINECO under the fellowship program “Juan de la Cierva incorporacion” (IJCI-2015-26034). S.M. acknowledges support from the Ramon y Cajal fellowship number RYC-2015-17697.
References
- Adibekyan, V. Z., Santos, N. C., Sousa, S. G., & Israelian, G. 2011, A&A, 535, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Figueira, P., Santos, N. C., et al. 2013, A&A, 554, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V., Figueira, P., Santos, N. C., et al. 2015, A&A, 583, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anders, F., Chiappini, C., Santiago, B. X., et al. 2018, A&A, 619, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, D. R., Collier Cameron, A., Hellier, C., et al. 2011, ApJ, 726, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Ansdell, M., Williams, J. P., van der Marel, N., et al. 2016, ApJ, 828, 46 [Google Scholar]
- Armstrong, D. J., Santerne, A., Veras, D., et al. 2015, A&A, 582, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barclay, T., Pepper, J., & Quintana, E. V. 2018, ApJS, 239, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Barragán, O., Gandolfi, D., Dai, F., et al. 2018, A&A, 612, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barragán, O., Gandolfi, D., & Antoniciello, G. 2019, MNRAS, 482, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Barros, S. C. C., Gosselin, H., Lillo-Box, J., et al. 2017, A&A, 608, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Batalha, N. E., Mandell, A., Pontoppidan, K., et al. 2017, PASP, 129, 064501 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., Bodenheimer, P. H., & Laughlin, G. P. 2016, ApJ, 829, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Bean, J. L., Désert, J.-M., Seifahrt, A., et al. 2013, ApJ, 771, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Bertran de Lis, S., Delgado Mena, E., Adibekyan, V. Z., Santos, N. C., & Sousa, S. G. 2015, A&A, 576, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Lambrechts, M., & Johansen, A. 2015, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blecic, J. 2016, Ph.D Dissertation [arXiv:1604.02692] [Google Scholar]
- Blecic, J., Harrington, J., & Bowman, M. O. 2016, ApJS, 225, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J. 2016, Rep. Progr. Phys., 79, 036901 [Google Scholar]
- Borysow, A. 2002, A&A, 390, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borysow, A., & Frommhold, L. 1989, ApJ, 341, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Borysow, J., Frommhold, L., & Birnbaum, G. 1988, ApJ, 326, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Borysow, A., Frommhold, L., & Moraldi, M. 1989, ApJ, 336, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Borysow, A., Jorgensen, U. G., & Fu, Y. 2001, J. Quant. Spectr. Rad. Transf., 68, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Bourrier, V., Lovis, C., Beust, H., et al. 2018, Nature, 553, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Brahm, R., Espinoza, N., Jordán, A., et al. 2018, ApJ, submitted [arXiv:1811.02156] [Google Scholar]
- Bruntt, H., Bedding, T. R., Quirion, P.-O., et al. 2010, MNRAS, 405, 1907 [NASA ADS] [Google Scholar]
- Burrows, A., Marley, M. S., & Sharp, C. M. 2000, ApJ, 531, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., & VandenBerg, D. A. 2018, MNRAS, 479, L102 [NASA ADS] [CrossRef] [Google Scholar]
- Christiansen, J. L., Jenkins, J. M., Caldwell, D. A., et al. 2012, PASP, 124, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2017, A&A, 600, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cubillos, P. E. 2016, Ph.D. Dissertation [arXiv:1604.01320] [Google Scholar]
- Cubillos, P. E. 2017, ApJ, 850, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, 2MASS All Sky Catalog of Point Sources [Google Scholar]
- Cutri, R. M., Wright, E. L., Conrow, T., et al. 2013, Explanatory Supplement to the AllWISE Data Release Products, Tech. rep. [Google Scholar]
- Dai, F., Winn,J. N., Gandolfi, D., et al. 2017, AJ, 154, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Delgado Mena, E., Israelian, G., González Hernández, J. I., et al. 2010, ApJ, 725, 2349 [NASA ADS] [CrossRef] [Google Scholar]
- Delgado Mena, E., Israelian, G., González Hernández, J. I., et al. 2014, A&A, 562, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delgado Mena, E., Tsantaki, M., Adibekyan, V. Z., et al. 2017, A&A, 606, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erkaev, N. V., Kulikov, Y. N., Lammer, H., et al. 2007, A&A, 472, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fossati, L., Erkaev, N. V., Lammer, H., et al. 2017, A&A, 598, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1993, A&A, 271, 451 [NASA ADS] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gandolfi, D., Alcalá, J. M., Leccia, S., et al. 2008, ApJ, 687, 1303 [NASA ADS] [CrossRef] [Google Scholar]
- Gandolfi, D., Barragán, O., Hatzes, A. P., et al. 2017, AJ, 154, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Gandolfi, D., Barragán, O., Livingston, J. H., et al. 2018, A&A, 619, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [Google Scholar]
- Huang, C.X., Shporer, A., Dragomir, D., et al. 2018a, AJ, submitted [arXiv:1807.11129] [Google Scholar]
- Huang, C. X., Burt, J., Vanderburg, A., et al. 2018b, ApJ, 868, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Ionov, D. E., Pavlyuchenkov, Y. N., & Shematovich, V. I. 2018, MNRAS, 476, 5639 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, A. P., Davis, T. A., & Wheatley, P. J. 2012, MNRAS, 422, 2024 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, M. C., Gandolfi, D., Fridlund, M., et al. 2016, AJ, 151, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, M. I., Brahm, R., Espinoza, N., et al. 2019, A&A, in press DOI: 10.1051/0004-6361/201834640 [Google Scholar]
- Kubyshkina, D., Fossati, L., Erkaev, N. V., et al. 2018, ApJ, 866, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Kuerster, M., Schmitt, J. H. M. M., Cutispoto, G., & Dennerl, K. 1997, A&A, 320, 831 [NASA ADS] [Google Scholar]
- Kurucz, R. L. 1970, SAO Special Report, 309 [Google Scholar]
- Kurucz, R. L. 1993, SYNTHE spectrum synthesis programs and line data (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
- Kurucz, R. L. 2013, Astrophysics Source Code Library [record ascl:1303.024] [Google Scholar]
- Lam, K. W. F., Santerne, A., Sousa, S. G., et al. 2018, A&A, 620, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A&A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lecavelier Des Etangs, A., Pont, F., Vidal-Madjar, A., & Sing, D. 2008, A&A, 481, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Leleu, A., Robutel, P., Correia, A. C. M., & Lillo-Box, J. 2017, A&A, 599, L7 [Google Scholar]
- Li, G., Gordon, I. E., Rothman, L. S., et al. 2015, ApJS, 216, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Lillo-Box, J., Demangeon, O., Santerne, A., et al. 2016, A&A, 594, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lillo-Box, J., Barrado, D., Figueira, P., et al. 2018a, A&A, 609, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lillo-Box, J., Leleu, A., Parviainen, H., et al. 2018b, A&A, 618, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lopez, E. D., & Fortney, J. J. 2014, ApJ, 792, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lovis, C., & Pepe, F. 2007, A&A, 468, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, ArXiv e-prints [arXiv:1107.5325] [Google Scholar]
- Lucy, L. B., & Sweeney, M. A. 1971, AJ, 76, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Lundkvist, M. S., Kjeldsen, H., Albrecht, S., et al. 2016, Nat. Commun., 7, 11201 [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Matsakos, T., & Königl, A. 2016, ApJ, 820, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumoto, Y., & Kokubo, E. 2017, AJ, 154, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mazeh, T., Holczer, T., & Faigler, S. 2016, A&A, 589, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mortier, A., Santos, N. C., Sousa, S. G., et al. 2013, A&A, 558, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelson, B. E., Ford, E. B., & Rasio, F. A. 2017, AJ, 154, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Nielsen, L. D., Bouchy, F., Turner, O., et al. 2019, A&A, 623, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Ogihara,M., Kokubo, E., Suzuki, T. K., & Morbidelli, A. 2018, A&A, 615, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owen, J. E., & Lai, D. 2018, MNRAS, 479, 5012 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F. A., Cristiani, S., Rebolo Lopez, R., et al. 2010, Proc. SPIE, 7735, 77350F [CrossRef] [Google Scholar]
- Piskunov, N., & Valenti, J. A. 2017, A&A, 597, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prieto-Arranz, J., Palle, E., Gandolfi, D., et al. 2018, A&A, 618, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, G., & Vanderspek, R. 2018, Data Products From TESS Data Alerts [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2018, ApJ, 861, 126 [Google Scholar]
- Rothman, L. S., Gordon, I. E., Barber, R. J., et al. 2010, J. Quant. Spectr. Rad. Transf., 111, 2139 [NASA ADS] [CrossRef] [Google Scholar]
- Santerne, A., Brugger, B., Armstrong, D. J., et al. 2018, Nat. Astron., 2, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C., Sousa, S. G., Mortier, A., et al. 2013, A&A, 556, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silva Aguirre, V., Davies, G. R., Basu, S., et al. 2015, MNRAS, 452, 2127 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C. A. 1973, Ph.D. Thesis, The University of Texas at Austin, Austin [Google Scholar]
- Snellen, I. A. G., de Kok, R. J., de Mooij, E. J. W., & Albrecht, S. 2010, Nature, 465, 1049 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sousa, S. G. 2014, in Determination of Atmospheric Parameters of B-, A-, F- and G-Type Stars, eds. E. Niemczura, B. Smalley, & W. Pych (Springer, Cham), 297 [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., et al. 2011, A&A, 526, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Adibekyan, V., Delgado-Mena, E., & Israelian, G. 2015, A&A, 577, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Southworth, J. 2011, MNRAS, 417, 2166 [NASA ADS] [CrossRef] [Google Scholar]
- Stassun, K. G., & Torres, G. 2018, ApJ, 862, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Stassun, K. G., Oelkers, R. J., Pepper, J., et al. 2018, AJ, 156, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Szabó, G. M., & Kiss, L. L. 2011, ApJ, 727, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Triaud, A. H. M. J. 2017, Handbook of Exoplanets, (New York: Springer International Publishing) [Google Scholar]
- Tu, L., Johnstone, C. P., Güdel, M., & Lammer, H. 2015, A&A, 577, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Twicken, J. D., Catanzarite, J. H., Clarke, B. D., et al. 2018, PASP, 130, 064502 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A.,& Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Valenti, J. A.,& Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanderspek, R., Huang, C. X., Vanderburg, A., et al. 2019, ApJ, 871, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Van Eylen, V., Albrecht, S., Gandolfi, D., et al. 2016, AJ, 152, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, A., & Schlattl, H. 2008, Ap&SS, 316, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Johnson, J. A., Howard, A. W., et al. 2010, ApJ, 723, L223 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T. N., Chamberlin, P. C., Harder, J. W., et al. 2009, Geophys. Res. Lett., 36, L01101 [NASA ADS] [CrossRef] [Google Scholar]
- Yurchenko, S. N., & Tennyson, J. 2014, MNRAS, 440, 1649 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zeng, L., Sasselov, D. D., & Jacobsen, S. B. 2016, ApJ, 819, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Zinn, J. C., Pinsonneault, M. H., Huber, D., & Stello, D. 2018, ApJ, submitted [arXiv:1805.02650] [Google Scholar]
Mikulski Archive for Space Telescopes, https://archive.stsci.edu/prepds/tess-data-alerts/
Available at http://archive.stsci.edu/cgi-bin/dss_form
Computed following the Monte Carlo bootstrap method described in Kuerster et al. (1997).
The last version of the ARES code (ARES v2) can be downloaded at http://www.astro.up.pt/~sousasag/ares
All Tables
Main identifiers, coordinates, parallax, and optical and infrared magnitudes of HD 219666.
All Figures
 |
Fig. 1 5′ × 5′ archival image taken in 1980 from the SERCJ survey, with the SPOC photometric aperture overplotted in blue (TESS pixel size is 21′′), and the positions of Gaia DR2 sources (J2015.5) within 2′ of HD 219666 indicated by circles. HD 219666 is in red, nearby sources contributing more than 1% of their flux to the aperture arein orange (see Sect. 2.2), and other sources are in green. |
| In the text | |
 |
Fig. 2 TESS light curve of HD 219666. The red arrows point to the four planet-transit occurrences. |
| In the text | |
 |
Fig. 3 Generalised Lomb-Scargle periodogram of the HARPS RVs (first panel), the CCF BIS and FWHM (second and third panels, respectively), the Ca II H and K S-index (fourth panel), and of the window function (fifth panel). The vertical dashed red line marks the frequency of the transit signal. The horizontal dashed blue line marks the FAP = 0.1% level. |
| In the text | |
 |
Fig. 4 Phase-folded and normalized TESS photometric data with our best fitting transit light curve. |
| In the text | |
 |
Fig. 5 Phase-folded HARPS RV data points with our best fitting circular RV curve. The blue error bars correspond to the nominal RV uncertainties calculated by the HARPS DRS while the grey ones account for the RV jitter term. The bottom panel shows the RV residuals that have a rms of 1.7 m s −1. |
| In the text | |
 |
Fig. 6 Mass−radius diagram for planets with masses Mp < 25 M⊕ and radii Rp < 6 R⊕, as retrieved from the catalogue for transiting planets TEPCat (available at http://www.astro.keele.ac.uk/jkt/tepcat/; Southworth 2011). Planets whose masses and radii are known with a precision better than 25% are plotted with grey circles. Composition models from Zeng et al. (2016) are displayed with different lines and colours. The red circle marks the position of HD 219666 b. Planets closer in mass to HD 219666 b are labelled. |
| In the text | |
 |
Fig. 7 Planet radius as a function of the orbital period. As for Fig. 6, data are retrieved from TEPCat. The position of HD 219666 b is shown by a red circle. The black dashed lines delimit the hot-Neptunes desert as derived in Mazeh et al. (2016). |
| In the text | |
 |
Fig. 8 Model transmission spectra of HD 219666 b (top panel). The dots and error bars denote simulated single-transit JWST transmission observations with NIRISS SOSS and NIRSpec G395H (wavelength coverage at bottom) for two underlying models (solid curves) at temperatures of 600 and 1000 K (see legend). CH4 shows strongabsorption bands at 1.7, 2.3, and 3.3 μm in the 600 Kmodel; whereas CO and CO2 show their strongest absorption features at wavelengths beyond 4 μm in the 1000 K model. Bottom panels: composition of the main species that shape the transmission spectrum. Depending on the atmospheric temperature, carbon favours either higher CH4 (temperatures lower than ~900 K) or CO/CO2 abundances (otherwise). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


