| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A166 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201834776 | |
| Published online | 27 March 2019 | |
Hot Exoplanet Atmospheres Resolved with Transit Spectroscopy (HEARTS)★
II. A broadened sodium feature on the ultra-hot giant WASP-76b
1
Observatoire astronomique de l’Université de Genève,
chemin des Maillettes 51,
1290 Versoix, Switzerland
e-mail: julia.seidel@unige.ch
2
Leiden Observatory, Leiden University,
Postbus 9513,
2300 RA Leiden, The Netherlands
3
Space Research Institute, Austrian Academy of Sciences,
Schmiedlstr. 6,
8042 Graz, Austria
4
Anton Pannekoek Institute for Astronomy, University of Amsterdam,
Science Park 904,
1098 XH Amsterdam, The Netherlands
5
SNSF NCCR-PlanetS,
Bern, Switzerland
6
Departamento Astrofísica, Centro de Astrobiología (INTA-CSIC), ESAC campus, Camino Bajo del Castillo s/n,
28692 Villanueva de la Cañada, Spain
7
Department of Physics, University of Warwick,
Gibbet Hill Rd.,
Coventry CV4 7AL, UK
8
Departamento de Astronomía, Universidad de Concepción,
Casilla 160-C, Concepción, Chile
9
University of Bern, Center for Space and Habitability,
Gesellschaftsstrasse 6, 3012 Bern, Switzerland
10
Laboratoire d’Astrophysique, École Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
11
European Southern Observatory,
Alonso de Córdova 3107,
Vitacura, Región Metropolitana, Chile
Received:
4
December
2018
Accepted:
29
January
2019
High-resolution optical spectroscopy is a powerful tool to characterise exoplanetary atmospheres from the ground. The sodium D lines, with their large cross sections, are especially suited to studying the upper layers of atmospheres in this context. We report on the results from Hot Exoplanet Atmosphere Resolved with Transit Spectroscopy survey (HEARTS), a spectroscopic survey of exoplanet atmospheres, performing a comparative study of hot gas giants to determine the effects of stellar irradiation. In this second installation of the series, we highlight the detection of neutral sodium on the ultra-hot giant WASP-76b. We observed three transits of the planet using the High-Accuracy Radial-velocity Planet Searcher (HARPS) high-resolution spectrograph at the European Southern Observatory (ESO) 3.6 m telescope and collected 175 spectra of WASP-76. We repeatedly detect the absorption signature of neutral sodium in the planet atmosphere (0.371 ± 0.034%; 10.75σ in a 0.75 Å passband). The sodium lines have a Gaussian profile with full width at half maximum (FWHM) of 27.6 ± 2.8 km s−1. This is significantly broader than the line spread function of HARPS (2.7 km s−1). We surmise that the observed broadening could trace the super-rotation in the upper atmosphere of this ultra-hot gas giant.
Key words: planets and satellites: atmospheres / planets and satellites: individual: WASP-76b / techniques: spectroscopic / instrumentation: spectrographs / methods: observational / planetary systems
© ESO 2019
1 Introduction
The field of exoplanetary research has moved firmly into the era of atmospheric characterisation. To learn more about the planet atmospheric composition and conditions, the light arriving from the host star during the transit is commonly used to extract the spectrum generated by the atmosphere of the planet. Based on theoretical work describing transmission spectroscopy and its potential (Marley et al. 1999; Seager & Sasselov 2000; Brown 2001), the first attempts to detect reflected light from the day side (Charbonneau et al. 2000) or the absorption of light through limb transmission (Moutou et al. 2001) were unsuccessful.
It took until 2002 to observe the first exoplanetary atmosphere on HD 209458b via the detection of atmospheric neutral sodium (Na i) at 589 nm (Charbonneau et al. 2002). These milestone measurements were performed with the Space Telescope Imaging Spectrograph (STIS) on board the 2.4 m Hubble Space Telescope (HST). The spectral resolution of STIS is 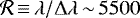 (~55 km s−1). Due to terrestrial atmospheric variation and telluric line contamination, ground-based observations were unable to reproduce the success of space-based missions until six years later when Redfield et al. (2008) and Snellen et al. (2008) detected atmospheric sodium in HD 189733b and HD 209458b, respectively.
(~55 km s−1). Due to terrestrial atmospheric variation and telluric line contamination, ground-based observations were unable to reproduce the success of space-based missions until six years later when Redfield et al. (2008) and Snellen et al. (2008) detected atmospheric sodium in HD 189733b and HD 209458b, respectively.
Neutral sodium is a sensitive probe for the higher atmosphere of exoplanets. Strong signatures in transit spectroscopy arise in the doublet resonant lines (Na I D1 and D2) at 589 nm even for small amounts of sodium in the atmosphere. Given these unique features, ground-based observations have led to a wealth of sodium detections in hot exoplanet atmospheres since then (Wood et al. 2011; Jensen et al. 2011, 2018; Zhou & Bayliss 2012; Murgas et al. 2014; Burton et al. 2015; Wyttenbach et al. 2015, 2017; Casasayas-Barris et al. 2017; Khalafinejad et al. 2017; Sing et al. 2016; Nikolov et al. 2016; Chen et al. 2017) using spectrographs with resolutions of ~100 000, making sodium one of the most detected species to date.
Atmospheric neutral sodium is not only a powerful tool to detect exoplanetary atmospheres, but also to characterise their properties. With a high cross section, the Na i doublet (at 589 nm, also called the Frauenhofer D line) probes the atmosphere up to high altitudes, thus constraining the temperature pressure profile (Vidal-Madjar et al. 2011a,b; Heng et al. 2015)and other dynamical processes up to the thermosphere (Louden & Wheatley 2015; Wyttenbach et al. 2015).
This technique was successfully applied to HD 189733b (Wyttenbach et al. 2015; Pino et al. 2018a) with HARPS, a high-resolution spectrograph stabilised in temperature and pressure at the 3.6 m telescope of ESO at La Silla Observatory, Chile. Wyttenbach et al. (2015) thus established the usefulness of HARPS in the search for atmospheric signatures during exoplanet transits. Based on this benchmark result the Hot Exoplanet Atmosphere Resolved with Transit Spectroscopy survey (HEARTS) was created to observe a large sample of gas giants with different masses and irradiation with HARPS.
The first result from this study was the detection of hot neutral sodium at high altitudes on WASP-49b (Wyttenbach et al. 2017). This paper is the second installation from the HEARTS survey and reports on the detection of neutral sodium in WASP-76b, which allows us to unveil the upper atmosphere properties of the planet. WASP-76b is a gas giant of approximately one Jupiter mass, but roughly twice its radius. The WASP-76b properties are listed in Tables 1 and 5 and a comparison to similar planets of sub-Jupiter mass with high irradiation can be seen in Fig. 1.
In the following section, we describe the observations with HARPS and their data reduction (Sect. 2), followed by Sect. 3 describing the simultaneous photometric observations of WASP-76 with EulerCam. Section 4 highlights the detection of neutral sodium from the transmission spectrum and the evolution of the signal with time. The observed sodium line profile is also discussed.
 |
Fig. 1 Mass of the planet vs. bolometric optical and infrared incident flux in units of flux received at Earth. In grey, transiting exoplanets are shown with V < 16 and masses determined with a precision better than 20%. WASP-76b is shown in orange. For comparison WASP-49b (Wyttenbach et al. 2017), HD 189733b (Wyttenbach et al. 2015), and HD 209458b (for reference) are shown in red, blue, and green, respectively. |
Orbital and physical parameters of the WASP-76 system (West et al. 2016).
2 Observations and data reduction
2.1 HARPS observations
We collected data of three transits of the hot gas giant planet WASP-76b with its host star WASP-76, a F7 star with a visual apparent magnitude of V = 9.5. The observations were made with the HARPS spectrograph at the ESO 3.6 m telescope in La Silla Observatory, Chile (Mayor et al. 2003). We performed observations on 2017-10-24 and 2017-11-22 as part of the HEARTS survey (ESO programme: 100.C-0750; PI: Ehrenreich) and combined them with an archival data set obtained on 2012-11-11 (ESO programme: 090.C-0540; PI: Triaud; Brown et al. 2017).
In the HEARTS survey, each target is observed for multiple transits to ensure reproducibility of the recorded spectra and a high signal-to-noise ratio (S/N). The HARPS spectra are extracted order by order from the 2D echelle spectral images (stored in e2ds files) by the HARPS Data Reduction Pipeline (DRS v3.5) In this study, we concentrated our analysis on order number 56, which contains the sodium doublet. The spectral order 56 samples the wavelength region from 5850.24 to 5916.17 Å. The data are corrected for the blaze and the pixel grid is calibrated to the wavelength solution grid using the daily afternoon calibration. The wavelengths are extracted from the header provided by HARPS and are given in air in the solar system barycentric rest frame. Each observation is started as early as possible with respect to the transit and ends when the star is no longer observable, which allows us to record the transit event and the best possible out-of-transit baseline before and after the transit. A good baseline is necessary to build an accurate out-of-transit master spectrum (“master out” spectrum) and thus an accurate spectrum ratio. A log of the observations can be found in Table 2. All transits were observed with one fibre on the target (fibre A) and one fibre on the sky (fibre B). This technique makes a correction for telluric contamination necessary (see Sect. 2.2). The exposure times varied from 300 to 600 s depending on seeing conditions on the respective nights. The three nights resulted in a total of 175 spectra with 68 in-transit and 107 out-of-transit. In the third night, the out-of-transit exposures after the transit (15 spectra) show a lower signal-to-noise ratio due to cirrus clouds and were discarded from the analysis. This leaves ten out-of-transit exposures taken before the ingress to build the out-of-transit baseline. The in-transit exposures are defined as spectra recorded fully or partially during the transit of the planet (i.e. between the first and fourth contacts), and the out-of-transit exposures are recorded before and after the transit event with ~ 1 h before and ~2–3 h after the transit.
Log of observations.
 |
Fig. 2 Telluric correction highlighted for an out-of-transit exposure during the first observation night on 2012-11-11. Upper panel: applied model of telluric lines. Middle panel: uncorrected flux in red and the corrected flux in black, which cannot be distinguished. We note the different scales for the two panels. Lower panel: difference between the corrected and uncorrected spectra for better visualisation. The impact of tellurics in the wavelength range of the cores of the sodium doublet is negligible. Nonetheless, a good telluric correction is crucial to clean the continuum baseline used for normalisation and where more telluric lines are situated. |
2.2 Telluric correction with molecfit
Figure 2 shows the influence of telluric lines in the optical ground-based observations of the HARPS spectral order containing sodium. As can be seen in Fig. 2, the optimal telluric correction does not impact the exposures in the wavelength range of the sodium doublet. However, telluric lines can influence the normalisation processes during the analysis since the lines appear stronger in the continuum. Furthermore we wish to use this pipeline for future observationswith HARPS, HARPS-N and ESPRESSO which are at different locations. A stable correction for tellurics becomes more influencial when dealing with HARPS-N (Roque de los Muchachos, La Palma) or during different seasons. To perform the correction we used molecfit version 1.5.1. (Smette et al. 2015; Kausch et al. 2015), a tool to correct telluric features in ground-based observations provided by ESO. This approach was used for the first time on a HARPS spectrum by Allart et al. (2017). The molecfit software computes a high-resolution (λ∕Δλ ~ 4 000 000) telluric spectrum with a line-by-line radiative-transfer model (LBLRTM).
The LBLRTM uses an atmospheric profile as input to calculate the spectrum that depends on the temperature, pressure, humidity, and abundance of the molecular species by height for a specific location and time with known airmass. To generate the input profilean atmospheric standard profile is merged with a Global Data Assimilation System (GDAS) profile. Atmospheric standard profiles provide pressure, temperature, and abundance for up to tens of molecular species for different altitudes at specific latitudes and were computed by the Reference Forward Model (Remedios et al. 2001). Additionally the GDAS profiles provided by the National Oceanic and Atmospheric Administration (NOAA) contain meteorological information such as pressure, temperature, and relative humidity as a function of height for specific locations and are updated every three hours.
The GDAS grid of pressure, temperature, abundance, and humidity with 100–150 layers in height is used to calculate the model spectrum. The model spectrum is adjusted to the observed spectrum by changing the continuum, the wavelength calibration, and the instrument resolution. The only element creating telluric lines in the spectral order of sodium is H2 O, which allows us to omit O2 and all other telluric elements from the calculation.
2.2.1 Application of molecfit to WASP-76b e2ds spectra
The e2ds pipeline of the HARPS spectrograph provides the spectra in the observer rest frame with the wavelength calibration adapted to air. Before using molecfit on the observed spectra we correct for the blaze on each night. The telluric features are not prominent in the spectral order of sodium and the modelling regions have to be selected meticulously by hand to not only avoid stellar features, but also to find telluric lines above the noise level. The fitting process aims at adjusting the continuum, the wavelength calibration, and the instrumental resolution for the telluric band of each spectrum. The convergence criteria (Levenberg–Marquardt χ2 and parameter convergence criterion) were set to 10−9, the continuum adjusted with a first degree polynomial and the wavelength calibrated with a Chebyschev third-degree polynomial (see Allart et al. 2017). The instrumental profile is set to have a Gaussian form with a FWHM of 3.5 pixels. For a detailed description of all molecfit free parameters, see Smette et al. (2015). The specific values for all molecfit parameters used herein can be found in Table 3.
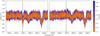 |
Fig. 3 All exposures for the second night (2017-10-24) plotted before (left panel) and after (right panel) telluric correction coloured by airmass. The strong telluric line (line centre indicated by the black dashed line) merged with a stellar line is corrected down to the noise level for high and low airmasses. This window is illustrative of the corrections performed on all three observation nights. |
Initial parameters for molecfit on each night based on Allart et al. (2017).
2.2.2 Assessment of the telluric correction
The molecfit output file contains all the fitted parameters as well as the uncorrected spectrum (the input spectrum), the modelled telluric spectrum, and the corrected spectrum. In Fig. 3 all the corrected spectra are plotted for one night with the airmass indicated via a colour spectrum. As we can see by comparing the left and right panels of Fig. 3, the telluric lines are corrected down to the noise level for all airmasses (including the lines merged with stellar lines). We checked that the telluric line highlighted in Fig. 3 is indeed a telluric line by comparison with the master-out spectrum for the night. Additionally, sodium emission lines can be present in the Earth’s atmosphere, an effect molecfit does not correct for. This effect can be estimated from our data taken with fibre B on the sky. Building master-out spectra for all nights from the fibre B data reveals no emission lines of sodium beyond the noise level. Sodium emission from Earth’s atmosphere has therefore no impact on our findings.
Overview of the simultaneous EulerCam photometric observations.
3 Simultaneous photometry with EulerCam
We obtained photometry simultaneous to our spectroscopic HARPS observations using EulerCam, the charged coupled device (CCD) imager at the 1.2 m Euler-Swiss telescope, also located at La Silla Observatory. For each transit event, we extracted differential light curves using relative aperture photometry, iteratively choosing a set of stable reference stars. Details on EulerCam and the related data-reduction procedures can be found in Lendl et al. (2012). The individual time-series observations are listed in Table 4, together with a number of key properties and the light curves are shown in Fig. 4.
We jointly analysed the ensemble of photometric data using the differential-evolution Markov chain Monte Carlo (MCMC) code described in Lendl et al. (2017), which makes use of the transit model of Mandel & Agol (2002) and the MC3 sampler (Cubillos et al. 2017). To account for instrumental systematics, we tested a range of photometric baseline models for each light curve, selecting the optimal model via comparison of the Bayesian information criterion. For all three light curves, we found significant (Bayes factor > 100) improvements when including a linear trend in stellar FWHM next to our minimal model of a linear trend in time. For the light curve of night two (2017-10-24), we found further improvements when including a second-order polynomial in coordinate shifts of the stellar PSF centre.
To account for additional red noise, we rescaled photometric errors via the βr and βw factors as describedin Gillon et al. (2010) and Winn et al. (2008). We assumed a quadratic limb-darkening law and used the routines of Espinoza & Jordán (2015) to compute coefficients tailored to WASP-76, the EulerCam detector efficiency, and filter transmission. To account for the uncertainty affecting the limb-darkening coefficients, we assumed Gaussian prior distributions in our analysis, centred on the computed values, with widths corresponding to the offsets incurred when altering the stellar parameters within the 1-σ uncertainties given in Brown et al. (2017).
Based on the observed light curves, we recomputed stellar and planetary parameters using the newly available stellar radius measurement of WASP-76 from Gaia (Gaia Collaboration 2018). With a revised stellar radius of 1.969 ± 0.035 R⊙ (compared to 1.7 ± 0.03 R⊙, Brown et al. 2017), we find a ~20% larger planetary radius of 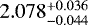 RJ (compared to 1.73 ± 0.03 RJ). As already suggested by Brown et al. (2017), we find a larger impact parameter compared to that stated in the discovery paper (West et al. 2016). A full list of the derived stellar and planetary parameters is given in Table 5.
RJ (compared to 1.73 ± 0.03 RJ). As already suggested by Brown et al. (2017), we find a larger impact parameter compared to that stated in the discovery paper (West et al. 2016). A full list of the derived stellar and planetary parameters is given in Table 5.
Planetary and stellar parameters inferred from EulerCam photometry.
 |
Fig. 4 The three light curves obtained by EulerCam (top to bottom: 2012-11-11, 2017-10-24 and 2017-11-22) offset by 0.02 for visibility. The computed model is shown in red. |
4 Transmission spectroscopy of WASP-76b
4.1 Transmission light curve
To properly depict the transit of the planet in front of its host star from the spectroscopic observations, we use the overall change of flux for the different exposures to construct the relative transmission light curve as a function of time (Charbonneau et al. 2002; Snellen et al. 2008). Figure 5 depicts the transit depth as a function of time, which means that the wavelength dependence is lost. We derive the change of transit depth by comparing the relative flux at the centre of the stellar sodium lines to the relative flux in reference passbands for each telluric corrected exposure. The reference passbands should remain unchanged during planet transit given that they only contain stellar lines. The passbands at line centre however change relative flux depending on whether they were taken in or out of transit because they may contain the additional sodium absorption of the atmosphere of the planet. Common reference passbands to use around the sodium doublet are bands on the blue (B) and red (R) side of the sodium doublet (window of 12 Å) of 12 Å each in width (Wyttenbach et al. 2015). The passbands in the sodium line centres (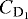 and
and 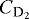 ) are of 0.75 Å in width. The relative flux (𝔉rel) is calculated by averaging over the spectrum in the mentioned bands (represented by a bar over the quantity in Eq. (1)). Further discussion of the passbands can be found in Sect. 4.3.
) are of 0.75 Å in width. The relative flux (𝔉rel) is calculated by averaging over the spectrum in the mentioned bands (represented by a bar over the quantity in Eq. (1)). Further discussion of the passbands can be found in Sect. 4.3.
The relative flux for each exposure is calculated as follows
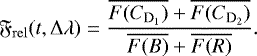 (1)
(1)
All light-curve points 𝔉rel(tout, Δλ) calculated with out-of-transit spectra are then used to normalise the out-of-transit light curve to zero. Astudillo-Defru & Rojo (2013) showed that this method, using simple average differences, produces reliable results because differential stellar limb-darkening does not affect the measurements on narrow passbands such as the ones selected in this work. The light curve obtained for the night of 2017-11-22shows a visible slope in the post-transit absorption depth with time (and airmass), which has a significant effect on the transmission spectrum as discussed in Sect. 4.3. The observer confirmed the presence of stratus clouds during these exposures.
The night in question has ten out-of-transit exposures before the start of the transit which allows for the affected exposures to be disregarded from the analysis of the transmission spectrum. The light curves for each of the three observed nights and the overall light curve is shown in Fig. 5.
The additional absorption depth during the planet transit can be seen for each of the three nights and is even clearer when combining all three transits by comparing the in-transit and out-of-transit data (highlighted with a green background in Fig. 5).
 |
Fig. 5 HARPS relative excess absorption in the sodium doublet compared to the white light curve of WASP-76b evolving in time. The upper three plots show the light curves for each night 2012-11-11, 2017-10-24, and 2017-11-22 from left to right. We note the different scales on the ordinate axis for upper and lower panels and the influence of stratus clouds in the out-of-transit exposures during the night of 2017-11-22. The grey data points show the relative absorption for each exposure; inblack the data is binned by five spectra. Lower panel: light curve for all three nights combined, with the original exposures averaged together for five spectra each in grey and binned by five averaged spectra in grey. The green background marks the exposures taken out-of-transit. |
4.2 Extraction of the transmission spectrum
Following Brown (2001) to calculate the spectral ratio, ℜ, all e2ds spectra are corrected for telluric signatures and stacked together, in and out of transit, respectively, to form a master spectrum in-transit (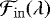 ) and a master spectrum out-of-transit (
) and a master spectrum out-of-transit (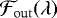 ). The divisionof master-in by master-out spectrum gives the classical spectrum ratio, eliminating the stellar features and leaving only the planetary atmospheric signature
). The divisionof master-in by master-out spectrum gives the classical spectrum ratio, eliminating the stellar features and leaving only the planetary atmospheric signature 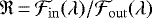 . Ground-based observations do not allow for a direct calculation of the spectrum ratio due to flux changes with time. To reduce this effect we fitted a three-order polynomial to the continuum of the ratio
. Ground-based observations do not allow for a direct calculation of the spectrum ratio due to flux changes with time. To reduce this effect we fitted a three-order polynomial to the continuum of the ratio 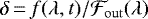 and divided each exposure f(λ, t) obtained at a given time t by the fitted continuum. The fit to the ratio δ assures that the stellar lines do not influence the fit (Allart et al. 2017).
and divided each exposure f(λ, t) obtained at a given time t by the fitted continuum. The fit to the ratio δ assures that the stellar lines do not influence the fit (Allart et al. 2017).
The normalised spectra 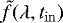 and
and 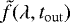 are then used to calculate the similarly self-normalised master-in
are then used to calculate the similarly self-normalised master-in 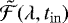 and master-out
and master-out 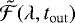 . We normalise all quantities on the in-transit spectra following
. We normalise all quantities on the in-transit spectra following
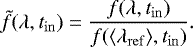 (2)
(2)
However the spectral ratio 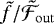 does not consider changes in radial velocity of the planet since it is calculated in the stellar rest frame. As WASP-76b transits its star, the radial velocity changes between the maximum values of − 50 and + 50 km s−1, which means that the planetary sodium signature shifts from the blue-shifted to the red-shifted part of the stellar sodium lines during the transit. In the wavelength range near the sodium doublet the shift is ≲ 1 Å during the transit. We correct for this shift by transferring each calculated spectral ratio in the planet rest frame.
does not consider changes in radial velocity of the planet since it is calculated in the stellar rest frame. As WASP-76b transits its star, the radial velocity changes between the maximum values of − 50 and + 50 km s−1, which means that the planetary sodium signature shifts from the blue-shifted to the red-shifted part of the stellar sodium lines during the transit. In the wavelength range near the sodium doublet the shift is ≲ 1 Å during the transit. We correct for this shift by transferring each calculated spectral ratio in the planet rest frame.
The end result of the new spectrum ratio is
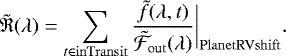 (3)
(3)
A more detailed description of the calculation of the spectrum ratio can be found in Wyttenbach et al. (2015). The transit spectrum of WASP-76b taking into account all three nights is plotted in the middle panel of Fig. 6.
4.3 Binned atmospheric absorption depth
The upper panel of Fig. 6 contains the transit spectrum of WASP-76b in the planetary rest frame and shows a double-peaked feature, one peak for each component of the sodium doublet.
The features are close to the wavelengths of the sodium doublet lines (D1 and D2) at wavelengths 5895.924 and 5889.951 Å, respectively. The systemic velocity of WASP-76 is γ = −1.07 km s−1, which shifts these features to 5895.903 (D1) and 5889.930 Å(D2) in the solar system barycentric reference frame. The telluric sodium lines should be located around the BERV values of − 12.6, − 3.6, and − 17.5 km s−1 for each of the nights and have no impact on the planetary signal.
The relative absorption depth can be calculated by averaging the flux in the sodium doublet line cores and comparing it to the average flux in specified reference bands in the continuum. Contrary to Snellen et al. (2008), who chose adjacent control passbands in the red (R) and blue (B) of the sodium doublet, we employ the approach of Charbonneau et al. (2002) with absolute reference bands outside of the sodium doublet. This approach is justified given that the high-resolution data resolve the doublet. The two reference bands were chosen as follows: [5874.89–5886.89] Å for the red band (R) and [5898.89–5910.89] Å for the blue band (B), corresponding to 12 Å each.
The central passband (C) containing the sodium signal is split in two centred passbands, one for each line of the doublet. The width of the passband is varied from containing only the line core to a broader passband reaching from the red to the blue reference band. We chose the following central passband widths in line with Wyttenbach et al. (2015, 2017): 2 × 0.75, 2 × 1.5, 2 × 3, 2 × 6 Å.
The relative depth caused by the exoplanetary atmospheric absorption is then obtained via the flux difference between the central and the reference passbands using the following equation
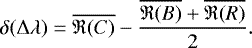 (4)
(4)
The detection levels for the different passbands can be found in Table 6 and show that the detection of planetary sodium in WASP-76b is independent of the passband choice. Nonetheless, the passband restricted around the line centre (2 × 0.75 Å) shows the strongest sodium feature, as expected, with a detection level of 10.75σ. The detection in this passband (see Table 6) corresponds to an atmospheric height of 28 800 ± 2600 km (0.19 ± 0.02Rp) (Pino et al. 2018b).
To establish the repeatability of the detection, we compare the relative depth for the 2 × 0.75 Å central passband for each of the nights separately (see Table 7 and Fig. 7). The values for all three nights lie within ± 1σ, which means the detection of sodium in the planetary atmosphere of WASP-76b is repeatable. The out-of-transit exposures affected by the drop in flux due to clouds during the last hours of the third night (2017-11-22) (see the data in the upper-right corner of Fig. 5) change the detection level significantly. As stated before, ten unaffected exposures were taken before the transit, which can be used to confidently establish a baseline without the contaminated exposures.
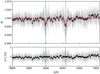 |
Fig. 6 HARPS transmission spectrum of WASP-76b centred around the sodium doublet in the planetary rest frame. Upper panel: light grey – full transmission spectrum for all nights combined in full resolution. Black – transmission spectrum binned by x20. The data has been corrected for tellurics and cosmics and shifted to the planetary rest frame. The absorption from the two Na I D lines from the planetary atmosphere can be seen clearly and the rest frame transition wavelengthsare marked with blue dashed lines. Red – Gaussian fits to each Na I line. We measure line contrasts of 0.373 ± 0.091% (D2) and 0.508 ± 0.083% (D1) and FWHMs of 0.619 ± 0.174 Å and 0.680 ± 0.128 Å, respectively. Lower panel: residuals of the Gaussian fit. |
Relative depth and detection level of atmospheric sodium on WASP-76b observed with HARPS for different central passbands.
4.4 Centre-to-limb variation and Rossiter–McLaughlin effect
Additional effects that could impact this analysis are centre-to-limb variation (CLV) and the Rossiter–McLaughlin effect (RM). As the stellar spectra obtained by HARPS are integrated over the stellar disc, both effects have the potential to significantly alter the transmission spectrum (Louden & Wheatley 2015).
To analyse the impact of the RM effect on our analysis, we built average transmission spectra in the star and planet rest frame (see Eq. (2) and Sect. 4.2) and calculated the cross correlation function (CCF) with the G2mask on the red detector (700 lines). This allows one to measure the average change in line shape imprinted by the RM effect on the transmission spectrum. This method is comparable to the transmission ccf method presented in Wyttenbach et al. (2017; see also Bourrier et al. 2018). The feature expected from the RM at 0 kms−1 is not detectedbeyond the noise level of 100 ppm. The small noise level is due to the peculiar characteristics of WASP-76, which is a slow rotator (vsini* < 2.3 km s−1) and has its planet, WASP-76b, in a polar orbit (Brown et al. 2017). As a conclusion, the planet always masks an area of the star with almost zero velocity during the whole transit. Since the 100 ppm value is much smaller than our detection, we conclude that the RM effect cannot explain our detection and is subsequently neglected.
For WASP-76, a F7 star, we assume that CLV effects can be disregarded given that CLV effects are less pronounced for earlier-type stars (Kostogryz & Berdyugina 2015; Czesla et al. 2015; Yan et al. 2017). According to the theoretical modelling of Czesla et al. (2015), the impact of CLV effects on our data should be negligible: these authors highlight a star similar to WASP-76 (F7, Teff = 6120 K) and CLV effects remain below the threshold of 200–500 ppm). Given that our light curve depth is about 0.005 (factor of 10 stronger) we do not take these effects into account during the following analysis.
Relative depth and detection level of atmospheric sodium on WASP-76b observed with HARPS for each of the nights separately in the 2 × 0.75 Å central passband.
 |
Fig. 7 Absorption depth of the three nights calculated from the transmission spectrum of the sodium doublet plotted with the value for all nights together and highlighted as a black horizontal line. The dashed lines mark one sigma around the main absorption depth. The data point in grey shows the value calculated for Night 3 when the cloud-contaminated exposures are not discarded. All values were taken from Tables 7 and 6. |
4.5 Systematic effects
To calculate the error on the relative absorption depth (δ(λ)) we propagated the error from the measured spectra through our analysis. The initial error is estimated as random photon noise obeying Poisson statistics. However, systematic errors and spurious signals cannot be ruled out. To further investigate their impact on our results we employ empirical Monte-Carlo (EMC) or bootstrapping methods following the approach in Redfield et al. (2008). The main goal is to verify that our signal is indeed produced by a planetary atmosphere and not by a random arrangement of the data, however statistically unlikely. To this end, wecreate different “scenarios” for comparison. The first scenario represents the case of an atmospheric detection: we select at random a sub-sample of spectra from the in-transit spectra and also at random the same number of out-of-transit spectra. These spectra are then used to calculate a randomised master-out spectrum (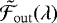 ) and subsequently δ(λ). This scenario should yield a detection and will be called the “in–out” scenario. Additionally a sub-sample containing only spectra from in-transit exposures was taken similarly and then split into two data sets of equal size. One half is labelled the “virtual in-transit” sample and the other the “virtual out-of-transit” sample.
) and subsequently δ(λ). This scenario should yield a detection and will be called the “in–out” scenario. Additionally a sub-sample containing only spectra from in-transit exposures was taken similarly and then split into two data sets of equal size. One half is labelled the “virtual in-transit” sample and the other the “virtual out-of-transit” sample.
This scenario is referred to hear as the “in–in” scenario. In the same fashion, “out–out” scenarios are created from the out-of-transit data. We created 10 000 of each of the “in–out”, “in–in”, and “out–out” scenarios, and ran our transmission spectroscopy analysis with them as described in Sect. 4.3. The resulting relative absorption depth distributions are plotted in Fig. 8 for the three observed nights. The red and blue distributions show the relative absorption depth for the “in–in” and “out–out” scenarios, respectively. A Gaussian fit to the distributions shows that both are centred at 0.0% as expected. The “in–out” distribution (in black) shows a relative absorption distribution centred around − 0.1%. This rules out a spurious detection of a planetary atmosphere as a statistical anomaly.
4.6 Broadening of the sodium feature
Both Na I lines are substantially broader than the instrumental line spread function of HARPS (2.7 km s−1) as shown in Fig. 9 where the two lines of the doublet are co-added. We first fit a Gaussian profile to measure the FWHM andthe amplitude of the sodium lines. We find that a Gaussian profile provides a good fit to the data (χ2 of 126.48 with 194 degrees of freedom).
First, we note that the depth of the D1 and D2 lines, as measured from the contrasts of the Gaussian fit in Fig. 6, is compatible to within 1–2σ, as expected for the depths of the Na I lines seen in absorption in a transit transmission spectrum.
The resulting FWHM is 27.6 ± 2.8 km s−1 which is 10.2 times broader than the resolution element of the spectrograph. The line is substantially broader than what we would expect from pure thermal broadening or a super-solar abundance of sodium. We verified this using the π η transit transmission spectroscopy code (Pino et al. 2018b). In contrast with previous work (Wyttenbach et al. 2015), we were not able to adjust the line profile either by increasing the temperature (up to ~17 000 K) or varying the mixing ratio of sodium (100 × solar abundance down to 10−6× solar abundance). The Na I lines in WASP-76b have a similar depth compared to HD 189733b (Wyttenbach et al. 2015), but are ~ 24% broader. Wetherefore attribute the broadening to missing physics in the hydrostatic atmospheric model used for the transit spectroscopy calculation.
One possibility is that the line broadening is of kinematic origin. A high-altitude atmospheric circulation around the planet (atmospheric super-rotation, typically not accounted for in 1D hydrostatic atmospheric models) could produce a Doppler broadening: sodium atoms moving towards and away from the observer at the evening (west) and morning (east) terminators, would respectively broaden the blue and red wings of the line.
Our data suggest that most sodium atoms have projected velocities below the escape velocity of 28 km s−1 calculated at a planetary radius of 2.08 RJup (Fig. 9). Assuming a Boltzmann distribution for the particle velocities, we calculate that only ~ 0.1% of all particles have velocities greater than or equal to the escape velocity. While these few sodium atoms in the tail of the velocity distribution may escape the planet, Fig. 9 shows that the bulk have velocities well within the escape velocity; therefore the absorption signature is mainly caused by atoms gravitationally bound to the planet. Because we only measure the projected velocities of the sodium atoms, the fraction of high-velocity sodium atoms might be higher, but this effect is unlikely to change our conclusion.
To better constrain atmospheric escape, follow-up studies need to trace layers above those probed by sodium, using lighter gases such as hydrogen and helium. Additionally, WASP-76b is too far away from Earth to measure UV transit absorption signal in the stellar Hi Lyman-α emission line (which is entirely absorbed by the interstellar medium), but there are good prospects for observations of escaping helium through high-resolution, near-infrared transit observations (Allart et al. 2018, 2019; Nortmann et al. 2018; Salz et al. 2018).
 |
Fig. 8 Distributions of the EMC analysis for the 12 Å passband. The resultsfor the transmission spectrum method are shown. As expected the “in–in” (red) and “out–out” (blue) distributions are centred around zero (no planetary detection) and the randomised “in–out” distribution shows a detection (black). On each night a different number of spectra was taken, which means that each randomisation will give a different number of counts, which results in a different scaling on the y-axis. This has no influence on the overall result. |
 |
Fig. 9 Co-added lines of the HARPS transmission spectrum sodium doublet as a function of velocity. The line centre was set to zero. The data are shown in grey and binned × 10 in black. A Gaussian fit derived as in Sect. 4.2 is shown in red with its FWHM marked by the red dashed lines. The HARPS instrumental line spread function (FWHM = 2.7 km s−1) is shown in orange and the escape velocity as green dotted-dashed lines. The FWHM velocity does not exceed the escape velocity at any point, making the atmospheric escape of sodium unlikely. The best Gaussian fit to the data is significantly wider than the instrumental response, but the corresponding velocity is well below the escape velocity of WASP-76b. Given that the conversion of relative depth to height depends on the choice of height at the continuum level (here: WASP-76b white light radius), the height is not an absolute height but an equivalence height (Pino et al. 2018b). |
5 Conclusion
We analysed 160 spectra of WASP-76, with 107 spectra while WASP-76b was in transit during three nights of observations with HARPS. This led to the first detection of sodium in the planet atmosphere from the transmission spectrum (0.371 ± 0.034%; 10.75σ in the 0.75 Å passband) in an ultra-hot Jupiter. The result was reproducible in each of the three obtained nights. We were able to rule out spurious signals from data artifacts via EMC analysis by testing for a detection from random exposures containing only in- or out-of-transit exposures, respectively. We co-added the sodium doublet and retrieved a FWHM of 27.6 ± 2.8 km s−1 for the fitted Gaussian. The significant line broadening could also be a result of rapid, large-scale circulation of hot atoms in the upper atmosphere of the planet, leading to Doppler broadening. These results suggest upper atmosphericsuper-rotation in an ultra-hot gas giant. The bulk of the population of hot neutral atoms do not escape the planet.
The HEARTS survey is intended as a pathfinder for a survey using the ESPRESSO spectrograph, which started operations in October 2018 at the 8-m-class Very Large Telescope. These new observations at high spectral resolution will substantially increase our understanding of exoplanetary atmospheres in different irradiation conditions and will shed light on atmospheric conditions such as winds and ionisation state.
Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (project FOUR ACES; grant agreement no 724427). This work has been carried out within the frame of the National Centre for Competence in Research “PlanetS” supported by the Swiss National Science Foundation (SNSF). A.W. and R.A. acknowledge the financial support of the SNSF (A.W.: Nr. P2GEP2_178191). N.A.-D. acknowledges support from FONDECYT Nr. 3180063. We are grateful to J. M. Désert and V. Panwar for allowing us to use their computational resources to run the πη code and thank L. DosSantos for his helpful comments. Additionally, we would like to highlight the contribution of the anonymous referee.
References
- Allart, R., Lovis, C., Pino, L., et al. 2017, A&A, 606, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allart, R., Bourrier, V., Lovis, C., et al. 2018, Science, 362, 1384 [NASA ADS] [CrossRef] [Google Scholar]
- Allart, R., Bourrier, V., Lovis, C., et al. 2019, A&A, 623, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astudillo-Defru, N., & Rojo, P. 2013, A&A, 557, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourrier, V., Dumusque, X., Dorn, C., et al. 2018, A&A, 619, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, T. M. 2001, ApJ, 553, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, D. J. A., Triaud, A. H. M. J., Doyle, A. P., et al. 2017, MNRAS, 464, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Burton, J. R., Watson, C. A., & Rodriguez-Gil, P. 2015, MNRAS, 446, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Casasayas-Barris, N., Palle, E., Nowak, G., et al. 2017, A&A, 608, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonneau, D., Noyes, R. W., Korzennik, S. G., et al. 2000, ApJ, 522, L145 [Google Scholar]
- Charbonneau, D., Brown, T. M., Noyes, R. W., & Gilliland, R. L. 2002, ApJ, 568, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, G., Palle, E., Nortmann, L., et al. 2017, A&A, 600, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cubillos, P., Harrington, J., Loredo, T. J., et al. 2017, AJ, 153, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Czesla, S., Klocova, T., Khalafinejad, S., Wolter, U., & Schmitt, J. H. M. M. 2015, A&A, 582, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinoza, N., & Jordán, A. 2015, MNRAS, 450, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Lanotte, A. A., Barman, T., et al. 2010, A&A, 511, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heng, K., Wyttenbach, A., Lavie, B., et al. 2015, ApJ, 803, L9 [Google Scholar]
- Jensen, A. G., Redfield, S., Endl, M., et al. 2011, ApJ, 743, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, A. G., Cauley, P. W., Redfield, S., et al. 2018, AJ, 156, 4 [Google Scholar]
- Kausch, W., Noll, S., Smette, A., et al. 2015, A&A, 576, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khalafinejad, S., von Essen, C., Hoeijmakers, H. J., et al. 2017, A&A, 598, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kostogryz, N. M., & Berdyugina, S. V. 2015, A&A, 575, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lendl, M., Anderson, D. R., Collier-Cameron, A., et al. 2012, A&A, 544, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lendl, M., Cubillos, P. E., Hagelberg, J., et al. 2017, A&A, 606, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Louden, T., & Wheatley, P. J. 2015, ApJ, 814, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Marley, M. S., Gelino, C., Stephens, D., Lunine, J. I., & Freedman, R. 1999, ApJ, 513, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Moutou, C., Coustenis, A., Schneider, J., et al. 2001, A&A, 371, 260 [CrossRef] [EDP Sciences] [Google Scholar]
- Murgas, F., Palle, E., Osorio, M. R. Z., et al. 2014, A&A, 563, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nikolov, N., Sing, D. K., Gibson, N. P., et al. 2016, ApJ, 832, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Nortmann, L., Palle, E., Salz, M., et al. 2018, Science, 362, 1388 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pino, L., Ehrenreich, D., Allart, R., et al. 2018a, A&A, 619, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pino, L., Ehrenreich, D., Wyttenbach, A., et al. 2018b, A&A, 612, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Redfield, S., Endl, M., Cochran, W. D., & Koesterke, L. 2008, ApJ, 673, L87 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Remedios, J. J., Gilles, J. C., Barnett, J. J., et al. 2001, Adv. Space Res., 27, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Salz, M., Czesla, S., Schneider, P. C., et al. 2018, A&A, 620, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seager, S., & Sasselov, D. 2000, A&A, 537, 916 [Google Scholar]
- Sing, D., Fortney, J. J., Nikolov, N., et al. 2016, Nature, 529, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snellen, I. A. G., Albrecht, S., de Mooij, E. J. W., & Poole, R. S. L. 2008, A&A, 487, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vidal-Madjar, A., Sing, D. K., Lecavelier des Etangs, A., et al. 2011a, A&A, 527, A110 [Google Scholar]
- Vidal-Madjar, A., Sing, D. K., Lecavelier des Etangs, A., et al. 2011b, A&A, 533, C4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- West, R. G., Hellier, C., Almenara, J.-M., et al. 2016, A&A, 585, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winn, J. N., Holman, M. J., Torres, G., et al. 2008, ApJ, 683, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, P. L., Maxted, P. F. L., Smalley, B., & Iro, N. 2011, MNRAS, 412, 2376 [NASA ADS] [CrossRef] [Google Scholar]
- Wyttenbach, A., Ehrenreich, D., Lovis, C., Udry, S., & Pepe, F. 2015, A&A, 577, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyttenbach, A., Lovis, C., Ehrenreich, D., et al. 2017, A&A, 602, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, F., Palle,E., Fosbury, R. A. E., Petr-Gotzens, M. G., & Henning, T. 2017, A&A, 603, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhou, G., & Bayliss, D. D. R. 2012, MNRAS, 426, 2483 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Relative depth and detection level of atmospheric sodium on WASP-76b observed with HARPS for different central passbands.
Relative depth and detection level of atmospheric sodium on WASP-76b observed with HARPS for each of the nights separately in the 2 × 0.75 Å central passband.
All Figures
 |
Fig. 1 Mass of the planet vs. bolometric optical and infrared incident flux in units of flux received at Earth. In grey, transiting exoplanets are shown with V < 16 and masses determined with a precision better than 20%. WASP-76b is shown in orange. For comparison WASP-49b (Wyttenbach et al. 2017), HD 189733b (Wyttenbach et al. 2015), and HD 209458b (for reference) are shown in red, blue, and green, respectively. |
| In the text | |
 |
Fig. 2 Telluric correction highlighted for an out-of-transit exposure during the first observation night on 2012-11-11. Upper panel: applied model of telluric lines. Middle panel: uncorrected flux in red and the corrected flux in black, which cannot be distinguished. We note the different scales for the two panels. Lower panel: difference between the corrected and uncorrected spectra for better visualisation. The impact of tellurics in the wavelength range of the cores of the sodium doublet is negligible. Nonetheless, a good telluric correction is crucial to clean the continuum baseline used for normalisation and where more telluric lines are situated. |
| In the text | |
 |
Fig. 3 All exposures for the second night (2017-10-24) plotted before (left panel) and after (right panel) telluric correction coloured by airmass. The strong telluric line (line centre indicated by the black dashed line) merged with a stellar line is corrected down to the noise level for high and low airmasses. This window is illustrative of the corrections performed on all three observation nights. |
| In the text | |
 |
Fig. 4 The three light curves obtained by EulerCam (top to bottom: 2012-11-11, 2017-10-24 and 2017-11-22) offset by 0.02 for visibility. The computed model is shown in red. |
| In the text | |
 |
Fig. 5 HARPS relative excess absorption in the sodium doublet compared to the white light curve of WASP-76b evolving in time. The upper three plots show the light curves for each night 2012-11-11, 2017-10-24, and 2017-11-22 from left to right. We note the different scales on the ordinate axis for upper and lower panels and the influence of stratus clouds in the out-of-transit exposures during the night of 2017-11-22. The grey data points show the relative absorption for each exposure; inblack the data is binned by five spectra. Lower panel: light curve for all three nights combined, with the original exposures averaged together for five spectra each in grey and binned by five averaged spectra in grey. The green background marks the exposures taken out-of-transit. |
| In the text | |
 |
Fig. 6 HARPS transmission spectrum of WASP-76b centred around the sodium doublet in the planetary rest frame. Upper panel: light grey – full transmission spectrum for all nights combined in full resolution. Black – transmission spectrum binned by x20. The data has been corrected for tellurics and cosmics and shifted to the planetary rest frame. The absorption from the two Na I D lines from the planetary atmosphere can be seen clearly and the rest frame transition wavelengthsare marked with blue dashed lines. Red – Gaussian fits to each Na I line. We measure line contrasts of 0.373 ± 0.091% (D2) and 0.508 ± 0.083% (D1) and FWHMs of 0.619 ± 0.174 Å and 0.680 ± 0.128 Å, respectively. Lower panel: residuals of the Gaussian fit. |
| In the text | |
 |
Fig. 7 Absorption depth of the three nights calculated from the transmission spectrum of the sodium doublet plotted with the value for all nights together and highlighted as a black horizontal line. The dashed lines mark one sigma around the main absorption depth. The data point in grey shows the value calculated for Night 3 when the cloud-contaminated exposures are not discarded. All values were taken from Tables 7 and 6. |
| In the text | |
 |
Fig. 8 Distributions of the EMC analysis for the 12 Å passband. The resultsfor the transmission spectrum method are shown. As expected the “in–in” (red) and “out–out” (blue) distributions are centred around zero (no planetary detection) and the randomised “in–out” distribution shows a detection (black). On each night a different number of spectra was taken, which means that each randomisation will give a different number of counts, which results in a different scaling on the y-axis. This has no influence on the overall result. |
| In the text | |
 |
Fig. 9 Co-added lines of the HARPS transmission spectrum sodium doublet as a function of velocity. The line centre was set to zero. The data are shown in grey and binned × 10 in black. A Gaussian fit derived as in Sect. 4.2 is shown in red with its FWHM marked by the red dashed lines. The HARPS instrumental line spread function (FWHM = 2.7 km s−1) is shown in orange and the escape velocity as green dotted-dashed lines. The FWHM velocity does not exceed the escape velocity at any point, making the atmospheric escape of sodium unlikely. The best Gaussian fit to the data is significantly wider than the instrumental response, but the corresponding velocity is well below the escape velocity of WASP-76b. Given that the conversion of relative depth to height depends on the choice of height at the continuum level (here: WASP-76b white light radius), the height is not an absolute height but an equivalence height (Pino et al. 2018b). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


