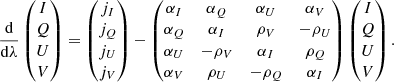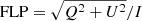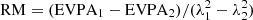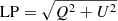| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A152 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201834503 | |
| Published online | 22 March 2019 | |
Linear and circular polarization of a 1D relativistic jet model
Department of Astrophysics/IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
e-mail: m.moscibrodzka@astro.ru.nl
Received:
24
October
2018
Accepted:
28
January
2019
Context. Polarimetric observations of black holes allow us to probe structures of magnetic fields and plasmas in strong gravity.
Aims. We present a study of the polarimetric properties of a synchrotron spectrum emitted from a relativistic jet using a low-dimensional model.
Methods. A novel numerical scheme is used to integrate relativistic polarized radiative transfer equations in a slab geometry where the plasma conditions change along the integration path.
Results. We find that the simple model of a non-uniform jet can recover basic observational characteristics of some astrophysical sources with a relativistic jet, such as extremely high rotation measures. Our models incorporate a time-dependent component. A small fluctuation in density or temperature of the plasma along the jet produces significant amounts of fluctuations not only in the fractional linear and circular polarizations, but also in the jet internal rotation measures.
Conclusions. The low-dimensional models presented here are developed within the same computational framework as the complex three-dimensional general relativistic magnetohydrodynamics simulations of black hole disks and jets, and they offer guidance when interpreting the results from more complex polarization models. The models presented here are scalable to stationary and transient polarized radio emissions produced by relativistic plasma ejected from around compact objects, in both stellar-mass and supermassive black hole systems.
Key words: black hole physics / magnetohydrodynamics (MHD) / polarization / radiative transfer / relativistic processes
© ESO 2019
1. Introduction
The compact flat-spectrum radio emissions from the cores of active galactic nuclei (AGN), low-luminosity AGN (LLAGN; Boccardi et al. 2017 and references therein), and quiescent/hard-state X-ray black hole binaries (XBHB; e.g., Connors et al. 2017) are all thought to be produced by synchrotron processes in a optically thick relativistic jet (Blandford & Königl 1979). The conditions of jet launching can now be studied in more detail. The detections of polarization in the synchrotron radiation from (LL)AGN at millimeter wavelengths (Plambeck et al. 2014; Bower et al. 2017; Hovatta et al. 2019) and from XBHB at NIR/optical wavelengths (Russell et al. 2016; Dinçer et al. 2018) allow us to probe the properties of magnetic fields and plasma in accretion flows in the vicinity of black holes, and also the structure of magnetic fields in relativistic jets at various distances from the black hole, and in two sources, down to scales of the black hole event horizon (Johnson et al. 2015; Bower et al. 2018).
The polarimetric observations of black hole jets and their launching zones can currently be modeled using complex three-dimensional general relativistic magnetohydrodynamics (3D-GRMHD) global simulations of magnetized accretion flows, combined with general relativistic polarized radiative transfer models (e.g., Shcherbakov et al. 2012; Gold et al. 2017; Mościbrodzka et al. 2017; Jiménez-Rosales & Dexter 2018). However, 3D-GRMHD models are complex, time-dependent, and numerical resolution dependent, hence the interpretation of polarimetric observations of LLAGN, especially time variable behavior of polarimetric observables, via these simulations is challenging. This motivates the development of simple, computationally cheap relativistic jet models carried out (semi-)analytically.
In this work we present a very simple analytic jet model inspired by the theoretical model of Blandford & Königl (1979), and additionally guided by the results of the radiative 3D-GRMHD simulations of jets presented earlier (Mościbrodzka & Falcke 2013; Mościbrodzka et al. 2014, 2016, 2017). The essential component of the presented model is the self-consistent radiative transfer simulation that predicts the polarimetric properties of the synchrotron emission (polarized spectra, rotation measures, and light curves) generated by plasma moving at a relativistic bulk speed.
Our relativistic jet model is developed within a simple polarized radiative transfer (PRT) integrator. The model assumes Minkowski space-time described by Cartesian coordinates. The underlying plasma moves at bulk relativistic speeds; the special relativistic effects are self-consistently included in the model. The integrator requires specification of (i) the plasma three-velocity along the line of sight, (ii) the three-vector magnetic fields, (iii) the plasma density, and (iv) the distribution function of emitting particles. These quantities can be non-uniform in this space-time. The result are Stokes parameters at a chosen observing frequency and time. We note that our model does not incorporate any dispersive effects (i.e., we assume that the plasma refractive index is one). The simple model allows a quick interpretation of polarimetric data without invoking a general relativity (GR) or a complex, usually time-dependent, MHD model. Instead, it only follows the rules of special relativity (including effects of finite speed of light) and the transfer equations for the Stokes parameters. A general relativistic version of the same numerical scheme (ipole) coupled to a 3D-GRMHD simulation is publicly available (see Mościbrodzka & Gammie 2018).
The paper is organized as follows. In Sect. 2 we detail the radiative transfer model. In Sect. 3 we present example calculations for a static background with a time-variable component. In Sect. 4 we summarize the results.
2. Polarized synchrotron emission
We solve the equations of the PRT with synchrotron radiation including emission, self-absorption, and Faraday effects:
Here, the absence of subscript ν implies that a term appears in invariant form, i.e., ρV = νρν, V, and the derivative is understood to follow an individual photon in frequency space. When integrating Eq. (1), the analytical fits for the synchrotron emissivities in ultra-relativistic electron-proton plasma (jIQUV), the corresponding absorptivities (αIQVU) and Faraday rotativities (ρQUV) are described by analytical fit functions presented by Shcherbakov (2008) and Dexter (2016).
Equation (1) is integrated numerically following a framework laid out in Gammie & Leung (2012) and its numerical implementation in Mościbrodzka & Gammie (2018; see their Sects. 2 and 3). In this approach, the polarized radiation field is represented by a coherency tensor Nμν which relates to Stokes parameters defined in an orthonormal tetrad 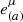 . Two orthonormal tetrads are relevant in the current setup. The first tetrad is associated with the fluid frame in which the Stokes parameters are evolved. The first three fluid frame tetrad vectors are
. Two orthonormal tetrads are relevant in the current setup. The first tetrad is associated with the fluid frame in which the Stokes parameters are evolved. The first three fluid frame tetrad vectors are 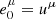 ,
, 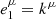 , and
, and 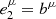 , where uμ, kμ, and bμ are the plasma four-velocity, wavevector, and magnetic field four-vector, respectively. The fourth vector is set by ortho-normalization operation. The Lorentz transformation of Nμν to and from the plasma tetrad is equivalent to self-consistently including special relativistic effects in the model. All synchrotron emissivities, absorptivities, and rotativities are derived in the plasma tetrad; the Stokes parameters are evolved in the plasma tetrad using analytic solutions (Eq. (23) in Mościbrodzka & Gammie 2018). This analytic solution assumes that the transfer coefficients are constant within one integration step. Next, Stokes parameters are packed back to Nμν, which is converted into a coordinate frame. The transport step of the Stokes parameters (which has to be taken into account in curved space-time) can be skipped in a Minkowski space-time described by Cartesian coordinates as it does not affect Nμν. The second tetrad is associated with the Cartesian coordinates in which the Stokes parameters are read out as
, where uμ, kμ, and bμ are the plasma four-velocity, wavevector, and magnetic field four-vector, respectively. The fourth vector is set by ortho-normalization operation. The Lorentz transformation of Nμν to and from the plasma tetrad is equivalent to self-consistently including special relativistic effects in the model. All synchrotron emissivities, absorptivities, and rotativities are derived in the plasma tetrad; the Stokes parameters are evolved in the plasma tetrad using analytic solutions (Eq. (23) in Mościbrodzka & Gammie 2018). This analytic solution assumes that the transfer coefficients are constant within one integration step. Next, Stokes parameters are packed back to Nμν, which is converted into a coordinate frame. The transport step of the Stokes parameters (which has to be taken into account in curved space-time) can be skipped in a Minkowski space-time described by Cartesian coordinates as it does not affect Nμν. The second tetrad is associated with the Cartesian coordinates in which the Stokes parameters are read out as 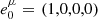 ,
, 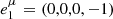 ,
, 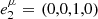 , and
, and 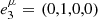 . The schematic diagram of the model geometry is shown in Fig. 1.
. The schematic diagram of the model geometry is shown in Fig. 1.
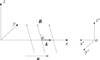 |
Fig. 1. Schematic diagram of the model geometry. The coordinate system (x, y, z) is that in which the PRT equations are integrated. The symbols have the following meanings: k is the spatial component of the wavevector, B is the three-vector of the magnetic field, u is the spatial component of the plasma bulk four-velocity, θ is the angle between the x-axis and the B-field vector measured in the frame of the adopted coordinate system; it has different values when measured in the rest-frame co-moving with the plasma. Finally, the coordinate system (x0, y0, x0) is the frame in which the Stokes parameters are observed. |
To demonstrate the validity of our numerical PRT scheme, we repeated two simple tests described by Dexter (2016; see their Appendix C) and Mościbrodzka & Gammie (2018; see their Sect. 4.2). The details and results of these tests are presented in the Appendix. The tests were carried out in dimensionless units. To integrate PRT for the synchrotron process, the underlying plasma density, magnetic field, and temperature are given in cgs units. The photon frequency is given in Hz (the photon wavevector unit is hν/mec2). The coordinate x unit is Lunit [cm] and time is measured in Tunit = Lunit/c. Here we assume that the plasma electrons have a thermal distribution function. In our model, a thermal and/or a non-thermal (power-law) electron distribution function can be used.
3. Polarized emission from plasma moving at relativistic speed towards an observer
Our simple jet model consists of two components: the first component is static (time-independent), and the second component is variable (time-dependent). In the following, we describe the implementation of both components in our model, and discuss their importance.
3.1. Static background component
3.1.1. Plasma configuration
The structure of the background component is inspired by the jet models of Blandford & Königl (1979) and by those realized in 3D-GRMHD simulations (Mościbrodzka & Falcke 2013; Mościbrodzka et al. 2014). In our static background model, we assume a jet propagates along the x-axis (Fig. 1), and assume that its electron density (ne[ cm−3]), magnetic field strength (B [Gauss]), and dimensionless electron temperature (Θe = kTe/me c2) all scale with the distance along the x-axis, i.e., ne = ne, 0x−2, B = B0x−1, and Θe = Θe, 0x−0.5, where (ne, 0, B0, Θe, 0) = (104, 27, 20). The values of plasma density, magnetic field strength, and the electron temperature at the jet launching point are compatible with those found in our 3D GRMHD models of jets (Mościbrodzka et al. 2016). Our jet model is not in equipartition because it is not strictly isothermal (this is motivated by jets in 3D-GRMHD models that experience adiabatic expansion). With this setup, the magnetic fields are dominating at the jet base, i.e., at x = 1, β = Pgas/Pmag = 0.16, where Pmag = B2/2 and Pgas = neΘemec2.
We assume that the magnetic field is inclined at a fiducial angle of θ = const = 120° with respect to the direction the electromagnetic wavevector k (along the x-axis) (Fig. 1); we note that this angle is slightly different from the angle between kμ and bμ measured in the frame co-moving with the plasma. We further assume that the plasma is moving along the x-axis with vx = 0.7c so that uμ = (γ, γvx, 0, 0), where 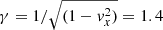 is the corresponding Lorentz factor. We integrate the PRT equations along the x-axis from x = 1 to x = 20 Lunit, where Lunit = 9 × 1014 cm. The chosen Lunit corresponds to the length-scale of the jet near a supermassive black hole with its mass of a few ×109 M⊙ (Lunit ≈ GMBH/c2). The corresponding unit in which time is measured is Tunit = 3000 s = 8 h. The initial wavevector (k) is pointing along the x-axis and the corresponding four-vector (kμ) remains constant over the integration range.
is the corresponding Lorentz factor. We integrate the PRT equations along the x-axis from x = 1 to x = 20 Lunit, where Lunit = 9 × 1014 cm. The chosen Lunit corresponds to the length-scale of the jet near a supermassive black hole with its mass of a few ×109 M⊙ (Lunit ≈ GMBH/c2). The corresponding unit in which time is measured is Tunit = 3000 s = 8 h. The initial wavevector (k) is pointing along the x-axis and the corresponding four-vector (kμ) remains constant over the integration range.
3.1.2. Polarization of spectral energy distribution
Figure 2 (left panel) shows the spectral energy distribution (SED) computed with the background component of the model. In Stokes I, the optically thick part of the spectrum (below the synchrotron peak frequency, i.e., ν < 3 × 1011 Hz) has a spectral slope of −2. Such a steep spectral slope is expected with this setup. Here we perform the integration of the PRT along a single line of sight which results in intensity of radiation as an end product. The observed flux, however, is proportional to the intensity multiplied by the surface area of the synchrotron photosphere. The size of the synchrotron photosphere is expected to increase with decreasing photon frequency as νp, where p ∈ ( − 1, −2) (depending on the jet geometry). Hence, the resulting observed spectrum would have a slightly inverted spectrum resulting in a flatter slope, as is observed is observed in many astrophysical jets (e.g., Nagar et al. 2000; Hada et al. 2013, 2016). The optically thin part of the SED (ν > 3 × 1011 Hz) has a high fractional linear polarization that changes from 30% (near the peak) to 100% (at higher energies), as expected from intrinsic synchrotron emissivities. In the optically thick part, the SED is depolarized due to self-absorption and Faraday effects. The SEDs of fractional linear and circular polarization have steep and nearly flat spectral slope, respectively. This is consistent with the observations of jets in some of the LLAGN (Boccardi et al. 2017). Figure 2 (left panel) also shows that the circular polarization of the background plasma is rather low everywhere with a maximum of ∼7% around the synchrotron emission peak. Near the synchrotron peak, intrinsic emission and Faraday conversion both contribute to the flux in Stokes V; however, circular polarization of the self-absorbed part of the spectrum is mainly produced via Faraday conversion. The circular polarization of the optically thin part of the spectrum is due to intrinsic emission. This is evident by comparing the middle and right panels of Fig. 2 where we show how the SEDs look when emissivity in Stokes V and Faraday conversion are switched off.
3.1.3. Circular polarization
Circular polarization is observed in the radio cores of some AGN and, in a few sources, in regions downstream of the core (Irwin et al. 2018) and often associated with processes in relativistic jets (Homan & Wardle 1999). It is not clear whether in these sources the observed circular polarization is produced intrinsically from the incoherent synchrotron emission from within the jet or is instead produced via internal Faraday conversion. However, the Faraday conversion is usually regarded as a more efficient mechanism in producing the observed levels of circular polarization. The efficiency of Faraday conversion depends on the details of the jet structure (MacDonald & Marscher 2018). Wardle & Homan (2003) discuss the expected circular polarization from an inhomogeneous self-absorbed jet model introduced by Blandford & Königl (1979). The expectations of Wardle & Homan (2003) are as follows: if the jet is isothermal the fractional circular polarization (FCP, which is ≡V/I) spectrum is either flat or inverted (FCP ∼ ν0, −1) regardless of the mechanism of production; in contrast, for a non-isothermal jet, the FCP should be steep, FCP ∼ ναV, where the exact slope αV depends on the details of the model. By performing numerical integration, we demonstrate that we can recover the previous theoretical expectations and make new predictions that may help us to distinguish the origins of circular polarization in AGN jets. Although not shown in the paper, we find that a nearly isothermal jet produces FCP ∼ ν0. In Fig. 2 (left panel) the jet with decreasing temperature produces FCP ∼ ναV where αV > 0, as expected.
3.1.4. Linear polarization and rotation measure
Figure 3 shows how the Stokes parameters and other observables such as fractional polarization, electric vector position angle, and rotation measure change along the integration path. These values are evaluated at putative frequencies of ν = 225 and 241 GHz1. The figure shows that the quantities approach the asymptotic values within the first few Lunit of integration. In our model, the optical depth and Faraday depth are close to one for photons around the synchrotron peak frequency. Interestingly, our models naturally show high rotation measures on the order of 105 [rad m−2], which is similar to the values measured towards accreting black holes (e.g., Sgr A*, 3C 84, or 3C 273; Mościbrodzka et al. 2017 and references therein).
 |
Fig. 2. Left panel: spectral energy distribution of the Stokes parameters (I, Q, U, V, where I ≡ Iν is the specific intensity in cgs units [ergs s−1 cm−2 ster−1 Hz−1]) computed with the static background jet model described in Sect. 3.1 and the corresponding fractional linear and circular polarizations. Middle panel: same as the left panel, but assuming no emission/absorption in Stokes V (jV = aV = 0). Right panel: same as the left panel, but assuming no Faraday conversion (ρQ = 0). The flux in Stokes V (left panel) in the optically thick part of the spectrum is mainly produced by Faraday conversion. In the optically thin part of SED, Stokes V is due to intrinsic emission. In this jet model the spectra of fractional linear and circular polarization have steep and nearly flat spectral slope, respectively. When the values of Q, U, and V are negative, −Q, −U, and −V are plotted here. |
3.2. Variable component: dense vs. hot plasmoid
In GRMHD simulations the accretion onto a black hole is inherently time-variable. Jets produced in these models are not static structures: they are either non-uniformly mass loaded or they are perturbed by the surrounding dynamic accretion disk (e.g., Beckwith et al. 2008). This motivates adding a variable component to the jet model.
The variable component of our simple model is described by a Gaussian function to emulate a perturbation (sometimes referred to as a plasmoid) propagating in a jet. We assume that the Gaussian has a varying amplitude and the fixed standard deviation, i.e., σx = 2 Lunit. This variable component is added to the static component discussed in Sect. 3.1. The variable component is injected at the jet base (x = 1) at a random moment in time, approximately 4.2 Tunit. It then propagates with the background flow which is moving at a speed vx = 0.7c. It takes about 27.1 Tunit for the Gaussian fluctuation to cross the entire computational domain so the fluctuation leaves the computational domain at t ≈ 31.3 Tunit.
We consider two scenarios. In the first (Model A) the electron density (ne) of the variable component is set to twice the value of the background density, which decreases with x (see Sect. 3.1). The other field values (B and Θe) are unchanged from those of the background component. In the second scenario (Model B), the electron temperature (Θe) in the variable component is set to twice the background temperature, which also decreases with x (Sect. 3.1). With these setups, we examine how the observed nature of the polarimetric values change in time, and how they react to the introduction of the simulated perturbation.
Figure 4 (upper four panels) show the light curves for the Stokes parameters computed for both Model A and B. These light curves are computed around the synchrotron peak frequency. The lower four panels show the corresponding time evolutions of the secondary polarimetric quantities computed from the Stokes parameters. These values are computed at the same two ALMA frequencies (ν = 225 and 241 GHz) used in Sect. 3.1 (Fig. 3).
 |
Fig. 3. Changes in polarimetric quantities along the integration path in the static background jet component model. The calculations are performed for photons at ν = 230 GHz, which corresponds to τ ≈ 1 in the SED plot (left panel of Fig. 2). Shown are the following quantities: panel a: Stokes I (where I ≡ Iν is the specific intensity in cgs units [ergss−1 cm−2ster−1Hz−1]); panel b: optical and Faraday depths (τabs and τF), where τF = ∫ρVdl; panel c: fractional linear and circular polarization (FLP and FCP), where |
 |
Fig. 4. Light curves of the Stokes parameters and the secondary polarimetric quantities computed with a dense plasmoid (Model A: left column) and with a hot plasmoid component (Model B: right column) moving along with the background flow (see Sect. 3.2 for the model descriptions). In both models the plasmoid is injected into the computational domain at t ≈ 4.2Tunit and it reaches the position where we make a measurement at t ≈ 31.3Tunit. The four upper panels show the model light curves of the Stokes parameters (I, Q, U, V), and the four lower panels show the corresponding time evolution of the optical and Faraday depths (τabs and τF: fifth row), the fractional linear and circular polarizations (FLP and FCP: sixth row), the rotation measure (RM: seventh row), and the electric vector position angle (EVPA; eighth row). The Stokes parameters and EVPA are computed at the two frequencies (ν = 225 GHz and 241 GHz). The other polarimetric quantities are computed around the synchrotron peak frequency (Fig. 2). In the plot for RM, the maximum possible RM value (π/Δλ2) is the maximum RM that can be resolved within the chosen frequency range. |
The figure shows that the polarimetric properties of the synchrotron radiation reaching the observer are sensitive to the conditions of the plasma in the jet. In Model A, when a dense plasmoid appears along the line of sight, the optical and Faraday depths increases by a factor of a few above the background. This results in a temporary decrease in the fractional linear polarization and a temporary increase in the rotation measure. The fractional circular polarization also decreases to below 1%. In Model B, the hot plasmoid along the line of sight decreases the optical and Faraday depths of the plasma for the millimeter photons. This results in an increase in the fractional linear polarization, and a decrease in the rotation measure. In both models, the amount of fluctuation in the fractional linear polarization can readily reach 30%. The rotation measure can change by a factor of two or more, easily reaching extreme values of 106 [rad m−2].
4. Discussions and conclusions
The low-dimensional models presented here are developed within the same computational framework as the 3D-GRMHD simulations of disks and jets (Mościbrodzka & Gammie 2018). Our future PRT calculations will be based on 3D-GRMHD simulations of an accretion disk with a jet to model the emission from the cores of sub-Eddington black holes. However, 3D-GRMHD models are complex and time-dependent, hence the interpretation of variable polarimetric observations of LLAGN, e.g., Sgr A*, via these simulations is challenging. The simple jet polarization model presented here is intended to be a useful guide when interpreting the results from a more complex polarization model or when interpreting observations.
We have examined the polarimetric properties of jets using the simplest scenarios. The main findings of this study are as follows.
Below the synchrotron peak, the depolarization of the synchrotron radiation from the jet can be very strong due to the self-absorption processes and Faraday effects within the jet itself. The high rotation measures reproduced in our simple jet scenario suggest that the RM towards some of the accreting black holes in LLAGN (when jet sources have a small inclination angle, e.g., the core of M87) could be partially internal to the outflows (instead of inflows). Consequently, the accretion rates estimates based on RM could be underestimated (e.g., Kuo et al. 2014).
In addition, a small fluctuation (of a factor of two) in the electron density or electron temperature (or in the particle distribution function) can lead to notable changes in linear and circular polarizations. It can also lead to significant fluctuations in rotation measures. Hence, the rotation measures detected towards accreting black holes could display variability.
Relativistic jets can be circularly polarized and the spectrum of fractional circular polarization is possibly a useful diagnostic tool to reveal the electron distribution function (or particle acceleration) along the jet. The models and consideration presented in Sect. 3.1 show that the fractional circular polarization is an interesting observable that is, in contrast to linear polarization, not affected by the external medium, which in the case of linear polarization may scramble coherent polarization signals. Hence investigating the origin and behavior of circular polarization in future GRMHD simulations of jets, which have complex structures of magnetic fields and particle distribution functions, may give us hints to how energy should be dissipated along the jet in these complex models. An interesting source where it is possible to test the models of particle acceleration along the jet is Sgr A*, the compact radio core in the center of the Milky Way, whose radio spectrum has long been thought to be produced by a compact relativistic jet. Muñoz et al. (2012) shows that all measurements of FCP in the optically thick part of Sgr A* form a slightly inverted spectrum, FCP ∼ ν0.35 ± 0.03. Investigating the exact slope of FCP produced in numerical simulations of a jet is an interesting direction for future developments of particle acceleration models in GRMHD simulations.
Our simple model can also be easily extended to include: (1) self-consistently evolved electron distribution function (instead of assuming Maxwellian distribution), (2) jets with multiple components, and (3) turbulent magnetic fields along the line of sight. These additions will be developed in future works. The simple models presented here are scalable to the stationary and transient polarized radio emissions from jets not only in supermassive black holes, but also in stellar-mass black holes in XBHB, gamma-ray, bursts or jets produced during stellar tidal disruptions by massive black holes.
These putative frequencies were chosen because they are within band 6 of The Atacama Large Millimeter/submillimeter Array (ALMA) receivers, which are used to measure RM in astrophysical jets (e.g., Hovatta et al. 2019; Bower et al. 2018).
Acknowledgments
I thank Jim Moran for his comments and suggestions. This research has made use of NASA’s Astrophysics Data System Bibliographic Services; matplotlib, a Python package developed by Hunter (2007); and the publicly available code ipole github.com/moscibrodzka/ipole described in Mościbrodzka & Gammie (2018).
References
- Beckwith, K., Hawley, J. F., & Krolik, J. H. 2008, ApJ, 678, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Königl, A. 1979, ApJ, 232, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Boccardi, B., Krichbaum, T. P., Ros, E., & Zensus, J. A. 2017, A&ARv, 25, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Dexter, J., Markoff, S., Rao, R., & Plambeck, R. L. 2017, ApJ, 843, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Broderick, A., Dexter, J., et al. 2018, ApJ, 868, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Connors, R. M. T., Markoff, S., Nowak, M. A., et al. 2017, MNRAS, 466, 4121 [NASA ADS] [Google Scholar]
- Dexter, J. 2016, MNRAS, 462, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Dinçer, T., Bailyn, C. D., Miller-Jones, J. C. A., Buxton, M., & MacDonald, R. K. D. 2018, ApJ, 852, 4 [NASA ADS] [Google Scholar]
- Gammie, C. F., & Leung, P. K. 2012, ApJ, 752, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Gold, R., McKinney, J. C., Johnson, M. D., & Doeleman, S. S. 2017, ApJ, 837, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Hada, K., Kino, M., Doi, A., et al. 2013, ApJ, 775, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Hada, K., Kino, M., Doi, A., et al. 2016, ApJ, 817, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, D. C., & Wardle, J. F. C. 1999, AJ, 118, 1942 [NASA ADS] [CrossRef] [Google Scholar]
- Hovatta, T., O’Sullivan, S., Martí-Vidal, I., Savolainen, T., & Tchekhovskoy, A. 2019, A&A, 623, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J. A., Henriksen, R. N., Weżgowiec, M., et al. 2018, MNRAS, 476, 5057 [Google Scholar]
- Jiménez-Rosales, A., & Dexter, J. 2018, MNRAS [Google Scholar]
- Johnson, M. D., Fish, V. L., Doeleman, S. S., et al. 2015, Science, 350, 1242 [NASA ADS] [CrossRef] [Google Scholar]
- Kuo, C. Y., Asada, K., Rao, R., et al. 2014, ApJ, 783, L33 [NASA ADS] [CrossRef] [Google Scholar]
- MacDonald, N. R., & Marscher, A. P. 2018, ApJ, 862, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Mościbrodzka, M., & Falcke, H. 2013, A&A, 559, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mościbrodzka, M., & Gammie, C. F. 2018, MNRAS, 475, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Mościbrodzka, M., Falcke, H., Shiokawa, H., & Gammie, C. F. 2014, A&A, 570, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mościbrodzka, M., Falcke, H., & Shiokawa, H. 2016, A&A, 586, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mościbrodzka, M., Dexter, J., Davelaar, J., & Falcke, H. 2017, MNRAS, 468, 2214 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz, D. J., Marrone, D. P., Moran, J. M., & Rao, R. 2012, ApJ, 745, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Nagar, N. M., Falcke, H., Wilson, A. S., & Ho, L. C. 2000, ApJ, 542, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Plambeck, R. L., Bower, G. C., Rao, R., et al. 2014, ApJ, 797, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Russell, D. M., Shahbaz, T., Lewis, F., & Gallo, E. 2016, MNRAS, 463, 2680 [NASA ADS] [CrossRef] [Google Scholar]
- Shcherbakov, R. V. 2008, ApJ, 688, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Shcherbakov, R. V., Penna, R. F., & McKinney, J. C. 2012, ApJ, 755, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Wardle, J. F. C., & Homan, D. C. 2003, Ap&SS, 288, 143 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Tests of the numerical integrator
The PRT integrator that solves Eq. (1) is tested in Minkowski space-time. Two simple tests assume that the light propagating media (plasma) are uniform in space and time. In the first test we set jIQ ≠ 0 and αIQ ≠ 0, while the other transfer coefficients are set to zero. In the second test, we set jQUV ≠ 0, ρQV ≠ 0, while other transfer coefficients are set to zero. In both test cases the PRT has an analytic solution in a simple functional form (see Dexter 2016) to which our numerical solutions are to be compared.
Figure A.1 shows the results of the tests and difference between the numerical and analytic solution. As can be seen from the figure, the numerical models and the analytical solutions are in excellent agreement (the equations are integrated with significantly better than single precision accuracy). This demonstrates that our numerical scheme is working correctly as the solutions are stable for small and large optical and Faraday depths for long integration paths Here, the integration of the transfer equation is carried out over a distance 10 times larger than used in the original tests in Dexter (2016).
 |
Fig. A.1. Tests of the numerical scheme demonstrating the performance of the numerical scheme. PRT solutions are stable and accurate (better than single precession accuracy). In test 1, Stokes I and Q are smooth functions of λ. In test 2, Stokes Q, U, and V show oscillatory behavior due to non-zero emissivity in Stokes U and a non-zero Faraday rotation coefficient. The errors in test 2 also show that the oscillation amplitudes, as expected, grow with x. |
All Figures
 |
Fig. 1. Schematic diagram of the model geometry. The coordinate system (x, y, z) is that in which the PRT equations are integrated. The symbols have the following meanings: k is the spatial component of the wavevector, B is the three-vector of the magnetic field, u is the spatial component of the plasma bulk four-velocity, θ is the angle between the x-axis and the B-field vector measured in the frame of the adopted coordinate system; it has different values when measured in the rest-frame co-moving with the plasma. Finally, the coordinate system (x0, y0, x0) is the frame in which the Stokes parameters are observed. |
| In the text | |
 |
Fig. 2. Left panel: spectral energy distribution of the Stokes parameters (I, Q, U, V, where I ≡ Iν is the specific intensity in cgs units [ergs s−1 cm−2 ster−1 Hz−1]) computed with the static background jet model described in Sect. 3.1 and the corresponding fractional linear and circular polarizations. Middle panel: same as the left panel, but assuming no emission/absorption in Stokes V (jV = aV = 0). Right panel: same as the left panel, but assuming no Faraday conversion (ρQ = 0). The flux in Stokes V (left panel) in the optically thick part of the spectrum is mainly produced by Faraday conversion. In the optically thin part of SED, Stokes V is due to intrinsic emission. In this jet model the spectra of fractional linear and circular polarization have steep and nearly flat spectral slope, respectively. When the values of Q, U, and V are negative, −Q, −U, and −V are plotted here. |
| In the text | |
 |
Fig. 3. Changes in polarimetric quantities along the integration path in the static background jet component model. The calculations are performed for photons at ν = 230 GHz, which corresponds to τ ≈ 1 in the SED plot (left panel of Fig. 2). Shown are the following quantities: panel a: Stokes I (where I ≡ Iν is the specific intensity in cgs units [ergss−1 cm−2ster−1Hz−1]); panel b: optical and Faraday depths (τabs and τF), where τF = ∫ρVdl; panel c: fractional linear and circular polarization (FLP and FCP), where |
| In the text | |
 |
Fig. 4. Light curves of the Stokes parameters and the secondary polarimetric quantities computed with a dense plasmoid (Model A: left column) and with a hot plasmoid component (Model B: right column) moving along with the background flow (see Sect. 3.2 for the model descriptions). In both models the plasmoid is injected into the computational domain at t ≈ 4.2Tunit and it reaches the position where we make a measurement at t ≈ 31.3Tunit. The four upper panels show the model light curves of the Stokes parameters (I, Q, U, V), and the four lower panels show the corresponding time evolution of the optical and Faraday depths (τabs and τF: fifth row), the fractional linear and circular polarizations (FLP and FCP: sixth row), the rotation measure (RM: seventh row), and the electric vector position angle (EVPA; eighth row). The Stokes parameters and EVPA are computed at the two frequencies (ν = 225 GHz and 241 GHz). The other polarimetric quantities are computed around the synchrotron peak frequency (Fig. 2). In the plot for RM, the maximum possible RM value (π/Δλ2) is the maximum RM that can be resolved within the chosen frequency range. |
| In the text | |
 |
Fig. A.1. Tests of the numerical scheme demonstrating the performance of the numerical scheme. PRT solutions are stable and accurate (better than single precession accuracy). In test 1, Stokes I and Q are smooth functions of λ. In test 2, Stokes Q, U, and V show oscillatory behavior due to non-zero emissivity in Stokes U and a non-zero Faraday rotation coefficient. The errors in test 2 also show that the oscillation amplitudes, as expected, grow with x. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.