© J. Vos et al. 2022

1. Introduction

The supermassive black hole (SMBH) at the center of the Milky Way, Sagittarius A* (hereafter Sgr A*), is surrounded by a radiatevely inefficient accretion flow (RIAF) with bolometric luminosity at a strongly sub-Eddington level (L_bol ≈ 10⁻¹⁰ L_Edd, where L_Edd is the Eddington luminosity; for reviews of Sgr A* observational properties see, e.g., Genzel et al. 2010; Morris et al. 2012). The environment surrounding the SMBH emits photons across the entire electromagnetic spectrum from radio to γ−rays, but the source spectral energy distribution peaks in the millimeter band. The millimeter band emission is dominated by the synchrotron process occurring in the immediate vicinity of the SMBH (e.g., Narayan et al. 1995; EHTC et al. 2022a,d). Sagittarius A* is known to display flaring behavior on the top of the base “quiescent” stochastic variability. During these flaring events, observed on a daily basis, the signal can increase by up to ∼100 times the mean quiescent flux density in the near-infrared (NIR; e.g., Dodds-Eden et al. 2009; Witzel et al. 2018, 2021) and X-ray (e.g., Porquet et al. 2008; Nowak et al. 2012; Do et al. 2019). The flux density is much larger at millimeter to radio wavelengths than the mean NIR and X-ray values, and displays only marginal flaring behavior (e.g., EHTC et al. 2022b; Wielgus et al. 2022a). This apparent discrepancy is attributed to effects associated with particle heating and acceleration occurring near the SMBH, but the details of such flaring sites, such as their location, geometry, magnetization, and evolution, are currently not well understood (Witzel et al. 2018, and references therein).

One of the proposed models for explaining the flaring activity of Sgr A* is the formation of plasmoids¹ near the black hole (BH) event horizon. The term “plasmoid” is broadly used, but we employ the term to describe a “localized energized accretion flow feature.” These bright blob-like features are also referred to as “hot spots” or “bright spots.” Such a scenario has been adopted to explain NIR flares observed using the GRAVITY instrument (GRAVITY Collaboration 2018, 2020) and polarimetric variability at millimeter wavelengths (Wielgus et al. 2022b) observed with the Atacama Large Millimeter/submillimeter Array (ALMA).

It is still largely unknown how a plasmoid would observationally manifest itself at millimeter wavelengths. With the Event Horizon Telescope (EHT; EHTC et al. 2019a,b), it has recently become possible to reach a sufficient angular resolution to image event horizon scale features of Sgr A*, both in total intensity (EHTC et al. 2022a,c) and in linear polarization (so far only published for the M87* SMBH; EHTC et al. 2021a,b). While no unambiguous trace of orbiting hot spots in the EHT images of Sgr A* has been published as yet, we turn to investigating their impact on millimeter light curves. In particular, Sgr A*’s linear polarization observations (during flares) in both the NIR and millimeter bands display similar looping behavior in the Stokes 𝒬 − 𝒰 diagrams (Marrone 2006; GRAVITY Collaboration 2020; Wielgus et al. 2022b), suggesting that the flaring events should manifest themselves in the millimeter band light curves of the unresolved compact source. Additionally, in the millimeter band, we observe persistent net circular polarization (Stokes 𝒱) of the Sgr A* light curves at the level of ∼ − 1% (Muñoz et al. 2012; Goddi et al. 2021; Wielgus et al. 2022b). Circular polarization measurements obtained during a 𝒬 − 𝒰 loop may help us to further constrain the physics of the flares.

On the theoretical front, there has been a significant effort to model Sgr A* flares with plasmoids. Plasmoid emission or their formation are currently modeled using a few distinct approaches: (i) semi-analytic geometric models (Gelles et al. 2021), (ii) semi-analytic accretion flow models with a Gaussian fluctuation in it (Broderick & Loeb 2005, 2006; GRAVITY Collaboration 2020), (iii) general relativistic magnetohydrodynamic (MHD/GRMHD) simulations (see, e.g., Murphy et al. 2013; Ripperda et al. 2020, 2022), and (iv) general relativistic particle-in-cell (PIC/GRPIC) simulations (see, e.g., Cerutti et al. 2014; Sironi et al. 2016; Crinquand et al. 2021). The approaches (ii), (iii), and (iv) include all general relativistic effects. Approaches (i) and (ii) focus on predicting radiative properties of plasmoids; approaches (iii) and (iv) mostly aim at following plasmoid formation and dynamics. In approaches (iii) and (iv), plasmoids are associated with magnetic reconnection events that heat the plasma (e.g., Rowan et al. 2017). Under certain conditions the reconnection current sheets break into a chain of plasmoids that then grow by merging with other plasmoids and evolve further (Loureiro et al. 2012). Plasmoids may therefore observationally appear as hot spots.

The main advantage of semi-analytic models of plasmoids (approaches (i) and (ii)) is that their observational appearance can be accurately predicted using first-principle radiative transfer calculations. The first semi-analytical radiative models of plasmoid were developed in Broderick & Loeb (2005), where the authors investigated the total intensity and polarized light curves and images of an optically thick sphere that orbits the BH in the equatorial plane. In Broderick & Loeb (2006), the previous models are expanded by adding a RIAF background emission and a different underlying magnetic field. Other notable papers that discuss radiation from (semi-analytical) Gaussian structures include: Hamaus et al. (2009), Zamaninasab et al. (2010), Broderick et al. (2011a,b), Pu et al. (2016), Tiede et al. (2020). Another class of these models discusses the hot spot’s formation and evolution along the jet of the BH (Younsi & Wu 2015; Ball et al. 2021).

The main focus of this work is to investigate the Stokes ℐ, 𝒬, 𝒰, and 𝒱 properties of the semi-analytic Kerr BH RIAF + hot spot model, and their dependence on the model parameters, particularly the magnetic field topology. We argue that the polarimetric features introduced by an equatorially orbiting hot spot, in addition to a RIAF background, are indicative of the underlying magnetic field geometry and spacetime. More specifically, we demonstrate the utility of Stokes 𝒬 − 𝒰 diagrams (first shown in Marrone 2006; also discussed in GRAVITY Collaboration 2020; Gelles et al. 2021) for differentiating between a wide variety of simulated scenarios that can help constrain BH spin, inclination, and orbital velocity of the entire system. Additionally, we discuss how circular polarization from orbiting plasmoids can help differentiate between dominant magnetic field geometries. While the NIR emission is well explained by an orbiting hot spot alone, the millimeter emission is expected to be dominated by the accretion disk background. The interplay between the background and the orbiting hot spot is another problem of interest that is investigated in this work.

Our work is motivated by the new full Stokes, high-sensitivity millimeter light curve datasets available for Sgr A* (Wielgus et al. 2022a,b), and in particular by the identification of orbiting hot spot signatures in ALMA 230 GHz observations (Wielgus et al. 2022b). The paper is structured as follows. We describe our model and its parameters in Sect. 2. In Sect. 3 we report the polarimetric properties of hot spots as a function of the model’s free parameters. We focus on discussing polarimetric light curves, the 𝒬 − 𝒰 loops, and circular polarization. We discuss our results and compare them to previous works in Sect. 4. Finally, we summarize our main findings and conclude in Sect. 5.

2. Model

2.1. Numerical setup

Our semi-analytic model of the accretion flow with an orbiting bright spot around a Kerr BH is built within ipole - a ray-tracing code for covariant general relativistic transport of polarized light in curved spacetimes. A detailed description of the numerical scheme is presented by Mościbrodzka & Gammie (2018). The radiative transfer model requires defining the underlying plasma density, electron temperature, and magnetic field strength and geometry to calculate thermal synchrotron emission. Given a plasma configuration, ipole generates maps of Stokes ℐ, 𝒬, 𝒰, and 𝒱 at chosen observing frequencies, including emission, self-absorption, and Faraday effects (rotation and conversion). In this work, we limit ourselves to modeling thermal synchrotron emission at 230 GHz (λ = 1.3 mm, i.e., millimeter band) with a standard image resolution of 256 × 256 (pixels). The images are pixel integrated to generate light curves. The radiative transfer model takes into account the finite speed of light, which indicates a “slow light” approach.

All calculations are carried out using the Kerr metric described by the Kerr-Schild coordinate system (t, r, θ, ϕ) (which is well-described in, e.g., McKinney & Gammie 2004) with the standard metric signature (- + + +). In the following sections, we measure distances in units of gravitational radii (r_g = GM/c², where G and c are the gravitational constant and the speed of light, respectively). Time is measured in units of r_g/c.

2.2. Background accretion flow

Our background accretion flow model is inspired by a radiatively inefficient accretion disk presented in Broderick & Loeb (2006; see also Fraga-Encinas et al. 2016). At the equator, we assume that the accretion flow around the Kerr BH is Keplerian. The dimensionless BH spin parameter is defined as a_* ≡ Jc/GM², where J is the BH angular momentum. In this work, we consider a_* = 0, ±0.5, ±0.9375. The various quantities describing the disk properties, with the subscript b for background, are denoted by:

$$\begin{array}{cc}& n_{e,b}=n_0{\left(\frac{r}{r_g}\right)}^{-3/2}exp(-\frac{{cos}^2(\theta )}{2{\sigma }^2}),\hfill \end{array}$$(1)

$$\begin{array}{cc}\hfill & {\mathrm{\Theta }}_{e,b}={\mathrm{\Theta }}_0{\left(\frac{r}{r_g}\right)}^{-0.84},\hfill \end{array}$$(2)

$$\begin{array}{cc}\hfill & B=B_0{\left(\frac{r}{r_g}\right)}^{-1}.\hfill \end{array}$$(3)

Here, n_e is the electron density, Θ_e ≡ k_BT_e/m_ec² is the dimensionless electron temperature, B is the magnetic field strength, and σ parameter characterizes the accretion disk vertical thickness.

All user-defined scaling factors and variables (including n₀ and Θ₀) are listed in Table 1. It should be noted that we do not fit these parameters to any existing observations of Sgr A* in this work, because the source is variable and our static background model is not. Nevertheless, we gauge the model parameters so that the radial, i = 30° case approximately matches the observed flux density of Sgr A* at 230 GHz, which is ∼2.5 Jy (Johnson et al. 2015; Bower et al. 2019; Wielgus et al. 2022a).

The electron density n_e is set to a small value for radii smaller than the innermost stable circular orbit (ISCO, see Bardeen et al. 1972). Therefore, emission from within this region is minimal, except from the photon ring in certain configurations. Additionally, as the ISCO is an spin-dependent quantity (see Table 2) that becomes smaller for increasing a_*, we find that the overall n_e, b is higher for the positive spin cases. Therefore, as the spot’s n_e, s (see next subsection) is unchanged for all cases, the background emission is more pronounced in the cases of positive spin (a_* > 0) than in the cases of negative spin (a_* < 0).

We investigate three basic magnetic field topologies denoted simply as radial, toroidal, and vertical. In purely poloidal cases (radial and vertical topology), the magnetic fields, in a given coordinate frame, are described with the azimuthal component of the vector potential. For the radial (monopolar) magnetic field this is

$$\begin{array}{c}\hfill A_{\varphi }=1-cos(\theta ),\end{array}$$(4)

and for the vertical magnetic field this is

$$\begin{array}{c}\hfill A_{\varphi }=rsin(\theta ).\end{array}$$(5)

While the magnetic fields of the former cases are defined through the vector potential, the toroidal magnetic field is straightforwardly defined by

$$\begin{array}{c}\hfill B_{\varphi }=1.\end{array}$$(6)

2.3. Orbiting spot

In addition to the background, we introduce a spot in a circular orbit in the equatorial plane at a fixed distance to the SMBH. The spot’s location is denoted, in Kerr-Schild coordinates (t, r, θ, ϕ), by:

$$\begin{array}{cc}& x_s^0=t,\hfill \end{array}$$(7)

$$\begin{array}{cc}\hfill & x_s^1=r_{\text{spot}}=11r_{\text{g}},\hfill \end{array}$$(8)

$$\begin{array}{cc}\hfill & x_s^2={\theta }_{\text{spot}}=\pi /2,\hfill \end{array}$$(9)

$$\begin{array}{cc}\hfill & x_s^3={\varphi }_{\text{spot}}=2\pi t/P.\hfill \end{array}$$(10)

Here, t is the time coordinate along the null-geodesic, which implies that the spot’s position is not fixed as a light ray moves through it. The radius at which the spot orbits, r_spot, is fixed for the majority of this work. Only the ϕ_spot coordinate changes over time and is determined by the orbital period P (see Table 2). We typically assume Keplerian rotation, that is

$$\begin{array}{c}\hfill P=2\pi (r^{3/2}+a_{\ast })[r_{\mathrm{g}}/c],\end{array}$$(11)

and that the spot corotates with the background RIAF. For observers with viewing angles i < 90° (i > 90°), the spot orbits the SMBH counterclockwise (clockwise).

Our implementation of a bright spot can be thought of as an overdensity with a higher temperature, which effectively makes the spot brighter than the background emission. The spot’s electron density n_e, s and dimensionless electron temperature Θ_e, s are defined as:

$$\begin{array}{cc}& n_{e,s}=\frac{n_0}{3}exp(-\frac{\mathrm{\Delta }{x}^k\mathrm{\Delta }{x}_k}{2R_s^2}),\hfill \end{array}$$(12)

$$\begin{array}{cc}\hfill & {\mathrm{\Theta }}_{e,s}={\mathrm{\Theta }}_0{\left(\frac{r}{r_g}\right)}^{-0.84}exp(-\frac{\mathrm{\Delta }{x}^k\mathrm{\Delta }{x}_k}{2R_s^2}),\hfill \end{array}$$(13)

where $\mathrm{\Delta }{x}^k\equiv x^k-x_s^k$, with k ∈ {1, 2, 3}, is the Euclidean distance from the spot center ($x_s^k$) to the photon (on the null-geodesic), which eventually falls on the camera. We note that in our model, the spot continues its orbit while the radiative transfer equations are evolved (also known as “slow light”). The entire, disk + spot, system is then simply described by:

$$\begin{array}{cc}& n_e=n_{e,b}+n_{e,s},\hfill \end{array}$$(14)

$$\begin{array}{cc}\hfill & {\mathrm{\Theta }}_e={\mathrm{\Theta }}_{e,b}+{\mathrm{\Theta }}_{e,s}.\hfill \end{array}$$(15)

The characteristic radius of the Gaussian hot spot is fixed to R_s = 1.5 r_g, which makes it consistent with the assumptions of Broderick & Loeb (2005, 2006). Additionally, we enforce a sharp spot boundary by only including matter if n_e, s > 10⁵ cm⁻³. Compared with plasmoids formed in recent GRMHD studies (Ripperda et al. 2020; Bransgrove et al. 2021), our spot’s size is large but still possible. On the other hand, simulations of Ripperda et al. (2022) indicate the formation of flux tubes that could manifest as observable orbiting hot spots, and are generally larger than the size that we assume.

3. Results

3.1. Definitions

In the following subsections, we present results in terms of net fractional linear (LP) and net fractional circular polarization (CP), which are defined as:

$$\begin{array}{cc}& \text{LP}=\frac{\sqrt{{(\sum _i{\mathcal{Q}}_i)}^2+{(\sum _i{\mathcal{U}}_i)}^2}}{{\sum }_i{\mathcal{I}}_i},\hfill \end{array}$$(16)

$$\begin{array}{cc}\hfill & \text{CP}=\frac{{\sum }_i{\mathcal{V}}_i}{{\sum }_i{\mathcal{I}}_i},\hfill \end{array}$$(17)

where ℐ, 𝒬, 𝒰, and 𝒱 are the Stokes parameters, and the sums (∑_i) are over image pixels. We also define:

$$\begin{array}{cc}& \stackrel{\sim }{\text{LP}}=\frac{\sqrt{{\mathcal{Q}}^2+{\mathcal{U}}^2}}{\mathcal{I}},\hfill \end{array}$$(18)

$$\begin{array}{cc}\hfill & \stackrel{\sim }{\text{CP}}=\frac{\mathcal{V}}{\mathcal{I}},\hfill \end{array}$$(19)

where $\stackrel{\sim }{\mathrm{LP}}$ and $\stackrel{\sim }{\mathrm{CP}}$ denote the linear and circular polarization per pixel. Additionally, we often discuss the net Stokes parameters’ behavior, which are denoted as: F_ν = ∑_iℐ_i, U = ∑_i𝒰_i, Q = ∑_i𝒬_i, and V = ∑_i𝒱_i. The net electric vector position angle (EVPA) is defined as:

$$\begin{array}{c}\hfill \text{EVPA}=\frac{1}{2}\arg {\displaystyle (\sum _i{\mathcal{Q}}_i+j\sum _i{\mathcal{U}}_i)},\end{array}$$(20)

where j is the imaginary unit and EVPA ∈ ( − 90° ,90° ]. The EVPA is measured east of north on the sky. Therefore, increasing the EVPA indicates counterclockwise rotation of the EVPA. Also, EVPA = 0° translates into the polarization tick being aligned with the north-south direction and EVPA = ±90° with the east-west direction in the sky (or image).

In the following subsections, we outline distinguishing features for the suite of models. To characterize the spot’s position in the image (over time), and thereby the behavior of ℐ, 𝒬, 𝒰, 𝒱, we introduce the concept of a location angle ζ. This angle is a simple aiding quantity to specify the spot’s location in the image (and therefore does not outline the geometrical location of the spot in Kerr-Schild coordinates). For a face-on view of the system (i = 0°), ζ is equal to ϕ_spot, but this is not the case for other inclination angles. From this viewing angle, the spot’s (counterclockwise) orbit describes a circle. Then, ζ = 0° corresponds to the spot being in the topmost position and ζ = 180° to the spot being in the bottommost position. ζ = 90° and ζ = 270° correspond to the spot being in leftmost and rightmost positions, respectively.

3.2. Static background emission: Stokes ℐ and polarization

The left panels of Fig. 1 display images of the background emission of the zero-spin (a_* = 0) model for the three different magnetic field configurations as seen from an edge-on viewing angle (i = 90°). For this viewing angle, the radial and vertical flux density F_ν structure is similar – a bright (relativistically beamed) left side of the disk, a faint (relativistically debeamed) right side of the disk, and a faint lensed ring surrounding the BH shadow. We notice that the photon ring around the central BH shadow is only weakly visible in the Stokes ℐ maps. Total intensity images are similar for different magnetic field geometries, although the radial and vertical cases look slightly different to the toroidal case.

Fig. 1. Edge-on view (i = 90°) of the disk background in the radial (top row), toroidal (middle row), and vertical (bottom row) magnetic field configurations for a field of view of 40 rg × 40 rg. Left panel: displays the zero-spin cases (a* = 0), while the right panel gives an overview of the other spin-cases. The white ticks, plotted over the Stokes ℐ maps, denote the EVPA scaled according to the linearly polarized flux ($\sqrt{{\mathcal{Q}}^2+{\mathcal{U}}^2}$).

Linear polarization carries information about the magnetic field topology. Generally, for all magnetic field topologies, $\stackrel{\sim }{\mathrm{LP}}$ is lowest for the brightest (beamed) region and highest for the diffuse halo. The toroidal case differs substantially from the others as it has two lower $\stackrel{\sim }{\mathrm{LP}}$ (of ∼50%) lobes above and below the equatorial plane. This behavior is specific to this particular case and is not recovered for other configurations based on inclination or otherwise. For the radial and vertical cases, the higher flux density regions are less polarized (60%–65%). Polarization ticks in the total intensity maps show the direction of the linear polarization vector (𝒬, 𝒰). These are different for different magnetic field geometries.

For $\stackrel{\sim }{\mathrm{CP}}$, the structural differences based on magnetic field configuration are even more substantial and they reflect the underlying magnetic field polarity (as we have checked that in our models, most of the $\stackrel{\sim }{\mathrm{CP}}$ is produced intrinsically rather then via the Faraday conversion process). The radial case $\stackrel{\sim }{\mathrm{CP}}$ image is predominantly negatively circularly polarized with positive polarization in the Doppler beamed part of the image where the sign (handedness) of the $\stackrel{\sim }{\mathrm{CP}}$ is due to the arbitrarily assumed magnetic field polarity (the inversion of the B sign produces the opposite polarity of $\stackrel{\sim }{\mathrm{CP}}$ maps). In the toroidal case, the $\stackrel{\sim }{\mathrm{CP}}$ map is positive on the Doppler beamed side and negative elsewhere. The vertical case displays a positive $\stackrel{\sim }{\mathrm{CP}}$ for the top half and a negative $\stackrel{\sim }{\mathrm{CP}}$ for the lower half, resulting in null total CP, as expected. We notice that in all cases, the magnitude of the $\stackrel{\sim }{\mathrm{CP}}$ is much lower when compared to the $\stackrel{\sim }{\text{LP}}$.

The photon ring (and emission from its direct vicinity) is another feature that differs per magnetic field case. Overall, the photon ring is expected to be relatively less linearly polarized than other regions due to a combinations of plasma (i.e., absorption and Faraday rotation) and gravitational effects, which are further elaborated in Jiménez-Rosales et al. (2021). However, since photon rings are not the main topic of this paper, we discuss the linear and circular polarization of the photon ring for different magnetic field geometries in Appendix B.

The right panels of Fig. 1 display the model background emission for rotating BHs for an edge-on view with a_* = ±0.5, ±0.9375. There, we find that both the flux density and linear polarization change significantly when the BH spin becomes negative. The cases with negative spin (a_* = −0.5, −0.9375) have a higher $\stackrel{\sim }{\text{LP}}$ (and LP) than those with positive spin (a_* = 0.5, 0.9375) for all magnetic field configurations. This is explained by the increased contribution of relativistic beaming (to the flux) and the higher electron densities, especially in the inner regions, for the positive spin cases. As we set the electron density to a floor value for radii smaller than the ISCO, the emission from this region is small. Additionally, the emission from these inner regions experience more Doppler boosting as the (Keplerian) orbital velocity is greater close to the BH. This explains why the Stokes ℐ maps of these (a_* = 0.5, 0.9375) cases are dominated by a relatively small emission region. Why the cases of negative spin (a_* = −0.5, −0.9375) have a bigger emission structure is explained with the same arguments, namely the relatively lower densities and lower orbital velocities at these radii result in an emission structure that is more diffuse and not dominated by a singular (strongly beamed) feature. For a fixed magnetic field configuration, changing the BH spin from positive to negative produces a significantly different $\stackrel{\sim }{\text{LP}}$ map. Importantly, two observables remain weakly affected by the BH spin value and sign: the EVPA orientation and the $\stackrel{\sim }{\mathrm{CP}}$ structure.

Figure 2 shows images of the zero-spin (a_* = 0) models as a function of the viewing angle. Starting with i = 0°, the total intensity maps show background disk emission where the inner edge corresponds to the ISCO and the photon ring is located around the BH shadow. As the viewing angle increases, a characteristic brightness depression appears in the upper left of the flux density maps for the vertical case. This “hollow” region is present for viewing angles that are considered, broadly speaking, to be face-on (0° < i ≲ 45°) and is due to relativistic aberration, which facilities the alignment of the wave vector k with the magnetic field vector B and effectively results in the suppression of the synchrotron emissivity (that is ∝k × B, see Eq. (12) in Narayan et al. 2021) as measured in the comoving fluid frame. This effect will be critical when describing the variability of the models (presented in Sect. 3.3).

Fig. 2. Stokes ℐ and polarimetric images of the background accretion flow as a function of the observer’s viewing angle i and magnetic field topology. The left panel corresponds to i = 0° while i = 20°, 40°, 60°, and 80° are shown in the right panel. Total intensity and polarimetric maps are displayed in the same fashion as in Fig. 1.

In Fig. 2 the $\stackrel{\sim }{\text{LP}}$ at i = 0° varies per magnetic field configurations. The EVPAs form distinct patterns: for radial fields the polarization ticks are purely azimuthal, for toroidal fields they are purely radial, and for vertical field, the ticks are nearly azimuthal. This is consistent with previous predictions (EHTC et al. 2021c). Such EVPA patterns are determined by the relative orientation of the electromagnetic wave vector k and magnetic field vector B, and relativistic aberration (as part of the relativistic beaming effect) that affects this orientation. This is explained by and in agreement with Narayan et al. (2021). For the face-on viewing angle(s), the circular polarization of the radial field configuration is similar to the vertical one, with positively polarized disk emission and photon ring emission with opposite polarization. The radial and vertical $\stackrel{\sim }{\mathrm{CP}}$ maps are similar because both of these fields have a poloidal component that is visible at this viewing angle. The toroidal field model, on the other hand, has a $\stackrel{\sim }{\mathrm{CP}}$ that is entirely negative. For small viewing angles (up to about i ≤ 30°), the polarimetric properties of the background emission are similar to the properties of models viewed face-on. For i > 30°, the $\stackrel{\sim }{\text{LP}}$ and $\stackrel{\sim }{\mathrm{CP}}$ maps become more complex. For the vertical magnetic field models, it is important to note that when $\stackrel{\sim }{\mathrm{CP}}$ is produced intrinsically, there is a degeneracy between inverting the viewing angle (from i = 30° to i = 150°, for example) and reversal of the polarity of the field. We extensively comment on this in Appendix B.

We conclude that while the background emission EVPA and $\stackrel{\sim }{\mathrm{CP}}$ depend more on the observer’s viewing angle than the BH spin, the background emission $\stackrel{\sim }{\text{LP}}$ is strongly dependent on both the viewing angle and the BH spin. This gives us a hint as to what polarimetric properties of the bright spot emission may be more geometry (viewing angle and magnetic field) dependent and less dependent on the model details.

3.3. Variable emission: Stokes ℐ

Before we discuss the polarimetric findings for an orbiting spot, we outline a number of characteristic features that appear in Stokes ℐ. We discuss in more detail two cases with an edge-on viewing angle and a nearly face-on viewing angle.

In Fig. 3, in the left panels, we show model images with a_* = 0 and all three magnetic field configurations for an edge-on viewing angle (i = 90°). These images are naturally paired with the light curves shown in the right panels in Fig. 3. Our full (background plus spot) model describes a periodic system, and thus the light curves can be arbitrarily shifted. Therefore, we align the light curves in such a way that the spot’s position is similar between different magnetic field cases. The maximum flux density in the light curve, shown in Fig. 3, always corresponds to the formation of an “Einstein ring”-like image at edge-on viewing angles. Then, as the Einstein ring disappears, we perceive a decrease in flux density. This decrease is slight for the radial case, more substantial for the vertical case, and significant for the toroidal case. After this decrease, the flux density increases again as the spot moves in view and is relativistically beamed (or Doppler boosted) toward the observer. The recovery of the flux density is also highly dependent on the magnetic field geometry. The second peak of the radial case almost reaches the level of the first maximum. For the vertical case, we see that the second peak recovers to about half of the first maximum amplitude. The toroidal case only increases to a third of the first maximum. These “recoveries” are all quantified with respect to the corresponding curves’ minimum.

Fig. 3. Stokes ℐ and polarimetric images, as well as image-integrated quantities of the full (disk + spot) models. Left panels: edge-on views (i = 90°) of the non-spinning (a* = 0) model in radial (top), toroidal (middle), and vertical (bottom) magnetic configurations for a field of view of 40 rg × 40 rg. The rows, within each panel, display Stokes ℐ, $\stackrel{\sim }{\mathrm{LP}}$, and $\stackrel{\sim }{\mathrm{CP}}$ at times t = 25, 50, 75, and 100 rg/c. The EVPA orientation is represented with white ticks on top of the Stokes ℐ panels. Their length is determined by the linearly polarized flux strength ($\sqrt{{\mathcal{Q}}^2+{\mathcal{U}}^2}$). Right panels: comparison of the evolution of the flux density Fν (top), LP (middle), and CP (bottom) over time for radial (solid), toroidal (dashed), and vertical (dotted) magnetic fields. Here, we additionally plot light curves for BHs with a* ≠ 0 (different BH spins are color coded).

Figure 4 shows the same models as in Fig. 3 but for the nearly face-on viewing angle (i = 20°). Here the observer has an unobstructed view of the spot during the entire orbit. As the emission of the spot is not heavily distorted by strong gravitational lensing, we recover a simpler, single-peaked, structure in the light curve. The flux density maximum occurs when the spot’s emission is beamed toward the observer (at t ≈ 100 r_g/c or ζ ≈ 90°). However, contrary to the edge-on case, the vertical (i = 20°) case has a “minimum” at this point in the spot’s orbit, where the wave vector (k) and the magnetic field vector (B) are parallel to each other and the synchrotron emissivity emission becomes negligible.

Fig. 4. Same as for Fig. 3, except for the viewing angle, which is i = 20°, and showing maps corresponding to times t = 25, 75, 125, and 175 rg/c.

We find that the contribution of the variable component to the total intensity is affected by the BH spin. For the edge-on cases (in Fig. 3), we see that the contribution of the spot is largest for the a_* = −0.9375 case, with (up to) 50% being determined by the variable component, and smallest for the a_* = 0.9375 case, with only (up to) 25% being determined by the variable component. Since the orbital velocity increases as a_* decreases, the contribution of the spot increases as a result of relativistic beaming. Additionally, this difference in contribution to the total flux density is also partly explained by the r < r_ISCO cut we apply to the disk background. For the nearly face-on cases (in Fig. 4), the spot’s contribution to the total flux density is less dependent on spin and seems to be roughly 10%−20%. As the observer inclination no longer lines up with spot’s orbital plane, relativistic beaming is less strong than for the edge-on case. It also no longer has the first (greater) flux density peak, which corresponds to the occurrence of the Einstein ring.

3.4. Variable emission: Polarization

3.4.1. Polarimetric signatures of bright spots: 𝒬 − 𝒰 loops

The evolution of EVPA is best described using 𝒬 − 𝒰 diagrams. The looping structure in the 𝒰 versus 𝒬 diagram (or put simply as the “𝒬 − 𝒰 diagram”) is a hallmark signature of an orbiting hot spot (GRAVITY Collaboration 2018). However, one could argue that the (disk) background emission is equally important in shaping the loop structure and position in the 𝒬 − 𝒰 diagram. This is illustrated in Fig. 5, where we show 𝒬 − 𝒰 diagrams for both the spot-only and the full (disk+spot) configurations for radial (left panel), toroidal (middle panel), and vertical (right panel) magnetic fields. Without commenting yet on the loops’ finer substructures, we find that the spot-only loops are greater in size and broadly describe a circle for the radial and toroidal configurations, which are largely independent of the viewing angle. The vertical configuration is more dependent on the system’s inclination angle - only the i = 20° case shows the looping structure. The smaller size of the full configuration’s 𝒬 − 𝒰 loops is largely due to the compensation with the flux density F_ν. As was commented in Sect. 3.2, the spot-only configuration has much smaller flux densities than the full model. Surprisingly, there are clear structural differences between the spot-only and full model descriptions for the 𝒬/ℐ, 𝒰/ℐ loops, whereas this is not the case for the 𝒬 − 𝒰 loops (unnormalized diagrams where 𝒬 and 𝒰 are shown in units of Jansky). For the latter diagrams, which are currently not shown, we find an identical 𝒬 − 𝒰 structure for both the spot-only and full configurations but they are displaced from each other by an offset as a result of the disk background. Therefore, the clear differences in the 𝒬/ℐ,𝒰/ℐ diagrams (between the spot-only and full models) originate from the disk component that dominates the flux density (or Stokes ℐ), especially when the spot is receding from the observer. The (near) circular structure in the 𝒬/ℐ,𝒰/ℐ diagrams for the spot-only cases is an indication that the variations in ℐ, 𝒬, and 𝒰 are largely (but not perfectly) correlated. This circular symmetry for the radial and toroidal cases is mainly broken by relativistic beaming and partially broken by Faraday rotation – see Appendix A.

Fig. 5. Normalized 𝒬 − 𝒰 diagrams for the three basic magnetic field configurations and a BH spin of a* = 0. Both the spot-only (dotted lines) and full models’ (solid lines) 𝒬 − 𝒰 loops are shown for four viewing angles i = 20°, 40°, 60°, and 80°.

The properties of the 𝒬 − 𝒰 loops depend on a number of model parameters. However, before we describe how the 𝒬 − 𝒰 loops depend on them, we introduce metrics to quantitatively describe the loops. Figure 6 displays a schematic overview of the typical 𝒬 − 𝒰 loop structures that appears in our models. Similar to Wielgus et al. (2022b), we describe the loops (i.e., a pretzel-like shape) using two dimensionless metrics. Another, additional metric we consider (which Wielgus et al. 2022b does not) is the total area of the loop structure in the 𝒬 − 𝒰 space, S = S₁ + S₂. The first of the dimensionless metrics is the ratio of total loop area (S) to small loop area (S₁), which is denoted as $\overline{S}=S/S_1$. The last metric is the inner loop timing ratio $\overline{R}=P/(T_{\mathrm{exit}}^c-T_{\mathrm{enter}}^c)$. Here, the $T_{\text{enter}}^c$ is the time at which the 𝒬 − 𝒰 signature enters the inner loop and $T_{\text{exit}}^c$ is the time at which it exits the inner loop. Then, $\overline{R}$ gives the period P divided by the time spent within the inner loop.

Fig. 6. Schematic diagrams of normalized 𝒬 − 𝒰 loops of the full models (for i = 20°, a* = 0) with the radial, toroidal, and vertical magnetic field configurations in the left, middle, and right panels, respectively. The loop color encodes the model LP. The inner loop surface S1 (in pink) and rest of surface (excluding S1) enclosed by the entire 𝒬 − 𝒰 loop structure is denoted by S2 (in yellow). The total surface is S = S1 + S2, surface fraction is $\overline{S}=S/S_1$, and time spent in the inner loop with respect to the total period is $\overline{R}=P/(T_4^c-T_2^c)$ (similar to Wielgus et al. 2022b). The “+” symbol marks the normalized 𝒬 − 𝒰 value of the static background emission. All shown loops are traversed in the counterclockwise direction.

By inspecting Fig. 6, one finds that for radial and toroidal magnetic fields, the 𝒬 − 𝒰 signature follows the inner loop when the spot is receding from the observer (ζ = 180° to ζ = 360° = 0°). The 𝒬 − 𝒰 signature follows the outer loop as the spot approaches the observer (ζ = 0° to ζ = 180°). For the vertical magnetic field case, this behavior is quite the opposite. Broadly speaking, the vertical magnetic field’s 𝒬 − 𝒰 signature traverses the left half of the 𝒬 − 𝒰 loop, roughly the outer loop, for ζ ≈ 160° to 320°. There, generally speaking, the spot recedes with respect to the observer. Therefore, the right half of the 𝒬 − 𝒰 diagram, including the inner loop, corresponds to the approaching spot. The 𝒬 − 𝒰 signature follows the inner loop when the contribution of the spot (almost completely) disappears in the region where synchrotron emission is suppressed (as at T₃ we can only see a lensed image of the spot). The vertical cases that do not possess an inner 𝒬 − 𝒰 loop (for i ≳ 25°) are still affected by the emission suppression region. Then, the indentation (where the inner loop would have been) corresponds to the part of the spot’s orbit where the emission is suppressed (for i = 25°). When we look at Fig. 6, we find that for the vertical cases, only a relatively small part of the spot’s orbital period is spent inside the inner 𝒬 − 𝒰 loop when compared to toroidal and radial cases.

Next, we investigate the 𝒬 − 𝒰 loop characteristics, (using the metrics defined above) as a function of a few model parameters, such as magnetic field geometry, the observers’ viewing angle, radius of the spot, BH spin, and plasma parameters (we consider only small deviations from our fiducial values of density, temperature, and magnetic field strength). We summarize our main findings in the paragraphs below.

Viewing angle. Figure 7 shows that the dominant decider for the shape of 𝒬 − 𝒰 loops is the inclination angle of the system. For a face-on viewing angle (i = 0°), we only recover circle-shaped loops, regardless of the field configuration. We notice that for a single orbital period, this circle is traversed two times, which indicates that the inner and outer loops are still present but have the same size (corresponding to $\overline{S}=1$ and $\overline{R}=2$). We also notice that all our loops are traversed in the counterclockwise direction because the spot is orbiting counterclockwise on the sky (we only show results for viewing angles i > 90°). As the inclination i increases, the properties of the 𝒬 − 𝒰 loops strongly depend on the underlying magnetic field geometry. For the radial and toroidal cases, for increasing i, the inner loop starts to shrink, while the outer loop remains the same size. For the vertical cases, we find that the inner loop disappears already for i ≳ 25° (with the last inner loop structure being present at i ≈ 24° to be more exact). For radial and toroidal cases, the loop persists for all viewing angles, except the exact edge-on case. For all three magnetic field topologies, $\overline{S}$ increases with increasing viewing angle, but for the vertical field, the dependency is stronger. $\overline{R}$ can be used to discriminate radial and toroidal cases from vertical cases: $\overline{R}$ slowly decreases with i for radial and toroidal fields, while $\overline{R}$ increases with i for vertical field. The sharp increase in $\overline{R}$ as a function of i is related to the duration of the k × B suppression as a result of relativistic beaming, which is a strong function of viewing angle.

Fig. 7. Normalized 𝒬 − 𝒰 diagrams of the full model, colored according to their LP fraction as a function of increasing inclination i (panels from top to bottom). Each column corresponds to a different magnetic field configuration. All models have a* = 0. While for the vertical magnetic field, the 𝒬 − 𝒰 loops disappear for i ≳ 25°, for other field geometries, they are present for all viewing angles, except exact edge-on cases (see also Fig. 5). The bottom row shows the behavior of $\overline{S}$ (in blue) and $\overline{R}$ (in orange) as a function of inclination i. The observables S, $\overline{S}$, and $\overline{R}$ are explained in Fig. 6.

Spot orbital radius. Figure 8 displays the 𝒬 − 𝒰 loop structure as a function of the spot’s orbiting radius r_spot. The viewing angle and spin are fixed to 20° and a_* = 0, respectively. For the vertical case with r_spot ≤ 11 r_g, we still find an inner loop, but the inner loop decreases in size for increasing r_spot until it is no longer present, which becomes clear for r_spot = 15 r_g. For the radial and toroidal cases, we recover the double 𝒬 − 𝒰 loop structure for all r_spot values. Their total surface S increases till r_spot = 9 r_g, after which it decreases. 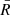$\overline{R}$ seems insensitive to variations in r_spot and $\overline{S}$ also varies minimally, except for r_spot = 6 r_g. This slight increase in $\overline{S}$ is likely related to cut-off at ISCO radius. The vertical magnetic field cases display a largely constant $\overline{R}$ for increasing r_spot, but $\overline{S}$ does increase with r_spot. This behavior has the same explanation as was stated in the previous paragraph, namely the orbital speed increases for decreasing r_spot.

Fig. 8. Normalized 𝒬 − 𝒰 diagrams colored according to their LP fraction. Each row corresponds to a different orbital radius rspot. The inclination and BH spin are set to i = 20° and a* = 0, respectively. The bottom row shows the behavior of $\overline{S}$ (in blue) and $\overline{R}$ (in orange) as a function of orbital radius rspot. The observables S, $\overline{S}$, and $\overline{R}$ are explained in Fig. 6.

Black hole spin. Figure 9 displays 𝒬 − 𝒰 loops and their properties as a function of BH spin. We find that the size of the 𝒬 − 𝒰 loop is greatest for the lowest spin (a_* = −0.9375). This behavior is a direct result of our model assumptions. We assume a low floor electron density n_e at radii below the ISCO. The contribution of the disk background therefore varies between spin cases, while the contribution of spot remains unaffected. Hence, the a_* = 0.9375 case has the largest disk background contribution, whereas the a_* = −0.9375 case has the lowest disk background contribution. This is an explanation for the increase in 𝒬 − 𝒰 loop size (S) with a decreasing spin parameter. The toroidal cases’ 𝒬 − 𝒰 loops are similar between the five spin cases. To a lesser extent, this can also be stated about the vertical cases. However, for the most positive (a_* = 0.9375) spin-case, we observe that the upper part of the loop is relatively larger with respect to the lower part. For the most negative (a_* = −0.9375) spin, this is the other way around but less pronounced. The other spin-cases (a_* = 0, ±0.5) display a clearer symmetry between the upper and lower halves of the loop.

Fig. 9. Normalized 𝒬 − 𝒰 diagrams colored according to their LP fraction. The inclination is set to i = 20°. Each row corresponds to a different BH spin parameter a*. The bottom row shows the behavior of $\overline{S}$ (in blue) and $\overline{R}$ (in orange) as a function of a*. The observables S, $\overline{S}$, and $\overline{R}$ are explained in Fig. 6.

We find that the total surface S increases when the spin decreases for all cases. For the radial and toroidal cases, we recover an almost constant $\overline{S}$ and $\overline{R}$, similar to what we saw in the previous paragraph (for r_spot). For the vertical case, we find that $\overline{R}$ is only a weak function of spin, but $\overline{S}$ is an exceptionally strong function of spin. Given the immutable nature of the 𝒬 − 𝒰 loop geometry and the strong dependence of $\overline{S}$ (and S) on spin, it would be possible to assess the BH spin a_* of the system for the vertical case (if the inclination is well constrained). For the radial and toroidal cases, this is less promising. However, the total surface S displays a stronger dependence on spin than it has shown for the other investigated quantities. We do recover near identical S between the radial and toroidal fields (as we have seen previously for other 𝒬 − 𝒰 figures).

Lastly, we discuss the radial cases in the left column of Fig. 9 in more detail. Each 𝒬 − 𝒰 loop has a point where one crosses from the inner to the outer loop. This point is henceforth referred to as the crossing point. For the radial cases, we find that the crossing point lies in the upper half of the 𝒬 − 𝒰 loop for the positive spin cases. However, as the spin decreases, the crossing point gradually moves toward the lower half of the 𝒬 − 𝒰 loop. This behavior is still present if we remove the background, which indicates that it is likely related to the underlying spacetime.

Spot size. Figure 10 displays the dependency of 𝒬 − 𝒰 loops on the spot size parameter R_s. Variations in R_s bring about significant changes especially in the 𝒬 − 𝒰 loop size, but not so much in the structure, except for the R_s = 3.0 r_g. It should be noted that the (𝒬/ℐ, 𝒰/ℐ) domain shown in this figure is significantly greater than for the other 𝒬 − 𝒰 figures. The spot’s contribution to the overall flux density increases with increasing spot size. This is reflected in the total loop size S. $\overline{R}$ remains independent of the spot size. $\overline{S}$, on the other hand, tends to decrease for increasing R_s in the radial and toroidal magnetic field configurations. As was established in the previous paragraphs (and shown schematically in Fig. 6), the inner 𝒬 − 𝒰 loop is followed when the spot recedes from the observer. For the vertical configuration, the inner loop has a different origin, namely a region where k × B ∼ 0. This explains why the R_s = 3.0 r_g case breaks the trend of steadily decreasing $\overline{S}$ for increasing R_s, as the spot has become sufficiently large to no longer be fully suppressed in the k × B ∼ 0 region. We note that the relative growth of the inner loop size indicates that the spot’s emission starts eclipsing the contribution of the disk. If this were to continue, then we find that we end up with a 𝒬 − 𝒰 loop behavior that is similar to what we see in Fig. 5 for the spot-only case(s).

Fig. 10. Normalized 𝒬 − 𝒰 diagrams colored according to their LP fraction for i = 20° and a* = 0 cases. Each row corresponds to a different spot size (Rs). The default in the rest of this work is Rs = 1.5 rg. The observables S, $\overline{S}$, and $\overline{R}$ are explained in Fig. 6.

Orbital velocity. Figure 11 displays the 𝒬 − 𝒰 loop behavior for deviations from the base model’s Keplerian orbital velocity (shown in the middle row). We modify the orbital velocity (v) of the entire system (disk + spot) with a factor so that it ranges from 0.6 v_kep (sub-Keplerian) to 1.4 v_kep (super-Keplerian). For the radial and toroidal cases, where the inner and outer 𝒬 − 𝒰 loops correspond to the receding and approaching spots, we find that the inner and outer loops become more similar in size (lower $\overline{S}$ but higher $\overline{R}$) for a decreasing orbital speed. This behavior is explained by the increased (decreased) contribution of relativistic beaming for increasing (decreasing) orbital velocity, which makes the inner and outer loops diverge more (less) from each other. For the vertical cases, we find an opposite relation (in the metrics) as the inner loop has a different physical cause, namely a suppression of the emission in the k × B ∼ 0 region. This is also explained by the varying strength of relativistic beaming for the different orbit velocities, but it has the opposite effect with respect to the other magnetic field configurations, that is a decreasing (increasing) inner loop size for a decreasing (increasing) orbital speed. This indicates that k, and subsequently k × B, are, unsurprisingly, quite sensitive to the orbital velocity. The increase in $\overline{R}$ indicates that the k × B ∼ 0 region grows in size for an increasing orbital velocity.

Fig. 11. Normalized 𝒬 − 𝒰 diagrams colored according to their LP fraction for i = 20° and a* = 0 cases. Each row corresponds to a different orbital velocity (v), denoted as a fraction of the standard velocity in this work, which is Keplerian (vkep). The observables S, $\overline{S}$, and $\overline{R}$ are explained in Fig. 6.

Plasma parameters. Figure 12 displays an exploratory model where we half our base electron density n_e and double both the electron temperature Θ_e and the magnetic field strength B. Unsurprisingly, the (Stokes) quantities have changed with respect to the base model (shown in the top row of the figure). The most notable differences are in LP and total 𝒬 − 𝒰 surface S of the system, which have both decreased substantially. The overall shape of the 𝒬 − 𝒰 structure remains relatively unaffected. Variations in $\overline{S}$ and $\overline{R}$ are consistent with what was found in earlier figures. Stokes ℐ has almost quadrupled but Stokes 𝒬 and 𝒰 have only doubled and/or tripled, respectively, which explains the decrease in both LP and the 𝒬 − 𝒰 loop metrics. Additionally, the intensity-averaged Faraday depth τ_V is three times smaller, but this is largely inconsequential as both cases are still very Faraday-thin at τ_V ∼ 10⁻²−−10⁻³. In the exploratory model, we have entered a relatively less polarized regime (at 230 GHz). This example is illustrative of the fact that (polarized) synchrotron emission is highly sensitive to the underlying plasma quantities and is affected differently per magnetic field configuration. This illustrates that fitting these models to observations would, therefore, be a nontrivial multiparameter endeavor.

Fig. 12. Normalized 𝒬 − 𝒰 diagrams colored according to their LP fraction. The top row corresponds to the base model with rspot = 11 rg, a* = 0, and i = 20°. The bottom row shows some exploratory models with doubling of Θe and B and halved ne. The observables S, $\overline{S}$, and $\overline{R}$ are explained in Fig. 6.

3.4.2. Linear and circular polarization of bright spots

Bright spots orbiting in the disk periodically highlight (and add to) emission regions with different linear and circular polarization. We want to understand if we can use LP and CP light curves to infer the magnetic field topology or remove degeneracy between, for instance, radial and toroidal cases (since they look similar in the EVPA evolution). The interpretation of LP and CP evolution, in observations, is challenging because the polarization of light curves is modified by the beam depolarization. Also, LP and CP magnitudes depend strongly on the underlying plasma parameters. However, the models we discuss in this work are all Faraday-thin, which implies that almost all CP emission is intrinsic and Faraday conversion and rotation plays a negligible role in shaping $\stackrel{\sim }{\mathrm{CP}}$ maps. This helps us to understand the behavior of the CP light curves.

In Fig. 3 Stokes ℐ exhibits variations that are expected for an edge-on viewing angle. During the spot’s passage, the double peaked light curve is produced by the Einstein ring and followed by emission from Doppler beaming of the spot along its orbit, as was already explained. The LP is mostly constant in all cases, except during the Einstein ring phase where LP decreases and the Doppler beamed phase where LP increases – as is clearly seen in the radial case, but the LP reaction is somewhat spin-dependent in the toroidal case. The decrease in LP is caused by the cancellation effect (beam depolarization) because places with opposite polarization direction cancel out. The LP increase is caused by amplification of the spot emission, which is small in size and therefore amplifies only one polarization direction. Due to symmetry, for the edge-on inclination with a vertical magnetic field geometry, CP becomes zero independently of the BH spin. For the toroidal case, CP decreases during the Einstein ring moment, due to the cancellation effect, and then increases during the Doppler beaming time. For the radial case, we see that CP flips sign during the spot’s passage. When the Einstein ring forms, CP is most negative and then gains a positive sign during Doppler beaming, which is a direct result of the underlying field topology.

In Fig. 4 the flux density (F_ν) exhibits small variations that are expected for low viewing angles. For the radial and toroidal cases, we find a slightly enhanced flux when the spot approaches the observer, but for the vertical case, the total intensity decreases due to suppression of synchrotron emissivity at ζ ≈ 45° (or inner 𝒬 − 𝒰 loop passage). For radial fields the increase in flux density, when the spot approaches the observer, is accompanied with a single peak in LP. For toroidal fields, the increase in flux density (F_ν) is associated with two peaks in LP. Finally, for vertical fields, the decrease in the flux density in the middle of the spot’s approach, is associated with a single peak in LP. When the spot recedes from the observer, LP increases to the maximum for the vertical case. For the vertical field case, the background flow polarity $\stackrel{\sim }{\mathrm{CP}}$ is uniform across the image and the bright spot added to the model simply amplifies the CP, except during the ζ ≈ 45° time moment (the inner 𝒬 − 𝒰 loop time moment) when the CP light curves tend to show a small decrease. For the toroidal field case, we find a fully negative $\stackrel{\sim }{\mathrm{CP}}$ (for low viewing angles), but we also notice that $\stackrel{\sim }{\mathrm{CP}}$ has a strong positive region in Fig. 3 (on the left side of the maps for the edge-on viewing angle). Finally, the radial field case is more complex because the top part of the $\stackrel{\sim }{\mathrm{CP}}$ map has an opposite polarity to the bottom one. Here one observes the decrease in CP light curves just before the Doppler boost moment marked with a hump in flux density (F_ν).

We conclude with a number of statements about CP and how one could utilize it to differentiate between the underlying magnetic field topologies during a 𝒬 − 𝒰 loop event (utilizing Figs. 4 and 6). We notice that our models assume that the spot contributes significantly to both LP and CP, which in reality may not be always the case. Starting with the vertical topology, we immediately find that the 𝒬 − 𝒰 loop structure has a significant offset in 𝒬 − 𝒰 space with respect to the other magnetic field cases. The 𝒬 − 𝒰 loop signature alone would, therefore, be sufficient to identify the vertical magnetic field (at this inclination and orbital velocity, see Fig. 11). Additionally, during the inner 𝒬 − 𝒰 loop passage, a slight drop in CP is perceivable. Although the 𝒬 − 𝒰 loops of the radial and toroidal cases span a similar 𝒬 − 𝒰 range, they have a different CP behavior (and 𝒬 − 𝒰 loop structure). Due to the underlying $\stackrel{\sim }{\mathrm{CP}}$ morphology, we only see an increase in CP when the spot approaches the observer (and the outer 𝒬 − 𝒰 loop is traversed) for the toroidal case. For radial, we find the most complex $\stackrel{\sim }{\mathrm{CP}}$ (image) morphology with an overall positive $\stackrel{\sim }{\mathrm{CP}}$ structure with a section at ζ = 0° ±25° where $\stackrel{\sim }{\mathrm{CP}}$ is negative. This implies that when the inner 𝒬 − 𝒰 loop is traversed (as the spot recedes from the observer), the CP continues to decrease over time. It should be noted that the CP minimum is not reached when the inner 𝒬 − 𝒰 loop is still begin traversed, but rather when it has just entered the outer 𝒬 − 𝒰 loop, after which CP quickly increases.

4. Discussion

In this work we have studied polarimetric signatures of bright spots produced in the accretion flow close to the BH event horizon. Semi-analytic modeling enables the exploration of a parameter space without needing to run computationally expensive plasma simulations (GRMHD or GRPIC) where the plasma simulations’ resolutions may impact the results. Although not as complex as a full plasma simulation, our simplified approach allows for a relatively straightforward decomposition of the various physical effects that are important in the system.

Even for semi-analytic models the parameter space is very large, so we can still only present a limited number of models. All models studied here have small optical depths τ_ν ≪ 1 and small Faraday depths τ_F ≪ 1 (see Appendix C for detailed definitions of optical and Faraday depths, and their values for all models). We also fixed the magnetic field polarities and the orbital direction of the spot. In Appendix C we discuss the impact of the magnetic field’s polarity, Faraday effects, and spot rotation direction on all polarimetric observables of a bright spot.

Several works have presented polarized emission from hot spots around the Kerr BH. Broderick & Loeb (2005) is one of the pioneering works on the semi-analytical modeling of spot polarization. They use an “optically thick sphere” to investigate the effect of a curved spacetime on polarized emission in a single vertically aligned magnetic field configuration. In particular, the gravitational magnifying effect and the image centroid motion are topics they comment on. In Broderick & Loeb (2006), they include a disk background and change the magnetic field to toroidal. Additionally, they improve their (optically thin) hot spot description by including a localized population of nonthermal electrons. Much of our work is inspired by Broderick & Loeb (2005, 2006), but there are numerous differences – mostly with respect to our focus that lies predominantly in the polarimetric signatures. While the aforementioned works mainly display net polarization fractions, we focus on the entire structure of the Stokes parameters (especially in 𝒬 − 𝒰 diagrams). Overall, when directly comparing the net polarization, there is little similarity between our model and the aforementioned ones by Broderick & Loeb (2005, 2006).

A more recent study by Gelles et al. (2021) outlines a toy model for synchrotron point source emission by analytically computing Kerr spacetime null-geodesics (Gralla & Lupsasca 2020) and enforcing conservation of the Penrose-Walker constant, without any more sophisticated radiative transfer considerations. This approach is fundamentally different from the numerical radiative transfer approach used in ipole (while it is also a Penrose-Walker constant conserving scheme). The authors comment extensively on the 𝒬 − 𝒰 loop structure they find. However, they only model a hot spot without a disk background, which makes their result better comparable with NIR emission observed during flares in Sgr A* than with observations at millimeter wavelengths. Additionally, they effectively adopt a “fast light” approach where the spot is stationary when the geodesics are evaluated. In our work, the spot continues its orbit while the radiative transfer equations are being integrated along the null geodesics. Lastly, it is important to note that they display 𝒬 − 𝒰 loops and not the normalized 𝒬 − 𝒰 loops that we show in this work, so they are not intuitively comparable. Their methodology does not produce images, which makes tracking down underlying effects difficult. Even though our magnetic field descriptions are not identical (and the disk background is missing), we find very consistent 𝒬 − 𝒰 loops structures in the low Faraday depth regime. The direct comparison of our model with 𝒬 − 𝒰 loops from Gelles et al. (2021) is shown in Wielgus et al. (2022b).

Another aspect investigated in this work, which was not addressed in detail previously, is the potential of using the circular polarization (or Stokes 𝒱) to further constrain the underlying magnetic field structure. If it is difficult to identify the model unambiguously based on the 𝒬 − 𝒰 loop behavior alone, then it is possible to get additional information from the CP signature, as we discussed in Sect. 3.4.2. A simple measurement of the CP sign can already help break this ambiguity, although imaging circular polarization structure (as shown in, e.g., Fig. 4) would be even more effective. We note that polarity of the magnetic field is arbitrarily chosen and can possibly be reversed in reality, but the behavior of CP, especially while traversing an inner 𝒬 − 𝒰 loop, remain diverging (even when inverted) for the magnetic field cases evaluated in this work.

In a parallel work, we demonstrated a remarkable consistency between predictions of our model and the full Stokes light curves of Sgr A* observed with ALMA at 230 GHz shortly after an X-ray flare (Wielgus et al. 2022b). Our findings strongly suggest a low inclination of the Sgr A* system and dominance of the vertical magnetic field component. In the future, one can expand the semi-analytic hot spot model in a number of ways, including, but not limited to, elliptical and/or non-equatorial orbits, a separate magnetic field description for the spot, mixed (global) magnetic field descriptions, cooling of the hot spot over time, and the presence of a nonthermal electron population. These more sophisticated models may provide a better fit to the existing data and a deeper understanding of the physical processes.

Our current base model consists of a RIAF disk and a hot spot, but one would expect an additional contribution of the jet (Blandford et al. 2019). If one were to consider a disk-jet model (e.g., Vincent et al. 2019) instead of a pure disk model, the emission from the disk would need to be reduced for the full model to end up at the same flux density. As this would require rebalancing the plasma parameters (mainly through the electron temperature and density), it is possible that the disk would enter a more optically and/or Faraday-thick regime. Then, the background flow could become an internal Faraday screen, which might severely alter the polarimetric characteristics of the models (Mościbrodzka et al. 2017; Jiménez-Rosales & Dexter 2018). Additionally, it has been shown that strong variations in rotation measure as a result of the internal Faraday screen are expected from GRMHD simulations (Ricarte et al. 2020).

The physical origin and lifetime of hot spots are also uncertain. Alternatively to the plasmoid interpretation, the orbiting hot spots reported in Sgr A* by GRAVITY Collaboration (2018) and Wielgus et al. (2022b) may correspond to flux tubes powered by reconnection and filled with hot electrons confined by the vertical magnetic field. Such features have been observed in numerical GRMHD simulations of magnetically arrested accretion disks (Ripperda et al. 2022). This origin would also support the notion that the hot spot emission should be (at least partially) described by nonthermal electron population, which is especially needed to explain the NIR observations (Chael et al. 2017; Davelaar et al. 2018, 2019; Fromm et al. 2022). The persistence and integrity of an orbiting hot spot also remain largely unknown. We expect hot spots to be disrupted by effects such as shearing in a differentially rotating flow (Tiede et al. 2020) or by the Rayleigh-Taylor instability (Ripperda et al. 2022) on dynamical timescales. Accounting for these effects would further modify the outcome of our calculations.

These topics are best investigated in dedicated GRMHD and/or GRPIC simulations. A number of studies have been conducted to better understand the behavior and evolution of plasmoids, but these typically do not include a study of the radiation. These simulations can be run within a shearing box (see, e.g., Murphy et al. 2013; Cerutti et al. 2014; Sironi et al. 2016) or global GRMHD and GRPIC simulations of magnetized accretion disks around a SMBH. There, one generally finds more erratic plasmoid chains due to the less confining nature of the setup (Crinquand et al. 2021; Bransgrove et al. 2021; Ripperda et al. 2020, 2022).

5. Summary

This study has outlined the various distinguishing polarimetric signatures of a circularly orbiting bright spot on top of a disk background at a frequency of 230 GHz. For this model, we have showcased the utility of 𝒬 − 𝒰 loops and circular polarization for establishing an underlying magnetic field structure. We have shown what signatures are indicative of the underlying radial, toroidal, and vertical magnetic fields. In the following paragraphs, we summarize the main findings of this work.

• (i)

  The shape and size of a 𝒬 − 𝒰 loop is indicative for at least three parameters that we investigate: inclination i, magnetic field, and BH spin (a_*). The inner 𝒬 − 𝒰 loop structure is particularly informative. The point where the 𝒬 − 𝒰 path moves from the outer to inner loop over time was previously referred to as the crossing point. This point lies on opposite sides for the toroidal and vertical magnetic field cases and the radial case. This does not change with inclination (including i > 90°), but the exact position of the crossing point is sensitive to rotation of the image. Additionally, as becomes clear from Fig. 6, the timing (of entering and exiting of the inner loop) is strikingly different in the radial and toroidal cases, to the vertical cases. While for the former cases, the division between the inner and outer 𝒬 − 𝒰 loops lies in the approaching versus receding part of the orbit, while for the vertical case, it is connected to the part of the orbit where the direct emission from the spot disappears (as outlined in Sect. 3.4).

• (ii)

  Moreover, inclination (i) is especially influential on the 𝒬 − 𝒰 loop structure for the vertical magnetic field case, as demonstrated in Figs. 5 and 7. In this configuration the inner loop structure disappears for i ≳ 25° and for even greater inclination angles, one only recovers thin crescents that have little resemblance to the typical 𝒬 − 𝒰 loop structure. Another influential parameter is the orbital velocity of the system, particularly for the vertical case (as highlighted in Fig. 11). To a lesser degree, this behavior is also present for the radial and toroidal cases, as the inner loop’s relative size decreases as function of inclination. However, for those cases, we find that even for near edge-on viewing angles, there is still some inner loop structure present, as shown in Fig. 5.

• (iii)

  The vertical magnetic field case behaves substantially different from the two others – both in terms of 𝒬 − 𝒰 loop structure and LP strength. Overall, the vertical cases are more 𝒬-negative and the variation of certain parameters results in a significant shift in Stokes 𝒬 (as shown in Figs. 7, 9, and 11 for i, a_*, and v, respectively). The radial and toroidal cases generally span an almost identical 𝒬 − 𝒰 range and display only minor variations in Stokes 𝒬. Interestingly, Stokes 𝒰 is (almost) insensitive to any of the parameter variations with an average value of 𝒰/ℐ ≈ 0 for the radial and toroidal cases. Some variation in 𝒰 is found for the vertical case (where it becomes more positive), but this remains minimal when compared to the variations in 𝒬.

• (iv)

  When the 𝒬 − 𝒰 structure is similar or unclear, circular polarization could break the degeneracy. Radial and toroidal cases for low inclinations (i ≲ 30°) would, observationally, be hard to differentiate. However, they do differ structurally in $\stackrel{\sim }{\mathrm{CP}}$. The region close to the photon ring has a negative $\stackrel{\sim }{\mathrm{CP}}$ (for all cases), while the surrounding emission structure (from radii beyond ISCO) has a predominantly positive $\stackrel{\sim }{\mathrm{CP}}$ for the radial case and negative $\stackrel{\sim }{\mathrm{CP}}$ for the toroidal case for 40° ≳i ≳ 150°. For edge-on viewing angles (70° ≲i ≲ 110°), the $\stackrel{\sim }{\mathrm{CP}}$ structure becomes more similar, but then one can differentiate based on $\stackrel{\sim }{\text{LP}}$. The same argument applies, to a lesser extent, to the image-integrated quantities CP and LP. Therefore, we argue that all Stokes parameters, ℐ, 𝒬, 𝒰, and 𝒱, are required to robustly determine the dominant underlying magnetic field structure.

Acknowledgments

We thank Alejandra Jiménez-Rosales, Hector Olivares, Aristomenis Yfantis, and Zachary Gelles for the insightful discussions and comments that have improved the quality of the manuscript. Additionally, we thank the internal EHTC reviewer Michi Bauböck for his comments. M.M. acknowledges support by the Dutch Research Council (NWO) grant No. OCENW.KLEIN.113. MW thanks Alexandra Elbakyan for her contributions to the open science initiative.

References

Appendix A: Linear and circular polarization

Figure A.1 displays the relation between LP and CP for all spins and inclinations of i = 20° , 40° , 60° , and 80°. Each magnetic field configuration displays a unique relation between LP and CP. For increasing inclination, LP rises for all cases. However, for an increasing inclination, we find that the CP decreases for the radial and vertical cases, and increases for the toroidal case. Another diverging feature is the size of the path followed in the LP and CP. The radial case is more variable in both LP and (especially) CP than the other cases. Additionally, it has a clear crescent-like shape, which is only deformed for the higher-inclination cases (due to boosting). The toroidal case has a vaguely similar shape, but it has almost no difference between the part of the orbit when the spot recedes (lower part of CPLP structure) and when the spot approaches (upper part of CPLP structure). Lastly, for the vertical case, we observe that there is little CP and LP variation during the spot’s orbit for any inclination. Overall, for all cases, we find that CP and LP variability decreases with increasing spin, which is due to the increased contribution of the spot to the overall flux density for lower-spin cases.

Fig. A.1. Linear polarization versus CP diagrams for models with different magnetic fields, BH spins, and viewing angles. The crosses denote the disk-only values. The dotted lines are shown to highlight a trend.

Figure A.2 continues to outline the relation between LP and CP, but here we vary the underlying plasma parameters modestly to investigate slight deviations from our base configuration. The base model has a_* = 0 and i = 20° and corresponds to the modification factor of one in the figure. In the top row, we vary only the electron (number) density n_e. There, we find that LP is almost invariant for variations in n_e. The LP-CP structure decreases slightly and CP becomes more negative as the n_e modification factor increases. This effect is largest for the radial case, but is also present for the toroidal case. For the vertical case, we find that the relation is reversed - CP increases minimally with an increasing multiplication factor. In the second row, we vary the electron temperature Θ_e. There, we find a larger response both in LP-CP structure alterations and the corresponding CP values. For the radial case, we observe that both the LP and CP variations decreases if the temperature increases. For the toroidal case, CP is most negative and largest in size for the smallest Θ_e value, but it increases when the multiplication factor increases. A similar relation is observed for the vertical case, but again in reverse - CP becomes smaller for an increasing multiplication factor. In the third row, we observe that variations in the magnetic field strength B once again produce unique alterations to the model’s LP and CP. For the radial case, we find that LP decreases and CP increases for increasing B. For the toroidal case, both LP and CP increase as B increases. For the vertical case, LP remains constant but we observe a significant increase in CP. For the bottom row, all quantities (n_e, Θ_e, B) are scaled simultaneous. The behavior here clearly shows that trying to predict the plasma behavior based on slight deviations to the base model is already a nontrivial endeavor. Each model once again describes a relation between LP and CP that is different from the behavior in the three top rows. Interestingly, both the radial and toroidal cases react similarly, but the vertical case is most similar to the B variation.

Fig. A.2. Linear polarization versus CP diagrams for models with different magnetic fields, BH spin of a* = 0, and viewing angle of i = 20°. In each row we show the base plasma property (i.e., ne, Θe, B), which are color-coded according to the multiplication factor with which they are scaled. The bottom row shows the behavior where all quantities (ne, Θe, B) are scaled simultaneously.

Appendix B: Circular polarization from regions close to the photon ring

A feature that further magnifies the differences between the magnetic field cases is the $\stackrel{\sim }{\mathrm{CP}}$ signature of the lensed emission directly outside the photon ring. The photon ring is a infinitesimal feature, with a well-defined radius (see, e.g., Bardeen et al. 1972), which is not well-resolved in our images but generally has a similar polarization (if slightly reduced) with respect to the lensed emission directly outside it (Jiménez-Rosales et al. 2021). For the rest of the section, we discuss the emission that comes from the vicinity of the photon ring, which we simply refer to as “emission” from now on. We would like to note that as we assume a small (floor) electron density for radii smaller than the ISCO the (near photon ring) emission one sees, is strongly lensed emission that has orbited the black hole multiple times. If one were to extend the electron density (inflow) description beyond the ISCO, then we expect our following findings to be affected. Nevertheless, one would still expect there to be at least a trace of the behavior we describe.

For the radial case, we find a strictly negative $\stackrel{\sim }{\mathrm{CP}}$, which is most pronounced for face-on viewing angles (110° ≲i ≲ 70°), as demonstrated in Figs. 2 and B.1. For the toroidal case, we find the vertical division as outlined in Sect. 3.4.2 persists in the photon ring’s $\stackrel{\sim }{\mathrm{CP}}$ signature (as shown in Figs. 1 and 2) - positive $\stackrel{\sim }{\mathrm{CP}}$ on the left and negative $\stackrel{\sim }{\mathrm{CP}}$ on the right. For the face-on viewing angle (from top or bottom), we find no apparent difference in the sign of $\stackrel{\sim }{\mathrm{CP}}$ between the photon ring and the disk, as shown in Fig. B.2.

Fig. B.1. Stokes ℐ (left panel), LP (middle panel), and CP (right panel) images of the background accretion flow for observer viewing angles of i = 10° and i = 170°, and a radial magnetic field topology.

Fig. B.2. Same as for Fig. B.1, but for the toroidal magnetic field topology.

The vertical case deviates in the sense that the $\stackrel{\sim }{\mathrm{CP}}$ signature of the emission directly outside the photon ring is strongly determined by the viewing angle. For i < 90°, we find negative $\stackrel{\sim }{\mathrm{CP}}$ for the photon ring and an overall positive $\stackrel{\sim }{\mathrm{CP}}$ from the (direct) disk and spot emission. For i > 90°, the situation is reversed. This is clearly shown in Fig. B.3. As can be seen in Fig. 1, the edge-on view reveals two modes - a top half that has a negative $\stackrel{\sim }{\mathrm{CP}}$ and a bottom half with a positive $\stackrel{\sim }{\mathrm{CP}}$ for the photon ring. This overall $\stackrel{\sim }{\mathrm{CP}}$ structure is oppositely polarized with respect to the photon ring. The dividing line, which lies along the equatorial plane, is unpolarized and splits these regions.

Fig. B.3. Same as for Fig. B.1, but for the vertical magnetic field topology.

If we were to look at $\stackrel{\sim }{\text{LP}}$ alone, then the radial and toroidal case describe similar structures that would be hard to differentiate. For $\stackrel{\sim }{\mathrm{CP}}$, however, the structure is completely different, which allows for a straightforward identification.

Appendix C: Optical and Faraday Depths, and other effects

Models considered in this work are mostly optically thin, with an optical depth of τ_a ∼ 10⁻³ − 10⁻². Models are also Faraday-thin, with Faraday depths of τ_V ∼ 10⁻³ − 10⁻². The Faraday thickness defined as τ_V = ∫ρ_Vdl (where ρ_V is the transfer coefficient for Faraday rotation) gives us an estimate of how many rotations (in radians) the EVPA is undergoing when a ray of light is transported from the emission origin to the observer. This means that Faraday rotation has small impact on the linear polarization of models.

Nevertheless, we discuss in more detail how Faraday effects impact the linear and circular polarization of our models. This is done for two reasons: i) Faraday conversion can alter circular polarization; and ii) Faraday effects may break degeneracies in observables such as LP (or $\stackrel{\sim }{\text{LP}}$) and CP (or $\stackrel{\sim }{\mathrm{CP}}$) of hot spot models rotating in different directions (on clockwise and counterclockwise orbits) or in models with opposite magnetic field polarity. Even for completely Faraday-thin models, changing the magnetic field polarity results in Stokes 𝒰 with the opposite sign.

The discussion is based on the analysis of a model of an accretion disk with a spot around a nonrotating BH threaded by a vertical magnetic field seen at a viewing angle of 20°. In this model a 𝒬 − 𝒰 loop is formed and CP experiences significant variation.

First, we consider a case when both Faraday rotation and Faraday conversion are absent (ρ_Q, V = 0). Changing the direction of system rotation from clockwise to counterclockwise reverses the sign of Stokes 𝒰, and thus the direction in which the 𝒬 − 𝒰 loop is traversed (the clockwise or counterclockwise rotating systems with display clockwise or counterclockwise 𝒬 − 𝒰 loops). The fractional LP and CP remain intact. In the model without Faraday effects, the CP is produced intrinsically, and thus the change in the system rotation changes neither the sign nor the magnitude of the CP. In Fig. C.1 (left panel) we demonstrate that this is true for our chosen model, as expected. We also notice that, for optically thin emission, when Faraday conversion is absent, the sign of the Stokes 𝒱 depends only on the polarity of the magnetic fields. Changing the magnetic field polarity to the opposite one simply reverses the sign of 𝒱.

Fig. C.1. Impact of Faraday effects on the Stokes parameters(ℐ, 𝒬, and 𝒰), LP, and CP evolution in a model with the vertical magnetic field viewed at i = 20deg. In the left panel, we show light curves of a model where we disabled the Faraday rotation and conversion effects by setting the Faraday rotativities to zero (radiative transfer model with ρQV = 0). In the right panels, we show the same model but with the Faraday effects taken into account. Solid and dashed lines in each subpanel indicate the model with the accretion disk and the bright spot on a clockwise (C) and counterclockwise (CC) orbit, respectively. Arrows in the 𝒬 − 𝒰 panels indicate the direction of time evolution.

Secondly, we consider the same model but with the Faraday effects included (shown in the right panels in Fig. C.1). Stokes 𝒬 and 𝒰 are slightly rotated by Faraday rotation, and thus clockwise and counterclockwise rotating models have slightly different LPs and the clockwise system 𝒬 − 𝒰 loop is not an identical reflection of the counterclockwise rotating system; the LP is changed. It is interesting to note that reversing the sign of the magnetic fields in this case results in Faraday rotation in the opposite direction (since ρ_V ∼ B_|| along the line of sight), so the 𝒬 − 𝒰 loop of clockwise model with +B should be a reflection of the 𝒬 − 𝒰 loop of the counterclockwise model with −B (this should be true only for spin zero). We also notice that when Faraday effects are included, the magnitude of Stokes 𝒱 is changed, meaning that in our models, a significant portion of the observed CP is produced in the process of Faraday conversion.

All Tables

All Figures

Fig. 1. Edge-on view (i = 90°) of the disk background in the radial (top row), toroidal (middle row), and vertical (bottom row) magnetic field configurations for a field of view of 40 rg × 40 rg. Left panel: displays the zero-spin cases (a* = 0), while the right panel gives an overview of the other spin-cases. The white ticks, plotted over the Stokes ℐ maps, denote the EVPA scaled according to the linearly polarized flux ($\sqrt{{\mathcal{Q}}^2+{\mathcal{U}}^2}$).

In the text

	Fig. 2. Stokes ℐ and polarimetric images of the background accretion flow as a function of the observer’s viewing angle i and magnetic field topology. The left panel corresponds to i = 0° while i = 20°, 40°, 60°, and 80° are shown in the right panel. Total intensity and polarimetric maps are displayed in the same fashion as in Fig. 1.
In the text

Fig. 3. Stokes ℐ and polarimetric images, as well as image-integrated quantities of the full (disk + spot) models. Left panels: edge-on views (i = 90°) of the non-spinning (a* = 0) model in radial (top), toroidal (middle), and vertical (bottom) magnetic configurations for a field of view of 40 rg × 40 rg. The rows, within each panel, display Stokes ℐ, $\stackrel{\sim }{\mathrm{LP}}$, and $\stackrel{\sim }{\mathrm{CP}}$ at times t = 25, 50, 75, and 100 rg/c. The EVPA orientation is represented with white ticks on top of the Stokes ℐ panels. Their length is determined by the linearly polarized flux strength ($\sqrt{{\mathcal{Q}}^2+{\mathcal{U}}^2}$). Right panels: comparison of the evolution of the flux density Fν (top), LP (middle), and CP (bottom) over time for radial (solid), toroidal (dashed), and vertical (dotted) magnetic fields. Here, we additionally plot light curves for BHs with a* ≠ 0 (different BH spins are color coded).

In the text

	Fig. 4. Same as for Fig. 3, except for the viewing angle, which is i = 20°, and showing maps corresponding to times t = 25, 75, 125, and 175 rg/c.
In the text

	Fig. 5. Normalized 𝒬 − 𝒰 diagrams for the three basic magnetic field configurations and a BH spin of a* = 0. Both the spot-only (dotted lines) and full models’ (solid lines) 𝒬 − 𝒰 loops are shown for four viewing angles i = 20°, 40°, 60°, and 80°.
In the text

Fig. 6. Schematic diagrams of normalized 𝒬 − 𝒰 loops of the full models (for i = 20°, a* = 0) with the radial, toroidal, and vertical magnetic field configurations in the left, middle, and right panels, respectively. The loop color encodes the model LP. The inner loop surface S1 (in pink) and rest of surface (excluding S1) enclosed by the entire 𝒬 − 𝒰 loop structure is denoted by S2 (in yellow). The total surface is S = S1 + S2, surface fraction is $\overline{S}=S/S_1$, and time spent in the inner loop with respect to the total period is $\overline{R}=P/(T_4^c-T_2^c)$ (similar to Wielgus et al. 2022b). The “+” symbol marks the normalized 𝒬 − 𝒰 value of the static background emission. All shown loops are traversed in the counterclockwise direction.

In the text

Fig. 7. Normalized 𝒬 − 𝒰 diagrams of the full model, colored according to their LP fraction as a function of increasing inclination i (panels from top to bottom). Each column corresponds to a different magnetic field configuration. All models have a* = 0. While for the vertical magnetic field, the 𝒬 − 𝒰 loops disappear for i ≳ 25°, for other field geometries, they are present for all viewing angles, except exact edge-on cases (see also Fig. 5). The bottom row shows the behavior of $\overline{S}$ (in blue) and $\overline{R}$ (in orange) as a function of inclination i. The observables S, $\overline{S}$, and $\overline{R}$ are explained in Fig. 6.

In the text

Fig. 8. Normalized 𝒬 − 𝒰 diagrams colored according to their LP fraction. Each row corresponds to a different orbital radius rspot. The inclination and BH spin are set to i = 20° and a* = 0, respectively. The bottom row shows the behavior of $\overline{S}$ (in blue) and $\overline{R}$ (in orange) as a function of orbital radius rspot. The observables S, $\overline{S}$, and $\overline{R}$ are explained in Fig. 6.

In the text

	Fig. 9. Normalized 𝒬 − 𝒰 diagrams colored according to their LP fraction. The inclination is set to i = 20°. Each row corresponds to a different BH spin parameter a*. The bottom row shows the behavior of $\overline{S}$ (in blue) and $\overline{R}$ (in orange) as a function of a*. The observables S, $\overline{S}$, and $\overline{R}$ are explained in Fig. 6.
In the text

	Fig. 10. Normalized 𝒬 − 𝒰 diagrams colored according to their LP fraction for i = 20° and a* = 0 cases. Each row corresponds to a different spot size (Rs). The default in the rest of this work is Rs = 1.5 rg. The observables S, $\overline{S}$, and $\overline{R}$ are explained in Fig. 6.
In the text

	Fig. 11. Normalized 𝒬 − 𝒰 diagrams colored according to their LP fraction for i = 20° and a* = 0 cases. Each row corresponds to a different orbital velocity (v), denoted as a fraction of the standard velocity in this work, which is Keplerian (vkep). The observables S, $\overline{S}$, and $\overline{R}$ are explained in Fig. 6.
In the text

	Fig. 12. Normalized 𝒬 − 𝒰 diagrams colored according to their LP fraction. The top row corresponds to the base model with rspot = 11 rg, a* = 0, and i = 20°. The bottom row shows some exploratory models with doubling of Θe and B and halved ne. The observables S, $\overline{S}$, and $\overline{R}$ are explained in Fig. 6.
In the text

	Fig. A.1. Linear polarization versus CP diagrams for models with different magnetic fields, BH spins, and viewing angles. The crosses denote the disk-only values. The dotted lines are shown to highlight a trend.
In the text

	Fig. A.2. Linear polarization versus CP diagrams for models with different magnetic fields, BH spin of a* = 0, and viewing angle of i = 20°. In each row we show the base plasma property (i.e., ne, Θe, B), which are color-coded according to the multiplication factor with which they are scaled. The bottom row shows the behavior where all quantities (ne, Θe, B) are scaled simultaneously.
In the text

	Fig. B.1. Stokes ℐ (left panel), LP (middle panel), and CP (right panel) images of the background accretion flow for observer viewing angles of i = 10° and i = 170°, and a radial magnetic field topology.
In the text

	Fig. B.2. Same as for Fig. B.1, but for the toroidal magnetic field topology.
In the text

	Fig. B.3. Same as for Fig. B.1, but for the vertical magnetic field topology.
In the text

Fig. C.1. Impact of Faraday effects on the Stokes parameters(ℐ, 𝒬, and 𝒰), LP, and CP evolution in a model with the vertical magnetic field viewed at i = 20deg. In the left panel, we show light curves of a model where we disabled the Faraday rotation and conversion effects by setting the Faraday rotativities to zero (radiative transfer model with ρQV = 0). In the right panels, we show the same model but with the Faraday effects taken into account. Solid and dashed lines in each subpanel indicate the model with the accretion disk and the bright spot on a clockwise (C) and counterclockwise (CC) orbit, respectively. Arrows in the 𝒬 − 𝒰 panels indicate the direction of time evolution.

In the text