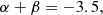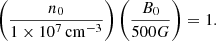| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202347772 | |
| Published online | 09 February 2024 | |
The internal Faraday screen of Sagittarius A*⋆
1
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: maciek@wielgus.info
2
Institute of Physics, Silesian University in Opava, Bezručovo nám. 13, 746 01 Opava, Czech Republic
3
Center for Astrophysics | Harvard & Smithsonian, 60 Garden Street, Cambridge, MA 02138, USA
4
Departament d’Astronomia i Astrofísica, Universitat de València, C. Dr. Moliner 50, 46100 Burjassot, València, Spain
5
Observatori Astronòmic, Universitat de València, C. Catedrático José Beltrán 2, 46980 Paterna, València, Spain
6
Department of Astrophysics, Institute for Mathematics, Astrophysics and Particle Physics (IMAPP), Radboud University, PO Box 9010 6500 GL Nijmegen, The Netherlands
7
Instituto de Astronomia, Geofísica e Ciências Atmosféricas, Universidade de São Paulo, R. do Matão, 1226, São Paulo, SP 05508-090, Brazil
8
Dipartimento di Fisica, Università degli Studi di Cagliari, SP Monserrato-Sestu km 0.7, 09042 Monserrato, CA, Italy
9
INAF – Osservatorio Astronomico di Cagliari, Via della Scienza 5, 09047 Selargius, CA, Italy
10
INFN, Sezione di Cagliari, 09042 Monserrato, CA, Italy
11
National Radio Astronomy Observatory, 520 Edgemont Road, Charlottesville, VA 22903, USA
Received:
21
August
2023
Accepted:
8
November
2023
We report on 85−101 GHz light curves of the Galactic Center supermassive black hole, Sagittarius A* (Sgr A*), observed in April 2017 with the Atacama Large Millimeter/submillimeter Array (ALMA). This study of high-cadence full-Stokes data provides new measurements of the fractional linear polarization at a 1−2% level resolved in 4 s time segments, and stringent upper limits on the fractional circular polarization at 0.3%. We compare these findings to ALMA light curves of Sgr A* at 212−230 GHz observed three days later, characterizing a steep depolarization of the source at frequencies below about 150 GHz. We obtain time-dependent rotation measure (RM) values, with the mean RM at 85−101 GHz being a factor of two lower than that at 212−230 GHz. Together with the rapid temporal variability of the RM and its different statistical characteristics in both frequency bands, these results indicate that the Faraday screen in Sgr A* is largely internal, with about half of the Faraday rotation taking place inside the inner 10 gravitational radii, contrary to the common external Faraday screen assumption. We then demonstrate how this observation can be reconciled with theoretical models of radiatively inefficient accretion flows for a reasonable set of physical parameters. Comparisons with numerical general relativistic magnetohydrodynamic simulations suggest that the innermost part of the accretion flow in Sgr A* is much less variable than these models predict; in particular, the observed magnetic field structure appears to be coherent and persistent.
Key words: black hole physics / magnetic fields / polarization / techniques: interferometric / techniques: polarimetric / Galaxy: center
A table of the light curve data is available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/682/A97
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open Access funding provided by Max Planck Society.
1. Introduction
Sagittarius A* (Sgr A*) is the radio source associated with a 4 × 106 M⊙ supermassive black hole (SMBH) located in our Galactic Center (Do et al. 2019; GRAVITY Collaboration 2022; Event Horizon Telescope Collaboration 2022a). The source is characterized by a particularly low mass accretion rate of ∼10−8 M⊙ yr−1 (Quataert & Gruzinov 2000; Yuan et al. 2003; Event Horizon Telescope Collaboration 2022b). Spectral energy distribution (SED) analysis allowed it to be identified as an advection dominated, radiatively inefficient type of accretion flow (ADAF/RIAF; Narayan et al. 1995; Yuan & Narayan 2014; Event Horizon Telescope Collaboration 2022c,b). The SED of Sgr A* exhibits a maximum at a turnover frequency in the range of several hundred GHz that can be attributed to synchrotron emission from the hot thermal electrons in the marginally optically thin innermost region of the accretion disk (Yuan et al. 2003). Despite significant progress on the theoretical front and multiple observational studies across the electromagnetic spectrum since Sgr A* was first identified in 1974 (Balick & Brown 1974), our detailed understanding of this object and the accretion flow surrounding it remains incomplete (for a recent review see, e.g., Morris 2023).
Very long baseline interferometric (VLBI) radio observations indicate that the intrinsic size of Sgr A* decreases with frequency, reaching event horizon scales at ∼230 GHz (e.g., Doeleman et al. 2008; Event Horizon Telescope Collaboration 2022a). At ∼90 GHz the intrinsic diameter of the VLBI image corresponds to about 20 gravitational radii rg = GM•/c2 (Shen et al. 2005; Bower et al. 2006; Lu et al. 2011; Issaoun et al. 2019), hence the emission originates in large part from a layer external to the innermost scales ≲5 rg. Therefore, observations at different radio frequencies can be used to probe distinct regions of the accretion flow. Linear and circular polarization (LP and CP), rotation measure (RM), and temporal variability of these observed quantities provide additional constraints on Sgr A* models (e.g., Quataert & Gruzinov 2000; Bower et al. 2003; Marrone et al. 2007; Sharma et al. 2007; Pang et al. 2011; Ressler et al. 2023).
The CP of Sgr A* was first reported by Bower et al. (1999a) at 4.8 GHz, while the first LP detections were obtained by Aitken et al. (2000) in the 150−400 GHz range. Multiple subsequent observations showed LP values of ∼5−10% at around 230 GHz (Bower et al. 2003, 2018; Marrone et al. 2007; Wielgus et al. 2022a). The source becomes strongly depolarized at lower frequencies, and there is a very limited number of LP detections below 150 GHz in the literature (Bower et al. 1999b; Macquart et al. 2006; Liu et al. 2016). Measurements of weak negative CP have been reported at frequencies below 20 GHz (Bower et al. 1999a, 2002). Above 200 GHz a stronger CP ∼ − 1% appears (Muñoz et al. 2012; Bower et al. 2018; Wielgus et al. 2022a; Michail et al. 2023). Only weak upper limits are currently known for intermediate frequencies (Tsuboi et al. 2003).
In this paper we present a study of ALMA light curves in the 85−101 GHz range (ALMA band 3), including unambiguous high-time-cadence detections of variable LP, stringent upper limits on CP, and time-resolved measurements of Faraday rotation. We compare these results to the study of 212−230 GHz (ALMA band 6) light curves obtained in a quasi-contemporaneous epoch (Wielgus et al. 2022a,b). At both frequency bands we build on the results of Goddi et al. (2021), where a preliminary analysis of Sgr A* polarization in the same ALMA observations, reduced under an unphysical static source assumption, was presented. The main consequence of our results for the Sgr A* system is the observationally demonstrated presence of a significant internal component of the Faraday screen, which must be located within the central 10 rg region (Sect. 2). We discuss the implications of this measurement for the RIAF accretion flow model, utilizing VLBI observations to constrain the radial distribution of the electron temperature (Sect. 3). We also compare the measurements with predictions from general relativistic magnetohydrodynamic (GRMHD) simulations (Sect. 4). A brief summary is given in Sect. 5.
2. Observations and data analysis
2.1. Data reduction and conventions
The high sensitivity of ALMA enabled detailed recent studies of the rapid variability of Sgr A* (Iwata et al. 2020; Murchikova & Witzel 2021; Wielgus et al. 2022b). In April 2017, Sgr A* was observed by ALMA during its participation in the VLBI campaigns with the Global mm-VLBI Array (GMVA; Issaoun et al. 2019; Goddi et al. 2019) and with the Event Horizon Telescope (EHT; Event Horizon Telescope Collaboration 2022a; Goddi et al. 2021) as a compact phased array (Matthews et al. 2018; Goddi et al. 2019). Algorithms enabling the extraction of ALMA-only time-dependent light curves of the compact Sgr A* source from these data were developed and extensively discussed in Wielgus et al. (2022b), where the data reduction pipeline used in this paper was described as intrafield flux density ALMA calibration (A1). The method is based on the well-motivated assumption of negligible variation of the arc-minute scale radio emission surrounding Sgr A* (Lo & Claussen 1983; Mus et al. 2022), allowing us to self-calibrate to the extended source structure and to extract the time-dependent point source component, reducing the impact of fluctuating amplitude gains. This robust approach, employed following the ALMA QA2 calibration (Goddi et al. 2019), has been applied to band 6 observations at 212−230 GHz, obtained on 2017 April 6, 7, and 11, and presented in Wielgus et al. (2022a,b). In this paper, we employ a very similar calibration algorithm to the data obtained on 2017 April 3 in ALMA band 3, with four frequency sub-bands, each 2 GHz wide, centered at 86.3, 88.3, 98.3, and 100.3 GHz. The sub-band depolarization and decorrelation effects are negligible in all cases, hence we work with the data averaged in sub-bands. The only difference with respect to the procedure of Wielgus et al. (2022b) was motivated by the wide total fractional bandwidth in ALMA band 3 observations (∼15%, as opposed to ∼7% in ALMA band 6). In order to account for the frequency dependence of the extended source structure across a wider frequency coverage we tested two approaches: carrying out an independent CLEAN deconvolution of each sub-band and using a CLEAN multifrequency-synthesis first-order expansion (Conway et al. 1990; McMullin et al. 2007). Both variants of the extended emission modeling resulted in very consistent light curves of the compact component, fitted individually in each sub-band. The latter approach was adopted for the final data set presented in this paper.
The data set contains all Stokes parameters: total intensity ℐ, linear polarization 𝒫 = 𝒬 + i𝒰, and circular polarization 𝒱, observed with a time cadence of 4 s. We define the fractional LP p and fractional CP v as
Furthermore, we define the electric vector position angle (EVPA) as χ = 0.5Arg(𝒬 + i𝒰).
2.2. Intensity and polarization
The obtained Sgr A* light curves are summarized in Fig. 1, with mean values and standard deviations reported in Table 1. The reported uncertainties are strongly dominated by the intrinsic source variability, with the effective signal-to-noise ratio (S/N) of each 4 s ALMA measurement: ∼200 for the Stokes ℐ component (Wielgus et al. 2022b). We focus on comparisons between band 3 observations on 2017 April 3 and band 6 observations on 2017 April 6, given that these light curves are closest in time and are of similar total duration. Generally, similar mean parameters were found on other days of the band 6 observations (see Appendix A and Wielgus et al. 2022a,b), with some discrepancies highlighted in Appendix A. We employed an identical flagging procedure for each data set presented in Fig. 1 in order to remove points for which the calibration procedures did not converge. The sparser time coverage after ∼12:30 UT reflects the decreasing elevation of Sgr A* at ALMA by the end of the observing epoch. We verified that flagging these data does not appreciably impact the reported results. Our physically motivated analysis (Figs. 1–3) confirms that there is a remarkable change in the degree of polarization between the two ALMA bands, first reported under a static source assumption by Goddi et al. (2021)1. Furthermore, the EVPA is significantly more variable at 85−101 GHz than at 212−230 GHz on the same timescales (Figs. 1 and 2).
 |
Fig. 1. Overview of the ALMA light curves of Sgr A* obtained in band 3 (left column) and band 6 (right column), each with four 2 GHz-wide sub-bands, spanning 85−101 GHz and 212−230 GHz, respectively. A significant reduction of the fractional polarization and an increase in the EVPA variability in the lower frequency band are visible. |
 |
Fig. 2. Time-dependent fractional LP measurements obtained at 86.3, 100.3, and 229.1 GHz presented on the 𝒬/ℐ − 𝒰/ℐ plane of linear polarization, compared with the past measurements at the corresponding frequencies. The colors denote the time progression, following the colorbars. The polar coordinates indicate fractional polarization (in %) and EVPA (in degrees; 0° ≡180° corresponds to EVPA aligned with the north-south axis). |
Summary of the Sgr A* light curves observed with ALMA in April 2017.
We also present time-dependent fractional LP vector measurements obtained at 86.3, 100.3, and 229.1 GHz (the latter following Wielgus et al. 2022a) in Fig. 2. We compare these measurements with the results reported by Macquart et al. (2006) at 86.3 GHz (low S/N measurements not shown), Liu et al. (2016) at 105−107 GHz, Marrone et al. (2007) at 230.6−231.9 GHz, Bower et al. (2018) at 226.0 GHz, and Wielgus et al. (2022a) at 229.1 GHz. We observe consistency between these historical measurements and our light curves at 86.3 and 100.3 GHz. The large temporal variations of the EVPA that we observe on a timescale of a few hours explain the EVPA changes reported by Macquart et al. (2006) between subsequent observing days. These variations appear as a full counterclockwise loop on the plane of linear polarization executed between 8:00 and 11:30 UT on 2017 April 3 (see the
EVPA panel in Fig. 1 and the first two panels in Fig. 2). If we attempted to explain this loop in the framework of a coherent orbital motion, we would conclude a Keplerian orbit of ∼20 rg radius. However, the direction of the loop is opposite to the one observed by Wielgus et al. (2022a) and GRAVITY Collaboration (2023), challenging that interpretation. At 230 GHz, we generally see a slightly increased degree of LP in 2017 with respect to the previous measurements, which can be related to the lower total compact flux density reported in April 2017 (mean 2.4 Jy in April 2017 comparing to mean 3.2 Jy in 2005−2019; Wielgus et al. 2022b). The 230 GHz EVPA, while variable, appears to have a preference for values χ ∼ 120° (derotated EVPA χ0 = χ − RMλ2 ∼ 170°), and almost never takes values in the range between −20° and 80°, which constitutes a potentially powerful constraint on theoretical models, particularly for the on-sky position angle of the system. As an example, for a toy model in which the observed nonzero net LP is a consequence of Doppler boosting of the approaching side of the inclined accretion disk, we expect the on-sky projected disk spin axis to align with the intrinsic EVPA χ0 for the predominantly azimuthal magnetic field, and to be perpendicular to χ0 if the magnetic field is predominantly vertical.
2.3. Depolarization at lower frequencies
A significant change in the fractional polarization with the observing frequency is summarized in Fig. 3, where we fitted the spectral indices of p and |v|, as reported in Table 1, across ALMA sub-bands. In band 3 we measured a steep depolarization toward lower frequencies p ∝ ν3, inconsistent with the milder depolarization p ∝ ν seen in band 6. Similarly, the fractional CP has a weak dependence on the frequency in band 6, inconsistent with the upper limits on |v| that we report in band 3, which we give as |v|< 0.3%, based on the time-resolved analysis. An increase in LP fraction with frequency has been observed in active galactic nuclei (AGN); for example, Agudo et al. (2014) reported a mean factor of ∼1.5 change between 86 and 229 GHz, corresponding to a fractional LP spectral index αp ≈ 0.5. A plausible explanation is that the higher frequency emission originates from a more compact region, with a more ordered magnetic field, or that the changes are related to the optical depth variation. However, the effect observed in Sgr A* is far more extreme, hinting at a prominent transition in the system in its innermost part, at around 5 − 10 rg, possibly separating strong and ordered magnetic fields near the event horizon (Johnson et al. 2015) from a weaker and more chaotic component farther away. The depolarization could also be caused by the optical depth τ increasing at lower frequencies, as polarization from the optically thick thermal synchrotron emission is suppressed exponentially with τ (Pacholczyk 1970). Hence, an increase in the optical depth by Δτ ≲ 2 would suffice to explain the change in fractional polarization. However, the opacity interpretation is only straightforward under the assumption of a uniform optical depth in the emission zone, which is likely an oversimplification.
 |
Fig. 3. Spectral dependence of Sgr A* fractional polarization, fitted with a power-law p(ν)∝να. Both LP and CP measurements indicate a rapid depolarization with decreasing frequency at about 100 GHz (2017 April 3) in contrast to a weak dependence of fractional polarization at observing frequencies above 200 GHz (2017 April 6). The error bars represent the standard deviation in the samples and are dominated by the intrinsic source variability, while the formal uncertainties of the spectral index fits are very small (see Table 1). |
2.4. Faraday rotation
Linearly polarized radiation undergoes a change in EVPA as it propagates through a Faraday screen, the magnetized plasma located between the emitter and the observer. This effect is quantified with rotation measure (RM), which can be defined as
for two observing wavelengths λ1, λ2. If the Faraday depth is small and the Faraday screen is external with respect to the emitting region, the RM is independent of the observing wavelength and the approximation in Eq. (2) turns into a strict equality. The intrinsic (derotated) EVPA of the emission can then be calculated as
On the other hand, measuring inconsistent values of RM at different wavelengths indicates a deviation from the λ2 relation, implying either a complex unresolved source structure involving multiple Faraday screens or an internal Faraday screen overlapping with the emission zone at some wavelengths (Burn 1966; Brentjens & de Bruyn 2005). These effects have been observed, for example in the quasar 3C 273 (Hovatta et al. 2019). In the case of Sgr A*, VLBI observations reveal a persistent, simple, compact, single-component source morphology across frequencies, and hence the internal Faraday screen interpretation is favored.
The RM toward Sgr A* has been well established through measurements at frequencies near 230 GHz (λ = c/ν ≈ 1.3 mm), with RM ≈ −5 × 105 rad m−2 (Bower et al. 2003, 2018; Marrone et al. 2007; Wielgus et al. 2022a), which is a rather large value when compared to what is typically observed toward AGN sources (e.g., Goddi et al. 2021). The RM was shown to fluctuate significantly (Bower et al. 2018), even on very short (sub-hour) timescales (Wielgus et al. 2022a). This poses a difficulty in estimating the RM based on nonsimultaneous EVPA measurements, with both RM and EVPAs fluctuating in time; the short associated timescales generally point toward the Faraday screen compactness.
There are not many RM measurements in Sgr A* available at different frequencies. They involve estimates at 345 GHz by Marrone et al. (2007), who found a mean RM in excess of −106 rad m−2, but large measurement uncertainties did not allow us to exclude consistency with the values observed at 230 GHz. At longer wavelengths, Macquart et al. (2006) calculated RM between 86 GHz and 230 GHz, but concluded that consistency with 230 GHz measurements depended on shifting the (180°-periodic) EVPA measurement by 180°, and a significantly lower RM was estimated without the shift. A preliminary discussion of ALMA bands 3 and 6 RM measurements (under the static source assumption) and their implications was presented in Goddi et al. (2021).
Following our time-dependent calibration of the ALMA observations, we estimated RM as a function of time by fitting a linear model for the EVPA as a function of squared wavelength across four sub-bands in band 3, independently for each timestamp. Subsequently, we compared these measurements with the band 6 results, already discussed in Appendix A of Wielgus et al. (2022a). While the time-dependent model linear in λ2 provides a good fit quality across each ALMA band individually, the resulting RM measurements significantly differ between the two bands. This is shown in Fig. 4, where high time cadence RM measurements in ∼6 h duration observing windows are presented for the mean band 3 frequency of 93 GHz (2017 April 3) and mean band 6 frequency of 221 GHz (2017 April 6). RM values observed at the lower frequency band are incompatible with both quasi-contemporaneous and historical measurements near 230 GHz, demonstrating a deviation from the λ2 relation defined in Eq. (2). This implies that about one-half of the Faraday rotation occurs internally with respect to the 93 GHz emission region, at most several rg away from the SMBH’s event horizon. The two measurements give an approximate scaling relation RM ∝ r−1.
 |
Fig. 4. Studies of RM in Sgr A*. Left and center: Time-resolved RM measurements in ALMA band 3 (85−101 GHz, blue) and band 6 (212−230 GHz, orange) in 2017 April, and corresponding histograms of the observed RM. The dashed lines represent mean values. The rapid variability of RM hints at the internal character of the Faraday screen, which is further supported by a significant discrepancy between the measurements obtained for the two bands, also including historical data, and a joint histogram of the 2017 April 6, 7, and 11 data (dashed gray line). Right: SF analysis of the RM variability, indicating more variability at higher frequencies, with a stronger contribution from the shortest timescales. A 0.5 h variability decorrelation timescale is found for the 221 GHz RM data, which is absent at 93 GHz. |
Furthermore, in the EVPA panels of Fig. 1 we show the intrinsic EVPA values χ0(t), derotated using the time-dependent RM measurements and Eq. (3). If the Faraday screen was external, but variable on short timescales, derotating χ(t) should reduce its variability. Since the shape of derotated χ0(t) and its measured variability remain overall very similar to those of the observed χ(t), we conclude that the intrinsic variability of the emitter dominates over the variability in the external Faraday screen, consistent with the dominant character of the internal Faraday screen component.
Simultaneous measurements of LP at distinct frequencies are necessary in order to provide an ultimate and “bulletproof” argument for the λ2 relation violation, otherwise one could still attempt to explain our results with an unusually low, but λ-independent RM on 2017 April 3. Nonetheless, these findings constitute by far the most convincing observational demonstration of an internal Faraday screen component in Sgr A* to date.
2.5. Quantifying the RM variability
We investigate the RM variability with the structure function (SF) approach (Simonetti et al. 1985), which is the time-domain analog of the power spectrum analysis, defined as
where the averaging is taken over all times t. Hence, the SF effectively splits the observed variation across timescales τ (lags). The results of the SF analysis are shown in the right panel of Fig. 4, where we compare 2017 April 3 and 6 analysis, as well as the joint analysis of band 6 RM calculated for April 6, 7, and 11, with a total of ∼20 h of data, increasing the formal robustness of the obtained estimates, although under the uncertain assumption of a stationary character of the RM time series. We confirm significantly less variation in the lower frequency band across the sampled timescales in the absolute sense (unnormalized RM variance, as shown in Fig. 4). Relative to the mean value, RM fluctuates by ∼24% at the lower frequency and by ∼16% at the higher one (Table 1). These fluctuations are strongly dominated by the intrinsic source variability rather than by the measurement errors. Furthermore, the short timescale variability slope in band 3 is significantly steeper than the one revealed by the joint analysis of band 6, implying less power at the shortest timescales in the band 3 data, consistent with the Faraday rotation occurring on larger physical scales at the lower frequency. We observe a similar dependence in the SF of RM in a numerical GRMHD simulation of Sgr A* (see also Sect. 4), with the lower frequency slope α = 0.5 steeper than the higher frequency slope α = 0.2. However, both slopes in the simulation are significantly less steep than the observations, indicating a larger contribution from variability occurring on the shortest timescales in the numerical model than in the real source. In the joint analysis of the April 6, 7, and 11 data, an SF maximum occurs at around 0.2−0.3 h, and for timescales longer than 0.5 h SF becomes flat, indicating an uncorrelated variability structure for larger time lags. Hence, we identify 0.5 h as a characteristic timescale for the 221 GHz Faraday screen variability. A similar flattening is not apparent at 93 GHz, but the reason is most likely related to the short total duration of the observed light curve. We predict that a longer decorrelation timescale will be identified in band 3 with additional observations, allowing us to contrast the characteristic timescales at different frequencies. The frequency dependence of the statistical characteristics of the RM variability is yet another hint that the Faraday screen is different for the two observed bands, and at least partly cospatial with the compact emission region. Additionally, in Appendix A we present SF analysis of RM performed individually for all three band 6 observing days.
3. Implications for the RIAF model
3.1. Electrons temperature profile
In order to study the implications of our findings for the RIAF model (Yuan et al. 2003), we first used the quasi-simultaneous VLBI observations of Sgr A* from April 2017 to constrain the radial distribution of the electron temperature. These data sets are summarized in Table 2. The VLBI observations measure flux density Sν and allow us to estimate the intrinsic (descattered, see Johnson et al. 2018) angular size of the source θmaj × θmin, modeled as an elliptical Gaussian. Hence, they allow us to estimate the brightness temperature of Sgr A*, a proxy for the temperature of the emitting electrons under the assumption of a thermal energy distribution
VLBI measurements of the intrinsic morphology and brightness temperature of Sgr A* in April 2017.
where flux density is given in Jy, frequency in GHz, and angular dimensions in mas. Furthermore, the observed intrinsic size of the source allows us to estimate the characteristic emission radius re as
where θg = rg/D is the angular size of the source gravitational radius rg viewed from a distance D, and following GRAVITY Collaboration (2022) we take θg = 5.1 μas. The subtraction of 1 in Eq. (6) approximately accounts for the geometric lensing around the black hole regardless of the detailed spacetime geometry (Gralla & Lupsasca 2020; Wielgus 2021). The emission from the vicinity of the SMBH’s event horizon is affected by the gravitational redshift, which scales the intrinsic brightness temperature by a factor of (1 + z) = [−gtt(re)]−0.5 = (1 − 2M/re)−0.5, TB, int = (1 + z)TB, obs (see Fig. 5 and Table 2).
 |
Fig. 5. Fitting intrinsic brightness temperature TB, int as a function of the emission radius re. TB, int is a proxy for the temperature of the emitting electrons Te. The measurements are based on the gravitational-redshift-corrected VLBI observations performed on 2017 April 3–7, with 20% errorbars assumed on the TB and re estimates. |
The EHT measurement deviates from a power-law characterizing TB, int at lower frequencies, which can be clearly seen in Fig. 5. We verify that the choice of an elliptical Gaussian model rather than a ring model with parameters reported in Event Horizon Telescope Collaboration (2022a) does not impact the Tb estimates by more than ∼20%. A possible explanation for the lower TB, int is either that the emission at 230 GHz, corresponding to re ≈ 4 rg, is optically thin and nonthermal, violating assumptions of the Tb calculation, and/or that the emission is produced by plasma plunging into the black hole with a relativistic radial velocity component and thus experiencing Doppler deboosting. Hence, we fit a power-law Te(r) = T0(r/rg)γ only to the three 22−86 GHz data points, obtaining γ = −0.87 ± 0.20 and T0 ≈ 2.0 × 1011 K. The estimated power-law index is consistent with the values commonly assumed for Te(r) in RIAF models (e.g., Broderick et al. 2011; Vincent et al. 2022; Vos et al. 2022) based on spectral energy density fitting (Yuan et al. 2003). Additionally, based on the four VLBI measurements reported in Table 2, we model the intrinsic source size dependence on frequency, finding a scaling of re ∝ ν−1.2, between the values reported by Shen et al. (2005) and Bower et al. (2006).
3.2. RM in a RIAF model
We study the properties of a simple spherically symmetric RIAF power-law model to see whether the observed wavelength-dependent RM can be reconciled with the theoretical expectations. In this framework, we can compute RM with the integral along the line of sight from the emitter to the observer (e.g., Mościbrodzka et al. 2017)
for the electron number density ne measured in cm−3 and magnetic field component along the line of sight B∥ measured in G. The additional dimensionless multiplier fe(Θe) is related to the reduced impact of hot relativistic electrons, and can be expressed as a function of dimensionless electron temperature Θe = kTe/mec2 (Quataert & Gruzinov 2000; Ressler et al. 2023)
The presence of this correction factor was raised as an argument against the internal Faraday screen in a RIAF system, since the contribution from the very hot innermost region would be strongly reduced (e.g., Marrone et al. 2006; Macquart et al. 2006). The argument appears reasonable, as the suppression factor from fe(Θe) reaches 0.008 at Te = 1011 K (Θe = 16.8). Moreover, the characteristic linear scale of a compact system is small in comparison to what the thickness of the external Faraday screen could be. Nevertheless, we show that constructing a RIAF flow model with significant internal Faraday rotation occurring inside the 10 rg radius is feasible regardless of the fe(Θe) factor.
For the RIAF model we assume the electron temperature distribution estimated in Sect. 3.1
We also assume power-law distributions for the electron number density ne and magnetic field parallel to the line of sight B∥
To simplify the problem further, we assume the emission at each separate frequency band to originate from a sphere located at the radius re, as estimated in Sect. 3.1: an onion-like model of the Sgr A* radio source. Particularly in case of a low optical depth these radii may only have an effective, approximate sense. We then require for the RM, integrated between the respective re and the distant observer (robs = 105 rg for practical purposes) using Eq. (7), to match the ALMA measurements. We assume a background RM value of −7 × 104 rad m−2, following the measurement of RM toward the Galactic Center magnetar J1745−2900 (Eatough et al. 2013), located ∼106 rg from Sgr A* (projected distance of ∼0.1 pc), with a caveat that the RM toward the magnetar is itself variable, and may involve a contribution from its compact vicinity. Since the sign of RM depends only on the polarity of the uniform magnetic field, we work with absolute values of the RM. With two RM measurements corresponding to different re, we can then fit for the two model parameters, α + β, and n0B0. In Fig. 6 we show a solution, corresponding to
 |
Fig. 6. Predicted value of RM as a function of the emission radius for a RIAF toy-model fitted to the ALMA data. The background RM corresponding to the value observed toward the magnetar J1745−2900 is assumed. Accounting for the relativistic correction fe decreases the RM significantly, by a factor of 20 for re = 4 rg, but does not preclude the dominant contribution to the Faraday rotation from the innermost part of the flow. |
Comparing our results to the thermal synchrotron one-zone emission model given by Event Horizon Telescope Collaboration (2022b), with ne, zone = 106 cm−3 and Bzone = 29 G, we can reproduce these numbers reasonably well as ne(re) and B∥(re) for α = −1.5, β = −2, and re = 4 rg. In Fig. 6 we also show the RM from the same model, computed neglecting the fe(Θe) factor. Accounting for this correction has a big impact on the results, but regardless of its presence Faraday rotation may be dominated by the plasma in the innermost part of the accretion flow.
To reproduce the observed ratio of the two RM measurements, around a factor of 2, we generally need a high value of α + β in the RIAF model. As an example, α + β = −2.5 assumed by Vos et al. (2022) appears insufficient, yielding a ratio of 1.4. Steeper radial decay favors the interpretation involving vertical rather than azimuthal magnetic fields, but on the other hand it may also correspond to a partially inhomogeneous magnetic field, where contributions from different emission regions cancel one another out. If we attribute the large contribution to the Faraday rotation from the innermost region of the flow to the partially ordered (Johnson et al. 2015) vertical magnetic field then it also suggests a relatively low viewing angle, so that a significant component of the magnetic field is oriented along the line of sight. Both vertical magnetic field and low inclination are consistent with the conclusions of GRAVITY Collaboration (2018), Wielgus et al. (2022a), and Event Horizon Telescope Collaboration (2022b). A low viewing angle and a dominant RM contribution from compact scales were also concluded by Sharma et al. (2007) based on the analysis of global MHD simulations of accretion in Sgr A*.
As an additional sanity check we estimate the locations of photospheres rph for the observing frequencies in the model with the parameters estimated above, following the calculations of Mahadevan et al. (1996) and integrating the resulting thermal synchrotron opacities inward. Interestingly, we obtain rph around 4 rg at 228.1 GHz and rph around 7 rg at 86.3 GHz, which are not terribly inconsistent with the estimated emission radii re. At lower frequencies rph are too low and generally smaller than 20 rg. We do not attempt to fit the locations of photospheres by tuning the model parameters.
Since the presented model constitutes an extreme simplification of reality, our findings should be considered primarily as a demonstration that an internal Faraday screen in Sgr A*, dominated by the contribution from very compact scales, is to be expected for a reasonable set of physical parameters in a RIAF system. Any more quantitative conclusions should be taken with a sizeable grain of salt.
4. Comparisons to general relativistic magnetohydrodynamics
Models more physically self-consistent than a power-law RIAF are obtained through numerical GRMHD simulations. RM in GRMHD simulations was studied by Mościbrodzka et al. (2017) and Ricarte et al. (2020), among others, in the context of M 87*, and more recently by Ressler et al. (2023) for Sgr A*. Event Horizon Telescope Collaboration (2022b) considered a large library of GRMHD models in order to identify ones that fulfill observational constraints. Here we investigate one of the models favored by the EHT analysis (the “best-bet” model), corresponding to a magnetically arrested disk (MAD; Narayan et al. 2003) system, viewed at low inclination of 30 deg. High magnetization and a small viewing angle are also supported by the analysis of GRAVITY Collaboration (2018) and Wielgus et al. (2022a). The model considered is also characterized by a moderate SMBH spin a* = 0.5 and an ion-to-electron temperature ratio parameterized by Rhigh = 160 (relatively cold accretion disk electrons; Mościbrodzka et al. 2016; Event Horizon Telescope Collaboration 2022b). While the model passed the majority of observational total intensity constraints, it has been reported (Event Horizon Telescope Collaboration 2022b) that much like other GRMHD MAD models it significantly overproduces the variability in total intensity light curves when compared to observations (Wielgus et al. 2022b). The selected GRMHD simulation was performed using the KHARMA code (a GPU-enabled extension of the iharm3D code; Prather et al. 2021) and consecutively ray-traced in a curved Kerr spacetime using ipole (Mościbrodzka & Gammie 2018; see Wong et al. 2022 for details of the simulation generation pipeline). During ray-tracing a scaling of the plasma density was selected in order to match the 2.4 Jy total compact flux density observed at 228 GHz in April 2017 (Wielgus et al. 2022b). Ray-traced images were then averaged over the entire field of view for each Stokes component at every time step to obtain full-Stokes simulated light curves.
In order to study the polarimetric properties of the simulated GRMHD light curves, we performed ray-tracing at four frequencies, 86.3, 100.3, 213.1, and 229.1 GHz, to be able to mimic the RM measurements at ALMA band 3 and band 6. Each light curve corresponds to the same GRMHD output of 1000 snapshots with a cadence of 5 rg/c ≈ 100 s. Since the light curves observed on 2017 April 3 and 6 have a duration of about 1000 rg/c (about 6 h), we effectively analyze five different realizations of the theoretical GRMHD model.
The GRMHD light curves from the selected best-bet model generally do not match the observed polarimetric properties of Sgr A*. The modeled fractional LP is p = 4 ± 2% across frequencies, with no sign of depolarization in the lower band. Compared to the Sgr A* values presented in Table 1, the model’s polarization is too low in band 6, and too high in band 3. The EVPA in the simulation wanders much more than it does in the band 6 data. The model fractional CP is strongly variable, and while the model mean values at 213−229 GHz are around −1%, similar to the observed quantities, there is about seven times more variability in the simulation than in the observations. Hence, the modeled CP sign flips on a ∼1 h timescale, while it appears to never change in the observed light curves (e.g., Bower et al. 2002; Muñoz et al. 2012; Wielgus et al. 2022a).
The RM in the simulation is evaluated from the EVPA differences between 86.3 and 100.3 GHz, and between 213.1 and 229.1 GHz, following Eq. (2). We only ray-trace the innermost 300 rg zone of the GRMHD simulation, hence there is no large-scale Faraday screen present. Since we find significantly different values of RM at each band for the same time snapshots, the Faraday screen in the simulations is necessarily largely internal (located between the 93 and 221 GHz emission region), consistently with our interpretation of the observations. This is illustrated in Fig. 7 where we show the cumulative distribution function (CDF) of the ratio of RM at 93 GHz (corresponding to the Faraday screen component located roughly between ∼9 rg and 300 rg) to the difference between RM at 221 GHz and 93 GHz (corresponding to the Faraday screen component located roughly between ∼4 rg and 9 rg). The figure indicates that in the GRMHD simulation the more compact component is typically dominating the total RM measured at 221 GHz with a factor of |RM93/(RM221 − RM93)| ∼ 0.1 − 0.2. Hence, the numerical model appears to be on average even more strongly dominated by the compact Faraday screen component than the observations, where the similar ratio is |RM93/(RM221 − RM93)| ∼ 1. Moreover, in the simulation the signs of the two components are uncorrelated, with 49% of snapshots indicating sign differences between the components. On the contrary, both components are persistently negative in the observations.
 |
Fig. 7. CDF of the ratio of RMs measured in the GRMHD simulation at 93 GHz (sensitive to the Faraday screen external with respect to the 93 GHz emission zone) and the difference between RM measured at 221 GHz and 93 GHz (sensitive to the screen component located between the 221 GHz and 93 GHz emission zones). Simultaneous ray-traced snapshots were considered to construct this empirical CDF. These results demonstrate that in the simulation the Faraday screen is typically (in 88% of snapshots) dominated by the contribution from the very compact region. |
While the observed RMs vary by ∼20 − 30% around the median values and (almost) never change sign, in the simulations the RM sign flips often, on a ∼1 h timescale. In order to maximize the consistency, in Fig. 8 we flip the sign of the model RM and shift the RM values by the Galactic Center magnetar RM to roughly represent the contribution from the Faraday rotation occurring outside of the GRMHD simulation domain. Accounting for the external Faraday rotation is sufficient for the model band 3 RM to mostly remain negative, although they are about a factor of two lower than the observed values. Recently Ressler et al. (2023) suggested, based on multiscale MHD/GRMHD modeling of the Sgr A* accretion flow fed by stellar winds, that the constant observed RM sign is related to a large and stable external contribution, dominating over the rapidly varying RM component from the compact region. This interpretation is challenged by our results. While it is easy to imagine a larger RM bias related to an external Faraday screen, allowing us to match the 93 GHz observations, a more challenging endeavor is to reproduce the large and strictly negative difference between RM at 221 and 93 GHz, necessarily caused by an intrinsic and very compact Faraday screen component. Not only are the RM values in our GRMHD simulation at band 6 smaller (in a mean sense) than observed, they are also dramatically more variable with respect to the median value, which is close to zero in the simulation (see also Sharma et al. 2007; Pang et al. 2011). This discrepancy can be understood in the framework of the magnetic field variability, which is the only signed quantity contributing to the RM. It appears that the magnetic field is far more turbulent and variable in the simulations than in reality, which echoes the total intensity light curve variability discrepancy of Event Horizon Telescope Collaboration (2022b).
 |
Fig. 8. Smoothed histograms of RM extracted from the GRMHD simulation (sign-flipped and shifted by the Galactic Center magnetar RM = −7 × 104 rad m−2) compared to the ranges inferred from observations on 2017 April 3 and 6, discussed in Sect. 2.4 (vertical bands). Shaded and hatched regions denote intervals containing 68% of the distribution around the median value. |
MAD models with lower Rhigh parameter (Rhigh = 160 is the largest value considered in the EHT simulation library) will have hotter electrons than the best-bet model studied here. Hotter electrons would only further decrease the mean value of RM with little impact on its stability because the emission would still emerge from the disk with turbulent magnetic fields. An interesting alternative is the observed millimeter radiation originating predominantly in the jet sheath region, which is typically threaded by a more stable, nearly vertical magnetic field in GRMHD simulations (Mościbrodzka & Falcke 2013). A subsequent detailed comparison of the simulations from the EHT library (and beyond it) with polarimetric observations at different wavelengths should provide more insight in the future.
5. Summary and conclusions
Using high sensitivity ALMA observations, we characterized the full-Stokes light curves of Sgr A* in the 85−101 GHz range, and compared them with a complementary data set obtained at 212−230 GHz. The two data sets were obtained just three days apart, on 2017 April 3 and 6. We provided new measurements of linear polarization at 85−101 GHz as well as stringent upper limits on circular polarization. The fractional polarization of Sgr A* decreases rapidly below 150 GHz, which we interpret as a transition in the accretion flow, possibly in magnetic field geometry, strength, or coherence, occurring at around 5 − 10 rg, but it could also be related to the transition to an optically thin flow at higher frequencies. Our observations yield time-dependent measurements of the RM in the 85−101 GHz band, which we find to be lower than the established measurements at higher frequencies by a factor of two. Together with the rapid temporal variability of the RM, lack of variability reduction in the derotated EVPA, and different statistical characteristics of RM temporal variability in the two frequency bands, these results show that the Faraday screen in Sgr A* is most likely largely of internal character, cospatial with the compact region of the synchrotron emission. We demonstrate how these findings can be reproduced using a simple theoretical model of a radiatively inefficient accretion flow. Finally, we demonstrate that the Faraday screen is largely internal in the numerical GRMHD simulations of Sgr A*. However, the particular simulation that we considered, while mostly consistent with the observational total intensity constraints, did not quantitatively reproduce the observed parameters of polarization, and indicated significantly more variability in the polarization fractions and in the rotation measure than is observed in Sgr A*.
The results of Goddi et al. (2021) follow the publicly available ALMA QA2 calibrated data reduction path, without the subsequent intrafield calibration step of Wielgus et al. (2022b) that enables time-dependent light curve analysis.
Acknowledgments
We thank Geoff Bower, Ilje Cho, Michael D. Johnson, Thomas Krichbaum, Dan Marrone, Ue-Li Pen, Venkatessh Ramakrishnan, Sean Ressler, Angelo Ricarte, Pablo Torne, Sebastiano von Fellenberg, and Guang-Yao Zhao for their helpful comments and enlightening discussions, as well as Vedant Dhruv, Charles Gammie, Abhishek Joshi, Ben Prather, and George Wong for performing the GRMHD simulation that we analyzed. We also thank Alexandra Elbakyan for her contributions to the open science initiative. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2016.1.01404.V and ADS/JAO.ALMA#2016.1.00413.V ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. This research is supported by the European Research Council advanced grant “M2FINDERS – Mapping Magnetic Fields with INterferometry Down to Event hoRizon Scales” (Grant No. 101018682). S.I. is supported by Hubble Fellowship grant HST-HF2-51482.001-A awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555. I.M.V. acknowledges partial support from Generalitat Valenciana (GenT Project CIDEGENT/2018/021), the MICINN Research Project PID2019-108995GB-C22 and the ASTROVIVES FEDER infrastructure IDIFEDER-2021-086. I.M.V. also acknowledges support from the Project European Union NextGenerationEU (PRTR-C17I1). M.M. acknowledges support by the NWO grant No. OCENW.KLEIN.113 and support by the NWO Science Athena Award. R.E. acknowledges the support from grant numbers 21-atp21-0077, NSF AST-1816420, and HST-GO-16173.001-A as well as the Institute for Theory and Computation at the Center for Astrophysics. C.G. was supported by FAPESP (Fundação de Amparo á Pesquisa do Estado de São Paulo) under grant 2021/01183-8.
References
- Agudo, I., Thum, C., Gómez, J. L., & Wiesemeyer, H. 2014, A&A, 566, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aitken, D. K., Greaves, J., Chrysostomou, A., et al. 2000, ApJ, 534, L173 [Google Scholar]
- Balick, B., & Brown, R. L. 1974, ApJ, 194, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Falcke, H., & Backer, D. C. 1999a, ApJ, 523, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Wright, M. C. H., Backer, D. C., & Falcke, H. 1999b, ApJ, 527, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Falcke, H., Sault, R. J., & Backer, D. C. 2002, ApJ, 571, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Wright, M. C. H., Falcke, H., & Backer, D. C. 2003, ApJ, 588, 331 [Google Scholar]
- Bower, G. C., Goss, W. M., Falcke, H., Backer, D. C., & Lithwick, Y. 2006, ApJ, 648, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Broderick, A., Dexter, J., et al. 2018, ApJ, 868, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Brentjens, M. A., & de Bruyn, A. G. 2005, A&A, 441, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Broderick, A. E., Fish, V. L., Doeleman, S. S., & Loeb, A. 2011, ApJ, 735, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Burn, B. J. 1966, MNRAS, 133, 67 [Google Scholar]
- Cho, I., Zhao, G.-Y., Kawashima, T., et al. 2022, ApJ, 926, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Conway, J. E., Cornwell, T. J., & Wilkinson, P. N. 1990, MNRAS, 246, 490 [Google Scholar]
- Do, T., Hees, A., Ghez, A., et al. 2019, Science, 365, 664 [Google Scholar]
- Doeleman, S. S., Weintroub, J., Rogers, A. E. E., et al. 2008, Nature, 455, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Eatough, R. P., Falcke, H., Karuppusamy, R., et al. 2013, Nature, 501, 391 [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022a, ApJ, 930, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022b, ApJ, 930, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022c, ApJ, 930, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022d, ApJ, 930, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Goddi, C., Martí-Vidal, I., Messias, H., et al. 2019, PASP, 131, 075003 [Google Scholar]
- Goddi, C., Martí-Vidal, I., Messias, H., et al. 2021, ApJ, 910, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Gralla, S. E., & Lupsasca, A. 2020, Phys. Rev. D, 101, 044031 [NASA ADS] [CrossRef] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2018, A&A, 618, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2022, A&A, 657, L12 [NASA ADS] [CrossRef] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2023, A&A, 677, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hovatta, T., O’Sullivan, S., Martí-Vidal, I., Savolainen, T., & Tchekhovskoy, A. 2019, A&A, 623, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Issaoun, S., Johnson, M. D., Blackburn, L., et al. 2019, ApJ, 871, 30 [Google Scholar]
- Iwata, Y., Oka, T., Tsuboi, M., Miyoshi, M., & Takekawa, S. 2020, ApJ, 892, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, M. D., Fish, V. L., Doeleman, S. S., et al. 2015, Science, 350, 1242 [Google Scholar]
- Johnson, M. D., Narayan, R., Psaltis, D., et al. 2018, ApJ, 865, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H. B., Wright, M. C. H., Zhao, J.-H., et al. 2016, A&A, 593, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lo, K. Y., & Claussen, M. J. 1983, Nature, 306, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, R. S., Krichbaum, T. P., Eckart, A., et al. 2011, A&A, 525, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Macquart, J.-P., Bower, G. C., Wright, M. C. H., Backer, D. C., & Falcke, H. 2006, ApJ, 646, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Mahadevan, R., Narayan, R., & Yi, I. 1996, ApJ, 465, 327 [Google Scholar]
- Marrone, D. P., Moran, J. M., Zhao, J.-H., & Rao, R. 2006, ApJ, 640, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Marrone, D. P., Moran, J. M., Zhao, J.-H., & Rao, R. 2007, ApJ, 654, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, L. D., Crew, G. B., Doeleman, S. S., et al. 2018, PASP, 130, 015002 [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 127 [Google Scholar]
- Michail, J. M., Yusef-Zadeh, F., Wardle, M., & Kunneriath, D. 2023, MNRAS, 520, 2644 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, M. R. 2023, ArXiv e-prints [arXiv:2302.02431] [Google Scholar]
- Mościbrodzka, M., & Falcke, H. 2013, A&A, 559, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mościbrodzka, M., & Gammie, C. F. 2018, MNRAS, 475, 43 [CrossRef] [Google Scholar]
- Mościbrodzka, M., Falcke, H., & Shiokawa, H. 2016, A&A, 586, A38 [Google Scholar]
- Mościbrodzka, M., Dexter, J., Davelaar, J., & Falcke, H. 2017, MNRAS, 468, 2214 [CrossRef] [Google Scholar]
- Muñoz, D. J., Marrone, D. P., Moran, J. M., & Rao, R. 2012, ApJ, 745, 115 [CrossRef] [Google Scholar]
- Murchikova, L., & Witzel, G. 2021, ApJ, 920, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Mus, A., Martí-Vidal, I., Wielgus, M., & Stroud, G. 2022, A&A, 666, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narayan, R., Yi, I., & Mahadevan, R. 1995, Nature, 374, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., Igumenshchev, I. V., & Abramowicz, M. A. 2003, PASJ, 55, L69 [NASA ADS] [Google Scholar]
- Pacholczyk, A. G. 1970, Radio Astrophysics. Nonthermal Processes in Galactic and Extragalactic Sources (San Francisco: Freeman) [Google Scholar]
- Pang, B., Pen, U.-L., Matzner, C. D., Green, S. R., & Liebendörfer, M. 2011, MNRAS, 415, 1228 [NASA ADS] [CrossRef] [Google Scholar]
- Prather, B., Wong, G., Dhruv, V., et al. 2021, J. Open Source Softw., 6, 3336 [NASA ADS] [CrossRef] [Google Scholar]
- Quataert, E., & Gruzinov, A. 2000, ApJ, 545, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Ressler, S. M., White, C. J., & Quataert, E. 2023, MNRAS, 521, 4277 [CrossRef] [Google Scholar]
- Ricarte, A., Prather, B. S., Wong, G. N., et al. 2020, MNRAS, 498, 5468 [NASA ADS] [CrossRef] [Google Scholar]
- Sharma, P., Quataert, E., & Stone, J. M. 2007, ApJ, 671, 1696 [Google Scholar]
- Shen, Z.-Q., Lo, K. Y., Liang, M. C., Ho, P. T. P., & Zhao, J. H. 2005, Nature, 438, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Simonetti, J. H., Cordes, J. M., & Heeschen, D. S. 1985, ApJ, 296, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuboi, M., Miyahara, H., Nomura, R., Kasuga, T., & Miyazaki, A. 2003, Astron. Nachr. Suppl., 324, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Vincent, F. H., Gralla, S. E., Lupsasca, A., & Wielgus, M. 2022, A&A, 667, A170 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vos, J., Mościbrodzka, M. A., & Wielgus, M. 2022, A&A, 668, A185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wielgus, M. 2021, Phys. Rev. D, 104, 124058 [NASA ADS] [CrossRef] [Google Scholar]
- Wielgus, M., Moscibrodzka, M., Vos, J., et al. 2022a, A&A, 665, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wielgus, M., Marchili, N., Martí-Vidal, I., et al. 2022b, ApJ, 930, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, G. N., Prather, B. S., Dhruv, V., et al. 2022, ApJS, 259, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F., & Narayan, R. 2014, ARA&A, 52, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F., Quataert, E., & Narayan, R. 2003, ApJ, 598, 301 [Google Scholar]
Appendix A: 2017 April 7 and 11 data
We present a summary of the analysis of ALMA light curves obtained on 2017 April 7 and 11, in the same fashion as presented in Table 1 for the 2017 April 3 and 6 data. On April 11 an X-ray flare occurred shortly before the ALMA observations (Event Horizon Telescope Collaboration 2022c; Wielgus et al. 2022a). On this day the 230 GHz light curves were significantly more variable, with a more negative spectral index and lower RM. These changes are broadly consistent with a hotter, more optically thin accretion disk on April 11 (see also Wielgus et al. 2022a,b).
Summary of the properties of Sgr A* light curves observed with ALMA in April 2017.
Furthermore, in Fig. A.1 we study the time variability of the measured RM, elaborating on the analysis presented in Section 2.5. The short timescale slopes of SF at 221 GHz correspond to α = 0.6 − 0.7 on April 7, 11, and in the joint analysis of the April 6, 7, and 11 data. The April 6 data indicate a steeper SF slope more consistent with the April 3 result at 93 GHz. We conclude that the SF slope is typically less steep at higher frequencies, consistently with the interpretation of a more compact Faraday screen, characterized by shorter variability timescales. The flattening of SF for timescales longer than 0.5 h, discussed in Section 2.5, is most prominently visible on April 6, April 7, and in the joint analysis.
 |
Fig. A.1. SF analysis of the RM variability at 93 GHz and 221 GHz separately for the three observing days, and combined. The figure shows more absolute variability at 221 GHz in all cases, with a typically less steep SF slope at the short timescales range than in case of 93 GHz. A 0.5 h variability decorrelation timescale, corresponding to flattening of the SF at longer timescales, is found for some 221 GHz RM data sets, and appears absent at 93 GHz. |
All Tables
VLBI measurements of the intrinsic morphology and brightness temperature of Sgr A* in April 2017.
Summary of the properties of Sgr A* light curves observed with ALMA in April 2017.
All Figures
 |
Fig. 1. Overview of the ALMA light curves of Sgr A* obtained in band 3 (left column) and band 6 (right column), each with four 2 GHz-wide sub-bands, spanning 85−101 GHz and 212−230 GHz, respectively. A significant reduction of the fractional polarization and an increase in the EVPA variability in the lower frequency band are visible. |
| In the text | |
 |
Fig. 2. Time-dependent fractional LP measurements obtained at 86.3, 100.3, and 229.1 GHz presented on the 𝒬/ℐ − 𝒰/ℐ plane of linear polarization, compared with the past measurements at the corresponding frequencies. The colors denote the time progression, following the colorbars. The polar coordinates indicate fractional polarization (in %) and EVPA (in degrees; 0° ≡180° corresponds to EVPA aligned with the north-south axis). |
| In the text | |
 |
Fig. 3. Spectral dependence of Sgr A* fractional polarization, fitted with a power-law p(ν)∝να. Both LP and CP measurements indicate a rapid depolarization with decreasing frequency at about 100 GHz (2017 April 3) in contrast to a weak dependence of fractional polarization at observing frequencies above 200 GHz (2017 April 6). The error bars represent the standard deviation in the samples and are dominated by the intrinsic source variability, while the formal uncertainties of the spectral index fits are very small (see Table 1). |
| In the text | |
 |
Fig. 4. Studies of RM in Sgr A*. Left and center: Time-resolved RM measurements in ALMA band 3 (85−101 GHz, blue) and band 6 (212−230 GHz, orange) in 2017 April, and corresponding histograms of the observed RM. The dashed lines represent mean values. The rapid variability of RM hints at the internal character of the Faraday screen, which is further supported by a significant discrepancy between the measurements obtained for the two bands, also including historical data, and a joint histogram of the 2017 April 6, 7, and 11 data (dashed gray line). Right: SF analysis of the RM variability, indicating more variability at higher frequencies, with a stronger contribution from the shortest timescales. A 0.5 h variability decorrelation timescale is found for the 221 GHz RM data, which is absent at 93 GHz. |
| In the text | |
 |
Fig. 5. Fitting intrinsic brightness temperature TB, int as a function of the emission radius re. TB, int is a proxy for the temperature of the emitting electrons Te. The measurements are based on the gravitational-redshift-corrected VLBI observations performed on 2017 April 3–7, with 20% errorbars assumed on the TB and re estimates. |
| In the text | |
 |
Fig. 6. Predicted value of RM as a function of the emission radius for a RIAF toy-model fitted to the ALMA data. The background RM corresponding to the value observed toward the magnetar J1745−2900 is assumed. Accounting for the relativistic correction fe decreases the RM significantly, by a factor of 20 for re = 4 rg, but does not preclude the dominant contribution to the Faraday rotation from the innermost part of the flow. |
| In the text | |
 |
Fig. 7. CDF of the ratio of RMs measured in the GRMHD simulation at 93 GHz (sensitive to the Faraday screen external with respect to the 93 GHz emission zone) and the difference between RM measured at 221 GHz and 93 GHz (sensitive to the screen component located between the 221 GHz and 93 GHz emission zones). Simultaneous ray-traced snapshots were considered to construct this empirical CDF. These results demonstrate that in the simulation the Faraday screen is typically (in 88% of snapshots) dominated by the contribution from the very compact region. |
| In the text | |
 |
Fig. 8. Smoothed histograms of RM extracted from the GRMHD simulation (sign-flipped and shifted by the Galactic Center magnetar RM = −7 × 104 rad m−2) compared to the ranges inferred from observations on 2017 April 3 and 6, discussed in Sect. 2.4 (vertical bands). Shaded and hatched regions denote intervals containing 68% of the distribution around the median value. |
| In the text | |
 |
Fig. A.1. SF analysis of the RM variability at 93 GHz and 221 GHz separately for the three observing days, and combined. The figure shows more absolute variability at 221 GHz in all cases, with a typically less steep SF slope at the short timescales range than in case of 93 GHz. A 0.5 h variability decorrelation timescale, corresponding to flattening of the SF at longer timescales, is found for some 221 GHz RM data sets, and appears absent at 93 GHz. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



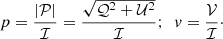
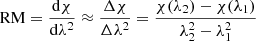
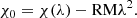
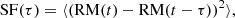
![$$ \begin{aligned} T_{\rm B, obs} = 1.22 \times 10^{12} \frac{S_\nu }{\nu ^2 \theta _{\rm maj} \theta _{\rm min}} \; \mathrm{[K]}, \end{aligned} $$](/articles/aa/full_html/2024/02/aa47772-23/aa47772-23-eq5.gif)
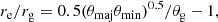
![$$ \begin{aligned} \mathrm{RM} = 10^4 \frac{e^3}{2 \pi m_{\rm e}^2 c^4} \int \limits ^\mathrm{r_{\rm obs}}_{r_{\rm e}} n_{\rm e} B_{\parallel } f_{\rm e}(\Theta _{\rm e}) \mathrm{d}r \ [\mathrm{rad\,m}^{-2}], \end{aligned} $$](/articles/aa/full_html/2024/02/aa47772-23/aa47772-23-eq7.gif)
![$$ \begin{aligned} f_{\rm e}(\Theta _{\rm e}) = {\left\{ \begin{array}{ll} 1&\mathrm{if}\,\,\Theta _{\rm e} \le 1,\\ \Theta _{\rm e}^{-2} \left[0.5 \log (\Theta _{\rm e}) \left(1 - \Theta _{\rm e}^{-1}\right) + 1\right]&\mathrm{if}\,\,\Theta _{\rm e} > 1. \end{array}\right.} \end{aligned} $$](/articles/aa/full_html/2024/02/aa47772-23/aa47772-23-eq8.gif)
![$$ \begin{aligned} T_{\rm e}(r) = 2 \times 10^{11} \left(\frac{r}{r_{\rm g}}\right)^{-0.87}\;\mathrm{[K]}. \end{aligned} $$](/articles/aa/full_html/2024/02/aa47772-23/aa47772-23-eq9.gif)
![$$ \begin{aligned}&n_{\rm e}(r) = n_0 \left(\frac{r}{r_{\rm g}}\right)^{\alpha }\;\mathrm{[cm^{-3}]}, \end{aligned} $$](/articles/aa/full_html/2024/02/aa47772-23/aa47772-23-eq10.gif)
![$$ \begin{aligned}&B_{\parallel }(r) = B_0 \left(\frac{r}{r_{\rm g}} \right)^{\beta }\;\mathrm{[G]}. \end{aligned} $$](/articles/aa/full_html/2024/02/aa47772-23/aa47772-23-eq11.gif)