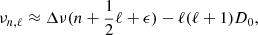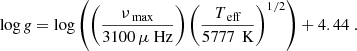| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A190 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201834690 | |
| Published online | 18 February 2019 | |
Asteroseismology of the Hyades red giant and planet host ϵ Tauri⋆,⋆⋆
1
Stellar Astrophysics Centre, Dept. of Physics and Astronomy, Aarhus University, Ny Munkegade, 8000 Aarhus C., Denmark
e-mail: toar@phys.au.dk
2
Key Laboratory of Optical Astronomy, National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100101, PR China
3
Department of Astronomy, China West Normal University, Nanchong 637002, PR China
4
Center for Cosmology and Particle Physics, Dept. of Physics, New York University, 726 Broadway, New York, NY 10003, USA
5
Institute for Astronomy, University of Hawai‘i, 2680 Woodlawn Drive, Honolulu, HI 96822, USA
6
Sydney Institute for Astronomy (SIfA), School of Physics, University of Sydney, NSW 2006, Australia
7
Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
8
Universidad de La Laguna, Dpto. Astrofísica, 38206 La Laguna, Tenerife, Spain
9
IRFU, CEA, Université Paris-Saclay, 91191 Gif-sur-Yvette, France
10
Université Paris Diderot, AIM, Sorbonne Paris Cité, CEA, CNRS, 91191 Gif-sur-Yvette, France
11
School of Physics, The University of New South Wales, Sydney, NSW 2052, Australia
12
Centre for Star and Planet Formation, Niels Bohr Institute, University of Copenhagen, Øster Voldgade 5, 1350 Copenhagen, Denmark
Received:
20
November
2018
Accepted:
4
January
2019
Context. Asteroseismic analysis of solar-like stars allows us to determine physical parameters such as stellar mass, with a higher precision compared to most other methods. Even in a well-studied cluster such as the Hyades, the masses of the red giant stars are not well known, and previous mass estimates are based on model calculations (isochrones). The four known red giants in the Hyades are assumed to be clump (core-helium-burning) stars based on their positions in colour-magnitude diagrams, however asteroseismology offers an opportunity to test this assumption.
Aims. Using asteroseismic techniques combined with other methods, we aim to derive physical parameters and the evolutionary stage for the planet hosting star ϵ Tau, which is one of the four red giants located in the Hyades.
Methods. We analysed time-series data from both ground and space to perform the asteroseismic analysis. By combining high signal-to-noise radial-velocity data from the ground-based SONG network with continuous space-based data from the revised Kepler mission K2, we derive and characterize 27 individual oscillation modes for ϵ Tau, along with global oscillation parameters such as the large frequency separation Δν and the ratio between the amplitude of the oscillations measured in radial velocity and intensity as a function of frequency. The latter has been measured previously for only two stars, the Sun and Procyon. Combining the seismic analysis with interferometric and spectroscopic measurements, we derive physical parameters for ϵ Tau, and discuss its evolutionary status.
Results. Along with other physical parameters, we derive an asteroseismic mass for ϵ Tau of M = 2.458 ± 0.073 M⊙, which is slightly lower than previous estimates, and which leads to a revised minimum mass of the planetary companion. Noting that the SONG and K2 data are non-simultaneous, we estimate the amplitude ratio between intensity and radial velocity to be 42.2 ± 2.3 ppm m−1 s, which is higher than expected from scaling relations.
Key words: asteroseismology / techniques: radial velocities / techniques: photometric / stars: individual: HD 28305 / stars: oscillations / planetary systems
Time-series data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/622/A190
Based on observations made with the SONG telescopes operated on the Spanish Observatorio del Teide (Tenerife) and at the Chinese Delingha Observatory (Qinghai) by the Aarhus and Copenhagen Universities, by the Instituto de Astrofísica de Canarias and by the National Astronomical Observatories of China, and with NASA’s K2 mission.
© ESO 2019
1. Introduction
Stellar open clusters are testbeds for stellar astrophysics because the common distance, chemical composition, formation history and age of the stars in a cluster limits the number of free parameters when fitting models to multiple cluster members. Furthermore, clusters often include objects that provide even more detailed information, such as stars in eclipsing binary systems, stars with exoplanets, and oscillating stars. Nearby clusters offer even better prospects, as they can be studied using multiple complementary techniques, including interferometry and time-resolved spectroscopic observations.
As the nearest open cluster, the Hyades is very well-studied, and even a casual inspection of the literature shows it to be an important laboratory for studying stellar evolution and stellar properties in great detail. With an age around 650 Myr (Lebreton et al. 2001) the cluster stars span a large range in mass. The highest masses are represented by the four brightest giants (γ, ϵ, θ1, and δ1 Tau), which are all thought to be in the core-helium-burning stage (de Bruijne et al. 2001) based on their location in the cluster colour–magnitude diagram. If this is indeed the case, ϵ Tau, which is the subject of this paper, would belong to the secondary clump given its mass of around 2.5 M⊙ (Girardi 1999; Montalbán et al. 2013). ϵ Tau is furthermore a known exoplanet host, with a massive planet (m2 sin i = 7.6 ± 0.2 MJ) in an 595-d orbit (Sato et al. 2007).
The revised Kepler mission, K2 (Howell et al. 2014), has uncovered several planetary systems in the cluster (Mann et al. 2018; Ciardi et al. 2018; Livingston et al. 2018). The high-precision photometry from K2 has also allowed the detection of solar-like oscillations in two main–sequence stars (Lund et al. 2016) and in the four bright giants (White et al., in prep.). Prior to this, Ando et al. (2010) detected oscillations in ϵ Tau based on a few nights of data, with an oscillation signal which is in good agreement with our analysis below. Furthermore, Beck et al. (2015) reported the detection of oscillations in θ1 Tau.
We have used the two nodes of the Stellar Observations Network Group (SONG) to obtain high-precision radial velocities from the sites in Tenerife (Grundahl et al. 2017) and the Delingha observing station in China (Deng et al. 2013) for ϵ Tau. The goal was to provide a dataset of radial velocities of the same duration as the K2 photometric data, such that a combined analysis could be carried out. Space-based photometry offers uninterrupted observations over long time spans and thus provide a good window function for the frequency analysis, whereas radial-velocity (RV) observations have a much higher sensitivity to the oscillations. This is because the background from stellar granulation is much lower in RV than in photometry (Bedding & Kjeldsen 2006; García et al. 2013). Since the RV observations are ground-based, the window function is not as good as from K2, which complicates the detection of true oscillation modes versus aliases. Thus, in the ideal case the combination of space- and ground-based observations will allow a correct identification of oscillation modes and provide a high signal-to-noise ratio (S/N).
With the seismic data presented here, we provide an updated estimate of the evolutionary state and mass for ϵ Tau and a precise value for its surface gravity. From our high-resolution spectra we derived the effective temperature and abundances. We also measured the ratio between the photometric and RV amplitudes as a function of frequency, an important measurement that can be used to test models of the stellar atmosphere (Houdek 2010). To our knowledge this represents only the second star with solar-like oscillations (apart from the Sun itself) with such a measurement; the other being Procyon (Huber et al. 2011).
2. Observations and data reduction
As part of this project, ϵ Tau was, as mentioned, observed with the Hertzsprung SONG telescope in Tenerife (Grundahl et al. 2017) and the Chinese SONG telescope at the Delingha Observing Station (Deng et al. 2013). We also include data from the revised Kepler mission K2 (Howell et al. 2014), taken during campaign 13 in which ϵ Tau was observed.
2.1. Tenerife data
The 1 m Hertzsprung SONG telescope on Tenerife observes in an fully automated mode (Andersen et al. 2016), and all the ϵ Tau data were collected in this way. The frequency of maximum oscillation power, νmax, is around 60 μHz, or ∼4.5 hrs (see preliminary results presented by Stello et al. 2017), and we therefore allowed other observing programmes to be executed as short (typically 1 hour) interruptions of the ϵ Tau time-series observations two or three times per night. We used an iodine cell for precise wavelength calibration, providing a single-point precision of 2–3 m s−1. The observation of the needed stellar template, spectral extraction and velocity calculations followed closely the method employed in Grundahl et al. (2017). For constructing the stellar template we obtained nine spectra with the highest spectral resolution (110 000), resulting in a S/N above 300 at wavelengths longer than 5000 Å (the spectrograph has a spectral range of 440 nm–690 nm). This combined spectrum was used for the abundance analysis presented in Sect. 4. In total, 5766 spectra were obtained for ϵ Tau (see Table 1). The first 941 spectra were obtained in November 2015 (Stello et al. 2017), while the majority of the spectra (4825) were obtained in the period of October 2016 to January 2017. Only the latter data were used in our asteroseismic analysis. We discarded a few outliers and ended up with a time series from Tenerife consisting of 4811 RV measurements for ϵ Tau.
Observational data from Tenerife and Delingha, and from K2.
2.2. Delingha data
The Delingha site is the second SONG node. It has a 1 m diameter telescope and as for the Tenerife node, the main instrument is a high-resolution échelle spectrograph (designed with the same throughput and resolution) located at the coudé focus. The building is insulated and temperature-controlled, since the temperature variation at the site can be somewhat larger than at Tenerife. In general, the site has slightly poorer weather conditions than the Tenerife site. The best observing conditions occur during the September–April season.
The spectrograph is very similar to the one in Tenerife; the main difference is that the spectral range is slightly smaller (440 nm–680 nm), with 50 spectral orders. The iodine cell uses counter-rotated wedged end windows to avoid fringing in the stellar spectra. The calibration, spectral extraction and velocity calculation are done by the same software as for the Tenerife data.
Since the operation of this telescope is not yet automated, all observations were carried out with an observer present. The RV precision obtained is close to 4 m s−1, somewhat worse than for Tenerife. This is probably due to non-automatic guiding and a lower signal due to the seeing. We do, however, note that during individual nights with the best observing conditions, a single-point precision better than 3 m s−1 has been reached. We collected in total 849 RV measurements from China; however, the data from some of the nights were of low quality and have been omitted in the analysis. We retained 590 RV measurements for use in the asteroseismic analysis.
2.3. The combined SONG data
The data from Tenerife and Delingha were combined by shifting each series to a common RV zero-point. The combined time series can be seen in Fig. 1a. There is a slow variation with an amplitude of about 20 m s−1 clearly visible in the data; similar drifts are visible in other SONG time-series and are most likely instrumental, although part of the variations may also be caused by rotational modulation or stellar activity, as they resemble variations seen in the RV data of θ1 Tau by Beck et al. (2015). The length of our time series is less than 20% of the orbital period of the exoplanet, so we expect only very-low-frequency modulation caused by the planet. We therefore filtered the data by subtracting a number of dominating, low-frequency sinusoidal signals, resulting in the combined time-series seen in Fig. 1b. The two lowest panels in Fig. 1 are close-up views from Tenerife and Delingha, respectively. Oscillations with a period of roughly 0.2 d are clearly visible in the data from both telescopes.
 |
Fig. 1. SONG data from Tenerife and Delingha, the combined, unfiltered time-series (panel a) the combined, filtered time-series (panel b). Panels c and d: close-ups of individual nights of RV observations from Tenerife (panel c) and from Delingha (panel d). |
2.4. K2 data
The K2 mission observed ϵ Tau during Campaign 13 (2017 March 8 to May 27) under Guest Observer Programme 13047 (P.I. D. Huber), with an observing cadence of one measurement per 30 minutes. Due to its brightness, ϵ Tau saturates the Kepler detector, with excess flux bleeding along CCD columns. Due to limitations of on-board data storage and telemetry from Kepler, it is not practical to record all the flux from such a bright star because of the large number of pixels this would require. Instead, ϵ Tau was observed with a circular mask with a radius of 20 pixels, with the time-series constructed from a weighted sum of the unsaturated pixels in the halo of scattered light surrounding the star. This method, referred to as ‘halo’ photometry, removes trends in the time-series that are due to the drift of the telescope, and has been successfully demonstrated with K2 observations of the bright B-stars in the Pleiades (White et al. 2017), as well as the red giant Aldebaran (Farr et al. 2018).
The K2 time-series, which can be seen in Fig. 2a, has an average precision per point of 218 ppm. The dominating low-frequency variations were again subtracted, providing us with the filtered time-series seen in panels b and c of Fig. 2. In the filtered time-series, the average noise per point is 160 ppm.
 |
Fig. 2. K2 data for ϵ Tau. The unfiltered time-series (panel a), a version of the time series (panel b) where dominating low-frequency variations up to 42 μHz have been subtracted (see text), a zoomed view of the filtered data (panel c) for the same length in time as in Fig 1c (we note the different zero points in time between the SONG and the K2 data). The data shown in panel c have been smoothed to enhance the oscillation signal. |
3. Data analysis
3.1. Power spectra and global oscillation parameters
The power spectra of the SONG and K2 time-series data were calculated using unweighted sine wave fitting to the data (Frandsen et al. 1995). We did try to use statistical weights for the SONG data, based on either the overall noise level in the data from each of the two sites, the flux levels of the individual measurements, or the local scatter in the time-series (obtained by running a boxcar through a version of the time series where all signals, including the oscillations, had been removed). We were only able to obtain a marginal improvement in the white-noise level as a result of the statistical weights, at the cost of degrading the spectral window by downweighting the data from China. We ascribe the ineffectiveness of using weights to the fact that the SONG data are dominated by the data from Tenerife, which are very homogeneous. Statistical weights were therefore not used in our analysis. The power density spectra and the corresponding spectral windows are shown in Fig. 3.
 |
Fig. 3. Power density spectra and spectral windows (in power) for the SONG and K2 data, respectively. The white curves are fits to the data to determine νmax, see text for a discussion. |
Although the SONG data were obtained from two sites, the final time-series still contains gaps, which result in 1 d−1 sidelobes of about 40% in power (65% in amplitude), which complicates the frequency analysis. The spectral window for the K2 data is excellent; there is, however, a significant rise in power at low frequencies due to stellar granulation. The oscillation envelope is clearly visible in both power spectra, with a frequency of maximum power (νmax) just below 60 μHz. The white-noise level in amplitude at high frequencies (above 500 μHz) is 7.0 cm s−1 for the SONG data, translating to an average noise of 2.9 m s−1 per data point. This is in good agreement with the noise estimates in Table 1 and given that the combined dataset is dominated by the data from Tenerife. The white-noise level in the K2 spectrum is 4.88 ppm, which translates into the noise per data-point of 160 ppm in the filtered time series, as mentioned above.
Following the approach of Mosser & Appourchaux (2009), which was also applied to SONG data by Stello et al. (2017), the frequency of maximum power (νmax) was determined from the SONG ϵ Tau data by applying a Gaussian fit combined with a linear trend to the filtered data, in order to take background signals into account. This is shown in the upper panel of Fig. 3; the full white line is the combined linear and Gaussian fit, while the dashed line is the linear fit to the background. From these fits, the frequency of maximum power was found to be 56.4 μHz. The oscillations are stochastic, which means that the distribution of oscillation power (i.e. which modes have highest amplitude) will differ from one instant to the next, providing slightly different values for νmax depending on when the star is observed. We used the actual SONG time-series to quantify this effect, and hence to estimate the uncertainty on νmax. We did this in the following way: we created 10 versions of the time series in each of which we had subtracted one of the dominant oscillation signals using CLEAN (the details of this method are described in Sect. 3.2 below). In order to avoid a bias, the 10 subtracted signals were evenly distributed around νmax, in a range between 35.93 and 87.79 μHz. We then calculated the power spectra based on these 10 modified time series, and determined νmax for each one of them. In this way we found 10 slightly different νmax values, which turned out to have a mean value of 56.4 μHz, and a standard deviation of 1.05 μHz which we round up to 1.1 μHz and adopt as our uncertainty estimate on νmax, as reported in Table 2. To test if this uncertainty is realistic, we used a 4-year Kepler time-series of KIC9716522, which is very similar to ϵ Tau, see Arentoft et al. (2017), but with a clearer oscillation signal, so that an 80-d segment of the KIC9716522 data resembles more our ϵ Tau RV data than the ϵ Tau K2 data where the oscillation signal is less pronounced. We split the time series into 18 80-d segments, filtered each of the segments for low-frequency signals, as we have done for the ϵ Tau data, and determined νmax in the same way as for ϵ Tau. In this way we found 18 values of νmax for KIC9716522, which turned out to have a standard deviation of 0.9 μHz, in good agreement with our estimated uncertainty of 1.1 μHz for ϵ Tau. Although the spectral windows of these 18 space-based data segments are cleaner than the SONG spectral window, this test supports our estimated uncertainty for the ϵ Tau νmax value of 1.1 μHz.
Global asteroseismic parameters for ϵ Tau.
Finally, we also performed the Gaussian fit to the K2 data and show the results in the lower panel of Fig. 3; the value of νmax determined in this way is 56.1±2.4 μHz, in good agreement with the value of 56.4±1.1 μHz found from the SONG data. In this case the uncertainty was found following the approach of Arentoft et al. (2017); the K2 time series was split in two, νmax was found from each of the two halves series, and the uncertainty was taken as the difference between these two values divided by 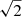 . Given the higher S/N in the spectroscopic data, we retain the value from SONG as our final result for νmax.
. Given the higher S/N in the spectroscopic data, we retain the value from SONG as our final result for νmax.
We then proceeded to determine the large frequency separation Δν, which is the frequency separation between oscillation modes of consecutive radial order (n) with the same angular degree (ℓ), assuming that the oscillations follow the asymptotic relation (see Sect. 3.2). Because of the expected regularity of the frequency spectrum, we first looked at the autocorrelation of each of the two power spectra, based on the SONG- and K2-data. The results are shown in Fig. 4. The autocorrelation of the SONG power spectrum is, not surprisingly, dominated by a peak from the 1 d−1 aliases originating from the spectral window. There is a minor peak at 5.0 μHz in both autocorrelations, marked by an arrow in Fig. 4; this peak becomes more prominent when we multiply the two autocorrelations, as seen in the lower panel. This is a signature of the large frequency separation for ϵ Tau, but we only have a marginal detection of Δν based on the autocorrelation method alone. Instead we applied a method described in Christensen-Dalsgaard et al. (2008), and in Arentoft et al. (2017) for the stars in NGC 6811, with a slight modification. For each trial Δν value in a range where we expect to find Δν for ϵ Tau, we cut the region of the SONG and K2 power spectra (respectively) containing the oscillations in bins of Δν, added the bins and found the highest peak in the summed spectrum. In this way, modes of ℓ = 0 will add up in the summed spectrum and create a strong peak when the correct value for Δν is used. We have previously cut the spectrum in bins of Δν/2, in order to make modes of ℓ = 0, 1 to add up. However in evolved stars like ϵ Tau, the ℓ = 1 modes are expected to be mixed (Dziembowski et al. 2001; Christensen-Dalsgaard 2004; Dupret et al. 2009) and their frequencies will therefore deviate from the values expected from the asymptotic relation for pure p-modes (Eq. (1)). We show the results of this analysis in Fig. 5. The figure plots the summed value for the highest peak as a function of the trial Δν-value. In the SONG data, we again see peaks at fractions of the daily aliases, but also a relatively strong peak near 5.0 μHz. The same peak is present in the K2 data, and when multiplying the two (bottom panel), we obtain a very clear peak just slightly below 5.0 μHz which we interpret as the large frequency separation. In the following, we identify a number of modes separated almost exactly by 5.0 μHz. We assume these to be equidistant ℓ = 0 modes and use these modes below to refine the Δν-value for ϵ Tau, based on the SONG data alone. The uncertainty value quoted in Table 2 for Δν of 0.01 μHz for SONG originates from this analysis, which is presented in the next section. The uncertainty value for K2 was again found by splitting the K2 time series in two, repeating the analysis on the two half series, and taking the uncertainty as the difference between the two values, divided by 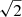 .
.
 |
Fig. 4. Autocorrelations of the power spectra, for the SONG spectrum in the upper panel, and K2 in the middle panel. Bottom panel: the two autocorrelations multiplied together. The vertical dashed lines in the upper panel indicate the signals originating from the 1 d−1 aliases in the spectral window, at 11.574 μHz and integer fractions thereof. The arrows indicate a value of 5.0 μHz, which we identify as Δν for ϵ Tau using various methods (see text). |
 |
Fig. 5. Results of using a modified version of an analysis method developed for solar-like oscillations observed with Kepler, as described in the text. Upper panel: results based on the SONG power spectrum. Middle panel: results for K2. As in Fig 4, the dashed lines in the upper panel indicate signals originating from the 1 d−1 aliases in the spectral window, and the arrow indicates the Δν-value of 5.0 μHz. Bottom panel: SONG and K2 results from the two upper panels are multiplied, resulting in a very clear peak near 5.0 μHz. |
3.2. Individual frequencies
The individual oscillation frequencies were found from the SONG data. We then used the K2 data, where the oscillation modes have lower S/N but a much cleaner spectral window, to distinguish between true oscillation modes and daily aliases. ϵ Tau is an evolved star, so we assume that the modes with angular degree ℓ = 0 and ℓ = 2 will largely follow the asymptotic relation (Vandakurov 1967; Tassoul 1980; Gough et al. 1986);
while there will be multiplets of mixed ℓ = 1 modes that do not follow this relation. The frequency analysis was an iterative procedure where we first ran a simple CLEAN (Frandsen et al. 1995) on the SONG data, where the dominating modes are subtracted one by one from the time series, with the power spectrum being recomputed in each step, and with the criterion that modes were included in the frequency list if their amplitudes were above 3.0 times the mean level of the amplitude spectrum between 130 and 150 μHz. All our detected modes have frequencies below 100 μHz. The average noise level in this part of the spectrum is more than three times higher than if we had used the noise level at even higher frequencies (e.g. above 500 μHz), which is likely due to spectral leakage through the window function of undetected modes in the frequency range where we detect the modes. However, finding the noise estimate close to the oscillation frequencies gives a more realistic estimate of the noise level in the region where we detect the modes, even if part of the noise is due to undetected modes, and results in a conservative frequency analysis and conservative estimates for the final S/N values of the detected modes.
At this point of our analysis we could potentially have detected peaks that are daily aliases of true oscillation modes, which would mean that we obtain wrong frequency values. As a result, the CLEAN procedure would become sub-optimal when we subtract these wrong frequencies during the analysis. We therefore looked for a regular pattern among the 20 frequencies detected in this first run of CLEAN, to identify a series of regularly spaced ℓ = 0 modes. This turned out to be possible. In Fig. 6 we show a number of modes which are all separated by 5.00 μHz, in good agreement with the value of the large frequency separation, Δν, found above, and to which we could assign a radial order (n). In Fig. 6 the black diamonds indicate detected modes that fit this regular structure, while the red triangles mark the positions of expected ℓ = 0 modes that were undetected in the first run of CLEAN. The blue squares indicate a mode for which CLEAN most likely picked up a 1 d−1 alias. The original frequency at 57.415 μHz lies almost exactly 11.574 μHz above the predicted ℓ = 0 mode with n = 8. To check this interpretation, we looked at the power spectra based on SONG, K2 and SONG multiplied by K2 near the detected frequency, and its ± 1d−1 aliases. This is shown in Fig. 7. The SONG data shown in the upper panels favour the originally detected frequency in the middle panel, while the K2 data and the product of the SONG and K2 data support that the true mode is the one near 45.8 μHz, which also fits into the regular ℓ = 0 structure shown in Fig. 6. The 1d−1 alias is probably dominating in the SONG spectrum because its amplitude is influenced by nearby modes, or by the spectral window of adjacent modes.
 |
Fig. 6. Upper panel: frequencies as a function of radial order (n) for the first stage of our frequency analysis. The dotted line has a slope of 5.00 μHz, in agreement with Δν found in Fig. 5. The black diamonds are detected modes that fit into a regular structure of expected ℓ = 0 modes, red triangles mark the positions of expected ℓ = 0 modes that were undetected in our first run of CLEAN, and the two blue squares represent the detected ℓ = 0, n = 8 mode, for which the first run of CLEAN picked up the +1 d−1 alias (see text). Lower panel: differences between the detected ℓ = 0 frequencies and those predicted by the asymptotic relation (Eq. (1)), also in μHz. |
 |
Fig. 7. As shown in Fig. 6, one of the modes detected in the original run of CLEAN on the SONG data was likely an 1 d−1 alias of a true ℓ = 0 mode. Three upper panels: SONG data near the originally detected frequency (middle column of panels), and minus (left panel) and plus (right panel) 1 d−1 corresponding to 11.574 μHz. Middle panels: same for the K2 data, and the lower panels for the product of the two. The K2 power spectrum and the product of the SONG and K2 spectra support the interpretation that the originally detected mode was in fact a 1 d−1 alias of the actual mode, which is indicated by an arrow in the lower-left panel. |
As a next step, we used the expected positions of the ℓ = 0 modes shown in Fig. 6 as input to a second iteration of CLEAN on the SONG data. We included the positions of the undetected ℓ = 0 modes (the red triangles in Fig. 6) in order to obtain a residual time-series and power spectrum, which were unaffected by the ℓ = 0 modes and their corresponding spectral window functions. We then ran CLEAN on the residual data, in order to detect ℓ = 1, 2 and possible ℓ = 3 modes. The final frequency list with all detected modes is given in Table 3, including frequency uncertainties determined in the same way as in Arentoft et al. (2017), amplitudes, and S/N-values. We have included the mode identification based on the position in the échelle diagram shown in Fig. 8 for ℓ = 0, and for a single mode, which we identify as ℓ = 2. Most of the remaining modes are likely mixed ℓ = 1 modes, although some of them may be ℓ = 3 modes, but due to the lack of regularity among the possible ℓ = 1 modes in Fig. 8, we cannot be sure of the mode identification for these modes. Some of them might also be aliases. The detected frequencies are also marked in the power spectra shown in Fig. 9 (see figure caption for details). We note that we have included the ℓ = 0, n = 13, 14 modes in our final frequency list, although they were not detected in our first run of CLEAN. The ℓ = 0, n = 14 mode has a S/N-value of 4.32 in amplitude and is therefore statistically significant, while the ℓ = 0, n = 13 mode has a S/N-value of only 2.52 in amplitude and is not statistically significant. There is, however, evidence in the K2 data for this mode, see Fig. 9, and the mode has therefore been included in the final frequency list.
List of the 27 mode frequencies (with uncertainties) in ϵ Tau, their amplitude, S/N value in amplitude (not power), and mode-identification (ℓ, n) for the ℓ = 0, 2 modes.
 |
Fig. 8. Échelle diagram for the 27 oscillation modes. The x-axis was shifted to place ℓ = 0, 2 modes close to each other in the diagram. Filled red circles are ℓ = 0 modes, the green triangle is ℓ = 2, and blue diamonds are for the remaining peaks, of which most are likely ℓ = 1 modes. |
 |
Fig. 9. Top panel: close-up of the power spectrum based on the SONG data, centred at the ℓ = 0, n = 11 mode just below 61 μHz. The over-plotted, red curve shows the spectral window for this central ℓ = 0 mode. The detected modes are indicated at the top of the panel, with an identification as in Fig. 8. The ℓ = 0 mode above 70 μHz has a low S/N of only 2.5 in the SONG data, but is more pronounced in the lower panel, where the K2 and SONG spectra are multiplied, as indicated by the arrow. The mode is therefore included in our final frequency list. Relatively strong but undetected peaks are sidelobes of modes outside the frequency range in the close-up view. Two lower panels: full SONG power spectrum and the product of the SONG and K2 power spectra, with the detected modes indicated using the same symbols as in the top panel. The three panels are aligned according to the ℓ = 0 mode just below 61 μHz. |
We end up with nine regularly spaced ℓ = 0 modes, for which we plot the frequency as a function of n-value in Fig. 10. Following the asymptotic relation (Eq. (1)) we again fitted a straight line to obtain values for the large frequency separation Δν and ϵ including uncertainty estimates, as shown in Fig. 10 and as listed in Table 2. The value for Δν is in excellent agreement with the value just below 5 μHz found in the previous section. This is, however, not surprising, as the methods applied in Sect. 3.1 also searched for regularly spaced modes, and therefore also relies on the ℓ = 0 modes shown in Fig. 10.
 |
Fig. 10. Frequencies of the nine ℓ = 0 modes included in Table 3 as a function of their n-values. According to the asymptotic relation in Eq. (1), the slope provides the large frequency separation Δν while the intersection with the ordinate is Δν ⋅ ϵ, leading to the value for ϵ quoted in the figure and listed in Table 2. |
4. Atmospheric parameter analysis
The atmospheric parameters of ϵ Tau were determined spectroscopically from an equivalent-width analysis. We used DAOSPEC (Stetson & Pancino 2008) to measure the equivalent widths using a line list published in Slumstrup et al. (2019). The auxiliary programme Abundance with SPECTRUM (Gray & Corbally 1994) was used to determine the atmospheric parameters, which are based on solar abundances from Grevesse & Sauval (1998) and ATLAS9 stellar atmosphere models (Castelli & Kurucz 2004). We assumed local thermodynamic equilibrium (LTE) because non-LTE effects are expected to be negligible in this parameter regime (Asplund 2005; Mashonkina et al. 2011). The atmospheric parameters were determined by invoking excitation and ionization equilibrium, and further requiring that [Fe/H] should have no systematic dependence on the strength of the line. Excitation equilibrium was reached by requiring the metallicity to show no trend with excitation potential, which is sensitive to the effective temperature, Teff. Ionization equilibrium was reached by ensuring the average [Fe/H] agreed for absorption lines of different ionization stages, FeI and FeII. This is sensitive to the surface gravity, log g, because FeII lines are more sensitive to pressure changes than FeI lines for this type of star. However, this balance is also affected by Teff and abundances of heavier elements, so several iterations were necessary. Lastly, the trend of [Fe/H] vs. the reduced equivalent width (log(EW)/λ) of an absorption line is sensitive to the microturbulence, a fitting parameter introduced to describe broadening of absorption lines by turbulence on small scales, that cannot otherwise be included in 1D stellar atmosphere models.
The analysis was carried out in two different ways, both with and without the strong asteroseismic constraint on log g, calculated using the νmax scaling relation (Brown et al. 1991; Kjeldsen & Bedding 1995):
The results are presented in Table 4 with only internal uncertainties. The asteroseismic log g is within the uncertainty of the spectroscopic log g, which makes the two sets of results consistent.
Stellar atmospheric parameters determined from spectroscopy, with and without a surface gravity constraint from asteroseismology.
With the set of atmospheric parameters determined without a log g constraint, the [Y/Mg] abundance was also determined as in Slumstrup et al. (2017) to be 0.21 ± 0.05. With a cluster age of 650 Myr for the Hyades (Lebreton et al. 2001), it leaves ϵ Tau just outside one sigma agreement with the [Y/Mg] – age relation for solar twins by Nissen et al. (2017), their Fig. 5, which was shown to also hold for lower-mass solar-metallicity red-clump giants (≲1.5 M⊙) by Slumstrup et al. (2017). It has been suggested in the literature that the Hyades could be as old as 800 Myr (Brandt & Huang 2015) but this would slightly worsen the agreement with the [Y/Mg] – age relation. To reach exact agreement, the cluster would instead have to be as young as 300 Myr. However, it should be noted that Slumstrup et al. (2017) only tested the relation for lower-mass giants (≲1.5 M⊙) and it is therefore not certain that the relation can be applied to giants of masses similar to ϵ Tau.
5. Physical parameters and evolutionary status
The angular diameter of ϵ Tau has been measured several times with different interferometric instruments at visible and infrared wavelengths (van Belle et al. 1999; Nordgren et al. 2001; Mozurkewich et al. 2003; Boyajian et al. 2009; van Belle & von Braun 2009; Baines et al. 2018). After correcting for limb-darkening, the measured values of the angular diameter, θLD, are not all in agreement, ranging from 2.41±0.11 mas (Nordgren et al. 2001) to 2.733±0.031 mas (Boyajian et al. 2009). One possible source for the disagreement may be the adopted limb-darkening corrections, which are based on model atmospheres and may not be consistent between the different studies. Alternatively, it has been observed that a systematic bias towards larger angular diameter measurements exists when a star is under-resolved (Casagrande et al. 2014; White et al. 2018). We adopt an angular diameter of θLD = 2.493 ± 0.019 mas from recent measurements with the PAVO beam combiner at the CHARA Array (White et al., in prep.). These observations have higher resolution than the previous measurements, allowing for the amount of limb darkening to be directly measured and lifting the degeneracy with the angular diameter.
Combining the angular diameter with the HIPPARCOS parallax π = 22.24 ± 0.25 mas (van Leeuwen 2007) gives a linear radius of 12.06±0.16 R⊙. From the angular diameter and bolometric flux, Fbol = (1.27 ± 0.06) × 10−6 erg s−1 cm−2 (Baines et al. 2018), we find an effective temperature of 4976±63 K. These values are in excellent agreement with the radius calculated from Teff, V-mag, parallax distance, and bolometric correction from Casagrande & VandenBerg (2014). This demonstrates excellent consistency between parameters and supports the spectroscopic Teff of 4950 K. The Gaia DR2 parallax for ϵ Tau is π = 20.31 ± 0.43 mas (Gaia Collaboration 2018), which is in poor agreement with the value and uncertainty reported for HIPPARCOS. The Gaia data product is not yet in its final version and for very bright stars, the full mission data will probably be needed to provide optimal results, and the present values are uncertain due to calibration issues (Lindegren et al. 2018). We will therefore not include an analysis based on the Gaia-DR2 parallax in this paper.
To determine the mass of ϵ Tau, we used the asteroseismic scaling relations (e.g. Kallinger et al. 2010). We used the global asteroseismic parameters in Table 2 along with solar reference values from Handberg et al. (2017). For atmospheric parameters, we adopted the spectroscopic Teff = 4950 K and [Fe/H] = 0.15, as derived in the previous section. To ensure exact agreement between the interferometric radius and that obtained from the asteroseismic scaling relations, we adjusted the Δν correction factor fΔν in the asteroseismic scaling relations (e.g. Sharma et al. 2016; Brogaard et al. 2018) until we reached this agreement. This way we obtained an empirical value of the correction factor of fΔν = 0.98993 and we found the asteroseismic mass for ϵ Tau to be M = 2.458 ± 0.073 M⊙. The uncertainty is based on propagating internal uncertainties on parallax, θLD, Teff, νmax, and Δν.
The similarity in CMD position between ϵ Tau and the other cluster giants suggests they are all in the core-He-burning evolutionary phase. However, the empirical correction factor, fΔν, we have found is in excellent agreement with the theoretically predicted fΔν by Rodrigues et al. (2017) if ϵ Tau is assumed to be an RGB star (their Fig. 3, panels 6 and 7 counted from the top), but not if ϵ Tau is in the core-He-burning phase. Complicating the issue, Fig. 6 (bottom panel) in Brogaard et al. (2018) reveals that the same value for fΔν is not found if one uses Teff as reference to determine fΔν instead of νmax, as in Rodrigues et al. (2017), even if everything else is unchanged. This may be caused by a too low temperature scale for the models used by Rodrigues et al. (2017), as also discussed by Brogaard et al. (2018). Retaining the view from Brogaard et al. (2018) that it is better to use νmax than Teff to estimate fΔν, we find evidence based on our empirical correction factor pointing to the RGB as the present evolutionary phase of ϵ Tau. If ϵ Tau is actually a clump star, this would suggest that a slight offset is needed for the fΔν values predicted by Rodrigues et al. (2017).
Kallinger et al. (2012) found that H-shell-burning stars and core-He-burning stars could be distinguished using the central modes closest to νmax to determine Δνc and ϵc (see their Fig. 4). This was also investigated theoretically by Christensen-Dalsgaard et al. (2014), who found the effect to be caused by differences in the convective envelopes. Using the radial oscillation modes in ϵ Tau closest to νmax (ℓ = 0, n = 9–11), we find Δνc = 5.04 ± 0.02 μHz and ϵc = 1.1 ± 0.2. This places ϵ Tau among the H-shell-burning stars in the upper panel in Fig. 4 in Kallinger et al. (2012). However, given the uncertainty on ϵc, the measurement is also consistent with ϵ Tau being at the top of the distribution of core-He-burning stars, within 1 σ.
We can also look at other asteroseismic indicators. Based only on a single ℓ = 2 mode, we have determined the small frequency separation δ02 to be 0.76 μHz. Using the lower panel in Fig. 4 in Kallinger et al. (2012), this places ϵ Tau in a region of the diagram where we cannot discriminate between RGB and clump stars. We would most likely be able to determine the evolutionary stage of ϵ Tau if we could determine the asymptotic period spacing of the mixed ℓ = 1 modes, as this allows for a discrimination between core-He-burning and H-shell-burning red giants (Bedding et al. 2011). For ϵ Tau, however, the échelle diagram shown in Fig. 8 displays a sparse set of mixed ℓ = 1 modes, some of which may be daily aliases. Our attempts to determine the period spacing, following the methods described in Arentoft et al. (2017), were unsuccessful.
We have also determined stellar properties using the BAyesian STellar Algorithm (BASTA; Silva Aguirre et al. 2015, 2017), fitting the asteroseismic parameters (Δν, νmax), the interferometric temperature and spectroscopic metallicity, and available Strömgren photometry assuming E(B − V)=0 to determine distance. The Bayesian scheme points to the core-He-burning stage as the most likely evolutionary stage of ϵ Tau. The preferred model is slightly more massive than the value of M = 2.458 ± 0.073 M⊙ found from the asteroseismic scaling relations above; the model has a mass of 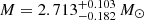 , however the 1σ errorbars exactly touch each other in between the two mass estimates. In the model fits, there are also core-He-burning solutions near 2.5 M⊙, however with lower probability, and we note that also these model fits are sensitive to systematic shifts in the effective temperature, so if the effective temperature scale is shifted by, say 100 K, the results of the model fits would be different. The radius and effective temperature of the preferred model solution (
, however the 1σ errorbars exactly touch each other in between the two mass estimates. In the model fits, there are also core-He-burning solutions near 2.5 M⊙, however with lower probability, and we note that also these model fits are sensitive to systematic shifts in the effective temperature, so if the effective temperature scale is shifted by, say 100 K, the results of the model fits would be different. The radius and effective temperature of the preferred model solution (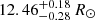 and
and 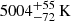 , respectively) are slightly larger than the values found from interferometry above, which would suggest a slightly larger distance to ϵ Tau, and hence a smaller value of the parallax, as also indicated by the preliminary Gaia parallax. We will have further constraints on the model comparison once the Gaia parallax of ϵ Tau is final. The Bayesian scheme returns a model age of
, respectively) are slightly larger than the values found from interferometry above, which would suggest a slightly larger distance to ϵ Tau, and hence a smaller value of the parallax, as also indicated by the preliminary Gaia parallax. We will have further constraints on the model comparison once the Gaia parallax of ϵ Tau is final. The Bayesian scheme returns a model age of 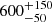 Myr, consistent with the isochrone age of the Hyades. This is one of only a few cases where an asteroseismic age can be compared to other robust methods for age determination, another one being for the open cluster M67 (Stello et al. 2016).
Myr, consistent with the isochrone age of the Hyades. This is one of only a few cases where an asteroseismic age can be compared to other robust methods for age determination, another one being for the open cluster M67 (Stello et al. 2016).
Finally, we applied the method of Hon et al. (2018), which uses a neural network to classify a star as being in the RGB or core-He-burning phase, based on the oscillation power spectrum. The network has been trained on power spectra from 82-d time series, corresponding to the K2 time-series for ϵ Tau, for which it has a classification accuracy of 95.4 per cent (Hon et al. 2018). The neural network classified ϵ Tau as a core-He-burning clump star, with a probability of p = 0.986 ± 0.012, where 1 corresponds to a clump star and 0 to a RGB star. Hence, comparing the ϵ Tau oscillation spectrum to the oscillation spectra of tens of thousands of red giants observed by the Kepler telescope, points to the clump as the current evolutionary status of ϵ Tau.
6. Oscillation amplitudes and amplitude ratio
Apart for the Sun, the amplitude ratio between intensity measurements and radial velocities for solar-like oscillations as a function of frequency has so far only been observed for Procyon (Huber et al. 2011). The amplitude ratio as a single value has also been derived for ϵ Oph (Kallinger et al. 2008). For Procyon, Huber et al. (2011) used observations from MOST (Walker et al. 2003; Matthews 2007) that were obtained simultaneously with the RV campaign of Arentoft et al. (2008) to derive an amplitude ratio between intensity and RV of Aℓ = 0, Phot/Aℓ = 0, RV = 0.23 ± 0.01 ppm cm−1 s. Determining the amplitude ratio allows tests of scaling relations (Kjeldsen & Bedding 1995, 2011), and allows a more robust comparison between observations and models than does comparing the intensity and RV amplitudes individually (Houdek 2010).
Amplitudes can be derived following the method of Kjeldsen et al. (2008), which involves heavily smoothing the power spectrum with a Gaussian, converting the spectrum to power density and scaling the signal to amplitude per radial mode. This method was used by Huber et al. (2011), who compared the results for Procyon to the expected amplitude ratio based on the scaling relations in Kjeldsen & Bedding (1995). They found the measured amplitude ratio to be considerably higher than the predicted value, by about 35%. They also found the amplitude ratio measured at the frequency of maximum power to be in better agreement with models from Houdek (2010) than with the scaling relations.
The method for deriving the amplitude per radial mode, which involves smoothing the power spectrum with a Gaussian with a full width at half maximum (FWHM) of 4Δν (Kjeldsen et al. 2008), was developed for solar-like main-sequence stars, which have higher oscillation frequencies and broader oscillation envelopes than is the case for evolved stars like ϵ Tau. When we applied the width of 4Δν to ϵ Tau, it was evident from the resulting, smoothed power spectra of the SONG and K2 data, that the oscillation signal was too heavily smoothed. We therefore tested FWHM-values of 2Δν and 3Δν, and found that those widths worked better for ϵ Tau, as the oscillation signal (similar to the white curves in Fig. 3) was better retained after smoothing than was the case when using the width of 4Δν. The results for the amplitude ratio of ϵ Tau using these two different widths (2Δν and 3Δν) agreed within the uncertainties. We used the width of 3Δν in the analysis described below.
In the case of ϵ Tau, the photometric K2 data and the SONG RV data were not obtained simultaneously. We can still measure the amplitude ratio but, given the stochastic nature of the solar-like oscillations, there will be an additional source of uncertainty in our measurement. In order to quantify this, we used the 18 low-frequency filtered, 80-d segments of the KIC9716522 Kepler-data described in Sect. 3.1. We determined the amplitude per radial mode following Kjeldsen et al. (2008) for each of these segments (see Fig. 11), where we smoothed the power spectrum with a Gaussian with a FWHM of 3Δν, and used c = 3.06 based on a central wavelength of 650 nm for K2 observations. We found a mean amplitude for KIC9716522 of 45.8 ppm, with a standard deviation from the 18 segments of 1.6 ppm, corresponding to an uncertainty of 3.5%. We have no available data which allow us to perform a similar analysis for RV data, but it seems reasonable to assume that the effect will be similar, and we adopt 4% as our uncertainty estimate for the photometric and radial velocity amplitudes.
 |
Fig. 11. Smoothed power spectra based on 80 d segments for KIC9716522 in NGC 6811, which is similar to ϵ Tau and which was observed for four years by Kepler. The data were used to estimate the uncertainty arising from the fact that the SONG and K2 data for ϵ Tau were non-simultaneous. |
Another factor to consider is the very different spectral windows for the SONG and K2 data (see Fig. 3). The K2 spectral window is very clean (i.e. no sidelobes), while the SONG spectral window contains significant sidelobes. Because the distribution of power in the spectral window covers a relatively broad frequency range compared with the oscillation envelope for ϵ Tau, some fraction of the power will be located outside the frequency region of the oscillations. This will be the case for both the K2- and the SONG-data; however, the effect is expected to be larger for the SONG data due to the worse spectral window. We would expect to underestimate the oscillation amplitudes due to this effect, and more so for SONG than for K2. In order to quantify this effect, we performed the simulations illustrated in Fig. 12. We created a simulated power spectrum based on the oscillation envelope observed for ϵ Tau (see Fig. 3). Using the observed Δν of 5.0 μHz, we placed a number of oscillation orders between 10 and 110 μHz, and placed 3 peaks in each order, so that the factor c (Kjeldsen et al. 2008) was set at c = 3. The heights (in power) were distributed according to the observed oscillation envelope, peaking at 1.0 at νmax. We convolved this synthetic spectrum with the SONG and the K2 spectral windows, resulting in the spectra shown in the two upper panels of Fig. 12. We then followed the prescription for determining the amplitude per radial mode from Kjeldsen et al. (2008), both using 2Δν and 3Δν for the width in the Gaussian smoothing.
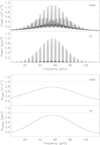 |
Fig. 12. Simulated power spectra to estimate the effect of the window function on the determination of oscillation amplitudes, see text. |
The results are shown in the two bottom panels of Fig. 12 for a width of 3Δν. If there were no effect of the spectral window function on the derived amplitudes, the maximum amplitude in both curves would reach 1.0. This is not the case and, as expected, the simulated SONG spectrum is more affected than the simulated K2 spectrum: the amplitude per radial mode reaches a maximum of 0.774 m s−1 for SONG, and 0.903 ppm for K2. This means that we will underestimate the amplitudes of ϵ Tau by similar factors and hence that we will underestimate the RV amplitude more than the intensity amplitude. We therefore used these two numbers to correct the amplitudes determined from the SONG and the K2 data.
The final step was to determine the amplitude ratio for ϵ Tau. The power spectra were again smoothed using a Gaussian with a FWHM of 3Δν, converted to power density, and converted to amplitude per radial mode using c = 4.09 for the SONG radial velocities and c = 3.06 for the K2 data. Using the corrections described above, we measured the amplitudes of ϵ Tau to be Aℓ = 0, RV = 0.94 ± 0.04 m s−1 and Aℓ = 0, Phot = 39.8 ± 1.4 ppm (see Fig. 13), and hence estimated the amplitude ratio between intensity and RV to be Aℓ = 0, Phot/Aℓ = 0, RV = 42.2 ± 2.3 ppm m−1 s (lower panel in Fig. 13). We note that the uncertainty on the amplitude ratio was estimated based on the analysis of the KIC9716522 data described above, and does not include systematic effects arising from, for example, the way we treat the noise background in the data. The true uncertainty may therefore be larger.
 |
Fig. 13. Measured amplitudes in RV (top panel) and intensity (middle panel), and the amplitude ratio as a function of frequency (bottom panel), for ϵ Tau. The dashed line indicates νmax |
The value for the amplitude ratio is significantly higher than expected from scaling relations: using the relations in Kjeldsen & Bedding (1995) and repeated in Huber et al. (2011), we obtain an expected value of only 23.2 ppm m−1 s. We are not able to explain this difference without model calculations, which are beyond the scope of this paper, but we note again that the amplitude ratio of Procyon was also higher than expected from the scaling relations (Huber et al. 2011). We do not see a shift in our ϵ Tau data towards higher frequencies for νmax in intensity as compared to velocity; such a shift was observed for Procyon (Huber et al. 2011). Finally, the shape of the amplitude ratio as a function of frequency for ϵ Tau agrees better with the models of Houdek (2010) than was the case for Procyon, see Huber et al. (2011), their Fig. 9. We note that the rise in the amplitude ratio at frequencies below 40 μHz in the lower panel in Fig. 13 is due to the residual granulation noise at low frequencies in the K2 power density spectrum which is visible in Fig. 3 (compare the upper and lower panels of Fig. 3 at frequencies below 40 μHz), so this part of the amplitude ratio curve should be discarded in a forthcoming comparison with model calculations.
The intensity and RV measurements of ϵ Tau were not obtained simultaneously, which weakens conclusions based on the measured amplitude ratio. However, it does seem that the amplitude ratio is higher than expected from simple scaling relations and in better agreement with the model calculations of Houdek (2010). Our results act as a proof-of-concept for combining RV measurements from SONG with space-based intensity data for measuring amplitude ratios of solar-like stars. This opens for new opportunities with the recent launch of TESS (Ricker et al. 2015), which will observe bright, solar-like stars for which we will obtain simultaneous SONG RV time-series data.
7. Updated parameters for the planetary system
Sato et al. (2007) found a planetary companion to ϵ Tau, which was the first exoplanet found in an open cluster. Based on a stellar mass of M = 2.7 ± 0.1 M⊙, they derived a planetary mass of m2 sin i = 7.6 ± 0.2 MJ. With our slightly lower stellar mass of M = 2.458 ± 0.073 M⊙, in agreement with Stello et al. (2017), we can redetermine the minimum mass of the planet, using the velocity semi-amplitude, orbital period, and eccentricity presented in Sato et al. (2007). We find the new minimum mass of the planet to be m2 sin i = 7.1 ± 0.2 MJ.
8. Conclusions and outlook
We have determined asteroseismic parameters and combined those with interferometric and spectroscopic data to derive physical parameters for ϵ Tau, including its mass. This leads to a slightly lower revised mass for its planetary companion. By combining high-S/N radial-velocity ground-based data from SONG with continuous space-based data from K2, we were able to extract 27 individual oscillation modes in addition to the global asteroseismic parameters. Although ϵ Tau most likely is a (secondary) clump star, various signatures, including the asteroseismic quantities, model fits and deep learning, gave diverging results on the evolutionary stage of the star, making it unclear whether the star is on the red-giant branch or in the core-helium-burning clump stage. Due to the fact that ϵ Tau displays a relatively sparse set of ℓ = 1 modes, we were unable to determine its asymptotic period spacing, which would allow us to determine if the star is in the red-giant-branch phase or already in the core-helium-burning phase (Bedding et al. 2011). In NGC 6811, Arentoft et al. (2017) found two groupings within the eight secondary clump stars in that cluster; four of the giants displayed rich sets of ℓ = 1 modes, which allowed for a determination of the asymptotic period spacing, while the other four stars were more like ϵ Tau, and no period spacing could be determined. If something similar is at play among the Hyades giants, time-series observations of the three other giants may allow for a determination of the asymptotic period spacing for some of the stars, and hence allow us to determine their evolutionary stage.
We have demonstrated the potential of combining ground-based data with space-based data, taking advantage of the strengths of both types of observations. Although the spectroscopic and intensity time-series were non-simultaneous, we were also able to determine the amplitude ratio between intensity and radial velocities as a function of frequency, which previously has been done only for the Sun and Procyon. The determination of the amplitude ratio of the ϵ Tau oscillations was found to be higher than expected from simple scaling relations. This illustrates the importance of obtaining measurements for a larger number of stars, and we plan to do this by obtaining ground-based radial-velocities with SONG that are simultaneous with TESS observations.
Acknowledgments
Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation (Grant agreement no.: DNRF106). The research was supported by the ASTERISK project (ASTERoseismic Investigations with SONG and Kepler) funded by the European Research Council (Grant agreement no.: 267864). This work was performed in part under contract with the Jet Propulsion Laboratory (JPL) funded by NASA through the Sagan Fellowship Program executed by the NASA Exoplanet Science Institute. D.H. acknowledges support by the National Aeronautics and Space Administration under Grants NNX17AF76G and 80NSSC18K0362 issued through the K2 Guest Observer Program. This paper includes data collected by the K2 mission. Funding for the K2 mission is provided by the NASA Science Mission directorate.
References
- Andersen, M. F., Grundahl, F., Beck, A. H., & Pallé, P. 2016, Rev. Mex. Astron. Astrofis. Conf. Ser., 48, 54 [NASA ADS] [Google Scholar]
- Ando, H., Tsuboi, Y., Kambe, E., & Sato, B. 2010, PASJ, 62, 1117 [NASA ADS] [Google Scholar]
- Arentoft, T., Kjeldsen, H., Bedding, T. R., et al. 2008, ApJ, 687, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Arentoft, T., Brogaard, K., Jessen-Hansen, J., et al. 2017, ApJ, 838, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baines, E. K., Armstrong, J. T., Schmitt, H. R., et al. 2018, AJ, 155, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, P. G., Kambe, E., Hillen, M., et al. 2015, A&A, 573, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bedding, T. R., & Kjeldsen, H. 2006, Mem. Soc. Astron. It., 77, 384 [NASA ADS] [Google Scholar]
- Bedding, T. R., Mosser, B., Huber, D., et al. 2011, Nature, 471, 608 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Boyajian, T. S., McAlister, H. A., Cantrell, J. R., et al. 2009, ApJ, 691, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, T. D., & Huang, C. X. 2015, ApJ, 807, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Brogaard, K., Hansen, C. J., Miglio, A., et al. 2018, MNRAS, 476, 3729 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Gilliland, R. L., Noyes, R. W., & Ramsey, L. W. 1991, ApJ, 368, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., & VandenBerg, D. A. 2014, MNRAS, 444, 392 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Casagrande, L., Portinari, L., Glass, I. S., et al. 2014, MNRAS, 439, 2060 [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004, ArXiv e-prints [arXiv:astro-ph/0405087] [Google Scholar]
- Christensen-Dalsgaard, J. 2004, Sol. Phys., 220, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., Arentoft, T., Brown, T. M., et al. 2008, J. Phys. Conf. Ser., 118, 012039 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., Silva Aguirre, V., Elsworth, Y., & Hekker, S. 2014, MNRAS, 445, 3685 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardi, D. R., Crossfield, I. J. M., Feinstein, A. D., et al. 2018, AJ, 155, 10 [NASA ADS] [CrossRef] [Google Scholar]
- de Bruijne, J. H. J., Hoogerwerf, R., & de Zeeuw, P. T. 2001, A&A, 367, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deng, L., Xin, Y., Zhang, X., et al. 2013, in Astrophysics from Antarctica, eds. M. G. Burton, X. Cui, & N. F. H. Tothill, IAU Symp., 288, 318 [NASA ADS] [Google Scholar]
- Dupret, M.-A., Belkacem, K., Samadi, R., et al. 2009, A&A, 506, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dziembowski, W. A., Gough, D. O., Houdek, G., & Sienkiewicz, R. 2001, MNRAS, 328, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Farr, W. M., Pope, B. J. S., Davies, G. R., et al. 2018, ApJ, 865, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Frandsen, S., Jones, A., Kjeldsen, H., et al. 1995, A&A, 301, 123 [NASA ADS] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García, R. A., Davies, G. R., Jiménez, A., et al. 2013, J. Phys. Conf. Ser., 440, 012040 [CrossRef] [Google Scholar]
- Girardi, L. 1999, MNRAS, 308, 818 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gough, D. O. 1986, in Hydrodynamic and Magnetodynamic Problems in the Sun and Stars, ed. Y. Osaki, 117 [Google Scholar]
- Gray, R. O., & Corbally, C. J. 1994, AJ, 107, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Sp. Sci. Rev., 85, 161 [CrossRef] [Google Scholar]
- Grundahl, F., Fredslund Andersen, M., Christensen-Dalsgaard, J., et al. 2017, ApJ, 836, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Handberg, R., Brogaard, K., Miglio, A., et al. 2017, MNRAS, 472, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Hon, M., Stello, D., & Yu, J. 2018, MNRAS, 476, 3233 [NASA ADS] [CrossRef] [Google Scholar]
- Houdek, G. 2010, Ap&SS, 328, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Bedding, T. R., Arentoft, T., et al. 2011, ApJ, 731, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Kallinger, T., Guenther, D. B., Matthews, J. M., et al. 2008, A&A, 478, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallinger, T., Weiss, W. W., Barban, C., et al. 2010, A&A, 509, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallinger, T., Hekker, S., Mosser, B., et al. 2012, A&A, 541, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 2011, A&A, 529, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kjeldsen, H., Bedding, T. R., Arentoft, T., et al. 2008, ApJ, 682, 1370 [NASA ADS] [CrossRef] [Google Scholar]
- Lebreton, Y., Fernandes, J., & Lejeune, T. 2001, A&A, 374, 540 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Livingston, J. H., Dai, F., Hirano, T., et al. 2018, AJ, 155, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Lund, M. N., Basu, S., Silva Aguirre, V., et al. 2016, MNRAS, 463, 2600 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, A. W., Vanderburg, A., Rizzuto, A. C., et al. 2018, AJ, 155, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Mashonkina, L. I., Gehren, T., Shi, J.-R., Korn, A. J., & Grupp, F. 2011, A&A, 528, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matthews, J. M. 2007, Commun. Asteroseismol., 150, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Montalbán, J., Miglio, A., Noels, A., et al. 2013, ApJ, 766, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Mosser, B., & Appourchaux, T. 2009, A&A, 508, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mozurkewich, D., Armstrong, J. T., Hindsley, R. B., et al. 2003, AJ, 126, 2502 [NASA ADS] [CrossRef] [Google Scholar]
- Nissen, P. E., Silva Aguirre, V., Christensen-Dalsgaard, J., et al. 2017, A&A, 608, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordgren, T. E., Sudol, J. J., & Mozurkewich, D. 2001, AJ, 122, 2707 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telescopes Instrum. Syst., 1, 014003 [Google Scholar]
- Rodrigues, T. S., Bossini, D., Miglio, A., et al. 2017, MNRAS, 467, 1433 [NASA ADS] [Google Scholar]
- Sato, B., Izumiura, H., Toyota, E., et al. 2007, ApJ, 661, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Sharma, S., Stello, D., Bland-Hawthorn, J., Huber, D., & Bedding, T. R. 2016, ApJ, 822, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Silva Aguirre, V., Davies, G. R., Basu, S., et al. 2015, MNRAS, 452, 2127 [NASA ADS] [CrossRef] [Google Scholar]
- Silva Aguirre, V., Lund, M. N., Antia, H. M., et al. 2017, ApJ, 835, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Slumstrup, D., Grundahl, F., Brogaard, K., et al. 2017, A&A, 604, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Slumstrup, D., Grundahl, F., Aguirre, V. S., & Brogaard, K. 2019, A&A, 622, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stello, D., Vanderburg, A., Casagrande, L., et al. 2016, ApJ, 832, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Stello, D., Huber, D., Grundahl, F., et al. 2017, MNRAS, 472, 4110 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B., & Pancino, E. 2008, PASP, 120, 1332 [Google Scholar]
- Tassoul, M. 1980, ApJS, 43, 469 [NASA ADS] [CrossRef] [Google Scholar]
- van Belle, G. T., & von Braun, K. 2009, ApJ, 694, 1085 [NASA ADS] [CrossRef] [Google Scholar]
- van Belle, G. T., Lane, B. F., Thompson, R. R., et al. 1999, AJ, 117, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Vandakurov, Y. V. 1967, AZh, 44, 786 [NASA ADS] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, G., Matthews, J., Kuschnig, R., et al. 2003, PASP, 115, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- White, T. R., Pope, B. J. S., Antoci, V., et al. 2017, MNRAS, 471, 2882 [NASA ADS] [CrossRef] [Google Scholar]
- White, T. R., Huber, D., Mann, A. W., et al. 2018, MNRAS, 477, 4403 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
List of the 27 mode frequencies (with uncertainties) in ϵ Tau, their amplitude, S/N value in amplitude (not power), and mode-identification (ℓ, n) for the ℓ = 0, 2 modes.
Stellar atmospheric parameters determined from spectroscopy, with and without a surface gravity constraint from asteroseismology.
All Figures
 |
Fig. 1. SONG data from Tenerife and Delingha, the combined, unfiltered time-series (panel a) the combined, filtered time-series (panel b). Panels c and d: close-ups of individual nights of RV observations from Tenerife (panel c) and from Delingha (panel d). |
| In the text | |
 |
Fig. 2. K2 data for ϵ Tau. The unfiltered time-series (panel a), a version of the time series (panel b) where dominating low-frequency variations up to 42 μHz have been subtracted (see text), a zoomed view of the filtered data (panel c) for the same length in time as in Fig 1c (we note the different zero points in time between the SONG and the K2 data). The data shown in panel c have been smoothed to enhance the oscillation signal. |
| In the text | |
 |
Fig. 3. Power density spectra and spectral windows (in power) for the SONG and K2 data, respectively. The white curves are fits to the data to determine νmax, see text for a discussion. |
| In the text | |
 |
Fig. 4. Autocorrelations of the power spectra, for the SONG spectrum in the upper panel, and K2 in the middle panel. Bottom panel: the two autocorrelations multiplied together. The vertical dashed lines in the upper panel indicate the signals originating from the 1 d−1 aliases in the spectral window, at 11.574 μHz and integer fractions thereof. The arrows indicate a value of 5.0 μHz, which we identify as Δν for ϵ Tau using various methods (see text). |
| In the text | |
 |
Fig. 5. Results of using a modified version of an analysis method developed for solar-like oscillations observed with Kepler, as described in the text. Upper panel: results based on the SONG power spectrum. Middle panel: results for K2. As in Fig 4, the dashed lines in the upper panel indicate signals originating from the 1 d−1 aliases in the spectral window, and the arrow indicates the Δν-value of 5.0 μHz. Bottom panel: SONG and K2 results from the two upper panels are multiplied, resulting in a very clear peak near 5.0 μHz. |
| In the text | |
 |
Fig. 6. Upper panel: frequencies as a function of radial order (n) for the first stage of our frequency analysis. The dotted line has a slope of 5.00 μHz, in agreement with Δν found in Fig. 5. The black diamonds are detected modes that fit into a regular structure of expected ℓ = 0 modes, red triangles mark the positions of expected ℓ = 0 modes that were undetected in our first run of CLEAN, and the two blue squares represent the detected ℓ = 0, n = 8 mode, for which the first run of CLEAN picked up the +1 d−1 alias (see text). Lower panel: differences between the detected ℓ = 0 frequencies and those predicted by the asymptotic relation (Eq. (1)), also in μHz. |
| In the text | |
 |
Fig. 7. As shown in Fig. 6, one of the modes detected in the original run of CLEAN on the SONG data was likely an 1 d−1 alias of a true ℓ = 0 mode. Three upper panels: SONG data near the originally detected frequency (middle column of panels), and minus (left panel) and plus (right panel) 1 d−1 corresponding to 11.574 μHz. Middle panels: same for the K2 data, and the lower panels for the product of the two. The K2 power spectrum and the product of the SONG and K2 spectra support the interpretation that the originally detected mode was in fact a 1 d−1 alias of the actual mode, which is indicated by an arrow in the lower-left panel. |
| In the text | |
 |
Fig. 8. Échelle diagram for the 27 oscillation modes. The x-axis was shifted to place ℓ = 0, 2 modes close to each other in the diagram. Filled red circles are ℓ = 0 modes, the green triangle is ℓ = 2, and blue diamonds are for the remaining peaks, of which most are likely ℓ = 1 modes. |
| In the text | |
 |
Fig. 9. Top panel: close-up of the power spectrum based on the SONG data, centred at the ℓ = 0, n = 11 mode just below 61 μHz. The over-plotted, red curve shows the spectral window for this central ℓ = 0 mode. The detected modes are indicated at the top of the panel, with an identification as in Fig. 8. The ℓ = 0 mode above 70 μHz has a low S/N of only 2.5 in the SONG data, but is more pronounced in the lower panel, where the K2 and SONG spectra are multiplied, as indicated by the arrow. The mode is therefore included in our final frequency list. Relatively strong but undetected peaks are sidelobes of modes outside the frequency range in the close-up view. Two lower panels: full SONG power spectrum and the product of the SONG and K2 power spectra, with the detected modes indicated using the same symbols as in the top panel. The three panels are aligned according to the ℓ = 0 mode just below 61 μHz. |
| In the text | |
 |
Fig. 10. Frequencies of the nine ℓ = 0 modes included in Table 3 as a function of their n-values. According to the asymptotic relation in Eq. (1), the slope provides the large frequency separation Δν while the intersection with the ordinate is Δν ⋅ ϵ, leading to the value for ϵ quoted in the figure and listed in Table 2. |
| In the text | |
 |
Fig. 11. Smoothed power spectra based on 80 d segments for KIC9716522 in NGC 6811, which is similar to ϵ Tau and which was observed for four years by Kepler. The data were used to estimate the uncertainty arising from the fact that the SONG and K2 data for ϵ Tau were non-simultaneous. |
| In the text | |
 |
Fig. 12. Simulated power spectra to estimate the effect of the window function on the determination of oscillation amplitudes, see text. |
| In the text | |
 |
Fig. 13. Measured amplitudes in RV (top panel) and intensity (middle panel), and the amplitude ratio as a function of frequency (bottom panel), for ϵ Tau. The dashed line indicates νmax |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.