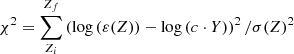| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A159 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201834241 | |
| Published online | 13 February 2019 | |
Unusual neutron-capture nucleosynthesis in a carbon-rich Galactic bulge star
1
Zentrum für Astronomie der Universität Heidelberg, Astronomisches Rechen-Institut, Mönchhofstr. 12, 69120 Heidelberg, Germany
e-mail: andreas.koch@uni-heidelberg.de
2
Institut für Kernphysik, Technische Universität Darmstadt, Schlossgartenstr. 2, 64289 Darmstadt, Germany
3
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
4
Dark Cosmology Centre, The Niels Bohr Institute, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
5
Monash Centre for Astrophysics, School of Phyics and Astronomy, Monash University, 3800, Australia
6
E. A. Milne Centre for Astrophysics, Department of Physics & Mathematics, University of Hull, HU6 7RX, UK
7
GSI Helmholtzzentrum für Schwerionenforschung GmbH, Planckstr. 1, 64291 Darmstadt, Germany
Received:
12
September
2018
Accepted:
14
December
2018
Metal-poor stars in the Galactic halo often show strong enhancements in carbon and/or neutron-capture elements. However, the Galactic bulge is notable for its paucity of these carbon-enhanced metal-poor (CEMP) and/or CH-stars, with only two such objects known to date. This begs the question whether the processes that produced their abundance distribution were governed by a comparable nucleosynthesis in similar stellar sites as for their more numerous counterparts in the halo. Recently, two contenders of these classes of stars were discovered in the bulge, at [Fe/H] = −1.5 and −2.5 dex, both of which show enhancements in [C/Fe] of 0.4 and 1.4 dex (respectively), [Ba/Fe] in excess of 1.3 dex, and also elevated nitrogen. The more metal-poor of the stars can be well matched by standard s-process nucleosynthesis in low-mass asymptotic giant branch (AGB) polluters. The other star shows an abnormally high [Rb/Fe] ratio. Here, we further investigate the origin of the abundance peculiarities in the Rb-rich star by new, detailed measurements of heavy element abundances and by comparing the chemical element ratios of 36 species to several models of neutron-capture nucleosynthesis. The i-process with intermediate neutron densities between those of the slow (s-) and rapid (r)-neutron-capture processes has been previously found to provide good matches of CEMP stars with enhancements in both r- and s-process elements (class CEMP-r/s), rather than invoking a superposition of yields from the respective individual processes. However, the peculiar bulge star is incompatible with a pure i-process from a single ingestion event. Instead, it can, statistically, be better reproduced by more convoluted models accounting for two proton ingestion events, or by an i-process component in combination with s-process nucleosynthesis in low-to-intermediate mass (2–3 M⊙) AGB stars, indicating multiple polluters. Finally, we discuss the impact of mixing during stellar evolution on the observed abundance peculiarities.
Key words: nuclear reactions, nucleosynthesis, abundances / stars: abundances / stars: carbon / stars: Population II / Galaxy: abundances / Galaxy: bulge
© ESO 2019
1. Introduction
Nuclei heavier than Z ≳ 30 can be created via neutron-captures, which can be separated into the slow (s) and rapid (r) neutron-capture processes (Burbidge et al. 1957), as determined by the relative efficiency of the capture rates vs. competing beta-decay timescales. Rare isotopes of heavy elements are formed by neutron captures with large cross sections, or by disintegration reactions or various other flavours of the p-process such as (p, γ) reactions. Since the slow and rapid processes require significantly different neutron densities, they have accordingly been assigned to different sites such as asymptotic giant branch (AGB) stars for the s-process (e.g., Busso et al. 1999; Gallino et al. 1998; Käppeler et al. 2011; Karakas & Lattanzio 2014) vs. supernova (SN) nucleosynthesis (Qian & Wasserburg 2007; Sneden et al. 2008; Winteler et al. 2012) or neutron star mergers for the r-process (e.g., Lattimer & Schramm 1974; Freiburghaus et al. 1999; Chornock et al. 2017; Watson et al. 2019).
Recent observations suggested the need for an additional process acting at conditions between s and r, viz. the intermediate neutron-capture process (i-process), originally proposed by Cowan & Rose (1977). Rather than invoking a pollution of the interstellar material with both r- and s-enhanced material from different sites to account for the abundance peculiarities seen in, for example, a sub-class of carbon-enhanced metal-poor stars (CEMP r/s1), the i-process acts at neutron densities between the r- and s-process in a single site, thus producing a markedly different abundance pattern. It is not straightforward to draw a distinction between the i- and s-processes at one definitive value for the neutron density. Fishlock et al. (2014) suggested that, while N exceeded 1013 cm−3 in their intermediate-mass AGB models, the resulting abundance distribution was still very much that of an s-process, while being dominated by first peak elements due to 22Ne(α, n)25Mg providing the neutrons. The reality is more likely that there is some overlap between neutron densities that are classically considered “s” and are “i”. Moreover, a distinction in terms of the τ–n-density space occupied by these two processes may be possible.. Calculations of the i-process are able to provide good fits to observations of strongly enhanced Ba and Eu abundances and in particular to reproduce the stars’ high [hs/ls] ratios2 (e.g., Hampel et al. 2016; Denissenkov et al. 2018). Indications of i-process signatures have been observed in grains (Jadhav et al. 2013), post-AGB stars (Lugaro et al. 2015), open-cluster stars (Mishenina et al. 2015), CEMP stars (e.g., Hampel et al. 2016), the most metal-poor stars known (Clarkson et al. 2018), and a carbon-normal, metal-poor field dwarf with enhanced s- and r-process abundances (Roederer et al. 2016). Proposed sites for i-process nucleosynthesis are, amongst others, the He-core and He-shell flashes in low-mass, low-metallicity stars (Campbell & Lattanzio 2008; Campbell et al. 2010; Cristallo et al. 2009; Stancliffe et al. 2011), Super-AGB stars (Doherty et al. 2015; Jones et al. 2016), and rapidly accreting white dwarfs (Denissenkov et al. 2017).
Here, we have investigated the nucleosynthetic signatures of a metal-poor ([Fe/H] = −1.5 dex) star in the Galactic bulge that shows evidence of strong s-process enhancements (Koch et al. 2016) without indication for strong over-abundances of the r-process elements. This CH-star shows a peculiar signature of two abundance peaks with similar enhancements, namely around Rb (Z = 37)3 and Ba (Z = 56). In Koch et al. (2016) we found that the abundance pattern of this star suggested enrichment from an intermediate mass AGB star of ∼4 M⊙, although the entire distribution could not be satisfactorily fitted. Such a deficiency of standard s-process nucleosynthesis prompts the need for further complexity in the form of admixing other nucleosynthetic channels. We therefore performed a detailed comparison of the observed abundance pattern in this bulge CH-star with calculations of s- and r-processes, combined with predictions from i-process nucleosynthesis.
This paper is organized as follows. In Sect. 2 we place this object in the context of other C-rich stars in the Milky Way’s components and we recapitulate the observed abundance details that are complemented with new measurements of several heavy elements; in Sect. 3 we introduce the s, r, and i-process models used to represent the targets’ abundance patterns, while, in Sect. 4, we describe the best-fit models to investigate, which processes dominated this bulge star’s enrichment. To improve the results, we consider enrichment from multiple sites in Sect. 5 and discuss alternative scenarios in Sect. 6. Finally, Sect. 7 summarizes our findings.
2. Metal-poor bulge stars
While the Galactic bulge is predominantly old and metal-rich (McWilliam & Rich 1994; Clarkson et al. 2008; McWilliam 2016), recent studies have focused on the detection and analysis of metal-poor stars toward the bulge, which are predicted by cosmological models to reside in those central regions (e.g., Tumlinson 2010). In fact, Casey & Schlaufman (2015) measured depleted [Sc/Fe] ratios in three metal-poor bulge stars, which they interpreted as a signature of enrichment by the first, massive Population III stars, while no other such sample shows any such evidence (Koch et al. 2016).
2.1. Carbon-rich bulge stars
In Koch et al. (2016) we detected two stars with strong carbon enhancements toward the Galactic bulge. Subsequent analyses classified them as a CEMP-s star (star-ID #277934; [Fe/H] = −2.52; [C/Fe] = 1.44; [Ba/Fe] = 1.31) and a moderately metal-poor CH-star (star-ID #10464; [Fe/H] = −1.53; [C/Fe] = 0.41; [Ba/Fe] = 1.35). These are the first known contenders of these classes of stars in the Galactic bulge.
In order to understand the origin of these stars’ abundance pattern and to connect it to any peculiar class of objects it is indispensable to detect and characterize more, similar candidates. However, so far no other CH- or CEMP-stars have been found in the bulge, save for very few of their metal-rich counterparts, the Ba-stars (Lebzelter et al. 2013), that follow the dominant metallicity distribution function (MDF) of the bulge. The target of the present study (#10464) and the bulge CEMP-s star #27793 (Koch et al. 2016) are such rare exceptions. This keeps the fraction of CEMP stars in the bulge down at the 2% level. The reason for this can be sought in the currently observed, overall, more metal-rich nature of the bulge, albeit theories predict the occurrence of such very metal-poor stars toward the Galactic centre regions (e.g., Tumlinson 2010; Ness et al. 2013; Casey & Schlaufman 2015; Koch et al. 2016).
The fraction of CEMP stars in the halo and in metal-poor dwarf spheroidal galaxies is known to significantly increase with decreasing metallicity (e.g., Norris et al. 2010; Carollo et al. 2012; Salvadori et al. 2015; Skúladóttir et al. 2015; Hansen et al. 2015b, 2016a; Susmitha et al. 2017) and also the bulge’s metal-poor population can be expected to follow this trend (Tumlinson 2007, 2010). It is then interesting to note that the bulge CH-star falls right on the peak of the halo MDF, and the CEMP-s lies at the peak of the halo CEMP star distribution. Moreover, the commonly accepted scenario for the origin of the s-process enhancements in the CEMP-s stars is mass transfer from an (AGB) companion in a binary system (e.g., Bisterzo et al. 2011; Starkenburg et al. 2014; Hansen et al. 2016c). Apart from the obvious contenders such as survey target selection biases (Jacobson et al. 2015), evolutionary mixing on the red giant branch that depletes the surface abundance of C (Placco et al. 2014), and overall low number statistics of metal-poor bulge stars (e.g., Koch et al. 2016), the present paucity of bulge CEMP-s stars could therefore also bear implications for the binary fraction in the early bulge, which to date has been difficult to determine (e.g., Holtzman et al. 1998; Miszalski et al. 2009). On the other hand, surveys to date failed to detect even the CEMP-no stars in the bulge (e.g., Howes et al. 2016); in the Galactic halo, this subclass, not over-enhanced in any of the heavy elements5, are not part of binary systems (Hansen et al. 2016a) so the very low fraction of CEMP stars of any class in the bulge indicates that their absence has multiple origins rather than only being related to the bulge binary fraction, which can differ from that of the halo (e.g., Ryan 1992).
2.2. Chemical peculiarities in metal-poor bulge stars
In Koch et al. (2016), comparison with standard AGB yields (Cristallo et al. 2011) indicated that the C- and s-process enhancements in the regular CEMP-s star #27793 were best matched with mass transfer from a low-mass AGB companion, although details of the AGB nucleosynthesis such as the size of the 13C-pocket and mass loss suggest a more complicated picture. More complications arose in the attempt to reproduce the abundance pattern of the target of this present study, star #10464, which shows contributions from AGB nucleosynthesis. However, no satisfactory fit to the hs- and simultaneously the ls-peak elements could be obtained, leaving a large uncertainty beyond the “low-to-intermediate mass AGB” enrichment. Here, the largest deviation from model fits (e.g., Cristallo et al. 2011) occurred for Rb, which, at [Rb/Fe] = 1.29 ± 0.16 dex, remains inexplicably high.
2.3. Stellar parameters and additional abundance measurements
The stellar parameters of the peculiar object #10464 we found in Koch et al. (2016) are (Teff, log g, ξ, [Fe/H]) = (5400 K, 1.7, 2.64 km s−1, −1.53). In that work, as well as in the following, we had performed an abundance analysis using the LTE abundance code MOOG (Sneden 1973) and building on the plane-parallel, one-dimensional grid of ATLAS model atmospheres6. This choice is adequate for star #10464 as it is a non-variable Horizontal Branch star and furthermore, a proper modeling of dynamic atmospheres is non-trivial and thus, to date, often approximated by static theory (Hansen et al. 2016b; Vasilyev et al. 2018; cf. García-Hernández et al. 2007). We also note that our working hypothesis is that the unusual chemical abundances found in the present-day star are the product of nucleosynthesis in a long-perished generation of polluters. The evolutionary state of the latter, whether with strong atmospheric dynamics or not, is thus irrelevant for the abundance derivation in the present object.
In Koch et al. (2016), we employed an equivalent width analysis and enforced excitation and ionization balances to obtain the stellar parameters. Here, we verified these parameters using the novel code ATHOS (“A Tool for HOmogenizing Stellar parameters”, Hanke et al. 2018), which uses flux ratios within an optimized set of spectral ranges. The resulting temperature and metallicity are in excellent agreement with the previous results. The gravity returned by ATHOS is marginally lower, but as Table 7 of Koch et al. (2016) indicates, this has only a minor influence on the derived abundances ratios. In particular, as a neutral species, Rb is highly insensitive to this parameter. Therefore we conclude that the set of stellar parameters we use in this work is reliable.
Table 1 recapitulates the abundance measurements in this star obtained in the latter work. In addition, we were able to extract further elemental abundances not included in the latter study. Here, we also list the total error bar on our measurements, which is based on the contribution from the statistical and systematic uncertainties. The former was based on the 1σ-scatter of lines in case that several transitions were measurable, and estimated from the quality of the fitting procedures otherwise. Systematic errors, in turn, were derived from the standard technique of varying the stellar models by one parameter about its uncertainty at a time, thereby re-deriving a new set of abundances (Koch et al. 2016). This full set of abundances will be the basis of our comparison with various models in Sect. 4.
Abundance ratios in the C-rich bulge star #10464 from Koch et al. (2016) and our present measurements.
In our previous work, the C-abundance of this star had been derived by spectral synthesis of the CH G-band at 4300 Å, yielding a [C/Fe] ratio of 0.4 dex. Here, from spectral synthesis of the CN-band at 3883 Å, we derived a nitrogen abundance ratio of [N/Fe] = 0.75 ± 0.15, with an uncertainty mainly driven by the continuum placement. The low [C/N] of −0.34 ± 0.19 dex in this CH-star is close to the limit that separates mixed and unmixed metal-poor stars (Spite et al. 2005; Hansen et al. 2016a). This will be further discussed in Sect. 6. In spite of its larger [N/Fe] ratio in excess of 0.5 dex, the [C/N] ratio of star #10464 is marginally too high for it to qualify as a “nitrogen-enhanced metal-poor” star (Johnson et al. 2007; Pols et al. 2012). An O-abundance from the triplet lines at 7770 Å could be determined and yielded a value of [O/Fe] = 0.63 ± 0.13 dex.
The blue spectral range of our spectra allowed us to complement our earlier, basic abundance ratios by a wealth of measurements for neutron-capture elements (Hansen et al. 2015a). To this end, we employed spectral synthesis for stronger lines that were chosen from the list of Roederer et al. (2014). Hyperfine structure was included where appropriate, and a line list providing the base for the additional measurements is given in Table 2. Thus we were able to determine additional abundances for Li, N, O, Ga, Ce, Pr, Sm, Gd, Tb, Dy, Ho, Er, Hf, and Pb that were not included in our original work (Koch et al. 2016).
Line list for heavy elements in #10464 that were not covered in Koch et al. (2016).
To illustrate the range of our measurements, we show in Fig. 1 the full abundance pattern for #10464 together with an exemplary range of AGB models from the F.R.U.I.T.Y. database (Cristallo et al. 2011), highlighting the difficulty in simultaneously reproducing all heavy-element peaks, in particular the star’s high [Rb/Fe] ratio.
 |
Fig. 1. Full abundance distribution of the bulge star #10464 from Koch et al. (2016) and this work. The AGB yields with progenitor masses as labeled were taken from Cristallo et al. (2011). The bottom panels are a zoom into the regions of the first and second n-capture element peaks. |
3. Model details of s-, r-, and i-process nucleosynthesis
3.1. s-process yields from AGB nucleosynthesis
Here, we employed the metal-poor (Z = 0.0001; [M/H]= −2.2 dex) AGB models of Lugaro et al. (2012). In order to determine the best model to describe this star, we applied our fitting routines (Sect. 4) to the entire, broad range of stellar masses (0.9–6 M⊙) provided by these models. This set of AGB calculations also accounted for varying initial chemical compositions (e.g., in terms of varying heavy element contributions from early Galactic chemical enrichment, Kobayashi et al. 2006) and one of the, to date, still most uncertain parameters in AGB nucleosynthesis – the size of the 13C pocket (see, e.g., Buntain et al. 2017 for a detailed discussion). Observations indicate a variety of pocket sizes; the convective boundary mixing that is relevant for transporting H into the intershell is not well understood, even though many processes have been proposed.
Similar tests were carried out using the more metal-rich models of Fishlock et al. (2014, [Z = 0.001]) and Karakas & Lugaro (2016, [Z = 0.007 and Z = 0.014]), but those resulted in considerably larger χ2 values when fitted to the observations. Coupled with the low metallicity of the star to be described, at [Fe/H] = −1.5 dex, we discard these metal-rich yields from the following considerations. The overall, best-fit s-process-alone model (viz. a 3 M⊙ AGB) will be described in detail in Sect. 4.2.
3.2. r-process yields from neutron star mergers
The r-process calculation was performed with the WinNet nucleosynthesis network (Thielemann et al. 2011; Winteler 2014) that contains almost 6000 nuclei, using ∼65 000 reaction rates of the Jina Reaclib Database V2.0 (Cyburt et al. 2010), using the Finite-Range droplet mass model (Möller et al. 1995). In addition, we used neutron capture and neutron-induced fission rates given by Panov et al. (2010). For temperatures lower than T ≤ 0.01 GK some electron-capture and β-decay rates are replaced by the ones of Langanke & Martínez-Pinedo (2001). Here, the r-process is calculated in the environment of dynamical ejecta from compact neutron star mergers using temperature and density profiles from the Newtonian simulations of Price & Rosswog (2006). Korobkin et al. (2012) investigated the r-process nucleosynthesis for these ejecta and found a very robust abundance pattern for heavy nuclei, caused by the low electron fractions of ∼0.035 that leads to fission cycling. Therefore, we chose one representative temperature and density profile to calculate the typical r-process abundances. Despite recent direct evidence for r-process nucleosynthesis in neutron star mergers (e.g., Chornock et al. 2017; Watson et al. 2019) other hosts are also promising astrophysical sites, for example, magnetohydrodynamically driven supernovae. Besides uncertain astrophysical conditions, most of the nuclear reactions involved in the r-process nowadays still rely on theoretical predictions rather than experimental data. As a consequence, theoretical nucleosynthesis predictions are not able to fully reproduce the solar r-process abundances. Therefore, we also considered the abundance pattern of the metal-poor star CS 22892-052 as a reference set, assuming that its heavy elements are produced by the r-process only (Sneden et al. 2003). Even with this pattern we reach the same conclusion that the contribution of r-process to the bulge star #10464 is negligible, as also illustrated below in Fig. 4.
3.3. Basics of the i-process
The i-process is thought to occur when H is advected into a convective zone that is driven by helium burning. Hydrogen reacts with 12C to produce 13N, which can decay to 13C. The latter isotope finally reacts with the available He via 13C(α,n)16O reaction, producing the necessary neutrons. Contrary to 13C-pockets in regular AGB models, which hold all material including heavy (s-process) elements in very localized regions, freshly produced nuclei in common i-process models can be distributed throughout the entire convective zone. The high temperatures lead to rapid neutron production and a characteristic neutron density of ∼1014–1015 cm−3 (Cowan & Rose 1977; Herwig et al. 2011; Roederer et al. 2016; Hampel et al. 2016). The energy release through these hydrogen-burning chains could lead to the expelling of the envelope and self-quenching (Jones et al. 2016). This terminates the i-process, although the time until termination will likely vary between different stellar sites, down to the order of days as in the case of Sakurai’s object (Herwig et al. 2011).
There is as yet no concrete site for the i-processes and many have been proposed, including proton ingestions in AGB stars, very late thermal pulses, Super-AGB stars and rapidly accreting white dwarfs. While we are not attempting to choose between them here, the physical conditions in our models were based on the first the ones mentioned above. Similarly, the metallicity constraints of this process are not clear, yet: observationally, the i-process is seen to operate at very low metallicity (CEMP-i stars; Hampel et al. 2016), but there is also evidence at higher metallicities, for example, in Sakurai’s object that shows in situ i-process nucleosynthesis at solar metallicity (Herwig et al. 2011). The latter situation is different from the star of our present analysis, which has not produced its heavy elements itself, but it had formed out of material enriched in these metals by a previous generation of events.
3.4. Equilibrium i-process with fixed neutron exposure
Using the suite of codes NucNet Tools (Meyer 2012) we created a one-zone model with given initial composition under conditions of fixed temperature and density. The latter were chosen as representing the mid-point of the intershell region in a low-metallicity AGB model (see Stancliffe et al. 2011 for further details of the structure), at values of T = 1.5 × 108 K and ρ = 1600 g cm−3. The initial chemical composition of this region represents the intershell of a low-metallicity (Z = 0.0001), low-mass (M = 1 M⊙) AGB model after the second thermal pulse (Abate et al. 2015b, and references therein). The nuclear network was followed with 5442 isotopes and 45 831 reactions from the JINA Reaclib V0.5 database (Cyburt et al. 2010) with further α-decay rates from Tuli (2011)7.
The evolution of the abundance distribution was followed at a fixed neutron density of N = 1015 cm−3 for 0.1 yr, which resulted in a neutron exposure of τ = 495 mbarn−1. This short time was sufficient to result in an equilibrium abundance pattern of the heavy elements, independently of the initial chemical composition. As elaborated in Hampel et al. (2016), the runtimes of models at lower neutron densities (down to 10−9 cm−3) were scaled with N to ensure the same neutron exposure. While this chosen exposure has the advantage of ensuring the robust equilibrium-abundance pattern, it has the drawback that Pb (Z = 82) abundances cannot be predicted, because the reaction flows around lead cannot reach equilibrium – this results in an implausibly high level of Pb production despite the otherwise very robust i-process pattern. Details of the shortcomings in a proper prediction of Pb are discussed in detail in Hampel et al. (2016). While lead represents, alone, the third s-process peak and thus is useful to verify the robustness of nucleosynthesis models, we explicitly removed Pb from all further consideration in our statistics given the above complications with its modeling.
The run-times of all other models with differing neutron densities from N = 109 cm−3 to N = 1015 cm−3 were finally scaled with neutron density to ascertain the same, constant neutron exposure in all models. to allow for comparisons of the different equilibrium patterns. We refer the reader to Hampel et al. (2016) for details on the i-process models.
4. Model results
4.1. Formalism
Next, we applied the setups laid out in Sect. 3 to test if the bulge star #10464 shows signatures indicative of s-, r-, or i-process nucleosynthesis, or combinations thereof. We assumed that the nucleosynthetic processes described did not take place in this star itself, but occurred in an earlier generation which polluted the gas from which this star formed. In the following, we only considered elements with 31 ≤ Z ≤ 72 (Ga through Hf in the statistics, since nuclei below Z ≲ 30 are not significantly produced in the neutron-capture reactions and in order to properly model light isotopes (such as 13C or 14N), a careful treatment of the entrainment and nucleosynthesis processes in multi-dimensional simulations is needed (Herwig et al. 2011, 2014). We note, however, that the C-, N-, and O-abundances in this star agree very well to within the uncertainties with model predictions of, for example, the AGB models detailed in Sect. 3.1. As explicated above, Pb was excluded from our statistics as well.
The results of the fitting are summarized in Table 3, where the mass of the s-process contributing AGB-star is indicated in Solar masses as a subscripts (ala “sm2” for a 2 M⊙ star and the i-process is identified by the log of its neutron density. The quality of each scenario was judged in terms of the χ2 statistics for each of the enrichment scenarios. This statistical estimator, within the element range of Zi ≤ Z ≤ Zf, is given by
Results for various linear combinations of nucleosynthetic processes in the fitting range of 31 ≤ Z ≤ 72.
where σ(Z) is the error on the observationally derived logε abundances (Table 1), and Y are the model yields from either process. The fit of one distribution was obtained by a multiplicative scaling factor c of the abundances Y, which translates into an additive scaling in logarithmic space. This is equivalent to an admixture of the individual processes with pure hydrogen. Under the assumption of Gaussian errors and considering that we have N = 18 elements in our fit range of 31 ≤ Z ≤ 72, we can estimate that a statistically good fit corresponds to a χ2 of about 40, while an excellent result should yield values on the order of ten.
The resulting abundance distributions for a chosen set are shown in Figs. 2–4. As Table 3 implies, admixtures of the Solar abundance distribution (Lodders 2003) has an adverse effect on the statistics and we do not consider this option any further.
 |
Fig. 2. Heavy element pattern in #10464 in comparison with i-process model calculations for various neutron densities reaching from N = 109 cm−3 to N = 1015 cm−3. Here, the s-process curve is for the best-fit 3 M⊙ AGB composition of Lugaro et al. (2012; case “sm3”; Table 3). Top panel: absolute abundances, lower panel: resulting residuals of the individual fits, and errorbars of the abundances as squares. Pb (Z = 82) was excluded from our statistical tests and is thus not shown in this and the following figures. |
 |
Fig. 3. Same as Fig. 2, but for various mixtures of s-process with i-process models. Shown are the curves for the overall, best-fit version (sm2 + sn15; blue), a 2 M⊙ AGB component plus a lower neutron density (red), and an s-process from a high-mass AGB model plus the two extreme neutron density i-processes (black and magenta). Shown as dashed lines are two s-process models from different AGB masses. |
 |
Fig. 4. Same as Fig. 2, but for a linear combination of all three nucleosynthetic channels (s + r + i). The bottom panel indicates the relative contributions from each process. We note that no r-process component is required. |
4.2. s- vs. i-process
Figure 2 shows the best-fit s-process results from the AGB models of Lugaro et al. (2012), and also different undiluted i-process models with neutron densities of N = 109 cm−3 up to 1015 cm−3 (Hampel et al. 2016). We did not attempt to fit a pure r-process pattern to the star given its higher metallicity where Galactic chemical evolution dictates that already several other sites have contributed to its chemical enrichment.
Our least-squares fitting emphasizes that the pure, diluted s-process pattern of the Lugaro et al. (2012) yields already provide a good agreement with the observed data. Here, we find a progenitor with an initial mass (Minit) of 3.0 M⊙ (Mevol = 2.51 M⊙ after evolution including 20 thermal pulses) to provide the best fit of the observations8; specifically it is characterized by core and envelope masses of MCore = 0.81 M⊙ and MEnv. = 1.70 M⊙, respectively, also implying a fairly massive white dwarf companion.
In comparison, the sole assumption of an i-process enrichment provides a larger χ2, which was smallest for a neutron density of N = 109 cm−3. The differences between model and observations are minimal for the second s-process peaks, while, for the light s-elements, this scenario only succeeds in reproducing either Y or Zr. Overall, the χ2 values in the hundreds indicate that these fits can be considered bad and statistically insignificant. Here, it is worth pointing out that an overproduction of Pb, as described in Sect. 3.4, is also seen in the s-process calculations (e.g., Fig. 1) and therefore not only inherent in the i-process models – conversely, the latter can actually aid to help with solving these problems in a bigger frame, although this endeavour is far beyond the scope of this work in a single, peculiar star.
Denissenkov et al. (2017) suggested that the i-process in rapidly accreting white dwarfs can account for about a third of the intermediate n-capture elements (31 ≤ Z ≤ 42) within Galactic chemical evolution. The abundance pattern from their model does not match our observations in the bulge star #10464 as none of the element abundances seen in this star reaches the over-enhancements predicted in that scenario (cf. their Fig. 4). We note, however, that the respective calculations have been carried out for explicitly higher metallicities ([Fe/H] > −1 dex) than the one found in this bulge object.
Based exclusively on the high Rb/Zr ratio, Koch et al. (2016) suggested that the AGB progenitor was likely of intermediate mass, at ∼4 M⊙, although a detailed match of the remaining abundance pattern (of 10 elements with Z ≥ 30) could not be reached. Similarly, either set of models employed in the present work fails to make sense of the very high [Rb/Fe] abundance of this star (cf. Abia et al. 2001). Even more severe is the trend of strongly decreasing [ls/Fe] ratios when moving from Rb to Zr (Fig. 1). This is not reproduced in any of our simulations and poses a challenge to nucleosynthetic calculations. A decrease from Sr through Zr is seen in models of fast rotating massive (∼25 M⊙) stars (Frischknecht et al. 2012), yet those have the tendency to produce low amounts of Rb. The latter is predominantly produced in AGB stars, but constructing a superposition of such enrichment with the more regular intermediate-mass pollution (van Raai et al. 2012) to account for #10464’s heavy element patterns seems unlikely. High Rb can also be indicative of high neutron-density (Pignatari et al. 2010). In turn, comparison with the models of Pérez-Mesa et al. (2017) indicate that ∼6 M⊙ AGB star can indeed produce the high, observed Rb abundance, but this conflicts with a too high Rb/Zr ratio of our observations. Indeed, our fitting of a pure higher-mass (5 M⊙) AGB s-process component (“sm5” in Fig. 3 and Table 3) leads to a deterioration of our statistics.
If we only assume a short neutron burst in our i-process calculations, which does not provide enough neutrons to establish a typical equilibrium-abundance pattern, the heavy element production is only driven up to the ls peak. In such a scenario, a neutron density of N = 109 cm−3, leading to an exposure of τ = 0.3 mbarn−1, can reproduce the observed characteristics of the Rb peak. However, any further neutron irradiation, as is needed for the production of heavier elements including the hs-peak elements and Pb, would destroy the reproduced ls pattern. Therefore it cannot be assumed that the i-process can produce both the Rb peak and the heavier elements in one single event.
As for the second-peak elements, none of the models we employed is able to reproduce the shape of the heavy-s peak (e.g., the observed [Ba/La] ratio), which renders a pure s-process origin unlikely; this is, for example, manifested in the [Ba/La] vs. [Eu/La] plane (Fig. 6 in Mishenina et al. 2015), where our star grazes the lowest boundary of open cluster and Galactic disk stars’ [Eu/La] values. While models of the i-process generally succeed in reproducing a higher [Ba/La] compared to the s- or r-process (e.g., Hampel et al. 2016), the observed Ba/La ratio of #10464 is, per se, too low for a substantial i-process contribution characterized by N = 1015 cm−3. Moreover, the shape of the hs-peak is remarkable, since [Ba/La] ≫ [Ba/Ce]. An increased neutron density shapes the hs-peak predominantly through contributions of additional Ba resulting from the decay of radioactive 135I, which, however, has trouble explaining both the Ba- and Ce-to-La ratio being 0.3 dex higher than solar.
5. Multiple enrichment sites
As we have shown in the previous section, it is hard to reconcile the observed heavy-element abundance pattern in #10464 with only one nucleosynthetic event at a time. Therefore, in the following we will focus on exploring the possibility that this bulge object was enriched by more than one progenitor, each having contributed some fraction of the two or three nucleosynthesis processes described above. In order to fit these processes to the observed abundance distribution of the star, we adopt a linear superposition of N individual nucleosynthetic processes, j, following the formalism of Hansen et al. (2014):
where Yj(Z) denotes the absolute abundances and cj are the weights assigned to each of the contributing processes (s,r,i), respectively. Since Yj includes an arbitrary scaling factor, the actual values of these weights have no physical meaning. We note that implementing N weights without additional constraints will include an additional additive freedom. However, there are other mixing techniques as shown in, e.g., Hampel et al. (2016), where the weighting factors are constrained by ∑ cj = 1. We want to stress that the choice of the mixing techniques does not affect the conclusion of this work. In the minimization process, Y was substituted by Ycalc in Eq. (1). If more than three different processes were included, convergence could not be achieved. The results for Zi = 31 and Zf = 72 are again indicated in Table 3.
In the following, we used the entire set of s-process patterns from Lugaro et al. (2012) as described above (Sects. 3.1 and 4.2), the Solar abundance scale from Lodders (2003), the diluted i-process pattern from Hampel et al. (2016; Sect. 3.4), and the theoretical r-process, calculated from the dynamical ejecta of a neutron star merger (Sect. 3.2). In total, more than 10 000 different model combinations were thus tested. In Figs. 3 and 4 we show the observed abundances logϵ for the star #10464 together with several exemplary combinations, and the best-fit linear combinations of the various processes.
As a result, the linear admixture of other processes to the s-process prescription improved the fits slightly. If we a priori assume that the s-process must come from the same, fiducial source as derived above from a single site (viz., a metal-poor 3 M⊙ AGB star) and the i-process would act as a mere perturbation on top of the AGB yields, we need to invoke the highest tested neutron density for a “best” match (case sm3 + in15 in Table 3). However, an even better χ2 was obtained for the case of an s-process from a 2 M⊙ AGB star plus the highest n-density (in15) i-process.
Conversely, the most neutron rich scenario we tested, the r-process, leads again to no significant improvement of the χ2 (labeled “s + r + i”). Moreover, for three production processes, the best fit was achieved without any fraction of the r-process, thereby leading us back to the above s + i scenarios. This can be seen in the lower panel of Fig. 4, where the contributions of the specific processes to each isotope are shown. The r-process does not contribute to any isotope, but a small fraction of i-process is seen to contribute to the region between 56 ≤ Z ≤ 72. We note that, still, none of the mixtures are able to reproduce the high amount of Rb and Sr.
In the framework of considering multiple individual enrichment events, it is standing to reason to consider the occurrence of two distinct proton-ingestion events in the same donor, each of different strength. Our current understanding of the site(s) of the i-process does not allow us to make firm constraints on the exact number of successive proton-ingestion events and it has been shown that, for example, super-AGB stars could host multiple such events (Jones et al. 2016). While a shorter neutron bursts with τ = 0.30 mbarn−1 can reproduce the light-s peak, adding a separate event with τ = 0.96 mbarn−1 gives the best fit to the observed abundances of elements with Z > 50. Two separate bursts are required because the peak abundance moves to higher Z as the exposure increases, building up first the light s peak but then moving on to the heavy s peak. If the exposure is high enough, Pb is built up. This is similar to the way heavy elements are produced in the s-process.
A combination of these two individual events thereby leads to the overall, best (in a χ2-sense) explanation of the peculiar abundance pattern of #10464 (Fig. 5), although the high complexity of this scenario renders it, statistically, equally (im-)probable as a 3 M⊙ AGB pollution plus single i-process contributions. At respective χ2 values on the order of 50 vs. 60, the differences are marginal. Typically, in abundance fitting excellent χ2 statistics as low as ∼10 can be reached (see also Hansen et al. 2014; Abate et al. 2015a). Our higher values in Table 3 indicate that the composition of this star is not fully understood, yet, and cannot be explained satisfactorily with any of the processes considered, or combinations thereof.
 |
Fig. 5. Same as Fig. 2, but for a two-step i-process with two separate ingestion events of τ = 0.30 and 0.96 mbarn−1. Such a superposition is better able to reproduce both the light and heavy s-peaks. |
6. The impact of self-pollution
The stellar parameters of Teff = 5400 K and log g = 1.7 derived by Koch et al. (2016) place this star on the horizontal branch, where evolutionary tracks indicate a mass of ∼0.55 M⊙ (e.g., Cassisi et al. 2004; Hansen et al. 2011). As the spectroscopic gravities of the sample of Koch et al. (2016) were based on accurate ionization equilibrium, also the stars’ distances could be determined; in turn, we estimate that star #10464 has a luminosity of ∼220 L⊙.
At this evolved level it is likely that this star has undergone deep evolutionary mixing toward the tip of the RGB, which will have altered its surface composition. For the case of carbon, this can be quantified using the evolutionary calculations of Placco et al. (2014), which suggest a upward correction in [C/Fe] on the order of 0.2 dex, bringing the carbon ratio of #10464 to ∼0.6 dex. These effects were also recently discussed by Henkel et al. (2018) in the context of an improved formalism for thermohaline mixing in metal-poor stars.
In addition to the moderately enhanced carbon-level of this star, we found a strong enhancement in nitrogen (Table 1), resulting in a [C/N] ratio of −0.34 ± 0.26 dex, or, accounting for the aforementioned correction for stellar evolution, [C/N] ∼ −0.54 dex. This value is close to the boundary of −0.6 dex that separates evolved, mixed stars from objects that are unaffected by mixing (Spite et al. 2005; Hansen et al. 2016a).
This is strongly manifested in Fig. 6, where we distinguish mixed and unmixed stars in the metal-poor halo sample of Spite et al. (2005, their Fig. 11). Here, the fact that mixed stars have converted C to N in the CN cycle is seen through their systematically higher [N/O]. Spite et al. (2005) also note a strong correlation between the [N/O] and [O/H] ratios in the mixed stars (solid/dotted lines in Fig. 6), which is not seen in the unmixed counterparts (dashed line). This is due to an overabundance of N in the surface of the mixed stars on top of the large, initial abundance spread. Assuming that this extra, secondary nitrogen is independent of the stellar metallicity, the [N/O] ratio would decrease with increasing metallicity, [O/H], as is seen in the observed abundances for the mixed stars. The bulge star 10464 lies marginally above the extrapolated trend of the mixed halo stars. Nonetheless, its elevated [N/O] ratio places it uniquely in the regime of mixing.
 |
Fig. 6. N and O abundances in metal-poor halo stars from Spite et al. (2005). A typical error bar is indicated top left; the bulge star 10 464 is shown as a green star symbol. Solid (open) symbols indicate unmixed (mixed) stars and the dashed line illustrates the mean value of the unmixed sample. The red line is the best-fit relation for the mixed stars, determined by Spite et al. (2005), extrapolated toward our bulge star (dotted line). |
A strong level of self-pollution would indicate that the presently observed surface abundance has been significantly altered from its initial composition. Thus it is possible that the abundance peculiarities seen in #10464 do not reflect an external polluter’s signatures only, aggravating a meaningful comparison with the models as described in the previous sections. The extent to which the signatures of an external polluter are disguised by mixing events depends on how the pollution has occurred. If the pollution was already present in the gas from which the star formed, then evolutionary mixing only plays a minor role in altering the composition. While on the main sequence, settling and levitation may change the surface layers, but these effects are removed once a deep convective envelope starts to develop (Richard et al. 2002; Matrozis & Stancliffe 2016). Processing of material near the tip of the giant branch only affects the lighter elements (Gratton et al. 2000; Stancliffe et al. 2009), with oxygen and beyond remaining unaffected. The heavy elements should therefore be representative of the material the gas formed from.
When pollution occurs from a companion star, the situation is more complex. Accreted material, which has undergone nuclear processing in the companion, will have a higher mean molecular weight than the unprocessed material of the star that receives it. The accreted layer will thus be unstable to thermohaline mixing, which has the effect of mixing the accreted layer into the recipient’s interior very rapidly, typically a small fraction of the main-sequence lifetime (Stancliffe et al. 2007). In addition, rotation may also cause mixing of accreted material (Matrozis & Stancliffe 2017). If the accreted material is mixed to less than the depth that the convective envelope reaches during the ascent of the main sequence (roughly 0.45 M⊙; Stancliffe & Glebbeek 2008) further dilution will occur. After this, the light element surface abundances can still be changed by processing of material near the tip of the giant branch, as described in the previous paragraph, while the heavy elements will all have been diluted to the same extent.
7. Summary and conclusions
An investigation of several nucleosynthetic models indicated that the abundance distribution of the peculiar bulge CH-star #10464 cannot be satisfactorily explained by pure AGB s-process nucleosynthesis, nor with a single i-process under conditions as derived from an AGB star in Hampel et al. (2016). Its abundances are better fit by combinations of several nucleosynthetic processes.
Our study suggested that, if the enhancements were due to s-process pollution, the progenitor of this component was likely a low-to-intermediate mass AGB, in line with our conclusions in Koch et al. (2016) from the F.R.U.I.T.Y. database (Cristallo et al. 2011), although those findings were restricted to an assessment of the Rb/Zr and hs/ls ratios. Similarly, the aforementioned CEMP-s star 27793 was found by Koch et al. (2016) to have been enriched by a ∼4 M⊙ AGB star, although the predictions of Abate et al. (2015b) suggest lower-mass companions for CEMP-s stars of around 0.9–1.1 M⊙. The fact that our abundance matching results in fairly common progenitor masses implies that AGB companions to such metal-poor bulge stars were very similar in nature to the present-day, metal-rich bulge AGB population (e.g., Uttenthaler et al. 2015).
It is more likely (from a mere statistical point of view) that the abundance pattern in this star was caused by some i-process nucleosynthesis, albeit a more complex scenario than the simple picture including one ingestion event (Sect. 3.3) cannot statistically be ruled out.
In a single event, mass conservation would dictate a decline in the second-peak elements (around Ba) accompanying an enhancement in the first peak elements (such as Rb and Sr), and vice versa. This is in contrast to the high, relative strength of the light and heavy neutron-capture peaks, indicating the occurrence of at least two ingestion periods.
A zoo of other processes to have entertained the enrichment of this star is certainly conceivable, such as electron-capture SNe (at a similar outcome as the weak-r process), ν-driven winds, νp-processes, or an α-rich freeze-out. However, a decomposition of the heavy element pattern into two components – an AGB-dominated s-process with an admixture of r-process rich ejecta from neutron star mergers – already did not yield any significant improvement of the statistics.
More data for this class of stars are clearly needed, but this request comes at a price: most of the models considered here are most sensitive to heavy elements that are notoriously difficult to measure, such as Os or Ir, whereas most of the dominant heavy element transitions lie predominantly in the blue-to-UV spectral range (see also Hansen et al. 2015a), which is challenging for anything but the metal-poor halo (e.g., Roederer et al. 2016).
That is, CEMP stars with strong enhancements in r- and s-process elements (Beers & Christlieb 2005).
The ratio of heavier, second-peak s-process elements to the lighter, first-peak elements. In the following we will adopt [ls/Fe] = [Sr+Y+Zr/Fe]/3 and [hs/Fe] = [Ba+La+Ce/Fe]/3; e.g., Cristallo et al. (2011), Abate et al. (2015a). We further follow the usual spectroscopic notation in terms of the number densities NA and NB for elements A and B, relative to the Sun: [A/B] = log10(NA/NB)−log10(NA/NB)⊙.
Extremely Rb-rich, self-enriched AGB stars have been reported to exist (García-Hernández et al. 2006; Zamora et al. 2014), but no detailed abundance distributions are available for those objects.
Following the naming scheme of Koch et al. (2016). The IAU names for these objects are J183113.29–335148.3 (=#27793) and J183003.87–333423.6 (=#10464).
Sr may, relatively speaking, have higher abundance ratios than, for example, Ba, but typically it still shows abundance ratios that are at most mildly elevated to [Sr/Fe] ≲ 0.5 (Yong et al. 2013), but primarily Solar or below (Hansen et al. 2016a, 2019) in CEMP-no stars.
Acknowledgments
We are very grateful to M. Pignatari, and also J. Bliss, and C. Ritter for helpful discussions. The anonymous referee is thanked for a fast and constructive report, and M. Hanke for support with the ATHOS code. This work was supported by Sonderforschungsbereich SFB 881 “The Milky Way System” (subproject A04) of the German Research Foundation (DFG). M.R. and A.A. acknowledge support by the Helmholtz-University Young Investigator grant No. VH-NG-825 and ERC Starting Grant 677912 EUROPIUM. R.J.S. acknowledges the support of STFC through the University of Hull Consolidated Grant ST/R000840/1.
References
- Abate, C., Pols, O. R., Izzard, R. G., & Karakas, A. I. 2015a, A&A, 581, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abate, C., Pols, O. R., Stancliffe, R. J., et al. 2015b, A&A, 581, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abia, C., Busso, M., Gallino, R., et al. 2001, ApJ, 559, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., & Christlieb, N. 2005, ARA&A, 43, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., & Käppeler, F. 2011, MNRAS, 418, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Buntain, J. F., Doherty, C. L., Lugaro, M., et al. 2017, MNRAS, 471, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Burbidge, E. M., Burbidge, G. R., Fowler, W. A., & Hoyle, F. 1957, Rev. Mod. Phys., 29, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Busso, M., Gallino, R., & Wasserburg, G. J. 1999, ARA&A, 37, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, S. W., & Lattanzio, J. C. 2008, A&A, 490, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campbell, S. W., Lugaro, M., & Karakas, A. I. 2010, A&A, 522, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carollo, D., Beers, T. C., Bovy, J., et al. 2012, ApJ, 744, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, A. R., & Schlaufman, K. C. 2015, ApJ, 809, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Castellani, M., Caputo, F., & Castellani, V. 2004, A&A, 426, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chornock, R., Berger, E., Kasen, D., et al. 2017, ApJ, 848, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Clarkson, W., Sahu, K., Anderson, J., et al. 2008, ApJ, 684, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Clarkson, O., Herwig, F., & Pignatari, M. 2018, MNRAS, 474, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, J. J., & Rose, W. K. 1977, ApJ, 212, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Straniero, O., Gallino, R., et al. 2009, ApJ, 696, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Piersanti, L., Straniero, O., et al. 2011, ApJS, 197, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Cyburt, R. H., Amthor, A. M., Ferguson, R., et al. 2010, ApJS, 189, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Denissenkov, P. A., Herwig, F., Battino, U., et al. 2017, ApJ, 834, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Denissenkov, P., Herwig, F., Woodward, P., et al. 2018, MNRAS, submitted [arXiv:1809.03666] [Google Scholar]
- Doherty, C. L., Gil-Pons, P., Siess, L., Lattanzio, J. C., & Lau, H. H. B. 2015, MNRAS, 446, 2599 [Google Scholar]
- Fishlock, C. K., Karakas, A. I., Lugaro, M., & Yong, D. 2014, ApJ, 797, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Freiburghaus, C., Rosswog, S., & Thielemann, F.-K. 1999, ApJ, 525, L121 [Google Scholar]
- Frischknecht, U., Hirschi, R., & Thielemann, F.-K. 2012, A&A, 538, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallino, R., Arlandini, C., Busso, M., et al. 1998, ApJ, 497, 388 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- García-Hernández, D. A., García-Lario, P., Plez, B., et al. 2006, Science, 314, 1751 [NASA ADS] [CrossRef] [Google Scholar]
- García-Hernández, D. A., García-Lario, P., Plez, B., et al. 2007, A&A, 462, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Sneden, C., Carretta, E., & Bragaglia, A. 2000, A&A, 354, 169 [NASA ADS] [Google Scholar]
- Hampel, M., Stancliffe, R. J., Lugaro, M., & Meyer, B. S. 2016, ApJ, 831, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Hanke, M., Hansen, C. J., Koch, A., & Grebel, E. K. 2018, A&A, 619, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, C. J., Nordström, B., Bonifacio, P., et al. 2011, A&A, 527, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, C. J., Montes, F., & Arcones, A. 2014, ApJ, 797, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, C. J., Ludwig, H.-G., Seifert, W., et al. 2015a, Astron. Nachr., 336, 665 [Google Scholar]
- Hansen, T., Hansen, C. J., Christlieb, N., et al. 2015b, ApJ, 807, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, C. J., Nordström, B., Hansen, T. T., et al. 2016a, A&A, 588, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, C. J., Rich, R. M., Koch, A., et al. 2016b, A&A, 590, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, T. T., Andersen, J., Nordström, B., et al. 2016c, A&A, 588, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, C. J., Hansen, T. T., Koch, A., et al. 2019, A&A, in press, DOI: 10.1051/0004-6361/201834601 [Google Scholar]
- Henkel, K., Karakas, A. I., Casey, A. R., Church, R. P., & Lattanzio, J. C. 2018, ApJ, 863, 1 [CrossRef] [Google Scholar]
- Herwig, F., Pignatari, M., Woodward, P. R., et al. 2011, ApJ, 727, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F., Woodward, P. R., Lin, P.-H., Knox, M., & Fryer, C. 2014, ApJ, 792, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Holtzman, J. A., Watson, A. M., Baum, W. A., et al. 1998, AJ, 115, 1946 [NASA ADS] [CrossRef] [Google Scholar]
- Howes, L. M., Asplund, M., Keller, S. C., et al. 2016, MNRAS, 460, 884 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobson, H. R., Keller, S., Frebel, A., et al. 2015, ApJ, 807, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Jadhav, M., Pignatari, M., Herwig, F., et al. 2013, ApJ, 777, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Herwig, F., Beers, T. C., & Christlieb, N. 2007, ApJ, 658, 1203 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, S., Ritter, C., Herwig, F., et al. 2016, MNRAS, 455, 3848 [NASA ADS] [CrossRef] [Google Scholar]
- Käppeler, F., Gallino, R., Bisterzo, S., & Aoki, W. 2011, Rev. Mod. Phys., 83, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karakas, A. I., & Lattanzio, J. C. 2014, PASA, 31, e030 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I., & Lugaro, M. 2016, ApJ, 825, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, C., Umeda, H., Nomoto, K., Tominaga, N., & Ohkubo, T. 2006, ApJ, 653, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., McWilliam, A., Preston, G. W., & Thompson, I. B. 2016, A&A, 587, A124 [Google Scholar]
- Korobkin, O., Rosswog, S., Arcones, A., & Winteler, C. 2012, MNRAS, 426, 1940 [NASA ADS] [CrossRef] [Google Scholar]
- Langanke, K., & Martínez-Pinedo, G. 2001, At. Data Nucl. Data Tabl., 79, 1 [Google Scholar]
- Lattimer, J. M., & Schramm, D. N. 1974, ApJ, 192, L145 [Google Scholar]
- Lebzelter, T., Uttenthaler, S., Straniero, O., & Aringer, B. 2013, A&A, 554, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaro, M., Karakas, A. I., Stancliffe, R. J., & Rijs, C. 2012, ApJ, 747, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaro, M., Campbell, S. W., Van Winckel, H., et al. 2015, A&A, 583, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matrozis, E., & Stancliffe, R. J. 2016, A&A, 592, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matrozis, E., & Stancliffe, R. J. 2017, A&A, 606, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McWilliam, A. 2016, PASA, 33, e040 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., & Rich, R. M. 1994, ApJS, 91, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, B. 2012, Proceedings of the XII International Symposium on Nuclei in the Cosmos (NIC XII). August 5–12, 2012, Cairns, Australia, 96 [Google Scholar]
- Mishenina, T., Pignatari, M., Carraro, G., et al. 2015, MNRAS, 446, 3651 [NASA ADS] [CrossRef] [Google Scholar]
- Miszalski, B., Acker, A., Moffat, A. F. J., Parker, Q. A., & Udalski, A. 2009, A&A, 496, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Möller, P., Nix, J. R., Myers, W. D., & Swiatecki, W. J. 1995, At. Data Nucl. Data Tabl., 59, 185 [Google Scholar]
- Ness, M., Freeman, K., Athanassoula, E., et al. 2013, MNRAS, 430, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E., Gilmore, G., Wyse, R. F. G., Yong, D., & Frebel, A. 2010, ApJ, 722, L104 [NASA ADS] [CrossRef] [Google Scholar]
- Panov, I. V., Korneev, I. Y., Rauscher, T., et al. 2010, A&A, 513, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pérez-Mesa, V., Zamora, O., García-Hernández, D. A., et al. 2017, A&A, 606, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pignatari, M., Gallino, R., Heil, M., et al. 2010, ApJ, 710, 1557 [NASA ADS] [CrossRef] [Google Scholar]
- Placco, V. M., Frebel, A., Beers, T. C., & Stancliffe, R. J. 2014, ApJ, 797, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Izzard, R. G., Stancliffe, R. J., & Glebbeek, E. 2012, A&A, 547, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Price, D. J., & Rosswog, S. 2006, Science, 312, 719 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Qian, Y.-Z., & Wasserburg, G. J. 2007, Phys. Rep., 442, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, O., Michaud, G., & Richer, J. 2002, ApJ, 580, 1100 [NASA ADS] [CrossRef] [Google Scholar]
- Roederer, I. U., Preston, G. W., Thompson, I. B., et al. 2014, AJ, 147, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Roederer, I. U., Karakas, A. I., Pignatari, M., & Herwig, F. 2016, ApJ, 821, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Ryan, S. G. 1992, AJ, 104, 1144 [NASA ADS] [CrossRef] [Google Scholar]
- Salvadori, S., Skúladóttir, Á., & Tolstoy, E. 2015, MNRAS, 454, 1320 [NASA ADS] [CrossRef] [Google Scholar]
- Skúladóttir, Á., Tolstoy, E., Salvadori, S., et al. 2015, A&A, 574, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sneden, C., Cowan, J. J., Lawler, J. E., et al. 2003, ApJ, 591, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C., Cowan, J. J., & Gallino, R. 2008, ARA&A, 46, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sneden, C. A. 1973, PhD Thesis, The University of Texas at Austin [Google Scholar]
- Spite, M., Cayrel, R., Plez, B., et al. 2005, A&A, 430, 655 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stancliffe, R. J., & Glebbeek, E. 2008, MNRAS, 389, 1828 [Google Scholar]
- Stancliffe, R. J., Glebbeek, E., Izzard, R. G., & Pols, O. R. 2007, A&A, 464, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stancliffe, R. J., Church, R. P., Angelou, G. C., & Lattanzio, J. C. 2009, MNRAS, 396, 2313 [Google Scholar]
- Stancliffe, R. J., Dearborn, D. S. P., Lattanzio, J. C., Heap, S. A., & Campbell, S. W. 2011, ApJ, 742, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Starkenburg, E., Shetrone, M. D., McConnachie, A. W., & Venn, K. A. 2014, MNRAS, 441, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Susmitha, A., Koch, A., & Sivarani, T. 2017, A&A, 606, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thielemann, F.-K., Arcones, A., Käppeli, R., et al. 2011, Nucl. Phys., 66, 346 [Google Scholar]
- Tumlinson, J. 2007, ApJ, 664, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Tumlinson, J. 2010, ApJ, 708, 1398 [NASA ADS] [CrossRef] [Google Scholar]
- Uttenthaler, S., Blommaert, J. A. D. L., Wood, P. R., et al. 2015, MNRAS, 451, 1750 [NASA ADS] [CrossRef] [Google Scholar]
- van Raai, M. A., Lugaro, M., Karakas, A. I., García-Hernández, D. A., & Yong, D. 2012, A&A, 540, A44 [Google Scholar]
- Vasilyev, V., Ludwig, H.-G., Freytag, B., Lemasle, B., & Marconi, M. 2018, A&A, 611, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, D., Hansen, C., Selsing, J., et al. 2019, Nature, submitted [Google Scholar]
- Winteler, C. 2014, PhD Thesis, University of Basel [Google Scholar]
- Winteler, C., Käppeli, R., Perego, A., et al. 2012, ApJ, 750, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Yong, D., Norris, J. E., Bessell, M. S., et al. 2013, ApJ, 762, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Zamora, O., García-Hernández, D. A., Plez, B., & Manchado, A. 2014, A&A, 564, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Abundance ratios in the C-rich bulge star #10464 from Koch et al. (2016) and our present measurements.
Line list for heavy elements in #10464 that were not covered in Koch et al. (2016).
Results for various linear combinations of nucleosynthetic processes in the fitting range of 31 ≤ Z ≤ 72.
All Figures
 |
Fig. 1. Full abundance distribution of the bulge star #10464 from Koch et al. (2016) and this work. The AGB yields with progenitor masses as labeled were taken from Cristallo et al. (2011). The bottom panels are a zoom into the regions of the first and second n-capture element peaks. |
| In the text | |
 |
Fig. 2. Heavy element pattern in #10464 in comparison with i-process model calculations for various neutron densities reaching from N = 109 cm−3 to N = 1015 cm−3. Here, the s-process curve is for the best-fit 3 M⊙ AGB composition of Lugaro et al. (2012; case “sm3”; Table 3). Top panel: absolute abundances, lower panel: resulting residuals of the individual fits, and errorbars of the abundances as squares. Pb (Z = 82) was excluded from our statistical tests and is thus not shown in this and the following figures. |
| In the text | |
 |
Fig. 3. Same as Fig. 2, but for various mixtures of s-process with i-process models. Shown are the curves for the overall, best-fit version (sm2 + sn15; blue), a 2 M⊙ AGB component plus a lower neutron density (red), and an s-process from a high-mass AGB model plus the two extreme neutron density i-processes (black and magenta). Shown as dashed lines are two s-process models from different AGB masses. |
| In the text | |
 |
Fig. 4. Same as Fig. 2, but for a linear combination of all three nucleosynthetic channels (s + r + i). The bottom panel indicates the relative contributions from each process. We note that no r-process component is required. |
| In the text | |
 |
Fig. 5. Same as Fig. 2, but for a two-step i-process with two separate ingestion events of τ = 0.30 and 0.96 mbarn−1. Such a superposition is better able to reproduce both the light and heavy s-peaks. |
| In the text | |
 |
Fig. 6. N and O abundances in metal-poor halo stars from Spite et al. (2005). A typical error bar is indicated top left; the bulge star 10 464 is shown as a green star symbol. Solid (open) symbols indicate unmixed (mixed) stars and the dashed line illustrates the mean value of the unmixed sample. The red line is the best-fit relation for the mixed stars, determined by Spite et al. (2005), extrapolated toward our bulge star (dotted line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.