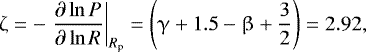EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 622 (February 2019) A&A, 622 (2019) A75 Full HTML
Free Access
Issue
A&A
Volume 622, February 2019
Article Number A75
Number of page(s) 11
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201834157
Published online 29 January 2019

© ESO 2019

1 Introduction

Protoplanetary disks are a natural outcome of angular momentum conservation during the collapse of a rotating molecular cloud (Terebey et al. 1984; Shu et al. 1987). These disks can be approximately characterized by a hot surface layer and a cool interior region close to the disk midplane (e.g., Calvet et al. 1991; Chiang & Goldreich 1997; Dullemond et al. 2001). Imaging disks at different wavelengths provides insights into a large number of fundamental physical properties of the disk population, which allow us to place constraints on models of disk evolution and planet formation. Observations in the infrared (IR) spectral range probe the distribution of small dust grains in the disk surface layer, whereas disk emission in the (sub-)millimeter regime is dominated by the thermal emission from large dust grains populating the regions close to the midplane, as a combined consequence of grain growth and vertical settling (e.g., Miyake & Nakagawa 1995; D’Alessio et al. 2001; Dullemond & Dominik 2004; Birnstiel et al. 2016; Pinte et al. 2016; Louvet et al. 2018). Investigating the detailed structure of the disk, in particular the disk interior and dense midplane probed by high-resolution millimeter observations, plays a key role in building the picture of planet formation and disk evolution.

With its unprecedented sensitivity and spatial resolution, the Atacama Large Millimeter/submillimeter Array (ALMA) has in recent years revealed a series of interesting structures in protoplanerary disks, such as gaps and rings (e.g., ALMA Partnership 2015; Andrews et al. 2016; Cieza et al. 2017; Dipierro et al. 2018; Fedele et al. 2018), horseshoe structures (e.g., Casassus et al. 2013; van der Marel et al. 2013; Kraus et al. 2017), and spiral arms (Tobin et al. 2016; Pérez et al. 2016). With the increasing number of targets observed by ALMA, gaps and rings appear to be prevalent in disks around T Tauri and Herbig stars regardless of their age (e.g., Zhang et al. 2016; Isella et al. 2016; Hendler et al. 2017; van der Plas et al. 2017). Several mechanisms have been proposed to explain the origin of the gap or ring structure, including sintering-induced dust rings (Okuzumi et al. 2016), dust coagulation or fragmentation triggered by condensation zones of volatiles (Zhang et al. 2015; Banzatti et al. 2015; Pinilla et al. 2017), dead zones (Pinilla et al. 2016), the operation of a secular gravitational instability (Takahashi & Inutsuka 2016), planet–disk interactions (e.g., Dipierro et al. 2015a, 2018; Jin et al. 2016; Rosotti et al. 2016; Fedele et al. 2018), and non-ideal magnetohydrodynamics (MHD) effects (Béthune et al. 2016).

In this paper, we present high angular resolution ALMA images of 1.3 mm continuum emission from the protoplanetary disk around MWC 480 (also frequently called HD 31648), and subsequently model the disk with hydrodynamic simulations to infer the mass of a possible planet within the disk. MWC 480 is a Herbig Ae star located at a Gaia DR2 distance1 of 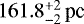161.8 −2 +2  pc $161.8_{-2}^{+2}\,\textrm{pc}$ (Gaia Collaboration 2016, 2018) with an age of ~7 Myr (Simon et al. 2000) in the Taurus star-forming region. The mid- to far-IR spectral energy distribution (SED) is consistent with a Group II Meeus disk (Juhász et al. 2010), following the grouping schemes of Meeus et al. (2001) and van Boekel et al. (2005). The SED does not show any evidence for an inner hole or an opacity gap, as there is no sharp flux deficit in the near-IR and/or mid-IR (Espaillat et al. 2007, 2010; Williams & Cieza 2011). Previous (sub-)millimeter observations suggested the presence of a bright emission from a smooth disk without significant substructures (Hamidouche et al. 2006; Piétu et al. 2006; Guilloteau et al. 2011; Huang et al. 2017). Polarization images of scattered light off the disk in H-band reveal that the small grains extend to ~ 160 au and are smoothly flared, with no significant substructures detected with a spatial resolution of 0.07′′ (Kusakabe et al. 2012). The Keplerian rotation measured in bright CO rotational line emission from the disk leads to a mass of ~ 2.0M⊙ (Simon et al. 2000; Piétu et al. 2007), after correcting for the updated distance. The star is actively accreting from the disk at a variable rate of ~1.2 × 10−7 M⊙ yr−1 (Mendigutía et al. 2012; see also, e.g., Donehew & Brittain 2011 and Salyk et al. 2013).

The MWC 480 disk is selected for this in-depth study as an initial result from an ALMA survey of 32 disks in the Taurus molecular cloud because of its prominent ring and gap structures. The observational details are given in Sect. 2. Section 3 describes our radiative transfer modeling with the goal of constraining the surface density profile and structural parameters of the disk. In Sect. 4, hydrodynamics simulations are performed to explore planet-disk interaction as the origin of the gap. We briefly discuss other potential interpretations of the ring structure in Sect. 5, followed by a summary in Sect. 6.

2 Observation, data reduction, and analysis

We observed MWC 480 with ALMA in Band 6 (230 GHz) as part of the Cycle 4 program (ID: 2016.1.01164.S; PI: G. Herczeg) on August 27, 2017. The observation was conducted using 47 12 m antennas with baselines ranging from 21 to 3638 m. Theon-source time was 4 min and the precipitable water vapor (PWV) was 0.5 mm during the integration. J0510+1800served as the flux calibrator, while J0510+1800 and J0512+2927 were observed for bandpass and phase calibration.

The data were calibrated using the Common Astronomy Software Applications (CASA, McMullin et al. 2007) package, version 5.1.1. Following the data reduction scripts provided by ALMA, the atmospheric phase noise was first reduced using water vapor radiometer measurements. Then the standard bandpass, flux, and gain calibrations were applied accordingly. Based on the phase and amplitude variations on calibrators, we estimated an absolute flux calibration uncertainty of ~ 10%. Self-calibration was performed to improve the signal-to-noise ratio. The continuum image was finally created from the calibrated visibilities using the CASA tclean task with Briggs weighting with a robust parameter of 0.5. The resulting beam size is 0.17′′× 0.11′′, corresponding to a physical scale of 27.5 × 17.8 au at a distance of 161.8 pc. The rms noise level of the image is ~0.07 mJy beam−1.

The cleaned image of 1.3 mm continuum emission (left panel of Fig. 1) reveals a pair of gap and ring. Figure 2 displays the radial brightness distribution along the major and minor axis of the disk, assuming a position angle (PA) of 148° obtained from the CASA imfit task. Modeling the visibility data yields a similar PA value and a total flux density at 1.3 mm of 268 ± 0.3 mJy (Long et al. 2018). The radial extent of thedisk is ~175 au, defined as the radius at 3 × rms noise level of the image (i.e., 0.21 mJy beam−1). The observed gap is deeper along the major axis than the minor axis. This difference in gap depth might be introduced artificially because the asymmetric beam (PA ~ 23°) has a major axis that is closely aligned with the minor axis of the disk, or may be the consequence of the projection effect of a geometrically thick disk.

Fitting a Gaussian profile to the brightness distribution along the major axis in the vicinity of the gap using the mpfit routine within IDL yields a gap location of 74.3 au (0.46′′) and a full-width at half-maximum (FWHM) of 23 ± 3 au. The same procedure yields a center for the bright ring of 97.5 au (0.6′′). There is a weak hint of a second ring at ~1′′, but it has a low significance. Follow-up observations are required to confirm the existence and place constraints on its properties.

3 Radiative transfer modeling

In order to constrain the surface density profile and structural parameters of the MWC 480 disk, we performed radiative transfer modeling of the broadband SED and the ALMA image using the radiative transfer code RADMC-3D2 (Dullemond et al. 2012). The disk is considered to be passively heated by stellar irradiation. The construction of the surface density is linked to the brightness distribution (see Sect. 3.2), because most parts of the disk are optically thin at 1.3 mm (see Fig. 6). Therefore, our modeling of the ALMA data was carried out in the image plane. However, we confirmed the quality of the fit in the UV space. Table 1 summarizes the model parameters.

We employed a two-dimensional flared disk model, which has been successfully used to explain observations of protoplanetary disks (e.g., Wolf et al. 2003; Sauter et al. 2009; Liu et al. 2012, 2017). The disk model includes distinct populations of small grains, which are used to set up the temperature structure and to reproduce the IR SED, and of large grains to reproduce the 1.3 mm dust continuum image. The density structure of both grain populations was fully parameterized rather than solved under an assumption of hydrostatic equilibrium. In particular, the flaring index and scale height were free parameters that were not self-consistently derived from the temperature calculation (see Sects. 3.1 and 3.2). This approach has the advantage that we were able to directly assess the effect of each model parameter on the simulated observable. The dust in the model was a mixture of 75% amorphous silicate and 25% carbon. For the complex refractive indices, we took the data from Dorschner et al. (1995) for silicate and from Jäger et al. (1998) for carbon at a pyrolysis temperature of 800 o C. We used the Mie theory to calculate the dust opacities. The grain size distribution followed the standard power law d n(a) ∝ a−3.5da with a minimum grain size of amin = 0.01 μm. The maximum grain size was set to amax = 2 μm for the small grain population (SGP) and amax = 3 mm for the largegrain population (LGP). The mass fraction of large dust grains relative to the total dust mass in the disk (Mdust,tot) is described as fLGP, so that small grains have a mass fraction of 1 − fLGP.

thumbnail Fig. 1

Comparison between the ALMA observation (left panel) and the model image (middle panel) atBand 6. The beam size is indicated by the white filled ellipse in the observed image. The residuals between the observed and model maps are shown in the right panel, in which σ refers to the rms level 0.07 mJy beam−1 of the CLEANed map. The dashed ellipses indicate the locations of the gap and ring.
thumbnail Fig. 2

Comparison between the observed brightness distribution and model prediction along the disk major (left panel) and minor (right panel) axis. Black solid lines show the observation with uncertainties indicated as gray shaded region, and blue dashed lines refer to model predictions.

3.1 Distribution of small grains

The surface density profile of the small grain population, ΣSGP, was modeled as a power law with an exponential taper, as Σ SGP (R)∝ ( R R C ) −γ exp[ − ( R R C ) 2−γ ], \begin{equation*} \Sigma_{\textrm{SGP}}(R) \propto \left(\frac{R}{R_{\textrm{C}}}\right)^{-\upgamma}\textrm{exp}\left[-\left(\frac{R}{R_{\textrm{C}}}\right)^{2-\upgamma}\right],\end{equation*}(1)

where RC = 200 au is a characteristic radius and γ = 1 is the gradient parameter. The vertical structure of the small grains was modeled as a Gaussian profile ρ SGP (R,z)∝ Σ SGP (R) h SGP (R)  exp[ − 1 2 ( z h SGP (R) ) 2 ], \begin{equation*} \rho_{\textrm{SGP}} (R,z)\propto\frac{\Sigma_{\textrm{SGP}}(R)}{h_{\textrm{SGP}}(R)}\,\exp\left[-\frac{1}{2}\left(\frac{z}{h_{\textrm{SGP}}(R)}\right)^2\right], \\\end{equation*}(2)

where R is the radial distance from the central star measured in the disk midplane. We fixed the disk inner radius to Rin = 0.15 au, which is consistent with the result from models of the SED (Fernandes et al. 2018) and the near- and mid-IR interferometric observations (Millan-Gabet et al. 2016). The outer radius of the small grain population was set to 750 au, close to the value from 12CO observations (Piétu et al. 2007), since small grains are expected to be well coupled with the gas.

The scale height of the small grain population, hSGP, follows a power-law profile 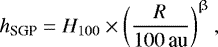h SGP = H 100 × ( R 100 au ) β , \begin{equation*} h_{\textrm{SGP}} = H_{100}\times\left(\frac{R}{100\,\textrm{au}}\right)^{\upbeta},\\\end{equation*}(3)

with β characterizing the degree of flaring and H100 representing the scale height at a distance of 100 au.

Table 1

Model parameters.

3.2 Distribution of large grains

The features of the high-resolution ALMA observations are difficult to parameterize with a simple analytic expression, such as a power-law profile with a Gaussian perturbation at the location of the gap (e.g., Liu et al. 2017). The surface density ΣLGP was instead built by reproducing the brightness distribution of 1.3 mm continuum emission along the disk major axis, following the iterative procedure introduced by Pinte et al. (2016).

For a given surface density distribution, the radiative transfer code RADMC-3D was used to produce a synthetic image of 1.3 mm continuum emission, which was then convolved with the beam of our ALMA observation. The initial surface density profile was obtained from a functional form analogous to Eq. (1), although the starting profile did not affect the final result. The distribution of the large grain population was truncated at Rout,LGP = 200 au, which is close to the boundary of emission from the disk shown in previous interferometric measurement at millimeter wavelengths (Piétu et al. 2006; Hamidouche et al. 2006; Guilloteau et al. 2011; Huang et al. 2017), as well as in our ALMA observation. The verticalstructure of large dust grains was described with a functional form analogous to Eq. (2). To account for the effect of dust settling, large grains are less vertically distributed, with a scale height of hLGH = ΛhSGP and a settling parameter Λ ≤ 1 constant over radius.

In order to keep the procedure as simple as possible, when we constructed the surface density distribution, we initially fixed H100 = 10 au and β = 1.1, as values that are typical of other disks (e.g., Andrews et al. 2009; Madlener et al. 2012; Liu et al. 2012; Kirchschlager et al. 2016). The total dust mass in the disk Mdust,tot was initially fixed to 2 × 10−3 M⊙, consistent with the results given by Piétu et al. (2007) and Guilloteau et al. (2011) assuming a gas-to-dust mass ratio of 100. The settling parameter Λ = 0.2 and fLGP = 0.85 were also fixed from previous models of protoplaneraty disks (e.g., Andrews et al. 2011; Fang et al. 2017; Fedele et al. 2018). The initial inclination of i = 36° is consistent with previous measurements (Simon et al. 2000; Piétu et al. 2006; Guilloteau et al. 2011).

The brightness distribution of the model was then compared to the radial brightness distribution extracted from the ALMA image along the disk major axis (see Fig. 2). In subsequent iterations, the large grain population surface density at each radius was corrected by the ratio of the observed and the modeled brightness profile. The iteration procedure converged after 30 iterations, when the change in model brightness profile was less than 5% at all radii. The profile of the constructed ΣLGP, shown in the bottom panel of Fig. 3, traces the gap and ring seen in the 1.3 mm continuum emission.

The surface density profile obtained from this fit was then used as an input for a simultaneous fit to the SED and ALMA image by exploring the parameter space that was initially fixed in this subsection.

thumbnail Fig. 3

Surface density profiles of the best-fit radiative transfer model. Top panel: surface density of the small grain population. It follows the profile described in Eq. (1) with RC = 200 au and γ = 1. Bottom panel: surface density of the large grain population. It is obtained by fitting the brightness distribution along the disk major axis, see Sect. 3.2.
thumbnail Fig. 4

SED of the MWC 480 disk. The black line represents the best-fit model, while red dots are photometry collected from the 2MASS (Cutri et al. 2003), WISE (Cutri & et al. 2013), IRAS (Beichman et al. 1988), and AKARI surveys (Ishihara et al. 2010), Herschel/PACS (Pascual et al. 2016), UBVRI (Mendigutía et al. 2012), and sub-mm bands (Mannings & Sargent 1997; Hamidouche et al. 2006; Piétu et al. 2006; Hughes et al. 2008; Öberg et al. 2010; Guilloteau et al. 2011; Huang et al. 2017). The flux density at ALMA Band 6 in this study is highlighted with a blue square. The contributions from the small grain population and large grain population to the total flux are indicated with the red and blue dashed lines, respectively. The green dash-dottedline gives the resulting SED when the raytracing only takes into account the central emission blob (Rin ≤ R ≤ 63 au) as seen in our ALMA image, see Sect. 5.1. The gray dashed line is the input photosphere model (Kurucz 1994).

3.3 Fit to the SED and brightness distribution

After constructing the surface density profile for the large grain population, the next step of our modeling was to search for a coherent model that can explain the SED and the brightness distribution along the major and minor axis simultaneously. To achieve this goal, we explored the parameter space {Mdust,tot, H100, β, Λ, fLGP, i} using the simulated annealing algorithm (Kirkpatrick et al. 1983). Based on the Metropolis–Hastings algorithm, simulated annealing creates a Markov chain Monte Carlo random walk through the parameter space, thereby gradually minimizing the discrepancy between observation and prediction by following the local topology of the merit function. This approach has specific advantages for high-dimensionality optimization because no gradients need to be calculated, and entrapment in local minima can be avoided regardless of the dimensionality. Details about the implementation of simulated annealing can be found in Madlener et al. (2012) and Liu et al. (2017).

In order to construct the observed SED with a complete wavelength coverage from optical to millimeter, we incorporated a variety of archival data and multiwavelength photometry. The IR excess from 1 to 10 μm of MWC 480 is known to vary by ~30% (Sitko et al. 2008; Kusakabe et al. 2012; Fernandes et al. 2018). Fernandes et al. (2018) explored two different possibilities: changing the height of the inner rim and using a structure that simulates an inner disk wind. They found that both scenarios can reproduce the near-IR variability, but only the disk wind model can produce flux levels in the far-IR that are consistent with existing data. We did not attempt to reinvestigate the same scenario because the ALMA data presented here are not sensitive enough to place additional constraints on the structure or geometry of the innermost region of the disk. The collected data points between 1 and 10 μm shown in Fig. 4 are close to the average level of the observed fluxes. Our radiative transfer analysis is devised to derive disk characteristics in a more general way, with the focus of constraining the surface density and model parameters that describe the overall structure of the disk. This information is useful for the hydrodynamical simulation of planet-disk systems, see Sect. 4.

The best-fit parameters are given in Table 1, with the results presented in Figs. 1, 2, 4, and 5. The best-fit model reproduces the ALMA image and the SED as well. The scale height H100 and total dust mass Mdust,tot are comparable to previous measurements for the MWC 480 disk (e.g., Piétu et al. 2006, 2007; Guilloteau et al. 2011)and are typical for other protoplanetary disks (e.g., Madlener et al. 2012; Gräfe et al. 2013; Garufi et al. 2014; Liu et al. 2017). The relatively flat IR SED of MWC 480 is consistent with being a member of the Meeus Group II (Meeus et al. 2001; Sitko et al. 2008). Therefore, a relatively small flaring index (β = 1.08) appears preferable for the disk vertical geometry.

The ring has a dust mass of 2 × 10−4 M⊙ (~ 67 M⊕), calculated by integrating the total surface density profile between 81 and 117 au, corresponding to the FWHM of the Gaussian fit to the brightness distribution in that ring. The ring mass of MWC 480 is about half of the mass of the B7 ring (at a similar location of ~ 97 au from the star) in the HL Tau disk (see Fig. 3 in ALMA Partnership 2015, Pinte et al. 2016; Liu et al. 2017). Figure 6 shows the two-dimensional temperature structure of the best-fit model, in which contours at 25, 130, and 150 K are also marked. The temperature in the disk midplane generally follows a power law Tmidplane ∝ R−0.51 with T~ 30 K at the gap location. The midplane temperature gradient is consistent with the results from previous parameter studies using a similar model setup (e.g., Pinte & Laibe 2014).

thumbnail Fig. 5

Comparison between the observed (red dots) and model (black line) visibilities. The errors of the observation are smaller than the symbol size.

4 Modeling the dust gap with hydrodynamics gas and dust simulations

Planet–disk interaction is an attractive mechanism to create gap-like structures in protoplanetary disks. To explore this hypothesis, we modeled thefeatures of the dust continuum emission of the MWC 480 disk by assuming that the observed gap (ring) corresponds to a dip (bump) in the dust density distribution of large grains (as shown in the bottom panel of Fig. 3) induced by the presence of an embedded protoplanet. Any structure detected in optically thin disk emission may instead be caused by temperatureeffects or by changes in the optical properties of dust grains. In this work, we assumed that these two contributions have a negligible effect on the disk emission with respect to the effects of dust density. For this reason, we assumed a locally isothermal equation of state and an uniform choice for the shape, porosity and chemical composition of the dust across the disk.

Based on the result from the radiative transfer analysis described in Sect. 3, we performed three-dimensional simulations of a variety of dust- and gas-disk models hosting an embedded protoplanet. The dynamics of large dust grains yields an estimate of the main physical properties of a planet that could carve such a gap in the dust density distribution of millimeter grains. Given the large number of parameters involved in our analysis and the computationally expensive approach, the fitting procedure was done by eye without performing any statistical test to quantify the goodness of fit.

We performed a set of three-dimensional smoothed particle hydrodynamics (SPH) simulations of gas and dust disks with an embedded protoplanet using the PHANTOM code (Price et al. 2018). The dust disk was approximated as a two-component system in terms of dust species: a population of micron-size grains perfectly mixed with the gas and a population of millimeter-size dust grains. The dynamics of dust grains were simulated using the one-fluid algorithm (Price & Laibe 2015) based on the terminal velocity approximation (e.g. Youdin & Goodman 2005) and because it is best suited to simulate particles that are tightly coupled to the gas (Ballabio et al. 2018). We represented the protoplanet and the central star using sink particles (Bate et al. 1995). The sinks were free to migrate and were able to accrete gas and dust particles due to their interaction with the disk. Particles were accreted onto the sinks when two conditions were fulfilled: i) the SPH particle was found to be gravitationally bound the sink, and ii) the divergence of the velocity field at the location of the particle was negative (Bate et al. 1995).

Each simulation was evolved for a maximum time of 100 orbits at the initial planet distance from the central star. The gas and dust density distributions at the end of our simulations were not in a steady state. Since in our simulations the planet was allowed to migrate and accrete due to the tidal interaction with the surrounding disk, the planet properties and the tidal effect on the surrounding disks evolved with time without reaching a steady state. It is therefore reasonable to expect a degree of degeneracy with the simulation parameters (e.g., initial planet mass, location, and gas disk mass). However, given the wide range of parameters involved in the fitting procedure, we cannot reasonably quantify this degeneracy. This limits our analysis to a set of initial disk and planet properties that are able to reproduce the dust disk model of MWC 480, as obtained from the radiative transfer modeling.

thumbnail Fig. 6

Two-dimensional temperature structure of the best-fit radiative transfer model. Overplotted are contours at 25, 130, and 150 K, which are relevant to the discussion on the origin of the ring structure (see Sect. 5.2). The vertical dotted line marks the center of the ring, i.e., R = 97.5 au. The dashed curve indicates the surface of dust opacity being one (τ1.3 mm = 1), where τ1.3 mm is vertically integrated from the disk surface layer down to the midplane.

4.1 Initial conditions

Our reference model for the total dust mass, grain size distributions, and the disk structural properties were adapted from the results of the radiative transfer modeling described in Sect. 3. The system consists of a central star of mass M⋆ (see Table 1) surrounded by a gas and dust disk extending from Rin = 1 au to Rout = 150 au that we modeled as a set of 5 × 105 SPH gas and dust particles. To simplify our analysis, gas and dust were assumed to be initially well mixed across the disk and the dust and gas surface density profile were initially assumed to be power laws with the same exponential index (γ = 1), without the tapering of Eq. (1). However, our simulations showed that the dynamics of large grains naturally produces a tapering of the dust surface density in the outer disk region. This shows that the choice of the shape of the initial dust surface density in the outer disk does not have a significant effect on the results at the end of the simulation.

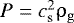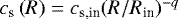The disk was vertically extended by assuming Gaussian profiles for the volume density in the vertical direction with a thickness expressed by Eq. (3). We adopted a vertically isothermal equation of state P= c s 2 ρ g $P=c_{\textrm{s}}^{2} \rho_{\mathrm{g}}$ with c s ( R )= c s,in (R/ R in ) −q $c_{\textrm{s}}\left(R\right) = c_{\textrm{s,in}} (R/R_{\textrm{in}})^{-q}$ with a value cs,in and q computed by assuming vertically hydrostatic equilibrium across the disk, that is, Hg = cs∕Ωk. Using the model parameters shown in Table 1, we obtained Hg ∕Rin = 0.083 and q = 3∕2 − β = 0.42. We set the SPH αAV viscosity parameter to ~0.15, resulting in an effective Shakura & Sunyaev (1973) viscosity αSS ≈ 5 × 10−3.

In order to explore the different dust density structures resulting from different gas and planet properties, we performed asuite of simulations by varying the total dust-to-gas ratio and the planet properties (mass and initial separation).

4.1.1 Dust-to-gas mass ratio

One of the key parameters in disk modeling is the gas disk mass, which is colocated with the dusty disk emission shown in the ALMA image. The local gas surface density regulates the aerodynamical coupling between the gas and the dust (e.g. Weidenschilling 1977) and the accretion and migration efficiency of the planet (D’Angelo & Lubow 2008; D’Angelo et al. 2010). Aerodynamical coupling is usually described in terms of the Stokes number St: 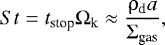St= t stop Ω k ≈ ρ d a Σ gas , \begin{equation*} {St}= t_{\textrm{stop}} \Omega_{\mathrm{k}}\approx \frac{\rho_{\textrm{d}}{a}}{\Sigma_{\textrm{gas}}}, \end{equation*}(4)

where tstop is the aerodynamical stopping time, Ωk is the Keplerian angular velocity, ρd is the internal dust density, and a is the grain size.

The typical approach is to assume a fixed value throughout the entire disk given by the typical interstellar medium (ISM) dust-to-gas mass ratio Mdust∕Mgas = 0.01. However, the small grains (and thus the gas) have been observed to extend up to Rout,SGP ~ 750 au, while the millimeter-size grains extend up to Rout,LGP ~ 200 au (Fig. 3). When we assume that originally, the two dust populations had the same radial distribution and that the discrepancy between them is only due to the radial drift of large grains (e.g. Birnstiel & Andrews 2014), it is reasonable to believe that the dust-to-gas mass ratio has increased by a factor 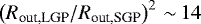( R out,LGP / R out,SGP ) 2  ~ 14 $\left(R_{\textrm{out,LGP}}/R_{\textrm{out,SGP}}\right)^2\,{\sim}\,14$ with respect to the value at birth (i.e., Mdust∕Mgas ≈ 0.01) in the regions of the MWC 480 disk where millimeter-size grains reside. Therefore, our simulations used dust-to-gas mass ratios that spanned the range Mdust∕Mgas ∈ [0.01, 0.2]. Given the best-fit total dust mass Mdust,tot from the radiative transfer modeling, this choice of Mdust∕Mgas corresponds to a disk gas mass of between 0.008 M⊙ < Mdisk,g < 0.16 M⊙.

Adopting the ISM value Mdust∕Mgas = 0.01 would have yielded a gas disk that is close to be gravitationally unstable, as assessed by the stability criterion of Toomre (1964) of 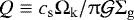Q≡ c s Ω k /πG Σ g $Q\equiv c_{\mathrm{s}} \Omega_{\mathrm{k}}/\uppi \mathcal{G} \Sigma_{\mathrm{g}}$, where 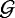G $\mathcal{G}$ is the gravitational constant. In the outer disk, the value of the Q parameter would reach values close to 3, which implies that the disk would be marginally prone to be gravitational unstable (Kratter & Lodato 2016). In this case, the disk would show the development of large-scale density fluctuations in the form of a spiral pattern (e.g. Cossins et al. 2009) that would have been observed by our observations (e.g. Dipierro et al. 2015b). Recent ALMA surveys also found a dust-to-gas mass ratio higher than the ISM value in many protoplanetary disks (e.g., Ansdell et al. 2016, 2017; Long et al. 2017). Therefore, it is reasonable to assume Mdust∕Mgas > 0.01.

In our simulations, millimeter-sized dust particles are characterized by a Stokes number in the range ~ [0.001, 0.1], with a value of St ~ 0.05 at the planet location for Mdust∕Mgas = 0.1. The value of the Stokes number in the outer disk affects the shape of the dust surface density of millimeter grains. As shown in the bottom panel of Fig. 3, the ring structure is just outside the gap, which suggests that the ring might be a trap of millimeter-sized grains due to the presence of a pressure maximum at the outer edge of the gap carved by the planet. The efficiency of dust trapping, and thus, the shape of the dust surface density in the outer disk region, depends on the local gas properties. Moreover, this shape can also be explained by the drift-dominated dynamics of non-growing grains with St < 1 (Youdin & Shu 2002; Birnstiel & Andrews 2014) migrating from the outer disk toward the planet location (see Sect. 3.3.1 in Dipierro et al. 2018). Analyzing dust settling of large dust grains constrained through radiative transfer modeling (see Sect. 3) can yield a rough estimate of the gas disk mass. The uncertainty of the result is connected with how well αSS is constrained. In detail, the vertical balance between the gravitational settling and turbulent diffusion determines the thickness of the dust disk, given by (Dubrulle et al. 1995; Fromang & Nelson 2009) 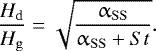H d H g = α SS α SS +St . \begin{equation*} \frac{H_{\mathrm{d}}}{H_{\mathrm{g}}} = \sqrt{\frac{\alpha_{\mathrm{SS}}}{\alpha_{\mathrm{SS}}&#x002B;{St}}}. \end{equation*}(5)

Assuming αSS = 5 × 10−3 and St computed by assuming Mdust∕Mgas = 0.1, we obtain a dust-to-gas height ratio ~0.28, averaged over a distance from the central star R ∈ [30 au, Rout]. This value is quite close to the value of Λ = 0.25 (see Table 1) inferred from the radiative transfer modeling, which implies that the dust vertical structure generated by a dust-to-gas mass ratio of 0.1 would reproduce the expected level of dust settling.

4.1.2 Analytical estimate of the planet properties

We ran simulations by adopting different planet masses and radial distances from the central star. Owing to the uncertainties in the planet properties, we considered a range of planet masses and distances based on analytical estimates of their fiducial values.

Numerical simulations have shown that the width Δ of dust gaps opened by planets is a few times the Hill radius Δ ≈ xRHill, where x = 4–8 (Rosotti et al. 2016), and 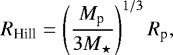R Hill = ( M p 3 M ⋆ ) 1/3 R p , \begin{equation*} R_{\textrm{Hill}}=\left(\frac{M_{\textrm{p}}}{3M_{\star}}\right)^{1/3}R_{\textrm{p}}, \end{equation*}(6)

where Rp is the radial distance of the planet. Therefore, we can qualitatively estimate the planet mass producing the dust density depletion seen in our ALMA continuum data as 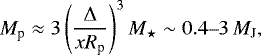M p ≈3 ( Δ x R p ) 3 M ⋆ ~0.4--3  M J , \begin{equation*} M_{\textrm{p}}\approx 3\left(\frac{\Delta}{xR_{\textrm{p}}} \right)^3 M_{\star}\sim 0.4 \textrm{--}3\, {M_{\textrm{J}}}, \end{equation*}(7)

assuming Rp = 73.4 au and Δ = 23 au.

This range of planet masses is consistent with the minimum planet mass required in order to carve a gap in the dust density profile (Rosotti et al. 2016; Dipierro & Laibe 2017; Facchini et al. 2018), M p ≈min[ 0.3 ( H R ) R p 3 ,1.38 ( ζ St ) 3/2 ( H R ) R p 3 ] M ⋆ ~1 M J , \begin{equation*} M_{\textrm{p}}\approx \min\left[0.3\left(\frac{H}{R}\right)^3_{R_{\textrm{p}}}, 1.38\left(\frac{\upzeta}{St}\right)^{3/2}\left(\frac{H}{R}\right)_{R_{\textrm{p}}}^3 \right]M_{\star}\sim 1 {M_{\textrm{J}}}, \end{equation*}(8)

where ζ=− ∂lnP ∂lnR | R p =( γ+1.5−β+ 3 2 )=2.92, \begin{equation*} \upzeta=-\left.\frac{\partial \ln P}{\partial \ln R}\right|_{R_{\textrm{p}}}=\left(\upgamma&#x002B;1.5-\upbeta&#x002B;\frac{3}{2}\right)=2.92, \end{equation*}(9)

using the parameters shown in Table 1. Recently, Ataiee et al. (2018) found the following criterion to produce a pressure bump able to trap dust grains as 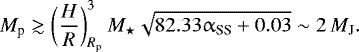M p ≳ ( H R ) R p 3 M ⋆ 82.33 α SS +0.03 ~2  M J . \begin{equation*} M_{\textrm{p}}\gtrsim \left(\frac{H}{R}\right)_{R_{\textrm{p}}}^{3}M_{\star} \sqrt{82.33\alpha_{\textrm{SS}}&#x002B;0.03}\sim 2 \,{M_{\textrm{J}}}.\end{equation*}(10)

Based on this analysis, our numerical simulations adopted planet masses spanning Mp= [0.4, 2] MJ.

We now check whether the masses inferred from the previous analysis are expected to carve a deep gap in the gas as well. In order to open a deep gap (corresponding to a depletion of ~ 90% of the unperturbed value), a planet needs to satisfy the criterion (Crida et al. 2006) 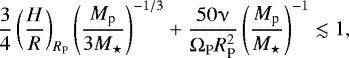3 4 ( H R ) R P ( M p 3 M ⋆ ) −1/3 + 50ν Ω P R P 2 ( M p M ⋆ ) −1 ≲1, \begin{equation*} \frac{3}{4}\left(\frac{H}{R}\right)_{R_{\textrm{P}}}\left(\frac{M_{\textrm{p}}}{3M_{\star}}\right)^{-1/3}&#x002B;\frac{50 \upnu}{\Omega_{\textrm{P}}R_{\textrm{P}}^2}\left(\frac{M_{\textrm{p}}}{M_{\star}}\right)^{-1}\lesssim 1,\end{equation*}(11)

where Ωp = 2π∕tp is the Keplerian orbital frequency of the planet, and tp its orbital period. The criterion in Eq. (11) requires a satellite with Mp ≳ 16 MJ in order to open a deep gap in the gas. This result suggests that the planet masses simulated here will carve a gap in the dust, and will produce only a slight depletion (10 – 20%) in the gas density at the planet location (Ataiee et al. 2018).

As soon as the simulation began, the planet started to migrate inward as a consequence of the interaction with the disk. Since the planet was initially completely embedded in the disk, it migrated according to type I migration on a timescale from Paardekooper et al. 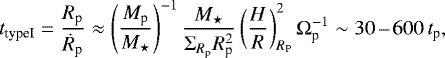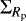(2010) of t typeI = R p R ˙ p ≈ ( M p M ⋆ ) −1 M ⋆ Σ R p R p 2 ( H R ) R P 2 Ω p −1 ~30 – 600  t p , \begin{equation*} t_{\textrm{typeI}}=\frac{R_{\textrm{p}}}{\dot R_{\textrm{p}}} \approx \left(\frac{M_{\textrm{p}}}{M_{\star}}\right)^{-1}\frac{M_{\star}}{\Sigma_{R_{\textrm{p}}}R_{\textrm{p}}^2}\left(\frac{H}{R}\right)_{R_{\textrm{P}}}^{2}\Omega_{\textrm{p}}^{-1}\sim 30\,\textrm{--}\,600 \,t_{\textrm{p}},\end{equation*}(12)

where Σ R p $\Sigma_{R_{\textrm{p}}}$ is the gas surface density at the planet radial distance from the star. On the right-hand side of Eq. (12), the shortest timescale is the one for Mdust∕Mg = 0.01 and the longest is the one for Mdust∕Mg = 0.2.

Since the planet should migrate inward due to the planet-disk interaction in our disk model, we initially locate the planet on an outer orbit (Rp = 85–120 au, depending on the migration timescale) with respect to the position of the minimum of the intensity profile in the gap region (i.e. Rp ≳ 74.3 au).

thumbnail Fig. 7

Rendered images of gas (left panel) and millimeter dust grain (right panel) surface density (in units of g cm-2 on a logarithmic scale) of our best-fit disk model hosting a planet with an initial mass of 1.25 MJ that is initially located at a distance of 85 au from the central star.

4.2 Results

Our best model consists of an initial well-mixed gas and dust disk with Mdust,tot∕Mgas = 0.1, hosting a planet with an initial mass of 1.25 MJ located at a distance of 85 au from the central star. We stopped the simulations after ~ 50 orbits at the initial location of the planet. Figure 7 shows the rendered images of gas and millimeter dust grain surface density of our best-fit model. The surface density structure of the dust phase shows an annular gap around the planet location. In contrast, the gas phase shows a weak depletion asymmetric with respect to the planet location and a spiral structure across the disk. The fast radial drift of dust grains in the outer disk toward the inner disk regions produces the accumulation of dust grains at the gap outer edge. After 50 orbits (measured at 85 au), the planet reaches a distance of 78.4 au from the central star, and its mass is ~ 2.3 MJ, with an average mass accretion rate of ~3 × 10−5 MJ yr−1. Moreover, the star accretes mass from the surrounding gas and dust disk at a rate given by ~ 2.5 × 10−7 M⊙ yr−1. This value is consistent with the average stellar accretion rate of 1.2 × 10−7 M⊙ yr−1 measured byMendigutía et al. (2013)3. It is worth remarking that the fast planet migration and accretion can be slowed down in our model by running the simulation for longer, letting the planet carve a deep gas gap.

Figure 8 shows the azimuthally averaged surface density of the gas and dust at the end of the simulation, compared tothe fit for the dust surface density of large grains described in Sect. 3. As expected, the gap in the dust component is deeper than the (barely visible) gap in the gas due to both the higher efficiency of the tidal torque and the dust radial motion induced by drag (Paardekooper & Mellema 2006; Fouchet et al. 2007; Pinilla et al. 2015; Dipierro & Laibe 2017). Our simulation shows that the planet perturbs the local pressure profile and creates a pressure maximum at the gap outer edge. As a result, millimeter grains accumulate at the location of the pressure maximum, forming a deeper dust gap than in the gas. At the inner edge, the perturbation of the pressure profile induced by the tidal torque does not exceed the background pressure gradient, leading to a weak pile-up at the inner gap edge and an accelerated radial inflow toward the central star (Fouchet et al. 2010). The discrepancy in the density profiles with respect to the radiative transfer model inside ~ 20 au is most likely a numerical effect that is due to the resolution-dependent SPH numerical viscosity, which causes an artificially fast depletion of the innermost disk regions (Lodato & Price 2010).

thumbnail Fig. 8

Azimuthally averaged dust (dashed) and gas (solid) surface density for our best disk hosting a planet with an initial mass of 1.25 MJ after 50 orbits, initially located at 85 au from the central star. The gas surface density is scaled down by a factor of 10 at the end of the simulation, for a direct comparison with the dust phase. The dotted line indicates the surfacedensity profile of large dust grains inferred from the radiative transfer analysis (bottom panel of Fig. 3). After 50 orbits (measured at 85 au), the planet is at 78.4 au from the central star and its mass is 2.3 MJ.

5 Discussion

5.1 Why the SED does not show evidence of the gap

The SED serves as an important diagnostic for substructures, including large inner holes (or cavities) and opacity gaps in protoplanetary disks. The significant depletion of small dust grains inside the hole and gap leads to a clear flux deficit in the near- and/or mid-IR wavelength domain (e.g., Espaillat et al. 2007, 2010, 2014; Williams & Cieza 2011). High-resolution (sub-) millimeter observations confirm the presence of such holes and gaps that are indirectly inferred from the SEDs (e.g., Andrews et al. 2011), and also yield hole sizes that generally match estimates from SED modeling well (van der Marel et al. 2016).

However, the SED of MWC 480 does not show any significant decrease in the near- or mid-IR wavelength regime (see Fig. 4), even though our ALMA observation clearly reveals a large and deep gap in the disk. This apparent discrepancy can be explained in two ways. First, the 1.3 mm continuum observation is sensitive only to millimeter dust grains and does not probe the distribution of small grains in the disk. The polarimetric differential imaging in the H band obtained with Subaru/HiCIAO indicates that small dust grains are smoothly distributed up to ~ 160 au (Kusakabe et al. 2012). These small grains are efficiently heated, and their thermal re-emission contributes a vast majority of the observed flux at IR wavelengths (see the red dashed line in Fig. 4). Second, the gap is too far from the central star to have a significant impact on the IR SED. Based on our ALMA observations, the disk can be generally divided into three parts: a central bright blob, a gap, and a bright ring. The green dash-dotted line in Fig. 4 shows the SED of the central bright blob defined with a radius range of Rin ≤ R ≤ 63 au. Subtracting the gap location with half of the gap width gives 63 au as the outer radius. The central blob is already sufficient to shape the SED up to a wavelength of ~ 50 μm. However, most criteria (e.g., using color–color diagram) for selecting disks with inner holes or gaps rely on data shorter than ~ 24 μm (e.g., Fang et al. 2009; Cieza et al. 2010; Merín et al. 2010). Quantifying the impact of gaps located at large radii on the appearance of the SED would require a detailed parameter study that covers a broad range of gap location, width, and depth, and also considers multiple gaps in a disk.

A few disks have also been found to have inner holes in millimeter imaging without evidence for IR dips in their SEDs, including MWC 758 (Isella et al. 2010a; Boehler et al. 2018; Dong et al. 2018), RY Tau (Isella et al. 2010b; Pinilla et al. 2018; Long et al. 2018), and several disks in the Ophiuchus star-forming region (Andrews et al. 2011).

5.2 On the origin of the gap or ring structure

In Sect. 4, we explored planet–disk interaction as the origin of the gap or ring structure in the MWC 480 disk. The hydrodynamics simulations suggest that the observed gap is caused by gravitational perturbations from a planet with a mass of 2.3 MJ embedded in the gap. It is interesting to determine whether the disk, particularly in the vicinity of the gap region, had sufficient material to form such a planet. For this purpose, we first performed a power-law fit to the best-fit surface density profile (the bottom panel of Fig. 3) outside the gap. The result is assumed to be the initially unperturbed surface density profile of large dust grains. We integrated this power-law fitted profile within the gap region and derived an initial mass of the material. By integrating the best-fit surface density profile in the same radius range, we obtained an after-perturbed mass. The difference between these two integrated masses is ~ 5 MJ, which can be considered as the “missing material” in the gap during the process of planet formation. This calculation uses a dust-to-gas mass ratio of 0.1 from the best hydrodynamical model. An assumption of a standard dust-to-gas mass ratio of 0.01 (i.e., for the interstellar medium), which is believed valid at the early stage of disk evolution, would increase the missing mass. This simple analysis indicates that there is a possibility for the formation of the planet.

Using polarimetric differential imaging in the H band obtained with Subaru/HiCIAO, Kusakabe et al. (2012) found that the radial polarized intensity profile drops as R−2 from 0.2′′ to 0.6′′ (32 − 97 au), while it is steeper, R−3, in the outer disk from 0.6′′ to 1.0′′ (97 − 162 au). The authorscompared the outer disk properties of MWC 480 with the roughly coeval SAO 206462 and the younger LkCa 15, both of which share similar characteristics in the radial polarized intensity profile. The evidence of spiral arms in SAO 206462 (Muto et al. 2012; Maire et al. 2017) and planet candidates in LkCa 15 (Kraus & Ireland 2012; Sallum et al. 2015) drove the authors to suggest that the outer disks in these systems are dynamically excited by massive planets. Our hydrodynamics modeling coupled with detailed radiative transfer analysis for MWC 480 supports this hypothesis. Nevertheless, deep high-contrast searches for planets in the gap are required to confirm the presence of a planet (e.g., Testi et al. 2015; Ruane et al. 2017; Keppler et al. 2018).

Alternative mechanisms in addition to planets can also create gap or ring structures in protoplanetary disks. Dust coagulation or fragmentation (Zhang et al. 2015; Banzatti et al. 2015; Pinilla et al. 2017) and sintering-induced dust rings (Okuzumi et al. 2016) near condensation fronts are believed to be universal, although it is unclear whether they can produce gaps. In cold disk regions, dust grains are expected to be covered by ice mantles of volatile molecules. The condensation fronts, also known as snow lines, are defined as the location where the ice mantles evaporate during the inward drift of dust grains. Phase transition occurs when the dust grains cross the condensation fronts relative to the molecules that form their ice mantles, which alters the opacity, coagulation, and fragmentation properties of dust grains, leading to the accumulation of dust particles in ring structures. In Fig. 6, we draw temperature contours of 25, 130, and 150 K corresponding to the condensation temperatures4 of CO and H2O that are abundant and commonly observed in protoplanetary disks. The center of the ring marked with the vertical dotted line appears associated with the CO snow line. In the disk midplane, the H2 O snow line is quite close to the central star and beyond the spatial resolution of our ALMA observation. One of the key feature of the condensation front as the origin of ring structure is that the total gas surface density is not expected to have strong variations (Pinilla et al. 2017; Stammler et al. 2017). However, gas observations toward the MWC 480 disk so far lack sufficient spatial resolution to confirm a small variation in the gas surface density near the CO snow line. Future high-resolution observations of the gas components are highly desired to constrain the gas surface density profile of the MWC 480 disk (e.g., Isella et al. 2016).

The dead zone is another potential cause for the ring structures (Pinilla et al. 2016). Protoplanetary disks embedded in a weak magnetic field are expected to be subject to the magnetorotational instability, which induces MHD turbulence to transfer angular momentum outward and therefore sustain accretion onto the central star (Balbus & Hawley 1991, 1998). The low degree of gas ionization in the dead zone suppresses the magnetorotational instability. Consequently, accretion slows down and a gas pressure bump is formed at the outer edge of the dead zone (Flock et al. 2015). The pressure bump is capable of trapping particles and enhancing grain growth, leading to ring-like structures. In addition, the magnetized disk model has been supported further from comparisons between simulation and observation (Flock et al. 2017; Bertrang et al. 2017). Follow-up observations are required to investigate whether dead zones are responsible for the ring observed in the MWC 480 disk. For example, spatially resolved measurements of the turbulence through different layers in the disk (e.g., Flaherty et al. 2015; Teague et al. 2016) will help to test the size of dead zones.

6 Summary

We identified a gap and bright dust ring in the MWC 480 disk for the first time using high-resolution (0.17′′× 0.11′′) ALMA Band 6 continuum observations. The gap is located at 74.3 au from the central star and has a width of 23 au. The ring is centered at 97.5 au. In order to constrain the surface density and structural parameters of the disk, we performed detailed radiative transfer modeling, in which two grain populations (i.e., a small and large grain population) with different spatial distribution and dust properties were considered in the setup. The ALMA image at 1.3 mm and the broadband SED were taken into account in the modeling procedure.

Planet–disk interactions are one of the most attractive mechanisms for the formation of gap or ring structures. For MWC 480, we tested this scenario by performing global three-dimensional SPH gas and dust simulations of disks hosting a migrating and accreting planet. The dust emission across the disk is consistent with the presence of an embedded planet with a mass of ~ 2.3 MJ at an orbital radius of ~78 au. Given the surface density of the best-fit radiative transfer model, the amount of depleted mass in the gap is higher than the planet mass, which means that the disk had the potential to form such a planet at this location. Therefore, the MWC 480 disk deserves follow-up deep and high-contrast search for planets. We also briefly discussed condensation fronts and dead zones as the origin of the gap or ring structure. Future high-resolution observations of the gas and multiwavelength measurements of the depth and width of the gap are indispensable to identify the dominant mechanism that carves out gaps in disks.

Acknowledgements

Y.L. acknowledges supports by the Natural Science Foundation of Jiangsu Province of China (Grant No. BK20181513) and by the Natural Science Foundation of China (Grant No. 11503087). G.D. acknowledges financial support from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 681601). G.L. and B.N. thank the support by the project PRIN-INAF 2016 The Cradle of Life – GENESIS-SKA (General Conditions in Early Planetary Systems for the rise of life with SKA). G.J.H. is supportedby general grants 11473005 and 11773002 awarded by the National Science Foundation of China. D.H. is supported by European Union A-ERC grant 291141 CHEMPLAN, NWO and by a KNAW professor prize awarded to E. van Dishoeck. Y.B., F.M. and G.v.d.P. acknowledge funding from ANR of France under contract number ANR-16-CE31-0013. D.J. is supported by NRC Canada and by an NSERC Discovery Grant. C.F.M. acknowledges an ESO Fellowship. This research used the ALICE High Performance Computing Facility and the DiRAC Data Intensive service operated by the University of Leicester IT Services. These resources form part of the STFC DiRAC HPC Facility (www.dirac.ac.uk), jointly funded by STFC and the Large Facilities Capital Fund of BIS via STFC capital grants ST/K000373/1 and ST/R002363/1 and STFC DiRAC Operations grant ST/R001014/1. This paper makes use of the following ALMA data: 2016.1.01164.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.

References

  1. Alecian, E., Wade, G. A., Catala, C., et al. 2013, MNRAS, 429, 1001 [NASA ADS] [CrossRef] [Google Scholar]
  2. ALMA Partnership (Brogan, C. L., et al.) 2015, ApJ, 808, L3 [NASA ADS] [CrossRef] [Google Scholar]
  3. Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2009, ApJ, 700, 1502 [NASA ADS] [CrossRef] [Google Scholar]
  4. Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011, ApJ, 732, 42 [NASA ADS] [CrossRef] [Google Scholar]
  5. Andrews, S. M., Wilner, D. J., Zhu, Z., et al. 2016, ApJ, 820, L40 [NASA ADS] [CrossRef] [Google Scholar]
  6. Ansdell, M., Williams, J. P., van der Marel, N., et al. 2016, ApJ, 828, 46 [Google Scholar]
  7. Ansdell, M., Williams, J. P., Manara, C. F., et al. 2017, AJ, 153, 240 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Ataiee, S., Baruteau, C., Alibert, Y., & Benz, W. 2018, A&A, 615, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
  10. Balbus, S. A.,& Hawley, J. F. 1998, Rev. Mod. Phy., 70, 1 [Google Scholar]
  11. Ballabio, G., Dipierro, G., Veronesi, B., et al. 2018, MNRAS, 477, 2766 [NASA ADS] [CrossRef] [Google Scholar]
  12. Banzatti, A., Pinilla, P., Ricci, L., et al. 2015, ApJ, 815, L15 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bate, M. R., Bonnell, I. A., & Price, N. M. 1995, MNRAS, 277, 362 [NASA ADS] [CrossRef] [Google Scholar]
  14. Beichman, C. A., Neugebauer, G., Habing, H. J., Clegg, P. E., & Chester, T. J. 1988, Infrared Astronomical Satellite (IRAS) Catalogs and Atlases. Volume 1: Explanatory supplement [Google Scholar]
  15. Bertrang, G. H.-M., Flock, M., & Wolf, S. 2017, MNRAS, 464, L61 [NASA ADS] [CrossRef] [Google Scholar]
  16. Béthune, W., Lesur, G., & Ferreira, J. 2016, A&A, 589, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Birnstiel, T., & Andrews, S. M. 2014, ApJ, 780, 153 [NASA ADS] [CrossRef] [Google Scholar]
  18. Birnstiel, T., Fang, M., & Johansen, A. 2016, Space Sci. Rev., 205, 41 [NASA ADS] [CrossRef] [Google Scholar]
  19. Boehler, Y., Ricci, L., Weaver, E., et al. 2018, ApJ, 853, 162 [Google Scholar]
  20. Calvet, N., Patino, A., Magris, G. C., & D’Alessio, P. 1991, ApJ, 380, 617 [NASA ADS] [CrossRef] [Google Scholar]
  21. Casassus, S., van der Plas, G., M, S. P., et al. 2013, Nature, 493, 191 [NASA ADS] [CrossRef] [Google Scholar]
  22. Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [NASA ADS] [CrossRef] [Google Scholar]
  23. Cieza, L. A., Schreiber, M. R., Romero, G. A., et al. 2010, ApJ, 712, 925 [NASA ADS] [CrossRef] [Google Scholar]
  24. Cieza, L. A., Casassus, S., Pérez, S., et al. 2017, ApJ, 851, L23 [NASA ADS] [CrossRef] [Google Scholar]
  25. Cossins, P., Lodato, G., & Clarke, C. J. 2009, MNRAS, 393, 1157 [Google Scholar]
  26. Crida, A., Morbidelli, A., & Masset, F. 2006, Icarus, 181, 587 [Google Scholar]
  27. Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
  28. Cutri, R. M., et al. 2013, VizieR Online Data Catalog: II/328 [Google Scholar]
  29. D’Alessio, P., Calvet, N., & Hartmann, L. 2001, ApJ, 553, 321 [NASA ADS] [CrossRef] [Google Scholar]
  30. D’Angelo, G., & Lubow, S. H. 2008, ApJ, 685, 560 [NASA ADS] [CrossRef] [Google Scholar]
  31. D’Angelo, G., Durisen, R. H., & Lissauer, J. J. 2010, Exoplanets, ed. S. Seager (Tucson, AZ: University Press of Arizona), 319 [Google Scholar]
  32. Dipierro, G., & Laibe, G. 2017, MNRAS, 469, 1932 [NASA ADS] [CrossRef] [Google Scholar]
  33. Dipierro, G., Price, D., Laibe, G., et al. 2015a, MNRAS, 453, L73 [NASA ADS] [CrossRef] [Google Scholar]
  34. Dipierro, G., Pinilla, P., Lodato, G., & Testi, L. 2015b, MNRAS, 451, 974 [Google Scholar]
  35. Dipierro, G., Ricci, L., Pérez, L., et al. 2018, MNRAS, 475, 5296 [NASA ADS] [CrossRef] [Google Scholar]
  36. Donehew, B., & Brittain, S. 2011, AJ, 141, 46 [NASA ADS] [CrossRef] [Google Scholar]
  37. Dong, R., Liu, S.-y., Eisner, J., et al. 2018, ApJ, 860, 124 [NASA ADS] [CrossRef] [Google Scholar]
  38. Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A, 300, 503 [Google Scholar]
  39. Dubrulle, B., Morfill, G., & Sterzik, M. 1995, Icarus, 114, 237 [NASA ADS] [CrossRef] [Google Scholar]
  40. Dullemond, C. P., & Dominik, C. 2004, A&A, 421, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
  42. Dullemond, C. P., Juhasz, A., Pohl, A., et al. 2012, Astrophysics Source Code Library [record ascl:1202.015] [Google Scholar]
  43. Espaillat, C., Calvet, N., D’Alessio, P., et al. 2007, ApJ, 670, L135 [NASA ADS] [CrossRef] [Google Scholar]
  44. Espaillat, C., D’Alessio, P., Hernández, J., et al. 2010, ApJ, 717, 441 [NASA ADS] [CrossRef] [Google Scholar]
  45. Espaillat, C., Muzerolle, J., Najita, J., et al. 2014, Protostars and Planets VI (Tucson, AZ: University of Arizona Press), 497 [Google Scholar]
  46. Facchini, S., Pinilla, P., van Dishoeck, E. F., & de Juan Ovelar, M. 2018, A&A, 612, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Fang, M., van Boekel, R., Wang, W., et al. 2009, A&A, 504, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Fang, M., Sicilia-Aguilar, A., Wilner, D., et al. 2017, A&A, 603, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Fedele, D., Tazzari, M., Booth, R., et al. 2018, A&A, 610, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Fernandes, R. B., Long, Z. C., Pikhartova, M., et al. 2018, ApJ, 856, 103 [NASA ADS] [CrossRef] [Google Scholar]
  51. Flaherty, K. M., Hughes, A. M., Rosenfeld, K. A., et al. 2015, ApJ, 813, 99 [NASA ADS] [CrossRef] [Google Scholar]
  52. Flock, M., Ruge, J. P., Dzyurkevich, N., et al. 2015, A&A, 574, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Flock, M., Nelson, R. P., Turner, N. J., et al. 2017, ApJ, 850, 131 [NASA ADS] [CrossRef] [Google Scholar]
  54. Fouchet, L., Maddison, S. T., Gonzalez, J.-F., & Murray, J. R. 2007, A&A, 474, 1037 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Fouchet, L., Gonzalez, J.-F., & Maddison, S. T. 2010, A&A, 518, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Fromang, S., & Nelson, R. P. 2009, A&A, 496, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Garufi, A., Podio, L., Kamp, I., et al. 2014, A&A, 567, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Gräfe, C., Wolf, S., Guilloteau, S., et al. 2013, A&A, 553, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Guilloteau, S., Dutrey, A., Piétu, V., & Boehler, Y. 2011, A&A, 529, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Hamidouche, M., Looney, L. W., & Mundy, L. G. 2006, ApJ, 651, 321 [NASA ADS] [CrossRef] [Google Scholar]
  63. Hendler, N. P., Pinilla, P., Pascucci, I., et al. 2017, MNRAS, submitted [arXiv:1711.09933] [Google Scholar]
  64. Huang, J., Öberg, K. I., Qi, C., et al. 2017, ApJ, 835, 231 [NASA ADS] [CrossRef] [Google Scholar]
  65. Hughes, A. M., Wilner, D. J., Qi, C., & Hogerheijde, M. R. 2008, ApJ, 678, 1119 [NASA ADS] [CrossRef] [Google Scholar]
  66. Isella, A., Natta, A., Wilner, D., Carpenter, J. M., & Testi, L. 2010a, ApJ, 725, 1735 [NASA ADS] [CrossRef] [Google Scholar]
  67. Isella, A., Carpenter, J. M., & Sargent, A. I. 2010b, ApJ, 714, 1746 [NASA ADS] [CrossRef] [Google Scholar]
  68. Isella, A., Guidi, G., Testi, L., et al. 2016, Phys. Rev. Lett., 117, 251101 [NASA ADS] [CrossRef] [Google Scholar]
  69. Ishihara, D., Onaka, T., Kataza, H., et al. 2010, A&A, 514, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Jäger, C., Mutschke, H., & Henning, T. 1998, A&A, 332, 291 [NASA ADS] [Google Scholar]
  71. Jin, S., Li, S., Isella, A., Li, H., & Ji, J. 2016, ApJ, 818, 76 [NASA ADS] [CrossRef] [Google Scholar]
  72. Juhász, A., Bouwman, J., Henning, T., et al. 2010, ApJ, 721, 431 [NASA ADS] [CrossRef] [Google Scholar]
  73. Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] [Google Scholar]
  74. Keppler, M., Benisty, M., Müller, A., et al. 2018, A&A, 617, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Kirchschlager, F., Wolf, S., & Madlener, D. 2016, MNRAS, 462, 858 [NASA ADS] [CrossRef] [Google Scholar]
  76. Kirkpatrick, S., Gelatt, C. D., & Vecchi, M. P. 1983, Science, 220, 671 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
  77. Kratter, K. M., & Lodato, G. 2016, ARA&A, 54, 271 [NASA ADS] [CrossRef] [Google Scholar]
  78. Kraus, A. L., & Ireland, M. J. 2012, ApJ, 745, 5 [NASA ADS] [CrossRef] [Google Scholar]
  79. Kraus, S., Kreplin, A., Fukugawa, M., et al. 2017, ApJ, 848, L11 [NASA ADS] [CrossRef] [Google Scholar]
  80. Kurucz, R. 1994, Kurucz CD-ROM No. 19. (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  81. Kusakabe, N., Grady, C. A., Sitko, M. L., et al. 2012, ApJ, 753, 153 [NASA ADS] [CrossRef] [Google Scholar]
  82. Liu, Y., Madlener, D., Wolf, S., Wang, H., & Ruge, J. P. 2012, A&A, 546, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Liu, Y., Henning, T., Carrasco-González, C., et al. 2017, A&A, 607, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Lodato, G., & Price, D. J. 2010, MNRAS, 405, 1212 [NASA ADS] [Google Scholar]
  85. Long, F., Herczeg, G. J., Pascucci, I., et al. 2017, ApJ, 844, 99 [NASA ADS] [CrossRef] [Google Scholar]
  86. Long, F., Pinilla, P., Herczeg, G. J., et al. 2018, ApJ, 869, 17 [NASA ADS] [CrossRef] [Google Scholar]
  87. Louvet, F., Dougados, C., Cabrit, S., et al. 2018, A&A, 618, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Luhman, K. L., Mamajek, E. E., Shukla, S. J., & Loutrel, N. P. 2017, AJ, 153, 46 [NASA ADS] [CrossRef] [Google Scholar]
  89. Madlener, D., Wolf, S., Dutrey, A., & Guilloteau, S. 2012, A&A, 543, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Maire, A.-L., Stolker, T., Messina, S., et al. 2017, A&A, 601, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Mannings, V., & Sargent, A. I. 1997, ApJ, 490, 792 [NASA ADS] [CrossRef] [Google Scholar]
  92. McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 127 [NASA ADS] [Google Scholar]
  93. Meeus, G., Waters, L. B. F. M., Bouwman, J., et al. 2001, A&A, 365, 476 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Mendigutía, I., Mora, A., Montesinos, B., et al. 2012, A&A, 543, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  95. Mendigutía, I., Brittain, S., Eiroa, C., et al. 2013, ApJ, 776, 44 [NASA ADS] [CrossRef] [Google Scholar]
  96. Merín, B., Brown, J. M., Oliveira, I., et al. 2010, ApJ, 718, 1200 [NASA ADS] [CrossRef] [Google Scholar]
  97. Millan-Gabet, R., Che, X., Monnier, J. D., et al. 2016, ApJ, 826, 120 [NASA ADS] [CrossRef] [Google Scholar]
  98. Miyake, K., & Nakagawa, Y. 1995, ApJ, 441, 361 [NASA ADS] [CrossRef] [Google Scholar]
  99. Mora, A., Merín, B., Solano, E., et al. 2001, A&A, 378, 116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  100. Muto, T., Grady, C. A., Hashimoto, J., et al. 2012, ApJ, 748, L22 [NASA ADS] [CrossRef] [Google Scholar]
  101. Öberg, K. I., Qi, C., Fogel, J. K. J., et al. 2010, ApJ, 720, 480 [NASA ADS] [CrossRef] [Google Scholar]
  102. Öberg, K. I., Murray-Clay, R., & Bergin, E. A. 2011, ApJ, 743, L16 [NASA ADS] [CrossRef] [Google Scholar]
  103. Okuzumi, S., Momose, M., Sirono, S.-i., Kobayashi, H., & Tanaka, H. 2016, ApJ, 821, 82 [NASA ADS] [CrossRef] [Google Scholar]
  104. Paardekooper,S.-J., & Mellema, G. 2006, A&A, 453, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  105. Paardekooper,S.-J., Baruteau, C., Crida, A., & Kley, W. 2010, MNRAS, 401, 1950 [NASA ADS] [CrossRef] [Google Scholar]
  106. Pascual, N., Montesinos, B., Meeus, G., et al. 2016, A&A, 586, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  107. Pérez, L. M., Carpenter, J. M., Andrews, S. M., et al. 2016, Science, 353, 1519 [NASA ADS] [CrossRef] [Google Scholar]
  108. Piétu, V., Dutrey, A., Guilloteau, S., Chapillon, E., & Pety, J. 2006, A&A, 460, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Piétu, V., Dutrey, A., & Guilloteau, S. 2007, A&A, 467, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  110. Pinilla, P., de Juan Ovelar, M., Ataiee, S., et al. 2015, A&A, 573, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  111. Pinilla, P., Flock, M., Ovelar, M. d. J., & Birnstiel, T. 2016, A&A, 596, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  112. Pinilla, P., Pohl, A., Stammler, S. M., & Birnstiel, T. 2017, ApJ, 845, 68 [NASA ADS] [CrossRef] [Google Scholar]
  113. Pinilla, P., Tazzari, M., Pascucci, I., et al. 2018, ApJ, 859, 32 [Google Scholar]
  114. Pinte, C., & Laibe, G. 2014, A&A, 565, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  115. Pinte, C., Dent, W. R. F., Ménard, F., et al. 2016, ApJ, 816, 25 [NASA ADS] [CrossRef] [Google Scholar]
  116. Price, D. J., & Laibe, G. 2015, MNRAS, 451, 813 [NASA ADS] [CrossRef] [Google Scholar]
  117. Price, D. J., Wurster, J., Nixon, C., et al. 2018, PASA, 35, e031 [Google Scholar]
  118. Rosotti, G. P., Juhasz, A., Booth, R. A., & Clarke, C. J. 2016, MNRAS, 459, 2790 [NASA ADS] [CrossRef] [Google Scholar]
  119. Ruane, G., Mawet, D., Kastner, J., et al. 2017, AJ, 154, 73 [NASA ADS] [CrossRef] [Google Scholar]
  120. Sallum, S., Follette, K. B., Eisner, J. A., et al. 2015, Nature, 527, 342 [NASA ADS] [CrossRef] [Google Scholar]
  121. Salyk, C., Herczeg, G. J., Brown, J. M., et al. 2013, ApJ, 769, 21 [NASA ADS] [CrossRef] [Google Scholar]
  122. Sauter, J., Wolf, S., Launhardt, R., et al. 2009, A&A, 505, 1167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  123. Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
  124. Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23 [Google Scholar]
  125. Simon, M., Dutrey, A., & Guilloteau, S. 2000, ApJ, 545, 1034 [NASA ADS] [CrossRef] [Google Scholar]
  126. Sitko, M. L., Carpenter, W. J., Kimes, R. L., et al. 2008, ApJ, 678, 1070 [NASA ADS] [CrossRef] [Google Scholar]
  127. Stammler, S. M., Birnstiel, T., Panić, O., Dullemond, C. P., & Dominik, C. 2017, A&A, 600, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  128. Takahashi, S. Z., & Inutsuka, S.-i. 2016, AJ, 152, 184 [NASA ADS] [CrossRef] [Google Scholar]
  129. Teague, R., Guilloteau, S., Semenov, D., et al. 2016, A&A, 592, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  130. Terebey, S., Shu, F. H., & Cassen, P. 1984, ApJ, 286, 529 [NASA ADS] [CrossRef] [Google Scholar]
  131. Testi, L., Skemer, A., Henning, T., et al. 2015, ApJ, 812, L38 [NASA ADS] [CrossRef] [Google Scholar]
  132. Tobin, J. J., Kratter, K. M., Persson, M. V., et al. 2016, Nature, 538, 483 [NASA ADS] [CrossRef] [Google Scholar]
  133. Toomre, A. 1964, ApJ, 139, 1217 [NASA ADS] [CrossRef] [Google Scholar]
  134. van Boekel, R., Min, M., Waters, L. B. F. M., et al. 2005, A&A, 437, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  135. van der Marel,N., van Dishoeck, E. F., Bruderer, S., et al. 2013, Science, 340, 1199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  136. van der Marel,N., Verhaar, B. W., van Terwisga, S., et al. 2016, A&A, 592, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  137. van der Plas, G., Ménard, F., Canovas, H., et al. 2017, A&A, 607, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  138. Weidenschilling, S. J. 1977, Ap&SS, 51, 153 [Google Scholar]
  139. Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
  140. Wolf, S., Padgett, D. L., & Stapelfeldt, K. R. 2003, ApJ, 588, 373 [NASA ADS] [CrossRef] [Google Scholar]
  141. Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [NASA ADS] [CrossRef] [Google Scholar]
  142. Youdin, A. N., & Shu, F. H. 2002, ApJ, 580, 494 [NASA ADS] [CrossRef] [Google Scholar]
  143. Zhang, K., Blake, G. A., & Bergin, E. A. 2015, ApJ, 806, L7 [NASA ADS] [CrossRef] [Google Scholar]
  144. Zhang, K., Bergin, E. A., Blake, G. A., et al. 2016, ApJ, 818, L16 [NASA ADS] [CrossRef] [Google Scholar]
1

This distance is consistent with the distance of 160 pc, calculated from the weighted mean of Gaia DR2 parallax measurements, of the 16 previously identified Taurus members (Luhman et al. 2017) that are located within one degree of MWC 480. All values from the literature used in this paper are updated to this new distance, from previous distance estimates of ~140 pc.

3

The original value reported in the paper has been corrected to nearly the same value by accounting for the updated distance, stellar mass, and stellar radius adopted in our analysis.

4

The condensation temperature of volatiles can vary under different assumptions for the composition and surface area of the dust grains and the gas number density in the disk midplane. For instance, Öberg et al. (2011) suggested an average condensation temperature of 20 K for CO ice, while Zhang et al. (2015) adopted a higher value of 25 K.

All Tables

Table 1

Model parameters.

In the text

All Figures

thumbnail Fig. 1

Comparison between the ALMA observation (left panel) and the model image (middle panel) atBand 6. The beam size is indicated by the white filled ellipse in the observed image. The residuals between the observed and model maps are shown in the right panel, in which σ refers to the rms level 0.07 mJy beam−1 of the CLEANed map. The dashed ellipses indicate the locations of the gap and ring.
In the text
thumbnail Fig. 2

Comparison between the observed brightness distribution and model prediction along the disk major (left panel) and minor (right panel) axis. Black solid lines show the observation with uncertainties indicated as gray shaded region, and blue dashed lines refer to model predictions.
In the text
thumbnail Fig. 3

Surface density profiles of the best-fit radiative transfer model. Top panel: surface density of the small grain population. It follows the profile described in Eq. (1) with RC = 200 au and γ = 1. Bottom panel: surface density of the large grain population. It is obtained by fitting the brightness distribution along the disk major axis, see Sect. 3.2.
In the text
thumbnail Fig. 4

SED of the MWC 480 disk. The black line represents the best-fit model, while red dots are photometry collected from the 2MASS (Cutri et al. 2003), WISE (Cutri & et al. 2013), IRAS (Beichman et al. 1988), and AKARI surveys (Ishihara et al. 2010), Herschel/PACS (Pascual et al. 2016), UBVRI (Mendigutía et al. 2012), and sub-mm bands (Mannings & Sargent 1997; Hamidouche et al. 2006; Piétu et al. 2006; Hughes et al. 2008; Öberg et al. 2010; Guilloteau et al. 2011; Huang et al. 2017). The flux density at ALMA Band 6 in this study is highlighted with a blue square. The contributions from the small grain population and large grain population to the total flux are indicated with the red and blue dashed lines, respectively. The green dash-dottedline gives the resulting SED when the raytracing only takes into account the central emission blob (Rin ≤ R ≤ 63 au) as seen in our ALMA image, see Sect. 5.1. The gray dashed line is the input photosphere model (Kurucz 1994).
In the text
thumbnail Fig. 5

Comparison between the observed (red dots) and model (black line) visibilities. The errors of the observation are smaller than the symbol size.
In the text
thumbnail Fig. 6

Two-dimensional temperature structure of the best-fit radiative transfer model. Overplotted are contours at 25, 130, and 150 K, which are relevant to the discussion on the origin of the ring structure (see Sect. 5.2). The vertical dotted line marks the center of the ring, i.e., R = 97.5 au. The dashed curve indicates the surface of dust opacity being one (τ1.3 mm = 1), where τ1.3 mm is vertically integrated from the disk surface layer down to the midplane.
In the text
thumbnail Fig. 7

Rendered images of gas (left panel) and millimeter dust grain (right panel) surface density (in units of g cm-2 on a logarithmic scale) of our best-fit disk model hosting a planet with an initial mass of 1.25 MJ that is initially located at a distance of 85 au from the central star.
In the text
thumbnail Fig. 8

Azimuthally averaged dust (dashed) and gas (solid) surface density for our best disk hosting a planet with an initial mass of 1.25 MJ after 50 orbits, initially located at 85 au from the central star. The gas surface density is scaled down by a factor of 10 at the end of the simulation, for a direct comparison with the dust phase. The dotted line indicates the surfacedensity profile of large dust grains inferred from the radiative transfer analysis (bottom panel of Fig. 3). After 50 orbits (measured at 85 au), the planet is at 78.4 au from the central star and its mass is 2.3 MJ.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.