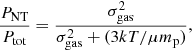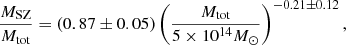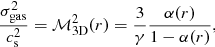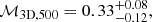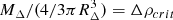| Issue |
A&A
Volume 621, January 2019
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 11 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201833324 | |
| Published online | 03 January 2019 | |
Non-thermal pressure support in X-COP galaxy clusters
1 Max-Planck-Institut für extraterrestrische Physik, Giessenbachstrasse 1, 85748 Garching, Germany
e-mail: deckert@mpe.mpg.de
2 Dipartimento di Fisica e Astronomia Università di Bologna, Via Piero Gobetti, 93/2, 40129 Bologna, Italy
3 INAF, Osservatorio di Astrofisica e Scienza dello Spazio, Via Pietro Gobetti 93/3, 40129 Bologna, Italy
4 INFN, Sezione di Bologna, viale Berti Pichat 6/2, 40127 Bologna, Italy
5 INAF, Osservatorio Astronomico di Trieste, Via Tiepolo 11, 34131 Trieste, Italy
6 Dipartimento di Fisica dell’Università di Trieste, Sezione di Astromia, Via Tiepolo 11, 34131 Trieste, Italy
7 IRAP, Université de Toulouse, CNRS, CNES, UPS, Toulouse, France
8 INAF – IASF Milano, Via E. Bassini 15, 20133 Milano, Italy
9 Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 40131 Hamburg, Germany
10 Department of Astrophysical Sciences, Princeton University, 4 Ivy Lane, Princeton, NJ, 08544-1001, USA
11 INAF-Osservatorio Astronomico di Brera, Via E. Bianchi 46, 23807 Merate, Italy
12 Dipartimento di Fisica, Università degli Studi di Roma “Tor Vergata”, Via della Ricerca Scientifica 1, 00133 Roma, Italy
13 Center for Astronomy, Institute for Theoretical Astrophysics, Heidelberg University, Philosophenweg 12, 69120 Heidelberg, Germany
Received:
30
April
2018
Accepted:
4
October
2018
Galaxy clusters are the endpoints of structure formation and are continuously growing through the merging and accretion of smaller structures. Numerical simulations predict that a fraction of their energy content is not yet thermalized, mainly in the form of kinetic motions (turbulence, bulk motions). Measuring the level of non-thermal pressure support is necessary to understand the processes leading to the virialization of the gas within the potential well of the main halo and to calibrate the biases in hydrostatic mass estimates. We present high-quality measurements of hydrostatic masses and intracluster gas fraction out to the virial radius for a sample of 13 nearby clusters with available XMM-Newton and Planck data. We compare our hydrostatic gas fractions with the expected universal gas fraction to constrain the level of non-thermal pressure support. We find that hydrostatic masses require little correction and infer a median non-thermal pressure fraction of ∼6% and ∼10% at R500 and R200, respectively. Our values are lower than the expectations of hydrodynamical simulations, possibly implying a faster thermalization of the gas. If instead we use the mass calibration adopted by the Planck team, we find that the gas fraction of massive local systems implies a mass bias 1 − b = 0.85 ± 0.05 for Sunyaev–Zeldovich-derived masses, with some evidence for a mass-dependent bias. Conversely, the high bias required to match Planck cosmic microwave background and cluster count cosmology is excluded by the data at high significance, unless the most massive halos are missing a substantial fraction of their baryons.
Key words: X-rays: galaxies: clusters / large-scale structure of Universe / galaxies: clusters: intracluster medium / galaxies: clusters: general
© ESO 2019
1. Introduction
Galaxy clusters form hierarchically through the merging of smaller halos throughout cosmic time. The gravitational energy released during cluster mergers is responsible for heating the intracluster medium (ICM) to the very high temperatures observed in today’s clusters. The kinetic energy developed by merging subunits while falling into the main cluster is progressively dissipated into heat and the plasma is virialized, thereby forming ever more massive systems (e.g. Kravtsov & Borgani 2012). Although we expect that the majority of the energy in today’s clusters is virialized, the timescale over which the kinetic energy is dissipated is currently unknown. Hydrodynamical simulations predict that non-thermal processes in the form of turbulence, bulk motions, magnetic fields or cosmic rays contribute at the level of ∼15 − 30% to the pressure support in present-day galaxy clusters (Lau et al. 2009; Vazza et al. 2009; Battaglia et al. 2012; Nelson et al. 2014; Shi et al. 2015; Biffi et al. 2016). In the case of substantial non-thermal pressure, the hydrostatic masses estimated under the assumption that the kinetic energy is fully thermalized should be biased low (e.g. Rasia et al. 2006; Nagai et al. 2007; Nelson et al. 2012; Shi et al. 2016; Khatri & Gaspari 2016). Non-thermal pressure would also affect the measured thermodynamic properties of the ICM by reducing the fraction of energy that is thermalized (Kawaharada et al. 2010; Fusco-Femiano & Lapi 2013).
Observationally, the integrated non-thermal pressure fraction is difficult to measure. While the fraction of energy contained within magnetic fields and cosmic rays is known to be small (≲1%, e.g. Brunetti & Jones 2014; Huber et al. 2013; Ackermann et al. 2014), the kinetic energy content in the form of bulk motions and turbulence is currently unknown. Indeed, while the exquisite spectral resolution of the Hitomi spacecraft allowed us to assess directly the presence of bulk and turbulent motions for the first time (Hitomi Collaboration 2016, 2018) in the Perseus cluster, setting an upper limit of 4% on the turbulent-to-thermal energy ratio, the measurement was limited to a small fraction of the cluster’s volume in the cluster core, where the non-thermal pressure fraction is expected to be small, especially in relaxed systems.
An alternative way of estimating the integrated contribution of non-thermal pressure is to look for deviations of ICM quantities (gas fraction, entropy) from the predictions of simple gravitational collapse. In particular, the total baryon fraction of massive clusters is one of the most robust quantities derived in cosmological simulations (White et al. 1993; Evrard 1997; Kravtsov et al. 2005; Mantz et al. 2014). Since massive local clusters originate from the collapse of very large regions of the early Universe (∼30 comoving Mpc at z ∼ 2, Muldrew et al. 2015), their composition should be representative of the Universe as a whole, with little scatter. Recent simulations confirm that while the gas and stellar fractions strongly depend on the adopted baryonic physics (cooling, star formation, feedback from supernovae and active galactic nuclei), the total baryonic fraction of massive clusters is nearly independent of the adopted baryonic setup (Planelles et al. 2013; Le Brun et al. 2014; Sembolini et al. 2016a,b). Thus, the baryon fraction of the most massive local clusters can be used to test the validity of the hydrostatic equilibrium assumption and estimate the integrated non-thermal pressure fraction (Ghirardini et al. 2018).
In this paper, we use high-precision hydrostatic masses obtained from the XMM-Newton cluster outskirts project (X-COP; Eckert et al. 2017a) out to R2001 to estimate the level of non-thermal pressure. We present a high-confidence estimate of the universal gas fraction of galaxy clusters and use our assessment of the universal gas fraction to probe the level of systematics in our hydrostatic mass measurements. We apply the same technique to examine potential systematics in the mass calibration adopted by the Planck team to derive cosmological parameters from Sunyaev–Zeldovich (SZ) cluster counts, which has resulted in the well-known tension between cosmic microwave background (CMB) and cluster counts (Planck Collaboration XXIV 2016). In companion papers we present our measurements of the thermodynamic properties of X-COP clusters (Ghirardini et al. 2019) and our high-precision hydrostatic mass estimates (Ettori et al. 2019).
The paper is organized as follows. In Sect. 2 we present the dataset and the methods used to derive gas fraction profiles. In Sect. 3 we estimate the universal gas fraction and describe the method we used to derive the non-thermal pressure fraction. Our results are presented in Sect. 4 and discussed in Sect. 5.
Throughout the paper, we assume a ΛCDM cosmology with Ωm = 0.3, ΩΛ = 0.7 and H0 = 70 km s−1 Mpc−1. We note that since our clusters are local (z < 0.1) the results have a very mild dependence on the adopted cosmology.
2. Data analysis
2.1. The X-COP sample
X-COP (Eckert et al. 2017a) is a very large program on XMM-Newton (proposal ID 074441, PI: Eckert) designed to advance our understanding of the physics of the ICM throughout the entire cluster volume. It targets 12 local, massive galaxy clusters selected from the Planck all-sky SZ survey. The selected clusters are the most significant Planck detections (S/N > 12 in the PSZ1 sample, Planck Collaboration XXIX 2014) in the redshift range 0.04 < z < 0.1. The selected systems span a mass range 3 × 1014 M⊙ < M500 < 1.2 × 1015 M⊙. The high signal-to-noise ratio of our clusters in the Planck survey allows us to perform a joint analysis of the X-ray and SZ properties of X-COP clusters and to extend our reconstruction of the properties of the ICM out to the virial radius. Detection at the virial radius is achieved both in X-rays and in SZ for 11 out of 12 objects. In the remaining case (A3266), the XMM-Newton mosaic does not extend far enough to cover all the way out to R200.
In Ghirardini et al. (2019) we present in detail our data analysis technique. Here we briefly summarize the main steps of the procedure.
-
The XMM-Newton data are processed using the XMMSASv13.5 software and the extended source analysis software (ESAS) package (Snowden et al. 2008). Count images, exposure maps, and particle background maps are extracted in the [0.7 − 1.2] keV band to maximize the source-to-background ratio (Ettori et al. 2010). To model the contribution from soft protons, we follow the procedure described in Ghirardini et al. (2018; see Appendix A). We used a large set of ∼500 blank-sky pointings to show that this procedure leads to an overall precision of ∼3% on the subtraction of the background in the [0.7 − 1.2] keV band.
-
SZ pressure profiles are extracted from the Plancky-maps extracted with the MILCA algorithm (Hurier et al. 2013) on the multifrequency information provided by the high-frequency instrument (HFI) from all the available Planck data. The procedure for the extraction of the pressure profiles closely follows Planck Collaboration Int. V (2013).
-
XMM-Newton spectra are extracted in concentric annuli out to ∼R500 using the ESAS package. We apply a full-blown modeling technique to determine the source parameters, simultaneously fitting source and background spectra to determine the contribution of each background component jointly (quiescent particle background cosmic X-ray background, Galactic foregrounds, and soft protons). A single-temperature APEC model (Smith et al. 2001) is used to describe the plasma emissivity, leaving temperature, normalization and metal abundance as free parameters. Temperature profiles are then constructed by fitting the full spectral model to the observed spectra.
-
Gas density profiles are reconstructed from the X-ray maps using the azimuthal median method proposed by Eckert et al. (2015). Binned surface-brightness maps are constructed using an adaptive Voronoi tessellation algorithm to ensure a minimum of 20 counts per bin. To reconstruct gas emissivity profiles that are unbiased by the presence of accreting clumps, we determine the median of the surface-brightness distributions in concentric annuli (Eckert et al. 2015).
For more details on the analysis procedure, we refer the reader to Ghirardini et al. (2019).
2.2. Hydrostatic masses and gas fraction
Our hydrostatic mass measurements and the procedure to obtain them are described in detail in Ettori et al. (2019). We use as our reference mass model the “backward NFW” model (Ettori et al. 2010), which describes the mass profile using a Navarro-Frenk-White (NFW; Navarro et al. 1996) model. We assume that the ICM is in hydrostatic equilibrium (HSE) within the potential well and that the kinetic energy has been fully converted into thermal energy, in which case the HSE equation reads
with Pgas, ρgas the pressure and density of the ICM, G the gravitational constant and MHSE the total hydrostatic mass enclosed within a radius r. We use the multiscale technique introduced in Eckert et al. (2016) to deproject the gas density profile. The concentration and scale radius of the NFW profile and the parameters describing the gas density profile are fit jointly to the measured thermodynamic quantities (X-ray emissivity, spectroscopic X-ray temperature, and SZ pressure) and the global likelihood is sampled using the Markov chain Monte Carlo (MCMC) sampler emcee (Foreman-Mackey et al. 2013). The high statistical quality of the X-COP data results in relative uncertainties of around 5% on MHSE. In Ettori et al. (2019) we compare our results with several other methods to reconstruct the hydrostatic mass (forward fitting, Gaussian processes) and show that all the methods provide consistent results. We also compare our mass estimates with literature values obtained using weak lensing, caustics and integrated SZ signal and find a good agreement between the various methods.
At each radius, we integrate the model gas density profiles to determine the enclosed gas mass,
where ρgas = μmp(ne + np), with ne = 1.17np the number densities of electron and proton in a fully ionized gas, μ = 0.61 the mean molecular weight, and mp the mass of the proton. The hydrostatic gas fraction profiles are then computed as fgas, HSE(r)= Mgas(< r)/MHSE(< r). In Fig. 1 we show the hydrostatic gas fraction profiles as a function of the scale radius R500, HSE for the 13 X-COP clusters. The radial range of each profile corresponds to the regions for which information on both the density and the pressure are available. For 10 objects out of 13 our gas fraction profiles extend out to R200 without requiring any extrapolation. The typical statistical uncertainties in fgas, HSE are ∼5% at R500 and ∼10% at R200. In the case where our measurements do not extend all the way out to R200 (A3266), the NFW mass model is extrapolated out to R200 to estimate the values of fgas, HSE.
 |
Fig. 1. Hydrostatic gas fraction profiles fgas, HSE(R)=Mgas(< R)/MHSE(< R) as a function of scale radius R/R500 for the X-COP clusters. The gray shaded area shows the Planck universal baryon fraction Ωb/Ωm (Planck Collaboration XIII 2016). |
3. Methodology
3.1. Universal gas fraction
As described in the introduction, the gas fraction of galaxy clusters is a fundamental prediction of cosmological simulations. In this section we review the current knowledge on the universal gas fraction and provide an assessment of the expected true gas fraction. We also conservatively discuss the associated uncertainties.
In a general way, the universal gas fraction within a given radius can be written as
with Yb(r) the baryon depletion factor, Ωb/Ωm the universal baryon fraction, and f⋆ the fraction of baryons converted into stars. Baryons in other forms such as warm and molecular gas or dust typically represent less than 0.1% of the mass content of a galaxy cluster (e.g. Edge et al. 2002; Salomé & Combes 2003) and for the present study we neglect their contribution. The universal baryon fraction is determined with very high precision by the CMB power spectrum. Here we assume the Planck value Ωb/Ωm = 0.156 ± 0.003 (Planck Collaboration XIII 2016). This value is slightly lower than, although consistent with, the WMAP9 measurement (0.166 ± 0.009, Hinshaw et al. 2013). The baryon depletion factor encodes the fraction of the baryons that is enclosed within a given radius; Yb = 1 implies no depletion. We expect from numerical simulation that its value at large cluster-centric radii depends very little on the adopted physical setup, such that the value of Yb can be calibrated using numerical simulations. Finally, the stellar fraction has been the subject of many studies and its value is well known. In the following we provide estimates of Yb and f⋆.
3.1.1. Baryon depletion factor
The baryon depletion factor Yb integrated over large fractions of the cluster volume is one of the quantities most robustly predicted by numerical simulations. A recent comparison of 13 different codes including modern and legacy SPH and grid codes (Sembolini et al. 2016a,b) shows that codes implementing vastly different hydrodynamical solvers and baryonic physics make very consistent predictions on the baryon budget integrated within the virial radius, whereas in the inner regions (R ≲ 0.5R500) different codes and simulation setups lead to substantial differences in the predicted baryon fraction.
In the present work, we utilize simulated clusters with masses in the X-COP range extracted from The Three Hundred Project simulations (hereafter The300, Chiu et al. 2018). This project comprises zoom-in re-simulations of more than 300 Lagrangian regions, of 15 − 20 h −1 Mpc radius, centered on the most massive cluster-size halos selected from one of the dark-matter-only MultiDark Simulation run carried out with Planck cosmology (Planck Collaboration XIII 2016). All the regions have been re-simulated at higher resolution (with dark matter particle mass around 2 × 109 M⊙) with a modified version of the Smoothed-Particle-Hydrodynamics GADGET-3 code Springel (2005). The re-simulations include the treatment of a large variety of physical processes to describe the baryonic component, such as gas cooling and star formation, chemical enrichment, stellar, and active galactic nuclei (AGN) feedback (see Rasia et al. 2015 and references therein for a more detailed description of the hydrodynamical code used, and Cui et al. (in prep.), for details on the re-simulation technique.
Thanks to the large statistics afforded by these simulations, we can constrain the value of Yb and its scatter with good precision. In Fig. 2 we show the measurements of Yb at R500 for the whole sample of simulated clusters. As noted in previous studies (e.g. Planelles et al. 2013), the value of Yb is typically 5 − 10% lower than 1, a value that is reached at a few times the virial region (see also Kravtsov et al. 2005). For masses M500 ≥ 2 × 1014 M⊙, the baryon depletion factor is approximately constant albeit with a large scatter. Smaller systems are instead largely influenced by the active galactic nuclei activity that on the one hand pushes out the hot gas and on the other hand quenches star formation, consequentially reducing both baryonic components. If we restrict our analysis to the subsample of 295 systems with masses M500 > 3 × 1014 M⊙, corresponding to the X-COP mass range, we obtain a median depletion factor of 6.2% at R500 and 4.9% at R200. The median, 1σ percentiles, and extreme values of Yb at R500 and R200 are provided in Table 1.
 |
Fig. 2. Baryon depletion factor Yb at R500 for the clusters in The300 simulation (filled circles). The blue points show the objects with a mass M500 > 3 × 1014 M⊙. The hashed gray shaded area shows the mass range covered by X-COP clusters and our determination of the universal baryon depletion factor and its scatter. |
Baryon depletion factor in the simulated clusters from the clusters in The300 project with M500 > 3 × 1014 M⊙.
3.1.2. Stellar fraction
While the ICM is known to contain the vast majority of the baryons in galaxy clusters, a fraction of the baryons are locked into stars, both inside galaxies and in the form of intracluster light (ICL; Zibetti et al. 2005; Budzynski et al. 2014; Montes & Trujillo 2014). Predicting the exact number of stars in numerical simulations is a difficult endeavor; the star formation rate and its evolution depend critically on the adopted setup describing gas cooling and feedback from supernovae and AGN (e.g. Kravtsov et al. 2005). However, the stellar content of galaxy clusters has been extensively studied in the literature (Giodini et al. 2009; Gonzalez et al. 2007, 2013; Laganá et al. 2013; Andreon 2010; Chiu et al. 2018) and the stellar fraction can be robustly set to its observed value.
In Fig. 3 we present a compilation of recent results on the stellar fraction of dark-matter halos as a function of their mass. Results obtained by directly integrating the stellar mass of member galaxies (Giodini et al. 2009; Gonzalez et al. 2013; Laganá et al. 2013; Andreon 2010; Chiu et al. 2018) and from the halo occupation distribution (Leauthaud et al. 2012; Coupon et al. 2015; Zu & Mandelbaum 2015; Eckert et al. 2016) are compared. While the results obtained with the two methods differ substantially in the galaxy group regime (M500 ≲ 1014 M⊙), in the mass range covered by X-COP clusters (3 × 1014 < M500 < 1.2 × 1015 M⊙) all studies are broadly consistent and converge to a median stellar fraction of 1.2%, with the notable exception of Giodini et al. (2009). The contribution of ICL was included in some, but not all cases; measurements indicate that ICL can account for ∼20 − 30% (Lin & Mohr 2004; Zibetti et al. 2005) of the total stellar mass. To encompass the uncertainty associated with the ICL fraction and with the various studies shown in Fig. 3, for the present study we conservatively set the value of the stellar fraction to
 |
Fig. 3. Stellar fraction within R500 estimated in several works from the literature. The hashed grey area represents the mass range of X-COP clusters and the range of f⋆ adopted in this work. |
Beyond the central regions the stellar fraction has been shown to be nearly constant (Andreon 2015; van der Burg et al. 2015), thus we adopt the same value for f⋆, 200.
Combining the results from the two previous sections through Eq. (3), we estimate the following values for the universal gas fraction:
The errors reported here include both the actual uncertainties in Ωb/Ωm and f⋆ and the measured scatter in Yb.
3.2. Non-thermal pressure fraction
Since our X-ray emissivity profiles are corrected for the effects of gas clumping (Eckert et al. 2015) down to the limiting resolution of our observations (10 − 20 kpc), we expect that residual deviations of the gas mass fraction with respect to the universal gas fraction should be caused by an additional, non-thermal pressure component. In the presence of isotropic non-thermal pressure, the hydrostatic equilibrium equation can be generalized as
with Pth and PNT the thermal and non-thermal pressure components, respectively. We set α(r)=PNT(r)/Ptot(r) the non-thermal pressure fraction, i.e. 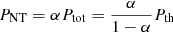 . Using this formulation, Eq. (6) can be rewritten as
. Using this formulation, Eq. (6) can be rewritten as
with 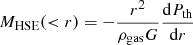 . The gas fraction as a function of radius can be written as
. The gas fraction as a function of radius can be written as
Thus, if the true gas fraction is known, the non-thermal pressure fraction α(r) can be estimated by comparing the measured fgas, HSE with the universal value (Ghirardini et al. 2018).
For α(r) we use the functional form introduced by Nelson et al. (2014),
with A, B, and γ being free parameters. This functional form was shown to reproduce the behavior of the non-thermal pressure fraction in the simulations of Nelson et al. (2014) and should be approximately valid in the range [0.3 − 2]R200. For the present work, we fix B = 1.7 to the best-fitting The300 simulation value. We note that when α(r) is constant this quantity is simply equal to the usual hydrostatic bias b = 1 − MHSE/Mtot.
As already discussed in Sect. 3.1, the gas fraction predicted by various simulations was found to be consistent (Sembolini et al. 2016a,b), including the setup used here (labelled G3X in Sembolini et al. 2016b). However, the predictions diverge in the inner regions (see their Fig. 10). Thus, we focus on the gas fraction at large radii to compare fgas, HSE to fgas, univ and determine the parameters of α(r). We set the universal gas fraction at R500 and R200 to the values derived in Sect. 3.1, and solve numerically Eq. (8) for the parameters A and γ. Since this procedure results in a corrected estimate for M500 and M200, we iteratively repeat the procedure with the revised mass estimates until it converges.
We use the output MCMC chains of our mass models to propagate the uncertainties in fgas, HSE into our estimate of α(r). We also propagate the dispersion and uncertainties in the universal gas fraction (see Sect. 3.1) by randomizing the value of fgas in Eq. (8). The best-fit curves for α(r) are then computed from the posterior distributions of the parameters.
4. Results
4.1. Non-thermal pressure fraction in X-COP clusters
In Fig. 4 we show the values of fgas, HSE for the 13 X-COP clusters at R500, HSE and R200, HSE compared to the universal baryon fraction (Planck Collaboration XIII 2016) and the universal gas fraction predicted from the The300 simulation. With the exception of A2319 (Ghirardini et al. 2018), for which a substantial non-thermal pressure support was clearly detected, at R500 our measurements of fgas, HSE lie very close to the universal gas fraction, although ∼7% higher on average (median fgas, 500 = 0.141 ± 0.005, with 12% scatter), implying a mild contribution of non-thermal pressure. Conversely, at R200, the majority of the measurements (9 out of 12) slightly exceed the universal gas fraction (median 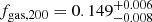 ). With just two exceptions (A3266 and ZwCl 1215), the gas fraction of all systems is at least as large as our determination of the Universal gas fraction.
). With just two exceptions (A3266 and ZwCl 1215), the gas fraction of all systems is at least as large as our determination of the Universal gas fraction.
 |
Fig. 4. Hydrostatic gas fractions at R500, HSE (blue points) and R200, HSE (red points) obtained from our reference hydrostatic mass model as a function of cluster mass. The dashed magenta line and shaded area represent the universal gas fraction at R500 estimated in Sect. 3.1 and its uncertainty. The green shaded area indicates the cosmic baryon fraction (Planck Collaboration XIII 2016). |
To investigate any dependence of the measured gas fraction on the core state, we split our sample into cool core (CC) and non-cool core (NCC) classes based on their central entropy K0 as measured by Chandra (Cavagnolo et al. 2009) because of its higher resolution in the core, using a threshold of 30 keV cm2 as a boundary between the two populations. Using this definition, four of our systems are classified as CC, and the remaining eight as NCC. At R500, we estimate median values fgas, CC = 0.142 ± 0.006 and fgas, NCC = 0.141 ± 0.008, i.e. there is no difference in the hydrostatic gas fraction of the two subpopulations. The values of fgas, HSE in the NCC population appear to be more scattered than in the CC population (15% versus < 7%). However, the small number of objects in our sample makes it difficult to make any strong statistical claim about the scatter of the two populations.
We used the distribution of output values for the parameters of the non-thermal pressure fraction (Eq. (9)) to determine the non-thermal pressure fraction at R500 and R200. The normalization of the non-thermal pressure term A in Eq. (9) is usually well determined and lies in the range 0.4 − 0.8 (median 0.65). The slope γ is poorly constrained, however, given that we are constraining it using only two anchor points (R500, R200). In the cases where no modification to the gas fraction was required we computed upper limits at the 90% confidence level. In Table 2 we provide our measurements of the hydrostatic gas fraction, of the non-thermal pressure ratio, and of the total cluster masses after applying the method described in Sect. 3.2 (hereafter labeled Mtot). The uncertainties on PNT were propagated to the estimated total mass using the MCMC chain (see Sect. 3.2). In the cases where no evidence of non-thermal pressure was found, Mtot is just equal to MHSE.
Hydrostatic gas fraction, non-thermal pressure fraction, and total (bias-corrected) masses at R500 and R200 in X-COP clusters.
In Fig. 5 we show the non-thermal pressure fractions at R500 and R200 for the entire X-COP sample. We immediately see that in the vast majority of cases non-thermal support in X-COP clusters is mild. We use a bootstrap method to compute the median of the distribution and the uncertainties on the median. We find a median non-thermal pressure of 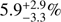 and
and 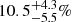 at R500 and R200, respectively. For comparison, in Fig. 5 we show the average non-thermal pressure ratio in two sets of numerical simulations (Ω500, Nelson et al. 2014; The300, Rasia et al., in prep.), with the scatter of the population indicated as the shaded areas. Assuming that the non-thermal pressure support is due to random gas motions, the level of non-thermal pressure in numerical simulations was defined as the ratio of the pressure induced by random motions
at R500 and R200, respectively. For comparison, in Fig. 5 we show the average non-thermal pressure ratio in two sets of numerical simulations (Ω500, Nelson et al. 2014; The300, Rasia et al., in prep.), with the scatter of the population indicated as the shaded areas. Assuming that the non-thermal pressure support is due to random gas motions, the level of non-thermal pressure in numerical simulations was defined as the ratio of the pressure induced by random motions 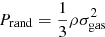 to the sum of random and thermal pressure (Nelson et al. 2014; Biffi et al. 2016),
to the sum of random and thermal pressure (Nelson et al. 2014; Biffi et al. 2016),
 |
Fig. 5. Non-thermal pressure fraction in X-COP clusters at R500 and R200. The positions on the x-axis are slightly shifted for clarity. The blue and green curves and shaded areas show the mean non-thermal pressure ratio predicted from the numerical simulations of Nelson et al. (2014) and Rasia et al. (in prep.), respectively. |
with σgas the velocity dispersion of gas particles in spherical shells, k the Boltzmann constant, μ the mean molecular weight and mp the proton mass. Interestingly, most of our measurements lie substantially below the Nelson et al. (2014) curve, possibly indicating a higher level of thermalization in the real population compared to the simulations. A somewhat lower level of non-thermal pressure is predicted in the The300 simulation, in better agreement with our results. We discuss this comparison in further detail in Sect. 5.2.
4.2. Impact of missing clusters and sample selection
While the selection of the X-COP sample was designed to be fairly clean (see Sect. 2.1), our original selection excluded four systems for which we were unsure whether the strategy adopted for the project could be applied. This includes clusters with obvious substructures, aspherical morphology, bad visibility for XMM-Newton, or an apparent size barely larger than the Planck beam (see Sect. 2.1 of Ghirardini et al. 2019). Two of these systems (A754 and A3667) are extreme mergers which may deviate substantially from hydrostatic equilibrium in a way similar to A2319, thus the average level of non-thermal pressure support in our sample may be biased by the exclusion of these objects. To investigate the potential impact of these systems on our results, we assumed that these two missing objects show a level of non-thermal pressure similar to that of A2319 and that the remaining two are representative of the population. Such a choice has no influence on the median non-thermal pressure fraction, but increases the mean value from 9% to 13% at R500. We can thus conclude that our analysis sets an upper limit of 13% to the mean level of non-thermal pressure in the Planck cluster population. We were recently allocated observing time on XMM-Newton (PI: Ghirardini) to extend the X-COP strategy to the missing objects discussed here, which will allow us to set firm limits on the level of non-thermal pressure support.
Another issue that cannot be addressed with the current X-COP sample is any possible evolution of non-thermal pressure and hydrostatic mass bias with redshift. Nelson et al. (2014) showed that the expected level of non-thermal pressure is expected to increase substantially with redshift when scaled by the critical density (see also Shi et al. 2016). By design, the X-COP sample was selected to contain only systems that are well resolved by Planck, which limits our study to local (z < 0.1) systems. Further studies with higher resolution SZ data (e.g. NIKA2, MUSTANG2) will allow us in the near future to test whether the findings reported here can be applied to clusters located at higher redshifts.
4.3. Comparison with Planck SZ masses
Following the discovery of the tension between Planck CMB cosmology and SZ number counts (Planck Collaboration XXIV 2016), considerable effort has been devoted to evaluating the accuracy of the mass calibration adopted by the Planck collaboration. Planck SZ masses were derived from a relation between SZ flux YSZ and total mass that was calibrated using XMM-Newton HSE masses. Biases in the estimation of the mass might arise from the potential impact of non-thermal pressure in the calibration sample, from uncertainties in the calibration of the XMM-Newton effective area and/or from the measurement of the total SZ flux from Planck data. Cosmological constraints from Planck CMB and cluster counts could be reconciled in the case where the YSZ − M500 relation adopted by the Planck team is biased low by a factor 1 − b = MSZ/Mtrue = 0.58 ± 0.04, presumably because of strong non-thermal pressure support (Rasia et al. 2006; Nagai et al. 2007). Numerous studies have addressed this issue by directly comparing masses derived using X-ray and weak lensing techniques (e.g. Hoekstra et al. 2015; von der Linden et al. 2014; Smith et al. 2016), resulting in somewhat divergent values for the Planck mass bias (1 − b in the range 0.7–1.0, Sereno & Ettori 2015). Here we take a different route and combine our high-quality measurements of hydrostatic masses with our robust assessment of the universal gas fraction to probe the reliability of Planck SZ masses. If SZ masses are incorrect, we expect the corresponding gas fractions to deviate from the universal gas fraction, which can be easily tested with our data.
We retrieved the masses of X-COP clusters from the PSZ2 catalog (Planck Collaboration XXVII 2016) and determined the value of R500, SZ accordingly. We recall that the PSZ2 masses were determined by applying a relation between SZ signal Y500 and total mass M500, SZ calibrated using HSE masses (Planck Collaboration XI 2011). ZwCl 1215 does not have an associated mass in PSZ2 because of the mask used (point sources and Galactic cuts, see Sect. 6.3 in Planck Collaboration XXVII 2016), thus in this case we use the mass provided in PSZ1. Although the SZ mass estimate for ZwCl 1215 is low, there is no contaminating point source at radio or submillimeter wavelengths that could bias the SZ signal. However, the overall consistency between the PSZ1 and PSZ2 mass proxy and mass estimates provided by Planck Collaboration XXIX (2014), Planck Collaboration XXVII (2016) cannot account for features or structures intrinsic to the cluster.
We integrated our gas masses out to R500, SZ and computed the corresponding values of fgas, SZ. We repeated the exercise by correcting the PSZ2 masses assuming a mass bias 1 − b = 0.58 ± 0.04, and derived the corresponding gas fractions. In Fig. 6 we show the gas fractions determined using the hydrostatic equilibrium assumption (see Table 2) as a function of total cluster masses corrected for non-thermal pressure support. We also show the gas fractions fgas, SZ measured from the PSZ2 masses and from the masses corrected to reconcile CMB and SZ number count cosmology.
 |
Fig. 6. Intracluster medium gas fraction at R500 obtained from our reference hydrostatic-based mass model (blue squares) as a function of the total mass corrected for non-thermal pressure support (see Sect. 4.3). The red points show the gas fraction obtained using the Planck PSZ2 masses estimated from the YSZ − M500 relation (Planck Collaboration XXVII 2016), whereas the green triangles show the gas fraction that would be obtained by correcting the PSZ2 masses with a uniform mass bias 1 − b = 0.58 ± 0.04 (Planck Collaboration XXIV 2016). The dashed magenta line and shaded area represent the universal gas fraction estimated in Sect. 3.1. |
In Fig. 6 we can clearly see that the gas fraction of X-COP clusters exceeds the expected value when the Planck masses are assumed to be correct. The median gas fraction is 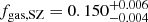 , i.e ∼15% higher than the universal gas fraction. We also notice a trend of increasing gas fraction with cluster mass, which may indicate a mass-dependent bias. Conversely, when correcting the SZ masses by a factor 1 − b = 0.58 the gas fraction is substantially lower than expected, with a median value fgas, 1 − b = 0.58 = 0.108 ± 0.006. All objects but one would lie outside of the allowed range for fgas, univ. Reconciling CMB and SZ cosmology would thus imply that the most massive local clusters are missing about a third of their baryons.
, i.e ∼15% higher than the universal gas fraction. We also notice a trend of increasing gas fraction with cluster mass, which may indicate a mass-dependent bias. Conversely, when correcting the SZ masses by a factor 1 − b = 0.58 the gas fraction is substantially lower than expected, with a median value fgas, 1 − b = 0.58 = 0.108 ± 0.006. All objects but one would lie outside of the allowed range for fgas, univ. Reconciling CMB and SZ cosmology would thus imply that the most massive local clusters are missing about a third of their baryons.
As shown in Fig. 6, measurements of fgas, 500 are very sensitive to the adopted mass calibration and thus they can be used to assess systematics in the Planck mass calibration. We compared our masses corrected for non-thermal pressure support under the assumption of a universal gas fraction (see Table 2) to the Planck SZ-derived masses. In Fig. 7 we show the ratio of SZ masses to total masses. We measure a median value 1 − b = M500, SZ/M500, tot = 0.85 ± 0.05 for the Planck mass bias in our systems. This value could be increased by 3 − 15% to take Eddington bias into account (Battaglia et al. 2016). As noted in several previous studies (von der Linden et al. 2014; Ettori 2015), we observe a substantial mass dependence of the SZ mass bias, with the most massive objects (M500 ∼ 1015 M⊙) being biased at the ∼25% level, while for M500 ∼ 4 × 1014 M⊙ SZ masses appear to be unbiased. For comparison, in Fig. 7 we also show the ratio of our direct HSE measurements to the masses corrected for non-thermal pressure support. In this case, we find that with the notable exception of A2319 our masses require little correction, with a median bias M500, HSE/M500, tot = 0.94 ± 0.04.
 |
Fig. 7. Comparison between HSE (blue squares)/SZ (red dots) and total masses corrected for non-thermal pressure as a function of mass. The magenta line and shaded area show our best fit to the SZ data with a power law, whereas the green area displays the expectation for a constant mass bias 1 − b = 0.58 ± 0.04. |
To assess the dependence of the Planck bias on the mass, we describe the relation between SZ mass and total mass as a power law and use the Bayesian mixture model code linmix_err (Kelly 2007) to fit the data. The resulting parameters read
i.e. a mass dependence is detected at ∼2σ. The best-fitting curve and error envelope are displayed in Fig. 7. A high, constant bias 1 − b = 0.58 ± 0.04 is rejected at the 4.4σ level for the specific case of the 12 X-COP clusters. We note that the value estimated here for the Planck mass bias encompasses all possible kinds of biases in the original Planck mass calibration (not restricted to hydrostatic bias), as the gas fractions computed using SZ masses were calculated using the original M500 − YSZ relation.
5. Discussion
5.1. Systematic uncertainties
Beyond uncertainties associated with the determination of the universal gas fraction (see Sect. 3.1), our results can also be affected by potential systematics in our measurements of fgas, HSE. Here we review potential sources of systematic uncertainties.
-
Reconstruction of MHSE: As described in Sect. 2.2, we adopt as our reference mass reconstruction method the backward NFW method (Ettori et al. 2010), which assumes that the mass profile can be accurately described by a NFW parametric form. However, this method may be inaccurate if the true mass distribution differs substantially from NFW. In Ettori et al. (2019) we compare the results obtained with our reference backward NFW method with the results obtained with methods that do not make any assumption on the shape of the dark matter halo (forward fitting, Gaussian processes). We find that the results obtained with the various methods agree within ∼5% at a radius of 1.5 Mpc, with the NFW method returning on average slightly higher masses. This propagates to a systematic uncertainty of ∼5% on the hydrostatic gas fraction, and thus on the non-thermal pressure fraction.
-
Gas mass measurements: The gas mass of local clusters is one of the quantities that can be most robustly computed from X-ray observations. Studies on mock X-ray observations of simulated clusters have shown that measurements of Mgas are accurate down to the level of a few percent and exhibit very little scatter, even in situations of violent mergers (Nagai et al. 2007; Rasia et al. 2011; Eckert et al. 2016). The measured gas densities tend to be biased high in cluster outskirts by the presence of accreting substructures and large-scale asymmetries (Mathiesen et al. 1999; Nagai & Lau 2011; Roncarelli et al. 2013), which introduces a systematic uncertainty of 5 − 10% on the true gas mass at R200. However, thanks to the use of the azimuthal median as a robust estimator of the surface brightness (Eckert et al. 2015), the bias introduced by infalling substructures has been taken into account in our study. Residual clumping on scales smaller than the resolution of our study (≲20 kpc) can still introduce a slight positive bias in our estimates of Mgas; however, we expect the residual effect to be less than a few percent.
-
Calibration uncertainties: Temperature measurements are known to be affected by systematics of the order of ∼15% in the high-temperature regime because of uncertainties in the calibration of the effective area of the instrument (Nevalainen et al. 2010; Schellenberger et al. 2015), with Chandra returning systematically higher gas temperatures than XMM-Newton. If Chandra temperatures are correct, our masses should be underestimated by ∼15%, meaning that our estimates of the non-thermal pressure should be overestimated. However, we note that our mass reconstruction makes use of joint XMM-Newton and Planck data. In the radial range where data from both instruments are available, we do not observe a systematic offset between X-ray and SZ pressure (see also Adam et al. 2017). While effective area calibration introduces some uncertainty in the recovered temperature, its effect on the gas density and gas mass is mild. Bartalucci et al. (2017) compared XMM-Newton and Chandra reconstructions of gas density profiles and gas masses and found an exquisite agreement between the two missions at the level of 2.5%.
-
Helium sedimentation: Several works suggest that helium nuclei can sediment within cluster cores (e.g. Ettori & Fabian 2006; Markevitch 2007; Peng & Nagai 2009). Helium abundance cannot be directly measured in the ICM, and it is assumed here. We cannot exclude that some sedimentation under the effect of the gravitational potential occurred and is biasing our estimates of the gas mass and total hydrostatic mass (e.g. Ettori & Fabian 2006). However, theoretical models predict that any possible rise in the He abundance by up to about 50% over the cosmic value (Peng & Nagai 2009) induces a bias of a few percent restricted to the inner (< R2500) cluster regions where sedimentation is more effective, thus not affecting our conclusion at R ≥ R500.
We note that most of the effects discussed here are potential positive biases in the reconstruction of fgas, HSE. If present, the measured hydrostatic gas fraction is thus more likely to be biased high, which would lower even the required non-thermal pressure and hydrostatic mass bias.
5.2. Implications on the thermalization of the ICM
As described in Sect. 4.1, our gas fraction data imply a low level of non-thermal pressure in our population, α = PNT/Ptot = 6% and 10% at R500 and R200, respectively. If we ascribe the excess gas fraction entirely to residual isotropic gas motions (Eq. (10)), we can relate the measured non-thermal pressure to the velocity dispersion by rewriting Eq. (10) as
with cs = (γkT/μmp)1/2 the sound speed in the medium, ℳ3D the Mach number of residual gas motions, γ = 5/3 the polytropic index, and α(r) the functional form for PNT/Ptot(r) following the definition of Eq. (9). The values estimated here thus imply an average Mach number at R500
i.e. isotropic gas motions in the X-COP cluster population are clearly subsonic. This value broadly agrees with the Mach numbers estimated from the amplitude of relative ICM fluctuations (Hofmann et al. 2016; Zhuravleva et al. 2015; Eckert et al. 2017b).
As shown in Fig. 5, our values are somewhat smaller than the predictions of non-radiative adaptive mesh refinement (AMR) simulations by Nelson et al. (2014) and closer to the curves extracted from the The300 simulation with the smoothed particle hydrodynamics (SPH) code GADGET-3. While in the past legacy SPH codes (employing a typically large artificial viscosity to handle shocks) tended to predict a more clumped and inhomogeneous ICM than grid codes did (Rasia et al. 2014), we observe the opposite here.
A few possible reasons can be given for this difference. First, to better reproduce standard hydrodynamics tests, the The300 simulation incorporates a number of advanced features compared to previous SPH codes, including a higher order Wendland C 4 kernel function, the implementation of a time-dependent artificial viscosity scheme, and artificial conduction (Beck et al. 2016). Compared to previous SPH codes, the SPH scheme included in the The300 leads to a more efficient mixing of the gas phases with different entropies. This promotes a faster thermalization of the accreting gas and of small merging substructures, thus reducing the non-thermal pressure fraction. On top of that, The300 simulation implements a wide range of baryonic processes (including radiative cooling, star formation, and AGN and supernova feedback) whereas the predictions of Nelson et al. (2014) are extracted from non-radiative simulations. The balance of cooling and AGN feedback implemented in these simulations substantially changes the appearance of galaxy- and group-scale halos by removing the most structured phase of the ICM from the X-ray emitting phase and by increasing their gas entropy, which leads to smoother and flatter density profiles compared to simulations without powerful feedback mechanisms. The AGN activity provides extra energy to the gas residing in the shallow potential well of small systems, further enhancing its mixing with the cluster ICM during, or immediately after, a merger. The subsequent clumping factor is thus reduced compared to the non-radiative case (Planelles et al. 2017) where the entropy difference between the medium and the denser, colder substructure is substantially greater. As a result, infalling motions get virialized on shorter timescales and the non-thermal pressure fraction is reduced.
It should be noted that the estimate of the non-thermal pressure support in the simulated ICM is by itself non-trivial, owing to the complexity of gas motions in the stratified cluster atmosphere. While all modern simulations overall agree on the predicted radial trend of turbulent motions moving from the cluster centers to the periphery (e.g. Vazza et al. 2011; Nelson et al. 2014; Miniati 2014; Biffi et al. 2016), their quantitative answer may change depending on the adopted filtering techniques to disentangle the various velocity components of the ICM (e.g. bulk motions, shock jumps and small-scale chaotic motions), which is particularly crucial in cluster outskirts (e.g. Vazza et al. 2017; Schmidt et al. 2017). For example, if motions along the radial direction are predominantly directed inwards, the missing pressure estimated with radial averages in simulations may overestimate the non-thermal pressure recovered here using the method devised in Sect. 3.2. More detailed comparisons using exactly the same technique as used here are necessary to test this hypothesis.
5.3. Implications for cosmology
The results presented in Sect. 4.3 have important implications for the use of galaxy clusters as cosmological probes. They imply that galaxy cluster masses derived under the assumption of hydrostatic equilibrium in a fully thermalized ICM require little correction from non-thermal pressure support, provided that the 12 X-COP clusters are representative of the Planck population. This conclusion is further supported by our direct comparison of hydrostatic and weak lensing masses when available (see Sect. 4 of Ettori et al. 2019), which finds a median ratio M500, HSE/M500, WL = 0.87 ± 0.10 and M200, HSE/M200, WL = 0.86 ± 0.13 for the six X-COP clusters with available weak lensing measurements, fully consistent with the non-thermal pressure and the mass ratio M500, HSE/M500, tot = 0.94 ± 0.04 estimated from the universal gas fraction method used here.
At face value, our results strongly disfavor a large hydrostatic bias as the origin of the tension in the Ωm − σ8 plane between SZ cluster counts and primary CMB. As shown in Fig. 6, our hydrostatic gas fraction measurements are very close to the values obtained with the Planck mass calibration, although we note a mildly significant trend of increasing bias in the Planck calibration with cluster mass. However, the median mass of the systems in the Planck cosmological sample is ∼5 × 1014 M⊙, where our analysis shows that the SZ masses are biased only at the 10% level. Although quantifying the exact impact of our results on the cosmological parameters is beyond the scope of this paper, it is fair to say that our study favors lower values of σ8 compared to primary CMB, similar to what was obtained from essentially all cluster count studies (Vikhlinin et al. 2009; de Haan et al. 2016) and weak lensing tomography studies (Heymans et al. 2013; Hildebrandt et al. 2017).
The conclusions reached here clearly rest on the premise that our determination of the universal gas fraction is accurate. As shown in Fig. 6, a large, constant hydrostatic bias would imply that the most massive galaxy clusters are missing about a third of their baryons. We also note that our estimate of the stellar fraction (Sect. 3.1.2) lies on the high side of the published measurements (see Fig. 3), thus our estimate of fgas is probably on the low side. Extreme AGN feedback would be required to push a substantial fraction of the baryons outside of R200, which would lead to high-entropy cores and large offsets from the observed scaling relations (e.g. Le Brun et al. 2014). High-resolution hydrodynamic simulations testing different AGN feedback models have shown that the feedback must be gentle and tightly self-regulated (e.g. Gaspari et al. 2014), thus affecting only the regions within ∼0.1R500. An extreme thermal/Sedov blast (∼1062 erg) would be required to evacuate a substantial fraction of the gas away from R500, which would transform any CC cluster into a NCC cluster, with cooling times well above the Hubble time. The gentle preservation of many cool cores up to redshift ∼2 (e.g. McDonald et al. 2017) rules out the strong and impulsive AGN feedback scenario. In the absence of evidence of such extreme phenomena, we conclude for the time being that our estimate of the universal gas fraction does not need to be revised.
6. Conclusion
In this paper, we presented high-precision measurements of the hydrostatic gas fraction from the X-COP project, a sample of 13 clusters with high-quality X-ray and SZ data from XMM-Newton and Planck. The statistical uncertainties in fgas, HSE are less than 10% in all cases and measurements at R200 are achieved for 10 out of 13 objects without requiring any extrapolation. We used our measurements to estimate the level of non-thermal pressure in our sample. Our results can be summarized as follows.
-
Combining a large set of clusters simulated with a state-of-the-art SPH code with literature measurements of the stellar fraction in observed clusters, we robustly estimate the universal gas fraction of massive clusters to be fgas, 500 = 0.131 ± 0.009 and fgas, 200 = 0.134 ± 0.007 at R500 and R200, respectively. The uncertainties quoted here include both statistical uncertainties and scatter in the simulated cluster population.
-
Our hydrostatic gas fractions are on average consistent with the estimated universal gas fraction, lying just 7% and 11% above the universal value at R500 and R200, respectively, with 12% scatter.
-
To determine the integrated level of non-thermal pressure support, we modified the hydrostatic equilibrium equation to incorporate the contribution of a non-thermal pressure term, which we describe using the parametric function of Nelson et al. (2014; see Sect. 3.2). The parameters of the non-thermal pressure component were then determined by comparing the measured hydrostatic gas fraction profiles with the universal gas fraction. Our procedure leads to revised mass measurements that incorporate the contribution of non-thermal pressure.
-
With the notable exception of A2319 (Ghirardini et al. 2018), the required levels of non-thermal pressure are mild, with median values PNT/Ptot(R500)∼6% and PNT/Ptot(R200)∼10%, with missing clusters possibly raising the non-thermal pressure fraction to a maximum of 13% at R500. These values are lower than the predictions of numerical simulations (Nelson et al. 2014; Biffi et al. 2016), possibly implying a faster thermalization of the kinetic energy in the real population compared to hydrodynamical simulations.
-
Assuming that the residual non-thermal pressure can be entirely ascribed to random gas motions, we infer an average Mach number
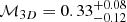 , implying that residual kinetic motions are clearly subsonic.
, implying that residual kinetic motions are clearly subsonic. -
We used our masses corrected for the effects of non-thermal pressure to test the accuracy of Planck SZ masses in our systems. We find that PSZ2 masses lead to an average gas fraction fgas, SZ = 0.150 ± 0.005 at R500, indicating that SZ masses are slightly underestimated. Comparing PSZ2 masses with our masses corrected for non-thermal pressure support, we infer a median bias 1 − b = 0.85 ± 0.05. As noted in previous studies (Ettori 2015; von der Linden et al. 2014), the bias appears to depend slightly on cluster mass,
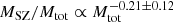 .
. -
If instead we assume that the PSZ2 masses are biased low by a constant factor MSZ/Mtrue = 0.58 ± 0.04 to reconcile Planck primary CMB and SZ cluster counts, the gas fraction of X-COP clusters would fall short of the universal baryon fraction (median fgas, 1 − b = 0.58 = 0.108 ± 0.006), implying that the most massive local clusters would be missing about one-third of their baryons. This would pose a serious challenge to our understanding of cluster formation processes and feedback energetics.
Acknowledgments
X-COP data products are available for download at https://www.astro.unige.ch/xcop. We thank Ricardo Herbonnet and Henk Hoekstra for providing us with their weak-lensing results in advance of publication, and the anonymous referee for helpful comments. The research leading to these results has received funding from the European Union’s Horizon 2020 Programme under the AHEAD project (grant agreement no. 654215). Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA. S.E. acknowledges financial contribution from contracts NARO15 ASI-INAF I/037/12/0, ASI 2015-046-R.0 and ASI-INAF n.2017-14-H.0. F.V. acknowledges financial support from the ERC Starting Grant “MAGCOW”, no.714196. M.G. is supported by NASA through Einstein Postdoctoral Fellowship Award Number PF5-160137 issued by the Chandra X-ray Observatory Center, which is operated by the SAO for and on behalf of NASA under contract NAS8-03060. Support for this work was also provided by Chandra grant GO7-18121X. E.R acknowledges the ExaNeSt and Euro Exa projects, funded by the European Union’s Horizon 2020 research and innovation programme under grant agreements no. 671553 and no. 754337 and financial contribution from the agreement ASI-INAF n.2017-14-H.0. H.B. acknowledges financial support from ASI Grant 2016-24-H.0.
References
- Ackermann, M., Ajello, M., Albert, A., et al. 2014, ApJ, 787, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Adam, R., Arnaud, M., Bartalucci, I., et al. 2017, A&A, 606, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S. 2010, MNRAS, 407, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S. 2015, A&A, 575, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bartalucci, I., Arnaud, M., Pratt, G. W., et al. 2017, A&A, 608, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battaglia, N., Bond, J. R., Pfrommer, C., & Sievers, J. L. 2012, ApJ, 758, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Battaglia, N., Leauthaud, A., Miyatake, H., et al. 2016, J. Cosmol. Astropart. Phys., 8, 013 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, A. M., Murante, G., Arth, A., et al. 2016, MNRAS, 455, 2110 [Google Scholar]
- Biffi, V., Borgani, S., Murante, G., et al. 2016, ApJ, 827, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., & Jones, T. W. 2014, Int. J. Mod. Phys. D, 23, 1430007 [Google Scholar]
- Budzynski, J. M., Koposov, S. E., McCarthy, I. G., & Belokurov, V. 2014, MNRAS, 437, 1362 [NASA ADS] [CrossRef] [Google Scholar]
- Cavagnolo, K. W., Donahue, M., Voit, G. M., & Sun, M. 2009, ApJS, 182, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Chiu, I., Mohr, J. J., & McDonald, M. 2018, MNRAS, 478, 3072 [NASA ADS] [CrossRef] [Google Scholar]
- Coupon, J., Arnouts, S., van Waerbeke, L., et al. 2015, MNRAS, 449, 1352 [NASA ADS] [CrossRef] [Google Scholar]
- de Haan, T., Benson, B. A., Bleem, L. E., et al. 2016, ApJ, 832, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Eckert, D., Roncarelli, M., Ettori, S., et al. 2015, MNRAS, 447, 2198 [NASA ADS] [CrossRef] [Google Scholar]
- Eckert, D., Ettori, S., Coupon, J., et al. 2016, A&A, 592, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eckert, D., Ettori, S., Pointecouteau, E., et al. 2017a, Astron. Nachr., 338, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Eckert, D., Gaspari, M., Vazza, F., et al. 2017b, ApJ, 843, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Edge, A. C., Wilman, R. J., Johnstone, R. M., et al. 2002, MNRAS, 337, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S. 2015, MNRAS, 446, 2629 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., & Fabian, A. C. 2006, MNRAS, 369, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., Gastaldello, F., Leccardi, A., et al. 2010, A&A, 524, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ettori, S., Ghirardini, V., Eckert, D., et al. 2019, A&A, 621, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evrard, A. E. 1997, MNRAS, 292, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Fusco-Femiano, R., & Lapi, A. 2013, ApJ, 771, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Fusco-Femiano, R., & Lapi, A. 2018, MNRAS, 475, 1340 [NASA ADS] [CrossRef] [Google Scholar]
- Gaspari, M., Brighenti, F., Temi, P., & Ettori, S. 2014, ApJ, 783, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirardini, V., Ettori, S., Eckert, D., et al. 2018, A&A, 614, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghirardini, V., Eckert, D., Ettori, S., et al. 2019, A&A, 621, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giodini, S., Pierini, D., Finoguenov, A., et al. 2009, ApJ, 703, 982 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, A. H., Zaritsky, D., & Zabludoff, A. I. 2007, ApJ, 666, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, A. H., Sivanandam, S., Zabludoff, A. I., & Zaritsky, D. 2013, ApJ, 778, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Heymans, C., Grocutt, E., Heavens, A., et al. 2013, MNRAS, 432, 2433 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrandt, H., Viola, M., Heymans, C., et al. 2017, MNRAS, 465, 1454 [Google Scholar]
- Hinshaw, G., Larson, D., Komatsu, E., et al. 2013, ApJS, 208, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Hitomi Collaboration 2016, Nature, 535, 117 [Google Scholar]
- Hitomi Collaboration 2018, PASJ, 70, 9 [NASA ADS] [Google Scholar]
- Hoekstra, H., Herbonnet, R., Muzzin, A., et al. 2015, MNRAS, 449, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Hofmann, F., Sanders, J. S., Nandra, K., Clerc, N., & Gaspari, M. 2016, A&A, 585, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huber, B., Tchernin, C., Eckert, D., et al. 2013, A&A, 560, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurier, G., Macías-Pérez, J. F., & Hildebrandt, S. 2013, A&A, 558, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kawaharada, M., Okabe, N., Umetsu, K., et al. 2010, ApJ, 714, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, B. C. 2007, ApJ, 665, 1489 [NASA ADS] [CrossRef] [Google Scholar]
- Khatri, R., & Gaspari, M. 2016, MNRAS, 463, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., & Borgani, S. 2012, ARA&A, 50, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., Nagai, D., & Vikhlinin, A. A. 2005, ApJ, 625, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Laganá, T. F., Martinet, N., Durret, F., et al. 2013, A&A, 555, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lau, E. T., Kravtsov, A. V., & Nagai, D. 2009, ApJ, 705, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Le Brun, A. M. C., McCarthy, I. G., Schaye, J., & Ponman, T. J. 2014, MNRAS, 441, 1270 [NASA ADS] [CrossRef] [Google Scholar]
- Leauthaud, A., Tinker, J., Bundy, K., et al. 2012, ApJ, 744, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y.-T., & Mohr, J. J. 2004, ApJ, 617, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Mantz, A. B., Allen, S. W., Morris, R. G., et al. 2014, MNRAS, 440, 2077 [NASA ADS] [CrossRef] [Google Scholar]
- Markevitch, M. 2007, ArXiv e-prints [arXiv:0705.3289] [Google Scholar]
- Mathiesen, B., Evrard, A. E., & Mohr, J. J. 1999, ApJ, 520, L21 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, M., Allen, S. W., Bayliss, M., et al. 2017, ApJ, 843, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Miniati, F. 2014, ApJ, 782, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Montes, M., & Trujillo, I. 2014, ApJ, 794, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Muldrew, S. I., Hatch, N. A., & Cooke, E. A. 2015, MNRAS, 452, 2528 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, D., & Lau, E. T. 2011, ApJ, 731, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, D., Vikhlinin, A., & Kravtsov, A. V. 2007, ApJ, 655, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, K., Rudd, D. H., Shaw, L., & Nagai, D. 2012, ApJ, 751, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, K., Lau, E. T., & Nagai, D. 2014, ApJ, 792, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Nevalainen, J., David, L., & Guainazzi, M. 2010, A&A, 523, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peng, F., & Nagai, D. 2009, ApJ, 705, L58 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XI. 2011, A&A, 536, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIV. 2016, A&A, 594, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVII. 2016, A&A, 594, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIX. 2014, A&A, 571, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. V. 2013, A&A, 550, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planelles, S., Borgani, S., Dolag, K., et al. 2013, MNRAS, 431, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Planelles, S., Fabjan, D., Borgani, S., et al. 2017, MNRAS, 467, 3827 [NASA ADS] [CrossRef] [Google Scholar]
- Rasia, E., Ettori, S., Moscardini, L., et al. 2006, MNRAS, 369, 2013 [NASA ADS] [CrossRef] [Google Scholar]
- Rasia, E., Mazzotta, P., Evrard, A., et al. 2011, ApJ, 729, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Rasia, E., Lau, E. T., Borgani, S., et al. 2014, ApJ, 791, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Rasia, E., Borgani, S., Murante, G., et al. 2015, ApJ, 813, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Roncarelli, M., Ettori, S., Borgani, S., et al. 2013, MNRAS, 432, 3030 [NASA ADS] [CrossRef] [Google Scholar]
- Salomé, P., & Combes, F. 2003, A&A, 412, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schellenberger, G., Reiprich, T. H., Lovisari, L., Nevalainen, J., & David, L. 2015, A&A, 575, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmidt, W., Byrohl, C., Engels, J. F., Behrens, C., & Niemeyer, J. C. 2017, MNRAS, 470, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Sembolini, F., Elahi, P. J., Pearce, F. R., et al. 2016a, MNRAS, 459, 2973 [NASA ADS] [CrossRef] [Google Scholar]
- Sembolini, F., Yepes, G., Pearce, F. R., et al. 2016b, MNRAS, 457, 4063 [NASA ADS] [CrossRef] [Google Scholar]
- Sereno, M., & Ettori, S. 2015, MNRAS, 450, 3633 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, X., Komatsu, E., Nelson, K., & Nagai, D. 2015, MNRAS, 448, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, X., Komatsu, E., Nagai, D., & Lau, E. T. 2016, MNRAS, 455, 2936 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. P., Mazzotta, P., Okabe, N., et al. 2016, MNRAS, 456, L74 [NASA ADS] [CrossRef] [Google Scholar]
- Snowden, S. L., Mushotzky, R. F., Kuntz, K. D., & Davis, D. S. 2008, A&A, 478, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Tchernin, C., Eckert, D., Ettori, S., et al. 2016, A&A, 595, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Burg, R. F. J., Hoekstra, H., Muzzin, A., et al. 2015, A&A, 577, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazza, F., Brunetti, G., Kritsuk, A., et al. 2009, A&A, 504, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazza, F., Brunetti, G., Gheller, C., Brunino, R., & Brüggen, M. 2011, A&A, 529, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazza, F., Jones, T. W., Brüggen, M., et al. 2017, MNRAS, 464, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A. V., Burenin, R. A., et al. 2009, ApJ, 692, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- von der Linden, A., Mantz, A., Allen, S. W., et al. 2014, MNRAS, 443, 1973 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., Navarro, J. F., Evrard, A. E., & Frenk, C. S. 1993, Nature, 366, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Zhuravleva, I., Churazov, E., Arévalo, P., et al. 2015, MNRAS, 450, 4184 [Google Scholar]
- Zibetti, S., White, S. D. M., Schneider, D. P., & Brinkmann, J. 2005, MNRAS, 358, 949 [Google Scholar]
- Zu, Y., & Mandelbaum, R. 2015, MNRAS, 454, 1161 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The case of A2142
For one cluster in our sample (A2142), in Tchernin et al. (2016) we published a similar analysis presenting the gas fraction of this system out to R200 based on a joint XMM-Newton and Planck reconstruction. Noting the convergence of fgas, HSE close to the universal baryon, we concluded that this system requires a modest level of non-thermal pressure, in agreement with the results presented here (15% and 18% at R500 and R200, respectively). Recently, Fusco-Femiano & Lapi (2018) re-analyzed our data and came to the contradicting conclusion that non-thermal pressure support at the level of ∼30% is required in the outskirts of A2142. To reach this conclusion, Fusco-Femiano & Lapi (2018) neglected the Planck constraints while fitting their model and extrapolated their fitted temperature profile beyond the range accessible to XMM-Newton. However, as shown in Appendix D of Tchernin et al. (2016), the outermost spectral measurement in A2142 is affected by the presence of accreting substructures which bias the measured temperature low. As a result, the extrapolation of the model fitted by Fusco-Femiano & Lapi (2018) underestimates the Planck data beyond R500 (see their Fig. 1), and their hydrostatic mass reconstruction is biased low. This issue highlights the need to use all the available information in a self-consistent manner.
All Tables
Baryon depletion factor in the simulated clusters from the clusters in The300 project with M500 > 3 × 1014 M⊙.
Hydrostatic gas fraction, non-thermal pressure fraction, and total (bias-corrected) masses at R500 and R200 in X-COP clusters.
All Figures
 |
Fig. 1. Hydrostatic gas fraction profiles fgas, HSE(R)=Mgas(< R)/MHSE(< R) as a function of scale radius R/R500 for the X-COP clusters. The gray shaded area shows the Planck universal baryon fraction Ωb/Ωm (Planck Collaboration XIII 2016). |
| In the text | |
 |
Fig. 2. Baryon depletion factor Yb at R500 for the clusters in The300 simulation (filled circles). The blue points show the objects with a mass M500 > 3 × 1014 M⊙. The hashed gray shaded area shows the mass range covered by X-COP clusters and our determination of the universal baryon depletion factor and its scatter. |
| In the text | |
 |
Fig. 3. Stellar fraction within R500 estimated in several works from the literature. The hashed grey area represents the mass range of X-COP clusters and the range of f⋆ adopted in this work. |
| In the text | |
 |
Fig. 4. Hydrostatic gas fractions at R500, HSE (blue points) and R200, HSE (red points) obtained from our reference hydrostatic mass model as a function of cluster mass. The dashed magenta line and shaded area represent the universal gas fraction at R500 estimated in Sect. 3.1 and its uncertainty. The green shaded area indicates the cosmic baryon fraction (Planck Collaboration XIII 2016). |
| In the text | |
 |
Fig. 5. Non-thermal pressure fraction in X-COP clusters at R500 and R200. The positions on the x-axis are slightly shifted for clarity. The blue and green curves and shaded areas show the mean non-thermal pressure ratio predicted from the numerical simulations of Nelson et al. (2014) and Rasia et al. (in prep.), respectively. |
| In the text | |
 |
Fig. 6. Intracluster medium gas fraction at R500 obtained from our reference hydrostatic-based mass model (blue squares) as a function of the total mass corrected for non-thermal pressure support (see Sect. 4.3). The red points show the gas fraction obtained using the Planck PSZ2 masses estimated from the YSZ − M500 relation (Planck Collaboration XXVII 2016), whereas the green triangles show the gas fraction that would be obtained by correcting the PSZ2 masses with a uniform mass bias 1 − b = 0.58 ± 0.04 (Planck Collaboration XXIV 2016). The dashed magenta line and shaded area represent the universal gas fraction estimated in Sect. 3.1. |
| In the text | |
 |
Fig. 7. Comparison between HSE (blue squares)/SZ (red dots) and total masses corrected for non-thermal pressure as a function of mass. The magenta line and shaded area show our best fit to the SZ data with a power law, whereas the green area displays the expectation for a constant mass bias 1 − b = 0.58 ± 0.04. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



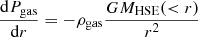
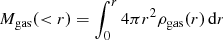
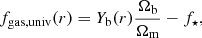
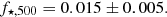
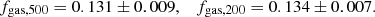
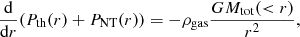
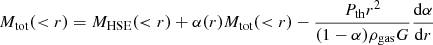
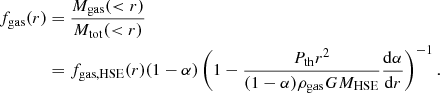
![$$ \begin{aligned} \frac{P_{\rm NT}}{P_{\rm tot}}(r)=1-A\left(1+\exp \left\{ -\left[\frac{r}{Br_{200}}\right]^\gamma \right\} \right) \end{aligned} $$](/articles/aa/full_html/2019/01/aa33324-18/aa33324-18-eq11.gif)