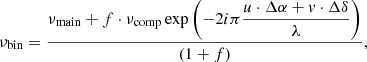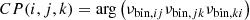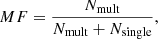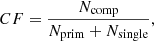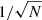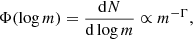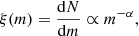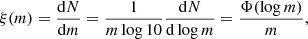| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A116 | |
| Number of page(s) | 26 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201833575 | |
| Published online | 07 December 2018 | |
Multiple star systems in the Orion nebula
1
MPE – Max Planck Institute for Extraterrestrial Physics, Gießenbachstraß, 85741
Garching, Germany
2
Department of Physics, Le Conte Hall, University of California, Berkeley, CA, 94720
USA
3
Physikalisches Institut, Universität zu Köln, Zülpicher Str. 77, 50937
Köln, Germany
4
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748
Garching, Germany
5
CENTRA – Centro de Astrofísica e Gravitação, IST, Universidade de Lisboa, 1049-001 Lisboa, Portugal; Universidade de Lisboa – Faculdade de Ciências, Campo Grande, 1749-016 Lisboa, Portugal
6
CENTRA – Centro de Astrofísica e Gravitação, IST, Universidade de Lisboa, 1049-001 Lisboa, Portugal; Faculdade de Engenharia, Universidade do Porto, Rua Dr. Roberto Frias, 4200-465 Porto, Portugal
7
Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
8
Observatoire de Genève, Université de Genève, 51 Ch. des Maillettes, 1290 Versoix, Switzerland
9
European Southern Observatory, Casilla, 19001 Santiago 19, Chile
10
MPIA – Max-Planck-Institut für Astronomie, Königstuhl 17, 69117
Heidelberg, Germany
11
LESIA – Observatoire de ParisUniversitè PSL, CNRS, Sorbonne Universitè, Univ. Paris Diderot, Sorbonne Paris Cité, 5 place Jules Janssen, 92195
Meudon, France
12
Sterrewacht Leiden, Leiden University, Postbus 513, 2300 RA
Leiden, The Netherlands
13
Max-Planck-Institute for Radio Astronomy, Auf dem Hügel 69, 53121
Bonn, Germany
14
ESA – European Space Agency, Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD, 21218
USA
15
Dublin Institute for Advanced Studies, Astronomy & Astrophysics Section, 31 Fitzwilliam Place, D02 XF86
Dublin, Ireland
16
University of Vienna, Universitätsring 1, 1010
Wien, Austria
17
School of Physics, Astrophysics Group, University of Exeter, Stocker Road, Exeter EX4 4QL UK
Received:
30
May
2018
Accepted:
26
September
2018
This work presents an interferometric study of the massive-binary fraction in the Orion Trapezium cluster with the recently comissioned GRAVITY instrument. We observed a total of 16 stars of mainly OB spectral type. We find three previously unknown companions for θ1 Ori B, θ2 Ori B, and θ2 Ori C. We determined a separation for the previously suspected companion of NU Ori. We confirm four companions for θ1 Ori A, θ1 Ori C, θ1 Ori D, and θ2 Ori A, all with substantially improved astrometry and photometric mass estimates. We refined the orbit of the eccentric high-mass binary θ1 Ori C and we are able to derive a new orbit for θ1 Ori D. We find a system mass of 21.7 M⊙ and a period of 53 days. Together with other previously detected companions seen in spectroscopy or direct imaging, eleven of the 16 high-mass stars are multiple systems. We obtain a total number of 22 companions with separations up to 600 AU. The companion fraction of the early B and O stars in our sample is about two, significantly higher than in earlier studies of mostly OB associations. The separation distribution hints toward a bimodality. Such a bimodality has been previously found in A stars, but rarely in OB binaries, which up to this point have been assumed to be mostly compact with a tail of wider companions. We also do not find a substantial population of equal-mass binaries. The observed distribution of mass ratios declines steeply with mass, and like the direct star counts, indicates that our companions follow a standard power law initial mass function. Again, this is in contrast to earlier findings of flat mass ratio distributions in OB associations. We excluded collision as a dominant formation mechanism but find no clear preference for core accretion or competitive accretion.
Key words: techniques: interferometric / astrometry / celestial mechanics / binaries: close / binaries: general / stars: massive
GRAVITY is developed in a collaboration by the Max Planck Institute for extraterrestrial Physics, LESIA of Paris Observatory/CNRS/UPMC/Univ. Paris Diderot and IPAG of Université Grenoble Alpes/CNRS, the Max Planck Institute for Astronomy, the University of Cologne, the Centro de Astrofísica e Gravitação, and the European Southern Observatory.
© ESO 2018
1. Introduction
Massive stars, defined as those with masses higher than 8 M⊙, have an intense impact on the evolution of galaxies. The winds, UV radiation, massive outflows, and the heavy elements produced by high-mass stars influence the formation of stars and planets (see e.g., Bally et al. 2005) as well as the structure of galaxies (e.g., Kennicutt 1998). Despite their important role, the formation of massive stars is not well understood. High-mass stars have short lifetimes and spend a significant part of their life hidden within their parental dust and gas clouds. During this embedded phase, some fundamental evolutionary processes are difficult to observe. For a detailed review of high-mass star formation, see for example Shu et al. (1987), Zinnecker & Yorke (2007), Tan et al. (2014) and Motte et al. (2018).
There are several indications that high-mass star formation is not just a scaled-up version of low-mass star formation. One indication is that massive stars tend to appear more often in multiple systems than lower mass stars (e.g., Chini et al. 2011; Sana et al. 2012). Zinnecker & Yorke (2007) found that the number of companions per star increases with stellar mass. For example, Duchêne & Kraus (2013) found 0.22 ± 0.06 companions for stars with masses ≲0.1 M⊙ and 1.3 ± 0.2 companions for primary stars with masses ≳16 M⊙. They also found more multiple systems for stars with higher mass. At least 60% of stars with 8–16 M⊙ are part of a multiple system. For stars ≳16 M⊙, at least 80% are found in multiple systems (Duchêne & Kraus 2013; Sana et al. 2014). The higher number of companions and multiple systems is most likely a result of their formation process. Massive stars are short-lived and thus it is unlikely that they assemble all of their companions by random interactions in reasonable timescales. Duchêne & Kraus (2013) provides a review about stellar multiplicity. Moe & Di Stefano (2017) present a detailed study of the distribution and properties of early-type binaries.
In the case of massive star formation, two different scenarios try to explain the birth of a protostellar object from molecular gas. McKee & Tan (2002) proposed that molecular condensations in turbulent gas form a single massive protostar or several gravitationally bound protostars. For this “monolithic collapse”, the mass of the final product is directly associated with the mass needed for star formation. Thus, the final material for the resulting star is already gathered before the beginning of star formation. Monolithic collapse or core accretion, assumes that the initial conditions are similar to low-mass star formation. An isolated core collapses and accretes mass with a disk (Yorke & Sonnhalter 2002). McKee & Tan (2002) proposed the turbulent core model, assuming mainly non-thermal internal pressure. Tan et al. (2014) pointed out that the accretion rate of the turbulent core model is higher than for competitive accretion. In the past it was believed that radiation pressure of young massive stars could halt accretion (see e.g., Zinnecker & Yorke 2007; Krumholz 2015). This has been solved by introducing non-spherical accretion (see e.g., Krumholz et al. 2009).
Bonnell et al. (1997, 2001) described an alternative scenario in which the core or resulting protostar moves within the cloud, independent of the movement of the surrounding gas. Thus, the material can come from different parts of the parent cloud, as well as from material infalling onto the cloud. Each of the forming protostars competes for the material; this mechanism is therefore called “competitive accretion”. Competitive accretion starts with many low-mass seeds in a parent cloud, which start to accrete mass, for example Krumholz (2016, 213). Two factors influence the amount of growth for stars with competitive accretion (see e.g., Bonnell et al. 1997, 2001). One is the accretion radius or the accretion domain, meaning the range where gas is gravitationally attracted to the star. The second factor is the gas density of the accretion domain. Because gas flows down to the center of clusters, the central position in a cluster is beneficial for mass growth. When the accretion volumes start to overlap, the stars are competing for the available material. This might explain why massive stars are rare and mainly form in the most favorable, that is, the densest, conditions. However, there are also a few examples of O-type stars born in isolation (de Wit et al. 2004, 2005; Oskinova et al. 2013).
The accretion rate for competitive accretion is lower than for monolithic collapse (see e.g., Tan et al. 2014; Krumholz 2016). The angular momentum of gas in both cases is large enough to form an accretion disk.
Companion stars can be formed by various mechanisms. In the monolithic collapse scenario, a massive core can fragment into several smaller cores and form a binary or multiple system (see e.g., Krumholz 2016; Tan et al. 2014; and references therein). Disk fragmentation can also produce companion stars, see for example Kratter & Lodato (2016). They concluded that for a star with 8 M⊙, the disk cools down sufficiently to undergo disk fragmentation for separations ≥50 astronomical units (AU). Krumholz (2016, 296) stated that the typical accretion rates on a stellar core lead to a high surface density of the disk and eventually result in disk fragmentation.
Another possible scenario for the formation of companions is the failed merging of two stars. This process requires a high stellar density, which is much higher than the typical observed density in our Galaxy. Zinnecker & Yorke (2007) concluded that the cross section is small and that the collision impact parameter requires fine tuning. If there is a disk, the capture of a companion star becomes more likely.
Additionally, a binary system can capture a third, massive companion – a mechanism called “three-body capture”. In a simulation of a protostellar cluster with more than 400 stars, Bonnell et al. (2003) demonstrated that dynamical three-body capture is common in protoclusters.
In order to gain a deeper understanding of massive star and cluster formation, the characteristics of binaries need to be determined. Lada & Lada (2003), Briceño et al. (2007) found that massive star formation results in either dense OB clusters or unbound OB associations. The Orion nebula cluster, at a distance of 414 pc (Menten et al. 2007; Reid et al. 2014), is one of the closest active star-forming regions. For a general overview see for example Genzel & Stutzki (1989), Hillenbrand (1997), Muench et al. (2008). The Orion nebula cluster comprises an expanding blister HII region with the Orion Trapezium cluster (θ1), an open cluster of young massive stars, at its center. These centrally concentrated young stars cause the ionization of the surrounding cloud. The Orion Trapezium cluster has six principal components, θ1 Ori A to θ1 Ori F. The stars θ1 Ori (A, B, C, D) are all known to have companions.
The Orion nebula cluster has already been thoroughly observed in recent decades. Deep spectroscopic surveys probed for close companions on scales ≲1 AU (e.g. Morrell & Levato 1991; Abt et al. 1991). Adaptive optic assisted imaging and speckle interferometry resolved companions ≳14–few 100 AU (e.g., Weigelt et al. 1999; Preibisch et al. 1999; Schertl et al. 2003). While these ranges have been covered, there is still a gap in the separations where observations are scarce. The region ∼1–few 10 AU can only be resolved with long baseline interferometry.
In the following, we present the observational data obtained with GRAVITY (Gravity Collaboration 2017), a K-band interferometric instrument at the Very Large Telescope Interferometer (VLTI). In Sect. 2, we describe our observations. Section 3 introduces the data analysis. We present our results in Sect. 4, discuss the results in Sect. 5, and conclude in Sect. 6.
2. Observations
Data were taken with GRAVITY, a novel instrument at the VLTI for ∼10 micro-arcsec astrometric precision measurements with K-band interferometry (Gravity Collaboration 2017). GRAVITY coherently combines the light of all four UTs (8.2 m diameter) or all four ATs (1.8 m diameter) with two interferometric beam combiners for fringe tracking and observing science objects, respectively. A star up to 10 mag in K-band can be used for fringe tracking faint objects up to 17 mag in the science channel using the UTs. The spectrometers provide three spectral resolutions: low, medium, and high, with R ∼ 22, 500, 4000, respectively.
Table B.1 provides an overview of all observations. The 16 brightest objects in the Orion nebula were selected for this study. Observations were primarily performed in medium resolution with the astrometric configuration of the ATs at the stations A0-G1-J2-K0. The detector integration time – DIT – depends on the source luminosity. A higher DIT is needed for fainter objects (e.g., a DIT of 30 s was used for θ1 Ori F with a K-magnitude of 8.38) whereas shorter DITs are possible for bright objects (e.g., 3 s or 5 s for θ1 Ori C with a K-magnitude of 4.57). The integration on the source is repeated several times, usually followed by a sky background observation with the same DIT and number of repetitions (NDIT). Data were reduced with the standard GRAVITY pipeline (Gravity Collaboration 2017). The reduction algorithm follows the approach of Tatulli et al. (2007) and creates a Pixel to Visibility Matrix (P2VM). The visibility is measured by combining the telescope beams with a relative phase shift of 0 ° ,90 ° ,180°, and 270°. Thus, we get four signals per baseline, resulting in 4 × 6 = 24 channels for the science object (Gravity Collaboration 2017). The P2VM provides the phase relations, photometry, and coherence of the four incoming telescope beams and the 24 outgoing signals. A detailed description of the reduction is provided in Lapeyrere et al. (2014) and an additional example of the use of GRAVITY to the study of massive multiple systems can be found in Sanchez-Bermudez et al. (2017).
For the instrument calibration, we also need to calibrate the wavelength of the fringe tracker and science channel, as well as to determine the dark field, bad pixels, and to compute the profile of the spectra with a flat field. Using the P2VM, we then compute real-time visibilities. Each file has several frames, one for each integration. The frames are averaged during reduction.
For the calibration of the visibilities we observe point-like objects with a known diameter and which can be considered single stars. As we know the true shapes of the calibrator visibilities, we compute a visibility transfer function to adjust the measured visibilities to match the expected visibilities. This visibility transfer function is then applied to the visibilities of the science object.
3. Data analysis
In this section, we provide an overview of the modeling functions and tools used for data analysis. In the beginning, the observed data is fitted according to a binary model. For sufficiently well-sampled data, we are able to determine the orbital parameters of the binaries. In order to accurately determine the companion magnitude, we need to consider the effects of dust extinction. Finally, we provide a detection limit for our observations.
3.1. Modeling a binary star
We introduce the modeling functions that were used for analyzing the data. We assume a binary model and use it to fit the squared visibilities, closure phase and triple amplitude of our observational data.
3.1.1. Visibility.
Visibility of a binary model is described as:
where νmain and νcomp are the complex visibilities for the primary and the companion star, respectively (see, for example, Lawson 2000). In the case of an unresolved star, νmain = νcomp = 1. The parameters u and v are the spatial frequencies of the telescope baselines; λ is the observed wavelength; Δα and Δδ are the angular distances of the companion star from the primary star in RA and Dec, respectively; and f = fcomp/fmain is the mean flux ratio over all wavelengths of the system, where fcomp and fmain are the flux of the companion star and primary star, respectively.
The parameters u, v, and λ are provided by the observational data, while the distances Δα and Δδ together with the flux ratio f are variable parameters to be fitted. To find starting values for these parameters, we use a grid-search algorithm. We scan Δα and Δδ between either ±200 mas, ±100 mas or ±50 mas in steps of either 1 or 0.5 mas, and the flux ratio f between 0 and 1 in steps of 0.1. The best result of the grid-search forms the starting values for the subsequent weighted least-squares optimization, using the Levenberg-Marquardt algorithm and the LMFIT package (Newville et al. 2014).
3.1.2. Closure phase and triple amplitude.
The closure phase (CP) is computed by taking the argument of the bispectrum of the visibility function. The bispectrum is the triple product of complex visibilites for the telescopes i, j, k:
where the complex visibilites νbin are computed using Eq. (1).
The triple amplitude is the modulus of the bispectrum. Most of the information is contained in the closure phase, thus, the triple amplitude is not always necessary for fitting the data. The optimization is done in the same way as for the visibility model.
3.2. Orbit modeling
For fitting the orbit, we use the KeplerEllipse class of PyAstronomy1 to determine the position at a given time for a set of orbital elements. This position is then compared with the positions obtained from the binary model fit (see Sect. 3.1). The optimization is done with the Trust-region method, which supports boundaries of variables in contrast to a regular least-squares minimization.
The parameters of the orbit are defined as follows: a is the semi-major axis of the Kepler ellipse, P is the orbital period, e the eccentricity, τ the time of periapsis passage, Ω the longitude of the ascending node, ω the argument of periastron, and i the inclination of the orbit. The ascending node is defined as the point where the orbiting object passes the plane of reference in the direction of the observer. All parameters are in units of the respective initial guess. The semi-major axis a is thus mostly reported in units of angular separation. For a more detailed discussion see for example Roy (2005, 22–24).
As an observer, we see the 3D-orbit projected on a 2D-plane. The projection of different orbits can appear similar on the plane of reference, for example a highly inclined and eccentric orbit can appear as a not inclined circular orbit.
In order to not get stuck in a local minimum of χ2, a good starting value is essential for optimization. If orbital elements are already determined in the literature, we take these elements as starting values for the optimization, for example the values from Kraus et al. (2009) for the orbit of θ1 Ori C2 (see Sect. 4.1.3). If there are no previously determined orbital elements, we use the Basin-Hopping algorithm (Wales & Doye 1997), to find a global minimum and use the result as starting value for the Trust-region method.
3.3. Dust extinction
For calculating the luminosity or absolute magnitude of a star, we need to consider its spectral type and extinction effects of the interstellar and circumstellar medium. A(λ) is the extinction at wavelength λ in magnitudes. The extinction of color is described by for example E(B − V)=A(B)−A(V), with B as the filter for ∼440 ± 90 nm and V as the filter for ∼545 ± 84 nm. The interstellar reddening law is RV = A(V)/E(B − V). For the diffuse interstellar medium, a typical value is RV = 3.1, whereas for dense clouds the value is RV = 5 (Allen & Cox 2000, 527). In the K-band and for RV = 3.1, we get A(K)=0.108A(V).
3.4. Photometric mass
To get a mass estimate based on the magnitude, we use the isochrones in Allen & Cox (2000, 151, 388, and references therein) and Salaris & Cassisi (2005, 130). With the first and second table, we get MK for different spectral types and temperatures. With the effective temperatures in both tables, we link MK to stellar masses using the third table. Now we can compare the values for MK from the table to MK(Star) and get an estimate of mass and spectral type. The tables are for class V stars, meaning hydrogen-burning main sequence stars. For premain sequence (PMS) stars, the values are not accurate, merely representing a rough estimation.
3.5. Companion detection limits
We use CANDID (Gallenne et al. 2015) for determining detection limits of companion stars. CANDID is a Python tool which looks for high contrast companions. It provides two methods for computing limits.
The first method follows the approach of Absil et al. (2011). Absil et al. (2011) inserted a binary model at different positions (α, β). They then compared the probability of the binary model with the probability of a uniform disk model, assuming the uniform disk is the true model.
The second approach changes the null hypothesis. They injected companions at different positions with different flux ratios. Then, they determined the probability of the binary model being the true model, compared with the model of a uniform disk. In other words, the first approach tries to reconstruct a uniform disk model from binary data. The second approach tries to reconstruct a binary model from binary data. The second method yields more conservative results, which is why we choose it to determine our detection limits. Figure 1 shows an example of the companion detection limit for θ1 Ori C. We take the worst limit as our companion detection limit.
 |
Fig. 1. Example for the companion detection limit for θ1 Ori B, observed at the 12th October 2017, as determined with CANDID. The detection limit on the y-axis is denoted as a magnitude difference to the main star. The x-axis shows the separation in mas. |
4. The Orion nebula cluster M 42
One of the closest active star forming regions is the Orion Nebula Cluster (ONC), at a distance of 414 ± 7 (Menten et al. 2007; Reid et al. 2014). The ONC is located in a giant molecular cloud, at the sword of Orion. A young star cluster (younger than 1 Myr) is located in the center of the Nebula – see for example Muench et al. (2008). This central region is called the “Orion Trapezium Cluster” (OTC) or θ1 Orionis. The OTC is dominated by θ1 Ori C, a young O-star with ∼34 M⊙. The radiation and outflow of θ1 Ori C caused the ionization of its vicinity. The H II region expanded into the surrounding molecular cloud and dissolved the molecular gas in which the young stars had been born. This process exposed large parts of the embedded star clusters and created the ONC.
4.1. Orion Trapezium cluster stars
In this study, we concentrate on the most luminous stars of the ONC. In the Trapezium Cluster, we observe stars with apparent K-magnitudes ranging from 4.57 to 8.38. In the following, we summarize previous results and present our findings for each of the observed targets.
4.1.1. θ1 Ori A (HD 37020, Brun 587, TCC 45, Parenago 1865)
θ1 Ori A1 is a B0.5-type star (Levato & Abt 1976; Simón-Díaz et al. 2006) with a K-band magnitude mK = 5.67 (Cutri et al. 2003). Hillenbrand (1997) found a mass of 18.91 M⊙ and an extinction of AV = 1.89 mag. Weigelt et al. (1999) calculated a mass of 20 M⊙ and Schertl et al. (2003) assumed a mass of 16 M⊙, whereas Simón-Díaz et al. (2006) found a mass of 14 ± 5 M⊙ and a radius of 6.3 ± 0.9 R⊙.
Lohsen (1975) found an eclipsing binary with a period of 65.43 days (Mattei & Baldwin 1976), which we will refer to as A3. Abt et al. (1991) derived a period of 65.09 ± 0.07 days from their measured radial velocities for θ1 Ori A3. Bossi et al. (1989) concluded that the thermal spectrum and features correspond to a T Tauri companion with a mass between 2.5 and 2.7 M⊙ at a separation of 0.71 AU. However, Vitrichenko & Plachinda (2001) determined a greater distance of 0.93 ± 0.07 AU.
Petr et al. (1998) discovered a third companion (A2) at a separation of ∼200 mas, which corresponds to a projected distance of ∼90–100 AU (see e.g., Weigelt et al. 1999; Preibisch et al. 1999; Close et al. 2012). Schertl et al. (2003) determined a mass of 4 M⊙ for θ1 Ori A2 and suggested a period of P ∼ 214 yr. θ1 Ori A2 is an F-type star extincted by AV ∼ 3.8 mag (Schertl et al. 2003).
Until now, it has not been entirely clear whether A2 is gravitationally bound to θ1 Ori A1, 3. We used GRAVITY data taken between November 2015 and January 2018 (Table B.1) to get precise separation vectors. Our position measurements show an acceleration toward the primary star, proving that the system is gravitationally bound. In Fig. 2 one can see a motion of the companion star toward the main object. We use only the position measurements, because the spectral resolution is too low for precise radial velocity measurements. From the measured flux ratio f ∼ 0.23 ± 0.05 we infer a magnitude of mK = 7.3 ± 0.3.
 |
Fig. 2. Measured positions of θ1 Ori A2, with east to the left. The primary star θ1 Ori A1 is located at position (0,0). Blue dotted positions were observed with GRAVITY. For some of the dots, the errorbar is smaller than the symbol displayed. Gray square positions are taken from Close et al. (2012), Schertl et al. (2003), Petr et al. (1998), Weigelt et al. (1999), Balega et al. (2004, 2007), and Grellmann et al. (2013). |
4.1.2. θ1 Ori B (HD 37021, Brun 595, TCC 56, TCC 60, Parenago 1863)
θ1 Ori B consists of at least six hierarchical components. θ1 Ori B1 is a B1V-type star (Mason et al. 1998) with a magnitude mK = 6.00 (Cutri et al. 2003). Hillenbrand (1997) determined a mass of 7.18 M⊙ for an extinction of AV = 0.49. Weigelt et al. (1999) estimated a consistent mass of m = 7 M⊙.
Petr et al. (1998) found a visual companion at a separation of approximately 1″, corresponding to 415 AU projected distance (Close et al. 2012) at 450 pc. Taking the 414 ± 7 pc from Menten et al. (2007); Reid et al. (2014), the projected separation becomes 382 ± 6 AU. This companion itself is a resolved binary (θ1 Ori B2, 3, see Fig. 3) with 49 ± 1 AU projected separation and a period of ∼200 yr (Close et al. 2013). Their K-magnitudes are estimated to be 7.6 and 8.6 (Close et al. 2012). According to Close et al. (2013), B2, 3 has a system mass of ∼5.5 M⊙, which is in the same order of magnitude as the masses determined by Schertl et al. (2003) with mB2 = 4 M⊙, and mB3 = 3 M⊙. However, it differs from the values found by Preibisch et al. (1999), which are mB2 = 1.6 M⊙, and mB3 = 0.7 M⊙. The inferred orbital period of B2, 3 around the main star depends on the inclination of the orbit. For a less inclined orbit, Close et al. (2012) determined a period of P ∼ 1920 yr, whereas in Close et al. (2013) a highly inclined orbit was assumed and resulted in a period of P ∼ 11 000 yr with an absolute separation of ∼820 ± 14 AU.
 |
Fig. 3. Main image: θ1 Ori B group imaged in H-band. B1 is an eclipsing binary B1, 5. It was created with NaCo data, based on data obtained from the ESO Science Archive Facility under request number 342335, ESO program 60.A-9800(J). Additionally, with GRAVITY we detected another companion B6 at a separation of ∼13 mas, shown in the zoomed image of B1, 5, 6 (K-band). The image of B6 orbiting B1, 5 is reconstructed from our observations. The zoom into the spectroscopic binary B1, 5 is only a representative image and was not created with observational data. |
Located 0.6″ ∼248 ± 4 AU northwest of B1 is another faint companion (Fig. 3), θ1 Ori B4 (Simon et al. 1999) with mK = 11.66 (Close et al. 2012). Close et al. (2013) determined a period of ∼2000 ± 700 yr. Preibisch et al. (1999) estimated the mass of B4 to be mB4 = 0.2 M⊙ and sets an upper mass limit of < 2 M⊙. In contrast, we estimate the mass of B4 to be mB4 ∼ 1 M⊙, which is consistent with the limit of Preibisch et al. (1999).
Considering an extinction of AV = 0.49 (Hillenbrand 1997), we calculate an absolute magnitude 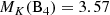 and compare the magnitude with the isochrones. This yields the mass estimate of 1 M⊙. Because of its low mass, B4 may be ejected from the system at a certain point, but appears temporarily stable (Close et al. 2013).
and compare the magnitude with the isochrones. This yields the mass estimate of 1 M⊙. Because of its low mass, B4 may be ejected from the system at a certain point, but appears temporarily stable (Close et al. 2013).
Hartwig (1921) and Schneller (1948) found θ1 Ori B1 to be an eclipsing binary (θ1 Ori B1, 5) with a 6.47 day period (Abt et al. 1991). Popper & Plavec (1976) determined θ1 Ori B5 to be a late A-type star and a mass ratio of q = mB5/mB1 ∼ 0.3, which leads to mB5 ∼ 2 M⊙. On the other hand, Close et al. (2003, 2012, 2013) assumed a mass of 7 M⊙ for B5, but did not justify their assumption. Close et al. (2012) determined a separation of 0.13 AU assuming a distance to the OTC of 450 pc. With the distance of 414 ± 7 pc determined by Menten et al. (2007), Reid et al. (2014), this converts to a separation of 0.120 ± 0.002 AU.
Vitrichenko et al. (2006) claim the detection of a late type companion based on radial velocity anomalies. Further observations are needed to verify the detection.
With GRAVITY, we detect a previously unknown companion B6 at separations between 8.5–17.2 mas, corresponding to a projected distance between 3.52 ± 0.05 AU and 7.12 ± 0.12 AU. The average flux ratio is 0.31 ± 0.06 and corresponds to an apparent K-magnitude of mK = 7.3 ± 0.5. Considering the absorption, the absolute K-magnitude is 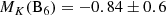 . The comparison with isochrones from Allen & Cox (2000, 150, 388) and Salaris & Cassisi (2005, 130) yields a mass mB6 ∼ 4–6 M⊙, which corresponds to a B-type star. Vasileiskii & Vitrichenko (2000) suggested a close B-type companion to explain a secondary minimum observed in the eclipse of B1. This supports our spectral classification of B6.
. The comparison with isochrones from Allen & Cox (2000, 150, 388) and Salaris & Cassisi (2005, 130) yields a mass mB6 ∼ 4–6 M⊙, which corresponds to a B-type star. Vasileiskii & Vitrichenko (2000) suggested a close B-type companion to explain a secondary minimum observed in the eclipse of B1. This supports our spectral classification of B6.
θ1 Ori B6 was observed between January 2017 and January 2018 (see Table B.1). The position of the star relative to θ1 Ori B1, 5 is presented in Fig. 4 and shows orbital motion. For the determination of orbital parameters further observations are needed. We approximate the orbital path by fitting values for Δα and Δδ over time with a quadratic function. The resulting path is the black line in Fig. 4. The residuals to this fit scatter by a root mean square (rms) of 0.05 mas in δ and 0.06 mas in α as can be seen in Fig. 5.
 |
Fig. 4. Positions of B6 between January 2017 and January 2018. We see orbital motion around B1, 5 at (0,0), moving from east (left) to west (right). |
 |
Fig. 5. Residuals of the Δα (top) and Δδ (bottom) positions from the best fit. The rms is 0.05 mas in δ and 0.06 mas in α. |
With CANDID (Gallenne et al. 2015, see Sect. 3.5), we can exclude further companions at a 3σ level with Δm < 3.5, thus a mass > 1.9 M⊙ for separations of 1.7–8.3 AU. For the range of 8.3–16.6 AU, the limit is 5 mag (≈1.5 M⊙) and for 16.6–46.8 AU, we can exclude companions with Δm = 5.2 (≈1.1 M⊙).
4.1.3. θ1 Ori C (HD 37022, Brun 598, TCC 68, Parenago 1891)
θ1 Ori C1 is a O7V-type star (Sota et al. 2011) and the brightest and most massive member of the Trapezium Cluster with mK = 4.57 (Ducati 2002). Furthermore, it is one out of few O-stars with detected magnetic fields (Stahl et al. 1996; Donati et al. 2002; Grunhut et al. 2017). Stahl et al. (1993) discovered variations in the spectrum with a 15.43 day period. This variation also appears in X-ray, radial velocities, and magnetic fields, discussed by, for example, Stahl et al. (2008), Wade et al. (2006), Simón-Díaz et al. (2006), and references therein. The magnetic field direction does not match the spin axis, which is an indication that θ1 Ori C1 was formed in a collision process (Zinnecker & Yorke 2007).
Weigelt et al. (1999) discovered a close visual companion C2 at a separation of 33 mas. Kraus et al. (2009) determined the orbital parameters in Table 1 and a resulting mass ratio of q(414 pc)=mC2/mC1 = 0.23 ± 0.05. They estimate a total system mass of 44 ± 7 M⊙ and a dynamical distance of 410 ± 20 pc.
Orbital parameter for θ1 Ori C determined by Kraus et al. (2009), Balega et al. (2015), and in this work including GRAVITY data.
Using the calibration models from Martins et al. (2005), Kraus et al. (2007) derived a mass of mC1 = 34 M⊙, an effective temperature Teff, C1 = 39 900 K, and logLC1/L⊙ = 5.41. The resulting parameters for the companion star are mC2 = 15.5 M⊙, Teff, C2 = 31 900 K and logLC2/L⊙ = 4.68, thus implying a O9.5-type star. The temperatures are in accordance with Simón-Díaz et al. (2006), who found temperatures of Teff, C1 = 39 000 ± 1000 K and derived a stellar radius of RC1 = 10.6 ± 1.5 R⊙. The spectroscopic mass of 45 M⊙ and evolutionary mass of 33 M⊙ for θ1 Ori C1 by Simón-Díaz et al. (2006) differ. Herrero et al. (1992) described a discrepancy between spectroscopic masses and masses determined using an evolutionary model. Habibi et al. (2017) pointed out that spectroscopic masses are sensitive to logg and that an error of 0.1 (as in Simón-Díaz et al. 2006) in logg translates to a factor of 100.1 ≈ 1.26, or an uncertainty of 126% for spectroscopic masses. Balega et al. (2015) added spectroscopic observations to the previous data and determined a total system mass of 45.5 ± 10 M⊙, a mass ratio of q = 0.36 ± 0.05 and derived mC1 = 33.5 ± 5.2 M⊙ and mC2 = 12 ± 3 M⊙. The separation of 44 ± 3 mas corresponds to 18.2 ± 1.2 AU.
GRAVITY observations from November 2015 to January 2018 (for a list of observations see Table B.1) show a variation of the flux ratio f = fC2/fC1 between 0.18 and 0.36, which points to a non-constant brightness of either the primary or the companion star or both stars. We compute an average K-magnitude of 6.0 ± 0.4. The extinction is AV = 1.74 (Hillenbrand 1997) and using the method described in the previous section, we infer a spectral type of B1 or younger and thus a stellar mass > 10 M⊙ (Allen & Cox 2000, 389). Looking at the flux ratio f depending on wavelength (Fig. 6), we notice a drop at 2166 nm – the Br-γ line. This points to an absorption of C2 in the Br-γ line. For the given example in Fig. 6, C2 is 1.3 times fainter at the Br-γ line than at other wavelengths. With the new GRAVITY data, we fit the orbit of C2 (see Fig. 7) and find that our results agree with the parameters from Kraus et al. (2009). Table 1 presents both outcomes, and the orbital elements determined by Balega et al. (2015).
 |
Fig. 6. Flux ratio f = fC2/fC1 as a function of observed wavelength. The vertical dashed gray line is at 2.166 microns, the Br-γ line. The drop indicates that C1 has a much higher flux at that wavelength than C2. Data were observed at January 9th 2016. |
 |
Fig. 7. Orbit of θ1 Ori C2. Orange dots are observed with GRAVITY, blue squares are positions taken from Weigelt et al. (1999), Schertl et al. (2003), Kraus et al. (2007, 2009), Patience et al. (2008), and Grellmann et al. (2013). The error bars of GRAVITY data are within the marker. The orbital parameters are listed in Table 1. |
Vitrichenko (2002b) and Lehmann et al. (2010) found another spectroscopic companion C3 with a period of 61.5 days, resulting in an estimated separation of ∼1 mas. They derived masses of 31 M⊙ for C1, 12 M⊙ for C2, and 1.0 ± 0.2 M⊙ for C3. For a primary star with 33 M⊙ and a companion star with 1 M⊙, we expect a reflex motion of ∼60 μas for C1. To this point, we have not detected such wobbling, probably because the position scattering was too large. The residuals from the orbit are shown in Fig. 8. The rms of the residuals is 0.07 mas for Δα and 0.05 mas for Δδ.
 |
Fig. 8. Residuals of the Δα (top) and Δδ (bottom) positions from the orbit of θ1 Ori C2. The blue circles represent the residuals of GRAVITY data and their respective uncertainties. The gray squares are the residuals from non-GRAVITY observations. The rms of the GRAVITY residuals is 0.07 mas for Δα, and 0.05 mas for Δδ. |
With CANDID, we set a limit on further companions at a 3σ level. For separations of 1.70–8.3 AU, we compute Δm < 3.2 (≈3 M⊙). For the range of 8.3–46.8 AU, we can exclude companions with Δm < 4.2 (≈2.2 M⊙).
4.1.4. θ1 Ori D (HD 37023, Brun 612, Parenago 1889)
θ1 Ori D is a premain sequence B1.5V-type star (Levenhagen & Leister 2006) with a K-magnitude of 5.75 (Cutri et al. 2003). Hillenbrand (1997) found a mass of 16.6 M⊙, whereas Simón-Díaz et al. (2006) derived a mass of 18 ± 6 M⊙. Levenhagen & Leister (2006) found a mass of 11 ± 1 M⊙ and Voss et al. (2010) determined a mass of 17.7 M⊙ using rotating stellar models.
Close et al. (2012) found a wide visual companion D2 at a distance of ∼1.4″ = 580 ± 10 AU. Currently it is not clear if D2 is physically bound to D1. In order to estimate the mass of the companion, we used archival imaging data2 of the Trapezium. We retrieved a NaCo image from 2005 and the corresponding calibration files. After calibrating the image with the NaCo reduction pipeline, we extracted the total flux of D2 and Ori F as a magnitude reference and compared the flux D2 with the flux of θ1 Ori F. With the flux ratio, we determine a magnitude of mK = 11.69 ± 0.06. We assume that the extinction is comparable with the value for the primary (AV = 1.79 Hillenbrand 1997) and get MK = 3.4 ± 0.1. This corresponds to a mass of ∼1 ± 0.1 M⊙.
A spectroscopic companion with a period of either 20.25 or 40.5 days was claimed by Vitrichenko (2002a). Another indication for a companion at a separation of 18.4 mas (≈7.6 ± 0.2 AU) and with a flux ratio of 0.14 was suggested by Kraus et al. (2007). Grellmann et al. (2013) found indications for a structure at 2 mas or 4 mas, which is consistent with a close companion, but could not provide further constraints due to large uncertainties.
With GRAVITY, we detected a star θ1 Ori D3 with a flux ratio f = 0.34 ± 0.04 at separations between 1.9 mas ≈ 0.79 ± 0.2 AU and 2.6 mas ≈1.08 ± 0.2 AU. The observed separations could correspond to the spectroscopic companion reported by Vitrichenko (2002a), since the inferred separations match quite well. However, we find no evidence for a companion at 18 mas. The trajectory of the detected companion does not favor a very eccentric orbit, that is, it cannot be related to the detection claim of Kraus et al. (2007). The positions of D3 are plotted in Fig. 9. We calculate the apparent magnitude of D3 to be 6.9 ± 0.3 mag and use AV = 1.79 (Hillenbrand 1997) to estimate a mass of 6 ± 1 M⊙ and a B spectral type. This agrees with Allen et al. (2017), who determined that the temperature of the spectroscopic companion of D1 has to be ∼20 000 K, which corresponds to ∼7 M⊙. The determined orbital parameters are shown in Table 2. The angles ω and Ω are not well constrained. With the orbit and a distance of 414 ± 7 pc (Menten et al. 2007; Reid et al. 2014), we get a system mass of 21.68 ± 0.05 M⊙. This corresponds to a companion mass of ∼6 ± 1 M⊙ and a primary mass of ∼16 ± 1 M⊙. Our data scatter with an rms of 0.02 mas for Δα and 0.03 mas for Δδ (see Fig. 10).
 |
Fig. 9. Positions of the newly detected θ1 Ori D3 around the primary D1 at (0,0). The orbital parameters are listed in Table 2. |
 |
Fig. 10. Residuals of the Δα (top) and Δδ (bottom) positions from the fitted orbit of θ1 Ori D3. The rms of the residuals is 0.02 mas for Δα and 0.03 mas for Δδ. |
Orbital parameters of the best fit for the positions of θ1 Ori D3.
We set a 3σ detection limit with CANDID, excluding companions with Δm < 2.5 (≈2.8 M⊙) in a range of 1.70–8.3 AU. For the 8.3–16.6 AU range the detection limit is Δm = 3.9 (≈1.9 M⊙) and for 16.6–46.8 AU we set a limit of Δm = 4.4 (≈1.9 M⊙).
4.1.5. θ1 Ori E (Brun 584, TCC 40, Parenago 1864)
θ1 Ori E is the second-strongest X-ray source in the Trapezium, exceeded only by θ1 Ori C (Ku et al. 1982). Its K-magnitude is 6.9 (Muench et al. 2002) and Morales-Calderón et al. (2012) determined a spectral type of G2IV. The extinction is AV = 3.8 (Feigelson et al. 2002).
Costero et al. (2006) and Herbig & Griffin (2006) discovered θ1 Ori E to be a double lined spectroscopic binary, which consists of two approximately identical stars. Herbig & Griffin (2006) concluded that the components of θ1 Ori E are located in the G-K region, but otherwise do not resemble typical T Tauri stars. They assumed masses of 3–4 M⊙. Costero et al. (2008) determined a period of P = 9.89520 ± 0.00069 d and a mass ratio q = 1.004 ± 0.018. The period corresponds to a semi-major axis of 0.22 mas or 0.091 ± 0.001 AU. They also concluded that the binary system is escaping the Trapezium Cluster. Morales-Calderón et al. (2012) determined masses of 2.81 ± 0.05 M⊙ and 2.80 ± 0.05 M⊙. The eclipsing companions cannot be resolved with GRAVITY. We did not find evidence for further companions.
With CANDID, we set a 3σ detection limit of Δm = 2.8 (≈1.8 M⊙) for 1.70–8.3 AU. For 8.3–16.6 AU the limit is Δm = 3.9 (≈1.4 M⊙). In the range of 16.6–46.8 AU, we exclude companions with Δm = 4 (≈1.4 M⊙).
4.1.6. θ1 Ori F (Brun 603, TCC 72, Parenago 1892)
θ1 Ori F is a B8-type star (Herbig 1950) with a magnitude in K-band of 8.38 (Muench et al. 2002). Studies by Petr et al. (1998) and Simon et al. (1999) did not detect companions with a separation ≥55 AU. We did not find any values for the extinction of θ1 Ori F in the literature. With the method described in Sect. 4.1.2, we estimate a lower mass limit of 2.2 M⊙. The typical mass for an B8-star is ∼2.8 M⊙ (Allen & Cox 2000, 150, 388; Salaris & Cassisi 2005, 130), thus we estimate a mass range of 2.2–2.8 M⊙ for θ1 Ori F.
With the recent GRAVITY data, we can place a 3σ detection limit of Δm = 1.75 (≈1.5 M⊙) in the range of 1.70–8.3 AU using CANDID. For the range 8.3–16.6 AU, we set a limit of Δm = 2.6 (≈1.4 M⊙), and for 16.6–46.8 AU we get Δm = 2.89 (≈1.2 M⊙).
4.2. Orion Nebula cluster stars
The following stars are not strictly members of the Trapezium Cluster. However, they reside within 2.6 pc and belong to the youngest and most massive stars of the ONC. The apparent K-magnitudes are in the range of 4.49–11.05.
4.2.1. θ2 Ori A (HD 37041, Brun 682, Parenago 1993)
θ2 Ori A1 is of spectral type O9.5IV (Sota et al. 2011) with a K-magnitude of 4.94 (Ducati 2002). Preibisch et al. (1999) estimated a mass of ∼25 M⊙. Simón-Díaz et al. (2006) determined a mass of 39 ± 14 M⊙, an effective temperature of 35 000 K and a stellar radius of 8.2 ± 1.1 R⊙.
θ2 Ori A is a hierarchical system comprising a spectroscopic companion A2 with a period P = 20.9741 ± 0.0028 days (Aikman & Goldberg 1974; Abt et al. 1991). Assuming a circular orbit, this corresponds to a separation of ∼0.46 ± 0.04 AU (∼1 mas). With the mass ratio q ≈ 0.35 (Abt et al. 1991) the companion should be in the range of ∼9–19 M⊙.
Preibisch et al. (1999) discovered a visual companion A3 at a separation of 0.38″, corresponding to 157 ± 3 AU, and a mass ratio q ≈ 0.25 (≈6–13 M⊙). Grunhut et al. (2017) claimed the detection of another spectroscopic companion, but provided no orbital period or any further constraints on the companion.
With GRAVITY, we detect a companion at a separation of 1.3 mas (≈0.538 ± 0.011 AU), likely the spectroscopic companion A2. The observed positions are displayed in Fig. 11. We observe a flux ratio of f = 0.52 ± 0.04, which corresponds to mK = 5.7 ± 0.2. Using AV = 1.12 (Hillenbrand 1997) we find an absolute magnitude in K-band of MK = −2.5 ± 0.2. Comparing this magnitude with isochrones, we suggest a stellar mass of ∼10 ± 2 M⊙ and an early B spectral type. This result is consistent with previous estimates.
 |
Fig. 11. Positions observed with GRAVITY of θ2 Ori A2, relative to A1, 3 at (0,0). |
With CANDID, we set a 3σ detection limit for the range of 1.70–8.3 AU of Δm = 5.25 (≈1.6 M⊙) and a limit of Δm = 6.2 (≈1.5 M⊙) for the range 8.3–16.6 AU. For 16.6–46.8 AU, we place a limit of Δm = 6.47 (≈1.1 M⊙).
4.2.2. θ2 Ori B (HD 37042, Brun 714, Parenago 2031)
θ2 Ori B is a B2–B5 PMS star (Hillenbrand 1997) with a K-magnitude of 6.41 (Ducati 2002). Simón-Díaz et al. (2006) determined a mass of 9 ± 3 M⊙ and a temperature of 29 000 ± 1000 K together with a radius of 4.5 ± 0.6 R⊙. The values agree with the results of Nieva & Przybilla (2014), who obtained M = 14.8 ± 3.4 M⊙, Teff = 29 300 ± 300 K and R = 4.3 ± 0.4.
Previous observations, for example Abt et al. (1991) or Preibisch et al. (1999), did not find indications for a companion star. GRAVITY observations made in January 2018 (see Table B.1) allowed the detection of a companion at a separation of 95.8 mas ≈40 ± 1 AU with a small flux ratio of f = 0.02 ± 0.01. This yields an apparent magnitude of 10.6 ± 1.3. Using AV = 0.73 (Hillenbrand 1997), we obtain MK = 2.4 ± 1.3. A comparison with isochrones from Allen & Cox (2000, 150, 388) and Salaris & Cassisi (2005, 130) yields a mass estimate of 1.6 ± 0.7 M⊙ and thus a late-A- or early-F-type star.
Using CANDID, we set a 3σ detection limit of Δm = 2.7 (≈1.9 M⊙) for the 1.70–8.3 AU and Δm = 3.9 (≈1.6 M⊙) for 8.3–46.8 AU.
4.2.3. θ2 Ori C (HD 37062, Brun 760, Parenago 2085)
θ2 Ori C1 is a B5V-type star (Samus’ et al. 2017) with mK = 7.54 (Cutri et al. 2003). Stelzer et al. (2005) determined an effective temperature Teff = 13 800. Comparing Teff with typical values for main sequence stars (Salaris & Cassisi 2005, 130), we get a mass estimate of 4 ± 1 M⊙, which agrees with the mass for B5-type stars.
Corporon & Lagrange (1999) detected a spectroscopic binary C2 with a period P ≈ 13 days. This corresponds to a separation of 0.4 mas or 0.165 ± 0.003 AU, assuming a circular orbit.
With GRAVITY, we resolved for the first time a third companion C3 at 38 mas, a projected separation of 15.7 ± 0.2 AU. The detected flux ratio is f = 0.115 ± 0.003. With AV = 0.92 (Hillenbrand 1997), this results in an apparent magnitude of 9.89 ± 0.07. The absolute magnitude is MK = 1.7 ± 0.1. Thus, a comparison with isochrones yields an estimate of 1.7 ± 0.2 M⊙ and A spectral type.
4.2.4. NU Ori (HD 37061, Brun 747, Parenago 2074)
NU Ori1 is a O9V-type star (Bragança et al. 2012) with a K-magnitude of 5.49 (Cutri et al. 2003). Hillenbrand (1997) determined a stellar mass of 16.3 M⊙, whereas Landstreet et al. (2017) estimated ∼13 M⊙ using effective temperatures but flagged it as particularly uncertain. Wolff et al. (2004) estimated a mass of ∼14 M⊙, using the luminosity and the effective temperature but stated that there are systematic uncertainties from the evolutionary tracks of PMS stars. Thus, we assume that the mass of NU Ori1 is in the range of 16 ± 3 M⊙.
NU Ori has a spectroscopic companion NU Ori2, discovered by Morrell & Levato (1991). Its orbital elements were determined by Abt et al. (1991), who found a period of P = 19.1387 ± 0.0028 d. and the lower limit for the mass ratio q = 0.19. With a primary mass between 13 and 19 M⊙, the lower limit for NU Ori2 is 2.5–3 M⊙. Assuming a circular orbit, we get a separation of 0.35 ± 0.03 AU.
Preibisch et al. (1999) discovered a companion star NU Ori3 at 0.47″. At a distance of 414 ± 7 pc (Menten et al. 2007; Reid et al. 2014), this corresponds to 195 ± 4 AU. The mass estimate is 1 M⊙, with an upper limit < 4 M⊙. Köhler et al. (2006) also detected a companion at 0.47 ± 0.01″ with ΔmK = 3.23 ± 0.1 mag. With this magnitude we are now able to estimate the stellar mass using the method described in Sect. 4.1.2. For an apparent K-magnitude of 8.7 ± 0.1, we get an absolute magnitude of MK = 0.4 ± 0.1 using the extinction AV = 2.09 (Hillenbrand 1997). This yields a mass estimate of 2.4 ± 0.6 M⊙ and thus an early A or late B-type star.
Grellmann et al. (2013) presumed another companion at either 20 mas or 10 mas separation. With our interferometric data, we found a companion NU Ori4 at a distance of d = 8.6 mas ≈3.6 ± 0.1 AU with a flux ratio f = 0.184 ± 0.009 (see Fig. 12). This new detection is most likely a different star than the spectroscopic companion, because a period of 19 days translates to a distance of ≈0.9 mas, a factor of 10 smaller than the newly discovered separation of 8.6 mas. With the flux ratio of 0.184 ± 0.009, we get an apparent magnitude of 7.3 ± 0.1 and an absolute K-magnitude of −1 ± 0.1. This results in a mass estimate of 4 ± 1 M⊙ and B spectral type.
 |
Fig. 12. Positions of NU Ori4 with respect to NU Ori1, 2 at (0,0). |
We set a 3σ detection limit of Δm = 3.8 (≈2 M⊙) for separations of 1.70–8.3 AU. For the range 8.3–46.8 AU, we determine a limit of Δm = 4.6 (≈1.8 M⊙).
4.2.5. Brun 862 (Parenago 2208)
Brun 862 is a K3–M0I-type star (Hillenbrand 1997) with mK = 4.49 (Cutri et al. 2003). To get a mass estimate, we take the calibration of MK spectral types for supergiants (luminosity class I) from Allen & Cox (2000, 390, Table 15.8). For spectral type K3–M0, the corresponding mass is 13 M⊙.
With GRAVITY observations from January 2018 (Table B.1), we can either fit a companion Brun 8622 at a separation of 0.29 ± 0.01 AU or fit a single star with a diameter of 0.33 ± 0.01 AU (∼71 R⊙), represented by a uniform disk. Both models fit the data equally well. For the first model the resulting flux ratio is f = 0.26 ± 0.04. With AV = 6.78 (Hillenbrand 1997), this would result in an absolute magnitude of MK = −2.9 ± 0.4. Assuming a main sequence star, we could estimate a mass of ∼10 M⊙ and suggest a late O or early B spectral type. On the other hand, the latter model of a single extended star is more plausible, considering that Brun 862 is classified as a supergiant. We compare the radius of 71 R⊙ with values from Levesque et al. (2005), who list K2 and K2.5 stars with ∼100 R⊙. Thus, our determined radius agrees well with Levesque et al. (2005). We determine companion detection limits on a 3σ level for 1.70–46.8 AU of Δm = 4.75 (≈2.2 M⊙).
4.2.6. TCC 59
TCC 59 is a Young Stellar Object (YSO) with a protoplanetary disk (O’Dell & Wong 1996). It has a K-magnitude of 11.05 (Muench et al. 2002). For a lower mass limit, we compare the absolute K-magnitude with isochrones as described in Sect. 4.1.2, and get 1.5 M⊙. We found no extinction measurements for this star, but as a YSO, its reddening in K-band is supposedly non-negligible. The color of (J − K)=1.35 (Muench et al. 2002) is very red compared to the other stars in our sample. This indicates significant dust extinction or intrinsic infrared excess due to, for example, a circumstellar disk. Thus, we expect TCC 59 to be intrinsically brighter and more massive and only provide a lower limit. Close et al. (2012) claimed the detection of a companion star with 136 ± 3 mas (≈56 ± 2 AU) separation.
In the data taken with GRAVITY in January 2018, we find signatures in visibilities and closure phases, but cannot find a good fit. Thus, it is not clear whether there is a companion star or whether the signatures result from a potential disk.
4.2.7. TCC 43
TCC 43 has a K-magnitude of 10.44 (Muench et al. 2002). Petr et al. (1998) and Simon et al. (1999) observed TCC 43 and did not find a companion star. With GRAVITY we see minor signatures in visibilities and closure phase, but cannot find a good fit. We set a lower mass limit of ∼1.5–1.7 M⊙, that is, an A or F-type using the method described in Sect. 4.1.2. We have no value for the extinction, therefore the star might be brighter and more massive.
With GRAVITY we can exclude companions in the 1.70–16.6 AU range with Δm = 1.4 (≈0.9 M⊙) on a 3σ level. For separations of 16.6–46.8 AU, we place a limit of Δm = 0.61 (≈1.1 M⊙).
4.2.8. LP Ori (HD 36982, Brun 530, Parenago 1772)
LP Ori is a B1.5V-type star (Samus’ et al. 2017) with mK = 7.47 (Cutri et al. 2003). Hillenbrand (1997) found an extinction AV = 1.47 and a mass of 7.15 M⊙. Reiter et al. (2018) determined a mass of 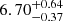 M⊙. Preibisch et al. (1999) and Abt et al. (1991) observed LP Ori but found no companion.
M⊙. Preibisch et al. (1999) and Abt et al. (1991) observed LP Ori but found no companion.
With GRAVITY we set a 3σ companion limit of Δm = 2.12 (≈1.9 M⊙) for separations of 1.70–8.3 AU and Δm = 2.87 (≈1.5 M⊙) for 8.3–46.8 AU.
4.2.9. HD 37115 (Brun 907, Parenago 2271)
HD 371151 is a B5-type star (Röser et al. 1994) with a K-magnitude of 7.13 (Cutri et al. 2003). Preibisch et al. (1999) estimated a mass of 5 M⊙, Hillenbrand (1997) of 5.7 M⊙ and Wolff et al. (2004) estimated a mass of 5.5 M⊙. We take the mean mass 5.4 ± 0.4 M⊙. Rio et al. (2016) determined AV = 5.9 ± 0.3.
Preibisch et al. (1999) found a companion at ∼890 mas separation, which corresponds to 368 ± 6 AU. The mass ratio is ∼0.29 and the estimated mass is ∼1.5 M⊙ with an upper limit of < 5 M⊙.
We do not detect a companion with GRAVITY but set a 3σ detection limit of Δm = 2 (≈2.2 M⊙) for the range of 1.70–8.3 AU. For 8.3–16.6 AU we get a limit of Δm = 2.42 (≈1.9 M⊙) and limit of Δm = 3.24 (≈1.5 M⊙) for separation range 16.6–46.8 AU.
4.2.10. HD 37150 (Brun 980, Parenago 2366)
HD 37150 is a B3III or -IV-type star (Houk & Swift 1999) with mK = 7.11 (Cutri et al. 2003). We estimate a lower mass limit of 7 M⊙, using the calibration table for MK spectral types from Allen & Cox (2000, 390, Table 15.8).
We do not detect a companion with GRAVITY. We set a 3σ detection limit of Δm = 2.29 (≈1.9 M⊙) in the range of 1.70–8.3 AU and Δm = 3.08 (≈1.5 M⊙) for separations of 8.3–46.8 AU.
4.3. Summary
We illustrate the observed companion systems in Fig. 13 and provide a summary of all stellar systems and their properties in Table B.2. Bold objects were observed with GRAVITY. For an overview of all observations, refer to Table B.1. In total, 16 objects were observed, out of which eleven are confirmed multiple systems. This leads to a multiplicity fraction of 11/16 = 0.688. All multiple systems combined have a total number of 22 confirmed companion stars. Thus, we get a companion fraction of 22/16 = 1.375.
 |
Fig. 13. Summary of the observed multiple systems in the Orion Nebula. We observed 16 multiple systems with a total number of 22 companion stars. The respective scales are indicated. The images of θ1 Ori B are from actual obervational data, except for the spectroscopic B1, B5 system, which is only a representation. The orbital positions for θ1 Ori D and θ1 Ori C are the positions obtained in this work and from the literature. All remaining close up depiction of stars (gray) are only for illustrative purposes and were not created with observational data. The background image of the Orion Nebula was created by ESO Igor Chekalin. The zoom of the Trapezium Cluster (θ1) is a cut from ESO M. McCaughrean et al. (AIP). |
Brun 862 is a supergiant with no clear detection of a companion star. The evolutionary stage of Brun 862 differs greatly from the remaining stars in our sample. Additionally, the Gaia parallax of Brun 862 (1.690 ± 0.094, Gaia Collaboration 2016, 2018; Luri et al. 2018) diverges significantly from the Gaia parallax of, for example θ1 Ori C (2.472 ± 0.082). We will not include Brun 862 in the following discussion.
5. Discussion
Our sample comprises 15 objects, excluding Brun 862. Eleven of them are multiple systems with up to six members. With long baseline interferometry observations performed using GRAVITY, we close the gap between close spectroscopic companions and more distant visual companions. This yields a complete sample of companions for our observed systems down to our detection limit of 1.5–3 M⊙.
5.1. Multiplicity
Duchêne & Kraus (2013) provided an overview of the multiplicity of stars. The multiplicity fraction MF is defined as
where Nmult, the number of multiple systems, is divided by the total number of systems, namely the sum of multiple star and single star systems. The companion frequency or companion fraction CF is the average number of companions per target
with Ncomp as the number of companion stars, Nprim = Nmult as the number of primary stars and Nsingle as the number of single stars.
We compare our resulting companion fraction with the values from Duchêne & Kraus (2013), Sana et al. (2014), and Moe & Di Stefano (2017), as shown in Fig. 14. Generally, we notice a rising companion fraction for higher masses. For stars with 3–7 M⊙, we obtain a companion fraction of 1 ± 0.6, which agrees well with Duchêne & Kraus (2013), and Moe & Di Stefano (2017). For 7–16 M⊙, our companion fraction is 2.0 ± 0.9 and agrees with 1.0 ± 0.2 by Duchêne & Kraus (2013), and 1.6 ± 0.2 by Moe & Di Stefano (2017) within the error bars. We get a companion fraction of 2.3 ± 0.4 for stars > 16 M⊙, which is nearly by a factor of two larger than the result 1.3 ± 0.2 obtained by Duchêne & Kraus (2013). Sana et al. (2014) presented the result of a survey of O stars and derived a companion fraction of 1.45 ± 0.5 for main sequence stars with companions at separations of 1–600 AU, which is comparable to our observed companion separations. Their survey covered companions up to separation ranges of 1–16 000 AU and yields a companion fraction of 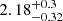 for O main sequence stars. We cannot assign companion stars at such large separations in the ONC, because the system would be unstable due to interactions with other cluster members. Still, our observed companion fraction of 2.3 ± 0.4, for separation ranges up to ∼600 AU, agrees with the result of
for O main sequence stars. We cannot assign companion stars at such large separations in the ONC, because the system would be unstable due to interactions with other cluster members. Still, our observed companion fraction of 2.3 ± 0.4, for separation ranges up to ∼600 AU, agrees with the result of 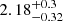 by Sana et al. (2014), for their full separation range of 1–16 000 AU. Our result is also in good agreement with the companion fraction of 2.1 ± 0.3, determined by Moe & Di Stefano (2017) for O-type stars with masses > 16 M⊙.
by Sana et al. (2014), for their full separation range of 1–16 000 AU. Our result is also in good agreement with the companion fraction of 2.1 ± 0.3, determined by Moe & Di Stefano (2017) for O-type stars with masses > 16 M⊙.
 |
Fig. 14. Companion fraction CF as measured with GRAVITY for mass ranges < 3 M⊙, 3–7 M⊙, 7–16 M⊙, > 16 M⊙ (red circles). The values from Duchêne & Kraus (2013) for very low mass stars (VLM), spectral types M, K, G, F, A, B, early B and O (from left to right), and the values from Sana et al. (2014) for O stars are plotted for reference. The companion fraction of Sana et al. (2014) depends on the considered separation range for companions. A range ≲600 AU is similar to the separations in our sample. |
The multiplicity fraction or multiplicity frequency (MF) is the number of multiple systems divided by the number of targets, as in Eq. (3). We compare our MF with previous results in Fig. 15. For stars > 3 M⊙, the MF of our sample is higher than the lower limits from Duchêne & Kraus (2013). For the mass range ≥16 M⊙ we obtain a MF of 100%. This agrees with the MF 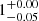 from Sana et al. (2014) and
from Sana et al. (2014) and 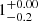 from Moe & Di Stefano (2017) for main sequence stars of type O. We consider our sample to be complete for stars > 3 M⊙. For each mass range we use
from Moe & Di Stefano (2017) for main sequence stars of type O. We consider our sample to be complete for stars > 3 M⊙. For each mass range we use 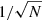 as uncertainty estimate. Thus, the actual MF of stars < 3 M⊙ is probably higher than our biased value.
as uncertainty estimate. Thus, the actual MF of stars < 3 M⊙ is probably higher than our biased value.
 |
Fig. 15. Multiplicity fraction MF as measured with GRAVITY for mass ranges < 3 M⊙, 3–7 M⊙, 7–16 M⊙, > 16 M⊙ (red circles). The values from Duchêne & Kraus (2013) for the whole mass range of ≲1 M⊙ to O stars and the values from Sana et al. (2014) for O stars are plotted for reference. For each mass range we use |
5.2. Initial mass function
In our discussion of the initial mass function (IMF), we will only consider stars ≥3 M⊙. This corresponds to our most conservative detection limit (see Table B.2). Down to this limit, we consider our sample to be complete for separations ≲600 AU.
The IMF describes the frequency of stars with masses in a given mass bin (m + dm) at birth. For a detailed review of the IMF see Bastian et al. (2010), Scalo (1986) or Kroupa et al. (2013) and references therein. Salpeter (1955) suggested a power law of the form:
with m as the mass, N as the number of stars in the mass range logm + dlogm and Γ = 1.35. The IMF can also be written in the form of
with the relation
yielding α = Γ + 1. For > 1 M⊙, Muench et al. (2002) suggested Γ = 1.21 for the Trapezium. More generally, Kroupa (2001) estimated Γ = 1.3 ± 0.7, which agrees with Chabrier (2003) and their result of Γ = 1.3 ± 0.3 for young clusters. Kroupa et al. (2013) noted that a good estimate for the intermediate mass regime 1 < m < 8 M⊙ is difficult, but suggested Γ = 1.3 as the best estimate Kroupa (2002, 2003) and Massey (2003) found slopes of −1.35 for massive stars. For example Muench et al. (2002); Da Rio et al. (2010) concluded that the IMF of the ONC is described by a Salpeter IMF for stars ≥0.6 M⊙. Further measurements of the exponent focused mainly on the low mass regime (≤1 M⊙), see for example Mužić et al. (2017), Drass et al. (2016), Da Rio et al. (2012) or Muench et al. (2002).
We bin our observed distribution of masses for all stars and compare the histogram with a model IMF suggested by Kroupa (2001) and Chabrier (2003), as shown in Fig. 16. The distribution is calculated by integrating the probability density f(m) = dN/dm ∝ m−2.3 ± 0.3. The cumulative distribution is depicted in Fig. 17. The observed mass distribution of the most massive ONC stars – including their companions – agrees remarkably well with the IMF for field stars proposed by Kroupa (2001, 2002, 2003), Massey (2003) and Chabrier (2003). This illustrates the importance of resolving companions to get a complete sample. Counting only the primary component would result in a smaller power-law index and yield the impression that massive stars were distributed differently than in the field. We estimate the uncertainties in Fig. 16 to be 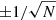 for each bin.
for each bin.
 |
Fig. 16. Normalized histogram of stars per mass. The observed distribution is compared with distribution functions of Chabrier (2003). We estimate the uncertainties to be |
 |
Fig. 17. Cumulative distribution of stars per mass with the respective distribution functions. |
5.3. Distribution of masses and mass ratios
We compare stellar masses, mass ratios q, and separations of companions by plotting different quantities against each other. It is important to stress that our sample is only complete for masses ≥3 M⊙. This leads to a bias, especially for the mass ratio, since we will be missing stars at the low mass end. We present our results here based on the observed stars, keeping in mind that we are missing a part of the population. Furthermore, photometric mass estimates rely strongly on evolutionary models and can comprise many uncertainties. It is only possible to provide a precise system mass if the orbit is known.
First, we look at the primary mass and the corresponding mass ratios for all companions. In Fig. 18, the mass ratio per primary mass is displayed. Different markers represent different systems. Additionally, the color categorizes the companions according to their order, going from the innermost to the outermost. We find high mass ratios ≳0.6 only for primary masses ≲8 M⊙. For stars with masses ≳8 M⊙, the mass ratio is ≲0.5. In every system, the most massive companion is either the closest or second-closest companion to the primary star.
 |
Fig. 18. Mass ratio per primary mass; each system is represented by a different marker. The colors indicate the companion order, starting from the innermost. Thus, the first companion (blue) means the companion closest to the primary, the second companion (orange) means the second-closest companion, etc. The gray area indicates the mass range ≤3 M⊙, for which we are no longer complete. The gray dotted line marks the individual mass limits for each system as given in Table B.2. |
The most massive companions ≳8 M⊙ belong to the most massive primary stars with ≥30 M⊙. They have a mass ratio in the range 0.3–0.4. We see no tendency for the companion to have a high mass similar to the primary – for example q ≈ 1 – if the primary is a high mass star. This disagrees with the result of Chini et al. (2012), who found that most massive stars have companions of similar mass. In our sample, only intermediate mass stars with masses between 3–8 M⊙ have a q ≳ 0.5.
A histogram of the mass ratio q is shown in Fig. 19 and the cumulative distribution in Fig. 20. We find a clear preference for small mass ratios, hence large mass differences. The most common values are ≤0.2. Our distribution is biased, because our sample is incomplete for stars with masses < 3 M⊙. Furthermore, small mass ratios (q < 0.01) are hard to detect with interferometry and imaging due to the extreme contrast ratios. In other words, any survey will be incomplete at low q. The underlying distribution is likely to show an even stronger preference for low q. We want to compare our distribution with other samples. Duchêne & Kraus (2013) stated that a power law is not an ideal representation for most distributions of q, but it is still the best way to compare multiple systems with different mass ranges. Thus, we follow their approach and fit our distribution with a power law dN/dq ∝ qγ, similar to Sect. 5.2. Our distribution of q is best fitted by γ = −1.7 ± 0.3 (see Fig. 19). Moe & Di Stefano (2017) found values for γ of −0.5 ± 0.3 for stars with a period of 10 days, γ = −1.7 ± 0.3 for stars with a period of 1000 days and masses > 5 M⊙, and γ = −2.0 ± 0.3 for stars with a period ≳270 years and masses > 5 M⊙. Our sample consists of stars with periods ranging from a few days to > 1000 yr (see Table B.2). These values agree well with our resulting γ of −1.7 ± 0.3. Thus, considering the uncertainties, our companion mass distribution can be described by an IMF with α = 2.3 ± 0.3. In Fig. 21, we calculate γ for Chabrier (2003) by taking a primary mass and considering companions down to q = 0.1. For stars ≤1 M⊙ the IMF follows a lognormal distribution. As soon as the primary mass is < 10 M⊙, the lognormal distribution changes the companion mass distributions of companions ≤1 M⊙. Hence, γ is no longer constant.
 |
Fig. 19. Normalized histogram of all mass ratios q and the best fit curve of a power law ∝qγ = q−1.7 ± 0.3. |
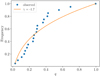 |
Fig. 20. Cumulative distribution of all mass ratios q and the best fit curve of a power law ∝qγ = q−1.7 ± 0.3. |
 |
Fig. 21. Power-law index γ of the mass ratio distribution with dN/dq ∝ qγ for different masses. The squares represent the fits of the overall population of multiple systems by Duchêne & Kraus (2013). The diamonds are the results for tight binaries (smaller separations than average) and the down-facing triangles the result for wide binaries (larger separations than average) by Duchêne & Kraus (2013). Our data is represented by a distribution with an index of −1.7 ± 0.3 (red circle). If the companion stars follow the IMF of Chabrier (2003), the index of q is equal to the index of the IMF with γ = −2.3 ± 0.3, for companions with masses 1 ≤ mcomp ≤ mprimary. The shaded area indicates the uncertainties of the IMF. |
We compare our distribution of q with the distributions in Duchêne & Kraus (2013). Figure 21 shows γ for systems with different primary mass ranges. Our sample is in the range ≳1 M⊙. The distributions by Duchêne & Kraus (2013) follow a nearly flat distribution γ ≲ 0.5 for masses ≳0.3 M⊙. We notice a steeper distribution in our sample with γ = −1.7 than Duchêne & Kraus (2013) for masses ≥3 M⊙. If we assume that the companion mass follows an IMF, the index γ will correspond to the power-law index α = −γ. Our result agrees within the uncertainties of an IMF according to Kroupa (2001) with α = 2.3 ± 0.6 and is consistent with the exponent 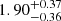 obtained by Schneider et al. (2018).
obtained by Schneider et al. (2018).
In Fig. 22, we compare the resulting mass ratios q with the corresponding companion separation. We notice no significant correlation between q and separation. The only system with q ≈ 1 has a small separation of ≈0.09 AU. But we also find systems with a separation of ∼400 AU and q ∼ 0.6, which is one of the highest mass ratios in our sample.
 |
Fig. 22. Separation in AU in a logarithmic scale per mass ratio q. |
Figure 23 shows the companion separation per system. There appears to be a preferred separation range for companion stars. We find eight companions within 1 AU, thus we notice a tendency for binaries with separation < 1 AU, which are typically spectroscopic binaries. Then there are only two companions within 1–10 AU. The next five companions cover the range 10–100 AU. This means, there are nearly as many companions within 1–100 AU as there are within 0.08–1 AU.
 |
Fig. 23. Companion separation per system with given primary mass in M⊙. In the range between 1–100 AU, we are sensitive down to 3 M⊙. There are equally many companion stars in the range 0.1–1 AU as in the range 1–100 AU. The colors indicate different systems, the marker size scales with the square root of the companion mass. The dashes indicate missing information about the mass of the first companion of θ2 Ori C and TCC 59. |
We present the distribution of companion separation in Fig. 24. Duchêne & Kraus (2013) described the orbital period distribution of OB stars with a peak at ∼0.2 AU and with a decreasing power-law tail for > 1 AU. They also determined the distribution for A stars, which is bimodal. A qualitative sketch is provided in Fig. 24 in comparison to the distribution of our observed separations. We also find a peak for companions in short distance but in a range up to ∼4 AU. Furthermore, we notice a decrease between 1–100 AU and a second peak at 400–600 AU, that is, a bimodal distribution. Our distribution more closely resembles that of the Duchêne & Kraus (2013) distribution for A stars, even though our sample consists mainly of O and B stars (see Table B.2).
 |
Fig. 24. Normalized histogram of companion separation. For comparison, we plot the qualitative distribution of Duchêne & Kraus (2013) for A (dotted) and OB stars (solid). The distribution of our separations for mainly B and O stars is bimodal and resembles more that of the Duchêne & Kraus (2013) distribution of A-type stars. We notice a decrease of companions in the range of 1–100 AU. |
On the top of Fig. 25, we compare the companion mass with separation. There appears to be no trend for the companion mass over the separations. Finally, we compare the multiplicity with the system distance from θ1 Ori C as shown in Fig. 25 on the bottom. In a comparable plot by Preibisch et al. (1999), there was a trend toward fewer companions for more distant objects from θ1 Ori C. We do not observe such a trend in our sample. It is possible that stars move away from their original birthplace, so that their location and multiplicity differs from their primordial distribution. It is also possible that the multiplicity was not triggered by winds and outflows of θ1 Ori C, but is universal. It could also depend on the stellar density of the cluster in general.
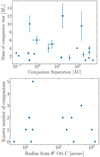 |
Fig. 25. Top: separation versus the companion mass. Bottom: multiplicity of objects plotted as a function of distance from θ1 Ori C in arcseconds. |
5.4. Comparison with star formation models
We compare our results with star formation models. The core accretion model predicts that the multiplicity and companion fraction rises with stellar mass (Clarke 2001). Disk fragmentation predicts low mass companions at 100-1000 AU (Kratter & Matzner 2006; Krumholz 2016). Krumholz (2006) suggested that high temperatures stabilize the core, leading to less fragmentation, even for high mass cores. This results in a small amount of massive protostars and a preference for binaries with high mass components. These massive components of high mass stars make the mass distribution of companion stars top-heavy. The massive core fragment also needs a larger volume to form, thus, we expect a correlation between system mass and separation.
Competitive accretion predicts a dependence of the separation r on the system mass M. In a turbulent medium, the relation is r ∝ M−2 (Bonnell & Bate 2005). The result of competitive accretion is a cluster with a large range of masses, where high mass stars are formed at the center of the cluster core (Bonnell 2005b) with close high mass companions. The companion frequency rises with stellar mass, see for example Peter et al. (2012).
Binaries with low masses and wide separations continue to accrete mass and evolve to a close high mass binary. The result is a close system with two massive components (Bonnell & Bate 2005). The fragmentation of clouds leads to clusters similar to the Trapezium Cluster (Bonnell & Bate 2005; Bonnell 2005a,b). The model also predicts three-body captures, where a high mass primary star with a low mass companion captures a massive wide companion star (Bonnell 2005b). The massive companion star absorbs most of the binding energy of the low mass star and the separation between the two high mass components shrinks. The low mass companion is either ejected or evolves to a wide binary. The resulting system is a close high mass binary with a high mass companion and a third low mass component at larger separations (Bate et al. 2002). This preference for high mass companions also yields a top-heavy companion mass distribution. Another important factor is the low mass accretion rate of competitive accretion. Wang et al. (2010) showed that star formation with competitive accretion requires 106 yr when considering protostellar outflows and magnetic fields. Dynamical processes also need time to take place.
For massive star formation through stellar collisions or mergers, the stellar mass distribution does not result in a Salpeter IMF. The collisions lead to runaway growth of a few objects, which does not produce a smooth mass distribution (Moeckel & Clarke 2011; Krumholz 2015). The collision of stars requires high densities > 106 stars pc−3. Massive stars are a merger product and become less likely to be close binary systems (Bonnell & Bate 2005).
Our observations of the stars in the ONC yield a Salpeter IMF for all stars, including the companions. We do not observe massive binaries with equally massive companion stars. Also, we find no preference for close massive systems. The mass of the companion star is not correlated with the separation. We only find high mass ratios (≳0.5) for primary stars with ≲7 M⊙. In our sample, we observe fewer companions in the range of 1–100 AU. This indicates different formation mechanism for‘ different separation ranges. This could be the transition of a mechanism responsible for tight binaries, for example failed mergers or accretion onto binaries, and for instance disk fragmentation. Kratter & Lodato (2016) concluded that the disk of a star with 8 M⊙ is sufficiently cool for fragmentation at ≥50 AU. This agrees with our gap between 1–10 AU and a slowly rising number of companions within 10–100 AU. Table 3 provides an overview of the various models and the predicted correlations. We compare the predictions with our findings.
Comparison of observable quantities from the star formation models with our observations.
We can exclude collisions as the main star formation process, because it does not represent our IMF and the density of the Trapezium (∼104 stars pc−3 Hillenbrand & Hartmann 1998) is lower than the required ∼106 stars pc−3. θ1 Ori C1 might still be the result of stellar merging, but the collision of stars is not a dominant process in the ONC. We find several aspects in favor of competitive accretion in our sample, for example, the formation of massive stars at the cluster center and the variety of the mass range. However, other features do not support competitive accretion, for instance we see no tight massive binaries or a preference for equal masses.
An important factor is that competitive accretion needs ∼1 Myr to form massive stars (Wang et al. 2010; Portegies Zwart et al. 2010), whereas the ONC has an average age of < 1 Myr with a spread of less than 2 Myr. Core accretion provides a mechanism of gaining mass without tightening the binary separation. Both models have difficulties with reproducing our observations. However, we clearly do not find a strong dependence of binary separation with system mass r ∝ M−2 and an anticorrelation of mass ratios and separation. This argues against a dominant mode of competitive accretion. We also need to consider that some dynamic processes may not be completed yet, which could change the masses or companion fraction of the ONC.
Krumholz et al. (2012) showed in a simulation that a combination of core accretion and competitive accretion is also possible. Massive stars started formation in distinct massive cores, according to the core accretion model. But the formed stars engaged in dynamical interactions while accreting mass, similar to the competitive accretion model. This resulted in hierarchical systems like the Trapezium Cluster. This combination could thus also be a possible scenario for the Trapezium, but needs further examination.
We note that both accretion scenarios initially form companions at large radii, which become eventually tight binaries, for example McKee & Ostriker (2007). This tightening process occurs through dynamical interactions with the disk or cluster members, or through ambient gas accretion and energy loss. It is therefore plausible that the observed fraction of close equal mass binaries depends on the cluster age. The ONC – with an age of 1 Myr (Hillenbrand 1997) – is one of the youngest massive star clusters in the Milky Way. Our finding of a large number of wide binaries with high mass ratios might reflect the fact that the binary population in the ONC did not have enough time to be altered by dynamical interactions (e.g., Moe & Kratter (2018) show different simulated scenarios of how close binaries can be formed, 60% form by unstable triples). Sana et al. (2017) also notice a lack of close companions and conclude their findings may support a theory in which binaries form initially at large separations and then harden to closer systems. This could explain why the companion separations and masses in the ONC are different than the distributions in more evolved clusters.
6. Conclusion
In order to gain a deeper understanding of massive star and cluster formation, this work presents an interferometric study of massive stars in the Orion Trapezium Cluster and its vicinity. The outstanding resolution of the VLTI (∼2 mas) and the sensitivity of GRAVITY allowed us to probe stars for companions in the widely unexplored range of 1–100 AU. We observed the 16 most massive stars with masses of 2–44 M⊙. We detected three new companions for the systems θ1 Ori B, θ2 Ori B, and θ2 Ori C. We confirmed the suspected companion for NU Ori and determined a separation of 3.6 ± 0.1 AU. Combined with the companions reported in the literature – based on speckle or AO imaging and spectroscopic surveys –, we find a total of 22 companion stars. θ1 Ori B6 is at a separation of 3.5–7.2 AU and we estimated a mass of 7.3 ± 0.5 M⊙. The new companion θ2 Ori B2 has a separation of 40 ± 1 AU and an approximate mass of 1.6 ± 0.7 M⊙. For θ2 Ori C2 we determined a separation of 15.7 ± 0.2 AU and estimated a mass of 1.7 ± 0.2. NU Ori4 has a separation of 3.6 ± 0.1 AU and an estimated mass of 4 ± 1 M⊙.
We confirmed companions for θ1 Ori A, θ1 Ori C, θ1 Ori D, and θ2 Ori A, all with substantially improved astrometry and photometric mass estimates. Additionally, we refined the orbit of the eccentric high-mass binary θ1 Ori C and obtained a period P = 11.4 ± 0.2 yr and a semi-major axis a = 18.2 ± 0.3 AU. Furthermore, we derived a new orbit for θ1 Ori D with a semi-major axis a = 0.77 ± 0.03 AU and a period P = 53.03 ± 0.06 d. The system mass is 21.7 M⊙, assuming a distance to the ONC of 414 ± 7 pc (Menten et al. 2007). We derived a multiplicity fraction of 0.69 and a companion fraction of 1.38 for our complete sample. Our observations are complete down to 3 M⊙. We illustrate the observed companion systems in Fig. 13.
The companion fraction rises with primary mass and extends from ∼0.6 for a mass range of ≤1–2 M⊙ to 2.3 ± 0.3 for objects with > 16 M⊙. The multiplicity fraction also increases with object mass. We obtain a multiplicity fraction of 0.5 for objects with ≤1–2 M⊙ and it rises up to 100% for stars with > 16 M⊙.
The companion mass distribution of our sample resembles an IMF with N ∝ m−2.3 ± 0.3. We fit the distribution of the mass ratio q with a power law ∝q−1.7 ± 0.1. The exponent of the power law is smaller compared to previous findings. We did not observe a preference for twin binaries in any mass range and more specifically, there is no tendency for high-mass stars to have companions of comparable masses in our sample. Additionally, we detected no correlation of the companion mass and the companion star separation.
We observed a bimodal distribution of the mass ratio q compared with the respective companion separation. This bimodal distribution resembles the distribution of A stars, even though our sample comprises mainly OB stars. We obtained a peak at separations ∼0.5 AU, followed by only few companions between 1–100 AU. This indicates a change of formation mechanism. Disk fragmentation becomes relevant at scales ≳50 AU. Hence, the observations indicate a transition to companions formed by disk fragmentation. We found a second peak for separations ≥100 AU. Our sample covers separations up to ∼600 AU, thus we limit our conclusion to this separation range.
Finally, we compared our observational results with the expected properties of star formation models. We found no clear tendency for either core accretion or competitive accretion. There are several aspects contradicting the predictions of core accretion, competitive accretion and stellar collisions. We excluded stellar collisions as the main formation mechanism.
We notice fundamental differences between our observations and previous observations of star forming regions. The main differences are that the companion mass distribution follows a Salpeter IMF, and that we find no tendency for high-mass binaries with equal mass companions. The differences in stellar mass distribution could result from the improved sensitivity with long baseline interferometry and GRAVITY. Another explanation could be the very young age of Orion, which is too short for a dynamical evolution of its binary systems. Close systems, as often observed for O-type stars, have not yet formed in the ONC. Further similar studies of other star forming regions are necessary.
Acknowledgments
This work is based on observations made with ESO Telescopes at the La Silla Paranal Observatory under program ID 0100.D-0576, ID 098.D-0322, ID 60.A-9102, and ID 0100.C-0608. This research has made use of the Jean-Marie Mariotti Center Aspro2 service (Available at http://www.jmmc.fr/aspro2) (Bourgès et al. 2013) and SearchCal service (available at http://www.jmmc.fr/searchcal) co-developped by LAGRANGE and IPAG, of CDS Astronomical Databases SIMBAD and VIZIER (available at http://cdsweb.u-strasbg.fr/) (Chelli et al. 2016), of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018), of PyAstronomy (https://github.com/sczesla/PyAstronomy), and of MiRA (https://github.com/emmt/MiRA). R.G.L has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie Grant Agreement No. 706320. J.S.B. acknowledges the support from the ESO fellowship program. A.A., N.A., P.G. & P.G. acknowledge support from FCT-Portugal with reference UIDFIS000992013. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. N.A. acknowledges the support from ERC Starting Grant (Grant Agreement No. 639889).
References
- Absil, O., Le Bouquin, J.-B., Berger, J.-P., et al. 2011, A&A, 535, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abt, H. A., Wang, R., & Cardona, O. 1991, AJ, 367, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Aikman, G. C. L., & Goldberg, B. A. 1974, JRASC, 68, 205 [NASA ADS] [Google Scholar]
- Allen, C., & Cox, A. 2000, Allen’s Astrophysical Quantities (Springer) [Google Scholar]
- Allen, C., Costero, R., Ruelas-Mayorga, A., & Sánchez, L. J. 2017, MNRAS, 466, 4937 [NASA ADS] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Balega, I., Balega, Y. Y., Maksimov, A. F., et al. 2004, A&A, 422, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balega, I. I., Balega, Y. Y., Maksimov, A. F., et al. 2007, Astrophys. Bull., 62, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Balega, Y. Y., Chentsov, E. L., Rzaev, A. K., & Weigelt, G. 2015, in Physics and Evolution of Magnetic and Related Stars, eds. Y. Y. Balega, I. I. Romanyuk, & D. O. Kudryavtsev, ASP Conf. Ser., 494, 57 [NASA ADS] [Google Scholar]
- Bally, J., Moeckel, N., & Throop, H. 2005, Chondrites Protoplanetary Disk, 341, 81 [NASA ADS] [Google Scholar]
- Bastian, N., Covey, K. R., & Meyer, M. R. 2010, ARA&A, 48, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R., Bonnell, I. A., & Bromm, V. 2002, MNRAS, 336, 705 [Google Scholar]
- Bonnell, I. A. 2005a, in The Initial Mass Function 50 Years Later, eds. E. Corbelli, F. Palla, & H. Zinnecker, Astrophys. Space Sci. Libr., 327, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A. 2005b, in Massive Star Birth: A Crossroads of Astrophysics, eds. R. Cesaroni, M. Felli, E. Churchwell, & M. Walmsley, IAU Symposium, 227, 266 [NASA ADS] [Google Scholar]
- Bonnell, I. A., & Bate, M. R. 2005, MNRAS, 362, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., Bate, M. R., Clarke, C. J., & Pringle, J. E. 1997, MNRAS, 285, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., Bate, M. R., Clarke, C. J., & Pringle, J. E. 2001, MNRAS, 323, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., Bate, M. R., & Vine, S. G. 2003, MNRAS, 343, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Bossi, M., Gaspani, A., Scardia, M., & Tadini, M. 1989, A&A, 222, 117 [NASA ADS] [Google Scholar]
- Bourgès, L., Mella, G., Lafrasse, S., & Duvert, G. 2013, Astrophysics Source Code Library [record ascl:1310.005] [Google Scholar]
- Bragança, G. A., Daflon, S., Cunha, K., et al. 2012, AJ, 144, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Briceño, C., Preibisch, T., Sherry, W. H., et al. 2007, Protostars Planets V, 345 [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chelli, A., Duvert, G., Bourgès, L., et al. 2016, A&A, 589, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chini, R., Nasseri, A., Hoffmeister, V. H., Buda, L., & Barr, A. 2011, in Evol. Compact Bin. ASP Conf. Ser., eds. L. Schmidtobreick, M. Schreiber, & C. Tappert, 447, 67 [NASA ADS] [Google Scholar]
- Chini, R., Hoffmeister, V. H., Nasseri, A., Stahl, O., & Zinnecker, H. 2012, MNRAS, 424, 1925 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, C. J. 2001, in The Formation of Binary Stars, eds. H. Zinnecker, & R. Mathieu, IAU Symp., 200, 346 [NASA ADS] [Google Scholar]
- Close, L. M., Wildi, F., Lloyd-Hart, M., et al. 2003, AJ, 599, 537 [CrossRef] [Google Scholar]
- Close, L. M., Puglisi, A., Males, J. R., et al. 2012, AJ, 749, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Close, L. M., Males, J. R., Morzinski, K., et al. 2013, AJ, 774, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Corporon, P., & Lagrange, A.-M. 1999, Astron. Astrophys. Suppl. Ser., 136, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Costero, R., Echevarria, J., Richer, M. G., Poveda, A., & Li, W. 2006, IAU Circ., 8669 [Google Scholar]
- Costero, R., Allen, C., Echevarr, J., et al. 2008, Rev. Mex. Astron. Astrofis. Ser. Conf., 34, 102 [NASA ADS] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Da Rio, N., Robberto, M., Soderblom, D. R., et al. 2010, ApJ, 722, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Da Rio, N., Robberto, M., Hillenbrand, L. A., Henning, T., & Stassun, K. G. 2012, ApJ, 748, 14 [NASA ADS] [CrossRef] [Google Scholar]
- de Wit, W. J., Testi, L., Palla, F., Vanzi, L., & Zinnecker, H. 2004, A&A, 425, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Wit, W. J., Testi, L., Palla, F., & Zinnecker, H. 2005, A&A, 437, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donati, J.-F., Babel, J., Harries, T. J., et al. 2002, MNRAS, 333, 55 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Drass, H., Haas, M., Chini, R., et al. 2016, MNRAS, 461, 1734 [NASA ADS] [CrossRef] [Google Scholar]
- Ducati, J. R. 2002, VizieR Online Data Catalog: II/237 [Google Scholar]
- Duchêne, G., & Kraus, A. 2013, Ann. Rev. Astron. Astrophys, 51, 269 [CrossRef] [Google Scholar]
- Feigelson, E. D., Broos, P., Gaffney, III., J. A., et al. 2002, ApJ, 574, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Mérand, A., Kervella, P., et al. 2015, A&A, 579, A1 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Genzel, R., & Stutzki, J. 1989, ARA&A, 27, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Gravity Collaboration (Abuter, R., et al.) 2017, A&A, 602, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grellmann, R., Preibisch, T., Ratzka, T., et al. 2013, A&A, 550, 531 [Google Scholar]
- Grunhut, J. H., Wade, G. A., Neiner, C., et al. 2017, MNRAS, 465, 2432 [NASA ADS] [CrossRef] [Google Scholar]
- Habibi, M., Gillessen, S., Martins, F., et al. 2017, ApJ, 847, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Hartwig, E. 1921, Astron. Nachr., 212, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H. 1950, ApJ, 11, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H., & Griffin, R. F. 2006, AJ, 132, 1763 [NASA ADS] [CrossRef] [Google Scholar]
- Herrero, A., Kudritzki, R. P., Vilchez, J. M., et al. 1992, A&A, 261, 209 [NASA ADS] [Google Scholar]
- Hillenbrand, L. A. 1997, AJ, 113, 1733 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L. A., & Hartmann, L. W. 1998, AJ, 492, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Houk, N., & Swift, C. 1999, Michigan Spectral Survey, Ann Arbor, Dep Astron., Univ. Michigan, 5 [Google Scholar]
- Kennicutt, R. C. 1998, Annu. Rev. Astron. Astrophys., 36, 189 [Google Scholar]
- Köhler, R., Petr-Gotzens, M. G., McCaughrean, M. J., et al. 2006, A&A, 458, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kratter, K. M., & Matzner, C. D. 2006, MNRAS, 373, 1563 [NASA ADS] [CrossRef] [Google Scholar]
- Kratter, K., & Lodato, G. 2016, Ann. Rev. Astron. Astrophys., 54, 271 [CrossRef] [Google Scholar]
- Kraus, S., Balega, Y. Y., Berger, J.-P., et al. 2007, A&A, 466, 649 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, S., Weigelt, G., Balega, Y. Y., et al. 2009, A&A, 497, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, 2002, Science, 295, 5552 [Google Scholar]
- Kroupa, 2003, ApJ, 598, 2 [NASA ADS] [Google Scholar]
- Kroupa, P., Weidner, C., Pflamm-Altenburg, J., et al. 2013, in The Stellar and Sub-Stellar Initial Mass Function of Simple and Composite Populations, eds. T. D. Oswalt, & G. Gilmore (Dordrecht, Netherlands: Springer), 115 [Google Scholar]
- Krumholz, M. R. 2006, ApJ, 641, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R. 2015, in The Formation of Very Massive Stars, ed. J. S. Vink (Cham: Springer International Publishing), 43 [Google Scholar]
- Krumholz, M. R. 2016,Notes on Star Form [arXiv: 1511.03457] [Google Scholar]
- Krumholz, M. R., Klein, R. I., Mckee, C. F., Offner, S. S. R., & Cunningham, A. J. 2009, Science, 323, 754 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Krumholz, M. R., Klein, R. I., & McKee, C. F. 2012, ApJ, 754, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Ku, W. H.-M., Righini-Cohen, G., & Simon, M. 1982, Science, 215, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, Ann. Rev. Astron. Astrophys, 41, 57 [Google Scholar]
- Landstreet, J. D., Kochukhov, O., Alecian, E., et al. 2017, A&A, 601, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lapeyrere, V., Kervella, P., Lacour, S., et al. 2014, in Optical and Infrared Interferometry IV, Proc. SPIE, 9146, 91462D [Google Scholar]
- Lawson, P. R. 2000, in Princ. Long Baseline Stellar Interferom., ed. P. R. Lawson [Google Scholar]
- Lehmann, H., Vitrichenko, É. A., Bychkov, V., Bychkova, L., & Klochkova, V. 2010, A&A, 514, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levato, H., & Abt, H. A. 1976, PASP, 88, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Levenhagen, R. S., & Leister, N. V. 2006, MNRAS, 371, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Levesque, E. M., Massey, P., Olsen, K. A. G., et al. 2005, ApJ, 628, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Lohsen, E. 1975, IBVS, 988 [Google Scholar]
- Luri, X., Brown, A. G. A., Sarro, L. M., et al. 2018, A&A, 616, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massey, 2003, ARA&A, 41, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, B. D., Gies, D. R., Hartkopf, W. I., et al. 1998, AJ, 115, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Mattei, J., & Baldwin, M. 1976, IAU Circ., 3004 [Google Scholar]
- McKee, C. F., & Tan, J. C. 2002, Nature, 416, 59 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moe, M., & Di Stefano, R. 2017, ApJS, 230, 15 [Google Scholar]
- Moe, M., & Kratter, K. M. 2018, ApJ, 854, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Moeckel, N., & Clarke, C. J. 2011, MNRAS, 410, 2799 [NASA ADS] [CrossRef] [Google Scholar]
- Morales-Calderón, M., Stauffer, J. R., Stassun, K. G., et al. 2012, AJ, 753, 17 [Google Scholar]
- Morrell, N., & Levato, H. 1991, ApJS, 75, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Bontemps, S., & Louvet, F. 2018, ARA&A, 56, 1 [Google Scholar]
- Muench, A. A., Lada, E. A., Lada, C. J., & Alves, J. 2002, AJ, 573, 366 [Google Scholar]
- Muench, A., Getman, K., Hillenbrand, L., & Preibisch, T. 2008, Star Form. Reg., I, 483 [Google Scholar]
- Mužić, K., Schödel, R., Scholz, A., et al. 2017, MNRAS, 471, 3699 [NASA ADS] [CrossRef] [Google Scholar]
- Newville, M., Stensitzki, T., Allen, D. B., & Ingargiola, A. 2014, LMFIT: Non-Linear Least-Square Minimization and Curve-Fitting for Python [Google Scholar]
- Nieva, M.-F., & Przybilla, N. 2014, A&A, 566, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Dell, C. R., & Wong, K. 1996, AJ, 111, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Oskinova, L. M., Steinke, M., Hamann, W.-R., et al. 2013, MNRAS, 436, 3357 [NASA ADS] [CrossRef] [Google Scholar]
- Patience, J., Zavala, R. T., Prato, L., et al. 2008, ApJ, 674, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Peter, D., Feldt, M., Henning, T., & Hormuth, F. 2012, A&A, 538, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petr, M. G., Coude du Foresto, V., Beckwith, S. V. W., Richichi, A., & McCaughrean, M. J. 1998, AJ, 500, 825 [Google Scholar]
- Popper, D. M., & Plavec, M. 1976, AJ, 205, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., McMillan, S. L. W., & Gieles, M. 2010, ARA&A, 48, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Preibisch, T., Balega, Y., Hofmann, K. H., Weigelt, G., & Zinnecker, H. 1999, New Astron., 4, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
- Reiter, M., Calvet, N., Thanathibodee, T., et al. 2018, ApJ, 852, 5 [Google Scholar]
- Rio, N. D., Tan, J. C., Covey, K. R., et al. 2016, ApJ, 818, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Röser, S., Bastian, U., & Kuzmin, A. 1994, A&AS, 105, 301 [NASA ADS] [Google Scholar]
- Roy, A. E. 2005, Orbital Motion, 4th edn. (Institute of Physics Publishing) [Google Scholar]
- Salaris, M., & Cassisi, S. 2005, Evolution of Stars and Stellar Populations, 400 [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Samus’, N. N., Kazarovets, E. V., Durlevich, O. V., Kireeva, N. N., & Pastukhova, E. N. 2017, Astron. Rep., 61, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Sana, H., Le Bouquin, J.-B., Lacour, S., et al. 2014, ApJS, 215, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., Ramírez-Tannus, M. C., de Koter, A., et al. 2017, A&A, 599, L9 [CrossRef] [EDP Sciences] [Google Scholar]
- Sanchez-Bermudez, J., Alberdi, A., Barbá, R., et al. 2017, ApJ, 845, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Scalo, J. M. 1986, Fundam. Cosmic Phys., 11, 1 [Google Scholar]
- Schertl, D., Balega, Y. Y., Preibisch, T., & Weigelt, G. 2003, A&A, 402, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, F. R. N., Sana, H., Evans, C. J., et al. 2018, Science, 359, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Schneller, H. 1948, Astron. Nachr., 276, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23 [Google Scholar]
- Simon, M., Close, L. M., & Beck, T. L. 1999, AJ, 117, 1375 [NASA ADS] [CrossRef] [Google Scholar]
- Simón-Díaz, S., Herrero, A., Esteban, C., & Najarro, F. 2006, AJ, 448, 351 [Google Scholar]
- Sota, A., Maíz Apellániz, J., Walborn, N. R., et al. 2011, ApJS, 193, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Stahl, O., Wolf, B., Gang, T., et al. 1993, A&A, 274, L29 [NASA ADS] [Google Scholar]
- Stahl, O., Kaufer, A., Rivinius, T., et al. 1996, A&A, 312, 539 [NASA ADS] [Google Scholar]
- Stahl, O., Wade, G., Petit, V., Stober, B., & Schanne, L. 2008, A&A, 487, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stelzer, B., Flaccomio, E., Montmerle, T., et al. 2005, ApJS, 160, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, J. C., Beltran, M. T., Caselli, P., et al. 2014, Protostars and Planets VI, 149 [Google Scholar]
- Tatulli, E., Millour, F., Chelli, A., et al. 2007, A&A, 464, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasileiskii, A. S., & Vitrichenko, É. A. 2000, Astron. Lett., 26, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Vitrichenko, É. A. 2002a, Astron. Lett., 12, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Vitrichenko, É. A. 2002b, Astron. Lett., 28, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Vitrichenko, É. A., & Plachinda, S. I. 2001, Astron. Lett., 27, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Vitrichenko, É. A., Klochkova, V. G., & Plachinda, S. I. 1998, Astron. Lett., 24, 296 [NASA ADS] [Google Scholar]
- Vitrichenko, É. A., Klochkova, V. G., & Tsymbal, V. V. 2006, Astrophysics, 49, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Voss, R., Diehl, R., Vink, J. S., & Hartmann, D. H. 2010, A&A, 520, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wade, G. A., Fullerton, A. W., Donati, J.-F., et al. 2006, A&A, 451, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wales, D. J., & Doye, J. P. K. 1997, J. Phys. Chem., 101, 5111 [CrossRef] [Google Scholar]
- Wang, P., Li, Z.-Y., Abel, T., & Nakamura, F. 2010, ApJ, 709, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Weigelt, G., Balega, Y., Preibisch, T., et al. 1999, A&A, 347, L15 [NASA ADS] [Google Scholar]
- Wolff, S. C., Strom, S. E., & Hillenbrand, L. A. 2004, ApJ, 601, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Yorke, H. W., & Sonnhalter, C. 2002, ApJ, 569, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Zinnecker, H., & Yorke, H. W. 2007, ARA&A, 45, 481 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Data Results
We present our resulting separations and flux ratios for object. We list the values for θ1 Ori A and θ1 Ori C that we took from the literature as well, but in separate tables.
A.1 θ1 Ori A
Results of the binary fit for GRAVITY data of θ1 Ori A.
Positions of θ1 Ori A2, in position angle (PA) and separation (Sep) with respect to the primary star.
A.2 θ1 Ori B
Results of the binary fit for GRAVITY data of θ1 Ori B.
A.3 θ1 Ori C
Results of the binary fit for GRAVITY data of θ1 Ori C.
Positions of θ1 Ori C2, in position angle (PA) and separation (Sep) with respect to the primary star.
A.4 θ1 Ori D
Results of the binary fit for GRAVITY data of θ1 Ori D.
A.5 θ2 Ori A
Results of the binary fit for GRAVITY data of θ2 Ori A.
A.6 θ2 Ori B
We observed θ2 Ori B on January 10th 2018 with: x = −66.93 ± 0.04, y = 68.52 ± 0.07, f = 0.022 ± 0.001.
A.7 θ2 Ori C
We observed θ2 Ori C on January 12th 2018 with: x = −36.74 ± 0.02, y = 10.21 ± 0.03, f = 0.114 ± 0.002.
A.8 NU Ori
Results of the binary fit for GRAVITY data of NU Ori.
Appendix B: Additional tables
GRAVITY observations of the Orion nebula.
Overview for all the observed stars.
All Tables
Orbital parameter for θ1 Ori C determined by Kraus et al. (2009), Balega et al. (2015), and in this work including GRAVITY data.
Comparison of observable quantities from the star formation models with our observations.
Positions of θ1 Ori A2, in position angle (PA) and separation (Sep) with respect to the primary star.
Positions of θ1 Ori C2, in position angle (PA) and separation (Sep) with respect to the primary star.
All Figures
 |
Fig. 1. Example for the companion detection limit for θ1 Ori B, observed at the 12th October 2017, as determined with CANDID. The detection limit on the y-axis is denoted as a magnitude difference to the main star. The x-axis shows the separation in mas. |
| In the text | |
 |
Fig. 2. Measured positions of θ1 Ori A2, with east to the left. The primary star θ1 Ori A1 is located at position (0,0). Blue dotted positions were observed with GRAVITY. For some of the dots, the errorbar is smaller than the symbol displayed. Gray square positions are taken from Close et al. (2012), Schertl et al. (2003), Petr et al. (1998), Weigelt et al. (1999), Balega et al. (2004, 2007), and Grellmann et al. (2013). |
| In the text | |
 |
Fig. 3. Main image: θ1 Ori B group imaged in H-band. B1 is an eclipsing binary B1, 5. It was created with NaCo data, based on data obtained from the ESO Science Archive Facility under request number 342335, ESO program 60.A-9800(J). Additionally, with GRAVITY we detected another companion B6 at a separation of ∼13 mas, shown in the zoomed image of B1, 5, 6 (K-band). The image of B6 orbiting B1, 5 is reconstructed from our observations. The zoom into the spectroscopic binary B1, 5 is only a representative image and was not created with observational data. |
| In the text | |
 |
Fig. 4. Positions of B6 between January 2017 and January 2018. We see orbital motion around B1, 5 at (0,0), moving from east (left) to west (right). |
| In the text | |
 |
Fig. 5. Residuals of the Δα (top) and Δδ (bottom) positions from the best fit. The rms is 0.05 mas in δ and 0.06 mas in α. |
| In the text | |
 |
Fig. 6. Flux ratio f = fC2/fC1 as a function of observed wavelength. The vertical dashed gray line is at 2.166 microns, the Br-γ line. The drop indicates that C1 has a much higher flux at that wavelength than C2. Data were observed at January 9th 2016. |
| In the text | |
 |
Fig. 7. Orbit of θ1 Ori C2. Orange dots are observed with GRAVITY, blue squares are positions taken from Weigelt et al. (1999), Schertl et al. (2003), Kraus et al. (2007, 2009), Patience et al. (2008), and Grellmann et al. (2013). The error bars of GRAVITY data are within the marker. The orbital parameters are listed in Table 1. |
| In the text | |
 |
Fig. 8. Residuals of the Δα (top) and Δδ (bottom) positions from the orbit of θ1 Ori C2. The blue circles represent the residuals of GRAVITY data and their respective uncertainties. The gray squares are the residuals from non-GRAVITY observations. The rms of the GRAVITY residuals is 0.07 mas for Δα, and 0.05 mas for Δδ. |
| In the text | |
 |
Fig. 9. Positions of the newly detected θ1 Ori D3 around the primary D1 at (0,0). The orbital parameters are listed in Table 2. |
| In the text | |
 |
Fig. 10. Residuals of the Δα (top) and Δδ (bottom) positions from the fitted orbit of θ1 Ori D3. The rms of the residuals is 0.02 mas for Δα and 0.03 mas for Δδ. |
| In the text | |
 |
Fig. 11. Positions observed with GRAVITY of θ2 Ori A2, relative to A1, 3 at (0,0). |
| In the text | |
 |
Fig. 12. Positions of NU Ori4 with respect to NU Ori1, 2 at (0,0). |
| In the text | |
 |
Fig. 13. Summary of the observed multiple systems in the Orion Nebula. We observed 16 multiple systems with a total number of 22 companion stars. The respective scales are indicated. The images of θ1 Ori B are from actual obervational data, except for the spectroscopic B1, B5 system, which is only a representation. The orbital positions for θ1 Ori D and θ1 Ori C are the positions obtained in this work and from the literature. All remaining close up depiction of stars (gray) are only for illustrative purposes and were not created with observational data. The background image of the Orion Nebula was created by ESO Igor Chekalin. The zoom of the Trapezium Cluster (θ1) is a cut from ESO M. McCaughrean et al. (AIP). |
| In the text | |
 |
Fig. 14. Companion fraction CF as measured with GRAVITY for mass ranges < 3 M⊙, 3–7 M⊙, 7–16 M⊙, > 16 M⊙ (red circles). The values from Duchêne & Kraus (2013) for very low mass stars (VLM), spectral types M, K, G, F, A, B, early B and O (from left to right), and the values from Sana et al. (2014) for O stars are plotted for reference. The companion fraction of Sana et al. (2014) depends on the considered separation range for companions. A range ≲600 AU is similar to the separations in our sample. |
| In the text | |
 |
Fig. 15. Multiplicity fraction MF as measured with GRAVITY for mass ranges < 3 M⊙, 3–7 M⊙, 7–16 M⊙, > 16 M⊙ (red circles). The values from Duchêne & Kraus (2013) for the whole mass range of ≲1 M⊙ to O stars and the values from Sana et al. (2014) for O stars are plotted for reference. For each mass range we use |
| In the text | |
 |
Fig. 16. Normalized histogram of stars per mass. The observed distribution is compared with distribution functions of Chabrier (2003). We estimate the uncertainties to be |
| In the text | |
 |
Fig. 17. Cumulative distribution of stars per mass with the respective distribution functions. |
| In the text | |
 |
Fig. 18. Mass ratio per primary mass; each system is represented by a different marker. The colors indicate the companion order, starting from the innermost. Thus, the first companion (blue) means the companion closest to the primary, the second companion (orange) means the second-closest companion, etc. The gray area indicates the mass range ≤3 M⊙, for which we are no longer complete. The gray dotted line marks the individual mass limits for each system as given in Table B.2. |
| In the text | |
 |
Fig. 19. Normalized histogram of all mass ratios q and the best fit curve of a power law ∝qγ = q−1.7 ± 0.3. |
| In the text | |
 |
Fig. 20. Cumulative distribution of all mass ratios q and the best fit curve of a power law ∝qγ = q−1.7 ± 0.3. |
| In the text | |
 |
Fig. 21. Power-law index γ of the mass ratio distribution with dN/dq ∝ qγ for different masses. The squares represent the fits of the overall population of multiple systems by Duchêne & Kraus (2013). The diamonds are the results for tight binaries (smaller separations than average) and the down-facing triangles the result for wide binaries (larger separations than average) by Duchêne & Kraus (2013). Our data is represented by a distribution with an index of −1.7 ± 0.3 (red circle). If the companion stars follow the IMF of Chabrier (2003), the index of q is equal to the index of the IMF with γ = −2.3 ± 0.3, for companions with masses 1 ≤ mcomp ≤ mprimary. The shaded area indicates the uncertainties of the IMF. |
| In the text | |
 |
Fig. 22. Separation in AU in a logarithmic scale per mass ratio q. |
| In the text | |
 |
Fig. 23. Companion separation per system with given primary mass in M⊙. In the range between 1–100 AU, we are sensitive down to 3 M⊙. There are equally many companion stars in the range 0.1–1 AU as in the range 1–100 AU. The colors indicate different systems, the marker size scales with the square root of the companion mass. The dashes indicate missing information about the mass of the first companion of θ2 Ori C and TCC 59. |
| In the text | |
 |
Fig. 24. Normalized histogram of companion separation. For comparison, we plot the qualitative distribution of Duchêne & Kraus (2013) for A (dotted) and OB stars (solid). The distribution of our separations for mainly B and O stars is bimodal and resembles more that of the Duchêne & Kraus (2013) distribution of A-type stars. We notice a decrease of companions in the range of 1–100 AU. |
| In the text | |
 |
Fig. 25. Top: separation versus the companion mass. Bottom: multiplicity of objects plotted as a function of distance from θ1 Ori C in arcseconds. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.