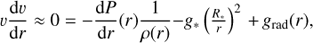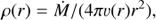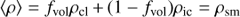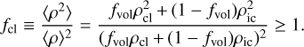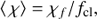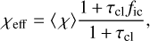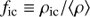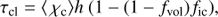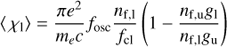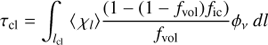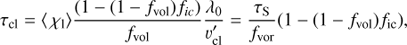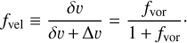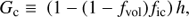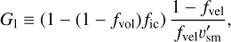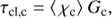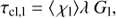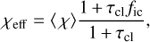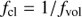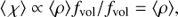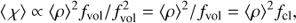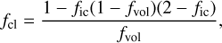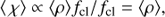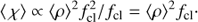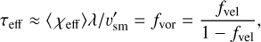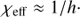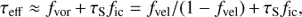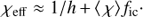| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A59 | |
| Number of page(s) | 11 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201832993 | |
| Published online | 07 November 2018 | |
Atmospheric NLTE models for the spectroscopic analysis of blue stars with winds
IV. Porosity in physical and velocity space
1 KU Leuven, Instituut voor Sterrenkunde, Celestijnenlaan 200D, 3001 Leuven, Belgium
e-mail: jon.sundqvist@kuleuven.be
2 LMU München, Universitätssternwarte, Scheinerstr. 1, 81679 München, Germany
Received:
9
March
2018
Accepted:
26
May
2018
Context. Clumping in the radiation-driven winds of hot, massive stars severly affects the derivation of synthetic observables across the electromagnetic spectrum.
Aims. We implement a formalism for treating wind clumping – focusing in particular on the light-leakage effects associated with a medium that is porous in physical and velocity space – into the global (photosphere + wind) NLTE model atmosphere and spectrum synthesis code FASTWIND.
Methods. The basic method presented here assumes a stochastic, two-component wind consisting of a mixture of optically thick and thin clumps embedded in a rarefied inter-clump medium. We have accounted fully for the reductions in opacity associated with porosity in physical and velocity-space (the latter due to Doppler shifts in an accelerating medium), as well as for the well-known effect that opacities depending on ⟨ρ2⟩ are higher in clumpy winds than in smooth ones of equal mass-loss rate. By formulating our method in terms of suitable mean and effective opacities for the clumpy wind, we are able to compute atmospheric models with the same speed (∼15 min on a modern laptop or desktop) as in previous generations of FASTWIND.
Results. After verifying important analytic limits (smooth, optically thin, completely optically thick), we present some first, generic results of the new models. These include: i) Confirming earlier results that velocity-space porosity is critical for analysis of UV wind resonance lines in O-stars; ii) for the optical Hα line, we show that optically thick clumping effects are small for O-stars, but potentially very important for late B and A-supergiants; iii) in agreement with previous work, we show that spatial porosity is a marginal effect for absorption of high-energy X-rays in O-stars, as long as the mean-free path between clumps are kept at realistic values ≲R*; iv) whereas radio absorption in O-stars shows strong spatial porosity effects in near photospheric layers, it is negligible at their typical radio-photosphere radii ∼100R*; v) regarding the wind ionization balance, a general trend is that increased rates of recombination in simulations with optically thin clumps lead to overall lower degrees of ionization than in corresponding smooth models, but that this effect now is counteracted by the increased levels of light-leakage associated with porosity in physical and velocity space (i.e., by an increase of ionization rates). We conclude by discussing future work and some planned applications for this new generation of FASTWIND models.
Key words: radiative transfer / techniques: spectroscopic / stars: early-type / stars: mass loss / stars: winds outflows
© ESO 2018
1. Introduction
Information about fundamental parameters of stars – like their mass, luminosity, surface temperature and chemical composition – comes primarily from matching observations to synthetic spectra computed using models of stellar atmospheres. For massive stars with hot surfaces, scattering and absorption in spectral lines further transfer momentum from the star’s intense radiation field to the plasma, and so provides a force that overcomes gravity and drives a wind-outflow directly from the stellar surface (Castor et al. 1975). These starlight-powered winds are very strong and fast, and can dramatically affect the star’s atmospheric structure (review by Puls et al. 2008) as well as the evolution of its mass and luminosity, chemical surface abundances, rotational velocity, and nuclear burning life-times (review by Smith 2014). Atmospheric models of such hot, massive stars must thus generally be constructed using a unified, or global, approach, wherein the basic structural equations for the quasi-static photosphere and the outflowing stellar wind are solved simultaneously (Gabler et al. 1989). In addition, the expanding atmospheres of these stars are characterized by their large departures from local thermodynamic equilibrium (LTE), meaning the full number density rate equations (typically reduced to statistical equilibrium, and often simply called non-LTE or NLTE) must be solved to obtain the atmospheric radiation field and the excitation and ionization balance. As such, quite intricate numerical solution techniques are normally required to compute synthetic observables, like spectral lines and energy distributions, for these objects (for details, see book by Hubeny & Mihalas 2014). Over the past decades, much effort has been devoted toward constructing such global NLTE, steady-state model atmospheres of hot stars with winds; several numerical computer codes meanwhile exist on the market, for example CMFGEN (Hillier & Miller 1998), POWR (Gräfener et al. 2002; Sander et al. 2015), PHOENIX (Hauschildt 1992), WM-BASIC (Pauldrach et al. 2001), and the subject of this paper, FASTWIND (Santolaya-Rey et al. 1997; Puls et al. 2005; Rivero González et al. 2011; Carneiro et al. 2016). FASTWIND is routinely applied for both photospheric and wind analyses of hot stars, and used for detailed studies of individual objects as well as in large spectroscopic surveys (like within the recent VLT-FLAMES survey of massive stars in the Tarantula giant star-forming region in the Large Magellanic Cloud, Evans et al. 2011). A critical component of all these codes regards their practical treatment of the stellar wind; traditionally this has been to assume a parametrized steady-state and smooth outflow, without any clumps or shocks. However, it has been known for quite many years now, that these line-radiation driven winds are in fact inhomogeneous and highly structured on small spatial scales (see overviews in Puls et al. 2008, 2015; Hamann et al. 2008; Sundqvist et al. 2012b). Such wind clumping arises naturally from the strong line-deshadowing instability, the LDI, a fundamental and inherent property of line driving (e.g., Owocki & Rybicki 1984, 1985). Radiation-hydrodynamic, time-dependent wind models (Owocki et al. 1988; Feldmeier et al. 1997; Owocki & Puls 1999; Dessart & Owocki 2003; Sundqvist & Owocki 2013, 2015; Sundqvist et al. 2018) following the non-linear evolution of this LDI show a characteristic two-component-like structure consisting of spatially small and dense clumps separated by large regions of very rarified material, accompanied by strong thermal shocks and a highly non-monotonic velocity field. Such clumpy winds then affect both the atmospheric structure and the radiative transfer needed to derive synthetic observables; as just one example of this, neglecting clumping typically leads to observationally inferred mass-loss rates that might differ by more than an order of magnitude for the same star, depending on which spectral diagnostic is used to estimate this mass loss (Fullerton et al. 2006). Global model atmospheres nowadays normally account for such wind inhomogeneities by simply assuming a two-component medium consisting of overdense, optically thin clumps of a certain volume filling factor, following a smooth, parametrized velocity law, and an inter-clump medium that is effectively void (e.g., Hillier 1991; Puls et al. 2006). However, if clumps become optically thick, it leads to an additional leakage of light – not accounted for in the filling factor approach – through porous channels in between the clumps. Such porosity can occur either spatially (e.g., Feldmeier et al. 2003; Owocki et al. 2004; Sundqvist et al. 2012a), or for spectral lines in velocity-space due to Doppler shifts in the rapidly accelerating wind (sometimes thus called velocity-porosity, or “vorosity”, Owocki 2008). Regarding spatial porosity, several studies over the past years have focused on examining potential effects on the bound-free absorption of X-ray photons by the bulk wind (e.g., Oskinova et al. 2006; Owocki & Cohen 2006; Sundqvist et al. 2012a; Leutenegger et al. 2013; Hervé et al. 2013). Regarding velocity-space porosity, similar studies (Oskinova et al. 2007; Hillier 2008; Sundqvist et al. 2010, 2011, 2014; Šurlan et al. 2012, 2013) have shown that clumps indeed very easily become optically thick in especially the strong UV wind-lines of hot stars (the so-called P-Cygni lines), and that the associated additional leakage of line-photons leads to weaker line profiles than predicted by smooth or volume filling factor models1. But constructing realistic, multi-dimensional ab-initio radiation-hydrodynamic wind simulations that account naturally for (time-dependent) spatial and velocity-field porosity is an extremely challenging and time-consuming task (Sundqvist et al. 2018). Thus there has also been a big need for developing simplified, parameterized models that can be more routinely applied to diagnostic work on samples of hot stars with winds. Building on their prior studies Sundqvist et al. (2010; 2011; 2012a; 2014, hereafter SPO14) developed and benchmarked such a method, using effective quantities to simulate the reduction in opacity associated with optically thick clumps. In contrast to some other models mentioned above, this “effective opacity” approach has the great advantage that it can be quite readily implemented into the already existing (time-independent) global NLTE atmosphere models discussed above.
This paper incorporates the SPO14 formalism into the FASTWIND computer code, and presents some first results. In Sect. 2 we briefly review the basic physics of FASTWIND, and Sect. 3 describes our methodology and practical implementation of wind clumping into the code. Sect. 4 then presents some first results, and in Sect. 5 we summarize and outline future work.
2. Basic physics of the global model atmosphere code FASTWIND
The versatile and fast (computing time ∼15 min on a modern desktop/laptop) global model atmosphere computer code FASTWIND solves the NLTE number-density rate equations within a spherically extended envelope containing both the stellar photosphere and the supersonic average wind, and including the effects from millions of metal spectral lines on the atmospheric structure. The present version is designed for analyzing stars of spectral types OBA, with winds that are not significantly optically thick in the optical continuum2.
2.1. Momentum and energy balance
As described in Santolaya-Rey et al. (1997), in the deep atmosphere FASTWIND neglects the advection term in the momentum equation and instead solves the equation of hydrostatic equilibrium in spherical symmetry:
where g* and R* are the (input parameters) surface gravity and radius, ρ is the mass density, dP/dr the gas pressure gradient, and grad the radiative acceleration in the photosphere. A novel feature of the basic methodology behind FASTWIND is the calculation of the flux-weighted opacities, needed above to compute grad, which in these deep atmospheric layers can be well approximated with a Kramer’s like opacity-formula (see Santolaya-Rey et al. 1997).
The photospheric structure is smoothly connected to the wind outflow at a pre-specified velocity, typically set to ≈10% of the isothermal sonic speed a for the assumed (input parameter) stellar effective temperature, vtrans ≈ 0.1a(Teff). The version of FASTWIND presented here further pre-specifies 3 the wind structure by adopting a “β” velocity law and a wind mass-loss rate Ṁ, i.e.,
where v∞ is the assumed terminal wind speed, and b is obtained from the calculated radius at the assumed wind boundary vtrans; the velocity field of the quasi-static photosphere then follows directly from mass conservation using the computed photospheric density.
As described in Puls et al. (2005), a consistent energy balance (temperature structure) is computed in parallel, using a flux-correction method in the lower atmosphere and the thermal balance of free electrons in the outer. As usual, the system of equations is closed by the ideal gas law, P(r)=ρ(r)a2(r)=ρ(r)kBT(r)/( μ(r)mH) for mean molecular weight μ(r) and with Boltzmann’s constant kB and hydrogen atomic mass mH.
We note further that when introducing wind clumping as described in Sect. 3, ρ and v in the equations above essentially are the mean density and velocity, respectively.
2.2. Detailed model atoms and background elements
To enable shorter computational times, FASTWIND separates between “explicit” elements considered in great detail and “background” elements treated in a somewhat more approximate way. Explicit elements use detailed model atoms and co-moving frame radiation transport for all line transitions, whereas the background elements use parameterized ionization cross-sections (see Puls et al. 2005) and co-moving frame transfer only for the most important, strong lines, whereas the rest of the lines are calculated using the (Sobolev 1960) approximation4. Model atoms for the explicit elements are provided by the user, and are typically those used for various diagnostic spectroscopic purposes (H, He, N, P, etc.; e.g., most recently a new carbon model atom has been implemented, see Carneiro et al. 2018). By contrast, the background elements are needed “only” for a consistent description of line blocking/blanketing (see below) and their data are pre-specified by our atomic data base (Pauldrach et al. 2001); this background then includes (almost) all elements up to Zn not treated as explicit ones in the particular calculations (for a more detailed description of the basic philosophy behind explicit and background elements, see Puls et al. 2005 and Rivero González et al. 2011). As is customary, also the metallicity and chemical composition of the atmosphere (including the helium abundance) are provided by the user, where we adopt solar abundances from Asplund et al. (2009) as default.
2.3. Line blocking and blanketing
As already mentioned, a key point of the philosophy behind FASTWIND is the speed of the program, which allows us to perform calculations much faster than comparable NLTE codes available on the market. In addition to the explicit/background element-approach described above, this computational speed is to a large extent due to the novel way of treating the opacity-effects of millions of weak spectral lines developed by Puls et al. (2005). In short, this method uses the way described above for solving the NLTE equations for the background elements, and then introduces a simple statistical approach for calculating the line opacities and emissivities (based on suitable averages) that are used within the radiative transfer to account for line blocking/blanketing (details given in Puls et al. 2005).
2.4. X-ray emission from embedded wind-shocks
Massive, hot stars are ubiquitous sources of high-energy X-ray emission, typically on order Lx/LBol ∼ 10−7 (e.g., Rauw et al. 2015). For putatively single, non-magnetic massive stars these X-rays are due to strong shocks embedded in the ambient stellar wind, and associated with the same fundamental instability of line-driven stellar winds that causes wind clumping (the LDI, see introduction). Recently, a module has been incorporated into FASTWIND that computes the ionization and absorption effects on the bulk wind stemming from such X-ray emission (Carneiro et al. 2016). In summary, in this method a (very) small fraction of the stellar wind is assumed to emit high-energy photons by means of thermal shocks, whereafter both the direct and Auger ionization effects arising from this are calculated, as well as the absorption (via valence and K-shell electrons) of the emitted high-energy photons by the ambient wind (for further details, see Carneiro et al. 2016).
Having summarized essential features and physical assumptions, the next section now describes in detail our implementation of wind clumping into FASTWIND.
3. Treatment of wind clumping
Our treatment of wind-clumping follows the formalism developed by SPO14. As shown in detail below, this methodology enables a simple and fast implementation, in both the NLTE rate equations and the computation of synthetic spectra, which accounts for the effects of porosity in physical and velocity space while preserving the (previously considered) limits of smooth winds and winds consisting of only optically thin clumps. Two key simplifying assumptions of our model are:
One-component average ionization description. Numerical NLTE computations like those performed by FASTWIND and similar computer codes are very challenging, and require much computational time. To avoid a full multi-component NLTE calculation of the structured wind5, we assume here that the wind excitation and ionization balance can be approximated from considering a suitable, single “effective” opacity of a two-component medium, accounting for contributions both from the dense clumps and the rarified medium in between them. As shown by SPO14 (see also Pomraning 1991), using such “effective” quantities then allows us to simply rescale the opacities of non-structured simulations, and so calculate new models that account for clumps of arbitrary optical depths without any essential loss of computation-time. While neglecting potential effects of a multi-component ionization balance (see Zsargó et al. 2008), this approach is thus very advantageous regarding, e.g., practical applications such as spectroscopy of larger stellar samples.
Absorption and emission. The formalism below is developed for absorption processes. An important assumption of our model is that corresponding emission coefficients are scaled analogously, using the same expressions for the clump optical depths (see next section). As shown by Pomraning (1991), this is indeed exact in the limit of only thermal absorption in a two-component model where both components have the same temperature. Although this procedure is formally not exact for scattering (see also discussion in Pomraning 1991, their Ch. 4), we here scale all emission processes in the same way, guided by the results of our previous multi-dimensional, Monte-Carlo line-scattering simulations (Sundqvist et al. 2010, 2011, 2014).
Having outlined above these two important physical assumptions, the below describes in detail our model. Limiting cases (particularly regarding an effectively void interclump medium) are provided in Sect. 4.
3.1. Mean and effective opacities
For a stochastic two-component medium consisting of dense clumps (hereafter subscripts “cl”) occupying a filling factor fvol of the total volume, and a rarified “inter-clump” (subscript “ic”) medium filling in the space in between clumps, the mean mass density is
where the last equality assumes mass-conservation with respect to a smooth medium of density ρsm. For notational simplicity, all expressions throughout this section suppress dependencies on the local radius. The mean density is related to the mean-square density via the so-called clumping factor
To avoid a full two-component NLTE computation, this paper introduces a formalism that preserves known limiting cases (see below) for the mean opacity per unit length, ⟨ χ⟩=κ⟨ρ⟩ with mass absorption coefficient κ, for processes where ⟨ χ⟩∼⟨ρ⟩ and ⟨ χ⟩∼⟨ρ2⟩.
The mean opacity is obtained by first computing the NLTE occupation numbers n within a “fiducial” clump of density ρf = ⟨ρ⟩fcl = ρsmfcl, and then reducing the fiducial clump opacity χf ≡ σnf by a clumping factor fcl,
where σ and nf above are the atomic cross-section and the number density of the fiducial clump, respectively, and where the underlying “smooth” scaling density ρsm = Ṁ/(4πvr2) is set by the wind mass-loss rate (Eq. (3)). We recall here again that this “average medium” treatment implicitly assumes that the (gas and radiation) temperatures of clump and inter-clump media are similar (see also above).
Formulated this way, Eq. (6) preserves the well-known results that ⟨ χ⟩ is unaffected by clumping if χ = σn ∼ ρ and enhanced (as compared to an unclumped medium) by a factor fcl if χ = σn ∼ ρ2, as can be shown by a simple calculation (see also Eqs. (25) and (26)).
Using this mean opacity, we then write the effective opacity of the two component medium as (SPO14)
where τcl is the clump optical depth and
sets the density of the rarefied medium in between the clumps. We note that Eq. (8) gives the inter-clump density in terms of the mean density; the density contrast between clumps and inter-clump medium, ρcl/ρic, is thus higher than 1/fic, and can be obtained from (Eqs. (4) and (5)).
These generic expressions are used to calculate all opacities in our clumpy models. However, as now described, the calculation of the clump optical depth τcl depends on the specific absorbing/emitting process.
3.2. Calculating the clump optical depth
The clump optical depth for continuum absorption is (SPO14)
where the porosity-length h ≡ lcl/fvol is the mean-free-path between clumps of characteristic length scale lcl, and the volume filling factor is related to the clumping factor via Eqs. (5) and (8). We note i) that for a void inter-clump medium (fic = 0), Eq. (9) depends exclusively on h and recovers the previously obtained result τcl = ⟨ χc⟩h (Owocki et al. 2004; Sundqvist et al. 2012a), and ii) that the above expression assumes statistically isotropic clump optical depths, as supported by the empirical porosity-studies of Leutenegger et al. (2013), Hervé et al. (2013) and by the theoretical models of Dessart & Owocki (2003), Sundqvist et al. (2018).
For line absorption, τcl may be similarly calculated from the mean line-integrated opacity
which yields for a frequency-normalized profile function ϕν
where the integration extends over the clump and ϕν is evaluated at the corresponding co-moving frame (cmf) frequency; in hot stellar winds Doppler broadening normally dominates so that 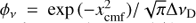 for Doppler width ΔνD = (ν0/c)vth and xcmf = (νcmf − ν0)/ΔνD. Other variables in Eqs. (10) and (11) have their usual meanings. However, we remind that fosc above denotes the oscillator strength (not to be confused here with the clumping factor fcl) and also that since ⟨ χl⟩ is integrated over the line-profile it has units of frequency over length (rather than just 1/length as for ⟨ χc⟩).
for Doppler width ΔνD = (ν0/c)vth and xcmf = (νcmf − ν0)/ΔνD. Other variables in Eqs. (10) and (11) have their usual meanings. However, we remind that fosc above denotes the oscillator strength (not to be confused here with the clumping factor fcl) and also that since ⟨ χl⟩ is integrated over the line-profile it has units of frequency over length (rather than just 1/length as for ⟨ χc⟩).
Sobolev approximation for line clump optical depth. For the rapidly accelerating hot stellar winds in focus here, we may safely assume that clumps cover their resonance zones of a few thermal widths vth ≈ 5 − 10 km s−1 in velocity space (Sundqvist et al. 2010, 2011, 2014)6. In full analogy with the standard assumptions of the Sobolev approximation then (Sobolev 1960), we can integrate (Eq. (11)) over the clump to obtain
where τS ≡ ⟨ χl⟩λ0/v′sm is the radial Sobolev optical depth for the mean wind with spatial velocity gradient v′sm = dv/drsm and line rest wavelength λ0. The last equality of (Eq. (12)) further uses the definition by SPO14 for the velocity clumping factor (see their Eq. (9) and Fig. 2)
for clump velocity span δv and velocity separation between clump-centers Δv, and where δvsm is the velocity-span the clump would have if it followed the underlying smooth velocity field. Note here that the special case of a clumped wind in which all clumps indeed follow this smooth velocity field, i.e. δv = δvsm, implies fvor = fvol and so in general high clump optical depths (τcl ≈ τSob/fvol) and thus very large velocity-porosity effects; under typical circumstances though, fvor > fvol (Sundqvist et al. 2010, see also Sect. 4).
The un-normalized velocity clumping factor is related to the normalized, and perhaps somewhat physically more intuitive, velocity filling factor, fvel, via
Eqs. (4)–(14) provide a full formalism toward implementing the effects of porosity in physical and velocity space into global NLTE model atmospheres like FASTWIND, using the four parameters fcl, fic, h, and fvel.
In FASTWIND, we use this particular set of independent parameters because we believe they best represent the underlying physics of the situation. In principle, however, using the equations above one can simply substitute fcl, h, and fvel, for, e.g., fvol, ℓcl, and the clump velocity span δv. The key point though, is that four independent parameters are needed to fully describe the radiative transfer effects in the assumed two-component structured, accelerating medium.
Nonetheless, as further discussed in Sects. 4 and 5, depending on which diagnostic feature in which wavelength-regime is targeted, not all four parameters are always important in practice. We also note here that fcl, fic and h are equivalents to the parameters used to describe continuum transport in a static two-component, stochastic Markovian mixture model (see book by Pomraning 1991, and also SPO14), whereas the last, fvel, accounts here for the additional effects of spectral line transport in accelerating media (SPO14).
3.3. Practical implementation into FASTWIND
This section summarizes some key points regarding our practical implementation of the above formalism into FASTWIND. The following radially dependent (but frequency independent) auxiliary quantities are pre-calculated within FASTWIND by a subroutine CLUMPING:
where the clump volume filling factor is obtained from (the input parameters) fcl and fic according to
Then, the frequency-dependent clump optical depths and effective opacities are computed within the code’s NLTE and radiative transfer networks from:
where subscripts “c” and “l”, denoting continuum and line, have been omitted for simplicity in Eq. (20), and where all mean opacities include corrections for clumping (cf. Eqs. (9) and (10)), with occupation numbers derived for density ρf = ρsmfcl.
Input. Four structure-parameters, the clumping factor fcl, the porosity length h, the inter-clump density contrast parameter fic, and the velocity filling factor fvel, are provided by the user as input. As described further below, these parameters are typically functions of radius (also controlled by user). If one chooses to pre-specify only fcl, we force all clump optical depths to be effectively zero, and so recover previous models assuming optically thin clumps7. Similarly, simply setting fcl = 1 means the two components are identical so that a smooth wind model with density ρsm is calculated, and the same is true also if fic = 1 is provided.
Velocity-space porosity in supersonic part of wind. As outlined above, we essentially use the Sobolev approximation to evaluate the clump optical depths for spectral lines. This method is only motivated for the supersonic parts of the wind8. As such, the present version of FASTWIND allows the consideration of such velocity-space porosity only for the supersonic parts v > a; to this end, we have for simplicity set the same lower boundary also for spatial porosity and optically thin clumping (i.e., we do not allow for any clumping in the sub-sonic parts).
Radial variation of porosity length. As default in FASTWIND, we assume a radial variation h = h∞v/v∞, where h∞ is the porosity-length at terminal wind speed (provided by user). Such a “velocity-stretch” law is consistent with various other models (e.g., Oskinova et al. 2004; Sundqvist et al. 2012a; Leutenegger et al. 2013; Grinberg et al. 2015), and follows naturally from considering mass-conserving clumps with characteristic length-scales that expand according to the local wind radius (Sundqvist et al. 2012a). We note that while this law certainly is very reasonable as default, the user can readily modify it (e.g., to account for collisional merging of clumps, Feldmeier et al. 1997) from within the above-mentioned subroutine CLUMPING.
Standard and background opacities. The implementation of the above formalism into any “standard” method for solving the coupled radiative transfer and NLTE rate equations is straightforward; for each considered process, “smooth” or mean opacities are converted to “effective” ones using the above expressions for the (frequency dependent) mean opacities and the (frequency independent) G-quantities (defined above to obtain clump optical depths and effective opacities). Whenever more than one process is present at a given frequency, the total clump optical depth is computed by summing up all individual components, and the corresponding effective opacities computed using this summed τcl. After this, calculations proceed as usual, but now using the new effective opacities χeff in the radiative transfer (instead of as in previous models mean opacities ⟨ χ⟩). We remind again here that the NLTE rate equations have to be solved for ρf = ρsmfcl.
For the so-called background line opacities included in FASTWIND (see previous section), the implementation becomes a bit more intricate. To this end, we proceed as follows: as explained in detail in Puls et al. (2005), these background line opacities are calculated by building suitable statistical averages within a number of pre-defined discrete frequency-bins. In each of these bins, we now also compute clump optical depths by summing up the opacities of the contributing line processes. These clump optical depths are then used to obtain an effective opacity for each of the bins; it is this effective opacity that then finally is used in all transfer calculations to obtain the line-blanketed pseudo-continuum radiation field. Whenever there is an overlap between these background lines and a line treated “explicitly” (see above), we compute τcl using both approaches and simply choose the highest one when calculating the effective opacity finally used in the radiative transfer.
4. Tests and first results
Let us now build physical insight by examining some important limits and basic results of the clumping model developed in Sect. 3.
4.1. Analytic limits
Smooth conditions. In the formalism above, setting fic = 1 (i.e., assuming two identical components) gives χeff = ⟨ χ⟩ and fcl = 1, thus recovering the smooth background model.
Optically thin clumps. For optically thin clumps, τcl ≪ 1, Eq. (7) always gives χeff = ⟨ χ⟩.
For a void inter-clump medium, fic = 0, this then results in
and
for processes depending on ρ and ρ2, respectively. This is consistent with previous FASTWIND versions (as well as with alternative NLTE global atmospheres codes like CMFGEN), and further demonstrates that in this case the fiducial clump density ρf = ⟨ρ⟩fcl = ⟨ρ⟩/fvol = ρcl indeed is the “real” clump density; that is, in models assuming an effectively void inter-clump medium the rate equations are solved within the clumps exactly.
Adding a non-negligible inter-clump medium to this changes the relation between the clumping and volume filling factor,
but, when expressed in terms of the clumping factor, preserves the scalings for ρ and ρ2 dependent opacities,
This illustrates the advantage of using the clumping factor instead of the volume filling factor as an independent parameter. Note though, that in this case of fic > 0 i) the clumping factor does not exactly equal the overdensity of clumps (i.e., ρcl ≠ ⟨ρ⟩fcl) and ii) the inverse of the clumping factor does not precisely equal the volume filling factor.
Optically thick clumps. Let us first consider the case of very optically thick clumps, τcl ≫ 1, and a void inter-clump medium, fic = 0.
For spectral lines, this limit is best illustrated by an effective optical depth in the Sobolev approximation,
which shows explicitly that the absorption here is controlled by how much of the wind velocity law is covered by clumps, i.e. by the velocity filling factor.
For continuum processes, on the other hand, it is more instructive to consider directly the effective opacity, for which one obtains (e.g., Feldmeier et al. 2003; Owocki et al. 2004)
This equation now illustrates how in this case the opacity (and thus the optical depth) is set by the mean free-path between clumps, that is by the porosity length.
Note that in these cases with fic = 0 the optical depth of the medium becomes gray (frequency independent), both for lines and continua, and further how the medium’s effective absorption becomes independent of the atomic opacity (i.e., independent of occupation numbers and cross sections).
Adding to this now a tenuous, but non-void, inter-clump medium (still considering optically thick clumps) yields for lines (SPO14)
and for the continuum case
These expressions show how the tenuous inter-clump medium now gradually fills in the porous channels (in velocity and physical space, for respectively lines and continuum) between the black clumps.
As discussed in SPO14, while in the clump + void model the opacity itself saturates (and thus becomes independent of the mean opacity), in this more general two-component model the ratio between the effective and mean opacities (optical depths) saturates; thus the medium can always become effectively optically thick provided this mean opacity is high enough.
The following sections now present some general, first results of our new clumpy numerical FASTWIND models. As directly evident from above, the key effect of optically thick clumps in the wind regards a potential reduction of opacities as compared to a wind consisting of only optically thin clumps. This may then, in turn, affect both the ionization balance and the derivation of synthetic observables, where a key point is that the potential opacity reduction depends on the clump optical depth, and so becomes highly frequency and process dependent.
4.2. Effects on ionization and opacities
Ionization balance. For the O-star models given in Table 1, Fig. 1 plots the ionization balance of (here the background elements) iron, phosphorus, and carbon, comparing now FASTWIND simulations accounting fully for clumping of arbitrary optical thickness (blue lines), with models assuming optically thin clumps (red) and a smooth wind (black). The clumping parameters have characteristic values chosen from current theoretical and observational constraints: fcl = 10 and h∞ = R⋆ are typical values found both in LDI models and observational studies (e.g., Puls et al. 2006; Leutenegger et al. 2013; Sundqvist & Owocki 2013; Grinberg et al. 2015) and fic = 0.01 and fvel = 0.5 are consistent with findings from the LDI (see Sundqvist et al. 2010). Regarding the velocity filling factor, we note that since fvol ≈ 1/fcl = 1/10, fvel = 0.5 represents a rather high |δv/δvsm|≈10; such values for the clump velocity spans are indeed what is typically found in present-day LDI simulations and models trying to mimic these (Sundqvist et al. 2010, e.g., see their Table 2).
 |
Fig. 1. Ionization balance of selected elements iron (Fe), phosphorus (P), and carbon (C) for FASTWIND models “O1” (top panels), “O2” (middle panels), and “O3” (lower panels) with parameters according to Table 1. Plotted in each panel are number density ratios log nj/ni for ion stage j of species i, with ni the total element abundance, as function of a radius coordinate log10(r/R* − 1). Blue lines are models “thick” including full effects of porosity in physical and velocity space; red lines are models “thin” assuming optically thin clumping; black lines are models “smooth” without any wind clumping. For iron (left panels), phosphorus (middle panels), and carbon (right panels), the displayed states are given in the upper right of each panel; solid lines then show the ion fraction in the lowest considered state j, the dotted lines show state j + 1 and the dashed ones j + 2. (For example the top left panel thus shows Fe 3+ − 5+ = Fe IV − VI in models O1 “thick” (blue), “thin” (red) and “smooth” (black), where solid lines are ion fractions of Fe IV, dotted lines of Fe V, and dashed lines of Fe VI.) |
Overall, Fig. 1 demonstrates clearly that quantitative effects vary significantly between elements and stellar parameters; nonetheless, it illustrates also a few quite general effects of clumping upon the wind ionization balance. In particular: i) the increased rates of recombination in models with optically thin clumps generally imply a lower degree of ionization than in corresponding smooth simulations; ii) this effect is then somewhat counteracted by the light-leakage and effective opacity reduction associated with optically thick clumps.
This quite general behavior can be understood by considering a simplified situation accounting only for ionization/recombination from/to the ground state of ion stage j to/from the ground state of stage j + 1. Following, e.g., Puls et al. (2005), an approximate NLTE number density ionization equilibrium equation can then be written9 as (their Eq. (18)):
where ne is the electron density, ϕ(Te) the Saha-Boltzmann factor (e.g., Hubeny & Mihalas 2014, their Eq. (9.5)) for electron temperature Te, and the radiation temperature Trad is defined from the mean intensity as J(ν, r)≡W(r)Bν(Trad(ν, r)) for Planck function Bν and dilution factor 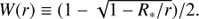 .
.
For a major ion stage nj + 1/ni ≈ 1, the product nj + 1ne ∼ ρ2 and so illustrates the first general effect discussed above (that clumped models tend to have lower degrees of ionization). But Eq. (31) also demonstrates explicitly the rather strong dependence on the local radiation field, where the exponential term on the right-hand-side decreases rapidly with an increasing Trad. For the three “O1” models in Table 1, Fig. 2 plots radiation temperatures in a wavelength range around important ionization edges in the extreme ultra-violet, for a typical wind radius r/R* ≈ 2. We note from the figure that around and shortward of the second helium ionization edge at 228 Å, the porous model yields radiation temperatures that are higher than in the simulation assuming optically thin clumps and more comparable to those seen in the smooth model (i.e., in this particular example 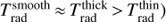 ). This is caused by the fact that χeff = ⟨ χ⟩ ≥ χsmooth in the model assuming optically thin clumps, whereas for the porous model χeff ≤ ⟨ χ⟩ (depending on τcl at the relevant frequency and radius, see also Fig. 3). In other words, porous models have reduced opacities when compared to equivalent models assuming optically thin clumping, which is an upper limit. And while changes may appear quite modest at first glance, we recall from Eq. (31) that increasing Trad by ∼1000 K in this range around ∼30 000 K already reduces nj by more than a factor of two (assuming nj + 1ne and Te remain unaltered).
). This is caused by the fact that χeff = ⟨ χ⟩ ≥ χsmooth in the model assuming optically thin clumps, whereas for the porous model χeff ≤ ⟨ χ⟩ (depending on τcl at the relevant frequency and radius, see also Fig. 3). In other words, porous models have reduced opacities when compared to equivalent models assuming optically thin clumping, which is an upper limit. And while changes may appear quite modest at first glance, we recall from Eq. (31) that increasing Trad by ∼1000 K in this range around ∼30 000 K already reduces nj by more than a factor of two (assuming nj + 1ne and Te remain unaltered).
 |
Fig. 2. Radiation temperature Trad vs. wavelength at a wind radius r/R* ≈ 2 for the three “O1” models in Table 1. Models are colored as in Fig. 1, i.e. the blue line is model thick, the red line model thin and the black line model smooth. |
 |
Fig. 3. Contour plot of effective to mean opacity ratio, χeff/⟨ χ⟩, for complete background opacities (i.e., sum of background lines + total continuum, see text), displayed as function of radius (abscissa) r/R* = 1 − 100 and the full considered wavelength range (ordinate) between 5 and 107 Å. Colors range between no opacity-reduction 1 (white) and the limiting value fic = 0.01 (black). Parameters according to ζ Pup like model thick1 in Table 1. |
Indeed, we can see this general ionization effect from a modified Trad directly in our clumpy FASTWIND models, for example in the ionization of trace ions of carbon in the outer wind: the upper right panel of Fig. 1 shows that optically thin clumping (red dashed line) reduces the relative number of CV atoms in the wind (as compared to the smooth model, the black dashed line), but how the addition here of porosity in physical and velocity space (blue dashed line) then increases the ionization to levels quite close to those of the smooth comparison model; the same behavior is also visible in the cooler “O3” carbon model to the lower right, however now it is the relative ionization of the minority stage CIV that is affected. Moreover, we note also that effects on the PV ion balance are quite moderate in the displayed models, thus providing some support of earlier phosphorus studies neglecting these ion feedback effects of velocity-space porosity (Oskinova et al. 2007; Sundqvist et al. 2010, 2011; Šurlan et al. 2013).
Continuum + line background opacities. For parameters of the ζ Pup like model thick1 in Table 1, Fig. 3 shows a contour-plot of the ratio effective to mean opacities. In order to illustrate both the effects from line blocking/blanketing and the continuum, we have summed up the contributions from background lines and all continuum opacities (i.e. from both background and explicit elements) when constructing this plot. The figure shows that, for this ζ Pup like model, the strong background opacities in the extreme ultraviolet are reduced to their saturation value χeff/⟨ χ⟩=0.01 set by the assumed inter-clump medium density (see Eq. (29)), whereas no effects of optically thick clumps are visible in the optical waveband. This illustrates that although the ζ Pup wind is optically thin in the visual waveband, the much higher opacities in the extreme ultra-violet are still subject to strong (velocity-)porosity effects.
Moreover, the figure illustrates that (the primarily bound-free) high-energy opacities below ≲ 10−20 Å are barely affected when terminal porosity-lenghts are on order h∞ ≲ R*; this is consistent with previous porosity-analysis of observed X-ray line-profiles in this high-energy regime (Leutenegger et al. 2013).
Finally, the plot demonstrates that at low wind radii continuum opacities at long radio wavelengths also reach the saturation value χeff/⟨ χ⟩=0.01; however, ⟨ χ⟩ is not affected at all in the outer wind beyond ∼10R*. And since the radio photosphere for O-supergiants typically is located well above 10R*, observations of radio emission in O-stars may thus be relatively free from severe porosity effects; this will be further investigated in an upcoming paper (del-Mar Rubio et al., in prep.).
4.3. Effects on line profiles
Ultra-violet resonance lines. For major-ion resonance lines with ⟨ χ⟩∼ρ, optically thin clumping affects computed profiles only through the potentially changed ionization balance (see above). On the other hand, because of their very strong and localized opacities, these lines are the ones most prone to experience effects of porosity in velocity space.
Fig. 4 shows the classical PV and NV P Cygni line doublets for the three ζ Pup like models of Table 1. The modeled phosphorus lines (upper panel) illustrate clearly the de-saturating effect of velocity-space porosity: The blue line shows strong PV lines emerging from simulations assuming optically thin clumping; the red dashed line then illustrates how velocity-porosity leads to significant additional light escape and so to weaker line profiles for a given Ṁ; finally, the black line shows how a tenuous inter-clump medium density of fic = 0.01 does not significantly affect this line (simply because the inter-clump densities are too low to contribute much to the total, effective line opacity). In agreement with previous studies (Oskinova et al. 2007; Sundqvist et al. 2010, 2011, 2014; Šurlan et al. 2013), this figure thus demonstrates explicitly how porosity in velocity space provides a natural explanation of the weak PV lines observed for O-stars in the Galaxy (Fullerton et al. 2006).
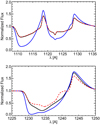 |
Fig. 4. Normalized flux profiles vs. wavelength for UV “P-Cygni” resonance doublets of PV (upper panel) and NV (lower panel). Profiles from the three ζ Pup like models in Table 1 are shown, where blue lines display model thin, black lines model thick1, and red dashed lines model thick2. See text. |
The lower panel then shows the same principal effects for the strong NV resonance doublet. Moreover, the red dashed line profile here also serves to demonstrate how a model with an effectively void medium actually never becomes completely “black”, since the absorptive intensity saturation value e−τeff(fvel) (=e−1 for the fvel = 0.5 assumed here) becomes independent of the atomic opacity (see Eq. (13) and previous discussion). However, unlike the weaker PV doublet, the strong NV lines are also sensitive to the inter-clump medium density; this is illustrated here by the black showing stronger absorption for the fic = 0.01 model than for the effectively void one (red dashed line). Physically, increasing the inter-clump density means the velocity-space holes between clumps are gradually “filled” in by absorbing material, until eventually the absorption profile becomes “black” at some saturation value ficτS (see Eq. (29)), which here clearly lies at fic > 0.01.
This essentially demonstrates how a combination of saturated and un-saturated UV P-Cygni lines may be used to constrain properties of both the high-density clumps and the sparse wind plasma in between them.
Hα. As discussed extensively in (Sundqvist et al. 2011, see also Oskinova et al. 2007), for O-stars the optical Hα line is generally less sensitive to velocity-space porosity effects than the UV resonance lines above. This is illustrated in the upper two panels of Fig. 5, displaying only small differences (actually quite negligible when the line is used for deriving Ṁ) between the “thin” and “thick” clumping simulations of the ζ Pup like and 03 models in Table 1. The marginal increase in Hα line emission of the “thick” models here is due to a small change in the NLTE number densities for the involved hydrogen atomic levels (neglected in previous work, which has only considered velocity-space porosity in the “formal integral” and not in the calculation of the NLTE number densities). Moreover, the principal recombination-line emission-measure scaling χ ∼ ⟨ρ2⟩ ∼ Ṁ2fcl (Sect. 4.1) is directly visible in the middle panel through the much stronger profiles of the clumped models than the smooth one. From the ζ Pup like models, we note finally that, as expected, the inter-clump density is not very important for the Hα line formation in this regime.
 |
Fig. 5. Modeled Hα line profiles. Profiles from the three ζ Pup like models in Table 1 are shown in the upper panel, with color coding as in Fig. 4. The middle and lower panels then display the O3 and B7 models in Table 1, respectively, with black lines showing models thick, blue lines models thin and orange lines models smooth. |
The lowest panel in Fig. 5 shows, however, that when changing the stellar parameters to those of typical late B- and A-supergiants, we see effects quite similar to those of the UV lines analyzed above. This was pointed out already by Sundqvist et al. (2010), but with our new FASTWIND models we are now able to quantify this potentially important effect. Namely, in this regime the lower level of the Hα transition becomes much more populated, and so the line transforms from being an almost optically thin recombination line to being much more optically thick (e.g., Kudritzki & Puls 2000). As such, Hα is much more prone to velocity-space porosity effects in this regime than for O-stars (as clearly seen in the lower panel of Fig. 5).
5. Summary and future work
We have developed a formalism that accounts for the leakage of light associated with porosity in physical and velocity space in a clumpy, accelerating medium, and incorporated this method into the global (photosphere + wind) NLTE model atmosphere code FASTWIND. Our method is included both in the general code network for solving the NLTE rate equations and in the “formal solver” used to produce synthetic spectra. As such, the new version of FASTWIND allows readily for investigations of optically thick clumping directly on line profiles, but also upon the wind ionization balance and NLTE number densities. Indeed, to date it is the only stellar atmosphere code on the market that includes these physical effects of clumping in the NLTE network; along with its quite remarkable computational speed (see below), the new version of FASTWIND is thus ideally suited for future multi-wavelength quantitative spectroscopic studies aiming to derive new improved wind parameters of individual stars in the local Universe.
The basic method is based on a description of the supersonic wind outflow as a stochastic two-component medium consisting of dense clumps (of arbitrary optical thickness) and a rarified “inter-clump” medium (filling in the space between the clumps). By formulating this in terms of effective and mean opacities scaled to corresponding “smooth” ones, we are able to compute models with the same speed as in previous FASTWIND programs (∼15 min on a modern laptop/desktop). Four parameters are required to fully specify the clumpy two-component medium; the clumping factor fcl, the inter-clump density parameter fic, the porosity length h and the velocity filling factor fvel. While the first three of these parameters are the equivalents of those used in previous stochastic transport models for static media (Pomraning 1991), the last one accounts here for line-absorption in accelerating, supersonic media (SPO14). As discussed in Sect. refclumping, we note also that the set fcl, h, and fvel is equivalent to a consideration of the clump volume filling factor, the clump length scale, and the clump velocity-span.
After confirming that relevant analytic limits are preserved (e.g., smooth, optically thin and completely optically thick cases), we present some first, generic FASTWIND results. A summary is as follows: i) We confirm earlier results (e.g., Oskinova et al. 2007; Sundqvist et al. 2011, 2014; Šurlan et al. 2013) that velocity-space porosity is critical for UV wind resonance lines in O-stars, and indeed provides a natural explanation for the overall weakness of, e.g., observed unsaturated PV lines in the Galaxy. In addition, we illustrate how a combination of saturated and un-saturated UV lines might be used to constrain not only the dense clumps, but also the rarefied material in between them (under the assumption made here of approximately equal gas and radiation temperatures for both components). ii) For the optical Hα line, we show that optically thick clumping effects are marginal for O-stars, but potentially very important for late B and A-supergiants (see also below). iii) In agreement with previous work, we show that spatial porosity is a marginal effect for absorption of high-energy X-rays below, say, ∼15 − 20Å in O-stars, as long as the terminal porosity lengths are kept at realistic values h∞ ≲ R* (Leutenegger et al. 2013; Hervé et al. 2013; Grinberg et al. 2015; Owocki & Sundqvist 2018). iv) Also, whereas radio absorption indeed shows strong spatial porosity effects in the inner wind, it is negligible at typical O-star radio-photosphere radii r ∼ 100R*. v) Regarding the wind ionization balance, quantitative effects depend significantly on the specific ion and stellar and wind parameter range. However, two general trends are 1) the increased rates of recombination in simulations with optically thin clumps lead to overallower degrees of ionization than in corresponding smooth models and 2) this effect is then counteracted by the increased light-leakage (i.e., the stronger radiation field) associated with porosity (in physical and/or velocity space).
An overall objective for the new version of FASTWIND now concerns application to multi-wavelength observations of samples of hot, massive stars, and corresponding derivation of empirical constraints on clumping parameters and mass-loss rates. Indeed, the paper here shows that, if enough suitable diagnostics are available one should be able to obtain direct constraints on the different clumping parameters (and their radial dependence). A rough outline for a 4-step procedure of such multi-wavelength analyses could be as follows: i) Use the relatively clumping-insensitive X-ray lines and/or broad-band spectrum to derive an empirical mass-loss rate (Cohen et al. 2011, 2014; Hervé et al. 2013); ii) then, obtain clumping factors for the near-photospheric layers using optical and/or infra-red (IR) recombination lines like Hα, HeII 4686, Brα, etc. (Puls et al. 2006; Sundqvist et al. 2011; Najarro et al. 2011); iii) then, obtain constraints on clumping factors in the intermediate/outer wind from IR/radio emission (Puls et al. 2006) and (at least) upper limits for porosity lengths by combining IR/radio and X-ray (Leutenegger et al. 2013) results; iv) then, obtain constraints on the velocity filling factor and the inter-clump density from a combination of saturated and un-saturated UV line profiles from different ions (see discussion above).
However, while this overall outline provides neat guidance for carrying out extensive analyses of nearby stars with a multitude of observational material available, for other cases (e.g., single line observations) one will have to rely on external constraints and knowledge for setting the clumping parameters. For such cases, reasonable input values (in overall agreement with various theoretical and empirical constraints, see also Sect. 4.2) might be fic ∼ 0.01 − 0.2, fvel ∼ 0.5 − 1.0, h∞/R* ∼ 0.5 − 1.0, and fcl ∼ 4 − 30. Also, let us repeat here again that, in practice, certainly not all clumping parameters will be relevant for all diagnostics (see previous sections).
In addition to UV P-Cygni lines in OB-stars, one interesting application regards Hα in late B and A-supergiants, for which the observed absorption troughs very often are shallower than predicted by smooth/optically thin clumping models (M. Urbaneja, private communication); this agrees well with the generic results from models including velocity-space porosity (Fig. 5, lower panel), and definitely deserves further studies. Indeed, such velocity-porosity effects may potentially be important also for quantifying mass loss from Hα across the broader B-star regime (Petrov et al. 2014), in particular in regions where the iron ion balance undergoes a quite sudden shift (at the so-called bistability-jump, Pauldrach & Puls 1990; Vink et al. 2000); this will be analyzed in detail in a forthcoming paper (Watts et al. in prep.). And in yet another waveband, a detailed analysis of (the potential lack of) porosity effects for deriving radio mass-loss rates from O-stars is also underway (del-Mar Rubio et al., in prep., but see also Ignace 2016 for alternative models).
Finally, key steps in future updates of FASTWIND will regard i) a CMF-solution of “all” contributing lines (see Puls 2017); ii) an extension toward modeling of optically thick Wolf-Rayet winds (where spatial/velocity-field porosity effects definitely should be very important, Sundqvist et al., in prep); and iii) solving the (steady-state) hydrodynamical equations in the wind in order to also predict average mass-loss rates and velocity fields (Sundqvist et al., in prep, but see also Sander et al. 2017; Krtička & Kubát 2017 for alternative models).
A note on terminology: Some authors collect the above effects of optically thick clumps under the umbrella-term “macroclumping”, and similarly name the case of only optically thin clumps “microclumping”. This essentially derives from the “microturbulence” and “macroturbulence” terminology traditionally used in spectroscopy of stellar photospheres. However, due to the quite different properties of line and continuum clumping-effects in accelerating media, as well as the risk of confusing optical depths with spatial scales within the micro- and macro-clumping terminology, this paper simply uses the denotation optically thin and thick clumping throughout, and describes effects of the latter using the more physical terms porosity in spatial and/or velocity-space.
Also here is a code-update under way, which will compute the full radiation field by means of co-moving frame transport (Puls 2017).
This does not include any phenomenological so-called “microturbulent” velocities in the wind, since such wind microturbulence typically is added in unclumped models in order to mimic just these effects of clumping; when synthesized directly from clumped LDI simulations, no ad-hoc microturbulence is required to model for example the extended black troughs of UV P-Cygni lines (see Fig. 1 of Sundqvist et al. 2012b).
Acknowledgments
JOS acknowledges previous support from DFG grant Pu117/8-1, and also previous support from the European UnionÕs Horizon 2020 researchand innovation program under the Marie Sklodowska-Curie grant agreement No 656725. JP gratefully acknowledges travel support by the Deutsche Forschungsgemeinschaft, under grant Pu117/9-1. We finally thank the referee, Ken Gayley, for useful comments on the manuscript.
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Carneiro, L. P., Puls, J., Sundqvist, J. O., & Hoffmann, T. L. 2016, A&A, 590, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carneiro, L. P., Puls, J., & Hoffmann, T. L. 2018, A&A, 615, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, D. H., Gagné, M., Leutenegger, M. A., et al. 2011, MNRAS, 415, 3354 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, D. H., Wollman, E. E., Leutenegger, M. A., et al. 2014, MNRAS, 439, 908 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., & Owocki, S. P. 2003, A&A, 406, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, C. J., Taylor, W. D., Hénault-Brunet, V., et al. 2011, A&A, 530, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feldmeier, A., Puls, J., & Pauldrach, A. W. A. 1997, A&A, 322, 878 [NASA ADS] [Google Scholar]
- Feldmeier, A., Oskinova, L., & Hamann, W.-R. 2003, A&A, 403, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fullerton, A. W., Massa, D. L., & Prinja, R. K. 2006, ApJ, 637, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Gabler, R., Gabler, A., Kudritzki, R. P., Puls, J., & Pauldrach, A. 1989, A&A, 226, 162 [NASA ADS] [Google Scholar]
- Gräfener, G., Koesterke, L., & Hamann, W.-R. 2002, A&A, 387, 244 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grinberg, V., Leutenegger, M. A., Hell, N., et al. 2015, A&A, 576, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamann, W.-R., Feldmeier, A., & Oskinova, L. M., eds. 2008, Clumping in Hot-Star Winds [Google Scholar]
- Hauschildt, P. H. 1992, J. Quant. Spectr. Rad. Transf., 47, 433 [Google Scholar]
- Hervé, A., Rauw, G., & Nazé, Y. 2013, A&A, 551, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillier, D. J. 1991, A&A, 247, 455 [NASA ADS] [Google Scholar]
- Hillier, D. J. 2008, in Clumping in Hot-Star Winds, ed. W.-R.Hamann, & A.Feldmeier, 93 [Google Scholar]
- Hillier, D. J., & Miller, D. L. 1998, ApJ, 496, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., & Mihalas, D. 2014, Theory of Stellar Atmospheres. [Google Scholar]
- Ignace, R. 2016, MNRAS, 457, 4123 [NASA ADS] [CrossRef] [Google Scholar]
- Krtička, J., & Kubát, J. 2017, A&A, 606, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kudritzki, R.-P., & Puls, J. 2000, ARA&A, 38, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Leutenegger, M. A., Cohen, D. H., Sundqvist, J. O., & Owocki, S. P. 2013, ApJ, 770, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Najarro, F., Hanson, M. M., & Puls, J. 2011, A&A, 535, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oskinova, L. M., Feldmeier, A., & Hamann, W.-R. 2004, A&A, 422, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oskinova, L. M., Feldmeier, A., & Hamann, W.-R. 2006, MNRAS, 372, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Oskinova, L. M., Hamann, W.-R., & Feldmeier, A. 2007, A&A, 476, 1331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owocki, S. P. 2008, in Clumping in Hot-Star Winds, ed. W.-R. Hamann, A. Feldmeier, & L. M. Oskinova, 121 [Google Scholar]
- Owocki, S. P., & Rybicki, G. B. 1984, ApJ, 284, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., & Rybicki, G. B. 1985, ApJ, 299, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., & Puls, J. 1999, ApJ, 510, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., & Cohen, D. H. 2006, ApJ, 648, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., & Sundqvist, J. O. 2018, MNRAS, 475, 814 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., Castor, J. I., & Rybicki, G. B. 1988, ApJ, 335, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., Gayley, K. G., & Shaviv, N. J. 2004, ApJ, 616, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Pauldrach, A. W. A., & Puls, J. 1990, A&A, 237, 409 [NASA ADS] [Google Scholar]
- Pauldrach, A. W. A., Hoffmann, T. L., & Lennon, M. 2001, A&A, 375, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrov, B., Vink, J. S., & Gräfener, G. 2014, A&A, 565, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pomraning, G. C. 1991, Linear Kinetic Theory and Particle Transport in Stochastic Mixtures [CrossRef] [Google Scholar]
- Puls, J. 2017, in The Lives and Death-Throes of Massive Stars, ed. J. J. Eldridge, J. C. Bray, L. A. S. McClelland, & L. Xiao, IAU Symposium, 329, 435 [Google Scholar]
- Puls, J., Urbaneja, M. A., Venero, R., et al. 2005, A&A, 435, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puls, J., Markova, N., Scuderi, S., et al. 2006, A&A, 454, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puls, J., Vink, J. S., & Najarro, F. 2008, A&ARv, 16, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puls, J., Sundqvist, J. O., & Markova, N. 2015, IAU Symposium, 307, 25 [Google Scholar]
- Rauw, G., Nazé, Y., Wright, N. J., et al. 2015, ApJS, 221, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Rivero González, J. G., Puls, J., & Najarro, F. 2011, A&A, 536, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rivero González, J. G., Puls, J., & Najarro, F. 2011, A&A, 536, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sander, A., Shenar, T., Hainich, R., et al. 2015, A&A, 577, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sander, A. A. C., Hamann, W.-R., Todt, H., Hainich, R., & Shenar, T. 2017, A&A, 603, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santolaya-Rey, A. E., Puls, J., & Herrero, A. 1997, A&A, 323, 488 [NASA ADS] [Google Scholar]
- Smith, N. 2014, ARA&A, 52, 487 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Sobolev, V. V. 1960, Moving Envelopes of Stars (Cambridge, UK: Harvard University Press) [CrossRef] [Google Scholar]
- Sundqvist, J. O., & Owocki, S. P. 2013, MNRAS, 428, 1837 [NASA ADS] [CrossRef] [Google Scholar]
- Sundqvist, J. O., & Owocki, S. P. 2015, MNRAS, 453, 3428 [NASA ADS] [CrossRef] [Google Scholar]
- Sundqvist, J. O., Puls, J., & Feldmeier, A. 2010, A&A, 510, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sundqvist, J. O., Puls, J., Feldmeier, A., & Owocki, S. P. 2011, A&A, 528, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sundqvist, J. O., Owocki, S. P., Cohen, D. H., Leutenegger, M. A., & Townsend, R. H. D. 2012a, MNRAS, 420, 1553 [NASA ADS] [CrossRef] [Google Scholar]
- Sundqvist, J. O., Owocki, S. P., & Puls, J. 2012b, in Proceedings of a Scientific Meeting in Honor of Anthony F. J. Moffat, ed. L. Drissen, C. Rubert, N. St-Louis, & A. F. J. Moffat, Astronomical Society of the Pacific Conference Series, 465, 119 [NASA ADS] [Google Scholar]
- Sundqvist, J. O., Puls, J., & Owocki, S. P. 2014, A&A, 568, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sundqvist, J. O., Owocki, S. P., & Puls, J. 2018, A&A, 611, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Šurlan, B., Hamann, W.-R., Kubát, J., Oskinova, L. M., & Feldmeier, A. 2012, A&A, 541, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Šurlan, B., Hamann, W.-R., Aret, A., et al. 2013, A&A, 559, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2000, A&A, 362, 295 [NASA ADS] [Google Scholar]
- Zsargó, J., Hillier, D. J., Bouret, J.-C., et al. 2008, ApJ, 685, L149 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Ionization balance of selected elements iron (Fe), phosphorus (P), and carbon (C) for FASTWIND models “O1” (top panels), “O2” (middle panels), and “O3” (lower panels) with parameters according to Table 1. Plotted in each panel are number density ratios log nj/ni for ion stage j of species i, with ni the total element abundance, as function of a radius coordinate log10(r/R* − 1). Blue lines are models “thick” including full effects of porosity in physical and velocity space; red lines are models “thin” assuming optically thin clumping; black lines are models “smooth” without any wind clumping. For iron (left panels), phosphorus (middle panels), and carbon (right panels), the displayed states are given in the upper right of each panel; solid lines then show the ion fraction in the lowest considered state j, the dotted lines show state j + 1 and the dashed ones j + 2. (For example the top left panel thus shows Fe 3+ − 5+ = Fe IV − VI in models O1 “thick” (blue), “thin” (red) and “smooth” (black), where solid lines are ion fractions of Fe IV, dotted lines of Fe V, and dashed lines of Fe VI.) |
| In the text | |
 |
Fig. 2. Radiation temperature Trad vs. wavelength at a wind radius r/R* ≈ 2 for the three “O1” models in Table 1. Models are colored as in Fig. 1, i.e. the blue line is model thick, the red line model thin and the black line model smooth. |
| In the text | |
 |
Fig. 3. Contour plot of effective to mean opacity ratio, χeff/⟨ χ⟩, for complete background opacities (i.e., sum of background lines + total continuum, see text), displayed as function of radius (abscissa) r/R* = 1 − 100 and the full considered wavelength range (ordinate) between 5 and 107 Å. Colors range between no opacity-reduction 1 (white) and the limiting value fic = 0.01 (black). Parameters according to ζ Pup like model thick1 in Table 1. |
| In the text | |
 |
Fig. 4. Normalized flux profiles vs. wavelength for UV “P-Cygni” resonance doublets of PV (upper panel) and NV (lower panel). Profiles from the three ζ Pup like models in Table 1 are shown, where blue lines display model thin, black lines model thick1, and red dashed lines model thick2. See text. |
| In the text | |
 |
Fig. 5. Modeled Hα line profiles. Profiles from the three ζ Pup like models in Table 1 are shown in the upper panel, with color coding as in Fig. 4. The middle and lower panels then display the O3 and B7 models in Table 1, respectively, with black lines showing models thick, blue lines models thin and orange lines models smooth. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.