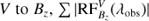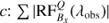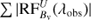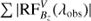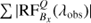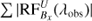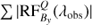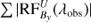| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 13 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201832955 | |
| Published online | 08 November 2018 | |
Magnetic field variations associated with umbral flashes and penumbral waves
1
Institute for Solar Physics, Department of Astronomy, Stockholm University, AlbaNova University Centre, 106 91 Stockholm, Sweden
2
Rosseland Centre for Solar Physics, University of Oslo, PO Box 1029 Blindern, 0315 Oslo, Norway
3
Institute of Theoretical Astrophysics, University of Oslo, PO Box 1029 Blindern, 0315 Oslo, Norway
e-mail: jayant.joshi@astro.uio.no
Received:
5
March
2018
Accepted:
24
August
2018
Context. Umbral flashes (UF) and running penumbral waves (RPWs) in sunspot chromospheres leave a dramatic imprint in the intensity profile of the Ca II 8542 Å line. Recent studies have focussed on also explaining the observed polarization profiles, which show even more dramatic variations during the passage of these shock fronts. While most of these variations can be explained with an almost constant magnetic field as a function of time, several studies have reported changes in the inferred magnetic field strength during UF phases. These changes could be explained by opacity effects or by intrinsic changes in the magnetic field strength.
Aims. In this study we investigate the origin of these periodic variations of the magnetic field strength by analyzing a time-series of high-temporal-cadence observations acquired in the Ca II 8542 Å line with the CRISP instrument at the Swedish 1-m Solar Telescope. In particular, we analyze how the inferred geometrical height scale changes between quiescent and UF phases, and whether those changes are enough to explain the observed changes in the magnetic field, B.
Methods. We have performed non local thermodynamical equilibrium (non-LTE) data inversions with the NICOLE code of a time-series of very high spatio-temporal-resolution observations in the Ca II 8542 Å, Fe I 6301.5, and Fe I 6302.5 Å lines. We analyze in detail the variations of the different physical parameters of the model as a function of time.
Results. Our results indicate that the Ca II 8542 Å line in sunspots is greatly sensitive to magnetic fields at log τ500 = −5 (hereafter log τ = −5) during UFs and quiescence. However this optical depth value does not correspond to the same geometrical height during the two phases. Our results indicate that during UFs and RPWs the log τ = −5 is located at a higher geometrical height than during quiescence. Additionally, the inferred magnetic field values are higher in UFs (up to ∼270 G) and in RPWs (∼100 G).
Conclusions. Our results suggest that opacity changes caused by UFs and RPWs cannot explain the observed temporal variations in the magnetic field, as the line seems to form at higher geometrical heights where the field is expected to be lower.
Key words: Sun: chromosphere / sunspots / Sun: magnetic fields / techniques: polarimetric / Sun: oscillations
© ESO 2018
1. Introduction
Oscillations in sunspots have been studied in the outer layers of the Sun, preferentially using intensity or Doppler measurements from different spectral diagnostics.
In the chromosphere the imprint of these waves is particularly dramatic as they become shocks due to the steep decrease of density between the photosphere and chromosphere (Lites 1984, 1986; Bloomfield et al. 2007). Beckers & Tallant (1969) and Wittmann (1969) identified for the first time sudden intensity enhancements in the core of the Ca II K line in sunspot umbrae (commonly known as umbral flashes), although most chromospheric lines show a similar behavior. A sawtooth pattern of an upward propagating shock wave in umbrae is observed using different chromospheric and transition region lines (e.g., Rouppe vander Voort et al. 2003; Centeno et al. 2006, de la Cruz Rodríguez et al. 2013; Tian et al. 2014; Kanoh et al. 2016).
The dominant period of these oscillations in umbrae is three minutes in the chromosphere as well as in the transition region and corona (Gurman et al. 1982; Gurman 1987; Thomas et al. 1987; Kentischer & Mattig 1995; De Moortel et al. 2002; Rouppe vander Voort et al. 2003; Centeno et al. 2006; Tian et al. 2014). Running penumbral waves (RPWs) are produced by a similar physical process to that responsible for umbral flashes, shock waves propagating along a magnetized atmosphere, but in this case the vertical propagation of the shock is slower than in the umbra because the magnetic field becomes more horizontal in the penumbra and the shock propagates along those field lines (e.g., Bloomfield et al. 2007).
Although magnetic fields have been studied in sunspot umbra (Socas-Navarro et al. 2000), only recently de la Cruz Rodríguez et al. (2013) analyzed magnetic field oscillations in the chromosphere. The latter found that the magnetic field oscillates with an amplitude of ∼200 G in the sunspot penumbra due to RPWs. However, de la Cruz Rodríguez et al. (2013) did not find significant variations of the magnetic field in the umbra. Henriques et al. (2017) also studied umbral flashes in a sunspot chromosphere and they found that the strength of the vertical component of the magnetic field is slightly reduced during the flash phase compared to that in the quiescent phase.
Several authors have studied magnetic field oscillations in the photosphere, but these studies do not present a consistent picture and often contradict each other. For example, variations in the magnetic field with different amplitudes, from zero to a few tens of Gauss, have been reported in a number of studies (see e.g., Landgraf 1997; Horn et al. 1997; Lites et al. 1998; Rueedi et al. 1998; Kupke et al. 2000; Balthasar 1990, 2003; Bellot Rubio et al. 2000; Kallunki & Riehokainen 2012).
Some authors, for example, Rüedi et al. (1999), Bellot Rubio et al. (2000), Rüedi & Cally (2003), Khomenko et al. (2003) and Khomenko & Collados (2015), have suggested that the observed temporal variations of photospheric magnetic fields in sunspots could be an opacity effect that changes the effective formation height of the line due to oscillations in the thermodynamical parameters. According to this idea, the vertical magnetic field gradient of a sunspot, in combination with oscillating formation height of the spectral line under consideration can lead to false observations of oscillation in the magnetic field. Similarly, in the chromosphere, Henriques et al. (2017) speculate that their results could be compatible with enhancements in the opacity of the Ca II 8542 Å line during the flash phase.
In this paper we study the evolution of physical parameters in a sunspot chromosphere during UFs, focusing our analysis on the temporal fluctuations of the derived magnetic field vector in the photosphere and chromosphere. We explore the origin of magnetic field oscillations in a sunspot and their relation to opacity changes in the Ca II 8542 Å line.
2. Observations
Our observations were recorded in full-Stokes mode on the 22 July 2013 starting at 08:33 UT using the CRISP spectropolarimeter (Scharmer 2006; Scharmer et al. 2008) at the Swedish 1-m Solar Telescope (SST; Scharmer et al. 2003). The observed field of view (FOV) consists of the leading sunspot in active region NOAA 11793.
The observations were acquired in the Ca II 8542 Å line at 21 wavelength points that sample a range of ±1.750 Å from line center in an irregular grid of line positions. Close to the line center, the line positions are sampled with a step of 70 mÅ and that grid becomes increasingly more sparse in the broad photospheric wings of this line. We also acquired co-temporal data in the Fe I 6301.5 and 6302.5 Å lines with 18 wavelength points. The Fe I 6301.5 and 6302.5 Å lines were observed with a sampling of 40 mÅ close to line centers and with relatively sparse sampling in line wings. The total cadence of these observations is 25 s and the duration of the complete time series is 25 min. The data were reduced using the CRISPRED pipeline (de la Cruz Rodríguez et al. 2015; Henriques 2012; Schnerr et al. 2011), including Multi-Object-Multi-Frame-Blind-Deconvolution processing (MOMFBD; van Noort et al. 2005) of the entire time series.
Figure 1a illustrates our target displayed in the line center of the Ca II 8542 Å line. Maps of Stokes V/Ic, Q/Ic, and, U/Ic at a wavelength offset of −350 mÅ from the line center are displayed in panels b, c and d, respectively; Ic represents average continuum intensity in the quiet Sun. The red slit marked on the FOV indicates the location of the spectra that we have extracted to perform our temporal analysis. The solar limb is located towards the upper part of the image.
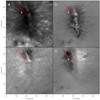 |
Fig. 1. Field of view comprising the leading sunspot in the active region NOAA 11793 observed on 22 July 2013. Panel a: image obtained at the line center of the Ca II 8542 Å spectral line using CRISP. Panels b–d: Stokes V/Ic, Q/Ic, and, U/Ic maps, respectively, at –350 mÅ from the line center. The red cut marked as r indicates the position for which the temporal evolution of the atmospheric parameters is analyzed in this study. |
3. Inversions
We used the non local thermodynamical equilibrium (non-LTE) inversion code NICOLE (Socas-Navarro et al. 2015) to obtain atmospheric parameters in the chromosphere and photosphere of our sunspot observations. The parameters of our model atmospheres are calculated in an optical-depth grid with five points per decade, which should suffice to compute very accurate intensities with DELO-Bezier formal solvers (see de la Cruz Rodríguez & Piskunov 2013; Janett et al. 2017). We refer to the code description paper for further details. We have included the effect of Ca II isotopic splitting in our inversions which can affect the derivation of Doppler velocities when it is not included in the inversion (see Leenaarts et al. 2014).
We only carried out the inversions for a time series extracted along the red cut shown in Fig. 1. We performed the inversions separately for the Ca II 8542 Å line and Fe I 6301.5 and 6302.5 Å lines. For the Ca II 8542 Å line, we used five nodes located at log τ = –7, –5, –3, –1 and, 1 for temperature, T, and four nodes at log τ = –7, –5, –3 and, 1 for line-of-sight (LOS) velocity, υLOS. τ represents the continuum optical depth at 500 nm. For all three components of the magnetic field, Bx, By, and, Bz, we used two nodes, that is, the magnetic field varies linearly with log τ. Bz is the LOS component of the magnetic field and Bx and By are the two components orthogonal to each other and Bz. The micro-turbulence, υturb, is assumed to be constant as a function of optical depth.
We have carried out test inversions to select the minimum number of nodes that allows to properly reproduce the observed spectra in the umbra, penumbra, and outside the sunspot. In the penumbra, good fits to the observed Stokes profiles were achieved even when we only allowed linear gradient in υLOS with respect to log τ. But UF atmospheres required more nodes in υLOS to fit the observed profiles. Hence, the inversions are carried out in two cycles; in the first cycle we used only two nodes for υLOS and a single node for Bx, By, and, Bz. In the second cycle, four nodes are used for υLOS and two nodes for Bx, By, and, Bz. The results from the first cycle are used as input in the second cycle.
We have another set of inversions for the Ca II 8542 Å line where the model atmosphere is very similar to that described above, except that the magnetic field is assumed to be constant with optical depth. This additional set of inversions allows us to compare the magnetic field properties of the sunspot obtained with two different approaches of the inversions.
Quintero Noda et al. (2016) analyzed response functions (RFs) of the Ca II 8542 Å line for different thermodynamical parameters and the magnetic field for the quiet-Sun FAL-C model (Fontenla et al. 1993). Their analysis showed that the Ca II 8542 Å line has almost negligible or zero response to υLOS in the atmosphere below log τ = −3, and for that reason we avoided adding a node for υLOS between log τ = −3 and 1 in our inversions. However, RFs could be significantly different for a sunspot model compared to that for FAL-C model.
For the photospheric magnetic field measurements, we inverted the Fe I 6301.5 and 6302.5 Å lines using four nodes, log τ = –5, –3, –1 and, 1 for T and two nodes for υLOS. We assume constant Bx, By, Bz and, υturb as a function of optical depth.
Since we are working with data that include the umbra-penumbra boundary, our data can be particularly affected by straylight from residual (uncorrected) atmospheric aberrations (Scharmer et al. 2010). Additionally, the flat-fielding method for the 8542 data includes a backscatter correction step that can slightly modify the contrast of the image (for more details see Appendix A1 of de la Cruz Rodríguez et al. 2013). For these reasons, and to avoid potentially controversial data deconvolutions, we decided to perform the inversion of the Ca II 8542 Å line separately from the Fe I 6301.5 and 6302.5 Å lines.
Hereafter, the chromospheric inversion results displayed at log τ = –5 and –3 are taken from the inversions of the Ca II 8542 Å line, whereas the photospheric parameters shown at log τ = −1 are obtained from the inversions of the Fe I 6301.5 and 6302.5 Å lines.
4. Results and analysis
4.1. Umbral flashes in temperature and LOS velocity
The temporal evolution of T and υLOS is presented in Fig. 2. At log τ = −5, T and υLOS reveal a clear oscillatory pattern in the umbra. At log τ = −3, the imprint of these oscillations is still visible but not as prominent as at log τ = −5. At log τ = −1, both quantities present spatial changes and a very smooth photospheric temporal evolution.
 |
Fig. 2. Temporal evolution of the temperature (top panels) and line-of-sight velocity (bottom panels) at log τ = −5, −3, and, −1. Panels a, b, d, and e illustrate the results from our inversions of the Ca II 8542 Å line, whereas panels c and f are taken from the inversion of the Fe I 6301.5 and 6302.5 Å lines. r = 0 corresponds to the outer-most point from the sunspot in the red cut marked in Fig. 1. |
In order to emphasize the smaller-scale fluctuations that are present in the penumbra, in Fig. 3 we have extracted the local background at each location by fitting a third-order polynomial along the temporal dimension for each slit position. Hereafter, these residual variations are denoted with a δ in front of the physical variable name.
 |
Fig. 3. As in Fig. 2, but in this case we illustrate the residual variations, δT and δυLOS after subtracting the local background. The green line in panels a and d traces an RPW. |
The signature of RPWs is now clearly visible in δT and δυLOS at log τ = –5 and –3. We have traced a RPW (see green line in panels a and d) which shows an outward motion from the inner penumbra towards the outer penumbra with a speed of ∼9kms−1.
Figures 2 and 3 show persistent variations in the temperature and LOS velocity during the passage of UFs and RPW that are believed to be responsible for opacity changes in the Ca II 8542 Å line.
We calibrated the absolute reference υLOS by assuming that the average photospheric velocity in the umbra is equal to zero. The Ca II 8542 Å line is not very sensitive to photospheric LOS velocities, so our calibration of υLOS may be affected by large uncertainties, but it is the best we can do based on prior knowledge of the observed target.
Average quiescent and flash atmospheres
Umbra. The average temperature stratification in UFs and quiescence in the umbra is relatively similar in both up to log τ = −3 (see Fig. 4). Around log τ = −5, atmosphere in UFs can be on average up to 1 kK hotter than the quiescent umbra as reported by de la Cruz Rodríguez et al. (2013). The LOS velocity shows an upflowing atmosphere during the UF phase in the chromsphere, but a rather static situation during quiescence. Below log τ = −3, υLOS is almost identical during UFs and in the quiescent phase.
 |
Fig. 4. Averaged stratification of T and υLOS as a function of optical depth obtained from the inversions of the Ca II 8542 Å line. Upper-left and lower-left panels: stratification of T and υLOS in the umbra, respectively. The red and blue curves represent the umbral flash and quiescent umbra atmosphere, respectively. Panels on the right: stratification of the same physical parameters in the penumbra. The shaded areas in all panels demonstrate the distribution of the parameters normalized at each log τ position. |
Penumbra. In the penumbra we find a similar behavior as in the umbra. At log τ = −5, T is 0.5 kK higher during the hotter phase of RPWs. Similarly, υLOS at log τ = −5 is on average around –1.2 km s−1 during the hotter phase of RPWs; otherwise it is close to zero.
We note that the average stratification of the parameters shown in Fig. 4 is calculated from the inversion results of the Ca II 8542 Å line. The latter provides limited velocity diagnostic capabilities in the photosphere due to the very broad (photospheric) wings of the Ca II line.
4.2. Time evolution of B
In the present study, we have assessed the quality of our fits during UFs and RPWs. We have also studied the sensitivity of the Ca II 8542 line to magnetic fields and magnetic field gradients in sunspot atmospheres using response functions. These studies can be found in Appendices A and B. The very short summary of that study is that in the derived sunspot atmospheres, the response function of the Ca II 8542 line peaks at approximately log τ = −5.
Our magnetic field maps show the oscillatory imprint of UFs and RPWs as a function of time (see Figs. 5 and 6 for the background compensated version). The amplitudes of these oscillations are larger in the umbra than in the penumbra, and they have the same phase and period as those detected in T . In the chromosphere, both components of the magnetic field show very similar behavior, except that Bt at the very end of the slit (in the umbra) does not show the imprint of UF because there is no signal in Q and U in those pixels. In the photosphere we detect a long period oscillation in δBz at r < 4′, but otherwise there is no obvious evidence of UF or RPW in any of the physical parameters.
 |
Fig. 5. Temporal evolution of the magnetic field in the chromosphere and in the photosphere. Panels a and c: LOS component of the magnetic field, Bz, and transverse component of the magnetic field, Bt,atlog τ = −5.0. Panels b and d: Bz and Bt at log τ = −1.0. These results are solely obtained from the inversion of the Ca II 8542 Å line. |
 |
Fig. 6. As in Fig. 5, but in this case we show the residual variations, δ|Bz| and δBt after removing the local background. The green line in panels a and c represents the same RPW as in Fig. 3. |
We have selected two locations along the slit in the umbra and in the penumbra. Figure 7 shows a comparison of all physical quantities at those locations. This figure greatly illustrates an almost perfect correlation of all parameters in the umbra, during UF passages. In the penumbra, υLOS seems to be slightly out of phase with T and B during RPWs. But the correlation between δT,δ|Bz| and δB in both cases is remarkable and seems to point to opacity effects. This figure also makes it very easy to appreciate how much larger the chromospheric oscillations are when compared to those in the photosphere. For clarity, we have summarized in Table 1 some of the peak-to-peak values that are observed in Fig. 7.
 |
Fig. 7. Temporal variations of the atmospheric parameters in the umbra (left column), and penumbra (right column) after removing the local background. The curves plotted in these panels correspond to r = 13″.8 and r = 7″.4 for the umbral and penumbral sets, respectively. From top to bottom,(panels a1–a3): δT, δυLOS and, δ|Bz| from the inversions of the Ca II 8542 Å line including a linear gradients in the magnetic field as a function of log τ. Panel a4: δ|Bz| from the inversions of the Ca II 8542 Å line (orange curve) and the Fe I line pair at 6302 Å (gray curve) separately with the assumption that the magnetic field is depth independent. Panels b1–b4 are similar to panels a1–a4, but the former depict δB instead of δ|Bz|. The red, blue, and green curves correspond to log τ = −5, −3, and, −1. |
4.3. Opacity changes during the UFs and RPWs
Both in the photosphere and chromosphere, several authors have suggested that the observed oscillations of the magnetic field in sunspots may be due to changes in line opacity induced by waves. The sunspot’s magnetic field has a gradient with height and if the line opacity changes during the passage of UFs, then the core of this spectral line can sample a different magnetic field regime. We analyze the changes in the geometrical height scale, z, as a consequence of changes in the thermodynamical parameters due to oscillations.
We have computed the geometrical height that corresponds to log τ = −5[z(log τ = −5)], assuming hydrostatic equilibrium. Although the latter is an approximation that may not reproduce the exact geometrical scale of the Sun, it allows to perform a differential study of z as a function of time, as illustrated in Fig. 8. Our results indicate that the magnetic field is amplified during UFs and RPWs, while the z(log τ = −5) increases.
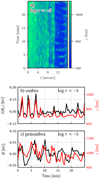 |
Fig. 8. Panel a: space-time variation of z(log τ = −5) . Panel b: temporal variations of δ|Bz| and z at log τ = −5 for an umbral pixel (r = 13″.8) and panel c: temporal variation of δB and z at log τ = −5 for a penumbral pixel (r = 7″.4). |
In the umbra, there is a clear variation of z(log τ = −5) during UF phases (up to 270 km), which is tightly correlated with the variations displayed in the space-time maps of T, υLOS, Bz, and Bt. In the penumbra this opacity effect has a somewhat smaller impact, and the variations of z(log τ = −5) are smaller (∼100 km).
In order to show some more statistics, we have computed scatter plots in a portion of the umbra and penumbra (see Fig. 9). The color scaling represents the corresponding T (log τ = −5). The clusters of hot points (higher T (log τ = −5)) in panel a have an average value of z(log τ = −5) ≈ 850 km and |Bz|(log τ = −5) equal to 1.45 kG. Cooler pixels are clustered around z(log τ = −5) = 700 km and |Bz|(log τ = −5) = 1.30 kG. A similar trend in the relation between |Bz|(log τ = −5) and z(log τ = −5) is present in panel b, which corresponds to a different location along the slit also in the umbra.
 |
Fig. 9. Distribution of |Bz| as a function of z(log τ = −5) for the time-series of two locations in the umbra (top) and two locations in the penumbra (bottom). Panel a: relation |Bz| and z in the umbra at r = 15″.0–15″.6. Panel b: similar to panel a but for r = 13″.2–13″.8. Panels c and d are taken at r = 10″.4–11″.0 and r = 7″.2–7″.8, respectively. The black lines show the average vertical gradient of |Bz| in the umbra (–0.7 G km−1) and penumbra (–0.5 G km−1). The points have been color-coded according to their temperature T (log τ = −5). |
This trend is completely different from what we expect from previous measurements of sunspot magnetic fields as a function of height. We have derived the vertical gradient of the magnetic field between log τ = −1 and log τ = −5 using our approximate (hydrostatic equilibrium) z-scale. As mentioned above, our inversions of Bx and By in the umbra are not very reliable. Therefore we have only calculated the vertical gradient of Bz in the umbra. On average, the umbral vertical gradient of Bz has a value around –0.7 G km−1, which is not the trend that we observe during the passage of shocks.
In the penumbra (panels c and d), there are no clear relations between B(log τ = −5) and z(log τ = −5). Although, there are signs of a trend suggesting that pixels with a higher value of z(log τ = −5) harbor higher values of B(log τ = −5). Intrinsically small temporal variations of B, z, and T in the penumbra might be the reason why no clear relation between these parameters is derived in the penumbra compared to that in the umbra. Moreover, the average vertical gradient of B in the penumbra is approximately –0.5 G km−1.
5. Discussion and conclusion
We have analyzed the temporal evolution of the magnetic field along a radial cut in the observed sunspot covering the umbra and penumbra. In the umbra, the observed Stokes Q and U profiles in the Ca II 8542 Å line do not have sufficient signal, so only LOS magnetic field is measured with confidence. However, in the penumbra, all Stokes profiles have significant signal allowing the reliable measurement of all the magnetic field components.
We have found that in the umbra the chromospheric LOS magnetic field, Bz(log τ = −5) varies periodically with a maximum variation in amplitude up to 270 G. The period of these oscillations is three minutes confirming the well known three-minute oscillations in the chromosphere of sunspots. In the chromosphere, LOS magnetic field variations due to UFs are correlated and anti-correlated to those in the temperature and LOS velocity, respectively. This means that during the passage of an UF, the chromospheric magnetic field increases along with the corresponding temperature increase.
Similarly, in the penumbra, the chromospheric magnetic field oscillates with an amplitude up to 100 G. These variations in the magnetic field are correlated with a temperature rise due to RPWs. de la Cruz Rodríguez et al. (2013) reported fluctuations in the magnetic field of RPWs with an amplitude of 200 G using the same spectral line and with similar observations as presented in the current paper. Nevertheless, these latter authors did not find any temporal variations of the magnetic field in the umbra. Our results indicate no significant variations in the photospheric magnetic field of the sunspot.
We have also calculated the vertical gradient of the magnetic field between the photosphere and chromosphere of the sunspot. The average vertical gradient of the LOS magnetic field in the umbra is –0.7 G km−1. In the penumbra, the magnetic field decreases with an average rate of –0.5 G km−1 in the vertical direction. The value of the estimated vertical gradient of the magnetic field is in agreement with those reported in the literature (see, e.g., Rueedi et al. 1995; Orozco Suarez et al. 2005; Schad et al. 2015; Joshi et al. 2016, 2017a). These authors report the vertical gradient of the sunspot’s magnetic field in the range of −0.3to −1.0Gkm−1.
Our analysis of the magnetic field response function indicates that the Ca II 8542 Å line is most sensitive to the magnetic field variations occurring at ∼ log τ = −5 in the sunspot atmosphere, and therefore the magnetic field measured at this depth is the most reliable. We investigated the temporal variations in the geometrical height at log τ = −5 and its relation to the observed magnetic field variations in the chromosphere. The geometrical height is calculated assuming hydrostatic equilibrium. We are aware that the obtained geometrical height with the approximation of hydrostatic equilibrium can be significantly different from reality because an effect of magnetic fields and plasma flows is neglected. Nevertheless, the obtained geometrical scale can be analyzed at least in qualitative (differential) terms. We found that the geometrical height corresponding to log τ = −5 also varies due to UFs and RPWs and it is correlated to the inferred magnetic field variations in the chromosphere. The observed oscillations in the magnetic field at log τ = −5 and corresponding geometrical height suggest that at the onset of a UF magnetic field increases and that it is also obtained higher in the atmosphere. There is a hint of a similar scenario in the penumbra, where both the magnetic field and its height of inference increases during the relatively hotter phase of RPWs. This increase in the magnetic field and at the same time in its inferred geometrical height due to oscillations indicate an opposite trend from the observed vertical gradient of the magnetic field in the sunspot. It is therefore unlikely that the observed temporal variations in the magnetic field are caused by an opacity effect as suggested by some authors (see, Rüedi et al. 1999; Bellot Rubio et al. 2000; Rüedi & Cally 2003, Khomenko et al. 2003; Khomenko & Collados 2015) to explain the observed oscillations in the sunspot’s magnetic field in the photosphere.
Felipe et al. (2014) predicted that the magnetic field retrieved from the Ca II IR triplet lines produces pseudo oscillations due to opacity effects. They used magnetohydrodynamic (MHD) simulations of wave propagation in a sunspot performed by Khomenko & Collados (2006) and Felipe et al. (2010). Felipe et al. (2014) found that the weak field approximation applied to the Ca II IR triplet lines leads to magnetic field oscillations with an amplitude of ∼100 G while the MHD simulations do not have such oscillations in the chromosphere. Felipe et al. (2014) attribute the pseudo-oscillations in the magnetic field to a change in the height at which the Ca II IR triple lines are sensitive to the magnetic field: during the quiescent phase, the Ca II IR triple lines are most sensitive to the upper photosphere while as the upward propagating shock develops the lines become more sensitive to the chromosphere.
Our results are computed in hydrostatic equilibrium and we do not perform a full radiation-MHD treatment when computing the gas pressure scale, but the value of our models is that they are reconstructed from real observations. Felipe et al. (2014) performs MHD simulations of sunspot umbra, but these simulations are also highly simplified in the treatment of heat conduction and radiation in the chromosphere.
The latter simulations seem to contradict our observational results, which suggest that the Ca II 8542 Å line is most sensitive to the magnetic field variations at the chromospheric height during UFs as well as the quiescent phase of the umbra (see, Fig. B.1). Another difference between the prediction of Felipe et al. (2014) and our results is that at the onset of UFs we found an increase in the chromospheric magnetic field whereas Felipe et al. (2014) suggest a decrease in the magnetic field during UFs compared to that in the quiescent phase of the umbra.
Recently, Henriques et al. (2017) reported reduced magnetic field in UFs compared to the quiescent umbra which contradicts our results. However, they also found an enhancement in the magnetic field at the edges of UFs. Moreover, Henriques et al. (2017) observed downflows in UFs and they interpreted these downflows as being in connected with sunspot plumes (Maltby et al. 1999; Brynildsen et al. 1998, 1999, 2001; Fludra 2001; Brosius & White 2004; Brosius 2005; Dammasch et al. 2008). However, we found that the umbral flashes predominantly show upflows and this might explain the discrepancy between results of Henriques et al. (2017) and those presented here.
Very recently, immediately before the submission of this paper, an independent study reported very similar results in the outer umbra of a sunspot (Houston et al. 2018) from the inversions of observations acquired in the He I 10830 Å line. They obtain a similar behavior in the outer umbra of a sunspot, although their analysis and inversion model are fundamentally different and the He I line has an intrinsically different formation mechanism (see Centeno et al. 2009; Leenaarts et al. 2016) than the Ca II 8542 Å line that we have used in the present study.
Along with the magnetic field, we have analyzed the oscillations in the temperature and LOS velocity in the sunspot. An increase in the temperature in the atmosphere above log τ = −3 is observed during UFs compared to that in the quiescent umbra. At log τ = −5, we found an average increase of 1 kK in the temperature due to UFs, which confirms the results of de la Cruz Rodríguez et al. (2013). In some of UFs the temperature increases by 1.5 kK, in addition to the temperature found in the quiescent umbra. The average UF atmosphere shows steep variation in the LOS velocity, where the plasma upflow increases from 3kms−1 at log τ = −3 to 11kms−1 at log τ = −5. Increase in the temperature and steep gradient in the LOS upflow velocity in the atmosphere above log τ = −3 support the hypothesis that shock waves are responsible for the formation of UFs as suggested by Rouppe vander Voort et al. (2003), Centeno et al. (2006), Bard & Carlsson (2010), Felipe et al. (2010), de la Cruz Rodríguez et al. (2013) and Tian et al. (2014). In the penumbra, we found variations in the temperature at log τ = −5 with an amplitude of 0.5 kK due to RPW.
Felipe et al. (2018) analyzed the effect that a tunable filter-graph instrument can have on inversions, due to the fact that the observed line profile is not strictly co-temporal at all wavelengths. They find that random errors can appear in the inverted parameters if very rapid events occur during the scanning of the instrument. In that case, their inversions could not properly reproduce the observed profile. Obviously our results can be affected by this source of error, but we want to point out that our results are systematic (not random) and we have not had any difficulty reproducing the observed profiles during UF, even with our inversion setup that uses very few nodes in all physical parameters. We therefore do not believe that these effects are dominating our results.
In summary, we report the observation of oscillations in the chromospheric magnetic field associated to UFs and RPWs in the outer umbra and in the penumbra. Our analysis of the magnetic field response function indicates that the observed oscillations in the sunspot magnetic field are not likely produced by an opacity effect.
Acknowledgments
This research was supported by the CHROMOBS grant of the Knut och Alice Wallenberg foundation. JJ is supported by the Research Council of Norway, project 250810, and through its Centres of Excellence scheme, project number 262622. JdlCR is supported by grants from the Swedish Research Council (2015-03994), the Swedish National Space Board (128/15) and the Swedish Civil Contingencies Agency (MSB, 2016-2102). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (SUN-MAG, grant agreement 759548). The Swedish 1-m Solar Telescope is operated by the Institute for Solar Physics of Stockholm University in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. Our computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the PDC Centre for High Performance Computing (PDC-HPC) at the Royal Institute of Technology in Stockholm as well as recourses at the High Performance Computing Center North (HPC2N).
Appendix A Quality of the fits
We have assessed the match between the observed and synthesized Stokes profiles from the inverted model atmosphere. We show some examples of the observed and best fitted Stokes profiles in the Ca II 8542 Å line in Fig. A.1. The top left panel in Fig. A.1 represents the variation in T and B at log τ = −5 during a passage of a UFs at r = 13″.8. The observed and fitted Stokes profiles at different phases of the UF are depicted in the lower panels marked as “A”, “B” and “C” in Fig. A.1. At location “B”, where the T is enhanced due to the UF, Stokes I profile shows a blue-shifted line core in emission. The match between the synthesized and observed Stokes I and V profiles is very good at all three locations. In the umbra, the Stokes Q and U signal is below the noise level. Therefore, hereafter we do not discuss the inferred transverse component of the umbral magnetic field.
 |
Fig. A.1. Examples of observed and best fitted profiles in the Ca II 8542 Å line in the umbra (right panels) and penumbra (left panels). For each set, the top panel shows T (black) and B (red) at log τ = −5. The observed (blue dots) and best fitted (red curves) Stokes I, V, Q, and U profiles are represented in each column for three different time stamps, which are indicated with capital letters. |
The top right panel in Fig. A.1 displays the variations of T and B at log τ = −5 during a passage of a RPW at r = 7″.4. Similar to the umbra, we plotted the observed and fitted Stokes profiles at different phases (marked as “P”, “Q” and, “R”) of the RPW. In the penumbra, Stokes I, V and U profiles are fitted very well, but not Stokes Q profiles. The Stokes Q profiles are weak and very noisy, and this is purely due to the choice of the red cut shown in Fig. 1 and the orientation of the sunspot’s magnetic field at that location in the penumbra. In other parts of the sunspot penumbra, Stokes Q profiles have a significant signal. The Stokes U profiles have as much as ∼0.013IC signal and they are very well fitted by the inversions which gives a somewhat reliable measurement of Bt.
Appendix B Sensitivity to the magnetic field vector
B.1. Response functions during UFs and quiescence
Using the resulting models from our inversions, we have calculated 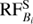 for the Ca II 8542 Å line in every pixel for all time steps. Here Bi denotes three components of the magnetic field and S represent Stokes Q, U and, V. Figure B.1 shows the sum of the absolute value of the RF over wavelength (Σλ |RF(λobs)|). Our results indicate that during UFs, the maximum response of the Stokes Q, U and, V profiles are located at lower log τ values compared to those during the quiescent phase in the umbra. We found log τ value corresponding to the maximum of Σ |RF(λobs)| for each pixel within the sunspot in our space-time map and histograms of obtained log τ values are plotted in Fig. B.2.
for the Ca II 8542 Å line in every pixel for all time steps. Here Bi denotes three components of the magnetic field and S represent Stokes Q, U and, V. Figure B.1 shows the sum of the absolute value of the RF over wavelength (Σλ |RF(λobs)|). Our results indicate that during UFs, the maximum response of the Stokes Q, U and, V profiles are located at lower log τ values compared to those during the quiescent phase in the umbra. We found log τ value corresponding to the maximum of Σ |RF(λobs)| for each pixel within the sunspot in our space-time map and histograms of obtained log τ values are plotted in Fig. B.2.
 |
Fig. B.1. Wavelength integrated magnetic field response functions of the Ca II 8542 Å line. Panel a: sum over observed wavelengths of the absolute value response function of Stokes V to |
Our results also indicate that for these models, the Ca II 8542 Å line has maximum response to the magnetic field between log τ = −4.8 and log τ = −5.2. These results also suggest that inversions assuming a constant magnetic field will greatly weight this range of the atmosphere.
B.2. The effect of gradients in the inversions of B
We have compared the magnetic field properties obtained from the inversion of the Ca II 8542 Å line with the assumption that the magnetic field varies linearly with log τ, to those retrieved by assuming that the magnetic field is constant. The latter comparison is illustrated in Fig. B.3 for the vertical and horizontal components of the magnetic field. In Fig. B.3, B(z,t)(log τ = −5, −1) represents the magnetic field retrieved through the inversions of the Ca II 8542 Å line under the assumption that the magnetic field varies linearly with log τ. Whereas, B(z,t)(Ca II) and B(z,t)(Fe I) corresponds to the magnetic field obtained from the inversions of the Ca II 8542 Å line and the Fe I 6301.5 and 6302.5 Å lines, assuming a depth-independent magnetic field. As expected from our tests in Appendix B.1, even when we allow for gradients in the magnetic field stratification, the retrieved values around the maximum of the RF, log τ = −5, greatly correlate with the results from the depth-independent magnetic field inversions. The Pearson coefficients, p, between Bz(log τ = −5) and Bz(Ca II) and between Bt(log τ = −5) and Bt(Ca II) are 0.83 and 0.81 (see panels a and b), respectively.
 |
Fig. B.2. Distribution of log τ values corresponding to the maximum value of |
Based on previous studies, the Fe I 6301.5 and 6302.5 Å lines are expected to have maximum response to the magnetic field at log τ ≈−1 (e.g., see Fig. 9 of Joshi et al. 2017b, among others). Our results for Bz(log τ = −1) from the inversion of the Ca II 8542 Å line are very well correlated (p = 0.83, panel c) with those from single node inversions of the Fe I 6301.5 and 6302.5 Å lines. The correlation for the transverse component is worse (p = 0.63, panel d) but the weaker Stokes Q and U signals may not encode sufficient information to accurately retrieve gradients in the horizontal component in our observations.
We note that although the Ca II 8542 Å line is not expected to have a strong response to photospheric magnetic fields, our inversions with gradients in this line yield similar values of Bz to those from the inversions of the Fe I 6301.5 and 6302.5 Å lines, and there is clear Stokes V signal present in the wings of the former line.
 |
Fig. B.3. Comparison of the magnetic field retrieved from the inversions with a single node in each component of the magnetic field vs. that from the inversions that includes a linear gradient in the magnetic field. B(z,t)(log = −5, −1) is taken from the inversions of the Ca II 8542 Å line including magnetic field gradient. The depth-independent magnetic field values derived from the inversions of the Ca II 8542 Å line and the Fe I 6301.5 and 6302.5 Å lines are indicated as B(z,t)(Ca II) and B(z,t)(Fe I), respectively. Panel a: normalized two-dimensional histogram of Bz(log τ = −5) vs. Bz(Ca II). Panel b: similar to panel a, but comparing Bt(log τ = −5) and Bt(Ca II). Panel c: normalized two-dimensional histogram of Bz(log τ = −1) vs. Bz(Fe I). Panel d: similar to panel c, but comparing Bt(log τ = −1) and Bt(Fe I). The red line in all the panels illustrates a one to one correspondence. |
References
- Balthasar, H. 1990, Sol. Phys., 125, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Balthasar, H. 2003, Sol. Phys., 218, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Bard, S., & Carlsson, M. 2010, ApJ, 722, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Beckers, J. M., & Tallant, P. E. 1969, Sol. Phys., 7, 351 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bellot Rubio, L. R., Collados, M., Ruiz Cobo, B., & Rodríguez Hidalgo, I. 2000, ApJ, 534, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Bloomfield, D. S., Lagg, A., & Solanki, S. K. 2007, ApJ, 671, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Brosius, J. W. 2005, ApJ, 622, 1216 [NASA ADS] [CrossRef] [Google Scholar]
- Brosius, J. W., & White, S. M. 2004, ApJ, 601, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Brynildsen, N., Maltby, P., Brekke, P., et al. 1998, ApJ, 502, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Brynildsen, N., Maltby, P., Brekke, P., Haugan, S. V. H., & Kjeldseth-Moe, O. 1999, Sol. Phys., 186, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Brynildsen, N., Maltby, P., Fredvik, T., Kjeldseth-Moe, O., & Wilhelm, K. 2001, Sol. Phys., 198, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Centeno, R., Collados, M., & Trujillo Bueno, J. 2006, ApJ, 640, 1153 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Centeno, R., Trujillo Bueno, J., Uitenbroek, H., & Collados, M. 2009, in Solar Polarization 5. In Honor of Jan Stenflo, eds. S. V. Berdyugina, K. N. Nagendra, & R. Ramelli, ASP Conf. Ser., 405, 297 [NASA ADS] [Google Scholar]
- Dammasch, I. E., Curdt, W., Dwivedi, B. N., & Parenti, S. 2008, Annal. Geophys., 26, 2955 [NASA ADS] [CrossRef] [Google Scholar]
- de la Cruz Rodríguez, J., & Piskunov, N. 2013, ApJ, 764, 33 [NASA ADS] [CrossRef] [Google Scholar]
- de la Cruz Rodríguez, J., Rouppe Vander Voort, L., Socas-Navarro, H., & Van Noort, M. 2013, A&A, 556, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de la Cruz Rodríguez, J., Löfdahl, M. G., Sütterlin, P., Hillberg, T., & Rouppe vander Voort, L. 2015, A&A, 573, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Moortel, I., Ireland, J., Hood, A. W., & Walsh, R. W. 2002, A&A, 387, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Felipe, T., Khomenko, E., & Collados, M. 2010, ApJ, 719, 357 [Google Scholar]
- Felipe, T., Socas-Navarro, H., & Khomenko, E. 2014, ApJ, 795, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Felipe, T., Socas-Navarro, H., & Przybylski, D. 2018, A&A, 614, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fludra, A. 2001, A&A, 368, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontenla, J. M., Avrett, E. H., & Loeser, R. 1993, ApJ, 406, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Gurman, J. B. 1987, Sol. Phys., 108, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Gurman, J. B., Leibacher, J. W., Shine, R. A., Woodgate, B. E., & Henze, W. 1982, ApJ, 253, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Henriques, V. M. J. 2012, A&A, 548, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henriques, V. M. J., Mathioudakis, M., Socas-Navarro, H., & de la Cruz Rodríguez, J. 2017, ApJ, 845, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Horn, T., Staude, J., & Landgraf, V. 1997, Sol. Phys., 172, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Houston, S. J., Jess, D. B., Asensio Ramos, A., et al. 2018, ApJ, 860, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Janett, G., Carlin, E. S., Steiner, O., & Belluzzi, L. 2017, ApJ, 840, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Joshi, J., Lagg, A., Solanki, S. K., et al. 2016, A&A, 596, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joshi, J., Lagg, A., Hirzberger, J., & Solanki, S. K. 2017a, A&A, 604, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joshi, J., Lagg, A., Hirzberger, J., Solanki, S. K., & Tiwari, S. K. 2017b, A&A, 599, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallunki, J., & Riehokainen, A. 2012, Sol. Phys., 280, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Kanoh, R., Shimizu, T., & Imada, S. 2016, ApJ, 831, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Kentischer, T. J., & Mattig, W. 1995, A&A, 300, 539 [NASA ADS] [Google Scholar]
- Khomenko, E., & Collados, M. 2006, ApJ, 653, 739 [Google Scholar]
- Khomenko, E., & Collados, M. 2015, Liv. Rev. Sol. Phys., 12, 6 [CrossRef] [Google Scholar]
- Khomenko, E. V., Collados, M., & Bellot Rubio, L. R. 2003, ApJ, 588, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Kupke, R., Labonte, B. J., & Mickey, D. L. 2000, Sol. Phys., 191, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Landgraf, V. 1997, Astron. Nachr., 318, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J., de la Cruz Rodríguez, J., Kochukhov, O., & Carlsson, M. 2014, ApJ, 784, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J., Golding, T., Carlsson, M., Libbrecht, T., & Joshi, J. 2016, A&A, 594, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lites, B. W. 1984, ApJ, 277, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W. 1986, ApJ, 301, 992 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Thomas, J. H., Bogdan, T. J., & Cally, P. S. 1998, ApJ, 497, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Maltby, P., Brynildsen, N., Fredvik, T., Kjeldseth-Moe, O., & Wilhelm, K. 1999, Sol. Phys., 190, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Orozco Suarez, D., Lagg, A., & Solanki, S. K. 2005, in Chromospheric and Coronal Magnetic Fields, eds. D. E. Innes, A. Lagg, & S. A. Solanki, ESA SP, 596, 59.1 [Google Scholar]
- Quintero Noda, C., Shimizu, T., de la Cruz Rodríguez, J., et al. 2016, MNRAS, 459, 3363 [NASA ADS] [CrossRef] [Google Scholar]
- Rouppe vander Voort, L. H. M., Rutten, R. J., Sütterlin, P., Sloover, P. J., & Krijger, J. M. 2003, A&A, 403, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rüedi, I., & Cally, P. S. 2003, A&A, 410, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rüedi, I., Solanki, S. K., Bogdan, T., & Cally, P. 1999, in Polarization, eds. K. N. Nagendra, & J. O. Stenflo, Astrophys. Space Sci. Lib., 243, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Rueedi, I., Solanki, S. K., & Livingston, W. 1995, A&A, 302, 543 [NASA ADS] [Google Scholar]
- Rueedi, I., Solanki, S. K., Stenflo, J. O., Tarbell, T., & Scherrer, P. H. 1998, A&A, 335, L97 [NASA ADS] [Google Scholar]
- Schad, T. A., Penn, M. J., Lin, H., & Tritschler, A. 2015, Sol. Phys., 290, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Scharmer, G. B. 2006, A&A, 447, 1111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharmer, G. B., Bjelksjo, K., Korhonen, T. K., Lindberg, B., & Petterson, B. 2003, in Innovative Telescopes and Instrumentation for Solar Astrophysics, eds. S. L. Keil, & S. V. Avakyan, Proc. SPIE, 4853, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Scharmer, G. B., Löfdahl, M. G., Van Werkhoven, T. I. M., & de la Cruz Rodríguez, J. 2010, A&A, 521, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharmer, G. B., Narayan, G., Hillberg, T., et al. 2008, ApJ, 689, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Schnerr, R. S., de la Cruz Rodríguez, J., & Van Noort, M. 2011, A&A, 534, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Socas-Navarro, H., Trujillo Bueno, J., & Ruiz Cobo, B. 2000, Science, 288, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Socas-Navarro, H., de la Cruz Rodríguez, J., Asensio Ramos, A., Trujillo Bueno, J., & Ruiz Cobo, B. 2015, A&A, 577, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thomas, J. H., Lites, B. W., Gurman, J. B., & Ladd, E. F. 1987, ApJ, 312, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, H., DeLuca, E., Reeves, K. K., et al. 2014, ApJ, 786, 137 [NASA ADS] [CrossRef] [Google Scholar]
- van Noort, M., Rouppe van der Voort, L., & Löfdahl, M. G. 2005, Sol. Phys., 228, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Wittmann, A. 1969, Sol. Phys., 7, 366 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Field of view comprising the leading sunspot in the active region NOAA 11793 observed on 22 July 2013. Panel a: image obtained at the line center of the Ca II 8542 Å spectral line using CRISP. Panels b–d: Stokes V/Ic, Q/Ic, and, U/Ic maps, respectively, at –350 mÅ from the line center. The red cut marked as r indicates the position for which the temporal evolution of the atmospheric parameters is analyzed in this study. |
| In the text | |
 |
Fig. 2. Temporal evolution of the temperature (top panels) and line-of-sight velocity (bottom panels) at log τ = −5, −3, and, −1. Panels a, b, d, and e illustrate the results from our inversions of the Ca II 8542 Å line, whereas panels c and f are taken from the inversion of the Fe I 6301.5 and 6302.5 Å lines. r = 0 corresponds to the outer-most point from the sunspot in the red cut marked in Fig. 1. |
| In the text | |
 |
Fig. 3. As in Fig. 2, but in this case we illustrate the residual variations, δT and δυLOS after subtracting the local background. The green line in panels a and d traces an RPW. |
| In the text | |
 |
Fig. 4. Averaged stratification of T and υLOS as a function of optical depth obtained from the inversions of the Ca II 8542 Å line. Upper-left and lower-left panels: stratification of T and υLOS in the umbra, respectively. The red and blue curves represent the umbral flash and quiescent umbra atmosphere, respectively. Panels on the right: stratification of the same physical parameters in the penumbra. The shaded areas in all panels demonstrate the distribution of the parameters normalized at each log τ position. |
| In the text | |
 |
Fig. 5. Temporal evolution of the magnetic field in the chromosphere and in the photosphere. Panels a and c: LOS component of the magnetic field, Bz, and transverse component of the magnetic field, Bt,atlog τ = −5.0. Panels b and d: Bz and Bt at log τ = −1.0. These results are solely obtained from the inversion of the Ca II 8542 Å line. |
| In the text | |
 |
Fig. 6. As in Fig. 5, but in this case we show the residual variations, δ|Bz| and δBt after removing the local background. The green line in panels a and c represents the same RPW as in Fig. 3. |
| In the text | |
 |
Fig. 7. Temporal variations of the atmospheric parameters in the umbra (left column), and penumbra (right column) after removing the local background. The curves plotted in these panels correspond to r = 13″.8 and r = 7″.4 for the umbral and penumbral sets, respectively. From top to bottom,(panels a1–a3): δT, δυLOS and, δ|Bz| from the inversions of the Ca II 8542 Å line including a linear gradients in the magnetic field as a function of log τ. Panel a4: δ|Bz| from the inversions of the Ca II 8542 Å line (orange curve) and the Fe I line pair at 6302 Å (gray curve) separately with the assumption that the magnetic field is depth independent. Panels b1–b4 are similar to panels a1–a4, but the former depict δB instead of δ|Bz|. The red, blue, and green curves correspond to log τ = −5, −3, and, −1. |
| In the text | |
 |
Fig. 8. Panel a: space-time variation of z(log τ = −5) . Panel b: temporal variations of δ|Bz| and z at log τ = −5 for an umbral pixel (r = 13″.8) and panel c: temporal variation of δB and z at log τ = −5 for a penumbral pixel (r = 7″.4). |
| In the text | |
 |
Fig. 9. Distribution of |Bz| as a function of z(log τ = −5) for the time-series of two locations in the umbra (top) and two locations in the penumbra (bottom). Panel a: relation |Bz| and z in the umbra at r = 15″.0–15″.6. Panel b: similar to panel a but for r = 13″.2–13″.8. Panels c and d are taken at r = 10″.4–11″.0 and r = 7″.2–7″.8, respectively. The black lines show the average vertical gradient of |Bz| in the umbra (–0.7 G km−1) and penumbra (–0.5 G km−1). The points have been color-coded according to their temperature T (log τ = −5). |
| In the text | |
 |
Fig. A.1. Examples of observed and best fitted profiles in the Ca II 8542 Å line in the umbra (right panels) and penumbra (left panels). For each set, the top panel shows T (black) and B (red) at log τ = −5. The observed (blue dots) and best fitted (red curves) Stokes I, V, Q, and U profiles are represented in each column for three different time stamps, which are indicated with capital letters. |
| In the text | |
 |
Fig. B.1. Wavelength integrated magnetic field response functions of the Ca II 8542 Å line. Panel a: sum over observed wavelengths of the absolute value response function of Stokes V to |
| In the text | |
 |
Fig. B.2. Distribution of log τ values corresponding to the maximum value of |
| In the text | |
 |
Fig. B.3. Comparison of the magnetic field retrieved from the inversions with a single node in each component of the magnetic field vs. that from the inversions that includes a linear gradient in the magnetic field. B(z,t)(log = −5, −1) is taken from the inversions of the Ca II 8542 Å line including magnetic field gradient. The depth-independent magnetic field values derived from the inversions of the Ca II 8542 Å line and the Fe I 6301.5 and 6302.5 Å lines are indicated as B(z,t)(Ca II) and B(z,t)(Fe I), respectively. Panel a: normalized two-dimensional histogram of Bz(log τ = −5) vs. Bz(Ca II). Panel b: similar to panel a, but comparing Bt(log τ = −5) and Bt(Ca II). Panel c: normalized two-dimensional histogram of Bz(log τ = −1) vs. Bz(Fe I). Panel d: similar to panel c, but comparing Bt(log τ = −1) and Bt(Fe I). The red line in all the panels illustrates a one to one correspondence. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.