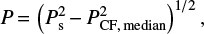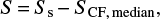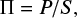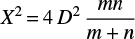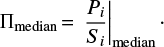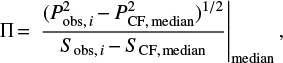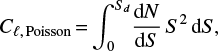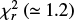| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 10 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201732342 | |
| Published online | 09 October 2018 | |
Average fractional polarization of extragalactic sources at Planck frequencies
1
INAF, Istituto di Radioastronomia, Via Piero Gobetti 101, 40129 Bologna, Italy
e-mail: trombetti@ira.inaf.it
2
Dipartimento di Fisica e Scienze della Terra, Università di Ferrara, Via Giuseppe Saragat 1, 44122 Ferrara, Italy
e-mail: burigana@ira.inaf.it
3
INFN, Sezione di Ferrara, Via Giuseppe Saragat 1, 44122 Ferrara, Italy
4
INFN, Sezione di Bologna, Via Irnerio 46, 40127 Bologna, Italy
5
INAF, Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
e-mail: gianfranco.dezotti@oapd.inaf.it
6
INAF, Osservatorio Astronomico di Trieste, Via Giambattista Tiepolo 11, 34143 Trieste, Italy
Received:
22
November
2017
Accepted:
22
May
2018
Recent detailed simulations have shown that an insufficiently accurate characterization of the contamination of unresolved polarized extragalactic sources can seriously bias measurements of the primordial cosmic microwave background (CMB) power spectrum if the tensor-to-scalar ratio r ∼ 0.001, as predicted by models currently of special interest (e.g., Starobinsky’s R2 and Higgs inflation). This has motivated a reanalysis of the median polarization fraction of extragalactic sources (radio-loud AGNs and dusty galaxies) using data from the Planck polarization maps. Our approach, exploiting the intensity distribution analysis, mitigates or overcomes the most delicate aspects of earlier analyses based on stacking techniques. By means of simulations, we have shown that the residual noise bias on the median polarization fraction, Πmedian, of extragalactic sources is generally ≲0.1%. For radio sources, we have found Πmedian ≃ 2.83%, with no significant dependence on either frequency or flux density, in good agreement with the earlier estimate and with high-sensitivity measurements in the frequency range 5–40 GHz. No polarization signal is detected in the case of dusty galaxies, implying 90% confidence upper limits of Πdusty ≲ 2.2% at 353 GHz and of ≲3.9% at 217 GHz. The contamination of CMB polarization maps by unresolved point sources is discussed.
Key words: polarization / cosmic background radiation / radio continuum: galaxies
© ESO 2018
1. Introduction
The detection of the primordial B-mode polarization of the cosmic microwave background (CMB) is currently the most pressing question of particle physics and cosmological research because the signal carries a clean signature of primordial inflation. It is very faint, however, because it is generated by tensor perturbations, which are so weak as to defy detection so far. The tightest upper limit on the ratio, r, of tensor-to-scalar fluctuations at the pivot scale of 0.05 Mpc−1 is r < 0.07 at the 95% confidence level (BICEP2 Collaboration & Keck Array Collaboration 2016).
Measurements of Galactic (Choi & Page 2015; Planck Collaboration Int. XXX 2016; Planck Collaboration XXV 2016; Krachmalnicoff et al. 2016; Planck Collaboration Int. L 2017) and estimates of extragalactic (Tucci et al. 2004; Tucci & Toffolatti 2012; Bonavera et al. 2017a,b) polarized foreground emission show that even in the cleanest 70% of the sky, this emission dominates both primordial B-modes and instrumental noise of the most sensitive forthcoming or proposed CMB polarization experiments, such as the Lite (Light) satellite for the studies of B-mode polarization and Inflation from cosmic background Radiation Detection (LiteBIRD)1, the Cosmic ORigins Explorer (CORE; Delabrouille et al. 2018), the Probe of Inflation and Cosmic Origin (PICO), one of the eight Probe-Scale space missions in the range of $ 400 M – $ 1000 M that are being funded by NASA2, the Primordial InflaXIon (Inflation) Explorer (PIXIE; Kogut et al. 2016) and the CMB-Stage IV experiment (CMB-S4; Abazajian et al. 2016).
Thus, the capability of future CMB observations to measure or constrain CMB B-mode power spectra will be limited not by sensitivity of the instrument, but by the ability of removing foreground contamination with extreme accuracy. According to Delabrouille et al. (2018), foreground cleaning must reach at least the 99.9% level at ℓ ≃ 10, at least the 99% level at ℓ ≃ 100 and at least the 90% level at ℓ ≃ 1000 to bring the residual contamination below noise and/or cosmic variance in multipole bins Δℓ/ℓ = 0.3.
Furthermore, the B-mode power spectrum exceeds that of primordial origin for ℓ ≳ 10 if r ≲ 10−2 due to gravitational lensing (cf. Fig. 1 of Delabrouille et al. 2018). Hence the detection of primordial B modes requires a very accurate control of lensing effects, which in turn are contaminated by fluctuations of unresolved extragalactic sources.
There is no definitive prediction for the magnitude of the tensor-to-scalar ratio, r. For inflationary models driven by a fundamental scalar field, the value of r is related to the total field excursion (i.e., to the inflation field range in Planck units; Lyth 1997; Baumann & McAllister 2007). Models currently of special interest (e.g., Starobinsky’s R2 and Higgs inflation) predict r ∼ 0.003 (Martin et al. 2014; Abazajian et al. 2016; Finelli et al. 2018). Large-field inflation with super-Planckian field excursions implies even lower values, r ≲ 0.001.
Accurate simulations (Remazeilles et al. 2018) showed that for r ≃ 10−3, the overall uncertainty on r is dominated by foreground residuals and that unresolved polarized point sources can be the dominant foreground contaminant over a broad range of angular scales (ℓ ≳ 50). An accurate understanding of the polarization properties of extragalactic sources is therefore crucial.
Root-mean-square temperature fluctuations due to unresolved extragalactic sources have a minimum around 120 GHz (cf. Fig. 2 of De Zotti et al. 2015), corresponding to the transition from the dominance of radio sources to that of dusty galaxies. The main radio source populations in the frequency range of CMB experiments (the so-called “cosmological window”) are the compact flat- and inverted-spectrum populations, primarily blazars (BL Lac objects and flat-spectrum radio quasars).
Our understanding of polarization properties of extragalactic radio sources in the cosmological window is still quite poor (for reviews, see Tucci & Toffolatti 2012; Galluzzi & Massardi 2016).
Direct WMAP detections in polarization are limited to small numbers of sources (Wright et al. 2009; López-Caniego et al. 2009). Planck, thanks to its higher sensitivity and angular resolution, has yielded more detections. The Second Planck Catalog of Compact Sources lists over 120 objects with polarized emission significant at a >99.99% level, not considering the PCCS2E sub-catalog, whose reliability is unknown (Table 14 of Planck Collaboration XXVI 2016). These sources, however, mostly lie at low Galactic latitudes so that only a minor fraction of them are expected to be extragalactic. The number of detections in the extragalactic zone (|b| > 30°) ranges from 28 at 30 GHz to ∼10 in the channels up to 217 GHz, to 1 at 353 GHz (De Zotti et al. 2018); the two highest Planck frequencies (545 and 857 GHz) were not polarization sensitive. All detected sources are radio-loud AGNs.
Follow-up polarization measurements at 8.4, 22, and 43 GHz of a complete sample of 199 extragalactic sources stronger than 1 Jy in the 5 yr WMAP catalog were carried out by Jackson et al. (2010). Polarimetric observations of 211 radio-loud active galactic nuclei (AGNs) at 86 and 229 GHz were performed by Agudo et al. (2014). Their ≥3σ detection rate was 88% at 86 GHz and 13% at 229 GHz. The sample selection was designed to be flux limited at 1 Jy at 86 GHz; however, 51% of the sources were found to have S86 < 1 Jy and 22% even had S86 < 0.5 Jy, probably due to variability.
Most recently, Galluzzi et al. (2017, 2018) presented high-sensitivity (σP ≃ 0.6 mJy) polarimetric observations at seven frequencies, from 2.1 to 38 GHz, of a complete sample of 104 compact extragalactic radio sources brighter than 200 mJy at 20 GHz. The observations achieved a 5σ detection rate of 90%. Individual sources showed a broad variety of spectral shapes (flat, steep, upturning, peaked, inverted, downturning) both in total intensity and in polarization, but with substantial variations with frequency of the polarization fraction from one object to another. Because of this complexity, extrapolations to frequencies of CMB experiments to mitigate the point source contamination of CMB maps are unreliable.
In the case of star-forming galaxies, the polarized emission above 100 GHz is dominated by dust. At lower frequencies, the synchrotron emission takes over, but at these frequencies, the extragalactic sky is far from being dominated by radio sources. Polarization properties of dusty galaxies as a whole at (sub-)millimeter wavelengths are almost completely unexplored. The only published measurement (Greaves & Holland 2002) yielded a polarization fraction Π = 0.4% for the prototype starburst galaxy M 82. Integrating the Planck dust polarization maps, De Zotti et al. (2018) found an average value of the Stokes Q parameter of about 2.7%. If this is typical for late-type galaxies seen edge-on and the polarization fraction scales as cos(θ), θ being the inclination angle, the mean polarization fraction, averaged over all possible inclinations, should be ≃1.4%.
It is particularly important to characterize the point source contamination in the 60–120 GHz frequency range, where Planck data (Planck Collaboration X 2016) have shown that the brightness temperature spectra of diffuse polarized foregrounds display a broad minimum (cf. Fig. 1 of Remazeilles et al. 2018).
Although the number of sources detected in polarization by Planck in the extragalactic zone is quite limited, estimates of the mean polarization fraction of fainter sources can be obtained using stacking techniques, that is, by co-adding the polarized signal from many objects detected in total intensity but not in polarization, to increase the signal-to-noise ratio (S/N). A first attempt in this direction was carried out by Bonavera et al. (2017a) for radio sources and by Bonavera et al. (2017b) for dusty galaxies.
Bonavera et al. (2017a) applied the stacking techniques to the 1560 30 GHz sources in the Second Planck Catalog of Compact Sources (PCCS 2; Planck Collaboration XXVI 2016), spanning about a factor of 20 in flux density, and followed them in all Planck maps in polarization (at 30, 44, 70, 100, 143, 217, and 353 GHz). The subsample outside the Planck GAL60 mask (covering about 40% of the sky, around the Galactic plane) and outside the Magellanic Cloud regions, contains 881, likely extragalactic, radio sources. The remaining 679 are probably mostly Galactic.
The application of stacking to high-resolution data is relatively straightforward, since only two ingredients need to be included: the (faint) signal of sources, and the noise. By coadding measurements at the positions of n sources, the signals add up while Gaussian noise decreases as n−1/2. In the case of the low-resolution Planck data, the situation is much more complicated because each resolution element containing a source also contains other polarized signals: the CMB itself, and diffuse synchrotron and dust emissions from the Galaxy. The Galactic contamination is particularly difficult to include because of its highly non-Gaussian statistics and its significant variations on the sky.
Furthermore, the mean polarized flux density, P, is computed from the Stokes parameters Q and U as P = (Q2 + U2)1/2. Any quadratic sum of this kind is liable to the so-called noise bias, however (e. g., Wardle & Kronberg 1974): the errors on Q and U add a contribution to P. The standard methods for correcting for this bias cannot be applied to stacking because sources are not individually detected.
Again, because sources are not detected, the desired result, that is, the mean polarization fraction, ⟨Π⟩ = ⟨P/S⟩, where S is the total flux density, cannot be computed directly but is approximated by ⟨P⟩/⟨S⟩. Recent studies (at lower frequencies) did not find evidence of systematic variations of the polarization fraction with S (Hales et al. 2014; Galluzzi et al. 2017), but on the other hand, the spectra of polarized emission of individual sources are generally substantially different from those in total intensity (Galluzzi et al. 2017, 2018). In addition, for the faintest sources the polarized signal is dominated by other components or by noise, so that it is unrelated to S. The combination of these effects may be a quite delicate point, in particular for flux densities differing by more than one order of magnitude. As described in next section, our approach does not rely at all on the ⟨Π⟩ = ⟨P/S⟩ ≃ ⟨P⟩/⟨S⟩ approximation.
When applied in this context, stacking techniques typically require simulations to include the noise bias. For example, the corresponding correction found in Bonavera et al. (2017a) is lower than ≃20% when applied to 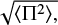 but reaches a factor of approximately 3–6, depending on frequency, when applied to ⟨Π⟩.
but reaches a factor of approximately 3–6, depending on frequency, when applied to ⟨Π⟩.
Bonavera et al. (2017b) applied the same approach to a sample of 4697 dusty galaxies drawn from the PCCS2 857 GHz catalog, deriving average corrected polarization fractions and corresponding median values at 217 and 353 GHz, with a tentative detection at 143 GHz.
Given the real, substantial difficulty of the problem and the importance of reaching an assessment as solid as possible of the mean polarization properties of extragalactic sources in the Planck frequency range, we decided to carry out a new investigation adopting an independent approach. In this paper we present a simpler analytical approach and describe how we control the critical aspects.
The layout of the paper is the following. In Sect. 2 we outline our method. In Sect. 3 we validate it by applying it to sources whose polarization has been measured by Jackson et al. (2010) at 43 GHz and by Agudo et al. (2014) at 86 and 229 GHz. In Sect. 4 we report our results, which are summarized in Sect. 5.
2. Outline of the method
Our approach uses the intensity distribution analysis (IDA; De Zotti et al. 1989; Barcons et al. 1995). Briefly, this method consists of measurements of signals in a map at the positions of a given source catalog. The distribution of signals is compared with that for the blank sky, measured at random positions, away from sources (control fields). If some statistical test detects a significant difference, in the sense that the source distribution is shifted toward higher values than that of control fields, a signal is detected. For this purpose, we use the one-sided Kolmogorov-Smirnov (KS) statistics.
The polarized flux density of sources is then estimated as
where Ps is the polarized signal in Planck maps at the source position and 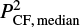 is the median value of P2 in the control fields. The subtraction removes, in a statistical sense, the contributions to P of the noise, of the CMB, and of polarized Galactic emissions. It thus largely corrects for the noise bias, as verified through a comparison with direct polarimetric measurements (Sect. 3) and via simulations (Sect. 4.3). When
is the median value of P2 in the control fields. The subtraction removes, in a statistical sense, the contributions to P of the noise, of the CMB, and of polarized Galactic emissions. It thus largely corrects for the noise bias, as verified through a comparison with direct polarimetric measurements (Sect. 3) and via simulations (Sect. 4.3). When 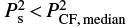 , we set P = 03.
, we set P = 03.
We have considered radio sources listed in the Second Planck Catalog of Compact Sources (PCCS2; Planck Collaboration XXVI 2016), selecting those detected at 143 GHz and located at high Galactic latitude (|b| ≥ 20°), excluding the areas inside the mask adopted for the Planck polarization analysis at 100 GHz at high resolution (COM_Mask_Likelihood-polarization-100_2048_R2.00.fits). We further excluded sources flagged as extended in the PCCS2. We repeated the analysis with a Galactic cut at |b| = 30°, obtaining consistent results but with a poorer statistics. Only the results for the cut at |b| = 20° are reported.
At high Galactic latitudes, objects above the the PCCS2 detection limit at 143 GHz are almost exclusively radio sources (cf. Negrello et al. 2013; Planck Collaboration Int. VII 2013; Mocanu et al. 2013). The contaminating fraction of dusty galaxies or Galactic sources is negligibly small at low frequencies, but increases with increasing frequency because dust emission steeply rises with frequency at millimeter/submillimeter wavelengths. An analysis of the brightest flux density bins at 353 GHz (S353 > 1780 mJy) has shown that about half of sources are either Galactic HII regions or nearby dusty galaxies. These objects are characterized by a strong upturn of the spectrum at submilimeter wavelengths that is due to dust emission. Thus, their contamination of the lower frequency samples is negligibly small. Nevertheless, they were excluded from all samples.
The Planck light maps in temperature (T) and in polarization (Stokes parameters Q and U) with Nside = 1024 at 30 and 44 GHz, and Nside = 2048 at higher frequencies were inspected at the source positions. For each source we summed the (positive and negative) signals in all pixels within a circle with FWHM/2 radius. Temperature and polarization signals, given in temperature units, were converted into flux densities using the unit conversion software provided by the Planck Collaboration4 (Planck Collaboration V 2014; Planck Collaboration IX 2014). We have checked that we obtain good agreement with the PCCS2 flux densities in this way.
The procedure was repeated for a large number of control fields. The centers of these fields were required to be separated by at least 2 FWHM from each other and from the sources. This was efficiently implemented using the properties of the hierarchical equal area isolatitude pixelation (HEALPix; Górski et al. 2005)4. It was enough to place the control field centers at the centers of the Nside = 64 and of the Nside = 128 pixels for the frequencies of the Low Frequency Instrument (LFI; 30, 44 and 70 GHz) and of the High Frequency Instrument (HFI; 100, 143, 217 and 353 GHz), respectively. We selected 26,231 and 111,442 control fields at the LFI and HFI frequencies, respectively.
Unlike the stacking technique, the IDA considers each source individually, therefore it allows us to compute the mean and the median P/S ratios directly. We preferred the median to the mean values because the latter are less stable, being very sensitive to the presence of a few objects with exceptionally high polarized flux densities. Analogously to the polarized flux density, the total flux density of sources is estimated by subtracting, in a statistical sense, the other contributions (mainly due to Galactic emissions) as
where Ss is the signal in Planck maps at the source position and SCF, median is the median value of S in control fields. Thus, the source polarization fraction is estimated by
with P and S given by Eqs. (1) and (2), respectively.
In order to investigate the possible flux-density dependence of the median polarization degree on flux density, we subdivided the samples selected at each frequency into flux density bins containing 30 sources each, starting from the 90% completeness limit given by the PCCS2 paper. This left fewer than 30 objects in the brightest bin, which has the strongest signal, which is also detectable with fewer sources. Since the dusty sources were removed after the bins were defined, the final number of sources in some bins is also slightly smaller than 30. For the source binning we used the DETFLUX photometry, as recommended for point sources up to 217 GHz (Planck Collaboration XXVI 2016). We checked that using APERFLUX, the recommended photometry above 217 GHz, the results at 353 GHz do not change significantly.
For each bin we compared the distribution of polarized signals with that of control fields using the one-sided KS statistics. Generally, no signal was detected for the faintest bins. When a signal was detected, the mean polarized flux density was computed using Eq. (1). This shows another advantage of the analysis by flux density bins over the stacking approach applied to the whole sample: it allows us to include for the final estimates only the flux density bins that include signals; fainter objects whose polarized emission is completely swamped by noise and fluctuations of other components can be excluded from the analysis.
While the DETFLUX photomery was used for the binning, for estimating the total flux densities used to compute ΠIDA = (P/S)median we adopted for uniformity the same approach as for the polarization signals: we summed signals in pixels within a radius of FWHM/2 from the source position.
3. Validation with external data
To validate our approach, we have exploited the ground-based polarization measurements by Jackson et al. (2010) and by Agudo et al. (2014) at frequencies close to those of a Planck channel.
At 43 GHz Jackson et al. (2010) detected 167 sources. We divided those detected by Planck in total flux density at 44 GHz (Planck Collaboration XXVI 2016) within the area specified above (135 sources) into bins containing 30 sources each, except for the brightest bin, which contains 15 sources. The KS test detected signal in Planck polarization maps for all bins, except for the 1740–3510 mJy bin. All detections are highly significant, as shown by the last column of Table 1. In this table (and in the following tables), D is the KS statistics, that is, the largest discrepancy between the cumulative distributions of sources in a bin and of control fields. The probability of the null hypothesis (no difference between the two) was computed by approximating the distribution of
with the chi-square distribution with two degrees of freedom (Siegel & Castellan 1988). Here m and n are the numbers of sources and of control fields, respectively.
For the full sample, the IDA method yielded estimates of the median polarization degrees consistent with those measured by Jackson et al. (2010), within the errors that correspond to the 16th and 84th percentiles of the polarization degree distribution, divided by the square root of the number of sources in the bin (cf. Table 1)6.
Agudo et al. (2014) reported ≥3σ linear polarization detections of 183 sources at 86 GHz (88% of the sample detected in total flux density at this frequency) and of 23 sources at 229 GHz (13% of those detected in total flux density); 156 of the sources detected in polarization at 86 GHz are listed in the PCCS2 100 GHz catalog within the area considered here. These sources were again divided into flux density bins containing 30 sources each, except for the brightest bin, which contains 6 sources. Highly significant polarization signals are detected for all bins (cf. Table 2). The method yields values of the median polarization degrees in close agreement with the ground-based measurements in this case as well.
Comparison of the median polarization degrees, ΠIDA = (P/S)median, at 44 GHz yielded by the IDA method with those measured by Jackson et al. (2010) at 43 GHz, within the flux density range Srange.
Comparison of the median polarization degrees, Π, at 100 GHz yielded by the IDA method with those measured by Agudo et al. (2014) at 86 GHz.
Of the 23 sources detected in polarization at 229 GHz by Agudo et al. (2014), 18 are within the region we considered, but one of them was not detected by Planck at 217 GHz. For the remaining 17 sources, the KS test gives a detection probability of 92% (i.e., a probability of the null hypothesis, sources extracted from the same distribution as control fields, of 8%). The median polarization degree measured on Planck maps is 4.8 (+1.7, −2.7)% to be compared with 7.9 (+2.2, −1.8)% measured by Agudo et al. (2014) for the same sources. Given that only a small fraction of observed sources were detected, it is quite likely that the detected sources, which are strongly variable, were preferentially caught by Agudo et al. (2014) in a high-polarization phase. Hence it is not surprising that the median value derived from Planck maps, which are averages over five scans of the sky spanning 2.5 yr, is somewhat lower.
4. Results
4.1. Radio sources
We detected significant polarization signals of PCCS2 radio sources in the region specified in Sect. 2 for more than two flux density bins at 30, 44, 100, and 143 GHz. The median polarization degrees yielded by the IDA method for each bin are reported in Tables 3–6. ΠIDA was computed using the median of Π, Eq. (3), over the considered sample. The errors correspond to the 16th and 84th percentiles of the polarization degree distribution, divided by the square root of the number of sources in the bin.
The first bin in each table is the faintest for which we detected a significant positive signal. The significance of the detections (not to be confused with the S/N) is at least at the ≃3σ level and in most cases is much higher, as shown in the last column of Tables 3–6. There is no significant dependence of ΠIDA on flux density at any frequency.
In Fig. 1 the distributions of polarized signals of radio sources is compared with those of control fields. The source distributions refer to the total flux densities above the Slim listed in Table 7. The shift of the distributions toward higher values of the polarized flux density, compared to control fields, can be perceived by eye.
Table 7 and Fig. 2 show the median polarization degrees, with their errors, for the full flux density ranges over which a signal was detected, at all the Planck polarization-sensitive frequencies. The KS test always detects signals with high significance, and the estimates have an S/N > 3 except at 44 and 353 GHz. Assuming that ΠIDA is frequency independent, a minimum χ2 fit gives ⟨ΠIDA⟩ = 2.83 (+0.18, −0.19)% with a reduced χ2, 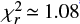 7.
7.
 |
Fig. 1. Distribution of the polarized signals of PCCS2 radio sources and dusty galaxies compared with those of control fields (signals within a radius of FWHM/2 from the corresponding centers). The total flux density limits for radio sources are those listed in Table 7. For dusty galaxies at 353 GHz we have kept the same limit as for radio sources (784 mJy). At 217 GHz, Slim, dusty = 300 mJy (see text). |
The median polarization degree does not show any statistically significant frequency dependence, consistent with the results of Battye et al. (2011) and Galluzzi et al. (2017, 2018), but not with the increase between 86 and 229 GHz by factors of ∼1.6 or ∼2.6 claimed by Agudo et al. (2014) and by Agudo et al. (2018), respectively.
Our results are generally in good agreement with ground-based high sensitivity polarization measurements at nearby frequencies. At 33 GHz, Galluzzi et al. (2018) found for their fainter sample ⟨Π⟩ = 1.85% with first and third quartile values of 1.17% and 3.29%, respectively, to be compared with our median values at 30 GHz of 3.3%. At 43 GHz, Battye et al. (2011) found Πmedian = 2.25%; our median value at 44 GHz is 2.2%. At 86 GHz, Agudo et al. (2014) found a median polarization degree, including upper limits, Πmedian = 2.9% with first and third quartiles of 1.8% and 4.8%, respectively, to be compared with our median value at 100 GHz of 1.9%.
We also agree with Bonavera et al. (2017a), who found that the average fractional polarization of radio sources is approximately frequency independent in the Planck range and derived a weighted mean over all the channels of Π = 3.08%. Their median values, Π = 1.9%, are slightly lower, and close to ours.
4.2. Dusty galaxies
The same approach was applied to investigate the polarization properties of dusty galaxies. Samples of these objects within the same area considered for radio sources were extracted from the PCCS2 at 217 and 353 GHz. The selection of dusty galaxies was made taking into account only sources without a counterpart at 143 GHz, where radio sources dominate, as mentioned above.
We collected 616 and 678 dusty galaxies brighter than 152 mJy at 217 GHz and than 304 mJy at 353 GHz. As in the case of radio sources, these objects were subdivided into total flux density bins containing 30 dusty galaxies each, except for the brightest bins, which contain 16 and 18 objects, respectively.
The KS test did not detect any significant positive shift of the distribution of polarized flux densities compared to that of control fields. Examples are shown in the bottom panels of Fig. 1. At 353 GHz, we adopted Slim = 784 mJy, the same as for radio sources. The 68% and 90% confidence upper limits to the polarization degree are Π353,dusty, ≲ 1.1% and ≲2.2%, respectively. We checked that these upper limits are stable by varying Slim8.
At 217 GHz, there are no objects above 1085 mJy (the limit for radio sources) and only 11 objects above 500 mJy. Thus, the histogram refers to Slim, dusty = 300 mJy. Correcting for the small bias, the 68% and 90% confidence upper limits are Π217, dusty ≲ 2.0% and ≲3.9%, respectively. The looser limits at 217 GHz, compared to those at 353 GHz, reflect the weakening of dusty galaxy flux densities. These limits do not vary appreciably when we decrease Slim. The number of sources rapidly decreases for higher Slim, and the limits become unstable.
 |
Fig. 2. Median polarization degrees for radio sources at Planck frequencies with their errors (blue data points), and upper limits (90% and 68% confidence) for dusty galaxies (red arrows). All values were corrected for the small biases discussed in Sect. 4.3. The solid blue line shows the minimum χ2 value of the median polarization degree of radio sources, assumed to be frequency independent. The dashed and dot-dashed lines show the 68% and 95% limits, respectively. |
We therefore do not confirm the conclusion by Bonavera et al. (2017b), who derived mean fractional polarizations of (3.65 ± 0.66)% and (3.10 ± 0.75)%, and corresponding median values of (2.0 ± 0.8)% and (1.3 ± 0.7)%, at 353 GHz and at 217 GHz, respectively. We note, however, that their median values are consistent with our 68% confidence upper limit at 217 GHz and with our 90% confidence upper limit at 353 GHz.
Median polarization degrees of radio sources at the Planck polarization-sensitive frequencies.
4.3. Validation through simulations
Although the comparison with the polarization measurements by Jackson et al. (2010) and by Agudo et al. (2014) has shown that the IDA approach accounts for and remarkably well corrects the noise bias (cf. Sect. 3), Eq. (1) can still be affected by bias residuals, whose magnitude can be estimated by means of Monte Carlo simulations.
In the ideal case, the polarized flux density of the ith source is 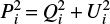 and, for an ensemble of Ns sources, the median polarization degree is
and, for an ensemble of Ns sources, the median polarization degree is
In our approach, Eq. (5) becomes
where (P or S)CF, median is the median over all the NCF control fields (with NCF ≫ Ns). The signal in the jth control field depends on noise and “foregrounds” (here including the CMB as well), that is, 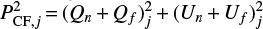 and SCF, j = (Sn + Sf)j, while for the ith source, we have
and SCF, j = (Sn + Sf)j, while for the ith source, we have 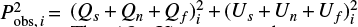 and Sobs,i = (Ss + Sn + Sf)i. The (Q, U) cross-product terms of source with noise and foregrounds are not subtracted in the numerator of Eq. (6) and their contribution is not fully negligible, in principle, even though they are uncorrelated, hence vanishing on average, and expected to be significantly suppressed in the median.
and Sobs,i = (Ss + Sn + Sf)i. The (Q, U) cross-product terms of source with noise and foregrounds are not subtracted in the numerator of Eq. (6) and their contribution is not fully negligible, in principle, even though they are uncorrelated, hence vanishing on average, and expected to be significantly suppressed in the median.
To quantify these potential residuals, we performed Monte Carlo simulations consisting of 1000 realizations. Since diffuse foregrounds vary especially with Galactic latitude, we analyzed the following cases: Galactic latitude |b| > 20°, |b| ∈ (20, 40)°, |b| ∈ (40, 60)°, and |b| ∈ 60°. The simulated sources in the mock catalogs (chosen in number as in Col. 3 of Table 7) were randomly located at the positions of some control fields, in order to avoid regions where real sources are detected. We generated source flux densities in the same ranges as real sources at each frequency, in keeping with their differential number counts.
Mock radio sources and dusty galaxies were assigned ΠRS = 2.75% and Πdusty = 1%, respectively; (Qi, Ui) were derived from a uniform distribution of polarization angles. Applying the IDA method, we generally found for radio sources bias values of δΠRS ≃ −(0.05−0.06)% except at 44 GHz (where Planck maps are particularly noisy) and at 353 GHz (where the statistics is poor); at these frequencies we have δΠRS, 44 ≃ −0.12% and δΠRS, 353 ≃ −0.31%. For dusty galaxies, simulated only at 217 and 353 GHz, we found δΠdusty,217 ≃ −0.1% and a negligible value at 353 GHz.
These results refer to |b| > 20°, but the bias amplitudes do not show any significant dependence on Galactic latitudes, except at 353 GHz, where they somewhat increase for |b| ∈ (40, 60)° and |b| > 60° because of the poorer statistics of control fields that is due to the smaller sky fraction. In general, the bias values are much lower than the uncertainties on Π; nevertheless, the median polarization degrees in Table 7 and in Fig. 2 include this correction. The errors on the retrieved median values are about a factor of 2 lower than those estimated for real sources. The reason probably is that the simulations do not allow for the intrinsic dispersion of the source fractional polarization.
4.4. Power spectra
Figure 3 compares the polarization power spectra of radio sources (solid blue lines) and of dusty galaxies (dashed red lines, shown only for ν ≥ 100 GHz) with the CMB power spectra. The dot-dashed and dotted green lines show the E-mode and lensing B-mode power spectra for the Planck best-fit cosmological parameters (Planck Collaboration XIII 2016). The dashed green lines show the primordial B-mode power spectra for four values of the tensor to scalar ratio.
The power spectra of sources are the sum of Poisson and clustering contributions. Poisson fluctuations have a white-noise power spectrum, independent of the multipole number ℓ:
where dN(S)/dS are the differential number counts per steradian of sources weaker than the detection limit Sd.
In the case of extragalactic radio sources, the contribution of clustering can be neglected (cf., e.g., Delabrouille et al. 2013). To compute the Poisson power spectrum, counts in polarized flux density were estimated from counts in total flux density, S, adopting a polarization fraction of 2.83%, that is, setting Sp = 0.0283 S. For the counts in total flux density, we exploited the models by de Zotti et al. (2005) up to 70 GHz and by Tucci et al. (2011) at higher frequencies. In the relevant flux-density range, the slope of the dN(S)/dS of extragalactic radio sources is ≲2, so that the largest contribution to Cℓ,Poisson comes from flux densities just below the detection limits in polarization. Figure 3 shows two cases, considering the polarized flux density detection limits expected for next-generation CMB experiments (cf. Fig. 8 of De Zotti et al. 2018).
 |
Fig. 3. Polarization E/B-mode power spectra of radio sources and of dusty galaxies compared with the CMB E mode and B mode for four values of the tensor to scalar ratio r = 0.01, 0.003, 0.001, 0.0003 (from top to bottom); see text and legend for details. Since unresolved point sources on average contribute equally to E and B mode, their total power spectra have been divided by a factor of 2. |
Conversely, in the case of dusty galaxies, the clustering contribution dominates most of the multipole range of interest here. The power spectra in polarized flux density were derived from those in total flux density given by the Cai et al. (2013) model that accurately reproduce both the Planck (Planck Collaboration XVIII 2011; Planck Collaboration XXX 2014) and the Herschel (Viero et al. 2013) measurements. For these objects, the counts are very steep (slope > 3), so that the main contribution to the power spectrum comes from faint sources, or in other words, the power spectrum amplitude is essentially independent of Sd. Again, the power spectra in polarization were scaled from those in total flux density for two choices of the polarization degree, 3%, close to the mean value found by Bonavera et al. (2017b), and 1%, close to our 68% confidence upper limit at 353 GHz. For the sake of illustration, we applied this approach down to 100 GHz. We note, however, that already at 143 GHz, the dusty galaxies in Planck maps are too faint to allow the derivation of reasonably accurate constraints on their average polarization degree.
Unresolved point sources contribute, on average, equally to E- and B-mode power spectra. Thus, for comparison with the CMB polarization modes (Fig. 3), the total power spectra discussed above were divided by a factor of 2.
The contamination of CMB polarization maps by extragalactic radio sources was previously discussed by Tucci et al. (2004), Tucci & Toffolatti (2012), and Curto et al. (2013). Our analysis agrees with their conclusion that these objects are not a strong contaminant to the CMB E-mode polarization, but can constrain the detection of cosmological B-modes if r ≲ 0.01.
Estimates of the power spectrum of dusty galaxies were presented by Curto et al. (2013), who assumed an average polarization level of 1%, and by Bonavera et al. (2017b). The latter authors used log-normal distributions for the polarization degrees and took into account only the Poisson contributions. Extrapolating to lower frequencies the estimates or the upper limits obtained at 217 and 353 GHz, we find that the contamination by dusty galaxies may be comparable to that of radio sources at 100–143 GHz; it becomes dominant at higher frequencies and rapidly fades away at lower frequencies.
5. Conclusions
We have revisited the estimates of the mean polarization fraction of extragalactic sources (radio-loud AGNs and dusty galaxies) based on data from the Planck polarization maps at 30, 44, 70, 100, 143, 217, and 353 GHz. Although the earlier analyses by Bonavera et al. (2017a,b) based on stacking techniques were carefully made, there are several tricky aspects and subtleties that call for an independent analysis. This is particularly important in relation to the forthcoming or proposed CMB polarization experiments aimed at detecting primordial B modes.
The importance of a careful control of foregrounds has been demonstrated by detailed sky simulations (Remazeilles et al. 2018), which included Galactic and extragalactic polarized emissions in addition to the CMB, based on state-of-the-art observations. These simulations have shown that for r at the per thousand level (i.e., at the level predicted by models currently of special interest), or smaller (as in the case of large-field inflation with super-Planckian field excursions), the overall uncertainty on this parameter can be dominated by the contamination of unresolved polarized extragalactic sources. An insufficiently accurate characterization of this component could lead to a bias in the reconstruction of the primordial CMB B-mode signal.
Our independent reanalysis overcomes the two most delicate aspects of the application of stacking techniques: the approximation of the average polarization fraction, ⟨Π⟩ = ⟨P/S⟩, with the ratio of the mean polarized flux density to the mean total flux density, ⟨P⟩/⟨S⟩, and the need of simulations to correct for the noise bias.
Our approach considered the objects one by one. This allowed us to identify the flux density range that contributes significantly to the polarization signal; thus we can exclude fainter objects from the analysis that may affect results because of the serious limitation by noise and background signals. For objects above the flux density threshold, we directly computed the median P/S. We find that the method allows us to detect, on Planck maps, mean polarized flux densities at few tens of mJy levels. For comparison, the detection limits in total intensity are at the few to several hundred mJy levels (cf. Table 13 of Planck Collaboration XXVI 2016).
In addition, the subtraction of the median of the polarization signal of control fields largely corrects for the contributions of the noise and of the other polarized components (CMB and Galactic emissions). By means of simulations, we have found that residual biases on the median polarization fractions are generally below 0.1%, which is much smaller than the estimated errors.
For radio sources, we find a median polarization degree, averaged over frequencies, ΠIDA,median ≃ 2.83%, in good agreement with Bonavera et al. (2017a) as well as with the ground-based measurements of a fainter sample at 33 and 38 GHz (Galluzzi et al. 2018) and of a bright sample at 86 GHz (Agudo et al. 2014). We do not find any significant dependence of Π on either flux density or frequency, in agreement with earlier analyses at frequencies up to 43 GHz, but not in agreement with the increase of Π from 86 to 229 GHz claimed by Agudo et al. (2014, 2018).
At variance with Bonavera et al. (2017b), we do not detect any polarization signal from dusty galaxies, although their median values are consistent with our upper limits. For these objects we derive a 90% confidence upper limit at 353 GHz Πdusty ≲ 2.2%. The upper limit at the same confidence level is looser (≲3.9%) at 217 GHz, where dusty galaxies are substantially fainter.
The contamination of CMB maps in polarization by extragalactic sources is dominated by radio-loud AGNs up to ∼100 GHz. The amplitude of their power spectra depends on their detection limit in polarization, Sd. For the values of Sd expected for next-generation CMB experiments, we confirm that at ≃70 GHz, that is, in correspondence to the minimum Galactic emission, the point source (radio source) contamination is well below primordial E modes, as found by previous analyses. On the other hand, it is close to the level of lensing B modes and of primordial B modes for r ≃ 0.01. The contribution of dusty galaxies to the point source power spectra is still poorly constrained, but may be substantial or even dominant at ≥100 GHz.
Acknowledgments
Thanks are due to Z.-Y. Cai and to M. Tucci for having provided the power spectra of dusty galaxies and the high-frequency counts of radio sources, respectively, yielded by their models. We also thank the anonymous referee for comments that helped improve the paper. We gratefully acknowledge financial support from ASI/INAF agreement n. 2014-024-R.1 for the Planck LFI Activity of Phase E2, from the ASI/Physics Department of the university of Roma–Tor Vergata agreement n. 2016-24-H.0 for study activities of the Italian cosmology community and from the Italian Ministero dell’Istruzione, Università e Ricerca through the grant “Progetti Premiali 2012-iALMA” (CUP C52I13000140001). Some of the results in this paper have been derived using the HEALPix (Górski et al. 2005) package.
References
- Abazajian, K. N., Adshead, P., Ahmed, Z., et al. 2016, ArXiv e-prints [arXiv:1610.02743] [Google Scholar]
- Agudo, I., Thum, C., Gómez, J. L., & Wiesemeyer, H. 2014, A&A, 566, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Agudo, I., Thum, C., Ramakrishnan, V., et al. 2018, MNRAS, 473, 1850 [NASA ADS] [CrossRef] [Google Scholar]
- Barcons, X., Franceschini, A., de Zotti, G., Danese, L., & Miyaji, T. 1995, ApJ, 455, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Battye, R. A., Browne, I. W. A., Peel, M. W., Jackson, N. J., & Dickinson, C. 2011, MNRAS, 413, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Baumann, D., & McAllister, L. 2007, Phys. Rev. D, 75, 123508 [NASA ADS] [CrossRef] [Google Scholar]
- BICEP2 Collaboration & Keck Array Collaboration. 2016, Phys. Rev. Lett., 116, 031302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bonavera, L., González-Nuevo, J., Argüeso, F., & Toffolatti, L. 2017a, MNRAS, 469, 2401 [NASA ADS] [CrossRef] [Google Scholar]
- Bonavera, L., González-Nuevo, J., De Marco, B., Argüeso, F., & Toffolatti, L. 2017b, MNRAS, 472, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Cai, Z.-Y., Lapi, A., Xia, J.-Q., et al. 2013, ApJ, 768, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, S. K., & Page, L. A. 2015, JCAP, 12, 020 [NASA ADS] [CrossRef] [Google Scholar]
- Curto, A., Tucci, M., González-Nuevo, J., et al. 2013, MNRAS, 432, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Delabrouille, J., Betoule, M., Melin, J.-B., et al. 2013, A&A, 553, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delabrouille, J., de Bernardis, P., Bouchet, F. R., et al. 2018, JCAP, 4, 014 [NASA ADS] [CrossRef] [Google Scholar]
- De Zotti, G., Danese, L., Franceschini, A., Persic, M., & Toffolatti, L. 1989, ESA SP, 296, 737 [NASA ADS] [Google Scholar]
- de Zotti, G., Ricci, R., Mesa, D., et al. 2005, A&A, 431, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Zotti, G., Castex, G., González-Nuevo, J., et al. 2015, JCAP, 018 [Google Scholar]
- De Zotti, G., González-Nuevo, J., Lopez-Caniego, M., et al. 2018, JCAP, 4, 020 [Google Scholar]
- Finelli, F., Bucher, M., Achúcarro, A., et al. 2018, JCAP, 4, 016 [Google Scholar]
- Galluzzi, V., & Massardi, M. 2016, Int. J. Mod. Phys. D, 25, 1640005 [NASA ADS] [CrossRef] [Google Scholar]
- Galluzzi, V., Massardi, M., Bonaldi, A., et al. 2017, MNRAS, 465, 4085 [NASA ADS] [CrossRef] [Google Scholar]
- Galluzzi, V., Massardi, M., Bonaldi, A., et al. 2018, MNRAS, 475, 1306 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Greaves, J. S., & Holland, W. S. 2002, in Astrophysical Polarized Backgrounds, eds. S. Cecchini, S. Cortiglioni, R. Sault, & C. Sbarra, AIP Conf. Ser., 609, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Hales, C. A., Norris, R. P., Gaensler, B. M., & Middelberg, E. 2014, MNRAS, 440, 3113 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, N., Browne, I. W. A., Battye, R. A., Gabuzda, D., & Taylor, A. C. 2010, MNRAS, 401, 1388 [NASA ADS] [CrossRef] [Google Scholar]
- Kogut, A., Chluba, J., Fixsen, D. J., Meyer, S., & Spergel, D. 2016, Proc. SPIE, 9904, 99040W [CrossRef] [Google Scholar]
- Krachmalnicoff, N., Baccigalupi, C., Aumont, J., Bersanelli, M., & Mennella, A. 2016, A&A, 588, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Caniego, M., Massardi, M., González-Nuevo, J., et al. 2009, ApJ, 705, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Lyth, D. H. 1997, Phys. Rev. Lett., 78, 1861 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, J., Ringeval, C., & Vennin, V. 2014, Phys. Dark Univ., 5, 75 [CrossRef] [Google Scholar]
- Mocanu, L. M., Crawford, T. M., Vieira, J. D., et al. 2013, ApJ, 779, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Negrello, M., Clemens, M., Gonzalez-Nuevo, J., et al. 2013, MNRAS, 429, 1309 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XVIII. 2011, A&A, 536, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration V. 2014, A&A, 571, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration IX. 2014, A&A, 571, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXX. 2014, A&A, 571, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration X. 2016, A&A, 594, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXV. 2016, A&A, 594, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVI. 2016, A&A, 594, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. VII. 2013, A&A, 550, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXX. 2016, A&A, 586, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. L. 2017, A&A, 599, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Remazeilles, M., Banday, A. J., Baccigalupi, C., et al. 2018, JCAP, 4, 023 [NASA ADS] [CrossRef] [Google Scholar]
- Siegel, S., & Castellan, N. 1988, Nonparametric Statistics for the Behavioral Sciences, 2nd edn. (McGraw–Hill, Inc.: New York) [Google Scholar]
- Tucci, M., & Toffolatti, L. 2012, Adv. Astron., 2012, 624987 [Google Scholar]
- Tucci, M., Martínez-González, E., Toffolatti, L., González-Nuevo, J., & De Zotti, G. 2004, MNRAS, 349, 1267 [NASA ADS] [CrossRef] [Google Scholar]
- Tucci, M., Toffolatti, L., de Zotti, G., & Martínez-González, E. 2011, A&A, 533, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viero, M. P., Wang, L., Zemcov, M., et al. 2013, ApJ, 772, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Wardle, J. F. C., & Kronberg, P. P. 1974, ApJ, 194, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Chen, X., Odegard, N., et al. 2009, ApJS, 180, 283 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Comparison of the median polarization degrees, ΠIDA = (P/S)median, at 44 GHz yielded by the IDA method with those measured by Jackson et al. (2010) at 43 GHz, within the flux density range Srange.
Comparison of the median polarization degrees, Π, at 100 GHz yielded by the IDA method with those measured by Agudo et al. (2014) at 86 GHz.
Median polarization degrees of radio sources at the Planck polarization-sensitive frequencies.
All Figures
 |
Fig. 1. Distribution of the polarized signals of PCCS2 radio sources and dusty galaxies compared with those of control fields (signals within a radius of FWHM/2 from the corresponding centers). The total flux density limits for radio sources are those listed in Table 7. For dusty galaxies at 353 GHz we have kept the same limit as for radio sources (784 mJy). At 217 GHz, Slim, dusty = 300 mJy (see text). |
| In the text | |
 |
Fig. 2. Median polarization degrees for radio sources at Planck frequencies with their errors (blue data points), and upper limits (90% and 68% confidence) for dusty galaxies (red arrows). All values were corrected for the small biases discussed in Sect. 4.3. The solid blue line shows the minimum χ2 value of the median polarization degree of radio sources, assumed to be frequency independent. The dashed and dot-dashed lines show the 68% and 95% limits, respectively. |
| In the text | |
 |
Fig. 3. Polarization E/B-mode power spectra of radio sources and of dusty galaxies compared with the CMB E mode and B mode for four values of the tensor to scalar ratio r = 0.01, 0.003, 0.001, 0.0003 (from top to bottom); see text and legend for details. Since unresolved point sources on average contribute equally to E and B mode, their total power spectra have been divided by a factor of 2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.