| Issue |
A&A
Volume 616, August 2018
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 9 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201833110 | |
| Published online | 22 August 2018 | |
Kinematics of outer halo globular clusters: M 75 and NGC 6426⋆
1
Zentrum für Astronomie der Universität Heidelberg, Astronomisches Rechen-Institut, Mönchhofstr. 12, 69120 Heidelberg, Germany
e-mail: andreas.koch@uni-heidelberg.de
2
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
Received:
27
March
2018
Accepted:
13
May
2018
Globular clusters (GCs) and their dynamic interactions with the Galactic components provide an important insight into the structure and formation of the early Milky Way. We present a kinematic study of two outer halo GCs based on a combination of VLT/FORS2, VLT/FLAMES, and Magellan/MIKE low- and high-resolution spectroscopy of 32 and 27 member stars, respectively. Although both clusters are located at Galactocentric distances of 15 kpc, they have otherwise very different properties. M 75 is a luminous and metal-rich system at [Fe/H] = −1.2 dex, which is a value that we confirm from the calcium triplet region. This GC shows mild evidence for rotation with an amplitude of Arot ~ 5 km s−1. One of the most metal-poor GCs in the Milky Way (at [Fe II/H] = −2.3 dex), NGC 6426 exhibits marginal evidence of internal rotation at the 2 km s−1 level. Both objects have velocity dispersions that are consistent with their luminosity. Although limited by small-number statistics, the resulting limits on their Arot/σ0 ratios suggest that M 75 is a slow rotator driven by internal dynamics rather than being affected by the weak Galactic tides at its large distances. In this work, M 75 (Arot/σ0 = 0.31) is fully consistent with the properties of other, younger halo clusters. At Arot/σ0 = 0.8 ± 0.4, NGC 6426 appears to have a remarkably ordered internal motion for its low metallicity, but the large uncertainty does not allow for an unambiguous categorization as a fast rotator. An accretion origin of M 75 cannot be excluded, based on the eccentric orbit, which we derived from the recent data release 2 of Gaia, and considering its younger age.
Key words: globular clusters: individual: M 75 / globular clusters: individual: NGC 6426 / Galaxy: kinematics and dynamics / Galaxy: structure / Galaxy: halo
© ESO 2018
1. Introduction
Globular clusters (GCs) are ideal tracers of the earliest phases of the Milky Way’s assembly because they are amongst the oldest stellar systems in the universe. A particular emphasis lies on objects at large Galactocentric distances, as they probe the outermost halo and its accreted, ex situ origin (Searle & Zinn 1978; Hartwick 1987; Carollo et al. 2007; Pillepich et al. 2015), or the important transition region between the inner and outer Galactic halo. Despite their, on average, younger ages (Mackey & Gilmore 2004; Marín-Franch et al. 2009), outer halo GCs are chemically very similar to halo clusters at smaller Galactocentric radii (Koch et al. 2009; Koch & Côté 2010; Çalışkan et al. 2012).
Internally, GCs deviate ever more from the historic view of simple stellar populations. Similarly, spherical symmetry and dynamic equilibrium are often too simplistic assumptions for many of these objects. It is nowadays well established that these object host multiple populations, indicating a great degree of complexity during their early formation epochs (Decressin et al. 2007; D’Ercole et al. 2008; Bastian et al. 2013; Milone et al. 2017; Martocchia et al. 2018), as is presently most pronounced in terms of their light chemical abundance variations (Osborn 1971; Kayser et al. 2008; Carretta et al. 2009b; Gratton et al. 2012). However, none of the models present a fully satisfactory formation picture yet (Bastian et al. 2015; Bastian & Lardo 2018).
In this context, a spatial segregation between first and second generations of stars has been observed (e.g., Carretta et al. 2010a), which is often accompanied by differences in their internal kinematics such as significantly different velocity dispersions and rotational amplitudes (Bellazzini et al. 2012). Furthermore, systematic correlations of the kinematic properties with other GC characteristics, such as their metallicity or age, have been reported (Carretta et al. 2010b; Bellazzini et al. 2012; Kacharov et al. 2014; Lardo et al. 2015). All these can be considered an imprint of the formation history of GCs rather than a result of long-term dynamical evolution, such that detailed dynamical models are in place (Bianchini et al. 2013; Vesperini et al. 2013; Cordero et al. 2017; Baumgardt 2017). Rotation has by now been observed in most GCs and it leads to their morphological flattening, although also external effects such as pressure anisotropy and the Galactic tidal field can play a significant role in affecting the dynamical evolution and shape of these systems (e.g., Tiongco et al. 2018). Observationally, systematic monitoring of the internal dynamics of GCs has started blooming owing to the large multiplexing capacities of multi-object spectrographs and with the latest developments in integral-field unit spectroscopy (e.g., Kamann et al. 2018; Ferraro et al. 2018).
In this paper, we determine the kinematic properties of two GCs that do not have many common characteristics (such as metallicity or mass) except for their location in the transition region between the inner and outer Galactic halos, at  = 14.4 and 14.6 kpc, respectively. M 75 (
= 14.4 and 14.6 kpc, respectively. M 75 ( NGC 6864) is a massive, metal-rich ([Fe/H] =
NGC 6864) is a massive, metal-rich ([Fe/H] = 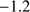 dex) GC that exhibits an extraordinary, trimodal horizontal branch (HB) morphology (Catelan et al. 2002; Kacharov et al. 2013). In contrast, the chemical abundance study of Kacharov et al. (2013) revealed only moderate light element anti-correlations, lacking a third, extreme component that would go in lockstep with the extended, hot HB, concluding that the HB peculiarity of this object has been shaped by processes that are yet unknown. On the other hand, the low-mass NGC 6426 is one of the three most metal-poor and oldest GCs in the Milky Way system (Salaris & Weiss 2002; Hanke et al. 2017). Owing to a limited spectral sample, Hanke et al. (2017) could not establish the presence of a Na-O anti-correlation in NGC 6426, but mild variations in other elements suggested that multiple populations are also likely present in this object. Both our target clusters are, kinematically, hitherto uncharted.
dex) GC that exhibits an extraordinary, trimodal horizontal branch (HB) morphology (Catelan et al. 2002; Kacharov et al. 2013). In contrast, the chemical abundance study of Kacharov et al. (2013) revealed only moderate light element anti-correlations, lacking a third, extreme component that would go in lockstep with the extended, hot HB, concluding that the HB peculiarity of this object has been shaped by processes that are yet unknown. On the other hand, the low-mass NGC 6426 is one of the three most metal-poor and oldest GCs in the Milky Way system (Salaris & Weiss 2002; Hanke et al. 2017). Owing to a limited spectral sample, Hanke et al. (2017) could not establish the presence of a Na-O anti-correlation in NGC 6426, but mild variations in other elements suggested that multiple populations are also likely present in this object. Both our target clusters are, kinematically, hitherto uncharted.
This paper is organized as follows: Sect. 2 presents the data and our velocity measurements. Additional measurements of metallicities for the M 75 stars are briefly discussed in Sect. 3, before describing the general kinematic properties of the two GCs in Sect. 4. Next, Sect. 5 focuses on an in-depth analysis of the internal rotation of the clusters before discussing our findings in Sect. 6.
2. Data and radial velocity measurements
2.1. M 75: MIKE high-resolution spectra
The spectra used in the present analysis are those already presented in Kacharov et al. (2013). In brief, high-resolution ( 40,000) spectra of 18 red giant member stars have been obtained with the Magellan Inamori Kyocera Echelle (MIKE) spectrograph at the 6.5 m Magellan2/Clay Telescope at Las Campanas Observatory, Chile. Out of these stars, 16 had a sufficient signal-to-noise ratio (S/N) for a detailed abundance analysis. We measured their radial velocities via a cross-correlation of the spectra against a synthetic template of a red giant branch (RGB) star of stellar parameters typical of the observed sample.
40,000) spectra of 18 red giant member stars have been obtained with the Magellan Inamori Kyocera Echelle (MIKE) spectrograph at the 6.5 m Magellan2/Clay Telescope at Las Campanas Observatory, Chile. Out of these stars, 16 had a sufficient signal-to-noise ratio (S/N) for a detailed abundance analysis. We measured their radial velocities via a cross-correlation of the spectra against a synthetic template of a red giant branch (RGB) star of stellar parameters typical of the observed sample.
2.2. M 75: VLT/FORS2 low-resolution data
Low-resolution spectroscopy of 37 stars within 3.8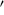 (7.5 half-light radii
(7.5 half-light radii 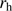 ) of the GC is available from the European Souther Observatory (ESO) archive. The location of these targets in a color magnitude diagram (CMD) is shown in Fig. 1. These spectroscopic data have been taken during one night in August 2002 with the Focal Reducer and low dispersion Spectrograph FORS2 at the Very Large Telescope (VLT) under proposal 69.B-0305 (P.I. E. Tolstoy). The filter used was OG590 with grism 1028z, centered around the near-infrared calcium triplet (CaT) lines at
) of the GC is available from the European Souther Observatory (ESO) archive. The location of these targets in a color magnitude diagram (CMD) is shown in Fig. 1. These spectroscopic data have been taken during one night in August 2002 with the Focal Reducer and low dispersion Spectrograph FORS2 at the Very Large Telescope (VLT) under proposal 69.B-0305 (P.I. E. Tolstoy). The filter used was OG590 with grism 1028z, centered around the near-infrared calcium triplet (CaT) lines at 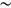 8500 Å, and the exposure time was 2
8500 Å, and the exposure time was 2 900 s. These data were reduced via the IRAF apall and other standard routines (see also Fraternali et al.2009) and have a resolving power of
900 s. These data were reduced via the IRAF apall and other standard routines (see also Fraternali et al.2009) and have a resolving power of 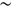 2500, as determined from the width of the sky emission lines. Typical S/N values range from 7 to 120 pixel
2500, as determined from the width of the sky emission lines. Typical S/N values range from 7 to 120 pixel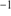 and have a median of
and have a median of  70 pixel
70 pixel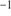 .
.
Heliocentric velocities of the target stars were determined by cross-correlation (within IRAF’s fxcor) against a synthetic spectrum of the three CaT lines, adopted as simple Gaussian profiles (Kleyna et al. 2004). One of the stars is a blue HB star and we measured its velocity from the Doppler shifts of the prominent, broad Paschen lines, yielding a larger uncertainty. The formal errors returned by fxcor are on the order of 1.5 km s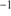 . As a result (Fig. 2), we find 21 stars within 3.3
. As a result (Fig. 2), we find 21 stars within 3.3 (6.7
(6.7 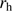 ) with velocities below
) with velocities below 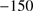 km s
km s that are clearly separated from the bulk of Galactic foreground stars. We therefore assume these as GC member candidates. Their properties are listed in Table 1 and Fig. 1 shows their spatial distribution and velocity histogram.
that are clearly separated from the bulk of Galactic foreground stars. We therefore assume these as GC member candidates. Their properties are listed in Table 1 and Fig. 1 shows their spatial distribution and velocity histogram.
The layout of FORS2 with its two separate CCD chips can, in principle, lead to systematic offsets in radial velocities if measured on different chips (e.g., Fraternali et al. 2009). In order to ascertain that our data are not affected by such systematics, we computed the kinematics of the subsamples from chip 1 and 2 separately and find only a marginal (0.7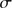 ) difference of the mean systemic velocity as computed from either chip. We deem chip offsets redundant for the remainder of this work and comment further on this option in the sections presenting our results below.
) difference of the mean systemic velocity as computed from either chip. We deem chip offsets redundant for the remainder of this work and comment further on this option in the sections presenting our results below.
 |
Fig. 1. Left panel: CMD of M75 from Kravtsov et al. (2007) with spectroscopic targets shown as red star symbols (FORS members), and green circles (MIKE targets). Right panel: CMD of NGC 6426 from the HST photometry of Dotter et al. (2011), indicating member candidates (red stars). Green circles show the four stars studied in high resolution by Hanke et al. (2017). |
 |
Fig. 2. Heliocentric radial velocity against radial distance (bottom panel) and CaT-based metallicity (middle panel) from the FORS data are shown in black. The histogram in the top panel indicates the peak of M 75 at |
Properties of M 75 member stars.
2.3. M 75: Combined sample
In the following, we determined mean heliocentric radial velocities and velocity dispersions in a maximum likelihood sense, by optimizing the probability 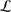 that the given ensemble of stars with velocities
that the given ensemble of stars with velocities 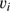 and errors
and errors 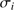 are drawn from a population with mean velocity
are drawn from a population with mean velocity 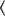

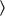 and dispersion
and dispersion 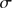 (e.g.,Walker et al. 2006) as follows:
(e.g.,Walker et al. 2006) as follows: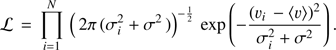 (1)
(1)
From the 21 stars observed with FORS alone, we thus derived a mean heliocentric radial velocity of  km s
km s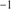 and a velocity dispersion
and a velocity dispersion 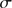 of 8.1
of 8.1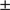 1.3 km s
1.3 km s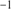 , both of which are consistent with earlier results (Pryor et al. 1993; Harris 2010). Similarly, the MIKE sample of 18 stars returns a value of
, both of which are consistent with earlier results (Pryor et al. 1993; Harris 2010). Similarly, the MIKE sample of 18 stars returns a value of 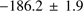 km s
km s with dispersion of 7.8
with dispersion of 7.8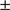 1.3 km s
1.3 km s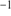 , which is in excellent agreement with the aforementioned values.
, which is in excellent agreement with the aforementioned values.
Seven stars have been targeted in common between both campaigns. The velocities agree excellently for three of those stars, while the difference is larger, up to 7 km s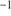 for the remainder. Such inconsistencies could, in principle, indicate that those stars are in binaries; however, the temporal sampling of the observing runs is insufficient to test for more systematic variations. Overall, the mean difference between the MIKE and FORS values is 0.7 km s
for the remainder. Such inconsistencies could, in principle, indicate that those stars are in binaries; however, the temporal sampling of the observing runs is insufficient to test for more systematic variations. Overall, the mean difference between the MIKE and FORS values is 0.7 km s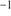 with a large scatter of 3.9 km s
with a large scatter of 3.9 km s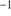 . These deviations are independent of the locations of the stars in the GC, their position in the CMD, and neither subset shows systematically lower or larger values alone.
. These deviations are independent of the locations of the stars in the GC, their position in the CMD, and neither subset shows systematically lower or larger values alone.
To construct a final, bona fide sample, we shifted the FORS velocities by the difference in mean velocity, thereby tying these velocities to the more precise MIKE scale. As a second test, we rejected those common stars with velocities that differ by more than the combined error bar and, for the remaining three overlapping stars, we computed an error-weighted mean value. We emphasize that the results of the kinematic analysis below are insensitive to the inclusion or exclusion of the common stars, or the employed combination scheme such that we continue with the sample after shifting to a common velocity scale and removal of the binary candidates (see also Koch et al. 2007).
2.4. NGC 6426: VLT/FLAMES
The central regions of this GC are heavily affected by crowding, which is unfortunate for efficient multi-object fiber spectroscopy. For target selection, we relied on infrared photometry from the Two Micron All Sky Survey (2MASS; Cutri et al. 2003). Furthermore, Hubble Space Telescope (HST) photometry is available in V and I for a pencil beam toward this GC (Dotter et al. 2011), which contains most of our target stars. The corresponding CMD is shown in the right panel of Fig. 1.
The observations were carried out using the HR13 grating of the GIRAFFE spectrograph as part of the Fibre Large Array Multi Element Spectrograph (FLAMES; Pasquini et al. 2002) at the ESO/VLT. This setting provides a wavelength coverage of 6100–6400 Å at a resolving power of 20 000, where 125 fibers were placed on stars.
After the loss of two entire runs over two ESO periods due to bad weather, data could finally be accrued on the two nights of August 21 and Sepember 19, 2017. While originally conceived as an abundance project, only two out of the six granted observing blocks were taken, which are the basis for the present, kinematic study, for which the lower S/N is sufficient. Here, the total exposure time was 1.4 h, split into 4 1240 s exposures. The data were reduced using ESO standard routines.
1240 s exposures. The data were reduced using ESO standard routines.
As above, we measured radial velocities from a cross-correlation of the spectra against a synthetic template spectrum with stellar parameters representative of the target stars. The errors returned by fxcor were rescaled using the (up to four) repeat observations following the formalism of Vogt et al. (1995) and Koch et al. (2007), resulting in a median velocity error of 1.5 km s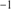 . The resulting measurements and target properties are listed in Table 2.
. The resulting measurements and target properties are listed in Table 2.
Properties of the NGC 6426 member stars from FLAMES.
The plot of velocity versus radial distance from the cluster center in Fig. 3 shows a clear signal of the GC population at a heliocentric velocity of 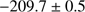 km s
km s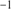 that is significantly detached from the Milky Way foreground. This value is considerably lower than that listed in the Harris (2010) catalog based on low-resolution spectra of a handful of stars. As for M 75, we also combined our sample with the MIKE data of (Hanke et al. 2017) by shifting the FLAMES velocities to the higher resolution MIKE scale. This yields a final sample of 27 member candidates with a dispersion of
that is significantly detached from the Milky Way foreground. This value is considerably lower than that listed in the Harris (2010) catalog based on low-resolution spectra of a handful of stars. As for M 75, we also combined our sample with the MIKE data of (Hanke et al. 2017) by shifting the FLAMES velocities to the higher resolution MIKE scale. This yields a final sample of 27 member candidates with a dispersion of 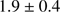 km s
km s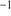 , and we discuss their kinematic properties in the following.
, and we discuss their kinematic properties in the following.
3. M 75: Calcium triplet metallicities
As a more detailed chemical abundance analysis of this GC exists from the MIKE spectra of Kacharov et al. (2013), we determined the equivalent widths (EWs) of the CaT lines from the FORS2 spectra as another means of membership assessment. To this end, we fitted Gaussian plus Lorentz line profiles (Cole et al. 2004) to each line using line and continuum band passes from Armandroff & Zinn (1988). Adopting the calibrations of line strength onto metallicity by Rutledge et al. (1997a; b), we find that 18 of the 21 likely radial velocity members also cluster in abundance space (Fig. 2, middle panel) around [Fe/H]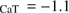 dex on the scale Carretta et al. (2009a). This compares favorably with previous photometric estimates of
dex on the scale Carretta et al. (2009a). This compares favorably with previous photometric estimates of 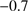 to
to 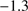 dex (Catelan et al. 2002; Kravtsov et al. 2007; Kacharov et al. 2013). The other three stars with lower metallicities at the systemic velocity of M 75 can still be considered likely members: these are the reddest bright objects at
dex (Catelan et al. 2002; Kravtsov et al. 2007; Kacharov et al. 2013). The other three stars with lower metallicities at the systemic velocity of M 75 can still be considered likely members: these are the reddest bright objects at 
 1.9 mag. Given the inflection of the RGB of this metal-rich GC near the tip, these are likely luminous AGB stars with notably narrow (CaT) absorption lines, for which the linear CaT calibration becomes unreliable (e.g., Garnavich et al. 1994). Moreover, the data of Corwin et al. (2003) indicate that at least two out these three are variable stars.
1.9 mag. Given the inflection of the RGB of this metal-rich GC near the tip, these are likely luminous AGB stars with notably narrow (CaT) absorption lines, for which the linear CaT calibration becomes unreliable (e.g., Garnavich et al. 1994). Moreover, the data of Corwin et al. (2003) indicate that at least two out these three are variable stars.
As a result, the mean metallicity of  dex, which has an intrinsic dispersion of 0.07
dex, which has an intrinsic dispersion of 0.07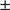 0.05 dex, is slightly more metal rich than the high-resolution, high-S/N MIKE study of Kacharov et al. (2013), who found a mean [Fe I/H] of
0.05 dex, is slightly more metal rich than the high-resolution, high-S/N MIKE study of Kacharov et al. (2013), who found a mean [Fe I/H] of 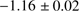 . This systematic overestimate from the low-resolution FORS2 spectra is also seen in the one-to-one comparison of the stars that overlap between the both samples. This discrepancy is considerably alleviated when comparing our results to the metallicity scale from ionized iron lines. Kacharov et al. (2013) found a GC mean of [Fe II/H] =
. This systematic overestimate from the low-resolution FORS2 spectra is also seen in the one-to-one comparison of the stars that overlap between the both samples. This discrepancy is considerably alleviated when comparing our results to the metallicity scale from ionized iron lines. Kacharov et al. (2013) found a GC mean of [Fe II/H] = 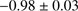 dex (random)
dex (random)  0.16 dex (systematic) with a 1
0.16 dex (systematic) with a 1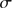 spread of 0.13 dex, which is fully compatible with our present finding. This strongly attests to favoring the use of Fe II as a prime metallicity scale (e.g., Kraft & Ivans 2003; Hanke et al. 2017), as it is also less prone to NLTE effects.
spread of 0.13 dex, which is fully compatible with our present finding. This strongly attests to favoring the use of Fe II as a prime metallicity scale (e.g., Kraft & Ivans 2003; Hanke et al. 2017), as it is also less prone to NLTE effects.
 |
Fig. 3. Heliocentric radial velocity against radial distance (bottom panel) for the entire NGC 6426 observations. The histogram in the top panel indicates the peak of the GC at |
4. General kinematics
Based on our measurement of 32 (27) heliocentric velocities in M 75 and NGC 6426, respectively, we determined the global kinematic properties of the GCs (as listed in Table 3) from the bona fide, combined samples.
For M 75, we determined a mean heliocentric velocity of 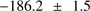 km s
km s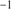 with a velocity dispersion of 8.2
with a velocity dispersion of 8.2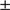 1.1 km s
1.1 km s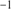 . While this dispersion seems high for a GC at a first glance, it has to be kept in mind that M 75 is a massive system such that our measured value is to be expected and fully compatible with the high values for
. While this dispersion seems high for a GC at a first glance, it has to be kept in mind that M 75 is a massive system such that our measured value is to be expected and fully compatible with the high values for 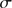 found in other luminous, dense systems (Fig. 4; Pryor et al. 1993).
found in other luminous, dense systems (Fig. 4; Pryor et al. 1993).
For NGC 6426, we find a mean velocity and dispersion of 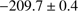 km s
km s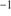 and 1.9
and 1.9 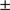 0.4 km s
0.4 km s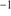 , respectively. The low, latter value is in line with the GC’s lower mass of this GC, as also suggested by Fig. 4. Hanke et al. (2017) found a mean systemic velocity that is lower by 2.4
, respectively. The low, latter value is in line with the GC’s lower mass of this GC, as also suggested by Fig. 4. Hanke et al. (2017) found a mean systemic velocity that is lower by 2.4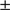 0.8 km s
0.8 km s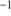 , which was, however, based on four stars. Accordingly, their velocity dispersion is considerably lower than our value, at 1.0
, which was, however, based on four stars. Accordingly, their velocity dispersion is considerably lower than our value, at 1.0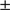 0.4 km s
0.4 km s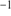 . One star in the present sample is in common with Hanke et al. (2017). The velocity from their MIKE spectra differs by 1.7 km s
. One star in the present sample is in common with Hanke et al. (2017). The velocity from their MIKE spectra differs by 1.7 km s (1.2
(1.2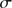 ). Since the latter work was focused on a high-resolution chemical abundance analysis, this discrepancy may hint at an underestimate of the velocity errors, which were not crucial for the chemical purpose. Likewise, the different result by Dias et al. (2015) of a mean velocity of
). Since the latter work was focused on a high-resolution chemical abundance analysis, this discrepancy may hint at an underestimate of the velocity errors, which were not crucial for the chemical purpose. Likewise, the different result by Dias et al. (2015) of a mean velocity of  km s
km s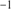 can be understood in terms of the small sample size (at five stars) and a low spectral resolution of
can be understood in terms of the small sample size (at five stars) and a low spectral resolution of 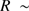 2000.
2000.
Since Galactic foreground stars at similar velocities can, in principle, inflate velocity dispersion measurements and corrupt kinematic analyses (e.g., Walker et al. 2009), we estimated the amount of contamination via the Besançon Galaxy model (Robin et al. 2003). As a result we do not expect a single foreground interloper within the CMD selection criteria and at velocities below 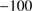 km s
km s drawn from samples such as our NGC 6426 observations. The same holds for M 75.
drawn from samples such as our NGC 6426 observations. The same holds for M 75.
Global and kinematic properties of the two targeted GCs.
 |
Fig. 4. Global velocity dispersion vs. absolute magnitude, using data from Pryor et al. (1993) and Harris (2010), and with the latest measurements of low-mass GCs from Koch et al. (2017a, b, 2018). Targets of this study are indicated by red stars. |
5. Rotation analysis
As a first step, we followed the standard procedure of dividing the data into bins of position angle (PA) and computing the mean velocity of the respective subsamples (e.g., Koch et al. 2007; Kacharov et al. 2014). The resulting difference in mean velocity from either side of a line passing through the GC center at that angle then yields the projected rotation curves in Fig. 5. These can be described by a simplistic sinusoidal with amplitude A and PA (counting north through east) as 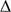 v =
v = 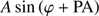 , where
, where 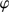 is the PA of each star with respect to the cluster center. As the spatial distribution of the stars in the bottom panel of Fig. 5 indicates, the main source of uncertainty in this analysis is the small-number statistics of the samples.
is the PA of each star with respect to the cluster center. As the spatial distribution of the stars in the bottom panel of Fig. 5 indicates, the main source of uncertainty in this analysis is the small-number statistics of the samples.
Next we performed a more advanced Bayesian fit to the discrete kinematic data of the two GCs (Mackey et al. 2013, see also Kacharov et al. 2014) accounting simultaneously for both the rotation profile 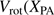 ) (Eq. (2)) and velocity dispersion profile
) (Eq. (2)) and velocity dispersion profile 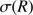 (Eq. (3)). The former parameterization adopts a cylindrical rotation and violent relaxation. Overall, this approach and the associated likelihood distributions follows closely the method described by Cordero et al. (2017, their Eqs. (2), (5)), that is
(Eq. (3)). The former parameterization adopts a cylindrical rotation and violent relaxation. Overall, this approach and the associated likelihood distributions follows closely the method described by Cordero et al. (2017, their Eqs. (2), (5)), that is (2)
(2)
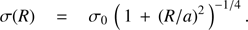 (3)
(3)
The adopted dispersion model follows the prediction for a Plummer sphere with one free parameter – the central velocity dispersion 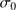 . We kept the half-mass radius a fixed at the half-light radius divided by a factor of 1.3.
. We kept the half-mass radius a fixed at the half-light radius divided by a factor of 1.3.
In contrast, the rotation parameterization has three free parameters: the position angle (PA) of the rotation axis, the amplitude of rotation (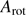 ), and the distance of the peak rotation from the center of the cluster,
), and the distance of the peak rotation from the center of the cluster, 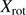 . As per Eq. (2), this rotation curve is given as a function of the distance along the major axis, also accounting for the unknown inclination i. As we found that the position of the peak rotation is not well constrained by the data, we used a normal distribution with a mean at the center of the cluster and a standard deviation of 2
. As per Eq. (2), this rotation curve is given as a function of the distance along the major axis, also accounting for the unknown inclination i. As we found that the position of the peak rotation is not well constrained by the data, we used a normal distribution with a mean at the center of the cluster and a standard deviation of 2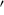 as a prior on this parameter. In practice, we sampled the joint posterior distribution of the four free parameters using the affine-invariant Markov Chain Monte Carlo algorithm (Goodman & Weare 2010; Foreman-Mackey et al. 2013). The resulting posteriori probability distributions are shown in Fig. 6, and in the following Section we summarize the resulting free parameters in terms of their median values and adopt the 15.9 and 84.1% percentiles as lower and upper error bounds. While the median values indicate a marginal level of rotation in either object, the full probability distributions suggest that an absence of rotation cannot be fully excluded.
as a prior on this parameter. In practice, we sampled the joint posterior distribution of the four free parameters using the affine-invariant Markov Chain Monte Carlo algorithm (Goodman & Weare 2010; Foreman-Mackey et al. 2013). The resulting posteriori probability distributions are shown in Fig. 6, and in the following Section we summarize the resulting free parameters in terms of their median values and adopt the 15.9 and 84.1% percentiles as lower and upper error bounds. While the median values indicate a marginal level of rotation in either object, the full probability distributions suggest that an absence of rotation cannot be fully excluded.
 |
Fig. 5. Top panels: Rotation curves and best-fit sinusoidal for both GCs. The bottom panels show the location of the target stars, colour-coded by radial velocity in units of their dispersion. Diamonds refer to M 75 targets on chip #1 on FORS2, circles indicate stars on chip #2, and MIKE targets are shown without extra delimiters. The gray shaded areas indicate the error margin of the rotation axis, which itself is shown as a dashed line. The major axis PAs of each cluster from Chen & Chen (2010) are plotted as thin red lines; finally, the direction of the Gaia DR2 proper motion is shown via a thick red line. |
 |
Fig. 6. Posterior probability distributions of our rotational analysis. Parameters are as defined in Eqs. (1) and (2). The top and |
5.1. M 75
Our tests for rotation suggest that the rotation axis of M 75 is inclined at a position angle of 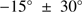 . Using 2MASS photometry and density distributions, Chen & Chen (2010) determined the morphological parameters for almost the entire GC population of the Galaxy. For M 75, their study implied a major axis position angle1 of
. Using 2MASS photometry and density distributions, Chen & Chen (2010) determined the morphological parameters for almost the entire GC population of the Galaxy. For M 75, their study implied a major axis position angle1 of 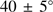 . Since morphological distortions would be manifest in a flattening that is aligned with the minor axis, we consider in the following rather the minor axis position angle, which for M 75 is thus
. Since morphological distortions would be manifest in a flattening that is aligned with the minor axis, we consider in the following rather the minor axis position angle, which for M 75 is thus 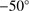 . In this regard, our kinematic rotation axis is offset to the minor axis of the cluster by 35
. In this regard, our kinematic rotation axis is offset to the minor axis of the cluster by 35 , but it should be kept in mind that the actual flattening of M 75 is very small, at an axis ratio of 0.92
, but it should be kept in mind that the actual flattening of M 75 is very small, at an axis ratio of 0.92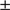 0.03 (Chen & Chen 2010), and that our kinematic analysis is aggravated by small-number statistics. However, as the distinction in Fig. 5 (bottom left) of stars on the two FORS2 chips indicates, the preferential rotation direction is not aligned with the instrument so that chip offsets are unlikely to be the cause of the rotation signal. This is bolstered by the independent confirmation of the additional MIKE data.
0.03 (Chen & Chen 2010), and that our kinematic analysis is aggravated by small-number statistics. However, as the distinction in Fig. 5 (bottom left) of stars on the two FORS2 chips indicates, the preferential rotation direction is not aligned with the instrument so that chip offsets are unlikely to be the cause of the rotation signal. This is bolstered by the independent confirmation of the additional MIKE data.
The amplitude of the sinusoidal in Fig. 4, which is statistically on the order of twice the overall average rotation signal (Bellazzini et al. 2012), is 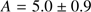 km s
km s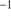 , while the more detailed Bayesian fit of Eq. (2) to the non-binned profile yielded a half-amplitude of
, while the more detailed Bayesian fit of Eq. (2) to the non-binned profile yielded a half-amplitude of 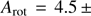 2.1 km s
2.1 km s around an axis that is offset from the center by some 1.6
around an axis that is offset from the center by some 1.6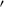 (Fig. 7; Table 3). At the half-light radius of 0.5
(Fig. 7; Table 3). At the half-light radius of 0.5 of the GC (Harris 2010), this would correspond to three such radii and would be remarkably large. Considering the poor sampling of our data in the central regions of M 75, we do not interpret this value any further.
of the GC (Harris 2010), this would correspond to three such radii and would be remarkably large. Considering the poor sampling of our data in the central regions of M 75, we do not interpret this value any further.
 |
Fig. 7. Rotation curve and best-fit curve following Eq. (2). The gray-shaded area indicates the margins imposed by the radial velocity dispersion profile (Eq. (3)). Different symbols for M 75 reflect targets on different FORS2 chips (filled) and those observed with MIKE (open). |
5.2. NGC 6426
The best-fit position angle for this GC is 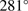 . This compares to a minor axis position angle from the morphological analysis of Chen & Chen (2010) of
. This compares to a minor axis position angle from the morphological analysis of Chen & Chen (2010) of 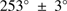 , which is marginally consistent with our measurement. On the other hand, our derived amplitudes of
, which is marginally consistent with our measurement. On the other hand, our derived amplitudes of 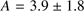 and
and 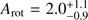 km s
km s , the latter with a nominal peak at
, the latter with a nominal peak at 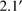
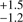 (thus well outside the cluster core, at
(thus well outside the cluster core, at 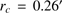 ), are clearly a limited representation of the kinematics of NGC 6426.
), are clearly a limited representation of the kinematics of NGC 6426.
6. Orbits
In order to obtain the full kinematic information on our clusters, we derived their proper motions using the recent second data release, DR2, of Gaia (Gaia Collaboration 2018). To identify the bona fide cluster signature in proper motion space, we selected stars within 1.5 times 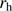 , vetting those with significant parallaxes as nearby foreground stars, and we demanded that the errors in either direction are
, vetting those with significant parallaxes as nearby foreground stars, and we demanded that the errors in either direction are 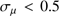 mas yr
mas yr . This way, we used 161 and 103 objects toward M 75 and NGC 6426, respectively. The resulting median values (with 15.9 and 84.1% percentile uncertainties) we find are (
. This way, we used 161 and 103 objects toward M 75 and NGC 6426, respectively. The resulting median values (with 15.9 and 84.1% percentile uncertainties) we find are (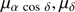 ) = (
) = ( mas yr
mas yr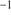 for M 75 and (
for M 75 and (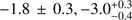 ) mas yr
) mas yr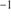 for NGC 6426. These values are in excellent agreement with the recent HST study of Sohn et al. (2018) for NGC 6426 and with the values for M 75 of Chemel et al. (2018), which are in turn based on a variety of surveys including Gaia DR1. It is interesting to note that, for M 75, the direction of motion is consistent with the rotation axis, while for NGC 6426 is it almost perpendicular. Our derived proper motions were then fed into the Galactic potential of Dehnen & Binney (1998), which contains contributions from the halo and disk, and spherical bulge. The orbital integrations were carried out backward for 12 Gyr and the resulting projections are shown in Fig. 8.
for NGC 6426. These values are in excellent agreement with the recent HST study of Sohn et al. (2018) for NGC 6426 and with the values for M 75 of Chemel et al. (2018), which are in turn based on a variety of surveys including Gaia DR1. It is interesting to note that, for M 75, the direction of motion is consistent with the rotation axis, while for NGC 6426 is it almost perpendicular. Our derived proper motions were then fed into the Galactic potential of Dehnen & Binney (1998), which contains contributions from the halo and disk, and spherical bulge. The orbital integrations were carried out backward for 12 Gyr and the resulting projections are shown in Fig. 8.
Both GCs show typical motions with apocenters of 17.5 kpc (M 75) and 19.4 kpc (NGC 6426) that lie close to their current Galactocentric distances. At 0.4 Gyr each, their orbital periods are fairly short. The eccentricities of these outer halo objects are high, at 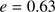 for NGC 6426, and even more notably for M 75, which shows an eccentric orbit with e = 0.87. The latter could indicate that M 75 has once been accreted, as also bolstered by its younger age compared to other GCs at similar metallicities (Catelan et al. 2002). However, while this object lies close in projection to the disrupted Sagittarius Stream, no tidal debris around M 75 has been observed (Carballo-Bello et al. 2014), and Majewski et al. (2004) argue that this GC is unlikely to be associated with Sagittarius based on its high approaching radial velocity. As for NGC 6426, Forbes & Bridges (2010) noted that this GC lies close to the purported orbit of the Canis Major overdensity, but given our present result, we cannot unambiguously constrain an in situ or ex situ origin of this metal-poor object. Globally speaking, the full, three-dimensional kinematics of stellar systems in the outer halo has further important implications for constraining the mass of the Milky Way (Watkins et al. 2018; Helmi et al. 2018).
for NGC 6426, and even more notably for M 75, which shows an eccentric orbit with e = 0.87. The latter could indicate that M 75 has once been accreted, as also bolstered by its younger age compared to other GCs at similar metallicities (Catelan et al. 2002). However, while this object lies close in projection to the disrupted Sagittarius Stream, no tidal debris around M 75 has been observed (Carballo-Bello et al. 2014), and Majewski et al. (2004) argue that this GC is unlikely to be associated with Sagittarius based on its high approaching radial velocity. As for NGC 6426, Forbes & Bridges (2010) noted that this GC lies close to the purported orbit of the Canis Major overdensity, but given our present result, we cannot unambiguously constrain an in situ or ex situ origin of this metal-poor object. Globally speaking, the full, three-dimensional kinematics of stellar systems in the outer halo has further important implications for constraining the mass of the Milky Way (Watkins et al. 2018; Helmi et al. 2018).
 |
Fig. 8. Orbit projections as a result of a backward computation. Only a timeframe of 6 Gyr is depicted. The present location of the GCs is shown as a red point. The cross and line denote the Galactic center and plane. |
7. Discussion
The ratio of a system’s rotation amplitude and central velocity dispersion, 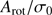 , versus its ellipticity (Fig. 9) is a representative measure for the importance of its dynamic-morphological interaction (e.g., Davies et al. 1983). While we were able to compute a meaningful global velocity dispersion for our two target GCs, the overall small number of sample stars aggravated a precise derivation of a dispersion profile, and the measurement of the central velocity dispersion
, versus its ellipticity (Fig. 9) is a representative measure for the importance of its dynamic-morphological interaction (e.g., Davies et al. 1983). While we were able to compute a meaningful global velocity dispersion for our two target GCs, the overall small number of sample stars aggravated a precise derivation of a dispersion profile, and the measurement of the central velocity dispersion  in our probabilistic fitting should be taken with caution. However, a radial dispersion gradient as seen in most GCs, for example, when following the common Plummer profile (Mackey et al. 2013; Cordero et al. 2017), can be assumed. Moreover, many GCs are well described by a truncated King (1966) profile, which is essentially flat within a few core radii. Thus we can state the measured, global velocity dispersion as a lower limit of
in our probabilistic fitting should be taken with caution. However, a radial dispersion gradient as seen in most GCs, for example, when following the common Plummer profile (Mackey et al. 2013; Cordero et al. 2017), can be assumed. Moreover, many GCs are well described by a truncated King (1966) profile, which is essentially flat within a few core radii. Thus we can state the measured, global velocity dispersion as a lower limit of 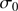 , as is indeed realized in our rotational analysis.
, as is indeed realized in our rotational analysis.
Despite the overall large error bars the outer halo GC M 75 can be firmly considered as a slow rotator. It is worth noting that M 75 is very similar to NGC 4372 in terms of its 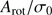 ratio and its ellipticity, although the latter is less massive and more metal poor (Kacharov et al. 2014; San Roman et al. 2015). In the parameter space of rotation versus metallicity, M 75 falls fully in line with the majority of other Milky Way GCs, which is also consistent with its peculiar HB morphology. In turn, the very metal-poor NGC 6426 has a nominal, very large
ratio and its ellipticity, although the latter is less massive and more metal poor (Kacharov et al. 2014; San Roman et al. 2015). In the parameter space of rotation versus metallicity, M 75 falls fully in line with the majority of other Milky Way GCs, which is also consistent with its peculiar HB morphology. In turn, the very metal-poor NGC 6426 has a nominal, very large 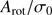 ratio of
ratio of 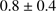 , although its large uncertainty renders it equally compatible with other GCs with slower rotation properties at comparable ellipticity. This cluster appears as an outlier, showing a more ordered dynamics given its low metallicity, which is, however, also seen in other metal-poor GCs below
, although its large uncertainty renders it equally compatible with other GCs with slower rotation properties at comparable ellipticity. This cluster appears as an outlier, showing a more ordered dynamics given its low metallicity, which is, however, also seen in other metal-poor GCs below  2 dex. It is interesting to note that the minor axis of its, relatively large flattening is consistent with the rotation axis found in the present study to within the uncertainties.
2 dex. It is interesting to note that the minor axis of its, relatively large flattening is consistent with the rotation axis found in the present study to within the uncertainties.
At their large distances in the halo, external tides from the Galactic disks are unlikely to play a significant dynamic role in shaping the outer halo clusters, and the observed, slow rotation favors internal dynamic processes as a cause for the mild observed flattening over tidal effects. In this context, N-body simulations (e.g., Tiongco et al. 2017) show that, as GCs dynamically evolve in a tidal field, they become progressively dominated by random motions while losing angular momentum. Nonetheless, even after many relaxation times and accounting for mass loss from the GCs, they can still be characterized by non-negligible  ratios.
ratios.
Moreover, Kacharov et al. (2014) conjecture that most of the slow rotators are located on the younger, presumably accreted branch in the age-metallicity space (Marín-Franch et al. 2009). Coupled with other evidence such as its very eccentric orbit, its younger age compared to other GCs at the same metallicity, a large enrichment in the r-process elements (Kacharov et al. 2013), and the slow rotation pattern, it is likely that the more metal rich of our targets, M 75, is a prime example of an accreted outer halo object, although the host to its accretion has still to be determined.
 |
Fig. 9. Ratio of rotation amplitude and central velocity dispersion, according to Kacharov et al. (2014) with additional measurements from Bellazzini et al. (2012). The solid line refers to an isotropic rotating sphere as described by Binney (2005). |
We note that Chen & Chen (2010) reported their parameters in Galactic coordinates, leading to an original angle with respect to the north Galactic pole of 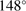 .
.
Acknowledgments
The authors are grateful to Eline Tolstoy for helpful comments on the FORS2 data set. The anonymous referee is thanked for a constructive and helpful report. This work was supported by Sonderforschungsbereich SFB 881 “The Milky Way System” (subproject A08) of the German Research Foundation (DFG).
References
- Armandroff, T. E., & Zinn, R. 1988, AJ, 96, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N.& Lardo, C. 2018, ARA&A, in press [arXiv:1712.01286] [Google Scholar]
- Bastian, N., Lamers, H. J. G. L. M., de Mink, S. E., et al. 2013, MNRAS, 436, 2398 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bastian, N., Cabrera-Ziri, I., & Salaris, M. 2015, MNRAS, 449, 3333 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H. 2017, MNRAS, 464, 2174 [NASA ADS] [CrossRef] [Google Scholar]
- Bellazzini, M., Bragaglia, A., Carretta, E., et al. 2012, A&A, 538, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchini, P., Varri, A. L., Bertin, G., & Zocchi, A. 2013, ApJ, 772, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J. 2005, MNRAS, 363, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Çalışkan, Ş., Christlieb, N., & Grebel, E. K. 2012, A&A, 537, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carballo-Bello, J. A., Sollima, A., Martínez-Delgado, D., et al. 2014, MNRAS, 445, 2971 [NASA ADS] [CrossRef] [Google Scholar]
- Carollo, D., Beers, T. C., Lee, Y. S., et al. 2007, Nature, 450, 1020 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., D’Orazi, V., & Lucatello, S., 2009a, A&A, 508, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., & Lucatello, S. 2009b, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., D’Orazi, V., Lucatello, S., & Gratton, R. G., 2010a, A&A, 519, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., & Gratton, R. G., et al. 2010b, A&A, 516, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Catelan, M., Borissova, J., & Ferraro, F. R., et al. 2002, AJ, 124, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Chemel, A. A., Glushkova, E. V., Dambis, A. K., et al. 2018, Astrophys. Bull., 73, 162 [Google Scholar]
- Chen, C. W., & Chen, W. P. 2010, ApJ, 721, 1790 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, A. A., Smecker-Hane, T. A., Tolstoy, E., Bosler, T. L., & Gallagher, J. S. 2004, MNRAS, 347, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Cordero, M. J., Hénault-Brunet, V., Pilachowski, C. A., et al. 2017, MNRAS, 465, 3515 [NASA ADS] [CrossRef] [Google Scholar]
- Corwin, T. M., Catelan, M., Smith, H. A., et al. 2003, AJ, 125, 2543 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F. & van Dyk, S., et al. 2003. 2MASS All Sky Catalog of point sources [Google Scholar]
- Davies, R. L., Efstathiou, G., Fall, S. M., Illingworth, G., & Schechter, P. L. 1983, ApJ, 266, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., & Ekström, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dehnen, W., & Binney, J. 1998, MNRAS, 294, 429 [NASA ADS] [CrossRef] [Google Scholar]
- D’Ercole, A., Vesperini, E., D’Antona, F., McMillan, S. L. W., & Recchi, S. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Dias, B., Barbuy, B., Saviane, I., et al. 2015, A&A, 573, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dotter, A., Sarajedini, A., & Anderson, J. 2011, ApJ, 738, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, F. R., Mucciarelli, A., Lanzoni, B., et al. 2018, ApJ, 860, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, D. A., & Bridges, T. 2010, MNRAS, 404, 1203 [NASA ADS] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Fraternali, F., Tolstoy, E., Irwin, M. J., & Cole, A. A. 2009, A&A, 499, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garnavich, P. M., Vandenberg, D. A., Zurek, D. R. & Hesser, J. E. 1994, AJ, 107, 1097 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. App. Math. Comput. Sci., 5, 65 [Google Scholar]
- Gratton, R. G., Carretta, E., & Bragaglia, A. 2012, A&ARv, 20, 50 [CrossRef] [Google Scholar]
- Hanke, M., Koch, A., Hansen, C. J., & McWilliam, A. 2017, A&A, 599, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, W. E. 2010, ArXiv, e-prints [arXiv:1012.3224]. [Google Scholar]
- Hartwick, F. D. A. 1987, in NATO Advanced Science Institutes (ASI) Series C, eds. G. Gilmore, & B. Carswell, NATO Advanced Science Institutes (ASI) Series C, 207 281 [Google Scholar]
- Helmi, A., van Leeuwen, F., McMillan, P. et al. 2018, A&A, 616, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kacharov, N., Koch, A., & McWilliam, A. 2013, A&A, 554, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kacharov, N., Bianchini, P., Koch, A., et al. 2014, A&A, 567, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamann, S., Husser, T.-O., Dreizler, S., et al. 2018, MNRAS, 473, 5591 [NASA ADS] [CrossRef] [Google Scholar]
- Kayser, A., Hilker, M., Grebel, E. K., & Willemsen, P. G. 2008, A&A, 486, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- King, I. R. 1966, AJ, 71, 64 [Google Scholar]
- Kleyna, J. T., Wilkinson, M. I., Evans, N. W., & Gilmore, G. 2004, MNRAS, 354, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A. & Côté, P. 2010, A&A, 517, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koch, A., Wilkinson, M. I., Kleyna, J. T., et al. 2007, ApJ, 657, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., Côté, P., & McWilliam, A. 2009, A&A, 506, 729 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koch, A., Hansen, C. J., & Kunder, A. 2017a, A&A, 604, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koch, A., Kunder, A., & Wojno, J., 2017b, A&A, 605, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koch, A., Hansen, T. T., & Kunder, A. 2018, A&A, 609, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraft, R. P. & Ivans, I. I. 2003, PASP, 115, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, V., Alcaíno, G., Marconi, G., & Alvarado, F. 2007, A&A, 469, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lardo, C., Pancino, E., Bellazzini, M., et al. 2015, A&A, 573, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mackey, A. D., & Gilmore, G. F. 2004, MNRAS, 355, 504 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mackey, A. D., Da Costa, G. S., Ferguson, A. M. N., & Yong, D. 2013, ApJ, 762, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Majewski, S. R., Kunkel, W. E., Law, D. R., et al. 2004, AJ, 128, 245 [Google Scholar]
- Marín-Franch, A., Aparicio, A., Piotto, G., et al. 2009, ApJ, 694, 1498 [NASA ADS] [CrossRef] [Google Scholar]
- Martocchia, S., Cabrera-Ziri, I., Lardo, C., et al. 2018, MNRAS, 473, 2688 [Google Scholar]
- Milone, A. P., Piotto, G., Renzini, A., et al. 2017, MNRAS, 464, 3636 [NASA ADS] [CrossRef] [Google Scholar]
- Osborn, W. 1971, Observatory, 91, 223 [Google Scholar]
- Pasquini, L., Avila, G., Blecha, A., et al. 2002, Messenger, 110, 1 [Google Scholar]
- Pillepich, A., Madau, P., & Mayer, L. 2015, ApJ, 799, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Pryor, C., & Meylan, G. 1993, in Structure and Dynamics of Globular Clusters, ed. S. G. Djorgovski, Astronomical Society of the Pacific Conference Series, 50, 357 [NASA ADS] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rutledge, G. A., Hesser, J. E., & Stetson, P. B. 1997a, PASP, 109, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Rutledge, G. A., Hesser, J. E., Stetson, P. B., et al. 1997b, PASP, 109, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., & Weiss, A. 2002, A&A, 388, 492 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- San Roman, I., Muñoz, C., Geisler, D., et al. 2015, A&A, 579, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Searle, L., & Zinn, R. 1978, ApJ, 225, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Sohn, S. T., Watkins, L. L., & Fardal, M. A. 2018, ApJ, 862, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Tiongco, M. A., Vesperini, E., & Varri, A. L. 2017, MNRAS, 469, 683 [NASA ADS] [Google Scholar]
- Tiongco, M. A., Vesperini, E., & Varri, A. L. 2018, MNRAS, 475, L86 [NASA ADS] [CrossRef] [Google Scholar]
- Vesperini, E., McMillan, S. L. W., D’Antona, F., & D’Ercole, A. 2013, MNRAS, 429, 1913 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, S. S., Mateo, M., Olszewski, E. W., & Keane, M. J., 1995, AJ, 109, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., Mateo, M., & Olszewski, E. W. 2006, AJ, 131, 2114 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., Mateo, M., Olszewski, E. W., Sen, B., & Woodroofe, M. 2009, AJ, 137, 3109 [NASA ADS] [CrossRef] [Google Scholar]
- Watkins, L. L., van der Marel, R. P., Sohn, S. T., & Evans, N. W. 2018. AAS J., submitted [arXiv:1804.11348] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Left panel: CMD of M75 from Kravtsov et al. (2007) with spectroscopic targets shown as red star symbols (FORS members), and green circles (MIKE targets). Right panel: CMD of NGC 6426 from the HST photometry of Dotter et al. (2011), indicating member candidates (red stars). Green circles show the four stars studied in high resolution by Hanke et al. (2017). |
| In the text | |
 |
Fig. 2. Heliocentric radial velocity against radial distance (bottom panel) and CaT-based metallicity (middle panel) from the FORS data are shown in black. The histogram in the top panel indicates the peak of M 75 at |
| In the text | |
 |
Fig. 3. Heliocentric radial velocity against radial distance (bottom panel) for the entire NGC 6426 observations. The histogram in the top panel indicates the peak of the GC at |
| In the text | |
 |
Fig. 4. Global velocity dispersion vs. absolute magnitude, using data from Pryor et al. (1993) and Harris (2010), and with the latest measurements of low-mass GCs from Koch et al. (2017a, b, 2018). Targets of this study are indicated by red stars. |
| In the text | |
 |
Fig. 5. Top panels: Rotation curves and best-fit sinusoidal for both GCs. The bottom panels show the location of the target stars, colour-coded by radial velocity in units of their dispersion. Diamonds refer to M 75 targets on chip #1 on FORS2, circles indicate stars on chip #2, and MIKE targets are shown without extra delimiters. The gray shaded areas indicate the error margin of the rotation axis, which itself is shown as a dashed line. The major axis PAs of each cluster from Chen & Chen (2010) are plotted as thin red lines; finally, the direction of the Gaia DR2 proper motion is shown via a thick red line. |
| In the text | |
 |
Fig. 6. Posterior probability distributions of our rotational analysis. Parameters are as defined in Eqs. (1) and (2). The top and |
| In the text | |
 |
Fig. 7. Rotation curve and best-fit curve following Eq. (2). The gray-shaded area indicates the margins imposed by the radial velocity dispersion profile (Eq. (3)). Different symbols for M 75 reflect targets on different FORS2 chips (filled) and those observed with MIKE (open). |
| In the text | |
 |
Fig. 8. Orbit projections as a result of a backward computation. Only a timeframe of 6 Gyr is depicted. The present location of the GCs is shown as a red point. The cross and line denote the Galactic center and plane. |
| In the text | |
 |
Fig. 9. Ratio of rotation amplitude and central velocity dispersion, according to Kacharov et al. (2014) with additional measurements from Bellazzini et al. (2012). The solid line refers to an isotropic rotating sphere as described by Binney (2005). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.