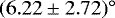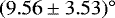| Issue |
A&A
Volume 616, August 2018
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 6 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201732451 | |
| Published online | 13 August 2018 | |
Study of the orientation of narrow-line Seyfert I
1
Dipartimento di Fisica G. Occhialini,
Università degli Studi di Milano Bicocca,
Piazza della Scienza 3,
20126
Milano,
Italy
e-mail: tullia.sbarrato@unimib.it
2
INFN, Sezione Milano-Bicocca,
Piazza della Scienza 3,
20126
Milano,
Italy
3
INAF – Osservatorio Astronomico di Brera,
Merate,
via E. Bianchi 46,
23807 Merate,
Italy
Received:
12
December
2017
Accepted:
7
May
2018
We study a sample of narrow-line Seyfert 1 galaxies (NLS1) in their optical and radio features to understand the differences between their radio silent, radio-loud, and radio-quiet subclasses. We first show that the different redshift and mass distributions of radio-loud and radio-quiet NLS1s could be ascribed to observational biases. We then present a geometrical model according to which most of the different observational features of radio-loud and radio-quiet NLS1s are ascribed to the orientation of an intrinsically structured jet. We estimate the fraction of intrinsically jetted sources among NLS1s that justifies the observed radio-detected population. Noticeably, under the assumptions of the geometrical model, we derive a fraction of jetted sources significantly larger than in standard AGN.
Key words: galaxies: active / galaxies: Seyfert / galaxies: jets / black hole physics
© ESO 2018
1 Introduction
Narrow-line Seyfert 1 galaxies (NLS1s) are a subclass of type I active galactic nuclei (AGN) characterized by the presence of broad emission lines (BELs) with a full width at half maximum (FWHM) ≲ 2000 km s−1 (Goodrich 1989), weak [OIII] lines (compared to the Hβ), and strong FeII emission (e.g. Osterbrock & Pogge 1985; Véron-Cetty et al. 2001). NLS1s often show a X-ray continuum that is steeper and more variable than the average AGN (e.g. Green et al. 1993; Boller et al. 1996; Hayashida 2000).
The narrow FWHM of the optical BELs has originally been ascribed to small BH masses, in some cases found smaller than predicted from MBH-host galaxy relations (Grupe & Mathur 2004). In this low MBH scenario, NLS1s would be characterized by close to Eddington accretion with a normalized accretion rate fEdd = L∕LEdd that is larger, on average, than Seyfert I with broader BELs (BLS1s) by an order of magnitude (e.g. Grupe & Mathur 2004).
Relatively narrow BELs can also be interpreted as the result of a projection effect if the broad line region (BLR) has a disc geometry. Such a configuration is only stable if the gas emitting the broad lines moves mostly in the disc plane and, as a consequence, lines emitted by the BLR discs that by chance are observed close to face-on would suffer a smaller Doppler broadening. Such dependence of the BELs FWHM on the BLR orientation has been commonly advocated to model the properties of blazars (Decarli et al. 2011), radio-loud (RL) AGN (e.g. Wills & Browne 1986; Fine et al. 2011; Runnoe et al. 2013), and for quasars in general (Labita et al. 2006; Decarli et al. 2008b; Shen & Ho 2014). The BLR geometry can be directly tested with high quality reverberation mapping data because the time and frequencies at which a single broad line responds to variations of the AGN continuum depend on the spatial distribution and velocity field of the emitting gas (Blandford & McKee 1982). Pancoast et al. (2014b) and Grier et al. (2017) succeeded only recently in constraining the disc geometry of a few BLRs taking advantage of high quality reverberation data coupled with the parametric dynamical model proposed by Pancoast et al. (2014a). The latter modelled the individual BLRs as a collection of clouds whose positions and velocities are extracted by parametric distributions. In particular, the spatial distribution of the clouds would depend on the geometrical thickness of the BLR θ0, ranging from 0° for a thin disc to 90° for a spherical distribution. A nested sampling search through the parameter space resulted in 8 BLR (out of 9 AGN studied by the two teams) described by discs with thickness θ0 < 40° and inclination with respect to the line of sight θi < 40°.
Decarli et al. (2008a) proposed a “geometrical scenario” for NLS1s assuming that these are standard Seyfert Is hosting BLRs with disc geometries observed close to face-on (see also Bian & Zhao 2004). The angle within which AGN are seen as NLS1 has hence been estimated from their relative abundance. The resulting correction factor to MBH obtained from the de-projection shifts the distributions of NLS1 masses and fEdd on the top of those obtained from BLS1s, in agreement with independent estimates of the NLS1 MBH (Calderone et al. 2013). Such a scenario could in principle be tested by reverberation mapping studies. Unfortunately, only three objects in Pancoast et al. (2014b) and Grier et al. (2017) are NLS1s, one of which (Mrk 1310) have been modelled as a disc with θi ≈ 8°, in agreement with the geometrical scenario, while the other two (Mrk 335 and PG 2130 + 099) are best modelled by higher inclinations (θi ~30° in both cases).
The recent developments in the study of RL-NLS1s and the detection of γ emission from NLS1s by the Fermi satellite (e.g. Abdo et al. 2009; Foschini 2011, 2012; D’Ammando et al. 2012, 2015) has re-ignited the interest in the field. The γ emission is caused by a relativistic jet quasi-aligned with the line of sight. Indeed RL-NLS1s have been interpreted as an early evolutionaryphase that would eventually lead to fully developed blazars (Foschini et al. 2015; Foschini 2017). It is interesting to note that the radio-to-optical spectral energy distribution (SED) and variability of a large percentage of RL-NLS1s seem to indicate that the low frequency emission is dominated by a relativistic jet pointing towards us (Lähteenmäki et al. 2017).
In the few NLS1s in which the jet orientation was derived, the observed degree of jet alignment supports the geometrical scenario1. Under the geometric assumption, RL-, radio-quiet (RQ), and radio-silent NLS1 should differ in the presence of a jet and its detectability. This assumption has been debated as the mass and redshift distributions of RL-NLS1s and RQ-NLS1s seem to differ (Järvelä et al. 2015). A tentative comparison between RL- and RQ-NLS1 populations was also performed by Berton et al. (2015) in their attempt to identify a parent population of the flat spectrum radio-loud NLS1s among steep spectrum RL-NLS1s, RQ-NLS1s, and disc-hosted radio galaxies. Unfortunately, the flat spectrum RL- and RQ-NLS1 samples are still too poorly populated to draw strong conclusions.
In this study we first highlight some observational biases that could account for such apparent discrepancies (Sect. 2), then we provide a physical interpretation of the observed γ-NLS1s and RL-NLS1s in the context of a simple model built on the assumptions of the geometrical scenario (Sect. 3). Possible implications of this geometrical scenario are discussed in Sect. 4.
2 Do RL-NLSy1 and RQ-NLSy1 belong to two distinct populations?
Järvelä et al. (2015) studied the sources in Zhou et al. (2006) sample of NLS1 galaxies from the Sloan Digital Sky Survey (SDSS) by classifying these sources on the basis of their radio emissions and studying the distribution of the subpopulations. Starting from a sample of 2011 sources in Zhou et al. (2006), Järvelä et al. (2015) classified the sources in radio-undetected NLS1s, RQ-NLS1s detected by the FIRST survey (97 sources with a radio-loudness parameter defined as the ratio of 1.4 GHz radio flux density over 400 nm optical flux density R < 10), and RL-NLS1s (195 sources with R > 10). Järvelä et al. (2015) found different redshift distributions for RQ-NLS1s and RL-NLS1s (mean z = 0.22 and z = 0.41, respectively), concluding that the two classes belong to intrinsically different populations. Most of radio-detected sources are close to the FIRST flux limit (i.e. 1mJy), possibly introducing some observational bias. While RL radio emission is dominated by the jet, detected RQ sources are often dominated by star formation in the same bands (Caccianiga et al. 2015; Järvelä et al. 2015; Padovani 2016), often not showing jet features at all. Being intrinsically fainter in radio, RQ-NLS1s are therefore biased towards lower z, while RL sources can be detected up to higher z. This can be inferred from Fig. 1, where we show the optical and radio luminosities (L5100, L1.4 GHz) versus the redshifts of Järvelä et al. (2015) NLS1 samples. RL-NLS1 sources are more uniformly distributed in both planes, as the non radio-detected sources. RQ-NLS1, instead, are mainly located at low z. We stress that less luminous but intrinsically RL-NLS1s could be classified as radio silent, if their radio fluxes are below the FIRST detection limit, affecting the population studies of jetted NLS1. Some of these, in fact, could be classified as radio-silent sources, preventing us from distinguishing between intrinsically jetted and non-jetted sources.
In addition to the properties directly measured from the observations, Järvelä et al. (2015) provided virial estimates of the MBH for each object following Greene & Ho (2005):
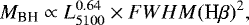 (1)
(1)
where the FWHM is that of the broad Hβ line2 and L5100 is the monochromatic luminosity at 5100 Å. Järvelä et al. (2015) concluded that the RQ- and RL-NLS1 populations have different MBH distributions (with mean log(MBH∕M⊙) = 6.96 and 7.18, respectively). The bias towards higher redshifts for RL-NLS1s can be (at least partially) responsible for the different MBH distributions. A second possible bias affecting the RL-NLS1s MBH is related to the non-thermal jet emission itself. As explored by Lähteenmäki et al. (2017), when observed at multiple radio frequencies (1.4, 37 GHz), RL-NLS1 often show beaming and variability features typical of blazars, i.e. sources with jets directed towards our line of sight. In that case, the jet emission often contributes to optical emission (Giommi et al. 2012; Ghisellini et al. 2017), resulting in an overestimate of the 5100 Å continuum luminosity henceforth of MBH. A significant contribution from the jet to the optical luminosity of RL-NLS1s has already been discussed in the literature. Calderone et al. (2012) studied the example of B2 0954 + 25A, a blazar that on different observations taken at different epochs shows an optical emission either dominated by the jet or by the accretion disc3. Jets have been demonstrated to play an important role in the optical variability of RL-NLS1s in the Catalina Real Time Transient Survey (Rakshit & Stalin 2017). We note that a substantial jet contamination in the optical luminosity could affect the observed NLS1 spectra. The equivalent widths of BELs in jet-dominated sources should be smaller than their non-jetted counterparts. This could serve as a possible diagnostic to understand whether RL-NLS1s are truly contaminated by jet emission in their optical luminosity.
To test whether a jet-like power law could contribute to the optical continuum in Järvela et al. RL-NLS1s, we studied their optical-UV slopes. At such frequencies, the jet emission is characterized by a negative power law in ν − νLν (see e.g. Ghisellini et al. 2017), which differs from the big blue bump typical of the disc emission. Hence, we studied the RL-NLS1 SEDs in the SDSS band. We noted that 152 out of 195 RL-NLS1s show a negative slope among the SDSS bands and have a profile similar to the blue data in Fig. 2. Of these, 23 out of 195 sources have a monotonically decreasing νLν or show a single fluctuation from the monotonic profile, such as the red and green examples in Fig. 2. We are aware that this characterization does not guarantee a good sampling of jet-dominated sources, and a broader band SED analysis would be needed to strongly confirm it. Nonetheless, this points towards a partial continuum contamination by the jet in a large number of RL-NLS1s, implying an overestimate of L5100, and therefore of MBH compared to RQ-NLS1s. Another possible cause for such a negative slope could be intrinsic dust absorption. Figure 2 includes three dashed lines, each representing a hypothetical accretion disc, modelled as a Shakura & Sunyaev (1973) multi-colour black body, which has virial masses derived by Järvelä et al. (2015) and accretion rates set by fitting the lowest frequency point to the continuum disc emission of each object with decreasing slopes. If reddening by absorption had an important role for these sources, these disc profiles would be the lowest accretion rate solutions possible. By forcing this fit, we obtain Eddington ratios of Ld∕LEdd ≃ 100, 10, and 420 for green, red, and blue data, respectively. A standard accretion disc with a fair amount of ionizing radiation is not stable at such high Eddington ratios. Dust absorption has most likely a minor role in shaping the UV-optical SEDs of these sources.
A definite interpretation of the relative jet and disc contributions in the optical, along with a demonstration that the two distributions may be extracted from the same population, would require a detailed SED modelling including the contributionof all the components of an AGN. We are currently working on implementing the required modifications in QSFIT4, a free software package to automatically perform the analysis of AGN spectra (Calderone et al. 2017). We postpone this analysis to a future investigation, while in this work we simply assume that orientation is the main parameter determining the classification of AGN as Seyfert I and NLS1s, and, for radio-detected sources, between RQ-NLS1s, RL-NLS1s, and γ-NLS1s. The consequences of such a model assumption are highlighted in the next section.
 |
Fig. 1 Distribution of 5100 Å (top panel) and radio (bottom panel) luminosities vs. redshift for the NLS1 subclasses. RQ-NLS1 (blue dots) are mainly located at low z. The few sources at higher z are among the most luminous: the radio flux sensitivity only allows us to observe the peak of the iceberg. RL-NLS1 (red dots), instead, are more evenly distributed in luminosities and z; thanks to their larger radio flux, they are less affected by this observational bias compared with RQ sources. They are missing in radio surveys from higher redshift than their RQ counterparts. |
 |
Fig. 2 Optical SEDs for three RL-NLS1s and a RQ-NLS1. Green, red, and blue data show decreasing profiles of SDSS J 224605.44 − 091925.1 (z = 0.119), SDSS J162458.42 + 423107.5 (z = 0.663), and SDSS J171930.56 + 293412.8 (z = 0.180), typical of jet-dominated optical emissions. The analogous dashed lines show Shakura & Sunyaev (1973) disc profiles for the three sources, drawn with the virial masses by Järvelä et al. (2015) and normalized by forcing them to pass through the lowest frequency data point. Violet data, instead, show the disc-dominated profile of the RQ-NLS1 SDSS J144012.76 + 615633.2 (z = 0.276). The RL-NLS1s have an SED that is clearly not disc-like. |
3 Geometrical unification model for NLS1s
In the geometrical, scenario, the critical angle that discriminates between NLS1s and BLS1s (θNLS1) can be obtained from the number ratio of the members of the two populations. Following this approach, Decarli et al. (2008a) found 13° ≲ θNLS1 ≲ 19°. We extend their model to the subsample of RL-NLS1s and γ-NLS1s under the assumptionsthat (i) only a fraction fjet of NLS1s possess a jet, and (ii) that only objects that are seen close to face-on would be observed in γ or selected as RL (within a maximum inclination of θγ−NLS1 and θRL-NLS1, respectively)5. The second assumption is motivated by the spine-layer (SL) jet model, in which the central and fastest part of the jet, responsible for the γ emission, is embedded in a slower layer contributing to the radio flux (Ghisellini et al. 2005). As reference values θRL-NLS1 ≈ 7° and θγ−NLS1 ≈ 4°, which is reasonable in the SL framework that we are following.
By simply comparing the solid angles involved, we can correlate the two critical angles with the ratio of the number of RL-NLS1s (NRL-NLS1) to that of all the NLS1 (NNLS1) as follows:
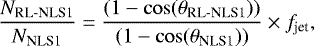 (2)
(2)
where fjet corrects for the intrinsic fraction of jetted sources. Under the assumption of a negligible radio flux limit effect, we can estimate fjet as the fraction of RL-NLS1 NRL-NLS1∕NNLS1 = 195∕2011 observed by Järvelä et al. (2015), we obtain 0.3 ≲ fjet ≲ 0.7, where the scatter depends on the assumed value of θNLS1. Interestingly, the fraction of intrinsically jetted NLS1s is much higher than what typically assumed for AGN. This is not unexpected, though, as the high degree of alignment of the jet with the line of sight allows for the observation of intrinsically faint radio sources.
As a consistency check that accounts for the radio flux limit effect, we performed a Monte Carlo simulation to reproduce the radio-detected NLS1 sample by Järvelä et al. (2015). We start from the NLS1 sample by Zhou et al. (2006) and randomly select a source with its z and observed optical luminosity. To this source, we assign (i) a random jet bulk velocity Γ and (ii) an intrinsic comoving radio luminosity 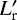 , both extracted from Gaussian distributions. Furthermore, we assigned a jet orientation θv (with respect to the observer line of sight) drawn from a solid angle weighted distribution within a maximum angle of 20°. With these parameters, we computed the source radio observed flux, i.e.
, both extracted from Gaussian distributions. Furthermore, we assigned a jet orientation θv (with respect to the observer line of sight) drawn from a solid angle weighted distribution within a maximum angle of 20°. With these parameters, we computed the source radio observed flux, i.e.
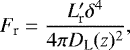 (3)
(3)
where δ = 1∕Γ(1 − βcosθv) is the jet beaming factor and DL(z) is the luminosity distance. For each source, we thus compute the radio-loudness R = Fr∕Fopt where for Fopt we used the observed optical flux of this source as reported in Zhou et al. (2006) catalogue. Our aim is to reproduce the radio-loudness properties of Järvelä et al. (2015) sample of NLS1 in terms of R and radio flux distributions, total number of radio-detected RL- and RQ-NLS1s, and the relative number of RL- and RQ-NLS1s (these are our constraints). Therefore, we select in our simulated sample only those source with a radio flux larger than FIRST radio flux limit (1 mJy) to be compared with Järvelä et al. (2015) sample. The free parameters of this Monte Carlo test are the central values and width of Γ and 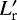 distributions. Since this is a consistency check, we do not aim at fully exploring their parameter space, but only testing if reasonable assumptions on their values can reproduce our constraints. Figure 3 shows the radio-loudness distribution as a function of the orientation in our simulated sample (top panel), obtained by sampling from distributions of Γ centred at 10 (σ = 0.2) and of
distributions. Since this is a consistency check, we do not aim at fully exploring their parameter space, but only testing if reasonable assumptions on their values can reproduce our constraints. Figure 3 shows the radio-loudness distribution as a function of the orientation in our simulated sample (top panel), obtained by sampling from distributions of Γ centred at 10 (σ = 0.2) and of 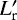 centred at 8 × 1035 erg s−1 (σ = 0.2 dex). The simulation needs fjet ~ 0.5 to reproduce the RL occurrence in the sample6 and suggests an average orientation angle of
centred at 8 × 1035 erg s−1 (σ = 0.2 dex). The simulation needs fjet ~ 0.5 to reproduce the RL occurrence in the sample6 and suggests an average orientation angle of 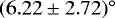 for RL-NLS1s, which is roughly consistent with our assumption on θRL-NLS1 (7°). Interestingly, our test suggests that ~1∕3 RQ-NLS1s are dominated by SF in their radio emission, since they are underestimated in proportion to RL-NLS1s, if only the jet emission is considered contributing to the radio luminosity (in agreement with Järvelä et al. 2015). As a note of caution, we stress that this test does not aim at reproducing source by source the NLS1s in Järvelä et al. (2015), but rather their distribution (of R, radio fluxes, and RL/RQ) as a radio flux-limited statistical sample. For completeness, we assumed an intrinsic optical-to-radio luminosity ratio for the jet component as in the jet-dominated state of B2 0954 + 25A (Calderone et al. 2012). We similarly beamed the optical luminosity, derived the optical flux (see Eq. (3)), and compared it with the observed optical flux. We find that in all the RQ sources the simulated optical flux is on average 1/50–1/100 of the observed flux. In RL sources, instead, a minor fraction (~ 5%) overestimates the observed optical flux, while in the majority of RL sources the jet emission likely contributes on the same level as the disc emission, which is comparable but less than the observed flux. This effect, coupled with the redshift bias introduced in Sect. 2, is likely responsible for the apparently different black hole mass distributions in the RQ- and RL-NLS1 subclasses.
for RL-NLS1s, which is roughly consistent with our assumption on θRL-NLS1 (7°). Interestingly, our test suggests that ~1∕3 RQ-NLS1s are dominated by SF in their radio emission, since they are underestimated in proportion to RL-NLS1s, if only the jet emission is considered contributing to the radio luminosity (in agreement with Järvelä et al. 2015). As a note of caution, we stress that this test does not aim at reproducing source by source the NLS1s in Järvelä et al. (2015), but rather their distribution (of R, radio fluxes, and RL/RQ) as a radio flux-limited statistical sample. For completeness, we assumed an intrinsic optical-to-radio luminosity ratio for the jet component as in the jet-dominated state of B2 0954 + 25A (Calderone et al. 2012). We similarly beamed the optical luminosity, derived the optical flux (see Eq. (3)), and compared it with the observed optical flux. We find that in all the RQ sources the simulated optical flux is on average 1/50–1/100 of the observed flux. In RL sources, instead, a minor fraction (~ 5%) overestimates the observed optical flux, while in the majority of RL sources the jet emission likely contributes on the same level as the disc emission, which is comparable but less than the observed flux. This effect, coupled with the redshift bias introduced in Sect. 2, is likely responsible for the apparently different black hole mass distributions in the RQ- and RL-NLS1 subclasses.
The previous analytic argument applied to the fraction of RL-NLS1 can be used to constrain the fraction of RL-NLS1s that would be observed with a γ-ray selection, i.e.
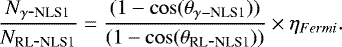 (4)
(4)
In this case, we assume that all the RL-NLS1s host a jet (i.e. the contamination by SF radio emission is negligible), such that ηFermi accounts forthe possible selection effects introduced by the Fermi/LAT flux limit. The ratio Nγ- NLS1∕NRL-NLS1 = 1∕7 observed by D’Ammando et al. (2015) results in ηFermi ≈ 0.43, i.e. about half of the NLS1s with very aligned jets have been observed by Fermi.
The critical angles for a jetted NLS1 to be classified as RL-NLS1 or γ-NLS1 can be used to improve the estimates of their masses. Under the assumption that the BLR is virialized and lies within the influence sphere of the BH, MBH can be estimated through
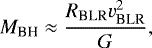 (5)
(5)
where RBLR is an estimate of the BLR size, and vBLR the typical velocity of BLR clouds. Equation (5) implies Eq. (1) when RBLR is estimated through RBLR-luminosity relations (Kaspi et al. 2000, 2005; Bentz et al. 2006, 2009) and vBLR is inferred from the Hβ width vBLR = f⋅FWHM. Here f is a fudge factor that depends on the geometry of the BLR that is usually set by comparing the MBH estimates obtained from Eq. (1) with independent mass estimates over a sample of Type I objects.
Under the assumption of a thick disc BLR (e.g. Collin et al. 2006), f can be expressed for any AGN as
![\begin{equation*}f=\left[2 \sqrt{\left(\frac{H}{R}\right)^2+\sin^2{\theta_i}}\right]^{-1}, \end{equation*}](/articles/aa/full_html/2018/08/aa32451-17/aa32451-17-eq10.png) (6)
(6)
where θi is the angle between the normal to the BLR disc and the line of sight, and the aspect ration H∕R is related tothe relative importance of isotropic (e.g. turbulent) versus rotational motions. We assume H∕R ≈ 0.1, since this value can resolve the possibly not physical discrepancy between NLS1 and BLS1 black hole masses (Decarli et al. 2008a). Each class of AGN has a different bias in the MBH estimates that is proportional to the average value of f2 (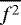 ) over all the allowed orientations as follows:
) over all the allowed orientations as follows:
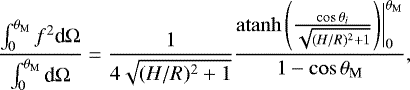 (7)
(7)
where θM is equal to θBLS1 = 40° for the whole Seyfert I population, θNLS1 = 15° for NLS1s, θRL-NLS1 = 7° for RL-NLS1s, and θγ−NLS1 = 4° for γ-NLS1s. The correction factor to remove the projection effects for a specific class of AGN is therefore 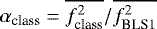 with αNLS1 ≈ 6.3, αRL-NLS1 ≈ 12.8, and αγ−NLS1 ≈ 17.1. We stress that the larger correction for the RL-NLS1s would increase the disagreement between the observed distributions of MBH in RQ-NLS1s and RL-NLS1s discussed by Järvelä et al. (2015), hinting at an even larger impact of the observational biases discussed in Sect. 2. In addition, the limited variation between αRL-NLS1 and αγ−NLS1 is due to the H∕R term in Eq. (6). A larger value of H∕R ≈ 0.2 would result in smaller and more similar correction factors, i.e. αNLS1 ≈ 3.6, αRL-NLS1 ≈ 5.2, and αγ−NLS1 ≈ 5.8.
with αNLS1 ≈ 6.3, αRL-NLS1 ≈ 12.8, and αγ−NLS1 ≈ 17.1. We stress that the larger correction for the RL-NLS1s would increase the disagreement between the observed distributions of MBH in RQ-NLS1s and RL-NLS1s discussed by Järvelä et al. (2015), hinting at an even larger impact of the observational biases discussed in Sect. 2. In addition, the limited variation between αRL-NLS1 and αγ−NLS1 is due to the H∕R term in Eq. (6). A larger value of H∕R ≈ 0.2 would result in smaller and more similar correction factors, i.e. αNLS1 ≈ 3.6, αRL-NLS1 ≈ 5.2, and αγ−NLS1 ≈ 5.8.
 |
Fig. 3 Top panel: radio-loudness as a function of the orientation angle for the simulated NLS1 sample. Middle panel: orientation angle distribution for simulated radio-detected NLS1s. Our simulated samples have average orientations of |
4 Discussion
We presented a simple geometrical unification model based on the assumption that a fraction of RQ-NLS1s (~ 50%), RL-NLS1s, and γ-NLS1s are classified as such only because of their orientation. We discuss our model in the broader context of NLS1s, commenting on possible tests.
Within the same scenario, Smith et al. (2004, 2005) have theoretically predicted that, when observed in polarized light, NLS1s should have a low polarization fraction, the polarization angle should change monotonically from one wing of the BELs to the other, and the BELs should be significantly broader than those observed in direct light (Smith et al. 2004, 2005). We assume that polarized BELs are scattered into the line of sight by material that is close to coplanar with the BLR (i.e. the torus). This prediction has been searched for in RQ-NLS1s, but many objects have not been detected in polarized light, and none of the detected show any significant broadening of the BELs (e.g. Goodrich 1989; Breeveld & Puchnarewicz 1998; Kay et al. 1999). On the other hand, only one RL-NLS1 (PKS 2004-447) has been the object of a spectropolarimetry study (Baldi et al. 2016), and the three predicted features have been observed that have a FWHM in the polarized Hα of ≈ 9000 km s−1. We propose for the first time a simple scenario that can resolve such apparent tension between the two classes of NLS1s. We speculate that in those NLS1s that are intrinsically without a jet (a fraction of the RQ-NLS1) a significant amount of polarized light could be due to polar scattering of the BELs, by material above the BLR, as observed for type II AGN (Antonucci 1983; Miller & Antonucci 1983; Antonucci & Miller 1985). A polar-scattered component could easily overwhelm the planar-scattering contribution, predicted to result in low polarization fractions for face-on objects because of the axi-symmetry of the scattering material. In RL-NLS1s, on the contrary, the jet could evacuate the intervening material, resulting in a lower degree of polarization in which only the broadened component of the BEL is left. The evacuation of the polar material by a jet closely aligned withthe line of sight has been already proposed by Ghisellini & Sbarrato (2016) to account for the lack of high-z blazar parent population. This simple speculative scenario can be tested through spectropolarimetry of a larger sample of RL-NLS1s.
As a note of caution, we discussed only the radio and γ features of NLS1s, and the properties of their optical BELs. Other peculiarities are characteristic of this classof AGN. As an example, NLS1s show weak [OIII] emission when normalized to the Hβ line, explained both by the low-MBH and geometrical scenarios as a consequence of weak thermal emission at high (UV) frequencies. While in the low-MBH scenario this high energy cut-off is supposedly caused by the self shielding of the optically and geometrically thick innermost (hotter) parts of a close to or super-Eddington accretion disc (see e.g. Boroson 2002), in the geometrical scenario such self-shielding is not required because the innermost parts of the accretion discs are naturally colder. We stress that such geometrical model is in agreement with the infrared-to-UV SED fitting discussed, for example, by Calderone et al. (2013). In addition, NLS1s show a steeper/more variable X-ray continuum with respect to the bulk of the type I AGN population. These features have been interpreted as due to higher Eddington ratios in the low-MBH scenario7, but they are also consistent with the “aborted jet” model (Ghisellini et al. 2004), in which a weak radio jet (similar to the jets discussed in the geometrical model for RL- and γ-NLS1s) is responsible for the highly variable X-ray emission. In both models the Comptonization of optical-UV photons produced in the accretion disc onto the non-thermal electrons is responsible for the steepness of the X-ray spectrum, as long as most of the accretion energy is released in the accretion disc and not directly into the non-thermal electrons of the corona/jet. Although the geometrical model explains many different aspects of the NLS1s and in particular jetted NLS1s, further theoretical effort is needed to reproduce all the features that characterize such class of AGN. In particular, to our knowledge the peculiar FeII intensity is not an immediate prediction of the geometrical model, and certainly requires some additional investigation.
In conclusion, the geometrical model has already been successfully applied to a RL-NLS1 (Baldi et al. 2016) and it could explain the blazar-like behaviour of the RL subclass. Nevertheless, we cannot firmly constrain the relative fraction of face-on NLS1s versus those powered by an undermassive BH accreting close to its Eddington limit. Of particular interest in this regard is the study by Sani et al. (2010), in which the ratio of star formation activity to AGN emission (R) has been estimated both for NLS1s and BLS1s. The R parameter does not depend in any way on the assumed mass of the central BH, hence is not affected by possible orientation effects. Although a significant number of NLS1s lie in the same region of the (MBH-R) plane as the BLS1s, the NLS1 sample shows overall an enhanced star formation with respect to the BLS1s. It would be interesting to check whether the star formation properties can be used to discriminate between the two scenarios.
Acknowledgements
We thank Luigi Foschini and Valentina Braito for useful discussions.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 707, L142 [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, R. R. J. 1983, Nature, 303, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, R. R. J., & Miller, J. S. 1985, ApJ, 297, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Baldi, R. D., Capetti, A., Robinson, A., Laor, A., & Behar, E. 2016, MNRAS, 458, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Peterson, B. M., Pogge, R. W., Vestergaard, M., & Onken, C. A. 2006, ApJ, 644, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Peterson, B. M., Netzer, H., Pogge, R. W., & Vestergaard, M. 2009, ApJ, 697, 160 [Google Scholar]
- Berton, M., Foschini, L., Ciroi, S., et al. 2015, A&A, 578, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bian, W., & Zhao, Y. 2004, MNRAS, 352, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & McKee, C. F. 1982, ApJ, 255, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boller, T., Brandt, W. N., & Fink, H. 1996, A&A, 305, 53 [NASA ADS] [Google Scholar]
- Boroson, T. A. 2002, ApJ, 565, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Breeveld, A. A., & Puchnarewicz, E. M. 1998, MNRAS, 295, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Caccianiga, A., Antón, S., Ballo, L., et al. 2015, MNRAS, 451, 1795 [NASA ADS] [CrossRef] [Google Scholar]
- Calderone, G., Ghisellini, G., Colpi, M., & Dotti, M. 2012, MNRAS, 424, 3081 [NASA ADS] [CrossRef] [Google Scholar]
- Calderone, G., Ghisellini, G., Colpi, M., & Dotti, M. 2013, MNRAS, 431, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Calderone, G., Nicastro, L., Ghisellini, G., et al. 2017, MNRAS, 472, 4051 [NASA ADS] [CrossRef] [Google Scholar]
- Collin, S., Kawaguchi, T., Peterson, B. M., & Vestergaard, M. 2006, A&A, 456, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Ammando, F., Orienti, M., Finke, J., et al. 2012, MNRAS, 426, 317 [NASA ADS] [CrossRef] [Google Scholar]
- D’Ammando, F., Orienti, M., Larsson, J., & Giroletti, M. 2015, MNRAS, 452, 520 [NASA ADS] [CrossRef] [Google Scholar]
- D’Ammando, F., Orienti, M., Finke, J., et al. 2016, Galaxies, 4, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Decarli, R., Dotti, M., Fontana, M., & Haardt, F. 2008a, MNRAS, 386, L15 [NASA ADS] [Google Scholar]
- Decarli, R., Labita, M., Treves, A., & Falomo, R. 2008b, MNRAS, 387, 1237 [NASA ADS] [CrossRef] [Google Scholar]
- Decarli, R., Dotti, M., & Treves, A. 2011, MNRAS, 413, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Fine, S., Jarvis, M. J., & Mauch, T. 2011, MNRAS, 412, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Foschini, L. 2011, Narrow-Line Seyfert 1 Galaxies and Their Place in the Universe, 24 [Google Scholar]
- Foschini, L. 2012, AIP Conf. Ser., 1505, 574 [NASA ADS] [Google Scholar]
- Foschini, L. 2017, Frontiers in Astronomy and Space Sciences, 4, 6 [Google Scholar]
- Foschini, L., Berton, M., Caccianiga, A., et al. 2015, A&A, 575, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., & Sbarrato, T. 2016, MNRAS, 461, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Haardt, F., & Matt, G. 2004, A&A, 413, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., Tavecchio, F., & Chiaberge, M. 2005, A&A, 432, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., Righi, C., Costamante, L., & Tavecchio, F. 2017, MNRAS, 469, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Giommi, P., Padovani, P., Polenta, G., et al. 2012, MNRAS, 420, 2899 [NASA ADS] [CrossRef] [Google Scholar]
- Goodrich, R. W. 1989, ApJ, 342, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Green, A. R., McHardy, I. M., & Lehto, H. J. 1993, MNRAS, 265, 664 [NASA ADS] [Google Scholar]
- Greene, J. E., & Ho, L. C. 2005, ApJ, 630, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Grier, C. J., Pancoast, A., Barth, A. J., et al. 2017, ApJ, 849, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Grupe, D., & Mathur, S. 2004, ApJ, 606, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashida, K. 2000, New Astron. Rev., 44, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Järvelä, E., Lähteenmäki, A., & León-Tavares, J. 2015, A&A, 573, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaspi, S., Smith, P. S., Netzer, H., et al. 2000, ApJ, 533, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, S., Maoz, D., Netzer, H., et al. 2005, ApJ, 629, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Kay, L. E., Magalhães, A. M., Elizalde, F., & Rodrigues, C. 1999, ApJ, 518, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Labita, M., Treves, A., Falomo, R., & Uslenghi, M. 2006, MNRAS, 373, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Lähteenmäki, A., Järvelä, E., Hovatta, T., et al. 2017, A&A, 603, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, J. S., & Antonucci, R. R. J. 1983, ApJ, 271, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Pogge, R. W. 1985, ApJ, 297, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P. 2016, A&ARv, 24, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Pancoast, A., Brewer, B. J., & Treu, T. 2014a, MNRAS, 445, 3055 [NASA ADS] [CrossRef] [Google Scholar]
- Pancoast, A., Brewer, B. J., Treu, T., et al. 2014b, MNRAS, 445, 3073 [NASA ADS] [CrossRef] [Google Scholar]
- Rakshit, S., & Stalin, C. S. 2017, ApJ, 842, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Runnoe, J. C., Brotherton, M. S., Shang, Z., Wills, B. J., & DiPompeo, M. A. 2013, MNRAS, 429, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Sani, E., Lutz, D., Risaliti, G., et al. 2010, MNRAS, 403, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shen, Y., & Ho, L. C. 2014, Nature, 513, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. E., Robinson, A., Alexander, D. M., et al. 2004, MNRAS, 350, 140 [Google Scholar]
- Smith, J. E., Robinson, A., Young, S., Axon, D. J., & Corbett, E. A. 2005, MNRAS, 359, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Véron-Cetty, M.-P., Véron, P., & Gonçalves, A. C. 2001, A&A, 372, 730 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wills, B. J., & Browne, I. W. A. 1986, ApJ, 302, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, H., Wang, T., Yuan, W., et al. 2006, ApJS, 166, 128 [NASA ADS] [CrossRef] [Google Scholar]
In the RL-NLS1 PKS 2004 – 447, such a scenario has been successfully tested through the spectropolarimetry of the broad Hα line (Baldi et al. 2016).
Similar results have been presented for NLS1 PKS 2004 – 447 by Abdo et al. (2009) and for PMN J0948 + 0022, SBS 0846 + 513, PMN J0948 + 0022, 1H 0323 + 342, and PKS 1502 + 036 in D’Ammando et al. (2016).
The fraction of intrinsically jetted sources increases up to 1 by increasing the maximum viewing angle up to ~30° in order to obtain a simulated sample consistent with that by Järvelä et al. (2015).
Although, a SED fitting including the soft X-ray part of the NLS1s spectra seems to indicate MBH masses larger than those obtained from the virial estimates and, as a consequence, smaller inclinations (within ~17°; Bian & Zhao 2004).
All Figures
 |
Fig. 1 Distribution of 5100 Å (top panel) and radio (bottom panel) luminosities vs. redshift for the NLS1 subclasses. RQ-NLS1 (blue dots) are mainly located at low z. The few sources at higher z are among the most luminous: the radio flux sensitivity only allows us to observe the peak of the iceberg. RL-NLS1 (red dots), instead, are more evenly distributed in luminosities and z; thanks to their larger radio flux, they are less affected by this observational bias compared with RQ sources. They are missing in radio surveys from higher redshift than their RQ counterparts. |
| In the text | |
 |
Fig. 2 Optical SEDs for three RL-NLS1s and a RQ-NLS1. Green, red, and blue data show decreasing profiles of SDSS J 224605.44 − 091925.1 (z = 0.119), SDSS J162458.42 + 423107.5 (z = 0.663), and SDSS J171930.56 + 293412.8 (z = 0.180), typical of jet-dominated optical emissions. The analogous dashed lines show Shakura & Sunyaev (1973) disc profiles for the three sources, drawn with the virial masses by Järvelä et al. (2015) and normalized by forcing them to pass through the lowest frequency data point. Violet data, instead, show the disc-dominated profile of the RQ-NLS1 SDSS J144012.76 + 615633.2 (z = 0.276). The RL-NLS1s have an SED that is clearly not disc-like. |
| In the text | |
 |
Fig. 3 Top panel: radio-loudness as a function of the orientation angle for the simulated NLS1 sample. Middle panel: orientation angle distribution for simulated radio-detected NLS1s. Our simulated samples have average orientations of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.