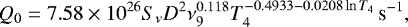| Issue |
A&A
Volume 616, August 2018
|
|
|---|---|---|
| Article Number | A126 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201732180 | |
| Published online | 28 August 2018 | |
Parsec-scale jets driven by high-mass young stellar objects
Connecting the au- and the parsec-scale jet in IRAS 13481-6124★
1
Dublin Institute for Advanced Studies, School of Cosmic Physics, Astronomy & Astrophysics Section,
31 Fitzwilliam Place,
Dublin 2,
Ireland
e-mail: fedriani@cp.dias.ie
2
School of Physics, University College Dublin, Belfield,
Dublin 4,
Ireland
3
School of Physics, Astrophysics Group, University of Exeter,
Stocker Road,
Exeter EX4 4WL,
UK
4
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
5
Thüringer Landessternwarte Tautenburg,
Sternwarte 5,
07778
Tautenburg,
Germany
Received:
26
October
2017
Accepted:
23
May
2018
Context. Protostellar jets in high-mass young stellar objects (HMYSOs) play a key role in the understanding of star formation and provide us with an excellent tool to study fundamental properties of HMYSOs.
Aims. We aim at studying the physical and kinematic properties of the near-infrared (NIR) jet of IRAS 13481-6124 from au to parsec scales.
Methods. Our study includes NIR data from the Very Large Telescope instruments SINFONI, CRIRES, and ISAAC. Information about the source and its immediate environment is retrieved with SINFONI. The technique of spectro-astrometry is performed with CRIRES to study the jet on au scales. The parsec-scale jet and its kinematic and dynamic properties are investigated using ISAAC.
Results. The SINFONI spectra in H and K bands are rich in emission lines that are mainly associated with ejection and accretion processes. Spectro-astrometry is applied to the Brγ line, and for the first time, to the Brα line, revealing their jet origin with milliarcsecond-scale photocentre displacements (11−15 au). This allows us to constrain the kinematics of the au-scale jet and to derive its position angle (~216°). ISAAC spectroscopy reveals H2 emission along the parsec-scale jet, which allows us to infer kinematic and dynamic properties of the NIR parsec-scale jet. The mass-loss rate inferred for the NIR jet is Ṁejec ~ 10−4 M⊙ yr−1 and the thrust is Ṗ ~ 10−2 M⊙ yr−1 km s−1, which is roughly constant for the formation history of the young star. A tentative estimate of the ionisation fraction is derived for the massive jet by comparing the radio and NIR mass-loss rates. An ionisation fraction ≲8% is obtained, which means that the bulk of the ejecta is traced by the NIR jet and that the radio jet only delineates a small portion of it.
Key words: ISM: jets and outflows / ISM: kinematics and dynamics / stars: pre-main sequence / stars: massive / stars: individual: IRAS 13481-6124 / techniques: spectroscopic
© ESO 2018
1 Introduction
In recent years, significant progress has been made in understanding the formation of high-mass young stellar objects (HMYSOs; i.e. M*≥ 8 M⊙, Lbol ≥ 5 × 103 L⊙). The latest observational and theoretical studies present evidence that tips the balance of favour in a key debate over how high-mass stars form. It now seems likely that HMYSOs are born in the same way as their low-mass counterparts, via disc accretion, rather than through coalescence of lower mass stars. The growing observational evidence to support this view includes (i) discovery of dusty discs around HMYSOs via near-infrared (NIR) interferometric image reconstruction (Kraus et al. 2010, 2017) and mid-infrared (MIR) interferometry (Boley et al. 2016), (ii) observations of HMYSO discs in Keplerian rotation through modelling of CO band-head emission (Ilee et al. 2013), (iii) direct detection of HMYSO discs in molecular tracers (Beltrán & de Wit 2016), (iv) detection of several parsec-scale collimated infrared jets (Caratti o Garatti et al. 2008, 2015a; Varricatt et al. 2010; Cesaroni et al. 2013), and (v) discovery of the first disc-mediated accretion burst in a 20 M⊙ YSO (Caratti o Garatti et al. 2017). If, as now appears likely, HMYSOs form through the accretion–ejection process, then studies of the jet and outflow have the potential to provide valuable insights into their accretion processes as well as how these processes scale with the mass of the young stars.
As HMYSOs are deeply embedded in their parental cloud, jet and outflow observations have traditionally relied on tracers at long wavelengths to minimise the effects of extinction. For example, HMYSO molecular outflows have been well studied in the molecular tracers of CO and SiO, observed in the sub-millimeter and millimeter regimes (see e.g. Beuther et al. 2002; Maud et al. 2015). However, these emission lines are generally considered tracers of the secondary outflow, that is, ambient material swept-up by the faster primary jet. Meanwhile, the primary jet has been well studied in radio emission (Guzmán et al. 2012; Masqué et al. 2015; Rosero et al. 2016; Purser et al. 2016). However, as radio emission traces only ionised gas, it may not trace the bulk of the ejecta since it depends on the degree of ionisation of the jet. Success in observing HMYSO primary jets at shorter wavelengths has been achieved, despite extinction, by moving to the NIR regime. The primary jet of HMYSOs has also been seen to emit in several NIR atomic (H I, [Fe II]) and molecular lines (H2) (Davies et al. 2010; Stecklum et al. 2012; Cooper et al. 2013; Caratti o Garatti et al. 2015a, 2016), which trace the warm/hot gas of these shocked jets (T > 2000 K). The instantaneous efficiency at which mass is accumulated is measured by Ṁejec∕Ṁacc. Conceivably, this ratio could vary not only with evolutionary phase, but also with the mass of the central object. In turn, this could give us clues as to the underlying ejection mechanism, because massive jets could be a scaled-up version of their low-mass counterparts.
A limited number of kinematic studies of HMYSO primary jets exist in the NIR, the majority focusing on a single object (Davis et al. 2004; Gredel 2006; Caratti o Garatti et al. 2008, 2015a, 2016). Therefore, improving jet statistics is crucial to facilitate conclusions on disc-mediated accretion in HMYSOs, because the discs and stars themselves suffer high visual extinction, thereby hindering access to direct observations.
In this paper we report our findings on IRAS 13481-6124 (G310.0135+00.3892), an HMYSO located at 3.1 ±1.1 kpc (Lumsden et al. 2013). This object has a mass of ~20 M⊙ (Lbol= 5.7 × 104 L⊙), a spectral type of O9, and an age of ~6 × 104 years (Grave & Kumar 2009). Detection of an accretion disc (inclination ~ 45°, position angle ~ 120°) was achieved via IR interferometry (Kraus et al. 2010; Boley et al. 2016). The central source drives a parsec-scale collimated bipolar jet with an extensionof ~7 pc (Stecklum et al. 2012; Caratti o Garatti et al. 2015a). The parsec-scale jet has a precession angle of ~ 8° (Caratti o Garatti et al. 2015a; see also Fig. 1). By means of NIR interferometry on the Brγ line, Caratti o Garatti et al. (2016) detected ejecta very close to the source (~few au) that extended for a few tens of au, suggesting that Brγ is tracing the inner jet and that the protostar is still accreting material. This system has also been studied at radio wavelengths, and its radio jet dynamic properties have been derived (Purser et al. 2016). A mass-loss rate of ~ 1.8 × 10−5 M⊙ yr−1 and momentum rate of ~1−2 × 10−2 M⊙ yr−1 km s−1 were found (assuming vjet = 500 km s−1 and xe = 0.2; Purser et al. 2016), consistent with typical values determined for a sample of HMYSOs. Here, we present the first detailed study of the NIR jet of IRAS 13481-6124. We examine the jet on small and large spatial scales, we compare it to the radio jet, and we thus present the first report on the kinematic and dynamic properties of the parsec-scale jet.
This paper is structured as follows. In Sect. 2 we describe our observations and in Sect. 3 we describe the data analysis. In Sect. 4 we present the results on source and along the jet at different spatial scales, including the kinematic and dynamic properties. Section 5 presents our local thermal equilibrium (LTE) model. Section 6 discusses the results we obtained. Finally, in Sect. 7 our conclusions are presented.
 |
Fig. 1 SOFI1 H2 continuum-subtracted image of IRAS 13481-6124 showing the blue-shifted jet knots, bow shock, and driving source. Knot positions are labelled A, B, D, and F, following the notation of Caratti o Garatti et al. (2015a). ISAAC slit positions (blue) are labelled SLIT 1, 2, and 3 for convenience, and correspond to observations on the source, jet, and bow shock, respectively. |
2 Observations
Observations of IRAS 13481-6124 were obtained using three ESO-Very Large Telescope (VLT) instruments: the spectrograph for integral field observations in the near-infrared (SINFONI; Eisenhauer et al. 2003); the CRyogenic high-resolution pre-dispersed InfraRed Echelle Spectrograph (CRIRES; Kaeufl et al. 2004), and the Infrared Spectrometer And Array Camera (ISAAC; Moorwood et al. 1998). Details of the observations can be found in Table 1.
Each instrument was used to study different regions of the IRAS 13481-6124 system at different scales: SINFONI was used to analyse the source and its immediate environment, and CRIRES and ISAAC were used to study the jet; the former focusing on the au-scale jet using the technique of spectro-astrometry and the latter focusing at the parsec-scale jet investigating its dynamic and kinematic properties.
Summary of the observations carried out with VLT/SINFONI, ISAAC, and CRIRES.
2.1 SINFONI data
VLT/SINFONI integral field unit (IFU) observations were obtained on 2011 April 27 (Program ID 087.C-0951(B)) in K band. The field of view of 8″ × 8″ was centred on the source, with a position angle (PA) east of north (E of N) of zero degrees. Spatial sampling was 125 × 250 mas pixel−1, with the smaller sampling in the northern direction. Total integration time was 3 s. Spectral resolution was 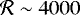 (75 km s−1), and spatial resolution achieved using AO + NGS was 0.1″. The natural guide star used for the AO system was 2MASS J13513620-6138563 (V =12.3, R = 12.6 mag and separation of 16″ from the target).
(75 km s−1), and spatial resolution achieved using AO + NGS was 0.1″. The natural guide star used for the AO system was 2MASS J13513620-6138563 (V =12.3, R = 12.6 mag and separation of 16″ from the target).
Additional SINFONI data were obtained on 2012 February 21 and 22 (Program ID 088.C-0575(C)) in H and H + K bands. The field of view of 3″ × 3″ was centred on the source, with a PA of − 31° in both bands. Spatial sampling was 50 × 100 and 125 × 250 mas pixel−1 for the H and H + K bands, respectively, with the smaller sampling in the jet direction. Total exposure time was 8 and 16 s for the H band (both were coadded to increase the signal-to-noise ratio, S/N) and 2 s for H + K band. The spectral resolution was 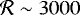 and 1500 (100 and 200 km s−1), respectively. Spatial resolution of 0.5″ (AO + NGS) was achieved for the H band and 1.0″ (seeing-limited) for the H + K band.
and 1500 (100 and 200 km s−1), respectively. Spatial resolution of 0.5″ (AO + NGS) was achieved for the H band and 1.0″ (seeing-limited) for the H + K band.
All data were reduced in the standard way, using dedicated instrument software, GASGANO, and standard IRAF routines for SINFONI. A wavelength accuracy of 0.31Å (or ~ 4.2−5.6 km s−1 for the H and K bands, respectively) was achieved. Flux calibration was performed using the photometric standard star Hip072690.
2.2 CRIRES data
VLT/CRIRES high spectral resolution observations were carried out on 2013 March 10, 15, and 16 in the L, K, and J bands, respectively (Program ID 090.C-0371(C)). A long slit of 0.4″ × 40″ was centred on Brα (λvac= 4.05226 μm), Brγ (λvac= 2.16612 μm), and Paβ (λvac= 1.28216 μm). This set-up achieved a spectral resolution of 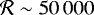 (6 km s−1). Spatial sampling was 86 mas pixel−1. The slit was placed first along the jet (204°), and then perpendicular to the jet (114°). The slit was also placed at two anti-parallel PA values (24° and 294°). This observing strategy allows for the identification and removal of artefacts before applying the technique of spectro-astrometry (see Sect. 3). Use of AO+NGS achieved spatial resolutions of 0.35″, 0.3″, and 0.2″ for the Paβ, Brγ, and Brα lines, respectively. The NGS used in CRIRES observations was the same as in SINFONI observations.
(6 km s−1). Spatial sampling was 86 mas pixel−1. The slit was placed first along the jet (204°), and then perpendicular to the jet (114°). The slit was also placed at two anti-parallel PA values (24° and 294°). This observing strategy allows for the identification and removal of artefacts before applying the technique of spectro-astrometry (see Sect. 3). Use of AO+NGS achieved spatial resolutions of 0.35″, 0.3″, and 0.2″ for the Paβ, Brγ, and Brα lines, respectively. The NGS used in CRIRES observations was the same as in SINFONI observations.
The data were reduced in the standard way using the GASGANO package, and following the CRIRES data reduction cookbook. A wavelength accuracy of 0.22, 0.25, and 0.61 Å (or ~5.1, 3.5, and 4.5 km s−1 for the J, K, and L bands, respectively) was achieved. The telluric standard star used was HR5071 to remove atmospheric features, for the Paβ and Brγ spectra. In the case of the Brα spectrum, due to the poor quality of the standard star in the L band, telluric features were modelled and removed using templates of the Earth’s telluric features. CRIRES spectra were not flux calibrated.
2.3 ISAAC data
High-resolution long-slit spectra were obtained with VLT/ISAAC on 2011 April 18 in H and K bands (Program ID 087.C0951(A)). High-resolution spectra around the [Fe II] (λvac = 1.6642 μm; from 1.4 to 1.82 μm), and around the 1 − 0 S(1) H2 (λvac = 2.12183 μm), and Brγ (λvac = 2.16612 μm) lines were obtained. The 0.3″ × 120″ long slit was positioned at three orientations: on-source (PA = −152.5°; slit 1, see Fig. 1), along the jet (PA = 27.5°; slit 2, see Fig. 1), and on the terminal bow shock (PA = 167.5°; slit 3, see Fig. 1). Spatial sampling was 146 mas pixel−1. Total integration time was 180 and 150 s for H and K bands, respectively. Spectral resolution was 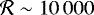 and 8900 (30−35 km s−1) for the H and K bands, respectively. Spatial resolution was seeing-limited (0.8−1.0″). The standard ABBA nodding strategy was used.
and 8900 (30−35 km s−1) for the H and K bands, respectively. Spatial resolution was seeing-limited (0.8−1.0″). The standard ABBA nodding strategy was used.
Data were reduced in the standard way using IRAF. Wavelength calibration relied on the OH atmospheric lines in each frame. The spatial distortion and curvature caused by the long slit were corrected using the calibration file STARTRACE. A wavelength accuracy of 0.061Å (or ~ 1.1 and 0.8 km s−1 for the H and K bands, respectively) was achieved. Atmospheric telluric lines were corrected for by observing the telluric standard star Hip058630. Additionally, the on-source spectra were flux calibrated using the photometric standard star Hip058630.
3 Data analysis
3.1 Spectra extraction and velocity calculation
To generate the SINFONI spectra, a region of 0.5″ × 0.5″ (i.e., 1550 × 1550 au at a distance of 3.1 kpc) was extracted from the data cubes. ISAAC and CRIRES spectra were extracted using specific IRAF tasks for long slit. The wavelength calibration was carried out via two different methods: for ISAAC and CRIRES spectra, atmospheric telluric lines were used; and for SINFONI spectra, calibration relied on arc lamp observations.
Radial velocities of the [Fe II], Brγ, and H2 lines were measured from the ISAAC spectra. These lines are used to compute kinematic and dynamic properties shown in Sect. 4. The emission lines were fitted by a Gaussian profile with a typical error of 5− 6 km s−1, given the high S/N (~100 for the brightest lines). All velocities in ISAAC and CRIRES spectra are with respect to the local standard of rest (LSR), and were corrected for the velocity of the parental cloud (− 37.9 km s−1; Lumsden et al. 2013).
3.2 Spectro-astrometry
Given the high spectral resolution of CRIRES and the excellent S/N of our observations, we are in a position to apply the technique of spectro-astrometry in order to retrieve spatial information on scales below the effective resolution of the observations (Bailey 1998; Takami et al. 2001, 2003; Whelan et al. 2005). The technique involves measuring the spatial offset of the emission centroid with respect to that of the continuum as a function of wavelength. The accuracy, σ, of the centroid position, well below the effective spatial resolution, is given by Whelan & Garcia (2008); nonetheless, the error given by this formula is likely underestimated:
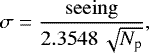 (1)
(1)
where the seeing is measured in the spatial direction and is determined by the FWHM of the observations (i.e. the FWHM of the continuum). Np is the number of photons at the peak of the line. Given the spectral resolution and S/N in our CRIRES observations, this equation provides an accuracy of up to ~0.65 milliarcsecond (mas) in our case, which implies that we can probe our target on au scales. Although the technique is powerful, it is prone to contamination by artefacts (Bailey 1998; Takami et al. 2001; Whelan & Garcia 2008). For example, the spectro-astrometric signal is affected by a misalignment of the detector with respect to the spatial direction, and therefore a second-order polynomial was fitted to correct for this distortion. To remove artefacts, the parallel (p) and the antiparallel (ap) slit measurements were subtracted from each other for each pixel (x) (Brannigan et al. 2006), as shown in Eq. (2):
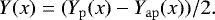 (2)
(2)
A fitting of the continuum was not possible due to the very broad nature of the lines, but instead we were able to estimate the continuum intensity level by examining the small portion of the continuum to the left of the line. The measured line displacement was corrected by multiplying by the following weight in order to derive theoffset of the line emitting region from the measured combined line and continuum emission offset (see e.g. Takami et al. 2001):
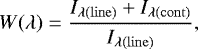 (3)
(3)
where Iλ(line) is the continuum-subtracted intensity in the line.
Finally, it is also important to correct for photospheric features. However, IRAS 13481-6124 is probably an O9 star (see Grave & Kumar 2009), and the H I photospheric contribution should be negligible. Nevertheless, we examined our data for such features (see Sect. 4.1).
4 Results
We have divided the results into three subsections, corresponding to the three main regions of our target: the source and its immediate circumstellar environment; the base of the jet, that is, the au-scale jet; and the parsec-scale jet.
4.1 Source and its immediate environment
Several emission lines on source and in the immediate environment are detected in both SINFONI and ISAAC data (see Table 2 and Fig. 2, upper and lower left panels). These lines mainly trace circumstellar features. Although the observed emission lines are not spatially resolved, they have different excitation energies and therefore trace a variety of processes at distinct spatial scales. In the H band, we detect the Brackett series lines (from Br26 1.4941 μm to Br10 1.7376 μm), which are mainly associated with accretion and ejection processes (Muzerolle et al. 1998; Garcia Lopez et al. 2006; Caratti o Garatti et al. 2015a). In addition, permitted and forbidden atomic lines are also identified. In particular, Fe II (1.6811 μm), C I (1.6894 μm), and Mg I (1.7113 μm) are believed to originate from chromospheric activity (Hamann & Persson 1992a,b; Kelly et al. 1994). However, in the early stage of HMYSOs, there is no clear evidence of the existence of chromospheres. Hence, these lines may trace fluorescent emission. Indeed, OB stars emit sufficient UV photons to pump those lines by fluorescence. The [Fe II] line traces the base of the jet very close to the central engine (Nisini et al. 2002; Caratti o Garatti et al. 2006). In the K band, we detect the prominent Brγ line at 2.1662 μm, as well as the Na I doublet at 2.2062/2.2089 μm, which originates in the disc (Lorenzetti et al. 2011). Detected lines and corresponding fluxes are listed in Table 2. Interestingly, no photospheric features were detected in any of our spectra from all three instruments. This is probably due to the high veiling. From our ISAAC spectra we estimate rK ≳ 35. Therefore, expected photospheric lines such as He I lines at 1.571, 1.691, and 1.700 μm in the H band (Blum et al. 1997), or He I lines at 2.058, 2.112, 2.113 μm, He II at 2.185 μm, Ne III at 2.115 μm, and the C IV at 2.069, 2.078, 2.083 μm in the K band (Bik et al. 2005) cannot be seen. As a consequence, we are not able to confirm the spectral type of the central source.
Figure 2 (bottom right) zooms in on the Brγ line of the K band ISAAC spectrum. Notably, the Brγ line of IRAS 13481-6124 displays a P Cygni profile. Such an asymmetric line profile is indicative of an absorbing blue-shifted outflow with a measurable bulk velocity. We measure for the centroid of the blue absorption of the P-Cygni profile for the Brγ vrad ~−290 ± 40 km s−1 (which corresponds to a total velocity of vtot ~ 410 km s−1, considering an inclination angle of 45°), which is tracing the bulk of the material of the wind close to the star. This velocity is likely very close to the terminal velocity of the jet. Velocities measured at large scales (with H2 and [Fe II] emission) are similar to the velocity found close to the star. We also measure a radial velocity peak of ~ 10 ± 5 km s−1 and a full width at zero intensity (FWZI) of ~900 km s−1.
Figure 2 (upper right panel) shows the spectral energy distribution (SED) of IRAS 13481-6124 in the H and K bands. An increase in continuum flux towards the longer wavelengths is observed. This IR-excess is due to the combined effect of dust extinction and dust emission towards the source.
Observed emission lines on IRAS13481-6124.
 |
Fig. 2 Top left panel: H-band SINFONI spectrum on source. Detected lines and telluric features (⊕) are labelled. Bottom left panel: K-band SINFONI spectrum on source. Top right panel: SED from the H and K spectra. Bottom right panel: zoom-in of the Brγ line of the ISAAC spectrum. Velocities are with respect to the local standard of rest (LSR). |
4.2 Jet base: H I emission lines and their spatial displacements
CRIRES spectro-astrometry on the Paβ, Brγ, and Brα lines was performed to retrieve photocentre shifts of the line with respect to the continuum on mas scales (see Sect. 3). Figure 3 shows the spectrum of the Paβ line. Part of the line is missing due to the wavelength coverage and the gaps between the chips. Nonetheless, the shape of the line is clearly asymmetric, that is, the blue-shifted wing is absent. This effect is produced by self-absorption along the flow caused by the strong wind. The FWZI of the Paβ line is ~ 900 km s−1, consistent with what we find with ISAAC for the Brγ line. This would then suggest not just a similar wind origin, but also that it is produced in the same region. Unfortunately, no significant spectro-astrometric signal was detected on the Paβ line due to the low S/N (~7) of the Paβ line. The upper limit on the spectro-astrometric signal is defined by the detection limit, which is ~ 23 mas.
By contrast, the Brγ and Brα lines (S/N ~62 and ~130, respectively) show a significant spectro-astrometric signal. To improve the S/N of these lines, emission was binned spectrally: 32 channels (or pixel columns) were binned in the case of Brγ, and 16 for Brα, corresponding to a velocity resolution of 55 and 38 km s−1, respectively. Centroid positions were measured for points above 3σ of the continuum intensity, namely in the velocity ranges approximately − 110 to 250 km s−1 for the Brγ line and approximately −100 to 160 km s−1 for the Brα line (Figs. 4 and 5, upper left panels).
The Brγ line offsets (continuum-compensated, as discussed in Sect. 3.2) extend up to ~ 4.5 mas (~ 14 au) in the direction of the jet (i.e. parallel slit observations; Fig. 4, middle left panel) and up to ~ 2.5 mas (~ 8 au) in the direction orthogonal to the jet (i.e. perpendicular slit observations; Fig. 4, bottom left panel). Figure 4, right panel, shows the centroid offset in the plane of the sky. The offset of the Brγ line emitting region with respect to the continuum in the plane of the sky is ~ 3.5 mas (~ 11 au), which is a lower limit because with spectro-astrometry one does not spatially resolve the emission. The red line is the linear fit to the points. From the slope of the fit (m), one can derive the PA of the jet (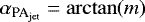 ). A value of
). A value of 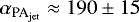 ° was found for the Brγ line. This result is in good agreement with previously derived values for the IRAS 13481-6124 jet (Kraus et al. 2010; Stecklum et al. 2012; Caratti o Garatti et al. 2015a), confirming that the Brγ is displaced along the jet axis (Fig. 4, right panel).
° was found for the Brγ line. This result is in good agreement with previously derived values for the IRAS 13481-6124 jet (Kraus et al. 2010; Stecklum et al. 2012; Caratti o Garatti et al. 2015a), confirming that the Brγ is displaced along the jet axis (Fig. 4, right panel).
Figure 5 shows the spectrum (upper left panel) and, for the first time in a HMYSO, the centroid offsets of the Brα line (middle and lower left panels). The line profile is clearly asymmetric, as seen in the previous H I lines. The FWZI of the three H I lines investigated with CRIRES are identical and coincident with the one obtained with ISAAC for the Brγ (~ 900 km s−1). As with the Brγ line, the Brα emission extends along the jet direction, up to ~ 5 mas (~ 15 au), which is again a lower limit. The blue-shifted wing of the Brackett lines extend towards to the south-west, and the red-shifted wing extend towards to the north-east. The magnitude of the centroid offset increases with increasing radial velocity; the blue-shifted wing offset reaches ~ 1.5 mas at approximately − 100 km s−1, while the red-shifted wing reaches ~ 5 mas at ~ 160 km s−1 (Fig. 5, right panel). These spectro-astrometric features reveal the presence of a bipolar jet close to the star (Takami et al. 2001), as previously detected through interferometric observations of the Brγ line (Caratti o Garatti et al. 2016). The red line indicates the linear fit to the Brα points. A PA of 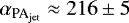 ° is derived. Reassuringly, both Brackett lines yield a similar jet PA and agree with previous studies, which relied on different techniques (Kraus et al. 2010; Stecklum et al. 2012; Caratti o Garatti et al. 2015a, 2016).
° is derived. Reassuringly, both Brackett lines yield a similar jet PA and agree with previous studies, which relied on different techniques (Kraus et al. 2010; Stecklum et al. 2012; Caratti o Garatti et al. 2015a, 2016).
However, it is worth noting that our spectro-astrometric results show a shift towards the north north-east with respect to the position of the central source, namely position (0,0) in Figs. 4 and 5. We would expect the red-shifted and blue-shifted jet offsets to straddle the continuum position. The simplest explanation is to consider that this effect is produced by a hypotheticalbinary companion in the surroundings of IRAS 13481-6124. However, there is no indication of a close (mas-scale) companion from NIR interferometry data (Kraus et al. 2010; Caratti o Garatti et al. 2016). In addition, there is no evidence of a companion in our SINFONI+AO observations, which achieved high spatial resolution (hundreds of mas). Finally, neither ISAAC nor CRIRES data show detection of a possible companion in the direction of the centroid offset. It would be detected as a second continuum in the CRIRES spectral images, which is not the case. Therefore, the spectro-astrometric offsets seem to have a different origin, such as an asymmetric FOV-dependent continuum distribution. We note that while the technique of spectro-astrometry cannot spatially resolve the emission, it does give information on the flux distribution. Conversely, interferometry resolves the jet at small (au) scales, but observes only a very small FOV around the star. As a consequence, it may partially resolve out extended, asymmetric continuum flux distribution. This explains why the AMBER Brγ emission is observed to be centred on the source, while the CRIRES spectro-astrometry reveals an offset. This offset can be explained by a contribution of large-scale circumstellar nebulosity.
 |
Fig. 3 CRIRES spectrum of the Paβ line. Intensity is normalised to the continuum. Velocity is with respect to the LSR. |
 |
Fig. 4 Left panel: CRIRES Brγ spectrum (top panel) along with the spectro-astrometric signal (in mas) detected in the jet parallel (middle panel) and perpendicular slit (bottom panel). The spectro-astrometric signal is continuum-corrected. Right panel: spectro-astrometric signal on the plane of the sky (north is up and east is to the left). The red line is the linear fit to the points giving a PA for the line-emitting region of 190 ± 15°. Error bars shown in both plots are 3σ. Velocities are colour coded and are the same in both panels. |
 |
Fig. 5 Left panel: CRIRES Brα spectrum (top panel) along with the spectro-astrometric signal (in mas) detected in the jet parallel (middle panel) and perpendicular slit (bottom panel). The spectro-astrometric signal is continuum-corrected. Right panel: spectro-astrometric signal on the plane of the sky (north is up and east is to the left). The red line is the linear fit to the points giving a PA for the line-emitting region of 216° ± 5°. Error bars shown in both plots are 3σ. Velocities are colour coded and are the same in both panels. |
4.3 Parsec-scale jet
H2 1 − 0 S(1) emission is detected along the whole jet, as well as on the leading bow shock (knots A and B), whereas a faint [Fe II] emission is detected on knots D and F along the jet (Fig. 6). No Brγ emission is detected along the parsec-scale jet, nor is it associated with the leading bow shock (Figs. 6 and 7). In addition to the 1 − 0 S(1) transition, other H2 lines (i.e. 1 − 0 S(10) 1.6665 μm, 2 − 1 S(3) 2.0734 μm, and 2 − 1 S(2) 2.1542 μm) are detectedin knot D and in the leading bow shock.
Figure 6 shows the position-velocity (PV) diagram for slit 2 encompassing the source and the jet, namely knots F and D. In the left panel, the SOFI H2 continuum-subtracted image of the knots (taken from Caratti o Garatti et al. 2015a) is shown as a reference. We note that the H2 knots at positive x-offsets extending to the south-east might belong to another outflow or be part of the outflow cavity (Caratti o Garatti et al. 2015a). The middle and right panels of the figure display the spectral images of the [Fe II] and H2 1 − 0 S(1) lines, respectively. In both images the YSO continuum has been subtracted (at Y = 0). Additionally, in the [Fe II] image an OH sky line was also subtracted, as evidenced by the residual noise at positive velocities. In this PV diagram, both atomic and molecular emission extend up to 70′′ (or ~1 pc), which corresponds to the tip of knot D. Along the F and D knots, the [Fe II] radial velocities range from approximately − 60 km s−1 up to approximately − 200 km s−1. On source, the H2 radial velocity is close to ~ 0 km s−1. Away from the source position (from 5″ on), the radial velocity ranges from approximately − 20 km s−1 to approximately − 200 km s−1. In particular, for knot D in [Fe II] and H2, we identify a high-velocity component (HVC) and a low-velocity component (LVC) (see Fig. 6, right panel, for the spectral image and Fig. 8 for the line profiles, top panels). Additionally, we identify in the [Fe II] spectral image a high- and low-velocity pair at 2″. The corresponding H2 emission is not detected, most likely because this position is so close to the source that H2 would be dissociated.
The H2 emission close to the source (i.e. from ~5″ to 25″, knot F) is indicative of jet emission, with each velocity component originating in a separate sub-structure (see Fig. 6, right panel). We note that the corresponding H2 line profile (upper left panel of Fig. 8) has been integrated over the whole knot F. In knot D, the H2 PV diagram clearly shows two velocity components at roughly the same spatial location, suggesting a bow shock structure (see, e.g. Hartigan et al. 1987), where the HVC is more likely to have a jet origin and the LVC an ambient material origin. However, the SOFI image of knot D does not show a clear bow shock morphology (Fig. 6, left panel). Observations at higher spatial resolution are required to fully disentangle the structure.
The PV diagram for slit 3 is shown in Fig. 7, where the slit was placed along the bow shock, encompassing both wing (knot B) and head (knot A). The left panel shows the SOFI H2 continuum-subtracted image of the blue-shifted bow shock (see Fig. 1). In the right panel, the emission of the H2 1 − 0 S(1) line is shown. Inspection of Fig. 1 reveals that A corresponds to the head of the bow shock and B the wing in this precessing jet. This interpretation is justified by the spectral image, which shows that A is mainly traced by the HVC and B is mainly traced by the LVC. The radial velocity ranges from a few km s−1 to approximately − 100 km s−1. Two velocity components are identified at some positions for each of the H2 transitions (see, e.g., Fig. 7, right panel and Fig. 8, bottom panels), and are indicative of a bow shock structure.
In orderto calculate dynamic properties, we must first determine the jet radial velocity. In the case of knot A + B and D, the two H2 velocity components are likely due to a bow shock geometry. Therefore, the radial velocity (vr) reported in Table 3 refers to the HVC. Meanwhile, in the case of knot F, an average radial velocity along the knot was considered. This is because the jet mass to be used in our calculation relies on lower resolution observations, which do not resolve the sub-structure (Caratti o Garatti et al. 2015a). Moreover, due to the disc geometry of this object (i ~45°; Kraus et al. 2010), the radial and tangential velocities of the jet can be assumed equal (i.e. vr = vt). This fact allows us to infer both tangential and total velocities. By combining the velocities with distance, length, and mass of each knot (by fitting several H2 transition intensities in a ro-vibrational diagram, based on low-resolution spectral data, Caratti o Garatti et al. 2015a), we can compute the main jet dynamic properties, reported in Table 3.
In particular, the mass-loss rate can be expressed as Ṁejec = Mknotvt∕l, where Mknot is the mass of the knot, vt is the tangential velocity, and l is the length of the knot, which is given by l = D × α, where D is the distance to the HMYSO and α is the extension of the knot on the sky. Values of the order of ~10−4 M⊙ yr−1 were found for all the knots, within the error, suggesting that the mass ejection rate has been roughly constant, within a factor of two, in the history of this source (see Table 3, Col. 4 for individual values of the various knots). A rough estimate of the mass-loss rate for the atomic component using the [Fe II] 1.644 μm line was made for the F knot (highest signal for this line, S∕N ~ 6.5). Using the same reasoning as Hartigan et al. (1994; see their Eqs. (5)–(10)) and using the atomic values and cosmic abundances for iron (Nussbaumer & Storey 1980; Mendoza 1983), an expression for the mass-loss rate based on the iron line was derived. The expression can be written as
![\begin{eqnarray*} \dot{M}_{[\ion{\textrm{Fe}}{\textrm{ii}}]}&=&1.9\times10^{-2}\left(\frac{N_e}{10^3({\,\textrm{cm}^{-3}})}\right)^{-1}\left(\frac{L}{L_{\odot}}\right)\frac{v_{\perp}}{l_{\perp}}\nonumber\\\nonumber\\&=&4.6\times10^{-6}\left(\frac{N_e}{10^3({\,\textrm{cm}^{-3}})}\right)^{-1}{\,\textrm{M}_{\odot}\,\textrm{yr}^{-1}} ,\end{eqnarray*}](/articles/aa/full_html/2018/08/aa32180-17/aa32180-17-eq11.png) (4)
(4)
where Ne is the electron density, L = 0.04406 L⊙ is the luminosity of the knot (after being dereddened using Rieke & Lebofsky 1985), v⊥ = 200 km s−1 is the velocity of the knot, and l⊥ = 2.5″ is the length of the knot. Assuming typical electron density values from protostellar jets (Ne ~ 5 × 104 cm−3), a mass-loss rate for the atomic component of the order of ~10−7 M⊙ yr−1 is obtained.
On the other hand, the jet momentum is P = Mknotvtotal, where 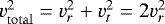 is the total velocity. Momentum values of 86, 44, and 80 M⊙ km s−1 for the F, D, and A + B knots were found, respectively (see Table 3, Col. 5).
is the total velocity. Momentum values of 86, 44, and 80 M⊙ km s−1 for the F, D, and A + B knots were found, respectively (see Table 3, Col. 5).
From the previous values, momentum rates can also be inferred, namely Ṗ = Ṁejecvtotal. Values of the momentum rate do not significantly vary along the jet, being of the order of 10−2 M⊙ yr−1 km s−1 (Table 3, Col. 6).
Inferred kinetic energies of the knots (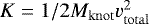 ) range from 1.1 × 1047 to 1.8 × 1047 erg (see Table 3, Col. 7). Finally, we also derive the dynamical time of each knot, that is, τdyn = d∕vt, where d is the distance of the knot from the central source. The dynamical time of the farthest bow shock provides us with an upper limit on the timescale of the ejecta, and, in turn, with an upper limit on the age of the central source. Values of the dynamical time range from 1800 to 26 800 yr for the closest and farthest emission, respectively (see Table 3, Col. 8).
) range from 1.1 × 1047 to 1.8 × 1047 erg (see Table 3, Col. 7). Finally, we also derive the dynamical time of each knot, that is, τdyn = d∕vt, where d is the distance of the knot from the central source. The dynamical time of the farthest bow shock provides us with an upper limit on the timescale of the ejecta, and, in turn, with an upper limit on the age of the central source. Values of the dynamical time range from 1800 to 26 800 yr for the closest and farthest emission, respectively (see Table 3, Col. 8).
 |
Fig. 6 PV diagram of slit 2. Left panel: SOFI H2 − K continuum subtracted image (Caratti o Garatti et al. 2015a). Contours are from 3σ to 20σ in steps of 5σ. Middle panel: [Fe II] (1.644 μm) line PV diagram tracing the atomic jet. Contours range from 3σ to 5σ in steps of 1σ. Right panel: H2 (2.12 μm) line PV diagram tracing the molecular jet. Contours are from 3σ to 20σ in steps of 5σ. Zoom-in panels of knots D (upper) and F (lower) with contours from 3σ to 80σ in steps of 20σ and from 3σ to 20σ in steps of 5σ, respectively.Radial velocities are in the LSR frame. |
 |
Fig. 7 PV diagram of slit 3. Left panel: SOFI H2 − K continuum subtracted of the blue bow shock. Right panel: H2 (2.12 μm) line showing the two velocity components of the bow shock. Contours are from 3σ to 20σ in steps of 5σ. Radial velocities are with respect to LSR. |
 |
Fig. 8 H2 1–0 S(1) line profiles for the investigated knots. Top left panel: F knot, top right panel: D knot, bottom left panel: A knot, and bottom right panel: B knot. Radial velocities are with respect to the LSR. |
Kinematic and dynamic properties of the IRAS 13481-6124 parsec-scale jet derived from the H2 1 − 0 S(1) line.
5 LTE model of the Brackett emitting region
To model the physical conditions of the H I emission detected on source in our SINFONI data, we used all the line fluxes from the Brackett series (Br26 to Brγ; see Table 2). Therefore, the main atomic gas parameters (close to the source), such as density, optical depth, and temperaturecan be derived. Homogeneous and isothermal conditions were assumed in the LTE model. Moreover, under LTE conditions, the kinetic temperature (Maxwell distribution) and excitation temperature (Boltzmann distribution) can be considered equal, that is, Tkin = Tex. Due to the high density and high temperature conditions expected, the LTE assumption is plausible for the system. One expects LTE to be valid for electron densities higher than ΣAul∕ΣCul, where Aul is the spontaneous radiation rates and Cul is the collisional de-excitation rates from level u to level l and the sum is over lower levels, that is, when collisions are the main source of excitation. Case B recombination can only reproduce our data when we set the density as high as n = 108 cm−3, which means that the gas would be in LTE.
In LTE conditions, the intensity can be written as
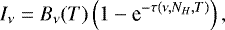 (5)
(5)
where Bν is the Planck function and τ is the optical depth. τ(ν, NH, T) can be calculated assuming a hydrogen column density (NH) and a temperature (T) for the system at a given frequency (ν). The line ratios among Brackett lines can be used to infer physical conditions of the emitting gas and discern an approximative size of the emitting region. The Brackett decrement was computed using the ratio of the various Brackett lines with respect to the Brγ line and assuming T = 10 000 K. Figure 9 shows the observed Brackett decrement (blue stars) and the best fit (red dots) corresponding to an optical depth of τbest = 2.5 at λ = 2.1662 μm. The observed data were fitted using Eq. (5).
To estimate the size of the Brγ emitting region, we used Eq. (6) assuming, for simplicity, a spherical geometry:
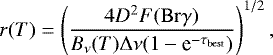 (6)
(6)
where D = 3.1 kpc is the distance to the star, F(Brγ) = 8.60 × 10−12 erg s−1 cm−2 is the integrated flux of the Brγ line (corrected by extinction using the extinction law of Rieke & Lebofsky 1985, and assuming a value of Av = 15 mag from Caratti o Garatti et al. 2015a), and Δν = Δv⋅ν∕c is the line width, using the optical depth obtained from the best fit. A value of ~ 1 au for the radius of theBrγ emitting region was inferred.
Using the estimated value of the radius of the Brγ emitting region, one can derive the density
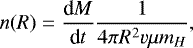 (7)
(7)
where dM∕dt = Ṁ = 1.8 × 10−5 M⊙ yr−1 is the mass-loss rate for the ionised jet (Purser et al. 2016), R = 1 au is the radius of the Brγ region derived before, v = 500 km s−1 is the velocity of the jet close to the star (Purser et al. 2016), μ = 1.24 is the mean atomic weight, and mH is the mass of the hydrogen atom. A value of ~2.5 × 109 cm−3 for the density was found for the Brγ emitting region.
 |
Fig. 9 Best fit of the observed Brackett decrement using our LTE model (red solid line). An optical depth of τ = 2.5 is inferred. |
6 Discussion
6.1 Atomic au-scale jet
Different approaches were used to study the innermost part of the parsec-scale jet of IRAS13481-6124. Examining the Brγ on source, the LTE model of the Brackett emitting region, and spectro-astrometry allows us to study the jet down to mas scales.
The P Cygni profile of the Brγ indicates the presence of a powerful ionised wind at the base of the au-scale jet (Fig. 2, bottom right panel). As the other H I line analysed, the line is clearly asymmetric, with strong self-absorption in the blue part of the line, produced by the outflow/wind, which reabsorbs the emission. The terminal radial velocity of the wind is around − 290 km s−1 (which corresponds to vtotal ~ 410 km s−1). The P Cygni profile is a peculiar feature that is not present in all HMYSOs. Cooper et al. (2013) found only 13 YSOs (in a sample of 195 objects) that also display a P Cygni profile, probably due to the geometry of these objects. Usually, the Brγ line in emission can have different origins: accretion of matter onto the star (Eisner et al. 2009; Tambovtseva et al. 2014), or ejected material in different manifestations –winds or jets (Weigelt et al. 2011; Stecklum et al. 2012; Garcia Lopez et al. 2015, 2016; Caratti o Garatti et al. 2015b). See also Coffey et al. (2010) and Tambovtseva et al. (2016) for a detailed discussion of the origin of Brγ emission. Nonetheless, one has to take into account that the broad profile of the H I around the line peak can also be accounted for by the significant contribution expected from the disc rotation motions very close to the base of the jet (vkep ~ 130 km yr−1, for M ~ 20 M⊙ and R ~ 10 R⊙). It seems clear, however, for this particular object that Brγ is tracing outflowing material and that the emission comes from the ionised jet (see also Caratti o Garatti et al. 2016).
The optical depth derived from the LTE model (τ = 2.5) suggests that the Brγ line is optically thick. Therefore, we can derive the density conditions of this region. A density of ~ 2.5 × 109 cm−3 was found. In addition, a radius of ~ 1 au was inferred assuming a circular shape for the Brγ emitting region. Using interferometric observations, Caratti o Garatti et al. (2016) found for the Brγ emitting region an extension of 6.4−13 au, observing a conical jet with an opening angle of ~ 30°. If the projected circular region from the model is transformed into two projected cones with the same opening angle, an extension of 4.8 au is found that matches the NIR interferometric observations reasonably well. This shows that it is important to study the Brγ line to constrain jet properties in YSOs, in particular of HMYSOs.
CRIRES spectro-astrometry shows a clear signature of well-collimated outflowing material close to the star for the H I Brγ and Brα lines. The increasing photocentre offset with increasing velocity proves that the emission is coming from ejected material (Takami et al. 2001; Whelan et al. 2005). For the first time, spectro-astrometry was performed in the Brα line, which has similar properties (in size and orientation) as the Brγ line. Position angles of 190° and 216° (and displacements of 11 and 15 au) were found for Brγ and Brα, respectively, suggesting that both lines might be tracing analogous regions. The good agreement between our results with those found by Caratti o Garatti et al. (2016) using interferometry on the Brγ line is quite remarkable. In both studies, the size of the line-emitting region is almost identical. The PA found by Caratti o Garatti et al. (2015a) for the parsec-scale jet (~ 206°) is consistent with the PA found in this study for the au-scale jet (~ 190−216°). The difference between the position angles might be due to the jet precession angle (~ 8°; Caratti o Garatti et al. 2015a). The consistency in size and position angle between the spectro-astrometry and the interferometry confirms the jet origin of the Brγ emission.
Summarising, these observations strongly suggest that the Brackett lines are tracing the jet and its outflowing material. On the one hand, the Brackett emission cannot be explained as magnetospheric accretion (i.e. extension of the magnetosphere). Nor can the H I emission originate from a Keplerian disc, as the spectro-astrometric results would not show a clear alignment with the jet axis and increasing velocity with increasing offset, but rather a displacement following the disc and with Keplerian rotation where the red and blue emission would be clearly differentiated with faster velocities closer to the star. On the other hand, H I emission from UV pumping seems apparent, as we clearly detect lines (namely, C I, Mg I, etc.), that seem to be connected to a photodissociation region (PDR). However, the Brackett line profiles show broad wings at high velocities. Moreover, one would expect a spherical shape in the distribution of PDR emission. We do not discard that some contribution of the Brackett lines may come from a PDR, but this seems negligible in comparison with the shocked emission. This can be shown by calculating the Ströngrem radius for IRAS13481-6124 (Draine 2011):
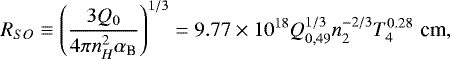 (8)
(8)
where Q0,49 ≡ Q0∕1049 s−1, Q0 is the rate of emission of hydrogen-ionising photons, n2 ≡ nH∕102 cm−3, T4 = T∕104 K, and αB is given by
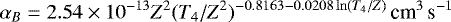 (9)
(9)
where Sν is the radio flux, D is the distance to the object, and ν9 = ν∕GHz is the frequency of the radio flux.
The Q0 value was calculated using the radio flux on source from (Purser et al. (2016; 9.1 ± 0.07 mJy at 17.0 GHz). Considering logQ0 = 44.75, T =10 000 K, and n =2.5 × 109 cm−3 (from the LTE model; see Sect. 5), a value of ~0.25 au for the Strömgren radius was inferred. The Strömgren radius for this star is much smaller than the extension of the Brackett lines found using interferometry (6.4–13 au; Caratti o Garatti et al. 2016), confirming that the H I Brackett lines are most likely tracing the au-scale jet.
6.2 Molecular parsec-scale jet in context
As was seen in the previous section, atomic hydrogen lines mainly trace the au-scale base of the jet. The composition of the NIR jet changes with distance from the source, with a smooth transition from atomic to molecular. At parsec scales, the observed jet becomes fully molecular, in the form of molecular hydrogen (H2). Close to the central engine, the molecular hydrogen cannot survive since UV photons would dissociate the molecule and only atomic hydrogen would survive. Therefore, there is a transition with distance between the atomic and the molecular component. From our observations, the molecular component starts at ~ 5″−10″ (i.e., 15 000−30 000 au) and extends up to ~170″−180″ (i.e., 2.5−2.7 pc).
Notably, very high radial velocities are found in the H2 emission lines along the knots of the parsec-scale jet: the F, D, and A + B knots. These values are well above the H2 velocity dissociation (~ 50 km s−1; Smith 1994), which can reach up to ~80 km s−1 if a strong magnetic field is present (Le Bourlot et al. 2002). This phenomenon has previously been reported in other studies of jets driven by low-mass (Davis et al. 2000; Chrysostomou et al. 2000) and high-mass protostars (Davis et al. 2004; Caratti o Garatti et al. 2008). Burton & Geballe (1986) proposed various mechanisms to explain the large line-widths observed in the H2 lines, favouring the scenario that the shocked H2 gas is in a medium that has been set in motion in fast-moving clumps. This scenario allows one to measure high-velocity H2 components (Chrysostomou et al. 2000), as the measured velocity is a combination of the medium and shock velocities. Davis et al. (2004) discussed that a combination of magnetically mediated C-type shock and inclination of the flow with respect to the plane of the sky, H2 line widths of up to 80−100 km s−1 are plausible. In this context, the radial velocity found in terminal bow shock (A + B knots; ~ 95 km s−1) can be easily explained. The leading bow shock must have moved in a steady medium and likely accelerated it as it propagated. This view is supported by the increasing velocity measured towards the central engine. The radial velocity found in knot D (~ 100 km s−1) is faster than the leading A + B bow shock. The gas observed in this knot is probably moving into a medium that has been set in motion before by the forward shocks. In addition, F is the fastest knot found along the parsec-scale jet (~ 200 km s−1), supporting the idea that this emission is embedded in an accelerated medium. Devine et al. (1997) and Chrysostomou et al. (2000) also reported a decrease in velocity with distance from the central source, which supports our results. This interpretation is also in agreement with the values of 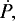 which slightly increase towards the central engine (see Fig. 10, bottom panel).
which slightly increase towards the central engine (see Fig. 10, bottom panel).
The, dynamical ages of the A + B knots are around ~ 26 800 yr, and they are the farthest structure in the system of the blue-shifted NIR jet. This value is consistent with the jet phase timescale of ~ 4 × 104 yr suggested by Guzmán et al. (2012). The dynamical age found for this knot is compatible, and might be even more accurate for the age of the star, with the age derived from SED modelling (~ 6 × 104 yr; Grave & Kumar 2009). Another interesting result concerns the roughly constant mass-loss rate value (~ 10−4 M⊙ yr−1) found along the various knots (see Fig. 10, top panel, and Table 3). This suggests that the ejection, and in turn, accretion of material has been constant in the formation history of IRAS 13481-6124. The ejection–accretion processes are indeed closely related (see, e.g., Cabrit 2007; Cabrit et al. 2010). For lower-mass YSOs, the ratios between the mass ejection rate (Ṁejec) and the mass-accretion rate (Ṁacc) are found to be ≳0.1 (Antoniucci et al. 2008). If one considers a similar relation for the high-mass regime (0.1≲Ṁejec∕Ṁacc ≲ 0.3; Cabrit 2007), one obtains a mass-accretion rate of 3.33 × 10−4 ≲Ṁacc ≲ 10−3 M⊙ yr−1. Then, one can estimate the mass of the central object multiplying the mass-accretion rate by the dynamical age giving rise to 12 ≲ M*≲ 35 M⊙, consistent with the mass derived from SED modelling (~20 M⊙; Grave & Kumar 2009). Therefore, itseems plausible that Ṁejec∕Ṁacc ratio for at least this HMYSO is similar to those found in low-mass YSOs.
 |
Fig. 10 Top panel: inferred mass-loss rates versus distance for the various knots. Bottom panel: inferred thrust versus distance. |
6.3 Comparison between the NIR and the radio jet
Our knowledge about HMYSOs is largely determined by radio observations, and fundamental dynamic properties, such as the mass-loss rate or mass-accretion rate, are based on radio measurements where only the ionised component is considered (see, e.g., Guzmán et al. 2012; Rosero et al. 2016; Sanna et al. 2016; Purser et al. 2016). Physical properties derived from radio should be compared with those obtained from NIR observations for a better understanding of the formation of massive stars. To discern whether there is significant difference, we compared the dynamical properties of the radio jet (Purser et al. 2016) with those of the NIR jet.
We are in the position to estimate the ionisation fraction (x0) of the HMYSO jet. Purser et al. (2016) give an ionised mass-loss rate of Ṁejec = 1.792 ± 1.338 × 10−5 M⊙ yr−1 assuming a jet velocity of 500 km s−1 and an ionisation fraction of 0.2. If we remove the velocity and ionisation fraction dependence from their Eq. (5), we can write 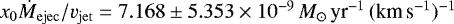 (see Cesaroni et al. 2018). From our NIR observations, we can assume that the mass-loss rate close to the star is similar to the one derived along the parsec-scale jet (Ṁejec ~ 1.766 ± 0.276 × 10−4 M⊙ yr−1, roughly constant in the formation history of the star). Meanwhile, the P Cygni profile of the Brγ gives a range of velocities for the wind at the base of the jet close to the central source, that is, vjet = 400−1100 km s−1. Combining the above results, we obtain x0 ~ 2−5% ± 3%. Therefore, a conservative upper limit of x0 ≲ 8% can be considered for the ionisation fraction of IRAS 13481-6124, suggesting that only a small portion of the whole jet is ionised. Notably, similar results have also been found in both high-mass (Cesaroni et al. 2018) and low-mass (Ainsworth et al. 2013) regimes. This calculation should be considered tentative because of the underlying assumptions and large uncertainties.
(see Cesaroni et al. 2018). From our NIR observations, we can assume that the mass-loss rate close to the star is similar to the one derived along the parsec-scale jet (Ṁejec ~ 1.766 ± 0.276 × 10−4 M⊙ yr−1, roughly constant in the formation history of the star). Meanwhile, the P Cygni profile of the Brγ gives a range of velocities for the wind at the base of the jet close to the central source, that is, vjet = 400−1100 km s−1. Combining the above results, we obtain x0 ~ 2−5% ± 3%. Therefore, a conservative upper limit of x0 ≲ 8% can be considered for the ionisation fraction of IRAS 13481-6124, suggesting that only a small portion of the whole jet is ionised. Notably, similar results have also been found in both high-mass (Cesaroni et al. 2018) and low-mass (Ainsworth et al. 2013) regimes. This calculation should be considered tentative because of the underlying assumptions and large uncertainties.
It is also worth pointing out that the low mass-loss rates of HMYSO radio jets seem to be a frequent characteristic in all ionised jets. For example, Sanna et al. (2016) find a mass-loss rate for the radio jet of ~ 8 × 10−6 M⊙ yr−1 in a 20 M⊙ protostar, and Purser et al. (2016) find a typical mass-loss rate of ~1.4 × 10−5 M⊙ yr−1 for a sampleof HMYSOs. This issue has previously been considered by Guzmán et al. (2012). To explain the discrepancy between the momentum of the radio jet and the molecular outflow, the authors suggested that the jet is not entirely ionised, as we are now demonstrating. Moreover, if one estimates the mass-accretion rate from the mass ejection rate of the radio jets (by assuming 0.1 ≲Ṁejec∕Ṁacc ≲ 0.3), one obtains a very low mass for the central object (assuming a typical age of few 104 yr). In particular, for IRAS 13481-6124, we would derive a value of Ṁacc ≲ 10−4 M⊙ yr−1, which yields M*~ 3.5−6 M⊙, in complete disagreement with the estimate of the central mass (M*~ 20 M⊙). Therefore, we conclude that the NIR jet is tracing the majority of the ejecta and the radio jet just a small portion of it. This is truly important because our mass-loss rate estimates for HMYSOs rely on radio measurements that trace a small percentage of the whole ejection. Nevertheless, both are likely part of the primary jet, as is revealed by comparing the thrust (Ṗ) for the radio (~ 10−2 M⊙ yr−1 km s−1 Purser et al. 2016) and the NIR (roughly constant to ~10−2 M⊙ yr−1 km s−1; see Fig. 10, bottom panel and Table 3) regimes.
7 Conclusions
We used three ESO-VLT instruments, SINFONI, CRIRES, and ISAAC, to study the au- and parsec-scale jet as well as the immediate environment of the HMYSO IRAS 13481-6124. Kinematic and dynamic properties were investigated at au and parsec scales, including the connection between the two. A comparison between the NIR jet and the radio jet was made. We summarise our main results and conclusions in the following points:
Several emission lines were detected on source that are mainly associated with accretion and ejection activity (H I, [Fe II]) with the presence of the disc (Na I), and with UV-pumped emission (Fe II, C I, K I, Mg I).
The Brγ line was detected on source with a terminal radial velocity of approximately −290 km s−1. From all three instruments, the characteristic P Cygni profile was identified, suggesting that the line is tracing ejection from a powerful bipolar wind very close to the central engine.
The technique of spectro-astrometry was applied to the Brγ line and for the first time to the Brα line, revealing the atomic nature of the au-scale jet. The PA (~190 ± 15° and ~216 ± 5° for Brγ and Brα, respectively) and the high collimation of the au-scale jet match the parsec-scale jet quite well. The photocentre offset with respect to the continuum of the Brγ and Brα emitting region is at least ~11 au and ~15 au, respectively.
Molecular hydrogen (H2) emission lines were used to derive dynamic and kinematic properties of the parsec-scale jet. Radial velocities were measured, and mass-loss rate, momentum, thrust, kinetic energy, and dynamical time were computed for the various knots that form the jet. Roughly constant mass-loss rates of the order of ~10−4 M⊙ yr−1 were found along the parsec-scale jet. From this value, a mass-accretion rate of ~3 × 10−4−10−3 M⊙ yr−1 was inferred. High H2 radial velocities (from 100 to 200 km s−1) were found likely due to the relative motion of the jet in an already-moving medium.
-
The ionisation fraction of the HMYSO jet driven was determined to have a tentative upper limit of x0 ≲ 8%, suggesting that the radio jet traces only a small fraction of the entire ejecta, whereas the NIR jet traces the majority.
In conclusion, the HMYSO jet of IRAS 13481-6124 is traced mainly by atomic species at au scales but molecular species at parsec scales. Our derived ionisation fraction implies that the NIR component traces the bulk of the ejecta.
Acknowledgements
We would like to acknowledge Simon Purser for his inestimable help in gently transferring his radio data for the object IRAS13481-6124, which improved the discussion of the paper. We thank the anonymous referee for constructive comments. R.F. acknowledges support from Science Foundation Ireland (grant No. 13/ERC/12907). A.C.G. and T.P.R. have received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 743029). R.G.L has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Grant (agreement No. 706320). S.K. acknowledges support from an STFC Rutherford Fellowship (ST/J004030/1) and ERC Starting Grant (grant agreement No. 639889).
References
- Ainsworth, R. E., Ray, T. P., Scaife, A. M. M., Greaves, J. S., & Beswick, R. J. 2013, MNRAS, 436, L64 [NASA ADS] [CrossRef] [Google Scholar]
- Antoniucci, S., Nisini, B., Giannini, T., & Lorenzetti, D. 2008, A&A, 479, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailey, J. 1998, MNRAS, 301, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Beltrán, M. T. & de Wit, W. J. 2016, A&ARv, 24, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Schilke, P., Sridharan, T. K., et al. 2002, A&A, 383, 892 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bik, A., Kaper, L., Hanson, M. M., & Smits, M. 2005, A&A, 440, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blum, R. D., Ramond, T. M., Conti, P. S., Figer, D. F., & Sellgren, K. 1997, AJ, 113, 1855 [NASA ADS] [CrossRef] [Google Scholar]
- Boley, P. A., Kraus, S., de Wit, W.-J., et al. 2016, A&A, 586, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brannigan, E., Takami, M., Chrysostomou, A., & Bailey, J. 2006, MNRAS, 367, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Burton, M. G., & Geballe, T. R. 1986, MNRAS, 223, 13P [NASA ADS] [CrossRef] [Google Scholar]
- Cabrit, S. 2007, in Star-Disk Interaction in Young Stars, eds. J. Bouvier & I. Appenzeller, IAU Symp., 243, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrit, S., Ferreira, J., Dougados, C., & Garcia, P. 2010, Highlights of Astronomy, 15, 261 [Google Scholar]
- Caratti o Garatti, A., Giannini, T., Nisini, B., & Lorenzetti, D. 2006, A&A, 449, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caratti o Garatti, A., Froebrich, D., Eislöffel, J., Giannini, T., & Nisini, B. 2008, A&A, 485, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caratti o Garatti, A., Stecklum, B., Linz, H., Garcia Lopez, R., & Sanna, A. 2015a, A&A, 573, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caratti o Garatti, A., Tambovtseva, L. V., Garcia Lopez, R., et al. 2015b, A&A, 582, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caratti o Garatti, A., Stecklum, B., Weigelt, G., et al. 2016, A&A, 589, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caratti o Garatti, A., Stecklum, B., Garcia Lopez, R., et al. 2017, Nat. Phys., 13, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Cesaroni, R., Massi, F., Arcidiacono, C., et al. 2013, A&A, 549, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cesaroni, R. M., Neri, R., Sanna, A., et al. 2018, A&A, 612, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chrysostomou, A., Hobson, J., Davis, C. J., Smith, M. D., & Berndsen, A. 2000, MNRAS, 314, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Coffey, D., Bacciotti, F., Podio, L., & Nisini, B. 2010, ApJ, 719, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, H. D. B., Lumsden, S. L., Oudmaijer, R. D., et al. 2013, MNRAS, 430, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, C. J., Berndsen, A., Smith, M. D., Chrysostomou, A., & Hobson, J. 2000, MNRAS, 314, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, C. J., Varricatt, W. P., Todd, S. P., & Ramsay Howat, S. K. 2004, A&A, 425, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davies, B., Lumsden, S. L., Hoare, M. G., Oudmaijer, R. D., & de Wit, W.-J. 2010, MNRAS, 402, 1504 [NASA ADS] [CrossRef] [Google Scholar]
- Devine, D., Bally, J., Reipurth, B., & Heathcote, S. 1997, AJ, 114, 2095 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton, NJ: Princeton University Press) [Google Scholar]
- Eisenhauer, F., Abuter, R., Bickert, K., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye & A. F. M. Moorwood, Proc. SPIE, 4841, 1548 [Google Scholar]
- Eisner, J. A., Graham, J. R., Akeson, R. L., & Najita, J. 2009, ApJ, 692, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia Lopez, R., Natta, A., Testi, L., & Habart, E. 2006, A&A, 459, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia Lopez, R., Tambovtseva, L. V., Schertl, D., et al. 2015, A&A, 576, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia Lopez, R., Kurosawa, R., Caratti o Garatti, A., et al. 2016, MNRAS, 456, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Grave, J. M. C., & Kumar, M. S. N. 2009, A&A, 498, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gredel, R. 2006, A&A, 457, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guzmán, A. E., Garay, G., Brooks, K. J., & Voronkov, M. A. 2012, ApJ, 753, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, F., & Persson, S. E. 1992a, ApJS, 82, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, F., & Persson, S. E. 1992b, ApJS, 82, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, P., Raymond, J., & Hartmann, L. 1987, ApJ, 316, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, P., Morse, J. A., & Raymond, J. 1994, ApJ, 436, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Ilee, J. D., Wheelwright, H. E., Oudmaijer, R. D., et al. 2013, MNRAS, 429, 2960 [NASA ADS] [CrossRef] [Google Scholar]
- Kaeufl, H.-U., Ballester, P., Biereichel, P., et al. 2004, in Ground-based Instrumentation for Astronomy, eds. A. F. M. Moorwood & M. Iye, Proc. SPIE, 5492, 1218 [CrossRef] [Google Scholar]
- Kelly, D. M., Rieke, G. H., & Campbell, B. 1994, ApJ, 425, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, S., Hofmann, K.-H., Menten, K. M., et al. 2010, Nature, 466, 339 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Kraus, S., Kluska, J., Kreplin, A., et al. 2017, ApJ, 835, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bourlot J., Pineau des Forêts, G., Flower, D. R., & Cabrit, S. 2002, MNRAS, 332, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Lorenzetti, D., Giannini, T., Larionov, V. M., et al. 2011, ApJ, 732, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Lumsden, S. L., Hoare, M. G., Urquhart, J. S., et al. 2013, ApJS, 208, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Masqué, J. M., Rodríguez, L. F., Araudo, A., et al. 2015, ApJ, 814, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Maud, L. T., Moore, T. J. T., Lumsden, S. L., et al. 2015, MNRAS, 453, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Mendoza, C. 1983, in Planetary Nebulae, ed. D. R. Flower, IAU Symp., 103, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Moorwood, A., Cuby, J.-G., Biereichel, P., et al. 1998, Messenger, 94, 7 [NASA ADS] [Google Scholar]
- Muzerolle, J., Hartmann, L., & Calvet, N. 1998, AJ, 116, 2965 [NASA ADS] [CrossRef] [Google Scholar]
- Nisini, B., Caratti o Garatti, A., Giannini, T., & Lorenzetti, D. 2002, A&A, 393, 1035 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nussbaumer, H., & Storey, P. J. 1980, A&A, 89, 308 [NASA ADS] [Google Scholar]
- Purser, S. J. D., Lumsden, S. L., Hoare, M. G., et al. 2016, MNRAS, 460, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Rosero, V., Hofner, P., Claussen, M., et al. 2016, ApJS, 227, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Sanna, A., Moscadelli, L., Cesaroni, R., et al. 2016, A&A, 596, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, M. D. 1994, MNRAS, 266, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Stecklum, B., Caratti o Garatti, A., & Linz, H. 2012, in Circumstellar Dynamics at High Resolution, eds. A. C. Carciofi & T. Rivinius, ASP Conf. Ser., 464, 369 [NASA ADS] [Google Scholar]
- Takami, M., Bailey, J., Gledhill, T. M., Chrysostomou, A., & Hough, J. H. 2001, MNRAS, 323, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Takami, M., Bailey, J., & Chrysostomou, A. 2003, A&A, 397, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tambovtseva, L. V., Grinin, V. P., & Weigelt, G. 2014, A&A, 562, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tambovtseva, L. V., Grinin, V. P., & Weigelt, G. 2016, A&A, 590, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Varricatt, W. P., Davis, C. J., Ramsay, S., & Todd, S. P. 2010, MNRAS, 404, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Weigelt, G., Grinin, V. P., Groh, J. H., et al. 2011, A&A, 527, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whelan, E., & Garcia, P. 2008, in Jets from Young Stars II, eds. F. Bacciotti, L. Testi, & E. Whelan, Lect. Notes Phys. (Berlin: Springer), 742, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Whelan, E. T., Ray, T. P., Bacciotti, F., et al. 2005, Nature, 435, 652 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
Kinematic and dynamic properties of the IRAS 13481-6124 parsec-scale jet derived from the H2 1 − 0 S(1) line.
All Figures
 |
Fig. 1 SOFI1 H2 continuum-subtracted image of IRAS 13481-6124 showing the blue-shifted jet knots, bow shock, and driving source. Knot positions are labelled A, B, D, and F, following the notation of Caratti o Garatti et al. (2015a). ISAAC slit positions (blue) are labelled SLIT 1, 2, and 3 for convenience, and correspond to observations on the source, jet, and bow shock, respectively. |
| In the text | |
 |
Fig. 2 Top left panel: H-band SINFONI spectrum on source. Detected lines and telluric features (⊕) are labelled. Bottom left panel: K-band SINFONI spectrum on source. Top right panel: SED from the H and K spectra. Bottom right panel: zoom-in of the Brγ line of the ISAAC spectrum. Velocities are with respect to the local standard of rest (LSR). |
| In the text | |
 |
Fig. 3 CRIRES spectrum of the Paβ line. Intensity is normalised to the continuum. Velocity is with respect to the LSR. |
| In the text | |
 |
Fig. 4 Left panel: CRIRES Brγ spectrum (top panel) along with the spectro-astrometric signal (in mas) detected in the jet parallel (middle panel) and perpendicular slit (bottom panel). The spectro-astrometric signal is continuum-corrected. Right panel: spectro-astrometric signal on the plane of the sky (north is up and east is to the left). The red line is the linear fit to the points giving a PA for the line-emitting region of 190 ± 15°. Error bars shown in both plots are 3σ. Velocities are colour coded and are the same in both panels. |
| In the text | |
 |
Fig. 5 Left panel: CRIRES Brα spectrum (top panel) along with the spectro-astrometric signal (in mas) detected in the jet parallel (middle panel) and perpendicular slit (bottom panel). The spectro-astrometric signal is continuum-corrected. Right panel: spectro-astrometric signal on the plane of the sky (north is up and east is to the left). The red line is the linear fit to the points giving a PA for the line-emitting region of 216° ± 5°. Error bars shown in both plots are 3σ. Velocities are colour coded and are the same in both panels. |
| In the text | |
 |
Fig. 6 PV diagram of slit 2. Left panel: SOFI H2 − K continuum subtracted image (Caratti o Garatti et al. 2015a). Contours are from 3σ to 20σ in steps of 5σ. Middle panel: [Fe II] (1.644 μm) line PV diagram tracing the atomic jet. Contours range from 3σ to 5σ in steps of 1σ. Right panel: H2 (2.12 μm) line PV diagram tracing the molecular jet. Contours are from 3σ to 20σ in steps of 5σ. Zoom-in panels of knots D (upper) and F (lower) with contours from 3σ to 80σ in steps of 20σ and from 3σ to 20σ in steps of 5σ, respectively.Radial velocities are in the LSR frame. |
| In the text | |
 |
Fig. 7 PV diagram of slit 3. Left panel: SOFI H2 − K continuum subtracted of the blue bow shock. Right panel: H2 (2.12 μm) line showing the two velocity components of the bow shock. Contours are from 3σ to 20σ in steps of 5σ. Radial velocities are with respect to LSR. |
| In the text | |
 |
Fig. 8 H2 1–0 S(1) line profiles for the investigated knots. Top left panel: F knot, top right panel: D knot, bottom left panel: A knot, and bottom right panel: B knot. Radial velocities are with respect to the LSR. |
| In the text | |
 |
Fig. 9 Best fit of the observed Brackett decrement using our LTE model (red solid line). An optical depth of τ = 2.5 is inferred. |
| In the text | |
 |
Fig. 10 Top panel: inferred mass-loss rates versus distance for the various knots. Bottom panel: inferred thrust versus distance. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.