| Issue |
A&A
Volume 615, July 2018
|
|
|---|---|---|
| Article Number | A139 | |
| Number of page(s) | 19 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201732546 | |
| Published online | 27 July 2018 | |
Effective temperature determinations of late-type stars based on 3D non-LTE Balmer line formation★
1
Max Planck Institute für Astronomy,
Königstuhl 17,
69117
Heidelberg,
Germany
e-mail: amarsi@mpia.de
2
Research School of Astronomy and Astrophysics, Australian National University,
Canberra,
ACT 2611,
Australia
e-mail: thomas.nordlander@anu.edu.au
3
ARC Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D),
Australia
4
Theoretical Astrophysics, Department of Physics and Astronomy, Uppsala University,
Box 516,
751 20
Uppsala,
Sweden
e-mail: paul.barklem@physics.uu.se
5
Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University,
Ny Munkegade 120,
8000
Aarhus C,
Denmark
Received:
24
December
2017
Accepted:
6
April
2018
Hydrogen Balmer lines are commonly used as spectroscopic effective temperature diagnostics of late-type stars. However, reliable inferences require accurate model spectra, and the absolute accuracy of classical methods that are based on one-dimensional (1D) hydrostatic model atmospheres and local thermodynamic equilibrium (LTE) is still unclear. To investigate this, we carry out 3D non-LTE calculations for the Balmer lines, performed, for the first time, over an extensive grid of 3D hydrodynamic STAGGER model atmospheres. For Hα, Hβ, and Hγ we find significant 1D non-LTE versus 3D non-LTE differences (3D effects): the outer wings tend to be stronger in 3D models, particularly for Hγ, while the inner wings can be weaker in 3D models, particularly for Hα. For Hα, we also find significant 3D LTE versus 3D non-LTE differences (non-LTE effects): in warmer stars (Teff ≈ 6500 K) the inner wings tend to be weaker in non-LTE models, while at lower effective temperatures (Teff ≈ 4500 K) the inner wings can be stronger in non-LTE models; the non-LTE effects are more severe at lower metallicities. We test our 3D non-LTE models against observations of well-studied benchmark stars. For the Sun, we infer concordant effective temperatures from Hα, Hβ, and Hγ; however the value is too low by around 50 K which could signal residual modelling shortcomings. For other benchmark stars, our 3D non-LTE models generally reproduce the effective temperatures to within 1σ uncertainties. For Hα, the absolute 3D effects and non-LTE effects can separately reach around 100 K, in terms of inferred effective temperatures. For metal-poor turn-off stars, 1D LTE models of Hα can underestimate effective temperatures by around 150 K. Our 3D non-LTE model spectra are publicly available, and can be used for more reliable spectroscopic effective temperature determinations.
Key words: radiative transfer / line: formation / line: profiles / stars: atmospheres / stars: late-type
The 3D non-LTE model spectra is also available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/615/A139
© ESO 2018
1 Introduction
Late-type stars can be described by a number of atmospheric parameters including effective temperature Teff, surface gravity logg, and metallicity ![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq1.png) 1. These parameters need to be precisely and accurately constrained before reliable surface chemical compositions can be obtained, and are needed to infer fundamental stellar parameters such as mass, radius, and age. Furthermore, these fundamental parameters, together with chemical compositions, are essential to constrain, for example, nucleosynthetic yields, Galaxy structure and formation, and Galactic chemical evolution.
1. These parameters need to be precisely and accurately constrained before reliable surface chemical compositions can be obtained, and are needed to infer fundamental stellar parameters such as mass, radius, and age. Furthermore, these fundamental parameters, together with chemical compositions, are essential to constrain, for example, nucleosynthetic yields, Galaxy structure and formation, and Galactic chemical evolution.
For dwarfs and giants with 4500eff∕K ≲ 8000, H I Balmer lines are useful spectroscopic diagnostics for the effective temperature (e.g. Cayrel de Strobel 1960; Searle & Oke 1962; Gehren 1981; Fuhrmann et al. 1993, 1994; Cayrel et al. 2011; Ruchti et al. 2013). For such stars, the emergent Balmer lines are characterised by pressure-broadened wings, with large sensitivity to the gas temperature. Furthermore, the wings have the same pressure dependence as the dominant source of continuous opacity, H−, such that, after continuum-normalisation, the wings are only weakly sensitive to the surface gravity (e.g. Gray 2008, Chap. 13). Lastly, H I is by far the dominant species in the photospheres of such stars, meaning that the line wings are only weakly sensitive to the surface metallicity and helium abundance. Consequently, the emergent Balmer lines can be used to measure effective temperatures to better than 100 K (Barklem et al. 2002, Table 4).
The usefulness of Balmer lines as effective temperature diagnostics is potentially limited by errors in the line formation models. The line broadening theory, for Stark broadening (Stehle 1994; Stehlé & Hutcheon 1999) and self-resonance broadening (Barklem et al. 2000; Allard et al. 2008), is now on firm footing (with a corresponding Teff error of the order 20 K; Barklem et al. 2002, Table 4). It has thus been suggested that the two factors limiting effective temperature determinations are the use of one-dimensional (1D) hydrostatic model atmospheres (e.g. Asplund 2005; Ludwig et al. 2009), and the assumption that the gas is in local thermodynamic equilibrium (LTE; e.g. Przybilla & Butler 2004a,b; Barklem 2007).
The problem with using 1D hydrostatic model atmospheres lies in their inability to describe stellar surface convection, which is a 3D and dynamic phenomenon. Thus, various mixing-length parameters (Böhm-Vitense 1958; Henyey et al. 1965) are usually employed in 1D simulations, to account for convective energy transport, alongside microturbulence and macroturbulence parameters (e.g. Gray 2008, Chap. 17), to account for the line broadening effects of the photospheric convective velocity field and temperature inhomogeneities. In contrast, ab initio 3D hydrodynamic stellar atmosphere simulations naturally encapsulate the physics of convection, and thus have no need to employ any such free parameters (e.g. Asplund et al. 2000; Nordlund et al. 2009; Magic et al. 2015).
Of the various parameters present in 1D analyses, the (dimensionless) mixing-length (αMLT) has the most influence on emergent Balmer lines, via its influence on the model temperature stratification. Fuhrmann et al. (1993, 1994) and Barklem et al. (2002) independently analysed observations of emergent Balmer lines and calibrated αMLT ≈ 0.5; while a degeneracy between the mixing-length and the y parameters (the latter describing the temperature profile within convective elements; e.g. Henyey et al. 1965) influences this calibration, the degeneracy is such that both low αMLT and low y are favoured. This reflects that the formation of Balmer line wings is biased towards the hot convective upflows. In contrast, calibrations that account for the overall effects of convective energy transport (i.e. that consider the role of both upflows and downflows), for example by matching the adiabatic entropy or the mean temperature structure of the deep convection zone (e.g. Ludwig et al. 1999; Trampedach et al. 2014; Magic et al. 2015), or by considering emergent continuum fluxes (e.g. Steffen & Ludwig 1999), give significantly higher values, typically in the range 1.6 ≲αMLT ≲ 2.1 after adopting standard values for y and the other mixing-length parameters.
Earlier works have already illustrated the importance of adopting 3D model atmospheres when modelling Balmer line formation. For example, Tremblay et al. (2011, 2013) demonstrated how 3D hydrodynamical modelling could resolve the problem of the surface gravity distribution of DA white dwarfs, wherein the surface gravities of cooler DA white dwarfs determined from Balmer line modelling based on 1D model atmospheres and mixing-length theory were up to 0.2 dex higher than expected (in white dwarfs, the Balmer lines are pressure-sensitive). For late-type stars, Ludwig et al. (2009) used a differential 1D LTE versus 3D LTE comparison to demonstrate how 1D modelling is unable to predict the same emergent Balmer line shapes as 3D modelling, for any choice of mixing-length. They further showed that, compared to 3D LTE, effective temperatures determined by 1D LTE model emergent Balmer lines have errors reaching up to 300 K, depending on the atmospheric parameters and the Balmer line in question.
Departures from LTE are an added complication. Using theoretical and semi-empirical 1D model atmospheres, and the most complete model hydrogen atom to date, Barklem (2007) showed that collisional processes are not necessarily efficient enough to make LTE valid for the Balmer line wings. Compared to 1D non-LTE modelling, effective temperatures that are determined using LTE models of the H α lines are potentially susceptible to errors reaching of the order 100 K. The predicted departures from LTE are generally expected to be larger in 3D hydrodynamic model atmospheres, where they are driven by the steep horizontal temperature gradients associated with overshooting convective upflows and downflows.
Motivated by these problems, we present a study of Balmer line formation on a grid of 3D hydrodynamic model atmospheres and 3D non-LTE radiative transfer. We describe the methodology in Sect. 2. We present the results of our simulations in Sect. 3, and present fits to well-studied benchmark stars in Sect. 4. We discuss the effective temperatures inferred for the benchmark stars in Sect. 5. We present 3D non-LTE model spectra for the astronomy community to use for effective temperature determinations in Sect. 6. We summarise our findings in Sect. 7.
2 Method
2.1 Model atmospheres
2.1.1 STAGGER-grid
Calculations were performed on 169 models of the STAGGER-grid of 3D hydrodynamic model atmospheres. We illustrate the gas temperature distributions of some typical model atmospheres in Fig. 1. We refer to Magic et al. (2013a) for a comprehensive description of the simulations. Here, we only provide an overview of the pertinent details.
The model atmospheres are characterised by three atmospheric parameters: ![$\left(T_{\mathrm{eff}},\log{g},\mathrm{\left[Fe/H\right]}\right)$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq2.png) . They assume standard chemical compositions: solar abundances from Asplund et al. (2009) scaled by
. They assume standard chemical compositions: solar abundances from Asplund et al. (2009) scaled by ![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq3.png) , with an implicit enhancement to α-element abundances of + 0.4 dex for
, with an implicit enhancement to α-element abundances of + 0.4 dex for ![$\mathrm{\left[Fe/H\right]}\leq-1.0$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq4.png) . The extent of the STAGGER-grid in each dimension is not regular (see Magic et al. 2013a, Fig. 1). The maximum extent in each dimension is 4000eff∕K ≲ 7000 in steps of roughly 500 K,
. The extent of the STAGGER-grid in each dimension is not regular (see Magic et al. 2013a, Fig. 1). The maximum extent in each dimension is 4000eff∕K ≲ 7000 in steps of roughly 500 K, 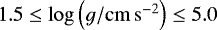 in steps of 0.5 dex, and
in steps of 0.5 dex, and ![$-4.0\leq\mathrm{\left[Fe/H\right]}\leq0.0$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq6.png) in steps of 1.0 dex; calculations were also performed on models with
in steps of 1.0 dex; calculations were also performed on models with ![$\mathrm{\left[Fe/H\right]}=+0.5$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq7.png) .
.
The original hydrodynamic simulations used a Cartesian mesh with 2403 grid-points. For this work, the snapshots were down-sampled in the two horizontal directions by a factor of three. Further, the optically thick layers (log τR ≳ 2) were trimmed, and the thermodynamic quantities were interpolated onto a new depth scale roughly equally spaced in the mean temperature so as to better resolve the steep, continuum-forming regions. The final number of grid-points was 80 × 80 × 220. Calculations were performed on typically five snapshots of each model spanning the entire sequence, so as to obtain temporally averaged emergent spectra. This number of snapshots is sufficient to obtain effective temperatures to better than 10 K precision (precluding any modelling or observational errors, which are typically much larger than 10 K).
 |
Fig. 1 Gas temperature-vertical optical depth distributions in 3D hydrodynamic models of turn-off stars (left panel) and sub-giants (right panel) with solar metallicity (top panel) and |
2.1.2 ATMO-grid
To understand the effect of using a consistent and realistic treatment of convection, calculations were also performed on a grid of 1D hydrostatic ATMO model atmospheres (Magic et al. 2013a, Appendix A). These were calculated on the same ![$\left(T_{\mathrm{eff}},\log{g},\mathrm{\left[Fe/H\right]}\right)$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq8.png) nodes as the 3D grid we described in Sect. 2.1.1. The ATMO simulations used the same equation of state and radiative transfer solver (angle quadrature, opacity-binning scheme, and numerical solver) as used by the STAGGER simulations, to facilitate a differential 1D vs. 3D comparison.
nodes as the 3D grid we described in Sect. 2.1.1. The ATMO simulations used the same equation of state and radiative transfer solver (angle quadrature, opacity-binning scheme, and numerical solver) as used by the STAGGER simulations, to facilitate a differential 1D vs. 3D comparison.
We illustrate the impact of the mixing-length on the 1D model atmospheres in Fig. 1. Lowering the mixing-length tends to steepen the temperature stratification in the deeper layers where the continuum forms. Since the Balmer lines are sensitive to the choice of mixing-length (e.g. Fuhrmann et al. 1993), line formation calculations were thus performed for three different mixing-lengths: αMLT = 1.0, 1.5, and 2.0. Other mixing-length parameters were set to standard values (y = 0.076, vconv = 8.0; e.g. Gustafsson et al. 2008). Turbulent pressure was neglected.
Line formation calculations based on 1D model atmospheres require extra microturbulent and macroturbulent broadening parameters (e.g. Gray 2008, Chap. 17) to reproduce the broadening effects of the photospheric convective velocity field and temperature inhomogeneities on lines without pronounced wings (e.g. Asplund et al. 2000). For simplicity we adopted throughout the study a depth-independent microturbulence of 1.0 km s−1, which is consistent with the value used to construct the model atmospheres, and neglected macroturbulence, which has no practical impact on the Balmer line profiles.
2.1.3 MARCS-grid
To quantify the 3D effects, the most differential approach is to compare results from the STAGGER-grid of 3D hydrodynamic model atmospheres(Sect. 2.1.1) with those from the ATMO-grid of 1D hydrostatic model atmospheres (Sect. 2.1.2). Nonetheless, we briefly note that calculations were also performed on an extensive grid of 1100 MARCS model atmospheres, with standard chemical compositions and standard mixing-length parameters (Gustafsson et al. 2008). The calculations on the 1D MARCS model atmospheres were performed in exactly the same way as those on the 1D ATMO model atmospheres.
The maximum extent in each dimension of the MARCS grid used here is 4000eff∕K ≤ 6750 in steps of 250 K, 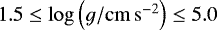 in steps of 0.5 dex, and
in steps of 0.5 dex, and ![$-4.0\leq\mathrm{\left[Fe/H\right]}\leq0.5$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq10.png) in steps of 0.25 dex for
in steps of 0.25 dex for ![$-1.0\leq\mathrm{\left[Fe/H\right]}\leq0.5$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq11.png) , 0.5 dex for
, 0.5 dex for ![$-3.0\leq\mathrm{\left[Fe/H\right]}\leq-1.0$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq12.png) , and 1.0 dex otherwise. The grid is complete in the parameter region of interest, and more finely-spaced in Teff and
, and 1.0 dex otherwise. The grid is complete in the parameter region of interest, and more finely-spaced in Teff and ![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq13.png) than the STAGGER-grid. Consequently, the resulting grid of model Balmer lines were used to estimate interpolation and extrapolation errors on the coarser and incomplete STAGGER-grid. We discuss this in Sect. 4.2.3.
than the STAGGER-grid. Consequently, the resulting grid of model Balmer lines were used to estimate interpolation and extrapolation errors on the coarser and incomplete STAGGER-grid. We discuss this in Sect. 4.2.3.
The MARCS-based results of the fits to benchmark stars that we present in Sect. 4 were found to be very similar to those from the 1D ATMO model atmospheres with the same mixing-length parameters (i.e. αMLT = 1.5, y = 0.076, vconv = 8.0), after accounting for interpolation and extrapolation errors. The largest differences in inferred effective temperatures were for H γ and only of the order 20 K, which is already much smaller than the uncertainties intrinsic to the method (mainly in placing the continuum). Consequently, for brevity, we do not discuss the results from the MARCS grid of model atmospheres in detail.
2.2 Post-processing line formation calculations
We used our 3D non-LTE radiative transfer code BALDER to calculate emergent Balmer line spectra for all of the models (1D and 3D; LTE and non-LTE). This code is originally based on the code MULTI3D (Botnen & Carlsson 1999; Leenaarts & Carlsson 2009), but with our own customisations (e.g. Amarsi et al. 2016a,b; Amarsi & Asplund 2017). We provide a brief overview of the code here.
The code employs the MALI algorithm (Rybicki & Hummer 1992) to find the statistical equilibrium of H I/H II simultaneously, assuming no feedback on the background atmosphere. The mean radiation field J was determined by solving the radiative transfer equation using a short characteristics integral solver (Ibgui et al. 2013), using the eight-point Lobatto quadrature on the interval ![$\left[-1,1\right]$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq14.png) for the integration over μ = cosθ, where θ is the angle relative to the vertical, and, for non-vertical rays, an equidistant four-point trapezoidal quadrature on the interval
for the integration over μ = cosθ, where θ is the angle relative to the vertical, and, for non-vertical rays, an equidistant four-point trapezoidal quadrature on the interval ![$\left[0,2\pi\right]$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq15.png) for the integration over the azimuthal angle ϕ.
for the integration over the azimuthal angle ϕ.
The equation-of-state (EOS) and background opacities were computed using our code BLUE, which was previously described in Amarsi et al. (2016b, Sect. 2.1.2). The EOS was recomputed in post-processing (i.e. with no feedback on the background atmosphere) assuming LTE with corrections − Δ χ to the ionisation potentials χ to account for Debye shielding. A more general treatment of perturbations caused by neighbouring particles exists in the occupation probability formalism (Däppen et al. 1987; Hummer & Mihalas 1988). Using the HBOP code, part of the HLINOP package (Barklem & Piskunov 2015), we tested the impact of adopting the occupation probability formalism on the emergent Balmer lines in 1D LTE. The Hγ line profiles become marginally weaker, with normalised flux residuals of the order 10−4, or of the order a few kelvin in effective temperature; the lower members of the Balmer series are even less affected. These errors are small, compared to other uncertainties inherent in the modelling. Background line opacities were precomputed on temperature-density grids for a given chemical composition, and interpolated onto the model atmosphere at runtime. On the other hand, background continuous opacities were computed at runtime for highest accuracy.
After the last iteration, the final emergent intensities were computed using an integral solver on a viewing-angle aligned grid (so as to avoid diffusion errors associated with interpolating the specific intensity; e.g. Peck et al. 2017). A monotonic cubic interpolation scheme was used to interpolate the extinction and source-function onto the ray-aligned grid; we found that the default linear interpolation scheme originally implemented in MULTI3D can lead to errors of up to 1000 K in the worst case (H γ in metal-poor red giants). The astrophysical fluxes were computed by disk-integrating the emergent intensities, using the seven-point Lobatto quadrature on the interval ![$\left[0,1\right]$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq16.png) for the integration over μ, and, for non-vertical rays, an equidistant eight-point trapezoidal quadrature on the interval
for the integration over μ, and, for non-vertical rays, an equidistant eight-point trapezoidal quadrature on the interval ![$\left[0,2\pi\right]$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq17.png) for the integration over the azimuthal angle ϕ. Since the integrand for the astrophysical flux is identically null at μ = 0, this amounts to 41 rays in total. Background line opacities were neglected at this stage. The spectra were trivially normalised, by repeating these radiative transfer calculations without any H I line opacities.
for the integration over the azimuthal angle ϕ. Since the integrand for the astrophysical flux is identically null at μ = 0, this amounts to 41 rays in total. Background line opacities were neglected at this stage. The spectra were trivially normalised, by repeating these radiative transfer calculations without any H I line opacities.
To calculate the hydrogen absorption line profiles 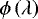 (which enter into the calculation of exctinction coefficients; e.g. Hubeny & Mihalas 2014, Chap. 8), we implemented into our code the Fortran modules HLINPROF and HLINOP (Barklem & Piskunov 2015). The former module was used for an accurate treatment of low Balmer absorption line profiles with lower state n = 2 and upper state n ≤ 6, and is based on Stehlé & Hutcheon (1999) for Stark broadening, and Barklem et al. (2000) for self-resonance broadening. The latter module was used for the remaining H I lines (in the solution of the statistical equilibrium); it is based on Griem (1960) and Vidal et al. (1973) for Stark broadening, and Ali & Griem (1966) for self-resonance broadening. More details can be found in Barklem (2007, Sect. 2.1.1; 2016, Sect. 4.1.1). Complete redistribution was assumed throughout, which means that the absorption line profiles are identical to the emission line profiles.
(which enter into the calculation of exctinction coefficients; e.g. Hubeny & Mihalas 2014, Chap. 8), we implemented into our code the Fortran modules HLINPROF and HLINOP (Barklem & Piskunov 2015). The former module was used for an accurate treatment of low Balmer absorption line profiles with lower state n = 2 and upper state n ≤ 6, and is based on Stehlé & Hutcheon (1999) for Stark broadening, and Barklem et al. (2000) for self-resonance broadening. The latter module was used for the remaining H I lines (in the solution of the statistical equilibrium); it is based on Griem (1960) and Vidal et al. (1973) for Stark broadening, and Ali & Griem (1966) for self-resonance broadening. More details can be found in Barklem (2007, Sect. 2.1.1; 2016, Sect. 4.1.1). Complete redistribution was assumed throughout, which means that the absorption line profiles are identical to the emission line profiles.
2.3 Hydrogen model atom and inelastic collisions
The model atom includes all H I states up to n = 20, as well as H II (so that the non-LTE excitation and ionisation balance were solved together, consistently). All lines and continua involving these levels were considered. Przybilla & Butler (2004a) recommended including at least the number of levels corresponding to the classical Inglis–Teller limit (e.g. Inglis & Teller 1939; Vidal 1966), for a given star. Using the semi-empirical solar model atmosphere of Holweger & Müller (1974), the limit at Tgas = 5772 K is n ≈ 11.6, which indicates that n = 20 is more than sufficient for this study of late-type stars.
Being very much a minority species in late-type stellar atmospheres, H− is not expected to influence the populations of H I or H II, and was thus treated in LTE. However, H− is the dominant source of background opacity in the optical region, so any departures from LTE in thisspecies would have a large influence on the results presented here. The non-LTE H− problem is highly non-trivial and is, to our knowledge, yet unsolved (Lites & Mihalas 1984). We intend to revisit this problem in a future study.
Since the energies and transition probabilities for hydrogen are known to exceptionally high precision, the main subtlety in constructingthe model atom is in the treatment of inelastic collisions. We based our construction on that presented in Barklem (2007, Sect. 2.1.2):
Inelastic H+e collisional excitation rate coefficients were taken from Przybilla & Butler (2004a), based on the R-matrix method in the close-coupling approximation, for the transitions between the states with n ≤ 7. Rate coefficients for the remaining transitions were calculated using the semi-empirical formula of Vriens & Smeets (1980).
Inelastic H+e collisional ionisation rate coefficients were based on the experimental results of Shah et al. (1987) for the n = 1 transition, and Defrance et al. (1981) for the n = 2 transition, both via the analytical formula of Barklem (2007). Rate coefficients for the remaining transitions were calculated using the semi-empirical formula of Vriens & Smeets (1980).
Inelastic H+H collisional excitation rate coefficients were taken from Bates & Lewis (1955), based on the Landau-Zener model, for the lone transition between the states with nlo = 2 and nup = 3. Rate coefficients for the transitions between the states with 4 ≤ nlo ≤ 10, 1 ≤ nup − nlo ≤ 5 were taken from Mihajlov et al. (2004), based on a semi-classical theory for resonant energy exchange in Rydberg atoms. In contrast to Barklem (2007), we used Kaulakys (1991, Eq. (18)), based on the free-electron model in the scattering length approximation, for the remaining transitions with nlo ≥ 4. These rates were calculated using the IDL packages MSWAVEF (Barklem 2017b), and KAULAKYS (Barklem 2017a). The remaining transitions, with nlo = 2, and nlo = 3, were neglected (see the end of this section).
Inelastic H+H collisional ionisation rate coefficients were taken from Mihajlov et al. (1996), based on a semi-classical theory for resonant energy exchange in Rydberg atoms, for the 4 ≤ nlo ≤ 10 transitions. A linear fit to the (logarithmic) rate coefficients against transition energy was obtained and extrapolated to obtain rate coefficients for transitions with nlo ≥ 11. The remaining transitions, with nlo = 2, and nlo = 3, were neglected (see the end of this section).
Inelastic H++H- mutual neutralisation rate coefficients were taken from Fussen & Kubach (1986), based on a quantum close-coupling treatment, for the nlo = 2 and nlo = 3 transitions, via the formula of Barklem (2007). More robust calculations were presented in Stenrup et al. (2009); however, their results compare well to those from Fussen & Kubach (1986), and Barklem (2007) demonstrated that these transitions are not very important for the Balmer line wings.
Here H+H refers to collisions with neutral hydrogen in the n = 1 ground state. Penning ionisation, involving collisions with neutral hydrogen in the n = 2 excited state (e.g. Bates et al. 1967), is not expected to be important (Barklem 2007) and was neglected here.
The treatment of inelastic H+H collisional ionisation from the nlo = 2 and nlo = 3 states, and also inelastic H+H collisional excitation from the nlo = 2 and nlo = 3 states into nup ≥ 4 states, are perhaps the main source of uncertainty in the non-LTE modelling. As discussed in Barklem (2007), there is presently no satisfactory description for these rates. The Drawin recipe (Drawin 1968, 1969), for example, predicts very small rates for these transitions, that have only a minor impact on the overall results. As we mentioned above, we thus decided to neglect these rates altogether, erring on the side of slightly overestimating the departures from LTE. We refer to Barklem (2007) for a detailed discussion of the sensitivity of the non-LTE effects on the collisional transitions.
3 Results
3.1 Formation depths
It is useful to first consider where in the model atmospheres that the Balmer lines form. The monochromatic contribution function to the flux depression in the lines, 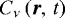 (Amarsi 2015, Eq. (14)), is useful here. For this discussion we define a monochromatic mean formation depth (Amarsi 2015, Sect. 2.4),
(Amarsi 2015, Eq. (14)), is useful here. For this discussion we define a monochromatic mean formation depth (Amarsi 2015, Sect. 2.4),
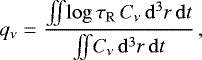 (1)
(1)
where we adopted logτR, the logarithmic vertical Rosseland-mean optical depth, as the reference depth scale.
In Fig. 2 we illustrate contribution functions for the H α and H γ lines in vertical slices of the turn-off model atmospheres shown in Fig. 1. Line formation generally follow the contours of vertical optical depth, rather than geometric height. In turn, in the deeper regions these contours trace the granulation pattern. It can be seen from the lighter shadings in the plots for H γ how the contribution function is sharply peaked around logτR ≈ 0; moreover, the line formation is biased towards the hot convective upflows, rather than the cool downflows. For H α, the contribution function extends further up into the atmosphere.
Across the grid, the Balmer line wings form mainly in the region − 1.0 ≲ logτR ≲ 0.5, with weaker lines forming in the more optically thick layers (thus, in cooler stars, or for higher members of the Balmer series, the formation region is pushed to deeper layers). For the metal-poor turn-off model atmosphere, the mean formation depths of the wings, here taken to be 0.2 nm redward of the line centre, are qν ≈−0.78 (Hα), − 0.43 (Hβ), and − 0.32 (Hγ). For the metal-poor sub-giant model atmosphere, the mean formation depths of the wings are qν ≈−0.35 (Hα), − 0.05 (Hβ), and 0.06 (Hγ).
Based on this discussion, the 3D effects on the Balmer line wings are expected to be more positive for H γ than for H β, and for H β than for H α (where a positive difference implies weaker, or less depressed absorption lines in 1D than in 3D), at least for higher values of mixing-length. The contribution functions for higher members of the Balmer series peak in deeper regions of the photosphere, probing regions in the (upflows of the) 3D model atmospheres that typically have increasingly steeper temperature gradients compared to in the corresponding 1D model atmospheres. It also follows that the 3D effects are expected to be more sensitive to the mixing-length for higher members of the Balmer series, since this parameter has a larger effect deeper in the photosphere (Fig. 1). However, the signs and absolute magnitudes of these 1D non-LTE versus 3D non-LTE differences depend on the atmospheric parameters, adopted mixing-length, and wavelength (Sect. 3.3).
We briefly note that the distribution of line formation of the Balmer wings is slightly skewed towards the optically thin regions of the photosphere. For Hα in particular, some line formation is able to occur very high up in the atmosphere, log τR ≈−3.0, in the regions where the local gas temperature is higher than its surroundings. These hot regions are associated with reversed granulation, and this effect is enhanced in the metal-poor regime (Magic et al. 2013b, Appendix A), as can be seen in Fig. 2.
For the Sun, Balmer line cores are known to have a significant chromospheric contribution (e.g. Leenaarts et al. 2012), despite the ability of 1D model photospheres to approximately reproduce time-averaged observations of the core flux (e.g. Przybilla & Butler 2004b). For cooler stars, such as the red giant Arcturus, 1D model photospheres fail to satisfactorily reproduce observations of the Balmer line cores (e.g. Przybilla & Butler 2004b; Bergemann et al. 2016). Modelling the chromospheric contribution to the emergent Balmer line cores is beyond the scope of the present work; we just note here that our models are not reliable for the emergent Balmer line cores.
 |
Fig. 2 Gas temperatures T (first row) and contribution functions Cν for the inner wings (0.2 nm redward of the line centre) of the Hα (second row) and Hγ (third row) lines, in vertical slices of the solar metallicity (left column) and metal-poor (right column) model atmospheres shown in Fig. 1. Lighter shading indicates larger temperatures (first row), and more emergent flux contribution (second and third rows). Contours of constant log τR are overdrawn. In each plot, the contribution functions are normalised such that their maximum values are unity. |
3.2 Departure coefficients
The departure coefficients are defined as the ratio of non-LTE to LTE level populations:
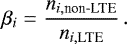 (2)
(2)
To first order, the non-LTE line opacity is enhanced by a factor βlo, while the non-LTE line source function is enhanced by a factor βup∕βlo (e.g. Rutten 2003, Chap. 2).
In Fig. 3 we illustrate departure coefficients in the model atmospheres shown in Fig. 1. They are plotted against the reference vertical optical depth (log τR); this correlates well with line formation, with the Balmer line wings mostly forming around − 1.0 ≲ logτR ≲ 0.5 (Sect. 3.1).
Figure 3 demonstrates broad distributions for the departure coefficients of the n = 2 and n > 2 levels, through which the Balmer lines form. The departure mechanisms (which we briefly describe at the end of this section) are similar in 1D and in 3D, and consequently the departure coefficients in the 1D model atmospheres follow the distributions in the 3D model atmospheres. A notable exception is for n = 2 in the metal-poor turn-off star. Here, the distribution of departure coefficients is bimodal. The mode corresponding to larger departures (reaching β2 ≈ 1.4 in the upper layers) corresponds to line formation in the regions of high temperature in the upper atmosphere (see Fig. 2, second column). These reverse granulation features are obviously not present in the 1D model atmospheres. As such, the departure coefficients from the 1D model atmospheres follows the other mode, which stays close to unity.
The departure coefficients have a strong dependence on metallicity. Generally, at solar metallicity, the departures in the region − 1.0 ≲ logτR ≲ 0.5 are not very severe. For the Balmer levels, they are less than around 5%. The departures grow towards lower metallicities. At ![$\mathrm{\left[Fe/H\right]}=-3.0$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq22.png) , the departures are of the order 10−20%. This dependence of the departure coefficients on metallicity translates into more severe non-LTE effects on the emergent Balmer line wings at lower
, the departures are of the order 10−20%. This dependence of the departure coefficients on metallicity translates into more severe non-LTE effects on the emergent Balmer line wings at lower ![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq23.png) , consistent with Barklem (2007), and with our own results in Sect. 3.3.
, consistent with Barklem (2007), and with our own results in Sect. 3.3.
The departure coefficients also have a dependence on effective temperature. At higher effective temperatures, there is predominantly a source function effect on the Balmer line wings: for the lower Balmer level β2 stays close to unity, while for the upper Balmer levels βup are larger than unity. The Balmer line wings are thus weaker when departures from LTE are taken into account. On the other hand, towards lower effective temperatures, an opacity effect becomes increasingly more important: β2 becomes larger than unity, and the ratios β2 to βup move closer to unity. The opacity effect strengthens the Balmer line wings, whereas the source function effect weakens them. Since these effects are in competition, the non-LTE effects on the emergent line profiles are not necessarily more severe at lower Teff, as we shall demonstrate in Sect. 3.3.
To aid intuition, we provide a brief, qualitative description on what causes these opacity and source function effects. The overpopulation of the n = 2 level, and thus the opacity effect, is largely driven by photon pumping through the Ly α line: the suprathermal UV radiation field leads to a flow from the n = 1 population reservoir into the n = 2 level; this effect is enhanced at lower metallicities and lower effective temperatures (Fig. 3). Were radiative coupling via the Ly α line to be omitted, the lower Balmer level would satisfy β2 ≈ 1, even at the top of the simulation domain logτR ≈−5. A careful treatment of Lyα and the UV flux is likely important for accurate non-LTE modelling of the Balmer lines: a future work should examine how relaxing the assumption of complete redistribution for the Ly α wings in the stellar photosphere, may affect the departure coefficients of the n = 2 level and through that the Balmer line wings (as was done for a solar chromospheric model by Leenaarts et al. 2012).
The statistical equilibrium of the n > 2 levels is more complicated. Close collisional coupling within these excited levels, as well as with H II, means that at high effective temperatures, numerous strong lines and continua significantly affect the statistical equilibrium. The picture becomes simpler towards lower effective temperatures, where H I lines are weaker and so collisional coupling with the n = 2 level becomes more effective at pushing the departure coefficients of the upper Balmer levels, βup towards that of the lower Balmer level, β2.
 |
Fig. 3 Departure coefficient-vertical optical depth distributions in the 3D hydrodynamic model atmospheres shown in Fig. 1. Darker shading indicates a larger density of grid-points. The departure coefficients of the lower and upper levels of the α line are shown. The departure coefficients of the heavily populated ground level (n = 1) always stay close to unity, while the departure coefficients of the more excited levels (n > 3) and the ionised state (H II) roughly follow those of the n = 3 state. |
3.3 Emergent Balmer lines
In Fig. 4 for Hα, Fig. 5 for Hβ, and Fig. 6 for Hγ, we illustratethe line profiles emergent from the model atmospheres shown in Fig. 1. These plots directly illustrate the impact of assuming LTE and of using 1D hydrostatic model atmospheres on the synthetic Balmer lines. We focus on the line wings, rather than the cores, for the reasons given in Sect. 3.1.
The far outer regions of the Balmer line wings are typically stronger in 3D non-LTE models than in 1D non-LTE models. The line formation in the (upflows of the) 3D model atmospheres is enhanced owing to their steeper temperature gradients relative to in the corresponding 1D model atmospheres. As expected from Sect. 3.1, this effect is more pronounced for higher values of mixing-length which predict shallower 1D temperature stratifications in the deepest regions (Fig. 1), and for higher members of the Balmer series (e.g. Fig. 6) rather than for H α, because the latter forms higher up in the atmosphere where differences in the temperature stratifications of the 1D and (upflowing columns of the) 3D model atmospheres are lesser. On its own, stronger outer wings implies lower inferred effective temperatures from the 3D models than from the 1D models (and this is in fact the case for e.g. Hγ and high αMLT; see Sect. 5.1).
On the other hand, the inner regions of the Balmer line wings can be weaker in 3D non-LTE models than in 1D non-LTE models, at least for stronger lines that form higher up in the atmosphere such as for example H α in the solar-metallicity turn-off star (Fig. 4). This result reflects how the average 3D temperature stratifications (⟨3D⟩ in Fig. 1) can be shallower than the 1D temperature stratifications, in the region 0.0 ≲ logτR ≲−1.0. On its own, weaker inner wings implies higher inferred effective temperatures from the 3D models than from the 1D models.
Figures 4–6 indicate that smaller values of mixing-length tend to reduce the 3D effects, particularly in the outer wings. This is because low mixing-lengths imply a 1D stratification below log τR = 0 closer to the high-temperature upflows in the 3D model (Fig. 1), which is where much of the Balmer line formation occurs (Sect. 3.1). This is consistent with the low mixing-lengths, αMLT ≈ 0.5, calibrated by Fuhrmann et al. (1993, 1994) and Barklem et al. (2002). However, there does not appear to be a value of αMLT for which the 1D model line shapes adequately reproduce the 3D model line shapes, for any particular set of atmospheric parameters (e.g. Ludwig et al. 2009), and inhomogeneities in the 3D model atmospheres have a non-negligible impact on the Balmer lines (e.g. Pereira et al. 2013).
The non-LTE effects are generally less pronounced than the 3D effects. They mainly affect the inner wings of H α, and become less severe for higher members of the Balmer series. This is because the stronger H α line forms in more optically thin regions (Sect. 3.1), where the departure coefficients deviate more significantly from unity (Sect. 3.2). For similar reasons, the non-LTE effects are most severe closer to the cores of the lines, whereas they are typically insignificant in the outer wings.
We discussed in Sect. 3.2 that the departure coefficients have a strong dependence on metallicity. Figures 4–6 show that this translates into more pronounced non-LTE effects on the inner wings (of all Balmer lines) towards lower metallicities. However, even at low metallicities, it is mainly H α that is influenced by departures from LTE.
We also discussed in Sect. 3.2 that the departure coefficients have a complicated dependence on effective temperature. A source function effect dominates at higher effective temperatures: it serves to weaken the Balmer line wings with respect to LTE. This is demonstrated in Figs. 4 and 5, in the inner wings of H α and H β, in the turn-off stars at either metallicity. The competing opacity effect becomes more important at lower effective temperatures: it serves to strengthen the Balmer line wings with respect to LTE. This is also demonstrated in these figures, in the inner wings of H α and H β, this time in the metal-poor sub-giant. Although the departures are more severe at lower effective temperature, this does not necessarily translate into more pronounced non-LTE effects towards lower effective temperatures, because the opacity and source function effects are in competition.
As a result of how the 3D non-LTE effects depend on distance from the line core of the Balmer line in question, it is not possible to define a definitive, quantitative 3D non-LTE versus 1D LTE (for example) effective temperature correction: the value inevitably depends on the adopted method of analysis. Nevertheless, some intuition for the errors incurred by a 1D LTE analysis can be drawn from our analysis of a sample of benchmark stars in Sect. 4.
 |
Fig. 4 Hα lines emergent from the model atmospheres shown in Fig. 1. Rotational broadening is neglected. The residuals are given with respect to the 3D non-LTE model. |
 |
Fig. 5 Hβ lines emergent from the model atmospheres shown in Fig. 1. Rotational broadening is neglected. The residuals are given with respect to the 3D non-LTE model. |
 |
Fig. 6 Hγ lines emergent from the model atmospheres shown in Fig. 1. Rotational broadening is neglected. The residuals are given with respect to the 3D non-LTE model. |
4 Fits to benchmark stars
4.1 Sample
The models that we presented in Sect. 3 were compared to high-quality observations of well-studied benchmark stars: the Sun, Procyon (HD 61421), HD 103095, HD 84937, HD 140283, and HD 122563. The effective temperatures as well as the surface gravities of these benchmark stars are well-constrained by photometric, interferometric, or astrometric measurements that are independent of spectrum analysis methods. Since rotational broadening is unimportant for fitting the Balmer line wings, the v sinι parameter was neglected here. We summarise the sample in Table 1.
For the Sun, the Fourier transform spectrometer (FTS) solar flux atlas of Wallace et al. (2011) was used, based on high-resolution, high signal-to-noise ratio observations taken at the Kitt Peak National Observatory (KPNO). For the other benchmark stars, high-quality spectra (Korn et al. 2003) taken with the FOCES spectrograph (Pfeiffer et al. 1998) were used. These have been proven to accurately reproduce the intrinsic shapes of broad lines thanks to the fibre-fed design of the instrument (Korn 2002).
High-resolution spectra from the UVES-POP catalogue (Bagnulo et al. 2003) are also available for some of the benchmark stars considered here. These data are generally unreliable for Balmer line analyses because of percent-level residuals from the flat-fielding process occurring over scales of 1.5−2.0 nm. This can be seen in the spectrum of HD 122563, which is the only star in the sample for which UVES data were used. As the line wings of this star are not very extended, our analysis is not significantly affected by these shortcomings, in comparison to the relatively large influence of blending lines. Percent-level residuals in the H α profile are apparent in most data sets based on cross-dispersed echelle spectrographs (e.g. Blanco-Cuaresma et al. 2014, Fig. 2); special care must be taken in the data reduction of such observations (e.g. Barklem et al. 2002, Sect. 2).
Benchmark stars, their literature atmospheric parameters, sources for their observed spectra, nominal spectral resolving power R = λ∕Δλ, and the assumed 1σ uncertainties in the atmospheric parameters and in the placement of the continuum.
4.2 Fitting procedure
Effective temperatures were determined from individual Balmer line wings by profile fitting of the continuum normalised model spectra. These were performed by χ2-minimisation, using the IDL routine MPFIT (Markwardt 2009). We discuss the line and continuum masks in Sect. 4.2.1, the continuum normalisation in Sect. 4.2.2, the interpolation procedure in Sect. 4.2.3, and the error analysis in Sect. 4.2.4. The only free parameters in the fits were Teff, and the continuum placement as we describe below.
4.2.1 Fitting masks
Following Barklem et al. (2002), wavelength masks were used to isolate unblended regions; the line cores were also avoided, for the reasons given in Sect. 3.1. Continuum masks were used to fit the observed continuum, while line masks were used to fit the Balmer lines and infer the effective temperature. We illustrate the masks in Figs. 7–9, and describe how these masks were constructed below.
Basic wavelength masks were constructed first, from which continuum and line masks were derived. For a particular benchmark star, the basic masks were constructed by comparing two sets of 1D LTE model spectra: one set containing all known blends in the vicinity of the Balmer lines, and one set without them. These model spectra were constructed on the adopted atmospheric parameters of the benchmark star (Table 1); for the metal-poor HD 84937 and HD 140283, the masks were based on the warm solar-metallicity benchmark star Procyon with only minor adjustments, instead. Clean wavelength regions were then identified using the criterion that the difference between the blended and unblended 1D LTE model spectra corresponds to an effect of less than 30 K. Following that, these masks were refined by using the observed, high-resolution KPNO spectrum of the Sun to identify and screen residual missing blends and telluric lines.
From these basic masks, continuum and line masks were constructed based on the sensitivity of the 1D non-LTE and 3D non-LTE model spectra to the effective temperature. The continuum masks were chosen so as to consider wavelength regions where neither the 1D nor the 3D model spectra had significant sensitivity to the effective temperature. Conversely, the line masks were chosen so as to consider wavelength regions where both the 1D and the 3D model spectra had significant sensitivity to the effective temperature. Owing to the severe line blending in the region surrounding H γ, especially in the nearby CH G-band, the continuum masks had to be placed closer to the line core. Consequently, for H γ, residual unresolved blends inside the continuum and line mask regions can affect the results at the level of 100 K.
4.2.2 Continuum normalisation
The observed spectra were continuum normalised during every step of the χ2 -minimisation using the median ratio between synthesis and observations, within the continuum mask windows; that is, the continuum and line fitting were performed simultaneously. For the continuum placement of the UVES spectra (HD 122563), small but significant residual slopes were identified; therefore for these data a robust slope fitting method (Sen 1968; Theil 1992) was adopted instead.
4.2.3 Interpolation procedure
It was necessary to interpolate (and moderately extrapolate) the model spectra onto arbitrary sets of atmospheric parameters when performing the fits. This interpolation was performed in several steps. Since the original Teff nodes are not regularly spaced but the logg and ![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq24.png) nodes are, in the first step the continuum and total model fluxes at each wavelength and on each log g and
nodes are, in the first step the continuum and total model fluxes at each wavelength and on each log g and ![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq25.png) node were interpolated onto a regular Teff grid spanning 4000eff∕K ≤ 6750 in steps of 50 K. Linear extrapolation with respectto Teff was permitted up to 25 K, at this stage.
node were interpolated onto a regular Teff grid spanning 4000eff∕K ≤ 6750 in steps of 50 K. Linear extrapolation with respectto Teff was permitted up to 25 K, at this stage.
In the second step, the resulting grid was interpolated onto a finer mesh in log g, spanning 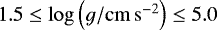 in steps of 0.1 dex. In the third step, this was repeated for
in steps of 0.1 dex. In the third step, this was repeated for ![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq27.png) , spanning
, spanning ![$-4.0\leq\mathrm{\left[Fe/H\right]}\leq0.5$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq28.png) in steps of 0.1 dex. The interpolations of the continuum and total model fluxes in these first three steps were done using cubic splines, or linearly when too few points were available. Only in the linear regime are the second and third steps commutable. In the fourth step, where necessary, linear extrapolations of the continuum and total model fluxes were performed with respect to log g,
in steps of 0.1 dex. The interpolations of the continuum and total model fluxes in these first three steps were done using cubic splines, or linearly when too few points were available. Only in the linear regime are the second and third steps commutable. In the fourth step, where necessary, linear extrapolations of the continuum and total model fluxes were performed with respect to log g, ![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq29.png) , or Teff, in order of preference.
, or Teff, in order of preference.
Finally, during the χ2-minimisation, the model fluxes on this fine, regular and complete grid were normalised, and were interpolated tri-linearly with respect to Teff, log g, and ![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq30.png) onto the desired parameters. The normalised model fluxes were interpolated onto a uniform wavelength basis, convolved with Gaussian instrumental profiles, then interpolated onto the observed wavelengths, using cubic splines.
onto the desired parameters. The normalised model fluxes were interpolated onto a uniform wavelength basis, convolved with Gaussian instrumental profiles, then interpolated onto the observed wavelengths, using cubic splines.
Interpolation and extrapolation errors were estimated by considering two different sets of model spectra. The first set of model spectra constitutes 1D non-LTE calculations across the entire, finely-spaced MARCS-grid (1100 model atmospheres; see Sect. 2.1.3). The second set is based on interpolating the first set of model spectra onto the stellar parameters of the coarsely-spaced STAGGER-grid using cubic splines. Both sets of model spectra were then interpolated and extrapolated into regular grids in the way that we described above, and used to analyse the benchmark stars. Then, under the assumption that errors incurred when interpolating across the finer grid of model spectra are much smaller than those incurred when interpolating across the coarser grid of model spectra, we used the differences in the inferred effective temperatures from the coarse and fine grids of model spectra to roughly quantify interpolation and extrapolation errors on the coarser grid. These errors in turn are indicative of interpolation and extrapolation errors on the grid of 3D non-LTE model spectra.
In Table 2 we illustrate the interpolation and extrapolation errors, estimated as described above. For Procyon and HD 122563, the errors are really extrapolation errors, because these stars lie slightly outside of the STAGGER-grid (see Magic et al. 2013a, Fig. 1). The extrapolation errors can be large (nearly 150 K for H γ in HD 122563), and we caution that our results for these stars are consequently less robust than our results for the other stars in our sample. For the Sun, HD 103095, HD 84937, and HD 140283, the errors mainly reflect interpolation errors on a coarser Teff and ![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq31.png) grid, as we discussed in Sect. 2.1.3. These errors are most severe for HD 140283, where their magnitudes are nevertheless still small (at most around 15 K). We note, however, that these values do not reflect interpolation errors in log g, for which the step-size is the same in the MARCS-grid as in the STAGGER-grid (0.5 dex); such errors are nevertheless expected to be small, since the normalised Balmer lines are not very sensitive to log g (Sect. 1).
grid, as we discussed in Sect. 2.1.3. These errors are most severe for HD 140283, where their magnitudes are nevertheless still small (at most around 15 K). We note, however, that these values do not reflect interpolation errors in log g, for which the step-size is the same in the MARCS-grid as in the STAGGER-grid (0.5 dex); such errors are nevertheless expected to be small, since the normalised Balmer lines are not very sensitive to log g (Sect. 1).
Interpolation/extrapolation errors, as estimated by the difference in effective temperatures inferred from a coarser and incomplete grid of model spectra, relative to those inferred from a finer and complete grid of model spectra, in both cases using 1D non-LTE calculations on MARCS model atmospheres (see Sect. 4.2.3).
4.2.4 Error analysis
To estimatethe residual systematic errors in the 3D non-LTE models, it was first necessary to quantify all other contributing sources of uncertainty. In Table 1 we list the assumed 1σ uncertainties in the adopted atmospheric parameters (logg and ![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq32.png) ), as well as in the continuum placement (arising from the finite signal-to-noise ratio of the observations, and imperfections in the continuum tracing and residual blends).The uncertainty in the continuum placement is only an estimate, since the influence of missing blends may be significantly larger in the case of H γ.
), as well as in the continuum placement (arising from the finite signal-to-noise ratio of the observations, and imperfections in the continuum tracing and residual blends).The uncertainty in the continuum placement is only an estimate, since the influence of missing blends may be significantly larger in the case of H γ.
These 1σ uncertainties were translated into effectivetemperature errors: 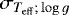 ,
, ![$\sigma_{T_{\mathrm{eff}};\,\mathrm{\left[Fe/H\right]}}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq34.png) , and
, and 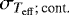 . This was done by repeatingthe 3D non-LTE analysis (using the interpolated regular 3D non-LTE grid we described in Sect. 4.2.3), but shifting logg or
. This was done by repeatingthe 3D non-LTE analysis (using the interpolated regular 3D non-LTE grid we described in Sect. 4.2.3), but shifting logg or ![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq36.png) relative to their reference values (Table 1), or shifting the continuum level relative to its best-fit value, by the stated 1σ uncertainties. To aid intuition on the relative magnitude of these three sources of error, we illustrate how sensitive the inferred effective temperatures are to perturbations of ± 0.3 dex in log g and
relative to their reference values (Table 1), or shifting the continuum level relative to its best-fit value, by the stated 1σ uncertainties. To aid intuition on the relative magnitude of these three sources of error, we illustrate how sensitive the inferred effective temperatures are to perturbations of ± 0.3 dex in log g and ![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq37.png) , and to perturbations of ± 0.3% in the continuum level in Table 3, based on the 1D non-LTE calculations across the entire, finely-spaced MARCS-grid (Sect. 2.1.3).
, and to perturbations of ± 0.3% in the continuum level in Table 3, based on the 1D non-LTE calculations across the entire, finely-spaced MARCS-grid (Sect. 2.1.3).
Under the assumption that all of these uncertainties are independent, they were combined in quadrature, together with the formal fitting error 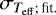 , to produce the final 1σ uncertainties given in Table 5:
, to produce the final 1σ uncertainties given in Table 5:
![\begin{eqnarray*}\sigma_{T_{\mathrm{eff}}}^2 &=& \sigma_{T_{\mathrm{eff}};\,\log{g}}^2 + \sigma_{T_{\mathrm{eff}};\,\mathrm{\left[Fe/H\right]}}^2 + \sigma_{T_{\mathrm{eff}};\,\text{cont.}}^2 + \sigma_{T_{\mathrm{eff}};\,\text{fit}}^2. \end{eqnarray*}](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq39.png) (3)
(3)
Interpolation errors (Sect. 4.2.3) were not folded into these uncertainties.
Sensitivity of the effective temperatures inferred from the 1D non-LTE Balmer lines (using MARCS model atmospheres) to changes in the atmospheric parameters log g or ![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq48.png) with respect to the adopted literature value, or to a change in the placement of the continuum with respect to the best-fitting value.
with respect to the adopted literature value, or to a change in the placement of the continuum with respect to the best-fitting value.
4.3 Inferred effective temperatures
We illustrate the 3D non-LTE model fits to the benchmark spectra in Fig. 7 for H α, Fig. 8 for Hβ, and Fig. 9 for Hγ. The qualityof the fits for the line wings remains satisfactory, in particular for H α, in the reduced χ2 sense, for the whole sample. This is despite the 3D non-LTE models lacking any leverage in the form of free parameters.
In Table 4 we tabulate the differences in the effective temperatures inferred, for a given benchmark star and Balmer line, from the 3D LTE models, and from the 1D non-LTE models, compared to those inferred from the 3D non-LTE models. We use these differences to quantify the non-LTE effects and the 3D effects, respectively. We also show the differences between the 1D LTE models and the 3D non-LTE models, that reflect the errors that may be present in standard 1D LTE Balmer line analyses. We tabulate the actual effective temperatures inferred from the 3D non-LTE models in Table 5. In Fig. 10 we plot the effective temperature errors as inferred from different models, as functions of literature atmospheric parameters. We discuss these results in the following section, Sect. 5.
 |
Fig. 7 Hα line profiles observed in benchmark stars, compared to the best-fitting 3D non-LTE model when effective temperature is taken as a free parameter. The reference parameters Teff / logg/ |
 |
Fig. 8 Hβ line profiles observed in benchmark stars, compared to the best-fitting 3D non-LTE model when effective temperature is taken as a free parameter. The reference parameters Teff / logg/ |
 |
Fig. 9 Hγ line profiles observed in benchmark stars, compared to the best-fitting 3D non-LTE model when effective temperature is taken as a free parameter. The reference parameters Teff / logg/ |
 |
Fig. 10 Differences between effective temperatures of benchmark stars inferred from 3D non-LTE or 1D LTE model spectra (the latter calculated on αMLT = 1.5 model atmospheres), and independent literature values, as functions of literature effective temperatures (left panel) and metallicities(right panel). Error bars are shown for the 3D non-LTE models, and omitted for the 1D LTE models for clarity. Also shown are lines of best fit that take uncertainties into account. |
5 Discussion
5.1 Quantifying the 3D non-LTE effects
Table 4 shows that the 3D effects, as quantified by the 1D non-LTE versus 3D non-LTE differences, are significant for all of the Balmer lines. Their magnitudes depend on the line and atmospheric parameters. For H α, the absolute differences range from negligible to around 100 K, and a typical absolute value is around 50 K. The 3D effects tend to grow in magnitude for higher members of the Balmer series, and for H β and H γ the differences are also sensitive to the adopted mixing-length (Sect. 3.1): typical absolute values are around 50− 150 K for H β and H γ, depending on the star and on the adopted mixing-length.
Table 4 shows that for Hα, the 3D effects tend to be negative. This is because the inner wings of H α tend to be weaker in the 3D non-LTE models than in the 1D non-LTE models (Sect. 3.3). For higher members of the Balmer series (H β and H γ), the 3D effects tend to be more positive, at least for larger values of mixing-length (Sect. 3.1); in particular, the differences are all positive for Hγ with αMLT = 2.0. Ludwig et al. (2009) also found that the differences get more positive for the higher members, based on a differential 1D LTE vs. 3D LTE comparison (see their Table 2, noting the opposite sign convention). Lowering αMLT generally acts to reduce the absolute differences in effective temperatures inferred from the 1D and 3D model spectra (as expected from the theoretical fluxes, in Sect. 3.3).
In contrast to the 3D effects, Table 4 shows that the non-LTE effects, as quantified by the 3D LTE versus 3D non-LTE differences, become less severe for higher members of the Balmer series. This is expected, since the higher members form deeper in the atmosphere, and the departure coefficients are much closer to unity there (Sect. 3.2). In warmer stars, the absolute differences are usually only significant for Hα; however in cooler stars, such as HD 103095, the non-LTE effects can remain significant even for H γ. For H α, the absolute non-LTE effects range from negligible to nearly 100 K and a typical absolute value is around 50 K.
We showed in Sect. 3.3 that the non-LTE effects are sensitive to the effective temperature. At high effective temperatures a source function effect dominates, weakening the Balmer lines, whereas towards lower effective temperatures a competing opacity effect becomes increasingly important (Sect. 3.2). This is somewhat apparent in Table 4, with the non-LTE effects being positive for HD 103095 and, at least for H β and H γ, for HD 122563, but negative (or negligible) for the other benchmark stars. In those sections we also explained that the non-LTE effects become more severe towards lower metallicities; accordingly, Table 4 shows larger absolute non-LTE effects for HD 84937 than for Procyon, two turn-off stars with similar effective temperatures and surface gravities but very different metallicities.
For Hα at high effective temperature, the non-LTE effects and the 3D effects tend to go in the same direction: they are usually both negative. Since the non-LTE effects are more severe towards lower metallicities, 3D non-LTE modelling of H α is especially important for warmer metal-poor stars. And indeed, Table 4 shows that some of the largest 1D LTE vs. 3D non-LTE differences for Hα are in HD 84937 and HD 140283.
5.2 Solar effective temperature
Table 5 shows that the solar effective temperature inferred from the 3D non-LTE models is too low. The effective temperature was inferred to be around 5710−5720 K, from the different Balmer lines. This corresponds to an error of around 50− 65 K in effective temperature, slightly larger than the 1σ uncertainty of around 20−40 K in placing the continuum. Other observations of the solar flux (Brault & Neckel 1987; Korn et al. 2003) tend to give similar results, as do observations of the solar disk-centre intensity (Neckel & Labs 1984). This solar effective temperature error is also consistent with the analysis of Pereira et al. (2013).
This systematic error is small (50 K in effective temperature corresponds to around 0.5% in the emergent flux), which makes it difficult to pin down exactly what is missing from the models. Uncertainties in the Stark-broadening and self-broadening theories may separately impart errors of the order 10− 15 K (Barklem et al. 2002, Table 4). Furthermore, considering these two mechanisms as independent of each other may also lead to a significant error on its own. On the other hand, tests on different tailored model solar atmospheres, with the chemical composition of Asplund et al. (2009) as well as the more metal-poor composition of Asplund et al. (2005), indicated a sensitivity of the results on the microphysics adopted in the model atmosphere, of the order 20− 30 K. Interpolation errors are apparently unimportant in this region of parameter space, at least according to Table 2. In practical applications, however, errors of the order 50− 65 K are usually smaller than the other uncertainties intrinsic to the method, in particular, in placing the continuum.
5.3 Use as effective temperature diagnostics
Table 5 and Fig. 10 show that the 3D non-LTE models are generally able to reproduce the effective temperatures of the benchmark stars to within the combined 1σ uncertainties; the only exceptions are the Sun (which we discussed in Sect. 5.2), H β and H γ in HD 103095 (which we discuss below), and Hβ in Procyon and HD 122563 (both of which are somewhat influenced by extrapolation errors). These 1σ uncertainties are mainly influenced by uncertainties in placing the continuum; this is very significant for H γ, because the spectral region is very blended, as can be seen in Fig. 9. Very blended stellar spectra combined with a finite spectral resolution can lead to the observed continuum being systematically underestimated by our fitting procedure, as can be seen by comparing the results for Hα with those for Hγ in Table 5 and Fig. 10.
All of the effective temperatures inferred from H α agree with the corresponding reference values to within 50 K. For the Sun, HD 84937, and HD 140283, the effective temperatures inferred from H α and H β agree to better than 70 K. These results suggest that our 3D non-LTE Hα and H β models can be used for reliable effective temperature determinations.
The results in Table 5 do however indicate some failure in the analysis for HD 103095. While H α gives an effective temperature that is consistent with the reference value to well within the 1σ uncertainties, H β and H γ do not. The 1D LTE models of HD 103095, perform similarly badly, if not slightly worse, than the 3D non-LTE models (Fig. 10). We note that HD 103095 has a non-standard chemical composition, having a lower α-enhancement than the value of 0.4 dex adopted here (Zhao et al. 2016, Fig. 8), and we suspect that this is the origin of the errors in the effective temperatures inferred from H β and H γ. Test calculations on MARCS model atmospheres that were both enhanced and not enhanced in α-element abundances (Gustafsson et al. 2008) support this hypothesis. These tests indicated significant differences that go in the opposite directions for Hα, as for Hβ and H γ, owing to the temperature structure in the α-poor model atmospheres being shallower in the region 0.0 ≲ logτR ≲ 1.0 (resulting in weaker Hβ and H γ line wings), and steeper in the region − 0.5 ≲ logτR ≲ 0.0 (resulting in stronger Hα line wings), compared to that in the standard-composition model atmospheres. Moreover, the residuals in Figs. 8 and 9 illustrate that small changes to the model H β and H γ fluxes have a large influence on the inferred effective temperature, at least compared to H α in Fig. 7. To confirm this hypothesis quantitatively, one would need to recalculate the 3D model atmospheresusing a custom chemical composition, and repeat the analysis; this is beyond the scope of the present work.
With the majority of analyses today still based on 1D LTE models, it is interesting to briefly consider how our 1D LTE H α models fare in comparison to our 3D non-LTE models. For Hα, Fig. 10 illustrates that the 1D LTE models tend to underestimate the effective temperatures. This is most apparent forthe warmer benchmark stars. As we discussed in Sect. 5.1, the 3D effects and the non-LTE effects go in the same direction at higher effective temperatures and lower metallicities; we thus find that the 1D LTE models perform worst for the metal-poor turn-off HD 84937, underestimating the effective temperature by around 150 K compared to the IRFM method (Casagrande et al. 2011). This highlights the importance of adopting the full 3D non-LTE approach in this regime.
6 Accessing the grid
We make publicly available the 3D non-LTE model spectra calculated on the STAGGER-grid nodes for the astronomy community to use for effective temperature determinations. The data can be accessed at an online repository2, or by contacting one of the authors directly. We also make our interpolation routines (Sect. 4.2.3) available. The grids span H α through to H γ. However, analyses of Hγ are usually prone to uncertainties caused by neighbouring blends (Sect. 5.3), so we recommend giving most weight to H α and H β in practice.
7 Conclusion
We carried out 3D non-LTE radiative transfer calculations for H I/H II on the extensive STAGGER grid of 3D hydrodynamic model atmospheres. We used these calculations to study Balmer line formation in the context of effective temperature determinations of late-type stars. We summarise our main findings below.
The absolute 3D effects, as quantified by the 1D non-LTE versus 3D non-LTE differences, are typically around 50 K for H α, and can reach around 100 K. The differences tend to be negative: the inner wings of Hα are significantly weaker in the 3D models compared to in the 1D models. The 3D effects tend to become more severe and more positive for higher members of the Balmer series and for higher values of mixing-length; they can reach around + 200 K for H γ when αMLT = 2.0.
The absolute non-LTE effects, as quantified by the 3D LTE versus 3D non-LTE differences, are typically around 50 K for H α, and can also reach around 100 K. The non-LTE effects become more severe towards lower metallicities. The signs of the non-LTE effects are sensitive to the effective temperature. At higher effective temperatures the non-LTE effects tend to be negative; the LTE models of H α usually underestimate the effective temperature. The non-LTE effects become less significant for higher members of the Balmer series.
At higher effective temperatures and lower metallicities the 3D effects and non-LTE effects go in the same direction. Consequently, 1D LTE models of Hα can underestimate the effective temperatures of metal-poor turn-off stars such as HD 84937 by around 150 K.
The ab initio 3D non-LTE model spectra are generally able to reproduce the effective temperatures of various benchmark stars to within the 1σ uncertainties in the reference effective temperatures. The solar analysis suggests that the error in the 3D non-LTE model spectra are only of the order 50−65 K in terms of theinferred effective temperature.
As demonstrated here, the use of 1D Balmer line profiles can lead to significant systematic errors. We therefore provided 3D non-LTE model spectra (Sect. 6) for the astronomy community to use to determine more reliable spectroscopic effective temperatures of late-type stars.
Acknowledgements
We thank the anonymous referee for their careful reading of and helpful suggestions on the manuscript, and Andreas Korn for providing the FOCES spectra used in this work. AMA and KL acknowledge funds from the Alexander von Humboldt Foundation in the framework of the Sofja Kovalevskaja Award endowed by the Federal Ministry of Education and Research, and KL also acknowledges funds from the Swedish Research Council (grant 2015-004153) and Marie Skłodowska Curie Actions (cofund project INCA 600398). TN and MA acknowledge funding from the Australian Research Council (grant DP150100250), and MA also acknowledges funding through ARC Laureate Fellowship (FL110100012). Parts of this research were conducted by the Australian Research Council Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013. PSB acknowledges financial support from the Swedish Research Council and the project grant “The New Milky Way” from the Knut and Alice Wallenberg Foundation. Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation (grant DNRF106). This work made use of data from the UVES Paranal Observatory Project (ESO DDT Program ID 266.D-5655). This work was supported by computational resources provided by the Australian Governmentthrough the National Computational Infrastructure (NCI) under the National Computational Merit Allocation Scheme.
References
- Ali, A. W., & Griem, H. R. 1966, Phys. Rev., 144, 366 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, N. F., Kielkopf, J. F., Cayrel, R., & van’t Veer-Menneret C. 2008, A&A, 480, 581 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amarsi, A. M. 2015, MNRAS, 452, 1612 [NASA ADS] [CrossRef] [Google Scholar]
- Amarsi, A. M., & Asplund, M. 2017, MNRAS, 464, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Amarsi, A. M., Asplund, M., Collet, R., & Leenaarts, J. 2016a, MNRAS, 455, 3735 [NASA ADS] [CrossRef] [Google Scholar]
- Amarsi, A. M., Lind, K., Asplund, M., Barklem, P. S., & Collet, R. 2016b, MNRAS, 463, 1518 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Nordlund, Å., Trampedach, R., Allende Prieto, C., & Stein, R. F. 2000, A&A, 359, 729 [NASA ADS] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes, & F. N. Bash, ASP Conf. Ser., 336, 25 [NASA ADS] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bagnulo, S., Jehin, E., Ledoux, C., et al. 2003, The Messenger, 114, 10 [NASA ADS] [Google Scholar]
- Barklem, P. S. 2007, A&A, 466, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barklem, P. S. 2016, A&ARv, 24, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S. 2017a, KAULAKYS: Inelastic Collisions between Hydrogen Atoms and Rydberg Atoms, Astrophysics Source Code Library [record ascl:1701.005] [Google Scholar]
- Barklem, P. S. 2017b, MSWAVEF: Momentum-Space Wavefunctions, Astrophysics Source Code Library [record ascl:1701.006] [Google Scholar]
- Barklem, P. S., & Piskunov, N. 2015, HLINOP: Hydrogen LINe OPacity in Stellar Atmospheres, Astrophysics Source Code Library [record ascl:1507.008] [Google Scholar]
- Barklem, P. S., Piskunov, N., & O’Mara, B. J. 2000, A&A, 355, L5 [NASA ADS] [Google Scholar]
- Barklem, P. S., Stempels, H. C., Allende Prieto, C., et al. 2002, A&A, 385, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bates, D. R., & Lewis, J. T. 1955, Proc.. Phys. Soc. A, 68, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Bates, D. R., Bell, K. L., & Kingston, A. E. 1967, Proc. Phys. Soc., 91, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Bergemann, M., & Gehren, T. 2008, A&A, 492, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergemann, M., Lind, K., Collet, R., Magic, Z., & Asplund, M. 2012, MNRAS, 427, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Bergemann, M., Serenelli, A., Schönrich, R., et al. 2016, A&A, 594, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanco-Cuaresma, S., Soubiran, C., Jofré, P., & Heiter, U. 2014, A&A, 566, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Botnen, A. & Carlsson, M. 1999, in Numerical Astrophysics, eds. S. M. Miyama, K. Tomisaka, & T. Hanawa, Astrophys. Space Sci. Lib., 240, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Brault, J., & Neckel, H. 1987, available from ftp.hs.uni-hamburg.de/pub/outgoing/FTS-Atlas/, 69 [Google Scholar]
- Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cayrel, R., van’t Veer-Menneret, C., Allard, N. F., & Stehlé, C. 2011, A&A, 531, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cayrel de Strobel, G. 1960, Ann. Astrophys., 23, 278 [NASA ADS] [Google Scholar]
- Chiavassa, A., Bigot, L., Kervella, P., et al. 2012, A&A, 540, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Däppen, W., Anderson, L., & Mihalas, D. 1987, ApJ, 319, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Defrance, P., Claeys, W., Cornet, A., & Poulaert, G. 1981, J. Phys. B Atom. Mol. Phys., 14, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Drawin, H.-W. 1968, Z. Phys., 211, 404 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drawin, H. W. 1969, Z. Phys., 225, 483 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1993, A&A, 271, 451 [NASA ADS] [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1994, A&A, 285, 585 [NASA ADS] [Google Scholar]
- Fussen, D., & Kubach, C. 1986, J. Phys. B Atom. Mol. Phys., 19, L31 [CrossRef] [Google Scholar]
- Gehren, T. 1981, A&A, 100, 97 [NASA ADS] [Google Scholar]
- Gray, D. F. 2008, The Observation and Analysis of Stellar Photospheres (Cambridge: Cambridge University Press) [Google Scholar]
- Griem, H. R. 1960, ApJ, 132, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiter, U., Jofré, P., Gustafsson, B., et al. 2015, A&A, 582, A49 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Henyey, L., Vardya, M. S., & Bodenheimer, P. 1965, ApJ, 142, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Holweger, H., & Müller, E. A. 1974, Sol. Phys., 39, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., & Mihalas, D. 2014, Theory of Stellar Atmospheres (Princeton, NJ: Princeton University Press) [Google Scholar]
- Hummer, D. G., & Mihalas, D. 1988, ApJ, 331, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Ibgui, L., Hubeny, I., Lanz, T., & Stehlé, C. 2013, A&A, 549, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inglis, D. R., & Teller, E. 1939, ApJ, 90, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Karovicova, I., White, T. R., Nordlander, T., et al. 2018, MNRAS, 475, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Kaulakys, B. P. 1991, J. Phys. B Atom. Mol. Phys., 24, L127 [Google Scholar]
- Korn, A. J. 2002, in Scientific Drivers for ESO Future VLT/VLTI Instrumentation, eds. J. Bergeron, & G. Monnet (Berlin: Springer), 199 [Google Scholar]
- Korn, A. J., Shi, J., & Gehren, T. 2003, A&A, 407, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leenaarts, J., & Carlsson, M. 2009, in The Second Hinode Science Meeting: Beyond Discovery-Toward Understanding, eds. B. Lites, M. Cheung, T. Magara, J. Mariska, & K. Reeves, ASP Conf. Ser., 415, 87 [NASA ADS] [Google Scholar]
- Leenaarts, J., Carlsson, M., & Rouppe van der Voort, L. 2012, ApJ, 749, 136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lites, B. W., & Mihalas, D. 1984, Sol. Phys., 93, 23 [NASA ADS] [Google Scholar]
- Ludwig, H.-G., Freytag, B., & Steffen, M. 1999, A&A, 346, 111 [NASA ADS] [Google Scholar]
- Ludwig, H.-G., Behara, N. T., Steffen, M., & Bonifacio, P. 2009, A&A, 502, L1 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Magic, Z., Collet, R., Asplund, M., et al. 2013a, A&A, 557, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magic, Z., Collet, R., Hayek, W., & Asplund, M. 2013b, A&A, 560, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magic, Z., Weiss, A., & Asplund, M. 2015, A&A, 573, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markwardt, C. B. 2009, in Analysis Software and Systems XVIII, Astronomical Data, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Mihajlov, A. A., Dimitrijević, M. S., & Djurić, Z. 1996, Phys. Scr., 53, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Mihajlov, A. A., Ignjatovic, L. M., Djuric, Z., & Ljepojevic, N. N. 2004, J. Phys. B Atom. Mol. Phys., 37, 4493 [NASA ADS] [CrossRef] [Google Scholar]
- Neckel, H. & Labs, D. 1984, Sol. Phys., 90, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Nordlund, Å., Stein, R. F., & Asplund, M. 2009, Liv. Rev. Sol. Phys., 6, 2 [Google Scholar]
- Peck, C. L., Criscuoli, S., & Rast, M. P. 2017, ApJ, 850, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira, T. M. D., Asplund, M., Collet, R., et al. 2013, A&A, 554, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfeiffer, M. J., Frank, C., Baumueller, D., Fuhrmann, K., & Gehren, T. 1998, A&AS, 130, 381 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prša, A., Harmanec, P., Torres, G., et al. 2016, AJ, 152, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Przybilla, N., & Butler, K. 2004a, ApJ, 609, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Przybilla, N., & Butler, K. 2004b, ApJ, 610, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Allende Prieto, C., & Lambert, D. L. 2013, ApJ, 764, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Ruchti, G. R., Bergemann, M., Serenelli, A., Casagrande, L., & Lind, K. 2013, MNRAS, 429, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Rutten, R. J. 2003, Radiative Transfer in Stellar Atmospheres, 8th edn (The Netherlands: Utrecht University) [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1992, A&A, 262, 209 [NASA ADS] [Google Scholar]
- Searle, L., & Oke, J. B. 1962, ApJ, 135, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Sen, P. K. 1968, J. Am. Stat. Assoc, 63, 1379 [Google Scholar]
- Shah, M. B., Elliott, D. S., & Gilbody, H. B. 1987, J. Phys. B Atom. Mol. Phys., 20, 3501 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, M., & Ludwig, H.-G. 1999, in Stellar Structure: Theory and Test of Connective Energy Transport, eds. A. Gimenez, E. F. Guinan, & B. Montesinos, ASP Conf. Ser., 173, 217 [NASA ADS] [Google Scholar]
- Stehle, C. 1994, A&AS, 104, 509 [Google Scholar]
- Stehlé, C., & Hutcheon, R. 1999, A&AS, 140, 93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stenrup, M., Larson, Å., & Elander, N. 2009, Phys. Rev. A, 79, 012713 [NASA ADS] [CrossRef] [Google Scholar]
- Theil, H. 1992, in Henri Theil’s Contributions to Economics and Econometrics, eds. B. Raj, & J. Koerts (Berlin: Springer), 345 [CrossRef] [Google Scholar]
- Trampedach, R., Stein, R. F., Christensen-Dalsgaard, J., Nordlund, Å., & Asplund, M. 2014, MNRAS, 445, 4366 [NASA ADS] [CrossRef] [Google Scholar]
- Tremblay, P.-E., Ludwig, H.-G., Steffen, M., Bergeron, P., & Freytag, B. 2011, A&A, 531, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tremblay, P.-E., Ludwig, H.-G., Steffen, M., & Freytag, B. 2013, A&A, 559, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- VandenBerg, D. A., Bond, H. E., Nelan, E. P., et al. 2014, ApJ, 792, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal, C. 1966, J. Quant. Spec. Rad. Transf., 6, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal, C. R., Cooper, J., & Smith, E. W. 1973, ApJS, 25, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Vriens, L., & Smeets, A. H. M. 1980, Phys. Rev. A, 22, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Wallace, L., Hinkle, K. H., Livingston, W. C., & Davis, S. P. 2011, ApJS, 195, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, G., Mashonkina, L., Yan, H. L., et al. 2016, ApJ, 833, 225 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Benchmark stars, their literature atmospheric parameters, sources for their observed spectra, nominal spectral resolving power R = λ∕Δλ, and the assumed 1σ uncertainties in the atmospheric parameters and in the placement of the continuum.
Interpolation/extrapolation errors, as estimated by the difference in effective temperatures inferred from a coarser and incomplete grid of model spectra, relative to those inferred from a finer and complete grid of model spectra, in both cases using 1D non-LTE calculations on MARCS model atmospheres (see Sect. 4.2.3).
Sensitivity of the effective temperatures inferred from the 1D non-LTE Balmer lines (using MARCS model atmospheres) to changes in the atmospheric parameters log g or ![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq48.png) with respect to the adopted literature value, or to a change in the placement of the continuum with respect to the best-fitting value.
with respect to the adopted literature value, or to a change in the placement of the continuum with respect to the best-fitting value.
All Figures
 |
Fig. 1 Gas temperature-vertical optical depth distributions in 3D hydrodynamic models of turn-off stars (left panel) and sub-giants (right panel) with solar metallicity (top panel) and |
| In the text | |
 |
Fig. 2 Gas temperatures T (first row) and contribution functions Cν for the inner wings (0.2 nm redward of the line centre) of the Hα (second row) and Hγ (third row) lines, in vertical slices of the solar metallicity (left column) and metal-poor (right column) model atmospheres shown in Fig. 1. Lighter shading indicates larger temperatures (first row), and more emergent flux contribution (second and third rows). Contours of constant log τR are overdrawn. In each plot, the contribution functions are normalised such that their maximum values are unity. |
| In the text | |
 |
Fig. 3 Departure coefficient-vertical optical depth distributions in the 3D hydrodynamic model atmospheres shown in Fig. 1. Darker shading indicates a larger density of grid-points. The departure coefficients of the lower and upper levels of the α line are shown. The departure coefficients of the heavily populated ground level (n = 1) always stay close to unity, while the departure coefficients of the more excited levels (n > 3) and the ionised state (H II) roughly follow those of the n = 3 state. |
| In the text | |
 |
Fig. 4 Hα lines emergent from the model atmospheres shown in Fig. 1. Rotational broadening is neglected. The residuals are given with respect to the 3D non-LTE model. |
| In the text | |
 |
Fig. 5 Hβ lines emergent from the model atmospheres shown in Fig. 1. Rotational broadening is neglected. The residuals are given with respect to the 3D non-LTE model. |
| In the text | |
 |
Fig. 6 Hγ lines emergent from the model atmospheres shown in Fig. 1. Rotational broadening is neglected. The residuals are given with respect to the 3D non-LTE model. |
| In the text | |
 |
Fig. 7 Hα line profiles observed in benchmark stars, compared to the best-fitting 3D non-LTE model when effective temperature is taken as a free parameter. The reference parameters Teff / logg/ |
| In the text | |
 |
Fig. 8 Hβ line profiles observed in benchmark stars, compared to the best-fitting 3D non-LTE model when effective temperature is taken as a free parameter. The reference parameters Teff / logg/ |
| In the text | |
 |
Fig. 9 Hγ line profiles observed in benchmark stars, compared to the best-fitting 3D non-LTE model when effective temperature is taken as a free parameter. The reference parameters Teff / logg/ |
| In the text | |
 |
Fig. 10 Differences between effective temperatures of benchmark stars inferred from 3D non-LTE or 1D LTE model spectra (the latter calculated on αMLT = 1.5 model atmospheres), and independent literature values, as functions of literature effective temperatures (left panel) and metallicities(right panel). Error bars are shown for the 3D non-LTE models, and omitted for the 1D LTE models for clarity. Also shown are lines of best fit that take uncertainties into account. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\mathrm{\left[Fe/H\right]}=-3.0$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq40.png)
![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq41.png)
![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq42.png)
![$\mathrm{\left[Fe/H\right]}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq43.png)
![${\mathrm{\left[A/B\right]}} =\left(\log{N_{\mathrm{A}}}/\log{N_{\mathrm{B}}}\right)_{*}-\left(\log{N_{\mathrm{A}}}/\log{N_{\mathrm{B}}}\right)_{\odot}$](/articles/aa/full_html/2018/07/aa32546-17/aa32546-17-eq59.png)