| Issue |
A&A
Volume 615, July 2018
|
|
|---|---|---|
| Article Number | A84 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201732399 | |
| Published online | 18 July 2018 | |
Coronal energy release by MHD avalanches: continuous driving
1
School of Mathematics and Statistics, University of St Andrews,
St Andrews,
Fife,
KY16 9SS,
UK
e-mail: jr93@st-andrews.ac.uk
2
Jodrell Bank Centre for Astrophysics, School of Physics and Astronomy, University of Manchester,
Manchester,
M13 9PL,
UK
e-mail: awh@st-andrews.ac.uk
3
Space and Atmospheric Physics, The Blackett Laboratory, Imperial College,
London,
SW7 2BW,
UK
Received:
1
December
2017
Accepted:
23
March
2018
Previous work has confirmed the concept of a magnetohydrodynamic (MHD) avalanche in pre-stressed threads within a coronal loop. We undertook a series of full, three-dimensional MHD simulations in order to create three threads by twisting the magnetic field through boundary motions until an instability ensues. We find that, following the original instability, one unstable thread can disrupt its neighbours with continued driving. A “bursty” heating profile results, with a series of ongoing energy releases, but no evident steady state. For the first time using full MHD, we show that avalanches are a viable mechanism for the storing and release of magnetic energy in the solar corona, as a result of photospheric motions.
Key words: Sun: corona / Sun: magnetic fields / magnetohydrodynamics (MHD) / methods: numerical
© ESO 2018
1 Introduction
The release of magnetic energy in the solar corona arises over a wide range of scales, ranging from large flares (1025 J) to microflares (1022 J), and to the small events (1017–1018 J) that may heat the quiet Sun and non-flaring coronal active regions. Although dissipation of magnetohydrodynamic (MHD) waves remains a popular mechanism for coronal heating (e.g. van Ballegooijen et al. 2011), the process, in particular, of magnetic reconnection is widely regarded as key to dissipation of magnetic energy. From the viewpoint of coronal heating, there is considerable interest in small, impulsive releases of magnetic energy, generally referred to as “nanoflares” (Parker 1988). In this scenario, the non-flaring corona is heated by a large number of small events although whether the physics of nanoflares is the same as flares is unclear. The size of a nanoflare is too small to be observed directly. By their nature, they must overlap and, hence, are difficult directly to detect individually. Evidence from EUV and X-ray observations suggests that they may exist (Reale 2014; Cargill et al. 2015). However, in the hard X-ray observations of RHESSI (Ramaty High Energy Solar Spectroscopic Imager, Lin et al. 2002), Christe et al. (2008) and Hannah et al. (2008) observed many thousands of microflares, and subsequent instruments with higher sensitivity have provided further information of their properties (Krucker et al. 2014; Glesener et al. 2017).
It is widely believed that non-potential coronal magnetic energy is built up either through direct injection of non-potential field through flux emergence, or through slow, horizontal photospheric motions. At some point, this energy can be accessed, either through the field entering a state of magnetic non-equilibrium, or through an instability. Since the coronal plasma is a nearly perfect conductor, magnetic reconnection can only occur in the presence of current sheets that enable changes in the topology of the magnetic field and the subsequent release of magnetic energy. Current sheet formation can arise as the magnetic field becomes increasingly complicated by the action of photospheric motions, and spontaneous magnetic reconnection results in the breaking and reformation of field lines in a more stable, lower-energy configuration. Examples of such studies can be found in Galsgaard & Nordlund (1996), De Moortel & Galsgaard (2006), O’Hara & De Moortel (2016), and Knizhnik et al. (2017). Ritchie et al. (2016) demonstrate the significance of the nature of the driving motions, with the associated helicity and topological entropy, for the scale and frequency of heating events. Rappazzo et al. (2008), followed by Rappazzo et al. (2010, 2013), use reduced MHD (RMHD) to consider the rate of heating for various shearing and rotational driving motions.
Much of the work on the non-linear kink instability in an individual twisted loop, and indeed in subsequent papers on avalanches, has considered an initial state composed of one loop initially in equilibrium, linearly unstable to the ideal kink mode, with a non-zero growth rate.In this line of work, Browning & Van der Linden (2003) argue that ideal MHD instabilities in an ordered magnetic field are likely to instigate reconnection, through their fast growth times and subsequent formation of strong currents. Using numerical simulations, Browning et al. (2008) and Hood et al. (2009) demonstrate that a kink instability led to very fine-scale currents and rapid dissipation of stored magnetic energy. The coronal magnetic field conserved helicity while relaxing to the constant-α field, as predicted in Taylor (1974).
Subsequent studies developed the model first by analysing the evolution of the kink instability with multiple twisted loops. Tam et al. (2015) consider a case of two neighbouring loops, where one was kink unstable and the other stable. They demonstratethat the instability in one loop led to energy release in the other one, as the unstable loop engulfed the stable one. Hood et al. (2016) consider twenty-three loops, one being unstable. An avalanche occurred, with most of the stable loops being engulfed, associated with a series of “bursty” energy releases. In all these simulations, there was no photospheric driving, the initial magnetic field being an unstable equilibrium.
Strictly, however, such an initial state, of a loop in equilibrium but unstable to a kink mode, cannot exist, since a field must evolve through driving across the stability boundary, and hence the instability would start to grow, albeit very slowly at first, as soon as the instability threshold is reached. It is much more realistic to consider a field driven by slow (sub-Alfvénic) motions of the photospheric footpoints. For such a system, the linear growth rate increases as the field evolves beyond marginal stability. Modelling this evolution is a complex, non-linear problem. However, one intuitively expects two types of evolution: firstly, with the instability growing more slowly than the field evolves through photospheric driving, the system continues to pass through a series of equilibria; secondly, once the instability grows faster than this, itwill dominate the subsequent dynamics. In the case of Rayleigh-Taylor-like instabilities, it has been shown that driving across the stability boundary can lead to the explosive growth of the instabilities (Hurricane et al. 1997; Cowley et al. 2003), but the position for current-driven instabilities, such as the ideal kink instability, is unclear. Therefore, it is difficult to identify exactly when the instability is triggered and its growth rate in evolving magnetic fields.
Gordovskyy et al. (2013) and Bareford et al. (2016) investigate continuous driving by rotating footpoint motions of a single loop, including also the effects of both the expansion and curvature of the loop. They demonstrate that the results are qualitatively similar to those predicted for models with initially unstable fields. In particular, there is a clear onset of dynamic behaviour, with subsequent energy release through reconnection, which appears to correspond to the kink instability.
The presence of such an avalanche as envisaged by Hood et al. (2016) has potentially widespread implications, although a number of questions remain unanswered. Among these is whether repeated episodes of instability and energy release can occur, as the field is continually twisted. Rappazzo et al. (2013) suggest that this is not possible, and that the disordering of the field prevents the onset of the kink instability; however, it is not clear whether their reduced MHD simulations can fully address the situation when footpoints undergo relatively large displacements, as must be the case for the field being continually twisted. For this reason, it is important to address the matter using full three-dimensional MHD simulations, as we do here. Another important question, addressed here, is the behaviour when different parts of the field experience twisting at different rates, producing several threads with unequal twists. A class of conceptual (i.e. non-MHD) coronal energy release models have been developed, where a driven system undergoes avalanches, prescribed by simple rules governing the implied currents (e.g. Lu & Hamilton 1991; Isliker et al. 2000; Vlahos et al. 2009). Good agreement with some observables, such as distribution of energies, is obtained. However, whether such behaviour represents the correct behaviour, as predicted by MHD, is unclear.
In this paper, we take a step towards addressing this question by developing the work of Tam et al. (2015) and Hood et al. (2016) to study a possible MHD avalanche in a driven system. A coronal loop model of three twisted threads is considered, with one thread being driven unstable while the others remain stable. In contrast to our earlier work, we continue to drive the system after the first instability. Section 2 introduces the basic model and the imposed boundary conditions. The evolution up to the kink instability is described in Sect. 3 and the main results presented in Sect. 5. The final section discusses the results and the conclusions.
2 Basic model
We modelled a straightened, line-tied coronal loop, with its footpoints anchored in the dense photosphere. The initial state comprises a uniform magnetic field along the loop axis (defined as the z direction) connecting the two photospheric boundaries. We imposed a rotational motion at the footpoints of three distinct cylindrical threads within the overall loop. In response to the motion, the magnetic field in the three threads becomes twisted. The remaining parts of the photosphere were assumed to be at rest throughout the simulation. The time-dependent evolution was followed by a three-dimensional MHD code described below. While the coronal parts of the twisted threads do not retain their simple initial topology, the photospheric motions were only applied to the initial footpoints. A schematic of the overall geometry is shown in Fig. 1.
2.1 Numerical method
The non-ideal MHD equations were solved numerically using the Lagrangian Remap code, Lare3d, of Arber et al. (2001). The equations are made dimensionless by choosing a typical length, magnetic field strength, and number density. For the simulations discussed below, we took these as L0 = 1 Mm, B0 = 0.002 T (20 G), and n0 = 1015 m−3, respectively. The initial plasma beta is 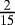 . Hence, the reference speed is the Alfvén speed, vA = 1381 km s−1, and the Alfvén time is tA = L0∕vA = 0.72 s. We note that the initial fast mode speed is 1455 km s−1 and the typical energy density W0 = 3.18 J m−3.
. Hence, the reference speed is the Alfvén speed, vA = 1381 km s−1, and the Alfvén time is tA = L0∕vA = 0.72 s. We note that the initial fast mode speed is 1455 km s−1 and the typical energy density W0 = 3.18 J m−3.
Thus, we solved the dimensionless equations:
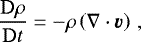 (1)
(1)
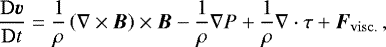 (2)
(2)
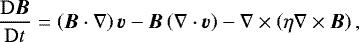 (3)
(3)
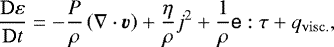 (4)
(4)
where ρ is the mass density, v the plasma velocity, B the magnetic field, P the gas pressure, η the dimensionless magnetic diffusivity, 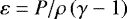 the specific internal energy (where γ = 5∕3 is the ratio of specific heats), and j the current density. In addition, e denotes the viscous strain rate tensor and τ the viscous stress tensor incorporating the artificial viscosity used in order to resolve shocks (cf. Arber et al. 2007). Further, Fvisc. is the uniform viscosity, discussed below, and qvisc. the associated heating. For simplicity and in order to reduce computational overheads, thermal conduction and optically thin radiation were both neglected. The boundary conditions were chosen to be periodic in x and y; in z, a prescribed velocity driver was imposed as discussed in detail below and, for all other quantities, the normal derivative was set to zero. In the initial state, the plasma is stationary, with uniform density and specific internal energy, and the magnetic field uniform in the z direction.
the specific internal energy (where γ = 5∕3 is the ratio of specific heats), and j the current density. In addition, e denotes the viscous strain rate tensor and τ the viscous stress tensor incorporating the artificial viscosity used in order to resolve shocks (cf. Arber et al. 2007). Further, Fvisc. is the uniform viscosity, discussed below, and qvisc. the associated heating. For simplicity and in order to reduce computational overheads, thermal conduction and optically thin radiation were both neglected. The boundary conditions were chosen to be periodic in x and y; in z, a prescribed velocity driver was imposed as discussed in detail below and, for all other quantities, the normal derivative was set to zero. In the initial state, the plasma is stationary, with uniform density and specific internal energy, and the magnetic field uniform in the z direction.
Combining the above equations gives the total energy equation:
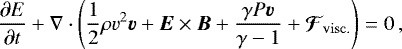 (5)
(5)
where the total energy density is
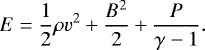 (6)
(6)
Of all the terms in the energy flux, only the Poynting flux, E ×B, and the significantly smaller viscous flux, 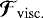 , are non-zero for the boundary conditions used.
, are non-zero for the boundary conditions used.
The computational domain had boundaries sited at x = ±w, y = ±w, z = ±L. Here, w = 3 and L = 10. Thus, for a thread of unit radius, the length-to-width aspect ratio is ten, as has been used in previous models (Browning & Van der Linden 2003; Browning et al. 2008; Hood et al. 2009). We used a computational grid of 5122 × 2048 points. This ensures thatthere are at least 160 grid points across the diameter of each thread. As noted below, we also performed simulations in coarser grids of 2562 × 1024 and 1282 × 512, but there were no qualitative differences in the results.
2.2 Viscosity and resistivity
In addition to the standard shock viscosities used in Lare3d, the code incorporates a uniform viscosity, in order to damp the Alfvén waves generated by the imposed footpoint motions. The heating associated with both viscosities and the Ohmic heating are added to the equation for internal energy. No other form of “background” coronal heating was imposed.
As used in previous work on the avalanche model (Tam et al. 2015), the non-uniform resistivity is defined as
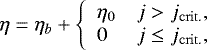 (7)
(7)
where ηb is a uniform background resistivity and jcrit. is a threshold current, above which an anomalous resistivity, η0, is added.
While we used ideal background conditions, ηb = 0.0, an anomalous resistivity η0 = 0.001 was used when current sheets were created. This ensures that resistivity, as opposed to a numerical diffusion, is responsible for any magnetic reconnection. The threshold current was taken as jcrit. = 5.0, set by reference to the peak current shortly before the kink instability and consistent with preceding papers (Hood et al. 2009; Tam et al. 2015).
2.3 Driving velocity
The centres of the three cylindrical threads that undergo twisting are defined as 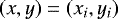 , with the radius defined for generality as a, but set to unity in this paper. The configuration of the three threads is shown in Fig. 1 and they were centred on
, with the radius defined for generality as a, but set to unity in this paper. The configuration of the three threads is shown in Fig. 1 and they were centred on  ,
, 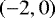 , and
, and 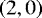 . Defining a local radial coordinate
. Defining a local radial coordinate 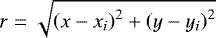 , for r < a, we imposed a localized, cylindrically symmetric azimuthal velocity on the photospheric boundaries. The photospheric velocity is assumed to vanish at the axis and edge of each thread, and, for sufficiently small r, the behaviour isapproximately linear,
, for r < a, we imposed a localized, cylindrically symmetric azimuthal velocity on the photospheric boundaries. The photospheric velocity is assumed to vanish at the axis and edge of each thread, and, for sufficiently small r, the behaviour isapproximately linear,
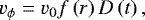 (8)
(8)
where v0 is a parameter governing the speed of the driving, and
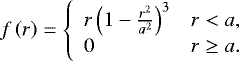 (9)
(9)
A rotation in opposite directions was imposed on the top and bottom boundaries to ensure twisting of the magnetic field lines along each thread. Three independent, cylindrical threads are created, but these are not part of any large-scale braided structure. Here, we refer to a “braided” structure as one where the magnetic field loses invariance in sequential cuts in the x, y-plane. However, one could consider this, and all other braided fields, using the definition and techniques of Yeates & Hornig (2013) and Wilmot-Smith (2015).
The function ![$D\left(t\right) = \left[1 - \cos\left(\pi t/T\right)\right]/2$](/articles/aa/full_html/2018/07/aa32399-17/aa32399-17-eq18.png) , for t < T, imposes a time-dependence on the driver, which allows it to be phased in very smoothly, over a rise-time T, after which
, for t < T, imposes a time-dependence on the driver, which allows it to be phased in very smoothly, over a rise-time T, after which 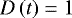 . Throughout, we assume T = 2. Nevertheless, the starting of the footpoint motion results in the generation of Alfvén waves. These are being damped out by viscosity such that the subsequent evolution is tending towards a steady nature until the central thread is destabilized by the ideal kink instability.
. Throughout, we assume T = 2. Nevertheless, the starting of the footpoint motion results in the generation of Alfvén waves. These are being damped out by viscosity such that the subsequent evolution is tending towards a steady nature until the central thread is destabilized by the ideal kink instability.
The magnitude of the driving speed was chosen in order that all footpoint motions should be sub-Alfvénic, yet sufficiently fast to overcome any slipping of the magnetic field at the boundaries of the domain associated with either numerical or physical diffusion (see Bowness et al. 2013, for discussion). Here, v0 was chosen such that the maximum magnitudes of the driving speeds (at 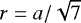 ) are 0.05 for the central thread (v0 = 0.21) and 0.02 for the other two (v0 = 0.084). The initial evolution of the magnetic field is through a sequence of equilibria. Since the central thread is twisted at a faster rate, it will become unstable to a kink instability before the other two and will correspond to the situation considered in Hood et al. (2016).
) are 0.05 for the central thread (v0 = 0.21) and 0.02 for the other two (v0 = 0.084). The initial evolution of the magnetic field is through a sequence of equilibria. Since the central thread is twisted at a faster rate, it will become unstable to a kink instability before the other two and will correspond to the situation considered in Hood et al. (2016).
 |
Fig. 1 Location of threads and direction of driving applied. Opposing rotational motions are applied on the top and bottom boundaries at three locations in order to create three independent threads. |
3 Basic theory
3.1 Initial predicted evolution
The initial evolution can be determined by linearizing the MHD equations about the uniform initial state. The imposed driver gives rise to a steady azimuthal velocity in the thread, of the form (cf. Goldstraw et al. 2018)
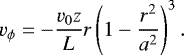 (10)
(10)
Integrating over the volume of a thread, one obtains an estimate for the steady-state kinetic energy in each thread:
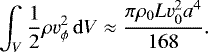 (11)
(11)
Through the induction equation, neglecting resistivity, this velocity produces an azimuthal component to the magnetic field:
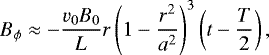 (12)
(12)
for t ≥ T. The azimuthal field is analogous to that studied in the previous papers (Tam et al. 2015; Hood et al. 2016), allowing this choice of radial dependence to emulate the field used in those papers. When the footpoint displacements become large (v0t∕L ≈ 1), the agreement between the field in this paper and the previous work is weaker.
The magnetic energy associated with the azimuthal field of each thread is
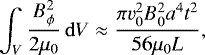 (13)
(13)
for 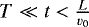 , until non-linear effects become important. The total magnetic energy will include that in the background, potential field.
, until non-linear effects become important. The total magnetic energy will include that in the background, potential field.
For such Bϕ, the angle through which the field is twisted is taken as
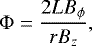 (14)
(14)
(e.g. Hood & Priest 1979). For the present form of Bϕ, in Eq. (12), the mean twist is defined as
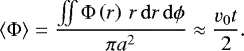 (15)
(15)
The linear behaviour of the axial current within each thread is
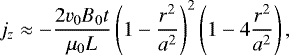 (16)
(16)
for t ≫ T. The integral across the radius of the thread vanishes, demonstrating that there is no net axial current here, as in the models previously studied (Hood et al. 2009, 2016; Tam et al. 2015), since the currents are generated by localized and finite footpoint motions (Tam et al. 2015).
3.2 Threshold for instability
For an azimuthal magnetic field
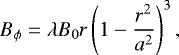 (17)
(17)
Hood et al. (2016) quote a threshold for the onset of a kink instability as λ ≥ λcrit. ≈ 1.586. Comparing with Eq. (12), we identify λ ≈ v0t∕L for t ≫ T. Hence, in principle, it is straightforward to estimate the time at which the kink instability is expected to start.
However, any comparison between the theoretically predicted instability threshold and those seen in the simulation is rendered difficult for a number of reasons, and these are of importance in understanding the results. Firstly, the marginal stability value is based on straight, cylindrically symmetric magnetic fields, with a specific radial profile. While the magnetic field generated by footpoint motions agrees with the analytical profile for short times, it may be significantly different for longer times as a result of rapid expansion or contraction near the photospheric boundaries, as discussed by Browning & Hood (1989). Secondly, the growth rate of the instability just beyond marginal stability is small and we know from Hood et al. (2016) that the kink instability can take around 50 reference Alfvén times to grow detectably out of a random disturbance. During this time, our field is still being driven and so the value of λ, corresponding to the time that the instability is identified, will be larger than the actual critical value, λcrit.. Thirdly, the linear stability results are based on a force-free field with a uniform density. Fourthly, as a consequence of numerical dissipation, the actual twist present in the magnetic field is less than that theoretically anticipated. In the driven case, the density and pressure change in response to the driving motions. While the plasma beta remains low, it is likely that these changes will not affect the stability properties much, but it does add to the difficulty of comparing results.
We estimate the time at which the central thread crosses the theoretical marginal stability threshold for the kink instability at t ≈ 76.5 and that for the two other threads at t ≈ 189.7. However, as we shall see in the next section, the instability in the numerical simulation occurs later owing to the slow, non-linear development of the instability, as discussed above. A more appropriate estimate, accounting also for the change in the vertical magnetic field and non-zero plasma beta, is inferred from the numerical solution.
4 Continued driving: evolution of magnetic and kinetic energies up to instability
Throughout the numerical experiment, the total energy is conserved with an error better than 0.5%. This is illustrated in Fig. 2, where the rate of change of the volume-integrated total energy and the total energy flux through the boundaries, 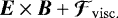 (the Poynting flux plus a small viscous energy flux), are plotted as functions of time. Whenever narrow current sheets form and fast reconnection occurs, there is a small loss of energy. However, as shown, this energy loss remains small and insignificant.
(the Poynting flux plus a small viscous energy flux), are plotted as functions of time. Whenever narrow current sheets form and fast reconnection occurs, there is a small loss of energy. However, as shown, this energy loss remains small and insignificant.
The numerical evolution of the magnetic and kinetic energies up to the onset of the kink instability can be compared with the estimates of the previous section. Fig. 3 shows the volume-integrated magnetic energy as a function of time as a solid black curve. The simple estimate in Eq. (13), based on linear MHD, is shown as the red dashed curve. The initial increase is correctly predicted by the quadratic expression for short times, with a slight departure occurring once the non-linear terms become important. The increase in magnetic energy continues until the kink instability occurs.
The volume-integrated kinetic energy is shown in Fig. 4 as a function of time and demonstrates the presence of Alfvén waves travelling across the length of the domain from the start-up of the photospheric driving. The amplitude of the Alfvén waves is damped by the diffusive effects and the kinetic energy tends towards the steady state predicted by Eq. (11) (shown as the horizontal dashed line). From Fig. 4, the period of the Alfvén waves is approximately 20, namely the propagation time for an Alfvén wave with a unit dimensionless Alfvén speed over a distance 2L = 20. The first indication of the presence of the kink instability is seen in the exponential growth in kinetic energy around t = 160. The nature of the instability is confirmed by plotting the logarithm of the kinetic energy as a function of time.
 |
Fig. 2 Rates of change of the total energy (the sum of internal, kinetic, and magnetic) in the system, plotted as functions of t, along with inward flux (red). Their closeness demonstrates approximate conservation in the domain. The dominant flux is the Poynting flux that adds to magnetic energy. |
 |
Fig. 3 Volume-integrated magnetic energy shown as a function of t (blue curve) prior to the first instability, along with the simple predicted value of Eq. (13) (red dashed curve). |
5 Results
5.1 Axial current
The development of current sheets is one key ingredient of the kink instability and is essential for the development of an MHD avalanche, as shown in Hood et al. (2016). Current sheet formation is clearly seen for the continually driven case too.
As expected from Eq. (16), the dominant component of the current is the vertical component, jz, which grows as a consequence of the rotational shearing of the magnetic field resulting from the photospheric driving motions. Initially, this is the generation of a distributed current. We note that, near the axis of each thread, the axial current is negative, but, surrounding this, there is a neutralizing positive current. As indicated above, the net axial current in each thread is zero. The distributed current remains up to t = 180. After this time, the kink instability creates a strong helical current sheet. Reconnection occurs and, in the non-linear development of the instability, the current sheet fragments.
In Fig. 5a, one can see the formation of thin, axial current structures from the current sheet fragmentation. In Fig. 5b, the unstable central thread starts to interact with the right-hand thread, creating a thin current sheet at the boundary between the two threads. Again reconnection occurs and the right-hand thread is disrupted and its magnetic energy released. At t = 310, Fig. 5c shows the formation of a current sheet in the left-hand thread, as this thread starts to disrupt. We note thepresence of a large number of thin current structures in the remains of the other two threads. By t = 450, the continued driving generates a large number of strong current regions where reconnection and heating can occur.
 |
Fig. 4 Total kinetic energy plotted against time, until the onset of disruption in the first thread. The horizontal red dashed line is the estimated steady state. |
5.2 Onset of instability
The first evidence of disruption of the central thread from the kink instability is readily identified through the temporal evolution of the kinetic energy. Once the kink instability in the central thread is triggered, the kinetic energy grows exponentially in time, at twice the linear MHD growth rate. This is clearly seen around t = 160 in Fig. 4. The identification of subsequent disruption times is more difficult. However, we can use the formation and growth of crescent-like structures in the axial current of a thread as an indicator of the approximate disruption time and, hence, determine the associated twist and value of λ. These times are shown in Table 1.
An alternative estimate of the first disruption time is obtained from the kinetic energy (see Fig. 4). However, this is a more difficult way in which to estimate the subsequent disruption times; the formation of a current crescent is more readily identified.
From the fact that the second and third threads are disrupted long before attaining that twist present in the first thread at the time of its disruption, it is clear that the very presence of the initial instability brings about the disruption of its neighbours.
In marked contrast to the time at which the kinetic energy and axial current identify the instability, the critical value of λ is exceeded around t = 95. When the rotational boundary driving is halted before t = 95, it subsequently remained stable. When the driving is halted slightly beyond t = 95, the instability eventually developed, although it was only identifiable after a further 100 Alfvén times. Finally, stopping the driving later than this, the instability developed in a similar manner to the continually driven case in this paper.
 |
Fig. 5 Contours of dimensionless axial current, jz, in the mid-plane at z = 0. The kink instability is characterized by the formation of a crescent of strong current, as is apparent in panel a. The times shown are the time at which the initial kink instability is seen (panel a), the time of disruption of the right-hand thread (panel b), the time of disruption of the left-hand thread (panel c), and a general time showing the large number of strong current layers (panel d). Where the magnitude of current exceeds jcrit. = 5.0, resistivity istriggered. |
Onset times for disruption of each thread.
5.3 Fieldline evolution and connectivity
To understand how the connectivity of the field evolves in time, field lines are traced from a given initial point on the photospheric boundary (z = ±L) until they either reach the other photospheric end, where their locations are recorded, or cross the side boundaries. Tracking field lines using the highest-resolution grid is computationally too intensive and so the results presented are for a grid with 2562 × 1024 points. There is no significant qualitative difference, but we can track the connectivity of many more field lines.
The starting points are distributed on the bottom and top boundaries and move with the imposed driving velocity. This allows us to track the same field lines and follow their evolution. The results are depicted in Fig. 6. In Fig. 6a, the twisted nature of the three threads is clearly seen. The central thread is more highly twisted and is beyond the point of marginal stability for the onset of the kink instability. Figure 6b shows the non-linear evolution of the kink instability in the central thread, where its field lines have started to untwist. There is some evidence that this thread is starting to interact with the right-hand thread: dark purple field lines can be seen crossing the bottom boundary within the central thread. Figure 6c shows that the right thread has disrupted because of the interaction with the central thread, while the left thread is still relatively isolated. However, by t = 450, Fig. 6d shows that all three threads are individually less twisted, but now completely intertwined with each other. This intertwined state will now continue and the imposed regular twisting of the footpoints will now create a much more complex magnetic structure.
To emphasize how complex the magnetic field becomes, we track the same field lines from their advected footpoints on the bottom boundary, and record the location where they cross the top boundary. The results are shown in Fig. 7. At t = 180, the left and right threads both have the same regular pattern, indicating that the field lines have not changed their connectivity. However, there is some evidence of a restructuring of the field in the central thread in that the pattern is not as regular as the other two threads. This is to be expected since this thread is already beyond the threshold for the kink instability. At t = 230, the mixture of colours in Fig. 7b clearly shows that the central and right threads have many reconnected field lines. Figure 7c shows that the field lines from the central and right threads have spread a significant distance into the surrounding potential field, outside the twisting region. Finally, Fig. 7d demonstrates how far the reconnected field lines have departed from their original threads after all the threads have been disrupted. Thus, the energy released as these field lines reconnect will spread into a significant volume surrounding the original threads.
Figures 6 and 7 demonstrate that the field lines remain within their original threads until the occurrence of the initial kink instability. Field lines within the unstable thread begin to connect with the field outside this thread. The general expansion of the unstable central thread, as it releases its stored magnetic energy, causes an initial interaction with the right thread and triggers reconnection, resulting in one thread’s magnetic field becoming connected with another. Indeed, by the end of the simulation, field lines connect across the entire width of the domain and, like the contours of axial current in Fig. 5, no longer exhibit any discernible shape of the three individual threads. It is particularly interesting to note that the highly complex pattern of the footpoint locations, and hence the complex topology of the magnetic field, has arisen from three well-ordered, coherent motions.
An alternative representation of the same effect is witnessed in Fig. 8, where the direction of the magnetic field in the plane normal to the axis of the threads is shown. The initial, ordered structure of the field, induced by the smooth driving motions, gives way, with the onset of the initial kink instability and subsequent disruptions, to a field without the previous clear pattern of the original threads.
 |
Fig. 6 Field lines traced from each driven boundary, z = ±L. Here, the field lines drawn at t = 180 (panel a), t = 230 (panel b), t = 310 (panel c), and t = 450 (panel d), corresponding with the times in Fig. 5, are visible. The darker field lines are traced from the bottom boundary, and the lighter from the top. These are produced from a lower resolution, 2562 × 1024, because of limits on computational resources. |
5.4 Volume-integrated heating
As can be seen in Fig. 9, in response to the photospheric driving motions and the generated Poynting flux, the magnetic energy increases until the first instability. Then, as the central thread and the right thread are disrupted, the magnetic energy drops rapidly between t = 180 and t = 220. It is slightly increased by the continued input of energy by the Poynting vector until t = 300, when the left thread is disrupted and the magnetic energy again drops. These major releases of magnetic energy correspond to the largest heating events shown in Fig. 10. The dashed vertical lines in each plot show the times at which strong peaks appear in the total heating, largely agreeing with falls in magnetic energy and growth in kinetic energy. After t = 400, all three original threads are disrupted and the field line connectivity is complex. There are many small-scale current sheets that are potential sites for reconnection and energy release. While there is now a general increase in the magnetic energy, we can observe a series of distinct releases of energy, marked by a slight decline in magnetic energy. There is no indication yet of the magnetic energy reaching an approximate steady state. It may be the case that imposed driving speeds increase the magnetic energy faster than reconnection can dissipate it. Much longer (and computationally more expensive) experiments are required. We have continued a lower-resolution simulation (1282 × 512) up to 10 000 Alfvén times, and no evidence of saturation of stored energy is seen. The release of this magnetic energy results in a small increase in kinetic energy, seen in Fig. 11, but the majority of the released energy goes into heat.
The total heating is the combined effect of viscous and Ohmic heating and we now investigate the temporal evolution of the volume-integrated heating, as shown in Fig. 10. Two clear features are visible after t = 400. Firstly, there are many heating events with a wide range of magnitudes and durations. Apart from the initiating kink instability and the initial thread disruptions, there are no very large releases of energy up to 1000 Alfvén times. There are only a large number of smaller events. These smaller heating events may be related to the hypothesized nanoflares. Secondly, there is a clear background heating after the initial instability. The heating never drops to zero after t = 100. Initial studies suggest that this background heating is not dependent on the grid resolution, although the exact timing of the individual small heating events is. A simple Fourier analysis of the total heating function does not pick out a preferred period for the “nanoflares” and, thus, suggests that the events are random.
Until the end of the simulation, with driving being continually applied, there is a consistent presence of such heating events recurring. The persistence of a background level of heating, seen in Fig. 10, above which there are sporadic “bursts” of heating, attests to the possibility of a consistent source of heating, long after the threads have become unstable and ceased to hold any of their recognizable cylindrical form. Although one finds, apparently, evidence of consistent heating of indefinite duration, the individual events which constitute this effect provide little evidence of strong, discernible periodicity, with no intervals appearing in a power spectrum.
 |
Fig. 7 Locations on z = L to which field lines traced from z = −L connect. These are shown for t = 180 (panel a), t = 230 (panel b), t = 310 (panel c), and t = 450 (panel d), corresponding with the times in Fig. 5. Field lines in blue begin in the central thread, those in orange in the left, and those in purple in the right. These are produced from a lower resolution, 2562 × 1024, as for Fig. 6. |
 |
Fig. 8 Arrows indicating the strength and direction of the magnetic field in the mid-plane in z. The times shown are for t = 180 (panel a), t = 230 (panel b), t = 310 (panel c), and t = 450 (panel d), corresponding with the times in Fig. 5. The longest arrows correspond to a field strength in the x, y-plane of 0.787 (panel a), 0.486 (panel b), 0.655 (panel c), and 0.369 (panel d). |
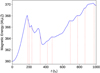 |
Fig. 9 Magnetic energy over time. Decreases in magnetic energy correspond to individual heating events. The red dashed lines match the times of large heating events identified in Fig. 10. |
 |
Fig. 10 Instantaneous total heating over time. This is the sum of Ohmic heating, heating by shock viscosities, and heating by uniform viscosity. The red dashed lines identify an illustrative sample of visibly large heating events. |
 |
Fig. 11 Volume-integrated kinetic energy over time. The red dashed lines match the times of large heating events identified in Fig. 10. |
6 Discussion and conclusions
This paper has addressed coronal energy release by considering the driven evolution of three neighbouring threads within a large-scale loop structure. Instability of one of the threads leads to the release of magnetic energy in all three, with bursty energy release continuing throughout the simulation.
An important outcome of this work is that, while the relatively simple driving of three vortex motions at the photospheric boundaries initially produces three coherent and distinct flux tubes, after the instability and subsequent disruptions, the magnetic field lines are connected to different vortices and the continued photospheric motions begin to braid the magnetic field in a much more complex manner. Indeed, there is little cylindrical symmetry left in the final field, and the complex three-dimensional magnetic field lines readily form numerous small current sheets and possible heating sites. This scenario differs from that proposed by others who argue that current sheets will always form in sufficiently tangled magnetic fields generated by complex motions (e.g. Hendrix & Van Hoven 1996; Ng et al. 2012). Here, the current sheets form spontaneously from a highly ordered initial state, with the photospheric motions bringing about braiding of the magnetic field, as has often been seen in such driven simulations (Wilmot-Smith 2015), and hence the possibility of the topological dissipation discussed by Parker (1972).
The field then attempts to relax to a lower-energy configuration, but nevertheless the constant imposition of the driving velocity necessitates a departure from the classical theory of Taylor (1974). The perpetual influx of energy by photospheric driving precludes the system attaining a minimal energy state. In addition, the work by Yeates et al. (2010) suggests that the constant-α state will not be reached, but instead a higher-energy state conserving topological degree. Nonetheless, the magnetic field is still non-potential and contains available energy. That external driving causes departures from a pure Taylor statehas been widely discussed in the case of laboratory plasmas (see Kitson & Browning 1990; Tang & Boozer 2005).
The temporal evolution of the total heating shows that, after the first few large releases of energy, there is a continued background level of heating and a large number of small heating events. There is no obvious periodicity or size for these events. The question of the origin of the background heating (in terms of viscosity models), and whether it is really steady or a series of very small events, will be presented in a subsequent paper. Future work will also address the spatial dependence of the heating, in order to ascertain whether the heating is likely to be localized (e.g. footpoint heating) or spread throughout the corona (quasi-uniform heating, see Klimchuk 2015).
The application of avalanches to coronal energy dissipation, posited by Lu & Hamilton (1991) and since then considered by several authors (Aschwanden et al. 2016), was noted earlier. In this and earlier work, we have demonstrated using full three-dimensional MHD simulations that the destabilization of large-scale magnetic fields by a single unstable “node” is indeed feasible. This is conceptually similar to the ideas arising in the concept of “self-organized criticality” (SOC), whereby an instability occurs following the breach by a certain parameter of some critical condition, and leads to a reconfiguration which affects neighbouring regions. As the disruption spreads, with neighbours successively impacting upon each other, an “avalanche” results (Bak et al. 1987; Bak 1997).
However, there are important differences between our results and those arising from SOC. In particular, these models iterate through external driving and dissipation in accordance with basic rules, with a marginally stable state being attained. We do not find evidence for this here. The reason is likely to be that, at this time, MHD simulations cannot be run for nearly long enough to attain the SOC marginal state. Thus, the major outstanding issue in applying SOC and cellular automata (CA) to the coronal energy release problem, namely the construction of rigorous rules governing the instability and subsequent redistribution of the field and, hence, heating of the plasma, remains untested. However, this and earlier work (Hood et al. 2016) do suggest merit in the idea of coronal avalanches, and more computational power will eventually bridge this gap.
Acknowledgements
AWH acknowledges the financial support of STFC through the Consolidated grant, ST/N000609/1, to the University of St Andrews and JR acknowledges the support of the Carnegie Trust for the Universities of Scotland. PKB acknowledges financial support of STFC through consolidated grant ST/P000428/1 at the University of Manchester. This work used the DIRAC 1, UKMHD Consortium machine at the University of St Andrews and the DiRAC Data Centric system at Durham University, operated by the Institute for Computational Cosmology on behalf of the STFC DiRAC HPC Facility (www.dirac.ac.uk). This equipment was funded by a BIS National E-infrastructure capital grant ST/K00042X/1, STFC capital grant ST/K00087X/1, DiRAC Operations grant ST/K003267/1 and Durham University. DiRAC is part of the National E-Infrastructure.
References
- Arber, T. D., Longbottom, A. W., Gerrard, C. L., & Milne, A. M. 2001, J. Comput. Phys., 171, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Arber, T. D., Haynes, M., & Leake, J. E. 2007, ApJ, 666, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Crosby, N. B., Dimitropoulou, M., et al. 2016, Space Sci. Rev., 198, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Bak, P. 1997, How Nature Works: The Science of Self-Organized Criticality (Oxford: Oxford University Press) [Google Scholar]
- Bak, P., Tang,C., & Wiesenfeld, K. 1987, Phys. Rev. Lett., 59, 381 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bareford, M. R., Gordovskyy, M., Browning, P. K., & Hood, A. W. 2016, Sol. Phys., 291, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Bowness, R., Hood, A. W., & Parnell, C. E. 2013, A&A, 560, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Browning, P. K., & Hood, A. W. 1989, Sol. Phys., 124, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Browning, P. K., & Van der Linden, R. A. M. 2003, A&A, 400, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Browning, P. K., Gerrard, C., Hood, A. W., Kevis, R., & Van der Linden, R. A. M. 2008, A&A, 485, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cargill, P. J., Warren, H. P., & Bradshaw, S. J. 2015, Phil. Trans. R. Soc. A, 373, 40260 [Google Scholar]
- Christe, S., Hannah, I. G., Krucker, S., McTiernan, J., & Lin, R. P. 2008, ApJ, 677, 1385 [NASA ADS] [CrossRef] [Google Scholar]
- Cowley, S. C., Wilson, H., Hurricane, O., & Fong, B. 2003, Plasma Phys. Control. Fusion, 45, A31 [CrossRef] [Google Scholar]
- De Moortel, I., & Galsgaard, K. 2006, A&A, 459, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galsgaard, K.,& Nordlund, Å. 1996, J. Geophys. Res., 101, 13445 [NASA ADS] [CrossRef] [Google Scholar]
- Glesener, L., Krucker, S., Hannah, I. G., et al. 2017, ApJ, 845, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstraw, E. E., Hood, A. W., Browning, P. K., & Cargill, P. J. 2018, A&A, 610, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gordovskyy, M., Browning, P. K., Kontar, E. P., & Bian, N. H. 2013, Sol. Phys., 284, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Hannah, I. G., Christe, S., Krucker, S., et al. 2008, ApJ, 677, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Hendrix, D. L., & Van Hoven, G. 1996, ApJ, 467, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Hood, A. W., & Priest, E. R. 1979, Sol. Phys., 64, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Hood, A. W., Browning, P. K., & Van der Linden, R. A. M. 2009, A&A, 506, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hood, A. W., Cargill, P. J., Browning, P. K., & Tam, K. V. 2016, ApJ, 817, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Hurricane, O. A., Fong, B. H., & Cowley, S. C. 1997, Phys. Plasmas, 4, 3565 [NASA ADS] [CrossRef] [Google Scholar]
- Isliker, H., Anastasiadis, A., & Vlahos, L. 2000, A&A, 363, 1134 [NASA ADS] [Google Scholar]
- Kitson, D. A.,& Browning, P. K. 1990, Plasma Phys. Control. Fusion, 32, 1265 [NASA ADS] [CrossRef] [Google Scholar]
- Klimchuk, J. A. 2015, Phil. Trans. R. Soc. A, 373, 20140256 [CrossRef] [Google Scholar]
- Knizhnik, K. J., Antiochos, S. K., & DeVore, C. R. 2017, ApJ, 835, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Krucker, S., Christe, S., Glesener, L., et al. 2014, ApJ, 793, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, R. P., Dennis, B. R., Hurford, G. J., et al. 2002, Sol. Phys., 210, 3 [Google Scholar]
- Lu, E. T., & Hamilton, R. J. 1991, ApJ, 380, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, C. S., Lin, L., & Bhattacharjee, A. 2012, ApJ, 747, 109 [NASA ADS] [CrossRef] [Google Scholar]
- O’Hara, J. P.,& De Moortel, I. 2016, A&A, 594, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parker, E. N. 1972, ApJ, 174, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1988, ApJ, 330, 474 [Google Scholar]
- Rappazzo, A. F., Velli, M., Einaudi, G., & Dahlburg, R. B. 2008, ApJ, 677, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Rappazzo, A. F., Velli, M., & Einaudi, G. 2010, ApJ, 722, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Rappazzo, A. F., Velli, M., & Einaudi, G. 2013, ApJ, 771, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Reale, F. 2014, Liv. Rev. Sol. Phys., 11, 4 [Google Scholar]
- Ritchie, M. L., Wilmot-Smith, A. L., & Hornig, G. 2016, ApJ, 824, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Tam, K. V., Hood, A. W., Browning, P. K., & Cargill, P. J. 2015, A&A, 580, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tang, X. Z., & Boozer, A. H. 2005, Phys. Rev. Lett., 94, 225004 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, J. B. 1974, Phys. Rev. Lett., 33, 1139 [NASA ADS] [CrossRef] [Google Scholar]
- van Ballegooijen, A. A., Asgari-Targhi, M., Cranmer, S. R., & DeLuca, E. E. 2011, ApJ, 736, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Vlahos, L., Krucker, S., & Cargill, P. 2009, The Solar Flare: A Strongly Turbulent Particle Accelerator, eds. L. Vlahos, & P. Cargill (Berlin: Springer-Verlag), 157 [Google Scholar]
- Wilmot-Smith, A. L. 2015, Phil. Trans. R. Soc. A, 373, 20140265 [Google Scholar]
- Yeates, A. R., & Hornig, G. 2013, Phys. Plasmas, 20, 012102 [NASA ADS] [CrossRef] [Google Scholar]
- Yeates, A. R., Hornig, G., & Wilmot-Smith, A. L. 2010, Phys. Rev. Lett., 105, 085002 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Location of threads and direction of driving applied. Opposing rotational motions are applied on the top and bottom boundaries at three locations in order to create three independent threads. |
| In the text | |
 |
Fig. 2 Rates of change of the total energy (the sum of internal, kinetic, and magnetic) in the system, plotted as functions of t, along with inward flux (red). Their closeness demonstrates approximate conservation in the domain. The dominant flux is the Poynting flux that adds to magnetic energy. |
| In the text | |
 |
Fig. 3 Volume-integrated magnetic energy shown as a function of t (blue curve) prior to the first instability, along with the simple predicted value of Eq. (13) (red dashed curve). |
| In the text | |
 |
Fig. 4 Total kinetic energy plotted against time, until the onset of disruption in the first thread. The horizontal red dashed line is the estimated steady state. |
| In the text | |
 |
Fig. 5 Contours of dimensionless axial current, jz, in the mid-plane at z = 0. The kink instability is characterized by the formation of a crescent of strong current, as is apparent in panel a. The times shown are the time at which the initial kink instability is seen (panel a), the time of disruption of the right-hand thread (panel b), the time of disruption of the left-hand thread (panel c), and a general time showing the large number of strong current layers (panel d). Where the magnitude of current exceeds jcrit. = 5.0, resistivity istriggered. |
| In the text | |
 |
Fig. 6 Field lines traced from each driven boundary, z = ±L. Here, the field lines drawn at t = 180 (panel a), t = 230 (panel b), t = 310 (panel c), and t = 450 (panel d), corresponding with the times in Fig. 5, are visible. The darker field lines are traced from the bottom boundary, and the lighter from the top. These are produced from a lower resolution, 2562 × 1024, because of limits on computational resources. |
| In the text | |
 |
Fig. 7 Locations on z = L to which field lines traced from z = −L connect. These are shown for t = 180 (panel a), t = 230 (panel b), t = 310 (panel c), and t = 450 (panel d), corresponding with the times in Fig. 5. Field lines in blue begin in the central thread, those in orange in the left, and those in purple in the right. These are produced from a lower resolution, 2562 × 1024, as for Fig. 6. |
| In the text | |
 |
Fig. 8 Arrows indicating the strength and direction of the magnetic field in the mid-plane in z. The times shown are for t = 180 (panel a), t = 230 (panel b), t = 310 (panel c), and t = 450 (panel d), corresponding with the times in Fig. 5. The longest arrows correspond to a field strength in the x, y-plane of 0.787 (panel a), 0.486 (panel b), 0.655 (panel c), and 0.369 (panel d). |
| In the text | |
 |
Fig. 9 Magnetic energy over time. Decreases in magnetic energy correspond to individual heating events. The red dashed lines match the times of large heating events identified in Fig. 10. |
| In the text | |
 |
Fig. 10 Instantaneous total heating over time. This is the sum of Ohmic heating, heating by shock viscosities, and heating by uniform viscosity. The red dashed lines identify an illustrative sample of visibly large heating events. |
| In the text | |
 |
Fig. 11 Volume-integrated kinetic energy over time. The red dashed lines match the times of large heating events identified in Fig. 10. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


