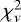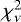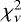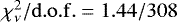| Issue |
A&A
Volume 615, July 2018
|
|
|---|---|---|
| Article Number | A150 | |
| Number of page(s) | 14 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201731583 | |
| Published online | 31 July 2018 | |
Asymmetric Type-Ia supernova origin of W49B as revealed from spatially resolved X-ray spectroscopic study
1
Anton Pannekoek Institute, University of Amsterdam,
PO Box 94249,
1090 GE
Amsterdam,
The Netherlands
e-mail: p.zhou,j.vink@uva.nl
2
School of Astronomy and Space Science, Nanjing University,
Nanjing
210023,
PR China
3
GRAPPA, University of Amsterdam,
PO Box 94249,
1090 GE
Amsterdam,
The Netherlands
Received:
17
July
2017
Accepted:
23
March
2018
The origin of the asymmetric supernova remnant (SNR) W49B has been a matter of debate: is it produced by a rare jet-driven core-collapse (CC) supernova, or by a normal supernova that is strongly shaped by its dense environment? Aiming to uncover the explosion mechanism and origin of the asymmetric, centrally filled X-ray morphology of W49B, we have performed spatially resolved X-ray spectroscopy and a search for potential point sources. We report new candidate point sources inside W49B. The Chandra X-ray spectra from W49B are well-characterized by two-temperature gas components (~0.27 keV + 0.6–2.2 keV). The hot component gas shows a large temperature gradient from the northeast to the southwest and is over-ionized in most regions with recombination timescales of 1–10 × 1011 cm−3 s. The Fe element shows strong lateral distribution in the SNR east, while the distribution of Si, S, Ar, Ca is relatively smooth and nearly axially symmetric. Asymmetric Type-Ia explosion of a Chandrasekhar-mass white dwarf (WD) well-explains the abundance ratios and metal distribution of W49B, whereas a jet-driven explosion and normal CC models fail to describe the abundance ratios and large masses of iron-group elements. A model based on a multi-spot ignition of the WD can explain the observed high MMn∕MCr value (0.8–2.2). The bar-like morphology is mainly due to a density enhancement in the center, given the good spatial correlation between gas density and X-ray brightness. The recombination ages and the Sedov age consistently suggest a revised SNR age of 5–6 kyr. This study suggests that despite the presence of candidate point sources projected within the boundary of this SNR, W49B is likely a Type-Ia SNR, which suggests that Type-Ia supernovae can also result in mixed-morphology SNRs.
Key words: ISM: individual objects: W49B – ISM: supernova remnants – nuclear reactions, nucleosynthesis, abundances – white dwarfs
© ESO 2018
1 Introduction
The study of supernova remnants (SNRs) provides information about both the supernova explosions themselves, and about the environments in which the supernova explosions took place. The environment often carries important information about the supernova progenitor itself, such as whether it formed in a star-forming region, and whether the progenitor shaped its own environment with a stellar wind. In particular, massive stars are known to create large wind-blown bubbles of several tens of parsecs in size (Weaver et al. 1977; Chevalier 1999).
The morphology and spectra of SNRs are determined by the combined effects of both the intrinsic explosion properties and the ambient medium in which they involve. Unfortunately, however, it is sometimes difficult to disentangle the effects of explosion properties and the environment in which they occurred. There are properties that can be firmly attributed to the explosion properties, but also properties that may be attributed to either the explosion characteristics or to the environment. For example, for young SNRs it is clear that the abundance pattern provides clear signatures of the type of explosion, with Type-Ia supernovae producing more iron-group elements (IGEs), whereas core-collapse (CC) SNRs are more abundant in oxygen, neon, and magnesium (Hughes et al. 1995; Vink 2012).
Mixed-morphology SNRs are a special class of SNRs characterized by bright thermal X-ray emission from their center, and a shell-type morphology in the radio. Initially, it was noted that mixed-morphology SNRs show thermal emission in the interior originating from low-abundant hot gas (Rho & Petre 1998; Jones et al. 1998). W49B was included in the list, but appeared to have enhanced abundances. However, increasingly more of the originally mixed-morphology SNRs appeared to also have enhanced abundances in their interiors (Lazendic & Slane 2006). It is clear that W49B, together with some other metal-rich cases such as Sgr A East (Sakano et al. 2004; Park et al. 2005) stand out. In most reviews of mixed-morphology SNRs, W49B is listed as a mixed-morphology SNR (Lazendic & Slane 2006; Vink 2012; Zhang et al. 2015; Dubner & Giacani 2015), and the definition of mixed-morphology SNR is in those cases based solely on different radio and X-ray morphology, and the fact that the X-ray emission is thermal in nature. It is thought that mixed-morphology SNRs evolve in denser environments, and since massive stars are associated with molecular cloud environments, it is usually assumed that these SNRs are remnants of CC supernovae. Indeed, some of the mixed-morphology SNRs have associated young pulsars, proving that these SNRs are indeed CC SNRs (e.g., W44, IC 443, Wolszczan et al. 1991; Olbert et al. 2001).
Thermonuclear (or Type-Ia) supernova progenitors are carbon–oxygen white dwarfs (WDs), which take a longer time to evolve (> 40 Myr), and, moreover, only explode if they accrete sufficient matter from a companion star (the single-degenerate scenario; Whelan & Iben 1973), or merge with a companion carbon–oxygen WD (the double-degenerate scenario; Webbink 1984). By the time they explode, their ambient medium does not necessarily contain any information anymore about their progenitors. The exact origin of Type-Ia supernovae is still a source of debate (see reviews Branch et al. 1995; Hillebrandt & Niemeyer 2000; Livio 2000; Wang & Han 2012; Maoz et al. 2014, and references therein), but also the manner in which the WDs explode is uncertain, with models involving deflagration (Nomoto et al. 1984), competing with so-called delayed detonation (DDT) models (Khokhlov 1991). In general, Type-Ia SNRs are often to be found in less dense regions of the Galaxy. For example, SN 1006 is found high above the Galactic plane (b =14.6°, corresponding to ~ 560 pc at a distance of 2.18 ± 0.08 kpc, Winkler et al. 2003). The less disturbed media in which they are often found may account for the generally more symmetric morphology, as comparedto CC SNRs (Lopez et al. 2011). On the other hand, the more symmetric morphologies of Type-Ia SNRs may also be caused by intrinsically more symmetric explosions.
The idea that Type-Ia progenitors do not shape the supernova environments has recently been challenged. For example, it is clear thatKepler’s SNR (Vink 2016, for a review), a Type-Ia SNR (Kinugasa & Tsunemi 1999; Reynolds et al. 1994), is evolving inside a bow-shock-shaped high-density region caused by the wind from a progenitor system (Chiotellis et al. 2012). In contrast, the likely Type-Ia SNR RCW 86 (see Gvaramadze et al. 2017, for a recent paper suggesting a CC origin) seems to evolve inside the low-density environment created by a powerful low-density wind (Williams et al. 2011; Broersen et al. 2014). Type-Ia SNR Tycho is suggested to be overrunning a slowly expanding molecular bubble created by its progenitor’s outflow (Zhou et al. 2016). The middle-aged SNR G299.2−2.9 is a Type-IaSNR showing asymmetries in the ejecta distribution due to an asymmetric explosion and/or a nonuniform surrounding medium (Post et al. 2014; Park et al. 2007). Moreover, some Type-Ia supernovae may explode with intrinsic asymmetries (Röpke et al. 2007; Maeda et al. 2010b), which has been used to interpret the spectral evolution diversity observed in Type-Ia supernovae (Maeda et al. 2010a).
Many of the above-mentioned issues of relating SNRs and their environments to the explosion types, come together in the peculiar SNR W49B, which is suggested at a distance of 8–11.3 kpc (Radhakrishnan et al. 1972; Brogan & Troland 2001; Chen et al. 2014; Zhu et al. 2014). The X-ray emission from W49B is dominated by emission from the center, which was initially attributed to the presence of a pulsar wind nebula (Pye et al. 1984), but was not much later discredited by the fact that the X-ray spectra obtained by the EXOSAT satellite displayed bright Fe–K lines (Smith et al. 1985). Due to the centrally enhanced X-ray morphology, it was listed in the first catalog of mixed-morphology SNRs, but with a metal-rich interior (Rho & Petre 1998). However, the brightness of the Fe–K lines and detailed spectroscopy with ASCA (Hwang et al. 2000) suggested that W49B is relatively young (1000–4000 yr) compared to most mixed-morphology SNRs, although it does share some characteristics with Sgr A East, a metal-rich, mixed-morphology SNR (Maeda et al. 2002). A property that W49B shares with many other mixed-morphology SNRs is that the plasma appears over-ionized (Kawasaki et al. 2005; Yamaguchi et al. 2009; Miceli et al. 2010), rather than under-ionized, as in most SNRs. Like many mixed-morphology SNRs, W49B is a GeV gamma-ray source, but it is also a TeV gamma-ray source, which is more rare for this class of SNRs (H. E. S. S. Collaboration 2018).
Although the X-ray spectrum of W49B shows the SNR to be very iron-rich, it is usually assumed that it is a CC SNR, like most mixed-morphology SNRs, albeit a peculiar one. Hwang et al. (2000) expressed some doubts, suggesting that neither a CC origin, nor a Type-Ia origin could explain the measured abundances. The brightness of the Fe–K lines, but also the peculiar, jet-like morphology of the ejecta, has been interpreted as evidence that W49B is the result of a hypernova explosion (Keohane et al. 2007). On the other hand, Miceli et al. (2006) compared the observed abundances with yields for hypernova and supernova nucleosynthesis and found better agreement for the abundances of W49B with models with a normal explosion energy (1051 erg). More recently, Lopez et al. (2013b), assuming W49B to be a CC SNR, presented evidence that the supernova produced a black hole rather than a neutron star (NS). The reason is that they did not find evidence for a cooling NS, similar to the X-ray point source in Cas A (Tananbaum 1999).
The study presented here was prompted by the many peculiarities of W49B. Most notably, we were puzzled by the fact that black holes are thought to be the end products of the most massive stars (>25 M⊙, e.g., Heger et al. 2003), but W49B seems to be evolving in a cavity of only ~5 pc radius (Keohane et al. 2007). In contrast, a progenitor more massive than 25 M⊙ is expected to create a cavity with a radius of at least 20 pc (Chen et al. 2013).
With our study we therefore tried to investigate, a) whether a cooling NS may, after all, be present, given that W49B provides a spatially non-uniform X-ray background that could hide a point source, and that the interstellar absorption is relatively high (NH > 1022 cm−2; and b) whether W49B is indeed a CC SNR or even a jet-driven CC SNR, as often assumed.
To answer these questions we reanalyzed the archival Chandra data, using a state-of-the-art adaptive binning method for spatially resolved X-ray spectroscopy, and we made a new search for X-ray point sources. We indeed found a few point sources, but our overall conclusion is that the X-ray spectra fit better with a Type-Ia origin for W49B, and in particular that the abundance pattern best fits the multi-point ignition DDT models of Seitenzahl et al. (2013b).
2 Data and analysis
2.1 Data
W49B was observed with Chandra in three epochs in 2000 (obs. ID: 117; PI: Stephen Holt) and 2011 (obs. IDs: 13440 and 13441; PI: Laura Lopez), with exposures of 54, 158, and 60 ks, respectively. We retrieve three sets of Chandra data, which covered the SNR with the backside-illuminated S3 chip in the faint mode. We use CIAO software (vers. 4.9 and CALDB vers. 4.7.7)1 to reduce the data, extract spectra, and detect the point-like sources. Xspec (vers. 12.9.0u)2 is used for spectral analysis.
2.2 Spatial-spectral analysis and adaptive binning method
To optimize the binning of the X-ray data for spatially resolved study, we employ a state-of-the-art adaptive spatial binning method called the weighted Voronoi tessellations (WVT) binning algorithm (Diehl & Statler 2006), which is a generalization of Cappellari & Copin (2003) Voronoi binning algorithm. The X-ray events taken from the event file are adaptively binned with the WVT binning algorithm.
First, we use the observation with longest exposure (obs. ID: 13440) to generate the bins, with each bin containing about 3600 counts in 0.3–10 keV. Among the 238 detected bins, 177 are located inside the SNR, with mean counts per pixel (1″) larger than 5. Subsequently, we extract spectra of the 177 regions from three Chandra data sets. The combined data provide ~6000 counts in each spatial bin. We then perform spectral analysis on the 177 bins associated with W49B by jointly fitting three groups of spectra from three observations. For each spatial bin and each observation, separate response matrix file and ancillary response file are generated. The background spectra are selected from a source-free region to the northeast of the SNR, which is at a similar Galactic latitude to the remnant.
Since previous studies (Kawasaki et al. 2005; Miceli et al. 2006, 2010; Ozawa et al. 2009; Lopez et al. 2013a,b) indicate that the spectrum of W49B is best fit with either a collisional ionization equilibrium (CIE) model or a recombining plasma model (a non-equilibrium ionization model with over-ionization), or a combination of the two models, we started our analysis by fitting each spatial bin twice, once with a CIE and once with an over-ionization model; in the end we selected the model that fits the spectra of a given spatial bin best with the smallest reduced chi-squared 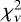 ; see Sect. 2.3).
; see Sect. 2.3).
Because this single-component model did not always give satisfactory fits, we decided to also use a two-component model, combining arelatively cool CIE component with a hotter component, which could be either a CIE or an over-ionized model (Sect. 2.4). The two component model gives better fits to the spectra, but a problem is that some of the parameters are correlated, so some additional constraints had to be imposed.
One should be aware that the recombining plasma model, with two more free parameters, may provide slightly smaller 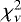 than the CIE model even though sometimes the two models are not statistically distinguished. Nevertheless, we found that for the single-component case discussed in Sect. 2.3 the two models can be distinguished in 90% of the extracted regions (based on the F-test, 2σ level), and for the two-component case in Sect. 2.4, the two groups of models are distinguishable in 80% of regions.
than the CIE model even though sometimes the two models are not statistically distinguished. Nevertheless, we found that for the single-component case discussed in Sect. 2.3 the two models can be distinguished in 90% of the extracted regions (based on the F-test, 2σ level), and for the two-component case in Sect. 2.4, the two groups of models are distinguishable in 80% of regions.
2.3 Single thermal component
We jointly fit the spectra in each bin with an absorbed CIE model (vapec) and an absorbed recombining plasma model (vrnei) in Xspec, and select the model with smaller 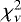 as the best-fit model. The two plasma models use the atomic data in the ATOMDB code3 version 3.0.7. The Tuebingen–Boulder interstellar medium (ISM) absorption model tbabs is used for calculation of the X-ray absorption due to the gas-phase ISM, the grain-phase ISM, and the molecules in the ISM (Wilms et al. 2000). The vrnei model describes a plasma that has cooled/heated rapidly from an initial temperature kTi to a temperatureof kT, whereas theionization state lags behind, and is characterized by a recombination/ionization timescale τr ∕τi applied to all ions. When the ions are in the recombining (overionized) state, kTi and the “ionization temperatures” of some ions kTz are larger than the current electron temperature kT. The lower limit on kTi is set to 2 keV to ensure that the recombining model is used, where the high ionization temperatures of Ar and Ca (kTz = 2.2–2.7 keV; Kawasaki et al. 2005) are also considered. We set the upper limit of kTi to 10 keV, which is a very high value for the plasma in an evolved SNR. We allow the abundances of Si, S, Ar, Ca, and Fe to vary and tie the abundance of Ni to Fe. Lower-mass elements, such as O, Ne, and Mg, have X-ray line emission below 1.8 keV, in the part of the spectrum that is heavily affected by interstellar absorption. The abundances of these elements are therefore unconstrained by the fits, and we fixed the abundances to their solar values. The solar abundances of Asplund et al. (2009) are adopted in plasma emission and photoelectric absorption models.Compared to the older widely used abundances obtained by Anders & Grevesse (1989), the O and Fe abundances in Asplund et al. (2009) decreased by 42% and 32%, respectively. Therefore, adopting different solar abundances can result in differences to the obtained abundances (especially for Fe) and absorption column density4.
as the best-fit model. The two plasma models use the atomic data in the ATOMDB code3 version 3.0.7. The Tuebingen–Boulder interstellar medium (ISM) absorption model tbabs is used for calculation of the X-ray absorption due to the gas-phase ISM, the grain-phase ISM, and the molecules in the ISM (Wilms et al. 2000). The vrnei model describes a plasma that has cooled/heated rapidly from an initial temperature kTi to a temperatureof kT, whereas theionization state lags behind, and is characterized by a recombination/ionization timescale τr ∕τi applied to all ions. When the ions are in the recombining (overionized) state, kTi and the “ionization temperatures” of some ions kTz are larger than the current electron temperature kT. The lower limit on kTi is set to 2 keV to ensure that the recombining model is used, where the high ionization temperatures of Ar and Ca (kTz = 2.2–2.7 keV; Kawasaki et al. 2005) are also considered. We set the upper limit of kTi to 10 keV, which is a very high value for the plasma in an evolved SNR. We allow the abundances of Si, S, Ar, Ca, and Fe to vary and tie the abundance of Ni to Fe. Lower-mass elements, such as O, Ne, and Mg, have X-ray line emission below 1.8 keV, in the part of the spectrum that is heavily affected by interstellar absorption. The abundances of these elements are therefore unconstrained by the fits, and we fixed the abundances to their solar values. The solar abundances of Asplund et al. (2009) are adopted in plasma emission and photoelectric absorption models.Compared to the older widely used abundances obtained by Anders & Grevesse (1989), the O and Fe abundances in Asplund et al. (2009) decreased by 42% and 32%, respectively. Therefore, adopting different solar abundances can result in differences to the obtained abundances (especially for Fe) and absorption column density4.
The single thermal component model gives a 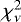 between 0.9 and 1.5 (degree of freedom (d.o.f.) = 222–365; mean
between 0.9 and 1.5 (degree of freedom (d.o.f.) = 222–365; mean 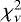 /d.o.f. = 1.16/291) across the remnant. Figure 1 displays the spatial distribution of the best-fit parameters, including the foreground absorption NH, electron temperature kT, initial temperature kTi (equal to kT when CIE is the best-fit model), recombination timescale τr (equal to the upper limit of 1014 cm−3 s when CIE is the best-fit model), and the abundances of Si, S, Ar, Ca, and Fe. The figure illustrates a large variation of the gas properties inside W49B. The kTi values can be constrained in only a small fraction of regions, while in the southwestern regions they run to the upper limit of 10 keV.
/d.o.f. = 1.16/291) across the remnant. Figure 1 displays the spatial distribution of the best-fit parameters, including the foreground absorption NH, electron temperature kT, initial temperature kTi (equal to kT when CIE is the best-fit model), recombination timescale τr (equal to the upper limit of 1014 cm−3 s when CIE is the best-fit model), and the abundances of Si, S, Ar, Ca, and Fe. The figure illustrates a large variation of the gas properties inside W49B. The kTi values can be constrained in only a small fraction of regions, while in the southwestern regions they run to the upper limit of 10 keV.
 |
Fig. 1 Distribution of the parameters fitted with the best-fit single component model, which, for every cell, was taken to be either the absorbed “vrnei” or the absorbed “apec” model, whichever produced the smallest |
2.4 Two thermal components
Previous studies suggest the existence of a cooler ISM component (~0.25 keV; Kawasaki et al. 2005)in addition to the hot, metal-rich component (Hwang et al. 2000; Miceli et al. 2006; Lopez et al. 2013a). Moreover, the infrared observations reveal that a large amount of dense gas (~500 cm−3 and ~800 M⊙) is shocked by W49B (Zhu et al. 2014), which implies that the SNR in such an inhomogeneous environment should consist of more than one density/temperature component. We, therefore also apply a two-thermal-component model to fit the spectra, in an attempt to check whether or not a cool component is needed across the SNR. The colder apec model with solar abundances is added to the absorbed vrnei/vapec model and then used to fit the 177 groups of spectra. The soft X-ray photons ≲2 keV (dominated by the cooler component) suffer heavy absorption, which results in some degeneracy between the cool component temperature kTc and NH in the spectral fit. We therefore assume that the foreground absorption of W49B is not changed across the small angular extent of the SNR (< 5′) and fix the NH value to 8 × 1022 cm−2. This value is close to the best-fit NH for the global spectra, and is also similar to the mean NH value if NH is allowed to vary for the 177 spectra. The upper limit for kTc is set to 0.7 keV to ensure that it is smaller than kTh.
Figure 2 shows the detailed distribution of the gas properties in W49B based on the two-component model, including 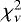 , the temperatures of the colder and hotter component (kTc and kTh, respectively), kTi, τr, and the abundances of Si, S, Ar, Ca, Fe elements. The Si distribution is smoother in the two-thermal-component model. Here the upper limit of kTi is set to 5 keV, which appears to be a limit to the electron temperatures found in young SNRs (Vink 2012). We note that the proton temperature may be higher, but the ionization properties of the plasma are determined by the electron temperatures. Moreover, the adopted upper limit value is indicated by the best-fit kTi values (~5 keV) in the SNR center.
, the temperatures of the colder and hotter component (kTc and kTh, respectively), kTi, τr, and the abundances of Si, S, Ar, Ca, Fe elements. The Si distribution is smoother in the two-thermal-component model. Here the upper limit of kTi is set to 5 keV, which appears to be a limit to the electron temperatures found in young SNRs (Vink 2012). We note that the proton temperature may be higher, but the ionization properties of the plasma are determined by the electron temperatures. Moreover, the adopted upper limit value is indicated by the best-fit kTi values (~5 keV) in the SNR center.
Although the overall temperature and abundance patterns obtained with single and double component models appear to be similar, the two-thermal-component model better describes the spectra than the model with only one thermal component: it results in smaller 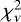 values (mean value of 1.06 and d.o.f. of 290), as well as smaller residuals in the spectral fit for the Si-XIII line emission for the range 1.8–2.2 keV (Fig. 3). The cooler component mainly affects the soft spectra ≲2 keV and the best-fit values of Si (see Fig. 3 for an example of the spectra fitted with one component and two components models, respectively). It is statistically meaningful to add the extra thermal component to the single-thermal-component model to improve the spectral fit of majority regions according to an F-test analysis (mean null hypothesis probability 10−7, adopting a mean d.o.f. of 291 and
values (mean value of 1.06 and d.o.f. of 290), as well as smaller residuals in the spectral fit for the Si-XIII line emission for the range 1.8–2.2 keV (Fig. 3). The cooler component mainly affects the soft spectra ≲2 keV and the best-fit values of Si (see Fig. 3 for an example of the spectra fitted with one component and two components models, respectively). It is statistically meaningful to add the extra thermal component to the single-thermal-component model to improve the spectral fit of majority regions according to an F-test analysis (mean null hypothesis probability 10−7, adopting a mean d.o.f. of 291 and 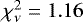 in the singlethermal model). For 92% of the bins, the two-component model significantly improves the fit with an F-test probability less than the typical value of 0.05 (2σ level), while for the other 8% bins near the western boundary the improvement is less significant.
in the singlethermal model). For 92% of the bins, the two-component model significantly improves the fit with an F-test probability less than the typical value of 0.05 (2σ level), while for the other 8% bins near the western boundary the improvement is less significant.
The X-ray flux of W49B is dominated by the hot component, as indicated by the large fraction of the hot-component flux to the total flux in 0.5–8 keV (flux_h/flux = 0.78–0.99; see the left panel of Fig. 4). The X-ray contribution from the cool component (1-flux_h/flux) is larger near the SNR shell than in the SNR interior. As a result, the single component fit with NH free gives smaller NH values near the SNR edge to compensate the flux of the missing cool component (see the NH distribution in Fig. 1). Therefore, the variation of NH is likely to be much smaller than suggested by the single-component model.
A temperature gradient for the hot component gas (kTh) is revealed with an orientation northeast to southwest (see Fig. 2). The kTh is as high as ~2.2 keV in the northeast but decreased to ~0.7 keV in the southwest. The kTc shows some variation across the SNR with a mean value of 0.27 keV. In a small fraction of regions with NH deviated largely from 8 × 1022 cm−2, kTc can be affected by NH due to the degeneracy between them. For example, a region in the southwest shows large kTc = 0.7 keV, which could be reduced to 0.18 keV if NH is free (~ 1023 cm−2).
The recombining plasma appears to be present throughout the SNR, except in the southeast shell, and occupies about three quarters of the studied area. The recombination timescale varies in the range 1–10 × 1011 cm−3 s. The recombining gas and CIE gas can be distinguished by comparing its kTi and kTh or by checking τr values: the recombining gas shows kTi > kTh and τr ≲ 1012 cm−3 s. The CIE region is colored in white in the τr panel of Fig. 2 (upper-right). Our study confirms the existence of recombining plasma in the center and west as pointed out by previous studies (e.g., Miceli et al. 2010; Lopez et al. 2013a). We note that the recombining plasma is also patchily distributed in the northern hemisphere of the remnant, but here the recombination timescales are generally much longer than in the southwest.
 |
Fig. 2 Distribution of the parameters fitted with the best-fit double component model, which was either an absorbed “hot vrnei + cool apec” model, or an absorbed “hot vapec + cool apec” model. First panel: |
 |
Fig. 3 Exemplified ACIS-S spectra from one bin in W49B fitted with one component (vapec; left: |
2.5 Density and mass of the shocked gas
W49B has a centrally bright X-ray morphology, indicating an enhanced plasma density in the interior, unlike the shell-type SNRs in Sedov phase with a density enhancement at the shells (Borkowski et al. 2001). Since the SNR is highly structured without a clear understanding of its three-dimensional density distribution, any complicate hypothesis on the gas distribution (e.g., bar + shell, disk + shell) could differ from the real distribution and introduce unknown uncertainties. Therefore, we take the simplest assumption that the plasma is uniform in each bin, so as to provide a mean gas density of the X-ray-emitting gas. We note that the following results are based on this oversimplified assumption of the geometry.
We estimate the mean density nH for a given bin using the normalization parameter in Xspec (norm = 10−14∕ (4πd2)∫ nenHdV, where d is the distance, ne and nH are the electron and H densities in the volume V; ne = 1.2nH for fully ionized plasma with solar or enhanced metal abundances in W49B) and an assumed prism geometry for each bin. Each prism has an area of the region and a depth across the SNR 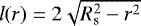 , where the radius of the SNR is Rs =2.′2, corresponding to 6.4 pc at a distance of 10 kpc, and r is its projection distance to the assumed SNR center. The SNR circle denoted in Fig. 4 encloses all regions, except a bin in the southwest, where its density and mass are not calculated. The two-temperature gas is assumed to fill the whole volume (fc + fh = 1) and in pressure balance (ncTc = nhTh), where f and n are the filling factor and hydrogen density, respectively, and the subscripts “c” and “h” denote the parameters for the cool and hot phases, respectively.
, where the radius of the SNR is Rs =2.′2, corresponding to 6.4 pc at a distance of 10 kpc, and r is its projection distance to the assumed SNR center. The SNR circle denoted in Fig. 4 encloses all regions, except a bin in the southwest, where its density and mass are not calculated. The two-temperature gas is assumed to fill the whole volume (fc + fh = 1) and in pressure balance (ncTc = nhTh), where f and n are the filling factor and hydrogen density, respectively, and the subscripts “c” and “h” denote the parameters for the cool and hot phases, respectively.
The distributions of the densities are displayed in Fig. 4. The brightness of the X-ray emission in 0.3–10 keV is overlaid with contours for comparison purposes. The hydrogen density nc in the cooler component gas is clearly enhanced along the “bar-like” feature across the SNR center and the shells in the eastern and western sides; it displays a good spatial correlation with the X-ray brightness. An enhancement of the density in those regions is also present in the hot component. The mean hydrogen density of the colder and hotter components are 24 cm−3 and 5 cm−3, respectively, and the mean filling factor of the hotter phase is 40%. The total masses of the X-ray-emitting gas are 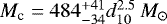 for the cool phase and
for the cool phase and 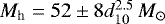 for the hot phase, where d10 = d∕(10 kpc) is the distance scaled to 10 kpc.
for the hot phase, where d10 = d∕(10 kpc) is the distance scaled to 10 kpc.
The mass uncertainties are calculated by using the 90% uncertainties of the normalization parameters and the filling factors of the 176 bins, where the uncertainties in the filling factors are incorporated into the overall error estimates, also taking into account uncertainties in the temperatures and normalizations of the two components. If the errors are asymmetric, we take the largest error. The systematic uncertainty is dominated by assumptions about the volume V or the depth l of the X-ray emitting gas, since the gas mass in bin i weakly depends on them (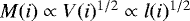 with given distance and norm). Since mixed-morphology SNRs generally have a relatively smooth radial density distribution, we assume the X-ray-emitting gas fills the whole SNR from front to back. This introduces some uncertainty, as the real depth, l(i), can be smaller. In the extreme case that the X-ray emission is only arising from a thin shell with a thickness of 1∕12RS,5 the masses are
with given distance and norm). Since mixed-morphology SNRs generally have a relatively smooth radial density distribution, we assume the X-ray-emitting gas fills the whole SNR from front to back. This introduces some uncertainty, as the real depth, l(i), can be smaller. In the extreme case that the X-ray emission is only arising from a thin shell with a thickness of 1∕12RS,5 the masses are 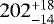 and 21 ± 3 M⊙ in the cool and hot components, respectively, which puts very conservative lower limits on the gas masses in W49B. We note that the thin shell geometry does not agree with the overall, center-filled, X-ray morphology of W49B.
and 21 ± 3 M⊙ in the cool and hot components, respectively, which puts very conservative lower limits on the gas masses in W49B. We note that the thin shell geometry does not agree with the overall, center-filled, X-ray morphology of W49B.
Mc is much larger than what could have been produced by the progenitor wind or the ejecta. Hence, the cool component is dominated by the heated interstellar gas. The mass of the hot component is also too large to correspond to the total supernova ejecta mass, which suggests that it consists of a mixture of ejecta and circumstellar material. An alternative could be that the hot component consists of almost pure ejecta material, with almost no hydrogen. In that case, the bremsstrahlung continuum is also dominated by electron-metal interactions rather than electron–proton interactions. The high average charge of the atoms and the enhanced ratio of electrons to atom results then in a higher emissivity per atom, which results in a lower mass for the hot component (Vink 2012, Sects. 6.1 and 10.3). Abundance ratios are not very sensitive to whether the gas is metal-pure, or hydrogen-rich with enhanced metal abundances. Currently with CCD X-ray spectroscopy we cannot distinguish between a pure metal plasma and a hydrogen-rich plasma withenhanced abundances. However, in the future, high-resolution imaging spectroscopy with the XARM (X-ray Astronomy Recovery Mission) and/or Athena could perhaps distinguish these two cases spectroscopically. Given the age of W49B (see also below) a mixture of hydrogen-rich and metal-rich ejecta seems the most likely scenario.
2.6 Abundance and distribution of the ejecta
The abundances and distribution of heavy elements have played an important role in probing the explosion mechanism of SNRs. We obtained average abundances [Si] = 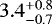 , [S] =
, [S] = 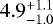 , [Ar] =
, [Ar] = 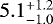 , [Ca] =
, [Ca] = 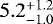 , and [Fe] =
, and [Fe] = 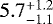 . The averageabundance values here are based on the weighted sum (by the estimated gas mass for each sub-region) over all individual sub-regions, and are insensitive to the emission volume assumption as long as the emission volume does not vary sharply at different regions. The abundance of Fe is greatly enhanced in the east of the SNR, while the Si, S, Ar, Ca elements are highly enhanced across the SNR, especially along the east and west (nearly axial symmetric distribution; see Sect. 3.2.2).
. The averageabundance values here are based on the weighted sum (by the estimated gas mass for each sub-region) over all individual sub-regions, and are insensitive to the emission volume assumption as long as the emission volume does not vary sharply at different regions. The abundance of Fe is greatly enhanced in the east of the SNR, while the Si, S, Ar, Ca elements are highly enhanced across the SNR, especially along the east and west (nearly axial symmetric distribution; see Sect. 3.2.2).
W49B is the first cosmic source in which Cr and possibly Mn emission were found (Hwang et al. 2000). The global spectra of W49B in 4.3–8.0 keV show a clear Cr line at ~5.6 keV and a Mn bump at ~6.1 keV (see Fig. 5). We fit the global spectra with the vvrnei model and obtained [Cr] = 6.6 ± 0.8, [Mn] = 12.5 ± 2.7 (see Fig. 5; 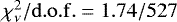 ;
; 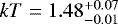 keV, NH is fixed to 8 × 1022 cm−2, kTi ≥ 4.6 keV, [Fe] = 3.2 ± 0.1; [Ni] cannot be constrained and thus tied to [Fe];
keV, NH is fixed to 8 × 1022 cm−2, kTi ≥ 4.6 keV, [Fe] = 3.2 ± 0.1; [Ni] cannot be constrained and thus tied to [Fe]; 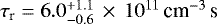 ). The thermal plasma model constrains the Mn K line flux to 1.6 × 10−5 cm−2 s−1, similar to that obtained by Miceli et al. (2006) and Yang et al. (2013). The CIE model gives a slightly larger
). The thermal plasma model constrains the Mn K line flux to 1.6 × 10−5 cm−2 s−1, similar to that obtained by Miceli et al. (2006) and Yang et al. (2013). The CIE model gives a slightly larger 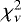 (1.78), with [Cr] = 5.9 ± 0.7, [Mn] =
(1.78), with [Cr] = 5.9 ± 0.7, [Mn] = 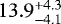 . Hereafter, we use the best-fit abundance results of the vvrnei model. The residuals at around 6.6 keV are likely due to the gain shifts for ACIS, but the shifts are within typical 0.3% systematic uncertainties in the ACIS gain (response from the CXC calibration scientists)6. The Fe abundance obtained by fitting the global spectra is smaller than the mass-weighted abundance (
. Hereafter, we use the best-fit abundance results of the vvrnei model. The residuals at around 6.6 keV are likely due to the gain shifts for ACIS, but the shifts are within typical 0.3% systematic uncertainties in the ACIS gain (response from the CXC calibration scientists)6. The Fe abundance obtained by fitting the global spectra is smaller than the mass-weighted abundance (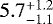 ), since the Fe element and the plasma properties vary across the SNR (see Fig. 2).
), since the Fe element and the plasma properties vary across the SNR (see Fig. 2).
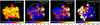 |
Fig. 4 Distribution of the hot-to-total flux ratio (0.75–0.99), hydrogen densities in the cold and hot phases, respectively, and recombination age of the hot components, overlaid with green contours the Chandra X-ray emission in 0.3–10 keV. The dashed circle denotes the SNR sphere for the density calculation. |
 |
Fig. 5 Global spectra of W49B in the 4.3–8.0 keV range fitted with a recombining plasma model vvrnei. The black, red, and green lines correspond to the spectra from observations 13 440, 13 441, and 117, respectively. |
2.7 Point-like sources in the vicinity
W49B has been considered to host a black hole, as no potential NS was detected down to an X-ray luminosity of 2.7 × 1031 erg s−1, and a core collapse origin was assumed (Lopez et al. 2013b). However, the remnant reveals a very nonuniform X-ray brightness, which provides a spatially varied background for point-source detection. After considering the bright background from the SNR plasma, we detected 24 point-like sources in, or in the vicinity of, W49B using the Mexican-Hat wavelet detection method (wavedetect in CIAO; see Fig. 6). The point spread function (PSF) of the chip and the vignetting effect are taken into account. The applied significance threshold of source identification (10−6) corresponds to one false detection in the image.
We derived the blackbody temperatures and luminosities of the sources based the photon fluxes f and hardness ratios (see Fig. 7). The luminosities of these sources are in the range 1032.1–36.2 erg s−1 at an assumed distance of 10 kpc. The details of the detection method and analysis are elaborated in Appendix A. Detailed information about these sources is summarized in Table A.1.
 |
Fig. 6 Detected point-like sources in the Chandra 0.7–5 keV raw image of W49B. The color-bar shows the scale of the counts per pixel (0.′′5). The details of the sources in the ellipses are summarized in Table A.1. The red regions denote the sources with best-fit blackbody luminosity in the range 7.0 × 1032– |
 |
Fig. 7 Hardness ratios (see the definition in Appendix A) and photon fluxes of the 24 point-like sources as a function of the blackbody temperature and luminosity at a distance of 10 kpc. The curved lines from the left to right indicate the luminosity from 1032 to 1036 erg s−1. An absorption of NH = 8 × 1022 cm−2 is assumed for all the sources. |
3 Discussion
Here we revisit the progenitor problems and discuss the CC (normal and energetic) and Type-Ia scenarios mainly based on three properties: metal abundances, metal distributions, and environment. The metal abundances can be compared to predictions of supernova nucleosynthesis models, the distribution of metals reveals explosion (a)symmetries, and the density distribution provides information on the circumstellar environment. We will also examine the SNR properties and discuss the origin of the bar-like morphology according to the spatially resolved spectroscopic analysis.
3.1 CC scenario and its problems
3.1.1 Cavity
W49B is suggested to be interacting with a molecular cavity surrounding the remnant (Chen et al. 2014; Zhu et al. 2014). A massive star can evacuate a hot, low-density bubble with its strong stellar wind during the main sequence stage. The slow and dense wind during its later red supergiant stage will, however, in most cases not reach the main sequence cavity shell. In the molecular environment with a typical pressure of p∕k ~ 105 cm−3 K (Chevalier 1999; Blitz 1993), the maximum radius of the bubble Rb is determined by the progenitor mass M*: Rb ≈ 1.22 M*∕M⊙− 9.16 pc (Chen et al. 2013). This linear relation is valid for stars with masses < 25 M⊙, while beyond the mass the bubble could be larger due to the contribution from the fast wind in Wolf–Rayet stage. If the molecular cavity surrounding W49B was created by the main sequence wind of a massive progenitor, a bubble with a radius of 6.′4 would suggest a progenitor mass of ~13 M⊙ (see also Chen et al. 2014; Zhang et al. 2015). A smaller bubble size (~5 pc) is also likely as suggested by Keohane et al. (2007), and indicates a progenitor mass ≲13 M⊙. This is inconsistent with the idea that the supernova explosion resulted in the creation of a black hole (Lopez et al. 2013a), which is considered to require a >25 M⊙ progenitor. A >25 M⊙ progenitor instead would create a wind bubble in the molecular cloud of ~21 pc.
3.1.2 Missing compact object?
A massive single star with M* ≲ 20–25 M⊙ ends its lifewith a NS (Heger et al. 2003). The NSs, which are born extremely hot (> 1010 K), cool predominantly via neutrino emission from the interior for ~ 104–105 yr after birth. The cooling curve or luminosity-age relation depends sensitively on the equation of state of dense matter, NS mass, and envelope composition. Page et al. (2004, 2009) proposed the minimal cooling scenario including Cooper pair breaking and formation process to explain the observed luminosities of considerably young NSs. According to the minimal cooling scenario, young NSs radiate X-ray emission in the initial few kyr and their temperatures and luminosities are a function of the NS age.
Figure 8 shows the cooling curve (luminosity evolution) of NSs based on the minimal cooling paradigm,7 which assumes that no enhanced neutrino emission is allowed in NSs (see Page et al. 2009). All models are for 1.4 M⊙ stars built using the NS equation of state of Akmal et al. (1998). The model predicts a luminosity range of L∞ = 7.0 × 1032–2.7 × 1034 erg s−1 for the NS at an age of W49B (5–6 kyr; see discussion in Sect. 3.4).
Nine of the 24 detected point-like sources are in the luminosity range predicted for an NS at an age of 5–6 kyr according to the minimal cooling paradigm (regions labeled in red in Fig. 6; distance of 10 kpc is assumed; between the dashed and dot-dashed curves in Fig. 7). We note that some of the sources may not be real point sources, but compact clumps of gas associated with W49B, while sources outside the SNR boundary would need a large transverse velocity (≳ 103 km s−1) to establish a connection with the SNR. As all the point sources are off-center, the NS may have been born with a high velocity (> 400 km s−1 assuming anSNR age of 6 kyr) if W49B was caused in a CC explosion. Therefore, even if W49B is a CC SNR, there is still the possibility that it contains a cooling NS, rather than a black hole, as suggested by Lopez et al. (2013b).
 |
Fig. 8 Predictions of NS cooling according to the minimal cooling paradigm (see Page et al. 2009). The light- and dark-gray lines represent the cooling curves of NSs with light- and heavy-element envelopes, respectively. The curves for intermediate-element envelopes are between them. Each envelope group includes 100 curves corresponding to four choices of 3P2 gaps, and five choices of neutron 1S0 and proton 1S0 gaps. The pink belt indicates the luminosity range of an NS in an age range of 5–6 kyr. |
3.1.3 Metal abundances and yields
For a CC SNR showing super-solar abundances, the progenitor mass could be estimated by comparing the abundance ratios with those predicted by the nucleosynthesis models, since the nucleosynthesis yields of CC SNe are related to the progenitor mass, stellar metallicity (solar assumed in this study), and explosion energy (e.g., Nomoto et al. 2006). Figure 9 shows the comparison of the abundances of Si, Ar, Ca, Cr, Mn, and Fe relative to Ar with the predictions of the spherical supernova explosion model (Sukhbold et al. 2016), hypernova model (Nomoto et al. 2006), and bipolar explosion model (Maeda & Nomoto 2003). The observed abundance ratios are ascending with the atomic weight from Si to Mn. We found that none ofthe available nucleosynthesis models explain the ascending abundance ratios. The less massive stars (12–13 M⊙) provide a flatter abundance pattern as function of element mass, whereas the very massive progenitors and energetic models produce sharper descending abundance ratio patterns (less IGEs), which are more deviated from the observed ratios.
Besides the inconsistent abundance ratios, none of the above-mentioned CC models explain the observed amount of IGEs. The Cr, Mn, and Fe ejecta masses in the hotter-phase gas are MCr = 4.9 ± 1.1 × 10−3 M⊙, MMn = 6.6 ± 1.9 × 10−3 M⊙, 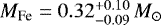 , respectively.The nucleosynthesis models used in this study predict higher iron-group production for the stars with higher masses. A 25.2 M⊙ star produces 6.4 × 10−4 M⊙ of Cr, 3.2 × 10−4 M⊙ of Mn, and 0.048 M⊙ of Fe in a spherical explosion, each of which is about an order of magnitude lower than the value obtained from X-ray observations. A 25 M⊙ undergoing energetic (1052 erg) spherical explosion produces slightly more Cr, Mn, and Fe (0.001 M⊙, 3.5 × 10−4 M⊙, and 0.007 M⊙, respectively) compared to normal explosion energies, but this remains insufficient to create the observed yields. Similarly, all of the bipolar CC explosion models predict much smaller IGE yields than the observed values. The bipolar energetic explosion of a 25 M⊙ star (model 25A) produces Cr, Mn and Fe masses of 7.5 × 10−4 M⊙, 2.3 × 10−4 M⊙, and 0.082 M⊙, respectively.
, respectively.The nucleosynthesis models used in this study predict higher iron-group production for the stars with higher masses. A 25.2 M⊙ star produces 6.4 × 10−4 M⊙ of Cr, 3.2 × 10−4 M⊙ of Mn, and 0.048 M⊙ of Fe in a spherical explosion, each of which is about an order of magnitude lower than the value obtained from X-ray observations. A 25 M⊙ undergoing energetic (1052 erg) spherical explosion produces slightly more Cr, Mn, and Fe (0.001 M⊙, 3.5 × 10−4 M⊙, and 0.007 M⊙, respectively) compared to normal explosion energies, but this remains insufficient to create the observed yields. Similarly, all of the bipolar CC explosion models predict much smaller IGE yields than the observed values. The bipolar energetic explosion of a 25 M⊙ star (model 25A) produces Cr, Mn and Fe masses of 7.5 × 10−4 M⊙, 2.3 × 10−4 M⊙, and 0.082 M⊙, respectively.
Hence, the CC models fail to explain the observed abundance ratios and under-predict the mass of IGEs. Due to the large abundances of Cr and Mn, this conclusion is unchanged, even taking into account the large systematic uncertainties in Mh (>18 M⊙; see Sect. 2.4).
3.2 Aspherical Type-Ia explosion
3.2.1 Metal abundances and yields
Type-Ia SNe are the dominant factories of IGEs (see a recent review of Seitenzahl & Townsley 2017). The large masses of Cr, Mn, and Fe and the high IGE/intermediate-mass element (IME) ratio in W49B clearly suggest a Type-Ia origin. As shown in the bottom panels of Fig. 9, we compare the abundances ratios of the SNR to the predicted results of different Type-Ia SNe models, including DDT models followed with spherical or extremely off-center slow flagrations, according to the three-dimensional model from Seitenzahl et al. (2013b) and two-dimensional models from Maeda et al. (2010b). The classical deflagration model W7 (Nomoto et al. 1984) was excluded since it over-predicts the Fe abundance.
For the models in the bottom-left panel of Fig. 9, the deflagration is assumed to be ignited from different numbers of sparks in a WD with a central density of 2.9 × 109 g cm−3. The model N1 is for the single spot ignition and N100 denotes the 100-spot ignition. The occurrence of multi-spot ignitions, which covers a range of offset radii, is a probable consequence of the turbulent convection of the WD prior to the thermonuclear runaway (Garcia-Senz & Woosley 1995; Woosley et al. 2004; Iapichino et al. 2006). The fewer sparks burn less materials to power the expansion of the WD and thus the deflagration is weaker. The moderately strong expansion causes a high central density at the onset of detonation, and most of the remaining fuel is burned to IGEs by detonation. Conversely, a larger number of ignition kernels produces relatively more IMEs during incomplete burning (Seitenzahl et al. 2013b).
The abundance ratios in W49B can be well described by the multi-spark ignition models N100 and N1600, except for the element Si. Hence, the model with moderate to large numbers of ignition sparks reproduces the abundances and yields in W49B well, whereas the fewer ignition sparks result in Fe/IME ratios that are too high.
 |
Fig. 9 Abundances of Si, Ar, Ca, Cr, Mn, and Fe relative Ar (with error bars) compared with the predictions of supernova nucleosynthesis models. Upper panels: CC spherical explosion models (left), and energetic spherical (middle) and bipolar explosion models (right; the explosion energy are 10–30 ×1051 erg, E51 stands for 1051 erg, θ is the opening half-angle of the jet) for different progenitor masses. Bottom-left panel: three-dimensional DDT Type-Ia models, where the deflagration is ignited in 1, 10, 100, and 1600 spherical sparks, respectively, near the WD center. Bottom-right panel: compares the DDT models which followed the two-dimensional spherical deflagration (C-DDT) and extremely off-center deflagration (O-DDT) ignitions, respectively. Solar progenitor metallicity is used for all models. |
3.2.2 Aspherical explosion
The ejecta distribution in W49B is not spherical, as shown in the abundance–position angle (PA) diagram (Fig. 10). Here the explosion center is assumed at the approximate geometric center αJ2000 = 19h11m07.s6, δJ2000 = 09°06′10.′′2, which is denoted by a green cross in the bottom-right panel of Fig. 2. In particular, the IGEs, synthesized in the densest part of the exploding WD, show strong lateral distribution. The abundance of Fe is evidently enhanced in the eastern part of W49B, and in the range PA ~10–130° (mean [Fe] > 6). The Si–Ca abundances are elevated in a similar P.A. range, but also in a nearly opposite PA range (~210–300°). The lateral distribution of Fe likely reflects intrinsic asymmetries of the SN explosion. The IMEs have a more axial symmetric morphology, which could be intrinsic to the explosion as well, but as discussed in Sect. 3.3 could also be caused by the structure of the circumstellar medium in which W49B is evolving.
A feasible explanation for an asymmetric Type-Ia SN explosion is off-center ignition of a WD (Röpke et al. 2007; Maeda et al. 2010b), which has been used to interpret the spectral evolution diversity observed in Type-Ia SNe (Maeda et al. 2010b). Maeda et al. (2010a) modeled nucleosynthesis results of an extremely off-center deflagration of a Chandrasekhar-mass WD followed with a DDT (model “O-DDT”), and compare them with those from a spherically symmetric explosion (model “C-DDT”). As shown in the bottom-right panel of Fig. 9, the off-center ignition model (29 sparks assumed) better describes the abundance ratios in W49B. Furthermore, the off-center ignition model predicts an offset distribution of stable Fe-peak elements, which appears to explain the lateral Fe distribution. The abundances and yields of two-dimensional simulations of an off-center SN explosion are identical to those of the 100 sparks ignition model as shown in the bottom-left panel of Fig. 9 (see Seitenzahl et al. 2013b, for more comparison of the two models), and also similar to the nucleosynthesis results of a recent gravitational detonation model with a single off-center bubble ignition (Seitenzahl et al. 2016).
Although the current study does not pin down a specific model among many Type-Ia models, we have found that W49B may provide a unique and important example of an asymmetric Type-Ia explosion, which may offer more clues about how WDs can explode asymmetrically.
 |
Fig. 10 Average abundances as a function of the P.A. (= 0° to the north); counter-clockwise orientation). The abundance of each element is averaged inside the dashed circle denoted in Fig. 4. |
3.2.3 The high Mn abundance and its implications
Most of the 55Mn is produced by the decay of 55Co via 55Fe, while the 55Co is mainly synthesized in the incomplete Si-burning and “normal” freeze-out from nuclear statistical equilibrium (NSE; Seitenzahl et al. 2013a). The production of the neutron-rich element 55Co (and hence 55Mn) requires the presence of neutron-rich elements (Badenes et al. 2008; Bravo 2013). The abundance of these elements are influenced by several effects. First of all, it may be caused by the presence of the initial abundance of the neutron-rich element 14N, in which case a high 55Mn yield may reflect the high initial metallicity of the progenitor (Timmes et al. 2003). Using a one-dimensional Type-Ia explosion model (spherical, single ignition), Badenes et al. (2008) proposed a relation MMn∕MCr = 5.3 × Z0.65 for estimating the progenitor Z with the Mn and Cr supernova yields. Secondly, in accreting C/O WDs close to the Chandrasekhar limit, the rise in temperatures in the core will result in carbon fusion several centuries before the onset of the explosion. During this so-called carbon-simmering phase, weak interactions enhance the neutron fraction in the core (Piro & Bildsten 2008), resulting in a higher 55Mn yield of the ensuing Type-Ia supernova. Finally, a high yield of 55Mn from “normal” freeze-out from NSE requires that the nucleosynthesis occurs under conditions of high density (ρ ≳ 2 × 108 cm−3; Thielemann et al. 1986). Such high density can be provided by WDs with masses larger than 1.2 M⊙, which is inconsistent with the sub-Chandrasekhar WD scenarios (Seitenzahl et al. 2013a). But the high yield of Mn is consistent with the single-degenerate Type-Ia scenario, for which the mass of the exploding WD should be close to the Chandrasekhar limit. Even for Chandrasekhar-limit explosions, the Mn/Fe abundance ratio is rather sensitive to the explosion conditions.
For a few young SNRs, such as Tycho’s and Kepler’s SNRs, the high Mn/Cr ratio has been taken as evidence for a high initial metallicity of the progenitor (Badenes et al. 2008; Park et al. 2013), since in these cases mostly the outer layers of the supernovae were assumed to be shocked, and the 55Mn yield in the outer layer does depend on the initial metallicity. Carbon simmering as the cause of the high Mn yield seems unlikely, since it onlyaffects the neutron excess of the core. However, a high metallicity was suggested in the young SNR N103B based on metal ratios, which seems highly unlikely given that this SNR is located in the low-metallicity environment of the Large Magellanic Cloud (Badenes 2016). In this case, but perhaps also in hindsight for the cases of Tycho’s and Kepler’s SNRs, the high yields may be affected by simmering, and radial mixing of material from the core and outer regions (e.g., Gamezo et al. 2005) may have affected the 55Mn abundance of outer ejecta (but see Badenes et al. 2005). Finally, a large Mn/Cr ratio was also found in the Type-Ia SNR candidate 3C 397, which could be contributed by the neutron-rich NSE region (Yamaguchi et al. 2015). On the other hand, a dense, low-carbon WD with a solar- and subsolar-metallicity progenitor can also produce the high Mn/Cr ratio in 3C 397 (Dave et al. 2017).
We report here a Mn mass of MMn = 6.6 ± 1.9 × 10−3 M⊙ for W49B, based on fitting the X-ray spectra with the vrnei model. The mass ratio of Mn and Cr is ~1.3 (0.8–2.2). If we would attribute this to the effect of progenitor metallicity, a super-solar metalicity of 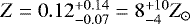 is implied (using the solar ratio of Asplund et al. 2009).
is implied (using the solar ratio of Asplund et al. 2009).
W49B is in a later stage of its SNR evolution than young SNRs like Tycho’s and Kepler’s SNR, so the Mn/Cr ratios reported here likely reflect the combination of both core and outer ejecta, that is, from both “normal” freeze-out from NSE and incomplete silicon burning. In this case, the ratio also depends on the selected initial parameters such as central density and numbers of flaming bubbles (Seitenzahl et al. 2013b) and the explosion mechanisms (e.g., Dave et al. 2017).
As shown in the bottom-left panel of Fig. 9, the three-dimensional models with solar-metallicity progenitor and different ignition sparks predict a range of MMn∕MCr (0.6–2.2), which overlaps with the mass ratio of 1.3 (0.8–2.2) reported here for W49B. Therefore, from the point of view of existing models, and the SNR phase W49B in super-solar metallicity models may not be required to explain our estimated high Mn/Cr mass ratio. Moreover, the high Mn/Cr ratio, and the high Mn/Fe ratio of [Mn/Fe]/[Mn/Fe]⊙ of 1.4–3.3 in W49B strongly suggest a WD explosion almost the mass of Chandrasekhar (sub-solar Mn/Fe ratio for sub-Chandrasekhar cases; Seitenzahl et al. 2013a), which is best explained by the single-degenerate scenario.
3.2.4 Properties for typing the SNR
Table 1 summarizes the main properties for typing an SNR and the results of W49B, in which their importance in reference is reflected in the sequence.
PWN/NS: There is no PWN detected inside W49B, or any clear evidence of an associated NS, although the presence of an NS cannot yet be excluded, as shown by the presence of numerous point sources in and around W49B (Fig. 6). An association of one of them with an NS would strongly suggest a CC origin.
Ejecta: The masses of the IGEs in the SNR are heavily overabundant compared to CC nucleosynthesis models. The observed abundance ratios instead suggest a Type-Ia origin.
Asymmetry: CC SNRs appear to be statistically more asymmetrical than Type-Ia SNRs (Lopez et al. 2011). However, there is emerging evidence that a fraction of the Type-Ia SN explosion is intrinsically aspherical (Maeda et al. 2010b; Uchida et al. 2013, for SN 1006). Moreover, the morphology of evolved SNR is subject to the shaping by the inhomogeneous environment. Given the nonuniform environment, Type-Ia SNe can also evolve to mixed-morphology SNRs. For W49B, the centrally filled morphology is mainly due to density enhancement in the SNR interior (see discussion below). We note that also the candidate Type-Ia SNR 3C 397 (Chen et al. 1999; Safi-Harb et al. 2000; Yang et al. 2013; Yamaguchi et al. 2014, 2015, the last reference suggests a CC origin) is highly aspherical, with many properties that are similar to W49B.
Wind bubble: The presence and size of a wind bubble, and/or the stellar environment itself provides clues about the progenitors of SNRs. W49B is suggested to be located inside a wind-blown bubble, whose relatively small size suggests that the progenitor had a mass of ~13 M⊙, or smaller (if the SNR shock has already transgressed sufficiently into the shell) if it is a CC SNR. However, Type-Ia SNRs can also be associated with wind bubbles if there is outflow driven by their single-degenerate progenitor systems, such as Tycho (Zhou et al. 2016)and the Type-Ia candidate RCW 86 (Badenes et al. 2007; Williams et al. 2011; Broersen et al. 2014). Moreover, observationsof Type-Ia SNe have shown that a considerable population explodes “promptly” and associated relatively young stellar populations, although the delay time of their explosions (40–420 Myr) is still larger than that of CC SNe (≲40 Myr; Maoz et al. 2012). The presence of a small cavity surrounded by a dense ambient medium therefore either suggests a CC SNR with a low-mass progenitor, or a Type-Ia SNR, with a moderately sized wind-blown bubble.
We favor the Type-Ia origin of W49B after a comparison of all direct and indirect properties for SNR typing, although some of its indirect properties can also be explained by a normal CC explosion. Both observations and models indicate that there is some diversity among Type-Ia SNe. In that regard, W49B is an intriguing object revealing some properties different from other Type-Ia SNRs. Further studies, especially on the details of the explosion process and its environment, are needed to achieve an integrated understanding of this remnant.
Properties for typing SNRs and W49B’s results.
3.3 “Bar-like” morphology due to a density enhancement
The bar-like X-ray morphology, which has an east-west orientation and is sharper in Fe–K emission, has been attributed to either an asymmetric SN explosion origin (Miceli et al. 2006; Lopez et al. 2013b), the density distribution of the ambient medium (Miceli et al. 2006) shaped by the progenitor winds (Keohane et al. 2007; Miceli et al. 2008; Zhou et al. 2011) or to two opposite SN jets perpendicular to the bar-like structure (Bear & Soker 2017).
Our density maps show that the cold component reveals a high-density distribution that has a similar east-west orientation, which is less prominently present in the hot component. The strong association with the cold component, which is likely shocked ambient medium, suggests that the bar-like structure is most likely the result of a structure in the ambient medium.
However, the X-ray morphology is clearly a combination of the metal-rich ejecta distribution and the density distribution. A possible explanation is that W49B evolves inside a more or less barrel-shaped cavity, with lower densities in the North and South, which agrees well with the shape of the infrared (Keohane et al. 2007) and radio emission (Moffett et al. 1993). The higher densities in the equatorial direction are reflected in the higher densities of the cold component along the bar. The high densities along the bar probably also triggered the early formation of the reverse shock, and therefore also resulted in the ejecta being shocked at higher densities in the central region of W49B.
The intrinsic asymmetry of the ejecta is reflected not in the overall bar-like morphology of the X-ray line emission, but in the abundance maps (Fig. 2), which indeed reveal not so much a bar-like morphology, but a fan-like region that reveals higher Fe abundances in the Eastern part of the bar-like region.
A bipolar explosion jet seems unlikely, since the base of the jet should be displaced several thousand years after the explosion (see the numerical simulation in González-Casanova et al. 2014). Instead the bar-like region goes through the center of the W49B, which is why this SNR is labeled a mixed-morphology SNR.
3.4 Recombining gas and SNR age
As mentioned in Sect. 2.4, the recombining plasma occupies the majority of the SNR regions of W49B (~3/4 by area), not only in the southwest, but also in the bar-like structure in the SNR interior and in the northeast. The recombination age in the northeast is larger than in the southwest (see Fig. 4). The gas that has reached CIE is distributed in the southeastern shell and spreads in patches throughout the northeastern part of the remnant.
The distribution and origin of the recombining/over-ionized plasma in W49B has been studied in several papers, and rapid cooling is regarded as the cause (e.g., Ozawa et al. 2009). Thermal conduction was initially proposed as the cooling mechanism (Kawasaki et al. 2005), but adiabatic expansion is more favored in the later studies (Miceli et al. 2010; Lopez et al. 2013a). Zhou et al. (2011) performed a hydrodynamic simulation of the W49B evolution in a circumstellar dense cylinder as indicated by the infrared observations. They found that the recombiningplasma originates in both cooling processes: (1) the mixing of hot plasma and cold gas evaporated from the dense circumstellar medium; and (2) rapid adiabatic expansion. The density enhancement along the bar-like structure (see Fig. 2) supports the existence of the dense circumstellar matter for process (1) to occur. The adiabatic expansion can explain the large-scale recombining plasma extended to the southwestern boundary.
The recombination age shown in Fig. 4 is derived from the recombination timescale and the electron density in the hot phase (tr = τr∕ne, where the density is assumed to be a constant with time). It describes the time elapse starting from the moment that plasma reached ionization equilibrium, and then began cooling. Our measurements indicate recombination ages between ~2000 and ~6000 yr, based on an over-ionization model. The true age of the plasma may well differ as the ionization state depends on the temperature and density history of the plasma. But one should also note that over-ionization can only occur once ionization equilibrium has been reached, and the plasma turns from under-ionized into over-ionized (Kawasaki et al. 2005). The latter would imply that our recombination age measurements even underestimate the true plasma age. Although the connection between recombination age and SNR age is complex, the recombination ages that we find have implications for the age of W49B.
In previous studies, the age of W49B was estimated to be between ~1000 yr (Pye et al. 1984; Lopez et al. 2013b) and ~4000 yr (Hwang et al. 2000). The recombination ages measured by us suggest that the SNR is older, as the SNR cannot be younger than the oldest plasma it contains, and the recombination age probably underestimates the true age of the plasma. Moreover, for the plasma to first reach ionization equilibrium, a timescale of ≳ 1012 cm−3 s (Smith & Hughes 2010) is needed. Even for densities around nH ≈ 10 cm−3, typical for the Western region, the associated timescale is ≳2600 yr. The recombination timescale of ~2000 yr for that region should be added to that. Therefore, the total plasma age must be of the order of 4000–5000 yr. In the eastern regions, the recombination ages are as high as 6000 yr, or the plasma is in equilibrium (white pixels in Fig. 4). Since the density is lower in that region (nH ≈ 4 cm−3), CIE implies plasma ages of ~6600 yr, close to maximum recombination ages we find. The recombination ages therefore suggest an age of at least 5000–6000 yr.
One can also estimate the age based on the Sedov model combined with an estimate of the forward shock velocity based on the plasma temperature. Here one has the choice between taking the hot plasma component or the cool plasma component. However, the hot plasma component seems to be very much metal enriched, and shows a lot of temperature variation. This component is likely associated with plasma shocked by the reverse shock. Associating the cooler component with the forward shock, we infer a forward shock velocity of ![$v_{\textrm{s}}=[16 kT_{\textrm{c}}/(3\bar{\mu} m_{\textrm{H}})]^{1/2} =476 (kT_{\textrm{c}}/0.27\,\textrm{keV})^{1/2} \,\textrm{km}\,\textrm{s}^{-1}$](/articles/aa/full_html/2018/07/aa31583-17/aa31583-17-eq27.png) , where the mean atomic weight
, where the mean atomic weight 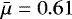 is taken for fully ionized plasma and mH is the hydrogen atomic mass. For a uniform ambient medium, the velocity corresponds to a Sedov age of
is taken for fully ionized plasma and mH is the hydrogen atomic mass. For a uniform ambient medium, the velocity corresponds to a Sedov age of 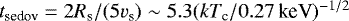 kyr, and an explosion energy
kyr, and an explosion energy 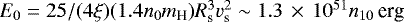 (Ostriker & McKee 1988), where we adopt an SNR radius Rs = 6.4 pc, and ξ = 2.026, with n10 the ambient density of hydrogen atom in units of 10 cm−3. The temperature of the cool component is therefore also consistent with an age of 5000–6000 yr, and the canonical supernova explosion energy of ~ 1051 erg for the high density environment in which W49B expands.
(Ostriker & McKee 1988), where we adopt an SNR radius Rs = 6.4 pc, and ξ = 2.026, with n10 the ambient density of hydrogen atom in units of 10 cm−3. The temperature of the cool component is therefore also consistent with an age of 5000–6000 yr, and the canonical supernova explosion energy of ~ 1051 erg for the high density environment in which W49B expands.
4 Conclusion
We have performed a spatially resolved X-ray study of SNR W49B using a state-of-the-art adaptive binning method in order to uncover its explosion mechanism and the origin of the centrally filled morphology. An asymmetric Type-Ia explosion is the most probable explanation for the abundances, yields, and metal distribution in W49B. A density enhancement with an east-west orientation is the main reason for the bar-like X-ray morphology. The detailed results are summarized as follows.
-
The X-ray emission in W49B is well characterized by two-temperature gas containing a cool component with kTc ~ 0.27 keV and a hot, ejecta-rich component with kTh ~ 0.6–2.2 keV. There is a large gradient of kTh from the northeast to the southwest. The detailed distribution of gas temperature and other physical parameters across the SNR are shown (see Figs. 2 and 4).
W49B isevolving in a dense environment. The mean densities are 24 and 5 cm−3 for the cool and hot X-ray components, respectively. The total masses of the X-ray-emitting gas are
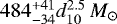 in the cool phase and
in the cool phase and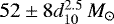 in the hot phase.
in the hot phase.We obtained the mass-weighted average abundances [Si] =
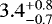 , [S] =
, [S] = 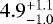 , [Ar] =
, [Ar] = 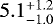 , [Ca] =
, [Ca] = 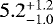 , and [Fe] =
, and [Fe] = 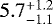 . The Cr, Mn, and Fe abundances according to a fit to the global spectra of W49B are [Cr] = 6.6 ± 0.8, [Mn] = 12.5 ± 2.7, and [Fe] = 3.2 ± 0.1.
. The Cr, Mn, and Fe abundances according to a fit to the global spectra of W49B are [Cr] = 6.6 ± 0.8, [Mn] = 12.5 ± 2.7, and [Fe] = 3.2 ± 0.1.The element Fe shows a strong lateral distribution. The abundance of Fe is evidently enhanced in PA range ~ 10–130° (SNR east). The Si–Ca abundances are also elevated in a similar PA range, but also in the nearly opposite P.A. range (~210–300°). The lateral distribution of Fe suggests intrinsic asymmetries of the SN explosion. The nearly axially symmetric distribution of IMEs may also reflect that the explosion was not sphericially symmetric, but in this case also the density distribution of the circumstellar medium may play a role (see point 8 below).
We have found 24 point-like sources in the vicinity of W49B with luminosities in the range
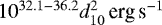 . Nine of them have the luminosities of a cooling NS at the age of W49B (at an assumed distance of 10 kpc). Therefore, even if W49B is a CC SNR, there is still the possibility that it contains a cooling NS, rather than a black hole.
. Nine of them have the luminosities of a cooling NS at the age of W49B (at an assumed distance of 10 kpc). Therefore, even if W49B is a CC SNR, there is still the possibility that it contains a cooling NS, rather than a black hole.None of the CC nucleosynthesis models (spherical explosion or bipolar explosion) explain the abundance ratios in W49B. The iron-group yields predicted by the CC models are insufficient to explain the observed masses in the hotter phase: MCr = 4.9 ± 1.1 × 10−3 M⊙, MMn = 6.6 ± 1.9 × 10−3 M⊙,
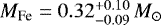 . The energetic CC explosion scenario matches even more poorly than the normal CC scenario given the small molecular cavity surrounding the SNR and nine point-like sources in the vicinity of W49B (probably only a projection effect).
. The energetic CC explosion scenario matches even more poorly than the normal CC scenario given the small molecular cavity surrounding the SNR and nine point-like sources in the vicinity of W49B (probably only a projection effect).A DDT Type-Ia model with multi-spot ignition of a Chandrasakhar-mass WD well describes the observed abundance ratios. This model based on solar-metallicity can also explain the high Mn-to-Cr ratio (MMn∕MCr = 0.8–2.2) found in W49B. A feasible explanation of the asymmetric Type-Ia SN explosion is off-center ignition of a WD.
The centrally filled/bar-like morphology of W49B is mainly due to density enhancement projected to the SNR center (nc > 30 cm−3), given the good spatial correlation between the gas density and the X-ray brightness. This suggests that W49B evolves in a barrel-shaped cavity, which also lead the ejecta to be shocked at higher densities and projected to the center. The overall morphology, triggered by the ambient medium structure, combined with our conclusion that W49B is a Type-Ia SNR, suggests that Type-Ia supernovae can also result in mixed-morphology SNRs.
The recombination age of the plasma suggests an SNR age of ~5–6 kyr, similar to the estimated Sedov age of 5.3 kyr.
Acknowledgements
P.Z. acknowledges the support from the NWO Veni Fellowship, grant no. 639.041.647 and NSFC grants 11503008, 11590781, and 11233001.
Appendix A Point-like sources in the vicinity of W49B
We detected 24 point-like sources in the 0.7–5 keV energy band in the vicinity of W49B using the Mexican-Hat wavelet source detection tool wavdetect in CIAO (see Fig. 6). We combined the three Chandra observations to detect faint sources, where the exposure-weighted PSF map was use to run wavdetect on the merged dataset8. The energy band is selected to highlight the emission of the point-like sources over the SNR background. The compact object is assumed to have an effective temperature of 0.07–0.5 keV for heavy element atmosphere or 0.11–0.5 keV for Hydrogen atmosphere, with a foreground absorption column density 5.5–8.8 × 1022 cm−2. Two criteriaare considered for the NS temperature range: (1) The observed central compact objects show blackbody temperatures in the range 0.2–0.5 keV (Pavlov et al. 2004) and (2) the minimal paradigm (Page et al. 2004) predicts a temperatureof 0.11 keV for the light elements envelop and 0.07 keV for the heavy envelop of an NS with an age of 6000 yr.
To minimize the contamination from the SNR structures, we extracted the most compact sources using the detection spatial scales of 1, 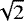 , and 2 pixels. Adding a larger spatial scale of
, and 2 pixels. Adding a larger spatial scale of 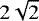 would result in a detection of 76 sources, while most of these sources are likely clumpy plasma inside the SNR. We examined the detected sources in the hard (2.5–5 keV) and soft (0.7–2.5 keV) bands in order to study their spectral properties. Table A.1 summarizes the coordinates, total (background-included) and net (background-subtracted) counts in the hard and soft bands, photon fluxes f, and hardness ratios HR of the sources, where f is the net count rate divided by the effective area of the camera. The hardness ratio defined as HR= (fH − fS)∕(fH + fS) has a value between −1 and 1, where the fH and fS are the photon fluxes in the hard and soft bands, respectively.
would result in a detection of 76 sources, while most of these sources are likely clumpy plasma inside the SNR. We examined the detected sources in the hard (2.5–5 keV) and soft (0.7–2.5 keV) bands in order to study their spectral properties. Table A.1 summarizes the coordinates, total (background-included) and net (background-subtracted) counts in the hard and soft bands, photon fluxes f, and hardness ratios HR of the sources, where f is the net count rate divided by the effective area of the camera. The hardness ratio defined as HR= (fH − fS)∕(fH + fS) has a value between −1 and 1, where the fH and fS are the photon fluxes in the hard and soft bands, respectively.
The blackbody temperatures kTBB and luminosities LBB of the point-like sources are estimated using hardness ratio HR and photon flux f (see Fig. 7). The foreground absorption and distance are assumed to be NH= 8 × 1022 cm−2 and 10 kpc, respectively, the same as those of W49B. The best-fit kTBB and LBB are also listed in Table A.1.
Information of the point-like sources in the vicinity of W49B.
References
- H. E. S. S. Collaboration (Abdalla, H., et al.) 2018, A&A, 612, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Badenes, C. 2016, Supernova Remnants: An Odyssey in Space After Stellar Death, 105 [Google Scholar]
- Badenes, C., Borkowski, K. J., & Bravo, E. 2005, ApJ, 624, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Badenes, C., Hughes, J. P., Bravo, E., & Langer, N. 2007, ApJ, 662, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Badenes, C., Bravo, E., & Hughes, J. P. 2008, ApJ, 680, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Bear, E., & Soker, N. 2017, MNRAS, 468, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Blitz, L. 1993, Protostars and Planets III, eds. E. H. Levy, & J. I. Lunine (Tucson: Univ. of. Arizona), 125 [Google Scholar]
- Borkowski, K. J., Rho, J., Reynolds, S. P., & Dyer, K. K. 2001, ApJ, 550, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Branch, D., Livio, M., Yungelson, L. R., Boffi, F. R., & Baron, E. 1995, PASP, 107, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Bravo, E. 2013, A&A, 550, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Broersen, S., Chiotellis, A., Vink, J., & Bamba, A. 2014, MNRAS, 441, 3040 [NASA ADS] [CrossRef] [Google Scholar]
- Brogan, C. L., & Troland, T. H. 2001, ApJ, 550, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Copin, Y. 2003, MNRAS, 342, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y., Sun, M., Wang, Z.-R., & Yin, Q. F. 1999, ApJ, 520, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y., Zhou, P., & Chu, Y.-H. 2013, ApJ, 769, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y., Jiang, B., Zhou, P., et al. 2014, in Supernova Environmental Impacts, eds. A. Ray, & R. A. McCray, IAU Symp., 296, 170 [NASA ADS] [Google Scholar]
- Chevalier, R. A. 1999, ApJ, 511, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Chiotellis, A., Schure, K. M., & Vink, J. 2012, A&A, 537, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dave, P., Kashyap, R., Fisher, R., et al. 2017, ApJ, 841, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Diehl, S., & Statler, T. S. 2006, MNRAS, 368, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Dubner, G., & Giacani, E. 2015, A&ARv, 23, 3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gamezo, V. N., Khokhlov, A. M., & Oran, E. S. 2005, ApJ, 623, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia-Senz, D., & Woosley, S. E. 1995, ApJ, 454, 895 [NASA ADS] [CrossRef] [Google Scholar]
- González-Casanova, D. F., De Colle, F., Ramirez-Ruiz, E., & Lopez, L. A. 2014, ApJ, 781, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Gvaramadze, V. V., Langer, N., Fossati, L., et al. 2017, Nat. Astron., 1, 0116 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Helfand, D. J., Becker, R. H., White, R. L., Fallon, A., & Tuttle, S. 2006, AJ, 131, 2525 [NASA ADS] [CrossRef] [Google Scholar]
- Hillebrandt, W., & Niemeyer, J. C. 2000, ARA&A, 38, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, J. P., Hayashi, I., & Helfand, D., et al. 1995, ApJ, 444, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Hwang, U., Petre, R., & Hughes, J. P. 2000, ApJ, 532, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Iapichino, L., Brüggen, M., Hillebrandt, W., & Niemeyer, J. C. 2006, A&A, 450, 655 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, T. W., Rudnick, L., Jun, B.-I., et al. 1998, PASP, 110, 125 [Google Scholar]
- Kawasaki, M., Ozaki, M., Nagase, F., Inoue, H., & Petre, R. 2005, ApJ, 631, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Keohane, J. W., Reach, W. T., Rho, J., & Jarrett, T. H. 2007, ApJ, 654, 938 [NASA ADS] [CrossRef] [Google Scholar]
- Khokhlov, A. M. 1991, A&A, 245, L25 [NASA ADS] [Google Scholar]
- Kinugasa, K., & Tsunemi, H. 1999, PASJ, 51, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Lazendic, J. S., & Slane, P. O. 2006, ApJ, 647, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M. 2000, eds. J. C. Niemeyer, & J. W. Truran, Type Ia Supernovae, Theory and Cosmology (Cambridge: Cambridge University Press), 33 [Google Scholar]
- Lopez, L. A., Ramirez-Ruiz, E., Huppenkothen, D., Badenes, C., & Pooley, D. A. 2011, ApJ, 732, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, L. A., Pearson, S., Ramirez-Ruiz, E., et al. 2013a, ApJ, 777, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, L. A., Ramirez-Ruiz, E., Castro, D., & Pearson, S. 2013b, ApJ, 764, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Maeda, K., & Nomoto, K. 2003, ApJ, 598, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Maeda, Y., Baganoff, F. K., Feigelson, E. D., et al. 2002, ApJ, 570, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Maeda, K., Benetti, S., Stritzinger, M., et al. 2010a, Nature, 466, 82 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Maeda, K., Röpke, F. K., Fink, M., et al. 2010b, ApJ, 712, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Mannucci, F., & Brandt, T. D. 2012, MNRAS, 426, 3282 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Mannucci, F., & Nelemans, G. 2014, ARA&A, 52, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Miceli, M., Decourchelle, A., Ballet, J., et al. 2006, A&A, 453, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miceli, M., Decourchelle, A., Ballet, J., et al. 2008, Adv. Space Res., 41, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Miceli, M., Bocchino, F., Decourchelle, A., Ballet, J., & Reale, F. 2010, A&A, 514, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moffett, D. A., Goss, W. M., & Reynolds, S. P. 1993, AJ, 106, 1566 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Thielemann, F.-K., & Yokoi, K. 1984, ApJ, 286, 644 [Google Scholar]
- Nomoto, K., Tominaga, N., Umeda, H., Kobayashi, C., & Maeda, K. 2006, Nucl. Phys. A, 777, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Olbert, C. M., Clearfield, C. R., Williams, N. E., Keohane, J. W., & Frail, D. A. 2001, ApJ, 554, L205 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, J. P., & McKee, C. F. 1988, Rev. Mod. Phys., 60, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ozawa, M., Koyama, K., Yamaguchi, H., Masai, K., & Tamagawa, T. 2009, ApJ, 706, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D., Lattimer, J. M., Prakash, M., & Steiner, A. W. 2004, ApJS, 155, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D., Lattimer, J. M., Prakash, M., & Steiner, A. W. 2009, ApJ, 707, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Park, S., Muno, M. P., Baganoff, F. K., et al. 2005, ApJ, 631, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Park, S., Slane, P. O., Hughes, J. P., et al. 2007, ApJ, 665, 1173 [NASA ADS] [CrossRef] [Google Scholar]
- Park, S., Badenes, C., Mori, K., et al. 2013, ApJ, 767, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlov, G. G., Sanwal, D., & Teter, M. A. 2004, in Young Neutron Stars and Their Environments, eds. F. Camilo, & B. M. Gaensler, IAU Symp., 218,239 [NASA ADS] [Google Scholar]
- Piro, A. L., & Bildsten, L. 2008, ApJ, 673, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Post, S., Park,S., Badenes, C., et al. 2014, ApJ, 792, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Pye, J. P., Becker, R. H., Seward, F. D., & Thomas, N. 1984, MNRAS, 207, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Radhakrishnan, V., Goss, W. M., Murray, J. D., & Brooks, J. W. 1972, ApJS, 24, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, S. P., Lyutikov, M., Blandford, R. D., & Seward, F. D. 1994, MNRAS, 271, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Rho, J., & Petre, R. 1998, ApJ, 503, L167 [NASA ADS] [CrossRef] [Google Scholar]
- Röpke, F. K., Hillebrandt, W., Schmidt, W., et al. 2007, ApJ, 668, 1132 [NASA ADS] [CrossRef] [Google Scholar]
- Safi-Harb, S., Petre, R., Arnaud, K. A., et al. 2000, ApJ, 545, 922 [NASA ADS] [CrossRef] [Google Scholar]
- Sakano, M., Warwick, R. S., Decourchelle, A., & Predehl, P. 2004, MNRAS, 350, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Seitenzahl, I. R., & Townsley, D. M. 2017, ArXiv e-prints [arXiv:1704.00415] [Google Scholar]
- Seitenzahl, I. R., Cescutti, G., Röpke, F. K., Ruiter, A. J., & Pakmor, R. 2013a, A&A, 559, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seitenzahl, I. R., Ciaraldi-Schoolmann, F., Röpke, F. K., et al. 2013b, MNRAS, 429, 1156 [Google Scholar]
- Seitenzahl, I. R., Kromer, M., Ohlmann, S. T., et al. 2016, A&A, 592, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, R. K., & Hughes, J. P. 2010, ApJ, 718, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, A., Peacock, A., Jones, L. R., & Pye, J. P. 1985, ApJ, 296, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Sukhbold, T., Ertl, T., Woosley, S. E., Brown, J. M., & Janka, H.-T. 2016, ApJ, 821, 38 [Google Scholar]
- Tananbaum, H. 1999, IAU Circ., 7246, 1 [NASA ADS] [Google Scholar]
- Thielemann, F.-K., Nomoto, K., & Yokoi, K. 1986, A&A, 158, 17 [NASA ADS] [Google Scholar]
- Timmes, F. X., Brown, E. F., & Truran, J. W. 2003, ApJ, 590, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Uchida, H., Yamaguchi, H., & Koyama, K. 2013, ApJ, 771, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. 2012, A&ARv, 20, 49 [Google Scholar]
- Vink, J. 2016, Supernova 1604, Kepler’s Supernova, and its Remnant (Cham: Springer), Handbook of Supernovae [arXiv:1612.06905] [Google Scholar]
- Wang, B., & Han, Z. 2012, New Astron. Rev., 56, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, R., McCray, R., Castor, J., Shapiro, P., & Moore, R. 1977, ApJ, 218, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Whelan, J., & Iben, Jr., I. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, B. J., Blair, W. P., Blondin, J. M., et al. 2011, ApJ, 741, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Winkler, P. F., Gupta, G., & Long, K. S. 2003, ApJ, 585, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Wolszczan, A., Cordes, J. M., & Dewey, R. J. 1991, ApJ, 372, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Wunsch, S., & Kuhlen, M. 2004, ApJ, 607, 921 [NASA ADS] [CrossRef] [Google Scholar]
- Yamaguchi, H., Ozawa, M., Koyama, K., et al. 2009, ApJ, 705, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Yamaguchi, H., Badenes, C., Petre, R., et al. 2014, ApJ, 785, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Yamaguchi, H., Badenes, C., Foster, A. R., et al. 2015, ApJ, 801, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X. J., Tsunemi, H., Lu, F. J., et al. 2013, ApJ, 766, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, G.-Y., Chen, Y., Su, Y., et al. 2015, ApJ, 799, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, X., Miceli, M., Bocchino, F., Orlando, S., & Chen, Y. 2011, MNRAS, 415, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, P., Chen, Y., Zhang, Z.-Y., et al. 2016, ApJ, 826, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, H., Tian,W. W., & Zuo, P. 2014, ApJ, 793, 95 [NASA ADS] [CrossRef] [Google Scholar]
For example, using the solar abundances of Anders & Grevesse (1989) result in ~30% smaller NH and Fe abundance for the spectra showed in Fig. 3 (for both of the single and two component models).
Cooling code from Dany P. Page: http://www.astroscu.unam.mx/neutrones/NSCool/
All Tables
All Figures
 |
Fig. 1 Distribution of the parameters fitted with the best-fit single component model, which, for every cell, was taken to be either the absorbed “vrnei” or the absorbed “apec” model, whichever produced the smallest |
| In the text | |
 |
Fig. 2 Distribution of the parameters fitted with the best-fit double component model, which was either an absorbed “hot vrnei + cool apec” model, or an absorbed “hot vapec + cool apec” model. First panel: |
| In the text | |
 |
Fig. 3 Exemplified ACIS-S spectra from one bin in W49B fitted with one component (vapec; left: |
| In the text | |
 |
Fig. 4 Distribution of the hot-to-total flux ratio (0.75–0.99), hydrogen densities in the cold and hot phases, respectively, and recombination age of the hot components, overlaid with green contours the Chandra X-ray emission in 0.3–10 keV. The dashed circle denotes the SNR sphere for the density calculation. |
| In the text | |
 |
Fig. 5 Global spectra of W49B in the 4.3–8.0 keV range fitted with a recombining plasma model vvrnei. The black, red, and green lines correspond to the spectra from observations 13 440, 13 441, and 117, respectively. |
| In the text | |
 |
Fig. 6 Detected point-like sources in the Chandra 0.7–5 keV raw image of W49B. The color-bar shows the scale of the counts per pixel (0.′′5). The details of the sources in the ellipses are summarized in Table A.1. The red regions denote the sources with best-fit blackbody luminosity in the range 7.0 × 1032– |
| In the text | |
 |
Fig. 7 Hardness ratios (see the definition in Appendix A) and photon fluxes of the 24 point-like sources as a function of the blackbody temperature and luminosity at a distance of 10 kpc. The curved lines from the left to right indicate the luminosity from 1032 to 1036 erg s−1. An absorption of NH = 8 × 1022 cm−2 is assumed for all the sources. |
| In the text | |
 |
Fig. 8 Predictions of NS cooling according to the minimal cooling paradigm (see Page et al. 2009). The light- and dark-gray lines represent the cooling curves of NSs with light- and heavy-element envelopes, respectively. The curves for intermediate-element envelopes are between them. Each envelope group includes 100 curves corresponding to four choices of 3P2 gaps, and five choices of neutron 1S0 and proton 1S0 gaps. The pink belt indicates the luminosity range of an NS in an age range of 5–6 kyr. |
| In the text | |
 |
Fig. 9 Abundances of Si, Ar, Ca, Cr, Mn, and Fe relative Ar (with error bars) compared with the predictions of supernova nucleosynthesis models. Upper panels: CC spherical explosion models (left), and energetic spherical (middle) and bipolar explosion models (right; the explosion energy are 10–30 ×1051 erg, E51 stands for 1051 erg, θ is the opening half-angle of the jet) for different progenitor masses. Bottom-left panel: three-dimensional DDT Type-Ia models, where the deflagration is ignited in 1, 10, 100, and 1600 spherical sparks, respectively, near the WD center. Bottom-right panel: compares the DDT models which followed the two-dimensional spherical deflagration (C-DDT) and extremely off-center deflagration (O-DDT) ignitions, respectively. Solar progenitor metallicity is used for all models. |
| In the text | |
 |
Fig. 10 Average abundances as a function of the P.A. (= 0° to the north); counter-clockwise orientation). The abundance of each element is averaged inside the dashed circle denoted in Fig. 4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.