EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 613 (May 2018) A&A, 613 (2018) A43 Full HTML
Free Access
Issue
A&A
Volume 613, May 2018
Article Number A43
Number of page(s) 19
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201732347
Published online 30 May 2018

© ESO 2018

1 Introduction

The infrared and submillimetre spectral energy distribution (SED) of galaxies provides a unique set of data to study how the dust is processed in galaxies and in the interstellar medium (ISM) in general. The emission from dust has been proposed as a probe of the amount of star formation within a galaxy, therefore understanding better how the dust physical properties change under different conditions of the ISM will help us to get a better picture on how the dust traces star formation rate (SFR) and how galaxies evolve with time.

The physical properties of the dust are directly linked to those of the ISM where it is located. The dust is not only heated by the interstellar radiation field (ISRF) but it is also affected by other mechanisms, such as destruction or coagulation of dust grain species (see Jones 2004, for a review) that are at play in the ISM and can lead to a change in its physical properties. Jones et al. (1994, 1996) set up a theoretical framework for dust destruction mechanisms in regions of the ISM affected by strong shocks. These studies have been recently updated by Bocchio et al. (2014) (see also Slavin et al. 2015). There is some observational evidence that dust is evolving under different environments: dust grains can fragment in the ISM (e.g. Paradis et al. 2011; Stephens et al. 2014) and very small grains (VSGs) can coagulate on the surfaces of big grains (BGs; Stepnik et al. 2003; Paradis et al. 2009; Köhler et al. 2012). In an observational study (Relaño et al. 2016, hereafter Paper I) found that the abundance of VSGs is higher in intense star-formingregions, where shocks might be present, than in more quiescent diffuse-type H II regions. Besides, it is also well known that the amount of polycyclic aromatic hydrocarbons (PAHs) are reduced in regions of intense ISRF (e.g. Madden et al. 2006) and that the dust abundance changes with the metallicity of the environment (Galliano et al. 2003, 2005, 2008).

The analysis of integrated SEDs in galaxies with different metallicity has shown that some low metallicity objects exhibit an excess emission above the modelled dust continuum in the submillimetre wavelength range, which is referred as submillimetre excess: in the Large Magellanic Cloud (LMC) and Small Magellanic Cloud (SMC; Israel et al. 2010; Bot et al. 2010) and in nearby galaxies (Galliano et al. 2003, 2005; Galametz et al. 2011; Dale et al. 2012; Kirkpatrick et al. 2013; Rémy-Ruyer et al. 2013). The origin of this excess is so far unknown. Some studies have tried to locally isolate this excess to shed light on to the origin of this phenomenon: Galliano et al. (2011) found that the excess is located in regions of low dust mass surface density in the LMC, and Galametz et al. (2014) studied a sample of KINGFISH (Key Insights on Nearby Galaxies: a Far-Infrared Survey with Herschel, Kennicutt et al. 2011) galaxies and found that the excess was located in the outer parts of the discs. Also Gordon et al. (2014) found that the excess in the 500 μm SPIRE band was located in the outer parts of the most intense star-forming regions in the LMC and SMC. Tabatabaei et al. (2014) showed that the emissivity coefficient β tends to take lower values in the outer parts of the disc of M 33. A similar result was found by Smith et al. (2012) for M 31. A lower β would be the required coefficient to fit the excess of the SED in the submillimetre wavelength range. Finally, Hermelo et al. (2016) presented observational evidence of excess in M 33 located mainly in the diffuse part of the disc of this galaxy. These authors made a careful analysis to fit the excess with the emission produced by different proposed mechanisms: they found that a change in the physical properties of the dust would be the best explanation for the excess in this galaxy. In this present study, the submillimetre excess is defined as it was done by Hermelo et al. (2016): the fraction of emission in the submillimetre range that is above a dust model having an emissivity coefficient β = 2. SEDs fitted with dust models with variable β would not, in principle, present any excess, as lower values of β ≤ 2 would be able to fit the observed SED.

The ratio between the gas and dust mass (GDR), gives an estimate of the amount of metals locked up in the dust compared to the ones still present in the gas phase. It is directly linked to the metallicity of the ISM (Dwek 1998; Lisenfeld & Ferrara 1998; Draine et al. 2007; Rémy-Ruyer et al. 2014), thus providing information about the evolutionary stage of the galaxy. Quantifying the GDR requires an estimation of the gas and dust masses of galaxies. Total gas masses are derived using neutral hydrogen and CO observations. The CO observations would lead, assuming a CO-to-H2 conversion factor X(CO), to an estimate of the amount of molecular mass traced by CO. Some difficulties in obtaining accurate molecular gas masses reside in the existence of a “CO-dark gas component”, a fraction of molecular gas that under certain physical conditions is not traced by CO observations (Pineda et al. 2014; Bolatto et al. 2013; Madden et al. 2012; Bernard et al. 2008), and in the variation of X(CO) with the metallicity of the galaxy (Boselli et al. 2002; Leroy et al. 2011; Schruba et al. 2012; Sandstrom et al. 2013; Accurso et al. 2017). The dust mass estimates are also affected by certain uncertainties: they are subject to the dust model assumed to explain the far infrared peak of the SED, for example, the assumed emissivity coefficient, and affected by the evolution of dust under different physical conditions (Galliano et al. 2011).

In this paper we present a study of the SED of the whole disc of M 33 in a pixel-by-pixel basis. We aim to better understand which mechanisms might produce the excess in the submillimetre wavelength range and how the GDR depends on other properties of the galaxy. M 33 is an ideal target on which to perform such a study, because its distance to the galaxy (840 kpc; Freedman et al. 1991) and high resolution of the available infrared (IR) observations allow us to perform an SED analysis at small galactic scales of ~170 pc. The disc also covers a wide range of physical interstellar conditions over a large number of pixels to give statistically significant conclusions. The submillimetre excess for the total SED of M 33 was observed for the first time by Hermelo et al. (2016), who found that the diffuse part of the galaxy exhibits a higher fraction of excess than the SED corresponding to the integrated emission coming from the star-forming regions. GDR measurements for M 33 were obtained by Gratier et al. (2017) who, following the method derived by Leroy et al. (2011) and Sandstrom et al. (2013), and assuming a single modified black body (MBB) with variable β for the dust emission derived in Tabatabaei et al. (2014), were able to estimate the GDR over the disc of M 33 taking into account the fraction of dark gas not traced by CO observations.

Our analysis goes a step further than these studies as we apply a dust model that assumes different dust grain species. We also vary the fraction of the different dust grains to fit the SED at local ~(170 pc) scales in the disc of M 33. With this approach we have been able to isolate the regions in which the submillimetre excess is located, and thus find out if these locations share similar physical conditions. Moreover, we were able to better estimate the dust mass at local scales as the variation of the different grain types in the model allows us to mimic the grain evolution across the disc of M 33.

The paper is outlined as follows. In Sect. 2 we present the data used in this study and the preliminary analysis to create the data cube that will be used to perform the SED fitting. In Sect. 3 we present the dust model and describe the fitting technique applied to each pixel inthe disc of M 33. In Sect. 4 we show the direct results from the fitting procedure: dust masses and grain abundances. The GDR and its relation to other physical properties is described in Sect. 5. We analyse how well the strength of the ISRF is linked to the amount of star formation at local scales in Sect. 6. In Sect. 7 we study the observed submillimetre excess and its trend with the spatial location within the disc of the galaxy. Finally, the conclusions are presented in Sect. 8.

2 Data sets

For the purpose of this study we have made use of the available data of M 33 covering the mid-IR to submillimetre wavelength range. We used Spitzer IRAC (3.6, 4.5, 5.8, and 8.0 μm) and Spitzer MIPS (24 and 70 μm) data already presented in Relaño et al. (2013). We refer the reader to this paper for further description of these particular datasets. We covered the gap between 8.0 and 24 μm with 12 μm (W3), and 22 μm (W4) Wide-field Infrared Survey Explorer (WISE; Wright et al. 2010) data. The data reduction has already been reported in Paper I. Herschel data (PACS: 70, 100, and 160 μm, and SPIRE: 250, 350, and 500 μm) were presented within the Herschel M33 extended survey (HerM33es) collaboration (Kramer et al. 2010; Xilouris et al. 2012; Boquien et al. 2011, 2015). We used the latest version of 100 μm PACS data reprocessed with Scanamorphos v16 (Roussel 2013) as described in Boquien et al. (2011), and the new observed 70 and 160 μm PACS data, obtained in a follow-up open time cycle 2 programme of Herschel (Boquien et al. 2015). The SPIRE images were obtained using version 10.3.0 of the Herschel data processing system (HIPE; Ott 2010, 2011) with the updated calibration scheme (spire−cal−10−1). The beam areas for the three SPIRE bands (250, 350 and 500 μm) are 431.7, 766.0, 1572.7 arcsec2, respectively. For a description of the data reduction the reader is referred to Xilouris et al. (2012). Finally, 12 CO(J = 2–1) and HI (21 cm) intensity maps were obtained from Druard et al. (2014) and Gratier et al. (2010), respectively. Each image in our data set was registered first and then convolved to the spatial resolution of the SPIRE 500 μm image using the convolution kernels of G. Aniano (Aniano et al. 2011). The final data set has a spatial resolution of ~ 38.1′′ × 35.1′′ and a pixel size of 14′′ (~56 pc) and will produce SEDs with the fluxes of 14 different filters spanning between 3.6 and 500 μm.

2.1 Uncertainties

We assumed the following uncertainties for our data set. For IRAC data we assume a conservative value of 10% uncertainty for all IRAC bands, as reported in the IRAC Instrument Handbook1. For WISE 12 μm (W3) and 22 μm (W4) we adopt a flux uncertainty of 10% to account for discrepancy between red and blue calibrators as reported in Explanatory Supplement to the WISE All-Sky Data Release Products. MIPS 24 and 70 μm uncertainties are 4% (Engelbracht et al. 2007) and 10% (Gordon et al. 2007), respectively. We assumed an uncertainty of 10% in the three PACS bands, which is a combination of the absolute uncertainty in the calibration plus an additional uncertainty to account for extended emission (Gordon et al. 2014). Finally, the uncertainty for SPIRE data is 15% (Swinyard et al. 2010; Kramer et al. 2010).

2.2 Masking

We are interested in fitting the SEDs of each pixel in the disc of M 33. However, in order to avoid bad fits which produce misleading conclusions we fitted only the SED with reliable flux measurements in all bands. We thus first masked in each image all the pixels with fluxes below 3 times the standard deviation of the background value. Then we produced another mask using the 250 μm image: all the pixels with fluxes below F(250 μm) = 10 MJy sr−1 were eliminated. The threshold was chosen to cover a wide area of the disc with diffuse and star-forming regions while avoiding low surface brightness areas that would lead to unreliable fits. The spatial coverage of the M 33 disc is shown in Fig. 1. We applied the mask to all the images in our data set and create a masked data-cube which will be used in our SED fitting procedure.

3 SED fitting technique

We make use of the tool DustEM (Compiègne et al. 2011) to obtain the emission of the different dust grain types in our dust model. The code allows the use of different dust models and ISRFs as inputs and gives the emissivity per hydrogen atom (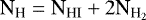) for each grain type based on the incident radiation field strength and the grain physics in the optically thin limit. We adopted here the classical dust model from Desert et al. (1990) and the ISRF from Mathis et al. (1983). Although more sophisticated dust models can be usedwith DustEM we decide not to adopt them here. The reason for this choice is that we are interested in studying the submillimetre excess, which is directly related to the emissivity index β (see Sect. 7) and most of the submillimetre excess reported in the literature is based on MBB fitting with β = 2. Making use of the average extinction of the dust distribution provided by DustEM we obtained a grain absorption cross section of κ 350 μm = 4.8 cm2g−1 and β = 2. Therefore, the submillimetre excess detected using the dust model from Desert et al. (1990) can be directly compared with the results obtained from fitting the SED with a MBB with β = 2. This model consists of three dust grain types: PAHs, VSGs of carbonaceous material, and BGs of astronomical silicates. For the purpose of this study we change the mass relative to hydrogen of each dust grain population (Y i = Mi∕MH, for i = PAH, VSG, and BG) and theISRF parameter G0, which is the scaling factor relative to the solar neighbourhood ISRF given in Mathis et al. (1983). The ISRF is measured as energy density per unit frequency as: 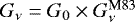, where 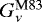is the ISRF for the solar neighbourhood. Finally, in order to fit the contribution of the stellar emission in the near-IR, we added a near-IR continuum modelled using a black body with a temperature of 1000 K following Relaño et al. (2016).

The fit of the observed SED in each pixel of the data cube generated in Sect. 2.2 was performed using a Bayesian approach similar to the one followed in da Cunha et al. (2008). We outline here the steps to perform the fit. We first created a library of models with different values of Y i, G0, and GNIR (the scale factor of the near-IR 1000 K black body continuum). Making use of the previous analysis of H II regions in M 33 (Relaño et al. 2016), the parameter values were generated within a wide range that covers possible solutions for this galaxy. For each combination of the input parameters, we obtained the dust emissivity per hydrogen atom with the use of DustEM and created a library of 7 695 000 dust models. In Table 1 we show the range and the sampling of the input parameters. We convolved the SEDs of each dust model in the library with the corresponding filter bandpass of our observations to obtain the fluxes in each band for each library model.

We obtained the parameters that best reproduce the observed data for each pixel in the following way. For each model in the library we compared the theoretical fluxes with the observed ones using the χ2 parameter and build up the probability density function (PDF) by weighting the input parameter distribution in each model i by the likelihood 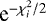. We take the mean of the PDF as the best parameter value and the 16th to 84th percentile range as an estimate of its uncertainty. In Fig. 2 we show two typical examples of PDFs derived with our fitting procedure.

In Fig. 3 we show two examples of the best fit SEDs for two different pixels within the disc of M 33. The far-IR peak is nicely fitted with this routine. The PAH features are not always well fitted with the dust model from Desert et al. (1990), as was already reported in Paper I. However, for the purpose of this study we are interested in deriving good estimates of the dust mass and the submillimetre excess, thus the lack of good fits in the PAH domain does not affect the conclusions of this paper. We analysed the robustness of the fit and the existence of double peaks in thePDF in Appendices A and B. In Fig. A.1 we show the 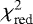distribution for all the fits. In general we were ableto get good fits ( 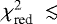8.0) for most of the pixels in our sample. For the rest of the study we took into account only those pixels with fits having 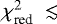8.0. The relationships between the best fit parameters are shown in Fig. B.2.

thumbnail Fig. 1

250 μm intensity image in MJy sr−1 masked using the constraints presented in Sect. 2.2.
Table 1

Input parameter range.

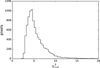thumbnail Fig. A.1

distribution for all the SEDs in the disc of M 33.
thumbnail Fig. B.2

Relations between the five parameters fitted with our technique described in Sect. 3.

4 Results from the fitting

In this section we present our analysis of the direct results from our fitting procedure. Although we show here maps of the parameters derived from the fit for the whole disc of M 33 (e.g. Fig. 4), in order to make a meaningful statistical analysis of the correlations presented in this paper we took into account only independent pixels. This was done by choosing pixels spaced roughly the spatial resolution of the data set (see Sect. 2), following Tabatabaei et al. (2013). In Sect. 4.1 we studied the dust mass derived in a pixel-by-pixel basis for the disc of M 33, in Sect. 4.2 we analysed the contribution of the different grain types to the emission of each filter. Finally, in Sect. 4.3 we compared the relative abundances for each grain type to other physical properties of the ISM.

thumbnail Fig. 2

Histograms derived in our fitting procedure for two different pixels (70, 123) (top) and (88, 144) (bottom) corresponding to star-forming and diffuse regions, respectively. The values of the best fit parameters obtained as described in the text are: G0 = 3.69 ± 0.97, Y PAH = (2.1 ± 0.4) × 10−3, Y VSG = (3.1 ± 1.8) × 10−3, and Y BG = (2.5 ± 0.6) × 10−2 for the top panel, and G0 = 3.17 ± 0.97, Y PAH = (2.6 ± 0.7) × 10−4, Y VSG = (4.1 ± 2.5) × 10−4, and Y BG = (5.5 ± 1.5) × 10−3 for the bottom panel. The dashed line corresponds to the Gaussian fitted to each PDF. We compare the results from the best fit parameters obtained with our procedure and those derived from the Gaussian fitting in Appendix A.

4.1 Dust mass

From the fitting we can estimate the dust mass in every pixel in the disc of M 33. The result is shown in Fig. 4. We see the spiral arms delineated in the map, showing that in general the dust mass surface density is higher at the location of the star-forming regions. This agrees with the correlation between the SFR and dust mass surface density found by Smith et al. (2012) for M31 using single-MBB fitting (top left panel of Fig. 11 in that paper). A similar trend is found by Tabatabaei et al. (2014) for the cold dust mass derived using two-MBBs corresponding to the warm and cold dust (see their Fig. 5). These authors kept fixed βw (β coefficient for the warm dust emission) to 1.5, while the one corresponding to the cold dust, βc, was left free. We re-gridded our images to a pixel size of 10′′ – as used byTabatabaei et al. (2014) – and perform the fitting routine for each pixel in the new dataset. We then produced a new dust mass map of M 33, which is directly comparable in a pixel by pixel basis with the results from Tabatabaei et al. (2014).

In Fig. 5, we show the comparison of the sum of the warm and cold dust mass derived by these authors and the dust masses derived with our fitting technique. In general the MBB dust masses are above those derived with the dust model from Desert et al. (1990). The mean value of the ratio between the dust mass derived from Tabatabaei et al. (2014) and the one derived in this study is 1.7, although there are ratios up to 4–5. The grain absorption cross section per unit mass that is used in Tabatabaei et al. (2014) is κ = 0.04 (ν∕250 GHz)2 m2 kg−1, which corresponds to κ 350 μm = 4.7 cm2 g−1, similar to the one used in Desert et al. (1990), κ 350 μm = 4.8 cm2 g−1. Therefore, the discrepancies cannot be attributed to different grain absorption cross sections.

The differences shown in Fig. 5 could be due to the use of a free β co-efficient and a κ350 μm from a dust model that assumes a β parameter close to two. As explained in Bianchi (2013), this procedure gives dust masses that depend on the wavelength chosen for normalisation, yielding differences of 50% between normalisations at 250 and 500 μm. Finally, differences between MBB fitting and more sophisticated dust models have been reported previously: Galametz et al. (2012) performed a two-MBB fitting to the integrated SEDs of the KINGFISH galaxies with photometric data from 24 to 500 μm and found discrepancies up to 35% between the dust masses from the MBB fitting and Draine & Li (2007) dust models.

thumbnail Fig. 3

Examples of SED fitting for pixels (70 123) (top) and (88 144) (bottom) corresponding to star-forming and diffuse regions, respectively. values are 5.1 and 3.7 for the top and bottom panels, respectively. The bottom panel shows submillimetre excess in the 500 μm band. We study this excess in Sect. 7.

4.2 Grain emission in different filters

Before looking for trends between the grain abundances and other physical properties of the ISM it is interesting to estimate how much emission of the different grain types is contributing to the fluxes in the Spitzer and Herschel bands. In Table 2 we show the mean values of the fraction of the emission of each grain type to the total emission in the 8 and 24 μm filters from Spitzer, and 70, 100 and 160 μm filters from Herschel. We can see, as expected, that the main contributors to the emission in the 8 μm filter are the PAHs, while the BGs contribute ~90% of the emission in the 100 and 160 μm filters. Emission in the 24 μm band is dominated by the VSGs (~60%), but there is a significant contribution(~40%) of the PAHs to the flux in this band. In the 70 μm filter, ~70% of the emission is coming from the BGs, whereas the remaining 30% are from VSGs. Thus, the emission of VSGs needs to be taken into account when including the 70 μm flux in the SED fit with MBBs, as not all the emission in 70 μm band comes from grains in thermodynamic equilibrium.

thumbnail Fig. 4

Map of the dust surface density in units of M⊙ pc−2 for M 33 derived from our fitting technique.
thumbnail Fig. 5

Comparison of the dust masses obtained in this paper and those derived by Tabatabaei et al. (2014) with two MBBs. Each point corresponds to one pixel on the sky. Only independent data points have been considered to compare both masses (see text for details). The mean value and standard deviation of the ratio between the dust mass derived from Tabatabaei et al. (2014) and from this study is 1.7 (dashed line) and 0.7, respectively. The relative uncertainties for the dust masses derived in this paper are ~25%.
Table 2

Average relative fraction of emission corresponding to PAHs, VSGs, and BGs in the 8 and 24 μm bands from Spitzer, and in the 70, 100 and 160 μm filters from Herschel.

4.3 Grain abundances

Our fitting technique gives the dust mass fraction relative to the hydrogen mass for each grain type in our model. With this information we were able to create maps of the dust abundance for each grain type for the whole surface in the disc of M 33. In Fig. 6 we show the maps for each grain type. In general, while the Y VSG∕Y TOTAL and Y BG∕Y TOTAL maps present distributions similar to the one of the star-forming regions, the Y PAH∕Y TOTAL map shows a more diffuse distribution across the disc of the galaxy.

In Fig. 7, we show the fraction of BGs (top left panel) and VSGs (top right panel) versus the logarithmic Hα luminosity for the individual pixels of the disc of M 33. Although both panels present a high dispersion we can see that Y VSG∕Y TOTAL tends to increase at locations of intense star formation, while Y BG∕Y TOTAL follows the opposite correlation. There are some data points outside of the main trend showing higher values of Y VSG∕Y TOTAL, these correspond to the same pixels with low Y BG∕Y TOTAL. For these pixels, a single ISRF might not be enough to describe the radiation field heating the dust, and a combination of several ISRFs might describe better the dust temperature distribution at these locations (see Chastenet et al. 2017).

The high values of Y VSG∕Y TOTAL and the corresponding low values of Y BG∕Y TOTAL at location where the Hα luminosity is high, could be explained by the reprocessing of the BGs fragmenting into VSGs. Relaño et al. (2016) shows that for a sample of H II regions in M 33 catalogued in terms of morphology, the most intense regions tend to have a higher fraction of VSGs than the more diffuse shell-type H II regions. The high velocity shocks occurring inside the most luminous H II regions can destroy the BGs giving as consequence an increase of the VSG fraction. The results shown here agree with those presented in Relaño et al. (2016) and are consistent with the framework of the dust evolution models in Jones et al. (1994, 1996), suggesting dust grain destruction and/or fragmentation by interstellar shocks in the warm medium. Finally, the data points in the top right panel with values of Y VSG∕Y TOTAL higher than 0.5 correspond to pixels in the outer parts of IC133, an H II complex with a very high emission at 24 μm. In these pixels the 22 and 24 μm emission from MIPS and WISE, respectively, is so high that the fluxes are comparable to the IR peak of the SED.

Interestingly, we do not find any relation between the fraction of PAHs and the Hα luminosity (bottom left panel of Fig. 7), nor the UV luminosity and G0 (plots not shown here). The reason for the lack of relation is that the linear scales of the individual SEDs, ~170 pc, include the H II region, Photodissociation Region, and molecular cloud, and thus, do not allow us to isolate the central parts of the H II regions where the strong ISRF would destroy the PAHs. There is a slight relation between Y PAH∕Y TOTAL and galactocentric radius (albeit with high dispersion), as it can be seen in the bottom left panel of Fig. 7: Y PAH∕Y TOTAL in the centre of the disc is around 0.08 and decreases to values of ~0.03 at R ≥ 3 kpc. This trend could be related to the metallicity (e.g. Engelbracht et al. 2008): the metallicity gradient of M 33 is quite shallow (0.045 dex/Rkpc, Bresolin 2011), which is consistent with the small differences of Y PAH∕Y TOTAL between the centre and the outer parts of the galactic disc. Y PAH∕Y TOTAL correlates with surfacedensity of the dust (bottom right panel of Fig. 7), but the correlation seems to be modulated by the radial distribution of the surface density of the dust.

Finally, we investigated how well the ratio between the 24 μm and the total-IR (TIR) luminosity (and between 24 and 250 μm luminosities) traces the abundance of VSGs. In the left-hand panel of Fig. 8, we show Y VSG∕Y TOTAL versus log (L24∕LTIR). For Y VSG∕Y TOTAL  > 0.2 (log (L24∕LTIR) > −1.08) there is a tight correlation between the fraction of VSGs and log (L24∕LTIR). The linear fit to the correlation is Y VSG∕Y TOTAL  =  (1.036 ± 0.003) × log(L24∕LTIR) + (1.282 ± 0.003). The correlation between Y VSG∕Y TOTAL and log (L24∕L250) (right-hand panel of Fig. 8) is not so tight. It is interesting that we find no correlation between Y PAH∕Y TOTAL and the ratio of L8 and LTIR.

5 Gas-to-dust mass ratio

The dust mass derived in the previous section can be combined with the gas mass obtained from observations to estimate the GDR over the whole face of M 33. The gas mass was obtained using the 12 CO(J = 2–1) and H I intensity maps presented in Druard et al. (2014) and Gratier et al. (2010), respectively. For the neutral hydrogen gas mass we used a conversion factor of X (H i) = 1.8 × 1018 cm−2 (K−1 km s−1), as in Gratier et al. (2010). The molecular gas mass was obtained using a CO-to-H2 conversion factor of 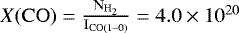cm−2 (K−1 km s−1), consistent with the metallicity of M 33. A constant ICO(2−1)∕ICO(1−0) = 0.8 was assumed following Druard et al. (2014). Both masses include a factor of 1.37 to account for the helium contribution. The total gas mass is the sum of the neutral H I and the molecular H 2 mass (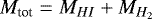). In Fig. 9 we show the GDR map for the whole disc of M 33. The map seems quite smooth with no significant structures across the disc.

5.1 Radial trend

In Fig. 10 we show the radial profile of the GDR for different values of X(CO). In general the profiles are quite constant up to R ~4 kpc, where they start to slightly increase. The value of X(CO) = 4.0 × 1020 cm−2 (K−1 km s−1) assumed in this paper to estimate the molecular gas mass gives a GDR of ~300 for the inner 4 kpc. This value is slightly higher than previous studies. Kramer et al. (2010) derived a GDR of 200 for the entire galaxy with variations between 120 and 200 at different annuli. Using radiation transfer models to fit the whole SED of M 33, Hermelo et al. (2016) derived a GDR of ~100, lower than what would be expected from the metallicity of M 33. These authors argue that dust properties different from those assumed in their radiation transfer model are the main explanation for the low values of the GDR. In a novel approach Leroy et al. (2011) solved simultaneously the conversion factor αCO2 and the GDR, assuming a constant value of GDR at local scales larger than typical individual molecular clouds. These authors find values for the GDR in the range of 100–200, lower than expected for the metallicity of M 33. The dust mass in Leroy et al. (2011) was derived using the Draine & Li (2007) dust model. The dust masses derived from this model are, on average, a factor of two too high (Planck Collaboration XXIX 2016), thus accounting for a dust mass lower by a factor of two would bring the GDR to200–400, closer to the expected value for the metallicity of M 33. A similar method as applied in Leroy et al. (2011), but accounting for a CO-dark gas component, was presented in Gratier et al. (2017). These authors find values of 250–400 for the GDR in the whole disc of M 33: in the inner R < 3 kpc the GDR has a constant value of ~250, at R > 3 kpc the GDR starts to increase up to 400 at R ~ 5 kpc. Assuming β = 2 they found constant values for the GDR ratio within the disc that are lower and do not increase with radius as much as when a variable β is adopted. The radial trend observed in Fig. 10 is in agreement with the trend found in Gratier et al. (2017).

The GDR radial profile increases slightly in the outer parts (R ≳ 4 kpc) of the galaxy. This mild increase is consistent with the shallow oxygen abundance gradient derived in Bresolin (2011): oxygen abundances vary from 12 + log(O/H) = 8.50 in the inner part of the galaxy to 12 + log(O/H) = 8.14 at 8 kpc. Based on the radial gradient given in Bresolin (2011), we assigned a metallicity to each pixel in the M 33 disc and present the relation between GDR and oxygen abundance for the disc of M 33 in Fig. 11. The GDR tends to increase for 12 + log(O/H) ≲ 8.32, which is the oxygen abundance at R ~ 4 kpc. As a comparison with M31, Smith et al. (2012) obtained a well defined radial increase of GDR that is consistent with the radial oxygen abundance gradient of M31 derived by Galarza et al. (1999), but steeper than the abundance gradient derived more recently using electron temperature determinations for this galaxy (Zurita & Bresolin 2012). For M33, we find that the relation between the GDR and 12 + log(O/H) at local scales agrees with the general relation found for nearby galaxies by Rémy-Ruyer et al. (2014).

thumbnail Fig. 6

YPAH∕Y TOTAL (left), Y VSG ∕Y TOTAL (middle), and Y BG∕Y TOTAL (right) maps for the disc of M 33 derived using our fitting procedure.

5.2 Dependence on other parameters

There are recent studies which claim a variation of the GDR with properties other than the metallicity of the ISM (Galliano et al. 2011; Roman-Duval et al. 2014, 2017). In particular, Galliano et al. (2011) found a correlation between the GDR and the mean value of the radiation field intensity (⟨U⟩) at local scales of 54 pc in the LMC (see Fig. 13 in that paper). These authors propose two explanations for the correlation: at locations with a weak radiation field, the GDR can be underestimated by the presence of undetected gas, while at the positions with an intense radiation field, shocks might destroy the grains and thus the dust mass derived by their models can be under-estimated (see Fig. B.2 in Galliano et al. 2011), producing an artificial correlation between the GDR and ⟨U⟩.

In Fig. 10 we see that the GDR for M 33 is relatively constant within a radius of ~4 kpc, which agrees with the results from Gratier et al. (2017). In this section we investigate if the GDR varies with other properties of the ISM. In Fig. 12 we investigate the relation with G0, the dust and gas surface densities. We show in the top panel of Fig. 12 that at the spatial scales of this study (~170 pc) the GDR is relatively constant with G0, with some hints of a decreasefor low values of G0. This decrease of the GDR has also been seen by Galliano et al. (2011) for the LMC, but these authors found a stronger variation than the one presented in the top panel of Fig. 12. We investigated if at low G0, the GDR can be under-estimated by the presence of CO-dark gas as suggested by Galliano et al. (2011). We made use of the radial dependence of the dark gas fraction obtained by Gratier et al. (2017) and created a new GDR map where the gas surface density is the combination of the gas surface density derived from CO observations and the fraction related to dark gas. In Fig. 12, we plot the mean values of the GDR in bins of G0 when the dark gas fraction has been considered. We can see that the dark gas fraction does not change the values of GDR at low G0, in disagreement with the idea proposed by Galliano et al. (2011) to explain the GDR and G0 relation.

In the bottom panel of Fig. 12 we present the relation between the GDR and Σ dust. There is slight trend of increasing GDR at low Σdust, while for Σ dust ≳0.05 M⊙ pc−2 the GDR is basically constant. Higher GDR values at low Σ dust was also found by Galliano et al. (2011) and Roman-Duval et al. (2014) for the LMC with a stronger trend than the one presented here. The relation between the GDR and Σgas is presented in the middle panel of Fig. 12. Lower values of GDR are found at low Σ gas, while at Σ gas ≳20 M⊙ pc−2, the GDR is constant. Galliano et al. (2011) also found a constant GDR for high values of Σ gas and a hint of a decrease of GDR at low Σgas. However, their data show a too high dispersion at low Σgas to establish a clear trend. We find agreement with the trends for the molecular data points of Roman-Duval et al. (2017), which seems plausible as the gas in M 33 is molecular dominated.

The trends presented here show that the GDR might vary with the physical conditions of the ISM. We also note here that we do not find any significant correlation in the three panels of Fig. 12 with the metallicity of each pixel and therefore we can conclude that the trends observed in Fig. 12 cannot be explained by the relation between the GDR and the metallicity in each point of the disc of M 33. Dark gas does not seem to explain the trends shown here. Therefore, reprocessing of dust, as Galliano et al. (2011) suggested, might play a role in the variations. Further investigation of the parameters that drive the variations in the GDR requires a larger dynamic range in GDR than that of M 33.

thumbnail Fig. 7

Top: Y BG∕Y TOTAL (left), Y VSG ∕Y TOTAL (right) versus the logarithmic Hα luminosity for the individual pixels in the disc of M 33 fitted with our code. Bottom: Y PAH ∕Y TOTAL versus logarithmic Hα luminosity (left) and dust surface density (right). The red squares and error bars correspond to the mean and standard deviation of the grain fractions for different bins in logarithmic Hα luminosity, which are overplotted to better show the trend between the quantities in both axis. The error bar corresponds to the median error: 0.04 for Y VSG∕Y TOTAL, 0.02 for Y PAH∕Y TOTAL, and 0.32 Y BG∕Y TOTAL.
thumbnail Fig. 8

YVSG∕Y TOTAL versus the ratio of 24 μm and the TIR luminosity (left) and the ratios of the 24 and 250 μm luminosities (right). The linear fit is performed for points with Y VSG∕Y TOTAL > 0.2, or alternatively for log(L24∕LTIR) > −1.08. The colour code corresponds to the emission fraction of the VSGs contributing to the 24 μm filter.
thumbnail Fig. 9

GDR map of the whole disc of M 33 obtained from the dust masses derived with our fitting procedure and total gas masses from the HI and CO observations of Gratier et al. (2010) and Druard et al. (2014), respectively.
thumbnail Fig. 10

Elliptical profiles of the GDR for M 33 for different values of X(CO). The differences in the profiles are more notable at R < 4 kpc, where the molecular gas mass fraction is high. At R > 4 kpc, the molecular hydrogen surface density, , is considerable smaller than the atomic hydrogen surface density, ΣHI (Druard et al. 2014; Gardan et al. 2007).

6 G0 as a tracer of the star formation rate

G0 is the scale factor of theintegral between 6 and 13.6 eV of the ISRF of the solar neighbourhood given by Mathis et al. (1983), which is the one used in our models. Therefore, G0 represents the energy density heating the dust in our models and the strength of the ISRF. Since the dust is heated by stars in the ISM, G0 should be related in principle to the amount of star formation. Despite the fact that some radiation from the stars could leak out of the regions where the dust is heated, it is interesting to investigate the relation between G0 and the SFR.

It is true that the concept of SFR at small spatial scales may not be valid for the following main reasons (Kennicutt & Evans 2012): incomplete sampling of the initial mass function for SFR below ~0.01 M⊙ yr−1, the breakdown of the assumption of continuous star formation implicit in the SFR calibrations, and larger spatial extension than the considered spatial scale of the emission that is used to calibrate the SFR. Keeping these warnings in mind, we look for a trend between the strength of the ISRF, G0, and the SFR estimations at the local scales of ~170 pc. Although atthese small spatial scales, Boquien et al. (2015) warns about the concept of SFR not being very suitable for the reasons we have presented above, they show that at local scales hybrid SFR estimators (those based on more than a single luminosity) reproduce better the SFR than the monochromatic SFR estimators. Therefore, we made use of the combination of Hα and 24 μm luminosities as well as the far-UV (FUV) and TIR luminosities to trace the SFR at these scales.

In the left panel of Fig. 13 we show the correlation between G0 and Σ SFR derived from Hα and 24 μm luminosities following the calibration of Calzetti et al. (2007) which is obtained for scales between ~30 pc and ~1.2 kpc, and is therefore valid for the spatial scales considered here (~170 pc). In the right panel we show the correlation when the SFR is derived using the combination of FUV and TIR luminosities from Murphy et al. (2012), derived for a star-forming complexes of ~1 kpc size. We checked that this calibration is consistent with the one presented in Boquien et al. (2016), who parameterised the linear coefficient for the combination of FUV and TIR luminosities with FUV-3.6 colours. It is interesting that the correlation holds for all values of ΣSFR, not only at the location of the star-forming regions corresponding to pixels with high SFR but also for pixels in the more diffuse ISM.

The SFR distribution derived from the Hα and 24 μm luminosities seems to extend to lower values than the SFR distribution derived from the FUV and TIR luminosities. The reason for this could be that at low SFRs the combination of Hα and 24 μm luminosity might underestimate the SFR due to stochasticity of the initial mass function (Lee et al. 2009), or that at local scales of ~170 pc we cannot account for some leakage of ionising photons which would underestimate the SFR when Hα luminosity is used (Relaño et al. 2012). Another possible explanation is that the radiation field of old stars contributing to the TIR emission is more extended than the radiation field responsible for the dust emission at 24 μm, which is more related to star forming regions. In this situation, at local scales the TIR emission can be contaminated by radiation of stars located at further distances, giving higher values of SFR than the ones estimated using the emission at Hα and 24 μm. For both hybrid SFR estimators, we find a correlation between the strength of the ISRF and the SFR. We note that although a relationship between the amount of energy heating the dust and the amount of star formed in the same area is expected, this is the first time such a relationship is empirically demonstrated.

thumbnail Fig. 11

GDR as a function of oxygen abundance for the disc of M 33. The abundances have been derived using the radial gradient obtained by Bresolin (2011).
thumbnail Fig. 12

GDRversus G0 (top), Σ gas (middle), and Σdust (bottom). We assumed a constant value of X(CO) = 4.0 × 1020 cm−2 (K−1 km s−1) to derive the gas mass in the disc of M 33. We colour-code the data with the oxygen abundance of each point obtained using the radial metallicity gradient from Bresolin (2011).

7 Submillimetre excess

We define the submillimetre excess as the fraction of observed luminosity in the SPIRE 500 μm band above the luminosity derived from the model in the same band. We note that the dust model we apply in this study has an emissivity coefficient β = 2 and therefore our results can be directly compared to what has been referred to in the literature as a submillimetre excess using MBBs (where a constant β = 2 is normally assumed). We parameterised the excess as 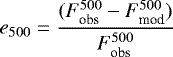(1)

where 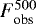and 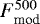are the observed and modelled fluxes in the SPIRE 500 μm band, respectively.

In Fig. 14 we show histograms of e500 for all the individual pixels fitted with our model in the three bands of SPIRE. The fluxes at 250 μm are very well fitted with our dust models: the histogram is centred at zero with a width of 15–20%, close to the uncertainty of the SPIRE fluxes (15%, see Sect. 2). However, in the 350 μm SPIRE band the centre of the histogram is shifted to positive values and at 500 μm the excess is as high as ~50%, clearly above the uncertainty of the 500 μm flux.

In Fig. 15 we show the map of excess at 500 μm for M 33. We confirm with these plots that M 33 exhibits an excess in the sub-millimetre wavelength range, which has already been reported before by Hermelo et al. (2016). Since we fit here the SED of the whole disc of M 33 in a pixel-by-pixel basis we are able to localise the regions of the disc where the excess is present. This will help us to better understand the main mechanisms which mightproduce this excess.

7.1 Radial trend

In Fig. 16 we show the variation of the mean e500 with the galactocentric distance. We see that the excess increases towards the outer parts of the galaxy and reaches values up to 38% in agreement with the analysis of the histograms shown in the previous section. The radial trend is in agreement with previous results shown in the literature. Using MBB fitting for M 33, Tabatabaei et al. (2014) report a decline of the emissivity co-efficient β with the radial distance of the galaxy (Fig. 3 in their paper): lower values of β correspond to a shallower slope in the SED (compared to β = 2), and therefore to an expected excess in the submillimetre wavelength range. An excess in 500 μm of 38% corresponds to a change of β from 2 to 1.1, which fits nicely with the β radial variation shown by Tabatabaei et al. (2014). The increase of e500 with the galactocentric radius is also seen in other galaxies: Paradis et al. (2012) studied the 500 μm excess in the Galactic plane with Herschel observations and found that the excess is located in the peripheral regions of the Galactic plane; Galametz et al. (2012, 2014) found that when the dust temperature and β are left free in the MBB fitting, β tends to decrease radially towards low surface brightness regions. Using MBB fitting, Smith et al. (2012) found a radial decrease of β for R > 3.1 kpc in M 31. The range of β values for M31 are however higher than those found in M 33 by Tabatabaei et al. (2014): β is ~1.8 at the centre of M 33 and decreases radially towards the outer parts of the galaxy, while for M 31 β ~ 2.5 at R ~ 3.1 kpc.

7.2 Relation to physical parameters

In this section we try to identify under which ISM conditions the submillimetre excess is prominent. This will shed light onto the mechanisms that might cause the excess. In Fig. 17 we show correlations between e500 and some parameters representative of the physical conditions of the ISM. We find an anti-correlation between e500 and the molecular hydrogen surface density mass in agreement with results from Tabatabaei et al. (2014), while no relation at all between e500 and the neutral hydrogen surface density mass was found (not shown here). A similar anti-correlation between e500 is seen for Σdust, Σ SFR and the relative mass fraction of PAHs. The anti-correlation between the excess and the dust surface density has also been observed in the LMC by Galliano et al. (2011). The excess is seen in regions with low SFR where the molecular gas and dust surface densities are low as well. These regions correspond to the diffuse ISM outside the main H II regions. Inside the main star-forming regions and molecular clouds the excess is in general close to zero.

The location of the excess within the galaxy, shown in the present work to be clearly associated with the diffuse ISM, is consistent with previous results given in the literature: Hermelo et al. (2016), fitting the global SED of M 33 with a radiation transfer model, found a higher submillimetre excess in the diffuse SED of M 33 than in the combined SED of all the H II regions of the galaxy. Gordon et al. (2014) performed a pixel-by-pixel SED fitting of the LMC and SMC using different versions of MBBs. For both LMC and SMC, these authors found higher values of e500 in the diffuse regions corresponding to low values of SPIRE 250 μm fluxes (Gordon et al. 2014, see Fig. 6 and 7). Finally, Planck Collaboration XXV (2011) reported a slight difference in the emissivity index between the dense (β ~ 2) and the diffuse medium (β ~ 1.7) of the Taurus complex, which agrees with the findings presented here.

We thus conclude that there is an excess in the SPIRE 500 μm band in M 33 which is significantly higher than the uncertainties (15%) in the observed 500 μm flux. The excess is mainly located in the diffuse part of the disc, while the star-forming regions present no excess within the uncertainty in the observed flux in this band. There is also a clear trend of the excess to increase with the galactocentric radius. Although we cannot rule out that the excess might have a dependence with the metallicity within the disc of the galaxy (indeed there is large evidence that the excess is mainly seen in low metallicity galaxies, e.g. Galametz et al. 2011), the metallicity gradient in M 33 is quite shallow (0.045 dex/Rkpc, Bresolin 2011) to establish a clear trend between e500 and metallicity in this galaxy. The radial trend observed in Fig. 16 could be a consequence of the fact that at larger radii the fraction of diffuse ISM is higher than in the inner parts of the disc of M 33.

In orderto investigate further the location of the excess we analysed the residuals of the excess relative to the radius. For that, we use the linear fit shown in Fig. 16 and obtained the deviation of the excess relative to this linear fit. In Fig. 18 we plot the residuals versus the same quantities as in Fig. 17. The correlations between the residuals and the surface density of the molecular gas, dust and the SFR are kept, showing that indeed the excess is more prominent in diffuse regions where these three quantities have low values independent of the galactic radius. There is no correlation between the residuals and Y PAH∕Y TOTAL, showing that the trend of the excess with Y PAH∕Y TOTAL presented in Fig. 17 was mainly driven by the fact that there is also a decrease of PAHs with the galactocentric radius in M 33.

thumbnail Fig. 13

G0 versus ΣSFR derived fromtwo different combinations of luminosities: Hα and 24 μm luminosities (left panel), and FUV and TIR luminosities (right panel). The colour bar corresponds to galactocentric distances in kpc. The coefficients of the linear combinations are taken from Calzetti et al. (2007) and Murphy et al. (2012) for Hα plus 24 μm luminosities and FUV plus TIR luminosities, respectively.

7.3 Other dust models

Several mechanisms have been invoked to explain the submillimetre excess in galaxies: the existence of a large amount of very cold dust, which would require a very high dust mass incompatible with the observations (Lisenfeld et al. 2002; Galliano et al. 2011; Galametz et al. 2011; Gordon et al. 2014), different dust grain properties producing a lower than two emissivity co-efficient β (Lisenfeld et al. 2002; Galliano et al. 2011; Gordon et al. 2014), emission of magnetic nanograins (Draine & Hensley 2012), and spinning grains (Draine & Lazarian 1998; Bot et al. 2010). We refer the reader to Hermelo et al. (2016) who analysed in very detail how these mechanisms contribute to the excess observed in the integrated SED of M 33. These authors showed that fitting the excess with very cold dust requires a high amount of dust mass giving an unreasonable GDR. Besides, the emission of spinning grains and magnetic nanoparticles are not able to reproduce completely the observed excess in the total SED of M 33 (see Fig. 9 in Hermelo et al. 2016).

Here we showed that the excess is present in the diffuse ISM (low gas and dust surface densities) whereas in star-forming regions (high gas and dust surface densities) no excess is found. The physical properties of the interstellar dust might be completelydifferent in both ISM phases, mainly because the evolutionary stage of the dust might be determined by the conditions of the ISM in both phases. Jones et al. (1994, 1996) proposed a theoretical framework where the dust grains are destroyed due to shocks in the ISM altering the grain size distribution of the dust. Recently, Jones et al. (2013, 2017) has proposed a new dust model based on three different components: small (a ≃ 0.4 to ~100 nm) and large amorphous hydrocarbon grains, a-C(:H), and large amorphous silicate grains. The small grains present a power-law size distribution, while the large grains are assumed to have a log-normal size distribution peaking at radii ≃200 nm. An extension of this model has been introduced by Köhler et al. (2014) adding a mix of amorphous olivine- and pyroxene-type silicate grains with iron nano-inclusions. This dust model has been successfully applied to the LMC and SMC by Chastenet et al. (2017).

The Jones et al. (2013, 2017) dust model, calibrated to reproduce the emission of the diffuse dust in the Milky Way, is mainly validfor dust located in the diffuse ISM where the gas and dust density is low, but it is flexible and can also accommodate the evolution of grains in different ISM phases. The model predicts that large a-C particles have a flat emissivity slope of β ≳ 1.2–1.3. On the contrary, within the molecular clouds coagulation of particles and a-C:H accretion leads to materials with β ~ 1.8–2.5. This model can naturally explain our results where the excess, quantified as e500, is mainly located in diffuse low dense regions of the ISM. Köhler et al. (2015) studied the evolution of the dust grains in the model proposed by Jones et al. (2013) and Köhler et al. (2014). They studied the transition from the diffuse ISM to denser regions assuming that the dust in the dense regions is affected by two mechanisms: i) accretion of C and H from the gas phase onto the surface of the dust grains, and ii) coagulation of grains into aggregates. They modelled the resulting dust emission and found that both processes make the dust temperature to decrease by 3 K and the emissivity coefficient to increase to β = 2 with respect to the assumed values of the dust model for the diffuse ISM, β ~ 1.8 (see Fig. 6 in Köhler et al. 2015). Our results are consistent with those from Köhler et al. (2015): the low density ISM medium has a low emissivity coefficient β, while the more intense star-forming regions surrounded by the molecular clouds and exhibiting higher gas and the dust mass surface density values, present no signatures of excess (i.e. emissivity coefficient values close to the one assumed by the dust model from Desert et al. 1990; β = 2).

thumbnail Fig. 14

Excess in % obtained using Eq. (1) for the three SPIRE bands: 250, 300, and 500 μm. There is no sign of excess at 250 μm, the excess starts to appear at 350 μm and clearly visible at 500 μm.
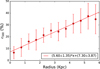thumbnail Fig. 15

Excess at at 500 μm derived using Eq. (1) for the whole disc of M 33.
thumbnail Fig. 16

Radial profile of e500. Each dot and its error bars correspond to the mean and the standard deviation of the e500 in each concentric 500 pc wide elliptical ring.
thumbnail Fig. 17

Top: excess in the SPIRE 500 μm band versus the molecular gas (left) and dust (right) surface density. Bottom: excess in the same band versus the SFR (left) and the mass fraction of PAHs (right). Each red square and its error bars correspond to the mean and the standard deviation of the magnitud represented in y axis. The colour bar corresponds to galactocentric distances in kiloparsecs.

8 Conclusions

We performed an analysis of the individual SEDs at scales of ~170 pc in the whole disc of M 33. Using a Bayesian statistical approach we fitted the individual SEDs with the classical dust model of Desert et al. (1990). This dust model has an emissivity index of β = 2, which allows us to make a direct comparison with MBB fitting reported in the literature. The best fit values representing the observed SEDs are obtained from the PDFs of each input parameter: the best value corresponds to the mean of the PDF, while the uncertainty is the corresponding 16th to 84th percentile range for each parameter. Our main conclusions are:

  • The relative fraction of the VSGs, Y VSG∕Y TOTAL, increasesat locations of intense star formation, while the relative fraction of BGs, Y BG∕Y TOTAL, follows the opposite correlation. These results agree with those presented in Relaño et al. (2016) and are consistent with theframework of dust evolution models of Jones et al. (1994, 1996) suggesting dust grain destruction and/or fragmentation by interstellar shocks in the warm medium.

  • We derive the GDR over the whole disc of M 33. The GDR is relatively constant with a value of ~300 up to a radius of 4 kpc where it starts to increase. The radial variation is consistent with the shallow metallicity gradient of this galaxy. We do not find a strong correlation between the GDR and the strength of the ISRF, as it was suggested by Galliano et al. (2011) for the LMC, even when including the dark gas fraction reported by Gratier et al. (2017).

  • We find a correlation between G0, the strength of the ISRF in the solar neighbourhood given by Mathis et al. (1983), and the SFR at each spatial location in the disc of M 33. The relation holds when the SFR is derived using a linear combination of Hα and 24 μm, or FUV and TIR luminosities. This relation shows that G0, derived from the models, can account for the amount of the star formation forming at these spatial locations.

  • We find a submillimetre excess, defined as the fraction of observed luminosity in the SPIRE 500 μm band above the luminosity derived from the model in the same band, that can be as high as ~50%, clearly above the uncertainty of the 500 μm flux. Theexcess increases at larger radii in agreement with the radial dependence of β reportedby Tabatabaei et al. (2014) for M 33.

  • The excess is prominent in regions of low surface densities of SFR, dust and gas mass. These regions correspond to the diffuse ISM outside the main star-forming H II regions.

  • Our findings are consistent with THEMIS dust model presented in Jones et al. (2013, 2017). This model is mainly valid for the diffuse ISM and predicts that large a-C(:H) particles exhibit a flat emissivity coefficient β ~ 1.2–1.3. A dust component (composed of carbon or silicate-type dust) with similarly flat dust emissivity coefficients than the large a-C(:H) particles in the THEMIS dust model could be invoked to explain the submillimetre excess in the diffuse disc of M 33.

thumbnail Fig. 18

Top: residual excess in the SPIRE 500 μm band versus the molecular gas (left) and dust (right) surface density. Bottom: excess in the same band versus the SFR (left) and the mass fraction of PAHs (right). Each red square and its error bars correspond to the mean and the standard deviation of the magnitud represented in y-axis. The colour bar corresponds to galactocentric distances in kpc.

Acknowledgements

We would like to thank the referee for the useful comments that helped to improve the first version of this paper. This work was partially supported by the Junta de Andalucía Grant FQM108 and Spanish MEC Grants, AYA-2011-24728 and AYA-2014-53506-P. MRP thanks to the Computational service PROTEUS at the Instituto Carlos I. This research made use of APLpy, an open-source plotting package for Python hosted at http://aplpy.github.com of TOPCAT & STIL: Starlink Table/VOTable Processing Software (Taylor 2005) of Matplotlib, a suite of open-source python modules that provide a framework for creating scientific plots.

Appendix A Robustness of the fit

The low values for the 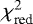in most of the fits (see Fig. A.1) show that in general the fits are reproducing quite well the observed SEDs. As a further step, we also analyse how robust our fitting methodology is. For this purpose we use two procedures: (i) generate mock SEDs and check if the fitting routine applied to the mock SEDs gives consistent results as the original ones, and (ii) fit each PDF with a single Gaussian and compare the results to the estimates of the best fit parameter values and corresponding uncertainties.

For the first procedure for each pixel we use the best fit SED and create a new mock SED. The fluxes of the mock SED in each band are chosen from a random Gaussian flux distribution having the best fit flux as a mean value and the observational uncertainty as σ (see Boquien et al. 2012). We then fit the mock SED with the same procedure explained in Sect. 3 and obtain the best mock parameters. The comparison between the best fit and the best mock parameter values for each pixel is shown in Fig. A.2. Most of the best mock parameter values agree with the original ones within 1 − σ, which reinforces that the fitting method is robust.

thumbnail Fig. A.2

Robustness of the best fit for the G0 (top left), Y VSG (top right), Y PAH (bottom left), and Y BG (bottom right). We use the best fit SEDs given by the method described in Sect. 3 and create new SEDs choosing random flux values in each band from a Gaussian distribution having the best fit flux as a mean value and the observational uncertainty as σ. The best fit parameters for the mock SEDs are then compared with those initially obtained. The dashed lines represents 1 + median(σ) of the original best fit parameters.

For the second procedure we fit the PDF of each parameter with a single Gaussian and compare the mean and the Full Width at Half Maximum (FWHM) with the best fit parameter value and the corresponding uncertainty. The result is shown in Fig. A.3. We can see that the mean of the fitted Gaussian agrees very well with the assumed best fit parameter value for the four input parameters, which shows that in general the PDFs are well fitted with a single Gaussian. Although with higher dispersion, the estimated uncertainties of the PDFs and the FWHM values given by the Gaussian fit are in agreement as well.

thumbnail Fig. A.3

Left: comparison of the best fit parameter values adopted here and the mean of the Gaussian fitted to each PDF in each pixel and for each parameter. The agreement between each magnitude shows that the PDF are well represented by a single Gaussian. Right: comparison of the adopted uncertainty -the 16th to 84th percentile range- and the FWHM value derived from the Gaussian fit in each pixel.

Appendix B Double-peak PDFs

We make use of the results of the Gaussian fitting to each PDF and consider the existence of double peaks in the PDFs in two ways. First, we checked if there are secondary peaks in the PDF outside the main one. To do this, we looked for peaks with an intensity higher than 0.3 the maximum of the fitted Gaussian and located at a distance larger than 7σ from the main peak. We did this for each parameter and pixel. We confirm there are no secondary peaks outside the main one of the PDF distribution.

Secondly, it might also happen that the PDF distribution could be described with two peaks close to each other, as shown in the lower right panel of Fig. B.1. To detect these cases, we look for peaks having an intensity higher than 0.5 the maximum of the PDF distribution and separated a distance higher than one ⟨σ⟩, where ⟨σ⟩ is the mean σ over all pixels in each parameter. We detect double peaks in 28 (0.3%), 108 (1.3%), 240 (2.9%) and 136 (1.6%) PDFs for G0, Y PAH, Y VSG, and Y BG, respectively. The low fraction of PDFs with double peaks confirms the assumption of single-peaked PDFs and reinforces the results presented here.

thumbnail Fig. B.1

PDF for pixel (70 189) where a double peak in the BG PDF has been detected. Our programme looks for secondary peaks with 0.5 times the intensity of the maximum of the PDF and located at a distance higher than 0.5 times the mean FWHM, where the mean has been taken over all the pixels in each parameter. The adopted uncertainty of Y BG for this pixel – the 16th to 84th percentile range – accounts for the double peak of the PDF for this particular pixel.

References

  1. Accurso, G., Saintonge, A., Catinella, B., et al. 2017, MNRAS, 470, 4750 [NASA ADS] [Google Scholar]
  2. Aniano, G., Draine, B. T., Gordon, K. D., & Sandstrom, K. 2011, PASP, 123, 1218 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bernard, J.-P., Reach, W. T., Paradis, D., et al. 2008, AJ, 136, 919 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bianchi, S. 2013, A&A, 552, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bocchio, M., Jones, A. P., & Slavin, J. D. 2014, A&A, 570, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
  7. Boquien, M., Calzetti, D., Combes, F., et al. 2011, AJ, 142, 111 [NASA ADS] [CrossRef] [Google Scholar]
  8. Boquien, M., Buat, V., Boselli, A., et al. 2012, A&A, 539, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Boquien, M., Calzetti, D., Aalto, S., et al. 2015, A&A, 578, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Boquien, M., Kennicutt, R., Calzetti, D., et al. 2016, A&A, 591, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Boselli, A., Lequeux, J., & Gavazzi, G. 2002, Ap&SS, 281, 127 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bot, C., Ysard, N., Paradis, D., et al. 2010, A&A, 523, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Bresolin, F. 2011, ApJ, 730, 129 [NASA ADS] [CrossRef] [Google Scholar]
  14. Calzetti, D., Kennicutt, R. C., Engelbracht, C. W., et al. 2007, ApJ, 666, 870 [NASA ADS] [CrossRef] [Google Scholar]
  15. Chastenet, J., Bot, C., Gordon, K. D., et al. 2017, A&A, 601, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Compiègne, M., Verstraete, L., Jones, A., et al. 2011, A&A, 525, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. da Cunha, E., Charlot, S., & Elbaz, D. 2008, MNRAS, 388, 1595 [NASA ADS] [CrossRef] [Google Scholar]
  18. Dale, D. A., Aniano, G., Engelbracht, C. W., et al. 2012, ApJ, 745, 95 [NASA ADS] [CrossRef] [Google Scholar]
  19. Desert, F.-X., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215 [NASA ADS] [Google Scholar]
  20. Draine, B. T., & Hensley, B. 2012, ApJ, 757, 103 [CrossRef] [Google Scholar]
  21. Draine, B. T., & Lazarian, A. 1998, ApJ, 508, 157 [NASA ADS] [CrossRef] [Google Scholar]
  22. Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
  23. Draine, B. T., Dale, D. A., Bendo, G., et al. 2007, ApJ, 663, 866 [NASA ADS] [CrossRef] [Google Scholar]
  24. Druard, C., Braine, J., Schuster, K. F., et al. 2014, A&A, 567, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Dwek, E. 1998, ApJ, 501, 643 [NASA ADS] [CrossRef] [Google Scholar]
  26. Engelbracht, C. W., Blaylock, M., Su, K. Y. L., et al. 2007, PASP, 119, 994 [NASA ADS] [CrossRef] [Google Scholar]
  27. Engelbracht, C. W., Rieke, G. H., Gordon, K. D., et al. 2008, ApJ, 678, 804 [NASA ADS] [CrossRef] [Google Scholar]
  28. Freedman, W. L., Wilson, C. D., & Madore, B. F. 1991, ApJ, 372, 455 [NASA ADS] [CrossRef] [Google Scholar]
  29. Galametz, M., Madden, S. C., Galliano, F., et al. 2011, A&A, 532, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Galametz, M., Kennicutt, R. C., Albrecht, M., et al. 2012, MNRAS, 425, 763 [NASA ADS] [CrossRef] [Google Scholar]
  31. Galametz, M., Albrecht, M., Kennicutt, R., et al. 2014, MNRAS, 439, 2542 [NASA ADS] [CrossRef] [Google Scholar]
  32. Galarza, V. C., Walterbos, R. A. M., & Braun, R. 1999, AJ, 118, 2775 [NASA ADS] [CrossRef] [Google Scholar]
  33. Galliano, F., Madden, S. C., Jones, A. P., et al. 2003, A&A, 407, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Galliano, F., Madden, S. C., Jones, A. P., Wilson, C. D., & Bernard, J.-P. 2005, A&A, 434, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Galliano, F., Dwek, E., & Chanial, P. 2008, ApJ, 672, 214 [NASA ADS] [CrossRef] [Google Scholar]
  36. Galliano, F., Hony, S., Bernard, J.-P., et al. 2011, A&A, 536, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Gardan, E., Braine, J., Schuster, K. F., Brouillet, N., & Sievers, A. 2007, A&A, 473, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Gordon, K. D., Engelbracht, C. W., Fadda, D., et al. 2007, PASP, 119, 1019 [NASA ADS] [CrossRef] [Google Scholar]
  39. Gordon, K. D., Roman-Duval, J., Bot, C., et al. 2014, ApJ, 797, 85 [NASA ADS] [CrossRef] [Google Scholar]
  40. Gratier, P., Braine, J., Rodriguez-Fernandez, N. J., et al. 2010, A&A, 522, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Gratier, P., Braine, J., Schuster, K., et al. 2017, A&A, 600, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Hermelo, I., Relaño, M., Lisenfeld, U., et al. 2016, A&A, 590, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Israel, F. P., Wall, W. F., Raban, D., et al. 2010, A&A, 519, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Jones, A. P. 2004, in Astrophysics of Dust, eds. A. N. Witt, G. C. Clayton, & B. T. Draine, ASP Conf. Ser., 309, 347 [Google Scholar]
  45. Jones, A. P., Tielens, A. G. G. M., Hollenbach, D. J., & McKee, C. F. 1994, ApJ, 433, 797 [NASA ADS] [CrossRef] [Google Scholar]
  46. Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [NASA ADS] [CrossRef] [Google Scholar]
  47. Jones, A. P., Fanciullo, L., Köhler, M., et al. 2013, A&A, 558, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Jones, A. P., Koehler, M., Ysard, N., Bocchio, M., & Verstraete, L. 2017, A&A, 602, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
  50. Kennicutt, R. C., Calzetti, D., Aniano, G., et al. 2011, PASP, 123, 1347 [NASA ADS] [CrossRef] [Google Scholar]
  51. Kirkpatrick, A., Calzetti, D., Galametz, M., et al. 2013, ApJ, 778, 51 [NASA ADS] [CrossRef] [Google Scholar]
  52. Köhler, M., Stepnik, B., Jones, A. P., et al. 2012, A&A, 548, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Köhler, M., Jones, A., & Ysard, N. 2014, A&A, 565, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Köhler, M., Ysard, N., & Jones, A. P. 2015, A&A, 579, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Kramer, C., Buchbender, C., Xilouris, E. M., et al. 2010, A&A, 518, L67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Lee, J. C., Gil de Paz, A., Tremonti, C., et al. 2009, ApJ, 706, 599 [NASA ADS] [CrossRef] [Google Scholar]
  57. Leroy, A. K., Bolatto, A., Gordon, K., et al. 2011, ApJ, 737, 12 [NASA ADS] [CrossRef] [Google Scholar]
  58. Lisenfeld, U., & Ferrara, A. 1998, ApJ, 496, 145 [NASA ADS] [CrossRef] [Google Scholar]
  59. Lisenfeld, U., Israel, F. P., Stil, J. M., & Sievers, A. 2002, A&A, 382, 860 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Madden, S. C., Galliano, F., Jones, A. P., & Sauvage, M. 2006, A&A, 446, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Madden, S. C., Rémy, A., Galliano, F., et al. 2012, in The Spectral Energy Distribution of Galaxies - SED 2011, eds. R. J. Tuffs, & C. C. Popescu, IAU Symp., 284, 141 [NASA ADS] [Google Scholar]
  62. Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
  63. Murphy, E. J., Bremseth, J., Mason, B. S., et al. 2012, ApJ, 761, 97 [NASA ADS] [CrossRef] [Google Scholar]
  64. Ott, S. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 139 [NASA ADS] [Google Scholar]
  65. Ott, S. 2011, in Astronomical Data Analysis Software and Systems XX, eds. I. N. Evans, A. Accomazzi, D. J. Mink, & A. H. Rots, ASP Conf. Ser., 442, 347 [NASA ADS] [Google Scholar]
  66. Paradis, D., Bernard, J.-P., & Mény, C. 2009, A&A, 506, 745 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Paradis, D., Paladini, R., Noriega-Crespo, A., et al. 2011, ApJ, 735, 6 [NASA ADS] [CrossRef] [Google Scholar]
  68. Paradis, D., Paladini, R., Noriega-Crespo, A., et al. 2012, A&A, 537, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Pineda, J. L., Langer, W. D., & Goldsmith, P. F. 2014, A&A, 570, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Planck Collaboration XXV. 2011, A&A, 536, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Planck Collaboration XXIX. 2016, A&A, 586, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Relaño, M., Kennicutt, Jr. R. C., Eldridge, J. J., Lee, J. C., & Verley, S. 2012, MNRAS, 423, 2933 [NASA ADS] [CrossRef] [Google Scholar]
  73. Relaño, M., Verley, S., Pérez, I., et al. 2013, A&A, 552, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Relaño, M., Kennicutt, R., Lisenfeld, U., et al. 2016, A&A, 595, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Rémy-Ruyer,A., Madden, S. C., Galliano, F., et al. 2013, A&A, 557, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Rémy-Ruyer,A., Madden, S. C., Galliano, F., et al. 2014, A&A, 563, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Roman-Duval,J., Gordon, K. D., Meixner, M., et al. 2014, ApJ, 797, 86 [NASA ADS] [CrossRef] [Google Scholar]
  78. Roman-Duval,J., Bot, C., Chastenet, J., & Gordon, K. 2017, ApJ, 841, 72 [NASA ADS] [CrossRef] [Google Scholar]
  79. Roussel, H. 2013, PASP, 125, 1126 [Google Scholar]
  80. Sandstrom, K. M., Leroy, A. K., Walter, F., et al. 2013, ApJ, 777, 5 [NASA ADS] [CrossRef] [Google Scholar]
  81. Schruba, A., Leroy, A. K., Walter, F., et al. 2012, AJ, 143, 138 [NASA ADS] [CrossRef] [Google Scholar]
  82. Slavin, J. D., Dwek, E., & Jones, A. P. 2015, ApJ, 803, 7 [NASA ADS] [CrossRef] [Google Scholar]
  83. Smith, M. W. L., Eales, S. A., Gomez, H. L., et al. 2012, ApJ, 756, 40 [NASA ADS] [CrossRef] [Google Scholar]
  84. Stephens, I. W., Evans, J. M., Xue, R., et al. 2014, ApJ, 784, 147 [NASA ADS] [CrossRef] [Google Scholar]
  85. Stepnik, B., Abergel, A., Bernard, J.-P., et al. 2003, A&A, 398, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Swinyard, B. M., Ade, P., Baluteau, J.-P., et al. 2010, A&A, 518, L4 [Google Scholar]
  87. Tabatabaei, F. S., Schinnerer, E., Murphy, E. J., et al. 2013, A&A, 552, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Tabatabaei, F. S., Braine, J., Xilouris, E. M., et al. 2014, A&A, 561, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Taylor, M. B. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, ASP Conf. Ser., 347, 29 [Google Scholar]
  90. Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
  91. Xilouris, E. M., Tabatabaei, F. S., Boquien, M., et al. 2012, A&A, 543, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Zurita, A., & Bresolin, F. 2012, MNRAS, 427, 1463 [NASA ADS] [CrossRef] [Google Scholar]
2

αCO is the conversion factor from integrated CO luminosity to molecular gas mass. It scales linearly with X(CO), which is the conversion factor from integrated CO luminosity to column density of H 2.

All Tables

Table 1

Input parameter range.

In the text
Table 2

Average relative fraction of emission corresponding to PAHs, VSGs, and BGs in the 8 and 24 μm bands from Spitzer, and in the 70, 100 and 160 μm filters from Herschel.

In the text

All Figures

thumbnail Fig. 1

250 μm intensity image in MJy sr−1 masked using the constraints presented in Sect. 2.2.
In the text
thumbnail Fig. A.1

distribution for all the SEDs in the disc of M 33.
In the text
thumbnail Fig. B.2

Relations between the five parameters fitted with our technique described in Sect. 3.
In the text
thumbnail Fig. 2

Histograms derived in our fitting procedure for two different pixels (70, 123) (top) and (88, 144) (bottom) corresponding to star-forming and diffuse regions, respectively. The values of the best fit parameters obtained as described in the text are: G0 = 3.69 ± 0.97, Y PAH = (2.1 ± 0.4) × 10−3, Y VSG = (3.1 ± 1.8) × 10−3, and Y BG = (2.5 ± 0.6) × 10−2 for the top panel, and G0 = 3.17 ± 0.97, Y PAH = (2.6 ± 0.7) × 10−4, Y VSG = (4.1 ± 2.5) × 10−4, and Y BG = (5.5 ± 1.5) × 10−3 for the bottom panel. The dashed line corresponds to the Gaussian fitted to each PDF. We compare the results from the best fit parameters obtained with our procedure and those derived from the Gaussian fitting in Appendix A.
In the text
thumbnail Fig. 3

Examples of SED fitting for pixels (70 123) (top) and (88 144) (bottom) corresponding to star-forming and diffuse regions, respectively. values are 5.1 and 3.7 for the top and bottom panels, respectively. The bottom panel shows submillimetre excess in the 500 μm band. We study this excess in Sect. 7.
In the text
thumbnail Fig. 4

Map of the dust surface density in units of M⊙ pc−2 for M 33 derived from our fitting technique.
In the text
thumbnail Fig. 5

Comparison of the dust masses obtained in this paper and those derived by Tabatabaei et al. (2014) with two MBBs. Each point corresponds to one pixel on the sky. Only independent data points have been considered to compare both masses (see text for details). The mean value and standard deviation of the ratio between the dust mass derived from Tabatabaei et al. (2014) and from this study is 1.7 (dashed line) and 0.7, respectively. The relative uncertainties for the dust masses derived in this paper are ~25%.
In the text
thumbnail Fig. 6

YPAH∕Y TOTAL (left), Y VSG ∕Y TOTAL (middle), and Y BG∕Y TOTAL (right) maps for the disc of M 33 derived using our fitting procedure.
In the text
thumbnail Fig. 7

Top: Y BG∕Y TOTAL (left), Y VSG ∕Y TOTAL (right) versus the logarithmic Hα luminosity for the individual pixels in the disc of M 33 fitted with our code. Bottom: Y PAH ∕Y TOTAL versus logarithmic Hα luminosity (left) and dust surface density (right). The red squares and error bars correspond to the mean and standard deviation of the grain fractions for different bins in logarithmic Hα luminosity, which are overplotted to better show the trend between the quantities in both axis. The error bar corresponds to the median error: 0.04 for Y VSG∕Y TOTAL, 0.02 for Y PAH∕Y TOTAL, and 0.32 Y BG∕Y TOTAL.
In the text
thumbnail Fig. 8

YVSG∕Y TOTAL versus the ratio of 24 μm and the TIR luminosity (left) and the ratios of the 24 and 250 μm luminosities (right). The linear fit is performed for points with Y VSG∕Y TOTAL > 0.2, or alternatively for log(L24∕LTIR) > −1.08. The colour code corresponds to the emission fraction of the VSGs contributing to the 24 μm filter.
In the text
thumbnail Fig. 9

GDR map of the whole disc of M 33 obtained from the dust masses derived with our fitting procedure and total gas masses from the HI and CO observations of Gratier et al. (2010) and Druard et al. (2014), respectively.
In the text
thumbnail Fig. 10

Elliptical profiles of the GDR for M 33 for different values of X(CO). The differences in the profiles are more notable at R < 4 kpc, where the molecular gas mass fraction is high. At R > 4 kpc, the molecular hydrogen surface density, , is considerable smaller than the atomic hydrogen surface density, ΣHI (Druard et al. 2014; Gardan et al. 2007).
In the text
thumbnail Fig. 11

GDR as a function of oxygen abundance for the disc of M 33. The abundances have been derived using the radial gradient obtained by Bresolin (2011).
In the text
thumbnail Fig. 12

GDRversus G0 (top), Σ gas (middle), and Σdust (bottom). We assumed a constant value of X(CO) = 4.0 × 1020 cm−2 (K−1 km s−1) to derive the gas mass in the disc of M 33. We colour-code the data with the oxygen abundance of each point obtained using the radial metallicity gradient from Bresolin (2011).
In the text
thumbnail Fig. 13

G0 versus ΣSFR derived fromtwo different combinations of luminosities: Hα and 24 μm luminosities (left panel), and FUV and TIR luminosities (right panel). The colour bar corresponds to galactocentric distances in kpc. The coefficients of the linear combinations are taken from Calzetti et al. (2007) and Murphy et al. (2012) for Hα plus 24 μm luminosities and FUV plus TIR luminosities, respectively.
In the text
thumbnail Fig. 14

Excess in % obtained using Eq. (1) for the three SPIRE bands: 250, 300, and 500 μm. There is no sign of excess at 250 μm, the excess starts to appear at 350 μm and clearly visible at 500 μm.
In the text
thumbnail Fig. 15

Excess at at 500 μm derived using Eq. (1) for the whole disc of M 33.
In the text
thumbnail Fig. 16

Radial profile of e500. Each dot and its error bars correspond to the mean and the standard deviation of the e500 in each concentric 500 pc wide elliptical ring.
In the text
thumbnail Fig. 17

Top: excess in the SPIRE 500 μm band versus the molecular gas (left) and dust (right) surface density. Bottom: excess in the same band versus the SFR (left) and the mass fraction of PAHs (right). Each red square and its error bars correspond to the mean and the standard deviation of the magnitud represented in y axis. The colour bar corresponds to galactocentric distances in kiloparsecs.
In the text
thumbnail Fig. 18

Top: residual excess in the SPIRE 500 μm band versus the molecular gas (left) and dust (right) surface density. Bottom: excess in the same band versus the SFR (left) and the mass fraction of PAHs (right). Each red square and its error bars correspond to the mean and the standard deviation of the magnitud represented in y-axis. The colour bar corresponds to galactocentric distances in kpc.
In the text
thumbnail Fig. A.2

Robustness of the best fit for the G0 (top left), Y VSG (top right), Y PAH (bottom left), and Y BG (bottom right). We use the best fit SEDs given by the method described in Sect. 3 and create new SEDs choosing random flux values in each band from a Gaussian distribution having the best fit flux as a mean value and the observational uncertainty as σ. The best fit parameters for the mock SEDs are then compared with those initially obtained. The dashed lines represents 1 + median(σ) of the original best fit parameters.
In the text
thumbnail Fig. A.3

Left: comparison of the best fit parameter values adopted here and the mean of the Gaussian fitted to each PDF in each pixel and for each parameter. The agreement between each magnitude shows that the PDF are well represented by a single Gaussian. Right: comparison of the adopted uncertainty -the 16th to 84th percentile range- and the FWHM value derived from the Gaussian fit in each pixel.
In the text
thumbnail Fig. B.1

PDF for pixel (70 189) where a double peak in the BG PDF has been detected. Our programme looks for secondary peaks with 0.5 times the intensity of the maximum of the PDF and located at a distance higher than 0.5 times the mean FWHM, where the mean has been taken over all the pixels in each parameter. The adopted uncertainty of Y BG for this pixel – the 16th to 84th percentile range – accounts for the double peak of the PDF for this particular pixel.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.