| Issue |
A&A
Volume 613, May 2018
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 32 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201731804 | |
| Published online | 04 June 2018 | |
Broadband radio spectro-polarimetric observations of high-Faraday-rotation-measure AGN
1
Istituto de Radioastronomía y Astrofísica (IRyA-UNAM), Antigua Carretera a Pátzcuaro,
Morelia,
Michoacán, Mexico
e-mail: a.pasetto@irya.unam.mx
2
Hamburger Sternwarte, Universität Hamburg,
Gojenbergsweg 112,
21029
Hamburg, Germany
3
Max-Planck Institut für Radioastronomie (MPIfR),
Auf dem Hügel 69,
53121
Bonn, Germany
4
Istituto di Astrofisica e Planetologia Spaziali (IAPS-INAF),
via Fosso del Cavaliere 100,
00133
Roma, Italy
5
Instituto de Astronomía, UNAM,
Apartado Postal 70-264,
04510
Mexico,
DF, Mexico
6
Istituto di Radioastronomia (IRA-INAF),
Via Gobetti 101,
40129
Bologna, Italy
Received:
20
August
2017
Accepted:
27
January
2018
We present broadband polarimetric observations of a sample of high-Faraday-rotation-measure (high-RM) active galactic nuclei (AGN) using the Karl. G. Jansky Very Large Array (JVLA) telescope from 1 to 2 GHz, and 4 to 12 GHz. The sample (14 sources) consists of very compact sources (linear resolution smaller than ≈5 kpc) that are unpolarized at 1.4 GHz in the NRAO VLA Sky Survey (NVSS). Total intensity data have been modeled using a combination of synchrotron components, revealing complex structure in their radio spectra. Depolarization modeling, through the so-called qu-fitting (the modeling of the fractional quantities of the Stokes Q and U parameters), has been performed on the polarized data using an equation that attempts to simplify the process of fitting many different depolarization models. These models can be divided into two major categories: external depolarization (ED) and internal depolarization (ID) models. Understanding which of the two mechanisms is the most representative would help the qualitative understanding of the AGN jet environment and whether it is embedded in a dense external magneto-ionic medium or if it is the jet-wind that causes the high RM and strong depolarization. This could help to probe the jet magnetic field geometry (e.g., helical or otherwise). This new high-sensitivity data shows a complicated behavior in the total intensity and polarization radio spectrum of individual sources. We observed the presence of several synchrotron components and Faraday components in their total intensity and polarized spectra. For the majority of our targets (12 sources), the depolarization seems to be caused by a turbulent magnetic field. Thus, our main selection criteria (lack of polarization at 1.4 GHz in the NVSS) result in a sample of sources with very large RMs and depolarization due to turbulent magnetic fields local to the source. These broadband JVLA data reveal the complexity of the polarization properties of this class of radio sources. We show how the new qu-fitting technique can be used to probe the magnetized radio source environment and to spectrally resolve the polarized components of unresolved radio sources.
Key words: polarization / radiation mechanisms: non-thermal / techniques: polarimetric / galaxies: active / radio continuum: galaxies
© ESO 2018
1 Introduction
Active galactic nuclei (AGN) are powered by the supermassive black hole (SMBH) at their centers. They can emit across the full electromagnetic spectrum, from low radio frequencies to high-energy X-ray and γ-ray. The radio emission of radio-loud AGN is dominated by synchrotron radiation from their core, jets and lobes. Understanding how these objects interact with the surrounding medium is important for studying the evolution and feedback of the radio sources and the formation of the radio jets. Important information can be extracted not only through studying the total intensity of the synchrotron radiation but also the polarization information. During the last years, polarization study has been playing an important role in the understanding of AGN jets and their surroundings (e.g., recent works done by Zavala & Taylor 2003; O’Sullivan & Gabuzda 2009; Hovatta et al. 2012; O’Sullivan et al. 2012; Farnes et al. 2014; Pasetto et al. 2016; Kravchenko et al. 2017). In the radio regime, the polarization state of the electromagnetic radiation of extragalactic sources is described using the Stokes parameters I, Q, U and V . Following Sokoloff et al. (1998), the complex linear polarization is:
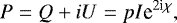 (1)
(1)
where I, Q, and U are the measured Stokes parameters, and p and χ are the fractional polarization and the polarization angle of the polarized wave, respectively, described as:
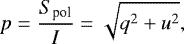 (2)
(2)
where we consider q = Q∕I and u = U∕I as the fractional values of the Stokes parameters Q and U, respectively, as used in Farnsworth et al. (2011), and
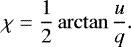 (3)
(3)
The study of the polarization state of radio sources provides the opportunity to analyze two important effects: Faraday rotation and Faraday depolarization. Characterizing the Faraday structure and studying the effect of Faraday depolarization in radio sources allows one to probe the properties of the magneto-ionic medium, such as the strength, degree of order, orientation of the magnetic field, and the distribution of the relativistic and thermal electron populations. Faraday rotation is the rotation of the plane of an electromagnetic wave as it passes through a magnetized medium; which for a particular region can be described by the Faraday depth (Burn 1966):
![\begin{equation*} \phi = 0.81\int^{\textrm{telescope}}_{\textrm{emission}} nB_{\parallel} \textrm{d}l \quad [\textrm{rad}\, \textrm{m}^{-2}],\end{equation*}](/articles/aa/full_html/2018/05/aa31804-17/aa31804-17-eq4.png) (4)
(4)
where n is the free electron density (in units of cm−3), B∥ is the parallel component of the magnetic field (in μG) and l is the distance along the line of sight (in parsec). In the simplest scenario, in which there is a background source emitting synchrotron radiation and only one single uniform Faraday screen in the foreground, the Faraday depth Φ is identical to the rotation measure (RM). Traditionally, the RM has been determined by fitting the equation:
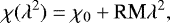 (5)
(5)
where χ0 is the intrinsic polarization angle. This equation is true when one restricts the RM fitting to regions of λ2 space, where the fractional polarization, p(λ2), is constant or decreases monotonically (e.g., Simard-Normandin et al. 1981), or when one restricts the fitting to λ < λ1∕2 (therefore, p(λ1∕2)∕p(0) = 0.5), beyond which Burn (1966) suggests a nonlinear behavior of the polarization angle, χ(λ2). In more realistic astrophysical cases, a nonlinear behavior of the polarization angle, therefore a complex Faraday structure, occurs (e.g., Roy et al. 2005; Anderson et al. 2015, 2016; Pasetto et al. 2016, hereafter Pa16). The presence of a magnetized and dense medium surrounding and/or interacting with the emitting radio source can depolarize the emission. This effect is generally seen as a decrease of the degree of polarization with increasing wavelength, and has been studied for many years (e.g., Burn 1966; Tribble 1991; Sokoloff et al. 1998). The depolarization can be caused internally, where the synchrotron emitting and the Faraday rotating regions are spatially coincident, or externally, where the synchrotron emitting and the Faraday rotation regions are different (see Sect. 4 for a more exhaustive explanation). To extract information about the magnet-ionic medium, it is necessary to study and model both the fractional polarization, p(λ2), and the polarization angle, χ(λ2), as suggested by Farnsworth et al. (2011). However, until now the lack of wide bandwidth coverage has made this kind of study difficult. To study the complex behavior of the several Faraday structures, well sampled polarized data and more sophisticated modeling are required. Very recently, thanks to new broadband receivers at radio facilities, spectropolarimetric studies have been performed by O’Sullivan et al. (2012); Anderson et al. (2015, 2016); O’Sullivan et al. (2017, hereafter OS17) on discrete sources. They selected polarized sources at 1.4 GHz and analyzed the complex behavior by studying and modeling the polarization signal. In this work we present well sampled, wide-band polarimetric data of a sample of AGN observed with the Karl. G. Jansky Very Large Array (JVLA) of the National Radioastronomy Observatory (NRAO)1 at L, C, and X bands (1–2 GHz bandwidth is L band; 4–8 GHz bandwidth is C band and 8–12 GHz bandwidth is X band). The sources have been selected from previous work: a polarimetric Effelsberg single-dish study by Pa16. The sources in Pa16 were selected to show strong depolarization in the 1.4 GHz NRAO VLA Sky Survey (NVSS, 45′′ FWHM resolution, effective continuum IF bandwidth of Δν ~ 42 MHz) with p ≤ 0.3 × 10−2 and sources with no polarization information (blanked sources in the NVSS, i.e., pixels with lower weight blanked to eliminate regions with inadequate coverage and poor sensitivity). Pa16 found that the strong depolarization of these sources is most likely related to the large values of RM derived from linear χ(λ2) fits (with RM measured with single-dish observations, RM dish > 500 rad m−2). In this work, we present and analyze their wide-band JVLA total intensity data and their polarimetric data (at L, C and X bands) by modelingthe total intensity radio spectra using a combination of several synchrotron components and by modeling the polarization information following the approach in O’Sullivan et al. (2012). We propose a general interpretation of the complex medium of these sources. In Sect. 2 we present the sample, in Sect. 3 we describe the observations and calibration process. In Sect. 4 we describe the polarization models and in Sect. 5 we describe the fitting of the depolarization modeling and how to extract the polarization and Faraday rotation parameters. Section 6 presents our results for all sources, with comments on individual sources in Sect. 7. In Section 8 we discuss possible implications and our summary and conclusion are in Sect. 9. Throughout this paper, we assume a cosmology with H0 = 71 km s−1 Mpc−1, Ω M = 0.27 and Ω Λ = 0.73, and define the spectral index, α, such that the observed flux density (S) at frequencyν follows the relation Sν ∝ να.
2 The sample
The sources have been selected from Pa16 where single-dish observations with the Effelsberg 100-m radio telescope of a sample of more than 500 AGN have been performed in order to search for sources with high RM. The two principal characteristics of Pa16 sources are (1) their lack of sufficient polarized flux density at 1.4 GHz in the NVSS (i.e., blanked polarized images and low polarization flux density detection) with 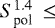 0.87 mJy, which represents the 3
0.87 mJy, which represents the 3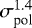 (the rms fluctuation level
(the rms fluctuation level 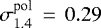 mJy/beam, for the NVSS survey, Condon et al. 1998) and (2) their compactness at arcsec scale; they are unresolved in the FIRST catalog (5′′ FWHM, White et al. 1997) after subsequent cross correlation with the NVSS catalog. The first characteristic was important for the previous project because of its possible relation with strong depolarization (with p ≤ 0.3 × 10−2) due to high RM. The second characteristic allowed us to select possibly compact/or high-redshift candidates and avoid extended structure sources that might be affected by beam depolarization (cancellation of the polarized vectors within the telescope beam) at the NVSS and FIRST resolution. High-frequency (10 GHz) single-dish observations of the initial big sample of more than 500 AGN resulted in a list of 30 targets with detectable polarization. Subsequent follow-up single-dish observations (from 1 to 10 GHz) have been performed in order to study the total intensity and polarized spectra. Pa16 found that almost half of the sample have high RM values with RM dish ≥ 500 rad m−2. Moreover, they noticed the first signs of complexity of the polarization information (i.e., fractional polarization and polarization angle) and deviations from the standard linear-λ2 behavior expected for simple RM structure.
mJy/beam, for the NVSS survey, Condon et al. 1998) and (2) their compactness at arcsec scale; they are unresolved in the FIRST catalog (5′′ FWHM, White et al. 1997) after subsequent cross correlation with the NVSS catalog. The first characteristic was important for the previous project because of its possible relation with strong depolarization (with p ≤ 0.3 × 10−2) due to high RM. The second characteristic allowed us to select possibly compact/or high-redshift candidates and avoid extended structure sources that might be affected by beam depolarization (cancellation of the polarized vectors within the telescope beam) at the NVSS and FIRST resolution. High-frequency (10 GHz) single-dish observations of the initial big sample of more than 500 AGN resulted in a list of 30 targets with detectable polarization. Subsequent follow-up single-dish observations (from 1 to 10 GHz) have been performed in order to study the total intensity and polarized spectra. Pa16 found that almost half of the sample have high RM values with RM dish ≥ 500 rad m−2. Moreover, they noticed the first signs of complexity of the polarization information (i.e., fractional polarization and polarization angle) and deviations from the standard linear-λ2 behavior expected for simple RM structure.
Here we present a study of this polarization complexity, performing high-sensitivity broadband JVLA observations on 14 sources, all Quasar (QSO) type, with RM dish ≥ 500 rad m−2 (see Table 1 for the complete list of the sources). We note that the source 0239–0234 show a RM dish value that is lower than 500 rad m−2. However, we decided to include this source to test if the broadband spectropolarimetry technique could reveal Faraday components with higher RM values previously hidden due to lack of data coverage. According to our previous single-dish work and based on the characteristics of the new JVLA observations, the sources have the following selection criteria:
-
Galactic latitude l > 30°: in order to avoid the contribution of the galactic plane.
-
Flux density at 1.4 GHz in the NVSS, S1.4 > 300 mJy.
-
Unpolarized at 1.4 GHz in the NVSS (
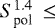 0.87 mJy or blank polarized images).
0.87 mJy or blank polarized images). -
RMdish ≥ 500 rad m−2.
-
Unresolved in the FIRST catalog and at all the JVLA configurations used (reaching a resolution of 0.6′′ at X band forthe B configuration).
This source selection resulted in a sample of 14 unresolved sources (see Table 1). We observed this sample at L, C, and X bands with the JVLA with the objective to study their total intensity spectra and their magneto-ionic media. Considering the highest angular resolution reached with these JVLA observations (0.6′′ at X band for the B configuration) and the redshift of the sources, we can give an upper limit on their linear sizes. Our observations are sensitive to regions smaller than ~5 kpc (see Linear Resolution – Lin. Res. – in Table 1). Therefore, the sample is composed of much more compact sources than those polarized at 1.4 GHz selected by OS17, for which the median linear size is of the order of ~100 kpc.
List of the high-RM sources.
3 Observations and data reduction
We observed our sample of 14 sources with the JVLA in full polarization mode. Observational details are summarized in Tables 2 and 3. Observations were made in different epochs during semesters 2013B (project code: 13B-236), 2014B, and 2015A (project code: 14B-184), and used different configurations of the JVLA (see Table 2). Different observational setups were used for C and X bands (2 GHz bandwidth in 13B-236, and 4 GHz bandwidth in 14B-184; see Table 2). For L band a bandwidth of 1 GHz was used.
The sources in our sample are cataloged as phase calibrators in the VLA calibrator manual. This means that all of them are bright and their emission is dominated by a point-like component. Therefore, for the phase calibration of the sources in our sample, we initially self-calibrated them by assuming a point-like model. After calibration, we checked for the possible presence of diffuse extended emission in high-sensitivity tapered images (using the full 4 GHz bandwidth and weighting the visibilities giving more weightto short baselines). We did not detect any evidence of an additional extended emission component in any of the sources, confirming that their emission is dominated by only a point-like component at the sensitivity and resolutions of our observations. Therefore, additional phase calibration on the sample sources was not necessary. On-source times were fixed around 1 min per source/band. This integration time was enough to obtain signal-to-noise ratios (S/Ns) larger than approximately 30 for the total intensity at all the observed frequencies, with 80% of the data points having S∕N ≈ 3500 (see Fig. 1 red histogram) and to have S/Ns larger than ≈3 for the polarized intensity, with 80% of the data points having S∕N ≈ 100 (see Fig. 1 green histogram). In each session, we included observations of a standard flux/polarization angle calibrator, as well as a leakage calibrator (see Table 3).
Data editing and calibration were done using the data-reduction package CASA (Common Astronomy Software Applications2; version 4.4.0) following standard JVLA procedures. We wrote scripts in order to perform calibration in a quasi-automatic way. Our calibration scripts use prior known corrections of the data provided by the NRAO (antenna positions, antenna gain curves, atmosphere opacity corrections, and requantizer gains). Subsequently, CASA performs bandpass and delay calibrations (using the flux calibrator of each run), and complex gain calibration (by self-calibrating each source) and polarization calibration. The procedure checks the calibrated data, makes additional flags when necessary after a visual inspection, and re-runs the calibration scripts.
For the flux calibration of the Stokes I, we used resolved models of the flux calibrators provided by the NRAO. Total flux density at each frequency is set by using their known spectrum (Perley & Butler 2013a). The polarization angle was calibrated using known polarization parameters of the flux calibrators3C286, 3C138, and 3C48. However, there are not yet models of the fractional polarization and the polarization angle at different frequencies for these calibrators. Therefore, in order to calibrate the linear polarization for our wide band observations, we used the known values of the fractional polarization (p) and polarization angle (χ) at different frequencies reported by Perley & Butler (2013b) and performed, within the 1–50 GHz frequency range, the following polynomial functions to the data:

where νc is the central frequency of the fitted frequency ranges. The results of these fittings are shown in Fig. 3 and the coefficients used for the fitting are listed in Table 4. For the calibrator 3C286 we performed a single model for the entire frequency range (1–50 GHz) while, for 3C138 and 3C48, because of the more complicated behavior of the polarized parameters, we divided their spectra into several frequency ranges; see Table 4. We therefore set the model for each spectral window (spw, 128 MHz bandwidth) using the standard “setjy” CASA task. For each spw we calculated the values of Stokes I (using the fit performed by Perley & Butler 2013a), the fractional polarization (p), and the polarization angle (χ) (using our fitting models) at the borders (I0, I1 , p0 , p1 and χ0 , χ1) and at the center (Ic, pc and χc) of each spw. We then assigned to each of the spws the central value of the Stokes Ic , pc and χc . We finally let them varying linearly with frequency within each spw.
We obtained solutions for the polarization angle and the D-terms, the instrumental polarization, for each channel. For the polarization angle calibration we constrained the solutions to short baselines (following the suggestions given by NRAO) in order to avoid effects due to possible extended structure emission of the polarization angle calibrators. To correct for the D-terms, we corrected using an unpolarized calibrator for each observational session.
From the calibrated data, wide band images of Stokes I were made for all the targets at L, C, and X bands. We ran the CLEAN task using the parameter nterms = 2 (that takes into account the spectral index of the source) and different weight values of the robust parameter (Briggs 1995). All the sources appear unresolved at the highest angular resolution of 0.6′′ , as assumed in the calibration. Images of Stokes parameters I, Q, and U were also made for each 64 MHz spw at L band and for each 128 MHz spw for C and X bands (using nterms = 1 in the task CLEAN). On the individual I, Q, and U spectral window images we perform a Gaussian fit to the source, considering a circular region with a diameter two times the deconvolved beam size of the image. In this way, information on the Stokes parameters for each 64 MHz sub-band and for each 128 MHz sub-band have been collected in order to study the total intensity spectra (at L, C, and X bands) and the polarized spectra (at C and X bands) of the sources in our sample.
The depolarization effects due to in-band depolarization have been estimated, that is, the depolarization due to the rotation of the polarization angle within a considered bandwidth due to high RM. We estimated the in-band depolarization effect considering the lowest frequency for each observed band (i.e., 1 GHz for L band, 4 GHz for C band and 8 GHz for X band) and their respective spw bandwidths (64 MHz for L band and 128 MHz for C and X bands) (see Fig. 2(a) and its zoom to low percentage (b)). Considering the lowest frequency at L band (i.e., 1 GHz), the in-band depolarization reaches values > 80% for a RM value of ~1000 rad m−2 , however in-band depolarization of ~50% can be reached already for a RM value of ~200 rad m−2. For the lowest frequency at C band (i.e., 4 GHz), we estimated an in-band depolarization of ~2% for RM of 1000 rad m−2, while for the same RM value, the in-band depolarization at the lowest frequency at X band (i.e., 8 GHz) is of the order of ~0.03%. With these calculations we want to show that the polarization information extracted at C and X band are not affected by observational effects such as the bandwidth of these receivers; therefore in-band depolarization is negligible at these bands and they are the best bands to perform a modeling of the polarization behavior. In contrast, at L band, even with low RM values of 200 rad m−2, we expect large in-band depolarization for a 64 MHz bandwidth. In order to relate the large RMs and the in-band depolarization at L band, one would extract polarization information within shorter bandwidths (i.e., BW < 64 MHz), but with an increase of the rms noise. We explored this in our sample and made total intensity and polarization intensity L band images considering smaller bandwidths of 30 MHz and 15 MHz. At the sensitivity we got at L band, we could detect polarized signal for four sources: 0239–0234, 0243–0550, 1246–0730 and 1405+0415; the overall total intensity and polarized behavior is shown in Fig. 9. For the last three sources (0243–0550, 1246–0730, and 1405+0415) we had enough data points to perform a depolarization modeling analysis at L band, after excluding a possible depolarization modeling considering the three bands together (see Sect. 6.3 for more details). Nevertheless, as mentioned, a proper polarization modeling could also be properly performed using the C and X bands.
General information of the projects.
Log file of the projects.
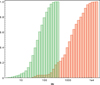 |
Fig. 1 Cumulative plot of the S/N distribution of the total intensity (red) and the polarized intensity (green) data points considering all the observed frequencies. |
4 Faraday screen and depolarization models
When synchrotron radiation passes through a magneto-ionic medium such as a Faraday screen, changes in the direction of its polarization angle, that is, Faraday rotation (FR), and a reduction of its polarization flux density (depolarization) can occur. When depolarization occurs, we can divide this effect into two main categories: external depolarization and internal depolarization (see Table 5 and Fig. 5 for a schematic and visual explanation of the depolarization equations). Several authors have described these two possible scenarios considering the presence in the following two depolarization families: a (1) uniform and a (2) uniform and turbulent magnetic field (for more details on the different depolarization equations see: Burn 1966; Tribble 1991; Sokoloff et al. 1998; Rossetti et al. 2008). To study the depolarization mechanism we use the complex representation of the polarized signal in the presence of a FR that does not depolarize (see Fig. 4; Burn 1966):
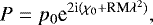 (8)
(8)
where p0 and χ0 are the intrinsic fractional polarization and the intrinsic polarization angle, respectively. This equation describes a constant behavior of p with λ2 and a linear behavior of χ with λ2 . To this equation we add the depolarization contributions.
When the synchrotron radiation is passing through a magneto-ionic medium that now contains a turbulent magnetic field, the depolarization is called external faraday dispersion/beam depolarization (EFD/Bd) and it is represented by the equation
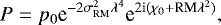 (9)
(9)
where σRM is the Faraday dispersion of the random field within the volume traced by the telescope beam (Farnsworth et al. 2011) and RM is the mean RM across the source on the sky. In this scenario, the depolarization occurs because of the presence of random magnetic cells or, in the case of regular magnetic field, because of the variation in the strength or direction of the field, both cases within the telescope beam.
The synchrotron-emitting regions and the Faraday rotating regions may also be mixed together. In this case the depolarization is internal. The main equations that describe this depolarization scenario are: (1) internal faraday dispersion (IFD) and the (2) differential faraday rotation (DFR; Gardner & Davies 1966) with its extension to the case of a RM gradient (Berkhuijsen & Beck 1990; Sokoloff et al. 1998). In these equations, the contribution from a single foreground magneto-ionic material (Eq. (8)) is also present.
In the case in which the synchrotron-emitting, Faraday-rotating region contains a turbulent and regular magnetic field together, that is, the IFD, the degree of polarization is then given by
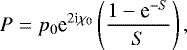 (10)
(10)
where 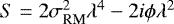 . In this case, the depolarization occurs because of the combination of both the presence of a regular magnetic field and the turbulent magnetic field. In this scenario, a random walk of the plane of polarization through the region occurs. In this equation σRM is the internal Faraday dispersion of the random field and ϕ is the Faraday depth through the region.
. In this case, the depolarization occurs because of the combination of both the presence of a regular magnetic field and the turbulent magnetic field. In this scenario, a random walk of the plane of polarization through the region occurs. In this equation σRM is the internal Faraday dispersion of the random field and ϕ is the Faraday depth through the region.
When σRM = 0 (i.e., no turbulent magnetic field component), the emitting and rotating regions are only co-spatial in the presence of a regular magnetic field, that is, the DFR. The complex degree of polarization is given by
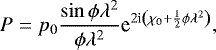 (11)
(11)
where ϕ is the Faraday depth through the region. In this case the radiation coming from the most distant part of the region (with respect the observer) undergoes a different amount of Faraday rotation with respect to the radiation coming from the nearest part of that region.
The case of a gradient in RM across the beam, discussed in the work by Berkhuijsen & Beck (1990) and studied in detail in Sokoloff et al. (1998), is of great interest. This special case of DFR occurs when the RM varies systematically across the beam, and therefore its magnetic field could be considered uniform. The RM gradient can originate in the synchrotron source and/or in a foreground screen but local to the radio emitting region. Following the detailed description in Sokoloff et al. (1998), the internal depolarization due to a smooth change in the RM across the beam (considering a flat beam profile) is given by
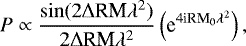 (12)
(12)
where ΔRM is the variation in RM across the beam and RM0 is the initial value of RM within the region. If the gradient of RM originates in a foreground Faraday screen, for example, for radio lobes embedded in a intra-cluster medium, the new equation is similar to Eq. (12) but with the addition of the random field effect, σRM. Therefore, we get (for a flat beam profile)
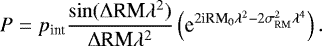 (13)
(13)
However, to describe the more realistic case of a Gaussian beam profile, the Δ RM has to be divided by a factor of 1.35 (Sokoloff et al. 1998).
Our JVLA observations revealed complex behavior both in the total intensity radio spectra and in polarization (see Sect. 6). In fact, the radio spectra were fitted with multiple synchrotron components. We therefore might expect a complex behavior also in the polarization information with the presence of multiple interfering RM components. To investigate this, we fitted the wide-band Stokes Q∕I (q) and U∕I (u) spectra following the procedure proposed by Farnsworth et al. (2011); O’Sullivan et al. (2012). The above equations cannot completely explain the complex scenarios revealed by our data. The scenario that seems to better represent them is when multiple emitting and/or rotating components exist and they are unresolved within the telescope beam. We proceed by simultaneously fitting both q(λ2) and u(λ2) using, first, the simplest equation of a one-component RM model (Eq. (8)); it cannot describe any of the polarized behavior of the fractional polarization and polarization angle. Therefore, we tried using one component of the depolarization equations listed above. This approach did not give us good results, and therefore we finally tried multiple-component RM models. Multiple component models are simply constructed as P = P1 + P2 + ⋯ + PN (O’Sullivan et al. 2012).
The model fitting used in this study (presented in Sect. 5) attempts to describe the data using the simplest possible parameterization of Faraday depolarization from uniform and random fields (Eq. (14)). We implicitly assume that the polarized emission comes from optically thin regions with similar spectral index values.
Coefficients used for the polynomial fits for the calibrators 3C286, 3C138, and 3C48.
 |
Fig. 2 In-band depolarization at all the frequency bands – a): L band (red), C band (green) and X band (blue); and b) a zoom to only 5% in-band depolarization for the three bands. |
Summary of the depolarization equations.
5 Fittingthe depolarization models and extracting the polarization parameters
Assuming that all the emission components have the same spectral index, the depolarization models (described in Sect. 4) can be broadly represented by the following complex polarization equation,
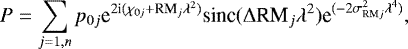 (14)
(14)
where j represents the several Faraday components used for the fitting, p0j is the intrinsic fractional polarization,χ0j is the intrinsic polarization angle, and ΔRMj and σRMj describe the variation of the RM in a regular and turbulent magnetic field, respectively. This is the only equation that we used to fit our data. We need to clarify that Eq. (10) is not exactly represented by Eq. (14). In fact, the depolarization behavior relatively closely matched but the polarization angle behavior often does not. Nevertheless, Eq. (14) is an attempt to simplify the process of fitting many different models.
We limit the number of the Faraday components to three therefore, P = P1 + P2 + P3. For all our sources, first we fit a “Faraday thin”, where no contribution of Δ RM and σRM are present, and then we fit the Eq. (14) with the contribution of Δ RM only, and then with σRM only, and finally with ΔRM and σRM together. This approach results in a total of twelve equations used for the qu-fitting. Reduced χ2 , standard deviation σ2, the Bayesian information criterion (BIC) and the Akaike information criterion (AIC) were performed in order to evaluate the quality of the fit. Visual inspection and the combination of the lowest values of all the statistics methods used help us to choose which equation, therefore which depolarization scenario, well represents the collected polarized data. In order to compare the several polarization properties (RM, ΔRM and σRM) for each source, we weighted the respective values to the number of components j. Therefore, we defined the polarization-weighted RM dispersion as:
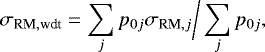 (15)
(15)
and the polarization-weighted RM gradient:
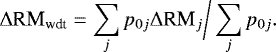 (16)
(16)
We corrected the measured RM for the Galactic foreground RM contribution (GRM) using the galactic RM map performed by Oppermann et al. (2015). Even though our sources are unpolarized, the Oppermann et al. (2015) galactic RM map allowed us to estimate the GRM. We obtained the residual rotation measure (RRM) subtracting the polarization-weighted RM (RMwtd) and the GRM correspondent at the position of the source (i.e., RRM = RMwtd − GRM). The RMwtd is calculated as
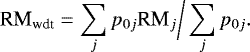 (17)
(17)
 |
Fig. 3 Modeling of the polarization parameters for the calibrators, 3C48, 3C138, and 3C286. Frequency coverage: from 1 to 50 GHz. For each of the sources, upper panel: the polarized flux density (black line) and the Stokes parameters, Q (blue line) and U (red line); middle panel: the polarization angle variation; and last panel: the polarization degree in percentage variation. The dashed vertical lines mark the frequency ranges used for the modeling. |
 |
Fig. 4 FR sketch. The radiation (red arrow) coming from a synchrotron-emitting region (yellow circle with nonthermal electrons) passes through a magneto-ionic region (blue cloud with thermal electrons) with regular magnetic field (black arrows) thatrotates the polarized vector of the radiation (blue arrow). In this scenario the fractional polarization remains constant. |
 |
Fig. 5 Depolarization mechanisms. The red undulated arrows represent the synchrotron radiation and the blue arrows represent the polarization vector of the radiation; the length of this vector decreases when depolarization occurs. The black arrows represent the magnetic field direction and its intensity is represented by the thickness of the arrows. The pictures (a), (b), and (c) represent the cases of internal depolarization where the synchrotron-emitting regions and the Faraday rotating regions coexist together (dark yellow with thermal, et , and nonthermal, eno-t, electrons). Picture (a) represents the DFR (Eq. (11)) where a regular magnetic field is present, picture (b) represents the IFD (Eq. (10)) where a turbulent and a regular magnetic field is present, and picture (c) represents the depolarization due to an internal gradient of RM (Δ RM int, Eq. (12)); the magnetic field is uniform and throughout the region the radiation undergoes both fractional polarization and polarization angle smooth changes. Picture (d) represents the case of external depolarization where the synchrotron-emitting region (yellow circle containing eno-t) and the Faraday rotating region (blue cloud containing et) are separated (Eq. (9)). Here the depolarization is due to the presence of a turbulent magnetic field or to the polarized vectors canceling each other out within the telescope beam (beam depolarization, Bd). Picture (e) represents the depolarization due to a gradient of RM due to the presence of a foreground region (Eq. (13)). |
6 Results
6.1 Radio spectrum
The radio spectra (Figs. 6 and 7) were made using our JVLA data at L, C, and X bands, as well as data at lower frequencies reported in several surveys, that is, the VLSS at 74 MHz (Cohen et al. 2007), the 7C at 151 MHz (Hales et al. 2007), the WENSS at 325 MHz (Rengelink et al. 1997) and the TEXAS at 365 MHz (Douglas et al. 1996). We also added recent low-frequency data from the new broadband total intensity GLEAM survey (Hurley-Walker et al. 2017). The sources in our sample have previously been observed with the Effelsberg 100-m single dish telescope at several frequencies (from 2 to 10 GHz). The radio single-dish spectra fitting has been reported in Pa16. In the previous work we fitted the data using apower law (representing pure optically thin synchrotron emission), one to three synchrotron self-absorption components, and a combination of power-law models and synchrotron self-absorption components (see previous paper for more details Pa16). These new broadband data were fitted following a similar approach where the total intensity spectra are a composition of multiple synchrotron-emitting volumes, considering homogeneous, self-absorbed sources with power-law electron energy distributions with spectral index in the optically thick and thin parts of the spectrum αthick = 2.5 and αthin = −0.7, respectively. Because of the better-sampled data at our disposal, we were forced to use more synchrotron-emitting components to fit the total intensity data. Indeed, to well represent the radio spectra we used mainly a combination of synchrotron self-absorption components (using a maximum of 5 synchrotron components) and a combination of a single synchrotron self-absorption component with a synchrotron component with a break (symptomatic of ageing of the radio source). The equations used for the radio spectra fitting are the following:
-
A combination of several synchrotron self-absorption components (
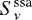 ):
):
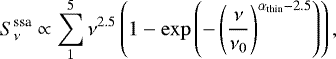 (18)
(18)
where ν0 is the frequency where the emission changes from optically thick, with a spectral index of 2.5, to optically thin with a spectral index αthin = −0.7;
-
a single synchrotron component with a break at frequency νb (
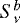 ):
):
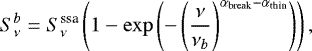 (19)
(19)
where αthin is the spectral index at frequencies lower than νb and αbreak is the spectral index after the frequency break;
-
and a combination of a synchrotron self-absorption component with a synchrotron component with a break at frequency νb (
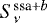 ),
),
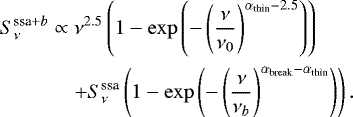 (20)
(20)
Although we used more synchrotron components with respect to the previous single dish radio spectra fitting, these results are consistent with those of the previous single dish observation campaign. Moreover, comparing the single dish and the interferometer fluxes, they are consistent. Therefore, no significant variability was detected within the two observational sessions (time between the two sessions was roughly 2 yr). We note that this modeling is not unique, there are other possibilities to model the data; for example, considering a thermal electron contribution with αthick = 2.0. In practice, this is not too different from a 2.5 slope; the data at our disposal cannot help us to discern which are the best total intensity components. Moreover, adding other, different kinds of total intensity components in the radio SED analysis would overly complicate the overall interpretation. The procedure we decided to follow is a simple one that gives us an idea of the complexity of the sources.
 |
Fig. 6 Radio spectra using L, C and X bands and literature. Total flux density is expressed in [mJy] and the frequency in [GHz]. Blue points are the JVLA and literature data and the green points are upper limits. Orange lines are the individual synchrotron componentsused for the radio spectra fit and the red line is their sum. The gray vertical dashed lines indicate the L to C band range and the C to X band range. |
 |
Fig. 7 Radio spectra using L, C, and X bands and literature. Total flux density is expressed in [mJy] and the frequency in [GHz]. Blue points are the JVLA and literature data and green points are upper limits. Orange lines are the individual synchrotron componentsused for the radio spectra fit and the red line is their sum. The gray vertical dashed lines indicate the L to C band range and C to X band range. |
 |
Fig. 8 Polarization information of the sources at C and X bands. For each plot, first upper panel: the total intensity S expressed in [mJy] (the black line simply connects the points), second panel: the polarized flux density Spol expressed in [mJy], the Stokes parameters Q (magenta dots) and U (green dots) expressed in [mJy] (the black, the magenta, and the green lines simply connect the points); the third middle panel reports the fractional polarization; the last bottom panel shows the polarization angle χ expressed in [deg]. All this information is represented in the λ2 domain. Thevertical dashed lines indicate the C to X band range. |
6.2 Polarization information
In Fig. 8 we show the observed polarization quantities (the Stokes Q and U together with the polarized flux density Spol, the fractional polarization fp and the polarization angle χ) together with the total intensity data points for each source at C and X bands. In Fig. 9 we show the same information but for those sources for which we also have polarization detection at L band (0239−0234, 0243−0550, 1246−0730 and 1405+0415). Previous single-dish data revealed the first signs of the complexity of the medium with a deviation from the linear fit in the determination of the RM value (Pa16). Now, with these new broadband data, the polarized signal clearly shows a complicated behavior, with the fractional polarization and the polarization angle changing in a non-trivial manner. Our JVLA observations confirmed the previous results from the Effelsberg campaign (Pa16), that is, for most of the sources the behavior of the polarization angle deviates significantly from a simple linear trend with λ2 . Thus, we cannot assign a single RM for these sources in the 4–12 GHz range (for the ten sources having C and X bands polarization data points) and in the 1–12 GHz range (for the four sources which also have polarized data points at L band). The polarization behavior for all the targets requires the presence of multiple synchrotron emission and Faraday rotation media.
This statement is reinforced after the qu-fitting (see Sect. 5 for more details) of the polarization data. The results of the qu-fitting are reportedin Figs. A.1–A.10 and in Figs. B.1–B.7. The plots show the behavior of the fractional Stokes parameters q and u, the fractional polarization p, the polarization angle χ versus λ2 , and the behavior of q versus u. The parameters that result from the depolarization modeling and their statistics for each of the targets are reportedin Tables 6 and 7. The depolarization modeling reveals the presence of several Faraday components (more than two) to explain the complexity of the polarized signal. Since all sources have C and X band polarization data available, we focused on the analysis and discussion of that frequency range, that is, 4–12GHz. In order to analyze the polarization properties for all sources, that is, RM, Δ RM and σRM for each source, we weighted the respective values to the number of the Faraday rotating components, as explained in Sect. 5. The discussion of these parameters is reported in Sect. 8. The RM wtd, the subsequent determined RRM, the σRM,wtd, and the ΔRMwtd values are reported in Table 8. The correction of the RRM in the rest frame of the targets is also reported in Table 8. Overall, these parameters intrinsically reveal, once again, the complexity of the medium surrounding the sources. Indeed the values are considerably large, suggesting a highly magnetized and dense medium in the vicinity of the central engine. The source 1616+0459 shows the highest RRM value; in the rest frame it assumes a value of RM rf ≈ 2.3 × 104 rad m−2.
 |
Fig. 8 continued. |
6.3 Depolarization modeling at L band
As mentioned above, we detected polarization at L band for four sources (0239–0234, 0243–0550, 1246–0730 and 1405+0415) by splitting each available spectral window (each with bandwidth of 64 MHz) into smaller bandwidth (BW): 30 MHz and 15 MHz. For approximately the first half of the L band (from 1 to ~1.5 GHz) we did not detect polarization for all the four sources (in Fig. 9 we omit the first half of L band in order to save space in the plots).
For sources 0239–0234 and 0243–0550, we obtained two and six data points, respectively, when splitting thespw into BW of 30 MHz and no data points when using the 15 MHz BW (because of the poor sensitivity obtained at these smaller bandwidths). These two sources have low polarized flux density at L band (both around 3 mJy). For sources 1246–0730 and 1405+0415, we obtained 14 and 12 data points, respectively, when using the 30 MHz BW, and 24 and 22 data points when using the 15 MHz BW. Because fluxes were consistent and the lower S/N in the 15 MHz BW images, we decided to analyze the data of the 30 MHz BW only. Figure 9 shows the polarization together with the total intensity for the four sources for which L band data have also been obtained when splitting the spw into BW of 30 MHz.
Depolarization modeling considering the three bands (L, C, and X bands) has been performed for these targets. However, for none of them could we find any good model that could represent the polarization behavior in the whole wide band. Indeed, the L-band data seem to behave very differently with respect to data from the C–X band. Figure 10 shows depolarization modeling for C–X bands (blue points) with the L-band data points (red points) over plotted. The low-frequency data do not follow the depolarization described using the high-frequency data. Therefore, we performed depolarization modeling considering C–X bands and L band separately. The source 0239–0234 was not considered for L-band depolarization modeling because it only has two data points at low frequency. Figures B.1–B.7 show the depolarization modeling for each of the targets considering C and X bands together and L band only (for the source 0239–0234, depolarization modeling is only available for C–X bands). The parameters resulting from the fitting are reported in Table 7.
 |
Fig. 9 Polarization information of the sources at L, C, and X bands. |
7 Comments on the individual sources
Here we comment on the observational and modeling results in the context of the AGN environment. We consider and combine all the wide-band observational results: the radio spectrum, the polarization information, and the depolarization modeling results. We also used the MOJAVE catalog (Lister et al. 2009) with milliarcsecond imaging in order to investigate, if possible, the source morphologies and resolved polarization information. When available, other information from the NED database and the literature is reported within the text.
Source 0239–0234. We fit this spectrum with four synchrotron components, with the oldest component peaking at a few MHz, and the other three peaking at ~1 GHz, ~4 GHz, and ~10 GHz (see Fig. 6). The polarization percentage decreases from 6% at X band to 3% at C band, dropping down to ~1% at L band. The source shows a deviation from a linear χ(λ2) relation in the determination of the RM value within the whole frequency range (C, X, and L bands; see Fig. 9). The broadband depolarization model fits the data very well within the C and X bands frequency range finding two Faraday components with random magnetic fields (see Fig. B.1 and Table 7), with the first Faraday component having a more turbulent magnetic field (σRM1CX of about 500 rad m−2) than the second.
These results suggest the presence of at least two emission components at high frequency that emit synchrotron and Faraday-rotate at the same time in the presence of turbulent magnetic field. Therefore, the two synchrotron components that are dominating the radio spectrum at C and X bands could be those that Faraday-depolarize at that range of frequency. In the previous single-dish study, Pa16 measured a RM lower than 500 rad m−2 for this source; in this new work we decided to include this source in order to test whether or not the broadband spectropolarimetry could reveal Faraday structures. Indeed, the Stokes qu-fitting reveals a much more complex polarized structure.
Source 0243–0550. The SED of this source was fit with four synchrotron components: one peaking at a low frequency (<74 MHz) and the other three peaking at higher frequencies (~1 GHz, ~3 GHz and ~10 GHz; see Fig. 6). Overall, the radio spectrum at high frequency is flat. The fractional polarization increases from X to C bands but it drops at L band (Fig. 9). This suggests some repolarization mechanism in the X and C band frequency range. Physical repolarization can be explained with an increase of the ordering of the magnetic field (Sokoloff et al. 1998), by partial coverage of the emission by a rotating and depolarizing layer (Mantovani et al. 2009), and/or through a helical magnetic field with a tangled component (Homan et al. 2002).
We fit the C–X bands global trend of the fractional polarization with two Faraday components with random magnetic fields (see Fig. B.2 and Table 7). Our modeling suggests one component with RM 1CX ≃ 610 rad m−2 and with a regular magnetic field, and a second component with RM 2CX ≃ 1630 rad m−2 with a more disordered magnetic field (σRM2CX ≃ 520 rad m−2). This suggests an ordering of the magnetic field in the environment towards lower frequency that seems to be consistent with the observed repolarization (Fig. 9). The repolarization visible in the fractional polarization versus λ2 panel could also be due to ordering of the magnetic field within the source. However, we cannot be sure, since the emission region is unresolved. We can also notice in the polarization plot (Fig. 9) and in the depolarization modeling plot (Fig. B.2) that the data points (the q and u values, p and χ) at short wavelength, exhibit a sharp turnover in a very small λ2 interval. This could be an indication of the presence of another Faraday component closer to the central region than those already fitted by the model.
The model predicts the source to show polarized signal at 1.4 GHz (with a fractional polarization of ~2%) but in fact it does not. Further depolarization occurs at longer wavelengths. Indeed, the polarization data available at L band were modeled with two simple Faraday components with two high RM values (see Fig. B.3 and Table 7). The low-frequency data were not in agreement with the depolarization modeling performed at C–X bands, suggesting no connection between the X–C band and L band data points. We had to treat the two intervals separately. This suggests that the Faraday components revealed by the Stokes qu-fitting are mapping different regions of the targets: structures close to the central engine at C and X bands and regions more distant from the central engine at L band.
Source 0751+2716. This source was fitted with a synchrotron component with a break (see Fig. 6). The spectrum is characteristic of a gigahertz peaked spectrum (GPS) source (it has been classified as a peaked-spectrum source at low-frequency, Callingham et al. 2017). This kind of source is believed to be an AGN in an early phase of evolution, which is very compact (~10–1000 pc) and has high radio luminosity (Lradio ~ 1045 erg s−1, O’Dea et al. 1991). The fractional polarization decreases from 15% to a few percent from X band to C band (Fig. 8). The RM at X band is relatively high (≃500 rad m−2), and at C band there seems to be no rotation of the polarization angle, except for a narrow frequency range in which a dramatic change of the polarization angle occurs and the fractional polarization reaches a minimum (see Fig. 8).
The depolarization modeling suggests that there are at least three different rotating components with random magnetic field intervening the synchrotron radiation (see Fig. A.1 and Table 6).
Source 0845+0439. The radio SED of this source was fit by four synchrotron components peaking at ~100 MHz, ~1 GHz, ~4 GHz and ~10 GHz (see Fig. 6). However, the spectrum is also consistent with a flat spectrum across the whole frequency range. The fractional polarization follows a sinusoidal-like behavior and its polarization angle clearly does not follow a linear χ(λ2) relation (see Fig. 8).
The depolarization model fit reveals the presence of two synchrotron-emitting and Faraday-rotating regions (Fig. A.2 and Table 6). We obtain two moderate RM dispersions, σRM (σRM1 ≃ 150 rad m−2 and σRM2 ≃ 230 rad m−2) components with two high values of RM (RM1 ≃ 790 rad m−2 and RM 2 ≃ 1600 rad m−2; see Table 6). In this case, it is possible that the two synchrotron components that contribute to the radio spectrum at high frequency are also those responsible for the Faraday depolarization.
Source 0958+3224. The spectrum of this source, also known as 3C232, was fit by three synchrotron components: the first peaking at low frequency (~100 MHz) and the other two at ~300 MHz and ~10 GHz respectively (see Fig. 6). The fractional polarization follows a sinusoid-like behavior (see Fig. 8).
The polarization properties are well described by three Faraday components with three Faraday RM gradients (Fig. A.3) with regular magnetic fields. The values of the RMs are very high (RM1 ≃ 3900 rad m−2, RM 2 ≃ 640 rad m−2, and RM 3 ≃ 1160 rad m−2, Table 6) with very high RM gradients (Δ RM1 ≃ 370 rad m−2, Δ RM2 ≃ 810 rad m−2, Δ RM3 ≃ 850 rad m−2, respectively) suggesting a very dense magnetized media. These RM gradients could be similar to those found through high-resolution imaging of AGN jets (e.g., O’Sullivan & Gabuzda 2009).
Véron-Cetty & Véron (2006) classify this object as Seyfert 1.8 (Sy 1.8). This optical classification is due to reddening by an obscuring torus or to low ionization of the medium. In the first case, the jet orientation is most likely in the plane of the sky. The kpc scale observations, from low to high frequency (data from literature and the L, C and X band JVLA data)are tracing different dominant emission regions. Low-frequency data from the literature and from our new broadband, L band JVLA data, are most likely dominated by extended, more diffuse emission from the radio galaxy, that is, the radio emission from the lobes. The high-frequency JVLA data, still unresolved at our kpc scale, should be dominated by the central core. This could explain the steep radio spectral shape at low frequency and its flattening towards high frequency. The source, then, could have a large viewing angle with respect to the observer and show different radio emission components on different scales.
Altogether this information suggests that the radio emission at high frequency comes from the central region of the galaxy and contains at least three Faraday screens with regular magnetic field that smoothly depolarize at C and X bands.
Source 1048+0141. The radio spectrum of this object was fit by two synchrotron components peaking at ~100 MHz and ~1 GHz respectively (see Fig. 6). The fractional polarization decreases following a sinc-like trend and reaches a roughly constant value of 1% across C band. The polarization angle increases at X band and reaches an approximately constant value at C band (see Fig. 8).
The polarization properties are well fitted by two Faraday components with turbulent magnetic fields (Fig. A.4) with a low RM1 (≃ −20 rad m−2) due to the constant value of the Stokes parameters at C band, and a very high RM2 (≃5100 rad m−2). We note in Table 6 that the σRM1 has a large error; this means that the first Faraday component with random magnetic field is, in principle, not necessary. At long wavelengths the q and u values do not cross each other, resulting in a constant fractional polarization and polarization angle with a low value of RM, suggesting a less dense magnetized medium. However, the model predicts constant polarization of the source at 1.4 GHz; but it is not the case. Therefore, further depolarization occurs at longer wavelengths. At short wavelength, the parameters cross very frequently. Moreover, the dashed and the straight lines of the qu-fitting versus λ2 show that at higher frequencies the q and u continue crossing each other, resulting in a possible increase of the RM value towards higher frequency.
Source 1146+5356. This source was fit by four synchrotron components: one at ~200 MHz and the other three at higher frequencies (~2 GHz, ~4 GHz, and ~10 GHz, respectively; see Fig. 6). Overall the radio spectrum could also be considered flat, consistent with a small viewing angle source. The polarized properties seem to follow a simple behavior with the fractional polarization decreasing exponentially with wavelength and the polarization angle following a linear χ(λ2) relation (see Fig. 8).
The depolarization model fit requires two Faraday components characterized by turbulent magnetic fields (Fig. A.5 and Table 6). Both the RM values are around −500 rad m−2, but with two different values of the RM dispersion (σRM1 of 100 rad m−2 and σRM2 of 630 rad m−2; see Table 6). This suggests that the magnetic field is more ordered within the first Faraday screen compared to the second Faraday screen that is more dominated by random magnetic fields.
Source 1246-0730. This source was fit by a synchrotron component at low frequency (peaking at frequencies smaller than 100 MHz) and three components peaking at ~500 MHz, ~3 GHz, and ~10 GHz, respectively (see Fig. 6). The spectrum looks flat at higher frequency. The fractional polarization decreases until roughly 6 GHz and then it increases, or repolarizes (Fig. 9). The polarization angle follows roughly a linear χ(λ2) relation among C and X bands but it stays constant at L band.
The polarization properties in the C–X bands range are well fit by two Faraday components with two gradients of RM (Fig. B.4 and Table 7), one of which has a very high value with Δ RM1CX ≃ −1300 rad m−2. This medium could be a large layer within which the radiation is subject to a smooth and large change of the polarization angle rising to a very high value of ΔRM.
The source is monitored in the MOJAVE program (Lister et al. 2009) and shows a very high apparent velocity with βapp = 22c, consistent with an abject with a small viewing angle. The MOJAVE polarization image shows that the polarized flux density is located within the central region and the value of the RM measured in that map is in agreement with the previous single dish measurement with RM ≈700 ± 150 rad m−2 (Hovatta et al. 2012; Pa16). However, this new modeling reveals the presence at C and X band of at least two Faraday components that depolarize and that can be associated to the two synchrotron components that are equally contributing to the radio spectrum.
At L band the source has been modeled with two simple Faraday components, the small depolarization of which came only from the presence of a simple external magneto-ionic material (Fig. B.5). The two RM values detected at low frequency are not as large (|RM1L,2L| ~ 20 rad m−2) as those detected at C and X bands. Thisis in agreement with the fact that the source shows large fractional polarization (~20%), almost constant polarization angle, and no cross of the Stokes parameters Q and U at low frequency.
As for the source 0243–0550, it was not possible to model the whole polarized data points; instead we had to treat the low-frequency range (L band) and the higher-frequency range (C and X band) separately. This suggests again no connection between the Faraday structures revealed by the Stokes qu-fitting in the two frequency ranges. The Faraday components mapped within the C–X bands range are different and closer to the central engine than those revealed by the Stokes qu-fitting at L band.
In this case, considering the radio spectrum and depolarization model fit information at C and X bands and the MOJAVE information, we would argue that the depolarization is most likely due to at least two Faraday screens originating in the synchrotron source itself that are producing a large gradient of RM across the beam. Since the gradient of RM is, in this case, symptomatic of regular magnetic field, it is possible that we are detecting depolarization due to helical magnetic field within the radio jet pointing toward the observer. The low-frequency Stokes qu-fitting is mapping two extra layers far from the central engine that are contributing little to the depolarization at that frequency range.
Source 1311+1417. This source was fit by two synchrotron components peaking at ~400 MHz and at ~2 GHz the second of which shows a break peaking around 8 GHz (see Fig. 7). The spectrum is characteristic of a GPS source. The fractional polarization decreases from ~7% to ~2% at roughly 7 GHz. At lower frequencies the fractional polarization decreases much more slowly, from ~2% to ~1%. In a similar way the polarization angle increases rapidly until 7 GHz where it reaches an approximately constant value (see Fig. 8).
The fit of the polarized properties find three Faraday components with highly turbulent magnetic fields (Fig. A.6 and Table 6). The high RM values, one of which is ≈ −1100 rad m−2, suggests a very dense magnetized medium. Looking at the σRM values of the qu-fitting, they are all very high compared to their respective RM values, indicating that the media is not only highly magnetized but also highly turbulent. As for source 1048+0141, the q and u values cross at higher frequency with resulting in a possible increase of the RM.
Gugliucci et al. (2005) reject this source as a possible GPS target; therefore, we can exclude the young nature of this radio galaxy. We suggest that the source, a complex bended core-jet (from VLBA image at 8 GHz, Gugliucci et al. 2005) is surrounded by at least three dense and turbulent Faraday-rotating clouds that are pierced by the synchrotron emission from the source.
Source 1312+5548. This source was fit by two synchrotron components: the first peaking at very low frequency (<100 MHz) and the second at ~1 GHz. The latter shows a break at ~8 GHz (see Fig. 7). The fractional polarization decreases exponentially from 7% to ~0%. The polarization angle has large variation within the C and X bands (see Fig. 8).
The depolarization modeling fit finds three Faraday components with very high RM values (RM1 ≃ −200 rad m−2, RM 2 ≃ −1600 rad m−2 and RM 3 ≃ 3400 rad m−2) and highly turbulent fields (σRM1 ≃ −360 rad m−2, σRM2 ≃ −970 rad m−2 and σRM3 ≃ −720 rad m−2, respectively); see Fig. A.7 and Table 6.
A high-resolution VLBI image at 5 GHz (Helmboldt et al. 2007) reveals a complex source morphology: a two sided radio source with a strongly bent jet. It appears to be a misaligned radio source. This complex morphology is likely related to the complex polarization behavior.
Source 1405+0415. This QSO was fit by a component peaking at very low frequency (<100 MHz) and one synchrotron component peaking at 1 GHz (see Fig. 7). The fractional polarization is approximately constant across the C and X bands with a value around 2%; however it decreases to less that 1% at L band. The polarization angle from 4 GHz to 7 GHZ remains constant at around 9°, before increasing up to 12° at 10 GHz. At high frequency it decreases, producing a high RM detected with qu-fitting.
This source could be a case in which an nπ ambiguity affects the data producing a misleadingly high RM detection or the source could be variable. From single-dish observations we determined a very high RM value (thousands of rad m−2) by adding nπ ambiguity to the polarization angle (Pa16). From the JVLA observations it turns out that this source seems to have a mainly low RM value within the whole observational frequency bands (L, C, and X bands), although the depolarization modeling identifies a Faraday component with a high RM value. Two Faraday components with turbulent magnetic fields fit the data at C and X bands (see Fig. B.6). Although the second Faraday component seems not to be necessary (the RM 2CX and the σRM2CX are very low with high errors); the fit is statistically better when the second components is present (see Table 7). This fit returns a high value of RM1CX (~ −850 rad m−2), relatively high turbulence (with a high σRM1CX of ~440 rad m−2) and a small value for RM2CX (≃ −3 rad m−2). The model also predicts the source to have a constant fractional polarization at low frequency; however this is not the case. L band polarized data are well fitted by two simple Faraday components, the small depolarization of which comes from the presence of simple external magneto-ionic medium which only rotates the polarized angle (Fig. B.7 and Table 7). The two RM values resulting from the Stokes qu-fitting are small (|RM1L,2L| ~ 20 rad m−2) consistent with the fact that no cross of the Stokes parameters q and u occurs within the low-frequency band. As for sources 0243–0550 and 1246–0730, it was not possible to study the depolarization considering the whole observational frequency range. We had to treat the high- and the low-frequency ranges separately. Once again, this implies that the two frequency ranges (C–X band and L band) are tracing different structures and are located far away from the central engine.
It is worth noting that this source is monitored in the MOJAVE program and shows variability in its total flux density (Lister et al. 2009). The polarized flux density could be affected by variability, a characteristic of emission dominated by the central region of a source.
Source 1549+5038. This source was fit by four synchrotron components (peaking at ~300 MHz, ~2 GHz, ~5 GHz and ~11 GHz; see Fig. 7). Overall the radio spectrum looks flat. The fractionals polarization decreases from 2.5% to 0.5%. The polarization angle and the fractional polarization displays complex behavior across the whole observed band (see Fig. 8).
The source shows complex behavior of the q and u values that are difficult to fit well, however three Faraday components with turbulent magnetic fields give a reasonable fit (Fig. A.8 and Table 6). The depolarization modeling returns relatively high values of RM and high σRM values, suggesting a dense and turbulent medium. This medium could be associated to some of the synchrotron components that characterize the radio spectrum at high frequency and/or some clumpy regions intercepting the synchrotron radiation.
Source 1616+0459. This source could be fitted with a component peaking at very low frequency (<100 MHz) and two components at higher frequencies (~2 GHz and ~6 GHz, respectively; see Fig. 7). This source forms part of a group of galaxies at redshift 3.2 (Djorgovski et al. 1987). The fractional polarization decreases with wavelength from 3% to 0.5%. The polarization angle increases with wavelength following an almost linear χ(λ2) relation (seeFig. 8).
The depolarization behavior has been fitted with two Faraday components with turbulent magnetic field (Fig. A.9 and Table 6). The two Faraday screens have high RM values (around 2100 rad m−2 and 500 rad m−2 for the first and second RM screens, respectively) and quite high values of the dispersion of the RM σRM (≈ −400 rad m−2 and ≈ −300 rad m−2 for the first and second RM dispersions, respectively).
Higher-angular resolution VLBI images at 5 and 8 GHz reveal a very compact source with a linear scale of the order of ~8 pc/mas (O’Sullivan et al. 2011). We note that, when corrected for the redshift, the RM value of the first Faraday component is ≈4 × 104 [rad m−2, the highest RM value in our sample. Since the source is part of a group of galaxies, with intergalactic medium surrounding the system, the two Faraday components that depolarize the radiation could be associated to either two different layers in the foreground (depolarization due to a gradient of RM in a foreground screen or external Faraday dispersion/beam depolarization) or two internal layers emitting and rotating at the same time (due to the presence of two synchrotron components in its radio spectrum at high frequency).
Source 2245+0324. This source was fit by three synchrotron components (peaking at ~1 GHz, ~4 GHz, and ~8 GHz; see Fig. 7). However, this is also consistent with a convex shape spectrum indicating a possible GPS nature of the source. The fractional polarization seems to follow a sinc-like trend. At C band the polarization angle remains almost constant, with very low RM value (see Fig. 8).
Three Faraday components with turbulent magnetic fields fit the data (Fig. A.10 and Table 6). Two of the resulting RM values are very high (thousands of rad m−2) with high RM dispersions (σRM), suggesting very dense and turbulent magnetized regions.
These three Faraday components can be considered as associated with the three synchrotron components of the radio spectrum.
Resulting parameters of the depolarization modeling for the 10 sources with data at C and X bands.
Resulting parameters of the depolarization modeling for the four sources at CX band and L band.
 |
Fig. 10 Depolarization models for the four sources at C and X bands with the L band data points over plotted. Shown for each source are behavior of the fractional Stokes parameters (q and u), the fractional polarization (p), and the polarization angle (χ) versus wavelength squared (λ2). Blue data points are for bands C and X, and red points are for L band. Black lines are the depolarization models fit considering bands C and X. |
Polarization-weighted parameters and RM corrected in the rest frame (RMrf) considering the C–X bands frequency range.
8 Discussion
We observed in full polarization a sample of AGN at L, C, and X bands with the JVLA. The sources were selected from Pa16 as those sources with no detected polarized flux density or blanked at 1.4 GHz (from the NVSS survey) and with large RM values (with RM > 500 rad m−2). The lack of polarized flux density at longer wavelengths could be due to strong depolarization due to high RM. Previous single-dish observations revealed a sample of sources with large RM values and strong depolarization (Pa16). However, it was not possible to study in detail the complexity of the polarization data due to insufficient data coverage. Therefore, we selected the most interesting sources to be observed using the broadband capability available at the JVLA: 14 sources with previous single-dish RM values larger than 500 rad m−2.
The sources of our sample show very complex behavior of the Stokes parameters. For four sources (0239–0234, 0245–0550, 1246–0730 and 1405+0415) we detected sufficient polarized signal also at L band when splitting the L band spw (64 MHz BW) into smaller BW (e.g., 30 MHz). We fit the total intensity using combinations of synchrotron components, and the polarization data using qu-fitting (as suggested by Farnsworth et al. 2011; O’Sullivan et al. 2012) with simple depolarization equations. The majority of the radio spectra were fit by several synchrotron components (all but the source 0751+2716 and the source 1311+1417). The fractional Stokes q and u parameters, the polarized intensity, the fractional polarization, and the polarization angle were fit by combining several Faraday components and considering the high-frequency range (C–X band range) and the low-frequency range (L band; when available) separately suggesting that the two frequency intervals are tracing different magneto-ionic plasma located away from the AGN core: medium close to the central engine at C and X bands, and structures far away from the central engine at L band. None of the sources in our sample were fit by one Faraday component; instead all the sources needed at least two Faraday components to describe the complex behavior in polarization. Moreover, although all the sources are unresolved at the higher JVLA resolution (0.6′′), visual inspection reveals a correspondence between the number of synchrotron components fitted in the total intensity radio spectrum and the number of Faraday components fitted in the polarization domain in the C–X band frequency range (~8 sources show a clear and a marginal correspondence while the remaining 6 other sources do not; see Table 9). Higher-angular-resolution observations, performed using VLBI technique, will help us to understand whether this is actually true (to be presented in a forthcoming paper). We also noticed that the depolarization occurring in the 4–12 GHz range for the majority of the sources of our sample (12 sources) is explained by Eq. (14) with only contribution from the σRM required. In this case, the depolarization is mainly related to the presence of turbulent magnetic fields, thus with possible scenarios of IFD or EFD/Bd. The remaining two sources: 0958+3224 and 1246–0730 need the contribution of Δ RM alone. Therefore, the depolarization is explained by the presence of a regular magnetic field. In this case the possible scenarios are the DFR and the gradient of RM for the internal case (Δ RMint). Interestingly, none of the sources required a combination of σRM and Δ RM to describe the depolarization behavior, for example, ΔRMext. Some support for the physical interpretation of these type of models already exists. For example, OS17 found a preference for the intrinsic polarization angle derived from the model-fitting to be aligned with the jet orientation, as often observed in FRI radio galaxies (e.g., Saikia & Salter 1988). However, in the study presented in this paper, higher-angular-resolution observations are required to determine how the true underlying polarization and Faraday-rotation distributions compare to the model-fit results. We plan to report on new VLBI observations for a subsample of these sources to investigate this issue.
The initial selection criteria (mainly the lack of polarization at 1.4 GHz in the NVSS survey) results in a sample of sources with very large Faraday rotation parameters (RRM, σRM and Δ RM) within the C and X bands frequency range. The sources can be considered Faraday thick. In only one case (the source 0243–0550), we found one Faraday component with a σRM2CX value that is close to zero; this could be associated with the repolarization that the source is subject to from X to C band (see Fig. B.2 and Table 7). The median value of the RRM in our sample is 617 ± 88 rad m−2, the median values of σRM,wtd and ΔRMwtd are 263 ± 28 rad m−2 and 772 ± 430 rad m−2, respectively.Figure 11 shows the cumulative plot of the polarization-weighted parameters. The red color represents the cumulative distribution of the RRM (for all the sources), the green color represents the cumulative distribution of the σRM,wtd (for 12 sources) and the blue color represents the cumulative distribution of the Δ RMwtd (for 2 sources).
In order to underline the peculiarity of our sources, we compare our work with that of OS17, a broadband polarization (1–10 GHz) study of 100 sources selected to be brightly polarized at 1.4 GHz. Both studies required only the σRM parameter to describe the depolarization for the majority of sources in the samples, and both required several Faraday components (more than two) to the data (only 20% of the sources in the sample have been fitted with one Faraday component due to relatively low S∕N: <25, OS17). Onthe other hand, the median values of the polarized parameters in OS17 are much lower than ours. In fact, the RRM in our sample is approximately 60 times larger that the RRM in OS17 and the σRM,wtd and Δ RMwtd are approximately 18 times and 13 times larger than the values in OS17.
It is worth noting that in our sample of unpolarized sources at 1.4 GHz we identified two sources (1246–0730 and 1405+0415) that are blazars, monitored in the MOJAVE program (Lister et al. 2009). Blazars are usually highly polarized at low frequency (Marscher 1980). This result implies that blazar polarization properties could also be affected by high RM and strong depolarization due to the presence of a complex medium of interfering Faraday screens.
We can conclude that the selection of unpolarized radio sources at low frequency (1.4 GHz in the NVSS) illuminates sources with strong depolarization due to very high RM values, and thus, with complex magneto-ionic media. These AGN all seem to be associated with very turbulent magnetic fields. The magneto-ionic medium that depolarizes these sources can be internal or external with respect to the synchrotron-emitting component but very close to the central engine of the targets. In fact, any contribution from very large structures, such as intergalactic medium, the galactic foreground that could be important at low frequency, can be neglected here because of the relatively high radio frequency used for this analysis (C and X bands) and the emission from small-scale structures. In fact, we can estimate an upper limit on the linear size of the sources, considering the highest angular resolution reached with these observations (0.6′′ at B configuration) and the redshift of the targets. The upper limit on the linear size is ≈5 kpc, much smaller if compared with the polarized sources at 1.4 GHz selected by OS17, which have linear sizes of the order of ≈100 kpc. Therefore, our observations are sensitive to emission coming from components smaller than ≈5 kpc. As a consequence, the sources in our study are probing more of the dense magneto-ionic medium of the host galaxy, while most of polarized regions of the sources in OS17 likely extend outside the host galaxy. The magneto-ionic medium that causes the Faraday rotation and depolarization in this sample can be considered to be local to the source with high electron densities and strong, turbulent magnetic fields. Therefore, it is most likely situated close to the central engine and not far away where the electron density would be much lower. This is true for the four sources which also show L band polarization data. The depolarization modeling at low frequency reveals structures with low RM values, most likely located far away from the central engine and less dense. Indeed, L band polarized data are sensitive to structures that are ≈30 kpc wide; therefore, structures that could include the far surroundings of an AGN. The complex media detected at C and X bands can be visualized with highly turbulent clouds in the proximity of the emitting radio source; therefore the radiation coming from the radio jets, the dominant synchrotron-emitting components containing nonthermal electrons, could be embedded or pass through very complex and turbulent clouds. Figure 12 shows an example of what can happen in the vicinity of the radio source.
Faraday components vs. synchrotron components correspondence.
 |
Fig. 11 Cumulative plot of the polarization-weighted parameters: RRM (red), σRM,wtd (green), and the ΔRMwtd (blue). |
9 Summary and conclusions
We have observed at L, C, and X bands (1–12 GHz) with the JVLA a sample of AGN which are unpolarized at 1.4 GHz (in the NVSS survey Condon et al. 1998) and have high RMs detected in previous single-dish observations (Pa16). We have collected total-intensity and polarized-intensity data among the whole observational frequency range. We analyzed broadband spectro-polarimetric data across the JVLA C and X bands (for four sources we also detected polarized signal at L band). A summary of our results are given below.
We fit the total intensity radio spectra with several synchrotron components. Overall the sources display a complex spectrum between L and X bands and no strong variability has been detected between previous single-dish radio spectra fitting (Pa16).
Polarization data, that is, the Stokes Q and U, the polarization flux density (Spol), the fractional polarization (p), and the polarization angle (χ), show complex behavior in the 4–12 GHz range. In particular, the p data do not show a simple exponential decay, as expected from the simplest depolarization case, that is, Eq. (8), and χ deviates significantly from a linear trend.
Depolarization modeling in the C and X band range has been performed for all the targets. We used several Faraday components, that is, at least two Faraday screens, to represent the complexity of the sources. We cannot assign a single RM to the sources, but several Faraday screens contribute to the complexity of the targets. It seems that there is a correspondence between the synchrotron components used to fit the radio spectra and the Faraday components used for the depolarization modeling. However, to verify whether this statement is correct, a higher-angular-resolution polarimetric study, presented in a forthcoming paper, is needed.
We detected polarization signal for four sources (0239–0234, 0243–0550, 1246–0730, 1405+0415) when splitting the available L band spws (64 MHz BW) into smaller BWs (i.e., 30 MHz BW). The L band data does not follow the trend of the C and X bands data; we could not include the low-frequency data points in the depolarization modeling of the high frequency data. We treated the two frequency intervals (4–12 GHz and 1–2 GHz) separately. This suggests that the low-frequency polarized data are tracing different structures with respect to the high-frequency data. In fact, the L band data (with a resolution of ~4.5′′) are sensitive to structure with sizes of the order of 30 kpc, larger than those detected by the high-frequency data sensible to structure with sizes of the order of 5 kpc.
For the majority of our targets (12 sources) the depolarization is caused by turbulent magnetic fields. Possible equations that contain the contribution of turbulent cells of magnetic field, the Faraday dispersion σRM, are the internal Faraday dispersion (Eq. (10)), or the external Faraday depolarization/beam depolarization (Eq. (9)). Only two sources have been fitted considering the contribution of a regular magnetic field (Δ RM). None of the sources have been fitted using the contribution of both regular and turbulent magnetic fields.
Nevertheless, the lack of polarized flux density at 1.4 GHz results in a sample of sources with very large Faraday-rotation parameters (RRM, σRM and Δ RM). The median values of the RRM, σRM and ΔRM are: 617 ± 88 rad m−2, 263 ± 28 rad m−2 and 772 ± 430 rad m−2, respectively. The highest value of RRM detected is 2020 ± 30 (for the source 1616+0459) which reaches values of ~2 × 104 in the rest frame.
Two sources (1246–0730 and 1405+0415) are blazars, monitored in the MOJAVE program (Lister et al. 2009). Most likely, blazar-type sources can be characterized by high RM and strong depolarization due to a complex intervening medium.
We provide an upper limit on the linear size of the sources of ≈5 kpc. The sources are thus probing dense magneto-ionic media with high electron density and strong, turbulent magnetic fields, most likely situated close to the central engine.
These broadband JVLA data show, without any doubt, the complexity of radio sources both in total intensity and in polarized intensity. Thanks to the high spectral resolution of these data, it has been possible to follow the dramatic changes of the polarization information of these AGN across a wide range of frequencies, and to model, with very good accuracy, the complexity of the polarization behavior. The new qu-fitting technique applied to broadband polarization data can be used to map the medium of these radio sources; specifically, it can be used to spectrally resolve polarized components of unresolved radio sources.
Radio spectro-polarimetric observations are an excellent tool to unveil magnetized structures in radio AGN. Overall, this study paves the way for future broadband and spectro-polarimetric studies with large-area surveys (e.g., VLASS, ASKAP-POSSUM) that will measure the polarization and Faraday-rotation properties of hundreds of thousands of radio-loud AGN. This will greatly improve the statistical study of the magnetized properties of radio AGN and their environments.
 |
Fig. 12 Sketch of the depolarization that occurs in an AGN. |
Acknowledgements
A. P. acknowledges support from CONACyT 238631. G. B. acknowledges financial support under the INTEGRAL ASI-INAF agreement 2013-025.R01. This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research has made use of data from the MOJAVE database that is maintained by the MOJAVE team (Lister et al. 2009). This work was supported by UNAM-PAPIIT IA101214 and IA102816. We thank Prof. Robert Antonucci for his careful revision of the paper and useful comments.
Appendix A Depolarization modeling plots: sources with C–X bands polarization data
 |
Fig. A.1 Depolarization model for the source 0751+2716: 3 components model. |
 |
Fig. A.2 Depolarization model for the source 0845+0439: 2 components model. |
 |
Fig. A.3 Depolarization model for the source 0958+3224: 3 components model. |
 |
Fig. A.4 Depolarization model for the source 1048+0141: 2 components model. |
 |
Fig. A.5 Depolarization model for the source 1146+5356: 2 components model. |
 |
Fig. A.6 Depolarization model for the source 1311+1417: 3 components model. |
 |
Fig. A.7 Depolarization model for the source 1312+5548: 3 components model. |
 |
Fig. A.8 Depolarization model for the source 1549+5038: 3 components model. |
 |
Fig. A.9 Depolarization model for the source 1616+0459: 2 components model. |
 |
Fig. A.10 Depolarization model for the source 2245+0324: 3 components model. |
Appendix B Depolarization modeling plots: sources with C–X bands and L band polarization data
 |
Fig. B.1 Depolarization model for the source 0239–0234 at C and X bands: 2 components model. L band depolarization modeling is not available because of insufficient data points at this frequency band. |
 |
Fig. B.2 Depolarization model for the source 0243–0550 at C and X bands: 2 components model. |
 |
Fig. B.3 Depolarization model for the source 0243–0550 at L band: 2 components model. |
 |
Fig. B.4 Depolarization model for the source 1246–0730 at C and X bands: 2 components model. |
 |
Fig. B.5 Depolarization model for the source 1246–0730 at L band: 2 components model. |
 |
Fig. B.6 Depolarization model for the source 1405+0415 at C and X bands: 2 components model. |
 |
Fig. B.7 Depolarization model for the source 1405+0415 at L band: 2 components model. |
References
- Anderson, C. S., Gaensler, B. M., Feain, I. J., & Franzen, T. M. O. 2015, ApJ, 815, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, C. S., Gaensler, B. M., & Feain, I. J. 2016, ApJ, 825, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Wampler, E. J., & Burbidge, E. M. 1981, ApJ, 243, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Berkhuijsen, E. M., & Beck, R. 1990, in Galactic and Intergalactic Magnetic Fields, eds. R. Beck, R. Wielebinski, & P. P. Kronberg, IAU Symp., 140, 201 [NASA ADS] [Google Scholar]
- Briggs, E. L. 1995, PhD Thesis, State University, North Carolina, USA [Google Scholar]
- Brotherton, M. S. 1996, ApJS, 102, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Burn, B. J. 1966, MNRAS, 133, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Callingham, J. R., Ekers, R. D., Gaensler, B. M., et al. 2017, ApJ, 836, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, A. S., Lane, W. M., Cotton, W. D., et al. 2007, AJ, 134, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Djorgovski, S., Strauss, M. A., Spinrad, H., McCarthy, P., & Perley, R. A. 1987, AJ, 93, 1318 [NASA ADS] [CrossRef] [Google Scholar]
- Douglas, J. N., Bash, F. N., Bozyan, F. A., Torrence, G. W., & Wolfe, C. 1996, AJ, 111, 1945 [NASA ADS] [CrossRef] [Google Scholar]
- Farnes, J. S., Gaensler, B. M., & Carretti, E. 2014, ApJS, 212, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Farnsworth, D., Rudnick, L., & Brown, S. 2011, AJ, 141, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Fricke, K. J., Kollatschny, W., & Witzel, A. 1983, A&A, 117, 60 [NASA ADS] [Google Scholar]
- Gardner, F. F., & Davies, R. D. 1966, Aust. J. Phys., 19, 129 [NASA ADS] [Google Scholar]
- Gugliucci, N. E., Taylor, G. B., Peck, A. B., & Giroletti, M. 2005, ApJ, 622, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Hales, S. E. G., Riley, J. M., Waldram, E. M., Warner, P. J., & Baldwin, J. E. 2007, MNRAS, 382, 1639 [NASA ADS] [Google Scholar]
- Helmboldt, J. F., Taylor, G. B., Tremblay, S., et al. 2007, ApJ, 658, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, D. C., Ojha, R., Wardle, J. F. C., et al. 2002, ApJ, 568, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Hovatta, T., Lister, M. L., Aller, M. F., et al. 2012, AJ, 144, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley-Walker, N., Callingham, J. R., Hancock, P. J., et al. 2017, MNRAS, 464, 1146 [NASA ADS] [CrossRef] [Google Scholar]
- Kravchenko, E. V., Kovalev, Y. Y., & Sokolovsky, K. V. 2017, MNRAS, 467, 83 [NASA ADS] [Google Scholar]
- Labiano, A., Barthel, P. D., O’Dea, C. P., et al. 2007, A&A, 463, 97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lister, M. L., Cohen, M. H., Homan, D. C., et al. 2009, AJ, 138, 1874 [NASA ADS] [CrossRef] [Google Scholar]
- Mantovani, F., Mack, K.-H., Montenegro-Montes, F. M., Rossetti, A., & Kraus, A. 2009, A&A, 502, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marscher, A. P. 1980, ApJ, 235, 386 [NASA ADS] [CrossRef] [Google Scholar]
- O’Dea, C. P., Baum, S. A., & Stanghellini, C. 1991, ApJ, 380, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Oppermann, N., Junklewitz, H., Greiner, M., et al. 2015, A&A, 575, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Sullivan, S. P., & Gabuzda, D. C. 2009, MNRAS, 393, 429 [NASA ADS] [CrossRef] [Google Scholar]
- O’Sullivan, S. P., Gabuzda, D. C., & Gurvits, L. I. 2011, MNRAS, 415, 3049 [NASA ADS] [CrossRef] [Google Scholar]
- O’Sullivan, S. P., Brown, S., Robishaw, T., et al. 2012, MNRAS, 421, 3300 [NASA ADS] [CrossRef] [Google Scholar]
- O’Sullivan, S. P., Purcell, C. R., Anderson, C. S., et al. 2017, MNRAS, 469, 4034 [NASA ADS] [CrossRef] [Google Scholar]
- Pasetto, A., Kraus, A., Mack, K.-H., Bruni, G., & Carrasco-González, C. 2016, A&A, 586, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peck, A. B., Taylor, G. B., Fassnacht, C. D., Readhead, A. C. S., & Vermeulen, R. C. 2000, ApJ, 534, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, R. A., & Butler, B. J. 2013a, ApJS, 204, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, R. A., & Butler, B. J. 2013b, ApJS, 206, 16 [Google Scholar]
- Rengelink, R. B., Tang, Y., de Bruyn, A. G., et al. 1997, A&AS, 124, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richards, G. T., Myers, A. D., Gray, A. G., et al. 2009, ApJS, 180, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Rossetti, A., Dallacasa, D., Fanti, C., Fanti, R., & Mack, K.-H. 2008, A&A, 487, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roy, S., Rao, A. P., & Subrahmanyan, R. 2005, MNRAS, 360, 1305 [NASA ADS] [CrossRef] [Google Scholar]
- Saikia, D. J., & Salter, C. J. 1988, ARA&A, 26, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Simard-Normandin, M., Kronberg, P. P., & Button, S. 1981, ApJS, 45, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Sokoloff, D. D., Bykov, A. A., Shukurov, A., et al. 1998, MNRAS, 299, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Souchay, J., Andrei, A. H., Barache, C., et al. 2012, A&A, 537, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stickel, M., & Kuehr, H. 1994, A&AS, 103, 349 [NASA ADS] [Google Scholar]
- Tonry, J. L., & Kochanek, C. S. 1999, AJ, 117, 2034 [NASA ADS] [CrossRef] [Google Scholar]
- Tribble, P. C. 1991, MNRAS, 250, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Tytler, D., & Fan, X.-M. 1992, ApJS, 79, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Véron-Cetty,M.-P., & Véron, P. 2006, A&A, 455, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, R. L., Becker, R. H., Helfand, D. J., & Gregg, M. D. 1997, ApJ, 475, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkes, B. J. 1986, MNRAS, 218, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Wolter, A., Ciliegi, P., della Ceca, R., et al. 1997, MNRAS, 284, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, W., Lawrence, C. R., Readhead, A. C. S., & Pearson, T. J. 1994, AJ, 108, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Zavala, R. T., & Taylor, G. B. 2003, New Astron. Rev., 47, 589 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Coefficients used for the polynomial fits for the calibrators 3C286, 3C138, and 3C48.
Resulting parameters of the depolarization modeling for the 10 sources with data at C and X bands.
Resulting parameters of the depolarization modeling for the four sources at CX band and L band.
Polarization-weighted parameters and RM corrected in the rest frame (RMrf) considering the C–X bands frequency range.
All Figures
 |
Fig. 1 Cumulative plot of the S/N distribution of the total intensity (red) and the polarized intensity (green) data points considering all the observed frequencies. |
| In the text | |
 |
Fig. 2 In-band depolarization at all the frequency bands – a): L band (red), C band (green) and X band (blue); and b) a zoom to only 5% in-band depolarization for the three bands. |
| In the text | |
 |
Fig. 3 Modeling of the polarization parameters for the calibrators, 3C48, 3C138, and 3C286. Frequency coverage: from 1 to 50 GHz. For each of the sources, upper panel: the polarized flux density (black line) and the Stokes parameters, Q (blue line) and U (red line); middle panel: the polarization angle variation; and last panel: the polarization degree in percentage variation. The dashed vertical lines mark the frequency ranges used for the modeling. |
| In the text | |
 |
Fig. 4 FR sketch. The radiation (red arrow) coming from a synchrotron-emitting region (yellow circle with nonthermal electrons) passes through a magneto-ionic region (blue cloud with thermal electrons) with regular magnetic field (black arrows) thatrotates the polarized vector of the radiation (blue arrow). In this scenario the fractional polarization remains constant. |
| In the text | |
 |
Fig. 5 Depolarization mechanisms. The red undulated arrows represent the synchrotron radiation and the blue arrows represent the polarization vector of the radiation; the length of this vector decreases when depolarization occurs. The black arrows represent the magnetic field direction and its intensity is represented by the thickness of the arrows. The pictures (a), (b), and (c) represent the cases of internal depolarization where the synchrotron-emitting regions and the Faraday rotating regions coexist together (dark yellow with thermal, et , and nonthermal, eno-t, electrons). Picture (a) represents the DFR (Eq. (11)) where a regular magnetic field is present, picture (b) represents the IFD (Eq. (10)) where a turbulent and a regular magnetic field is present, and picture (c) represents the depolarization due to an internal gradient of RM (Δ RM int, Eq. (12)); the magnetic field is uniform and throughout the region the radiation undergoes both fractional polarization and polarization angle smooth changes. Picture (d) represents the case of external depolarization where the synchrotron-emitting region (yellow circle containing eno-t) and the Faraday rotating region (blue cloud containing et) are separated (Eq. (9)). Here the depolarization is due to the presence of a turbulent magnetic field or to the polarized vectors canceling each other out within the telescope beam (beam depolarization, Bd). Picture (e) represents the depolarization due to a gradient of RM due to the presence of a foreground region (Eq. (13)). |
| In the text | |
 |
Fig. 6 Radio spectra using L, C and X bands and literature. Total flux density is expressed in [mJy] and the frequency in [GHz]. Blue points are the JVLA and literature data and the green points are upper limits. Orange lines are the individual synchrotron componentsused for the radio spectra fit and the red line is their sum. The gray vertical dashed lines indicate the L to C band range and the C to X band range. |
| In the text | |
 |
Fig. 7 Radio spectra using L, C, and X bands and literature. Total flux density is expressed in [mJy] and the frequency in [GHz]. Blue points are the JVLA and literature data and green points are upper limits. Orange lines are the individual synchrotron componentsused for the radio spectra fit and the red line is their sum. The gray vertical dashed lines indicate the L to C band range and C to X band range. |
| In the text | |
 |
Fig. 8 Polarization information of the sources at C and X bands. For each plot, first upper panel: the total intensity S expressed in [mJy] (the black line simply connects the points), second panel: the polarized flux density Spol expressed in [mJy], the Stokes parameters Q (magenta dots) and U (green dots) expressed in [mJy] (the black, the magenta, and the green lines simply connect the points); the third middle panel reports the fractional polarization; the last bottom panel shows the polarization angle χ expressed in [deg]. All this information is represented in the λ2 domain. Thevertical dashed lines indicate the C to X band range. |
| In the text | |
 |
Fig. 8 continued. |
| In the text | |
 |
Fig. 9 Polarization information of the sources at L, C, and X bands. |
| In the text | |
 |
Fig. 10 Depolarization models for the four sources at C and X bands with the L band data points over plotted. Shown for each source are behavior of the fractional Stokes parameters (q and u), the fractional polarization (p), and the polarization angle (χ) versus wavelength squared (λ2). Blue data points are for bands C and X, and red points are for L band. Black lines are the depolarization models fit considering bands C and X. |
| In the text | |
 |
Fig. 11 Cumulative plot of the polarization-weighted parameters: RRM (red), σRM,wtd (green), and the ΔRMwtd (blue). |
| In the text | |
 |
Fig. 12 Sketch of the depolarization that occurs in an AGN. |
| In the text | |
 |
Fig. A.1 Depolarization model for the source 0751+2716: 3 components model. |
| In the text | |
 |
Fig. A.2 Depolarization model for the source 0845+0439: 2 components model. |
| In the text | |
 |
Fig. A.3 Depolarization model for the source 0958+3224: 3 components model. |
| In the text | |
 |
Fig. A.4 Depolarization model for the source 1048+0141: 2 components model. |
| In the text | |
 |
Fig. A.5 Depolarization model for the source 1146+5356: 2 components model. |
| In the text | |
 |
Fig. A.6 Depolarization model for the source 1311+1417: 3 components model. |
| In the text | |
 |
Fig. A.7 Depolarization model for the source 1312+5548: 3 components model. |
| In the text | |
 |
Fig. A.8 Depolarization model for the source 1549+5038: 3 components model. |
| In the text | |
 |
Fig. A.9 Depolarization model for the source 1616+0459: 2 components model. |
| In the text | |
 |
Fig. A.10 Depolarization model for the source 2245+0324: 3 components model. |
| In the text | |
 |
Fig. B.1 Depolarization model for the source 0239–0234 at C and X bands: 2 components model. L band depolarization modeling is not available because of insufficient data points at this frequency band. |
| In the text | |
 |
Fig. B.2 Depolarization model for the source 0243–0550 at C and X bands: 2 components model. |
| In the text | |
 |
Fig. B.3 Depolarization model for the source 0243–0550 at L band: 2 components model. |
| In the text | |
 |
Fig. B.4 Depolarization model for the source 1246–0730 at C and X bands: 2 components model. |
| In the text | |
 |
Fig. B.5 Depolarization model for the source 1246–0730 at L band: 2 components model. |
| In the text | |
 |
Fig. B.6 Depolarization model for the source 1405+0415 at C and X bands: 2 components model. |
| In the text | |
 |
Fig. B.7 Depolarization model for the source 1405+0415 at L band: 2 components model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


