| Issue |
A&A
Volume 612, April 2018
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201732097 | |
| Published online | 13 April 2018 | |
Energy scaling of the “heartbeat” pulse width of GRS 1915+105, IGR J17091−3624, and MXB 1730−335 from Rossi-XTE observations
1
Università degli Studi di Cagliari – Dipartimento di Fisica, Complesso Universitario di Monserrato,
S.P. Monserrato-Sestu km 0,700,
09042
Monserrato (CA), Italy
e-mail: alessandro.maselli@dsf.unica.it
2
INAF, IAPS,
via del Fosso del Cavaliere 100,
00113
Roma, Italy
3
INFN,
Sezione Roma 1, Piazzale A. Moro 2,
00185
Roma, Italy
4
In Unam Sapientiam,
Piazzale A. Moro 5,
00185
Roma, Italy
5
INAF, IASF Palermo,
via U. La Malfa 153,
90146
Palermo, Italy
Received:
13
October
2017
Accepted:
15
January
2018
We investigate some key aspects of the “heartbeat” variability consisting of series of bursts with a slow rise and a fast decay, thus far detected only in GRS 1915+105, IGR J17091−3624, and MXB 1730−335. A previous analysis based on BeppoSAX data of GRS 1915+105 revealed a hard-X delay (HXD), that is a lag of the burst rise at higher energies with respect to lower ones; this leads to narrower pulse widths, w, at higher energies. We here use some light curves of Rossi-XTE observations of GRS 1915+105 for a deeper analysis of this effect and search for its presence in those extracted from some IGR J17091−3624 and MXB 1730−335 observations performed with the same satellite. Our results show that, at variance with GRS 1915+105, no HXD is evident in the light curves of MXB 1730−335 and only a marginal HXD may be argued for IGR J17091−3624. For GRS 1915+105 we find a decreasing trend of the pulse width with energy following a power law w = A ⋅ E−s with an index s ≈ 0.8. Furthermore, we confirm the increase of the HXD with the recurrence time Trec of the bursts in each series that was already found in previous works using BeppoSAX data. Based on a spectral analysis of these three sources we conclude that the differences highlighted in the properties of the “heartbeat” variability are probably related to the different accreting compact object and the eventual presence of a corona in these binary interacting systems.
Key words: binaries: close / X-rays: stars / X-rays: individuals: GRS 1915+105 / X-rays: individuals: IGR J17091–3624 / X-rays: individuals: MXB 1730–335
© ESO 2018
1 Introduction
To date, three sources are known to exhibit series of bursts, usually referred to as “heartbeat” variability. These bursts display a structure consistent with the ρ variability class first defined by Belloni et al. (2000) while studying microquasar GRS 1915+105. They are characterised by a typical slow rise fast decay (SRFD) time profile. This type of burst series was first observed in GRS 1915+105 on several occasions since 1997 and was explained in terms of thermal instability in a viscous disk (Taam et al. 1997). In the case of GRS 1915+105, the duration of these series can be of several days, as seen in the BeppoSAX pointing of October 2000 (Massaro et al. 2010) with a variable recurrence time, Trec, ranging from ~40 s to more than ~90 s and correlated to the source luminosity. A similar variability pattern, but with shorter Trec, was also observed in the source IGR J17091−3624 (Altamirano et al. 2011), and recently Bagnoli & in’t Zand (2015) reported the discovery of a behaviour similar to the ρ class in the X-ray binary MXB 1730−335 (also known as the Rapid Burster, discovered by Lewin et al. 1976), but exhibiting a longer recurrence time of about 7 min.
Several properties of this repeating bursting state of GRS 1915+105 were investigated in a series of papers (Massaro et al. 2010; Mineo et al. 2012, 2016, 2017; Massa et al. 2013) based on data series obtained in a long-duration study of this source with BeppoSAX in April 1999 and October 2000. According to the definition given in Mineo et al. (2012) we distinguish in a burst the following three main segments: an initial increase of the photon count rate, the slow leading trail (SLT), up to the development of a pulse, frequently structured in a few narrow peaks, and terminating with a final decaying trail (FDT) to the initial level. In particular, Massa et al. (2013) and Mineo et al. (2016) discussed the so called hard X delay (HXD): a time lag of the bursts’ rising times that increases with the mean photon energy. The HXD had been investigated previously by Janiuk & Czerny (2005) who, applying a cross-correlation analysis between light curves at different energies, found a delay of the high-energy signal shorter than 1 s, and interpreted it as due to the photon scattering in a hot corona near to the inner disk. As shown by Massa et al. (2013), however, the cross-correlation analysis is more sensitive to finding time shifts rather than changes in the pulse width, w. For this reason those authors developed a method to evaluate the HXD based on the study of the trajectories described during the burst evolution in the count rate versus mean photon energy bidimensional space. They reported HXD values ranging from about 2 s to about 9 s, correlated with the recurrence time of the bursts and the photon count rate. In a subsequent paper, Massaro et al. (2014) found that the time series of the count rate and mean photon energy can be reproduced by means of a mathematical model based on the well studied non-linear FitzHugh–Nagumo system of differential equations (FitzHugh 1961; Nagumo et al. 1962).
In the present paper we report the results of a comparativeanalysis of the HXD in a sample of ρ class bursts observed in GRS 1915+105, IGR J17091−3624, and MXB 1730−335 based on Rossi-XTE (RXTE) archive data. This phenomenon is clearly apparent in the segments of GRS 1915+105 light curve at the three energies of 3.6, 6.8, and 11.4 keV shown in Fig. 1 with burst profiles having largely different burst recurrence times. One can see that the rising portions of the three bursts are delayed and that this lag increases with the photon energy. A rather small time shift of the peak maxima of the order of 1 or 2 s, comparable with the delay found by Janiuk & Czerny (2005), appears in the data plotted in the upper panel of Fig. 1, while this effect isnot present in those plotted in the lower panel. FDT portions of the bursts at different energies are nearly simultaneous and this implies that the widths of the pulse segment of the burst (hereafter we use the same definitions for the burst segments given in Mineo et al. (2012)) become narrower for increasing energy. In this study we extend the previous results on HXD and test the possibility of establishing a simple relation between w and the energy for GRS 1915+105, and whether a similar relation holds for the other sources exhibiting the same behaviour.
Data and selection procedure are illustrated in Sect. 2, while in Sect. 3 we describe themethods used in the analysis and present the results. The comparison with previous results and some implications for the burst origin are discussed in Sect. 4.
 |
Fig. 1 Two segments of RXTE/PCA light curves of GRS 1915+105 in the ρ variability class at three energies showing the HXD phenomenon and the dependence of the pulse width, w, upon energy. Data, after the subtraction of a constant level, are scaled to obtain comparable pulse heights. Upper panel: RXTE G-2a data; lower panel: G-1 data. In the latter data set the recurrence time of the bursts was more than twice longer than that in the former one. We note in both panels the variable duration and shape of individual bursts and in the upper one the small time delay of the peak maxima, particularly in the first and in the third burst. |
2 Observations and data reduction
We considered data from RXTE/PCA (Jahoda et al. 1996) and created filter and good time intervals (GTI) files applying all standard criteria. The level of the background for the light curves of each of the three sources was evaluated with standard procedures1 and, for both MXB 1730−335 and IGR J17091−3624, the contamination from strong sources in the field of view was also studied. The log of all used observations is given in Table 1. The energy ranges used to accumulate the light curves were properly selected to maximise the differences in the time profile while keeping similar statistics. We carried out spectral analysis for IGR J17091−3624 and MXB 1730−335, in a bandpass limited to the range 2.5–20 keV where the PCA is well calibrated (Jahoda et al. 2006; Shaposhnikov et al. 2012)and contains most of the signal. A systematic error of 0.5 per cent per channel was included (following Shaposhnikov et al. 2012). All spectra were corrected for particle background and cosmic diffuse background as predicted through the PCABACKEST tool (version 3.8). The PCA response matrix was calculated with the PCARSP tool (version 11.7.1). Spectral bins were combined to obtain at least 20 counts per bin in order to ensure applicability of the χ2 statistic. The spectral modelling was carried out with XSPEC (version 12.9.1).
RXTE observations of the three sources showing heartbeat variability.
2.1 GRS 1915+105
RXTE observed GRS 1915+105 many times; a part of this large data collection was already used by Belloni et al. (2000) to define 12 variability classes and, in particular, the bursting ρ class. We considered only two pointings, G-1 and G-2, in which the source exhibited sequences of bursts with different Trec , as shown in Fig. 1. Furthermore, G-2 data present two subsets divided by a gap of ~2000 s that we analysed independently naming them G-2a and G-2b. The two subsets have small differences in the mean recurrence time and in the maximum pulse heights: the G-2a subset is the richest one with 113 bursts and a variable Trec in the range from 43 to 51 s (see Fig. 1) with a mean value around 47 s, while Trec increases to ~53 s in the G-2b subset. In the G-1 data set, Trec is longer and varies in the range 90–104 s. Further details about these RXTE observations are reported in Table 1. PCA light curves in 15 energy bands in the range from 3.2 to 13.0 keV with a time bin of 0.5 s were produced using binned-mode data with 8 ms timing in 16 energy channels. No background subtraction was applied in the light curve accumulation because it was found negligible compared to the source count rate even in the portions of the bursts with the lowest count rates at the highest energies: about 2.5 ct s−1 against 113 ct s−1, therefore much lower than the Poissonian error.
2.2 IGR J17091−3624
RXTE performed a large collection of pointed observations of IGR J17091−3624. A complete analysis of these data was recently presented by Court et al. (2017), who included many data from other space X-ray observatories. These authors defined nine classes of variability, and bursts rather similar to the ρ class appearin the classes III, IV, and V with different recurrence times and time profiles.
The RXTE campaign of pointed observations of IGR J17091−3624 considered in the present paper started on 2011 February 9 (MJD 55601) for a total exposure time of about 550 ks divided into 226 pointings. Among the RXTE/PCA observations, we selected only those in which the source was clearly in the ρ class (Pahari et al. 2014) or class IV according to Court et al. (2017). Moreover, because of the faintness of the source with respect to GRS 1915+105, we selected the PCA pointings with the highest signal to noise ratio (S/N) and rather regular burst sequences. We verified that during these pointings the source IGR J17098−3628, at an angular distance of 8. ′′ 5, was in a quiescent state and its emission did not affect the light curves of IGR J17091−3624. PCA light curves with a time binning of 0.125 s were extracted from science Data in GoodXenon mode without applying background subtraction. The background contribution to the extracted light curves is stable across both observations, with a mean of ~3 and ~5.7 ct s−1 in the low- (2–6 keV) and in the high- (6–20 keV) energy ranges, respectively, for the I-2, I-3, I-4 observations and doubled in I-1 where two PCUs were operating. Although higher than in the case of GRS 1915+105, the background contribution is stably lower than the source signal to alter the burst profile of IGR J17091−3624. Table 1 reports further details of the pointings considered in our analysis.
2.3 MXB 1730−335
As recently found by Bagnoli & in’t Zand (2015), ρ-class bursts were observed from MXB 1730−335 only on one occasion, during the RXTE visit of 1999 October 16. This consisted of two observations, here indicated by M-1 and M-2, separated by a gap of 68 s. As a whole, 15 complete bursts were observed; in the M-1 observation there is also one type-I burst superposed onto the FDT of one of the ρ bursts, and this data segment of 250 s was excluded from ouranalysis. Further details are given in Table 1.
The RXTE pointing changed between M-1 and M-2 to exclude from the PCA field of view the Low Mass X-ray binary 4U 1728−34, at an angular distance of ~0.5 degrees from MXB 1730−335. This change put MXB 1730−335 at an off-axis angle of 0.56 degrees in M-2, with a sensible reduction of the detected rate as a consequence of the smaller effective area (see also Bagnoli et al. 2014). However, as also shown by Bagnoli & in’t Zand (2015; their Fig. 1), the shape of the burst profiles and the peak-to-peak amplitude were not affected by this change. We noticed in the field of view of the M-2 observation the presence of the other potentially contaminating source IGR J17354−3255 (Bird et al. 2010). We evaluated the expected contribution from this object by means of the spectral model given by D’Aì et al. (2011) and obtained that the 2–10 keV count rate is lower than 1% of the signal from MXB 1730−335. We therefore concluded that neither 4U 1728−34 nor IGR J17354−3255 significantly affected the observed light curves of the Rapid Burster.
We then extracted two light curves of this source in the distinct energy ranges 2.1–3.8 keV and 11.4–15.2 keV, where statistics is good enough for evaluating the peaks’ width, with a time bin of 1 s; these curves were accumulated from PCA event-mode data with 16 μs timing in 64 energy channels. We verified that the background contribution to the extracted light curves was stable across both observations, with a mean of ~7 and ~9 ct s−1 in the low- (2.1–3.8 keV) and in the high- (11.4–15.2 keV) energy ranges, respectively, that is, too low to affect the rate variations of the source.
3 Data analysis and results
3.1 Methods
The burst profiles in Fig. 1 show that the HXD affects the pulse width, w, that becomes narrower with increasing energy. A simple and direct approach to obtain a relation between w and the photon energy E is that of measuring the former quantity from individual bursts in light curves at different energies and then computing averages and standard deviations for each set. It is reasonable to take w to be equal to the full width half maximum (FWHM) of the pulse including significant portions of the rising and decaying segments. We obtained this quantity by measuring the time difference at the half level between the lowest and the highest count rates. We then computed the mean width for every energy band and took as uncertainty the standard deviation which reflects the statistical scatter of the w values from these means. In the case of the G-2 observation (Fig. 1, upper panel), however, the pulse is generally structured in two or three narrow peaks and it is not easy to establish the actual half level. When there is a rather deep value between two peaks, we decided to take w to be the largest interval between the half peak levels in the initial rising and final decaying portion of the pulse as this structure could also be present in the G-1 data (Fig. 1, lower panel), but individual peaks are not always well resolved.
This method, however, applied to IGR J17091−3624 data failed to obtain significant results due to the low S/N and to the large fluctuations in amplitude, recurrence time, and burst structure. A simple approach, useful for a fast visualisationof the changes of the pulse width with energy, is the two-energy plot, an intensity-intensity plot, with each intensity measured in a different energy band. Given two simultaneous light curves at different energies, one makes the scatter plot of the count rate at lower energy on the abscissa against the simultaneous rate at higher energy on the ordinate. The points of similar burst profiles are distributed along a straight lineand, if bursts are normalised to the same amplitude, this is the bisecting line. A scattering of the burst pointsin the shape of a curved trajectory, with an upward or downward curvature, corresponds to a delayed or anticipated increase of the higher-energy count rate, with the minima and maxima points clustering on the bisecting line. Figure 2 shows an example of high-energy delayed trajectories for one burst of GRS 1915+105. Data were smoothed to eliminate the statistical noise and to show the typical pattern described in a burst. To highlight the curved trajectory a quadratic best fit (the simplest non-linear law) was also computed: for this purpose all the data were included in the fit. We note that the closed cycle is described in an anticlockwise direction, implying that pulse widths at higher energies are narrower because of the occurrence of the HXD. A loop in a clockwise direction would correspond to a high-energy rise preceding that in the lower-energy band. One has to take into accountthat both the high variability of burst profiles and the low S/N affect the point distribution that can exhibit a relatively large dispersion. In any case, a simple inspection of the plot is useful for deriving a qualitative indication of the possible changes of the pulse width with energy.
3.2 Results
3.2.1 GRS 1915+105
The two-energy plot for the data series at 3.6 keV and 11.4 keV shown in the upper panel of Fig. 1 is given in the left panel of Fig. 3. After a normalisation of the count-rate ranges to similar amplitudes, we found that the point distribution clearly shows the same pattern shown in Fig. 2 with the curvature expected for high-energy pulse widths narrower than the corresponding ones at low energy. This effect is also apparent from the deviation of the quadratic best fit line to all data (thick green line) from the straight (black) line that would imply an unchanged profile.
We evaluated the FWHM of all pulses in the light curves at 15 energy channels in the range from 3.5 keV to 12.5 keV and reported the resulting mean value versus the average energy of each channel. The resulting relations for the two considered pointings are given in the plot in the upper panel of Fig. 4. A clear monotonic decreasing trend is apparent in all the data sets that can be well described by a single power law w = A ⋅ E−s whose best-fit relations are plotted using thick dashed lines. This model is a good fit to the G-1 and G-2b points with an exponent equal to s = 0.81 ± 0.04 for both curves. The subset G-2a cannot be fitted by the same law (χ2 = 61 for 13 d.o.f.) because of a break around 5 keV. For these data we used a broken power law whose best fit parameters are: s1 = 0.50 ± 0.08, s2 = 0.76 ± 0.02 and a break energy fixed at Eb = 5.0 ± 0.5 keV. All these fits gave reduced χ2 values very close to or lower than unity (0.6 for G-1; 1.2 for G-2a; 0.9 for G-2b). A broken power law, but with a lower statistical significance, can actually be obtained also for the G-2b set. The need for considering a broken power law can be evaluated by means of a run test that takes into consideration the number r of sequences (runs) of the residuals’ sign (see, e.g. Barlow 1989). There are 4 and 3 runs for the G-2a and G-2b sets, respectively, while the expected number of runs for N = 15 points is ⟨r⟩ = 1 + 2(N+N−)∕N = 8.5, where N+ and N− are the numbers of positive and negative residuals, in the case of G-2b data equal to 8 and 7, respectively. The variance of r is ![$\sigma_r^2 = [2 N_+ N_- (2 N_+ N_- - N)]/[N^2(N - 1)]$](/articles/aa/full_html/2018/04/aa32097-17/aa32097-17-eq1.png) , that in our case gives a standard deviation equal to 1.86. Thus, the above number of runs is 2.7σ lower than the expected value, suggesting that a law with an increasing negative slope would better represent these data.
, that in our case gives a standard deviation equal to 1.86. Thus, the above number of runs is 2.7σ lower than the expected value, suggesting that a law with an increasing negative slope would better represent these data.
Considering that the change in w is mainly due to the HXD in the slow leading trail (SLT, see Fig. 11 in Massaro et al. 2010 for a precise definition) and in the rising portion of the pulse, we can use these values to investigate how the delay increases with the photon energy. In the lower panel of Fig. 4 we reported the w differences between the lowest-energy channel (3.6 keV) and the others for the G-1 and the G-2a sets. We note that, in both curves, HXD increases up to ~10 keV and approaches a constant value above this energy; moreover, the positive correlation is confirmed between the HXD and Trec already found by Massa et al. (2013) using BeppoSAX data.
 |
Fig. 2 Two-energy plot for one of the GRS 1915+105 bursts reported in Fig. 1 after a smoothing to reduce the statistical noise. Photon count rates have been scaledto the same range from zero, corresponding to the minimum rate, to 1000 at the highest value. The bisecting black thick straight line is the locus of two coincident burst profiles; the dashed green line is the quadratic best fit to the data and the arrows indicate the time direction of the loop. The loop shape and the anticlockwise direction due to the HXD are clearly apparent. |
 |
Fig. 3 Two-energy plots for the three sources. Data points, obtained by a scaling at the same highest amplitude of light curves witha time resolution of 0.5 s after a smoothing over five points, are represented in red; the thick black lines correspond to equally scaled count rates, and the green solid curves are the quadratic best fits to the data. Left panel: G-2 data in the energy bands 3.22–3.94 keV on the abscissa and 10.82–11.92 keV on the ordinate with a time bin size of 1 s and 3-point running average; central panel: I-2 data in the energy bands 2–6 keV on the abscissa and 6–20 keV on the ordinate with a time bin size of 1 s and 3-point running average; right panel: M-1 and M-2 data (excluding those of the type-I event) in the ranges 2.1–3.8 keV on the abscissa and 11.4–15.2 keV on the ordinate. |
 |
Fig. 4 Upperpanel: energy scaling of the pulse FWHM of the bursts in the pointings G-1 (green squares), G-2a (black circles), and G-2b (orange diamonds). Error bars of the G-2a data set are smaller than the symbols. Power law best fits for all data sets are given by dashed lines, while the broken power-law best fits for G-2a and G-2b data are given by dash-dotted lines. Lower panel: HXD plotted as a function of energy for the G-1 and G-2a data set; the mean recurrence times of the bursts are reported. Colour codes are as in the upper panel. The dashed lines are quadratic best fits. |
3.2.2 IGR J17091−3624
The relatively low count rate and the high intrinsic variability of the burst shapes of this source make the data analysis difficult. To accumulate light curves with a sufficient statistics one has to use broad energy intervals, which makes it harder to distinguish between slightly different pulse widths. A couple of short segments of the light curves in the energy ranges 2–6 keV and 6–20 keV are given in the two upper panels of Fig. 5 to show the high variability of the burst profiles. The nature of these changes is mostly intrinsic, as shown in the same panels of this figure where we plotted the same light curves shifted by 81 s to match together the first and the fifth burst. We note the large changes in the burst duration, in their shape and amplitude as in the case of the last two bursts which almost disappeared in the shifted curves. Nevertheless, a rather weak indication for a smaller w in the high-energy band in a few of these bursts is not completely excluded. Another marginal indication for the existence of HXD is suggested by the two-energy plot shown in the central panel of Fig. 3 for the I-2 set: datapoints are, in fact, scattered in a curved pattern similar to the one in Fig. 2. The quadratic best fit to these data, when compared with the extrapolation of the linear fit of data in the low-count-rate regime, indicates a deviation at high count rates. Similar patterns arealso apparent in the other three data sets indicating that it is not due to some random effects. In any case, a goodquantitative evaluation of the relation between w and E, like in the case of GRS 1915+105, cannot be performed due to the low S/N. A further issue is that one could not establish the direction of the loop if it were really present. This is a relevant point because, as noticed early on by Altamirano et al. (2011) and recently confirmed by Court et al. (2017), the loop in the count rate versus the X-ray colour plane is described in the clockwise direction at variance with the case of GRS 1915+105, indicating thus a Soft X-ray Delay rather than a HXD.
To complete our analysis we also obtained standard spectra of the PCA observations reported in Table 1. We considered an absorbed multicolour disk black-body plus a comptonisation component (wabs*(diskbb+compTT) in XSPEC).The resulting best fits gave spectra with a dominant accretion-disk emission and a comptonised component contributing about 10% of the total emission in the 2–5 keV energy range without any cutoff up to 40 keV. Due to the lack of cutoff energy in the spectra, we fixed the electron plasma temperature of the comptonisation model at the lowest possible value in order to achieve an acceptable χ2 corresponding to a temperature estimate kTc ≈ 60 keV or 70 keV (depending on the spectra). As a result of these fitting procedures, we obtained for the disk an inner temperature kTd of ~1.3 keV and an electron plasma optical depth of about 0.3.
 |
Fig. 5 Two segments of the I-2 light curve of IGR J17091−3624 in the energy bands 2–6 keV (top panel, black) and 6–20 keV (central panel, red) exhibiting a bursting behaviour with a profile typical of the ρ variability class. The bin duration is 0.125 s. The dashed light curves in the top and central panels are the same light curves backshifted to match the fifth burst to the first one, to show the high intrinsic variations of the burst pattern. The superposition of the two data sets, scaled to the same mean amplitude and with the same colours, is plotted in the bottom panel to show the high variability of the burst shape and in particular of the height of the main pulses. We note that in some bursts there is a marginal indication of a pulse width at higher energies shorter than at lower ones. |
3.2.3 MXB 1730−335
The two-energy plot (see Fig. 3, right panel) shows that data points for the energy bands 2.1–3.8 keV and 11.4–15.2 keV are distributed, with a very small dispersion, along a straight line practically coincident with the best fit line, indicating that the burst profiles at these energies are very similar and no HXD is appreciable. Furthermore, the quadratic best fit (green line) gave a negligible second-degree term. This result is also evident from the two segments of the light curves in different energy bands shown in the top and central panels of Fig. 6. The profile is typical of the ρ bursts with the SLT followed by broad pulses and by the FDT. In the bottom panel of Fig. 6 the same two segments are superposed after a scaling to the same amplitude; no apparent difference of the pulse width can be seen between the two curves (see also Fig. 7).
Bagnoli& in’t Zand (2015) described the results of a phase-resolved spectral analysis using a comptonised model and found that a thick corona, with an optical depth ranging from 5 to 7, is necessary. We also performed a spectral analysis from data corresponding to one of the two bursts in the M-2 observation, excluding any contribution by 4U 1728−34: we included both a disk component and a comptonising corona – wabs*(diskbb + compTT), in XSPEC – and obtained results in very good agreement with Bagnoli & in’t Zand (2015), confirming that the emission is dominated by a thick corona without any significant contribution from the disk.
Finally, it is interesting to underline the different behaviour of type-I bursts, frequently observed in this source, whose FWHM exhibits a much lower width at high energies, due to a faster decay at high energies rather than to a delayed increase (see the review paper by Lewin et al. 1993).
 |
Fig. 6 Two segments of the RXTE/PCA light curves of MXB 1730−335 in the ρ variability class in the energy bands 2.1–3.8 keV (top panel, black) and 11.4–15.2 keV (central panel, red). A running average smoothing over five bins was applied to reduce the fluctuations and to show clearly the burst structure. The dashed violet horizontal lines correspond to the mean level of the background and the error bar is the statistical error. The superposition of the two data sets, scaled to the same mean amplitude and with the same colours, is plotted in the bottom panel to show that the pulse width does not change with energy. |
 |
Fig. 7 A segment of the RXTE/PCA M-1 light curves of MXB 1730−335 in the energy bands 2.1–3.8 keV (black) and 11.4–15.2 keV (red), in which at the time of 1250 s a type-I burst is superposed onto the heartbeat variability. These light curves were not rescaled at the same amplitude to better distinguish them. |
4 Discussion
The so-called ρ class of bursting variability, named after the classification introduced by Belloni et al. (2000) for GRS 1915+105, is characterised by a slow brightness increase followed by a much faster rate up to the pulse development, that can be structured either in a single or in a few narrow peaks, terminating through a fast decay to the initial level. This particular structure is observed not only in this unique source, but also in two interesting objects, namely the other microquasar IGR J17091−3624 and the peculiar accreting neutron star binary MXB 1730−335, generally referred to as Rapid Burster. Our aim was to investigate whether the ρ-class bursts of these sources exhibit similar characteristics in an attempt to find a common physical interpretation of the mechanism generating the bursts. In particular, we focused our analysis on the search of a relation between the pulse width and the photon energy.
In a previous paper on GRS 1915+105, Massa et al. (2013) found that the bursts’ structure is related to changes in the mean photon energy, which can be used for measuring the HXD; its occurrence implies that the pulse width w decreases with energy. It is interesting to recall that a similar phenomenon was already noticed in the prompt emission of gamma-ray bursts (GRBs) by Fenimore et al. (1995) who found that the typical burst duration, as measured by their autocorrelation functions, has a power-law dependence on the photon energy as E−s , with ⟨s⟩ = 0.45.
The results of our analysis show that for GRS 1915+105 the decreaseof the pulse width for increasing energies is remarkably regular and can be rather well described by a power law with a mean exponent close to ~0.8, but a slope that increases with energy is also suggested by the data. A similar behaviour cannot be firmly established for IGR J17091−3624 because of the poor statistics and the highly variable burst profiles; we were, therefore, able to find only a very marginal indication on the basis of the two-energy plot and it was practically impossible to obtain a description by means of any functional behaviour. Finally, the decrease of the pulse width with energy is excluded for the Rapid Burster from burst series at energies differing by a factor of about four and not exhibiting any change.
A simple mathematical model of the heating of the disk gas during the unstable growing phase of a burst is the one of an exponentially increasing photon flux with an energy-dependent scale τe (E):
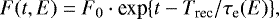 (1)
(1)
up to a peak value followed by a very sharp decrease, as shown in Fig. 8, where the initial values of the curves are neglected with respect to the much higher peak values which are normalised to unity. It is easy to demonstrate that if τe (E) is given by a power law like 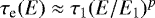 , it results in p = s.
, it results in p = s.
One can derive a relationship between the photon flux time scale and the emitting electron process in a simple dimensional approach by assuming that the energy losses (or gains) of the electrons having energy Ee and the resulting photon energy E can be expressed by power laws:
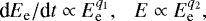 (2)
(2)
from which it is easy to derive
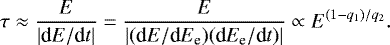 (3)
(3)
For synchrotron or inverse Compton radiation q1 = 2 and q2 = 2, one has s = (q1 − 1)∕q2 = 0.5, a value close to the typical exponent found for GRBs as already noticed by Tavani (1996), but clearly this value is too low for GRS 1915+105. Assuming s ≈ 0.8 = 4∕5, that is, the value that we found in our analysis (see Sect. 3.2.1), one obtains the following relation:
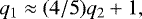 (4)
(4)
which, for a thermal emission process with q2 = 1, gives q1 ≈ 9∕5, a value close to 2 that should be compatible with the results from disk-instability numerical calculations.
The case of the Rapid Burster (MXB 1730−335) presents very interesting differences with respect to GRS 1915+105: the much longer Trec of bursts and their profile independent of energy. One has to take into account the physical structures of these systems. Both GRS 1915+105 and IGR J17091−3624 have accretion disks around black holes and spectral data indicate that ρ-class bursts are practically unaffected by photon scattering in an energetic corona, as discussed in Mineo et al. (2012, 2016) for the former source and in Capitanio et al. (2012) for the latter one. We verified that when IGR J17091−3624 exhibits ρ bursting series, the luminosity fraction from the corona does not exceed 10% and its optical depth is of the order of ~0.03 and likely compatible with zero.
Accretion in the Rapid Burster instead occurs onto a neutron star and therefore the disk, if and when existing, has its inner boundary at the star surface. Moreover, Bagnoli & in’t Zand (2015) and our spectral results indicate the presence of a thick corona, differently from the two other sources. The existence of a thick corona may be relevant for the development of ρ bursts in MXB 1730−335; in particular, it is interesting to verify whether these oscillations may be due to the onset of a limit cycle in the corona itself.
As reported by Bagnoli & in’t Zand (2015), an event, classified forits duration and time evolution as a type-I burst, was observed just at the beginning of one of the ρ bursts in the M-1 data series (see Fig. 7), exhibiting a faster decay at higher energies with respect to lower ones (see also Bagnoli et al. 2013). This event did not affect the simultaneous heartbeat variability and there is no evidence of a related effect in the corona: in particular the rising front is very sharp and independent of energy. This occurrence suggests that type-I and ρ bursts couldoriginate from different sites without any apparent relation. One has, therefore, to introduce either a particular geometric structure of the corona or to require that only a rather smallfraction of photons emitted in the type-I burst would be directed towards the corona.
Physical models for the bursting behaviour of GRS 1915+105 have been proposed since the paper by Taam et al. (1997) reporting its discovery. Neilsen et al. (2011, 2012), on the basis of the phase-resolved spectral analysis, explained the bursts’ structure by means of the superposition of two componentswith different energy spectra and time profiles. These two pulses, one soft and the other one hard, have a different origin. In particular, the latter one should originate in an outflow of energetic plasma from the inner disk as a consequence of the thermal-viscous instability (see Janiuk & Czerny 2005). Our results on the decreasing behaviour ofthe pulse width with the energy then provide an interesting constraint for a realistic modelling of these two components.
More recently, Mir et al. (2016) proposed a model in which the inner radius of the accretion disk changes during the burst with a delayed response to the accretion rate raised to an exponent less than or equal to unity. In this model, however, the origin of the lag is not explained but is rather assumed as a parameter to be derived from best-fit data. Moreover, these authors consider the lag as being due to a phase shift of sinusoidal modulation of the accretion rate, while we demonstrated that it corresponds to a decrease of the pulse width with energy. It would be interesting to verify whether the model proposed by Mir et al. (2016) is able to reproduce the observed burst profiles. Yan et al. (2013, 2017) performed a timing analysis in different segments of the ρ burst profile aimed at studying the properties of quasi-periodic oscillations detected in the Fourier spectra at frequencies higher than ~0.5 Hz. In the more recent paper, these authors considered only two wide energy bands, approximately below and above 5 keV, and found a hard phase lag up to 50 ms. This result, lower than HXDs measured by us, is not in conflict with our finding because it is clearly not related to the decrease of the pulse width for increasing energies.
The complex processes presented in this paper require further ad-hoc analysis and the development of a dedicated physical model that could be addressed in a future paper.
 |
Fig. 8 Approximate modelling of the rising portions of ρ bursts of GRS 1915+105 with exponential law with three e-folding scales: 14 s (black), 8 s (red), 4 s (blue). The corresponding half widths, w, are also indicated. |
Acknowledgements
The authors are grateful to the anonymous referee for comments that helped to improve the paper.
References
- Altamirano, D., Belloni, T., Linares, M., et al. 2011, ApJ, 742, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Bagnoli, T., & in’t Zand, J. J. M. 2015, MNRAS, 450, L52 [NASA ADS] [CrossRef] [Google Scholar]
- Bagnoli, T., in’t Zand, J. J. M., Galloway, D. K., & Watts, A. L. 2013, MNRAS, 431, 1947 [NASA ADS] [CrossRef] [Google Scholar]
- Bagnoli, T., in’t Zand, J. J. M., Patruno, A., & Watts, A. L. 2014, MNRAS, 437, 2790 [NASA ADS] [CrossRef] [Google Scholar]
- Barlow, R. 1989, Statistics. A Guide to the Use of Statistical Methods in the Physical Sciences (Wiley) [Google Scholar]
- Belloni, T., Klein-Wolt, M., Méndez, M., van der Klis, M., & van Paradijs, J. 2000, A&A, 355, 271 [NASA ADS] [Google Scholar]
- Bird, A. J., Bazzano, A., Bassani, L., et al. 2010, ApJS, 186, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Capitanio, F., Del Santo, M., Bozzo, E., et al. 2012, MNRAS, 422, 3130 [NASA ADS] [CrossRef] [Google Scholar]
- Court, J. M. C., Altamirano, D., Pereyra, M., et al. 2017, MNRAS, 468, 4748 [NASA ADS] [CrossRef] [Google Scholar]
- D’Aì, A., La Parola, V., Cusumano, G., et al. 2011, A&A, 529, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fenimore, E. E., in ’t Zand, J. J. M., Norris, J. P., Bonnell, J. T., & Nemiroff,R. J. 1995, ApJ, 448, L101 [NASA ADS] [CrossRef] [Google Scholar]
- FitzHugh, R. 1961, Biophys. J, 1, 445 [CrossRef] [PubMed] [Google Scholar]
- Jahoda, K., Swank, J. H., Giles, A. B., et al. 1996, in EUV, X-Ray, and Gamma-Ray Instrumentation for Astronomy VII, eds. O. H. Siegmund, & M. A. Gummin, Proc. SPIE, 2808, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Jahoda, K., Markwardt, C. B., Radeva, Y., et al. 2006, ApJS, 163, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Janiuk, A., & Czerny, B. 2005, MNRAS, 356, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Lewin, W. H. G., Doty, J., Clark, G. W., et al. 1976, ApJ, 207, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Lewin, W. H. G., van Paradijs, J., & Taam, R. E. 1993, Space Sci. Rev., 62, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Massa, F., Massaro, E., Mineo, T., et al. 2013, A&A, 556, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massaro, E., Ventura, G., Massa, F., et al. 2010, A&A, 513, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massaro, E., Ardito, A., Ricciardi, P., et al. 2014, Ap&SS, 352, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Mineo, T., Massaro, E., D’Ai, A., et al. 2012, A&A, 537, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mineo, T., Massa, F., Massaro, E., & D’Aì, A. 2016, A&A, 586, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mineo, T., Del Santo, M., Massaro, E., Massa, F., & D’Aì, A. 2017, A&A, 598, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mir, M. H., Misra, R., Pahari, M., Iqbal, N., & Ahmad, N. 2016, MNRAS, 457, 2999 [NASA ADS] [CrossRef] [Google Scholar]
- Nagumo, J., Arimoto, S., & Yoshizawa, S. 1962, Proc. IRE, 50, 2061 [Google Scholar]
- Neilsen, J., Remillard, R. A., & Lee, J. C. 2011, ApJ, 737, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Neilsen, J., Remillard, R. A., & Lee, J. C. 2012, ApJ, 750, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Pahari, M., Yadav, J. S., & Bhattacharyya, S. 2014, ApJ, 783, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Shaposhnikov, N., Jahoda, K., Markwardt, C., Swank, J., & Strohmayer, T. 2012, ApJ, 757, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Taam, R. E., Chen, X., & Swank, J. H. 1997, ApJ, 485, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Tavani, M. 1996, ApJ, 466, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, S.-P., Wang, N., Ding, G.-Q., & Qu, J.-L. 2013, ApJ, 767, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, S.-P., Ji, L., Méndez, M., et al. 2017, MNRAS, 465, 1926 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Two segments of RXTE/PCA light curves of GRS 1915+105 in the ρ variability class at three energies showing the HXD phenomenon and the dependence of the pulse width, w, upon energy. Data, after the subtraction of a constant level, are scaled to obtain comparable pulse heights. Upper panel: RXTE G-2a data; lower panel: G-1 data. In the latter data set the recurrence time of the bursts was more than twice longer than that in the former one. We note in both panels the variable duration and shape of individual bursts and in the upper one the small time delay of the peak maxima, particularly in the first and in the third burst. |
| In the text | |
 |
Fig. 2 Two-energy plot for one of the GRS 1915+105 bursts reported in Fig. 1 after a smoothing to reduce the statistical noise. Photon count rates have been scaledto the same range from zero, corresponding to the minimum rate, to 1000 at the highest value. The bisecting black thick straight line is the locus of two coincident burst profiles; the dashed green line is the quadratic best fit to the data and the arrows indicate the time direction of the loop. The loop shape and the anticlockwise direction due to the HXD are clearly apparent. |
| In the text | |
 |
Fig. 3 Two-energy plots for the three sources. Data points, obtained by a scaling at the same highest amplitude of light curves witha time resolution of 0.5 s after a smoothing over five points, are represented in red; the thick black lines correspond to equally scaled count rates, and the green solid curves are the quadratic best fits to the data. Left panel: G-2 data in the energy bands 3.22–3.94 keV on the abscissa and 10.82–11.92 keV on the ordinate with a time bin size of 1 s and 3-point running average; central panel: I-2 data in the energy bands 2–6 keV on the abscissa and 6–20 keV on the ordinate with a time bin size of 1 s and 3-point running average; right panel: M-1 and M-2 data (excluding those of the type-I event) in the ranges 2.1–3.8 keV on the abscissa and 11.4–15.2 keV on the ordinate. |
| In the text | |
 |
Fig. 4 Upperpanel: energy scaling of the pulse FWHM of the bursts in the pointings G-1 (green squares), G-2a (black circles), and G-2b (orange diamonds). Error bars of the G-2a data set are smaller than the symbols. Power law best fits for all data sets are given by dashed lines, while the broken power-law best fits for G-2a and G-2b data are given by dash-dotted lines. Lower panel: HXD plotted as a function of energy for the G-1 and G-2a data set; the mean recurrence times of the bursts are reported. Colour codes are as in the upper panel. The dashed lines are quadratic best fits. |
| In the text | |
 |
Fig. 5 Two segments of the I-2 light curve of IGR J17091−3624 in the energy bands 2–6 keV (top panel, black) and 6–20 keV (central panel, red) exhibiting a bursting behaviour with a profile typical of the ρ variability class. The bin duration is 0.125 s. The dashed light curves in the top and central panels are the same light curves backshifted to match the fifth burst to the first one, to show the high intrinsic variations of the burst pattern. The superposition of the two data sets, scaled to the same mean amplitude and with the same colours, is plotted in the bottom panel to show the high variability of the burst shape and in particular of the height of the main pulses. We note that in some bursts there is a marginal indication of a pulse width at higher energies shorter than at lower ones. |
| In the text | |
 |
Fig. 6 Two segments of the RXTE/PCA light curves of MXB 1730−335 in the ρ variability class in the energy bands 2.1–3.8 keV (top panel, black) and 11.4–15.2 keV (central panel, red). A running average smoothing over five bins was applied to reduce the fluctuations and to show clearly the burst structure. The dashed violet horizontal lines correspond to the mean level of the background and the error bar is the statistical error. The superposition of the two data sets, scaled to the same mean amplitude and with the same colours, is plotted in the bottom panel to show that the pulse width does not change with energy. |
| In the text | |
 |
Fig. 7 A segment of the RXTE/PCA M-1 light curves of MXB 1730−335 in the energy bands 2.1–3.8 keV (black) and 11.4–15.2 keV (red), in which at the time of 1250 s a type-I burst is superposed onto the heartbeat variability. These light curves were not rescaled at the same amplitude to better distinguish them. |
| In the text | |
 |
Fig. 8 Approximate modelling of the rising portions of ρ bursts of GRS 1915+105 with exponential law with three e-folding scales: 14 s (black), 8 s (red), 4 s (blue). The corresponding half widths, w, are also indicated. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


