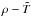| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 18 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201731866 | |
| Published online | 10 January 2018 | |
Magnetic neutron star cooling and microphysics
1 Centre de Recherche Astrophysique de Lyon, Université de Lyon, Université Lyon 1, Observatoire de Lyon, École Normale Supérieure de Lyon, CNRS, UMR 5574, 46 allée d’Italie, 69364 Lyon Cedex 07, France
2 Ioffe Institute, Politekhnicheskaya 26, 194021 Saint Petersburg, Russia
e-mail:
palex@astro.ioffe.ru
3 Central Astronomical Observatory at Pulkovo, Pulkovskoe Shosse 65, 196140 Saint Petersburg, Russia
4 School of Physics, University of Exeter, Exeter, EX4 4QL, UK
Received: 31 August 2017
Accepted: 24 October 2017
Aims. We study the relative importance of several recent updates of microphysics input to the neutron star cooling theory and the effects brought about by superstrong magnetic fields of magnetars, including the effects of the Landau quantization in their crusts.
Methods. We use a finite-difference code for simulation of neutron-star thermal evolution on timescales from hours to megayears with an updated microphysics input. The consideration of short timescales (≲1 yr) is made possible by a treatment of the heat-blanketing envelope without the quasistationary approximation inherent to its treatment in traditional neutron-star cooling codes. For the strongly magnetized neutron stars, we take into account the effects of Landau quantization on thermodynamic functions and thermal conductivities. We simulate cooling of ordinary neutron stars and magnetars with non-accreted and accreted crusts and compare the results with observations.
Results. Suppression of radiative and conductive opacities in strongly quantizing magnetic fields and formation of a condensed radiating surface substantially enhance the photon luminosity at early ages, making the life of magnetars brighter but shorter. These effects together with the effect of strong proton superfluidity, which slows down the cooling of kiloyear-aged neutron stars, can explain thermal luminosities of about a half of magnetars without invoking heating mechanisms. Observed thermal luminosities of other magnetars are still higher than theoretical predictions, which implies heating, but the effects of quantizing magnetic fields and baryon superfluidity help to reduce the discrepancy.
Key words: stars: neutron / stars: magnetars
© ESO, 2018
1. Introduction
Heat stored in neutron stars after their birth is gradually lost to neutrino emission and surface radiation. The rate of these losses depends on the characteristics of a neutron star: its mass, magnetic field, and composition of heat-blanketing envelopes. Theoretically calculated luminosity of the star as a function of its age (the cooling curve) is sensitive to the details of the theory of matter in extreme conditions: high densities, temperatures, and magnetic fields, not reachable in the terrestrial laboratory. Therefore, a comparison of observed surface luminosity with theoretical predictions can potentially provide information not only on the characteristics of a given star, but also on the poorly known properties of matter in extreme conditions. The theory of neutron star cooling has been developed in many papers, starting from the pioneering works by Chiu & Salpeter (1964) and Tsuruta & Cameron (1966). For a recent review of this theory, see Potekhin et al. (2015).
Thermal or thermal-like radiation has been detected from several classes of neutron stars. Particularly interesting are isolated neutron stars with confirmed thermal emission, whose thermal X-ray spectra are not blended with emission from accreting matter or magnetosphere. A comprehensive list of such objects found before 2014 has been compiled by Viganò et al. (2013). Many neutron stars from this list are satisfactorily explained by the cooling theory (see, e.g., Yakovlev et al. 2008; Viganò et al. 2013, and Sect. 4 below). However, the magnetars, a special class of neutron star with superstrong magnetic fields (see Mereghetti et al. 2015; Turolla et al. 2015; Kaspi & Beloborodov 2017, for recent reviews), are much more luminous than ordinary cooling neutron stars of the same age. For example, at age t ~ 10 kyr, typical thermal luminosities are ~(1031−1033) erg s-1 for ordinary neutron stars and several times (1033−1035) erg s-1 for magnetars. Their high luminosities are believed to be fed by magnetic energy stored in the neutron star (Duncan & Thompson 1992), but the mechanism of the release of this energy is uncertain. Several possible heating mechanisms suggested by different authors have recently been analyzed by Beloborodov & Li (2016).
The characteristic magnetic fields of magnetars, determined from their spindown according to the standard model of a rotating magnetic dipole in vacuum, range from ~1013 G to ≈2 × 1015 G (Olausen & Kaspi 2014). In addition to the poloidal magnetic field at the surface, the magnetars are believed to have much stronger toroidal magnetic field embedded in deeper layers (Geppert et al. 2006; Pérez-Azorin et al. 2006), which is corroborated by observations of free precession of the magnetars (Makishima et al. 2014, 2016). For a characteristic poloidal component Bpol of a neutron-star magnetic field to be stable, a toroidal component Btor must be present, such that, by order of magnitude, Bpol ≲ Btor ≲ 1016 G (Bpol/ 1013 G)1/2 (Akgün et al. 2013). Moreover, theoretical arguments (e.g., Bonanno et al. 2005), numerical simulations (e.g., Braithwaite 2008; Lasky et al. 2011; Kiuchi et al. 2011; Mösta et al. 2015), and observational evidence (e.g., Tiengo et al. 2014) show that magnetars possess highly tangled, small-scale magnetic fields, which can be several times stronger than their dipole component (see also Mereghetti et al. 2015; Link & van Eysden 2016, and references therein).
In this paper, we analyze the relative importance of different microphysics inputs in cooling of ordinary neutron stars and magnetars. We model both neutron stars with ground-state and accreted envelopes. We study the sensitivity of the cooling to different microphysics ingredients of the theory, including the equation of state (EoS), baryon superfluidity, opacities, and neutrino emission mechanisms, putting emphasis on the role of recent updates of corresponding theoretical models. We demonstrate the importance of the effects of Landau quantization in the crust of the magnetars on the EoS and thermal conductivity tensor, as well as formation of a condensed radiating surface, possibly covered by a dense atmosphere. The latter effects make the heat-blanketing envelope much more transparent than predicted by the classical theory.
The paper is organized as follows. In Sect. 2, we state the main assumptions, recall the basic equations of the cooling theory, and describe our numerical cooling code. In Sect. 3 we briefly recall the essential physics of neutron star cooling and summarize physics input. In Sect. 4, we examine the influence of different physics input ingredients on cooling of nonmagnetized neutron stars, with special attention being paid to several modern microphysics updates. Section 5 is devoted to the cooling of strongly magnetized neutron stars and the role of Landau quantization. Conclusions are summarized in Sect. 6. Appendices A and B specify some details of our treatment of the EoSs of nonmagnetic and strongly magnetized neutron stars.
2. Simulation of thermal evolution
The most massive central part of a neutron star, its core, consists of a uniform mixture of baryons and leptons. The core is surrounded by the crust, where atomic nuclei form a crystalline lattice, and the electrons form almost ideal, strongly degenerate Fermi gas. In an inner part of the crust, the lattice of nuclei is immersed in a liquid of “dripped” (quasi-free) neutrons. The crust is covered by a liquid layer, the ocean, where the lattice is destroyed by thermal fluctuations. As the star cools down, the bottom layers of the ocean freeze into the crust. The ocean, in turn, is usually covered by a gaseous atmosphere, where the spectrum of outgoing thermal radiation is formed.
About a day after the birth of a neutron star, the temperature everywhere in its interior drops below 1010 K. At this temperature, the chemical potentials of nucleons at densities ρ ≳ 1012 g cm-3 and of electrons at ρ ≳ 108 g cm-3 (without the rest energies) are much higher than their kinetic thermal energies. At these conditions, a good approximation is to describe the state of matter as cold nuclear matter in beta equilibrium, resulting in an effectively barotropic EoS. Therefore neutron-star cooling simulations are traditionally performed by treating the internal mechanical structure of the star as decoupled from its thermal structure. The outer boundary condition for simulations of thermal evolution is then provided by a solution of the stationary heat transport equation at ρ<ρb, where the commonly accepted value ρb = 1010 g cm-3 (Gudmundsson et al. 1983) is a trade-off between the applicability of a barotropic EoS at ρ>ρb and the stationary approximation at ρ<ρb.
This approach simplifies the cooling simulations, but it does not allow one to trace the rapid processes in the crust, accompanied by sudden heat release, which may result from accretion episodes, starquakes, magnetic reconnection events, and so on, and which are probably common in the magnetars (Mereghetti et al. 2015; Turolla et al. 2015; Kaspi & Beloborodov 2017). In this paper we follow a different approach, which is traditional for the nondegenerate, nonrelativistic stars, and which was extended to the case of general relativity by Richardson et al. (1979).
We assume the mechanical structure to be spherical. Appreciable deviations from the spherical symmetry can be caused by ultra-strong magnetic fields (B ≳ 1017 G) or by rotation with ultra-short periods (less than a few milliseconds), but we will not consider such extreme cases. We also assume a spherically symmetric thermal structure. This assumption can be violated by local heat releases or by large-scale (e.g., dipolar) strong magnetic fields. For highly tangled small-scale fields, the spherical symmetry is a reasonable first approximation.
In the spherical symmetry, the thermal and mechanical structure are governed by six first-order differential equations for radius r, gravitational potential Φ, gravitational mass Mr inside a sphere of radius r, luminosity Lr passing through this sphere, pressure P, and temperature T as functions of the baryon number a interior to a given shell (Richardson et al. 1979; cf. Thorne 1977). The time t enters only the equation for Lr in the form of the coordinate time derivative of the entropy per baryon.
The mechanical structure of the star is defined by equations
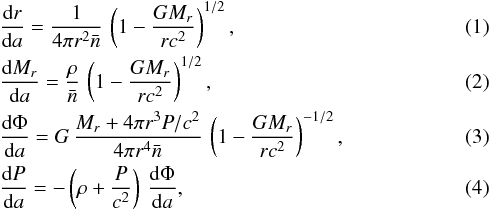 where
where 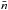 is the mean number density of baryons, G is the Newtonian constant of gravitation and c is the speed of light in vacuum. These equations are integrated from r = 0 and Mr = 0 at the center of the star outwards, starting from a predefined central baryon density and keeping ρ and P related to
is the mean number density of baryons, G is the Newtonian constant of gravitation and c is the speed of light in vacuum. These equations are integrated from r = 0 and Mr = 0 at the center of the star outwards, starting from a predefined central baryon density and keeping ρ and P related to 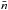 via the EoS, until the outer boundary condition is satisfied (e.g., a predefined mass density at the outer boundary ρb is reached). The boundary condition for Φ is provided by the Schwarzschild metric outside the star,
via the EoS, until the outer boundary condition is satisfied (e.g., a predefined mass density at the outer boundary ρb is reached). The boundary condition for Φ is provided by the Schwarzschild metric outside the star, 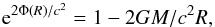 (5)where R and M = MR are the stellar radius and mass. In practice, Eq. (3) is integrated for a shifted potential Φ(r)−Φ(0), with the initial value equal to zero at the center of the star, and afterwards the value of the shift Φ(0) is found from Eq. (5).
(5)where R and M = MR are the stellar radius and mass. In practice, Eq. (3) is integrated for a shifted potential Φ(r)−Φ(0), with the initial value equal to zero at the center of the star, and afterwards the value of the shift Φ(0) is found from Eq. (5).
The heat flux through a spherical surface is related to gradient of the redshifted temperature 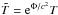 by equation
by equation 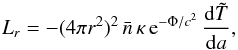 (6)where κ is the thermal conductivity measured in the local. Finally, time-dependence is introduced by equation (Richardson et al. 1979)
(6)where κ is the thermal conductivity measured in the local. Finally, time-dependence is introduced by equation (Richardson et al. 1979) 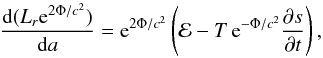 (7)where ℰ is the net rate of energy generation per baryon and ∂s/∂t is the coordinate time derivative of the entropy per baryon (e− Φ /c2∂s/∂t is the derivative evaluated in the local rest frame of matter). Equation (7) can be combined with Eq. (6) to form
(7)where ℰ is the net rate of energy generation per baryon and ∂s/∂t is the coordinate time derivative of the entropy per baryon (e− Φ /c2∂s/∂t is the derivative evaluated in the local rest frame of matter). Equation (7) can be combined with Eq. (6) to form 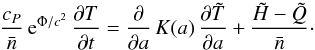 (8)Here, cP is the heat capacity per unit volume at constant pressure,
(8)Here, cP is the heat capacity per unit volume at constant pressure, 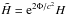 and
and 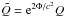 are redshifted powers of energy sources and sinks, respectively, per unit volume, and
are redshifted powers of energy sources and sinks, respectively, per unit volume, and 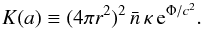 (9)Equation (8) can be written in the form of the usual thermal diffusion equation
(9)Equation (8) can be written in the form of the usual thermal diffusion equation 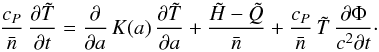 (10)In practice, the last term on the right-hand side is small compared to typical values of the left-hand side. Therefore, in a finite-difference scheme of solution, this term can be treated as an external source, with ∂Φ /∂t evaluated from the solution at the preceding time step. The boundary condition to Eq. (10) at the stellar center is
(10)In practice, the last term on the right-hand side is small compared to typical values of the left-hand side. Therefore, in a finite-difference scheme of solution, this term can be treated as an external source, with ∂Φ /∂t evaluated from the solution at the preceding time step. The boundary condition to Eq. (10) at the stellar center is 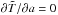 . The outer boundary condition follows from Eq. (6):
. The outer boundary condition follows from Eq. (6): 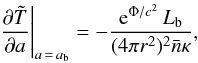 (11)where Lb is the energy flux through the outer boundary a = ab, which is provided by the quasi-stationary thermal structure of a thin envelope outside this boundary. Since we solve the nonstationary problem using the temperature-dependent EoS in the outer crust, the position of the boundary is not restricted by the requirement that the plasma should be degenerate at ρb = ρ(ab). Therefore, the thickness of the quasi-stationary envelope can be adapted to an astrophysical problem of interest. In the present work, we choose the mass of the quasi-stationary envelope ΔM so as to ensure that plasma is fully ionized at ρ>ρb. At B = 0, this condition is guaranteed for the mass of an envelope ΔM = 10-12M⊙. In the case of strong magnetic fields we find it appropriate to increase the envelope mass to ΔM = (10-11−10-9) M⊙, because the Landau quantization suppresses opacities (see Sect. 3.3), which results in quick thermal relaxation of such massive envelopes. We take the partial ionization into account in the outer quasi-stationary boundary layer only. In the deeper layers, where the time-dependent problem is being solved, we use the fully ionized plasma model.
(11)where Lb is the energy flux through the outer boundary a = ab, which is provided by the quasi-stationary thermal structure of a thin envelope outside this boundary. Since we solve the nonstationary problem using the temperature-dependent EoS in the outer crust, the position of the boundary is not restricted by the requirement that the plasma should be degenerate at ρb = ρ(ab). Therefore, the thickness of the quasi-stationary envelope can be adapted to an astrophysical problem of interest. In the present work, we choose the mass of the quasi-stationary envelope ΔM so as to ensure that plasma is fully ionized at ρ>ρb. At B = 0, this condition is guaranteed for the mass of an envelope ΔM = 10-12M⊙. In the case of strong magnetic fields we find it appropriate to increase the envelope mass to ΔM = (10-11−10-9) M⊙, because the Landau quantization suppresses opacities (see Sect. 3.3), which results in quick thermal relaxation of such massive envelopes. We take the partial ionization into account in the outer quasi-stationary boundary layer only. In the deeper layers, where the time-dependent problem is being solved, we use the fully ionized plasma model.
We solve the set of Eqs. (1)–(10) by a finite-difference scheme on a non-uniform, adaptive grid in a and t. First, at t = 0, we define a starting temperature profile (usually constant 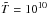 K, but we have checked that the start from
K, but we have checked that the start from 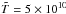 K changes the surface temperature by <1% at t ≳ 1 h) and solve the set of Eqs. (1)–(4) by the Runge-Kutta method. In order to prevent accuracy loss in the outer crust and ocean, where a is nearly constant as a function of ρ, we use the difference (ab−a) as an independent variable. At each t = tj, we introduce a nonuniform grid in this variable and choose a time step Δtj so as to ensure smallness of variations of T and P between the neighboring grid points and between the time tj and tj + 1 = tj + Δtj. We solve the difference equation, that approximates Eq. (10), by a purely time-implicit energy-conservative scheme (Samarskii 2001, Chapter 8, Eqs. (35), (36), (39)). This scheme would be unconditionally stable if
K changes the surface temperature by <1% at t ≳ 1 h) and solve the set of Eqs. (1)–(4) by the Runge-Kutta method. In order to prevent accuracy loss in the outer crust and ocean, where a is nearly constant as a function of ρ, we use the difference (ab−a) as an independent variable. At each t = tj, we introduce a nonuniform grid in this variable and choose a time step Δtj so as to ensure smallness of variations of T and P between the neighboring grid points and between the time tj and tj + 1 = tj + Δtj. We solve the difference equation, that approximates Eq. (10), by a purely time-implicit energy-conservative scheme (Samarskii 2001, Chapter 8, Eqs. (35), (36), (39)). This scheme would be unconditionally stable if 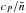 , K(a),
, K(a), 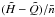 were constant, so the time step Δtj is not limited by the Courant-Friedrichs-Lewy condition. The values of the coefficients are evaluated at the next layer tj + 1, so the scheme is nonlinear. Self-consistent solution for
were constant, so the time step Δtj is not limited by the Courant-Friedrichs-Lewy condition. The values of the coefficients are evaluated at the next layer tj + 1, so the scheme is nonlinear. Self-consistent solution for 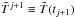 and coefficients of the difference equation at t = tj + 1 is found by an iterative method. At each iteration, the coefficients of the equation, found on the previous iteration, are kept fixed, so that the scheme becomes linear and the values of
and coefficients of the difference equation at t = tj + 1 is found by an iterative method. At each iteration, the coefficients of the equation, found on the previous iteration, are kept fixed, so that the scheme becomes linear and the values of 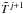 on the new layer tj + 1 are found by the elimination method in terms of the function
on the new layer tj + 1 are found by the elimination method in terms of the function 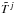 on the current layer tj (Samarskii 2001). If a variation of
on the current layer tj (Samarskii 2001). If a variation of 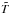 at the time step Δtj proves to be insufficiently small at some point, we diminish Δtj and repeat the calculation for a new layer tj + 1. After the solution is found for
at the time step Δtj proves to be insufficiently small at some point, we diminish Δtj and repeat the calculation for a new layer tj + 1. After the solution is found for 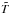 on a given layer, the mechanical structure is adjusted (if necessary) using Eqs. (1)–(4). After the adjustment, the values of
on a given layer, the mechanical structure is adjusted (if necessary) using Eqs. (1)–(4). After the adjustment, the values of 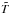 on the new grid in a are obtained by interpolation from the values on the previous grid. The overall accuracy of the solution has been checked by variation of the criteria for choosing steps in t and a and the number of iterations.
on the new grid in a are obtained by interpolation from the values on the previous grid. The overall accuracy of the solution has been checked by variation of the criteria for choosing steps in t and a and the number of iterations.
3. Physics input
3.1. The essential physics of neutron star cooling
The essential physics ingredients needed to build a model of a cooling neutron star, are the EoS (including P, ρ, and cP as functions of 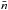 and T), rates of different neutrino emission mechanisms responsible for the energy sink, and thermal conductivity. These ingredients are substantially different in different shells of the star: the atmosphere and outer ocean, where ionization of atoms can be incomplete; the inner ocean and outer crust, which consist of fully ionized electron-ion Coulomb plasmas, liquid or solid depending on ρ, T, and chemical composition; the inner crust at ρnd<ρ<ρcc, where free neutrons are present; and the core at ρ>ρcc, consisting of a uniform matter. Here, ρnd ≈ 4.3 × 1011 gcm-3 is the neutron drip density, and ρcc ≈ (1.0−1.5) × 1014 g cm-3 is the density at the crust-core phase transition. For the present work, we have restricted ourselves by the npeμ matter, that is, matter composed of nucleons and leptons without free hyperons, mesons, or quarks.
and T), rates of different neutrino emission mechanisms responsible for the energy sink, and thermal conductivity. These ingredients are substantially different in different shells of the star: the atmosphere and outer ocean, where ionization of atoms can be incomplete; the inner ocean and outer crust, which consist of fully ionized electron-ion Coulomb plasmas, liquid or solid depending on ρ, T, and chemical composition; the inner crust at ρnd<ρ<ρcc, where free neutrons are present; and the core at ρ>ρcc, consisting of a uniform matter. Here, ρnd ≈ 4.3 × 1011 gcm-3 is the neutron drip density, and ρcc ≈ (1.0−1.5) × 1014 g cm-3 is the density at the crust-core phase transition. For the present work, we have restricted ourselves by the npeμ matter, that is, matter composed of nucleons and leptons without free hyperons, mesons, or quarks.
The heat capacity, neutrino emissivity, and heat transport by nucleons can be strongly affected by nucleon superfluidity in the inner crust and the core, by many-body in-medium effects in the core, and by magnetic field in any region of the star, if the field is sufficiently strong (see Potekhin et al. 2015, for review).
In magnetic fields, the heat transport becomes anisotropic, so that the conductivity is a tensor. For the dominant electron heat conduction mechanisms, this effect is important if the Hall magnetization parameter ωg/νcoll is large enough. Here, ωg is electron gyrofrequency and νcoll is an effective collision frequency of heat carriers (for quantitative estimates in different heat-transport regimes see, e.g., Potekhin et al. 2015). The scalar κ that is needed in the spherically symmetric model, Eqs. (6)–(11), is an appropriate effective value. If the field is large-scale, for example dipolar, then a locally one-dimensional approximation can be applied with effective κ = κ∥ cos2θB + κ⊥ sin2θB, where κ∥ and κ⊥ are the conductivities along and across the field, respectively, and θB is the angle between the magnetic field and the normal to the surface. In the case of highly tangled magnetic fields, which we consider here, a more appropriate model is the local average, κ = κ∥/ 3 + 2κ⊥/ 3 (e.g., Potekhin et al. 2005).
In the npeμ matter of the core of a neutron star, heat is carried mainly by electrons, muons, neutrons, and protons. In the crust, the main heat carriers are electrons (contributions from neutrons in the inner crust and from phonons are less important). In the ocean and atmosphere, the competing heat transport mechanisms are the radiative and electron conduction.
If the magnetic field is nonquantizing, it does not affect heat transport by uncharged carriers (photons, phonons, and neutrons). It also does not affect the longitudinal transport by charged particles (electrons, muons, and protons), but suppresses the corresponding transverse heat transport. In the degenerate matter, the suppression factor is ≈1/ [1 + (ωg/νcoll)2]. The nonquantizing magnetic field does not affect the EoS.
A quantizing magnetic field affects both longitudinal and transverse conductivities and the EoS. If the field is strongly quantizing, so that all particles reside on the ground Landau level, these effects are quite pronounced. For the electrons in the crust, the field is strongly quantizing if T ≪ Tcycl = ħeB/meckB = 1.3434 × 108B12 K and ρ<ρB, where 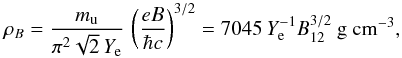 (12)mu is the unified atomic mass unit, Ye is the number of electrons per baryon, and B12 ≡ B/ 1012 G (see, e.g., Potekhin & Chabrier 2013, Sect. 4.2.2). For example, if the crust has the ground-state composition and B = 1016 G, then ρB ≈ 1.8 × 1010 g cm-3. In practice, magnetic field can be considered as nonquantizing if either ρ ≫ ρB or T ≫ Tcycl.
(12)mu is the unified atomic mass unit, Ye is the number of electrons per baryon, and B12 ≡ B/ 1012 G (see, e.g., Potekhin & Chabrier 2013, Sect. 4.2.2). For example, if the crust has the ground-state composition and B = 1016 G, then ρB ≈ 1.8 × 1010 g cm-3. In practice, magnetic field can be considered as nonquantizing if either ρ ≫ ρB or T ≫ Tcycl.
3.2. Equation of state
The EoS for the core of neutron stars is sensitive to the details of fundamental physical theory of matter at extreme densities. There is thus an intrinsic connection between the macroscopic structure and evolution of the neutron stars and the underlying fundamental interactions between the constituent particles at the microscopic level. There is a large number of different theoretical approaches to construction of the EoS of superdense matter (see, e.g., the excellent recent review by Oertel et al. 2017). Here we mainly use the results by Pearson et al. (in prep.), who have developed a unified treatment of the outer and inner crusts and the core of a neutron star, calculating the zero-temperature equation of state in each region with the same energy-density functional from the “Brussels-Skyrme” (BSk) family of functionals. They considered three such functionals, labeled BSk22, BSk24 and BSk25, which are based on generalized Skyrme-type forces supplemented with realistic contact pairing forces. The parameters of these models are constrained by Goriely et al. (2013) to fit the database of 2353 nuclear masses (Audi et al. 2014) and to be consistent with the EoS of neutron-star core calculated by Li & Schulze (2008) within the Brueckner-Hartree-Fock approach, using the realistic Argonne v18 nucleon-nucleon potential (Wiringa et al. 1995) and the phenomenological three-body forces that employ the same meson-exchange parameters as the Argonne v18 potential. We have selected to use the EoS BSk24 as our basic model, because it provides the best agreement with various experimental constraints (nuclear mass measurements, restrictions derived from heavy-ion collision experiments, etc.). It is very similar to the BSk21 EoS model (Potekhin et al. 2013, and references therein), based on the generalized Skyrme functional fitted to the previous atomic mass evaluation.
In view of a considerable theoretical uncertainty in EoS properties at supranuclear densities ρ ≳ ρ0, where ρ0 ≈ 2.7 × 1014 g cm-3 is the normal nuclear density, we also use an alternative APR EoS (Akmal et al. 1998), based on variational calculations. We adopt the version of the APR model, named A18+δv+UIX∗ in Akmal et al. (1998), where the Argonne v18 potential is supplemented by three-body force UIX∗ and so-called relativistic boost interaction (Forest et al. 1995). The force UIX∗ is the phenomenological Urbana UIX three-body force model (Pudliner et al. 1995), refitted to take account of the relativistic boost. The APR EoS is not unified: it is applicable only to the core but not to the crust. In the crust, therefore, we continue using the BSk24 model. For comparison, we also consider the ground-state nuclear composition of the crust calculated in the Hartree-Fock approximation by Negele & Vautherin (1973; hereafter NV) and the EoS, calculated by Douchin & Haensel (2001) using the liquid-drop model with parameters derived from the Skyrme-Lyon effective potential SLy4.
Accretion of fresh material onto a neutron star can change the crust composition. We include this possibility by using the model of consecutive layers of H, 4He, 12C, and 16O, previously employed in Potekhin et al. (2003), but with more accurate 12C and 16O boundaries (Potekhin & Chabrier 2012), determined by the balance between the cooling due to neutrino emission and heating due to thermonuclear burning. Beyond the 16O boundary, we adopt the composition of the accreted crust obtained by Haensel & Zdunik (1990).
Most of the quantities related to the inner crust and the core that are needed for modeling thermal evolution of a nonmagnetized neutron star (pressure and energy density, number fraction of electrons in the core, characteristics of nuclei in the inner crust, effective masses of nucleons, etc.) are implemented in our code via explicit parametrizations (see Appendix A). They are based on the theoretical models (BSk, APR, SLy4) which neglect the effects of finite temperature and strong magnetic fields (T = 0, B = 0 approximation).
In the outer crust and the ocean, all thermodynamic functions at any B and T are provided by the model of a fully ionized magnetized Coulomb plasma (Potekhin & Chabrier 2013). This model is not directly applicable in the inner crust and the core, because it does not take into account thermodynamic effects of weak and strong interactions between free nucleons, which are important at ρ>ρnd. In this density range, we use the nonmagnetic EoS models described above and add corrections due to the magnetic field according to an approximate model described in Appendix B. The same model is used to calculate specific heat contributions of all particles at all densities and magnetic fields (with the use of effective masses of neutrons and protons, 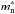 and
and 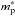 ).
).
Specific heat contributions of free baryons can be affected by their superfluidity. The principal types of superfluidity arise from the singlet Cooper pairing of protons in the core, triplet pairing of neutrons in the core, and singlet pairing of free neutrons in the inner crust of the star. The modifications of the heat capacity by these types of superfluidity are described by reduction factors, presented by Yakovlev et al. (1999; with a typo fixed according to footnote 1 in Potekhin et al. 2015) as functions of T/Tcrit, where Tcrit is the critical temperature for a given type of superfluidity. In the dense matter, different types of triplet pairs of neutrons can form a superposition (Leinson 2010). For simplicity hereafter we restrict ourselves by considering the 3P2, mJ = 0 superfluidity in the case of triplet pairing (“Type B superfluidity” of Yakovlev et al. 1999).
The critical temperatures Tcrit are related to the gaps in the energy spectra of the baryons, which are sensitive to the details of underlying microscopic theory. A wealth of models have been developed in the literature, resulting in different dependencies Tcrit on the number densities of neutrons nn and protons np. In general, these dependencies have an umbrella shape, with a maximum typically ~109−1010 K for singlet type and ≲109 K for triplet type of the Cooper pairs. We adopt the gap parametrization of Kaminker et al. (2001) and take the parameter values from Table 1 of Ho et al. (2015).
3.3. Heat transport
In the core of a neutron star, the heat is carried by baryons (n, p) and leptons (e, μ). This heat transport is sensitive to the baryon superfluidity. The conduction by baryons is also affected by the in-medium effects.
The most advanced studies of these heat transport mechanisms with allowance for the effects of superfluidity have been performed by Shternin & Yakovlev (2007; in the case of transport by leptons) and by Shternin et al. (2013; in the case of transport by baryons). The results of Shternin & Yakovlev (2007) are given by analytical fits, which we have incorporated in the cooling code. The results of Shternin et al. (2013) are taken into account in an approximate manner, according to Potekhin et al. (2015), who find it sufficient to multiply the conductivities obtained in the effective-mass approximation (Baiko et al. 2001) by a factor of 0.6 to reproduce the thermal conductivity of Shternin et al. (2013) with an accuracy of several percent in the entire density range of interest.
The most important heat carriers in the crust and ocean of the neutron star are the electrons. In the atmosphere, the heat is carried mainly by photons. In general, the two mechanisms work in parallel, hence κ = κr + κe, where κr and κe denote the radiative (r) and electron (e) components of the thermal conductivity κ.
We calculate the electron thermal conductivities in the crust and ocean, including the effects of strong magnetic fields, as described in Potekhin et al. (2015). The radiative conductivity is calculated in the model of fully ionized plasma, taking into account free-free transitions and scattering, 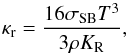 (13)where KR is the Rosseland mean radiative opacity, and σSB is the Stefan-Boltzmann constant. For nondegenerate, nonrelativistic electron-ion plasma without a quantizing magnetic field, the photon-electron scattering opacity Ksc equals neσT/ρ, where ne is the number density of electrons and σT is the Thomson cross section. Under the same conditions, the Rosseland opacities due to the free-free transitions Kff and due to the combined action of both free-free transitions and scattering were calculated and fitted by analytical formulae (Potekhin & Yakovlev 2001), based on a fit to the frequency-dependent Gaunt factor obtained by Hummer (1988).
(13)where KR is the Rosseland mean radiative opacity, and σSB is the Stefan-Boltzmann constant. For nondegenerate, nonrelativistic electron-ion plasma without a quantizing magnetic field, the photon-electron scattering opacity Ksc equals neσT/ρ, where ne is the number density of electrons and σT is the Thomson cross section. Under the same conditions, the Rosseland opacities due to the free-free transitions Kff and due to the combined action of both free-free transitions and scattering were calculated and fitted by analytical formulae (Potekhin & Yakovlev 2001), based on a fit to the frequency-dependent Gaunt factor obtained by Hummer (1988).
Quantizing magnetic fields reduce the Rosseland mean radiative opacities. The reduction factors for the nondegenerate, nonrelativistic plasmas were calculated by Silant’ev & Yakovlev (1980) and fitted by Potekhin & Yakovlev (2001).
Propagation of electromagnetic waves is quenched at photon frequencies below the plasma frequency. The resulting increase of the Rosseland opacity can be approximated by a density-dependent multiplication factor, which equals 1 at low ρ and high T and increases at high ρ or low T (Potekhin et al. 2003).
The scattering opacities are modified by the electron degeneracy at high ρ and by the Compton effect at T ≳ 108 K. An accurate analytical description of both these effects is given by Poutanen (2017).
The free-free opacities are suppressed by electron degeneracy. In the absence of the Landau quantization, the free-free opacities at arbitrary degeneracy have been fitted by Schatz et al. (1999), based on numerical calculations of Itoh et al. (1991). The latter calculations, as well as the above-mentioned results of Hummer (1988), were based on the tables of free-free absorption coefficient as a function of the electron velocity and photon frequency, calculated by Karzas & Latter (1961).
The fit of Schatz et al. (1999) is inapplicable in the case of quantizing magnetic fields. On the other hand, the results of Silant’ev & Yakovlev (1980) and Potekhin & Yakovlev (2001) are only applicable for nondegenerate nonrelativistic plasmas. In practice, for the T and B values typical for neutron star crusts, the effects of electron degeneracy are most important at ρ ≳ ρB, where the field is only weakly quantizing. Therefore we neglect the effect of quantizing magnetic field on the radiative opacities of degenerate electrons and apply the magnetically modified opacities for nondegenerate electrons. A smooth transition between the two regimes is provided by the weight factor exp(−T/TF,e), where TF,e is the electron Fermi temperature in a strongly quantizing magnetic field (Potekhin & Chabrier 2013).
At high temperatures T ≳ 109 K, electron-positron pairs become abundant and contribute to the radiative opacities. We calculate the abundance of the e+e− pairs from the standard relation μ+ + μ− = 0 (Landau & Lifshitz 1980), where μ± are the chemical potentials of e±, including the rest energy, calculated with allowance for the quantizing magnetic field.
Figure 1 shows examples of radiative opacities, calculated at different temperatures, densities, and magnetic field strengths in the model of a fully ionized iron plasma. We see that strong magnetic fields reduce the opacities at lower densities by orders of magnitude. At high densities, the plasma becomes degenerate, and the opacities merge with nonmagnetic ones. The increase of the opacities at small ρ and high T is due to the contribution of the e+e− pairs. The sharp increase at high ρ and at low T is due to the plasma-frequency cutoff. However, the electron conduction anyway dominates at high ρ and low T, so the cutoff is unimportant for cooling simulations. If we replace iron by light chemical elements, which is appropriate in the case of accreted envelopes, the opacities decrease (e.g., for He the decrease reaches nearly an order of magnitude at T ≲ 108 K), but the picture remains qualitatively the same.
In the atmosphere, which provides the outer boundary condition to Eq. (10), plasma can be partially ionized. For the nonmagnetic atmospheres, we use the EoS and Rosseland mean opacities provided either by the Opacity Library (opal; Rogers & Iglesias 1998) or by the Opacity Project (op; Mendoza et al. 2007, and references therein). We have checked that the differences between the opal and op opacities are negligible for the conditions of our interest. For strongly magnetized atmospheres, we use the model of fully ionized plasma for iron and the EoS and opacities from Potekhin & Chabrier (2004) for hydrogen.
 |
Fig. 1 Rosseland mean radiative opacities due to the free-free transitions and Compton scattering in the model of fully ionized iron plasma as functions of mass density at different temperatures (marked near the curves) and magnetic fields B = 0, 1012 G, 1014 G, and 1016 G (shown by different line styles). |
3.4. Neutrino emission
Yakovlev et al. (2001) reviewed the rich variety of reactions with neutrino emission in the compact stars and presented convenient fitting formulae for applications. The rates of reactions with participation of free neutrons and protons are strongly changed if these particles are superfluid. Moreover, the very existence of nucleon superfluidity gives rise to a new neutrino emission mechanism by Cooper pair breaking and formation (PBF), most powerful at T ~ Tcrit.
The most important reactions in the neutron-star crust and npe matter in the core with references to the appropriate fitting formulae are collected in Table 1 of Potekhin et al. (2015). In the crust, they are plasmon decay, electron-nucleus bremsstrahlung, and electron-positron annihilation. In the core, the most important reactions are different branches of direct and modified Urca processes, baryon bremsstrahlung, and the PBF at T ~ Tcrit. The reactions with participation of muons, fully analogous to those with the electrons, should be included for the npeμ matter. A strong magnetic field brings about additional neutrino emission processes: electron synchrotron radiation and, if protons are superconducting, bremsstrahlung due to scattering of electrons on fluxoids (Yakovlev et al. 2001).
The direct Urca processes are most powerful, but operate only if the proton fraction is large enough, which occurs above a certain threshold baryon density 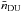 (e.g., Haensel 1995). Therefore, those neutron stars whose mass M exceeds a threshold MDU, where
(e.g., Haensel 1995). Therefore, those neutron stars whose mass M exceeds a threshold MDU, where 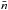 exceeds
exceeds 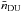 at the center of the star, rapidly cool down via the direct Urca processes (Lattimer et al. 1991; Page & Applegate 1992).
at the center of the star, rapidly cool down via the direct Urca processes (Lattimer et al. 1991; Page & Applegate 1992).
It is worthwhile noticing several updates in the relevant neutrino reaction rates that have been developed recently, which improve the results of Yakovlev et al. (2001). An improved fit to the emission rate due to plasmon decay, which has a larger validity range, has been constructed by Kantor & Gusakov (2007). Electron-nucleus bremsstrahlung rates for arbitrary (not only ground state) composition of the crust have been calculated and fitted by Ofengeim et al. (2014). The reduction of the neutrino emissivity of modified Urca and nucleon-nucleon bremsstrahlung processes by superfluidity of neutrons and protons in neutron-star cores has been revised by Gusakov (2002), who also presented a corrected phase-space factor for the modified Urca process in the case of a large proton fraction. Neutrino emission caused by the Cooper PBF has been recalculated by accurately taking into account conservation of the vector weak currents by Leinson & Pérez (2006) for the singlet Cooper pairing of baryons and by Kolomeitsev & Voskresensky (2008) for the triplet pairing. Leinson (2010) described a modification of the PBF neutrino emission rate due to the anomalous contribution to the axial current, arising from the off-diagonal components of the vertex matrix in the Nambu-Gorkov formalism for the nucleon interactions with the external neutrino field.
Not all of these improvements have been so far accurately included in the widely used neutron-star cooling codes and recent calculations (e.g., Page et al. 2009, 2011; Ho et al. 2015; Shternin & Yakovlev 2015; Page 2016; Taranto et al. 2016). For example, the anomalous axial PBF contribution results in a multiplication of the PBF neutrino-emission rate in the case of triplet pairing by a factor of 0.19 compared to Yakovlev et al. (2001), which is four times smaller than the factor 0.76 effectively used in the recent cooling calculations. Besides, the suppression of the contribution to the PBF emission rate in the vector channel of weak interactions (Leinson & Pérez 2006; Kolomeitsev & Voskresensky 2008) is usually taken into account by setting this contribution to zero, whereas a more accurate estimate is given by a small but non-zero multiplication factor ~(pF/m∗c)2, where pF is the Fermi momentum of the relevant nucleons.
In the superdense matter of the core, the neutrino emission rates are affected by the many-body “in-medium effects” (e.g., Voskresensky 2001, and references therein). We take account of these effects following Shternin & Baldo (in prep.) and Shternin (priv. comm.), who have obtained in-medium enhancement factors for the modified Urca emission rates. They also found an additional enhancement of the modified Urca emission rate near the threshold for the opening of the direct Urca process, which results in a non-standard temperature dependence of the emission rate Q ∝ T7, intermediate between Q ∝ T8 and T6 for the modified and direct Urca processes, respectively.
Some neutrino emission rates can be modified by strong magnetic fields. For instance, Baiko & Yakovlev (1999) showed that the threshold for the opening of the direct Urca processes is smeared out over some B-dependent scale, and described this smearing by simple formulae, which we include in the present treatment of the cooling. They also showed that a strong magnetic field causes oscillations of the reaction rate in the permitted domain of the direct Urca reaction, but the latter effect, albeit interesting, appears to be unimportant for the cooling.
 |
Fig. 2 Theoretical cooling curves (redshifted thermal luminosity |
4. Cooling of nonmagnetized neutron stars
Before considering the effects of superstrong magnetic fields on neutron star cooling, let us examine the role of the microphysics updates mentioned in Sect. 3. The solid black curve in Fig. 2 is the cooling curve of our fiducial basic model: neutron star mass M = 1.4 M⊙, BSk24 EoS, which gives stellar radius R = 12.6 km for this M, boundary layer of mass ΔM = 10-12M⊙, which is assumed quasi-stationary and may be partially ionized, and the physics input described in Sect. 3, but without baryon superfluidity. Although the absence of baryon superfluidity seems unrealistic, it is a convenient starting approximation for the basic model, to which all comparisons will be made.
In the main frame of the figure we show evolution of the redshifted surface luminosity, 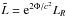 . Errorbars and arrows show observational estimates of the ages and thermal luminosities of 44 neutron stars with confirmed thermal emission. The first 41 sources are taken from Table 3 of Potekhin et al. (2015), and are numbered according to their order in that table, which was derived from the catalog of Viganò et al. (2013) with the addition of one source, PSR J1741−2054 (object number 13, Karpova et al. 2014; Marelli et al. 2014). For the thermal luminosity of the neutron star CXO J232327.9+584842 in the supernova remnant Cassiopeia A (object number 4, often dubbed Cas A NS) we have adopted improved observational data on
. Errorbars and arrows show observational estimates of the ages and thermal luminosities of 44 neutron stars with confirmed thermal emission. The first 41 sources are taken from Table 3 of Potekhin et al. (2015), and are numbered according to their order in that table, which was derived from the catalog of Viganò et al. (2013) with the addition of one source, PSR J1741−2054 (object number 13, Karpova et al. 2014; Marelli et al. 2014). For the thermal luminosity of the neutron star CXO J232327.9+584842 in the supernova remnant Cassiopeia A (object number 4, often dubbed Cas A NS) we have adopted improved observational data on  (Posselt et al. 2013). We have supplemented this catalog with three neutron stars with recently measured thermal fluxes: two neutron stars with carbon envelopes (sources 42 and 43, Klochkov et al. 2015, 2016), and one pulsar (source 44, Danilenko et al. 2015; Karpova et al. 2017; in this case, we adopt the interpretation of the thermal spectrum with the model of a partially ionized magnetized hydrogen atmosphere nsmax, Ho et al. 2008). Objects 25 through 41 (red symbols) are magnetars.
(Posselt et al. 2013). We have supplemented this catalog with three neutron stars with recently measured thermal fluxes: two neutron stars with carbon envelopes (sources 42 and 43, Klochkov et al. 2015, 2016), and one pulsar (source 44, Danilenko et al. 2015; Karpova et al. 2017; in this case, we adopt the interpretation of the thermal spectrum with the model of a partially ionized magnetized hydrogen atmosphere nsmax, Ho et al. 2008). Objects 25 through 41 (red symbols) are magnetars.
The horizontal errorbars show estimates of the lower and upper bounds on the kinematic age of the star, determined from observations of the related supernova remnants. In the cases where only an estimate without errors is available, we replace the errorbar by a short double-sided arrow. In the cases where the kinematic age is unavailable, we use an estimate of the characteristic age, determined from the stellar spin period and its derivative in the canonical model of the rotating magnetic dipole in vacuum. The characteristic ages are measured very accurately, but they are rather poor estimators of a true age, therefore we plot longer horizontal arrows in these cases.
In the inset we show evolution of the nonredshifted effective temperature Teff in a restricted time interval. Here, the points represent estimates of Teff for the Cas A NS from Table I of Ho et al. (2015). The difference between the vertical position of these points in the inset and the errorbar 4 in the main frame is caused by the use of a different neutron star model, which gives a larger redshift and higher Teff (see Elshamouty et al. 2013).
4.1. Thickness of the quasi-stationary envelope
The cooling curves marked “a” and “b” in Fig. 2 are obtained for a model, which differs from the basic model by the thickness of the envelope that is treated in the quasi-stationary approximation, ΔM = 10-6M⊙ (in addition, curve “b” differs by the radiative opacity approximation, see Sect. 4.2). For the given M and R, the mass density at the bottom of this “thick” envelope is ρ ≈ 1.7 × 1010 g cm-3, which is close to the traditional ρb value. Comparison of the curve “a” with the basic cooling curve shows that the simulations with the traditional blanketing envelope are quite accurate on the timescales t ≳ 1 yr, but not on shorter timescales. The reason for this can be understood from inspection of Fig. 3, which shows temperature as function of density. At early ages the temperature profile in the thick envelope obtained in the quasi-stationary approximation (lines “a” and “b”) strongly differs from the profile calculated with the full account of time dependence in the thermal evolution Eq. (10) (the solid line, “basic model”). The solution of this equation in the quasi-stationary approximation is equivalent to setting cP = 0. Thus we see that the accurate evaluation of cP is important in the outer crust and ocean of a neutron star at relatively short timescales t ≲ 1 yr.
 |
Fig. 3 Redshifted temperature as a function of mass density inside a neutron star with M = 1.4 M⊙ at different ages (marked near the curves) according to different theoretical models. Line styles correspond to theoretical models in the same way as in Fig. 2. The three parts of the figure show the thermal structure of the envelopes comprising the ocean and the outer crust (left), the inner crust (middle), and the core (right) at different density scales. In the gray-cross-hatched |
4.2. Opacities
The influence of the model for radiative opacities on the cooling curves can be seen from comparison of the basic (solid) curve in Fig. 2 with the dot-long-dashed curve (marked “opac. PY’01”), which is calculated with simplified opacities following a model that does not include the plasma cutoff, electron-positron pairs, Compton effect, or electron degeneracy (Potekhin & Yakovlev 2001). The difference between the two cooling curves is noticeable only at high 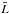 (the difference can exceed 10%, only if
(the difference can exceed 10%, only if 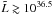 erg s-1; in the latter case, the effect is mainly due to the importance of Compton scattering at high temperatures).
erg s-1; in the latter case, the effect is mainly due to the importance of Compton scattering at high temperatures).
In the atmosphere, ionization can be incomplete, which is especially important in the case of heavy elements or strong magnetic fields. For the nonmagnetic iron atmosphere, we use the opal radiative opacities. There can be an ambiguity in connecting this opacity to the radiative opacity calculated in the model of a fully ionized plasma, shown in Fig. 1. In the case of the thick blanketing envelope, there are two curves in Fig. 2, long-dashed and dotted ones, corresponding to different prescriptions for the connection. The first one (curve “a”) is obtained by using the opal opacities in the density-temperature range where they are tabulated and replacing them by the fully ionized plasma model beyond the tables. The second one (curve “b”) is obtained with extrapolation of the tabular data to the bottom of the blanketing envelope, using the Kramers opacity law. The thermal structure of the envelopes with using these two prescriptions is illustrated in Fig. 3 by the red lines of the same styles (dotted and long-dashed) as corresponding lines “a” and “b” in Fig. 2. We see that these two ways of handling the radiative opacity data can result in noticeably different cooling curves, the difference being especially pronounced at t ≲ 100 yr, because at early ages the radiative transport dominates in a large part of the envelope due to the high temperatures.
4.3. Anomalous axial PBF contribution
To check the importance of the recent advances in the treatment of the Cooper PBF neutrino emission mechanism, we first include the superfluidity with the accurate treatment of this emission mechanism according to Leinson (2010; the dot-dashed lines in Figs. 2 and 3), and then switch off the anomalous contribution into the axial channel of weak interactions (the short-dashed lines). For illustration, we have chosen the superfluidity type SF081326. Here and hereafter, the first (08), second (13), and third (26) pair of digits compose the entry number in Table II of Ho et al. (2015). Thus, SF081326 stands for the superfluid gap model SFB for the neutron singlet superfluidity (Schwenk et al. 2003), CCDK for the proton singlet superfluidity (Chen et al. 1993; Elgarøy et al. 1996a), and TToa for the neutron triplet superfluidity (Takatsuka & Tamagaki 2004). This combination has been selected by Ho et al. (2015) as the best fit to the apparent surprisingly rapid decline of luminosity of the Cas A NS, first reported by Heinke & Ho (2010). In the inset of Fig. 2 we can see that the short-dashed curve Teff(t) is indeed close to the plotted Cas A NS data in the common approximation neglecting the anomalous axial contribution, but it is not the case if the PBF emission is calculated accurately. This conclusion confirms the statement by Leinson (2016) about the importance of the latter contribution.
Let us note that Shternin et al. (2011) were the first who encountered the impossibility of fitting the apparent fast decline of the Cas A NS luminosity with the results of Leinson (2010). In order to obtain an acceptable fit to this decline, they (as later Elshamouty et al. 2013) arbitrarily increased the PBF reaction rate by changing the coefficient 0.19, mentioned in Sect. 3.4, to 0.4, which does not follow from any theory. This artificial enhancement of the PBF rate is however unnecessary, since the fast cooling of Cas A NS has been put in doubt by Posselt et al. (2013), who suggested possible alternative explanations to the observational data.
4.4. In-medium effects
The importance of the in-medium effects can be seen from comparison of the corresponding cooling curves in Fig. 2 and temperature profiles in Fig. 3. Simulations without account of these effects substantially overestimate luminosities and effective temperatures of middle-aged neutron stars. We have checked that this effect is caused mainly by the in-medium enhancement of the modified Urca reactions (Shternin & Baldo, in prep.; Shternin, priv. comm.). The in-medium effects on thermal conductivities (Baiko et al. 2001; Shternin et al. 2013) turn out to be unimportant.
4.5. Equation of state and direct Urca processes
Figures 4 and 5 illustrate the effects of varying neutron star mass and equation of state on the cooling curves and thermal structure of neutron stars. In Fig. 4 we show a sequence of cooling curves for stellar masses M from 1.0 M⊙ to 2.0 M⊙ and the maximum mass Mmax, according to two EoSs, BSk24 (Mmax = 2.28 M⊙) and APR (Mmax = 2.21 M⊙).
 |
Fig. 4 Cooling curves for neutron stars with M = 1.0 (green), 1.2 (blue), 1.4 (black), 1.6 (magenta), 1.8 (orange), 2.0 M⊙ (violet), and the maximum mass Mmax (red lines), calculated using the same basic theoretical model as in Fig. 2, for the EoS models BSk24/21 (solid/dotted lines, Mmax = 2.28 M⊙, MDU = 1.596/1.587 M⊙) and APR+NV (dashed lines, Mmax = 2.21 M⊙, MDU = 2.01 M⊙) compared with observations (the same symbols as in Fig. 2). |
The cooling curves are close to the basic curve until M exceeds the direct Urca threshold MDU, which is equal to 1.596 M⊙ for BSk24 and to 2.01 M⊙ for APR. The difference of MDU for different EoSs is caused by different density-dependence of the electron fraction, which is obtained along with the thermodynamic functions while calculating the EoS by the free energy minimization. For M>MDU, a powerful cooling occurs in the central part of the core.
We have also performed analogous calculations for the EoS model BSk21, but found that the results are almost indistinguishable from those obtained with BSk24, except for values of M close to MDU. In Fig. 4, the difference is noticeable only for M = 1.6 M⊙ (the dotted curve). This is because the sensitivity of the cooling to the mass of the central region where the direct Urca processes operate. For BSk21, MDU = 1.587 M⊙, the threshold at M = 1.6 M⊙ is exceeded by M−MDU = 0.013 M⊙, compared to 0.004 M⊙ for BSk24. A change of M by −0.009 M⊙ brings the dotted cooling curve in Fig. 4 to the solid one. Such a small difference in M seems to be practically insignificant.
Figure 5 shows temperature profiles for several masses and ages. We see that some of the red and magenta lines go down towards the right edge of the figure, indicating temperature decrease with increasing density towards the center of the most massive stars. At early ages (t ≲ 1 yr), this temperature decrease exceeds an order of magnitude for the models with M = 2 M⊙ and M = Mmax using the BSk24 EoS and for the model with M = Mmax using the APR EoS. Thus the central region of the massive neutron star works as a cooler. As seen from Fig. 5, it is effective until the temperature falls to ~107 K. Afterwards the neutrino cooling dyes away and the temperature profile flattens out.
The total neutrino emissivities for several neutron star models and two ages are shown in Fig. 6. We see that for M = 1.8 M⊙>MDU(BSk24) the emission rate at ρ> 8.25 × 1014 g cm-3 is enhanced by several orders of magnitude compared to the rates at lower densities.
 |
Fig. 5 Redshifted temperature as function of mass density inside neutron stars with masses M = 1.0 (dot-long-dash lines), 1.4 (solid lines), 2.0 (short-dashed lines), and Mmax = 2.28 M⊙ (dot-short-dash lines) for the unified EoS model BSk24, and with mass Mmax = 2.21 M⊙ for the APR+NV EoS model (dotted lines) at ages of 10-3, 1, and 50 yr. The vertical lines separate three density regions: the ocean and outer crust, the inner crust, and the core, displayed using different density scales. |
4.6. Superfluidity
It is well known that superfluid energy gaps for different types of nucleon pairing have an important influence on the neutron star-cooling curves. When temperature falls substantially below Tcrit for some kind of the baryons, the superfluidity reduces their heat capacity (Levenfish & Yakovlev 1994; Yakovlev et al. 1999). The baryon superfluidity may also either reduce or increase the conductivity in the core (Baiko et al. 2001). These effects are seen respectively in the lower and upper panels of Fig. 7.
The baryon superfluidity affects the neutrino emissivity in different ways (Yakovlev et al. 2001, and references therein). Neutrino emission by the modified and direct Urca processes and by baryon bremsstrahlung gets strongly suppressed at T ≪ Tcrit. However, when T is close to Tcrit, the total neutrino emission is greatly enhanced due to the PBF mechanism. Since Tcrit for each type of superfluidity depends on baryon density, the overall picture is complicated, as we see in Fig. 6.
As a result, some parts of a neutron star may have higher- while other parts lower temperature than it would be for a neutron star without superfluidity. We see this in Figs. 3 and 9, which show temperature profiles in superfluid and nonsuperfluid neutron stars of different ages. The cooling can be accelerated or decelerated, depending on the interplay of the superfluidity-related mechanisms, as we see in Fig. 8 where the effects of three different models of superfluidity are demonstrated.
The model SF081326, which is also used in Figs. 2 and 3, is characterized by a relatively weak neutron singlet-pairing superfluidity SFB in the crust (maximum of the critical temperature maxTcrit ~ 5 × 109 K), rather strong proton singlet superfluidity CCDK in the core (maxTcrit ≈ 7 × 109 K), and moderate neutron triplet superfluidity TToa in the core (maxTcrit ≈ 6 × 108 K). In Fig. 8 we reproduce the corresponding cooling curve (line 4) and compare it with the curves calculated using two different combinations of the superfluidity models (lines 5 and 6). Retaining the same singlet-type superfluidities but replacing the moderate neutron triplet model TToa by the weak neutron triplet superfluidity model EEHOr with maxTcrit< 2 × 108 K (Elgarøy et al. 1996b), we effectively suppress the PBF neutrino emission at moderate ages, which helps to keep a neutron star relatively hot for a long time (curves 6 and 7 in Fig. 8). This model is sufficient for explanation of several sources showing luminosities above those predicted by the basic cooling curve; nevertheless, there remain many still hotter neutron stars, which require another explanation.
 |
Fig. 6 Neutrino emission power density as function of mass density at ages 50 yr (upper curves) and 5 kyr (lower curves of each type) for different neutron star models: the basic model (EoS BSk24, ground state composition, M = 1.4 M⊙, no superfluidity; solid lines), the neutron star with fully accreted envelope (short-dashed lines), three different combinations of the three types of superfluidity (dot-long-dash, dot-short-dash, and dotted curves), and a model without superfluidity but with the direct Urca processes due to the higher mass M = 1.8 M⊙ (long-dashed lines). The density scale is different in the left and right parts of the figure, separated by the vertical solid line. The vertical dotted lines mark the outer and inner boundaries of the inner crust. |
 |
Fig. 7 Thermal conductivity (upper panel) and heat capacity per baryon in units of kB (lower panel) as functions of mass density at age t = 1 kyr for the same neutron star models as in Fig. 6. The crosses mark the melting points for the models with M = 1.4 M⊙: to the left of them, the Coulomb plasma forms a liquid ocean. For the M = 1.8 M⊙ model, the crust does not melt in the displayed density range, because it is relatively cold at this age (cf. Fig. 4). The vertical dotted lines mark the outer and inner boundaries of the inner crust. |
As another example, we choose model combination SF061220: the strong neutron singlet superfluidity MSH (maxTcrit > 1010 K, Margueron et al. 2008; Gandolfi et al. 2009), moderate proton singlet superfluidity BS (maxTcrit ~ 5 × 109 K, Baldo & Schulze 2007), and moderate neutron triplet superfluidity BEEHS (maxTcrit ~ 4 × 108 K, Baldo et al. 1998). In this case, cooling is accelerated at early and late ages (line 4 in Fig. 8).
4.7. Accreted envelopes
The neutron star envelopes are more transparent to the heat flux if they are composed of light chemical elements. Previously we studied this effect in the quasi-stationary approximation for nonmagnetic (Potekhin et al. 1997) and strongly magnetized envelopes (Potekhin et al. 2003). The main effect is related to the Z-dependence of the electron-ion collision frequencies. The higher the ion charge number Z, the larger the collision frequency and the lower the conductivity. Another effect concerns radiative opacities in the photosphere, which are also smaller for light elements than for iron.
Here we more accurately simulate the cooling of neutron stars with accreted envelopes by relaxing the quasi-stationary approximation. The cooling curves for nonsuperfluid (lines 1–3) and superfluid (lines 4–7) neutron stars with nonaccreted (lines 1, 4, 5, 6) and accreted (lines 2, 3, 7) envelopes are compared in Fig. 8 and their thermal structures are shown in Fig. 9.
For the accreted envelopes, we use either hydrogen (lines 2 and 7) or helium (line 3) atmosphere models. An interesting effect, first noticed by Beznogov et al. (2016), is that the replacement of H by 4He increases the photon luminosity. This effect is caused by the different mass to charge ratio of H, which results in the discontinuity of ρ and is related to the lower opacities of He at high Tand fixed ρ, revealed in both op and opal tables. These discontinuities are seen in the left part of Fig. 9 at the H/He interface, which is set at T = 4 × 107 K (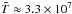 K), for the accreted-envelope models (dashed lines). On the other hand, the kinks at the temperature profiles for nonaccreted envelopes (solid lines in Fig. 9) at
K), for the accreted-envelope models (dashed lines). On the other hand, the kinks at the temperature profiles for nonaccreted envelopes (solid lines in Fig. 9) at 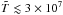 K are caused by the switch to the fully ionized plasma model for radiative opacities at the boundary of the opal tables for iron (see Sect. 4.2).
K are caused by the switch to the fully ionized plasma model for radiative opacities at the boundary of the opal tables for iron (see Sect. 4.2).
 |
Fig. 8 Cooling curves for a neutron star with M = 1.4 M⊙ according to the BSk24 EoS model with iron (lines 1, 4, 5, 6) or accreted envelopes (lines 2, 3, 7), iron (lines 1, 4, 5, 6), hydrogen (lines 2, 7), or helium atmosphere (line 3), without nucleon superfluidity (lines 1–3) and with different models of nucleon superfluidity (lines 4–7; see text for explanation of the SF-notations), compared with observations (the same symbols as in Fig. 2). |
 |
Fig. 9 Redshifted temperature as a function of mass density inside a neutron star for three of the seven different models considered in Fig. 8 (namely, models 1, 2, and 7), plotted using the same line styles, at different ages marked near the curves. The two parts of the figure, separated by the vertical solid line, show the regions before and after neutron drip at different density scales. The dotted lines in the left half of the figure show the adopted density-temperature domains for different chemical elements (H, 4He, 12C, 16O) in the accreted envelope. To the right of the last of these lines, the composition of the accreted crust is adopted from Haensel & Zdunik (1990). For the nonaccreted crust, we use the ground-state composition of matter according to the BSk24 model. The vertical dotted line in the right half of the figure separates the crust and the core. |
The composition of the accreted crust at larger densities, beyond the C and O layers, is produced by a sequence of nuclear transformations during accretion (Haensel & Zdunik 1990). This leads to different thermal conductivities and heat capacities, as seen in Fig. 7, and to different rates of neutrino bremsstrahlung, as seen in Fig. 6. The latter differences, however, are not sufficiently strong to noticeably affect the cooling curves.
Figure 8 shows that the largest theoretical luminosities are obtained by the use of the model with strong proton singlet and weak neutron triplet superfluidity (SF081322) and the accreted He envelope.
4.8. Other effects
We have additionally tested a number of other updates to the neutron star microphysics, which however proved to be unimportant. Two examples, the in-medium corrections to thermal conductivities and the upgrade of the BSk21 to the BSk24 EoS, have been mentioned above. Another example is latent heat of the crust. As a neutron star cools down, its frozen crust grows, gradually replacing the ocean. We have included the latent heat released during this process as a heat source 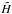 in Eq. (10), but found the cooling curves unchanged. This should have been anticipated, because the crust contains only a small fraction (less than 2%) of the total mass M of a neutron star.
in Eq. (10), but found the cooling curves unchanged. This should have been anticipated, because the crust contains only a small fraction (less than 2%) of the total mass M of a neutron star.
The replacement of the fit of Yakovlev et al. (2001) to bremsstrahlung neutrino energy losses in the crust by a more detailed fit of Ofengeim et al. (2014) also does not affect the cooling curves, even in the case of accreted crust
We have also checked that the replacement of the fit of Yakovlev et al. (2001) to the plasmon decay rate by the more accurate fit of Kantor & Gusakov (2007) does not have a noticeable effect on the cooling curves (this statement pertains to neutron stars, but not to white dwarfs, where the plasmon decay is an important channel of energy losses at early ages).
5. Cooling of magnetars
The effects of quantizing magnetic fields on the thermal structure of neutron-star envelopes were first studied by Hernquist (1985) and somewhat later by Van Riper (1988) and Schaaf (1990). Van Riper (1988) considered a neutron star with a constant radial magnetic field. In this model, the quantum enhancement of longitudinal electron conductivity κ∥ at ρ ~ ρB (where ρB is given by Eq. (12)) results in an overall enhancement of the neutron-star photon luminosity at a fixed internal temperature. However, Shibanov & Yakovlev (1996) showed that, for the dipole field distribution, the effects of suppression of the heat conduction across the field near the magnetic equator compensate or even overpower the effect of the conductivity increase near the normal direction of the field lines. This conclusion was also shown to be valid for small-scale fields at B ≲ 1014 G (Potekhin et al. 2005). However, in superstrong fields (B ≳ 1014 G) the quantum enhancement of the longitudinal conductivity and the corresponding increase of the stellar photon luminosity are more important. This enhancement overpowers the decrease of the luminosity in the regions of almost tangential field lines, so that overall photon luminosity increases (Kaminker et al. 2009, 2014). This may not be the case in the configurations where the field is nearly tangential over a significant portion of the stellar surface as, for example, in the case of a superstrong toroidal field (Pérez-Azorin et al. 2006; Page et al. 2007). We do not study the latter possibility in the present paper, assuming that the superstrong magnetar field is highly tangled.
 |
Fig. 10 Cooling curves for neutron stars with M = 1.4 M⊙ according to the BSk24 EoS model with B = 0 (solid line), 1014 G (short-dashed line), 1015 G (long-dashed line), and 1016 G (dot-dashed line). The three dotted lines result from simulations with the same three strong fields, but treated classically. |
Figure 10 shows cooling curves of neutron stars with B = 1014 G, 1015 G, and 1016 G, compared with the cooling of a nonmagnetic neutron star. We see the strong enhancement of the luminosity for middle-aged neutron stars with superstrong magnetic fields. As a consequence of rapid energy loss, the stored thermal energy is spent more rapidly, and the luminous lifetime of the magnetars becomes shorter. We intentionally leave aside additional heating by the magnetic energy consumption (e.g., by one of the mechanisms considered by Beloborodov & Li 2016), which may become the subject of a separate study. Here we aim at revealing the luminosity increase that can be provided by the effects of the quantizing magnetic fields on the crust of the star.
For comparison, we plot the cooling curves obtained using classical treatment of the magnetic fields (i.e., without allowance for the Landau quantization). At the middle ages of the stars, the latter curves pass below the nonmagnetic curve, which is explained by the magnetic suppression of the electron heat transport across the field lines.
Figure 11 shows thermal structure of magnetars at different ages. For comparison, we reproduce the thermal structure of a nonmagnetized neutron star with iron envelopes from Sect. 4. The temperature profiles of the strongly magnetized neutron stars reveal series of kinks, which are related to the magnetic quantization. They are located near the points where degenerate electrons fill consecutively excited Landau levels at densities ρ ≳ ρB. At these densities, the average conductivities have peaks and dips, as shown in Fig. 12.
Only part of the enhancement of luminosity in Fig. 10 is due to the above-mentioned increase of conductivity at ρ ~ ρB. Equally important is the magnetic condensation, the phenomenon predicted by Ruderman (1971) and studied by Lai & Salpeter (1997) and Medin & Lai (2006, 2007). In a nonmagnetized dense nonideal electron-ion plasma, the pressure of degenerate electrons overpowers the negative electrostatic pressure at high densities. In the superstrong fields of magnetars, however, the Fermi temperature is so strongly reduced at ρ ≪ ρB, that the electrons become nondegenerate, and hydrostatic instability develops, leading to formation of a condensed surface at high density. The radiation escapes directly from this hot surface, without diffusion through a gaseous atmosphere. Such a neutron star is said to be “naked” (Turolla et al. 2004).
 |
Fig. 11 Redshifted temperature as a function of mass density inside neutron stars with B = 0 (solid lines), 1015 G (long-dashed and dotted lines), and 1016 G (dot-dashed lines) at four ages t from 8 h to 2 × 104 yr, marked near the curves. The dotted line illustrates the model with superfluidity SF081322; the other lines are calculated without superfluidity. The two parts of the figure, separated by the vertical solid line, show the regions before and after neutron drip at different density scales. Inset: temperature profiles in the envelopes of a neutron star with B = 1014 G at ages t = 1, 5, 20, and 100 kyr. |
The process of formation of the naked neutron star is elucidated by Fig. 11. At early times, when a magnetar is sufficiently hot, its thermal structure is smooth because it possesses a thick atmosphere. As the magnetar cools down, a sharp condensed surface appears. Nevertheless, in the case of B = 1015 G, we see that the neutron star retains a finite atmosphere with densities ρ ≳ 103 g cm-3 above the condensed surface.
The inset in Fig. 11 illustrates the structure of the envelopes of a neutron star with B = 1014 G at the middle ages t = 104 ± 1 yr, around the time of magnetic condensation. The two upper profiles are smooth, without a condensed surface, and the two lower curves reveal a density gap, which corresponds to an atmosphere and ocean above a dense solid crust. As the star cools down, the ocean depth decreases. The condensation is accompanied by increasing heat-transparency of the envelope. For this reason, the decrease of the surface luminosity stalls, and the two profiles in the middle (at t = 5 kyr and 20 kyr, before and after the condensation) are close to each other at low densities. The slowdown of the luminosity decrease is clearly distinguishable on the cooling curve for B = 1014 G at t ~ 104 yr in Figs. 10 and 14.
 |
Fig. 12 Effective thermal conductivity as a function of density in the ocean and crust of a kyr-old magnetar with magnetic fields B = 1014 G, 1015 G, and 1016 G. The vertical dotted line marks the neutron drip density. |
Figure 13 shows neutrino emission rates inside nonsuperfluid magnetars with B = 1014 G, 1015 G, and 1016 G and a magnetar with superfluidity type SF081322 and B = 1016 G. For reference, neutrino emission of the basic nonmagnetic neutron star model is also shown. For ease of comparison with Fig. 6, we have chosen the same two ages, 50 yr and 5 kyr, and the same scale as in that figure. The most remarkable difference is the enhanced emission in the inner crust for B = 1014 G and 1015 G. The increase is due to the contribution of the synchrotron neutrino emission. At the strongest considered field B = 1016 G, however, the synchrotron contribution disappears, which looks surprising at the first glance. Actually the synchrotron emission is quenched at 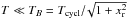 (Bezchastnov et al. 1997), where Tcycl is the electron cyclotron temperature defined in Sect. 3 and xr = pF,e/mec is the usual parameter of relativity. At B = 1016 G the condition T ≪ TB is fulfilled in the inner crust. The quenching is described by a factor SBC in Sect. 2.4b of Yakovlev et al. (2001), which is exponentially small at TB/T ≫ 1.
(Bezchastnov et al. 1997), where Tcycl is the electron cyclotron temperature defined in Sect. 3 and xr = pF,e/mec is the usual parameter of relativity. At B = 1016 G the condition T ≪ TB is fulfilled in the inner crust. The quenching is described by a factor SBC in Sect. 2.4b of Yakovlev et al. (2001), which is exponentially small at TB/T ≫ 1.
 |
Fig. 13 Neutrino emission power density as a function of mass density at ages 50 yr (upper curves) and 5 kyr (lower curves of each type) for nonsuperfluid magnetars with B = 1014 G (short-dashed lines), 1015 G (long-dashed lines), and 1016 G (dot-dashed lines) and for a magnetar with B = 1015 G and nucleon superfluidity (dotted lines), compared with neutrino emission of a nonmagnetic, nonsuperfluid neutron star (solid lines). The density scale is different in the left and right parts of the figure, separated by the vertical solid line. The vertical dotted lines mark the outer and inner boundaries of the inner crust. |
We have seen that strong proton superfluidity in the core, accreted envelopes, and superstrong magnetic fields enhance luminosities of neutron stars at t ~ 102−104 yr. One might expect that joint effect of these factors would help to explain observations of the most luminous magnetars. However, this is not the case. Figure 14 shows cooling of magnetars without and with strong proton superfluidity along with an example of a superfluid magnetar with an accreted envelope. We see that the stronger the magnetic field, the smaller the additional enhancement of the photon luminosity due to the superfluidity. Replacement of the iron envelope by an accreted envelope does not produce any appreciable effect on the cooling of those magnetars, whose luminosity has been already enhanced by a magnetic field B ≳ 1015 G and strong proton superfluidity.
The cooling curves in Fig. 14 are compatible with the observed luminosities and estimated ages of several magnetars without involving heating mechanisms. However, most of the data on magnetars are barely compatible with the theoretical cooling curves, and several objects (e.g., objects number 26, 4U 0142+614; 37, SGR 0526−66; 40, SGR 0526-66) are clearly incompatible with them. This indicates that heating mechanisms are probably important for the thermal evolution of magnetars, in agreement with previously published conclusions (e.g., Kaminker et al. 2009; Viganò et al. 2013; Beloborodov & Li 2016). Nonetheless, Fig. 14 demonstrates that combined effects of Landau quantization, magnetic condensation, and strong proton superfluidity substantially reduce the discrepancies without resorting to accreted envelopes of light elements, which would hardly survive on the surface of magnetars, due to high temperatures and bursting activity.
 |
Fig. 14 Comparison of cooling of nonsuperfluid (solid lines) and superfluid (dot-dashed lines) magnetars with superfluidity type SF081322 and magnetic fields B = 1014 G, 1015 G, and 1016 G. The dotted line shows the joint effect of superfluidity and accreted envelope for the magnetar with B = 1015 G. |
6. Conclusions
We have performed simulations of cooling of nonmagnetic neutron stars and neutron stars with tangled superstrong magnetic fields. We have studied the influence of various recent updates to microphysics input and the effects brought about by superstrong magnetic fields of magnetars. We treat the fully ionized envelopes uniformly with the interior of the star while taking into account the T-dependence of the EoS in the outer crust. We have considered both neutron stars with ground-state composition and with accreted envelopes.
We demonstrate that cooling simulations based on the approximation of a quasi-stationary envelope, which extends to ρb ~ 1010 g cm-3, are accurate on the timescales ≳1 yr, but not on the shorter timescales. The accurate treatment of the PBF neutrino emission, including the effect of suppression of axial channel for triplet type of Cooper pairing of neutrons, caused by contribution of the anomalous weak interaction (Leinson 2010), can be important. In particular, it is shown that the inclusion of this effect invalidates the tentative explanation of the apparent rapid cooling of the Cas A NS by the PBF emission mechanism (Page et al. 2011; Ho et al. 2015), in agreement with Leinson (2016). The enhancement of the Urca reactions by the in-medium effects (Voskresensky 2001; Shternin & Baldo, in prep.; Shternin, priv. comm.) are equally important.
On the other hand, the latent heat of the crust, the in-medium effects on baryon thermal conduction, the upgrade of BSk21 to BSk24 EoS model, and the recent improvements in treatments of neutrino bremsstrahlung and plasmon decay in the crust proved to have almost no effect on the cooling. Allowance for the electron-positron pairs, electron degeneracy, Compton effect, and plasma cutoff in the treatment of radiative opacities can noticeably (by >10%) improve accuracy of the simulations of thermal evolution only for very hot neutron stars, with photon luminosities above 1036 erg s-1, and are unimportant for colder sources.
In agreement with previous studies, we find that accreted envelopes and superstrong magnetic fields make the neutron-star envelope more heat-transparent, which results in an increase of the surface luminosity at the neutrino cooling stage and quick fading at a later photon cooling stage. The cooling can be decelerated at the middle ages by a combination of weak neutron and strong proton superfluidities. However, the effects of the accreted envelopes and superstrong magnetic fields are not additive. Thus the highest luminosity of a cooling magnetar (without heating sources) at the middle ages t ~ 104 yr is provided by the superstrong magnetic field and superfluidity without an accreted envelope. This maximum luminosity is still not sufficient to explane observations of the most luminous magnetars, which implies the importance of heating. A study of the magnetar heating problem is beyond the scope of the present paper.
We did not consider magnetic fields stronger than 1016 G for two reasons. First, the strongest observed dipole component of a magnetic field of a neutron star, evaluated from the star spindown rate, is 2 × 1015 G. While several times stronger small-scale fields look plausible, orders of magnitude stronger fields do not. The second reason is more fundamental. At B> 1016 G, a number of physical effects come into play, which can be safely neglected at lower fields and have not been included in the present study. Examples of such effects are the B-dependence of the neutron drip transition pressure (Chamel et al. 2016), a possible influence of the field on nuclear shell energies and magic numbers, which may substantially change the composition and structure of the crust (Kondratiev et al. 2000, 2001; Stein et al. 2016), and the shift of the muon production threshold in the core (Suh & Mathews 2001).
Acknowledgments
We are grateful to Peter Shternin and Marcello Baldo for sharing their results with us before publication. We thank the anonymous referee for many valuable comments and suggestions, which helped us to improve the paper. A.P. thanks Peter Shternin for critical remarks, which have been taken into account in the final version of the text. The work of A.P. was supported by the Russian Science Foundation (grant 14-12-00316).
References
- Akgün, T., Reisenegger, A., Mastrano, A., & Marchant, P. 2013, MNRAS, 433, 2445 [NASA ADS] [CrossRef] [Google Scholar]
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Audi, G., Wang, M., Wapstra, A. H., et al. 2014, Nuclear Data Sheets, 120, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Baiko, D. A., & Yakovlev, D. G. 1999, A&A, 342, 192 [NASA ADS] [Google Scholar]
- Baiko, D. A., Haensel, P., & Yakovlev, D. G. 2001, A&A, 374, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldo, M., & Schulze, H.-J. 2007, Phys. Rev. C, 75, 025802 [NASA ADS] [CrossRef] [Google Scholar]
- Baldo, M., Elgarøy, Ø., Engvik, L., Hjorth-Jensen, M., & Schulze, H.-J. 1998, Phys. Rev. C, 58, 1921 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Baldo, M., Burgio, G. F., Schulze, H.-J., & Taranto, G. 2014, Phys. Rev. C, 89, 048801 [NASA ADS] [CrossRef] [Google Scholar]
- Beloborodov, A., & Li, X. 2016, ApJ, 833, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Bezchastnov, V. G., Haensel, P., Kaminker, A. D., & Yakovlev, D. G. 1997, A&A, 328, 409 [NASA ADS] [Google Scholar]
- Beznogov, M. V., Potekhin, A. Y., & Yakovlev, D. G. 2016, MNRAS, 459, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Bonanno, A., Urpin, V., & Belvedere, G. 2005, A&A, 440, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braithwaite, J. 2008, MNRAS, 386, 1947 [NASA ADS] [CrossRef] [Google Scholar]
- Broderick, A., Prakash, M., & Lattimer, J. M. 2000, ApJ, 537, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., Goriely, S., & Pearson, J. M. 2009, Phys. Rev. C, 80, 065804 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., Stoyanov, Zh. K., Mihailov, L. M., et al. 2016, Phys. Rev. C, 91, 065801 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1957, An Introduction to the Study of Stellar Structure (New York: Dover) [Google Scholar]
- Chen, J. M. C., Clark, J. W., Davé, R. D., & Khodel, V. V. 1993, Nucl. Phys. A, 555, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Chiu, H.-Y., & Salpeter, E. E. 1964, Phys. Rev. Lett., 12, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Danilenko, A., Shternin, P., Karpova, A., Zyuzin, D., & Shibanov, Yu. 2015, PASA, 32, e038 [NASA ADS] [CrossRef] [Google Scholar]
- Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duncan, R. C., & Thompson, C. 1992, ApJ, 392, L9 [Google Scholar]
- Elgarøy, Ø., Engvik, L., Hjorth-Jensen, M., & Schulze, H.-J. 1996a, Nucl. Phys. A, 604, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Elgarøy, Ø., Engvik, L., Hjorth-Jensen, M., & Osnes, E. 1996b, Phys. Rev. Lett., 77, 1428 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Elshamouty, K. G., Heinke, C. O., Sivakoff, G. R., et al. 2013, ApJ, 777, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Forest, J. L., Pandharipande, V. R., & Friar, J. L. 1995, Phys. Rev. C, 52, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Gandolfi, S., Illarionov, A. Yu., Pederiva, F., Schmidt, K. E., & Fantoni, S. 2009, Phys. Rev. C, 80, 045802 [NASA ADS] [CrossRef] [Google Scholar]
- Geppert, U., Küker, M., & Page, D. 2006, A&A, 457, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goriely, S., Chamel, N., & Pearson, J. M. 2013, Phys. Rev. C, 88, 024308 [NASA ADS] [CrossRef] [Google Scholar]
- Gudmundsson, E. Y., Pethick, C. J., & Epstein, R. I. 1983, ApJ, 272, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Gusakov, M. E. 2002, A&A, 389, 702 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haensel, P. 1995, Space Sci. Rev.,74, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., & Potekhin, A. Y. 2004, A&A, 428, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 1990, A&A, 229, 117 [NASA ADS] [Google Scholar]
- Heinke, C. O., & Ho, W. C. G. 2010, ApJ, 719, L167 [NASA ADS] [CrossRef] [Google Scholar]
- Hernquist, L. 1985, MNRAS, 213, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, W. C. G., Potekhin, A. Y., & Chabrier, G. 2008, ApJS, 178, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, W. C. G., Elshamouty, K. G., Heinke, C. O., & Potekhin, A. Y. 2015, Phys. Rev. C, 91, 015806 [NASA ADS] [CrossRef] [Google Scholar]
- Hummer, D. G. 1988, ApJ, 327, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, N., & Kohyama, Y. 1983, ApJ, 275, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, N., Kuwashima, F., Ichihashi, K., & Mutoh, H. 1991, ApJ, 382, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Kaminker, A. D., Haensel, P., & Yakovlev, D. G. 2001, A&A, 373, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaminker, A. D., Potekhin, A. Y., Yakovlev, D. G., & Chabrier, G. 2009, MNRAS, 395, 2257 [NASA ADS] [CrossRef] [Google Scholar]
- Kaminker, A. D., Kaurov, A. A., Potekhin, A. Y., & Yakovlev, D. G. 2014, MNRAS, 442, 3484 [NASA ADS] [CrossRef] [Google Scholar]
- Kantor, E. M., & Gusakov, M. E. 2007, MNRAS, 381, 1702 [NASA ADS] [CrossRef] [Google Scholar]
- Karpova, A., Danilenko, A., Shibanov, Yu., Shternin, P., & Zyuzin, D. 2014, ApJ, 789, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Karpova, A., Zyuzin, D., Danilenko, A., & Shibanov, Yu. 2017, in Proc. of the International Conference Physics of Neutron Stars – 2017, 50 years after the Pulsar Discovery (Saint Petersburg, Russia, July 10–14, 2017), J. Phys. Conf. Ser., accepted [Google Scholar]
- Karzas, W. J., & Latter, R. 1961, ApJS, 6, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, V. M., & Beloborodov, A. 2017, ARA&A, 55, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Kiuchi, K., Yoshida, S., & Shibata, M. 2011, A&A, 532, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klochkov, D., Suleimanov, V., Pühlhofer, G., et al. 2015, A&A, 573, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klochkov, D., Suleimanov, V., Sasaki, M., & Santangelo, A. 2016, A&A, 592, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kolomeitsev, E. E., & Voskresensky, D. N. 2008, Phys. Rev. C, 77, 065808 [NASA ADS] [CrossRef] [Google Scholar]
- Kondratiev, V. N., Maruyama, T., & Chiba, S. 2000, Phys. Rev. Lett., 84, 1086 [NASA ADS] [CrossRef] [Google Scholar]
- Kondratiev, V. N., Maruyama, T., & Chiba, S. 2001, ApJ, 546, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, D., & Salpeter, E. E. 1997, ApJ, 491, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1980, Statistical Physics, Part 1 (Course of Theoretical Physics, Vol. 5), 3rd edn. (Oxford: Butterworth-Heinemann) [Google Scholar]
- Lasky, P. D., Zink, B., Kokkotas, K., & Glampedakis, K. 2011, ApJ, 735, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J. M., Prakash, M., Pethick, C. J., & Haensel, P. 1991, Phys. Rev. Lett., 66, 2701 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Leinson, L. B. 2010, Phys. Rev. C, 81, 025501 [NASA ADS] [CrossRef] [Google Scholar]
- Leinson, L. B. 2016, ArXiv e-prints [arXiv:1611.03794] [Google Scholar]
- Leinson, L. B., & Pérez, A. 2006, Nucl. Phys. B, 638, 114 [Google Scholar]
- Levenfish, K. P., & Yakovlev, D. G. 1994, Astron. Rep., 38, 247 [NASA ADS] [Google Scholar]
- Li, Z. H., & Schulze, H. J. 2008, Phys. Rev. C, 78, 028801 [NASA ADS] [CrossRef] [Google Scholar]
- Link, B., & van Eysden, C. A. 2016, ApJ, 823, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Makishima, K., Enoto, T., Hiraga, J. S., et al. 2014, Phys. Rev. Lett., 112, 171102 [NASA ADS] [CrossRef] [Google Scholar]
- Makishima, K., Enoto, T., Murakami, H., et al. 2016, PASJ, 68, S12 [NASA ADS] [CrossRef] [Google Scholar]
- Marelli, M., Belfiore, A., Saz Parkinson, P., et al. 2014, ApJ, 790, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Margueron, J., Sagawa, H., & Hagino, K. 2008, Phys. Rev. C, 77, 054309 [NASA ADS] [CrossRef] [Google Scholar]
- Medin, Z., & Lai, D. 2006, Phys. Rev. A, 74, 062508 [NASA ADS] [CrossRef] [Google Scholar]
- Medin, Z., & Lai, D. 2007, MNRAS, 382, 1833 [NASA ADS] [Google Scholar]
- Mendoza, C., Seaton, M. J., Buerger, P., et al. 2007, MNRAS, 378, 1031; opacity database URL http://opacities.osc.edu/rmos.shtml [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mereghetti, S., Pons, J. A., & Melatos, A. 2015, Space Sci. Rev., 191, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Mösta, P., Ott, C. D., Radice, D., et al. 2015, Nature, 528, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Negele, J. W., & Vautherin, D. 1973, Nucl. Phys. A, 207, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Oertel, M., Hempel, M., Klahn, T., & Typel, S. 2017, Rev. Mod. Phys., 89, 015007 [NASA ADS] [CrossRef] [Google Scholar]
- Ofengeim, D. D., Kaminker, A. D., & Yakovlev, D. G. 2014, Europhys. Lett., 108, 31002 [NASA ADS] [CrossRef] [Google Scholar]
- Olausen, S. A., & Kaspi, V. M. 2014, ApJS, 212, 6; magnetar catalog URL http://www.physics.mcgill.ca/~pulsar/magnetar/main.html [NASA ADS] [CrossRef] [Google Scholar]
- Page, D. 2016, Astrophysics Source Code Library, [record ascl:1609.009] [Google Scholar]
- Page, D., & Applegate, J. H. 1992, ApJ, 394, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D., Geppert, U., & Küker, M. 2007, Ap&SS, 308, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D., Lattimer, J. M., Prakash, M., & Steiner, A. W. 2009, ApJ, 707, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D., Prakash, M., Lattimer, J. M., & Steiner, A. W. 2011, Phys. Rev. Lett., 106, 081101 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Pérez-Azorin, J. F., Miralles, J. A., & Pons, J. A. 2006, A&A, 451, 1009 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Posselt, B., Pavlov, G. G., Suleimanov, V., & Kargaltsev, O. 2013, ApJ, 779, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y., & Chabrier, G. 2004, ApJ, 600, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y., & Chabrier, G. 2010, Contrib. Plasma Phys., 50, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y., & Chabrier, G. 2012, A&A, 538, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Potekhin, A. Y., & Chabrier, G. 2013, A&A, 550, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Potekhin, A. Y., & Yakovlev, D. G. 2001, A&A, 374, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Potekhin, A. Y., Chabrier, G., & Yakovlev, D. G. 1997, A&A, 323, 415 [NASA ADS] [Google Scholar]
- Potekhin, A. Y., Yakovlev, D. G., Chabrier, G., & Gnedin, O. Y. 2003, ApJ, 594, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y., Urpin, V. A., & Chabrier, G. 2005, A&A, 443, 1025 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Potekhin, A. Y., Fantina, A. F., Chamel, N., Pearson, J. M., & Goriely, S. 2013, A&A, 560, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Potekhin, A. Y., Pons, J. A., & Page, D. 2015, Space Sci. Rev., 191, 239; open conductivity codes URL http://www.ioffe.ru/astro/conduct/ [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J. 2017, ApJ, 835, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Pudliner, B. S., Pandharipande, V. R., Carlson, J., & Wiringa, R. B. 1995, Phys. Rev. Lett., 74, 4396 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Richardson, M. B., Van Horn, H. M., & Savedoff, M. P. 1979, ApJS, 39, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., & Iglesias, C. A. 1998, Space Sci. Rev., 85, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. A. 1971, Phys. Rev. Lett., 27, 1306 [NASA ADS] [CrossRef] [Google Scholar]
- Samarskii, A. A. 2001, The Theory of Difference Schemes (New York–Basel: Marcel Dekker, Inc.) [Google Scholar]
- Schaaf, M. E. 1990, A&A, 227, 61 [NASA ADS] [Google Scholar]
- Schatz, H., Bildsten, L., Cumming, A., & Wiescher, M. 1999, ApJ, 524, 1014 [NASA ADS] [CrossRef] [Google Scholar]
- Schwenk, A., Friman, B., & Brown, G. 2003, Nucl. Phys. A, 713, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Schwinger, J. 1988, Particles, Sources, and Fields (Redwood: Addison-Wesley) [Google Scholar]
- Shibanov, Yu. A., & Yakovlev, D. G. 1996, A&A, 309, 171 [NASA ADS] [Google Scholar]
- Shternin, P. S., & Yakovlev, D. G. 2007, Phys. Rev. D, 75, 103004 [NASA ADS] [CrossRef] [Google Scholar]
- Shternin, P. S., & Yakovlev, D. G. 2015, MNRAS, 446, 3621 [NASA ADS] [CrossRef] [Google Scholar]
- Shternin, P. S., Yakovlev, D. G., Heinke, C. O., Ho, W. C. G., & Patnaude, D. J. 2011, MNRAS, 412, L108 [NASA ADS] [Google Scholar]
- Shternin, P. S., Baldo, M., & Haensel, P. 2013, Phys. Rev. C, 88, 065803 [NASA ADS] [CrossRef] [Google Scholar]
- Silant’ev, N. A., & Yakovlev, D. G. 1980, Ap&SS, 71, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, M., Maruhn, J., Sedrakian, A., & Reinhard, P.-G. 2016, Phys. Rev. C, 94, 035802 [NASA ADS] [CrossRef] [Google Scholar]
- Suh, I.-S., & Mathews, G. J. 2001, ApJ, 546, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Takatsuka, T., & Tamagaki, R. 2004, Progr. Theor. Phys., 48, 1517 [NASA ADS] [CrossRef] [Google Scholar]
- Taranto, G., Burgio, G. F., & Schulze, H.-J. 2016, MNRAS, 456, 1451 [NASA ADS] [CrossRef] [Google Scholar]
- Thorne, K. S. 1977, ApJ, 212, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Tiengo, A., Esposito, P., Mereghetti, S., et al. 2014, Astron. Nachr., 335, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuruta, S., & Cameron, A. G. W. 1966, Can. J. Phys., 44, 1863 [NASA ADS] [CrossRef] [Google Scholar]
- Turolla, R., Zane, S., & Drake, J. J. 2004, ApJ, 603, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Turolla, R., Zane, S., & Watts, A. L. 2015, Rep. Prog. Phys., 78, 116901 [Google Scholar]
- Viganò, D., Rea, N., Pons, J. A., Aguilera, D. N., & Miralles, J. A. 2013, MNRAS, 434, 123; thermally emitting neutron star catalog URL http://www.neutronstarcooling.info/ [NASA ADS] [CrossRef] [Google Scholar]
- Van Riper, K. A. 1988, ApJ, 329, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Voskresensky, D. N. 2001, Lect. Notes Phys., 578, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Wiringa, R. B., Stoks, V. G. B, & Schiavilla, R. 1995, Phys. Rev. C, 51, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Y., Goriely, S., Jorissen, A., Chen, G., & Arnould, M. 2013, A&A, 49, A106; nuclear isotope properties database, URL http://www.astro.ulb.ac.be/bruslib/index.html [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yakovlev, D. G., Levenfish, K. P., & Shibanov, Yu. A. 1999, Phys. Usp., 42, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Yakovlev, D. G., Kaminker, A. D., Gnedin, O. Y., & Haensel, P. 2001, Phys. Rep., 354, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Yakovlev, D. G., Gnedin, O. Y., Kaminker, A. D., & Potekhin, A. Y., 2008, in 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, eds. C. Bassa, Z. Wang, A. Cumming, & V. M. Kaspi, AIP Conf. Proc., 983, 379 [Google Scholar]
Appendix A: Analytical parametrizations at B = 0
For modeling stellar structure and evolution, analytical parametrizations of the quantities of astrophysical interest can be useful. We have constructed such parametrizations for the BSk24 and APR EoS models, following the approach previously developed by Haensel & Potekhin (2004) for Sly4 EoS and Potekhin et al. (2013) for BSk21 EoS. The unified fits to pressure and energy density cover a broad density range including the inner crust and the core. These unified fits smear away all density discontinuities between layers of different composition. Other quantities that are required in modeling neutron-star structure and evolution, such as particle fractions, are given by separate parametrizations for the inner crust and the core.
In the case of BSk24, the analytical fitting formulae for pressure P as a function of mass density ρ, energy per baryon as a function of baryon number density 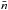 , number fractions of the electrons Ye in the core and free nucleons (Yn, Yp) in the inner crust, sizes and shapes of nuclei in the inner crust, chemical potentials of neutrons and protons in the inner crust and the core will be presented in Pearson et al. (in prep.). We do not reproduce them here, but refer the reader to the web site1, dedicated to Fortran implementations of the EoS fits mentioned in this Appendix.
, number fractions of the electrons Ye in the core and free nucleons (Yn, Yp) in the inner crust, sizes and shapes of nuclei in the inner crust, chemical potentials of neutrons and protons in the inner crust and the core will be presented in Pearson et al. (in prep.). We do not reproduce them here, but refer the reader to the web site1, dedicated to Fortran implementations of the EoS fits mentioned in this Appendix.
For the APR EoS, we have constructed parametrizations of pressure and density in exactly the same form as those presented by Haensel & Potekhin (2004) for the SLy4 EoS model of Douchin & Haensel (2001) in a wide density range including the core and crust. Since APR does not apply in the crust, the present unified fits rely on the SLy4 EoS at 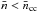 , where
, where 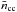 is the baryon number density at the crust-core transition (
is the baryon number density at the crust-core transition (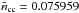 fm-3 according to Douchin & Haensel 2001).
fm-3 according to Douchin & Haensel 2001).
The parametrization of pressure P as a function of mass density ρ is ![\appendix \setcounter{section}{1} \begin{eqnarray} &&\!\!\!\!\! \log_{10}\left(\frac{P}{\mbox{dyn cm}^{-2}}\right) = \frac{6.22+6.121\xi+0.006035\,\xi^3}{(1+0.16354 \,\xi) \big[\ee^{4.73\, (\xi-11.5831)}+1\big]} \nonumber\\&&\qquad + \frac{12.589+1.4365\,\xi}{\ee^{4.75\,(11.5756-\xi)}+1} + \frac{3.8175\,\xi-42.489}{\ee^{2.3\,(14.81 -\xi)}+1} \nonumber\\&&\qquad + \frac{29.80-2.976\,\xi}{\ee^{1.99\, (14.93 -\xi)}+1} , \label{Pfit} \end{eqnarray}](/articles/aa/full_html/2018/01/aa31866-17/aa31866-17-eq257.png) (A.1)where ξ ≡ log 10(ρ/ gcm-3). The typical fit error of P is ≈1–2% for 6 ≲ ξ ≲ 16; the maximum error of ≲4% is due to the continuous fitting across the discontinuity of density at the phase boundary between the crust and the core.
(A.1)where ξ ≡ log 10(ρ/ gcm-3). The typical fit error of P is ≈1–2% for 6 ≲ ξ ≲ 16; the maximum error of ≲4% is due to the continuous fitting across the discontinuity of density at the phase boundary between the crust and the core.
The mass density ρ and the baryon number density 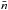 are approximated as functions of each other by the formulae
are approximated as functions of each other by the formulae  where
where 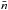 is in fm-3, ρ is in g cm-3, and n0 = ρ/ 1.66 × 1015.
is in fm-3, ρ is in g cm-3, and n0 = ρ/ 1.66 × 1015.
The APR model predicts a phase transition at 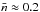 fm-3, which is accompanied by a drop of the charged fraction, as illustrated in Figs. 8 and 9 of Akmal et al. (1998). These results can be approximately described by the formulae
fm-3, which is accompanied by a drop of the charged fraction, as illustrated in Figs. 8 and 9 of Akmal et al. (1998). These results can be approximately described by the formulae 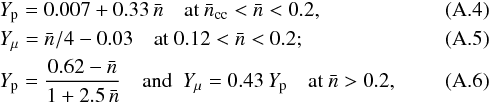 where
where 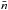 is in fm-3, Yμ = 0 at
is in fm-3, Yμ = 0 at 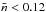 , and Ye = Yp−Yμ.
, and Ye = Yp−Yμ.
Calculations of thermal conductivity in the core, the neutron and proton contributions to the specific heat, and some neutrino reaction rates require knowledge of the effective neutron and proton masses, 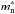 and
and 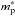 . For the BSk family of models, the effective masses are readily provided in an explicit analytical form as functions of the baryon number density
. For the BSk family of models, the effective masses are readily provided in an explicit analytical form as functions of the baryon number density 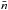 and proton number fraction Yp by the same generalized Skyrme parametrization that underlies the EoS calculations, according to Chamel et al. (2009). In the case of the APR model, the effective masses for the AV18+UIX∗ forces that underlie the EoS are given at
and proton number fraction Yp by the same generalized Skyrme parametrization that underlies the EoS calculations, according to Chamel et al. (2009). In the case of the APR model, the effective masses for the AV18+UIX∗ forces that underlie the EoS are given at 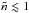 fm-3 by (Baldo et al. 2014)
fm-3 by (Baldo et al. 2014) 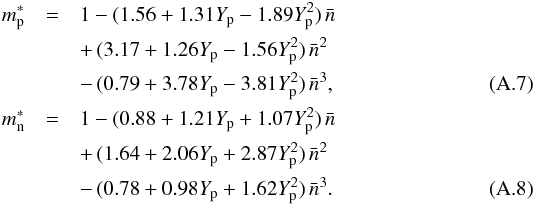 Calculations of electron thermal conductivity (Potekhin et al. 2015, and references therein) and neutrino bremsstrahlung (Ofengeim et al. 2014) in the neutron star crust involve the proton equivalent size parameter
Calculations of electron thermal conductivity (Potekhin et al. 2015, and references therein) and neutrino bremsstrahlung (Ofengeim et al. 2014) in the neutron star crust involve the proton equivalent size parameter 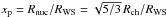 , where Rnuc is the nuclear radius in the model of the rectangular profile of proton charge distribution, Rch is the root mean squared radius of the proton charge distribution, and RWS is the equivalent Wigner-Seitz cell radius (the ion sphere radius). For the BSk24 model, the size parameter is given as function of
, where Rnuc is the nuclear radius in the model of the rectangular profile of proton charge distribution, Rch is the root mean squared radius of the proton charge distribution, and RWS is the equivalent Wigner-Seitz cell radius (the ion sphere radius). For the BSk24 model, the size parameter is given as function of  by the fit
by the fit  (A.9)where
(A.9)where 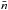 is in fm-3. This fit is accurate to within 1.8%, with typical residuals ~0.4%. For the NV model and the accreted crust model, we use the estimate Rnuc ≈ 1.83Z1/3 fm by Itoh & Kohyama (1983). In the outer crust, we use the values of Rch provided by the bruslib database (Xu et al. 2013).
is in fm-3. This fit is accurate to within 1.8%, with typical residuals ~0.4%. For the NV model and the accreted crust model, we use the estimate Rnuc ≈ 1.83Z1/3 fm by Itoh & Kohyama (1983). In the outer crust, we use the values of Rch provided by the bruslib database (Xu et al. 2013).
Appendix B: Equation of state of a strongly magnetized fermion plasma
The EoS of a fully degenerate nuclear matter in strong magnetic fields was studied by Broderick et al. (2000), using the relativistic mean field model. Here we apply an approximation, which is quite accurate at B ≲ 1016 G and is not bound to using a specific field-theoretical model of nucleon interactions. It relies on the fact that the magnetic field B ≲ 1016 G can be only weakly quantizing at ρ > ρnd, and for this reason its effects on the EoS in the inner crust and the core can be treated perturbatively. We calculate these effects approximately by adding to the free energy at B = 0, provided by a nonmagnetic EoS, the difference ΔFB = FB−F0 between the values for the given B and for B = 0, provided by a generalization of the fully ionized electron-ion plasma model.
The free energy FB includes contributions due to the electrons (FB,e), positrons (FB,e+), neutrons (FB,n), nuclei in the inner crust (FB,Z,A), protons (FB,p) in the core (and in the deepest inner crust layers, where free protons are present according to the BSk model), and muons (FB,μ) in the core at the densities where free muons exist. For FB,Z,A, the known analytical formulae for the magnetized Coulomb crystal (Potekhin & Chabrier 2013) are directly applicable. The other contributions are computed using the model of free Dirac fermions with an addition of the anomalous magnetic moments. We employ the thermodynamic relation 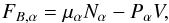 (B.1)where V is the volume, μα is an effective chemical potential of the particles of type α (α = e, e+, p, n, μ),
(B.1)where V is the volume, μα is an effective chemical potential of the particles of type α (α = e, e+, p, n, μ), 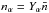 is their number density, Nα = nαV, and Pα is their partial pressure.
is their number density, Nα = nαV, and Pα is their partial pressure.
Anomalous magnetic moments affect the energies of relativistic particles in a nontrivial way (see Broderick et al. 2000). Moreover, the g-factors of fermions are constant only in the perturbative QED regime (e.g., Schwinger 1988), that is at bα ≪ 1, where 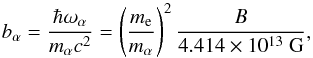 (B.2)mα is the fermion mass, ωα = eB/mαc, and e is the elementary charge. For the leptons, however, the anomalous magnetic moments can be neglected (see Suh & Mathews 2001), while for baryons we always have bα ≪ 1. Thus, in general, we have
(B.2)mα is the fermion mass, ωα = eB/mαc, and e is the elementary charge. For the leptons, however, the anomalous magnetic moments can be neglected (see Suh & Mathews 2001), while for baryons we always have bα ≪ 1. Thus, in general, we have 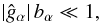 (B.3)where ĝα is the anomalous part of the g-factor (for protons ĝp = gp−2 = 3.586, for neutrons ĝn = gn = −3.826, and for leptons ĝα = gα−2 ≈ 0). Under condition (B.3), the energy due to the anomalous magnetic moment can be approximately treated as an additive constant, positive of negative depending on the magnetic moment direction. In this approximation, the energy of a free charged relativistic fermion in a magnetic field, including rest energy mαc2, can be written in a unified form,
(B.3)where ĝα is the anomalous part of the g-factor (for protons ĝp = gp−2 = 3.586, for neutrons ĝn = gn = −3.826, and for leptons ĝα = gα−2 ≈ 0). Under condition (B.3), the energy due to the anomalous magnetic moment can be approximately treated as an additive constant, positive of negative depending on the magnetic moment direction. In this approximation, the energy of a free charged relativistic fermion in a magnetic field, including rest energy mαc2, can be written in a unified form, 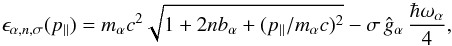 (B.4)(α = e, e+, μ, p). Here, p∥ is the momentum along the field and n = nρ + (1 + σ)/2 is the conventional Landau quantum number, nρ = 0,1,2,... being the radial Landau quantum number; σ = ± 1 controls the spin projection on the magnetic field. A straightforward generalization of Eqs. (51) and (52) of Potekhin & Chabrier (2013) then reads
(B.4)(α = e, e+, μ, p). Here, p∥ is the momentum along the field and n = nρ + (1 + σ)/2 is the conventional Landau quantum number, nρ = 0,1,2,... being the radial Landau quantum number; σ = ± 1 controls the spin projection on the magnetic field. A straightforward generalization of Eqs. (51) and (52) of Potekhin & Chabrier (2013) then reads ![\appendix \setcounter{section}{2} \begin{eqnarray} n_\alpha &=& \frac{1}{\pi^{3/2}\,\am^2\,\lambda_\alpha} \sum_{\sigma\,=\,\pm1} \,\sum_{n\,=\,(1\,+\,\sigma)/2}^{\infty} (1+2nb_\alpha )^{1/4}\, \frac{\partial I_{1/2}(\chi_{\alpha,n,\sigma},\tau_{\alpha,n})}{ \partial \chi_{\alpha,n,\sigma}}, \nonumber\\[-2ex]&& \label{densmag} \\ P_\alpha &=& \frac{\kB T}{\pi^{3/2}\,\am^2\,\lambda_\alpha} \sum_{\sigma\,=\,\pm1} \,\sum_{n\,=\,(1\,+\,\sigma)/2}^{\infty} (1+2nb_\alpha )^{1/4}\, I_{1/2}(\chi_{\alpha,n,\sigma},\tau_{\alpha,n}), \nonumber\\[-2ex]&& \label{presmag} \end{eqnarray}](/articles/aa/full_html/2018/01/aa31866-17/aa31866-17-eq311.png) where
where 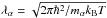 is the thermal de Broglie length,
is the thermal de Broglie length, 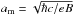 is the magnetic length,
is the magnetic length, 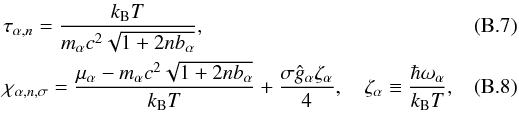 and
and 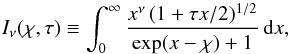 (B.9)which is the relativistic Fermi-Dirac integral.
(B.9)which is the relativistic Fermi-Dirac integral.
For neutrons, in the same approximation, the energy is 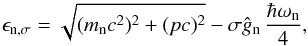 (B.10)where p is the momentum. This leads to
(B.10)where p is the momentum. This leads to ![\appendix \setcounter{section}{2} \begin{eqnarray} n_\alpha &=& \frac{2}{\sqrt{\pi}\,\lambda_\alpha^3} \sum_{\sigma=\pm1} \left[ I_{1/2}(\chi_{\alpha,0,\sigma},\tau_{\alpha,0}) + \tau_{\alpha,0} I_{3/2}(\chi_{\alpha,0,\sigma},\tau_{\alpha,0}) \right], \nonumber\\[-2ex]&& \label{n_e} \\ P_\alpha &=& \frac{4}{3\sqrt\pi}\,\frac{\kB T }{ \lambda_\alpha^3} \sum_{\sigma=\pm1} \Big[ I_{3/2}(\chi_{\alpha,0,\sigma},\tau_{\alpha,0}) + \frac{\tau_{\alpha,0}}{ 2} I_{5/2}(\chi_{\alpha,0,\sigma},\tau_{\alpha,0}) \Big]. \nonumber\\[-1ex]&& \label{P_e} \end{eqnarray}](/articles/aa/full_html/2018/01/aa31866-17/aa31866-17-eq317.png) Equations (B.11) and (B.12) are valid not only for neutrons (α = n), but also for other fermions in a nonquantizing magnetic field or at B = 0 (in the latter case, ∑ σ amounts to the factor 2), so they yield F0.
Equations (B.11) and (B.12) are valid not only for neutrons (α = n), but also for other fermions in a nonquantizing magnetic field or at B = 0 (in the latter case, ∑ σ amounts to the factor 2), so they yield F0.
At given nα, T, and B, we find μα by numerical inversion of Eqs. (B.5) or (B.11). Then the above expressions for nα and Pα provide the partial free energy FB,α, from which we can derive the magnetic contributions of the fermions α into the total free energy F, entropy S = −(∂F/∂T)V, internal energy U = F + TS, heat capacity at constant volume CV = (∂S/∂lnT)V, derivatives of pressure (∂P/∂T)V and (∂P/∂V)T, heat capacity at constant pressure 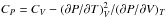 , and so on.
, and so on.
Analytical approximations for the Fermi-Dirac integrals Iν(χ,τ) (see Potekhin & Chabrier 2013, and references therein) provide nα(μα,T), Pα(μα,T), and consequently FB,α(μα,T) in an explicit form. Using relations 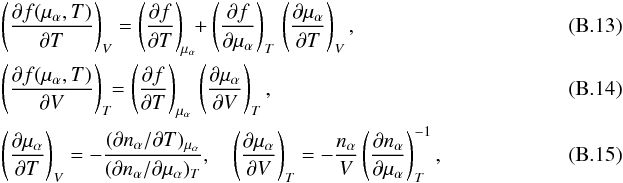 we can now write explicit analytical approximations to first, second, and mixed partial derivatives of FB,α over V and T, which provide magnetic contributions to the above-mentioned thermodynamic functions.
we can now write explicit analytical approximations to first, second, and mixed partial derivatives of FB,α over V and T, which provide magnetic contributions to the above-mentioned thermodynamic functions.
In the particular case of nonrelativistic nondegenerate particles with spin 1/2, we have 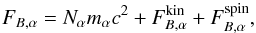 (B.16)where
(B.16)where ![\appendix \setcounter{section}{2} \begin{equation} F_{B,\alpha}^\mathrm{kin} = N_\alpha \kB T \left[ \ln(2\pi\lambda_\alpha\am^2) + \ln\left(\ee^{\zeta_\alpha/2}-\ee^{-\zeta_\alpha/2}\right) - 1 \right], \end{equation}](/articles/aa/full_html/2018/01/aa31866-17/aa31866-17-eq336.png) (B.17)which is the kinetic contribution for charged particles,
(B.17)which is the kinetic contribution for charged particles, ![\appendix \setcounter{section}{2} \begin{equation} F_{B,\alpha}^\mathrm{kin} = N_\alpha \kB T \left[ \ln(2\pi\lambda_\alpha^3) - 1 \right], \end{equation}](/articles/aa/full_html/2018/01/aa31866-17/aa31866-17-eq337.png) (B.18)which is the kinetic contribution for neutrons (or in nonquantizing magnetic field), and
(B.18)which is the kinetic contribution for neutrons (or in nonquantizing magnetic field), and ![\appendix \setcounter{section}{2} \begin{equation} F_{B,\alpha}^\mathrm{spin} = - \,N_\alpha \kB T \left[ \frac{g_\alpha\zeta_\alpha}{4} + \ln\left(\frac{1-\ee^{-g_\alpha\zeta_\alpha}}{ 1-\ee^{-g_\alpha\zeta_\alpha/2}} \right) \right], \end{equation}](/articles/aa/full_html/2018/01/aa31866-17/aa31866-17-eq338.png) (B.19)which is the magnetic moment contribution in both cases. The pressure of nondegenerate particles is not affected by the magnetic field (Pα = nαkBT), but the internal energy
(B.19)which is the magnetic moment contribution in both cases. The pressure of nondegenerate particles is not affected by the magnetic field (Pα = nαkBT), but the internal energy 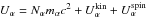 and heat capacity
and heat capacity 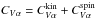 are affected by the B-dependent spin contributions
are affected by the B-dependent spin contributions 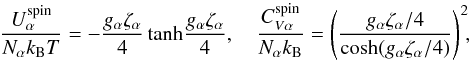 (B.20)and for charged particles also by the B-dependent kinetic contributions,
(B.20)and for charged particles also by the B-dependent kinetic contributions, 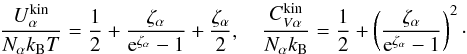 (B.21)In the opposite case of strongly degenerate fermions (μα−mαc2 ≫ kBT), one can use the Sommerfeld expansion (e.g., Chandrasekhar 1957, Chapter X),
(B.21)In the opposite case of strongly degenerate fermions (μα−mαc2 ≫ kBT), one can use the Sommerfeld expansion (e.g., Chandrasekhar 1957, Chapter X),  (B.22)where
(B.22)where 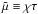 ,
, 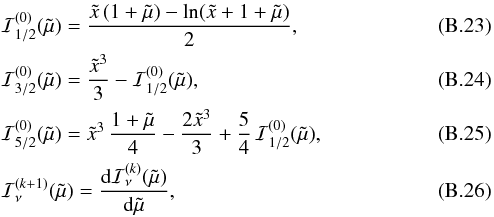 and
and 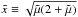 . At a fixed nα, to the lowest order in T2, Eqs. (B.1), (B.5), and (B.22) yield
. At a fixed nα, to the lowest order in T2, Eqs. (B.1), (B.5), and (B.22) yield 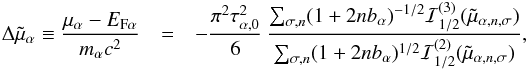 (B.27)where summation indices run over the same values as before (σ = ± 1; n = 0,1,2,... for σ = −1 and n = 1,2,3,... for σ = 1),
(B.27)where summation indices run over the same values as before (σ = ± 1; n = 0,1,2,... for σ = −1 and n = 1,2,3,... for σ = 1), 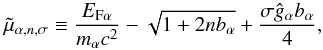 (B.28)and EFα is the Fermi energy, which is found from the condition
(B.28)and EFα is the Fermi energy, which is found from the condition 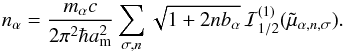 (B.29)The pressure is given, to the same order of approximation, by
(B.29)The pressure is given, to the same order of approximation, by  (B.30)where
(B.30)where 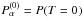 and
and 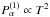 are given by
are given by ![\appendix \setcounter{section}{2} \begin{eqnarray} P_\alpha^{(0)} &=& \frac{m_\alpha^4 c^5}{\hbar^3}\, \frac{b_\alpha}{2\pi^2}\,\sum_{\sigma, n} (1+2nb_\alpha)\mathcal{I}_{1/2}^{(0)}(\tilde\mu_{\alpha,n,\sigma}), \\ P_\alpha^{(1)} &=& \frac{m_\alpha^4 c^5}{\hbar^3}\, \frac{b_\alpha}{2\pi^2}\,\sum_{\sigma, n} \Bigg[ \Delta\tilde\mu_\alpha (1+2nb_\alpha)\,\mathcal{I}_{1/2}^{(1)}(\tilde\mu_{\alpha,n,\sigma}) \nonumber\\&& +\, \frac{\pi^2\tau_{\alpha,0}^2}{6}\, \mathcal{I}_{1/2}^{(2)}(\tilde\mu_{\alpha,n,\sigma}) \Bigg]. \end{eqnarray}](/articles/aa/full_html/2018/01/aa31866-17/aa31866-17-eq361.png) For the degenerate neutrons, in the same approximation, Eq. (B.22) and Eqs. (B.1), (B.11), and (B.12) yield
For the degenerate neutrons, in the same approximation, Eq. (B.22) and Eqs. (B.1), (B.11), and (B.12) yield ![\appendix \setcounter{section}{2} \begin{equation} \Delta\tilde\mu_\alpha = - \frac{\pi^2\tau_{\alpha,0}^2}{6}\, \frac{\sum_\sigma \left[\mathcal{I}_{1/2}^{(2)}(\tilde\mu_{\alpha,0,\sigma}) + \mathcal{I}_{3/2}^{(2)}(\tilde\mu_{\alpha,0,\sigma}) \right]}{ \sum_{\sigma} \left[ (\mathcal{I}_{1/2}^{(1)}(\tilde\mu_{\alpha,0,\sigma}) + \mathcal{I}_{3/2}^{(1)}(\tilde\mu_{\alpha,0,\sigma}) \right]}, \end{equation}](/articles/aa/full_html/2018/01/aa31866-17/aa31866-17-eq362.png) (B.33)where EFα is found from the condition
(B.33)where EFα is found from the condition ![\appendix \setcounter{section}{2} \begin{equation} n_\alpha = \frac{1}{2\pi^2}\left(\frac{\hbar}{m_\alpha c}\right)^3 \sum_\sigma \left[ \mathcal{I}_{1/2}^{(0)}(\tilde\mu_{\alpha,0,\sigma}) + \mathcal{I}_{3/2}^{(0)}(\tilde\mu_{\alpha,0,\sigma}) \right]. \end{equation}](/articles/aa/full_html/2018/01/aa31866-17/aa31866-17-eq363.png) (B.34)Then the two lowest-order contributions to pressure are
(B.34)Then the two lowest-order contributions to pressure are ![\appendix \setcounter{section}{2} \begin{eqnarray} P_\alpha^{(0)} &=& \frac{m_\alpha^4 c^5}{3\pi^2\hbar^3}\, \sum_{\sigma} \left[ \mathcal{I}_{3/2}^{(0)}(\tilde\mu_{\alpha,0,\sigma}) + \frac12\,\mathcal{I}_{5/2}^{(0)}(\tilde\mu_{\alpha,0,\sigma}) \right],~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \\ P_\alpha^{(1)} &=& \frac{m_\alpha^4 c^5}{3\pi^2\hbar^3}\, \Delta\tilde\mu_\alpha \sum_{\sigma} \left[ \mathcal{I}_{3/2}^{(1)}(\tilde\mu_{\alpha,0,\sigma}) + \frac12\,\mathcal{I}_{5/2}^{(1)}(\tilde\mu_{\alpha,0,\sigma}) \right] \nonumber\\&& + \frac{m_\alpha^2 c}{18\hbar^3}\,(\kB T)^2 \sum_{\sigma} \left[ \mathcal{I}_{3/2}^{(2)}(\tilde\mu_{\alpha,0,\sigma}) + \frac12\,\mathcal{I}_{5/2}^{(2)}(\tilde\mu_{\alpha,0,\sigma}) \right]. \end{eqnarray}](/articles/aa/full_html/2018/01/aa31866-17/aa31866-17-eq364.png) These approximations give the free energy with the lowest-order T-dependent terms in the form
These approximations give the free energy with the lowest-order T-dependent terms in the form 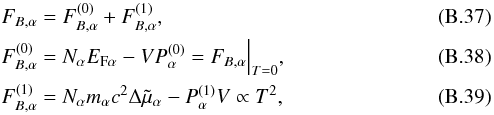 from which the first- and second-order thermodynamic functions are easily derived. They take particularly simple forms for the nonrelativistic fermions, for which EFα−mαc2 ≪ mαc2. Then we can consider
from which the first- and second-order thermodynamic functions are easily derived. They take particularly simple forms for the nonrelativistic fermions, for which EFα−mαc2 ≪ mαc2. Then we can consider 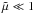 in Eqs. (B.23)–(B.26), and they simplify to
in Eqs. (B.23)–(B.26), and they simplify to 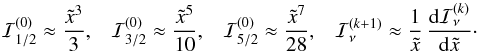 (B.40)Taking into account that for the baryons bα ≪ 1, we find, for example, that the Fermi energy of strongly degenerate neutrons EFn(nn,B) ≈ EFn(nn,0)[1−(gnħωn/ 8EFn)2], and that the temperature corrections
(B.40)Taking into account that for the baryons bα ≪ 1, we find, for example, that the Fermi energy of strongly degenerate neutrons EFn(nn,B) ≈ EFn(nn,0)[1−(gnħωn/ 8EFn)2], and that the temperature corrections  and
and  are shifted relative to the nonmagnetic expressions (Eq. (6) in Potekhin & Chabrier 2010) by the same fractional order of magnitude ~(ħωn/EFn)2. Analogous corrections for nonrelativistic protons are, by order of magnitude, ~(ħωp/EFp)2. Thus the contributions to the thermodynamic functions (in particular, heat capacity) of strongly degenerate baryons, caused by their anomalous magnetic moments, prove to be unimportant, in contrast to the case of nondegenerate baryons.
are shifted relative to the nonmagnetic expressions (Eq. (6) in Potekhin & Chabrier 2010) by the same fractional order of magnitude ~(ħωn/EFn)2. Analogous corrections for nonrelativistic protons are, by order of magnitude, ~(ħωp/EFp)2. Thus the contributions to the thermodynamic functions (in particular, heat capacity) of strongly degenerate baryons, caused by their anomalous magnetic moments, prove to be unimportant, in contrast to the case of nondegenerate baryons.
All Figures
 |
Fig. 1 Rosseland mean radiative opacities due to the free-free transitions and Compton scattering in the model of fully ionized iron plasma as functions of mass density at different temperatures (marked near the curves) and magnetic fields B = 0, 1012 G, 1014 G, and 1016 G (shown by different line styles). |
| In the text | |
 |
Fig. 2 Theoretical cooling curves (redshifted thermal luminosity |
| In the text | |
 |
Fig. 3 Redshifted temperature as a function of mass density inside a neutron star with M = 1.4 M⊙ at different ages (marked near the curves) according to different theoretical models. Line styles correspond to theoretical models in the same way as in Fig. 2. The three parts of the figure show the thermal structure of the envelopes comprising the ocean and the outer crust (left), the inner crust (middle), and the core (right) at different density scales. In the gray-cross-hatched |
| In the text | |
 |
Fig. 4 Cooling curves for neutron stars with M = 1.0 (green), 1.2 (blue), 1.4 (black), 1.6 (magenta), 1.8 (orange), 2.0 M⊙ (violet), and the maximum mass Mmax (red lines), calculated using the same basic theoretical model as in Fig. 2, for the EoS models BSk24/21 (solid/dotted lines, Mmax = 2.28 M⊙, MDU = 1.596/1.587 M⊙) and APR+NV (dashed lines, Mmax = 2.21 M⊙, MDU = 2.01 M⊙) compared with observations (the same symbols as in Fig. 2). |
| In the text | |
 |
Fig. 5 Redshifted temperature as function of mass density inside neutron stars with masses M = 1.0 (dot-long-dash lines), 1.4 (solid lines), 2.0 (short-dashed lines), and Mmax = 2.28 M⊙ (dot-short-dash lines) for the unified EoS model BSk24, and with mass Mmax = 2.21 M⊙ for the APR+NV EoS model (dotted lines) at ages of 10-3, 1, and 50 yr. The vertical lines separate three density regions: the ocean and outer crust, the inner crust, and the core, displayed using different density scales. |
| In the text | |
 |
Fig. 6 Neutrino emission power density as function of mass density at ages 50 yr (upper curves) and 5 kyr (lower curves of each type) for different neutron star models: the basic model (EoS BSk24, ground state composition, M = 1.4 M⊙, no superfluidity; solid lines), the neutron star with fully accreted envelope (short-dashed lines), three different combinations of the three types of superfluidity (dot-long-dash, dot-short-dash, and dotted curves), and a model without superfluidity but with the direct Urca processes due to the higher mass M = 1.8 M⊙ (long-dashed lines). The density scale is different in the left and right parts of the figure, separated by the vertical solid line. The vertical dotted lines mark the outer and inner boundaries of the inner crust. |
| In the text | |
 |
Fig. 7 Thermal conductivity (upper panel) and heat capacity per baryon in units of kB (lower panel) as functions of mass density at age t = 1 kyr for the same neutron star models as in Fig. 6. The crosses mark the melting points for the models with M = 1.4 M⊙: to the left of them, the Coulomb plasma forms a liquid ocean. For the M = 1.8 M⊙ model, the crust does not melt in the displayed density range, because it is relatively cold at this age (cf. Fig. 4). The vertical dotted lines mark the outer and inner boundaries of the inner crust. |
| In the text | |
 |
Fig. 8 Cooling curves for a neutron star with M = 1.4 M⊙ according to the BSk24 EoS model with iron (lines 1, 4, 5, 6) or accreted envelopes (lines 2, 3, 7), iron (lines 1, 4, 5, 6), hydrogen (lines 2, 7), or helium atmosphere (line 3), without nucleon superfluidity (lines 1–3) and with different models of nucleon superfluidity (lines 4–7; see text for explanation of the SF-notations), compared with observations (the same symbols as in Fig. 2). |
| In the text | |
 |
Fig. 9 Redshifted temperature as a function of mass density inside a neutron star for three of the seven different models considered in Fig. 8 (namely, models 1, 2, and 7), plotted using the same line styles, at different ages marked near the curves. The two parts of the figure, separated by the vertical solid line, show the regions before and after neutron drip at different density scales. The dotted lines in the left half of the figure show the adopted density-temperature domains for different chemical elements (H, 4He, 12C, 16O) in the accreted envelope. To the right of the last of these lines, the composition of the accreted crust is adopted from Haensel & Zdunik (1990). For the nonaccreted crust, we use the ground-state composition of matter according to the BSk24 model. The vertical dotted line in the right half of the figure separates the crust and the core. |
| In the text | |
 |
Fig. 10 Cooling curves for neutron stars with M = 1.4 M⊙ according to the BSk24 EoS model with B = 0 (solid line), 1014 G (short-dashed line), 1015 G (long-dashed line), and 1016 G (dot-dashed line). The three dotted lines result from simulations with the same three strong fields, but treated classically. |
| In the text | |
 |
Fig. 11 Redshifted temperature as a function of mass density inside neutron stars with B = 0 (solid lines), 1015 G (long-dashed and dotted lines), and 1016 G (dot-dashed lines) at four ages t from 8 h to 2 × 104 yr, marked near the curves. The dotted line illustrates the model with superfluidity SF081322; the other lines are calculated without superfluidity. The two parts of the figure, separated by the vertical solid line, show the regions before and after neutron drip at different density scales. Inset: temperature profiles in the envelopes of a neutron star with B = 1014 G at ages t = 1, 5, 20, and 100 kyr. |
| In the text | |
 |
Fig. 12 Effective thermal conductivity as a function of density in the ocean and crust of a kyr-old magnetar with magnetic fields B = 1014 G, 1015 G, and 1016 G. The vertical dotted line marks the neutron drip density. |
| In the text | |
 |
Fig. 13 Neutrino emission power density as a function of mass density at ages 50 yr (upper curves) and 5 kyr (lower curves of each type) for nonsuperfluid magnetars with B = 1014 G (short-dashed lines), 1015 G (long-dashed lines), and 1016 G (dot-dashed lines) and for a magnetar with B = 1015 G and nucleon superfluidity (dotted lines), compared with neutrino emission of a nonmagnetic, nonsuperfluid neutron star (solid lines). The density scale is different in the left and right parts of the figure, separated by the vertical solid line. The vertical dotted lines mark the outer and inner boundaries of the inner crust. |
| In the text | |
 |
Fig. 14 Comparison of cooling of nonsuperfluid (solid lines) and superfluid (dot-dashed lines) magnetars with superfluidity type SF081322 and magnetic fields B = 1014 G, 1015 G, and 1016 G. The dotted line shows the joint effect of superfluidity and accreted envelope for the magnetar with B = 1015 G. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.