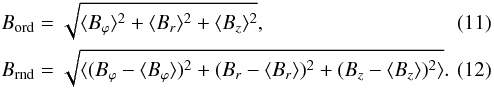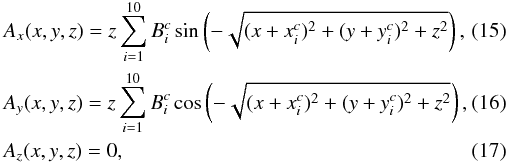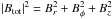| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 14 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201629988 | |
| Published online | 25 January 2018 | |
Global enhancement and structure formation of the magnetic field in spiral galaxies
1 GEPI, Observatoire de Paris, PSL Research University, CNRS, Place Jules Janssen, 92195 Meudon Cedex, France
e-mail: sergey.khoperskov@obspm.fr
2 Institute of Astronomy, Russian Academy of Sciences, Pyatnitskaya st. 48, Moscow 119017, Russia
3 Volgograd State University, Universitetsky pr., 100, Volgograd 400062, Russia
Received: 1 November 2016
Accepted: 10 October 2017
In this paper we study numerically large-scale magnetic field evolution and its enhancement in gaseous disks of spiral galaxies. We consider a set of models with the various spiral pattern parameters and the initial magnetic field strength with taking into account gas self-gravity and cooling and heating processes. In agreement with previous studies we find out that galactic magnetic field is mostly aligned with gaseous structures, however small-scale gaseous structures (spurs and clumps) are more chaotic than the magnetic field structure. In spiral arms magnetic field often coexists with the gas distribution, in the inter-arm region we see filamentary magnetic field structure. These filaments connect several isolated gaseous clumps. Simulations reveal the presence of the small-scale irregularities of the magnetic field as well as the reversal of magnetic field at the outer edge of the large-scale spurs. We provide evidences that the magnetic field in the spiral arms has a stronger mean-field component, and there is a clear inverse correlation between gas density and plasma-beta parameter, compared to the rest of the disk with a more turbulent component of the field and an absence of correlation between gas density and plasma-beta. We show the mean field growth up to 3−10 μG in the cold gas during several rotation periods (500−800 Myr), whereas ratio between azimuthal and radial field is equal to 4/1. We find an enhancement of random and ordered components of the magnetic field. Mean field strength increases by a factor of 1.5−2.5 for models with various spiral pattern parameters. Random magnetic field component can reach up to 25% from the total strength. By making an analysis of the time-dependent evolution of the radial Poynting flux, we point out that the magnetic field strength is enhanced more strongly at the galactic outskirts which is due to the radial transfer of magnetic energy by the spiral arms pushing the magnetic field outward. Our results also support the presence of sufficient conditions for the development of magnetorotational instability at distances >11 kpc after 300 Myr of evolution.
Key words: galaxies: spiral / galaxies: magnetic fields / galaxies: ISM
© ESO, 2018
1. Introduction
It has long been recognized that numerous nearby spiral galaxies contain a large-scale magnetic field (Beck 2009, 2016). Giant galaxies generate their regular magnetic fields already at z = 3−4 (Bernet et al. 2008; Arshakian et al. 2009). The general properties of magnetic fields and their variation as a function of resolution, seed field and baryon physics in cosmological simulations have been intensively studied by Pakmor et al. (2014), Marinacci et al. (2015), Marinacci & Vogelsberger (2016). Rieder & Teyssier (2016) suggest that weak initial seed fields were first amplified by a small-scale dynamo during a violent feedback-dominated early phase in the galaxy formation history.
In the disks of galaxies magnetic field pressure appears to be comparable with the thermal pressure of the interstellar medium (ISM) in the current epoch (Beck et al. 1996; Crutcher 1999). Magnetic field strength is also related to the galactic star formation rate (see, e.g., Beck 2009; Ostriker et al. 2010; Mikhailov et al. 2012). Indeed, total magnetic field strength grows non-linearly with star formation rate (SFR), while the regular magnetic field strength does not seem to depend on SFR (Krause 2009). The magnetic field structure in the Milky Way (Jansson & Farrar 2012) and its role in the gas kinematics are still under debate (see models of the Milky Way rotation Sánchez-Salcedo & Santillán 2013; Elstner et al. 2014).
Some grand design spiral galaxies demonstrate the presence of prominent magnetic arms, situated in the inter-arm regions, between the material arms (Shukurov 1998). The origin of this feature remains unclear and possible mechanisms have been discussed in a several works by Moss et al. (2013, 2015), Chamandy et al. (2013, 2015). Polarized synchrotron emission and Faraday rotation measurements suggest that in a number of disk galaxies regular magnetic field is generally aligned with the global gas motions (see e.g., Graeve & Beck 1988; Beck & Wielebinski 2013; Gießübel & Beck 2014) and molecular gas structures (Li & Henning 2011). There is observable evidence that the magnetic field can control the flow of the diffuse interstellar gas at kiloparsec scales (Beck et al. 2005). There are galaxies where a bisymmetric magnetic structure dominates (e.g., M 81, M 51 in Beck 2000). At the same time, in some galaxies the magnetic field is represented by axisymmetic spiral structures (Krause & Beck 1998). The mean magnetic field strength for a sample of spiral galaxies observed by Niklas (1995) is on average 9 ± 3 μG ; higher values can be found in spiral arms, up to 20 μG (Beck 1991). For barred galaxies, the strength of the total magnetic field can be even larger. For instance, in the knots of NGC 1097, it is about 60 μG (Beck et al. 2005).
The growth of magnetic field strength is clearly demonstrated in dynamo theory simulations of the ISM in spiral galaxies (Frick et al. 2016), barred galaxies (Beck et al. 1994), and ring galaxies (Moss et al. 2016). Numerical models of evolving galaxies show fast field amplification and ordering due to differential rotation (Kotarba et al. 2009; Wang & Abel 2009), possibly supported by the magneto-rotational instability (Gressel et al. 2013; Pakmor & Springel 2013). In these models the ordered magnetic field forms spiral arm segments. Shetty & Ostriker (2006) also established that the magnetic field plays an important role in the morphology of gas in spiral galaxies. They also claimed that the magnetic field distortion is due to spiral shocks evolution. By doing smooth particles hydrodynamics (SPH) simulations, Dobbs & Price (2008) showed that the magnetic field is able to inhibit the formation of structures in the disk, but small-scale features still appear even for highly magnetized gas (β ≤ 0.1). In this the paper we define the standard plasma beta parameter as: 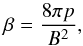 (1)which measures the ratio of the thermal to the magnetic pressure.
(1)which measures the ratio of the thermal to the magnetic pressure.
Apart from the large-scale magnetic field and random fields, there are several specific phenomena, related to the galactic magnetic field structure, for example, magnetic field reversals (see e.g., Vallee 1996). Magnetic field reversals from the early phases may survive up to more recent epochs (Moss et al. 2012). In simulations, large-scale field reversals are a common feature of the models by Poezd et al. (1993), Moss et al. (2012), Moss & Sokoloff (2013). Magnetic field reversal is studied in smooth particles magnetohydrodynamics (SPMHD) simulations of the Milky Way disk (Dobbs et al. 2016) in detail. It was shown that the magnetic field reversals occur when the velocity jump across the spiral shock is above ≈20 km s-1 . Reversals also occur at corotation and at the inner Lindblad resonance.
It is believed that spurs in spiral galaxies are formed due to Kelvin-Helmholtz-type instability in the vicinity of the galactic shock (Elmegreen 1980; Wada & Koda 2004). From another point of view, wiggle instability is originates from the generation of potential vorticity at a deformed shock front (Kim et al. 2014; Sormani et al. 2017). Kim et al. (2015) showed that magnetic fields suppress wiggle instability, but not completely, at least for β ≥ 1. The stabilizing role of magnetic fields is not from the perturbed fields but directly from the background unperturbed fields that tend to reduce the shock compression factor by exerting magnetic pressure. Despite these studies, magnetic field structure in the vicinity of galactic spurs has never been described in detail.
Current high-resolution galactic-scale simulations include detailed molecular chemistry of the ISM (Gnedin et al. 2009; Christensen et al. 2012; Smith et al. 2014), as well as star formation and feedback (Tasker & Tan 2009; Renaud et al. 2013; Pan et al. 2015; Padoan et al. 2016; Iffrig & Hennebelle 2017). These results suggest that hydrodynamic effects and the self-gravity of the gas play some important roles regarding the gas structures in the spiral (Dobbs & Bonnell 2006; Dobbs et al. 2006, 2008, 2011; Renaud et al. 2013) and bar potential (Fujimoto et al. 2014, 2016). The impact of MHD turbulence on the molecular clouds formation and evolution has been recently stressed by Inoue & Inutsuka (2009), Körtgen & Banerjee (2015). The morphology and evolution of molecular clouds in MHD converging flow simulations also have been studied by Banerjee et al. (2009) and Fogerty et al. (2016).
The effects of self-gravity and magnetic fields highly depend on the gaseous temperatures and phases (Banerjee et al. 2009; Federrath & Klessen 2012). However, it is not clear how the magnetic fields affect the stability of the multiphase ISM in a spiral potential. For instance, Dobbs & Price (2008) studied gas dynamics in a spiral potential, taking into account magnetic field evolution. However, in their non self-gravitating SPMHD simulations, they do not solve an energy equation with realistic cooling and heating processes where warm and cold components are treated separately as isothermal gases without phase exchange. In this paper we aim to explore the role of magnetic field in the structure of galactic gaseous disks as well as enhancement of various components of the magnetic field, taking into account gas self-gravity and multiphase ISM in the disks of spiral galaxies. We focus our analysis on the magnetic field structure in the simulated spiral galaxies with different morphology and pattern kinematics. Indeed star formation and feedback are very important for the structure and dynamics of the ISM, but instead of including all of the relevant detailed physics, here we focus on improving the initial parameters of the magnetic field (spatial structure and strength) the formation of small- and large-scale structures. The major interest of this work is the possibility of probing the physical quantities and structures in a consistent galactic context. Rather than studying the amplification of a primordial field, we start our calculations with magnetic field strengths closer to the present day values. However, we also study the simulation with an initially turbulent magnetic field, which already has significant strength. The paper is organized as follows. In Sect. 2 we describe our numerical models and introduce basic definitions. In Sect. 3 we present our results. In Sect. 4 we summarize and make some concluding remarks.
2. Model. Basic equations
The simulations have been run using the unsplit Total Variation Diminishing Multi Upstream Scheme for Conservation Laws (TVD MUSCL) code, which includes standard physics modules previously described in Khoperskov et al. (2013, 2014, 2016). For divergence cleaning we apply a constrained transport technique for magnetic field transport through the computational domain (Evans & Hawley 1988). In this approach, magnetic field strength is defined at the faces of a cell, while other gas dynamical variables are defined at the center of a cell. We numerically investigate the gas dynamics in 3D in a computational box of size 12 × 12 × 4 kpc, with a spatial resolution of 1600 × 1600 × 256 grid zones in the x, y, and z directions, respectively and the corresponding grid spacing is 15 pc. In the simulations we also implement gas self-gravity and the network of cooling and heating processes for a solar metallicity ISM (see details in Khoperskov et al. 2013). The equations considered in our simulations are: ![\begin{eqnarray} && \frac{\partial \rho }{\partial t} + \nabla \cdot \left( \rho \vec{u} \right) = 0, \\ && \frac{\partial (\rho \vec{u})}{\partial t} + \nabla\cdot\left[\rho \vec{u}\times\vec{u} - \frac{1}{4\pi}\vec{B}\times\vec{B} \right] = - \nabla p - \rho \nabla \Psi, \\ && \rho \frac{\partial e}{\partial t} +\nabla \cdot \left[ (e + p)\vec{u} - \frac{1}{4\pi} (\vec{B}\cdot\vec{u})\vec{B} \right] = \rho\Lambda, \\ &&\frac{\partial \vec{B}}{\partial t} - \nabla \times (\vec{u}\times \vec{B}) = 0, \end{eqnarray}](/articles/aa/full_html/2018/01/aa29988-16/aa29988-16-eq22.png) where ρ is the gas density, u and B are the vectors of the gas velocity and magnetic field correspondingly, p is the total gas pressure, e is the total gas energy, Ψ = Ψext + Ψgas is the sum of external gravitational potential Ψext and gas self-gravity Ψgas, and Λ is the loss function, including heating and cooling terms (see details in Khoperskov et al. 2013). Boundary conditions were chosen to allow for free outflow (see e.g., Dubois & Teyssier 2010). In our models the magnetic field at the outer border of the computational domain is much weaker than the average and the boundary conditions do not contribute significantly to the overall magnetic energy evolution.
where ρ is the gas density, u and B are the vectors of the gas velocity and magnetic field correspondingly, p is the total gas pressure, e is the total gas energy, Ψ = Ψext + Ψgas is the sum of external gravitational potential Ψext and gas self-gravity Ψgas, and Λ is the loss function, including heating and cooling terms (see details in Khoperskov et al. 2013). Boundary conditions were chosen to allow for free outflow (see e.g., Dubois & Teyssier 2010). In our models the magnetic field at the outer border of the computational domain is much weaker than the average and the boundary conditions do not contribute significantly to the overall magnetic energy evolution.
We consider the dynamics of the gaseous disk in external potential of the spherical isothermal halo Ψh, the Plummer model of spherical bulge Ψb, and the flat disk component in Myamoto-Nagai form Ψd (Miyamoto & Nagai 1975). The combination of the disk, bulge and halo parameters lets us study the dynamics of gas in the isolated Milky Way-type disk, with a flat rotation curve and circular velocity of ≈220 km s-1 at 8 kpc from the center. We investigate gas response in the presence of spiral potential described by the logarithmic spiral perturbation Ψsp of the axisymmetric potential of the stellar disk, and then the total external potential is the following: 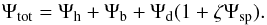 (6)The amplitude of spiral perturbation is adopted in the form:
(6)The amplitude of spiral perturbation is adopted in the form: 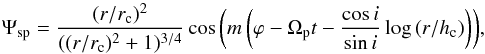 (7)where r and ϕ are the radial and azimuthal coordinates, respectively, i is the spiral pitch angle, Ωp is the pattern speed, rc is the spiral scale length, and hc is the spiral width. The amplitude of perturbation ζ is a function of time until t1 and it is used in the form proposed by Dehnen (2000):
(7)where r and ϕ are the radial and azimuthal coordinates, respectively, i is the spiral pitch angle, Ωp is the pattern speed, rc is the spiral scale length, and hc is the spiral width. The amplitude of perturbation ζ is a function of time until t1 and it is used in the form proposed by Dehnen (2000): 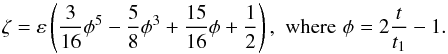 (8)After t1 the amplitude of perturbation is constant and is equal to ε. Such an approach guarantees a smooth transition from the axisymmetric potential to the spiral one during the time interval t1. In our simulations we adopted t1 = 100 Myr which enabled us to diminish the initial transient effects.
(8)After t1 the amplitude of perturbation is constant and is equal to ε. Such an approach guarantees a smooth transition from the axisymmetric potential to the spiral one during the time interval t1. In our simulations we adopted t1 = 100 Myr which enabled us to diminish the initial transient effects.
To avoid an initial magnetic field divergence in the computational domain, we introduce the magnetic field by using vector potential A: 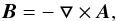 (9)where we set up A = { 0,0,exp(−r/rm) } for a purely toroidal initial magnetic field structure. Such an approach lets us set up values for the magnetic field on the faces of the computational cells, because these values are actually used in computations and divergence cleaning procedures.
(9)where we set up A = { 0,0,exp(−r/rm) } for a purely toroidal initial magnetic field structure. Such an approach lets us set up values for the magnetic field on the faces of the computational cells, because these values are actually used in computations and divergence cleaning procedures.
We set up the gaseous disk equilibrium state according to the radial balance of the gas rotation vs. radial gradient of gas pressure, gravitational forces (external potential and self-gravity) and magnetic field pressure. For the gaseous disk profile, we choose an exponential law with the radial scale length equal to 5 kpc. Our models are listed in Table 1, where we vary initial magnetic field strength, morphology of spiral potential, and the spiral pattern speed. We also simulated three special models: without magnetic field (pure hydrodynamics), without spiral pattern (axisymmetric external potential, or ε = 0), and with initial turbulent magnetic field structure. Our simulation was evolved for about 0.8−1 Gyr.
Parameters used in the calculations.
 |
Fig. 1 Face-on view of the surface density in the whole galactic disk at 500 Myr for three models with different initial magnetic field strength, from left to right: no magnetic field, β = 10, β = 1, β = 0.3. Rotation is clockwise. |
3. Results
First, we present the analysis of the evolution of both gas and magnetic field morphology in our fiducial simulation in Sect. 3.1 where we consider the response of a slightly magnetized medium β = 10 to the two-armed spiral potential perturbation representing the stellar spiral arms of a galaxy. We discuss the morphology of the magnetic field, and the magnetic field strengths of the spiral arm and inter-arm regions in Sects. 3.3 and 3.4. The evolution of various magnetic field components is considered in Sect. 3.5. We also examine the growth of magnetic field strength in models with various spiral perturbations (Sects. 3.6–3.8). Finally, turbulent magnetic field evolution and its impact on the gas dynamics is presented in Sect. 3.9.
3.1. Magnetic field impact on structure formation and gas kinematics
Large-scale disk galaxy morphology with magnetic fields looks similar to models without it. For a small initial magnetic field strength (β = 10) we see a very small difference from the pure hydro simulation (see Fig. 1). In both cases we observe the formation of a spiral structure is driven by the external potential perturbation. In the inter-arm region there is a number of small-scale isolated clumps. Various small-scale gas features, such as spurs, feathering, and clumps are formed due to gravitational, thermal and shear flow instabilities (Dobbs & Bonnell 2006; Dobbs et al. 2008; Wada 2008). The clumps are connected to large filaments which build up in the intersection region of the colliding flows. For larger initial magnetic fields (β ≤ 1), the difference in gas density distributions is clearly seen. In the very center, the formation of small-scale features is strongly suppressed where we see only global spiral shocks. At the same time, filaments are the dominant type of structures in the outer disk, instead of isolated clumps seen in models with much lower initial magnetic field strength. These filaments appear aligned with the ambient magnetic field, suggesting they are magnetically dominated. The degree of structure in the disk is reduced as the magnetic field strength increases. Comparison of our models with and without magnetic fields suggests that magnetic fields have only a minor effect on the global disk structure, merely smoothing out substructures in the disk similar to an extra pressure term. Here our models demonstrate a good agreement with the previous studies by Shetty & Ostriker (2006) and Dobbs & Price (2008).
 |
Fig. 2 Radial dependence of the gas velocity dispersion σgas (see Eq. (10)) at t = 500 Myr in models with different initial magnetic field strength: no magnetic field (solid blue line), β = 10 (red dashed line), β = 1 (yellow dash-dotted line), β = 0.3 (purple dotted line). |
We demonstrated that the formation of substructures in the gaseous component is reduced when we include magnetic fields in our models. However, magnetic field also affects the gas kinematics. To estimate the impact, we introduce the velocity dispersion of the gas σgas as the following: 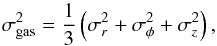 (10)where σr, σφ, and σz are the mass-weighted gas velocity dispersion components in radial, azimuthal and vertical directions respectively. The gas velocity dispersion is calculated over an annulus of width 100 pc located at the specified radius. In Fig. 2 we demonstrate radial profiles of the gas velocity dispersion computed in models with different initial magnetic field strength. An emerging trend for these simulations is that the rate of turbulence in the galactic disk decreases with increasing magnetic field strength. Differences between the purely hydrodynamical model (β = ∞) and our fiducial model (β = 10) are not particularly drastic, however, and the global decrease of the gas velocity dispersion is consistent.
(10)where σr, σφ, and σz are the mass-weighted gas velocity dispersion components in radial, azimuthal and vertical directions respectively. The gas velocity dispersion is calculated over an annulus of width 100 pc located at the specified radius. In Fig. 2 we demonstrate radial profiles of the gas velocity dispersion computed in models with different initial magnetic field strength. An emerging trend for these simulations is that the rate of turbulence in the galactic disk decreases with increasing magnetic field strength. Differences between the purely hydrodynamical model (β = ∞) and our fiducial model (β = 10) are not particularly drastic, however, and the global decrease of the gas velocity dispersion is consistent.
 |
Fig. 3 Time-dependent evolution of the gas surface density (top) and the magnetic field strength | Btot | in the disk plane (bottom) in the fiducial model. Rotation is clockwise. |
3.2. Basic model description
First, we analyze our basic model evolution. Global gas dynamics is mostly driven by the action of the large-scale spiral pattern (e.g., see also Gómez & Cox 2002). Global spiral shock amplitude increases rapidly in the simulation. It is initially very thick, but it starts to be narrower when the amplitude of spiral perturbation reaches the saturation level ε at t1 = 100 Myr. Shortly after t1, small-scale structures start forming due to shear instability (see e.g., Wada & Koda 2004; Shetty & Ostriker 2006). These basic stages of the gas density evolution can be seen in Fig. 3 (top row).
At early stages, the magnetic field structure mainly follows the gas distribution and it is characterized by the two-arm spiral structure (see Fig. 3, bottom row). Similar to Dobbs & Price (2008), we find that the magnetic field is compressed by the spiral shocks. The relative increase in the magnetic field strength is greater where the density wave is stronger. However, then small-scale magnetic field structure starts to be different from the gas density distribution (t> 250 Myr). In the inter-arm region, the magnetic field has a filamentary structure while a magnetic filament connects numerous substructures in the gas. Magnetic filaments look like curved structures, but they are mostly orientated along the azimuthal coordinate because of the galactic rotation. Radial scale lengths of the filaments do not exceed 1 kpc.
Our basic run starts from 1μG in the center and 0.1 μG at the outskirts (R ≈ 10 kpc). At initial stages of evolution (<200 Myr) we mostly see redistribution of the magnetic field, which increases in the spirals and decreases in the inter-arm region. In the inter-arm region, higher plasma-beta decreases the tension force acting on the flow, supporting the formation of higher density structures and corresponding field, for slightly higher efficient winding. Nevertheless, the density of filaments in the inter-arms is lower than that is in the spiral arms, and these high-density filaments tend to be parallel to the local magnetic field (see e.g., Peretto et al. 2012; Palmeirim et al. 2013). After that, in the filaments the magnetic field strength varies in the range 0.1−3 μG . In the very center and in the spiral arms, the magnetic field can reach up to 10 μG . Large fluctuations in magnitude for different clumps suggest that it can be distorted by the random motions of the dense gas clumps.
 |
Fig. 4 Face-on distributions of the gas surface density (top left), radial velocity component (top center), azimuthal velocity component (top right), azimuthal magnetic field component (bottom left), radial magnetic field component (bottom center), and total field strength (bottom right) in the part of the disk at t = 500 Myr for model O05 (with slow pattern speed rotation). We have labeled the spurs with letters A and B for easier reference. Magenta solid line shows the same surface density level in all frames. Rotation is clockwise. |
 |
Fig. 5 Probability density functions for logarithms of gas concentration (top left), temperature (top right), magnetic field strength (bottom left), and plasma beta (bottom right) at 500 Myr of the fiducial model. Distributions are plotted for the whole computational domain (solid black lines), for the spiral arms region (dashed blue lines), and for the inter-arm region (dash-dot lines). |
3.3. Spurs structure
Spurs are very well known features of spiral galaxies (Bingham 1967; Elmegreen 1980), which are clearly seen in a number of galaxies. From a theoretical point of view excitation of spur-like structures in spiral arms and the effect of magnetic fields on the wiggle instability have been investigated in MHD simulations by many authors (Kim & Ostriker 2002, 2006; Kim 2004). In our basic model the spiral arms fragmentation is very strong and it is not easy to identify large-scale spur-like structures. However, in model O05 (with the slower pattern speed rotation, see Table 1) we find several very extended spurs, which we analyze below in a more precise way.
In our simulations gas cools and becomes dense in the vicinity of galactic spiral arms, leading to the agglomeration of clumps into the large-scale structures, which shear off the spiral arms to become spurs. In Fig. 4 we plot the gas column density, velocity, and magnetic field components. Two large-scale spurs can be easily found and we marked these patterns as A (left) and B (right). Particular attention is paid to these structures because they are prominent, which facilitates our analysis and we are able to extract and more clearly demonstrate the key features that we want to identify, namely the magnetic field structure across the spurs. Here we define spur as a structure above the certain column density threshold 5M⊙ pc-2 (marked by magenta line in Fig. 4). As can be seen, spurs are not homogeneous structures. For instance, there are several substructures inside the left one (see A in Fig. 4). Inside the spurs the velocity components have a jump across the spurs with an amplitude of ≈20−30 km s-1 . The magnetic field structure looks very different from the density distribution. At the front edge of both spurs, the magnetic field is strongly positive and its strength is 1−3 μG which is much higher than in the surrounding medium. At the outer edge of the spurs, the azimuthal magnetic field component changes the direction and becomes negative. The positive and negative Bφ regions of enhanced magnetic field strength are separated by a strip of almost zero field along the spurs. The radial magnetic field component is maximal in the region where the azimuthal component is negative. Thus, there is a reversal of the azimuthal magnetic field across the spurs. The formation of a reversal field within the spurs in our models is consistent with the result by Dobbs et al. (2016) because they found that the magnetic field reversals occur when the velocity jump across the spiral shock is above ≈20 km s-1 . We note that similar small-amplitude reversals of the magnetic field are also seen for more tiny structures in the inter-arm region. These small-scale reversals can be consistent with polarization observations of pulsars in the disk of the Milky Way, which provided the evidence for the field reversal near the Perseus-arm as well as three reversals found in the solar circle (Han et al. 1999).
 |
Fig. 6 Relation between plasma beta (β) and the gas concentration (cm-3) for the whole disk (left), in the spirals arms (center), and in the inter-arm regions (right). The dashed line in the center frame is the distribution fit: β ∝ n-0.8. |
3.4. Plasma β – gas density relation
In this section, we focus on the properties of the magnetic field in different parts of the disk at a late epoch (t > 500 Myr) when the grand design spiral pattern is strong enough. ISM in the galactic disk rapidly segregates into two phases, as can be seen from Fig. 5, where we plot probability density functions for gas density, temperature, mean magnetic field strength, and plasma β. There is a warm phase, with typical temperatures of 104 K and concentration ≈0.1 cm-3, most of which is concentrated in between the spiral arms. The mean density of the cold gas (≈102 K) is typically of the order of 100 cm-3, high enough to allow gaseous clouds formation on a timescale of 10−30 Myr. We note also that all quantities of the distribution functions have a well-pronounced double-peaked shape.
Since we introduce the gas cooling, our simulations argue that plasma parameter β can vary with the gas parameters (see Fig. 6). Plasma beta appears to be decreasing with the gas concentration n and it varies in a wide range: from 10-3−10-2 cm-3 for the low density medium to 10−100 cm-3 in the densest parts of the spiral arms. Whereas we underline that the dense gas is much more magnetized than the low dense gas. However, as can be seen in the figure, for the whole galactic disk there is no clear relation β−n. Various galactic disk structures can develop the high-density contrasts. High-density regions in the galactic center or in spirals created by gravitational collapse and gas compression due to spiral potential co-exist with a low-density field at the galactic outskirts and in the inter-arm region. Since ISM physical conditions in spiral galaxies vary rapidly, the strength of the magnetic field also changes on short timescales and small spatial scales.
In the inter-arm regions, magnetic field strength is significantly lower 0.1 μG than in the arms where the magnetic field strength is 1−10 μG (see Figs. 3 and 5). It is clear that the inter-arm region is filled by the warm ~104 K medium, meanwhile in spirals gas mostly appears in the dense phase with temperature ≤100 K. Thus, it is natural to expect that magnetic field parameters would be different in these regions (see e.g., Dobbs & Price 2008). To check this point, we split the computational domain on spirals and inter-arm regions. We assume that gas is located in spirals if the gravitational potential of spiral perturbation (see Eq. (7)) is deeper than 0.5, otherwise gas is located in the inter-arm region. A potential threshold value 0.5 is chosen with the aim to have the gaseous arms located in the spiral region because of the possible spatial offset between minimum of the gravitational potential and the spiral shock (see e.g., Khoperskov et al. 2011). In general the field tends to be slightly more ordered, and stronger in the spiral arms, and more random in the inter-arm region. For spiral arms region we find a relation β ∝ n-0.8 (see middle frame in Fig. 6). In the spiral region such relation is rather clear because of the close coupling of magnetic fields to gaseous spirals. There are numerous dense clumps or filaments in the inter-arm region (see Fig. 3), which are supported by a high mean magnetic pressure and consequently they are characterized by a lower plasma β. However, filling factor of such clumps and filaments is very small and the warm, low-dense and less magnetized medium is dominant in the inter-arm region. Moreover, as we mentioned above, magnetic filaments can be spatially decoupled from the gaseous structures exactly in the inter-arm region (see Fig. 3). Such structures decoupling and a wide range of physical condition in the inter-arm region make the relation β−n insignificant.
 |
Fig. 7 Evolution of the magnetic field components. In all frames black line shows the total disk-averaged | B | value evolution. In the left frame evolution of | Br |, | Bφ |, and | Bz | is shown. In the center we show modules of the positive and negative components of azimuthal and radial magnetic field. In the right, we show ordered and random magnetic field components. |
3.5. Global field growth and evolution of various components
The enhancement of various components of the magnetic field is discussed in this paragraph. We employ this analysis to judge which component is dominant and has a larger growth rate in our fiducial model with two-arm spiral perturbation. In Fig. 7 we show a time-depended evolution of magnetic field projections (Br,Bϕ,Bz in left), positive and negative magnetic field components (center), and both ordered and random magnetic field strength (right). By initial parameters set up (see Eq. (9)) there is a pure ordered, azimuthal field in the disk Bϕ> 0. At latter times, the large scale field tends to be mostly connected with grand designed spiral perturbation during the whole simulation meanwhile in the inter-arm region the topology of the field is tangled. We find that the azimuthal field Bφ increases by a factor of 2 during the first 500−800 Myr of evolution since spiral pattern has been imposed. The maximum growth rate is between 200 and 500 Myr, and later magnetic field strength reaches saturation level. We also report on the noticeable growth of the radial component of the magnetic field which reaches up to 20% from the mean value of the magnetic field. Since spiral structure has a reasonable pitch angle (20°), the radial field can be partially driven by the spiral arms. In the absence of star formation and corresponding feedback, the magnetic field Bz stays negligible at a level of 0.1−1% of the total strength.
In the middle frame of Fig. 7 we plot the evolution of the positive and negative components of the radial and azimuthal magnetic field. Since the magnetic field shows a significant level of alignment with the velocity field, the positive azimuthal magnetic field component Bφ is characterized by the strongest enchantment, up to 1.8 times from the initial value. The reversal magnetic field component (Bϕ< 0) also appears in our simulations (up to 15%) and as has been shown above (see Sect. 3.3), most of this field is related to spurs and other tiny structures in the inter-arm region. Since these structures have a controversial direction of the magnetic field at the front and back sides, the radial field components (both negative and positive) are characterized by the same growth rate (see middle frame in Fig. 7).
We also calculate the evolution of the ordered Bord and random Brnd magnetic field components. We introduce these quantities similar to Dobbs & Price (2008):
In the right frame of Fig. 7 evolution of these components is shown. Ordered magnetic field is the dominant component at all the time and it reaches up to 75% from the final mean field. Random magnetic field is mostly driven by the wiggle instability in the inter-arm region where the gas motions are turbulent and the largest density fluctuations are seen on the small scales. However, relative increase (difference between final at 800 Myr and initial field) of ordered and random field is very similar and it equals to 0.25% from the final mean field strength. Thus, we claim that we observe growth of both components, but not a transformation of ordered component to the random field.
MHD studies of supernovae (SN)-driven turbulence have had considerable success in predicting the magnetic field growth rate. The main interest of such works is to simulate a turbulent galactic dynamo. For instance, Korpi et al. (1999) used a resolution of 10 pc for a local patch of the galactic disk, taking into account galactic shear. Their initial field 0.1 μG rapidly increases to 1.3 μG strength. Various models suggest that supernova-driven turbulence in conjunction with shear leads to an exponential increase of the mean magnetic field on timescales of 0.1−0.25 Gyr (Gressel et al. 2008a; Gent et al. 2013). By means of a cosmic ray driven dynamo, Hanasz et al. (2009) also found that the timescale of the large-scale magnetic field component growth is close to the disk rotation period.
Gressel et al. (2008a) claimed that the rotation frequency is the critical parameter allowing the dynamo to operate because for models without shear Gressel et al. (2008b) found no amplification of the mean field. Hence, we can compare the magnetic field enchantment rate found by Gressel et al. (2008a) with our model e0 (without spiral pattern) where the field radial migration is negligible. In all our models we adopted the same rotation curve and it matches the condition established by Gressel et al. (2008a): Ω > 25 km s-1 kpc-1 for galactocentric radii r < 8 kpc. We estimated total magnetic field growth rate as a function of angular velocity Ω(r) for the model without spiral perturbation. Since our model does not extend for a long time, beyond the apparent saturation of the magnetic field growth, we are able to detect a linear increase of regular field strength with the doubling times of ≈250, 150, and 80 Myr for rotation frequencies Ω = 50, 100, and 200 km s-1 kpc-1 , respectively. Meanwhile, Gressel et al. (2008a) found the exponential time-scales 147, 102, and 52 Myr for the same set of rotation rates. Thus in the absence of a dynamo, we obtained a much lower field growth rate in comparison to local dynamo models. We note also that the magnetic field enchantment we found is smaller by a factor of a few than Dobbs et al. (2016) found in similar galactic scale SPMHD simulations.
 |
Fig. 8 Mean magnetic field strength as a function of time in various models. In all frames, the fiducial model is shown by a black solid line. Other models are the following: a) blue dashed line, model without imposed spirals; b) models with a different pitch angle 10° (red dashed line) and 30° (blue dash-dot line); c) models with a different arm number m = 3 (red dashed line) and m = 4 (blue dash-dot line); d) models with a different initial magnetic field β = 1 (red dashed line) and β = 0.3 (blue dash-dot line). |
3.6. Comparison of different models with various spiral pattern parameters
In this paragraph we discuss the magnetic field evolution in models with a various spiral structure parameters. First we demonstrate the role of spiral arms. The density structure of the ISM in a spiral potential can be affected by three free parameters here: the pattern speed, strength of the spiral potential and the pitch angle. In Fig. 8a we compare our fiducial run with the model without any spiral perturbation. The absence of global structures in the disk enables the enhancement of the mean magnetic field by a factor of 1.5, which is 25% lower than in models with m = 2. Spiral arms play a significant role in the field generation, however the impact is comparable to the field growth driven by the gas random motions and differential rotation of the disk. In our fiducial model, the increase of gas density in the spiral arms (in comparison to the axisymmetric model, e0) increased the rate of winding of the field, hence the field strength is higher.
Tightly wound spirals generate larger magnetic fields in comparison to more open spirals (see Fig. 8b). For pitch angle i = 10°, the magnetic field strength increases much faster in comparison to models with i = 20° and i = 30°. The saturation level for this model is also higher by 10−15%. Multiple spiral arm models (m = 2,3) are characterized by a rapid mean magnetic strength growth. Mean magnetic field is higher by a factor of ≈2.5 in comparison to the initial field strength (see Fig. 8c). In the case of tightly wound spirals (i = 10°) and for a higher mode number (m = 3,4), the spiral structure action is stronger, and hence the rate of magnetic field winding is higher within a given disk radius. Hence, we detect a faster growth rate of magnetic field strength with a higher equilibrium value.
3.7. Conditions for MRI
SN-driven turbulent ISM dynamics have been studied numerically by numerous authors (see e.g., de Avillez & Mac Low 2002; Gressel et al. 2008a), but MRI has not been found in the inner disk part because it may be suppressed by SN-driven turbulence. For instance, Gressel et al. (2013) demonstrated that MRI turbulence can be sustained only for distances R> 14 kpc. Similar result was obtained by Korpi (2010) who estimated the limiting radius inside of which the SN activity can suppress the MRI for a Milky Way-type galaxy. Indeed, MRI might be important in extended HI disks including the outskirts of the Milky Way where star formation is almost impossible (Sellwood & Balbus 1999). For this reason, the absence of star formation in our models allows us to compare our simulations with conditions for MRI.
 |
Fig. 9 Comparison of simulated galaxy properties with MRI conditions from Korpi (2010): MRI damping curve (see Eq. (13)) for fiducial model (dashed line) and expected growth rate of the MRI Ωm (see Eq. (14)) at different times (solid lines). MRI is predicted to be damped by gas random motions in the regions where the solid line is above the dashed line. |
By using linear analysis of MHD equations, Korpi (2010) derived the limiting turbulence level and hence the turbulent diffusion needed to damp the MRI. From the linear stability analysis MRI is damped if 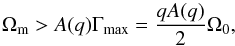 (13)where
(13)where 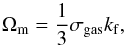 (14)and kf is the forcing wavenumber, A(q) varies from 1 to 3 (see Fig. 2 in Korpi 2010). All MRI modes to be damped for q = 1 (flat rotation curve) if A = 1.4.
(14)and kf is the forcing wavenumber, A(q) varies from 1 to 3 (see Fig. 2 in Korpi 2010). All MRI modes to be damped for q = 1 (flat rotation curve) if A = 1.4.
In Fig. 9 we show the corresponding damping curve and estimated turbulence diffusion rate at different times (125, 300, and 500 Myr). MRI is predicted to be damped by gas random motions in the regions where the solid lines are above the dotted line. For our estimation, we adopt the value of forcing wavelength as 100 pc, which is the typical spatial scale of small-scale structures in our models, but we neglect any variation in space and time. Large gas condensations, clumps and filaments with masses of 105–106M⊙ require ≈100 Myr to form via gravitational instabilities and accretion of mass from surrounding ISM (see e.g., Dobbs et al. 2011; Khoperskov et al. 2013; Dobbs & Pringle 2013). Until this timescale, gas velocity dispersion is not enough to stabilize the disk against MRI growth. In the inner regions of simulated spiral galaxies rapid formation of clumps and further gravity-driven random motions are the major source of turbulence. Once small-scale structures appear in the gas, velocity dispersion is increases rapidly and MRI is damped up to the radius of roughly <11 kpc at t> 200 Myr.
 |
Fig. 10 Radial profiles of the initial (red dash-dot line) and final (at t = 800 Myr, solid black line) magnetic field strength in models with a different initial magnetic field strength. The ratio between these quantities is shown by a blue dashed line. The filled area around the final magnetic field strength profile indicates the scatter at a given distance. |
 |
Fig. 11 Time dependence of radial component Poynting flux distribution in fiducial model. |
3.8. Radial profiles of the magnetic field
As we showed above, initial magnetic field strength plays the crucial role in further disk evolution (see Fig. 1). Indeed, the amount of small structures in gas rapidly decreases for lower values of β. For these models we have a very different magnetic field strength evolution and the relative value of the equilibrium magnetic field strength | Beq | / | B0 | is proportional to β (Fig. 8d). We compare the initial magnetic field profile with the final state for models with different initial β (see Fig. 10). We found that the magnetic field ratio is a function of radius for all models we analyze. We also claim flattening of the mean field radial profile. In the inner part, magnetic field amplification is negligible, but at the outer edge the magnetic field ratio is larger by a factor of 10 for models with initial β = 10. Hence the magnetic field growth rate increases from the inner to the outer galaxy. Such a picture is consistent with dynamo action models where the regular fields generated in the inner disk could be transported outwards by the joint action of a dynamo (see e.g., Moss et al. 1998).
The Poynting flux for MHD is interpreted as the rate at which energy is transported into (or out) of a given volume by the electromagnetic fields. To explore the transport of magnetic energy radially in our galactic disks we measure the Poynting flux in the radial direction. In Fig. 11 we show the radial component of Poynting flux at different times in our fiducial model. Positive values imply outward transport and negative values imply inward transport of the magnetic field. One can see that the positive values of Poynting flux is nicely coincide with the spiral pattern at all times, which means that the the spiral perturbation is responsible for the radial transport of the magnetic field.
In rotating spiral potential the gas density peaks occur downstream from the minimum of potential. In the outer region (beyond the corotation radius) the spiral pattern passes through the gas, leaving the shocked wave behind. The shock front itself is always upstream from the density peak and in the outer disk the shock forms on the outer face of the spiral arm (Khoperskov et al. 2011; Kim et al. 2014). Across the spiral shock both radial and tangential velocity rapidly increase their amplitude (Shetty & Ostriker 2006). This breaks the symmetry of the galactic velocity field and as the magnetic field variations are coupled to the velocity field variations, the magnetic field is wound up efficiently by the rotating non-axisymmetric structures. The winding of fields also enhances the radial diffusion for non-axisymmetric modes. Rapid increase of the gas velocity component implies an increase of the shear. The increase of shear leads to the radial diffusion of fields. Thus we conclude that in our models the non-axisymmetric spiral pattern is the driving force of the magnetic field transfer across the disk (see also Kotarba et al. 2009).
 |
Fig. 12 Time dependence of azimuthally-averaged radial component of Poynting flux in fiducial model (solid lines) and in model without spiral structure (e0). |
 |
Fig. 13 Model with turbulent initial magnetic field. Top: initial magnetic field components (Bx, By); bottom: gas density distribution and the total field strength at 500 Myr (see Fig. 3). |
To better understand how spirals act upon the Poynting flux we have checked the location of the Poynting flux peaks in the vicinity of gaseous spirals. At early periods (<200 Myr) we found that Poynting flux peaks are located on the outer surface of spirals with spatial offset ≈50−100 pc. However, later in our models we are not able to find any clear spatial offset between the gas density and Poynting flux peaks. Depending on the region in the disk we can see that either the Poynting flux has its maximum at the inner edge of spiral structure or we have the opposite configuration or Poynting flux peaks are coexistent with the gas density peaks. For well-developed spiral patterns, we obtained a mixture of these configurations due to a non-steady and non-linear evolution of gas in a rotating spiral potential.
In Fig. 12 we show azimuthally-averaged radial profiles of the mean radial component of the Poynting flux values at different times. In our fiducial model at early stages of evolution (<200 Myr), the Poynting flux profile does not expand out to the outer disk edge, its profile has a break at a given radius where the gaseous spirals significantly decrease their amplitude. However, gaseous spirals increase their amplitude in time and expand over an increasingly larger area. Consequently, at later periods (≥200 Myr) radial Poynting flux profile saturates at all radii. In the model without spiral perturbation (e0) we do not observe a significant increase of the Poynting flux in time and space. Thus we can finally summarize that in our simulations the action of spiral waves is indeed the major driver of the radial transport of the magnetic field outward.
3.9. Model with initial turbulent magnetic field structure
In this section we analyze the impact of the initial magnetic field structure on the formation of gaseous disk structures and the magnetic field growth. To mimic the turbulent structure of the magnetic field in the disk plane we set up its components as a superposition of ten modes with (pseudo-) random location in the disk and various amplitude (positive and negative). Similar to our basic approach, we set up the magnetic field through the vector potential which we introduce in the following form:
where Bcth is the amplitude of mode, and 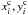 are the coordinates of ith mode. The initial magnetic field components were found according to Eq. (9). The initial magnetic field structure components in the disk plane are shown in Fig. 13. Initially the gas density profile is smoothly exponential as described in Sect. 2 and the external potential follows Eqs. (6) and (7) with the parameters of our fiducial model. For the magnetic field amplitude we assume that the mean beta parameter in the disk is β = 10.
are the coordinates of ith mode. The initial magnetic field components were found according to Eq. (9). The initial magnetic field structure components in the disk plane are shown in Fig. 13. Initially the gas density profile is smoothly exponential as described in Sect. 2 and the external potential follows Eqs. (6) and (7) with the parameters of our fiducial model. For the magnetic field amplitude we assume that the mean beta parameter in the disk is β = 10.
As the simulation begins the gas and magnetic field feel the impact of the potential. Since we drive the global spiral potential, the disk gas has a predominately two-arm spiral structure with a number of small-scale structures, which are formed in the galaxy disk through hydrodynamical and gravitational fragmentation. As it is clearly seen after 500 Myr of evolution the density distribution is almost identical to that we observe in our fiducial model (see right top frame in Fig. 3). Magnetic field spatial distribution (right frame in Fig. 9) is also very similar but it slightly enhanced in comparison to the purely toroidal initial field especially in the inter-arm region (see right bottom frame in Fig. 3). Comparison of the maps with the fiducial model suggests that initial magnetic field spatial structure is unlikely to be very important in the presence of the global spiral pattern.
In Fig. 14 we show the evolution of magnetic field components in the models with the random initial field. Since we impose random magnetic field at the initial phase, we have almost equal amplitudes in the radial and azimuthal fields. As seen from the evolution of magnetic field components, toroidal field Bφ becomes dominant very rapidly while the radial component decreases. A fast initial transformation of the turbulent magnetic field to the toroidal can be explained by differential rotation. Before the spiral pattern rises up (t< 100 Myr), radial gas flow is negligible, but the radial component of magnetic field is already present. Since azimuthal velocity in the disk is the dominant velocity component, one would expect the toroidal field to be wound up by a differential rotation Ω −effect (Krause & Raedler 1980; Widrow 2002). Toroidal magnetic field amplification is saturated when all of the radial field is wound up. Transformation of the random magnetic field component to the toroidal field leads to the decrease of radial field strength (t< 100 Myr). However, when angular momentum of gas is transported outward by spiral arms and the radial field is enhanced by a factor of ≈2 (100−300 Myr), at the end of the simulation its relative amplitude stays even smaller than the initial strength. Magnetic field strength across the disk plane (Bz) monotonically increases, but its strength stays relatively small.
 |
Fig. 14 Evolution of the magnetic field components as a fraction of the total field is shown versus time for model with the initial turbulent magnetic field (thick lines). For reference thin lines represent the same quantities evolution in our fiducial model. Total field strength is defined as |
 |
Fig. 15 Time evolution of the mean value of the total magnetic field strength (| Btot |) for simulations with different spatial resolution: 7.5 pc (solid black line), 15 pc (fiducial model, dashed red line) and 30 pc (blue dash-dotted line). The evolution is shown for central region <1 kpc. |
3.10. Resolution study
To check the effect of the grid resolution on the simulation results, we decrease the cell size to 7.5 pc in the fiducial model and we also repeat the simulation with the lower resolution 30 pc. Once we solve the equations for an ideal MHD, the magnetic field is frozen into the plasma. In this conception the magnetic field moves together with gas, especially at higher plasma-beta. In Fig. 15, we show the evolution in the total magnetic field strength in these simulations. The results obtained at the resolutions are evidently similar, although a slightly more rapid increase in magnetic field strength is observed in simulations performed at the higher resolution, which can be explained by numerical dissipation. Nonetheless, the tendency remains for the field strength to be strongly aligned with the gas density. As the disk rotates and the gas accumulates around the arms, the field aligns with the arms and wind up. We found the saturation of the field correlates to the limit of the maximum gas density related to the model resolution.
4. Conclusions
In our analysis, we rely on data from a suite of global spiral galaxy simulations that include the effects of self-gravity, magnetic fields and multiphase thermodynamics. A spiral structure in our simulations is the result of an externally-imposed rotating spiral potential, representing the stellar spiral arms of a galaxy. MHD simulations were used to follow the evolution and magnetic field amplification in disks of spiral galaxies. We explore a range of values for the physical parameters describing the properties of the gas, magnetic field and the external potential. We come to the following conclusions.
-
Similar to previous studies, we found that the magnetic field does not change dramatically the morphology and physical structure of ISM in simulated spiral galaxies. The disk structure is very similar in the gas and magnetic field distribution. Magnetic fields suppress a purely hydrodynamic shear instability as a means of growing inter-arm spurs and small-scale feathers. However, since our models include gas self-gravity and radiation cooling, we detect a number of filamentary structures that are more prominent in simulations with larger initial magnetic field strength. These gaseous filaments are coherent with the large-scale magnetic field structure.
-
We detect a magnetic filed reversal at the outer edge of the large-scale spurs. Meanwhile the front edges of the spurs are characterized by the increase of the positive magnetic field component. We note, that amplitudes of positive and negative components are very similar and reach up to several units of μG (see Fig. 4). The present treatment could be used for direct comparison with observations, coupled with radiative transfer calculations for various observational manifestations of the magnetic field.
-
Gas in the spiral arms is much more magnetized than it is in the inter-arm region. We found that the magnetic field in the spiral arms has a stronger mean-field component, and clear inverse correlation between the gas density and plasma-beta parameter β ∝ ρ-0.8, compared to the rest of the disk, with a more turbulent component than the field and an absence of correlation between gas density and plasma-beta (see Fig. 6). In the inter-arm the relation is less significant due to the presence of a large number of dense clumps and filaments which are surrounded by the warm, low-dense ISM. Moreover, magnetic filaments are seen to be disconnected from the gaseous structures exactly in the inter-arm region.
-
For various models we detect an amplification of the magnetic field by a factor of 2−2.5 during approximately two rotation periods of the galaxy (500 Myr). The mean value of the reversal magnetic field does not exceed 25% of the total field strength. Amplification of the ordered and random field is very similar, and since we start from the purely ordered state, at the end of simulation the amplitude of the ordered field component is three times higher than the random field (see right frame in Fig. 3).
-
Amplification of the magnetic field strongly depends on the initial magnetic field value (Fig. 8). A large initial magnetic field suppresses the formation of small-scale structures and smooth large-scale shocks, which in turn are less dense and generate less magnetic field. We also found that magnetic field amplification action is a function of radius: in the very center it is very small, meanwhile at the galactic outskirts (approximately three disk scales or 9 kpc) it can be larger by a factor of ≈10 than the initial magnetic field strength. At the same time the simulations where the initial magnetic field is turbulent demonstrate generically similar field configurations at the end of the run, but with slightly enhanced field strength in the inter-arm region in comparison to fiducial model (see Fig. 13). Initially disordered magnetic field contributions from randomly oriented field are efficiently ordered during one rotational period.
-
We found that the radial component of Poynting flux peaks near the spiral arms which spread the magnetic field towards the outer disk over time (see Figs. 11 and 12). Hence the magnetic field strength is enhanced more strongly at the galactic outskirts due to the radial transfer of magnetic energy by the spiral arms pushing the magnetic field outward.
-
Our models support the presence of MRI at distances >11 kpc (see Fig. 9) where we detect that the gas velocity dispersion is lower than the critical values suggested in linear analysis by Korpi (2010).
There are some processes which are likely to be important for the amplification of magnetic fields in galaxies but which are not included in our models, for example star formation and supernova feedback. Therefore, we miss a possible turbulent amplification of the magnetic field on small scales (Federrath et al. 2011; Schober et al. 2012; Sur et al. 2012). Such subgrid physics should comprise the α-effect, although the mechanism remains poorly understood (see e.g., Vainshtein & Cattaneo 1992, Beck et al. 1996; Brandenburg & Subramanian 2005). Because we evolve an isolated galaxy, it does not experience any large-scale shearing motions caused by infalling material or mergers with other galaxies that could lead to an additional amplification of the magnetic field (Dubois & Teyssier 2010; Geng et al. 2012; Pakmor et al. 2017). Nevertheless, in our limited model the magnetic field strength, its structure, and parameters of gaseous structures are comparable to the observations. The next step is to use the work presented here as a basis to reproduce galaxies with various morphology. To better match real external galactic gas structure it will be prudent to include the effects of live stellar disk, star formation, and feedback.
Acknowledgments
The authors thank the anonymous referee for his/her rapid reports and numerous very helpful comments and suggestions which improved this paper a lot. Authors also thank Dmitry Sokoloff and Eugeny Mikhailov for fruitful discussions of the paper. The authors are also grateful to Nicolas Leclerc and Yulia Venichenko for their assistance with the data processing. This work was supported by RFBR grant 16-32-60043. S.S.K. has been supported by the Ministry of Education and Science of the Russian Federation (government task No. 2.852.2017/4.6). The software used in this work was developed with the support of the Russian Foundation for Basic Research (grant 15-02-06204). The research is carried out using the equipment of the shared research facilities of HPC computing resources at Lomonosov Moscow State University.
References
- Arshakian, T. G., Beck, R., Krause, M., & Sokoloff, D. 2009, A&A, 494, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Banerjee, R., Vázquez-Semadeni, E., Hennebelle, P., & Klessen, R. S. 2009, MNRAS, 398, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R. 1991, A&A, 251, 15 [NASA ADS] [Google Scholar]
-
Beck, R. 2000, in Astronomy, physics and chemistry of H
 , Philos. Trans. Roy. Soc. London Ser. A, 358, 777
[Google Scholar]
, Philos. Trans. Roy. Soc. London Ser. A, 358, 777
[Google Scholar]
- Beck, R. 2009, Astrophys. Space Sci. Trans., 5, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R. 2016, A&ARv, 24, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., & Wielebinski, R. 2013, Magnetic Fields in Galaxies, eds. T. D. Oswalt, & G. Gilmore, 641 [Google Scholar]
- Beck, R., Carilli, C. L., Holdaway, M. A., & Klein, U. 1994, A&A, 292, 409 [NASA ADS] [Google Scholar]
- Beck, R., Brandenburg, A., Moss, D., Shukurov, A., & Sokoloff, D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Fletcher, A., Shukurov, A., et al. 2005, A&A, 444, 739 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernet, M. L., Miniati, F., Lilly, S. J., Kronberg, P. P., & Dessauges-Zavadsky, M. 2008, Nature, 454, 302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bingham, R. G. 1967, MNRAS, 137, 157 [NASA ADS] [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chamandy, L., Subramanian, K., & Shukurov, A. 2013, MNRAS, 428, 3569 [NASA ADS] [CrossRef] [Google Scholar]
- Chamandy, L., Shukurov, A., & Subramanian, K. 2015, MNRAS, 446, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen, C., Quinn, T., Governato, F., et al. 2012, MNRAS, 425, 3058 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M. 1999, ApJ, 520, 706 [NASA ADS] [CrossRef] [Google Scholar]
- de Avillez, M. A., & Mac Low, M.-M. 2002, ApJ, 581, 1047 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W. 2000, AJ, 119, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C. L., & Bonnell, I. A. 2006, MNRAS, 367, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C. L., & Price, D. J. 2008, MNRAS, 383, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C. L., & Pringle, J. E. 2013, MNRAS, 432, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C. L., Bonnell, I. A., & Pringle, J. E. 2006, MNRAS, 371, 1663 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dobbs, C. L., Glover, S. C. O., Clark, P. C., & Klessen, R. S. 2008, MNRAS, 389, 1097 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dobbs, C. L., Burkert, A., & Pringle, J. E. 2011, MNRAS, 413, 2935 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C. L., Price, D. J., Pettitt, A. R., Bate, M. R., & Tricco, T. S. 2016, MNRAS, 461, 4482 [NASA ADS] [CrossRef] [Google Scholar]
- Dubois, Y., & Teyssier, R. 2010, A&A, 523, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elmegreen, D. M. 1980, ApJ, 242, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Elstner, D., Beck, R., & Gressel, O. 2014, A&A, 568, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, C. R., & Hawley, J. F. 1988, ApJ, 332, 659 [Google Scholar]
- Federrath, C., & Klessen, R. S. 2012, ApJ, 761, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Sur, S., Schleicher, D. R. G., Banerjee, R., & Klessen, R. S. 2011, ApJ, 731, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Fogerty, E., Frank, A., Heitsch, F., et al. 2016, MNRAS, 460, 2110 [NASA ADS] [CrossRef] [Google Scholar]
- Frick, P., Stepanov, R., Beck, R., et al. 2016, A&A, 585, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fujimoto, Y., Tasker, E. J., Wakayama, M., & Habe, A. 2014, MNRAS, 439, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, Y., Bryan, G. L., Tasker, E. J., Habe, A., & Simpson, C. M. 2016, MNRAS, 461, 1684 [NASA ADS] [CrossRef] [Google Scholar]
- Geng, A., Kotarba, H., Bürzle, F., et al. 2012, MNRAS, 419, 3571 [NASA ADS] [CrossRef] [Google Scholar]
- Gent, F. A., Shukurov, A., Sarson, G. R., Fletcher, A., & Mantere, M. J. 2013, MNRAS, 430, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Gießübel, R., & Beck, R. 2014, A&A, 571, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gnedin, N. Y., Tassis, K., & Kravtsov, A. V. 2009, ApJ, 697, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, G. C., & Cox, D. P. 2002, ApJ, 580, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Graeve, R., & Beck, R. 1988, A&A, 192, 66 [NASA ADS] [Google Scholar]
- Gressel, O., Elstner, D., Ziegler, U., & Rüdiger, G. 2008a, A&A, 486, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gressel, O., Ziegler, U., Elstner, D., & Rüdiger, G. 2008b, Astron. Nachr., 329, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Gressel, O., Elstner, D., & Ziegler, U. 2013, A&A, 560, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, J. L., Manchester, R. N., & Qiao, G. J. 1999, MNRAS, 306, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Hanasz, M., Wóltański, D., & Kowalik, K. 2009, ApJ, 706, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Iffrig, O., & Hennebelle, P. 2017, A&A, 604, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inoue, T., & Inutsuka, S.-i. 2009, ApJ, 704, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Jansson, R., & Farrar, G. R. 2012, ApJ, 757, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Khoperskov, S. A., Khoperskov, A. V., Eremin, M. A., & Butenko, M. A. 2011, Astron. Lett., 37, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Khoperskov, S. A., Vasiliev, E. O., Sobolev, A. M., & Khoperskov, A. V. 2013, MNRAS, 428, 2311 [NASA ADS] [CrossRef] [Google Scholar]
- Khoperskov, S. A., Vasiliev, E. O., Khoperskov, A. V., & Lubimov, V. N. 2014, J. Phys. Conf. Ser., 510, 012011 [CrossRef] [Google Scholar]
- Khoperskov, S. A., Vasiliev, E. O., Ladeyschikov, D. A., Sobolev, A. M., & Khoperskov, A. V. 2016, MNRAS, 455, 1782 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, W.-T. 2004, J. Korean Astron. Soc., 37, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, W.-T., & Ostriker, E. C. 2002, ApJ, 570, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, W.-T., & Ostriker, E. C. 2006, ApJ, 646, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, W.-T., Kim, Y., & Kim, J.-G. 2014, ApJ, 789, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, Y., Kim, W.-T., & Elmegreen, B. G. 2015, ApJ, 809, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Korpi, M. J. 2010, Astron. Nachr., 331, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Korpi, M. J., Brandenburg, A., Shukurov, A., & Tuominen, I. 1999, A&A, 350, 230 [NASA ADS] [Google Scholar]
- Körtgen, B., & Banerjee, R. 2015, MNRAS, 451, 3340 [NASA ADS] [CrossRef] [Google Scholar]
- Kotarba, H., Lesch, H., Dolag, K., et al. 2009, MNRAS, 397, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, M. 2009, in Rev. Mex. Astron. Astrofis. Conf. Ser., 36, 25 [NASA ADS] [Google Scholar]
- Krause, F., & Beck, R. 1998, A&A, 335, 789 [NASA ADS] [Google Scholar]
- Krause, F., & Raedler, K.-H. 1980, Mean-field magnetohydrodynamics and dynamo theory (Oxford: Pergamon Press) [Google Scholar]
- Li, H.-B., & Henning, T. 2011, Nature, 479, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Marinacci, F., & Vogelsberger, M. 2016, MNRAS, 456, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Marinacci, F., Vogelsberger, M., Mocz, P., & Pakmor, R. 2015, MNRAS, 453, 3999 [NASA ADS] [CrossRef] [Google Scholar]
- Mikhailov, E. A., Sokoloff, D. D., & Efremov, Y. N. 2012, Astron. Lett., 38, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Miyamoto, M., & Nagai, R. 1975, PASJ, 27, 533 [NASA ADS] [Google Scholar]
- Moss, D., & Sokoloff, D. 2013, Geophys. Astrophys. Fluid Dyn., 107, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D., Shukurov, A., & Sokoloff, D. 1998, Geophys. Astrophys. Fluid Dyn., 89, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D., Stepanov, R., Arshakian, T. G., et al. 2012, A&A, 537, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Beck, R., Sokoloff, D., et al. 2013, A&A, 556, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Stepanov, R., Krause, M., Beck, R., & Sokoloff, D. 2015, A&A, 578, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Mikhailov, E., Silchenko, O., et al. 2016, A&A, 592, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Niklas, S. 1995, Ph.D. Thesis, Univ. Bonn [Google Scholar]
- Ostriker, E. C., McKee, C. F., & Leroy, A. K. 2010, ApJ, 721, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Pan, L., Haugbølle, T., & Nordlund, Å. 2016, ApJ, 822, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Pakmor, R., & Springel, V. 2013, MNRAS, 432, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Pakmor, R., Marinacci, F., & Springel, V. 2014, ApJ, 783, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Pakmor, R., Gomez, F. A., Grand, R. J. J., et al. 2017, MNRAS, submitted, ArXiv e-prints [arXiv:1701.07028] [Google Scholar]
- Palmeirim, P., André, P., Kirk, J., et al. 2013, A&A, 550, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pan, H.-A., Fujimoto, Y., Tasker, E. J., et al. 2015, MNRAS, 453, 3082 [NASA ADS] [CrossRef] [Google Scholar]
- Peretto, N., André, P., Könyves, V., et al. 2012, A&A, 541, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poezd, A., Shukurov, A., & Sokoloff, D. 1993, MNRAS, 264, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, F., Bournaud, F., Emsellem, E., et al. 2013, MNRAS, 436, 1836 [NASA ADS] [CrossRef] [Google Scholar]
- Rieder, M., & Teyssier, R. 2016, MNRAS, 457, 1722 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Salcedo, F. J., & Santillán, A. 2013, MNRAS, 433, 2172 [NASA ADS] [CrossRef] [Google Scholar]
- Schober, J., Schleicher, D., Federrath, C., Klessen, R., & Banerjee, R. 2012, Phys. Rev. E, 85, 026303 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Balbus, S. A. 1999, ApJ, 511, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Shetty, R., & Ostriker, E. C. 2006, ApJ, 647, 997 [NASA ADS] [CrossRef] [Google Scholar]
- Shukurov, A. 1998, MNRAS, 299, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., Glover, S. C. O., Clark, P. C., Klessen, R. S., & Springel, V. 2014, MNRAS, 441, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Sormani, M. C., Sobacchi, E., Shore, S. N., Treß, R. G., & Klessen, R. S. 2017, MNRAS, 471, 2932 [NASA ADS] [CrossRef] [Google Scholar]
- Sur, S., Federrath, C., Schleicher, D. R. G., Banerjee, R., & Klessen, R. S. 2012, MNRAS, 423, 3148 [NASA ADS] [CrossRef] [Google Scholar]
- Tasker, E. J., & Tan, J. C. 2009, ApJ, 700, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Vainshtein, S. I., & Cattaneo, F. 1992, ApJ, 393, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Vallee, J. P. 1996, A&A, 308, 433 [NASA ADS] [Google Scholar]
- Wada, K. 2008, ApJ, 675, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., & Koda, J. 2004, MNRAS, 349, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, P., & Abel, T. 2009, ApJ, 696, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Widrow, L. M. 2002, Rev. Mod. Phys., 74, 775 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Face-on view of the surface density in the whole galactic disk at 500 Myr for three models with different initial magnetic field strength, from left to right: no magnetic field, β = 10, β = 1, β = 0.3. Rotation is clockwise. |
| In the text | |
 |
Fig. 2 Radial dependence of the gas velocity dispersion σgas (see Eq. (10)) at t = 500 Myr in models with different initial magnetic field strength: no magnetic field (solid blue line), β = 10 (red dashed line), β = 1 (yellow dash-dotted line), β = 0.3 (purple dotted line). |
| In the text | |
 |
Fig. 3 Time-dependent evolution of the gas surface density (top) and the magnetic field strength | Btot | in the disk plane (bottom) in the fiducial model. Rotation is clockwise. |
| In the text | |
 |
Fig. 4 Face-on distributions of the gas surface density (top left), radial velocity component (top center), azimuthal velocity component (top right), azimuthal magnetic field component (bottom left), radial magnetic field component (bottom center), and total field strength (bottom right) in the part of the disk at t = 500 Myr for model O05 (with slow pattern speed rotation). We have labeled the spurs with letters A and B for easier reference. Magenta solid line shows the same surface density level in all frames. Rotation is clockwise. |
| In the text | |
 |
Fig. 5 Probability density functions for logarithms of gas concentration (top left), temperature (top right), magnetic field strength (bottom left), and plasma beta (bottom right) at 500 Myr of the fiducial model. Distributions are plotted for the whole computational domain (solid black lines), for the spiral arms region (dashed blue lines), and for the inter-arm region (dash-dot lines). |
| In the text | |
 |
Fig. 6 Relation between plasma beta (β) and the gas concentration (cm-3) for the whole disk (left), in the spirals arms (center), and in the inter-arm regions (right). The dashed line in the center frame is the distribution fit: β ∝ n-0.8. |
| In the text | |
 |
Fig. 7 Evolution of the magnetic field components. In all frames black line shows the total disk-averaged | B | value evolution. In the left frame evolution of | Br |, | Bφ |, and | Bz | is shown. In the center we show modules of the positive and negative components of azimuthal and radial magnetic field. In the right, we show ordered and random magnetic field components. |
| In the text | |
 |
Fig. 8 Mean magnetic field strength as a function of time in various models. In all frames, the fiducial model is shown by a black solid line. Other models are the following: a) blue dashed line, model without imposed spirals; b) models with a different pitch angle 10° (red dashed line) and 30° (blue dash-dot line); c) models with a different arm number m = 3 (red dashed line) and m = 4 (blue dash-dot line); d) models with a different initial magnetic field β = 1 (red dashed line) and β = 0.3 (blue dash-dot line). |
| In the text | |
 |
Fig. 9 Comparison of simulated galaxy properties with MRI conditions from Korpi (2010): MRI damping curve (see Eq. (13)) for fiducial model (dashed line) and expected growth rate of the MRI Ωm (see Eq. (14)) at different times (solid lines). MRI is predicted to be damped by gas random motions in the regions where the solid line is above the dashed line. |
| In the text | |
 |
Fig. 10 Radial profiles of the initial (red dash-dot line) and final (at t = 800 Myr, solid black line) magnetic field strength in models with a different initial magnetic field strength. The ratio between these quantities is shown by a blue dashed line. The filled area around the final magnetic field strength profile indicates the scatter at a given distance. |
| In the text | |
 |
Fig. 11 Time dependence of radial component Poynting flux distribution in fiducial model. |
| In the text | |
 |
Fig. 12 Time dependence of azimuthally-averaged radial component of Poynting flux in fiducial model (solid lines) and in model without spiral structure (e0). |
| In the text | |
 |
Fig. 13 Model with turbulent initial magnetic field. Top: initial magnetic field components (Bx, By); bottom: gas density distribution and the total field strength at 500 Myr (see Fig. 3). |
| In the text | |
 |
Fig. 14 Evolution of the magnetic field components as a fraction of the total field is shown versus time for model with the initial turbulent magnetic field (thick lines). For reference thin lines represent the same quantities evolution in our fiducial model. Total field strength is defined as |
| In the text | |
 |
Fig. 15 Time evolution of the mean value of the total magnetic field strength (| Btot |) for simulations with different spatial resolution: 7.5 pc (solid black line), 15 pc (fiducial model, dashed red line) and 30 pc (blue dash-dotted line). The evolution is shown for central region <1 kpc. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.