| Issue |
A&A
Volume 607, November 2017
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201629131 | |
| Published online | 20 November 2017 | |
Evidence for different accretion regimes in GRO J1008−57
1 Dr. Karl Remeis-Observatory & ECAP, Universität Erlangen-Nürnberg, Sternwartstr. 7, 96049 Bamberg, Germany
e-mail: matthias.kuehnel@sternwarte.uni-erlangen.de
2 Cahill Center for Astronomy and Astrophysics, California Institute of Technology, Pasadena, CA 91125, USA
3 European Space Astronomy Centre (ESA/ESAC), Operations Department, Villanueva de la Cañada, 28692 Madrid, Spain
4 CRESST/CSST/Department of Physics, UMBC, Baltimore, MD 21250, USA
5 NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
6 Center for Astrophysics and Space Sciences, University of California, San Diego, La Jolla, CA 92093, USA
7 Institut für Astronomie und Astrophysik, Universität Tübingen, Sand 1, 72076 Tübingen, Germany
Received: 16 June 2016
Accepted: 14 August 2017
We present a comprehensive spectral analysis of the BeXRB GRO J1008−57 over a luminosity range of three orders of magnitude using NuSTAR, Suzaku, and RXTE data. We find significant evolution of the spectral parameters with luminosity. In particular, the photon index hardens with increasing luminosity at intermediate luminosities in the range 1036–1037 erg s-1. This evolution is stable and repeatedly observed over different outbursts. However, at the extreme ends of the observed luminosity range, we find that the correlation breaks down, with a significance level of at least 3.7σ. We conclude that these changes indicate transitions to different accretion regimes, which are characterized by different deceleration processes, such as Coulomb or radiation breaking. We compare our observed luminosity levels of these transitions to theoretical predications and discuss the variation of those theoretical luminosity values with fundamental neutron star parameters. Finally, we present detailed spectroscopy of the unique “triple peaked” outburst in 2014/15 which does not fit in the general parameter evolution with luminosity. The pulse profile on the other hand is consistent with what is expected at this luminosity level, arguing against a change in accretion geometry. In summary, GRO J1008−57 is an ideal target to study different accretion regimes due to the well-constrained evolution of its broad-band spectral continuum over several orders of magnitude in luminosity.
Key words: X-rays: binaries / stars: neutron / stars: emission-line, Be / pulsars: individual: GRO J1008-57
© ESO, 2017
1. Introduction
The strong magnetic field of an accreting and pulsing neutron star channels accreted matter onto its magnetic poles. There, infalling plasma with velocities close to the speed of light is decelerated to rest on the surface. The X-ray spectrum of accreting neutron stars is therefore dominated by strong bulk-motion Comptonizaton caused by the interaction of primary soft X-rays from the accretion mound or column with hot electrons in the accretion column. A self-consistent model of the emerging X-ray spectrum requires relativistic magnetohydrodynamical calculations of this extreme plasma and is still outside of the range of capabilities of current computing facilities. However, in recent years some progress has been made and models have become available in which the radiative transfer equations are solved assuming thermal and bulk Comptonization (Becker & Wolff 2007; Marcu et al. 2015; Wolff et al. 2016) and which allow for different (phenomenological) velocity profiles (Farinelli et al. 2012, 2016). The details of the physical mechanisms decelerating the accreted material to rest above the neutron star’s surface are the topic of current theoretical investigations (see, e.g., discussions by Staubert et al. 2007; and Becker et al. 2012).
An ideal laboratory to investigate and check different theoretical predictions about accretion physics is the class of transient Be X-ray binaries (BeXRBs). Their luminosity changes by orders of magnitude during an outburst and the spectral evolution of the neutron star in different luminosity regimes can be studied in great detail. In previous works, using all available RXTE data, we have shown that the BeXRB GRO J1008−57 shows a tight correlation of its spectral shape with the 15–50 keV luminosity, which appears to be stable between outbursts (Kühnel et al. 2013, 2014, hereafter K13 and K14). GRO J1008−57 was discovered with the Compton Gamma Ray Observatory (CGRO) during a luminous outburst in 1993 July (Wilson et al. 1994; Stollberg et al. 1993). The system consists of a neutron star on a wide, eccentric orbit (asini = 530 lt-s, e = 0.68, Coe et al. 2007) around a B0e type companion star (Coe et al. 1994). In addition to the high eccentricity, the orbital period of Porb = 249.48 d (K13) is long enough for the circumstellar disk of the Be companion to be tidally truncated at the 7:1 or 8:1 resonance (Okazaki & Negueruela 2001), leading to regular type-I outbursts. The source showed a type-II giant outburst in 2012 November at an orbital phase of ~ 0.3 with a peak luminosity around 1 Crab in the 15–50 keV range (Fig. 1). After this outburst, GRO J1008−57 showed three regular type-I outbursts, the last of these on 2014 September (Nakajima et al. 2014a). This expected outburst was followed by two unusual type-II outbursts in 2014 November and 2015 January, occurring within the same orbit (Nakajima et al. 2014b; Kretschmar et al. 2015, and Fig. 1). To our knowledge, this “triple-peaked” outburst behavior had not been seen in any other source, although some sources, such as A 0535+262 (see, e.g., Caballero et al. 2013, and references therein) or GX 304−1 (Nakajima et al. 2012; Postnov et al. 2015b), feature rare “double-peaked” outbursts. What causes the source to undergo outbursts far away from periastron is not yet understood. A promising scenario proposed by Okazaki et al. (2013) is an inclined Be disk with respect to the orbital plane.
 |
Fig. 1 Swift-BAT (Krimm et al. 2013) light curve showing the activity of GRO J1008−57 between 2012 August and 2015 February. The arrows on top mark the times of observations by Swift (red), Suzaku-(green), and NuSTAR (blue). The numbers next to these arrows are the data epochs as defined in Table 1. The labeled dates correspond to these epochs. |
In this work, we compare our previous findings to observations performed by Suzaku, the Nuclear Spectroscopic Telescope Array (NuSTAR), and Swift from 2012 to 2015 in order to discuss implications on the theory of mass accretion onto magnetized neutron stars. Section 2 describes the data reduction of the observations and energy selection criteria applied to the resulting spectra. In addition, we discuss calibration uncertainties detected in the spectra. The actual spectral analysis of GRO J1008−57 is presented in Sect. 3 and the corresponding individual results and the outburst behavior of the source are discussed in Sect. 4. Section 5 focuses on the spectral evolution of GRO J1008−57, where we compare the results of the spectral analysis with our previous work and recent theoretical work. We conclude the paper with the discovery of different accretion regimes in this source.
2. Observations and data reduction
Figure 1 shows the light curves of GRO J1008−57 for all outbursts between 2012 August and 2016 February as recorded by the Swift Burst Alert Telescope (BAT). Arrows indicate the observations studied here (see also Table 1). During the peak of the type II giant outburst in 2012 November, GRO J1008−57 was observed with NuSTAR, Suzaku, and Swift. After this type-II outburst, the source went back to its normal behavior, featuring type-I outbursts at every periastron passage. Suzaku-observed the peak of such an outburst in 2014 January. The next observation by NuSTAR, which was simultaneous with Swift, was performed in 2014 December, after the second outburst of the triple-peaked outburst. Finally, NuSTAR and Swift also performed a joint observation slightly after the peak of the third outburst, which reached around 700 mCrab in Swift-BAT during 2015 January.
The light curve of GRO J1008−57 during 2005, as measured by the Proportional Counter Array (PCA, Jahoda et al. 1996) onboard RXTE (ObsID 90089-03-02-01) was used for the pulse profile analysis presented in Sect. 4.2. The GoodXenon events of the Proportional Counter Units (PCU) 2 and 3 were accumulated into a light curve with a time resolution of 1 s. Finally, the light curve was transformed into the barycenter of the solar system (see K13, for more details about the extraction of RXTE light curves).
Observations used in this work.
2.1. Suzaku
We reprocessed the Suzaku (Mitsuda et al. 2007) data following the Data Reduction (or ABC) Guide (ABC Guide, ISAS/JAXA et al. 2013). The data have been calibrated using aepipeline as distributed by HEASOFT v6.15.1. For the data of the Suzaku X-ray Imaging Spectrometers (XIS; Koyama et al. 2007), the XIS calibration database (CALDB) released on 2014-12-22 was used. For the calibration of the corresponding mirrors of the X-ray Telescopes (XRT; Serlemitsos et al. 2007), the releases 2011-05-05 (effective area) and 2009-06-05 (point spread function, PSF) are used. The High X-ray Detector (HXD; Takahashi et al. 2007) data were calibrated based on HXD CALDB release 2011-08-19.
Three of the four XIS (0, 1, and 3; data from XIS2 were no longer available) were operated in the 1/4 window mode during the 2012 November and 2014 January observations of GRO J1008−57. After extracting an image for each XIS and all editing modes using xselect, we applied the attitude correction by aeattcor2 using a preliminary source region. The final source spectra of GRO J1008−57 were extracted with xselect using a circular source region centered at the source. The radii were set to 80′′ in XIS0 and XIS3 for observation 408044010 and 90′′ otherwise. Pile-up needed to be investigated for each XIS and editing mode separately and was calculated for each pixel using pileest. During observation 408044010 pile-up of more than 4% was avoided by annuli source regions with inner radii of 13–30′′. Due to the very high count rate during observation 907006010, ellipsoidal areas within the source region with more than 2% pile-up were excluded. All background regions were chosen to avoid source photons from the area covered by the Point Spread Function (PSF) of the XRT with radii of 90′′. With these regions as input for xselect, the XIS-spectra of the source and background were extracted. The redistribution matrix function (RMF) and ancillary response function (ARF) were generated with xisrmfgen and xissimarfgen, respectively. For the spectral analysis we added the spectra of the different editing modes, ′′3 × 3′′ and ′′5 × 5′′, to generate one spectrum for each XIS.
The HXD (Kokubun et al. 2007) consisted of two detectors, the PIN diodes and the gadolinium silicate crystals (GSO). Spectra for both instruments were extracted using hxdpinxbpi and hxdgsoxbpi, respectively. These tools generate the background spectra based on the non X-ray background (NXB) using modeled events of the “tuned” background v2.2 (PIN) and v2.6 (GSO), and cosmic X-ray background (CXB), simulated following Boldt (1987). For PIN we used epoch number 11 (2011-06-01) and for GSO epoch 2010-05-24 for the response file (RSP). Additionally, the GSO ARF, calibrated on the Crab pulsar from epoch 2010-05-26, was used.
We restricted the energy range of the Suzaku observations (epochs 1a and 2, see Table 1) to 0.8–10 keV for the XISs, to 15−70 keV for PIN, and to 60–100 keV for GSO. The XIS-spectra have been rebinned following Nowak et al. (2011), that is, each energy bin has at least a minimum signal-to-noise (SNR) of 8 and a minimum number of channels close to the half-width half-maximum of the spectral resolution. For PIN and GSO, we applied a channel binning resulting in a minimum SNR of 15 and 5 in each energy bin, respectively.
During a preliminary spectral analysis we investigated possible calibration uncertainties of the Suzaku data. In both epochs, residual features in all XISs are found around the Au-edge at 2.19–2.37 keV, as already noticed by Nowak et al. (2011). Consequently, we ignored this energy range during the spectral analysis. Further calibration uncertainties around the Si-edge at 1.72–1.88 keV are known. Using the newer calibration, however, this calibration feature is only present in the backside illuminated XIS1, which we ignored appropriately in the analysis. In epoch 2 (2014 January), the front-illuminated XIS0 and XIS3 show residual emission at energies above 9 keV in contrast to XIS1. Thus, we ignored energies above 9 keV in these XISs. In addition, we found a slight discrepancy of the power-law photon index, Γ, determined by the spectrum of the back-illuminated XIS1 to the other XISs in epoch 2. This behavior is already known (see, e.g., Sect. 5.2.1 of Tsujimoto et al. 2011); the photon index shift of 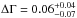 is, however, only significant on the ~90% confidence level.
is, however, only significant on the ~90% confidence level.
For epoch 1a we ignored PIN data below 20 keV because of a mismatch to NuSTAR as seen by Bellm et al. (2014), which is probably noise contamination due to the leakage current of the PIN sensors. Furthermore, we found a broad-band wave-like structure in PIN with an amplitude of 2–16% in flux, which can be described by a Gaussian absorption centered at 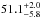 keV. Kokubun et al. (2007) noticed this feature in data of the Crab pulsar (in epoch 1a, GRO J1008−57’s flux was around 1 Crab), which they attributed to an insufficient modeling of the gadolinium fluorescent lines produced in the detector. During the spectral analysis of GRO J1008−57 we modeled this feature by the Gaussian as described above. In both epochs, the GSO-data in the four energy bins between 75 and 81 keV scatter strongly around any predicted model flux. Because the GSO background in this energy range is dominated by the decay of activated 151Gd and 149Eu (Kokubun et al. 1999) we ignored those bins in our analysis.
keV. Kokubun et al. (2007) noticed this feature in data of the Crab pulsar (in epoch 1a, GRO J1008−57’s flux was around 1 Crab), which they attributed to an insufficient modeling of the gadolinium fluorescent lines produced in the detector. During the spectral analysis of GRO J1008−57 we modeled this feature by the Gaussian as described above. In both epochs, the GSO-data in the four energy bins between 75 and 81 keV scatter strongly around any predicted model flux. Because the GSO background in this energy range is dominated by the decay of activated 151Gd and 149Eu (Kokubun et al. 1999) we ignored those bins in our analysis.
Among the calibration features we have described above and taken into account during the spectral fitting, we added 1% systematic uncertainties to the XIS-, PIN-, and GSO-spectra to achieve a reduced χ2 around unity. We have followed a slightly different treatment of calibration uncertainties compared to Bellm et al. (2014). In particular, they have not taken the Gaussian absorption feature caused by the gadolinium fluorescent lines or the photon index shift in XIS1 into account, but added higher systematic uncertainties of 3% to the spectra. However, their fit of the Suzaku data during GRO J1008−57’s giant outburst (epoch 1a) still resulted in a reduced χ2 of 3.15 (see their Table 2).
2.2. NuSTAR
Extraction of the NuSTAR data was performed separately for Focal Plane Module (FPM) A and B, following the NuSTAR Data Analysis Software Guide (Perri et al. 2015). The data were extracted using the standard nustardas pipeline (v1.4.1) and CALBD 20150316 as distributed with HEASOFT v6.16 and cleaned for source occultation by the Earth and SAA passages. Spectra in mode 01 (SCIENCE) event files were extracted for each of the three observations separately using a region with 120′′ diameter, centered on the J2000 coordinates of GRO J1008−57. The background was extracted from a region of the same size at the other end of the field of view to avoid contamination from source photons in the outer wings of the PSF. We additionally extracted data from mode 06 (SCIENCE_SC), in which the optical bench star tracker is occulted, and therefore the sky image reconstruction is solely based on the spacecraft attitude. This results in a smeared point source in the sky image. However, as the metrology system is still functional, the effective area is calculated correctly (see Walton et al. 2016, for details about mode 06 extract). We used a source region with 150′′ diameter to compensate for the increased apparent source size in the sky image. The mode 06 data added 16%, 20%, and 35% exposure time for epoch 1b, 3, and 4, respectively. We carefully checked that there were no significant differences between the mode 01 and 06 data and then combined them using addascaspec.
Although the NuSTAR and Suzaku data of the type-II giant outburst of GRO J1008−57 in 2012 November have already been published by Bellm et al. (2014), we analyze these data again for two reasons. First, our previous analysis of the spectral dependence on the source’s luminosity does not include these observations since the flux was higher than what had been observed until then. Secondly, by adding the mode 06 data, our statistical quality is improved compared to the spectra used by Bellm et al. (2014).
NuSTAR-FPMA and B data were fitted simultaneously between 4 and 78 keV. A first investigation of the spectra showed a significant mismatch between Swift and NuSTAR data below 4 keV across all epochs, which is why we did not use NuSTAR data down to 3 keV. This mismatch has been reported as well by Bellm et al. (2014) for epoch 1b. The NuSTAR data were rebinned to a signal-to-noise-ratio of 18 in the range 4–45 keV and 6 above 45 keV.
The barycentered NuSTAR-FPMA light curve of GRO J1008−57 during epoch 3 was extracted from the source region as defined above and with a 1 s time resolution.
2.3. Swift
The data of the X-Ray Telescope (XRT; Burrows et al. 2005; Godet et al. 2007) onboard Swift (Gehrels et al. 2004, 2005) were reprocessed following the Data Reduction Guide (Capalbi et al. 2005).
The observations of epoch 1b and 4 were operated in “Windowed Timing” mode (WT) and that of epoch 3 in “Photon Counting” mode (PC). The events of these observations were first calibrated and screened using xrtpipeline v0.13.2. The applied Telescope Definition File (teldef) was based on XRT CALDB release 2013-06-01. After having extracted an image of the observation using xselect, we created a circular source region with a radius of 47′′ corresponding to 90% of the PSF. In WT mode the circular background region of the same radius was selected at the edge of the one-dimensional image. During epoch 3 the count rate was, unfortunately, higher than 0.5 counts s-1, the nominal limit for pile-up since the outburst did not decay into quiescence as expected (see Fig. 1). To avoid pile-up in PC mode we compared the count rate profile with the expected PSF. We checked our results with the pileest tool, since the bad CCD columns due to a micro-meteorite hit might affect the count rate profile. The final source extraction region is an annulus with an outer radius of 47′′ and an inner radius of 22′′. The background region for epoch 3 is an annulus centered at the source position with an outer radius of 550′′ and an inner radius of 250′′.
The XRT-spectra were extracted using xselect. We only considered single events (grade 0) in the observations performed in PC mode (epoch 3). For the remaining observations in WT mode we also considered split events (grades 0–2). The spectra for each Good Time Interval (GTI) in WT mode were added into a final single spectrum. The ARF was generated by xrtmkarf taking the effective area and filter transmission into account and correcting for vignetting and PSF.
We rebinned the Swift-XRT spectra to a SNR of 12 for epochs 1b and 4, and to 6 for epoch 3, in order to retain enough spectral resolution around the iron line. These spectra were fitted in the 1−8 keV range.
3. Spectral analysis
The spectral analysis was performed using the Interactive Spectral Interpretation System (ISIS, Houck & Denicola 2000) v1.6.2-30. Unless stated otherwise, all uncertainties are given at the 90% confidence level and represent single parameter uncertainties (Δχ2 = 2.71).
As found in our previous work (K13), the RXTE broad-band spectra of GRO J1008−57 can be well described by a power-law with an exponential cutoff and an additional black body. This model provides very good fits over more than two orders of magnitude in the source’s flux. We applied the same model to the recent observations summarized in Table 1 in order to check and extend the covered range of fluxes. In K13 we found the temperature of the black body kT = 1.833 ± 0.019 keV1 and the folding energy of the cutoff power-law Efold = 15.9 ± 0.3 keV1 to be independent of the source’s flux and consistent among the outbursts. Furthermore, the bolometric flux of the black body, FBB, and the photon index of the power-law, Γ, were found to be well-defined functions of the source’s 15−50 keV flux, FPL. When checking these earlier results against the recent data analyzed here, we did not apply any of these findings a priori to the following spectral analysis.
We modeled the absorption by the interstellar medium (ISM) using TBnew2, a revised version of the model described by Wilms et al. (2000). Element abundances were set to Wilms et al. (2000) and cross-sections were taken from Verner et al. (1996). Furthermore, GRO J1008−57 shows fluorescent emission of iron at 6.4 keV and a CRSF around 78 keV, which we described by a Gaussian and a pseudo-Lorentzian absorption profile (CYCLABS, Makishima et al. 1990), respectively. Finally, we accounted for uncertainties in the flux calibration using a multiplicative constant, cx, for each instrument.
3.1. Suzaku (epoch 1a and 2)
For the analysis of the Suzaku spectra, all broad-band continuum parameters were allowed to vary, which are the black body temperature, kT, the folding energy, Efold, the power-law photon index, Γ, the black body flux, FBB, and the overall flux, FPL, in the 15–50 keV range. The absorption column density, NH, the energy of the iron Kα line, EFe Kα, and its flux, FFe Kα, were free parameters as well. The width of the iron line was kept narrow, that is, fixed to σFe Kα = 10-6 keV. From the best-fit we derived the iron line equivalent width, EWFe Kα. The flux calibration constants, cXIS0, cXIS1, cPIN, and cGSO were determined relative to cXIS3 = 1 (fixed). We note that during epoch 1a and 2 further calibration features were included in the fit as well (see Sect. 2.1). The CRSF was included in modeling epoch 1 only as it is not detected in epoch 2 (see the following for details).
 |
Fig. 2 a) The Suzaku-XIS (0: blue; 1: yellow; 3: green), -PIN (red), and -GSO (purple) spectra of the 2014 January observation of GRO J1008−57 (epoch 2) together with the best-fit model (black). b–d) The residuals to the best-fit model (b: XIS0, PIN, and GSO; c: XIS1; d: XIS3) showing the ignored energy bins due to calibration uncertainties (gray). The residuals of XIS1 (c) are shown without taking the photon index shift, ΔΓ, into account. |
Best-fit parameters of the Suzaku and simultaneous NuSTARSwift spectra analyzed here.
A first fit to the data of the 2014 January outburst (epoch 2) results in a very good description of the data. We found, however, a line-like feature around 7 keV that could be modeled by adding a second narrow Gaussian component. The fitted line energy of 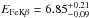 keV and relative flux
keV and relative flux 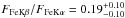 are in excellent agreement with fluorescent Kβ emission from neutral iron. The Suzaku spectrum together with the final best-fit model is shown in Fig. 2. The corresponding fit parameters are listed in Table 2.
are in excellent agreement with fluorescent Kβ emission from neutral iron. The Suzaku spectrum together with the final best-fit model is shown in Fig. 2. The corresponding fit parameters are listed in Table 2.
The Suzaku spectrum during the giant 2012 November outburst (epoch 1a) showed even more features. After applying the same K13 model as for epoch 2, strong residuals in absorption in PIN and GSO at energies above 60 keV remained, which we attributed to the high-energy CRSF (Bellm et al. 2014; Yamamoto et al. 2013, 2014). Adding such a feature with its width, Wcyc, fixed to 10 keV improved the fit significantly (Δχ2 = 353). The energy and depth of the CRSF, Ecyc and τcyc, respectively, were consistent with those found earlier. The XIS-spectra showed an excess towards lower energies, which could be described with a second black body at 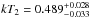 keV and improved the fit further (Δχ2 = 456). Finally, the emission lines of iron at 6.40, 6.67, and 7.00 keV, which we detected in our earlier analysis of this dataset (K13), were again detected. The line at 6.67 keV represents Kα emission from He-like iron (Fe xxiv), while the line at 7.00 keV is a combination of the Kβ from neutral iron and Kα from H-like iron (Fe xxv). The total flux in the fitted line was significantly higher than what is expected from neutral Kβ alone. The fit parameters of the final best-fit are listed in Table 2. For a figure showing the full Suzaku spectrum see Bellm et al. (2014, Fig. 4) and K13, Fig. 15, for a close-up of the iron line region.
keV and improved the fit further (Δχ2 = 456). Finally, the emission lines of iron at 6.40, 6.67, and 7.00 keV, which we detected in our earlier analysis of this dataset (K13), were again detected. The line at 6.67 keV represents Kα emission from He-like iron (Fe xxiv), while the line at 7.00 keV is a combination of the Kβ from neutral iron and Kα from H-like iron (Fe xxv). The total flux in the fitted line was significantly higher than what is expected from neutral Kβ alone. The fit parameters of the final best-fit are listed in Table 2. For a figure showing the full Suzaku spectrum see Bellm et al. (2014, Fig. 4) and K13, Fig. 15, for a close-up of the iron line region.
3.2. NuSTAR and Swift (epochs 1b, 3, and 4)
In a first step, we applied again the K13 model to the NuSTAR and Swift spectra (see Sect. 3.1). The broad-band continuum parameters were kept free as for the Suzaku analysis above. We added a Gaussian component in order to model the apparent neutral iron line with its centroid energy, EFe Kα, its flux and equivalent width, FFe Kα and EWFe Kα, respectively, and its width, which we fixed to σFe Kα = 10-6 keV. Flux calibration constants, cFPMB and cXRT, relative to cFPMA = 1 were included during the fit.
This model was able to describe the spectra taken during epoch 3, when GRO J1008−57’s luminosity was just above the detection limit of Swift-BAT (compare Fig. 1). The spectra during high luminosities of the source (epochs 1b and 4) could not, however, be fitted well with this model. There were clear indications for the CRSF towards the higher end of NuSTAR’s energy range. Including a CRSF with its width fixed to Wcyc = 10 keV as for the Suzaku data (see Sect. 3.1) led to a very good description of the spectra (Δχ2 = 527 for epoch 1b and Δχ2 = 286 for epoch 4). Slight residuals around the neutral iron line remained in all epochs. The energy resolution of the NuSTAR FPMs, however, does not allow resolution of further emission lines, such as iron Kβ or ionized iron, as was possible with the Suzaku-XISs. Nevertheless, varying the width of the iron Kα line, σFe Kα, was sufficient to get rid of these residuals. The best-fit energy, EFe Kα, was higher than the 6.4 keV expected from neutral iron. Together with a width of a few 100 eV these results point towards a blend of several emission lines, possibly from ionized iron as has been detected in the Suzaku data (see Sect. 3.1). For epoch 1b, the flux in the line of around 75 ph s-1 cm-2 agrees with the sum of the fluxes in the individual lines resolved in the Suzaku-XIS spectra (epoch 1a). The final fit-parameters for all epochs of NuSTAR and Swift observations are listed in Table 2. The spectra and corresponding models for epochs 3 and 4 are shown in Figs. 3 and 4, respectively. For epoch 1b see Bellm et al. (2014, Fig. 3). We note that the line-like residuals in Fig. 4b at ~ 1.8 keV and ~ 2.2 keV are only visible due to the coarser channel binning used in this figure. These features are calibration uncertainties in Swift-XRT around the Si K edge and the Au M edge, respectively (Godet et al. 2007; Hurkett et al. 2008). Due to their low significance they do not have any effect on the spectral parameters here.
 |
Fig. 3 a) NuSTAR-FPMA (dark blue), -FPMB (light blue), and Swift-XRT spectrum (red) of GRO J1008−57 in 2014 December after the second peak of its triple peaked outburst (epoch 3). The best-fit model is shown in black and the gray line shows its ratio to the spectral shape as predicted by our spectral evolution model (see Sect. 5 and Fig. 6). The data have been rebinned for display purposes. b) The residuals of the best-fit model. |
 |
Fig. 4 a) NuSTAR-FPMA (dark blue), -FPMB (light blue), and Swift-XRT spectrum (red) of GRO J1008−57 in 2015 January shortly after maximum flux of the third peak of the triple peaked outburst (epoch 4). The black line shows the best-fit model. The data have been rebinned for display purposes. b) The residuals of the best-fit model. |
4. Discussion on individual observations
We have successfully applied the model used in our previous study of GRO J1008−57 (K13) to recent Suzaku and simultaneous NuSTAR and Swift spectra. We compare the results of K13, especially the parameter evolution with the X-ray flux, with the results of the spectral analysis presented here in Sect. 5 separately. In this section we discuss our results in their individual context.
4.1. CRSF and 2nd black body
During the giant 2012 November outburst we can confirm the presence of a CRSF in the Suzaku and NuSTAR data (epochs 1a and 1b). Furthermore, we have detected the CRSF in the NuSTAR data during epoch 4, which happened at a source luminosity level comparable to that during epochs 1a and 1b. There is no hint of a cyclotron line in the NuSTAR data during epoch 3 and in the Suzaku data during epoch 2, when the source was at a much lower luminosity level. We cannot, however, exclude its presence due to the lower statistic. In the Suzaku data of the giant outburst (epoch 1a), we find the cyclotron line energy Ecyc = 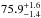 keV to be in excellent agreement with
keV to be in excellent agreement with 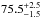 keV and
keV and 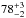 keV as found in the earlier analyses of these data by Yamamoto et al. (2013, 2014) and Bellm et al. (2014), respectively. The apparent difference in the measured CRSF energies between NuSTAR (epoch 1b and 4) and Suzaku (epoch 1a) is likely due to systematic uncertainties in this energy range, which is at the upper end of the useful energy range for both instruments. Furthermore, a slight change in the continuum parameters, especially the photon index, Γ, or the folding energy, Efold, influences the CRSF parameters at this high energy. Thus, we cannot draw definite conclusions from the apparent difference between the Suzaku (epoch 1a) and the NuSTAR results (epochs 1b and 4).
keV as found in the earlier analyses of these data by Yamamoto et al. (2013, 2014) and Bellm et al. (2014), respectively. The apparent difference in the measured CRSF energies between NuSTAR (epoch 1b and 4) and Suzaku (epoch 1a) is likely due to systematic uncertainties in this energy range, which is at the upper end of the useful energy range for both instruments. Furthermore, a slight change in the continuum parameters, especially the photon index, Γ, or the folding energy, Efold, influences the CRSF parameters at this high energy. Thus, we cannot draw definite conclusions from the apparent difference between the Suzaku (epoch 1a) and the NuSTAR results (epochs 1b and 4).
In the Suzaku data of the giant outburst of GRO J1008−57 in 2012 (epoch 1a) a second black body with 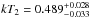 keV is required to fit the low-energy part of the XIS-spectra successfully. We had already detected this feature in our earlier analysis of these data together with Swift spectra (K13). On the other hand, the feature was not detected in the two Suzaku observations at lower luminosities (epoch 2 and during the decay of the 2007 data, see K13 for details) as well as in the Swift data during the maximum of the 2007 outburst (see K13). Thus, it is likely that the soft part of GRO J1008−57’s spectrum at ≲3 keV changed during the giant outburst. In combination with the evolution of the other spectral parameters with flux, as presented Sect. 5, this is evidence for the existence of different accretion regimes in GRO J1008−57. Bellm et al. (2014), who used the NPEX model for the broad-band continuum, found this second black body at the same temperature as we did, while they did not detect it in the NuSTAR data alone. We found that this feature is not significantly detected in the combined NuSTAR and Swift data as well. The broad-band continuum parameters agree, however, between Suzaku and NuSTAR. Thus, the presence of this feature does not significantly influence the remaining spectral parameters. Adding this feature to the NuSTAR spectrum at a fixed temperature indeed leads to consistent results with the Suzaku spectrum.
keV is required to fit the low-energy part of the XIS-spectra successfully. We had already detected this feature in our earlier analysis of these data together with Swift spectra (K13). On the other hand, the feature was not detected in the two Suzaku observations at lower luminosities (epoch 2 and during the decay of the 2007 data, see K13 for details) as well as in the Swift data during the maximum of the 2007 outburst (see K13). Thus, it is likely that the soft part of GRO J1008−57’s spectrum at ≲3 keV changed during the giant outburst. In combination with the evolution of the other spectral parameters with flux, as presented Sect. 5, this is evidence for the existence of different accretion regimes in GRO J1008−57. Bellm et al. (2014), who used the NPEX model for the broad-band continuum, found this second black body at the same temperature as we did, while they did not detect it in the NuSTAR data alone. We found that this feature is not significantly detected in the combined NuSTAR and Swift data as well. The broad-band continuum parameters agree, however, between Suzaku and NuSTAR. Thus, the presence of this feature does not significantly influence the remaining spectral parameters. Adding this feature to the NuSTAR spectrum at a fixed temperature indeed leads to consistent results with the Suzaku spectrum.
4.2. Spectral anomaly of epoch 3
 |
Fig. 5 Pulse profiles of GRO J1008−57 during epoch 3 (blue; NuSTAR-FPMA) and 2005 (red; RXTE-PCA). The RXTE observation was performed at a similar flux level of the source compared to the NuSTAR observation. The pulse profiles have been normalized to a mean count rate of zero and a standard deviation, σ, of unity. Pulse phase zero is defined as the minimum count rate. |
During the transition from the second to the third outburst (epoch 3) during GRO J1008−57’s “triple-peaked” outburst, the spectral parameters disagree with the correlation between spectral parameters as found in the other observations of this source (see Sect. 5 for details). In particular, the folding energy, Efold, of ~ 19.6 keV is significantly higher than the 15−16 keV as found during all other epochs (see Table 2). The gray line in Fig. 3a shows the ratio between the best-fit model spectrum and the predicted spectrum assuming the measured source flux at 15–50 keV as listed in Table 2. As can be seen, this flux ratio increases exponentially above ~30 keV up to a factor of 2 around 70 keV. These facts still hold true if the NuSTAR and Swift spectra are fitted with taking the CRSF into account, that is, the presence or absence of the CRSF has no influence on the model parameters.
To draw conclusions about the reason for this spectral anomaly we compared the pulse profile of the corresponding NuSTAR observation with an RXTE observation in 2005 at a similar flux level (ObsID 90089-03-02-01). As RXTE-PCA and NuSTAR-FPMA are sensitive over comparable energy ranges (3−60 and 3−78 keV), differences in the pulse profiles can be associated with changes in the accretion geometry. After correcting the light curves for binary motion using the orbital parameter listed in K13, we folded the NuSTAR and RXTE light curves on 93.445 s and 93.675 s, respectively, which correspond to the spin periods of GRO J1008−57 and were determined from the data using the epoch folding technique (see, e.g., Leahy et al. 1983).
The resulting pulse profiles shown in Fig. 5 were normalized to a mean count rate of zero and a standard deviation of unity (see, e.g., Ferrigno et al. 2011; Schönherr et al. 2014). Both pulse profiles are very similar in shape. We therefore concluded that the accretion geometry between these observations was very similar as well, which hints at an origin outside of the neutron star’s magnetosphere for the spectral anomaly. The observed changes in the pulse profile of A0535+26 during pre-outburst flares (Caballero et al. 2008) were explained by Postnov et al. (2008) as the result of magnetospheric instabilities. Since the pulse profile of GRO J1008−57 during the flaring epoch 3 is consistent with the expected pulse profile shape, it is unlikely that these instabilities are the origin for the observed flaring activity.
4.3. “Triple-peaked” outburst morphology
After the first confirmed giant outburst of GRO J1008−57 in 2012 November (epochs 1a and 1b) since its discovery in 1993, the source featured an expected type I outburst in January 2014 (epoch 2). Surprisingly, after the type-I outburst in September 2014, GRO J1008−57 went into a type-II outburst again. But instead of fading into quiescence after this second outburst (epoch 3), the source showed a third outburst in a single orbit (epoch 4). In fact, the peak of the third outburst was reached at apastron (see Fig. 1 and Kretschmar et al. 2015).
Figure 1 shows the light curve morphology of GRO J1008−57 during this “triple-peaked” outburst in 2014/2015, which lasted for half the orbital period of ~ 250 d. The transition between the first two outbursts occurred rather smoothly, which has also been observed during the known “double-peaked” outbursts of A 0535+262 (Caballero et al. 2013, Fig. 1) and GX 304−1 (Postnov et al. 2015b, Fig. 1). The peak separation in GRO J1008−57 of ~ 65 d = 0.25 Porb is, however, much larger than in these systems, which show separations of ~ 9 d = 0.08 Porb with Porb = 111.1 d in the case of A 0535+26 (Finger et al. 2006) and ~ 25 d = 0.19 Porb with Porb = 132.5 d in the case of GX 304−1 (Priedhorsky & Terrell 1983). As argued by Postnov et al. (2015b), the “double-peaked” outburst of GX 304−1 is due to a misaligned Be-disk with respect to the orbital plane. Once the disk has grown sufficiently beyond the distance between the stellar surface and the neutron star’s orbit a second intersection might be possible. This is consistent with recent theoretical investigations by Okazaki et al. (2013). The geometries of the Be-disk and the orbit are unique for each BeXRB, although there are similarities among this class. Thus, a difference of the peak separation up to a factor of ~3 in orbital phase is not astonishing. We note that the outbursts of XTE J1946+274 occurred twice per orbital period (Porb ~ 172 d; see, e.g., Marcu-Cheatham et al. 2015, and references therein), that is, the peak separation in this system is about 0.5 in orbital phase. As the system shows ≥ 5 outbursts in a row, this morphology is, however, different compared to the “double-peaked” outbursts.
Between the second and third peak of GRO J1008−57’s “triple-peaked” outburst, the light curve is not as smooth as the transition between the first two peaks. Rather, the source stayed at a more or less constant level for ~ 50 d with a weak flaring activity. A similar behavior was also observed before the giant 2012 November outburst (see Fig. 1), when the flaring activity was, however, much stronger and lasted for ~ 60 d. These flares occurred quasi-periodically with a period of around 9 d. A speculative explanation for this different behavior compared to the smooth transition might be external torques onto the accretion disk as studied by Doğan et al. (2015). They argue that for an accretion disk of a certain size and inclined with respect to the orbital plane, the torques might overpower the internal disk torques. Consequently, the disk would break up into slices, which would precess independently of each other. Doğan et al. (2015) thus conclude that the mass accretion rate onto the compact object gets modulated. In their example simulation (see Fig. 5 of Doğan et al. 2015) the period of this modulation is much longer than the orbital period, which makes it difficult to reconcile with the observed 9 d period.
5. Parameter evolution with flux
In K13 we found that the broad-band continuum of GRO J1008−57 is a function of the overall X-ray flux. The black body temperature, kT, and the folding energy, Efold, are independent of the 15–50 keV flux, FPL, and consistent among the outbursts. The power-law photon index, Γ, and the black body flux, FBB, show a tight correlation with FPL. These results are mainly based on observations taken by RXTE with the addition of one Swift and one Suzaku pointing.
The black body temperature found by analyzing the new Suzaku (epochs 1a and 2) and joint NuSTAR and Swift observations (epochs 1b, 3, and 4) are all within 0.15 keV of kT = 1.833 ± 0.019 keV as found by K13. Despite this small temperature range, the values during the bright NuSTAR observations (epochs 1b and 4) are, however, significantly lower than the mean value. The folding energy of 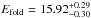 keV that we measured previously in K13 is consistent with the observations analyzed here with the exception of the NuSTAR epochs 1b and 3. While GRO J1008−57’s spectral anomaly during epoch 3 has been discussed in Sect. 4.2, Efold during epoch 1b is ~ 1 keV lower compared to the RXTE result of K13. In order to understand these apparent differences in kT and Efold we investigated contour maps of these parameters against other continuum parameters. We discovered parameter degeneracies, especially between the photon index, Γ, and the folding energy, Efold. In fact, the folding energy found previously by K13 is within 2.7σ (for two degrees of freedom) of the best-fit of epoch 1b as listed in Table 2. Fixing Efold = 15.92 keV indeed leads to a similar goodness of the fits for all epochs (except epoch 3 as discussed above). Thus, we conclude that the flux-independent parameters still seem to be the same for the newer data analyzed here (except epoch 3), which confirms our previous results (K13).
keV that we measured previously in K13 is consistent with the observations analyzed here with the exception of the NuSTAR epochs 1b and 3. While GRO J1008−57’s spectral anomaly during epoch 3 has been discussed in Sect. 4.2, Efold during epoch 1b is ~ 1 keV lower compared to the RXTE result of K13. In order to understand these apparent differences in kT and Efold we investigated contour maps of these parameters against other continuum parameters. We discovered parameter degeneracies, especially between the photon index, Γ, and the folding energy, Efold. In fact, the folding energy found previously by K13 is within 2.7σ (for two degrees of freedom) of the best-fit of epoch 1b as listed in Table 2. Fixing Efold = 15.92 keV indeed leads to a similar goodness of the fits for all epochs (except epoch 3 as discussed above). Thus, we conclude that the flux-independent parameters still seem to be the same for the newer data analyzed here (except epoch 3), which confirms our previous results (K13).
In K13 we also discovered that the photon index, Γ, and the black body flux, FBB, are functions of the overall 15–50 keV source flux, FPL. In particular, the same behavior is found in all outbursts. Figure 6 is an updated version of our previous RXTE results (Fig. 10 of K13), where the best-fit Γ and FBB over FPL of the newer data have been added (see Table 2). We note that since two fit parameters are plotted against each other in each panel, the uncertainties have to be calculated assuming two degrees of freedom. As we will fit these parameters below, we are providing 1σ uncertainties (Δχ2 = 2.30).
The parameters of the Suzaku epoch 2 (green triangle at ~ 1.5 × 10-9 erg s-1 cm-2) are consistent with the behavior seen earlier (black triangle). Furthermore, the NuSTAR and Suzaku observations during the giant 2012 outburst (the most luminous blue circle and green triangle) also give consistent results, although a second black body was necessary to describe the Suzaku data. Interestingly, the recent NuSTAR observation during the third outburst of the “triple-peaked” outburst (blue circle at ~ 7 × 10-9 erg s-1 cm-2) results in the same parameters as for the 2012 giant outburst, although the source was ~ 45% brighter then. The data from epoch 3 (blue circle marked with 1), where the folding energy, Efold, was not consistent with all the other observations (see Sect. 4.2 for a discussion), is almost consistent with the apparent parameter evolution. Due to the inconsistency in Efold we, however, ignore this observation until the end of this section.
In the following, we model the apparent evolution of the power-law photon index, Γ, and the black body flux, FBB, with the source flux, FPL, using phenomenological functions, 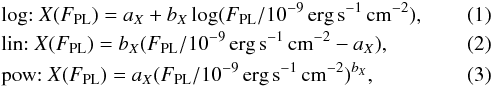 where X is either the photon index, Γ, or the black body flux, FBB. In the case of fitting the evolution of the black body flux, that is, X = FBB, we restrict the black body to be in emission only, that is, FBB(FPL) ≥ 0 for all source fluxes, FPL. In order to fit a model consisting of these functions to one of the parameter evolutions shown in Fig. 6 we minimize the χ2 accounting for the asymmetric uncertainties in both the flux, FPL, and the parameter of interest, X.
where X is either the photon index, Γ, or the black body flux, FBB. In the case of fitting the evolution of the black body flux, that is, X = FBB, we restrict the black body to be in emission only, that is, FBB(FPL) ≥ 0 for all source fluxes, FPL. In order to fit a model consisting of these functions to one of the parameter evolutions shown in Fig. 6 we minimize the χ2 accounting for the asymmetric uncertainties in both the flux, FPL, and the parameter of interest, X.
 |
Fig. 6 Evolution of the spectral parameters with the 15–50 keV flux, FPL, of GRO J1008−57. a) The power-law photon index, Γ, and b) the black body flux FBB (in erg s-1 cm-2), with the source’s flux (uncertainties represent 1σ uncertainties with two degrees of freedom). The black data points are the results of our previous RXTE and the black triangle the joined Suzaku RXTE analysis (K13). Their fluxes have been corrected for calibration uncertainties (see the text for details). The new results presented in this paper are the green triangles based on Suzaku and the blue circles based on NuSTAR data. The red lines show the empirical model with (solid) and without (dashed) the breaks at certain luminosity levels as described in the text. The NuSTAR results marked with 1) have been excluded from these fits. The bolometric luminosity for one accretion column has been calculated as described in Sect. 5. |
During a first investigation of the parameter evolutions, we have ignored data at FPL< 8 × 10-11 erg s-1 cm-2 in order to remove any possible bias introduced by the upper limits or large uncertainties at lower fluxes. Furthermore, we ignored data at FPL> 3 × 10-9 erg s-1 cm-2 due to an insufficient description of the observed parameter evolutions at these high fluxes regardless of the chosen model. We model and discuss this discrepancy further below. We find that the photon index evolution, Γ(FPL), is described best using a logarithmic function (log : χ2 = 97.0; pow: χ2 = 183.1; lin: χ2 = 399.3; all with 28 degrees of freedom). A power-law dependency fits the evolution of the black-body flux, FBB(FPL), well (pow: χ2 = 46.4; lin: χ2 = 69.1; log : χ2 = 185.9; all with 28 degrees of freedom).
Although the data follow these models well at first glance (see Fig. 6) the goodness of the fits as given above are not acceptable. A reduced χ2 near unity is, however, required for a reasonable interpretation of the resulting model parameters within their uncertainties. The reason for the large χ2 values is a few data points with very small uncertainties compared to the complete data set. These data points are, however, only a few percent off from the models. We have tried to fit these differences by introducing calibration constants similar to those during the spectral analysis (see Sect. 3). This approach failed due to the low number of data points for NuSTAR and Suzaku compared to RXTE and due to very similar spectral parameters among these missions at high luminosities of GRO J1008−57. To take into account the systematic effect of these offsets, we have added a systematic uncertainty of 0.03 in Γ (corresponding to 2–7% relative uncertainty) and a relative uncertainty of 3.5% in both flux parameters, FPL and FBB. These additional uncertainties are consistent with known energy and flux cross-calibration uncertainties between different X-ray missions and their instruments (see, e.g., Kirsch et al. 2005; Tsujimoto et al. 2011; or Madsen et al. 2017). We note that we cannot exclude source variability on a few percent level as a reason for the large χ2 values besides calibration uncertainties. This does not, however, affect any of the following conclusions given the overall change in Γ and FBB by a factor of 2–3 and by a few orders of magnitude, respectively.
When including all available data over the full flux range (with the exception of epoch 3), we find that the recent observations (when the source was at very high luminosities) are not consistent with a logarithmic function for Γ(FPL) and, especially, a power-law function for FBB(FPL) with a single slope. This is similar to what we found for lower fluxes in K14. For these three epochs (1a, 1b, and 4) we measure the same parameter values within their uncertainties, despite them being taken at very different fluxes. This behavior can be fitted much better by a flattening of the correlation towards higher fluxes, Fbrk, 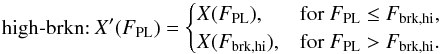 (4)Interestingly, the best-fit break fluxes for Γ(FPL) and FBB(FPL) are the same within their uncertainties. Thus, we tied the break fluxes, Fbrk,hi, for both parameter evolutions together. The observed parameter correlations can be described even better if we allow for an additional break of the photon index, Γ, to a constant at lower fluxes, Fbrk,lo, which we had noticed already in K14,
(4)Interestingly, the best-fit break fluxes for Γ(FPL) and FBB(FPL) are the same within their uncertainties. Thus, we tied the break fluxes, Fbrk,hi, for both parameter evolutions together. The observed parameter correlations can be described even better if we allow for an additional break of the photon index, Γ, to a constant at lower fluxes, Fbrk,lo, which we had noticed already in K14, 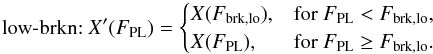 (5)This model for the spectral evolution of GRO J1008−57 including two breaks at different luminosity levels provides a good description of the data. The corresponding fit parameters are listed in Table 3.
(5)This model for the spectral evolution of GRO J1008−57 including two breaks at different luminosity levels provides a good description of the data. The corresponding fit parameters are listed in Table 3.
Since we interpret the artificial breaks in the model function as transitions between different accretion regimes, the statistical significance of their detection is crucial for our conclusion. The least prejudiced way to derive the significance of these model components is a Monte Carlo approach. Therefore, we simulated 1.77 × 106 data sets for both Γ(FPL) and FBB(FPL) based on our best-fit model without any breaks. A Gaussian randomization of the individual data points with their respective uncertainty has been applied for each simulated data set. The resulting data sets were then fitted both with the model with and without the two breaks. If the χ2 difference of those two fits was larger than the one obtained from fitting our measured data, we recorded this as a false-positive detection. The fraction of false-positive detections in the complete simulation directly translates to the significance of the modeled break. We find a significance of the high-luminosity break in FBB of ≥ 5σ as a lower limit. The high- and low-luminosity breaks of the photon index, Γ, are significant at the 2.35σ and 3.73σ level, respectively. We thus conclude that the high-luminosity break in FBB and the low-luminosity break in Γ are most likely real, while the high-luminosity break of Γ is only moderately significant. We note that the chosen additional uncertainties as described above move these significances to the conservative side. For instance, the significane of the low-luminosity break in Γ increases to 4.12 once no systematic uncertainty is added and only RXTE data are taken into account (this is the only data set relevant at this luminosity level, see Fig. 6).
We stress that other models for the spectral evolution of GRO J1008−57 as a function of luminosity might provide an equivalent description of the data. However, regardless of the chosen model or approach (e.g., investigating hardness ratios) we significantly detect changes near Fbrk,lo and Fbrk,hi. We do not claim that our (phenomenological) model or the way in handling systematic uncertainties is generally valid. Thus, the spectral shape of GRO J1008−57 for any flux as predicted by our model should be taken with care.
Accretion regimes in GRO J1008 − 57.
The detailed analysis of the evolution of the photon index and black body flux presented in Sect. 5 revealed two flux levels, where a change in the evolution is happening (see Fig. 6). At fluxes below Fbrk,lo ~ 10-10 erg s-1 cm-2 (between 15–50 keV) the photon index seems to be independent of flux and stays constant. For higher fluxes, the photon index starts to harden, while the black body flux increases. Once the flux exceeds Fbrk,hi ~ 3 × 10-9 erg s-1 cm-2 a saturation effect is observed, where the photon index is no longer hardening and the black body does not increase in flux further. In addition, during the giant 2012 November outburst (epoch 1a and 1b), when GRO J1008−57 reached its highest known flux so far3, another soft component below 3 keV shows up in the Suzaku spectrum (the second black body, see Sect. 3.1). This feature is not detected in any other observation at lower fluxes. We interpret these facts as observational evidence for three different accretion regimes in GRO J1008−57.
 |
Fig. 7 Comparison of the derived luminosities at the breaks of the spectral evolution (Lbrk,lo and Lbrk,hi, vertical dashed lines) with Lcoul and Lcrit of Becker et al. (2012, Eqs. (A.1A.2panel a, |
In order to connect these different accretion regimes of GRO J1008−57 with the physics of the accretion process, we have compared our findings with recent theoretical investigations by Becker et al. (2012), Postnov et al. (2015a), and Mushtukov et al. (2015a). These authors estimate the so-called critical luminosity, which can be interpreted as a transition between two accretion regimes: above this luminosity the radiation pressure inside the column dominates the deceleration of the infalling plasma, while Coloumb interactions dominate at lower luminosities. In addition, Becker et al. (2012) expect these Coloumb interactions to be unable to stop the material to rest for even lower luminosities. This so-called Coloumb braking luminosity would mark another transition between accretion regimes. The theoretical assumptions and calculations of these three works result, however, in differences by orders of magnitude. More details and the actual equations for the transition luminosities are given in Appendix A.
Figure 7 compares the luminosities of GRO J1008−57 at the observed breaks in the spectral parameter evolution, Lbrk,lo and Lbrk,hi, with the theoretically expected luminosities at the transition between different accretion regimes after Becker et al. (2012), Postnov et al. (2015a), and Mushtukov et al. (2015a) (Eqs. (A.1)−(A.3)). To derive the bolometric luminosities in the neutron star’s rest-frame, L, from the observed fluxes, Fbrk,lo and Fbrk,hi, we need to
-
a)
extrapolate the model to the full electromagnetic spectrum inorder to calculate the unabsorbed bolometric flux, F⋆;
-
b)
correct for the gravitational redshift, z;
-
c)
take into account a factor, g, describing the emission geometry;
-
d)
and, correct for the distance, d, to the source.
In summary, 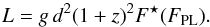 (6)We describe the details of the corrections a) to d) in the following and discuss their uncertainties.
(6)We describe the details of the corrections a) to d) in the following and discuss their uncertainties.
-
a)
The unabsorbed bolometric flux, F⋆, is a non-linear function of the power-law flux, FPL. We have used our spectral evolution model (see Table 3) in order to extrapolate the observed spectral shape to the 0.01 to 100 keV energy range. From this extended spectrum we determine the bolometric flux. The uncertainty of the extrapolation is caused by the unknown spectral shape outside of the observed energy band. Here, we assume a thermal Comptonization spectrum4 below 1 keV, that is, below the Swift-XRT and Suzaku-XIS sensitivities. Furthermore, the uncertainty in the estimated bolometric flux takes the uncertainty of the measured absorption column density, NH, into account. It is unlikely that the observed X-ray absorption mimics an actual Comptonization turn-over since we do not observe a change in NH with time or flux in GRO J1008−57(K13). Due to the exponential rollover at higher energies the spectral shape above ~ 80 keV (NuSTAR and Suzaku GSO) does not influence the bolometric flux significantly. We found that the extrapolation of the energy band results in a 0.01–100 keV flux uncertainty of 15% when comparing thermal Comptonization with the power-law spectrum used for spectral analysis (see Sect. 3).
-
b)
The gravitational redshift, 1 + z = (1−2GM/Rc2)− 1/2 with the mass, M, and radius, R, of the neutron star results in an observed luminosity of Lobs = L/ (1 + z)2 compared to the intrinsic one (Thorne 1977). For a typical neutron star with M = 1.4 M⊙ and R = 12 km, we find z ≈ 0.235. Assuming ΔM = 0.5 M⊙ and ΔR = 6 km we find an uncertainty of Δz = 0.1 in z, which corresponds to a 17% uncertainty in the derived intrinsic luminosity.
-
c)
The emission geometry of GRO J1008−57 is unknown and, thus, we assume isotropic emission of each pole into its hemisphere, that is, g = 2π (the theoretical expectations apply to one pole only). According to Martínez-Núñez et al. (2017), who estimate the effects of light bending (e.g., Kraus 2001), the real luminosity for a typical fan beam accretion geometry can differ by ~ 25% relative to the derived luminosity assuming isotropic emission. Due to the higher accretion rate in BeXRBs compared to low-mass X-ray binaries (LMXBs), which usually emit via a pencil beam geometry (see, e.g., Basko & Sunyaev 1975), the fan beam is a justified geometry for GRO J1008−57. Thus, we assume a systematic uncertainty of 25% due to the unknown emission geometry.
-
d)
The distance to the source was determined as d = 5.8(5) kpc by Riquelme et al. (2012), which propagates to a further 17% uncertainty in the luminosity.
Using Eq. (6) we converted the measured fluxes where we observed changes in the spectral behavior of GRO J1008−57, Fbrk,lo and Fbrk,hi, into the luminosities shown in Fig. 7, Lbrk,lo and Lbrk,hi (vertical dashed lines). Besides the corresponding measurement uncertainties of these luminosities (dark gray bands) we added a systematic uncertainty of 74% to the data (light gray bands) which corresponds to the sum of the additional sources of uncertainty, a−d, as described above5. In order to calculate the theoretical luminosities after Eqs. (A.1)−(A.3) (black stars), we assumed typical neutron star parameters (see Eqs. (A.1)−(A.3) and the respective references) with the exception of the surface cyclotron line energy, E⋆, which we assumed to be the redshift corrected cyclotron line energy, E⋆ = (1 + z)Ecyc = 90 keV, with the mean value of Ecyc as listed in Table 2. The dependencies of the different luminosities on the neutron star parameters are shown by the colored lines. Because Mushtukov et al. (2015a) solved Eq. (A.3) numerically they presented the dependencies of their critical luminosity, 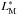 , on the neutron star parameters in their Fig. 5 instead of providing an analytical equation. From this figure, we have extracted the values of the critical luminosity assuming the same redshift corrected cyclotron line energy as above. In order to include the dependency of the critical luminosity,
, on the neutron star parameters in their Fig. 5 instead of providing an analytical equation. From this figure, we have extracted the values of the critical luminosity assuming the same redshift corrected cyclotron line energy as above. In order to include the dependency of the critical luminosity, 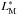 (Eq. (A.3)), on neutron star parameters in Fig. 7, we assumed a linear dependency between the extracted values. By drawing the resulting dependencies as dashed lines (panel b) we stress that this is for illustrating the basic dependence, that is, its sign, only.
(Eq. (A.3)), on neutron star parameters in Fig. 7, we assumed a linear dependency between the extracted values. By drawing the resulting dependencies as dashed lines (panel b) we stress that this is for illustrating the basic dependence, that is, its sign, only.
The facts from Fig. 6, which shows the spectral parameter evolution of GRO J1008−57, and Fig. 7, which compares the changes in this parameter evolution at Lbrk,lo and Lbrk,hi with recent theoretical investigations, can be summarized as follows.
-
Between the observed luminosities, Lbrk,lo and Lbrk,hi, the spectrum of GRO J1008−57 is hardening with increasing luminosity. This is in line with theoretical expectations by Postnov et al. (2015a) for sources in the subcritical accretion regime.
-
If Lbrk,hi can indeed be associated with the source exceeding the critical luminosity, then parameter combinations can be found such that each of the three theories summarized in Appendix A predict the expected value for this luminosity correctly:
-
Lbrk,hi ~ Lcrit for w> 1.9 after Becker et al. (2012, Eq. (A.2, that is, the spectrum inside the column is a mixture between a Plank spectrum (w = 3) and pure Comptonized bremsstrahlung radiation (w = 1).
-
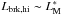 after Mushtukov et al. (2015a, Eq. (A.3 for canonical neutron star parameters.
after Mushtukov et al. (2015a, Eq. (A.3 for canonical neutron star parameters. -
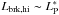 after Postnov et al. (2015a, Eq. (A.4 for b ≪ 1, that is, a hollow accretion
column. We note that Eq. (A.4) depends equally on b and κ⊥/κT,
that is, the same effect is achieved for κ⊥/κT ≪
1.
after Postnov et al. (2015a, Eq. (A.4 for b ≪ 1, that is, a hollow accretion
column. We note that Eq. (A.4) depends equally on b and κ⊥/κT,
that is, the same effect is achieved for κ⊥/κT ≪
1.
-
-
The change of the spectral evolution at Lbrk,lo is consistent with
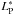 after Postnov et al. (2015a, Eq. (A.4 for a filled accretion column with a radius of r0 ≤ 935 m. The corresponding luminosity around 1036 erg s-1 is, however, too low for the transition to supercritical accretion as expected by all these theories. Even Postnov et al. (2015a) expect this transition to occur around 1037 erg s-1.
after Postnov et al. (2015a, Eq. (A.4 for a filled accretion column with a radius of r0 ≤ 935 m. The corresponding luminosity around 1036 erg s-1 is, however, too low for the transition to supercritical accretion as expected by all these theories. Even Postnov et al. (2015a) expect this transition to occur around 1037 erg s-1. -
The ratio between the Coulomb braking and the critical luminosity, Lcoul/Lcrit, after Becker et al. (2012, Eqs. (A.1A.2 matches almost perfectly the observed ratio Lbrk,lo/Lbrk,hi. The individual theoretical luminosities for canonical neutron star parameters are, however, a factor of ~ 6 higher than compared to observed ones.
-
The observed spectral change at high luminosities, Lbrk,hi, is also consistent with the saturation of the hardness as expected by Postnov et al. (2015a) due to reflection from the neutron star’s surface in case of a filled accretion column.
We have further investigated the dilemma that Lbrk,hi is consistent with reflection from a filled accretion column, but also with 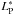 for a hollow accretion column after Postnov et al. (2015b). From our best-fit parameter evolution (see Table 3) we calculated the hardness ratio using the same energy bands as Postnov et al. (2015b, 5−12 keV over 1.3−. The resulting evolution of the hardness ratio does not increase above a hardness of ~ 6. This is in very good agreement with the expected value for the hardness ratio in case of a filled accretion column, whereas a hardness in the range of 10−16 is expected for a hollow accretion column (see Figs. 6 and 7 of Postnov et al. 2015b). Furthermore, the derived hardness saturates above a (one-column) accretion rate of 1 × 1017 g s-1, while the evolution of the hardness shown in Fig. 6 of Postnov et al. (2015b) suggests a saturation above 5−7 × 1017 g s-1. This value scales with the height of the filled accretion column, which itself anti-correlates with the magnetic field strength at a given mass accretion rate (K. Postnov, priv. comm.). The required magnetic field strength to achieve a match between the observed Lbrk,hi and the expected saturation of the hardness due to reflection is, however, far lower than compared to GRO J1008−57’s CRSF. In summary, the match of
for a hollow accretion column after Postnov et al. (2015b). From our best-fit parameter evolution (see Table 3) we calculated the hardness ratio using the same energy bands as Postnov et al. (2015b, 5−12 keV over 1.3−. The resulting evolution of the hardness ratio does not increase above a hardness of ~ 6. This is in very good agreement with the expected value for the hardness ratio in case of a filled accretion column, whereas a hardness in the range of 10−16 is expected for a hollow accretion column (see Figs. 6 and 7 of Postnov et al. 2015b). Furthermore, the derived hardness saturates above a (one-column) accretion rate of 1 × 1017 g s-1, while the evolution of the hardness shown in Fig. 6 of Postnov et al. (2015b) suggests a saturation above 5−7 × 1017 g s-1. This value scales with the height of the filled accretion column, which itself anti-correlates with the magnetic field strength at a given mass accretion rate (K. Postnov, priv. comm.). The required magnetic field strength to achieve a match between the observed Lbrk,hi and the expected saturation of the hardness due to reflection is, however, far lower than compared to GRO J1008−57’s CRSF. In summary, the match of 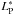 with Lbrk,hi in the case of a hollow column is ruled out by the observed hardness ratio. Once a filled column is assumed, the overall hardness ratio matches the predicted value. The dependence of
with Lbrk,hi in the case of a hollow column is ruled out by the observed hardness ratio. Once a filled column is assumed, the overall hardness ratio matches the predicted value. The dependence of 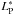 on the luminosity due to reflection at the neutron star’s surface requires, however, a much weaker magnetic field than what is found for GRO J1008−57.
on the luminosity due to reflection at the neutron star’s surface requires, however, a much weaker magnetic field than what is found for GRO J1008−57.
We notice that the observed break at high luminosities, Lbrk,hi, agrees well with the critical luminosity, 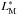 , as predicted by Mushtukov et al. (2015a), at least for the case of GRO J1008−57. The theories by Postnov et al. (2015b) and Becker et al. (2012) have difficulties explaining our observations since unlikely parameter combinations are necessary in order to achieve a match with their predicted critical luminosities,
, as predicted by Mushtukov et al. (2015a), at least for the case of GRO J1008−57. The theories by Postnov et al. (2015b) and Becker et al. (2012) have difficulties explaining our observations since unlikely parameter combinations are necessary in order to achieve a match with their predicted critical luminosities, 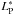 and Lcrit, respectively (see Fig. 7). The large systematic uncertainties when deriving luminosities from observational data as discussed above do not, however, allow us to favor unequivocally one of the discussed theories for the prediction of the critical luminosity. Especially, the observed change of the spectral evolution of GRO J1008−57 at low luminosities, Lbrk,lo, cannot be explained by either theory. Furthermore, drawing general conclusions about these theories is statistically questionable as only observational data of a single source are used. In future work, a detailed study of the recently claimed accretion regimes in 4U 1901+03 (Reig & Milonaki 2016) and V 0332+53 (Doroshenko et al. 2016) combined with the results by Reig & Nespoli (2013) for various sources could help clarify this question. It should be noted, however, that thorough analysis methods are required and systematic effects (caused by detector calibration and due to the conversion to luminosities) have to be taken into account as, for example, discussed here. Nevertheless, the existence of different accretion regimes, which are driven by the mass accretion rate, seems to be confirmed.
and Lcrit, respectively (see Fig. 7). The large systematic uncertainties when deriving luminosities from observational data as discussed above do not, however, allow us to favor unequivocally one of the discussed theories for the prediction of the critical luminosity. Especially, the observed change of the spectral evolution of GRO J1008−57 at low luminosities, Lbrk,lo, cannot be explained by either theory. Furthermore, drawing general conclusions about these theories is statistically questionable as only observational data of a single source are used. In future work, a detailed study of the recently claimed accretion regimes in 4U 1901+03 (Reig & Milonaki 2016) and V 0332+53 (Doroshenko et al. 2016) combined with the results by Reig & Nespoli (2013) for various sources could help clarify this question. It should be noted, however, that thorough analysis methods are required and systematic effects (caused by detector calibration and due to the conversion to luminosities) have to be taken into account as, for example, discussed here. Nevertheless, the existence of different accretion regimes, which are driven by the mass accretion rate, seems to be confirmed.
In summary, however, the theories allow us to associate the following physical accretion regimes with the observed changes in the spectral evolution of GRO J1008−57:
-
L > Lbrk,hi ~ 2 × 1037 erg s-1: supercritical accretion, where radiation dominates the deceleration of the infalling plasma and stops the hardening of the X-ray spectrum.
-
1036 erg s-1 ~ Lbrk,lo < L < Lbrk,hi: subcritical accretion regime, where Comptonization effects scale with the mass accretion rate.
-
L < Lbrk,lo: very low subcritical regime, where physical effects depend only marginally on the mass accretion rate.
Further investigations of the source are required to confirm or reject these conclusions. In order to proceed, however, working self-consistent models should be applied to the spectra of GRO J1008−57 to reveal the evolution of its physical parameters with luminosity. Additionally, high-SNR observations of the source at very low (L < Lbrk,lo) and extremely high luminosities (L > Lbrk,hi) are required to investigate the existence of the different accretion regimes as proposed here. Finally, theory predicts different flux dependencies of the CRSF parameters depending on the accretion regime, which could be probed for GRO J1008−57 with future hard X-ray missions with a sufficiently high effective area around 100 keV.
The uncertainties of some of the flux-independent parameters listed in Table 4 of K13 have been accidentally given on a confidence level slightly smaller than the stated 90%. The affected parameters with correct uncertainties are the black body temperature kT = 1.833 ± 0.019 keV, the folding energy Efold = 15.9 ± 0.3 keV, the flux of the galactic ridge X-ray emission F3–10 keV = 4.25 ± 0.23 × 10-12 erg s-1 cm-2, and its iron line parameters E = 6.35 ± 0.03 keV, σ = 0.53 ± 0.06 keV, and F = 2.39 ± 0.18 × 10-4 photons s-1 cm-2.
The physical flux of GRO J1008−57 within 20 and 50 keV during its discovery outburst in 1993 was 2.2 × 10-9 erg s-1 cm-2 (Shrader et al. 1999).
compTT (Titarchuk 1994): seed photons of kT = 1.883 keV, plasma temperature of Efold = 15.9 keV, plasma optical depth of 20 (Becker et al. 2012), and normalized to match the source’s spectrum at 1 keV.
Acknowledgments
M.K. acknowledges support by the Bundesministerium für Wirtschaft und Technologie under Deutsches Zentrum für Luft- und Raumfahrt grants 50OR1113 and 50OR1207. We appreciate the useful discussions with K. Postnov and M. Gornostaev about accretion column physics. All figures shown in this paper were produced using the SLXfig module, developed by John E. Davis. We thank the Suzaku and NuSTAR teams for accepting our proposals and performing the observations. Finally, we thank the referee for her/his valuable comments, which helped improving the quality of our paper.
References
- Basko, M. M., & Sunyaev, R. A. 1975, A&A, 42, 311 [NASA ADS] [Google Scholar]
- Basko, M. M., & Sunyaev, R. A. 1976, MNRAS, 175, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, P. A., & Wolff, M. T. 2007, ApJ, 654, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, P. A., Klochkov, D., Schönherr, G., et al. 2012, A&A, 544, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellm, E. C., Fürst, F., Pottschmidt, K., et al. 2014, ApJ, 792, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Boldt, E. 1987, in Observational Cosmology, eds. A. Hewitt, G. Burbidge, & L. Z. Fang (Cambridge: Cambridge Univ. Press), IAU Symp., 124, 611 [Google Scholar]
- Bradt, H. V., Rothschild, R. E., & Swank, J. H. 1993, A&AS, 97, 355 [NASA ADS] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Caballero, I., & Wilms, J. 2012, Mem. Soc. Astron. It., 83, 230 [NASA ADS] [Google Scholar]
- Caballero, I., Santangelo, A., Kretschmar, P., et al. 2008, A&A, 480, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caballero, I., Pottschmidt, K., Marcu, D. M., et al. 2013, ApJ, 764, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Capalbi, M., Perri, M., Saija, B., et al. 2005, NASA Goddard Space Flight Center, The SWIFT XRT Data Reduction Guide, Version 1.2, http://swift.gsfc.nasa.gov/analysis/ [Google Scholar]
- Coe, M. J., Roche, P., Everall, C., et al. 1994, MNRAS, 270, L57 [NASA ADS] [Google Scholar]
- Coe, M. J., Bird, A. J., Hill, A. B., et al. 2007, MNRAS, 378, 1427 [NASA ADS] [CrossRef] [Google Scholar]
- Doğan, S., Nixon, C., King, A., & Price, D. J. 2015, MNRAS, 449, 1251 [NASA ADS] [CrossRef] [Google Scholar]
- Doroshenko, V., Tsygankov, S. S., Mushtukov, A. A., et al. 2016, MNRAS, 466, 2143 [Google Scholar]
- Farinelli, R., Ceccobello, C., Romano, P., & Titarchuk, L. 2012, A&A, 538, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farinelli, R., Ferrigno, C., Bozzo, E., & Becker, P. A. 2016, A&A, 591, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrigno, C., Falanga, M., Bozzo, E., et al. 2011, A&A, 532, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finger, M. H., Camero-Arranz, A., Kretschmar, P., Wilson, C., & Patel, S. 2006, in BAAS, 38, 359 [Google Scholar]
- Fürst, F., Pottschmidt, K., Wilms, J., et al. 2014, ApJ, 780, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2005, ApJ, 621, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Godet, O., Beardmore, A. P., Abbey, A. F., et al. 2007, in UV, X-ray, and Gamma-ray Space Instrumentation for Astronomy XV, eds. O. H. W. Siegmund, & M. A. Gummin, SPIE Conf. Ser., 6686, 66860 [Google Scholar]
- Houck, J. C., & Denicola, L. A. 2000, in Astronomical Data Analysis Software and Systems IX, eds. N. Manset, C. Veillet, & D. Crabtree, ASP Conf. Ser., 216, 591 [Google Scholar]
- Hurkett, C. P., Vaughan, S., Osborne, J. P., et al. 2008, ApJ, 679, 587 [NASA ADS] [CrossRef] [Google Scholar]
- ISAS/JAXA, et al. 2013, The Suzaku Data Reduction Guide, Version 5, http://heasarc.gsfc.nasa.gov/docs/suzaku/analysis/abc/ [Google Scholar]
- Jahoda, K., Swank, J. H., Giles, A. B., et al. 1996, in UV, X-ray, and Gamma-ray Space Instrumentation for Astronomy VII, eds. O. H. W. Siegmund, & M. A. Gummin, SPIE Conf. Ser., 2808, 59 [Google Scholar]
- Kirsch, M. G., Briel, U. G., Burrows, D., et al. 2005, in UV, X-Ray, and Gamma-Ray Space Instrumentation for Astronomy XIV, ed. O. H. W. Siegmund, SPIE Conf. Ser., 5898, 22 [Google Scholar]
- Kokubun, M., Fukazawa, Y., Idesawa, E., et al. 1999, IEEE Trans. Nucl. Sci., 46, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Kokubun, M., Makishima, K., Takahashi, T., et al. 2007, PASJ, 59, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Koyama, K., Tsunemi, H., Dotani, T., et al. 2007, PASJ, 59, 23 [Google Scholar]
- Kraus, U. 2001, ApJ, 563, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Kretschmar, P., Salazar, E., Laplace, E., et al. 2015, ATel, 6917, 1 [NASA ADS] [Google Scholar]
- Krimm, H. A., Holland, S. T., Corbet, R. H. D., et al. 2013, ApJS, 209, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Kühnel, M., Müller, S., Kreykenbohm, I., et al. 2013, A&A, 555, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kühnel, M., Müller, S., Kreykenbohm, I., et al. 2014, in Physics at the Magnetospheric Boundary, EPJ Web Conf., 64, 06003 [CrossRef] [EDP Sciences] [Google Scholar]
- Kühnel, M., Müller, S., Kreykenbohm, I., et al. 2015, Acta Polytechnica, 55, 123 [NASA ADS] [Google Scholar]
- Kühnel, M., Falkner, S., Grossberger, C., et al. 2016, Acta Polytechnica, 56, 41 [Google Scholar]
- Lamb, F. K., Pethick, C. J., & Pines, D. 1973, ApJ, 184, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Leahy, D. A., Darbro, W., Elsner, R. F., et al. 1983, ApJ, 266, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Madsen, K. K., Beardmore, A. P., Forster, K., et al. 2017, AJ, 153, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Makishima, K., Mihara, T., Ishida, M., et al. 1990, ApJ, 365, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Marcu, D. M., Pottschmidt, K., Gottlieb, A. M., et al. 2015, in Proc. the 10th INTEGRAL Workshop “A Synergistic View of the High Energy Sky” (INTEGRAL 2014), PoS [Google Scholar]
- Marcu-Cheatham, D. M., Pottschmidt, K., Kühnel, M., et al. 2015, ApJ, 815, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Núñez, S., Kretschmar, P., Bozzo, E., et al. 2017, Space Sci. Rev., in press DOI: 10.1107/s11214-017-0340-1 [Google Scholar]
- Mitsuda, K., Bautz, M., Inoue, H., et al. 2007, PASJ, 59, 1 [Google Scholar]
- Mushtukov, A. A., Suleimanov, V. F., Tsygankov, S. S., & Poutanen, J. 2015a, MNRAS, 447, 1847 [NASA ADS] [CrossRef] [Google Scholar]
- Mushtukov, A. A., Tsygankov, S. S., Serber, A. V., Suleimanov, V. F., & Poutanen, J. 2015b, MNRAS, 454, 2714 [NASA ADS] [CrossRef] [Google Scholar]
- Nakajima, M., Mihara, T., Sugizaki, M., et al. 2012, ATel, 4420, 1 [NASA ADS] [Google Scholar]
- Nakajima, M., Ohtsuki, H., Ueno, S., et al. 2014a, ATel, 6465, 1 [NASA ADS] [Google Scholar]
- Nakajima, M., Sugizaki, M., Mihara, T., et al. 2014b, ATel, 6819, 1 [NASA ADS] [Google Scholar]
- Nowak, M. A., Hanke, M., Trowbridge, S. N., et al. 2011, ApJ, 728, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Okazaki, A. T., & Negueruela, I. 2001, A&A, 377, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Okazaki, A. T., Hayasaki, K., & Moritani, Y. 2013, PASJ, 65, 41 [NASA ADS] [Google Scholar]
- Perri, M., Puccetti, S., Spagnuol, N., et al. 2015, The NuSTAR Data Analysis Software Guide, Version 1.8.0, http://heasarc.gsfc.nasa.gov/docs/nustar/analysis/nustar_swguide.pdf [Google Scholar]
- Postnov, K., Staubert, R., Santangelo, A., et al. 2008, A&A, 480, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Postnov, K. A., Gornostaev, M. I., Klochkov, D., et al. 2015a, MNRAS, 452, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Postnov, K. A., Mironov, A. I., Lutovinov, A. A., et al. 2015b, MNRAS, 446, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Priedhorsky, W. C., & Terrell, J. 1983, ApJ, 273, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Reig, P., & Milonaki, F. 2016, A&A, 594, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reig, P., & Nespoli, E. 2013, A&A, 551, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riquelme, M. S., Torrejón, J. M., & Negueruela, I. 2012, A&A, 539, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schönherr, G., Schwarm, F.-W., Falkner, S., et al. 2014, A&A, 564, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Serlemitsos, P. J., Soong, Y., Chan, K.-W., et al. 2007, PASJ, 59, 9 [CrossRef] [EDP Sciences] [Google Scholar]
- Shrader, C. R., Sutaria, F. K., Singh, K. P., & Macomb, D. J. 1999, ApJ, 512, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Staubert, R., Shakura, N. I., Postnov, K., et al. 2007, A&A, 465, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stollberg, M. T., Finger, M. H., Wilson, R. B., et al. 1993, IAU Circ., 5836, 1 [NASA ADS] [Google Scholar]
- Takahashi, T., Abe, K., Endo, M., et al. 2007, PASJ, 59, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thorne, K. S. 1977, ApJ, 212, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L. 1994, ApJ, 434, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Tomsick, J. A., Nowak, M. A., Parker, M., et al. 2014, ApJ, 780, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Tsujimoto, M., Guainazzi, M., Plucinsky, P. P., et al. 2011, A&A, 525, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Walton, D. J., Tomsick, J. A., Madsen, K. K., et al. 2016, ApJ, 826, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. B., Harmon, B. A., Fishman, G. J., et al. 1994, in The Evolution of X-ray Binaries, eds. S. Holt, & C. S. Day, AIP Conf. Ser., 308, 451 [Google Scholar]
- Wolff, M. T., Becker, P. A., Gottlieb, A. M., et al. 2016, ApJ, 831, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Yamamoto, T., Mihara, T., Sugizaki, M., et al. 2013, ATel, 4759, 1 [NASA ADS] [Google Scholar]
- Yamamoto, T., Mihara, T., Sugizaki, M., et al. 2014, PASJ, 66, 59 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Critical luminosity
At the critical luminosity of an accreting neutron star the radiation pressure generated at the base of the accretion column contributes significantly to the deceleration of the infalling plasma (Basko & Sunyaev 1975). In the past many attempts have been made to derive this critical luminosity theoretically. Three of these theories are summarized in the following.
The X-ray spectra of several accreting neutron stars exhibit so-called cyclotron resonant scattering features (CRSFs; see, e.g., Caballero & Wilms 2012, for a review). These absorption features arise from transitions between the Landau levels of electrons in the accreted plasma, which are quantized due to the strong magnetic field of these neutron stars on the order of 1012 G. The observed cyclotron line energy, Ecyc, is found to show a positive or negative correlation with the mass accretion rate, Ṁ (see, e.g., Caballero & Wilms 2012; and Becker et al. 2012, and references therein).
In order to explain theoretically the different types of behavior of CRSF energy with luminosity, Becker et al. (2012) investigated the characteristic height of the X-ray emission region in the accretion column as a function of the mass accretion rate. These authors proposed different Ṁ regimes in which the height of the shock positively correlates (negative Ecyc correlation) or negatively correlates (positive Ecyc correlation) with Ṁ. The luminosities at which the transitions between these regimes occur, are known as Lcoul and Lcrit, and are given by (Eqs. (59) and (55) of Becker et al. 2012) ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:lcoul} L_\mathrm{coul} &=& 1.23 \times 10^{37}\,\mathrm{erg}\,\mathrm{s}^{-1} \left(\frac{\Lambda}{0.1}\right)^{-7/12} \left(\frac{\tau_\star}{20}\right)^{7/12} \nonumber \\[2mm] && \times \left(\frac{M_\star}{1.4\,\msol}\right)^{11/8} \left(\frac{R_\star}{10\,\mathrm{km}}\right)^{-13/24} \left(\frac{E_\star}{10\,\mathrm{keV}}\right)^{-1/3} \end{eqnarray}](/articles/aa/full_html/2017/11/aa29131-16/aa29131-16-eq291.png) (A.1)and
(A.1)and ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:lcrit} L_\mathrm{crit} &=& 1.28 \times 10^{37}\,\mathrm{erg}\,\mathrm{s}^{-1} \left(\frac{\Lambda}{0.1}\right)^{-7/5} w^{-28/15} \left(\frac{M_\star}{1.4\,\msol}\right)^{29/30} \nonumber\\[2mm] && \times \left(\frac{R_\star}{10\,\mathrm{km}}\right)^{1/10} \left(\frac{E_\star}{10\,\mathrm{keV}}\right)^{16/15}\cdot \end{eqnarray}](/articles/aa/full_html/2017/11/aa29131-16/aa29131-16-eq292.png) (A.2)Here, Λ is a parameter describing the accretion geometry (Λ = 1 for spherical accretion from a wind and Λ < 1 for accretion from a disk, see also Lamb et al. 1973), τ⋆ is the Thomson optical depth, M⋆ and R⋆ are the mass and radius of the neutron star, respectively, E⋆ is the CRSF energy related to the surface magnetic field, and w is a parameter describing the spectral shape inside the column (w = 1 for a Bremsstrahlung spectrum and w = 3 for a Planck spectrum). In the model of Becker et al. (2012), the in-falling matter is decelerated by passing through a radiation dominated shock. Above the so-called critical luminosity, Lcrit (in the supercritical accretion regime), the radiation pressure alone is able to stop the matter above the neutron star’s surface. Below this luminosity (in the subcritical regime), the radiation-dominated shock still exists, but the final deceleration occurs via Coulomb braking within the accretion flow. At very low luminosities, below a characteristic luminosity, Lcoul, Coulomb interactions are no longer sufficient to stop the matter. The detailed mechanism to decelerate the matter to rest is not yet clear (see., e.g. Fürst et al. 2014).
(A.2)Here, Λ is a parameter describing the accretion geometry (Λ = 1 for spherical accretion from a wind and Λ < 1 for accretion from a disk, see also Lamb et al. 1973), τ⋆ is the Thomson optical depth, M⋆ and R⋆ are the mass and radius of the neutron star, respectively, E⋆ is the CRSF energy related to the surface magnetic field, and w is a parameter describing the spectral shape inside the column (w = 1 for a Bremsstrahlung spectrum and w = 3 for a Planck spectrum). In the model of Becker et al. (2012), the in-falling matter is decelerated by passing through a radiation dominated shock. Above the so-called critical luminosity, Lcrit (in the supercritical accretion regime), the radiation pressure alone is able to stop the matter above the neutron star’s surface. Below this luminosity (in the subcritical regime), the radiation-dominated shock still exists, but the final deceleration occurs via Coulomb braking within the accretion flow. At very low luminosities, below a characteristic luminosity, Lcoul, Coulomb interactions are no longer sufficient to stop the matter. The detailed mechanism to decelerate the matter to rest is not yet clear (see., e.g. Fürst et al. 2014).
Alternatively, Mushtukov et al. (2015a) calculate the critical luminosity, that is, where the supercritical accretion sets in taking resonant scattering and photon polarization into account for the first time. For a circular hotspot on the neutron star’s surface, this luminosity is given by (Basko & Sunyaev 1975, 1976; Eq. (7) in Mushtukov et al. 2015a) 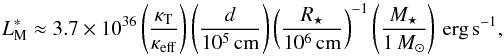 (A.3)where κeff is the effective scattering cross-section and d is the diameter of the hot spot. The key issue here is the calculation of the effective scattering cross-section, κeff, which is solved by Mushtukov et al. (2015a) numerically assuming specific accretion column geometries for wind- and disk-accretion, a linear velocity profile, and black body seed photons. Although these authors assumed a radiation dominated shock to exist for luminosities above the critical luminosity,
(A.3)where κeff is the effective scattering cross-section and d is the diameter of the hot spot. The key issue here is the calculation of the effective scattering cross-section, κeff, which is solved by Mushtukov et al. (2015a) numerically assuming specific accretion column geometries for wind- and disk-accretion, a linear velocity profile, and black body seed photons. Although these authors assumed a radiation dominated shock to exist for luminosities above the critical luminosity,  , they argue that the value of
, they argue that the value of  is mainly determined by the effective cross-section, κeff, due to resonant scattering of electrons. In contrast to Becker et al. (2012), they expect the X-ray emission region to settle down on the neutron star’s surface for luminosities below the critical luminosity,
is mainly determined by the effective cross-section, κeff, due to resonant scattering of electrons. In contrast to Becker et al. (2012), they expect the X-ray emission region to settle down on the neutron star’s surface for luminosities below the critical luminosity,  . In this subcritical regime, Mushtukov et al. (2015b) do not expect a radiation dominated shock to be formed. Instead, they explain the positive correlation of Ecyc with Ṁ by the (still) relativistic velocity of the in-falling plasma near the surface, which results in a Doppler shift of the CRSF energy.
. In this subcritical regime, Mushtukov et al. (2015b) do not expect a radiation dominated shock to be formed. Instead, they explain the positive correlation of Ecyc with Ṁ by the (still) relativistic velocity of the in-falling plasma near the surface, which results in a Doppler shift of the CRSF energy.
Another recent theoretical investigation by Postnov et al. (2015a) calculates the X-ray spectrum in the supercritical regime using the radiation diffusion approximation and assuming the emission emerging from the walls of the accretion column (known as the fan beam geometry). In this scenario the accretion column is assumed to be optically thick and the infalling matter is decelerated by a radiative shock similar to Becker et al. (2012). The minimum luminosity, 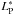 , at which an optically thick accretion column appears, is given by (Eq. (5) of Postnov et al. 2015a)
, at which an optically thick accretion column appears, is given by (Eq. (5) of Postnov et al. 2015a) 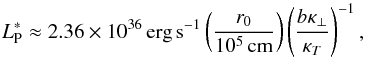 (A.4)with the radius r0 of the accretion column, the cross-sections κ⊥ and κT, and the thickness of the column walls, 0 < b ≤ 1, relative to its radius (b = 1 corresponds to a filled accretion column, while b ≪ 1 is a hollow column). In principle, their derived luminosity,
(A.4)with the radius r0 of the accretion column, the cross-sections κ⊥ and κT, and the thickness of the column walls, 0 < b ≤ 1, relative to its radius (b = 1 corresponds to a filled accretion column, while b ≪ 1 is a hollow column). In principle, their derived luminosity, 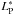 , describes the same physical condition as Lcrit after Becker et al. (2012) and
, describes the same physical condition as Lcrit after Becker et al. (2012) and 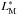 after Mushtukov et al. (2015a). For luminosities
after Mushtukov et al. (2015a). For luminosities 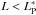 , that is, in the subcritical regime, Postnov et al. (2015a) showed that the observed X-ray spectrum hardens with increasing mass accretion rate, Ṁ, due to an increase in the Comptonization parameter. Finally, at very high luminosities around (3−7) × 1037 erg s-1 they observe a saturation in the hardness in some accreting pulsars using data from the All Sky Monitor (ASM) onboard the Rossi X-ray Timing Explorer (RXTE Bradt et al. 1993). They are able to explain this behavior by including reflected radiation from the neutron star’s surface, which is illuminated by the Doppler-boosted radiation of the column walls, while the spectrum continues to harden for increasing luminosities. Thus, in the model of Postnov et al. (2015a), the observed saturation is a purely geometric effect.
, that is, in the subcritical regime, Postnov et al. (2015a) showed that the observed X-ray spectrum hardens with increasing mass accretion rate, Ṁ, due to an increase in the Comptonization parameter. Finally, at very high luminosities around (3−7) × 1037 erg s-1 they observe a saturation in the hardness in some accreting pulsars using data from the All Sky Monitor (ASM) onboard the Rossi X-ray Timing Explorer (RXTE Bradt et al. 1993). They are able to explain this behavior by including reflected radiation from the neutron star’s surface, which is illuminated by the Doppler-boosted radiation of the column walls, while the spectrum continues to harden for increasing luminosities. Thus, in the model of Postnov et al. (2015a), the observed saturation is a purely geometric effect.
All Tables
Best-fit parameters of the Suzaku and simultaneous NuSTARSwift spectra analyzed here.
All Figures
 |
Fig. 1 Swift-BAT (Krimm et al. 2013) light curve showing the activity of GRO J1008−57 between 2012 August and 2015 February. The arrows on top mark the times of observations by Swift (red), Suzaku-(green), and NuSTAR (blue). The numbers next to these arrows are the data epochs as defined in Table 1. The labeled dates correspond to these epochs. |
| In the text | |
 |
Fig. 2 a) The Suzaku-XIS (0: blue; 1: yellow; 3: green), -PIN (red), and -GSO (purple) spectra of the 2014 January observation of GRO J1008−57 (epoch 2) together with the best-fit model (black). b–d) The residuals to the best-fit model (b: XIS0, PIN, and GSO; c: XIS1; d: XIS3) showing the ignored energy bins due to calibration uncertainties (gray). The residuals of XIS1 (c) are shown without taking the photon index shift, ΔΓ, into account. |
| In the text | |
 |
Fig. 3 a) NuSTAR-FPMA (dark blue), -FPMB (light blue), and Swift-XRT spectrum (red) of GRO J1008−57 in 2014 December after the second peak of its triple peaked outburst (epoch 3). The best-fit model is shown in black and the gray line shows its ratio to the spectral shape as predicted by our spectral evolution model (see Sect. 5 and Fig. 6). The data have been rebinned for display purposes. b) The residuals of the best-fit model. |
| In the text | |
 |
Fig. 4 a) NuSTAR-FPMA (dark blue), -FPMB (light blue), and Swift-XRT spectrum (red) of GRO J1008−57 in 2015 January shortly after maximum flux of the third peak of the triple peaked outburst (epoch 4). The black line shows the best-fit model. The data have been rebinned for display purposes. b) The residuals of the best-fit model. |
| In the text | |
 |
Fig. 5 Pulse profiles of GRO J1008−57 during epoch 3 (blue; NuSTAR-FPMA) and 2005 (red; RXTE-PCA). The RXTE observation was performed at a similar flux level of the source compared to the NuSTAR observation. The pulse profiles have been normalized to a mean count rate of zero and a standard deviation, σ, of unity. Pulse phase zero is defined as the minimum count rate. |
| In the text | |
 |
Fig. 6 Evolution of the spectral parameters with the 15–50 keV flux, FPL, of GRO J1008−57. a) The power-law photon index, Γ, and b) the black body flux FBB (in erg s-1 cm-2), with the source’s flux (uncertainties represent 1σ uncertainties with two degrees of freedom). The black data points are the results of our previous RXTE and the black triangle the joined Suzaku RXTE analysis (K13). Their fluxes have been corrected for calibration uncertainties (see the text for details). The new results presented in this paper are the green triangles based on Suzaku and the blue circles based on NuSTAR data. The red lines show the empirical model with (solid) and without (dashed) the breaks at certain luminosity levels as described in the text. The NuSTAR results marked with 1) have been excluded from these fits. The bolometric luminosity for one accretion column has been calculated as described in Sect. 5. |
| In the text | |
 |
Fig. 7 Comparison of the derived luminosities at the breaks of the spectral evolution (Lbrk,lo and Lbrk,hi, vertical dashed lines) with Lcoul and Lcrit of Becker et al. (2012, Eqs. (A.1A.2panel a, |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


